Methoden der Datenanalyse - Multiple Regression

Multiple Regression

Ziel dieser Lektion ist die Erweiterung des Konzepts des in der induktiven Statistik vorgestellten Konzeptes der einfachen linearen Regression (Anzur, 2007) auf mehrere erklärende Einflussgrößen.

Einleitung

Wie auch schon die einfache lineare Regression, ist die multiple lineare Regression ein Verfahren, um die (lineare) Beziehung verschiedener statistischer Merkmale abzuschätzen. Während bei der einfachen Regression nur eine erklärende und eine abhängige Variable vorhanden sind (daher auch der Name „Zwei-Variablen-Modell“), steht bei der multiplen Regression ein Satz von mehreren potentiellen erklärenden Variablen zur Verfügung. Lässt man auch mehr als eine abhängige Variable zu, spricht man üblicherweise von multivariater Regression, die aber hier nicht behandelt wird.

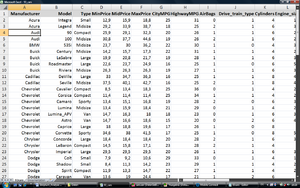
Beispiel 1 Gegeben sind Daten von 93 Modellen von Neuwagen aus dem Jahr 1993. In der Datentabelle (Abbildung 1) ersichtlich sind Kennzahlen wie z.B. Preis, Leistung (PS), Spritverbrauch in der Stadt bzw. auf der Autobahn, Hubraum, Anzahl der Zylinder, Umdrehungen pro Min., Tankkapazität und vieles mehr. (Datensatz cars.xlsx) Es soll nun mittels statistischer Analyse festgestellt werden, welche Variablen den Kaufpreis am besten erklären und welcher Art der Zusammenhang ist.

Die Fragestellung könnte dadurch beantwortet werden, dass mehrere lineare Einfachregressionen berechnet werden, jedoch hängen die verschiedenen Variablen auch untereinander zusammen. Man kann hierbei die Korrelationen der verschiedenen Variablen zueinander aber nicht berücksichtigen. Beispielsweise hängen der Hubraum und die PS-Zahl eines Motors positiv miteinander zusammen und es können in einer Einfachregression nicht die getrennten Anteile beider Größen bei der Erklärung des Kaufpreises eruiert werden. Man will nun ein möglichst sparsames Modell finden, dass die wichtigsten Variablen auswählt und deren einzelne Beiträge zur Zielgröße (dem Preis) darstellt.

In einem ersten Schritt wird nun wie bei der Einfachregression versucht, die Zusammenhänge zwischen der Zielgröße und den verschiedenen erklärenden Variablen zu visualisieren.

Ausschnitt des Datensatzes aus Beispiel 1

Scatterplots aus Beispiel 1 - Teil 1

Scatterplots aus Beispiel 1 - Teil 2

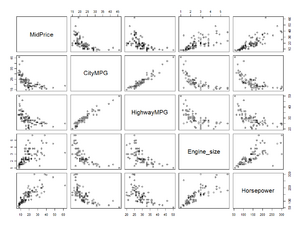
In Abbildung 2 und Abbildung 3 sind nun insgesamt acht Variablen ausgewählt, die einen mehr oder weniger inhaltlich begründeten Zusammenhang mit der Zielvariable „MidPrice“ aufweisen. Der Scatterplot in Abbildung 3 rechts oben zeigt beispiels­weise den Zusammenhang zwischen dem Preis und dem Gewicht des Wagens. Es zeigen sich mehrere einigermaßen lineare, jedenfalls monotone Zusammenhänge zur Zielvariable.

Modell und Schätzung der multiplen Regression

Das Modell der Daten lautet bei der multiplen Regression folgendermaßen:

$$y_{i}=\beta _{0}+\beta _{1}x_{i1}+\beta _{2}x_{i2}+\cdots \beta _{k}x_{ik}+\varepsilon _{i},(i=1,\ldots ,n;j=1,\ldots ,k);$$

wobei $y_{i}$ die Werte der abhängigen Variablen, $y_{i,j}$ die Werte der erklärenden Variablen und $\beta _{j}$ die Regressionsparameter, die das Ausmaß des Einflusses der Variablen kennzeichnen, sowie $+\varepsilon _{i}$ die durch das lineare Modell nicht erklärten „Reste“ (=Fehler) sind.

Es wird üblicherweise angenommen, dass die Fehler $+\varepsilon _{i}$normalverteilt sind mit Erwartungswert gleich Null und Varianz $\sigma ^{2}$. Das bedeutet einerseits, dass das Modell verlangt, dass die Varianzen für alle Fehler gleich groß sind. Andererseits ist die Verteilungsannahme notwendig, um statistische Tests über die geschätzten Parameter durchführen zu können. Weiters wird auch noch angenommen, dass es keine Zusammenhänge (Korrelationen) zwischen beliebigen Fehlern gibt.

Wie im einfachen Modell werden die Werte für die Regressionsparameter $\beta _{j}$ ermittelt, indem das Kriterium der kleinsten Quadrate angewandt wird.

$F\left(\beta _{0},\beta _{1},\ldots \beta _{k}\right)=\sum _{i=1}^{n}\left(y_{i}-\beta _{0}-\beta _{1}x_{i1}-\beta _{2}x_{i2}-\cdots \beta _{k}x_{ik}\right)^{2}\rightarrow \operatorname {Min} !$

Die Lösung dieses Optimierungsproblemes sind nun die geschätzten Regressions­parameter ${\widehat {\beta _{0}}},{\widehat {\beta }}_{1},\ldots {\widehat {\beta _{k}}}$.

Geometrisch bedeutet dies im Falle einer erklärenden Variable, dass die Gerade solange gedreht und verschoben wird, bis die Summe der Quadrate der vertikalen Abstände der Punkte zur Gerade im Scatterplot minimal wird. Im Falle zweier erklärender Variablen wird eine Ebene im dreidimensionalen Raum gedreht, bis sie „ideal passt“. Bei mehr als zwei erklärenden Variablen wäre es eine Hyperebene im $k$-dimensionalen Raum.

Auch hier ist es nun einfach, die durch die erklärenden Variablen prognostizierten Werte („fitted values“) ${\widehat {y_{i}}}$ zu berechnen:

$${\widehat {y_{i}}}={\widehat {\beta _{0}}}+{\widehat {\beta _{1}}}x_{i1}+{\widehat {\beta _{2}}}x_{i2}+\cdots {\widehat {\beta _{k}}}x_{ik}$$

Die nicht erklärten Differenzen ${\widehat {\epsilon _{i}}}=y_{i}-{\widehat {y_{i}}}$ werden als „Residuen“ bezeichnet. Die Optimierungsaufgabe kann daher auch als Minimierung der Residuen­quadrat­summe bezeichnet werden.

Fortsetzung Beispiel 1 In R können die Koeffizienten folgendermaßen berechnet werden: X93<-read.csv("C:\\...\\...\\93_cars.csv",header=TRUE,dec=",",sep=";") Einlesen der Daten names(X93) [1] "Manufacturer" "Model" "Type" "MinPrice" "MidPrice" [6] "MaxPrice" "CityMPG" "HighwayMPG" "AirBags" "Drive_train_type" [11] "Cylinders" "Engine_size" "Horsepower" "RPM" "ERM" [16] "ManualTransmissionAvailable" "FuelTankCapacity" "Passenger" "Length" "Wheelbase" [21] "Width" "UTurn" "Rear_seat_room" "Luggage" "Weight" [26] "Domestic" Variablennamen X93_sub<-X93[,c(5,7,8,12,13,17,19,20,25)] Subset an neun ausgewählten Variablen attach(X93_sub) Direkter Zugriff auf Variablennamen des Datensatzes „X93_sub“ lm1<-lm(MidPrice~CityMPG+HighwayMPG+Engine_size+Horsepower+FuelTankCapacity+Length+Wheelbase+Weight) Erstellen des linearen Modells (Schätzung des multiplen Regressionsmodells)

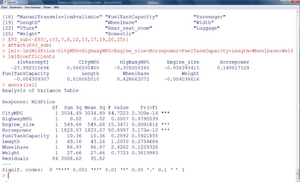
Die Fortsetzung und die geschätzten Parameter sind nun in Abbildung 4 ersichtlich.

Die erhaltene Gleichung zur Prognose des mittleren Preises eines Wagens lautet also folgendermaßen:

MidPrice (in T$)=

- 27,99 T$

+ Spritverbrauch in der Stadt (in “Miles“/Gallon) * 0,0865 T$

- Spritverbrauch auf der Autobahn (in “Miles“/Gallon) * 0,3050 T$

- Hubraum (in l) * 0,9364 T$

+ PS * 0,1498 T$

- Tankgröße (in gallons) * 0,0043 T$

+ Länge (in inch) * 0,0181 T$

+ Radstand (in inch) * 0,4287 T$

- Gewicht (in Pfund) * 0,0040 T$

Schätzung der Regressionsparameter

Der prognostizierte Preis eines Buick Century Midsize wäre dann beispielsweise:

-27,99 T$ + 22 * 0,0865 T$ - 31 * 0,3050 T$ - 2,2 * 0,9364 T$ + 110 * 0,1498 T$ - 16,4 * 0,0043 T$ + 189 * 0,0181 T$ + 105 * 0,4287 T$ - 2880 * 0,0040 T$ =

-27,99 T$ + 1,90 T$ - 9,46 T$ - 2,06 T$ + 16,48 T$ - 0,07 T$ + 3,42 T$ + 45,01 T$ -11,52 T$ =15,71 T$

Der tatsächliche Preis dieses Wagens beträgt 15.700 $. Damit ist die Prognose auf 10 $ genau.

Das ausgewählte Beispiel vermittelt jedoch einen falschen Eindruck, da hier jener Wagen ausgewählt wurde, für den die Prognose am besten zugetroffen hat. Um einen Eindruck zu bekommen, wie gut das Modell zu den Daten passt, müssen nun verschiedene andere Kriterien herangezogen werden.

Interpretation und Beurteilung der Güte des Regressionsmodells

Korrelation und Bestimmtheitsmaß

Ein notwendiges, aber nicht hinreichendes Kriterium für ein gut passendes Re­gressions­modell ist – wie schon im Zwei-Variablen-Modell – das Bestimmtheits­maß.

Dieses ist definiert als $R_{X,Y}^{2}={\frac {\sum _{i=1}^{n}\left({\hat {y}}_{1}-{\bar {y}}\right)^{2}}{\sum _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}}}$.

Es sagt also aus, welcher Anteil an der Variabilität der Zielvariable einzig durch die erklärenden Variablen erklärt wird. So wie bei jedem Anteil errechnet sich hier eine Zahl zwischen 0 und 1 (=100%).

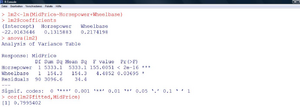
In Beispiel 1 kann man das Bestimmtheitsmaß aus der Aufstellung der Quadratsummen in der „Analysis of Variance“-Tabelle berechnen:

$$\sum _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}=3034,49+0,02+549,68+1823,07+10,36+43,16+86,97+27,66+3008,62=8584,33$$

$$\sum _{i=1}^{n}\left({\widehat {y_{i}}}-{\bar {y}}\right)^{2}=3034,49+0,02+549,68+1823,07+10,36+43,16+86,97+27,66=5575,71$$

$$R_{X,Y}^{2}={\frac {5575,71}{8584,33}}=65\%$$

Generell kann man sagen, dass eine Varianzerklärung von über 50% ganz gut ist. Das Bestimmtheitsmaß ist aber auch aus einer zweiten Sicht interessant, da es das Quadrat der linearen Korrelation der prognostizierten Werte mit der abhängigen Variable ist.

$$R_{X,Y}^{2}=[\operatorname {cor} ({\hat {Y}},Y)]^{2}$$

Daher kann der Betrag dieser Korrelation ebenfalls errechnet werden.

$$\operatorname {cor} ({\hat {Y}},Y)={\sqrt {R_{X,Y}^{2}}}={\sqrt {0,65}}=0,81$$

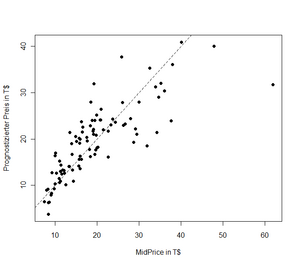
In der Gegenüberstellung der prognostizierten zu den tatsächlichen Preisen (Abbildung 5) kann man erkennen, welche Beobachtungen gut oder weniger gut geschätzt werden können. Hier sieht man auch beispielsweise sehr schön, dass der „Mercedes Benz 300E Midsize“ (ganz rechts) um ca. 30.000 $ teurer ist, als aufgrund seiner Leistungsdaten in diesem Beispiel prognostiziert.

Multikollinearität und Variablenselektion

Weder an der Tabelle in Abbildung 4, noch an den $-Beiträgen zum Gesamtpreis ist es aber möglich, festzustellen, welche Variablen nun die für den Preis wichtigsten sind. Die Komponenten der Varianz („Sum Sq“) sind davon abhängig, in welcher Reihenfolge das Modell spezifiziert wird. Es wird der Reihe nach untersucht, welchen Varianz-Anteil die jeweiligen Variablen an der Zielgröße haben. Nimmt man beispielsweise die „engine_size“ zuerst in das Modell, bleibt für die Variablen zum Spritverbrauch nicht mehr viel an Erklärung über, da dieser einigermaßen stark mit dem Motorvolumen korrelieren. Weiters führen viele hoch korrelierte Variablen dazu, dass schwerer bestimmbar ist, welchen Beitrag die einzelnen Variablen haben – die Varianzen dieser Schätzungen werden größer.

Prognostizierte Werte vs. Tatsächliche Werte

Gibt es potentielle erklärende Variablen, die sehr stark miteinander korrelieren (z.B. Spritverbrauch in der Stadt und auf der Autobahn), spricht man in diesem Zu­sammen­hang von „beinaher Multikollinearität“, bei perfekter linearer Korrelation von „exakter Multikollinearität“. Ein Satz von erklärenden Variablen, der Multi­kollineari­tät aufweist, ist daher problematisch.

Aufgabe 1 Berechnen Sie mit der Funktion „cor“ in R alle paarweisen Korrelationen der neun ausgewählten Variablen im obigen Regressionsmodell.

Wie kann nun ein „brauchbarer“ Satz von Variablen zusammengestellt werden?

Besteht bei allen acht Variablen die Möglichkeit, ins Modell aufgenommen zu werden oder nicht, müssten 2⁸-1=255 verschiedene Modelle miteinander verglichen werden (gegeben es wird zumindest eine Variable aufgenommen). Um diesen enormen Rechenaufwand zu vermindern gibt es nun verschiedene Methoden, die sich einer schrittweisen Vorgehensweise bedienen.

Ein weit verbreitetes Kriterium, dass die erklärte Varianz der Anzahl auf die Anzahl der verwendeten Variablen bezieht, ist das sogenannte „Akaike Information Criterion“ (AIC) von Akaike (1973, 1974, zitiert in Ripley, 1996, S. 34).

Fortsetzung Beispiel 1 library(MASS) lädt die Library, die die Funktion zur Modellwahl nach AIC enthält stepAIC(lm1) Als Ergebnis erscheint nun eine Prozedur, die, ausgehend vom Modell mit allen acht erklärenden Variablen jeweils einzelne Variablen entfernt, solange das AIC vermindert werden kann. Im konkreten Fall ergeben sich nur mehr die „Horsepower“ und die „Wheelbase“ als relevante Einflussgrößen.

Schätzung des nach AIC gewählten Regressionsmodells

Die erhaltene Gleichung zur Prognose des mittleren Preises eines Wagens lautet also nun:

MidPrice (in T$)= - 22,01 T$ + PS * 0,1316 T$ + Radstand (in inch) * 0,2174 T$

Der prognostizierte Preis des Buick Century Midsize wäre dann:

-22,01 T$ + 110 * 0,1316 T$ + 105 * 0,2174 T$ =15,30 T$

Wir erhalten also eine auf 400$ genaue Prognose, obwohl nun lediglich zwei statt acht Einflussgrößen im Modell sind.

Buick Century

Akzeptiert man dieses Modell, bedeutet dass, das ein Wagen mit 100 PS und 100 Inch Radstand im Mittel -22,01 T$ + 100 * 0,1316 T$ + 100 * 0,2174 T$ =12,89 T$ kostet. Jedes PS mehr oder weniger kostet/bringt im Mittel 131,6$ und jedes Inch mehr oder weniger beim Radstand kostet/bringt im Mittel 217,4$.

Abbildung 6 zeigt auch, dass die Korrelation zwischen dem Preis und der Prognose ebenfalls kaum merkbar gesunken ist (0,80 statt 0,81). Es findet daher quantitativ immer noch eine gute Erklärung durch das neue, deutlich sparsamere Modell statt.

Andere Variablenselektionskriterien nehmen, beginnend mit einem leeren Modell, die mit dem Zielkriterium jeweils am besten korrelierende Variable auf und prüfen, ob der Erklärungszuwachs noch statistisch signifikant ist („Vorwärtsselektion“; im Sinne eines statistischen Signifikanztests). Wieder andere Eliminieren aus dem vollen Satz an Variablen schrittweise jene, die nicht statistisch signifikant sind („Rückwärtsselektion“; ähnlich dem hier verendeten Verfahren). Das vorliegende Modell wäre auch mit den Standardeinstellungen der Vorwärts- und Rückwärts­selektion gewählt worden. Da die Korrelation zwischen Preis und PS-Stärke schon allein 0,79 beträgt, kann allerdings die PS-Stärke als weitaus wichtigere der beiden Variablen für die Erklärung des Preises identifiziert werden.

Residuenanalyse

Neben dem Bestimmtheitsmaß und der Sparsamkeit des Modells, ist es weiters bedeutend, die einzelnen Residuen der Regression zu untersuchen, und zwar in Hinblick auf

• Trend
• Ausreißer
• Heteroskedastizität
• Autokorrelation und
• Normalverteilung (NV)

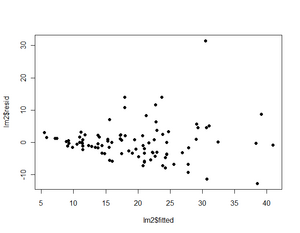
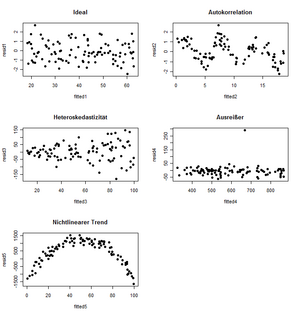
Eine Darstellung um die ersten vier genannten Punkte zu überprüfen ist in Abbildung 8 ersichtlich.

Trend

Es ist kein Trend zu erkennen. Mit wachsenden Prognosewerten bleibt das Niveau der Residuen im Mittel durchgehend auf Null.

Scatterplot Prognosewerte vs. Residuen

Ausreißer

Hier sieht man wieder den Mercedes Benz von vorhin als größtes der Residuen. Es empfiehlt sich, eine Analyse ohne diesen Datenpunkt zu machen um zu sehen, wie sehr die Schätzungen beeinflusst werden.

Aufgabe 2 Schätzen Sie die Koeffizienten des linearen Modells (Horsepower und Wheelbase) in R ohne den Mercedes 300E Midsize (Hinweis: Der Datensatz ohne die 59. Zeile – der entsprechende Wagen – wird in R folgendermaßen generiert: „X92_sub <- X93_sub[-59,]“). Wie stark ändern sich die Regressionskoeffizienten? Wie groß ist die Korrelation zwischen Preis und prognostiziertem Preis?

Heteroskedastizität

Es ist ersichtlich, dass die mittleren Abweichungen der Daten von der Prognose umso größer werden, je teurer der Wagen ist. Sind für ähnliche Prognosewerte die Abweichungen nicht im Mittel gleich, spricht man von Heteroskedastizität. So das Ausmaß dieser Heteroskedastizität quantifiziert werden kann, sollte diese in die Modellschätzung einfließen. Die Schätzungen für die Regressionskoeffizienten unterliegen dann einer geringeren Variabilität.

Autokorrelation

Autokorrelation besteht dann, wenn Residuen von ähnlichen Datenpunkten in etwa gleich groß sind. Zum Beispiel ist die Abweichung der Temperatur am 26. und am 27. Juli von der Jahresdurchschnittstemperatur jedes Jahr in etwa gleich. Umge­kehrt ist die Abweichung von der Durchschnittstemperatur im Jänner immer genau umgekehrt. Bei anderen Zeitreihen hat man ebenfalls solche Saisoneffekte (z.B. die Arbeitslosenrate) und das Ausmaß solcher Korrelationen sollte dort ebenfalls in die Modellschätzung einfließen.

Abbildung 9 zeigt nun nochmals zusammengefasst Darstellungen des „Idealfalles“ und verschiedene Modellverletzungen.

Ideales Residuenbild und verschiedene Abweichungen

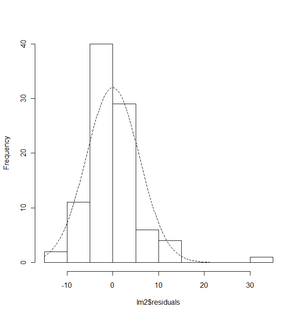
Die Annahme der Normalverteilung wird visuell mittels Histogramm (Abbildung 10) oder einem sogenannten Q-Q-Plot überprüft. Inferenzstatistisch wird der Kolmogo­rov-Smirnov-Anpassungstest verwendet.

Im Zuge der multiplen Regressionsanalyse können auch u.a. die einzelnen ge­schätzten Parameter auf Signifikanz geprüft werden, worauf aus Platzgründen hier verzichtet wird. Die Vorgehensweise ist in einführenden Büchern zu linearen Modellen beschrieben (z.B. Faraway, 2005, für eine Darstellung der Regressionsanalyse in R).

Fortsetzung Beispiel 1 hist(lm2$residuals,main=““) zeichnet ein Histogramm der Residuen ohne Titel; lm2 ist das analog zu lm1 gerechnete Modell ohne den Mercedes 300E midsize x<-seq(-15,35,by=0.1) fx<-dnorm(x,sd=sqrt(var(lm2$residuals)))*93*5 lines(x,fx,lty=2) zeichnet eine strichlierte, mit dem Stichprobenumfang n=93 und der Balkenbreite des Histogrammes (5) standardisierte Normalverteilungs-Dichtefunktion. Im vorliegenden Beispiel kann die NV-Annahme nicht widerlegt werden.

Histogramm der Residuen

Wiederholungsaufgaben und Zusammenfassung

1. Sie haben in ihrer Regression ein Bestimmtheitsmaß von 10% erhalten. Die Modellvoraussetzungen sind alle erfüllt. Was können Sie mit dieser Information anfangen?
2. Was sagt ein Bestimmtheitsmaß von 100% über

a) die Korrelation zwischen prognostizierten Werten und Zielvariable,

b) über die Varianz der Residuen, und

c) über die geometrische Lage der Beobachtungspunkte aus?

3. Sie ziehen drei Stichproben aus einer Population und berechnen jedesmal dasselbe multiple Regressionsmodell. Folgende Parameterschätzer ergeben sich:

	${\widehat {\beta _{0}}}$	${\widehat {\beta _{1}}}$	${\widehat {\beta _{2}}}$	${\widehat {\beta _{3}}}$	${\widehat {\beta _{4}}}$
Stichprobe 1	-0,3	-0,07	18,1	44,5	2,2
Stichprobe 2	-0,29	-0,09	22,4	21,9	1,7
Stichprobe 3	-0,32	0,04	19,3	2,6	-2,5

Welche Variablen würden Sie aufgrund der Vorzeichen der Regressionskoeffizienten jedenfalls ausschließen? Welcher Koeffizient erscheint Ihnen weiters nicht statistisch bedeutsam?

Zusammenfassung

Die multiple Regressionsanalyse prüft das Vorhandensein einer linearen Beziehung zwischen einer abhängigen Größe und einem Satz erklärender Einflussvariablen. Es wird zunächst unterstellt, dass diese abhängige Größe von allen gewählten Einflussvariablen linear abhängt und es werden durch Optimierung jene Regressionsparameter ermittelt, welche die Summe der Quadrate der Differenzen zwischen beobachteten Werten und durch das Modell geschätzten Werten kleinstmöglich machen.

In weiteren Schritten muss nun analysiert werden, ob wirklich jede Variable für sich einen von den anderen Variablen unabhängigen Beitrag liefert. Falls dies nicht der Fall ist, wird diese eliminiert. Dazu bedient man sich neben inhaltlichen Überlegungen auch automatisierten Ansätzen, den verschiedenen statistischen Methoden der Variablenselektion.

Ist schließlich ein Modell gefunden, in dem jede Variable einen wichtigen linearen Beitrag zur Zielgröße liefert, wird üblicherweise mittels visueller Verfahren unter­sucht, ob Modellverletzungen vorliegen (Heteroskedastizität, Autokorrelation, Aus­reißer oder nicht normalverteilte Residuen). Je nach Art einer gefundenen Modell­verletzung müssen entweder komplexere Modelle mit weiteren Spezifika­tionen (Heteroskedastizität, Autokorrelation) gerechnet, Daten ausgeschlossen werden (Ausreißer) oder Transformationen in den Daten geschehen (nicht normalverteilte Residuen).