Methoden der Datenanalyse - Strukturgleichungsmodelle: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „= Faktorenanalyse = ''Wichtiges Ziel der Lektion ist die Erkenntnis, welche Aussagen über nichtbeobachtbare Merkmale aufgrund der Korrelationsstruktur eines Satzes von vorhandenen Variablen abgeleitet werden können. Die Grundlagen der Faktorenanalyse als Basis von Strukturmodellen und die Darstellung der subjektiven Entscheidungen, die im Zuge einer Faktorenanalyse getroffen werden müssen sind ebenso Schwerpunkte, wie die Analyse der Daten in R.'' ==…“) |
|||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
= Strukturgleichungsmodelle = | = Strukturgleichungsmodelle = | ||
| Zeile 370: | Zeile 17: | ||
In der folgenden Darstellung geht es weniger um den komplexen mathematischen Hintergrund der Methode – dies würde den Rahmen deutlich sprengen – sondern um die Vorstellung der Idee dahinter. | In der folgenden Darstellung geht es weniger um den komplexen mathematischen Hintergrund der Methode – dies würde den Rahmen deutlich sprengen – sondern um die Vorstellung der Idee dahinter. | ||
== Grundlagen und Beispiele == | |||
=== Modelldarstellung, Terminologie und Notation === | |||
Die Datengrundlage für die Analyse mittels Strukturgleichungsmodellen sind wie in der Faktorenanalyse Kovarianzen bzw. Korrelationen zwischen den beobachtbaren Variablen. Output des Verfahrens sind wieder Modellparameter, zu denen in diesem Fall auch Signifikanzen berechnet werden können. Es kann also (wie übrigens auch bei der Regression) statistisch getestet werden, welche Parameter überzufällig von Null verschieden sind. Das Modell gilt dann als durch die Daten “bestätigt”, wenn sich die Korrelationen durch die Modellparameter (direkte oder indirekte Pfadkoeffizienten) rekonstruieren lässt. | Die Datengrundlage für die Analyse mittels Strukturgleichungsmodellen sind wie in der Faktorenanalyse Kovarianzen bzw. Korrelationen zwischen den beobachtbaren Variablen. Output des Verfahrens sind wieder Modellparameter, zu denen in diesem Fall auch Signifikanzen berechnet werden können. Es kann also (wie übrigens auch bei der Regression) statistisch getestet werden, welche Parameter überzufällig von Null verschieden sind. Das Modell gilt dann als durch die Daten “bestätigt”, wenn sich die Korrelationen durch die Modellparameter (direkte oder indirekte Pfadkoeffizienten) rekonstruieren lässt. | ||
| Zeile 389: | Zeile 33: | ||
Die dort dargestellte Struktur ist prototypisch für die Darstellung von Strukturgleichungsmodellen. Die Komponenten sind einerseits die Messmodelle der latenten Variablen. In ihnen wird spezifiziert, in welcher Form die entscheidenden latenten Variablen von den manifesten abhängen, also wie das, was von Interesse ist, gemessen wird. Es werden die latent endogenen Variablen (Zielvariablen, erklärten Variablen) und die latent exogenen Variablen (erklärenden Variablen) unterschieden. Die zweite Komponente ist das Strukturmodell, das angibt, wie die latenten Variablen untereinander zusammenhängen. Im vorliegenden Fall ist die Einstellung die verursachende Variable und das Kaufverhalten die davon abhängige Variable. Ein vollständiges Strukturgleichungsmodell besteht immer aus einem Strukturmodell und zwei Messmodellen. | Die dort dargestellte Struktur ist prototypisch für die Darstellung von Strukturgleichungsmodellen. Die Komponenten sind einerseits die Messmodelle der latenten Variablen. In ihnen wird spezifiziert, in welcher Form die entscheidenden latenten Variablen von den manifesten abhängen, also wie das, was von Interesse ist, gemessen wird. Es werden die latent endogenen Variablen (Zielvariablen, erklärten Variablen) und die latent exogenen Variablen (erklärenden Variablen) unterschieden. Die zweite Komponente ist das Strukturmodell, das angibt, wie die latenten Variablen untereinander zusammenhängen. Im vorliegenden Fall ist die Einstellung die verursachende Variable und das Kaufverhalten die davon abhängige Variable. Ein vollständiges Strukturgleichungsmodell besteht immer aus einem Strukturmodell und zwei Messmodellen. | ||
[[ | [[file:img1642212323899.png|300px|none|thumb|Pfaddiagramm eines Strukturgleichungsmodells]] | ||
Wie in Abbildung 38 ersichtlich, müssen auch die in den Gleichungen vorkommenden Fehler- bzw. Residualvariablen eingetragen werden. Hierfür werden die griechischen Buchstaben <math>\delta</math> („Delta“; Fehlerterm für Indikatoren der exogenen Variablen), <math>\varepsilon</math> („Epsilon“; Fehlerterm für die Indikatoren der endogenen Variablen) und <math>\zeta</math> („Zeta“; Fehlerterm für die latenten endogenen Variablen) verwendet. <math>\xi</math> („Ksi“) und <math>\eta</math> („Eta“) stehen für die latenten Variablen selbst. | |||
Aus der Darstellung der Wirkweise der Variablen zueinander folgen die resultierenden Gleichungen, die im Zuge der Analyse geschätzt werden müssen. Für das Beispiel in Abbildung 38 bedeutet das konkret: | |||
<math>X_{1}=\lambda_{x 1} * \xi_{1}+\delta_{1} </math> | |||
<math>X_{2}=\lambda_{x 2} * \xi_{1}+\delta_{2}</math> | |||
<math>Y_{1}=\lambda_{y 1} * \eta_{1}+\varepsilon_{1} </math> | |||
<math>\eta_{1}=\gamma * \xi_{1}+\zeta</math> | |||
Auf die übliche Notation in Matrixschreibweise wird an dieser Stelle verzichtet. Man beachte, dass in den Gleichungen lediglich <math>X_1</math>, <math>X_2</math> und <math>X_3</math> bekannt sind. Die Möglichkeit, die <math>\lambda</math>- und <math>\gamma</math>-Parameter dennoch zu schätzen ergibt sich aus der Erweiterung der einfachen Korrelation (vgl. Anzur, 2007) zur „partiellen Korrelation“. | |||
Auf die übliche Notation in Matrixschreibweise wird an dieser Stelle verzichtet. Man beachte, dass in den Gleichungen lediglich | |||
Wichtig ist hier, nochmals zu betonen, dass die Zusammenhänge und das daraus resultierende Gleichungssystem aus intensiven sachlogischen Überlegungen zustandekommen sollen. Dies erleichtert im Anschluss an die Parameterschätzungen das Auffinden etwaiger Widersprüche. | Wichtig ist hier, nochmals zu betonen, dass die Zusammenhänge und das daraus resultierende Gleichungssystem aus intensiven sachlogischen Überlegungen zustandekommen sollen. Dies erleichtert im Anschluss an die Parameterschätzungen das Auffinden etwaiger Widersprüche. | ||
| Zeile 425: | Zeile 56: | ||
=== Partielle Korrelation === | === Partielle Korrelation === | ||
Um zu widerlegen, dass zwei Variablen, | Um zu widerlegen, dass zwei Variablen, <math>X</math> und <math>Y</math>, vollständig kausal <ref>Vgl. dazu auch die Beispiele von Anzur (2007, S.95).</ref> miteinander in Zusammenhang stehen, muss eine Korrelation zwischen den beiden Variablen unter Ausschaltung potentieller Störvariablen berechnet werden. Im Falle einer Störvariable <math>Z</math> kann dies durch Berechnung der „partiellen Korrelation zwischen <math>X</math> und <math>Y</math> unter Auspartialisierung von <math>Z^{\prime \prime}</math>“ mittels folgender Formel erreicht werden: | ||
<math display="block"> | |||
r_{X Y, Z}=\frac{r_{X Y}-r_{X Z} r_{Y Z}}{\sqrt{\left(1-r_{X Z}^{2}\right) *\left(1-r_{Y Z}^{2}\right)}} | |||
</math> | |||
{| | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 14''' | ! width="100%" | '''Beispiel 14''' | ||
Zwischen Pro-Kopf-BIP ( | Zwischen Pro-Kopf-BIP (<math>X</math>) und Lebenserwartung ([<math>Y</math>) sei in verschiedenen Ländern eine Korrelation von 0,57 beobachtet worden. Bekannt sind aber auch Daten über die Bildung, beispielsweise die Analphabetenquote (<math>Z</math>). Hier sei weiters bekannt <math>r_{X Z}=-0,43</math> und <math>r_{Y Z}=-0,76</math>. Will man nun den Einfluss von <math>Z</math> ausschalten, berechnet man in Wirklichkeit so etwas wie die mittlere Korrelation zwischen <math>X</math> und <math>Y</math> für Gruppen von Länder, die jeweils dieselben (konstanten) <ref>Man spricht daher auch von „partieller Korrelation unter Konstanthaltung einer weiteren Variablen.</ref> Analphabetenquoten haben. Konkret ergibt sich: | ||
<math display="block"> | |||
r_{X Y . Z}=\frac{0,57-(-0,43) *(-0,76)}{\sqrt{\left(1-(-0,43)^{2}\right) *\left(1-(-0,76)^{2}\right)}}=0,41 | |||
</math> | |||
Der positive Zusammenhang zwischen pro-Kopf-BIP und Lebenserwartung reduziert sich bei Ausschaltung des Einflusses der Analphabetenrate und ist daher teilweise durch diese verursacht. | Der positive Zusammenhang zwischen pro-Kopf-BIP und Lebenserwartung reduziert sich bei Ausschaltung des Einflusses der Analphabetenrate und ist daher teilweise durch diese verursacht. | ||
| Zeile 453: | Zeile 90: | ||
<ul> | <ul> | ||
<li><p>Latente Variablen: Kaufsituation, Unternehmensgröße (exogen); Buying Center-Struktur, Geschäftsbeziehungen, Transaktionsprozess (endogen)</p></li> | <li><p>Latente Variablen: Kaufsituation, Unternehmensgröße (exogen); Buying Center-Struktur, Geschäftsbeziehungen, Transaktionsprozess (endogen)</p></li> | ||
<li><p>Indikatoren: Konjunktur, Produktwert, Größe, Technikerzahl (für die exogenen Variablen); Buying-Center-Größe, Umsatz, Aufträge, Verhandlungsdauer, Telefonkontakt (für die endogenen Variablen)</p> | <li><p>Indikatoren: Konjunktur, Produktwert, Größe, Technikerzahl (für die exogenen Variablen); Buying-Center-Größe, Umsatz, Aufträge, Verhandlungsdauer, Telefonkontakt (für die endogenen Variablen)</p></li> | ||
< | </ul> | ||
< | |||
== Durchführung == | |||
=== Vorgehen nach Vorliegen des Pfaddiagrammes === | |||
Nach Aufstellen von Hypothesen und der Spezifikation des Modells müssen – wie bei den meisten hier vorgestellten Verfahren – Zusatzannahmen getroffen werden. Auch hier ist die Unkorreliertheit der Fehler wieder eine entscheidende Annahme, sowohl untereinander (<math>\zeta</math>, <math>\varepsilon</math> und <math>\delta</math>) als auch mit den jeweils zugehörigen latenten Variablen (<math>\zeta</math> und <math>\delta</math> mit <math>\xi</math>, sowie <math>\varepsilon</math> mit <math>\eta</math>). | |||
Nach Aufstellen von Hypothesen und der Spezifikation des Modells müssen – wie bei den meisten hier vorgestellten Verfahren – Zusatzannahmen getroffen werden. Auch hier ist die Unkorreliertheit der Fehler wieder eine entscheidende Annahme, sowohl untereinander ( | |||
Bevor nun Parameter geschätzt werden können, ist weiters erforderlich, zu untersuchen, ob das vorliegende Gleichungssystem überhaupt gelöst werden kann. Hierfür muss sichergestellt sein, dass genügend viele Indikatoren in Bezug auf die Zahl der zu schätzenden Parameter im Modell enthalten sind. Sei | Bevor nun Parameter geschätzt werden können, ist weiters erforderlich, zu untersuchen, ob das vorliegende Gleichungssystem überhaupt gelöst werden kann. Hierfür muss sichergestellt sein, dass genügend viele Indikatoren in Bezug auf die Zahl der zu schätzenden Parameter im Modell enthalten sind. Sei <math>n</math> die Anzahl der verwendeten Indikatorvariablen, so darf die Anzahl der zu schätzenden Parameter maximal <math>\frac{n(n+1)}{2}</math> sein. Für das Pfaddiagramm in Abbildung 38 ergeben sich maximal <math>\frac{1}{2} * 3 * 4=6</math> Parameter. Daher sind die vier Parameter eindeutig schätzbar. | ||
Parameterschätzung | Parameterschätzung | ||
Ziel ist es nun, die Parameter derart zu schätzen, dass die durch die geschätzten Parameterwerte resultierenden Kovarianzen (Korrelationen) bestmöglich zur empirischen Varianz-Kovarianz-Matrix (Korrelationsmatrix) passt. Dieses Vorgehen ist schon aus der Faktorenanalyse bekannt. Dafür, was jedoch „bestmöglich“ heißen kann, gibt es ebenfalls wieder verschiedene Vorschläge, die aber überwiegend in den wichtigsten statistischen Schätzprinzipien „Kleinste quadrierte Abweichungen“ bzw. „Maximum Likelihood“ <ref>Vgl. ein grundlegendes Statistik-Lehrbuch (z.B. Bortz, 1999, Abschnitt 3.4).</ref> resultieren. Kriterien für die Wahl des Verfahrens sind (lt. Adler, 1996, zitiert in Backhaus et al., 2003) die Annahme der multivariaten Normalverteilung der Daten, die Skaleninvarianz der Schätzfunktion, der erforderliche Stichprobenumfang und ob Inferenzstatistiken verfügbar sein sollen. | Ziel ist es nun, die Parameter derart zu schätzen, dass die durch die geschätzten Parameterwerte resultierenden Kovarianzen (Korrelationen) bestmöglich zur empirischen Varianz-Kovarianz-Matrix (Korrelationsmatrix) passt. Dieses Vorgehen ist schon aus der Faktorenanalyse bekannt. Dafür, was jedoch „bestmöglich“ heißen kann, gibt es ebenfalls wieder verschiedene Vorschläge, die aber überwiegend in den wichtigsten statistischen Schätzprinzipien „Kleinste quadrierte Abweichungen“ bzw. „Maximum Likelihood“ <ref>Vgl. ein grundlegendes Statistik-Lehrbuch (z.B. Bortz, 1999, Abschnitt 3.4).</ref> resultieren. Kriterien für die Wahl des Verfahrens sind (lt. Adler, 1996, zitiert in Backhaus et al., 2003) die Annahme der multivariaten Normalverteilung der Daten, die Skaleninvarianz der Schätzfunktion, der erforderliche Stichprobenumfang und ob Inferenzstatistiken verfügbar sein sollen. | ||
Inferenzstatistische Beurteilung des geschätzten Modells | Inferenzstatistische Beurteilung des geschätzten Modells | ||
| Zeile 474: | Zeile 109: | ||
Hinweise, ob das geschätzte Modell die Daten gut beschreibt gibt es einige. Zuerst sollten die Schätzergebnisse auf Plausibilität überprüft werden. Korrelationen, die betragsmäßig größer als 1 sind, negative Varianzen, Koeffizienten, deren Vorzeichen umgekehrt zum postulierten Zusammenhang sind oder nicht positiv definite Korrelationsmatrizen sind einige Indikatoren, die auf eine Fehlspezifikation des Modells hinweisen. | Hinweise, ob das geschätzte Modell die Daten gut beschreibt gibt es einige. Zuerst sollten die Schätzergebnisse auf Plausibilität überprüft werden. Korrelationen, die betragsmäßig größer als 1 sind, negative Varianzen, Koeffizienten, deren Vorzeichen umgekehrt zum postulierten Zusammenhang sind oder nicht positiv definite Korrelationsmatrizen sind einige Indikatoren, die auf eine Fehlspezifikation des Modells hinweisen. | ||
Ist offensichtlich keine der Minimalforderungen verletzt, kann man für dieses Setting verschiedene prototypische statistische Tests, wie beispielsweise den t-Test oder den | Ist offensichtlich keine der Minimalforderungen verletzt, kann man für dieses Setting verschiedene prototypische statistische Tests, wie beispielsweise den t-Test oder den <math>\chi^{2}</math>-Test (Anzur, 2007) adaptieren. Während der t-Test Hypothesen über einzelne Parameter testet ([<math>H_{0}: \lambda_{i}=0 \text { versus } H_{1}: \lambda_{i} \neq 0</math>), führt der <math>\chi^{2}</math>-Test einen globalen Test durch (<math>H_{0}</math> „Die empirische Kovarianzmatrix entspricht dem Modell“ versus <math>H_{1}</math> „Die empirische Kovarianzmatrix entspricht nicht dem Modell“). | ||
Als Maßzahlen für die Zuverlässigkeit können außerdem noch das aus Lektion 1 bekannte Bestimmtheitsmaß (wie zuverlässig werden die latenten Variablen gemessen) sowie die paarweise Korrelationen zwischen den Parameterschätzungen angegeben werden. Falls sehr hohe Werte vorkommen, müssen einzelne Parameter entfernt werden. | Als Maßzahlen für die Zuverlässigkeit können außerdem noch das aus Lektion 1 bekannte Bestimmtheitsmaß (wie zuverlässig werden die latenten Variablen gemessen) sowie die paarweise Korrelationen zwischen den Parameterschätzungen angegeben werden. Falls sehr hohe Werte vorkommen, müssen einzelne Parameter entfernt werden. | ||
| Zeile 487: | Zeile 122: | ||
Zwei häufig in der Literatur genannten Softwarepakete zur Schätzung von Strukturgleichungsmodellen sind AMOS und LISREL, jedoch können derartige Analysen auch mit R durchgeführt werden. Wir werden uns nun ein kurzes Beispiel ansehen, wie ein Modelle in R spezifiziert und geschätzt werden kann. | Zwei häufig in der Literatur genannten Softwarepakete zur Schätzung von Strukturgleichungsmodellen sind AMOS und LISREL, jedoch können derartige Analysen auch mit R durchgeführt werden. Wir werden uns nun ein kurzes Beispiel ansehen, wie ein Modelle in R spezifiziert und geschätzt werden kann. | ||
{| | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 15''' | ! style="text-align: left;" width="100%" | '''Beispiel 15''' | ||
Die Daten stammen aus einer Untersuchung des Einflusses von Freunden („peer group“) und Familie auf den beruflichen Ehrgeiz (Duncan, Haller und Portes, 1968). In diesem einfachen Beispiel sollen die Zusammenhangsstrukturen von sechs manifesten Variablen untersucht werden. Gemessen wurde der berufliche Ehrgeiz („occupational aspiration“) der Respondenten („R“) bzw. des besten Freundes/der besten Freundin („F“) des/der Respondenten/in. Der Index korreliert u.a. mit persönliche Erfolgsorientierung, dem Selbstkonzept zur Zielerreichung und der „Wertigkeit“ des tatsächlich realisierten Berufes. | Die Daten stammen aus einer Untersuchung des Einflusses von Freunden („peer group“) und Familie auf den beruflichen Ehrgeiz (Duncan, Haller und Portes, 1968). In diesem einfachen Beispiel sollen die Zusammenhangsstrukturen von sechs manifesten Variablen untersucht werden. Gemessen wurde der berufliche Ehrgeiz („occupational aspiration“) der Respondenten („R“) bzw. des besten Freundes/der besten Freundin („F“) des/der Respondenten/in. Der Index korreliert u.a. mit persönliche Erfolgsorientierung, dem Selbstkonzept zur Zielerreichung und der „Wertigkeit“ des tatsächlich realisierten Berufes. | ||
| Zeile 494: | Zeile 129: | ||
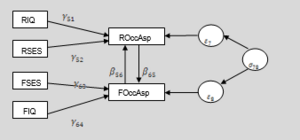
Für beide „Ehrgeiz“-Variablen gibt es je zwei erklärende Variablen, den Intelligenzquotienten („IQ“) und den sozioökonomische Status („SES“) der Familie der betreffenden Person. Folgendes Pfaddiagramm (Abbildung 40) veranschaulicht das zu spezifizierende Modell: | Für beide „Ehrgeiz“-Variablen gibt es je zwei erklärende Variablen, den Intelligenzquotienten („IQ“) und den sozioökonomische Status („SES“) der Familie der betreffenden Person. Folgendes Pfaddiagramm (Abbildung 40) veranschaulicht das zu spezifizierende Modell: | ||
<span id="_Toc249868226" class="anchor"></span> | <span id="_Toc249868226" class="anchor"></span> | ||
| Zeile 516: | Zeile 139: | ||
Für das Modell ergeben sich folgende Gleichungen: | Für das Modell ergeben sich folgende Gleichungen: | ||
<math display="block"> | |||
\text { ROccAsp }=\lambda_{51} * R I Q+\lambda_{52} * R S E S+\gamma_{56} * \text { FOccAsp }+\varepsilon_{7} | |||
</math> | |||
<math display="block"> | |||
\text { FOccAsp }=\lambda_{63} * \text { FIQ }+\lambda_{64} * \text { FSES }+\gamma_{65} * \text { ROccAsp }+\varepsilon_{8} | |||
</math> | |||
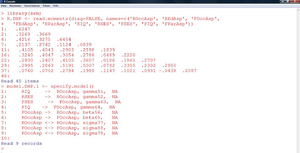
Ziel ist nun, die Koeffizienten dieser Gleichungen zu schätzen. In R kann das Modell mithilfe des Paketes „sem“ (structural bzw. simultaneous equation modeling) eingegeben werden. Abbildung 41 zeigt, wie die Matrix der Korrelationen als untere Dreiecksmatrix in R selbst eingegeben werden kann und wie anschließend das Modell spezifiziert wird. Alle Wirkungen in den Gleichungen müssen zeilenweise eingegeben werden, sowie der Name des Koeffizienten und – falls verfügbar – ein Startwert. | Ziel ist nun, die Koeffizienten dieser Gleichungen zu schätzen. In R kann das Modell mithilfe des Paketes „sem“ (structural bzw. simultaneous equation modeling) eingegeben werden. Abbildung 41 zeigt, wie die Matrix der Korrelationen als untere Dreiecksmatrix in R selbst eingegeben werden kann und wie anschließend das Modell spezifiziert wird. Alle Wirkungen in den Gleichungen müssen zeilenweise eingegeben werden, sowie der Name des Koeffizienten und – falls verfügbar – ein Startwert. | ||
| Zeile 529: | Zeile 156: | ||
* '''sem.DHP.1 <- sem(model.DHP.1, R.DHP, 329,fixed.x=c('RIQ', 'RSES', 'FSES', 'FIQ'))''' | * '''sem.DHP.1 <- sem(model.DHP.1, R.DHP, 329,fixed.x=c('RIQ', 'RSES', 'FSES', 'FIQ'))''' | ||
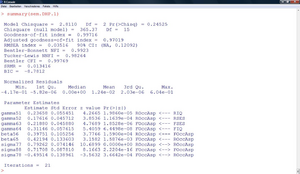
Die Zusammenfassung des Modells erscheint mittels der generischen Funktion „summary“ (Abbildung 42). Diese kann auf die verschiedensten R-Objekte angewandt werden. Ausgegeben werden zunächst die gängigen globalen Fit-Statistiken. Der oben erwähnte | Die Zusammenfassung des Modells erscheint mittels der generischen Funktion „summary“ (Abbildung 42). Diese kann auf die verschiedensten R-Objekte angewandt werden. Ausgegeben werden zunächst die gängigen globalen Fit-Statistiken. Der oben erwähnte <math>\chi^{2}</math>-Test erzielt einen p-Wert von 0,245. Dieser ist größer als der übliche <math>\alpha</math>-Fehler von 0,05 und damit entscheidet der Test für die Nullhypothese, dass die Varianz-Kovarianz-Matrix der Daten durch das Modell adäquat abgebildet wird. | ||
Unterhalb stehen die t-Tests für jeden einzelnen Koeffizienten. Die p-Werte sind allesamt kleiner als 0,05, daher sind alle Koeffizienten signifikant von Null verschieden. | Unterhalb stehen die t-Tests für jeden einzelnen Koeffizienten. Die p-Werte sind allesamt kleiner als 0,05, daher sind alle Koeffizienten signifikant von Null verschieden. | ||
| Zeile 535: | Zeile 162: | ||
Die geschätzten Gleichungen lauten: | Die geschätzten Gleichungen lauten: | ||
<math display="block"> | |||
R O C C A s p=0,24 * R I Q+0,18 * R S E S+0,40 * F O C C A s p+\varepsilon_{7} | |||
</math> | |||
<math display="block"> | |||
F O C C A s p=0,22 * F I Q+0,31 * F S E S+0,42 * R O C C A s p+\varepsilon_{8} | |||
</math> | |||
Als Varianzschätzungen ergeben sich: | Als Varianzschätzungen ergeben sich: <math>\sigma_{7}^{2}=0,79</math> und <math>\sigma_{8}^{2}=0,72</math> | ||
Als Kovarianzschätzung für die Fehlerterme ergibt sich: | Als Kovarianzschätzung für die Fehlerterme ergibt sich: <math>\sigma_{78}=-0,50</math> | ||
[[file:img1642238453677.png|300px|none|thumb|SEM-Analyse in R- Teil 2]] | [[file:img1642238453677.png|300px|none|thumb|SEM-Analyse in R- Teil 2]] | ||
Aktuelle Version vom 20. Jänner 2022, 10:43 Uhr
Strukturgleichungsmodelle
Die abschließende Lektion dient vor allem als Ausblick, wie die bestehenden Verfahren kombiniert bzw. erweitert werden können. Dies geschieht in der Theorie hinter Strukturgleichungsmodellen. Die Basiskomponenten und deren Darstellung, sowie eine überblicksartige Beschreibung des Prozesses vom Aufstellen von Hypothesen bis zur Schätzung des gewählten Modells sind Kernpunkt und Ziel dieser letzten Lektion.
Einführung und Begriffsabgrenzung
Die Strukturgleichungsmodelle stellen eine Kombination zweier in diesem Skriptum behandelter Verfahren dar. Wie in der Faktorenanalyse soll hier eine Korrelationsstruktur von manifesten Variablen durch latente Faktoren erklärt werden. Weiters sollen aber die Beziehungen zwischen verschiedenen latenten Faktoren durch regressionsanalytische Methoden festgestellt werden. Das ist hier gewissermaßen die Besonderheit. Wichtig ist dabei, dass die Art des kausalen Zusammenhanges identifiziert wird. Daher werden derartige Methoden auch als Kausalanalyse bezeichnet. Andere Bezeichnungen sind „Kovarianzstrukturanalyse“ oder auch Pfadanalyse, wobei letztere ein Spezialfall ist, da dort nur manifeste Variablen („Indikatoren“) im Kausalmodell zugelassen sind. Daher steht die Pfadanalyse auch der schon besprochenen Regressionsanalyse näher. Die „Latent Structure Analyse“ – ein ebenfalls verwandter Begriff – ist hingegen eine übergeordnete Bezeichnung für Verfahren, die auch diskrete, ordinale oder sogar dichotome Variablen zulassen.
Die Feststellung der Kausalität ist wichtig, da eine hohe Korrelation nur für „immer wenn, dann“ und nicht notwendig für „deswegen, weil“ steht. Mögliche Entsprechungen einer hohen Korrelation zwischen zwei Variablen X und Y können sein (vgl. Bortz, 1999, S. 226):
- X beeinflusst Y kausal
- Y beeinflusst X kausal
- X und Y werden von einer dritten Variable kausal beeinflusst
- X und Y beeinflussen sich wechselseitig kausal
Im Rahmen von Strukturgleichungsmodellen wird die Faktorenanalyse konfirmatorisch (im Gegensatz zur exploratorischen FA in Lektion 5) durchgeführt, d.h. es wird bereits konkret unterstellt von welchen latenten Variablen die manifesten abhängen. Mehr als bei anderen Verfahren ist der Anwender hier – auch in Hinblick auf Identifizierbarkeit und Eindeutigkeit der Schätzungen – gefordert, sich zu überlegen, welcher Art die Zusammenhänge sein könnten. Es fließen hier sehr viele unbekannte Größen in die Modellierung ein.
In der folgenden Darstellung geht es weniger um den komplexen mathematischen Hintergrund der Methode – dies würde den Rahmen deutlich sprengen – sondern um die Vorstellung der Idee dahinter.
Grundlagen und Beispiele
Modelldarstellung, Terminologie und Notation
Die Datengrundlage für die Analyse mittels Strukturgleichungsmodellen sind wie in der Faktorenanalyse Kovarianzen bzw. Korrelationen zwischen den beobachtbaren Variablen. Output des Verfahrens sind wieder Modellparameter, zu denen in diesem Fall auch Signifikanzen berechnet werden können. Es kann also (wie übrigens auch bei der Regression) statistisch getestet werden, welche Parameter überzufällig von Null verschieden sind. Das Modell gilt dann als durch die Daten “bestätigt”, wenn sich die Korrelationen durch die Modellparameter (direkte oder indirekte Pfadkoeffizienten) rekonstruieren lässt.
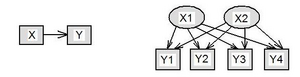
Die Modelle werden üblicherweise in Pfaddiagrammen dargestellt, wobei die Variablen als Knoten und die Wirkungen zwischen den Variablen als Kanten eingezeichnet werden. Manifeste Variablen („Indikatoren“) werden oft als Rechtecke und latente Variablen („Faktoren“) als Ellipsen gezeichnet. Abbildung 37 zeigt die Regressionsanalyse und die Faktorenanalyse als solches Pfaddiagramm. Für jeden Pfeil wird in den Verfahren ein Parameter geschätzt.
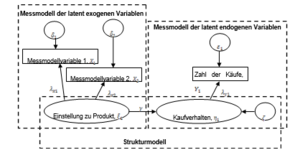
Die Erweiterung der Regressions- und Faktorenanalyse zu allgemeinen Strukturgleichungsmodellen besteht nun darin, dass Wirkungen zwischen latenten Variablen untersucht werden können, also auch „Pfeile zwischen Ellipsen“ zugelassen werden. Beispielsweise könnte man daran interessiert sein, inwiefern die Einstellung zu einem Produkt das Kaufverhalten beeinflusst. Die latente Variable „Einstellung zum Produkt“ kann durch verschiedene psychologische Einstellungsskalen z.B. mittels Fragebogen (manifest) erhoben werden, das Kaufverhalten womöglich am ehesten durch die Zahl der Käufe (manifest). Abbildung 38 zeigt das Pfaddiagramm eines solchen Modells (Backhaus et al., 2003).
Die dort dargestellte Struktur ist prototypisch für die Darstellung von Strukturgleichungsmodellen. Die Komponenten sind einerseits die Messmodelle der latenten Variablen. In ihnen wird spezifiziert, in welcher Form die entscheidenden latenten Variablen von den manifesten abhängen, also wie das, was von Interesse ist, gemessen wird. Es werden die latent endogenen Variablen (Zielvariablen, erklärten Variablen) und die latent exogenen Variablen (erklärenden Variablen) unterschieden. Die zweite Komponente ist das Strukturmodell, das angibt, wie die latenten Variablen untereinander zusammenhängen. Im vorliegenden Fall ist die Einstellung die verursachende Variable und das Kaufverhalten die davon abhängige Variable. Ein vollständiges Strukturgleichungsmodell besteht immer aus einem Strukturmodell und zwei Messmodellen.
Wie in Abbildung 38 ersichtlich, müssen auch die in den Gleichungen vorkommenden Fehler- bzw. Residualvariablen eingetragen werden. Hierfür werden die griechischen Buchstaben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} („Delta“; Fehlerterm für Indikatoren der exogenen Variablen), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon} („Epsilon“; Fehlerterm für die Indikatoren der endogenen Variablen) und („Zeta“; Fehlerterm für die latenten endogenen Variablen) verwendet. („Ksi“) und („Eta“) stehen für die latenten Variablen selbst.
Aus der Darstellung der Wirkweise der Variablen zueinander folgen die resultierenden Gleichungen, die im Zuge der Analyse geschätzt werden müssen. Für das Beispiel in Abbildung 38 bedeutet das konkret:
Auf die übliche Notation in Matrixschreibweise wird an dieser Stelle verzichtet. Man beachte, dass in den Gleichungen lediglich , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_2} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_3} bekannt sind. Die Möglichkeit, die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda} - und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma} -Parameter dennoch zu schätzen ergibt sich aus der Erweiterung der einfachen Korrelation (vgl. Anzur, 2007) zur „partiellen Korrelation“.
Wichtig ist hier, nochmals zu betonen, dass die Zusammenhänge und das daraus resultierende Gleichungssystem aus intensiven sachlogischen Überlegungen zustandekommen sollen. Dies erleichtert im Anschluss an die Parameterschätzungen das Auffinden etwaiger Widersprüche.
Partielle Korrelation
Um zu widerlegen, dass zwei Variablen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} , vollständig kausal [1] miteinander in Zusammenhang stehen, muss eine Korrelation zwischen den beiden Variablen unter Ausschaltung potentieller Störvariablen berechnet werden. Im Falle einer Störvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} kann dies durch Berechnung der „partiellen Korrelation zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} unter Auspartialisierung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z^{\prime \prime}} “ mittels folgender Formel erreicht werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{X Y, Z}=\frac{r_{X Y}-r_{X Z} r_{Y Z}}{\sqrt{\left(1-r_{X Z}^{2}\right) *\left(1-r_{Y Z}^{2}\right)}} }
| Beispiel 14
Zwischen Pro-Kopf-BIP (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} ) und Lebenserwartung ([Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} ) sei in verschiedenen Ländern eine Korrelation von 0,57 beobachtet worden. Bekannt sind aber auch Daten über die Bildung, beispielsweise die Analphabetenquote (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} ). Hier sei weiters bekannt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{X Z}=-0,43} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{Y Z}=-0,76} . Will man nun den Einfluss von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} ausschalten, berechnet man in Wirklichkeit so etwas wie die mittlere Korrelation zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} für Gruppen von Länder, die jeweils dieselben (konstanten) [2] Analphabetenquoten haben. Konkret ergibt sich: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{X Y . Z}=\frac{0,57-(-0,43) *(-0,76)}{\sqrt{\left(1-(-0,43)^{2}\right) *\left(1-(-0,76)^{2}\right)}}=0,41 }
|
|---|
Das Konzept der partiellen Korrelation kann für beliebig viele auszuschaltende Variablen verallgemeinert werden.
Beispielfragestellungen
Nachdem nun das Grundprinzip und die Bauart von Strukturgleichungsmodellen skizziert wurde, sollen nun einige Beispiele deren Einsatz zeigen:
- Welche Auswirkung haben Familie und Schule auf die Schulleistung eines Kindes?
- Latente Variablen: Familie und Schule (exogen); Schulleistung (endogen)
- Indikatoren: Beruf und Schulbildung der Eltern, Ausmaß an Nachhilfe, Ausbildungsniveau des Lehrers, Wissenstest, Interessentest
- Inwieweit nehmen Rollenunsicherheit und Arbeitsmotivation eines Verkäufers Einfluss auf seine Selbstwertschätzung, seine Berufszufriedenheit und den erzielten Umsatz?
- Latente Variablen: Rollenverständnis und Arbeitsmotivation (exogen); Selbstwertschätzung, Berufszufriedenheit und Leistung (endogen)
- Indikatoren: Verschiedene Messmodelle, Umsatz
- Wie beeinflussen bestimmte Rahmenbedingungen das Interaktionsverhalten bei Verhandlungsprozessen im Investitionsgüter-Marketing?
Latente Variablen: Kaufsituation, Unternehmensgröße (exogen); Buying Center-Struktur, Geschäftsbeziehungen, Transaktionsprozess (endogen)
Indikatoren: Konjunktur, Produktwert, Größe, Technikerzahl (für die exogenen Variablen); Buying-Center-Größe, Umsatz, Aufträge, Verhandlungsdauer, Telefonkontakt (für die endogenen Variablen)
Durchführung
Vorgehen nach Vorliegen des Pfaddiagrammes
Nach Aufstellen von Hypothesen und der Spezifikation des Modells müssen – wie bei den meisten hier vorgestellten Verfahren – Zusatzannahmen getroffen werden. Auch hier ist die Unkorreliertheit der Fehler wieder eine entscheidende Annahme, sowohl untereinander (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} ) als auch mit den jeweils zugehörigen latenten Variablen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi} , sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta} ).
Bevor nun Parameter geschätzt werden können, ist weiters erforderlich, zu untersuchen, ob das vorliegende Gleichungssystem überhaupt gelöst werden kann. Hierfür muss sichergestellt sein, dass genügend viele Indikatoren in Bezug auf die Zahl der zu schätzenden Parameter im Modell enthalten sind. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} die Anzahl der verwendeten Indikatorvariablen, so darf die Anzahl der zu schätzenden Parameter maximal Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{n(n+1)}{2}} sein. Für das Pfaddiagramm in Abbildung 38 ergeben sich maximal Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2} * 3 * 4=6} Parameter. Daher sind die vier Parameter eindeutig schätzbar.
Parameterschätzung
Ziel ist es nun, die Parameter derart zu schätzen, dass die durch die geschätzten Parameterwerte resultierenden Kovarianzen (Korrelationen) bestmöglich zur empirischen Varianz-Kovarianz-Matrix (Korrelationsmatrix) passt. Dieses Vorgehen ist schon aus der Faktorenanalyse bekannt. Dafür, was jedoch „bestmöglich“ heißen kann, gibt es ebenfalls wieder verschiedene Vorschläge, die aber überwiegend in den wichtigsten statistischen Schätzprinzipien „Kleinste quadrierte Abweichungen“ bzw. „Maximum Likelihood“ [3] resultieren. Kriterien für die Wahl des Verfahrens sind (lt. Adler, 1996, zitiert in Backhaus et al., 2003) die Annahme der multivariaten Normalverteilung der Daten, die Skaleninvarianz der Schätzfunktion, der erforderliche Stichprobenumfang und ob Inferenzstatistiken verfügbar sein sollen.
Inferenzstatistische Beurteilung des geschätzten Modells
Hinweise, ob das geschätzte Modell die Daten gut beschreibt gibt es einige. Zuerst sollten die Schätzergebnisse auf Plausibilität überprüft werden. Korrelationen, die betragsmäßig größer als 1 sind, negative Varianzen, Koeffizienten, deren Vorzeichen umgekehrt zum postulierten Zusammenhang sind oder nicht positiv definite Korrelationsmatrizen sind einige Indikatoren, die auf eine Fehlspezifikation des Modells hinweisen.
Ist offensichtlich keine der Minimalforderungen verletzt, kann man für dieses Setting verschiedene prototypische statistische Tests, wie beispielsweise den t-Test oder den Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^{2}} -Test (Anzur, 2007) adaptieren. Während der t-Test Hypothesen über einzelne Parameter testet ([Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{0}: \lambda_{i}=0 \text { versus } H_{1}: \lambda_{i} \neq 0} ), führt der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^{2}} -Test einen globalen Test durch (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{0}} „Die empirische Kovarianzmatrix entspricht dem Modell“ versus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{1}} „Die empirische Kovarianzmatrix entspricht nicht dem Modell“).
Als Maßzahlen für die Zuverlässigkeit können außerdem noch das aus Lektion 1 bekannte Bestimmtheitsmaß (wie zuverlässig werden die latenten Variablen gemessen) sowie die paarweise Korrelationen zwischen den Parameterschätzungen angegeben werden. Falls sehr hohe Werte vorkommen, müssen einzelne Parameter entfernt werden.
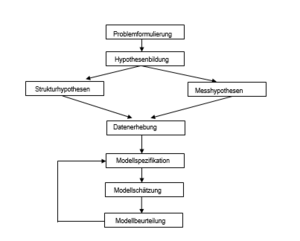
All diese Prüfungen (und einige mehr) bestimmen letztendlich, ob das gewählte Modell die Daten und damit den Sachverhalt gut erklärt. Abschließend sei hier nun nochmals der Gesamtablauf während der Analyse mit Strukturgleichungsmodellen schematisch dargestellt (Reinecke, 2005, S. 11):
Strukturgleichungsmodelle in R
Zwei häufig in der Literatur genannten Softwarepakete zur Schätzung von Strukturgleichungsmodellen sind AMOS und LISREL, jedoch können derartige Analysen auch mit R durchgeführt werden. Wir werden uns nun ein kurzes Beispiel ansehen, wie ein Modelle in R spezifiziert und geschätzt werden kann.
| Beispiel 15
Die Daten stammen aus einer Untersuchung des Einflusses von Freunden („peer group“) und Familie auf den beruflichen Ehrgeiz (Duncan, Haller und Portes, 1968). In diesem einfachen Beispiel sollen die Zusammenhangsstrukturen von sechs manifesten Variablen untersucht werden. Gemessen wurde der berufliche Ehrgeiz („occupational aspiration“) der Respondenten („R“) bzw. des besten Freundes/der besten Freundin („F“) des/der Respondenten/in. Der Index korreliert u.a. mit persönliche Erfolgsorientierung, dem Selbstkonzept zur Zielerreichung und der „Wertigkeit“ des tatsächlich realisierten Berufes. Für beide „Ehrgeiz“-Variablen gibt es je zwei erklärende Variablen, den Intelligenzquotienten („IQ“) und den sozioökonomische Status („SES“) der Familie der betreffenden Person. Folgendes Pfaddiagramm (Abbildung 40) veranschaulicht das zu spezifizierende Modell:
' . Für das Modell ergeben sich folgende Gleichungen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { ROccAsp }=\lambda_{51} * R I Q+\lambda_{52} * R S E S+\gamma_{56} * \text { FOccAsp }+\varepsilon_{7} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { FOccAsp }=\lambda_{63} * \text { FIQ }+\lambda_{64} * \text { FSES }+\gamma_{65} * \text { ROccAsp }+\varepsilon_{8} }
Die Berechnung der Parameter erfolgt hernach durch die Funktion „sem“, die als Input das spezifizierte Modell, den Stichprobenumfang (zur Bestimmung von Signifikanzen) und die Information, welches die manifesten exogenen Variablen sind, verlangt. Für sie müssen keine Varianzen und Kovarianzen spezifiziert werden. Das Ergebnis wird dem Objekt „sem.DHP.1“ zugewiesen:
Die Zusammenfassung des Modells erscheint mittels der generischen Funktion „summary“ (Abbildung 42). Diese kann auf die verschiedensten R-Objekte angewandt werden. Ausgegeben werden zunächst die gängigen globalen Fit-Statistiken. Der oben erwähnte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^{2}} -Test erzielt einen p-Wert von 0,245. Dieser ist größer als der übliche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fehler von 0,05 und damit entscheidet der Test für die Nullhypothese, dass die Varianz-Kovarianz-Matrix der Daten durch das Modell adäquat abgebildet wird. Unterhalb stehen die t-Tests für jeden einzelnen Koeffizienten. Die p-Werte sind allesamt kleiner als 0,05, daher sind alle Koeffizienten signifikant von Null verschieden. Die geschätzten Gleichungen lauten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R O C C A s p=0,24 * R I Q+0,18 * R S E S+0,40 * F O C C A s p+\varepsilon_{7} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F O C C A s p=0,22 * F I Q+0,31 * F S E S+0,42 * R O C C A s p+\varepsilon_{8} }
Als Kovarianzschätzung für die Fehlerterme ergibt sich: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{78}=-0,50} |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Wiederholen Sie die Schritte bei der Analyse eines Strukturgleichungsmodells
- Was ist ein Messmodell? Was ein Strukturmodell?
- Zeigen Sie anhand der Bedingung für die maximale Parameteranzahl, dass das Beispiel 15 lösbar ist.
Zusammenfassung
In der statistischen Analyse mittels Strukturgleichungsmodellen (SEM) steht wie in keinem anderen der in diesem Studienheft vorgestellten Verfahren die Bildung von Hypothesen über die Wirkzusammenhänge zwischen manifesten und latenten Variablen im Vordergrund. Dieses konfirmatorische Vorgehen unterscheidet sich wesentlich von der (explorativen) Faktorenanalyse, die sich „blind“ auf die Daten stürzt. Es können komplexe Abhängigkeitsstrukturen unterstellt werden und durch ein Pfaddiagramm beschrieben werden. Dies enthält im Allgemeinen sowohl Messmodelle für latente Variablen, als auch ein Strukturmodell für den Zusammenhang zwischen latenten Variablen. Für die Lösbarkeit des dadurch entstehenden Gleichungssystems ist es von Bedeutung, dass – bezogen auf die Zahl der zu schätzenden Parameter – genügend Daten in Form von Kovarianzen zwischen beobachtbaren Merkmalen verfügbar sind. Geschätzt werden die Gleichungssysteme dann mit der in der Statistik üblichen Methode der Kleinsten-Quadrate- bzw. der Maximum-Likelihood-Schätzung. Wesentlicher Unterschied zur Faktorenanalyse ist auch, dass Hypothesen über die geschätzten Parameter getestet werden können.