Methoden der Datenanalyse - Lösungen: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
= Lösungen zu den Aufgaben und zu den Wiederholungsaufgaben = | = Lösungen zu den Aufgaben und zu den Wiederholungsaufgaben = | ||
Lösungen zu den Aufgaben | == Lösungen zu den Aufgaben == | ||
Aufgabe 1 | Aufgabe 1 | ||
| Zeile 19: | Zeile 19: | ||
Analog zum Beispiel: | Analog zum Beispiel: | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! width="14%" | Versuch | ! width="14%" | Versuch | ||
! width="13%" | 1 | ! width="13%" | 1 | ||
| Zeile 60: | Zeile 60: | ||
Aufgabe 4 | Aufgabe 4 | ||
{| style="border-collapse: collapse; height: 197px;" border="1" | {| style="border-collapse: collapse; height: 197px;" border="1" | ||
! style="height: 28px; width: 111.771px;" | '''Datensatz 1''' | ! style="height: 28px; width: 111.771px;" | '''Datensatz 1''' | ||
! style="height: 28px; width: 58.2292px;" | | ! style="height: 28px; width: 58.2292px;" | | ||
| Zeile 70: | Zeile 70: | ||
! style="height: 28px; width: 58.2292px;" | | ! style="height: 28px; width: 58.2292px;" | | ||
! style="height: 28px; width: 58.2755px;" | | ! style="height: 28px; width: 58.2755px;" | | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 111.771px;" | Beobachtung Nr. | | style="height: 28px; width: 111.771px;" | Beobachtung Nr. | ||
| style="height: 28px; width: 58.2292px;" | | | style="height: 28px; width: 58.2292px;" | | ||
| Zeile 81: | Zeile 81: | ||
| style="height: 28px; width: 58.2292px;" | X<sub>2</sub> | | style="height: 28px; width: 58.2292px;" | X<sub>2</sub> | ||
| style="height: 28px; width: 58.2755px;" | X<sub>3</sub> | | style="height: 28px; width: 58.2755px;" | X<sub>3</sub> | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 111.771px;" | 1 | | style="height: 28px; width: 111.771px;" | 1 | ||
| style="height: 28px; width: 58.2292px;" | | | style="height: 28px; width: 58.2292px;" | | ||
| Zeile 92: | Zeile 92: | ||
| style="height: 28px; width: 58.2292px;" | 14 | | style="height: 28px; width: 58.2292px;" | 14 | ||
| style="height: 28px; width: 58.2755px;" | 7 | | style="height: 28px; width: 58.2755px;" | 7 | ||
|- style="height: 29px;" | |- style="height: 29px;" | ||
| style="height: 29px; width: 111.771px;" | 2 | | style="height: 29px; width: 111.771px;" | 2 | ||
| style="height: 29px; width: 58.2292px;" | | | style="height: 29px; width: 58.2292px;" | | ||
| Zeile 103: | Zeile 103: | ||
| style="height: 29px; width: 58.2292px;" | 2 | | style="height: 29px; width: 58.2292px;" | 2 | ||
| style="height: 29px; width: 58.2755px;" | 3 | | style="height: 29px; width: 58.2755px;" | 3 | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 111.771px;" | 3 | | style="height: 28px; width: 111.771px;" | 3 | ||
| style="height: 28px; width: 58.2292px;" | | | style="height: 28px; width: 58.2292px;" | | ||
| Zeile 114: | Zeile 114: | ||
| style="height: 28px; width: 58.2292px;" | 8 | | style="height: 28px; width: 58.2292px;" | 8 | ||
| style="height: 28px; width: 58.2755px;" | 3 | | style="height: 28px; width: 58.2755px;" | 3 | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 111.771px;" | 4 | | style="height: 28px; width: 111.771px;" | 4 | ||
| style="height: 28px; width: 58.2292px;" | | | style="height: 28px; width: 58.2292px;" | | ||
| Zeile 125: | Zeile 125: | ||
| style="height: 28px; width: 58.2292px;" | 1 | | style="height: 28px; width: 58.2292px;" | 1 | ||
| style="height: 28px; width: 58.2755px;" | 7 | | style="height: 28px; width: 58.2755px;" | 7 | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 111.771px;" | 5 | | style="height: 28px; width: 111.771px;" | 5 | ||
| style="height: 28px; width: 58.2292px;" | | | style="height: 28px; width: 58.2292px;" | | ||
| Zeile 141: | Zeile 141: | ||
Aufgabe 5 | Aufgabe 5 | ||
Bestimmtheitsmaß: | Bestimmtheitsmaß: <math>R^{2}=\frac{Q Z}{Q T}=\frac{Q Z}{Q Z+Q I}=\frac{123,744}{123,744+199,361}=38,3 \%</math> | ||
Aufgabe 6 | Aufgabe 6 | ||
| Zeile 147: | Zeile 147: | ||
Die Testentscheidung, ob H<sub>0</sub> oder H<sub>1</sub> gewählt werden soll, kann auf zwei Arten erfolgen. | Die Testentscheidung, ob H<sub>0</sub> oder H<sub>1</sub> gewählt werden soll, kann auf zwei Arten erfolgen. | ||
Entweder es wird die Prüfgröße (im Beispiel 4,655) mit einem kritischen Wert, der von | Entweder es wird die Prüfgröße (im Beispiel 4,655) mit einem kritischen Wert, der von <math>\alpha</math> abhängt und einer Verteilungstabelle entstammt verglichen (im Beispiel 3,68). In diesem Fall wird für H<sub>1</sub> entschieden, da 4,655>3,68. Im umgekehrten Fall wäre für H<sub>0</sub> entschieden worden. | ||
Die von Softwarepaketen durchgeführte, äquivalente Vorgehensweise dazu ist die Berechnung des p-Werts. Es wird also berechnet, mit welcher Wahrscheinlichkeit die F-Verteilung (im Beispiel mit 2 und 15 Freiheitsgraden) einen Wert größer als die Prüfgröße erzielt (in Excel: „'''FVERT(4,655;2;15)'''“ was als p-Wert 0,0267 liefert). Anschließend erfolgt die Testentscheidung, indem der p-Wert mit | Die von Softwarepaketen durchgeführte, äquivalente Vorgehensweise dazu ist die Berechnung des p-Werts. Es wird also berechnet, mit welcher Wahrscheinlichkeit die F-Verteilung (im Beispiel mit 2 und 15 Freiheitsgraden) einen Wert größer als die Prüfgröße erzielt (in Excel: „'''FVERT(4,655;2;15)'''“ was als p-Wert 0,0267 liefert). Anschließend erfolgt die Testentscheidung, indem der p-Wert mit <math>\alpha</math>verglichen wird. Im vorliegenden Fall gilt: p-Wert<math><\alpha=5%</math>, daher Entscheidung für H<sub>1</sub>. Der Vorteil nach letzterer Methode ist, dass auf einen Blick bestimmt werden kann, ab welchem <math>\alpha</math> der Test für H<sub>1</sub> entscheidet. Der p-Wert wird auch bei Publikationen verwendet. | ||
Aufgabe 7 | Aufgabe 7 | ||
| Zeile 159: | Zeile 159: | ||
Alpha=5%: in Excel: „'''FINV(0,05;2;15)'''“ liefert 3,68 (vgl. Aufgabe 6) | Alpha=5%: in Excel: „'''FINV(0,05;2;15)'''“ liefert 3,68 (vgl. Aufgabe 6) | ||
<math display="block"> | |||
\frac{Q Z}{Q I}=3,68 \Leftrightarrow \frac{Q Z}{Q Z+Q I}=\frac{3,68}{3,68+1}=78,6 \%=R^{2} | |||
</math> | |||
Alpha=1%: in Excel: „'''FINV(0,01;2;15)'''“ liefert 6,36 | Alpha=1%: in Excel: „'''FINV(0,01;2;15)'''“ liefert 6,36 | ||
<math display="block"> | |||
\frac{Q Z}{Q I}=6,36 \Leftrightarrow \frac{Q Z}{Q Z+Q I}=\frac{6,36}{6,36+1}=86,4 \%=R^{2} | |||
</math> | |||
Aufgabe 9 | Aufgabe 9 | ||
<math>\hat{\mu}=49,80 ; \widehat{\alpha_{1}}=59,05-49,80=9,25</math> (PP niedrig) | |||
<math>\widehat{\alpha_{2}}=49,45-49,80=-0,35</math> (PP mittel) | |||
<math>\widehat{\alpha_{3}}=40,90-49,80=-8,90</math> (PP hoch) | |||
<math>\widehat{\beta_{1}}=50,73-49,80=0,93</math> (Postwurf) | |||
<math>\widehat{\beta_{2}}=48,87-49,80=-0,93</math> (Anzeigen) | |||
Interaktionen: | Interaktionen: | ||
<math display="block"> | |||
\widehat{\alpha \beta_{11}}=63,80-(49,80+9,25+0,93)=3,82; | |||
\widehat{\alpha \beta_{12}}=54,30-(49,80+9,25-0,93)=-3,82; | |||
\widehat{\alpha \beta_{21}}=51,50-(49,80-0,35+0,93)=1,12; | |||
\widehat{\alpha \beta_{22}}=47,40-(49,80-0,35-0,93)=-1,12; | |||
\widehat{\alpha \beta_{31}}=36,90-(49,80-8,90+0,93)=-4,93; | |||
\widehat{\alpha \beta_{32}}=44,90-(49,80-8,90-0,93)=4,93 | |||
</math> | |||
Interpretation (Beispiel): Bei Hochpreispolitik und Anzeigenwerbung werden durchschnittlich um 4,93 Stück mehr verkauft als aufgrund der getrennten Effekte zu erwarten gewesen wäre (d.h. der reduzierte Verkauf bei Hochpreispolitik wirkt sich eher bei der Werbeart „Postwurfsendung“) aus. | Interpretation (Beispiel): Bei Hochpreispolitik und Anzeigenwerbung werden durchschnittlich um 4,93 Stück mehr verkauft als aufgrund der getrennten Effekte zu erwarten gewesen wäre (d.h. der reduzierte Verkauf bei Hochpreispolitik wirkt sich eher bei der Werbeart „Postwurfsendung“) aus. | ||
Aufgabe 10 | Aufgabe 10 | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! style="width: 69.4792px;" | | ! style="width: 69.4792px;" | | ||
! style="width: 69.4792px;" | | ! style="width: 69.4792px;" | | ||
| Zeile 242: | Zeile 257: | ||
Bei vier Objekten sind lt. Bell’schen Zahlen 15 Partitionen möglich: | Bei vier Objekten sind lt. Bell’schen Zahlen 15 Partitionen möglich: | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! width="20%" | 1 / 2 / 3 / 4 | ! width="20%" | 1 / 2 / 3 / 4 | ||
! width="20%" | 12 / 3 / 4 | ! width="20%" | 12 / 3 / 4 | ||
| Zeile 263: | Zeile 278: | ||
Aufgabe 12 | Aufgabe 12 | ||
Vollständige Rangordnung: | Vollständige Rangordnung: <math>\left(\begin{array}{c} | ||
15 \\ | |||
2 | |||
\end{array}\right)=105</math>]; Tetradenmethode: <math>\left(\begin{array}{c}\left(\begin{array}{c} | |||
15 \\ | |||
2 \\ | |||
\end{array}\right) | |||
2 | |||
\end{array}\right)=\left(\begin{array}{c} | |||
105 \\ | |||
2 | |||
\end{array}\right)=5460</math> | |||
Bei 105 Vergleichen werden die Paare schrittweise sortiert (alle Paare werden z.B. auf Kärtchen präsentiert; diese werden vorerst in ähnliche und unähnliche Paare geteilt; die Untergruppen werden weiter geteilt). Bei 5460 Vergleichen muss jede Person nur einige Vergleiche durchführen. | Bei 105 Vergleichen werden die Paare schrittweise sortiert (alle Paare werden z.B. auf Kärtchen präsentiert; diese werden vorerst in ähnliche und unähnliche Paare geteilt; die Untergruppen werden weiter geteilt). Bei 5460 Vergleichen muss jede Person nur einige Vergleiche durchführen. | ||
| Zeile 282: | Zeile 308: | ||
Aufgabe 14 | Aufgabe 14 | ||
Bei 2 Dimensionen muss | Bei 2 Dimensionen muss <math>\left(\begin{array}{l} | ||
K \\ | |||
2 | |||
\end{array}\right) \geq 2 * K * 2</math> gelten, also muss <math>K \geq 9</math> sein. | |||
Bei 3 Dimensionen muss | Bei 3 Dimensionen muss <math>\left(\begin{array}{l} | ||
K \\ | |||
2 | |||
\end{array}\right) \geq 2 * K * 3</math>, also muss <math>K \geq 13</math> sein. | |||
Aufgabe 15 | Aufgabe 15 | ||
| Zeile 290: | Zeile 322: | ||
<ol style="list-style-type: lower-alpha;"> | <ol style="list-style-type: lower-alpha;"> | ||
<li><p>Standardisierte Variablen haben Varianzen gleich Eins; die mittels Hauptachsentransformation rotierten Komponenten haben daher ebenfalls im Durchschnitt eine Varianz gleich Eins; es wird daher eine Varianzsumme gleich Acht aufgeteilt; die drei Achsen mit der höchsten Varianz haben demnach zumindest eine Varianzsumme größer als Drei, und…</p></li> | <li><p>Standardisierte Variablen haben Varianzen gleich Eins; die mittels Hauptachsentransformation rotierten Komponenten haben daher ebenfalls im Durchschnitt eine Varianz gleich Eins; es wird daher eine Varianzsumme gleich Acht aufgeteilt; die drei Achsen mit der höchsten Varianz haben demnach zumindest eine Varianzsumme größer als Drei, und…</p></li> | ||
<li><p>…erklären damit mindestens | <li><p>…erklären damit mindestens <math>\frac{3}{8}=37,5 \%</math> der Varianzsumme. Bei hochkorrelierten Variablen sollte die Varianzerklärung jedoch wesentlich höher liegen.</p></li> | ||
<li><p>Eine Varianzerklärung von 74% bedeutet, dass maximal fünf Achsen gewählt werden, da bei den besten sechs Achsen der erklärte Anteil jedenfalls zumindest | <li><p>Eine Varianzerklärung von 74% bedeutet, dass maximal fünf Achsen gewählt werden, da bei den besten sechs Achsen der erklärte Anteil jedenfalls zumindest <math>\frac{6}{8}=75 \%</math>wäre.</p></li> | ||
</ol> | </ol> | ||
Aufgabe 16 | Aufgabe 16 | ||
<math display="block"> | |||
\begin{array}{lr} | |||
h_{2}^{2}=0,843^{2}+(-0,160)^{2}=73,6 \% ; & h_{3}^{2}=0,929^{2}+(-0,254)^{2}=92,7 \% \\ | |||
h_{4}^{2}=0,342^{2}+0,936^{2}=99,3 \% ; h_{5}^{2}=0,277^{2}+0,957^{2}=99,2 \% & | |||
\end{array} | |||
</math> | |||
Die errechneten Kommunalitäten finden sich alle in der Hauptdiagonale der reproduzierten Korrelationsmatrix. „Haltbarkeit“ wird durch die gewählten Komponenten am besten erklärt (99,3%). | Die errechneten Kommunalitäten finden sich alle in der Hauptdiagonale der reproduzierten Korrelationsmatrix. „Haltbarkeit“ wird durch die gewählten Komponenten am besten erklärt (99,3%). | ||
Lösungen zu den Wiederholungsaufgaben | == Lösungen zu den Wiederholungsaufgaben == | ||
'''Lektion 1''' | '''Lektion 1''' | ||
| Zeile 305: | Zeile 342: | ||
<u>Aufgabe 1</u> | <u>Aufgabe 1</u> | ||
Da die Modellvoraussetzungen erfüllt sind, kann die geschätzte lineare Beziehung grundsätzlich vernünftig interpretiert werden, jedoch weist das niedrige Bestimmtheitsmaß auf eine schlechte Voraussage durch die erklärenden Variablen hin. Die Korrelation zwischen beobachteten Werten der Zielvariable und den geschätzten Werten beträgt lediglich | Da die Modellvoraussetzungen erfüllt sind, kann die geschätzte lineare Beziehung grundsätzlich vernünftig interpretiert werden, jedoch weist das niedrige Bestimmtheitsmaß auf eine schlechte Voraussage durch die erklärenden Variablen hin. Die Korrelation zwischen beobachteten Werten der Zielvariable und den geschätzten Werten beträgt lediglich <math>\pm \sqrt{0,1}=\pm 0,32</math>. | ||
<u>Aufgabe 2</u> | <u>Aufgabe 2</u> | ||
| Zeile 317: | Zeile 354: | ||
<u>Aufgabe 3</u> | <u>Aufgabe 3</u> | ||
Grundsätzlich ist der Einfluss einer Variablen, die einmal ein positives und einmal ein negatives Vorzeichen annimmt, fraglich. Man weiß nicht, ob der Einfluss nun positiv oder negativ ist (oder überhaupt Null?). Das trifft für die Variablen, zu denen die Koeffizienten | Grundsätzlich ist der Einfluss einer Variablen, die einmal ein positives und einmal ein negatives Vorzeichen annimmt, fraglich. Man weiß nicht, ob der Einfluss nun positiv oder negativ ist (oder überhaupt Null?). Das trifft für die Variablen, zu denen die Koeffizienten <math>\widehat{\beta_{1}}</math> und <math>\widehat{\beta_{2}}</math> geschätzt worden sind, zu. Auch <math>\widehat{\beta_{3}}</math> ist fraglich. Objektiv lässt sich das nachprüfen, indem jeweils der Mittelwert über die drei Stichproben der Standardabweichung gegenübergestellt wird: | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! width="36%" | | ! width="36%" | | ||
! width="12%" | | ! width="12%" | <math>\widehat{\beta_{0}}</math> | ||
! width="12%" | | ! width="12%" | <math>\widehat{\beta_{1}}</math> | ||
! width="12%" | | ! width="12%" | <math>\widehat{\beta_{2}}</math> | ||
! width="12%" | | ! width="12%" | <math>\widehat{\beta_{3}}</math> | ||
! width="12%" | | ! width="12%" | <math>\widehat{\beta_{4}}</math> | ||
|- | |- | ||
| Mittelwert | | Mittelwert | ||
| Zeile 390: | Zeile 427: | ||
<u>Aufgabe 5</u> | <u>Aufgabe 5</u> | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! width="30%" | Schritt Nr. | ! width="30%" | Schritt Nr. | ||
! width="30%" | Partition | ! width="30%" | Partition | ||
| Zeile 411: | Zeile 448: | ||
| 7,57 | | 7,57 | ||
|} | |} | ||
[[ | [[Datei:Mt422 a4.png|300px|none|thumb]] | ||
'''Lektion 4''' | '''Lektion 4''' | ||
| Zeile 429: | Zeile 467: | ||
<u>Aufgabe 3</u> | <u>Aufgabe 3</u> | ||
D: | D: <math>x_{41}^{+}=8,69 ; x_{42}^{+}=-12,34</math>; | ||
E: | E: <math>x_{51}^{+}=0,04 ; x_{52}^{+}=5,00</math> | ||
<u><br> | <u><br> | ||
Aufgabe 4</u> | Aufgabe 4</u> | ||
Die Disparitäten bilden eine monoton nicht fallende Funktion in | Die Disparitäten bilden eine monoton nicht fallende Funktion in <math>u_{k l}</math>. Daher sind (1) die richtigen Disparitäten. | ||
Das Stressmaß beträgt: | Das Stressmaß beträgt: <math>S T R E S S_{1}=\sqrt{\frac{\sum\left(d_{k !}-\alpha_{k !}^{2}\right)^{2}}{\sum d_{k !}^{2}}}=\sqrt{\frac{2,5}{91}}=0,17</math>. | ||
Daher kann die gefundene Konfiguration nur als „ausreichend“ bezeichnet werden. | Daher kann die gefundene Konfiguration nur als „ausreichend“ bezeichnet werden. | ||
| Zeile 448: | Zeile 486: | ||
Die Residuen der Korrelationen sind wie folgt: | Die Residuen der Korrelationen sind wie folgt: | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! width="21%" | | ! width="21%" | | ||
! width="22%" | Kaloriengehalt | ! width="22%" | Kaloriengehalt | ||
| Zeile 493: | Zeile 531: | ||
Nach dem Kaiser-Kriterium werden nur Komponenten gewählt, die einen Eigenwert größer Eins haben, also überdurchschnittlich beitragen. Im Beispiel wäre das nur die erste Komponente. | Nach dem Kaiser-Kriterium werden nur Komponenten gewählt, die einen Eigenwert größer Eins haben, also überdurchschnittlich beitragen. Im Beispiel wäre das nur die erste Komponente. | ||
Screeplot: Von rechts kommend wird der Linienverlauf erstmals merkbar an der Stelle | Screeplot: Von rechts kommend wird der Linienverlauf erstmals merkbar an der Stelle <math>x=3</math> abgelenkt. Das würde für zwei Komponenten sprechen. | ||
[[Datei:Mt422 a5.png|300px|none|thumb]] | |||
<u><br> | <u><br> | ||
Aufgabe 3</u> | Aufgabe 3</u> | ||
[[ | [[Datei:Mt422 a6.png|300px|none|thumb]] | ||
Die Darstellung zeigt, welche Variablen in den beiden Komponenten hoch laden. Komponente 1 fasst im wesentlichen die Variablen „Fettsäuren“, „Vitamingehalt“ und „Kaloriengehalt“, die untereinander hoch korrelieren zusammen. Haltbarkeit und Preis sind hier vernachlässigbar, jedoch am ehesten für Komponente 2 repräsentativ. Hier wird deutlich, was hohe bzw. niedrige Werte der beiden Komponenten bei den verschiedenen Produkten bedeuten. | Die Darstellung zeigt, welche Variablen in den beiden Komponenten hoch laden. Komponente 1 fasst im wesentlichen die Variablen „Fettsäuren“, „Vitamingehalt“ und „Kaloriengehalt“, die untereinander hoch korrelieren zusammen. Haltbarkeit und Preis sind hier vernachlässigbar, jedoch am ehesten für Komponente 2 repräsentativ. Hier wird deutlich, was hohe bzw. niedrige Werte der beiden Komponenten bei den verschiedenen Produkten bedeuten. | ||
| Zeile 516: | Zeile 553: | ||
<u>Aufgabe 3</u> | <u>Aufgabe 3</u> | ||
In Beispiel 15 werden die paarweisen Kovarianzen/Korrelationen von sechs verschiedenen Variablen verwertet. Dies sind | In Beispiel 15 werden die paarweisen Kovarianzen/Korrelationen von sechs verschiedenen Variablen verwertet. Dies sind <math>\frac{6 *(6+1)}{2}=21</math>. Da nur 9 Parameter geschätzt werden, ist das Gleichungssystem lösbar. | ||
Aktuelle Version vom 20. Jänner 2022, 13:31 Uhr
Lösungen zu den Aufgaben und zu den Wiederholungsaufgaben
Lösungen zu den Aufgaben
Aufgabe 1
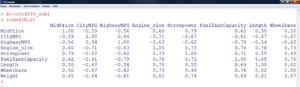
Wie auch schon Abbildung 2 vermuten lässt, ist – wenig überraschend – der lineare Zusammenhang zwischen dem Benzinverbrauch in der Stadt und auf der Autobahn betragsmäßig am größten (0,94).
Aufgabe 2
Die Regressionskoeffizienten ändern sich geringfügig. Die lineare Korrelation zwischen den Vorhersagewerten und der Originalvariable verändert sich durch Wegnahme einer einzigen Beobachtung immerhin von 0,80 auf 0,83.
Aufgabe 3
Analog zum Beispiel:
| Versuch | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Sorte 1 | 0,229 | 6,629 | -0,571 | -4,871 | -1,471 | 2,029 | -1,971 |
| Sorte 2 | -4,660 | 3,640 | 2,240 | 1,040 | -2,260 | - | - |
| Sorte 3 | 3,050 | -5,350 | -3,450 | 4,450 | 2,150 | -0,850 | - |
Draht Nr. 2 von Sorte 1 weicht am stärksten von der Prognose ab.
Aufgabe 4
| Datensatz 1 | Datensatz 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Beobachtung Nr. |
|
X1 | X2 | X3 | Beobachtung Nr. | X1 | X2 | X3 |
| 1 |
|
3 | 14 | 5 | 1 | 4 | 14 | 7 |
| 2 |
|
3 | 14 | 5 | 2 | 5 | 2 | 3 |
| 3 |
|
3 | 14 | 5 | 3 | 6 | 8 | 3 |
| 4 |
|
3 | 14 | 5 | 4 | 7 | 1 | 7 |
| 5 |
|
3 | 14 | 5 | 5 | 8 | 5 | 10 |
Datensatz 1 hat Bestimmtheitsmaß 100%, da alle drei Spalten (Variablen) keine Varianz aufweisen und die Mittelwerte unterschiedlich sind. Die Gesamtstreuung der Daten entfällt daher vollständig auf die Streuung zwischen den Gruppen(mittelwerten). Datensatz 2 hat Bestimmtheitsmaß 0, da alle drei Spalten den gleichen Mittelwert und Varianzen größer als Null aufweisen. Die Gesamtstreuung der Daten entfällt daher vollständig auf die Streuung innerhalb der einzelnen Gruppen.
Aufgabe 5
Bestimmtheitsmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R^{2}=\frac{Q Z}{Q T}=\frac{Q Z}{Q Z+Q I}=\frac{123,744}{123,744+199,361}=38,3 \%}
Aufgabe 6
Die Testentscheidung, ob H0 oder H1 gewählt werden soll, kann auf zwei Arten erfolgen.
Entweder es wird die Prüfgröße (im Beispiel 4,655) mit einem kritischen Wert, der von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} abhängt und einer Verteilungstabelle entstammt verglichen (im Beispiel 3,68). In diesem Fall wird für H1 entschieden, da 4,655>3,68. Im umgekehrten Fall wäre für H0 entschieden worden.
Die von Softwarepaketen durchgeführte, äquivalente Vorgehensweise dazu ist die Berechnung des p-Werts. Es wird also berechnet, mit welcher Wahrscheinlichkeit die F-Verteilung (im Beispiel mit 2 und 15 Freiheitsgraden) einen Wert größer als die Prüfgröße erzielt (in Excel: „FVERT(4,655;2;15)“ was als p-Wert 0,0267 liefert). Anschließend erfolgt die Testentscheidung, indem der p-Wert mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} verglichen wird. Im vorliegenden Fall gilt: p-WertFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle <\alpha=5%} , daher Entscheidung für H1. Der Vorteil nach letzterer Methode ist, dass auf einen Blick bestimmt werden kann, ab welchem der Test für H1 entscheidet. Der p-Wert wird auch bei Publikationen verwendet.
Aufgabe 7
Der p-Wert der Varianzanalyse ist 0,0264. Testet man auf 1%-Niveau, muss der p-Wert mit 1% verglichen werden. Da 0,0264>0,01 wird in diesem Fall die Nullhypothese H0 beibehalten.
Aufgabe 8
Alpha=5%: in Excel: „FINV(0,05;2;15)“ liefert 3,68 (vgl. Aufgabe 6)
Alpha=1%: in Excel: „FINV(0,01;2;15)“ liefert 6,36
Aufgabe 9
(PP niedrig) (PP mittel) (PP hoch) (Postwurf) (Anzeigen)
Interaktionen:
Aufgabe 10
| Objektpaar | |||||||
|---|---|---|---|---|---|---|---|
|
|
|
12 | 13 | 14 | 23 | 24 | 34 |
| L1-Distanz | Wert | 12 | 11 | 10 | 5 | 4 | 9 |
|
|
Rang | 6 | 5 | 4 | 2 | 1 | 3 |
| L2-Distanz | Wert | 7,87 | 6,71 | 8,12 | 3,61 | 2,45 | 5,74 |
|
|
Rang | 5 | 4 | 6 | 2 | 1 | 3 |
Die Rangfolgen der Distanzen zwischen den Objektpaaren sind nicht für beide Distanzmaße ident.
Aufgabe 11
Bei vier Objekten sind lt. Bell’schen Zahlen 15 Partitionen möglich:
| 1 / 2 / 3 / 4 | 12 / 3 / 4 | 13 / 2 / 4 | 14 / 2 / 3 | 23 / 1 / 4 |
|---|---|---|---|---|
| 24 / 1 / 3 | 34 / 1 / 2 | 12 / 34 | 13 / 24 | 14 / 23 |
| 123 / 4 | 124 / 3 | 134 / 2 | 234 / 1 | 1234 |
Aufgabe 12
Vollständige Rangordnung: ]; Tetradenmethode:
Bei 105 Vergleichen werden die Paare schrittweise sortiert (alle Paare werden z.B. auf Kärtchen präsentiert; diese werden vorerst in ähnliche und unähnliche Paare geteilt; die Untergruppen werden weiter geteilt). Bei 5460 Vergleichen muss jede Person nur einige Vergleiche durchführen.
Aufgabe 13
Die Distanz zwischen B und D ist am größten, jene zwischen A und D am kleinsten. Daher müssen die drei Objekte beispielsweise wie folgt liegen:
| B | A | D |
|---|
C und E müssten an den freien Stellen eingetragen werden. Nachdem die Distanz AE lt. Angabe größer als DE sein muss, ergibt sich hier ein Widerspruch.
Aufgabe 14
Bei 2 Dimensionen muss gelten, also muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K \geq 9} sein.
Bei 3 Dimensionen muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{l} K \\ 2 \end{array}\right) \geq 2 * K * 3} , also muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K \geq 13} sein.
Aufgabe 15
Standardisierte Variablen haben Varianzen gleich Eins; die mittels Hauptachsentransformation rotierten Komponenten haben daher ebenfalls im Durchschnitt eine Varianz gleich Eins; es wird daher eine Varianzsumme gleich Acht aufgeteilt; die drei Achsen mit der höchsten Varianz haben demnach zumindest eine Varianzsumme größer als Drei, und…
…erklären damit mindestens Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{3}{8}=37,5 \%} der Varianzsumme. Bei hochkorrelierten Variablen sollte die Varianzerklärung jedoch wesentlich höher liegen.
Eine Varianzerklärung von 74% bedeutet, dass maximal fünf Achsen gewählt werden, da bei den besten sechs Achsen der erklärte Anteil jedenfalls zumindest Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{6}{8}=75 \%} wäre.
Aufgabe 16
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{lr} h_{2}^{2}=0,843^{2}+(-0,160)^{2}=73,6 \% ; & h_{3}^{2}=0,929^{2}+(-0,254)^{2}=92,7 \% \\ h_{4}^{2}=0,342^{2}+0,936^{2}=99,3 \% ; h_{5}^{2}=0,277^{2}+0,957^{2}=99,2 \% & \end{array} }
Die errechneten Kommunalitäten finden sich alle in der Hauptdiagonale der reproduzierten Korrelationsmatrix. „Haltbarkeit“ wird durch die gewählten Komponenten am besten erklärt (99,3%).
Lösungen zu den Wiederholungsaufgaben
Lektion 1
Aufgabe 1
Da die Modellvoraussetzungen erfüllt sind, kann die geschätzte lineare Beziehung grundsätzlich vernünftig interpretiert werden, jedoch weist das niedrige Bestimmtheitsmaß auf eine schlechte Voraussage durch die erklärenden Variablen hin. Die Korrelation zwischen beobachteten Werten der Zielvariable und den geschätzten Werten beträgt lediglich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pm \sqrt{0,1}=\pm 0,32} .
Aufgabe 2
Die Korrelation ist 1
Die Varianz der Residuen ist gleich Null
Alle Punkte liegen in einer (Hyper-)Ebene
Aufgabe 3
Grundsätzlich ist der Einfluss einer Variablen, die einmal ein positives und einmal ein negatives Vorzeichen annimmt, fraglich. Man weiß nicht, ob der Einfluss nun positiv oder negativ ist (oder überhaupt Null?). Das trifft für die Variablen, zu denen die Koeffizienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{1}}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{2}}} geschätzt worden sind, zu. Auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{3}}} ist fraglich. Objektiv lässt sich das nachprüfen, indem jeweils der Mittelwert über die drei Stichproben der Standardabweichung gegenübergestellt wird:
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{0}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{1}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{2}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{3}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{4}}} | |
|---|---|---|---|---|---|
| Mittelwert | -0,30 | -0,04 | 19,93 | 23,00 | 0,47 |
| Standardabweichung | 0,02 | 0,07 | 2,22 | 20,97 | 2,58 |
| Mittelwert/Standardabweichung | -19,86 | -0,57 | 8,98 | 1,10 | 0,18 |
Die letzte Zeile zeigt auch die Prüfgröße, die üblicherweise bei einem statistischen Test für die Regressionsschätzer verwendet wird. Alle Zahlen nahe Null (insbesondere zwischen -2 und 2) deuten daraufhin, dass der zugrundeliegende Populations-Parameter eventuell nicht von Null verschieden ist.
Lektion 2
Aufgabe 1
Einerseits kann durch die Aufspaltung der gesamten Quadratsumme angegeben werden, welcher Anteil an der Gesamtstreuung durch die Faktoren erklärt wird (deskriptiv). Andererseits bilden die aufgespaltenen Quadratsummen „Zwischen“ und „Innerhalb“ die Basis für den statistischen Test, ob überzufällige Mittelwertsunterschiede existieren (induktiv).
Aufgabe 2
Weil sonst (insbesondere bei kleinen Stichproben) die Prüfgröße nicht F-verteilt ist und die Varianzanalyse ungültig ist.
Aufgabe 3
- Ja. Ein signifikanter Effekt ist bei einer größeren Stichprobe jedenfalls auch signifikant.
- Müsste konkret nachgeprüft werden. Je kleiner der Stichprobenumfang, desto eher wird für H0 entschieden, wenn alles andere konstant gehalten wird.
- Falls der p-Wert des Tests zwischen 1% und 5% liegt, wäre das Ergebnis nicht signifikant. Wenn er kleiner ist, schon.
Aufgabe 4
Der kritische Wert wird größer, da das 99%-Quantil größer als das 95%-Quantil ist. Dies führt dazu, dass H0 eher beibehalten wird.
Lektion 3
Aufgabe 1
Eine Partition ist ein System von Teilmengen der zu untersuchenden Objekte, wobei alle paarweisen Schnittmengen leer sind und die Vereinigung dieser Teilmengen die Objektmenge ergibt. Das Auffinden der in gewissen Sinne besten Partition ist das Ziel der Clusteranalyse.
Aufgabe 2
Eine Hierarchie ist eine Art Stammbaum, der angibt, in welcher Reihenfolge die Partitionen bei hierarchischen Clusterverfahren vergröbert bzw. verfeinert werden. In der Clusteranalyse ist die übliche Darstellungsform einer Hierarchie ein Dendrogramm.
Aufgabe 3
Bei hierarchischen Verfahren wird ein „Pfad“ abgesucht, der entweder von der Menge aller einelementigen Teilmengen der Untersuchungsobjekte zur Vereinigungsmenge (agglomerative Verfahren) führt, oder den umgekehrten Weg (divisive Verfahren). Hierbei werden der Reihe nach immer zwei Cluster vereinigt (Vergröberung) oder ein Cluster in zwei Teile aufgespalten (Verfeinerung). Damit wird untersucht, welche Clusteranzahl die beste ist. Bei partitionierenden Verfahren wird im vorhinein festgelegt, wieviele Cluster gewünscht sind und es werden verschiedene Partitionen derselben Clusteranzahl bezüglich eines Kriteriums optimiert.
Aufgabe 4
Von der Startpartition, die 20 Cluster zu je einem Element enthält, bis zur Zielpartition, die einen Cluster mit 20 Elementen enthält werden bei einem agglomerativen Verfahren insgesamt 20 Partitionen untersucht. Gesamt gibt es bei 20 Elementen 51724158235372 Partitionen.
Aufgabe 5
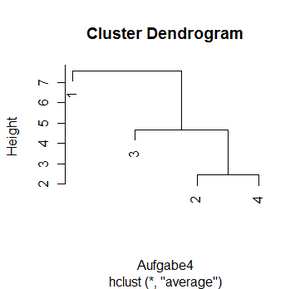
| Schritt Nr. | Partition | Heterogenität |
|---|---|---|
| 0 | 1 / 2 / 3 / 4 | 0 |
| 1 | 1 / 3 / 24 | 2,45 |
| 2 | 1 / 234 | 4,68 |
| 3 | 1234 | 7,57 |
Lektion 4
Aufgabe 1
Die Konfiguration ist die Anordnung der Beobachtungseinheiten in einem gewählten, meist zwei- oder dreidimensionalen Raum. Eine optimale Konfiguration zu finden, sodass ähnliche Objekte nahe bzw. unähnliche Objekte weit entfernt voneinander dargestellt werden ist das Ziel der MDS.
Die Distanz zwischen je zwei Objekten ist ein quantifiziertes Maß für ihre Unähnlichkeit. Je verschiedener eine Person zwei Objekte beurteilt bzw. je größer die Differenz zwischen einzelnen Merkmalen der Objekte sind, desto größer ist ihre Distanz zueinander.
Die Disparitäten sind Rechenhilfsgrößen bei der MDS. Sie modifizieren jede einzelne Distanz in der aktuellen Konfiguration um die kleinstmögliche Differenz, sodass die geforderte Distanzordnung eingehalten werden kann. Bei einer perfekt erstellten Ordnung gibt es keinen Unterschied zwischen den Disparitäten und den Distanzen.
Aufgabe 2
Sowohl die Clusteranalyse, als auch die MDS bewerten Distanzen der Objekte zueinander. Beide Verfahren benötigen nicht die Daten selbst, sondern kommen ausschließlich mit einer Distanzmatrix als Input aus. Die Clusteranalyse versucht, in bestehenden Daten homogene Gruppen zu finden. Ziel der MDS hingegen ist vor allem die Visualisierung der Abstände von Objekten zueinander.
Aufgabe 3
D: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{41}^{+}=8,69 ; x_{42}^{+}=-12,34} ;
E: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{51}^{+}=0,04 ; x_{52}^{+}=5,00}
Aufgabe 4
Die Disparitäten bilden eine monoton nicht fallende Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{k l}} . Daher sind (1) die richtigen Disparitäten.
Das Stressmaß beträgt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S T R E S S_{1}=\sqrt{\frac{\sum\left(d_{k !}-\alpha_{k !}^{2}\right)^{2}}{\sum d_{k !}^{2}}}=\sqrt{\frac{2,5}{91}}=0,17} .
Daher kann die gefundene Konfiguration nur als „ausreichend“ bezeichnet werden.
Lektion 5
Aufgabe 1
Die Residuen der Korrelationen sind wie folgt:
| Kaloriengehalt | Vitamingehalt | Haltbarkeit | Preis | |
|---|---|---|---|---|
| Fettsäuren | 0,115 | -0,033 | -0,003 | -0,003 |
| Kaloriengehalt |
|
0,119 | 0,001 | 0,014 |
| Vitamingehalt |
|
|
0,002 | -0,009 |
| Haltbarkeit |
|
|
|
0,007 |
Die Korrelation zwischen Kaloriengehalt und Vitamingehalt wird mittels der beiden gewählten Komponenten am schlechtesten erklärt.
Aufgabe 2
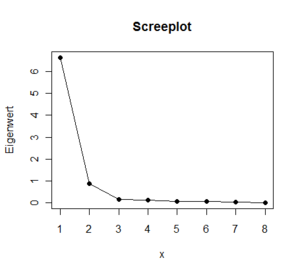
Für zumindest 90% der Varianz sind zwei Komponenten notwendig.
Nach dem Kaiser-Kriterium werden nur Komponenten gewählt, die einen Eigenwert größer Eins haben, also überdurchschnittlich beitragen. Im Beispiel wäre das nur die erste Komponente.
Screeplot: Von rechts kommend wird der Linienverlauf erstmals merkbar an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=3} abgelenkt. Das würde für zwei Komponenten sprechen.
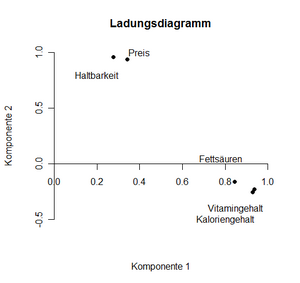
Aufgabe 3
Die Darstellung zeigt, welche Variablen in den beiden Komponenten hoch laden. Komponente 1 fasst im wesentlichen die Variablen „Fettsäuren“, „Vitamingehalt“ und „Kaloriengehalt“, die untereinander hoch korrelieren zusammen. Haltbarkeit und Preis sind hier vernachlässigbar, jedoch am ehesten für Komponente 2 repräsentativ. Hier wird deutlich, was hohe bzw. niedrige Werte der beiden Komponenten bei den verschiedenen Produkten bedeuten.
Lektion 6
Aufgabe 1
Vgl. Abbildung 39.
Aufgabe 2
Mess- und Strukturmodell sind die Komponenten eines allgemeinen Strukturgleichungsmodells. Das Messmodell gibt an, in welcher Form die latenten Faktoren durch die beobachteten Merkmale beschrieben/ gemessen werden können. Das Strukturmodellgibt an, wie die latenten Variablen untereinander wirken.
Aufgabe 3
In Beispiel 15 werden die paarweisen Kovarianzen/Korrelationen von sechs verschiedenen Variablen verwertet. Dies sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{6 *(6+1)}{2}=21} . Da nur 9 Parameter geschätzt werden, ist das Gleichungssystem lösbar.