Methoden der Datenanalyse - Clusteranalyse: Unterschied zwischen den Versionen
| (18 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 27: | Zeile 27: | ||
=== Ähnlichkeit und Distanzmaße === | === Ähnlichkeit und Distanzmaße === | ||
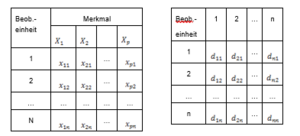
Um Beobachtungseinheiten gruppieren zu können, muss zunächst festgestellt werden, wie ähnlich sich die einzelnen Beobachtungen sind. Es muss also ein Maß für die Ähnlichkeit zwischen je zwei Beobachtungen definiert werden. Analog kann man statt Ähnlichkeiten auch Distanzen zwischen je zwei Beobachtungen angeben, die sich zu den Ähnlichkeiten in umgekehrter Relation verhalten. Der Ausgangspunkt einer Clusteranalyse ist bei den meisten Softwarepaketen daher entweder die Datenmatrix oder eine daraus abgeleitete Ähnlichkeits- oder Distanzmatrix (Abbildung 15). Da Ähnlichkeits- und Distanzmaße nur eine unterschiedliche Sicht des selben Sachverhalts ist, werden in weiterer Folge nur Distanzmaße betrachtet. | Um Beobachtungseinheiten gruppieren zu können, muss zunächst festgestellt werden, wie ähnlich sich die einzelnen Beobachtungen sind. Es muss also ein Maß für die Ähnlichkeit zwischen je zwei Beobachtungen definiert werden. Analog kann man statt Ähnlichkeiten auch Distanzen zwischen je zwei Beobachtungen angeben, die sich zu den Ähnlichkeiten in umgekehrter Relation verhalten. Der Ausgangspunkt einer Clusteranalyse ist bei den meisten Softwarepaketen daher entweder die Datenmatrix oder eine daraus abgeleitete Ähnlichkeits- oder Distanzmatrix (Abbildung 15). Da Ähnlichkeits- und Distanzmaße nur eine unterschiedliche Sicht des selben Sachverhalts ist, werden in weiterer Folge nur Distanzmaße betrachtet. | ||
<span id="_Ref249872823" class="anchor"></span> | <span id="_Ref249872823" class="anchor"></span> | ||
<span class="anchor"></span>[[file:img1642170327751.png|300px|none|thumb|Notation für die Datenmatrix | <span class="anchor"></span>[[file:img1642170327751.png|300px|none|thumb|Notation für die Datenmatrix und für die daraus berechnete Distanzmatrix]] | ||
Die Forderungen für ein Distanzmaß sind folgende: | Die Forderungen für ein Distanzmaß sind folgende: | ||
<math display="block"> | |||
- $d_{i i}=0 \forall i=1, \ldots, n$ | |||
- $d_{i j} \geq 0 \forall i \neq j=1, \ldots, n$ | |||
- $d_{i j}=d_{j i} \forall i, j=1, \ldots, n$ | |||
</math> | |||
Weiters wird zumeist gefordert, dass das Distanzmaß invariant bezüglich einer Klasse von bestimmten Transformationen ist (Umskalierungen, Verschiebungen). Es soll ja keinen Unterschied machen ob Werte in cm oder m, in kg oder g, in Schilling oder Euro gemessen werden. | Weiters wird zumeist gefordert, dass das Distanzmaß invariant bezüglich einer Klasse von bestimmten Transformationen ist (Umskalierungen, Verschiebungen). Es soll ja keinen Unterschied machen ob Werte in cm oder m, in kg oder g, in Schilling oder Euro gemessen werden. | ||
Bei metrischen Merkmalen werden nun am häufigsten die Minkowski-q-Metriken (L<sub>q</sub>-Distanzen) als Distanzmaß verwendet. Diese sind gegeben durch | Bei metrischen Merkmalen werden nun am häufigsten die Minkowski-q-Metriken (L<sub>q</sub>-Distanzen) als Distanzmaß verwendet. Diese sind gegeben durch | ||
<math display="block"> | |||
d_{m n}=\left(\sum_{i=1}^{p}\left|x_{i m}-x_{i n}\right|^{q}\right)^{1 / q} \text { für } q \geq 1 . | |||
</math> | |||
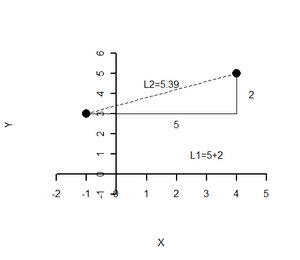
[[file:img1642150545739.png|300px|none|thumb| | [[file:img1642150545739.png|300px|none|thumb| L1 bzw. die L2 Distanz für zwei Datenpunkte]] | ||
Man beachte, dass alle L<sub>q</sub>-Distanzen (außer | Man beachte, dass alle L<sub>q</sub>-Distanzen (außer <math>q=2</math>) nicht invariant gegenüber Drehungen des Koordinatenkreuzes (orthogonale lineare Transformationen) sind. | ||
Ein alternatives Distanzmaß ist die „Mahalanobisdistanz“, der bei stark korrelierten Variablen der Vorzug gegeben wird. | Ein alternatives Distanzmaß ist die „Mahalanobisdistanz“, der bei stark korrelierten Variablen der Vorzug gegeben wird. | ||
| Zeile 128: | Zeile 60: | ||
Für einige Clusteralgorithmen ist nach Kenntnis der Distanzmatrix nur mehr die Reihenfolge der Distanzen zwischen je zwei Datenpunkten relevant. | Für einige Clusteralgorithmen ist nach Kenntnis der Distanzmatrix nur mehr die Reihenfolge der Distanzen zwischen je zwei Datenpunkten relevant. | ||
{| | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Aufgabe 10''' | ! width="100%" | '''Aufgabe 10''' | ||
| Zeile 141: | Zeile 73: | ||
Wichtig im Zusammenhang mit der Clusteranalyse ist nun auch der Begriff der „Klassifikation“. Eine Klassifikation Ω ist ein System von Teilmengen (Klassen, Gruppen, Cluster) der Menge aller Beobachtungseinheiten (Objekte). In Bezug auf die Clusteranalyse fordert man zumeist, dass eine Klassifikation disjunkt und exhaustiv ist. Ersteres meint, dass jede Beobachtung zu höchstens einer Teilmenge zugeordnet wird. Zweiteres meint, dass jede Beobachtung zu mindestens einer Teilmenge zugeordnet wird. Eine Klassifikation, die disjunktiv und exhaustiv ist, nennt man „Partition“. | Wichtig im Zusammenhang mit der Clusteranalyse ist nun auch der Begriff der „Klassifikation“. Eine Klassifikation Ω ist ein System von Teilmengen (Klassen, Gruppen, Cluster) der Menge aller Beobachtungseinheiten (Objekte). In Bezug auf die Clusteranalyse fordert man zumeist, dass eine Klassifikation disjunkt und exhaustiv ist. Ersteres meint, dass jede Beobachtung zu höchstens einer Teilmenge zugeordnet wird. Zweiteres meint, dass jede Beobachtung zu mindestens einer Teilmenge zugeordnet wird. Eine Klassifikation, die disjunktiv und exhaustiv ist, nennt man „Partition“. | ||
{| | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Aufgabe 11''' | ! width="100%" | '''Aufgabe 11''' | ||
Welche Partitionen können zu den Daten in Aufgabe 10 gefunden werden? | Welche Partitionen können zu den Daten in Aufgabe 10 gefunden werden? | ||
|} | |} | ||
Die Anzahl der möglichen verschiedenen Partitionen von | Die Anzahl der möglichen verschiedenen Partitionen von <math>n</math> Elementen ist durch die sogenannten BELLschen Zahlen <ref>Benannt nach dem schottisch-amerikanischen Mathematiker Eric Temple Bell. Berechenbar nach der Rekursionsformel <math>B_{n+1}=\sum_{k=0}^{n}\left(\begin{array}{l} n k \end{array}\right) B_{k} \text { mit } B_{0}=B_{1}=1</ref> gegeben. Diese „explodieren“ bei wachsender Anzahl von Beobachtungseinheiten. | ||
<span id="_Ref249872936" class="anchor"></span>Tabelle 3: Bell'sche Zahlen | <span id="_Ref249872936" class="anchor"></span>Tabelle 3: Bell'sche Zahlen | ||
| Zeile 225: | Zeile 157: | ||
== Hierarchische Verfahren == | == Hierarchische Verfahren == | ||
=== Grundbegriffe === | === Grundbegriffe === | ||
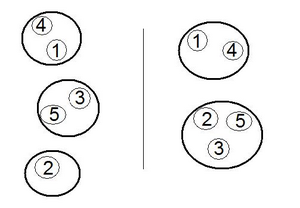
Hierarchische Verfahren stellen Hierarchien von Partitionen auf. Bewegt man sich in eine Richtung der Hierarchie, unterscheiden sich „benachbarte“ Partitionen dadurch, dass entweder zwei Klassen miteinander „verschmolzen“ werden („Vergröberung“) oder eine Klasse in zwei aufgespalten wird („Verfeinerung“). In Abbildung 17 erhält man die Partition rechts durch Vergröberung der Partition links bzw. jene links durch Verfeinerung der rechten. | Hierarchische Verfahren stellen Hierarchien von Partitionen auf. Bewegt man sich in eine Richtung der Hierarchie, unterscheiden sich „benachbarte“ Partitionen dadurch, dass entweder zwei Klassen miteinander „verschmolzen“ werden („Vergröberung“) oder eine Klasse in zwei aufgespalten wird („Verfeinerung“). In Abbildung 17 erhält man die Partition rechts durch Vergröberung der Partition links bzw. jene links durch Verfeinerung der rechten. | ||
| Zeile 241: | Zeile 173: | ||
<li><p>Frage 2: In wieviele und welche Gruppen sollen die Daten nun aufgeteilt werden?</p></li> | <li><p>Frage 2: In wieviele und welche Gruppen sollen die Daten nun aufgeteilt werden?</p></li> | ||
</ul> | </ul> | ||
=== Methoden zur Agglomeration === | === Methoden zur Agglomeration === | ||
| Zeile 257: | Zeile 190: | ||
Das Ward-Kriterium fusioniert jene beiden Klassen, bei denen ein minimaler Zuwachs an Varianz innerhalb der Klassen erreicht wird. | Das Ward-Kriterium fusioniert jene beiden Klassen, bei denen ein minimaler Zuwachs an Varianz innerhalb der Klassen erreicht wird. | ||
{| | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 4''' | ! style="text-align: left;" width="100%" | '''Beispiel 4''' | ||
Betrachten wir nochmals die Daten aus Aufgabe 10. Ziel ist nun, eine hierarchische Clusteranalyse mit den Daten durchzuführen. Wir wählen als Abstand die L<sub>2</sub>-Distanz und als Agglomerations-Methode „Complete Linkage“. | Betrachten wir nochmals die Daten aus Aufgabe 10. Ziel ist nun, eine hierarchische Clusteranalyse mit den Daten durchzuführen. Wir wählen als Abstand die L<sub>2</sub>-Distanz und als Agglomerations-Methode „Complete Linkage“. | ||
Zuerst Beginn besteht die Startpartition | Zuerst Beginn besteht die Startpartition <math>\mathcal{A}_{1}=\{\{1\},\{2\},\{3\},\{4\}\}</math>. Nun wird die Distanzmatrix berechnet: | ||
<math>d_{12}=\sqrt{(8-6)^{2}+(9-2)^{2}+(6-3)^{2}}=\sqrt{62}</math> | |||
{| | {| style="border-collapse: collapse; background-color: rgb(149, 165, 166); float: left;" border="1" | ||
! width="31%" | Beob.-Einheit | ! width="31%" | Beob.-Einheit | ||
! width="22%" | 2 | ! width="22%" | 2 | ||
| Zeile 273: | Zeile 206: | ||
|- | |- | ||
| 1 | | 1 | ||
| | | <math>\sqrt{62}</math> | ||
| | | <math>\sqrt{45}</math> | ||
| | | <math>\sqrt{66}</math> | ||
|- | |- | ||
| 2 | | 2 | ||
| | | | ||
<br> | <br> | ||
| | | <math>\sqrt{13}</math> | ||
| | | <math>\sqrt{6}</math> | ||
|- | |- | ||
| 3 | | 3 | ||
| Zeile 288: | Zeile 221: | ||
| | | | ||
<br> | <br> | ||
| | | <math>\sqrt{33}</math> | ||
|} | |} | ||
Der Heterogenitätsindex zu dieser Vergröberung ist gleich der maximal in einem Cluster vorkommenden Distanz. Daher: | |||
Die Beobachtungen 2 und 4 sind jene mit dem geringsten Abstand zueinander. Diese werden zur folgenden Partition fusioniert. Damit hat die erste Vergröberung stattgefunden.<math>\mathcal{A}_{1}=\{\{1\},\{2,4\},\{3\}\}</math>Der Heterogenitätsindex zu dieser Vergröberung ist gleich der maximal in einem Cluster vorkommenden Distanz. Daher: <math>h_{1}=\sqrt{6}</math> . | |||
Nach der „Complete Linkage“-Methode werden nun die neuen Abstände definiert, beispielsweise | Nach der „Complete Linkage“-Methode werden nun die neuen Abstände definiert, beispielsweise | ||
<math>d_{1,(2,4)}=\max \left(d_{12}, d_{14}\right)</math> | |||
{| | {| style="border-collapse: collapse; background-color: rgb(149, 165, 166);" border="1" | ||
! width="27%" | Beob.-Einheit | ! width="27%" | Beob.-Einheit | ||
! width="36%" | (2,4) | ! width="36%" | (2,4) | ||
| Zeile 305: | Zeile 244: | ||
|- | |- | ||
| 1 | | 1 | ||
| | | <math>\max (\sqrt{62}, \sqrt{66})=\sqrt{66}</math> | ||
| | | <math>\sqrt{45}</math> | ||
|- | |- | ||
| (2,4) | | (2,4) | ||
| | | | ||
<br> | <br> | ||
| | | <math>\max (\sqrt{13}, \sqrt{33})=\sqrt{33}</math> | ||
|}Damit findet im nächsten Schritt die Fusion zwischen Beobachtung 3 und dem Cluster bestehend aus 2 und 4 statt. Die neue Partition ist | |}Damit findet im nächsten Schritt die Fusion zwischen Beobachtung 3 und dem Cluster bestehend aus 2 und 4 statt. Die neue Partition ist<math>\mathcal{A}_{1}=\{\{1\},\{2,3,4\}\}</math>und der Heterogenitätsindex zu dieser Vergröberung ist <math>h_{2}=\sqrt{33}</math> | ||
Im letzten Schritt wird zur Partition <math>\mathcal{A}_{1}=\{\{1,2,3,4\}\}</math> fusioniert und <math>h_{3}=\max (\sqrt{66}, \sqrt{45}, \sqrt{33})=\sqrt{66}</math> . | |||
Im letzten Schritt wird zur Partition | |||
|} | |} | ||
| Zeile 358: | Zeile 293: | ||
Sie beträgt | Sie beträgt | ||
<math>L_{1}\left(x \mid \text { Einteilung } 1 ; \widehat{\mu_{2}} ; \widehat{\sigma_{l}}\right)=0,80 \times 0,80 \times 0.29 \times 0.51 \times 0.4 \times 0.88 \times 0.88 \approx 0.03</math>. | |||
Eine andere Partition wurde rechts gewählt. Dort wurden zwei Gruppen unterstellt (die kleinsten drei und die größten vier Beobachtungen). Wieder kann die Likelihood dieser Stichprobe berechnet werden. Diesmal ergibt sich: | Eine andere Partition wurde rechts gewählt. Dort wurden zwei Gruppen unterstellt (die kleinsten drei und die größten vier Beobachtungen). Wieder kann die Likelihood dieser Stichprobe berechnet werden. Diesmal ergibt sich: | ||
<math>L_{2}\left(x \mid \text { Einteilung } 2 ; \hat{\mu}_{\nu} ; \widehat{\sigma}_{2}\right)=0,22 \times 0,28 \times 0.16 \times 0.16 \times 0.19 \times 0.20 \times 0.15 \approx 9 * 10^{-6}</math>. | |||
Gewählt wird nun jene Partition, die die höchste Likelihood liefert. Für die Daten in Abbildung 19 ist die linke Gruppierung die bestmögliche. | Gewählt wird nun jene Partition, die die höchste Likelihood liefert. Für die Daten in Abbildung 19 ist die linke Gruppierung die bestmögliche. | ||
| Zeile 398: | Zeile 333: | ||
Code-Fortsetzung: | Code-Fortsetzung: | ||
[[file: | [[file:mt422_a7.png|300px|none|thumb|Fortsetzung des R-Codes zur Clusteranalyse]] | ||
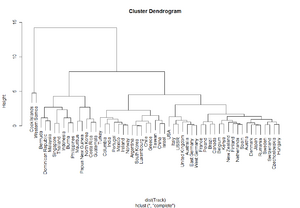
Das erzeugte Objekt „result1“ ist vom Typ „hclust“, beinhaltet daher alle Informationen, die bei einer hierarchischen Clusteranalyse berechnet werden. Es können auf Wunsch mehrere Attribute ausgegeben werden. Wird so ein Objekt mit dem „plot“-Befehl versehen, entsteht das Dendrogramm (Abbildung 22). Die Gruppen sollen nun so gewählt werden, dass sie untereinander homogen und zueinander heterogen sind. Der hier gewählte Kompromiss ist jener, der das Dendrogramm horizontal an der Stelle | Das erzeugte Objekt „result1“ ist vom Typ „hclust“, beinhaltet daher alle Informationen, die bei einer hierarchischen Clusteranalyse berechnet werden. Es können auf Wunsch mehrere Attribute ausgegeben werden. Wird so ein Objekt mit dem „plot“-Befehl versehen, entsteht das Dendrogramm (Abbildung 22). Die Gruppen sollen nun so gewählt werden, dass sie untereinander homogen und zueinander heterogen sind. Der hier gewählte Kompromiss ist jener, der das Dendrogramm horizontal an der Stelle <math>3,1<h<4,2</math> schneidet und sechs Gruppen liefert. Dies wird durch die Funktion „cutree“ (Abbildung 21) erzeugt. Das Ergebnis der Gruppenzuordnung wird sodann unter „partition1“ abgespeichert. | ||
Die beiden weiteren erstellten Partitionen wurden mit dem schon erwähnten k-Means-Algorithmus in R berechnet. Partition 2 verwendet die in Partition 1 gefundenen sechs Klassenschwerpunkte und ordnet jene Datenpunkte um, die näher zu einem anderen als dem eigenen Klassenschwerpunkt liegt. Nach einer Iteration werden die Schwerpunkte wieder neu berechnet. Das Verfahren konvergiert ziemlich schnell. Es müssen kaum Daten umgruppiert werden. | Die beiden weiteren erstellten Partitionen wurden mit dem schon erwähnten k-Means-Algorithmus in R berechnet. Partition 2 verwendet die in Partition 1 gefundenen sechs Klassenschwerpunkte und ordnet jene Datenpunkte um, die näher zu einem anderen als dem eigenen Klassenschwerpunkt liegt. Nach einer Iteration werden die Schwerpunkte wieder neu berechnet. Das Verfahren konvergiert ziemlich schnell. Es müssen kaum Daten umgruppiert werden. | ||
| Zeile 412: | Zeile 347: | ||
<span id="_Ref249873674" class="anchor"></span>Tabelle 4: Länderzuordnung zu den Clustern | <span id="_Ref249873674" class="anchor"></span>Tabelle 4: Länderzuordnung zu den Clustern | ||
{| | {| style="border-collapse: collapse;" border="1" | ||
! width="11%" | Cluster | ! width="11%" | Cluster | ||
! width="88%" | Länder | ! width="88%" | Länder | ||
| Zeile 436: | Zeile 371: | ||
<span class="anchor"></span> | <span class="anchor"></span> | ||
<span class="anchor"></span>[[file:img1642146023596.png|300px|none|thumb|Dendrogramm, L | <span class="anchor"></span>[[file:img1642146023596.png|300px|none|thumb|Dendrogramm, L-Distanz (euklidisch)]] | ||
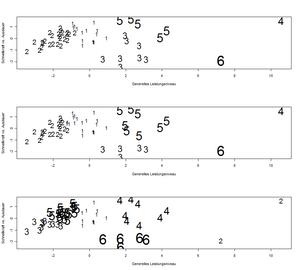
<span id="_Ref249873502" class="anchor"></span> [[file:img1642196418992.png|300px|none|thumb|Darstellung der drei ermittelten unterschiedlichen Partitionen]] | <span id="_Ref249873502" class="anchor"></span> [[file:img1642196418992.png|300px|none|thumb|Darstellung der drei ermittelten unterschiedlichen Partitionen]] | ||
Aktuelle Version vom 29. Jänner 2022, 10:56 Uhr
Clusteranalyse
Das Verständnis der Idee, die hinter clusteranalytischen Verfahren steckt, der Grundbegriffe und der Basis-Algorithmen, sowie die Durchführung einer Clusteranalyse in R sind die wesentlichen Ziele von Lektion 3.
Einführung und Beispielfragestellungen
Während in den beiden vorangegangenen Kapiteln jeweils untersucht wurde, in welcher Form eine oder mehrere Merkmale von einer Reihe von weiteren Merkmalen abhängen, ist man bei der Clusteranalyse daran interessiert, die unterschiedlichen Beobachtungseinheiten (Personen, Unternehmen, Produkte,usw.) in einzelne Gruppen – die sogenannten „Cluster“ – zu teilen. Die Einteilung soll jeweils Beobachtungseinheiten zusammenfassen, die untereinander recht ähnlich und von Einheiten anderer Gruppen recht unterschiedlich sind.
Die Clusteranalyse untersucht nun im Wesentlichen,
- ob und wie gut eine solche Einteilung möglich ist,
- in wieviele Gruppen die beobachtete Stichprobe geteilt werden soll und
- wie die verschiedenen gefundenen Gruppen charakterisiert werden können.
Ziel ist es also, die Daten derart zu strukturieren, damit die einzelnen Merkmalsträger mit verschiedenen „Etiketten“ versehen werden können (“Typenbildung“). Während insbesondere mit der Varianzanalyse, aber auch mit der Regressionsanalyse bestehende Hypothesen geprüft werden können, wird die Clusteranalyse zu den hypothesengenerierenden („exploratorischen“) Verfahren gezählt. Die Daten werden hier meistens ohne Vorstellungen über die statistische Verteilung der einzelnen Gruppen analysiert. Auch können die Variablen der Clusteranalyse beliebiges Skalenniveau aufweisen.
Im folgenden einige Beispiele für den Einsatz von Methoden zur Cluster-Bildung:
- Klassifikation von Verkehrsunfällen anhand von 20 binären Merkmalen (Vogel, 1975), die zum jeweiligen Unfall erhoben wurden, unter anderen anhand der Merkmale „Werktag vs. Wochenende“, „Autobahn vs. Stadtgebiet“, „Alkoholeinfluss ja/nein“,usw..
- Ein Marktforschungsinstitut analysiert Lifestyle und Konsumentenprofile und ermittelt daraus verschiedene Kundensegmente. Die Personen werden dann beispielsweise in „Weltoffene Etablierte“, „Konsumeinsteiger“, „Bodenständige“, usw. eingeteilt. Weiters werden die Marktanteile der einzelnen Segmente berechnet.
- „Semantisches Differential“: Es kann bestimmt werden wie ähnlich sich bestimmte Worte bezüglich ihrer konnotativen Bedeutung sind. Die verschiedenen Dimensionen, die die konnotative Bedeutung beschreiben, werden mittels faktorenanalytischer Methoden (Lektion 5) anhand einer Stichprobe von wertenden Personen bestimmt.
- Klassifikation verschiedener europäischer Länder nach Anteil der Angestellten in Landwirtschaft, Bauwirtschaft, Sozialarbeit, Finanzektor, usw..
- Biologie: Gruppierung von Bakterien und Mikroorganismen
Weitere Bezeichnungen für die Clusteranalyse sind „Klassifikationsverfahren“, „Unsupervised Learning“ oder auch „Pattern Recognition“.
Grundlagen der Clusteranalyse
Ähnlichkeit und Distanzmaße
Um Beobachtungseinheiten gruppieren zu können, muss zunächst festgestellt werden, wie ähnlich sich die einzelnen Beobachtungen sind. Es muss also ein Maß für die Ähnlichkeit zwischen je zwei Beobachtungen definiert werden. Analog kann man statt Ähnlichkeiten auch Distanzen zwischen je zwei Beobachtungen angeben, die sich zu den Ähnlichkeiten in umgekehrter Relation verhalten. Der Ausgangspunkt einer Clusteranalyse ist bei den meisten Softwarepaketen daher entweder die Datenmatrix oder eine daraus abgeleitete Ähnlichkeits- oder Distanzmatrix (Abbildung 15). Da Ähnlichkeits- und Distanzmaße nur eine unterschiedliche Sicht des selben Sachverhalts ist, werden in weiterer Folge nur Distanzmaße betrachtet.
Die Forderungen für ein Distanzmaß sind folgende:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle - $d_{i i}=0 \forall i=1, \ldots, n$ - $d_{i j} \geq 0 \forall i \neq j=1, \ldots, n$ - $d_{i j}=d_{j i} \forall i, j=1, \ldots, n$ }
Weiters wird zumeist gefordert, dass das Distanzmaß invariant bezüglich einer Klasse von bestimmten Transformationen ist (Umskalierungen, Verschiebungen). Es soll ja keinen Unterschied machen ob Werte in cm oder m, in kg oder g, in Schilling oder Euro gemessen werden.
Bei metrischen Merkmalen werden nun am häufigsten die Minkowski-q-Metriken (Lq-Distanzen) als Distanzmaß verwendet. Diese sind gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{m n}=\left(\sum_{i=1}^{p}\left|x_{i m}-x_{i n}\right|^{q}\right)^{1 / q} \text { für } q \geq 1 . }
Man beachte, dass alle Lq-Distanzen (außer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=2} ) nicht invariant gegenüber Drehungen des Koordinatenkreuzes (orthogonale lineare Transformationen) sind.
Ein alternatives Distanzmaß ist die „Mahalanobisdistanz“, der bei stark korrelierten Variablen der Vorzug gegeben wird.
Für einige Clusteralgorithmen ist nach Kenntnis der Distanzmatrix nur mehr die Reihenfolge der Distanzen zwischen je zwei Datenpunkten relevant.
| Aufgabe 10
Gegeben seien folgende vier Objekte, an denen jeweils drei Merkmale beobachtet wurden: (8/9/6), (6/2/3), (6/5/1), und (7/1/5). Berechnen Sie die L1- bzw. die L2-Distanzen und ordnen Sie die Objektpaare jeweils nach ihren Distanzen. Ist die Ordnung unterschiedlich? |
|---|
Im Falle von nominalskalierten Variablen müssen die Distanzen anders berechnet werden. Hier werden im wesentlichen die Übereinstimmungen zwischen je zwei Objekten gezählt und daraus Koeffizienten berechnet (siehe die entsprechenden Kapitel der vertiefenden Literatur).
Klassifikation - Partition
Wichtig im Zusammenhang mit der Clusteranalyse ist nun auch der Begriff der „Klassifikation“. Eine Klassifikation Ω ist ein System von Teilmengen (Klassen, Gruppen, Cluster) der Menge aller Beobachtungseinheiten (Objekte). In Bezug auf die Clusteranalyse fordert man zumeist, dass eine Klassifikation disjunkt und exhaustiv ist. Ersteres meint, dass jede Beobachtung zu höchstens einer Teilmenge zugeordnet wird. Zweiteres meint, dass jede Beobachtung zu mindestens einer Teilmenge zugeordnet wird. Eine Klassifikation, die disjunktiv und exhaustiv ist, nennt man „Partition“.
| Aufgabe 11
Welche Partitionen können zu den Daten in Aufgabe 10 gefunden werden? |
|---|
Die Anzahl der möglichen verschiedenen Partitionen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} Elementen ist durch die sogenannten BELLschen Zahlen [1] gegeben. Diese „explodieren“ bei wachsender Anzahl von Beobachtungseinheiten.
Tabelle 3: Bell'sche Zahlen
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| #Partitionen | 1 | 1 | 2 | 5 | 15 | 52 | 203 | 877 | 4140 | 21147 | 115975 |
| N | 20 |
|
|
|
|
50 |
|
|
|
|
|
| #Partitionen | 51724158235372 |
|
|
|
|
1,9*1047 |
|
|
|
|
|
Die „beste“ Partition zu finden ist nun die Aufgabe der Clusteranalyse und dies ist - in Anbetracht von Tabelle 3 - wenn nicht gerade drei bis fünf Objekte in Gruppen geteilt werden sollen, relativ schwierig. Analog zur Variablenselektion in der Regressionsanalyse gibt es aber nun Verfahren, die schrittweise durch Trennen oder Verbinden von Teilmengen eine möglichst gute Partitionen herausfinden sollen. Diese Methoden werden im folgenden Abschnitt diskutiert.
Hierarchische Verfahren
Grundbegriffe
Hierarchische Verfahren stellen Hierarchien von Partitionen auf. Bewegt man sich in eine Richtung der Hierarchie, unterscheiden sich „benachbarte“ Partitionen dadurch, dass entweder zwei Klassen miteinander „verschmolzen“ werden („Vergröberung“) oder eine Klasse in zwei aufgespalten wird („Verfeinerung“). In Abbildung 17 erhält man die Partition rechts durch Vergröberung der Partition links bzw. jene links durch Verfeinerung der rechten.
Je nachdem, ob das Verfahren kontinuierlich vergröbert oder verfeinert, spricht man von agglomerativen Verfahren bzw. divisiven Verfahren. Im weiteren Verlauf dieses Abschnitts soll nur auf agglomerative Verfahren eingegangen werden.
Bei agglomerativen Verfahren beginnt man mit jener Partition, in der jede Beobachtungseinheit eine Klasse definiert. Im weiteren Verlauf werden jeweils die beiden Klassen, die einander am ähnlichsten sind, miteinander zu einer Klasse verbunden. In jedem Schritt wird auch ein Heterogenitätsindex der erhaltenen Partition berechnet. Diese Prozedur geschieht solange, bis jene Klassifikation erreicht ist, die nur eine Klasse mit allen Werten enthält. Das Ergebnis eines agglomerativen Verfahrens ist eine Liste von durchgeführten Verbindungen und ein Vektor von Heterogenitätsmaßen.
Der Anwender hat nun zur genauen Durchführung der Analyse also zwei Fragen zu beantworten:
Frage 1: Was bedeutet „einander am ähnlichsten“ in Bezug auf Gruppen?
Frage 2: In wieviele und welche Gruppen sollen die Daten nun aufgeteilt werden?
Methoden zur Agglomeration
Frage 1 kann auf verschiedene Arten beantwortet werden und wieder hat der Anwender die Aufgabe, die Analyse genauer zu spezifizieren. Die Standardfunktion zur hierarchischen Clusteranalyse in R bietet beispielsweise sieben verschiedene Heterogenitätsmaße die die Unähnlichkeit zwischen je zwei Klassen ausdrücken.
Single Linkage, Complete Linkage und Average Linkage
Die Distanz zweier Klassen zueinander ist definiert als die kleinste („Single Linkage“), größte („Complete Linkage“) bzw. durchschnittliche („Average Linkage“) Distanz die zwischen beliebigen Paaren von Beobachtungen vorkommt. Die Paare bestehen dabei immer aus je einer Beobachtung aus beiden Klassen.
Median und Zentroid
Die Median- und die Zentroidmethode beziehen sich ebenfalls auf den „mittleren“ Abstand zwischen zwei Objektklassen. Der Nachteil ist hier, dass in Folge einer schrittweisen Fusionierung der Klassen das Heterogenitätsmaß nicht immer not-wendigerweise höher wird. So eine Hierarchie ist jedoch schwer zu interpretieren.
Ward
Das Ward-Kriterium fusioniert jene beiden Klassen, bei denen ein minimaler Zuwachs an Varianz innerhalb der Klassen erreicht wird.
| Beispiel 4
Betrachten wir nochmals die Daten aus Aufgabe 10. Ziel ist nun, eine hierarchische Clusteranalyse mit den Daten durchzuführen. Wir wählen als Abstand die L2-Distanz und als Agglomerations-Methode „Complete Linkage“. Zuerst Beginn besteht die Startpartition Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}_{1}=\{\{1\},\{2\},\{3\},\{4\}\}} . Nun wird die Distanzmatrix berechnet: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{12}=\sqrt{(8-6)^{2}+(9-2)^{2}+(6-3)^{2}}=\sqrt{62}}
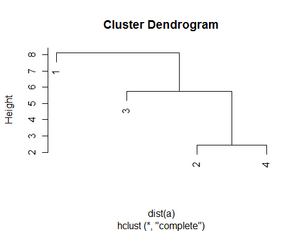
Die Beobachtungen 2 und 4 sind jene mit dem geringsten Abstand zueinander. Diese werden zur folgenden Partition fusioniert. Damit hat die erste Vergröberung stattgefunden.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}_{1}=\{\{1\},\{2,4\},\{3\}\}} Der Heterogenitätsindex zu dieser Vergröberung ist gleich der maximal in einem Cluster vorkommenden Distanz. Daher: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{1}=\sqrt{6}} . Nach der „Complete Linkage“-Methode werden nun die neuen Abstände definiert, beispielsweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{1,(2,4)}=\max \left(d_{12}, d_{14}\right)}
Im letzten Schritt wird zur Partition Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}_{1}=\{\{1,2,3,4\}\}} fusioniert und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{3}=\max (\sqrt{66}, \sqrt{45}, \sqrt{33})=\sqrt{66}} . |
|---|
Heterogenitätsindex und Dendrogramm
Ehe Frage 2 des vorletzen Abschnitts beantwortet werden kann, sollte das Ergebnis der Analyse graphisch aufbereitet werden. Bei hierarchischen Clusteranalysen geschieht dies zumeist durch das Dendrogramm. Dies ist eine Darstellung, in welcher Reihenfolge welche Fusionsschritte vollzogen worden sind und wie heterogen die gefundenen Cluster sind. Dadurch fließt auch der jeweils protokollierte Heterogenitätsindex in die Grafik ein.
Die Entscheidung, wieviele Gruppen gebildet werden sollen, ist nun dem Anwender überlassen. Wie heterogen die Mitglieder der jeweils selben Gruppe sein sollen, hängt auch von der inhaltlichen Fragestellung ab. Daher kann in Beispiel 4 darüber keine Empfehlung gegeben werden (Abbildung 18).
| Fortsetzung Beispiel 4'''' |
|---|
Weitere Clusteralgorithmen
Partitionierende Verfahren
Die partitionierenden Verfahren unterscheiden sich von den hierarchischen Clusterverfahren dadurch, dass hier versucht wird, eine bereits bestehende Partition durch Umgruppieren einzelner Beobachtungen bezüglich festgelegten Kriteriums zu optimieren. Man sollte hier aber eine Vorstellung bezüglich der Clusteranzahl haben, da diese jeweils zu den Standard-Inputs solcher Verfahren gehören. Die Ausgangspartition kann zum Beispiel durch ein hierarchisches Verfahren ermittelt werden, aber auch durch Gruppierung um Kristallisationskerne (potentielle Klassenschwerpunkte) oder durch Verwendung zufälliger Anfangspartitionen.
Die Vorgehensweise ist weiters wie folgt:
- Definiere zusätzlich zur Startpartition ein Optimierungskriterium
Prüfe bei jeder Beobachtung, ob das Kriterium durch Zuordnung der Beobachtung in einen anderen Cluster verbessert werden kann
Ordne jene Beobachtung um, die die beste Verbesserung des Kriteriums erzielt
Wiederhole die Schritte 2 und 3 bis keine Verbesserung mehr möglich ist.
Verwendung finden oft Kriterien, die in irgendeiner Form die Streuung innerhalb der verschiedenen Gruppen minimieren (wie das schon besprochene „Ward“-Kriterium). Eine bekannte Methode stellt hierbei die (auch in R implementierte) k-Means-Methode dar.
Modellbasiertes Clustering
Im Gegensatz zu den bisherigen Verfahren, die eher auf heuristischen Überlegungen beruhen, legt man beim modellbasierten Clustering ein stochastisches Modell zugrunde. Man betrachtet die verschiedenen Gruppen als Realisierung von verschiedenen Populationen, denen jeweils eine bestimmte statistische Verteilung unterstellt wird – meist die Normalverteilung.
Bei den Modellen wird dann die Auftrittswahrscheinlichkeit gegeben eine Klassenzugehörigkeit und den Verteilungsparametern berechnet und die Klassenzuordnungen werden solange geändert, bis diese Auftrittswahrscheinlichkeit maximiert wird.
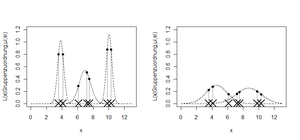
Abbildung 19 zeigt anhand einer Grafik, was hier passiert. Gegeben sind die sieben Datenpunkte, die auf der X-Achse mit einem Kreuz eingetragen sind. Es sollen nun zwei Kandidaten für eine Clustergruppierung gegenübergestellt werden. Auf der linken Seite wird die – intuitive – Lösung vorgeschlagen, eine Einteilung in drei Gruppen. Legt man die Einteilung fest, kann man daraus die Dichtefunktion der zugehörigen Normalverteilung schätzen. Führt man dies für alle drei Gruppen durch, erhält man nach Multiplikation der sieben Dichtefunktionswerte ein Maß für die Plausibilität der Stichprobe gegeben die Clustereinteilung, die „Likelihood“.
Sie beträgt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{1}\left(x \mid \text { Einteilung } 1 ; \widehat{\mu_{2}} ; \widehat{\sigma_{l}}\right)=0,80 \times 0,80 \times 0.29 \times 0.51 \times 0.4 \times 0.88 \times 0.88 \approx 0.03} .
Eine andere Partition wurde rechts gewählt. Dort wurden zwei Gruppen unterstellt (die kleinsten drei und die größten vier Beobachtungen). Wieder kann die Likelihood dieser Stichprobe berechnet werden. Diesmal ergibt sich:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{2}\left(x \mid \text { Einteilung } 2 ; \hat{\mu}_{\nu} ; \widehat{\sigma}_{2}\right)=0,22 \times 0,28 \times 0.16 \times 0.16 \times 0.19 \times 0.20 \times 0.15 \approx 9 * 10^{-6}} .
Gewählt wird nun jene Partition, die die höchste Likelihood liefert. Für die Daten in Abbildung 19 ist die linke Gruppierung die bestmögliche.
Im multivariaten Fall (der für die Clusteranalyse relevant ist) gibt es viele Möglichkeiten, welche Annahmen über die Varianzen bzw. Kovarianzen gemacht werden (Alle Varianzen gleich oder nicht? Kovarianzen gleich Null oder nicht? usw.). Die Clusteranalyse mittels Modellannahme hat aber auch noch einen weiteren Nutzen. Es zeigt sich, dass verschiedene heuristische Verfahren implizit dieselbe Optimierung durchführen. Dadurch können diese Verfahren im Nachhinein gerechtfertigt werden.
Clusteranalyse in R
Um die Arbeitsweise eines Clusteralgorithmus besser nachzuvollziehen zu können, soll eine Analyse nun an einem Beispiel, an dem die Daten leicht visualisiert werden können (zwei Dimensionen) gerechnet werden. Im allgemeinen werden die Daten durch mehrere Variablen charakterisiert.
Die vorliegenden Daten haben fast schon sporthistorischen Wert, geht es doch um die jeweils nationalen Bestleistungen in acht olympischen Laufbewerben (100m, 200m, 400m, 800m, 1500m, 5000m, 10000m, Marathon) aus dem Jahr 1984, protokolliert vor den olympischen Spielen in Los Angeles. Ziel der Analyse ist herauszufinden, welche Länder ähnliche Bestzeiten und über ein ähnliches Leistungsniveau im Laufsport verfügen.
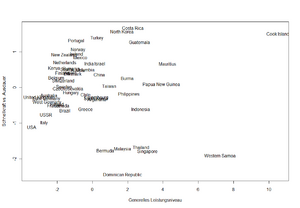
Mittels Hauptachsentransformation wurden bereits zwei Komponenten extrahiert, die über 90% an Varianz erklären. Diese können als „mittleres Leistungsniveau auf alle Strecken“ bzw. als „Ausdauer vs. Schnellkraft“ bezeichnet werden. Abbildung 20 zeigt die Länder in dem zweidimensionalen Raum. Nationen, die weit links stehen, haben ein hohes mittleres Leistungsniveau. Nationen, die oben stehen, haben bezogen auf ihr mittleres Leistungsniveau eine größere Bedeutung im Ausdauerbereich.
Die R-Sequenz, um aus den Daten Abbildung 20 zu erzeugen lautet wie folgt:
- Track.FA<-read.csv("C:\\...\\Track_FA.csv",header=TRUE,dec=",",sep=";")
- einlesen
- nam<-Track.FA[,1]
- dat<-Track.FA[,2:3]
- Trennung von Ländernamen und Werten
- plot(dat[,1],dat[,2],type="n",xlab="Generelles Leistungsniveau",ylab="Schnellkraft vs. Ausdauer")
- produziert einen XY-Scatterplot, allerdings ohne Punkte
- text(dat[,1], dat[,2],nam)
- trägt anschließend an den Stellen der Punkte die Ländernamen ein
Wieviele homogene Gruppen suggeriert Abbildung 20 nun? Wir haben einerseits zwei Ausreißern (Western Samoa und Cook Islands), sowie eine Gruppe von fünf Ländern im mittleren Leistungsniveau, die eher sprintstark bzw. schwach in Ausdauerbewerben sind (Dominikanische Republik, usw.). Die Topgruppe scheint vom Mittelfeld weniger gut trennbar.
Es wurde nun eine hierarchiche Clusteranalyse berechnet (Abbildung 21), die euklidische Distanzen und den „Complete-Linkage“-Algorithmus verwendet. Im Gegensatz zum „Single-Linkage“-Algorithmus, der zu bereits großen Gruppen immer noch einzelne Beobachtungen Schritt für Schritt dazuhängt, wachsen die Clustergrößen beim „Complete Linkage“ eher gleichmäßig.
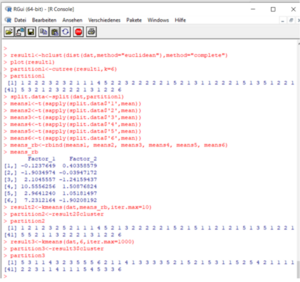
Code-Fortsetzung:
Das erzeugte Objekt „result1“ ist vom Typ „hclust“, beinhaltet daher alle Informationen, die bei einer hierarchischen Clusteranalyse berechnet werden. Es können auf Wunsch mehrere Attribute ausgegeben werden. Wird so ein Objekt mit dem „plot“-Befehl versehen, entsteht das Dendrogramm (Abbildung 22). Die Gruppen sollen nun so gewählt werden, dass sie untereinander homogen und zueinander heterogen sind. Der hier gewählte Kompromiss ist jener, der das Dendrogramm horizontal an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3,1<h<4,2} schneidet und sechs Gruppen liefert. Dies wird durch die Funktion „cutree“ (Abbildung 21) erzeugt. Das Ergebnis der Gruppenzuordnung wird sodann unter „partition1“ abgespeichert.
Die beiden weiteren erstellten Partitionen wurden mit dem schon erwähnten k-Means-Algorithmus in R berechnet. Partition 2 verwendet die in Partition 1 gefundenen sechs Klassenschwerpunkte und ordnet jene Datenpunkte um, die näher zu einem anderen als dem eigenen Klassenschwerpunkt liegt. Nach einer Iteration werden die Schwerpunkte wieder neu berechnet. Das Verfahren konvergiert ziemlich schnell. Es müssen kaum Daten umgruppiert werden.
Partition 3 wählt ebenfalls die k-Means-Methode für sechs Gruppen, jedoch mit sechs zufällig gewählten Beobachtungen als Anfangsschwerpunkten. Das Verfahren wurde mehrere Male mit jeweils 1000 Iterationen durchgeführt. Die am häufigsten gefundene Gruppierung wurde hier als „partition3“ gespeichert. Die Konvergenz ist hier allerdings sehr langsam.
Die Unterschiede zwischen den drei Verfahren sind in Abbildung 23 ersichtlich. Zu beachten ist, das Partition 3 die beiden Ausreißer in eine Gruppe gibt. Unter dieser Voraussetzung wären wohl fünf Gruppen ausreichend. Am ehesten ist Einteilung 2 zu bevorzugen, da hier das Ergebnis einer hierarchischen Analyse weiter optimiert wurde und der Algorithmuss konvergiert. Jeder Datenpunkt ist dort dem Mittelpunkt seiner jeweiligen Gruppe näher als jedem anderen Mittelpunkt.
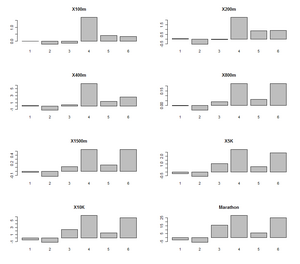
Abschließend sind die gefundenen Cluster nun noch zu charakterisieren. Tabelle 4 zeigt die Zuordnung der Länder zu den Clustern. Abbildung 24 stellt für alle acht Laufstrecken jeweils die Abweichung des Clustermittelwerts zum Gesamtmittelwert dar. Cluster 2 stellt sich als in jeder Disziplin überlegen heraus. Cluster 4 und 6 sind die beiden schwachen „Laufnationen“ am anderen Ende des Spektrums. Cluster 1 ist nach Cluster 2 die „zweite Leistungsgruppe“. Interessant sind nun Cluster 3 und 5. Cluster 3 ist in den beiden Sprintdistanzen besser als Cluster 1, in den drei längsten Distanzen jedoch nur besser als die beiden „Exoten“. Die Nationen von Cluster 5 sind bei diesen Distanzen am drittbesten, liegen aber beispielsweise auf 100m im Durchschnitt sogar hinter Western Samoa. Diese und weitere Erkenntnisse liefert also die durchgeführte Analyse.
Tabelle 4: Länderzuordnung zu den Clustern
| Cluster | Länder |
|---|---|
| 1 | Argentina, Austria, Chile, China, Columbia, Denmark, Greece, India, Ireland, Israel, Japan, South Korea, Luxembourg, Mexico, Norway, Portugal, Romania, Taiwan, Turkey |
| 2 | Australia, Belgium, Brazil, Canada, Czechoslovakia, Finland, France, East Germany, West Germany, United Kingdom, Hungary, Italy, Kenya, Netherlands, New Zealand, Poland, Spain, Sweden, Switzerland, USA, USSR |
| 3 | Bermuda, Dominican Republic, Malaysia, Singapore, Thailand |
| 4 | Cook Islands |
| 5 | Burma, Costa Rica, Guatemala, Indonesia, North Korea, Mauritius, Papua New Guinea, Philippines |
| 6 | Western Samoa |
Wiederholungsaufgaben und Zusammenfassung
- Was ist eine Partition?
Was ist eine Hierarchie?
Wie unterscheiden sich hierarchische Verfahren von partitionierenden Verfahren?
Wieviele Partitionen untersuchen Sie bei einem agglomerativen Verfahren mit gegebenen Algorithmus mit 20 Beobachtungen? Wieviele gibt es insgesamt?
Betrachten sie nochmals die vier Datenpunkte in Aufgabe 10. Führen Sie die „Average Linkage“-Methode unter Verwendung der L2-Distanzen durch und veranschaulichen Sie die Fusionsreihenfolge und die dazugehörigen Heterogenitätsindices anhand eines Dendrogramms.
Zusammenfassung
Die Clusteranalyse hat zum Ziel „ähnliche“ Objekte im Datensatz zu finden und diese dementsprechend in Gruppen (Cluster) zu ordnen. Diese Objekte sind Beobachtungseinheiten, von denen Messungen in mehreren Variablen vorhanden sind.
Zentrale Frage ist, wie „Abstand“ bzw. „Ähnlichkeit“ zwischen je zwei solcher Objekte definiert wird. Je nach Skalenniveau der Daten unterscheidet man zwischen Maßen, die die exakten Übereinstimmungen zählen oder Differenzen zwischen den einzelnen Komponenten der Beobachtungen messen. Zusätzlich muss jeweils ein Algorithmus gewählt werden, wie verschiedene Gruppierungen der Einheiten – Partitionen genannt – zu bewerten sind.
Die Gesamtzahl der Partitionen steigt rapide mit einem Zuwachs des Stichprobenumfangs. Daher ist es bereits bei Problemen mit moderaten Fallzahlen nicht möglich, alle möglichen Partitionen zu bewerten. Bei hierarchischen Verfahren werden verschiedene Partitionen schrittweise durch Verfeinerung bzw. Vergröberung erstellt. Hier wird nur ein sehr kleiner Bruchteil aller möglichen Partitionen bewertet. Bei partitionierenden Verfahren wird die Clusteranzahl festgelegt und dann ein Kriterium optimiert, das zumeist mit der Minimierung der Streuung der Datenpunkte innerhalb ihrer Cluster zu tun hat. Bei modellbasierten Verfahren verfolgt man einen stochastischen Ansatz.
Nachdem eine Partition gefunden ist, sind schließlich die gefundenen Gruppen auch zu charakterisieren und inhaltlich zu deuten.
- ↑ Benannt nach dem schottisch-amerikanischen Mathematiker Eric Temple Bell. Berechenbar nach der Rekursionsformel <math>B_{n+1}=\sum_{k=0}^{n}\left(\begin{array}{l} n k \end{array}\right) B_{k} \text { mit } B_{0}=B_{1}=1