Angewandte Makroökonomik - Wachstumstheorie: Unterschied zwischen den Versionen
| (35 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
= Wachstumstheorie = | = Wachstumstheorie = | ||
Gegenwärtig ist explizit oder implizit Ziel jeder Volkswirtschaft, die Produktion auszuweiten. Mit Fragen dieses Wachstums verbunden ist, ob sich das Outputniveau (die gesamte Produktion innerhalb einer Periode) verschiedener Ökonomien im Zeitverlauf angleicht, oder ob sich bestehende Disparitäten weiter vertiefen. Seit der Industriellen Revolution und insbesondere mit der zweiten Hälfte des 20. Jahrhunderts wird einerseits eine permanente Ausweitung der Produktion und somit ein langfristig positives Wirtschaftswachstum verzeichnet – zumindest in jenen Volkswirtschaften, die man als Industriestaaten bezeichnet. In Kapitel 1.1.1 wird das langfristige vom kurzfristigen Wachstum abgegrenzt, bevor in Kapiteln 1.1.2 die neoklassische Produktionsfunktion als Grundlage als grundlegende Annahme der modernen Wachstumstheorie vorgestellt wird; anschließend wird in Kapitel 1.1.3 die Dynamik des neoklassischen Wachstumsmodells diskutiert. In Kapitel 1.2 wird die Produktionsfunktion vom Typ Cobb-Douglas eingeführt, um das neoklassische Wachstumsmodell in Kapitel 1.2.1 in Verbindung mit technologischem Fortschritt, in Kapitel 1.2.2 mit Kapitalakkumulation und Wachstum, und in Kapitel 1.2.3 mit Humankapital zu anzuwenden. | Gegenwärtig ist explizit oder implizit Ziel jeder Volkswirtschaft, die Produktion auszuweiten. Mit Fragen dieses Wachstums verbunden ist, ob sich das Outputniveau (die gesamte Produktion innerhalb einer Periode) verschiedener Ökonomien im Zeitverlauf angleicht, oder ob sich bestehende Disparitäten weiter vertiefen. Seit der Industriellen Revolution und insbesondere mit der zweiten Hälfte des 20. Jahrhunderts wird einerseits eine permanente Ausweitung der Produktion und somit ein langfristig positives Wirtschaftswachstum verzeichnet – zumindest in jenen Volkswirtschaften, die man als Industriestaaten bezeichnet. In Kapitel 1.1.1 wird das langfristige vom kurzfristigen Wachstum abgegrenzt, bevor in Kapiteln 1.1.2 die neoklassische Produktionsfunktion als Grundlage als grundlegende Annahme der modernen Wachstumstheorie vorgestellt wird; anschließend wird in Kapitel 1.1.3 die Dynamik des neoklassischen Wachstumsmodells diskutiert. In Kapitel 1.2 wird die Produktionsfunktion vom Typ Cobb-Douglas eingeführt, um das neoklassische Wachstumsmodell in Kapitel 1.2.1 in Verbindung mit technologischem Fortschritt, in Kapitel 1.2.2 mit Kapitalakkumulation und Wachstum, und in Kapitel 1.2.3 mit Humankapital zu anzuwenden. | ||
== Grundlagen der Wachstumstheorie == | == Grundlagen der Wachstumstheorie == | ||
| Zeile 39: | Zeile 35: | ||
<math display="block"> | <math display="block"> | ||
Y_t=f(K_t, | Y_t=f(K_t,L_t ) | ||
</math> | </math> | ||
(1.1) | (1.1) | ||
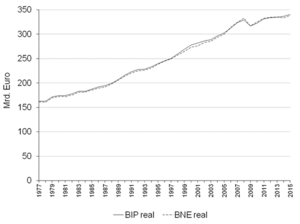
Wie bisher steht <math>Y</math> für Output, wobei die Betrachtung auf eine geschlossene Volkswirtschaft beschränkt ist und somit Output mit Einkommen gleichgesetzt werden kann. <ref>In Abb. 1.1 wäre somit das BIP identisch mit dem BNE.</ref> <math>K</math> bezeichnet den gesamten Sachkapitalbestand (Maschinen etc.) der Ökonomie und <math>L</math> das gesamte Arbeitsangebot, wobei Letzteres unter der Annahme von Vollbeschäftigung identisch mit der eingesetzten Arbeit ist. Die Zeit, gekennzeichnet als <math>t</math>, ist nur indirekt in der Produktionsfunktion über die Variablen <math>Y_t</math>, <math>K_t</math> und <math> | Wie bisher steht <math>Y</math> für Output, wobei die Betrachtung auf eine geschlossene Volkswirtschaft beschränkt ist und somit Output mit Einkommen gleichgesetzt werden kann. <ref>In Abb. 1.1 wäre somit das BIP identisch mit dem BNE.</ref> <math>K</math> bezeichnet den gesamten Sachkapitalbestand (Maschinen etc.) der Ökonomie und <math>L</math> das gesamte Arbeitsangebot, wobei Letzteres unter der Annahme von Vollbeschäftigung identisch mit der eingesetzten Arbeit ist. Die Zeit, gekennzeichnet als <math>t</math>, ist nur indirekt in der Produktionsfunktion über die Variablen <math>Y_t</math>, <math>K_t</math> und <math>L_t </math> vertreten. Die Gleichung (1.1) kann somit gelesen werden als: Der Output zum beliebigen Zeitpunkt <math>t</math> ist eine Funktion der zum selben Zeitpunkt eingesetzten Mengen von Arbeit und Kapital. | ||
Die Produktionsfunktion in Gleichung (1.1) stellt eine erhebliche Vereinfachung der Realität dar, als sie nur jeweils einen Typ Arbeit und Kapital kennt, also unterstellt, dass für jede Einheit Arbeit (ob Schweißer oder Krankenschwester) wie für jede Einheit Kapital (ob Traktor oder Bürogebäude) gilt, dass sie gleich produktiv sind und die gleiche Funktion erfüllen. In Kapitel 2.2.1 wird gezeigt, wie die Lockerung dieser Annahme das Modell realistischer macht, ohne die Hauptergebnisse zu ändern. Zunächst sei auf eine weitere implizite Annahme der Produktionsfunktion hingewiesen: Aus der Reduzierung auf Arbeit und Kapital ergibt sich, dass alle anderen Einflüsse in der langen Frist verhältnismäßig ''unwichtig'' sind, insbesondere Boden und natürliche Ressourcen. Das liegt zum einen daran, dass die Menge an Boden nicht veränderbar ist; insbesondere aber spielen diese Faktoren für moderne Ökonomien nur untergeordnete Rollen. <ref>In Österreich lag der Anteil der Land- und Forstwirtschaft inkl. Fischerei an der Bruttowertschöpfung (zu den Begriffen siehe Kapitel 1.4.1) im Jahr 2015 bei 1,29%, der Anteil des Bergbaus bei 0,39% (Berechnung nach Daten der Statistik Austria).</ref> In Man beachte außerdem, dass die Instrumente der Wirtschaftspolitik keine Berücksichtigung finden: Auf lange Sicht werden wirtschaftspolitisch- und konjunkturbedingte Schwankungen vom langfristigen Trend dominiert, in der Produktion also ausgeglichen. Ziel des Modells ist folglich, die ''Determinanten des langfristigen Trends'' zu identifizieren. <ref>Man kann sagen, dass das Modell nur anwendbar ist, wenn diese Annahmen erfüllt sind. Für Ökonomien, deren Realität von den Modellannahmen drastisch abweicht, hat das Modell folglich nur eingeschränkte Aussagekraft. Beispiele wären Ökonomien, die durch den Export von Rohstoffen sehr rasch wachsen wie etwa die OPEC-Länder in den 1970er- und 1980er-Jahren, oder Ökonomien, die die makroökonomischen Rahmenbedingungen wie Zinssatz, Inflation oder Staatsverschuldung nicht in den Griff bekommen, beispielsweise Japan oder die Ukraine in den 2000er- und 2010er-Jahren. Auch für die Ökonomien der Eurozone stellt sich angesichts der Euro-Dauerkrise zum Zeitpunkt der Drucklegung des vorliegenden Studienhefts schön langsam die Frage, ob die Modellannahmen noch zutreffen.</ref> | Die Produktionsfunktion in Gleichung (1.1) stellt eine erhebliche Vereinfachung der Realität dar, als sie nur jeweils einen Typ Arbeit und Kapital kennt, also unterstellt, dass für jede Einheit Arbeit (ob Schweißer oder Krankenschwester) wie für jede Einheit Kapital (ob Traktor oder Bürogebäude) gilt, dass sie gleich produktiv sind und die gleiche Funktion erfüllen. In Kapitel 2.2.1 wird gezeigt, wie die Lockerung dieser Annahme das Modell realistischer macht, ohne die Hauptergebnisse zu ändern. Zunächst sei auf eine weitere implizite Annahme der Produktionsfunktion hingewiesen: Aus der Reduzierung auf Arbeit und Kapital ergibt sich, dass alle anderen Einflüsse in der langen Frist verhältnismäßig ''unwichtig'' sind, insbesondere Boden und natürliche Ressourcen. Das liegt zum einen daran, dass die Menge an Boden nicht veränderbar ist; insbesondere aber spielen diese Faktoren für moderne Ökonomien nur untergeordnete Rollen. <ref>In Österreich lag der Anteil der Land- und Forstwirtschaft inkl. Fischerei an der Bruttowertschöpfung (zu den Begriffen siehe Kapitel 1.4.1) im Jahr 2015 bei 1,29%, der Anteil des Bergbaus bei 0,39% (Berechnung nach Daten der Statistik Austria).</ref> In Man beachte außerdem, dass die Instrumente der Wirtschaftspolitik keine Berücksichtigung finden: Auf lange Sicht werden wirtschaftspolitisch- und konjunkturbedingte Schwankungen vom langfristigen Trend dominiert, in der Produktion also ausgeglichen. Ziel des Modells ist folglich, die ''Determinanten des langfristigen Trends'' zu identifizieren. <ref>Man kann sagen, dass das Modell nur anwendbar ist, wenn diese Annahmen erfüllt sind. Für Ökonomien, deren Realität von den Modellannahmen drastisch abweicht, hat das Modell folglich nur eingeschränkte Aussagekraft. Beispiele wären Ökonomien, die durch den Export von Rohstoffen sehr rasch wachsen wie etwa die OPEC-Länder in den 1970er- und 1980er-Jahren, oder Ökonomien, die die makroökonomischen Rahmenbedingungen wie Zinssatz, Inflation oder Staatsverschuldung nicht in den Griff bekommen, beispielsweise Japan oder die Ukraine in den 2000er- und 2010er-Jahren. Auch für die Ökonomien der Eurozone stellt sich angesichts der Euro-Dauerkrise zum Zeitpunkt der Drucklegung des vorliegenden Studienhefts schön langsam die Frage, ob die Modellannahmen noch zutreffen.</ref> | ||
| Zeile 51: | Zeile 47: | ||
Während sich die klassische Ökonomie intensiv mit der Frage beschäftigte, wie eine stetig wachsende Bevölkerung bei konstantem Boden versorgt werden kann, bzw. wie sich der Einsatz von Maschinen auf den Faktor Arbeit auswirkt, führt die Vernachlässigung von natürlichen Ressourcen und Arbeitslosigkeit in der neoklassischen Wachstumstheorie zur zweiten kritischen Grundannahme, nämlich jener konstanter Skalenerträge. <ref>Vgl. im Zusammenhang mit einzelnen Betrieben hierzu ''Grundlagen der Volkswirtschaftslehre 2'' (Kapitel 1.1.4).</ref> Diese Annahme lässt sich einfach veranschaulichen: Sie bedeutet, dass bspw. eine Verdoppelung der Faktoren Arbeit und Kapital auch den Output verdoppeln wird. Formal muss für Gleichung (1.1) gelten: | Während sich die klassische Ökonomie intensiv mit der Frage beschäftigte, wie eine stetig wachsende Bevölkerung bei konstantem Boden versorgt werden kann, bzw. wie sich der Einsatz von Maschinen auf den Faktor Arbeit auswirkt, führt die Vernachlässigung von natürlichen Ressourcen und Arbeitslosigkeit in der neoklassischen Wachstumstheorie zur zweiten kritischen Grundannahme, nämlich jener konstanter Skalenerträge. <ref>Vgl. im Zusammenhang mit einzelnen Betrieben hierzu ''Grundlagen der Volkswirtschaftslehre 2'' (Kapitel 1.1.4).</ref> Diese Annahme lässt sich einfach veranschaulichen: Sie bedeutet, dass bspw. eine Verdoppelung der Faktoren Arbeit und Kapital auch den Output verdoppeln wird. Formal muss für Gleichung (1.1) gelten: | ||
<math display="block"> | <math display="block"> | ||
2Y_t=f(2K_t, | 2Y_t=f(2K_t,2L_t ) | ||
</math> | </math> | ||
(1.2) | (1.2) | ||
| Zeile 57: | Zeile 53: | ||
Oder allgemein für jede beliebige, nichtnegative Konstante <math>c</math>: | Oder allgemein für jede beliebige, nichtnegative Konstante <math>c</math>: | ||
<math display="block"> | <math display="block"> | ||
cY_t=f(cK_t, | cY_t=f(cK_t,cL_t ) | ||
</math> | </math> | ||
(1.3) | (1.3) | ||
| Zeile 65: | Zeile 61: | ||
Wenn hingegen nicht alle, sondern nur ''ein'' Faktor an Volumen zunimmt, gilt das Gesetz des abnehmenden Grenzprodukts. <ref>Vgl. ''Grundlagen der Volkswirtschaftslehre 2'' (Kapitel 1.1.1).</ref> Umgelegt auf eine Volkswirtschaft stellt sich auch hier die Frage, was passiert, wenn ein Faktor zunimmt, während der oder die anderen konstant bleiben. Ist etwa noch wenig Kapital vorhanden, so wird eine zusätzliche Einheit die Produktion erheblich erhöhen. Ist jedoch umgekehrt bereits reichlich Kapital vorhanden (etwa in Form von Traktoren oder Bürogebäuden), so werden weitere Einheiten kaum noch zur Produktion beitragen. Parallel verhält es sich mit dem Faktor Arbeit. | Wenn hingegen nicht alle, sondern nur ''ein'' Faktor an Volumen zunimmt, gilt das Gesetz des abnehmenden Grenzprodukts. <ref>Vgl. ''Grundlagen der Volkswirtschaftslehre 2'' (Kapitel 1.1.1).</ref> Umgelegt auf eine Volkswirtschaft stellt sich auch hier die Frage, was passiert, wenn ein Faktor zunimmt, während der oder die anderen konstant bleiben. Ist etwa noch wenig Kapital vorhanden, so wird eine zusätzliche Einheit die Produktion erheblich erhöhen. Ist jedoch umgekehrt bereits reichlich Kapital vorhanden (etwa in Form von Traktoren oder Bürogebäuden), so werden weitere Einheiten kaum noch zur Produktion beitragen. Parallel verhält es sich mit dem Faktor Arbeit. | ||
Die Annahme konstanter Skalenerträge erlaubt es, die Produktionsfunktion in ''intensiver Form'' darzustellen: Setzt man in Gleichung (1.3) <math>c=1/ | Die Annahme konstanter Skalenerträge erlaubt es, die Produktionsfunktion in ''intensiver Form'' darzustellen: Setzt man in Gleichung (1.3) <math>c=1/L_t </math> ein, so erhält man den Output je eingesetzter Einheit Arbeit: | ||
<math display="block"> | <math display="block"> | ||
\frac{Y_{t}}{L_{t}}=f\left(\frac{K_{t}}{L_{t}}, \frac{L_{t}}{L_{t}}\right)=f\left(\frac{K_{t}}{L_{t}}, 1\right) | |||
</math> | </math> | ||
(1.4) | (1.4) | ||
| Zeile 77: | Zeile 73: | ||
(1.5) | (1.5) | ||
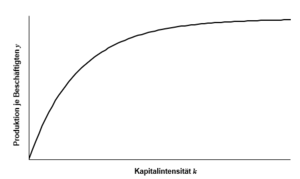
Die Produktion je Beschäftigten ist somit eine Funktion der Kapitalintensität. Die Annahme abnehmender Grenzerträge lässt sich durch die Bedingungen <math>f^ | Die Produktion je Beschäftigten ist somit eine Funktion der Kapitalintensität. Die Annahme abnehmender Grenzerträge lässt sich durch die Bedingungen <math>f^{\prime}(k)>0</math> und <math>f \prime \prime (k)<0</math> ausdrücken und wird in Abb. 1.2 veranschaulicht. | ||
Analog zur Kostengleichung eines einzelnen Anbieters <ref>Vgl. hierzu ''Grundlagen der Volkswirtschaftslehre 2'', Gleichung (1.10).</ref> folgen zwei wichtige Implikationen des Modells: Im Gleichgewicht werden beide Faktoren Arbeit wie Kapital nach ihrem jeweiligen ''Grenzprodukt'' bezahlt. Daraus folgen das '''Lohnniveau''' zum Zeitpunkt <math>t</math> | Analog zur Kostengleichung eines einzelnen Anbieters <ref>Vgl. hierzu ''Grundlagen der Volkswirtschaftslehre 2'', Gleichung (1.10).</ref> folgen zwei wichtige Implikationen des Modells: Im Gleichgewicht werden beide Faktoren Arbeit wie Kapital nach ihrem jeweiligen ''Grenzprodukt'' bezahlt. Daraus folgen das '''Lohnniveau''' zum Zeitpunkt <math>t</math> | ||
| Zeile 98: | Zeile 94: | ||
Aus der Identität der volkswirtschaftlichen Gesamtrechnung folgt, dass die Summe der Löhne und Gewinne dem Gesamtprodukt entsprechen: | Aus der Identität der volkswirtschaftlichen Gesamtrechnung folgt, dass die Summe der Löhne und Gewinne dem Gesamtprodukt entsprechen: | ||
<math display="block"> | <math display="block"> | ||
Y_t=w_t | Y_t=w_t L_t +r_t K_t | ||
</math> | </math> | ||
(1.8) | (1.8) | ||
| Zeile 114: | Zeile 110: | ||
Es wird angenommen, dass die Produktionsfaktoren mit exogen bestimmter, konstanter Rate wachsen. Unter der Annahme, dass das Arbeitsangebot mit derselben Rate wie die Bevölkerung wächst bzw. identisch mit ihr ist, gilt: | Es wird angenommen, dass die Produktionsfaktoren mit exogen bestimmter, konstanter Rate wachsen. Unter der Annahme, dass das Arbeitsangebot mit derselben Rate wie die Bevölkerung wächst bzw. identisch mit ihr ist, gilt: | ||
<math display="block"> | <math display="block"> | ||
L | \dot{L}_{t}=n L_{t} | ||
</math> | </math> | ||
(1.10) | (1.10) | ||
| Zeile 122: | Zeile 118: | ||
Es folgt aus Gleichung (1.10), dass zu jedem beliebigen Zeitpunkt <math>t</math> | Es folgt aus Gleichung (1.10), dass zu jedem beliebigen Zeitpunkt <math>t</math> | ||
<math display="block"> | <math display="block"> | ||
L_{t}=L_{0} e^{n t} | |||
</math> | </math> | ||
(1.11) | (1.11) | ||
| Zeile 130: | Zeile 126: | ||
Der Anteil des Outputs, der investiert wird, entspricht der Sparquote und ist exogen gegeben und konstant. Eine investierte Einheit Output entspricht einer neuen Einheit Kapital. Kapitalgüter müssen jedoch von Zeit zu Zeit erneuert werden, da der vorhandene Kapitalstock verfällt. Die Investitionsgleichung nimmt daher folgende Form an: | Der Anteil des Outputs, der investiert wird, entspricht der Sparquote und ist exogen gegeben und konstant. Eine investierte Einheit Output entspricht einer neuen Einheit Kapital. Kapitalgüter müssen jedoch von Zeit zu Zeit erneuert werden, da der vorhandene Kapitalstock verfällt. Die Investitionsgleichung nimmt daher folgende Form an: | ||
<math display="block"> | <math display="block"> | ||
K | \dot{K}_{t}=s_{K} f\left(K_{t}, L_{t}\right)-\delta K_{t}=s_{K} Y_{t}-\delta K_{t} | ||
</math> | </math> | ||
(1.12) | (1.12) | ||
Die Variable <math>s_K</math> bildet die Sparquote ab, während <math>\delta </math> die Abschreibungsrate bezeichnet. Gleichung (1.12) ist die Schlüsselgleichung des Solow-Modells und beschreibt die '''Kapitalakkumulation''' als elementaren Prozess der industriellen Produktion: Ein Teil der Produktion wird konsumiert, der andere Teil wird reinvestiert. Zugleich verbraucht sich der bereits vorhandene Kapitalstock und muss daher permanent erneuert werden. Der Term <math>s_K Y_t</math> entspricht folglich den ''Bruttoinvestitionen'' zum Zeitpunkt <math>t</math>, während die ''Nettoinvestitionen'' durch die gesamte Gleichung <math> | Die Variable <math>s_K</math> bildet die Sparquote ab, während <math>\delta </math> die Abschreibungsrate bezeichnet. Gleichung (1.12) ist die Schlüsselgleichung des Solow-Modells und beschreibt die '''Kapitalakkumulation''' als elementaren Prozess der industriellen Produktion: Ein Teil der Produktion wird konsumiert, der andere Teil wird reinvestiert. Zugleich verbraucht sich der bereits vorhandene Kapitalstock und muss daher permanent erneuert werden. Der Term <math>s_K Y_t</math> entspricht folglich den ''Bruttoinvestitionen'' zum Zeitpunkt <math>t</math>, während die ''Nettoinvestitionen'' durch die gesamte Gleichung <math>s_{K} Y_{t}-\delta K_{t}=\dot{K}_{t}</math> dargestellt sind. | ||
Für den gesamten Kapitalstock einer Ökonomie gilt somit, | Für den gesamten Kapitalstock einer Ökonomie gilt somit, | ||
<ul> | <ul> | ||
<li><p>dass er dann steigt, wenn der linke Term in Gleichung (1.12) größer ist als der rechte, d.h. wenn <math>s_K Y_t>\delta K_t</math>,</p> | <li><p>dass er dann steigt, wenn der linke Term in Gleichung (1.12) größer ist als der rechte, d.h. wenn <math>s_K Y_t>\delta K_t</math>,</p></li> | ||
</li> | <li><p>dass er konstant bleibt wenn <math>s_K Y_t=\delta K_t</math> und somit <math>\dot{K}_{t}=0</math></p></li> | ||
<li><p>dass er konstant bleibt wenn <math>s_K Y_t=\delta K_t</math> und somit <math>K | |||
</li> | |||
<li><p>dass er fällt, wenn <math>s_K Y_t<\delta K_t</math>.</p> | <li><p>dass er fällt, wenn <math>s_K Y_t<\delta K_t</math>.</p> | ||
<br></li> | <br></li> | ||
</ul> | </ul> | ||
Analog lässt sich die Investitionsgleichung je Beschäftigten ausdrücken: Da <math>k_t=K_t/ | Analog lässt sich die Investitionsgleichung je Beschäftigten ausdrücken: Da <math>k_t=K_t/L_t </math>, folgt aus der Quotientenregel | ||
<math display="block"> | <math display="block"> | ||
k | \dot{k}_{t}=\frac{\dot{K}_{t} L_{t}-K_{t} \dot{L}_{t}}{L_{t}^{2}}=\frac{\dot{K}_{t}}{L_{t}}-\frac{K_{t}}{L_{t}} \frac{\dot{L}_{t}}{L_{t}} | ||
</math> | </math> | ||
(1.13) | (1.13) | ||
| Zeile 154: | Zeile 148: | ||
Es folgt aus den Gleichungen (1.12) und (1.13) | Es folgt aus den Gleichungen (1.12) und (1.13) | ||
<math display="block"> | <math display="block"> | ||
k | \dot{k}_{t}=\frac{s_{K} Y_{t}-\delta K_{t}}{L_{t}}-\frac{K_{t}}{L_{t}} \frac{\dot{L}_{t}}{L_{t}}=s_{K} y_{t}-\delta k_{t}-n k_{t}=s_{K} y_{t}-(n+\delta) k_{t} | ||
</math> | </math> | ||
(1.14) | (1.14) | ||
| Zeile 161: | Zeile 155: | ||
<ul> | <ul> | ||
<li><p>Erstens, der Kapitalstock je Beschäftigten bleibt konstant wenn <math>s_K y_t=(n+\delta )k_t</math>: Demnach muss ein höheres Bevölkerungswachstum durch eine höhere Sparquote ausgeglichen werden. Passiert dies nicht, wird der Kapitalstock je Beschäftigten und somit die Produktion je Beschäftigten sinken, auch wenn gleichzeitig die Gesamtproduktion steigt.</p> | <li><p>Erstens, der Kapitalstock je Beschäftigten bleibt konstant wenn <math>s_K y_t=(n+\delta )k_t</math>: Demnach muss ein höheres Bevölkerungswachstum durch eine höhere Sparquote ausgeglichen werden. Passiert dies nicht, wird der Kapitalstock je Beschäftigten und somit die Produktion je Beschäftigten sinken, auch wenn gleichzeitig die Gesamtproduktion steigt.</p></li> | ||
</li> | <li><p>Zweitens, in einer betrachteten Ökonomie mag zu Beginn eines beliebigen Beobachtungszeitraums <math>0</math> der Fall <math>s_K y_t\neq (n+\delta )k_t</math> gegeben sein. Egal von welchem Punkt aus die Ökonomie startet, sie wird bei fixen <math>s_K</math>, <math>n</math> und <math>\delta </math> sowie <math>k_t>0</math> stets zum Gleichgewicht <math>\dot{k}_{t}=0</math> streben.</p></li> | ||
<li><p>Zweitens, in einer betrachteten Ökonomie mag zu Beginn eines beliebigen Beobachtungszeitraums <math>0</math> der Fall <math>s_K y_t\neq (n+\delta )k_t</math> gegeben sein. Egal von welchem Punkt aus die Ökonomie startet, sie wird bei fixen <math>s_K</math>, <math>n</math> und <math>\delta </math> sowie <math>k_t>0</math> stets zum Gleichgewicht <math>k | |||
</li> | |||
<li><p>Drittens muss für die Sparquote <math>s_K<1</math> gelten, da es sonst keinen Konsum (einschließlich Grundnahrungsmittel) gäbe. Sie kann also nicht beliebig erhöht werden.</p> | <li><p>Drittens muss für die Sparquote <math>s_K<1</math> gelten, da es sonst keinen Konsum (einschließlich Grundnahrungsmittel) gäbe. Sie kann also nicht beliebig erhöht werden.</p> | ||
<br></li> | <br></li> | ||
| Zeile 182: | Zeile 174: | ||
Einen häufig angewendeten, nichtsdestoweniger speziellen Fall einer Produktionsfunktion, die die geforderten Bedingungen erfüllt, ist jene vom Typ Cobb-Douglas: | Einen häufig angewendeten, nichtsdestoweniger speziellen Fall einer Produktionsfunktion, die die geforderten Bedingungen erfüllt, ist jene vom Typ Cobb-Douglas: | ||
<math display="block"> | <math display="block"> | ||
Y_{t}=K_{t}^{\alpha} L_{t}^{1-\alpha}, \quad 0<\alpha<1 | |||
</math> | </math> | ||
(1.15) | (1.15) | ||
| Zeile 188: | Zeile 180: | ||
wobei <math>\alpha </math> die Elastizität des Produktionsfaktors Kapital, und <math>1-\alpha </math> die Elastizität des Produktionsfaktors Arbeit bezeichnet. Indem beide Seiten der Gleichung (1.15) durch den Faktor Arbeit dividiert werden, erhält man die Produktion je Beschäftigten (Arbeitsproduktivität oder einfach Produktivität): | wobei <math>\alpha </math> die Elastizität des Produktionsfaktors Kapital, und <math>1-\alpha </math> die Elastizität des Produktionsfaktors Arbeit bezeichnet. Indem beide Seiten der Gleichung (1.15) durch den Faktor Arbeit dividiert werden, erhält man die Produktion je Beschäftigten (Arbeitsproduktivität oder einfach Produktivität): | ||
<math display="block"> | <math display="block"> | ||
y_{t}=\frac{Y_{t}}{L_{t}} \Rightarrow y_{t}=k_{t}^{\alpha} | |||
</math> | </math> | ||
(1.16) | (1.16) | ||
| Zeile 198: | Zeile 190: | ||
Das vorige Kapitel endete mit der Feststellung, dass zur langfristigen Produktionssteigerung die Produktivität des Faktors Arbeit erhöht werden muss. Um dies zu veranschaulichen, kann die Cobb-Douglas-Produktionsfunktion nun wie folgt angeschrieben werden: | Das vorige Kapitel endete mit der Feststellung, dass zur langfristigen Produktionssteigerung die Produktivität des Faktors Arbeit erhöht werden muss. Um dies zu veranschaulichen, kann die Cobb-Douglas-Produktionsfunktion nun wie folgt angeschrieben werden: | ||
<math display="block"> | <math display="block"> | ||
Y_{t}=K_{t}^{\alpha}\left(A_{t} L_{t}\right)^{1-\alpha}, \quad 0<\alpha<1 | |||
</math> | </math> | ||
(1.17) | (1.17) | ||
| Zeile 204: | Zeile 196: | ||
Die zusätzliche Variable <math>A_t</math> repräsentiert den technologischen Stand (das abstrakte Wissen) zum Zeitpunkt <math>t</math>. Diese allgemein verfügbare Technologie wächst mit konstanter Rate <math>g</math>, daher gilt analog zum Bevölkerungswachstum | Die zusätzliche Variable <math>A_t</math> repräsentiert den technologischen Stand (das abstrakte Wissen) zum Zeitpunkt <math>t</math>. Diese allgemein verfügbare Technologie wächst mit konstanter Rate <math>g</math>, daher gilt analog zum Bevölkerungswachstum | ||
<math display="block"> | <math display="block"> | ||
A | \dot{A}_{t}=g A_{t} | ||
</math> | </math> | ||
(1.18) | (1.18) | ||
| Zeile 210: | Zeile 202: | ||
und folglich zu jedem beliebigen Zeitpunkt <math></math> | und folglich zu jedem beliebigen Zeitpunkt <math></math> | ||
<math display="block"> | <math display="block"> | ||
A_{t}=A_{0} e^{g t} | |||
</math> | </math> | ||
(1.19) | (1.19) | ||
| Zeile 216: | Zeile 208: | ||
Daraus folgt, dass die gesamte Produktion zum Zeitpunkt <math></math> dargestellt werden kann als: | Daraus folgt, dass die gesamte Produktion zum Zeitpunkt <math></math> dargestellt werden kann als: | ||
<math display="block"> | <math display="block"> | ||
Y_{t}=K_{t}^{\alpha}\left(A_{0} e^{g t} L_{0} e^{n t}\right)^{1-\alpha} \Rightarrow Y_{t}=K_{t}^{\alpha}\left(A_{0} L_{0}\right)^{(1-\alpha)} e^{(1-\alpha)(g+n) t} | |||
</math> | </math> | ||
(1.20) | (1.20) | ||
| Zeile 227: | Zeile 219: | ||
Es gibt nun zwei Möglichkeiten, die Produktion je Beschäftigten in intensiver Form darzustellen: Erstens, beide Seiten aus Gleichung (1.17) werden durch den Faktor Arbeit dividiert, und man erhält die Produktion je Beschäftigten: | Es gibt nun zwei Möglichkeiten, die Produktion je Beschäftigten in intensiver Form darzustellen: Erstens, beide Seiten aus Gleichung (1.17) werden durch den Faktor Arbeit dividiert, und man erhält die Produktion je Beschäftigten: | ||
<math display="block"> | <math display="block"> | ||
\frac{Y_{t}}{L_{t}}=K_{t}^{\alpha} L_{t}^{-\alpha} A_{t}^{1-\alpha} \Rightarrow y_{t}=k_{t}^{\alpha} A_{t}^{1-\alpha} | |||
</math> | </math> | ||
(1.21) | (1.21) | ||
| Zeile 235: | Zeile 227: | ||
Die zweite Möglichkeit zur Darstellung in intensiver Form besteht darin, beide Seiten aus Gleichung (1.17) durch die Variablen Arbeit ''und'' Technologie zu dividieren und auf diese Weise Produktion je Beschäftigten um den technologischen Fortschritt zu korrigieren. Es mag an dieser Stelle zunächst verwirren, die Technologie zuerst einzuführen, bloß um sie anschließend wieder herauszurechnen, doch wie noch zu sehen ist, vereinfacht es die folgenden Berechnungen; dargestellt wird die Produktion ''je effektiver Arbeitseinheit'': | Die zweite Möglichkeit zur Darstellung in intensiver Form besteht darin, beide Seiten aus Gleichung (1.17) durch die Variablen Arbeit ''und'' Technologie zu dividieren und auf diese Weise Produktion je Beschäftigten um den technologischen Fortschritt zu korrigieren. Es mag an dieser Stelle zunächst verwirren, die Technologie zuerst einzuführen, bloß um sie anschließend wieder herauszurechnen, doch wie noch zu sehen ist, vereinfacht es die folgenden Berechnungen; dargestellt wird die Produktion ''je effektiver Arbeitseinheit'': | ||
<math display="block"> | <math display="block"> | ||
\frac{Y_{t}}{A_{t} L_{t}}=K_{t}^{\alpha} L_{t}^{-\alpha} A_{t}^{-\alpha} \Rightarrow \hat{y}_{t}=\hat{k}_{t}^{\alpha} | |||
</math> | </math> | ||
(1.22) | (1.22) | ||
wobei <math>\hat{y} =Y_t/A_t | wobei <math>\hat{y} =Y_t/A_t L_t </math> den Output je effektiver Arbeitseinheit darstellt, während <math>\hat{k}=K/AL</math> den Kapitalstock je effektiver Arbeitseinheit bezeichnet. Man sieht, dass | ||
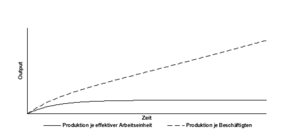
Gleichung (1.22) Gleichung (1.16) sehr ähnlich ist und kann nun festhalten, dass die Produktion je effektiver Arbeitseinheit in der langen Frist ''konstant'' bleibt. Dieser Zusammenhang wird in Abb. 1.4 veranschaulicht. | Gleichung (1.22) Gleichung (1.16) sehr ähnlich ist und kann nun festhalten, dass die Produktion je effektiver Arbeitseinheit in der langen Frist ''konstant'' bleibt. Dieser Zusammenhang wird in Abb. 1.4 veranschaulicht. | ||
| Zeile 247: | Zeile 239: | ||
Die Determinanten des Wachstums zeigen sich bei der weiteren Behandlung des Outputs je effektiver Arbeitseinheit. Analog zu Gleichung (1.12) gilt für die Gesamtwirtschaft unter Einbeziehung des technologischen Fortschritts: | Die Determinanten des Wachstums zeigen sich bei der weiteren Behandlung des Outputs je effektiver Arbeitseinheit. Analog zu Gleichung (1.12) gilt für die Gesamtwirtschaft unter Einbeziehung des technologischen Fortschritts: | ||
<math display="block"> | <math display="block"> | ||
K | \dot{K}_{t}=s_{K} f\left(K_{t}, A_{t} L_{t}\right)-\delta K_{t} | ||
</math> | </math> | ||
(1.23) | (1.23) | ||
da <math>\hat{ | da <math>\hat{k}_{t}=K_{t} /\left(A_{t} L_{t}\right)</math> folgen aus der Quotientenregel sowie der Produktregel | ||
<math display="block"> | <math display="block"> | ||
\hat{k | \dot{\hat{k}}_{t}=\frac{\dot{K}_{t} A_{t} L_{t}-K_{t}\left(\dot{A}_{t} L_{t}+A_{t} \dot{L}_{t}\right)}{A_{t}^{2} L_{t}^{2}}=\frac{\dot{K}_{t}}{A_{t} L_{t}}-\frac{K_{t} \dot{A}_{t} L_{t}}{A_{t}^{2} L_{t}^{2}}-\frac{K_{t} A_{t} \dot{L}_{t}}{A_{t}^{2} L_{t}^{2}} | ||
</math> | </math> | ||
(1.24) | (1.24) | ||
| Zeile 259: | Zeile 251: | ||
Es folgt daher aus den Gleichungen (1.12), (1.21) und (1.24) | Es folgt daher aus den Gleichungen (1.12), (1.21) und (1.24) | ||
<math display="block"> | <math display="block"> | ||
\hat{k | \dot{\hat{k}}_{t}=\frac{s_{K} f\left(K_{t}, A_{t} L_{t}\right)-\delta K_{t}}{A_{t} L_{t}}-\frac{K_{t} \dot{A}_{t} L_{t}}{A_{t}^{2} L_{t}^{2}}-\frac{K_{t} A_{t} \dot{L}_{t}}{A_{t}^{2} L_{t}^{2}}=s_{K} \hat{y}_{t}-\delta k_{t}-g k_{t}-n k_{t}=s_{K} \hat{y}_{t}-(n+g+\delta) \hat{k}_{t} | ||
</math> | </math> | ||
(1.25) | (1.25) | ||
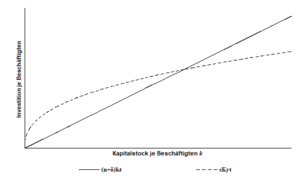
Gleichung (1.25) besagt, dass die Veränderung im Kapitalstock je effektiver Arbeitseinheit die Differenz aus zwei Termen ist: Der linke Term, <math>s_K \hat{y_t}</math>, entspricht den Bruttoinvestitionen je effektiver Arbeitseinheit; der rechte Term <math>(n+g+\delta ) \hat{k_t}</math>, entspricht den Investitionen, die nötig sind, um <math> \hat{y_t}</math> konstant zu halten. Dies ist folglich dann der Fall, wenn <math>s_K \hat{y_t}=(n+g+\delta ) \hat{k_t}</math> gilt. Wenn <math>s_K \hat{y_t}\neq (n+g+\delta ) \hat{k_t}</math> gilt, so steigt der Kapitalstock je effektiver Arbeitseinheit, <math> \hat{k_t}</math>, wenn <math>s_K \hat{y_t}>(n+g+\delta ) \hat{k_t}</math>, und umgekehrt. Dieser Prozess verläuft analog zum in Abb. 1.3 dargestellten Mechanismus, als die Ökonomie immer zum Schnittpunkt der beiden Kurven tendiert: Wenn <math>s_K \hat{y_t}=(n+g+\delta ) \hat{k_t}</math> und somit <math> \hat{k | Gleichung (1.25) besagt, dass die Veränderung im Kapitalstock je effektiver Arbeitseinheit die Differenz aus zwei Termen ist: Der linke Term, <math>s_K \hat{y_t}</math>, entspricht den Bruttoinvestitionen je effektiver Arbeitseinheit; der rechte Term <math>(n+g+\delta ) \hat{k_t}</math>, entspricht den Investitionen, die nötig sind, um <math> \hat{y_t}</math> konstant zu halten. Dies ist folglich dann der Fall, wenn <math>s_K \hat{y_t}=(n+g+\delta ) \hat{k_t}</math> gilt. Wenn <math>s_K \hat{y_t}\neq (n+g+\delta ) \hat{k_t}</math> gilt, so steigt der Kapitalstock je effektiver Arbeitseinheit, <math> \hat{k_t}</math>, wenn <math>s_K \hat{y_t}>(n+g+\delta ) \hat{k_t}</math>, und umgekehrt. Dieser Prozess verläuft analog zum in Abb. 1.3 dargestellten Mechanismus, als die Ökonomie immer zum Schnittpunkt der beiden Kurven tendiert: Wenn <math>s_K \hat{y_t}=(n+g+\delta ) \hat{k_t}</math> und somit <math>\hat{k}_{t}=0</math> gilt, befindet sich die Ökonomie im Steady-State. | ||
Bei näherer Betrachtung der Produktionsfunktion je effektiver Arbeitseinheit, <math> \hat{ | Bei näherer Betrachtung der Produktionsfunktion je effektiver Arbeitseinheit, <math>\hat{y}_{t}=\hat{k}_{t}^{\alpha}</math>, wird deutlich, dass der Output ''je effektiver Arbeitseinheit'' im Steady-State nicht wächst, sondern konstant bleibt. Was bedeutet das? Im Steady-State ist nicht die Produktion an sich, sondern die Produktion je effektiver Arbeitseinheit konstant. Aus <math>\hat{y}_{t}=\hat{k}_{t}^{\alpha}</math> folgt als Bedingung für den Steady-State | ||
<math display="block"> | <math display="block"> | ||
s_{K} \hat{k}_{t}^{* \alpha}=(n+g+\delta) \hat{k}_{t}^{*} | |||
</math> | </math> | ||
(1.26) | (1.26) | ||
| Zeile 273: | Zeile 266: | ||
wobei <math> \hat{k^*}</math> den Kapitalstock je effektiver Arbeitseinheit im Steady-State bezeichnet. Gleichung (1.26) lässt sich für <math>\hat{k^*}</math> ausdrücken und man erhält | wobei <math> \hat{k^*}</math> den Kapitalstock je effektiver Arbeitseinheit im Steady-State bezeichnet. Gleichung (1.26) lässt sich für <math>\hat{k^*}</math> ausdrücken und man erhält | ||
<math display="block"> | <math display="block"> | ||
\hat{k^*}=( | \hat{k}^{*}=\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{1}{1-\alpha}} | ||
</math> | </math> | ||
(1.27) | (1.27) | ||
| Zeile 279: | Zeile 272: | ||
Aus der Produktionsfunktion in Gleichung (1.22) folgt daher | Aus der Produktionsfunktion in Gleichung (1.22) folgt daher | ||
<math display="block"> | <math display="block"> | ||
\hat{y^*}=( | \hat{y}^{*}=\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{\alpha}{1-\alpha}} | ||
</math> | </math> | ||
(1.28) | (1.28) | ||
| Zeile 285: | Zeile 278: | ||
wobei <math>\hat{y^*}</math> den Output je effektiver Arbeitseinheit im Steady-State bezeichnet. Da der technologische Fortschritt <math>A</math> und die Bevölkerung (das Arbeitsangebot) <math>L</math> mit den konstanten Raten <math>g</math> bzw. <math>n</math> wachsen, kann der Output im Steady-State zu jedem beliebigen Zeitpunkt dargestellt werden als Steady-State-Output je Beschäftigten <math>y^*</math> zum Zeitpunkt <math>t</math> | wobei <math>\hat{y^*}</math> den Output je effektiver Arbeitseinheit im Steady-State bezeichnet. Da der technologische Fortschritt <math>A</math> und die Bevölkerung (das Arbeitsangebot) <math>L</math> mit den konstanten Raten <math>g</math> bzw. <math>n</math> wachsen, kann der Output im Steady-State zu jedem beliebigen Zeitpunkt dargestellt werden als Steady-State-Output je Beschäftigten <math>y^*</math> zum Zeitpunkt <math>t</math> | ||
<math display="block"> | <math display="block"> | ||
y_{t}^{*}=A_{t} \hat{y}^{*}=A_{0} e^{g t}\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{\alpha}{1-\alpha}} | |||
</math> | </math> | ||
(1.29) | (1.29) | ||
| Zeile 291: | Zeile 284: | ||
und der gesamte Steady-State-Output <math>Y^*</math> zum Zeitpunkt <math>t</math> als | und der gesamte Steady-State-Output <math>Y^*</math> zum Zeitpunkt <math>t</math> als | ||
<math display="block"> | <math display="block"> | ||
Y_{t}^{*}=A_{t} L_{t} \hat{y}^{*}=A_{0} L_{0} e^{(g+n) t}\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{\alpha}{1-\alpha}} | |||
</math> | </math> | ||
(1.30) | (1.30) | ||
| Zeile 304: | Zeile 297: | ||
Darüber hinaus ist das Solow-Modell in der Lage, einen langfristigen Wachstumspfad mit dem Phänomen temporärer Schwankungen zu verbinden. Wie in Abb. 1.1 am Beispiel Österreich veranschaulicht, kann das Wachstum in einzelnen Perioden zwar zum Teil recht erheblichen konjunkturellen Einfluss unterliegen, welche von der jeweiligen Wirtschaftspolitik oder äußeren Faktoren abhängig sind. Langfristig befindet sich die Wirtschaft jedoch offensichtlich auf einem bestimmten Wachstumspfad. Selbst wenn die Wirtschaft schwer erschüttert wird und ein großer Teil des Kapitalstocks etwa durch einen Krieg vernichtet wird, kehrt sie zum Gleichgewichtswachstum zurück. Wie in Abb. 1.3 zu sehen, gilt bei konstanter Sparquote während der Übergangsphase <math>s_K y_t>(n+\delta )k_t</math>, und die Ökonomie weist in dieser Zeit ein relativ hohes Wachstum auf. Auf diese Weise ist das Solow-Modell auch in der Lage, das hohe Wirtschaftswachstum in Österreich nach dem Zweiten Weltkrieg zu erklären („Wirtschaftswunderjahre“). | Darüber hinaus ist das Solow-Modell in der Lage, einen langfristigen Wachstumspfad mit dem Phänomen temporärer Schwankungen zu verbinden. Wie in Abb. 1.1 am Beispiel Österreich veranschaulicht, kann das Wachstum in einzelnen Perioden zwar zum Teil recht erheblichen konjunkturellen Einfluss unterliegen, welche von der jeweiligen Wirtschaftspolitik oder äußeren Faktoren abhängig sind. Langfristig befindet sich die Wirtschaft jedoch offensichtlich auf einem bestimmten Wachstumspfad. Selbst wenn die Wirtschaft schwer erschüttert wird und ein großer Teil des Kapitalstocks etwa durch einen Krieg vernichtet wird, kehrt sie zum Gleichgewichtswachstum zurück. Wie in Abb. 1.3 zu sehen, gilt bei konstanter Sparquote während der Übergangsphase <math>s_K y_t>(n+\delta )k_t</math>, und die Ökonomie weist in dieser Zeit ein relativ hohes Wachstum auf. Auf diese Weise ist das Solow-Modell auch in der Lage, das hohe Wirtschaftswachstum in Österreich nach dem Zweiten Weltkrieg zu erklären („Wirtschaftswunderjahre“). | ||
Das Solow-Modell wird recht häufig dafür kritisiert, dass es zwar die Bedeutung des technologischen Fortschritts veranschaulicht, aber keine Antwort auf die Frage gibt, wie dieser technologische Fortschritt entsteht. <ref>Die in den späten 1980er-Jahren entstandene endogene Wachstumstheorie (ausgehend von Arbeiten von Paul M. Romer sowie Robert E Lucas Jr.) versucht, die Determinanten der Höhe des technologischen Fortschritts zu modellieren und somit den technologischen Fortschritt als solchen zu bestimmen.</ref> Ein weiteres Problem ergibt sich beim Versuch einer Quantifizierung des ursprünglichen Solow-Modells. Ein Unterschied um das Zehnfache beim BIP je Arbeitseinheit ist nicht ungewöhnlich bei Vergleichen sowohl im Raum wie über die Zeit. Ein zehnfacher Unterschied in Bezug auf Arbeitsproduktivität bedingt im Solow-Modell jedoch einen Unterschied von <math>10^ | Das Solow-Modell wird recht häufig dafür kritisiert, dass es zwar die Bedeutung des technologischen Fortschritts veranschaulicht, aber keine Antwort auf die Frage gibt, wie dieser technologische Fortschritt entsteht. <ref>Die in den späten 1980er-Jahren entstandene endogene Wachstumstheorie (ausgehend von Arbeiten von Paul M. Romer sowie Robert E Lucas Jr.) versucht, die Determinanten der Höhe des technologischen Fortschritts zu modellieren und somit den technologischen Fortschritt als solchen zu bestimmen.</ref> Ein weiteres Problem ergibt sich beim Versuch einer Quantifizierung des ursprünglichen Solow-Modells. Ein Unterschied um das Zehnfache beim BIP je Arbeitseinheit ist nicht ungewöhnlich bei Vergleichen sowohl im Raum wie über die Zeit. Ein zehnfacher Unterschied in Bezug auf Arbeitsproduktivität bedingt im Solow-Modell jedoch einen Unterschied von <math>10^{1 / \alpha} )</math> bei der Kapitalausstattung – bei der üblichen Annahme von <math>\alpha \approx 1/3</math> ergibt sich daraus eine Kapitalausstattung je Arbeitseinheit um das Tausendfache. Das Verhältnis Kapital-Output mag sowohl über die Zeit wie in verschiedenen Ökonomien ganz erheblich variieren, derart gigantische Unterschiede sind jedoch empirisch nicht haltbar. | ||
Ein zweites Problem der Quantifizierung ergibt sich bei Vergleichen um die Welt. Aus <math>\alpha \approx 1/3</math> ergibt sich weiter, dass eine Differenz beim Output je Arbeiter um das Zehnfache eine Differenz bei der Grenzproduktivität des Kapitals um das Hundertfache bedingt. Im Kontext ganzer Volkswirtschaften folgt, dass da, wo bereits viel Kapital vorhanden ist, der Grenzertrag einer weiteren Einheit die Gesamtproduktion relativ wenig erhöhen wird – und umgekehrt da, wo noch wenig Kapital vorhanden ist, eine weitere Einheit sehr viel Ertrag bringt. Folglich wäre eine rege Investitionstätigkeit in Entwicklungs- und Schwellenländern zu erwarten, während Industrieländer eher unattraktiv für Investoren wären: Aus Gleichung (1.7) | Ein zweites Problem der Quantifizierung ergibt sich bei Vergleichen um die Welt. Aus <math>\alpha \approx 1/3</math> ergibt sich weiter, dass eine Differenz beim Output je Arbeiter um das Zehnfache eine Differenz bei der Grenzproduktivität des Kapitals um das Hundertfache bedingt. Im Kontext ganzer Volkswirtschaften folgt, dass da, wo bereits viel Kapital vorhanden ist, der Grenzertrag einer weiteren Einheit die Gesamtproduktion relativ wenig erhöhen wird – und umgekehrt da, wo noch wenig Kapital vorhanden ist, eine weitere Einheit sehr viel Ertrag bringt. Folglich wäre eine rege Investitionstätigkeit in Entwicklungs- und Schwellenländern zu erwarten, während Industrieländer eher unattraktiv für Investoren wären: Aus Gleichung (1.7) | ||
| Zeile 310: | Zeile 303: | ||
und der Cobb-Douglas-Produktionsfunktion aus Gleichung (1.15) ergibt sich als erwarteter Gewinn einer zusätzlichen Einheit Kapital zum Zeitpunkt <math>t</math>: | und der Cobb-Douglas-Produktionsfunktion aus Gleichung (1.15) ergibt sich als erwarteter Gewinn einer zusätzlichen Einheit Kapital zum Zeitpunkt <math>t</math>: | ||
<math display="block"> | <math display="block"> | ||
\frac{\partial Y_{t}}{\partial K_{t}}=\alpha K_{t}^{\alpha-1} L_{t}^{1-\alpha}=\alpha\left(\frac{L_{t}}{K_{t}}\right)^{1-\alpha}>0 | |||
</math> | </math> | ||
(1.31) | (1.31) | ||
| Zeile 316: | Zeile 309: | ||
Da <math>\alpha <1</math> gilt, ist die der erwartete Gewinn (rate of return) eindeutig positiv. Ein nochmaliges Ableiten der Produktionsfunktion zeigt, dass dieser zusätzliche Produktionsgewinn je Einheit <math>K_t</math> umso kleiner wird, je größer <math>K_t</math> ist: | Da <math>\alpha <1</math> gilt, ist die der erwartete Gewinn (rate of return) eindeutig positiv. Ein nochmaliges Ableiten der Produktionsfunktion zeigt, dass dieser zusätzliche Produktionsgewinn je Einheit <math>K_t</math> umso kleiner wird, je größer <math>K_t</math> ist: | ||
<math display="block"> | <math display="block"> | ||
\frac{\partial^{2} Y_{t}}{\partial K_{t}^{2}}=\alpha(\alpha-1) K_{t}^{\alpha-2} L_{t}^{1-\alpha}<0 | |||
</math> | </math> | ||
(1.32) | (1.32) | ||
| Zeile 328: | Zeile 321: | ||
N. Gregory Mankiw, David Romer und David N. Weil <ref>N. Gregory Mankiw, David Romer, David N. Weil: A Contribution to the Empirics of Economic Growth, Quarterly Journal of Economics 107, 1992</ref> haben kurz nach Lucas’ Beitrag Solows Modell erweitert, indem sie das Humankapital als zusätzlichen Faktor in die Produktionsfunktion aufnehmen: | N. Gregory Mankiw, David Romer und David N. Weil <ref>N. Gregory Mankiw, David Romer, David N. Weil: A Contribution to the Empirics of Economic Growth, Quarterly Journal of Economics 107, 1992</ref> haben kurz nach Lucas’ Beitrag Solows Modell erweitert, indem sie das Humankapital als zusätzlichen Faktor in die Produktionsfunktion aufnehmen: | ||
<math display="block"> | <math display="block"> | ||
Y_{t}=K_{t}^{\alpha} H_{t}^{\beta}\left(A_{t} L_{t}\right)^{1-\alpha-\beta}, \quad \alpha>0, \quad \beta>0, \quad \alpha+\beta<1 | |||
</math> | </math> | ||
(1.33) | (1.33) | ||
| Zeile 336: | Zeile 329: | ||
Die Dynamik des Modells folgt für Arbeit und Technologie den in den Gleichungen (1.10) und (1.18) dargestellten Prozessen. Für Sachkapital gilt in Analogie zu Gleichung (1.23) | Die Dynamik des Modells folgt für Arbeit und Technologie den in den Gleichungen (1.10) und (1.18) dargestellten Prozessen. Für Sachkapital gilt in Analogie zu Gleichung (1.23) | ||
<math display="block"> | <math display="block"> | ||
K | \dot{K}_{t}=s_{K} f\left(K_{t}, H_{t}, A_{t} L_{t}\right)-\delta K_{t}=s_{K} Y_{t}-\delta K_{t} | ||
</math> | </math> | ||
(1.34) | (1.34) | ||
| Zeile 342: | Zeile 335: | ||
Durch die Aufnahme einer zweiten Form von Kapital wird nun eine zweite Kapitalakkumulationsgleichung benötigt: | Durch die Aufnahme einer zweiten Form von Kapital wird nun eine zweite Kapitalakkumulationsgleichung benötigt: | ||
<math display="block"> | <math display="block"> | ||
H | \dot{H}_{t}=s_{H} f\left(K_{t}, H_{t}, A_{t} L_{t}\right)-\delta H_{t}=s_{H} Y_{t}-\delta H_{t} | ||
</math> | </math> | ||
(1.35) | (1.35) | ||
| Zeile 350: | Zeile 343: | ||
Das gesamte Lohnaufkommen <math>W</math> zum Zeitpunkt <math>t</math> beträgt somit | Das gesamte Lohnaufkommen <math>W</math> zum Zeitpunkt <math>t</math> beträgt somit | ||
<math display="block"> | <math display="block"> | ||
W_{t}=L_{t} w_{t}=L_{t} \frac{\partial Y_{t}}{\partial L_{t}}+H_{t} \frac{\partial Y_{t}}{\partial H_{t}} | |||
</math> | </math> | ||
(1.36) | (1.36) | ||
| Zeile 356: | Zeile 349: | ||
während der Gewinnsatz zum Zeitpunkt <math>t</math> unverändert bleibt und der Beziehung in Gleichung (1.7) mit <math>r_t=\partial Y_t/\partial K_t</math> folgt. Analog zu Gleichung (1.22) können wiederum beide Seiten der Produktionsfunktion in Gleichung (1.35) durch effektive Arbeit dividiert werden, und man erhält so die Produktion je effektiver Arbeitseinheit: | während der Gewinnsatz zum Zeitpunkt <math>t</math> unverändert bleibt und der Beziehung in Gleichung (1.7) mit <math>r_t=\partial Y_t/\partial K_t</math> folgt. Analog zu Gleichung (1.22) können wiederum beide Seiten der Produktionsfunktion in Gleichung (1.35) durch effektive Arbeit dividiert werden, und man erhält so die Produktion je effektiver Arbeitseinheit: | ||
<math display="block"> | <math display="block"> | ||
\hat{ | \hat{y}_{t}=\frac{Y_{t}}{A_{t} L_{t}} \Rightarrow \hat{y}_{t}=\hat{k}_{t}^{\alpha} \hat{h}_{t}^{\beta} | ||
</math> | </math> | ||
(1.37) | (1.37) | ||
| Zeile 364: | Zeile 357: | ||
Die Entwicklung der Ökonomie lässt sich darstellen über die beiden Schlüsselgleichungen des Mankiw-Romer-Weil-Modells | Die Entwicklung der Ökonomie lässt sich darstellen über die beiden Schlüsselgleichungen des Mankiw-Romer-Weil-Modells | ||
<math display="block"> | <math display="block"> | ||
\hat{k | \dot{\hat{k}}_{t}=s_{K} \hat{y}_{t}-(n+g+\delta) \hat{k}_{t} | ||
</math> | </math> | ||
(1.38) | (1.38) | ||
| Zeile 370: | Zeile 363: | ||
und | und | ||
<math display="block"> | <math display="block"> | ||
\hat{ | \dot{\hat{h}}_{t}=s_{H} \hat{y}_{t}-(n+g+\delta) \hat{h}_{t} | ||
</math> | </math> | ||
(1.39) | (1.39) | ||
| Zeile 376: | Zeile 369: | ||
die das Wachstum an Sachkapital je effektiver Arbeitseinheit, und das Wachstum an Humankapital je effektiver Arbeitseinheit darstellen. Setzt man jeweils die rechte Seite der beiden Gleichungen (1.38) und (1.39) gleich null und löst das entsprechende System aus zwei Gleichungen für <math> \hat{k}</math> und <math> \hat{h}</math>, so erhält man den Steady-State-Wert des Sachkapitals je effektiver Arbeitseinheit, | die das Wachstum an Sachkapital je effektiver Arbeitseinheit, und das Wachstum an Humankapital je effektiver Arbeitseinheit darstellen. Setzt man jeweils die rechte Seite der beiden Gleichungen (1.38) und (1.39) gleich null und löst das entsprechende System aus zwei Gleichungen für <math> \hat{k}</math> und <math> \hat{h}</math>, so erhält man den Steady-State-Wert des Sachkapitals je effektiver Arbeitseinheit, | ||
<math display="block"> | <math display="block"> | ||
\hat{k^*}=( | \hat{k}^{*}=\left(\frac{s_{K}^{1-\beta} s_{H}^{\beta}}{n+g+\delta}\right)^{\frac{1}{1-\alpha-\beta}} | ||
</math> | </math> | ||
(1.40) | (1.40) | ||
| Zeile 382: | Zeile 375: | ||
des Humankapitals je effektiver Arbeitseinheit, | des Humankapitals je effektiver Arbeitseinheit, | ||
<math display="block"> | <math display="block"> | ||
\hat{ | \hat{h}^{*}=\left(\frac{s_{K}^{\alpha} s_{H}^{1-\alpha}}{n+g+\delta}\right)^{\frac{1}{1-\alpha-\beta}} | ||
</math> | </math> | ||
(1.41) | (1.41) | ||
| Zeile 388: | Zeile 381: | ||
sowie, folgend aus Gleichung (1.37), Output im Steady-State je effektiver Arbeitseinheit: | sowie, folgend aus Gleichung (1.37), Output im Steady-State je effektiver Arbeitseinheit: | ||
<math display="block"> | <math display="block"> | ||
\hat{y^*}= \hat{k^ | \hat{y}^{*}=\hat{k}^{* a} \hat{h}^{* b}=\left(\frac{s_{K} s_{H}}{(n+g+\delta)^{\alpha+\beta}}\right)^{\frac{1}{1-\alpha-\beta}} | ||
</math> | </math> | ||
(1.42) | (1.42) | ||
| Zeile 396: | Zeile 389: | ||
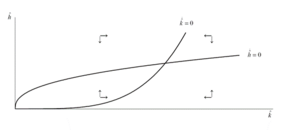
[[Datei:EC442 5.png|300px|none|thumb|Die dynamische Stabilität des Mankiw-Romer-Weil-Modells – unabhängig von der Ausgangslage strebt die Ökonomie stets zum Zustand ...]] | [[Datei:EC442 5.png|300px|none|thumb|Die dynamische Stabilität des Mankiw-Romer-Weil-Modells – unabhängig von der Ausgangslage strebt die Ökonomie stets zum Zustand ...]] | ||
<span id="_Toc251498197" class="anchor"></span>Abb. 1.5: Die dynamische Stabilität des Mankiw-Romer-Weil-Modells – unabhängig<br> | <span id="_Toc251498197" class="anchor"></span>Abb. 1.5: Die dynamische Stabilität des Mankiw-Romer-Weil-Modells – unabhängig<br> | ||
von der Ausgangslage strebt die Ökonomie stets zum Zustand <math>\hat{k}=0</math> und <math>\hat{h}=0</math> | von der Ausgangslage strebt die Ökonomie stets zum Zustand <math>\dot{\hat{k}}=0</math> und <math>\dot{\hat{h}}=0</math> | ||
Die Ökonomie befindet sich im Steady-State-Wachstum, wenn <math> \hat{k}=0</math> und <math> \hat{h}=0</math>: Sind beide Bedingungen erfüllt, beträgt wie im Solow-Modell das Wachstum je effektiver Einheit Null, und das Wachstum je Beschäftigten entspricht <math>g</math>. Dementsprechend werden positive oder negative Veränderung der Höhe von <math>s_K</math> oder <math>s_H</math> sich zwar entsprechend auf das langfristige Output-Niveau auswirken, nicht aber auf die langfristige Wachstumsrate. Die Auswirkungen auf das langfristige Outputniveau durch Veränderung von einer oder beiden Sparquoten (Sachkapital und/oder Humankapital) lassen sich aus Gleichung (1.42) ablesen. | Die Ökonomie befindet sich im Steady-State-Wachstum, wenn <math>\dot{\hat{k}}=0</math> und <math>\dot{\hat{h}}=0</math>: Sind beide Bedingungen erfüllt, beträgt wie im Solow-Modell das Wachstum je effektiver Einheit Null, und das Wachstum je Beschäftigten entspricht <math>g</math>. Dementsprechend werden positive oder negative Veränderung der Höhe von <math>s_K</math> oder <math>s_H</math> sich zwar entsprechend auf das langfristige Output-Niveau auswirken, nicht aber auf die langfristige Wachstumsrate. Die Auswirkungen auf das langfristige Outputniveau durch Veränderung von einer oder beiden Sparquoten (Sachkapital und/oder Humankapital) lassen sich aus Gleichung (1.42) ablesen. | ||
Durch die Berücksichtigung eines zusätzlichen Faktors wird das Mankiw-Romer-Weil-Modell im Vergleich zum Solow-Modell zwar komplexer, bleibt aber stabil: Was immer auch der Ausgangspunkt der Ökonomie hinsichtlich der Werte für <math> \hat{k}</math> und <math>\hat{h}</math> sein mag, das System konvergiert zu <math> \hat{k}=0</math> und <math> \hat{ h}=0</math> <ref>Ausgenommen ist hier ein Ausgangspunkt mit <math> \hat{k}=0</math> oder ; ein solcher Ausgangspunkt entspricht jedoch einer nicht existierenden Ökonomie und ist daher für die weitere Betrachtung belanglos.</ref> Dieser Zusammenhang wird im Phasendiagramm in Abb. 1.5 skizziert: Von einem beliebigen Ausgangspunkt strebt das System stets zum Schnittpunkt der beiden Kurven. | Durch die Berücksichtigung eines zusätzlichen Faktors wird das Mankiw-Romer-Weil-Modell im Vergleich zum Solow-Modell zwar komplexer, bleibt aber stabil: Was immer auch der Ausgangspunkt der Ökonomie hinsichtlich der Werte für <math> \hat{k}</math> und <math>\hat{h}</math> sein mag, das System konvergiert zu <math> \hat{k}=0</math> und <math> \hat{ h}=0</math> <ref>Ausgenommen ist hier ein Ausgangspunkt mit <math> \hat{k}=0</math> oder ; ein solcher Ausgangspunkt entspricht jedoch einer nicht existierenden Ökonomie und ist daher für die weitere Betrachtung belanglos.</ref> Dieser Zusammenhang wird im Phasendiagramm in Abb. 1.5 skizziert: Von einem beliebigen Ausgangspunkt strebt das System stets zum Schnittpunkt der beiden Kurven. | ||
| Zeile 404: | Zeile 397: | ||
Die ''qualitativen'' Schlussfolgerungen des Mankiw-Romer-Weil-Modells sind ähnlich zu jenen des Solow-Modells, die Einbeziehung des Humankapital führt jedoch zu erheblichen quantitativen Unterschieden. Dazu zählt insbesondere die Grenzproduktivität des Kapitals, die im Cobb-Douglas-Fall folgende Form annimmt: | Die ''qualitativen'' Schlussfolgerungen des Mankiw-Romer-Weil-Modells sind ähnlich zu jenen des Solow-Modells, die Einbeziehung des Humankapital führt jedoch zu erheblichen quantitativen Unterschieden. Dazu zählt insbesondere die Grenzproduktivität des Kapitals, die im Cobb-Douglas-Fall folgende Form annimmt: | ||
<math display="block"> | <math display="block"> | ||
\frac{\partial Y_{t}}{\partial K_{t}}=\alpha K_{t}^{\alpha-1} H_{t}^{\beta}\left(A_{t} L_{t}\right)^{1-\alpha-\beta} | |||
</math> | </math> | ||
(1.43) | (1.43) | ||
| Zeile 421: | Zeile 414: | ||
# Die Grenzproduktivität des Kapitals ist dort höher, wo noch wenig vorhanden ist – bei freien Kapitalflüssen und unter sonst identischen Bedingungen wird dort investiert werden, wo noch wenig vorhanden ist, wodurch ein Aufholprozess hinsichtlich der Produktivität in Gang gesetzt wird. | # Die Grenzproduktivität des Kapitals ist dort höher, wo noch wenig vorhanden ist – bei freien Kapitalflüssen und unter sonst identischen Bedingungen wird dort investiert werden, wo noch wenig vorhanden ist, wodurch ein Aufholprozess hinsichtlich der Produktivität in Gang gesetzt wird. | ||
# Output ist auch eine Funktion der Technologie. Daraus folgt, dass technologische Aufholprozesse zu einer Steigerung der Produktion führen. | # Output ist auch eine Funktion der Technologie. Daraus folgt, dass technologische Aufholprozesse zu einer Steigerung der Produktion führen. | ||
Modellendogene Konvergenz | |||
===== Modellendogene Konvergenz ===== | |||
Der erste Punkt ergibt sich aus dem Modell selbst, wonach eine Ökonomie stets zu ihrem ''eigenen'' Steady-State konvergieren wird. <ref>Für das Mankiw-Romer-Weil-Modell ist dieser Zusammenhang in Abb. 1.5 dargestellt.</ref> Die Stabilität des Modells gewährleistet eine Konvergenz der Produktionsfaktoren zu einem bestimmten Niveau – was auch immer die Ausgangslage sein mag. Dieser Zusammenhang wurde von Robert J. Barro und Xavier X. Sala-i-Martin <ref>Für eine ausführlichere Diskussion des Konzepts siehe: Robert J. Barro und Xavier X. Sala-i-Martin: Convergence, Journal of Political Economy 100, 1992</ref> formal aus dem Solow-Modell abgeleitet und mündet in die Gleichung | Der erste Punkt ergibt sich aus dem Modell selbst, wonach eine Ökonomie stets zu ihrem ''eigenen'' Steady-State konvergieren wird. <ref>Für das Mankiw-Romer-Weil-Modell ist dieser Zusammenhang in Abb. 1.5 dargestellt.</ref> Die Stabilität des Modells gewährleistet eine Konvergenz der Produktionsfaktoren zu einem bestimmten Niveau – was auch immer die Ausgangslage sein mag. Dieser Zusammenhang wurde von Robert J. Barro und Xavier X. Sala-i-Martin <ref>Für eine ausführlichere Diskussion des Konzepts siehe: Robert J. Barro und Xavier X. Sala-i-Martin: Convergence, Journal of Political Economy 100, 1992</ref> formal aus dem Solow-Modell abgeleitet und mündet in die Gleichung | ||
<math display="block"> | <math display="block"> | ||
1 | \frac{1}{T} \ln \left(\frac{y_{T}}{y_{0}}\right)=g+\frac{1-e^{-\tilde{\beta} T}}{T} \ln \left(\frac{y_{0}^{*}}{y_{0}}\right) | ||
</math> | </math> | ||
(1.44) | (1.44) | ||
| Zeile 431: | Zeile 425: | ||
wobei <math>ln</math> den natürlichen Logarithmus bezeichnet und <math>\tilde{\beta}=(1-\alpha )(n+g+\delta )</math> die Konvergenzgeschwindigkeit misst. <ref>Im Mankiw-Romer-Weil-Modell ergibt sich als Konvergenz-Geschwindigkeit <math>\beta \approx (1-\alpha -\beta )(n+g+\delta )</math></ref> Die linke Seite in Gleichung (1.44) entspricht einer Approximation des Wachstums zwischen den Zeitpunkten <math>=</math> und <math>T</math>. Nach einigen Umformungen erhält man die ökonometrische Spezifikation | wobei <math>ln</math> den natürlichen Logarithmus bezeichnet und <math>\tilde{\beta}=(1-\alpha )(n+g+\delta )</math> die Konvergenzgeschwindigkeit misst. <ref>Im Mankiw-Romer-Weil-Modell ergibt sich als Konvergenz-Geschwindigkeit <math>\beta \approx (1-\alpha -\beta )(n+g+\delta )</math></ref> Die linke Seite in Gleichung (1.44) entspricht einer Approximation des Wachstums zwischen den Zeitpunkten <math>=</math> und <math>T</math>. Nach einigen Umformungen erhält man die ökonometrische Spezifikation | ||
<math display="block"> | <math display="block"> | ||
\frac{\ln y_{T}-\ln y_{0}}{T}=\beta_{0}+\beta_{1} \ln y_{0} | |||
</math> | </math> | ||
(1.45) | (1.45) | ||
wobei <math>\ | wobei <math>\beta_{0}=g+\left[\left(1-e^{-\tilde{\beta} T}\right) / T\right] \ln y_{0}^{*}</math> der Konstanten und <math>\beta_{1}=\left(e^{-\tilde{\beta} T}-1\right) / T</math> der Steigung der Regressionsgeraden entspricht, woraus sich schließlich als empirisch messbare Konvergenzgeschwindigkeit <math>\tilde{\beta}=-\ln(1+Tb)/T</math> ergibt. In ökonometrischen Tests wird üblicherweise <math>\beta _1</math> geschätzt: Ist <math>\beta _1</math> negativ, so liegt Konvergenz vor – ein höheres Ausgangsniveau des BIP je Einwohner, <math>y_0</math>, führt der Hypothese zufolge zu einem langsameren Wachstum, daher besteht ein negativer Zusammenhang. Da <math>\beta _1</math> der entscheidende Parameter ist, spricht man auch von Beta-Konvergenz. | ||
Eine einfachere Methode, die Konvergenz-Hypothese zu prüfen, besteht darin, die Varianz des BIP je Einwohner für mehrere Zeitpunkte <math>t</math> zu messen: | Eine einfachere Methode, die Konvergenz-Hypothese zu prüfen, besteht darin, die Varianz des BIP je Einwohner für mehrere Zeitpunkte <math>t</math> zu messen: | ||
<math display="block"> | <math display="block"> | ||
\ | \sigma_{t}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(\ln y_{i, t}-\frac{1}{n} \sum_{i=1}^{n} \ln y_{i, t}\right)^{2} | ||
</math> | </math> | ||
(1.46) | (1.46) | ||
| Zeile 445: | Zeile 439: | ||
Um für allgemeine Wachstumsprozesse und Inflation zu kontrollieren, werden auch hier die Werte logarithmiert. Nimmt die Varianz im Zeitverlauf ab, so liegt Konvergenz vor. Da die Varianz üblicherweise durch <math>\sigma </math> symbolisiert wird, wird diese Art der Konvergenz auch Sigma-Konvergenz genannt. | Um für allgemeine Wachstumsprozesse und Inflation zu kontrollieren, werden auch hier die Werte logarithmiert. Nimmt die Varianz im Zeitverlauf ab, so liegt Konvergenz vor. Da die Varianz üblicherweise durch <math>\sigma </math> symbolisiert wird, wird diese Art der Konvergenz auch Sigma-Konvergenz genannt. | ||
Typen von Konvergenz | ===== Typen von Konvergenz ===== | ||
Ein Problem, das sich bei Prüfung der Konvergenz-Hypothesen auftritt, ist, dass ein Steady-State ein theoretisches Konstrukt darstellt, dessen wahre Höhe unbekannt ist – weshalb Annahmen darüber getroffen werden müssen, inwieweit sich die zu prüfenden Ökonomien hinsichtlich ihrer Steady-States voneinander unterscheiden. In empirischen Tests werden üblicherweise die Ausgangsdaten und die Wachstumsraten ausgewählter Ökonomien verglichen, gegebenenfalls ergänzt um weitere Variablen – d.h. es wird getestet, ob die Ökonomien ''zueinander'' konvergieren. Da das Solow-Modell als solches jedoch ein Modell für eine geschlossene Ökonomie ist, werden zwei Konzepte der Konvergenz ''unterschiedlicher'' Ökonomien unterschieden: | Ein Problem, das sich bei Prüfung der Konvergenz-Hypothesen auftritt, ist, dass ein Steady-State ein theoretisches Konstrukt darstellt, dessen wahre Höhe unbekannt ist – weshalb Annahmen darüber getroffen werden müssen, inwieweit sich die zu prüfenden Ökonomien hinsichtlich ihrer Steady-States voneinander unterscheiden. In empirischen Tests werden üblicherweise die Ausgangsdaten und die Wachstumsraten ausgewählter Ökonomien verglichen, gegebenenfalls ergänzt um weitere Variablen – d.h. es wird getestet, ob die Ökonomien ''zueinander'' konvergieren. Da das Solow-Modell als solches jedoch ein Modell für eine geschlossene Ökonomie ist, werden zwei Konzepte der Konvergenz ''unterschiedlicher'' Ökonomien unterschieden: | ||
| Zeile 455: | Zeile 449: | ||
Als Beispiel für bedingte Konvergenz aufgrund vergleichbarer Steady-States kann der Aufholprozess Österreichs gegenüber der Schweiz nach dem Zweiten Weltkrieg genannt werden: Die beiden Länder sind sich hinsichtlich ihrer wichtigsten Parameter ähnlich, allerdings war das Sachkapital in Österreich vom Krieg weitgehend zerstört. Das führte zu einer erhöhten Grenzproduktivität von Sachkapitalinvestitionen in Österreich, was das Wachstum temporär beschleunigt hat: Ausgehend von einem niedrigeren Niveau hat Österreich über Jahrzehnte zur Schweiz aufgeholt, bis sich der Abstand auf relativ niedrigem Niveau eingependelt hat. | Als Beispiel für bedingte Konvergenz aufgrund vergleichbarer Steady-States kann der Aufholprozess Österreichs gegenüber der Schweiz nach dem Zweiten Weltkrieg genannt werden: Die beiden Länder sind sich hinsichtlich ihrer wichtigsten Parameter ähnlich, allerdings war das Sachkapital in Österreich vom Krieg weitgehend zerstört. Das führte zu einer erhöhten Grenzproduktivität von Sachkapitalinvestitionen in Österreich, was das Wachstum temporär beschleunigt hat: Ausgehend von einem niedrigeren Niveau hat Österreich über Jahrzehnte zur Schweiz aufgeholt, bis sich der Abstand auf relativ niedrigem Niveau eingependelt hat. | ||
Kapitalflüsse | ===== Kapitalflüsse ===== | ||
Das Modell von Mankiw, Romer und Weil bietet eine bessere Erklärung für die empirisch beobachtbaren Kapitalströme, ändert aber nichts an einer der Grundaussagen des Modells: Wo die Grenzproduktivität des Sachkapitals höher ist, ist der erwartete Ertrag einer Neuinvestition höher, also wird Kapital dorthin fließen. Die Attraktivität des Ziellands hängt nicht nur davon ab, wie viel Sachkapital dort bereits vorhanden ist, sondern insbesondere, wie produktiv es eingesetzt wird. Die Hypothese, wonach unter sonst gleichen Bedingungen Kapital in kapitalärmere Regionen fließen wird, bleibt unter der Annahme konstanter Skalenerträge aufrecht. Der Fall steigender Skalenerträge wird im folgenden Kapitel 1.3.2 diskutiert. | Das Modell von Mankiw, Romer und Weil bietet eine bessere Erklärung für die empirisch beobachtbaren Kapitalströme, ändert aber nichts an einer der Grundaussagen des Modells: Wo die Grenzproduktivität des Sachkapitals höher ist, ist der erwartete Ertrag einer Neuinvestition höher, also wird Kapital dorthin fließen. Die Attraktivität des Ziellands hängt nicht nur davon ab, wie viel Sachkapital dort bereits vorhanden ist, sondern insbesondere, wie produktiv es eingesetzt wird. Die Hypothese, wonach unter sonst gleichen Bedingungen Kapital in kapitalärmere Regionen fließen wird, bleibt unter der Annahme konstanter Skalenerträge aufrecht. Der Fall steigender Skalenerträge wird im folgenden Kapitel 1.3.2 diskutiert. | ||
Technologische Aufholprozesse | ===== Technologische Aufholprozesse ===== | ||
Technologische Aufholprozesse als dritter Grund für Konvergenz können auf mannigfaltige Weise auftreten. Die Ausbreitung des Wissens ist bereits für die ältesten Hochkulturen kennzeichnend, ihre zum Teil jahrtausendealten Pfade wirken bis heute nach. Im Sinne ökonomischer Entwicklung kann Wissen dabei sehr umfassend begriffen werden und beschreibt sehr abstrakte Konzepte ebenso wie alltägliche Anwendungen. | Technologische Aufholprozesse als dritter Grund für Konvergenz können auf mannigfaltige Weise auftreten. Die Ausbreitung des Wissens ist bereits für die ältesten Hochkulturen kennzeichnend, ihre zum Teil jahrtausendealten Pfade wirken bis heute nach. Im Sinne ökonomischer Entwicklung kann Wissen dabei sehr umfassend begriffen werden und beschreibt sehr abstrakte Konzepte ebenso wie alltägliche Anwendungen. | ||
| Zeile 526: | Zeile 520: | ||
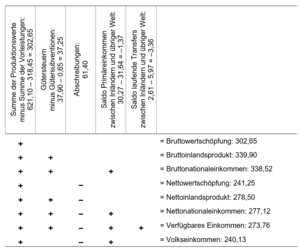
<ul> | <ul> | ||
<li><p>'''Bruttowertschöpfung''' (BWS): Sie ist die Grundlage der VGR und entspricht der Summe aller Produktionswerte abzüglich der Vorleistungen. In einer Welt ohne Ausland und ohne indirekte Steuern spiegelt sie das <math>Y</math> in den<br>Wachstumsmodellen wider. Die BWS entspricht der Produktion zu ''Herstellungspreisen'' oder ''Faktorkosten''.</p></li> | <li><p>'''Bruttowertschöpfung''' (BWS): Sie ist die Grundlage der VGR und entspricht der Summe aller Produktionswerte abzüglich der Vorleistungen. In einer Welt ohne Ausland und ohne indirekte Steuern spiegelt sie das <math>Y</math> in den<br>Wachstumsmodellen wider. Die BWS entspricht der Produktion zu ''Herstellungspreisen'' oder ''Faktorkosten''.</p></li> | ||
<li><p>Das '''Bruttoinlandsprodukt''' (BIP) ergibt sich durch Addition der indirekten Steuern abzüglich der Subventionen. Die Unterschiede zur BWS sind folglich die zusätzlichen Einnahmen und Ausgaben des Staates, der durch seine Politik in die Preissetzung am Markt eingreift. Das BIP entspricht daher der Produktion zu ''Marktpreisen''. | <li><p>Das '''Bruttoinlandsprodukt''' (BIP) ergibt sich durch Addition der indirekten Steuern abzüglich der Subventionen. Die Unterschiede zur BWS sind folglich die zusätzlichen Einnahmen und Ausgaben des Staates, der durch seine Politik in die Preissetzung am Markt eingreift. Das BIP entspricht daher der Produktion zu ''Marktpreisen''.</p> | ||
<p>Manchmal finden sich auch Ausdrücke wie „BIP zu Faktorkosten“, was daher der BWS entspricht.</p></li>minus Gütersubventionen:</ul> | <p>Manchmal finden sich auch Ausdrücke wie „BIP zu Faktorkosten“, was daher der BWS entspricht.</p></li>minus Gütersubventionen:</ul> | ||
</ul> | </ul> | ||
[[Datei:Ec a1.png|300px|none|thumb]] | |||
| Zeile 565: | Zeile 530: | ||
Diese ab- und zufließenden Primäreinkommen setzen sich aus Einkommen aus Besitz und Unternehmung sowie aus Arbeitseinkommen zusammen. Erstere entstehen insbesondere durch Vermögensbestände von Inländern im Ausland wie Beteiligungen an Unternehmen, ausländische Staatsanleihen etc. Letztere entstehen aus Arbeitseinkommen von Inländern im Ausland wie jene von Auslandspendlern (und jeweils umgekehrt von Ausländern im Inland). Man beachte, dass gemäß dem Europäischen System Volkswirtschaftlicher Gesamtrechnungen (ESVG) das Inländer-Konzept nicht Inländer im staatsrechtlichen Sinn umfasst, sondern dass sämtliche Erwerbspersonen, die ihren wirtschaftlichen Schwerpunkt | Diese ab- und zufließenden Primäreinkommen setzen sich aus Einkommen aus Besitz und Unternehmung sowie aus Arbeitseinkommen zusammen. Erstere entstehen insbesondere durch Vermögensbestände von Inländern im Ausland wie Beteiligungen an Unternehmen, ausländische Staatsanleihen etc. Letztere entstehen aus Arbeitseinkommen von Inländern im Ausland wie jene von Auslandspendlern (und jeweils umgekehrt von Ausländern im Inland). Man beachte, dass gemäß dem Europäischen System Volkswirtschaftlicher Gesamtrechnungen (ESVG) das Inländer-Konzept nicht Inländer im staatsrechtlichen Sinn umfasst, sondern dass sämtliche Erwerbspersonen, die ihren wirtschaftlichen Schwerpunkt | ||
{| | {| style="border-collapse: collapse; height: 224px;" border="1" | ||
! | ! style="height: 28px; width: 35.4051px;" | | ||
! | ! style="height: 28px; width: 423.519px;" | '''Bruttoinlandsprodukt: 339,90''' | ||
|- | |- style="height: 28px;" | ||
| '''-''' | | style="height: 28px; width: 35.4051px;" | '''-''' | ||
| Arbeitnehmerentgelte an die übrige Welt: 2,72 | | style="height: 28px; width: 423.519px;" | Arbeitnehmerentgelte an die übrige Welt: 2,72 | ||
|- | |- style="height: 28px;" | ||
| '''-''' | | style="height: 28px; width: 35.4051px;" | '''-''' | ||
| Vermögenseinkommen an die übrige Welt: 28,50 | | style="height: 28px; width: 423.519px;" | Vermögenseinkommen an die übrige Welt: 28,50 | ||
|- | |- style="height: 28px;" | ||
| '''-''' | | style="height: 28px; width: 35.4051px;" | '''-''' | ||
| Produktions- und Importabgaben an die Institutionen der EU: 0,42 | | style="height: 28px; width: 423.519px;" | Produktions- und Importabgaben an die Institutionen der EU: 0,42 | ||
|- | |- style="height: 28px;" | ||
| '''+''' | | style="height: 28px; width: 35.4051px;" | '''+''' | ||
| Arbeitnehmerentgelte aus der übrigen Welt: 2,29 | | style="height: 28px; width: 423.519px;" | Arbeitnehmerentgelte aus der übrigen Welt: 2,29 | ||
|- | |- style="height: 28px;" | ||
| '''+''' | | style="height: 28px; width: 35.4051px;" | '''+''' | ||
| Vermögenseinkommen aus der übrigen Welt: 27,24 | | style="height: 28px; width: 423.519px;" | Vermögenseinkommen aus der übrigen Welt: 27,24 | ||
|- | |- style="height: 28px;" | ||
| '''+''' | | style="height: 28px; width: 35.4051px;" | '''+''' | ||
| Subventionen aus der EU: 0,74 | | style="height: 28px; width: 423.519px;" | Subventionen aus der EU: 0,74 | ||
|- | |- style="height: 28px;" | ||
| '''=''' | | style="height: 28px; width: 35.4051px;" | '''=''' | ||
| '''Bruttonationaleinkommen: 338,52''' | | style="height: 28px; width: 423.519px;" | '''Bruttonationaleinkommen: 338,52''' | ||
|} | |} | ||
| Zeile 598: | Zeile 563: | ||
Insbesondere in Ländern, die einen hohen Zufluss an Auslandsdirektinvestitionen aufweisen, kommt es daher notwendigerweise mittelfristig zu einer erheblichen Diskrepanz zwischen Inlands- und Inländer-Produkt bzw -Einkommen. Während in Österreich das Verhältnis absolutes BNE/BIP bei 0,996 liegt, beträgt selbiges in der Republik Irland 0,792. <ref>Angabe für Irland berechnet laut ''Central Statistics Office Ireland'', nach Daten für 2015.</ref> Auch bei Vernachlässigung einiger Feinheiten der Berechnung bleibt der Schluss zulässig, dass in Österreich 0,4% des entstehenden Einkommens, in Irland hingegen 20,8% des produzierten Einkommens netto an das Ausland fließen. | Insbesondere in Ländern, die einen hohen Zufluss an Auslandsdirektinvestitionen aufweisen, kommt es daher notwendigerweise mittelfristig zu einer erheblichen Diskrepanz zwischen Inlands- und Inländer-Produkt bzw -Einkommen. Während in Österreich das Verhältnis absolutes BNE/BIP bei 0,996 liegt, beträgt selbiges in der Republik Irland 0,792. <ref>Angabe für Irland berechnet laut ''Central Statistics Office Ireland'', nach Daten für 2015.</ref> Auch bei Vernachlässigung einiger Feinheiten der Berechnung bleibt der Schluss zulässig, dass in Österreich 0,4% des entstehenden Einkommens, in Irland hingegen 20,8% des produzierten Einkommens netto an das Ausland fließen. | ||
{| | {| style="border-collapse: collapse; height: 308px;" border="1" | ||
! | ! style="height: 28px; width: 381.898px;" | '''Quelle''' | ||
! | ! style="height: 28px; width: 63.9815px;" | '''AT''' | ||
! | ! style="height: 28px; width: 63.9815px;" | '''HU''' | ||
! | ! style="height: 28px; width: 64.0046px;" | '''AT/HU''' | ||
|- | |- style="height: 28px;" | ||
| Der Spiegel Länderlexikon (BNE/EW in US-$) | | style="height: 28px; width: 381.898px;" | Der Spiegel Länderlexikon (BNE/EW in US-$) | ||
| 32.300 | | style="height: 28px; width: 63.9815px;" | 32.300 | ||
| 8.270 | | style="height: 28px; width: 63.9815px;" | 8.270 | ||
| 391% | | style="height: 28px; width: 64.0046px;" | 391% | ||
|- | |- style="height: 28px;" | ||
| OECD (BIP/EW zu KKP) | | style="height: 28px; width: 381.898px;" | OECD (BIP/EW zu KKP) | ||
| 31.944 | | style="height: 28px; width: 63.9815px;" | 31.944 | ||
| 15.946 | | style="height: 28px; width: 63.9815px;" | 15.946 | ||
| 200% | | style="height: 28px; width: 64.0046px;" | 200% | ||
|- | |- style="height: 28px;" | ||
| Weltbank (BNE/EW in US-$) | | style="height: 28px; width: 381.898px;" | Weltbank (BNE/EW in US-$) | ||
| 32.280 | | style="height: 28px; width: 63.9815px;" | 32.280 | ||
| 8.370 | | style="height: 28px; width: 63.9815px;" | 8.370 | ||
| 386% | | style="height: 28px; width: 64.0046px;" | 386% | ||
|- | |- style="height: 28px;" | ||
| Der Fischer Weltalmanach online (BNE/EW in US-$) | | style="height: 28px; width: 381.898px;" | Der Fischer Weltalmanach online (BNE/EW in US-$) | ||
| 32.300 | | style="height: 28px; width: 63.9815px;" | 32.300 | ||
| 8.270 | | style="height: 28px; width: 63.9815px;" | 8.270 | ||
| 391% | | style="height: 28px; width: 64.0046px;" | 391% | ||
|- | |- style="height: 28px;" | ||
| Economist Intelligence Unit (BIP/EW zu KKP) | | style="height: 28px; width: 381.898px;" | Economist Intelligence Unit (BIP/EW zu KKP) | ||
| 31.930 | | style="height: 28px; width: 63.9815px;" | 31.930 | ||
| 15.184 | | style="height: 28px; width: 63.9815px;" | 15.184 | ||
| 210% | | style="height: 28px; width: 64.0046px;" | 210% | ||
|- | |- style="height: 28px;" | ||
| Cambridge Econometrics (BIP/EW in ECU, fixe Preise) | | style="height: 28px; width: 381.898px;" | Cambridge Econometrics (BIP/EW in ECU, fixe Preise) | ||
| 26.209 | | style="height: 28px; width: 63.9815px;" | 26.209 | ||
| 4.720 | | style="height: 28px; width: 63.9815px;" | 4.720 | ||
| 555% | | style="height: 28px; width: 64.0046px;" | 555% | ||
|- | |- style="height: 28px;" | ||
| Eurostat (BIP/EW in Euro, jeweilige Preise) | | style="height: 28px; width: 381.898px;" | Eurostat (BIP/EW in Euro, jeweilige Preise) | ||
| 29.390 | | style="height: 28px; width: 63.9815px;" | 29.390 | ||
| 7.978 | | style="height: 28px; width: 63.9815px;" | 7.978 | ||
| 368% | | style="height: 28px; width: 64.0046px;" | 368% | ||
|- | |- style="height: 28px;" | ||
| Eurostat (BIP/EW in ECU, fixe Preise, Basisjahr 1995) | | style="height: 28px; width: 381.898px;" | Eurostat (BIP/EW in ECU, fixe Preise, Basisjahr 1995) | ||
| 27.413 | | style="height: 28px; width: 63.9815px;" | 27.413 | ||
| 4.770 | | style="height: 28px; width: 63.9815px;" | 4.770 | ||
| 575% | | style="height: 28px; width: 64.0046px;" | 575% | ||
|- | |- style="height: 28px;" | ||
| Eurostat (BIP/EW in ECU, Verkettung, Referenzjahr 1995) | | style="height: 28px; width: 381.898px;" | Eurostat (BIP/EW in ECU, Verkettung, Referenzjahr 1995) | ||
| 27.756 | | style="height: 28px; width: 63.9815px;" | 27.756 | ||
| 4.884 | | style="height: 28px; width: 63.9815px;" | 4.884 | ||
| 568% | | style="height: 28px; width: 64.0046px;" | 568% | ||
|- | |- style="height: 28px;" | ||
| Eurostat (BIP/EW zu KKP, EU-25 = 100) | | style="height: 28px; width: 381.898px;" | Eurostat (BIP/EW zu KKP, EU-25 = 100) | ||
| 122,6 | | style="height: 28px; width: 63.9815px;" | 122,6 | ||
| 60,2 | | style="height: 28px; width: 63.9815px;" | 60,2 | ||
| 204% | | style="height: 28px; width: 64.0046px;" | 204% | ||
|} | |} | ||
| Zeile 658: | Zeile 623: | ||
<ul>Tab. 1.3:. Das BIP und BNE je Einwohner (EW) in Österreich und Ungarn sowie das Verhältnis im Jahr 2004 nach verschiedenen Quellen und Berechnungsmethoden</ul> | <ul>Tab. 1.3:. Das BIP und BNE je Einwohner (EW) in Österreich und Ungarn sowie das Verhältnis im Jahr 2004 nach verschiedenen Quellen und Berechnungsmethoden</ul> | ||
</ul> | </ul> | ||
Bei der Interpretation der Daten kommt es daher darauf an, was gemessen wird. Das bei Wachstumsfragen relevante Problem nomineller versus realer Größen <ref>Vgl. ''Grundlagen der Volkswirtschaftslehre 1'', Kapitel 1.3.3.</ref> ist dabei ebenso zu berücksichtigen wie die sinnvolle Wahl einer Bezugsgröße. Bei internationalen Vergleichen üblich ist, das BIP je Einwohner (Österreich im Jahr 2015: 39.390 Euro) anzugeben. Die Zahl der Erwerbstätigen kann | Bei der Interpretation der Daten kommt es daher darauf an, was gemessen wird. Das bei Wachstumsfragen relevante Problem nomineller versus realer Größen <ref>Vgl. ''Grundlagen der Volkswirtschaftslehre 1'', Kapitel 1.3.3.</ref> ist dabei ebenso zu berücksichtigen wie die sinnvolle Wahl einer Bezugsgröße. Bei internationalen Vergleichen üblich ist, das BIP je Einwohner (Österreich im Jahr 2015: 39.390 Euro) anzugeben. Die Zahl der Erwerbstätigen kann sowohl im Zeitverlauf wie auch von Land zu Land schwanken, weshalb häufig die die Arbeitsproduktivität von Interesse ist: Sie ist definiert als Output je Arbeitseinheit und wird üblicherweise berechnet als BIP oder BWS je Erwerbstätigen oder je Arbeitsstunde (BWS je Erwerbstätigen in Österreich im Jahr 2015: 81.500 Euro). Nettolöhne und -gehälter (AT 2015: 92,17 Mrd. Euro) werden üblicherweise je Arbeitnehmer ausgewiesen (AT 2015: 28.800 Euro), zu beachten ist hier u.a., ob Erwerbstätige und Arbeitnehmer lediglich gezählt oder zu Vollzeitäquivalenten erfasst werden (hier: Vollzeitäquivalente), oder inwieweit sich die Gruppe der Erwerbstätigen mit jenen der Arbeitnehmer überschneidet (hier: 3.205.661 der 3.713.442 Erwerbstätigen waren 2015 Arbeitnehmer). Eine weitere Kennzahl stellt die ''Kapitalintensität'' dar, die das Verhältnis von BIP zum Bruttoanlagevermögen (Wert zu Wiederbeschaffungspreisen in Österreich 2015: 2,168 Billionen Euro) | ||
sowohl im Zeitverlauf wie auch von Land zu Land schwanken, weshalb häufig die die Arbeitsproduktivität von Interesse ist: Sie ist definiert als Output je Arbeitseinheit und wird üblicherweise berechnet als BIP oder BWS je Erwerbstätigen oder je Arbeitsstunde (BWS je Erwerbstätigen in Österreich im Jahr 2015: 81.500 Euro). Nettolöhne und -gehälter (AT 2015: 92,17 Mrd. Euro) werden üblicherweise je Arbeitnehmer ausgewiesen (AT 2015: 28.800 Euro), zu beachten ist hier u.a., ob Erwerbstätige und Arbeitnehmer lediglich gezählt oder zu Vollzeitäquivalenten erfasst werden (hier: Vollzeitäquivalente), oder inwieweit sich die Gruppe der Erwerbstätigen mit jenen der Arbeitnehmer überschneidet (hier: 3.205.661 der 3.713.442 Erwerbstätigen waren 2015 Arbeitnehmer). Eine weitere Kennzahl stellt die ''Kapitalintensität'' dar, die das Verhältnis von BIP zum Bruttoanlagevermögen (Wert zu Wiederbeschaffungspreisen in Österreich 2015: 2,168 Billionen Euro) | |||
darstellt und somit angibt, wie viel eine Kapitaleinheit im Durchschnitt zur Herstellung einer Einheit Bruttoinlandsprodukt beiträgt (Österreich 2015: 15,68 Cent). | darstellt und somit angibt, wie viel eine Kapitaleinheit im Durchschnitt zur Herstellung einer Einheit Bruttoinlandsprodukt beiträgt (Österreich 2015: 15,68 Cent). | ||
| Zeile 667: | Zeile 631: | ||
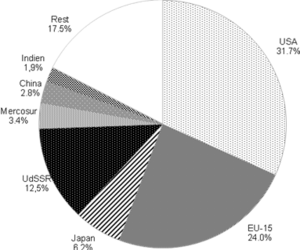
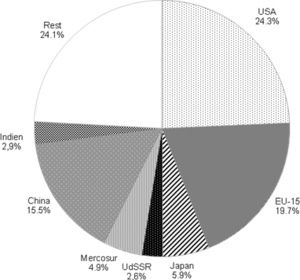
=== Globale Konvergenz? === | === Globale Konvergenz? === | ||
>Die in Kapitel 1.3.1 aus der neoklassischen Wachstumstheorie hergeleitete Konvergenz-Hypothese zählt zu den meistdiskutierten makroökonomischen Themen der vergangenen 25 Jahre. Zu den Hauptergebnissen zählt die von Sala-i-Martin geprägte Zwei-Prozent-Regel als Resultat zahlreicher Studien, wonach Ökonomien entsprechend einem <math>\tilde{\beta}</math> aus Gleichung (1.44) mit einer Geschwindigkeit von 2% pro Jahr zueinander konvergieren <ref>Siehe hierzu: Xavier X. Sala-i-Martin: The Classical Approach to Convergence Analysis, The Economic Journal 106, 1996</ref> Die beiden prominentesten Beispiele zur Stützung der Konvergenz-Hypothese sind einerseits die Aufholprozesse der großen westeuropäischen Ökonomien Deutschland, Frankreich und Italien gegenüber Großbritannien in den letzten 200 Jahren, sowie der Aufholprozess innerhalb der OECD gegenüber den USA in den vergangenen 50 Jahren. Betrachtungen dieser Art haben jedoch die Schwachstelle, dass sie ex post erfolgen: Verglichen wird, was heute ähnlich ist, um dann festzustellen, dass ein Angleichungsprozess zu beobachten war. Demgegenüber steht die Feststellung von Gunnar Myrdal, der bereits 1957 bemerkte, dass es die Industriestaaten sind, die sich weiter industrialisieren und in denen alle Indikatoren nach oben zeigen. Tatsächlich stimmen die wohlhabenden Ökonomien von heute mit jenen von 1957 weitgehend überein. Temporäre Aufholprozesse wie zurzeit der VR China oder Indiens können nicht darüber hinwegtäuschen, dass mit Ausnahme der Republik Korea seit Myrdals Analyse kein einziges Land das BIP-je-Einwohner-Niveau der etablierten Industriestaaten erreichen konnte (abgesehen von Stadtstaaten wie Singapur und Rohstoff exportierenden Ländern wie Kuwait). | |||
<math>\tilde{\beta}</math | |||
Wenn die gesamte Weltwirtschaft empirisch verglichen werden soll, stellt sich zunächst das Problem, dass es einige sehr, sehr große Länder und viele kleinere gibt. Ist es sinnvoll, eher kleinen Ländern wie Dänemark oder Guatemala bei einer Länder übergreifenden Studie denselben Stellenwert zuzuweisen wie etwa Russland oder Brasilien? Ein Lösungsansatz ist, statt einzelner Länder ökonomische Zonen und Blöcke zu betrachten: Abb. 1.6 zeigt das BIP als Anteil am Weltprodukt (= die Summe des absoluten BIP aller Länder = die Summe des absoluten BNE aller Länder) in den Jahren 1970 und 2015 für sieben Zonen bzw. Blöcke: Die USA, die EU innerhalb der Grenzen von 1995 bis 2004 („EU-15“), Japan, die UdSSR und ihre Nachfolgestaaten, die neun südamerikanischen Mitglied- und assoziierten Staaten des Mercosur, die Volksrepublik China (zu Grenzen von 2015) sowie Indien. Wie aus der Abbildung zu sehen ist, wurde 1970 rund 83%, und 2005 rund 76% des Weltprodukts in diesen sieben Zonen erwirtschaftet. Die Anteile der führenden Industriestaaten der USA, der EU-15 sowie Japans gingen im Beobachtungszeitraum zwar zurück, jedoch um weit weniger als der Anteil der betreffenden Länder an der Weltbevölkerung – was bedeutet, dass die Produktion je Einwohner in den führenden Industriestaaten im Vergleich zum Rest der Welt sogar noch zunahm. | Wenn die gesamte Weltwirtschaft empirisch verglichen werden soll, stellt sich zunächst das Problem, dass es einige sehr, sehr große Länder und viele kleinere gibt. Ist es sinnvoll, eher kleinen Ländern wie Dänemark oder Guatemala bei einer Länder übergreifenden Studie denselben Stellenwert zuzuweisen wie etwa Russland oder Brasilien? Ein Lösungsansatz ist, statt einzelner Länder ökonomische Zonen und Blöcke zu betrachten: Abb. 1.6 zeigt das BIP als Anteil am Weltprodukt (= die Summe des absoluten BIP aller Länder = die Summe des absoluten BNE aller Länder) in den Jahren 1970 und 2015 für sieben Zonen bzw. Blöcke: Die USA, die EU innerhalb der Grenzen von 1995 bis 2004 („EU-15“), Japan, die UdSSR und ihre Nachfolgestaaten, die neun südamerikanischen Mitglied- und assoziierten Staaten des Mercosur, die Volksrepublik China (zu Grenzen von 2015) sowie Indien. Wie aus der Abbildung zu sehen ist, wurde 1970 rund 83%, und 2005 rund 76% des Weltprodukts in diesen sieben Zonen erwirtschaftet. Die Anteile der führenden Industriestaaten der USA, der EU-15 sowie Japans gingen im Beobachtungszeitraum zwar zurück, jedoch um weit weniger als der Anteil der betreffenden Länder an der Weltbevölkerung – was bedeutet, dass die Produktion je Einwohner in den führenden Industriestaaten im Vergleich zum Rest der Welt sogar noch zunahm. | ||
| Zeile 693: | Zeile 648: | ||
=== Regionales Wachstum innerhalb der Europäischen Union === | === Regionales Wachstum innerhalb der Europäischen Union === | ||
Die bisherige Analyse hat gezeigt, dass es erstens Gesetzmäßigkeiten hinsichtlich der Entwicklung ''einer'' Ökonomie gibt, jedoch zweitens Ökonomien sich unterschiedlich entwickeln, wobei es keine automatische Angleichung gibt. Was für Europa gilt, gilt auch für die Europäische Union, die mittlerweile rund zwei Drittel der Bevölkerung Europas umfasst. Unterschiede hinsichtlich der Produktivität und des Wohlstands sind sowohl durch Nord-Süd-Gefälle wie durch Ost-West-Gefälle charakterisiert. Abb. 1.7 visualisiert diesen Sachverhalt durch eine Darstellung des Bruttoregionalprodukts (BRP) <ref>Das Bruttoregionalprodukt ist konzeptionell identisch mit dem Bruttoinlandsprodukt.</ref> für die EU: Es zeigt sich ein geographisches Muster, wobei die im Zentrum gelegenen Regionen jene mit dem höchsten BRP sind, während jene in Randlage benachteiligt scheinen. Die Regionen und Staaten innerhalb der Europäischen Union sind jedoch Teil desselben Wirtschaftsraums und unterliegen daher denselben Rahmenbedingungen, sie haben durch den Binnenmarkt prinzipiell Zugang zur selben Technologie und können bis zu einem gewissen Grad als ähnlich eingestuft werden. Deshalb folgt ein möglicher innereuropäischer Konvergenzprozess anderen Bedingungen als ein globaler. | |||
''einer'' | |||
Als die Europäischen Gemeinschaften 1957/1958 gegründet wurden, bestanden sie aus sechs Ländern der produktivsten Industrieregionen der Welt, die sich auf vergleichbarem Niveau befanden; lediglich in Süditalien war die Produktivität deutlich niedriger. Nichtsdestoweniger wurde bereits mit dem Vertrag von Rom (1957) auch die Gründung der Europäischen Investitionsbank festgelegt, um Investitionen in weniger entwickelten Regionen zu unterstützen. Mit den verschiedenen Beitrittsrunden der heutigen Europäischen Union haben die regionalen Disparitäten jedoch zugenommen, zunächst durch den Beitritt der Republik Irland 1973, in den 1980er-Jahren durch die Süderweiterungen 1981 (Griechenland) und 1986 (Portugal und Spanien) und schließlich durch die Osterweiterungen seit 2004. Parallel zu dieser Entwicklung wurden die Bemühungen um eine Verringerung der Disparitäten erhöht, zunächst 1975 mit der Gründung des ''Europäischen Fonds für regionale Entwicklung''. | Als die Europäischen Gemeinschaften 1957/1958 gegründet wurden, bestanden sie aus sechs Ländern der produktivsten Industrieregionen der Welt, die sich auf vergleichbarem Niveau befanden; lediglich in Süditalien war die Produktivität deutlich niedriger. Nichtsdestoweniger wurde bereits mit dem Vertrag von Rom (1957) auch die Gründung der Europäischen Investitionsbank festgelegt, um Investitionen in weniger entwickelten Regionen zu unterstützen. Mit den verschiedenen Beitrittsrunden der heutigen Europäischen Union haben die regionalen Disparitäten jedoch zugenommen, zunächst durch den Beitritt der Republik Irland 1973, in den 1980er-Jahren durch die Süderweiterungen 1981 (Griechenland) und 1986 (Portugal und Spanien) und schließlich durch die Osterweiterungen seit 2004. Parallel zu dieser Entwicklung wurden die Bemühungen um eine Verringerung der Disparitäten erhöht, zunächst 1975 mit der Gründung des ''Europäischen Fonds für regionale Entwicklung''. | ||
| Zeile 732: | Zeile 677: | ||
Niveau und Wachstum einer Ökonomie werden über die Größen der Volkswirtschaftlichen Gesamtrechnung erfasst, in welcher für verschiedene Fragestellungen eine Auswahl an Größen erfasst sind. Ein weltweiter Vergleich des Bruttoinlandsprodukts seit 1970 zeigt, dass eine allgemeingültige Konvergenz-Hypothese durch die Empirie generell nicht gestützt wird, wiewohl temporäre Aufholprozesse beobachtet werden können. Innerhalb der EU ließ sich bis zum Ausbruch der Krise ein allgemeiner Trend der interregionaler Konvergenz beobachten, der seit 2008 jedoch zum Erliegen gekommen ist. | Niveau und Wachstum einer Ökonomie werden über die Größen der Volkswirtschaftlichen Gesamtrechnung erfasst, in welcher für verschiedene Fragestellungen eine Auswahl an Größen erfasst sind. Ein weltweiter Vergleich des Bruttoinlandsprodukts seit 1970 zeigt, dass eine allgemeingültige Konvergenz-Hypothese durch die Empirie generell nicht gestützt wird, wiewohl temporäre Aufholprozesse beobachtet werden können. Innerhalb der EU ließ sich bis zum Ausbruch der Krise ein allgemeiner Trend der interregionaler Konvergenz beobachten, der seit 2008 jedoch zum Erliegen gekommen ist. | ||
== Übungen == | == Übungen == | ||
| Zeile 747: | Zeile 693: | ||
<li><p>Zeigen Sie formal, dass die Cobb-Douglas-Produktionsfunktion ohne technologischen Fortschritt konstante Skalenerträge aufweist!</p></li> | <li><p>Zeigen Sie formal, dass die Cobb-Douglas-Produktionsfunktion ohne technologischen Fortschritt konstante Skalenerträge aufweist!</p></li> | ||
<li><p>Zeigen Sie anhand von Gleichung (1.28), dass im Solow-Modell eine Erhöhung der Sparquote eindeutig zu einem höheren Steady-State-Output je effektiver Arbeitseinheit führt!</p></li> | <li><p>Zeigen Sie anhand von Gleichung (1.28), dass im Solow-Modell eine Erhöhung der Sparquote eindeutig zu einem höheren Steady-State-Output je effektiver Arbeitseinheit führt!</p></li> | ||
<li><p>Zeigen Sie, dass aus dem Solow-Modell mit Cobb-Douglas-Produktionsfunktion folgt, dass zehnfacher Unterschied bei der Arbeitsproduktivität <math>y_t</math> einen Unterschied von <math>10^(1/\alpha )</math> bei der Kapitalausstattung bedingt!</p>Zeigen Sie anhand von Gleichung (1.42), dass im Mankiw-Romer-Weil-Modell eine Erhöhung der Humankapitalinvestitionen eindeutig zu einem höheren Steady-State-Output je effektiver Arbeitseinheit führt. | <li><p>Zeigen Sie, dass aus dem Solow-Modell mit Cobb-Douglas-Produktionsfunktion folgt, dass zehnfacher Unterschied bei der Arbeitsproduktivität <math>y_t</math> einen Unterschied von <math>10^(1/\alpha )</math> bei der Kapitalausstattung bedingt!</p></li> | ||
<li>Zeigen Sie anhand von Gleichung (1.42), dass im Mankiw-Romer-Weil-Modell eine Erhöhung der Humankapitalinvestitionen eindeutig zu einem höheren Steady-State-Output je effektiver Arbeitseinheit führt.</li> | |||
<li><p>Wie hoch ist der Durchschnittslohn im Mankiw-Romer-Weil-Modell?</p></li> | <li><p>Wie hoch ist der Durchschnittslohn im Mankiw-Romer-Weil-Modell?</p></li> | ||
<li><p>Was wird als Lucas-Paradoxon bezeichnet?</p></li> | <li><p>Was wird als Lucas-Paradoxon bezeichnet?</p></li> | ||
| Zeile 761: | Zeile 708: | ||
</ol> | </ol> | ||
|} | |} | ||
<br><hr> | |||
<br> | |||
#Der stationäre Zustand bezeichnet eine Entwicklung, in der die Ökonomie nicht mehr wächst, da landwirtschaftliche Produktion und Kapitalakkumulation ihre theoretischen Maxima erreicht haben. | |||
#Der Steady-State bezeichnet eine Entwicklung, in der die Ökonomie mit konstanter Rate wächst. Diese Rate kann positiv, gleich null, oder theoretisch auch negativ sein. Eine positive Wachstumsrate der Gesamtwirtschaft kann mit einer negativen Wachstumsrate je Einwohner zusammenfallen. | |||
#Ab einer hinreichenden Größe kann eine Ökonomie von einer Spezialisierung nicht weiter profitieren: Die Verdopplung aller Inputs führt zu einer Verdopplung des Outputs. | |||
#Ist noch relativ wenig von einem Faktor vorhanden, so wird eine zusätzliche Einheit die Produktion erheblich erhöhen. Nimmt die Menge des Faktors weiter zu, während der oder die anderen konstant bleiben, so werden weitere Einheiten immer weniger zur Produktion beitragen. | |||
#Die Entwicklung des Kapitalstocks je Arbeitseinheit über die Zeit ist in der Differentialgleichung <math>\dot{k}_{t}=s_{K} y_{t}-(n+\delta) k_{t}</math> beschrieben. Daraus folgt, dass <math>\dot{k}_{t}>0</math> wenn <math>s_{K} y_{t}>(n+\delta) k_{t}</math>. | |||
</ | #Eine Senkung der Sparquote führt zu einem Rückgang des Wachstums, bis die Ökonomie beim neuen, niedrigeren Gleichgewichtspunkt angelangt ist. | ||
<math>\ | #Der Output ist durch die Funktion <math>\hat{y}_{t}=\hat{k}_{t}^{\alpha}</math> beschrieben. Die erste Ableitung ergibt <math>\partial \hat{y}_{t} / \partial \hat{k}_{t}=\alpha \hat{k}_{t}^{\alpha-1}</math> und ist eindeutig positiv, da alle Variablen positiv sind. | ||
< | #Aus <math>c Y_{t}=f\left(c K_{t}, c L_{t}\right)</math> folgt im Cobb-Douglas-Fall <math>f\left(c K_{t}, c L_{t}\right)=\left(c K_{t}\right)^{\alpha}\left(c L_{t}\right)^{1-\alpha}=c^{\alpha} c^{1-\alpha} K_{t}^{\alpha} L_{t}^{1-\alpha}=c f\left(K_{t}, L_{t}\right)</math> | ||
#Die erste Ableitung ergibt <math>\partial \hat{y}^{*} / \partial s_{K}=\alpha /\left[(1-\alpha) s_{K}^{1 /(1-\alpha)}(n+g+\delta)^{\alpha /(1-\alpha)}\right]</math>, da alle Variablen als positiv definiert sind und <math>\alpha<1</math> gilt. | |||
</ | #Eine Verzehnfachung der Produktionsfunktion lässt sich anschreiben als <math>10 y_{t}=10 k_{t}^{\alpha}</math>, woraus folgt <math>10 y_{t}=\left(10^{1 / \alpha} k_{t}\right)^{\alpha}</math>. Aus <math>\alpha=1/3</math> ergibt sich eine Kapitalausstattung je Arbeitseinheit um das Tausendfache. | ||
#Die erste Ableitung ergibt <math>\partial \hat{y}^{*} / \partial s_{H}=[1 /(1-\alpha-\beta)]\left[s_{K} s_{H}^{-\alpha-\beta}(n+g+\delta)^{-\alpha-\beta}\right]^{1 /(1-\alpha-\beta)}</math>, da alle Variablen als positiv definiert sind und <math>\alpha+\beta<1</math> gilt, ist die Ableitung positiv. | |||
< | #Aus der Produktionsfunktion folgt für das gesamte Lohnaufkommen <math>W_{t}=L_{t}\left(\partial Y_{t} / \partial L_{t}\right)+H_{t}\left(\partial Y_{t} / \partial H_{t}\right)=(1-\alpha-\beta) Y_{t}+\beta Y_{t}=(1-\alpha) Y_{t}</math>. Der Durchschnittslohn ergibt aus der Division des gesamten Lohnaufkommens durch das Arbeitsangebot: <math>W_{t} / L_{t}=w_{t}=(1-\alpha) A_{t} \hat{k}_{t}^{\alpha} \hat{h}_{t}^{\beta}</math> | ||
< | #Das Lucas-Paradoxon bezeichnet die empirische Beobachtung, dass Investitionen größtenteils in Ökonomien stattfinden, die bereits über eine hohe Kapitalausstattung je Arbeitseinheit verfügen. | ||
</ | #Nicht-Rivalität: Die Anwendung einer Einheit Wissens vermindert nicht den Bestand an vorhandenem Wissen. | ||
#Lokalisationsvorteile sind Kostenvorteile, die sich aus der räumlichen Ballung von Unternehmen der selben Industriebranche ergeben. | |||
#Zentripetale Entzugseffekte bezeichnen negative Auswirkungen des Wachstums einer Region auf eine andere, was zu einer Vertiefung bereits bestehender Disparitäten führt. | |||
#Das BIP entspricht der Wertschöpfung zu Marktpreisen nach dem Inlands-Prinzip, das BNE entspricht der Wertschöpfung zu Marktpreisen nach dem Inländer-Prinzip. Die Größen unterscheiden sich um den Saldo der Primäreinkommen zwischen Inländern und übriger Welt. | |||
#Hinweise: 1. Das BIP misst nicht das Vermögen, sondern das Einkommen. 2. Das BIP misst nicht das erhaltene, sondern das produzierte Einkommen. | |||
#U.a. Deutschland, Frankreich und Italien gegenüber Großbritannien im 19. und teilweise 20. Jh., europäische OECD gegenüber den USA in der zweiten Hälfte des 20. Jh., außerdem ostasiatische Länder wie Singapur oder die Republik Korea in den vergangenen 30 bis 40 Jahren. | |||
#Die Abstände zwischen den produktiven, wohlhabenden Ökonomien und den weniger produktiven Ökonomien blieben seit 1970 in den meisten Fällen konstant oder vergrößerten sich. | |||
#1. Liberalisierung des Außenhandels können zu überlegener Konkurrenz von außen führen.2. Freier Verkehr von Arbeit und Kapital führt zu einer tendenziellen Verstärkung räumlicher Konzentration der industriellen Produktion. | |||
#Innerhalb der Regionen und Länder der EU und EFTA lässt sich eine Konvergenz beobachten. Gleichzeitig zeigt sich jedoch eine Zunahme der regionalen Disparitäten innerhalb vieler Länder. | |||
< | |||
< | |||
< | |||
</ | |||
< | |||
< | |||
< | |||
Aktuelle Version vom 14. März 2022, 19:22 Uhr
Wachstumstheorie
Gegenwärtig ist explizit oder implizit Ziel jeder Volkswirtschaft, die Produktion auszuweiten. Mit Fragen dieses Wachstums verbunden ist, ob sich das Outputniveau (die gesamte Produktion innerhalb einer Periode) verschiedener Ökonomien im Zeitverlauf angleicht, oder ob sich bestehende Disparitäten weiter vertiefen. Seit der Industriellen Revolution und insbesondere mit der zweiten Hälfte des 20. Jahrhunderts wird einerseits eine permanente Ausweitung der Produktion und somit ein langfristig positives Wirtschaftswachstum verzeichnet – zumindest in jenen Volkswirtschaften, die man als Industriestaaten bezeichnet. In Kapitel 1.1.1 wird das langfristige vom kurzfristigen Wachstum abgegrenzt, bevor in Kapiteln 1.1.2 die neoklassische Produktionsfunktion als Grundlage als grundlegende Annahme der modernen Wachstumstheorie vorgestellt wird; anschließend wird in Kapitel 1.1.3 die Dynamik des neoklassischen Wachstumsmodells diskutiert. In Kapitel 1.2 wird die Produktionsfunktion vom Typ Cobb-Douglas eingeführt, um das neoklassische Wachstumsmodell in Kapitel 1.2.1 in Verbindung mit technologischem Fortschritt, in Kapitel 1.2.2 mit Kapitalakkumulation und Wachstum, und in Kapitel 1.2.3 mit Humankapital zu anzuwenden.
Grundlagen der Wachstumstheorie
Wenn in der Ökonomie von Wachstum die Rede ist, so ist damit grundsätzlich das gemeint, was im allgemeinen Sprachgebrauch Wirtschaftswachstum genannt wird. Das Einsparen zweier Silben im Jargon der Ökonomen verdeutlicht unmissverständlich die Bedeutung des Themas; dennoch ist es nötig, eine weitere Abgrenzung vorzunehmen: Wenn in der öffentlichen Diskussion das Wirtschaftswachstum zum Thema wird – und das ist ausgesprochen oft der Fall – so ist fast immer das kurzfristige Wachstum gemeint. Meistens bezieht man sich auf ein Jahr, ein mittlerer Horizont von drei bis fünf Jahren wird schon sehr viel seltener diskutiert. Die Wachstumstheorie hingegen geht weit darüber hinaus und legt das Erkenntnisinteresse vor allem auf die langfristige Entwicklung der Produktion. Um nationale und internationale Entwicklungen sowie politische Entscheidungen richtig interpretieren zu können ist es nötig, zu verstehen, nach welchen Mechanismen moderne Ökonomien funktionieren.
Kurzfristiges versus langfristiges Wachstum
In den bisherigen Lektionen des Bachelor-Studiengangs, die sich mit makroökonomischen Fragestellungen auseinandersetzen, [1] stand die Frage im Mittelpunkt, wie das Wirtschaftswachstum kurzfristig gesteuert werden kann. Es wurde gezeigt, wie die Produktion und somit das Einkommen via Geld- und Fiskalpolitik beeinflusst werden kann, etwa über Änderungen im Zinssatz, im Preisniveau oder bei der Nachfrage. Im Anschluss wurde der Einfluss des Auslands via Nachfrage und Wechselkurse diskutiert. Die entsprechende Politik dient vor allem der Stabilität, um hohe Inflation und Arbeitslosigkeit zu vermeiden. Marktwirtschaftliche Systeme sind durch Konjunkturzyklen gekennzeichnet, einem ständigen Auf und Ab der wirtschaftlichen Entwicklung: Auch ohne Rezession kann das Wachstum wie im Falle Österreichs seit den 1970er-Jahren von annähernd null bis über fünf Prozent jährlich betragen. [2] Ganz offensichtlich würde es langfristig einen enormen Unterschied machen, ob man nahe null über fünf Prozent wächst.
Angesichts solcher Schwankungen und der enormen Auswirkungen auf Lebensstandard und Wohlstand, den ein anhaltender Unterschied um das Vierfache bei der Wachstumsrate hätte, drängt sich die Frage auf, ob das langfristige Wachstum von den selben Determinanten bestimmt wird wie das kurzfristige Wachstum. Die Darstellung der Entwicklung in Österreich von 1977 bis 2015 in Abb. 1.1 zeigt, wie Krisen und Boom-Phasen aus der längerfristigen Perspektive
verblassen. Deutlich erkennbar ist hingegen bis zum Krisenjahr 2008 ein stetiges Wachstum im Lauf der Zeit. Die jährlichen Ausreißer im Rahmen der Konjunkturzyklen relativieren sich langfristig und fallen in der Abbildung kaum ins Auge: Im Mittel liegt das BIP-Wachstum im Beobachtungszeitraum bei 1,97%, es ist seit den 1970er-Jahren bis zum Ausbruch der Krise über die Jahre weder ein Abwärts- noch ein Aufwärtstrend der mittelfristigen Wachstumsrate zu beobachten. Seit Ausbruch der Krise 2008 wächst Österreichs Wirtschaft wieder, allerdings scheint es, als ob die Krise Österreichs Wachstum um eine Stufe gedrückt hätte: Die Kurven des BIP und des BNE zeigen einen Verlauf, als kostete die Krise Österreich 4 Prozent seines Wohlstands, seither entwickelt sich die Wirtschaft wie gehabt.
Man kommt der Frage nach den Determinanten des langfristigen Wachstums näher, wenn man sich vergegenwärtigt, dass Wirtschaftswachstum keine historische Notwendigkeit darstellt. Die Ökonomien Mitteleuropas wuchsen über Jahrhunderte kaum oder gar nicht, und auch heute ist in vielen Ländern der Erde das Wachstum der Gesamtwirtschaft geringer als jenes der Bevölkerung, sodass das BIP je Einwohner sogar schrumpft (z.B. in Ländern Zentralafrikas). Erst mit der Industriellen Revolution kam es zu einer erheblichen Ausweitung der Produktion, die in den Industrie-Staaten bis heute anhält. Wachstum lässt sich jedoch nicht nur in diesen, sondern in vielen, mitunter gänzlich unterschiedlich organisierten Ökonomien beobachten. Daraus folgt, dass eine Theorie, die das Wachstum in den wohlhabenden, kapitalistisch organisierten Volkswirtschaften erklären kann, auch erklären muss, warum es einerseits in anderen Systemen Wachstum gibt, aber andererseits in der Vergangenheit und in der Gegenwart in vielen Teilen der Welt kein Wachstum beobachtet wird.
Gedanken zum Wirtschaftswachstum als Folge von Produktivitätsfortschritten finden sich bereits bei den klassischen Ökonomen. Adam Smith [3] unterstreicht insbesondere die Bedeutung der Arbeitsteilung, [4] geht aber nur am Rande auf technologischen Fortschritt als solchen ein. David Ricardo [5] beschäftigt sich ausführlicher mit den Auswirkungen der Mechanisierung der Arbeitsprozesse, d.h. mit dem, was wir heute als „technologischen Fortschritt“ bezeichnen. Wie Smith vor ihm kommt jedoch auch Ricardo zu dem Schluss, dass auch die Entwicklung und der Einsatz von Maschinen die Ökonomie lediglich näher in Richtung eines stationären Zustands bringen: Demnach werden Produktivitätsfortschritte stets dazu führen, dass die Bevölkerung weiter wächst. Die Wirtschaft kann schließlich nur so lange wachsen, bis Kapitalakkumulation und Bevölkerungszahl ihr jeweiliges Maximum erreicht haben.
Karl Marx [6] greift die grundlegenden Gedanken von Smith und Ricardo auf und entwickelt ein Modell, das bereits die wesentlichen Aspekte der modernen Wachstumstheorie berücksichtigt, insbesondere die tragenden Rollen des technologischen Fortschritts und der Kapitalakkumulation. Die kapitalistisch organisierte Produktion führt zu einer ständigen Ausweitung der Produktion als Folge technischer Neuerungen und Investitionen. Marx kommt zum Schluss, dass dieser Prozess nicht endlos fortgesetzt werden kann, vielmehr führen mittel- bis langfristiges Wirtschaftswachstum zu einem Rückgang der Nachfrage nach dem Faktor Arbeit, was letztlich zu einem Systemwechsel führt. Marx’ Wachstumsmodell beschreibt das Wachstum einer kapitalistisch organisierten Ökonomie, und es bleibt offen, ob bzw. wie der Wachstumsprozess in einer kommunistisch organisierten Wirtschaft fortgesetzt würde.
Etwa 70 Jahre nach Marx finden sich auch bei John Maynard Keynes Gedanken über die langfristigen Auswirkungen technologischen Fortschritts, in seiner Theorie fokussiert er jedoch auf kurzfristige Wachstumspolitik. Allen vier genannten Ökonomen gemein ist, dass sie erhebliche Zweifel an einem immerwährenden Wirtschaftswachstum haben, bzw. ein solches erst gar nicht in Betracht ziehen. Die Frage, ob Wirtschaftswachstum auf Dauer möglich ist, stellt sich auch heute und hat insbesondere seit Ausbruch der Krise 2008 wieder an Aufmerksamkeit gewonnen. Die Diskussion über mögliche „Grenzen des Wachstums“ wird wissenschaftlich allerdings eher selten innerhalb der Ökonomie geführt, eher geht es um die Vereinbarkeit mit anderen Zielen, insbesondere Umweltschutz. Ob die Produktion in diesem Jahrhundert weiter steigen wird wie im vergangenen und welche Auswirkungen dies auf Gesellschaft und Umwelt hat, vermag niemand vorherzusehen. Festzuhalten ist allerdings, dass die Empirie bislang keine Hinweise auf ein Ende des Wachstums zeigt. Es kommt allerdings auch darauf an, was man unter „Wachstum“ konkret versteht. Wie weiter unten gezeigt wird, ist das BIP nur eine Möglichkeit, Wachstum zu messen, aber nicht notwendigerweise jene, die der Vorstellung von Wohlstandsvermehrung – denn darum geht es letzten Endes – tatsächlich entspricht. Ob etwa Umweltverschmutzung und Ressourcenabbau berücksichtigt werden, ist eine Frage der Konvention, aber kein konzeptioneller Widerspruch.
Ausgangspunkt der modernen Wachstumstheorie ist das Modell von Robert Solow [7] von 1956, auf dem die neoklassische Wachstumstheorie basiert. Ihr Modellrahmen hat sich bis heute als sehr robust erwiesen und repräsentiert in gewisser Weise eine ideale Theorie: Sie baut auf einigen wenigen, sinnvollen Annahmen auf, ist dabei in der Lage, eine Vielzahl beobachtbarer Phänomene zu erklären und schließt inkonsistente Entwicklungen aus. Im Unterschied zu den oben skizzierten Theorien ist sie nicht an ein bestimmtes Wirtschaftssystem gebunden, d.h. sie ist für kapitalistische, kommunistische und andere denkbare Organisationsformen anwendbar. In der Theorie gibt es im Gegensatz zur klassischen Ökonomie auch kein Ende des Wachstums: Statt eines stationären Zustands („stationary state“) strebt die Ökonomie einem Steady-State entgegen, womit ein Wachstum bei konstanter Rate gemeint ist. Anders formuliert gibt es in der modernen, neoklassischen Wachstumstheorie kein Ende des Wachstumsprozesses.
Die neoklassische Produktionsfunktion
Entscheidend für das Verständnis der neoklassischen Wachstumstheorie sind zwei kritische Annahmen: Erstens, die Ökonomie ist durch eine aggregierte Produktionsfunktion charakterisiert, in der im einfachsten Fall die beiden Faktoren Arbeit und Kapital in grundsätzlich beliebigen Einsatzverhältnissen berücksichtigt werden. [8] Zweitens ist diese Produktionsfunktion durch konstante Skalenerträge bei abnehmenden Grenzerträgen gekennzeichnet. Beide Annahmen werden im Folgenden beschrieben.
Die aggregierte Produktionsfunktion
Die neoklassische Produktionsfunktion hat die grundlegende Form:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_t=f(K_t,L_t ) } (1.1)
Wie bisher steht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} für Output, wobei die Betrachtung auf eine geschlossene Volkswirtschaft beschränkt ist und somit Output mit Einkommen gleichgesetzt werden kann. [9] Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K} bezeichnet den gesamten Sachkapitalbestand (Maschinen etc.) der Ökonomie und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} das gesamte Arbeitsangebot, wobei Letzteres unter der Annahme von Vollbeschäftigung identisch mit der eingesetzten Arbeit ist. Die Zeit, gekennzeichnet als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} , ist nur indirekt in der Produktionsfunktion über die Variablen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_t} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_t} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_t } vertreten. Die Gleichung (1.1) kann somit gelesen werden als: Der Output zum beliebigen Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} ist eine Funktion der zum selben Zeitpunkt eingesetzten Mengen von Arbeit und Kapital.
Die Produktionsfunktion in Gleichung (1.1) stellt eine erhebliche Vereinfachung der Realität dar, als sie nur jeweils einen Typ Arbeit und Kapital kennt, also unterstellt, dass für jede Einheit Arbeit (ob Schweißer oder Krankenschwester) wie für jede Einheit Kapital (ob Traktor oder Bürogebäude) gilt, dass sie gleich produktiv sind und die gleiche Funktion erfüllen. In Kapitel 2.2.1 wird gezeigt, wie die Lockerung dieser Annahme das Modell realistischer macht, ohne die Hauptergebnisse zu ändern. Zunächst sei auf eine weitere implizite Annahme der Produktionsfunktion hingewiesen: Aus der Reduzierung auf Arbeit und Kapital ergibt sich, dass alle anderen Einflüsse in der langen Frist verhältnismäßig unwichtig sind, insbesondere Boden und natürliche Ressourcen. Das liegt zum einen daran, dass die Menge an Boden nicht veränderbar ist; insbesondere aber spielen diese Faktoren für moderne Ökonomien nur untergeordnete Rollen. [10] In Man beachte außerdem, dass die Instrumente der Wirtschaftspolitik keine Berücksichtigung finden: Auf lange Sicht werden wirtschaftspolitisch- und konjunkturbedingte Schwankungen vom langfristigen Trend dominiert, in der Produktion also ausgeglichen. Ziel des Modells ist folglich, die Determinanten des langfristigen Trends zu identifizieren. [11]
Skalen- und Faktorerträge
Während sich die klassische Ökonomie intensiv mit der Frage beschäftigte, wie eine stetig wachsende Bevölkerung bei konstantem Boden versorgt werden kann, bzw. wie sich der Einsatz von Maschinen auf den Faktor Arbeit auswirkt, führt die Vernachlässigung von natürlichen Ressourcen und Arbeitslosigkeit in der neoklassischen Wachstumstheorie zur zweiten kritischen Grundannahme, nämlich jener konstanter Skalenerträge. [12] Diese Annahme lässt sich einfach veranschaulichen: Sie bedeutet, dass bspw. eine Verdoppelung der Faktoren Arbeit und Kapital auch den Output verdoppeln wird. Formal muss für Gleichung (1.1) gelten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2Y_t=f(2K_t,2L_t ) } (1.2)
Oder allgemein für jede beliebige, nichtnegative Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} : Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cY_t=f(cK_t,cL_t ) } (1.3)
Diese wichtige Annahme ist zugleich eine Einschränkung, denn sie besagt, dass die Ökonomie hinreichend groß ist, sodass sie von einer Spezialisierung nicht weiter profitieren kann. Dies ist wichtig zur Unterscheidung von kleineren, regionalen Ökonomien, die etwa aufgrund von Agglomerationseffekten mitunter steigende Skalenerträge aufweisen (vgl. Kapitel 1.3.2). Das Solow-Modell, wie es im Folgenden beschrieben wird, bildet hinreichend große Ökonomien, d.h. Volkswirtschaften bzw. relativ große Regionalökonomien, ab.
Wenn hingegen nicht alle, sondern nur ein Faktor an Volumen zunimmt, gilt das Gesetz des abnehmenden Grenzprodukts. [13] Umgelegt auf eine Volkswirtschaft stellt sich auch hier die Frage, was passiert, wenn ein Faktor zunimmt, während der oder die anderen konstant bleiben. Ist etwa noch wenig Kapital vorhanden, so wird eine zusätzliche Einheit die Produktion erheblich erhöhen. Ist jedoch umgekehrt bereits reichlich Kapital vorhanden (etwa in Form von Traktoren oder Bürogebäuden), so werden weitere Einheiten kaum noch zur Produktion beitragen. Parallel verhält es sich mit dem Faktor Arbeit.
Die Annahme konstanter Skalenerträge erlaubt es, die Produktionsfunktion in intensiver Form darzustellen: Setzt man in Gleichung (1.3) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c=1/L_t } ein, so erhält man den Output je eingesetzter Einheit Arbeit: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{Y_{t}}{L_{t}}=f\left(\frac{K_{t}}{L_{t}}, \frac{L_{t}}{L_{t}}\right)=f\left(\frac{K_{t}}{L_{t}}, 1\right) } (1.4)
Im Folgenden bezeichnet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_t=Y_t/L_t } die Produktion je Beschäftigten zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} , und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_t=K_t/\partial } die Kapitalintensität zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} . Gleichung (1.4) kann daher angeschrieben werden als: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_t=f(k_t) } (1.5)
Die Produktion je Beschäftigten ist somit eine Funktion der Kapitalintensität. Die Annahme abnehmender Grenzerträge lässt sich durch die Bedingungen und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f \prime \prime (k)<0} ausdrücken und wird in Abb. 1.2 veranschaulicht.
Analog zur Kostengleichung eines einzelnen Anbieters [14] folgen zwei wichtige Implikationen des Modells: Im Gleichgewicht werden beide Faktoren Arbeit wie Kapital nach ihrem jeweiligen Grenzprodukt bezahlt. Daraus folgen das Lohnniveau zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w_t=(\partial Y_t)/(\partial L_t ) } (1.6)
und der Gewinnsatz zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_t=(\partial Y_t)/(\partial K_t ) } (1.7)
[CHART]
Aus der Identität der volkswirtschaftlichen Gesamtrechnung folgt, dass die Summe der Löhne und Gewinne dem Gesamtprodukt entsprechen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_t=w_t L_t +r_t K_t } (1.8)
Während die Entstehungsrechnung durch Gleichung (1.1) repräsentiert ist, verdeutlicht Gleichung (1.8) die Verteilungsrechnung: Das zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} in einer Ökonomie entstandene Einkommen entspricht der Summe der Löhne Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w_t \partial } und der Gewinne (Kapitaleinkommen) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_t K_t} . Der gesamte Output als das gesamte produzierte Einkommen lässt sich außerdem aufteilen in Konsum und Investitionen, d.h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_t} lässt sich auch als Verwendungsrechnung darstellen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_t=C_t+I_t } (1.9)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C} den gesamten Konsum und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I} die gesamten Investitionen bezeichnet. In einer geschlossenen Ökonomie sind Produktion und Ausgaben somit zwangsläufig identisch. Eine offene Ökonomie unterscheidet sich insofern, als durch Einkommen, die im Ausland oder vom Ausland erzielt werden, Gleichungen (1.8) und (1.9) nicht zwangsläufig übereinstimmen.
Die Dynamik des Modells
Es wird angenommen, dass die Produktionsfaktoren mit exogen bestimmter, konstanter Rate wachsen. Unter der Annahme, dass das Arbeitsangebot mit derselben Rate wie die Bevölkerung wächst bzw. identisch mit ihr ist, gilt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{L}_{t}=n L_{t} } (1.10)
wobei ein Punkt über einer Variable deren Ableitung nach der Zeit symbolisiert und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} die Rate des Bevölkerungswachstums ist. Die neoklassische Wachstumstheorie zeigt hier eine wesentliche Abweichung von den Annahmen der klassischen Gedanken zum Wirtschaftswachstum: Die Bevölkerung wächst nicht mehr mit der Wirtschaft, sondern losgelöst von ihr. Folglich kommt es in der neoklassischen Theorie nicht zwangsläufig zu einem stationären Zustand, sondern ein stetiges Wachstum pro Kopf ist möglich.
Es folgt aus Gleichung (1.10), dass zu jedem beliebigen Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{t}=L_{0} e^{n t} } (1.11)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e} für die Eulersche Zahl steht und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} einen beliebigen Beginn eines Beobachtungszeitraums markiert. Man beachte, dass im Falle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n>0} aufgrund der abnehmenden, aber stets positiven Grenzproduktivität des Faktors Arbeit die gesamte Produktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} ceteris paribus ein positives Wachstum verzeichnet, während die Produktion je Beschäftigten zurückgeht. Anders formuliert: Ein positives Wirtschaftswachstum je Beschäftigten bei zugleich positivem Bevölkerungswachstum kann es nur geben, wenn zugleich die Kapitalintensität und/oder die Arbeitsproduktivität steigt. Die erste Möglichkeit soll im Folgenden behandelt werden, ehe im nächsten Kapitel die Bedeutung des technologischen Fortschritts beleuchtet wird:
Der Anteil des Outputs, der investiert wird, entspricht der Sparquote und ist exogen gegeben und konstant. Eine investierte Einheit Output entspricht einer neuen Einheit Kapital. Kapitalgüter müssen jedoch von Zeit zu Zeit erneuert werden, da der vorhandene Kapitalstock verfällt. Die Investitionsgleichung nimmt daher folgende Form an: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{K}_{t}=s_{K} f\left(K_{t}, L_{t}\right)-\delta K_{t}=s_{K} Y_{t}-\delta K_{t} } (1.12)
Die Variable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K} bildet die Sparquote ab, während Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta } die Abschreibungsrate bezeichnet. Gleichung (1.12) ist die Schlüsselgleichung des Solow-Modells und beschreibt die Kapitalakkumulation als elementaren Prozess der industriellen Produktion: Ein Teil der Produktion wird konsumiert, der andere Teil wird reinvestiert. Zugleich verbraucht sich der bereits vorhandene Kapitalstock und muss daher permanent erneuert werden. Der Term Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K Y_t} entspricht folglich den Bruttoinvestitionen zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} , während die Nettoinvestitionen durch die gesamte Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_{K} Y_{t}-\delta K_{t}=\dot{K}_{t}} dargestellt sind.
Für den gesamten Kapitalstock einer Ökonomie gilt somit,
dass er dann steigt, wenn der linke Term in Gleichung (1.12) größer ist als der rechte, d.h. wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K Y_t>\delta K_t} ,
dass er konstant bleibt wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K Y_t=\delta K_t} und somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{K}_{t}=0}
dass er fällt, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K Y_t<\delta K_t} .
Analog lässt sich die Investitionsgleichung je Beschäftigten ausdrücken: Da Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_t=K_t/L_t } , folgt aus der Quotientenregel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{k}_{t}=\frac{\dot{K}_{t} L_{t}-K_{t} \dot{L}_{t}}{L_{t}^{2}}=\frac{\dot{K}_{t}}{L_{t}}-\frac{K_{t}}{L_{t}} \frac{\dot{L}_{t}}{L_{t}} } (1.13)
Es folgt aus den Gleichungen (1.12) und (1.13) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{k}_{t}=\frac{s_{K} Y_{t}-\delta K_{t}}{L_{t}}-\frac{K_{t}}{L_{t}} \frac{\dot{L}_{t}}{L_{t}}=s_{K} y_{t}-\delta k_{t}-n k_{t}=s_{K} y_{t}-(n+\delta) k_{t} } (1.14)
Aus Gleichung (1.14), der Entwicklung des Kapitalbestands je Beschäftigten über die Zeit, lassen sich weitere Schlüsse ziehen:
Erstens, der Kapitalstock je Beschäftigten bleibt konstant wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K y_t=(n+\delta )k_t} : Demnach muss ein höheres Bevölkerungswachstum durch eine höhere Sparquote ausgeglichen werden. Passiert dies nicht, wird der Kapitalstock je Beschäftigten und somit die Produktion je Beschäftigten sinken, auch wenn gleichzeitig die Gesamtproduktion steigt.
Zweitens, in einer betrachteten Ökonomie mag zu Beginn eines beliebigen Beobachtungszeitraums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} der Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K y_t\neq (n+\delta )k_t} gegeben sein. Egal von welchem Punkt aus die Ökonomie startet, sie wird bei fixen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta } sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_t>0} stets zum Gleichgewicht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{k}_{t}=0} streben.
Drittens muss für die Sparquote Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K<1} gelten, da es sonst keinen Konsum (einschließlich Grundnahrungsmittel) gäbe. Sie kann also nicht beliebig erhöht werden.
Abb. 1.3 veranschaulicht diese Zusammenhänge: Die Gerade zeigt jenes Brutto-Investitionsniveau je Beschäftigten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (n+\delta )k_t} , das erforderlich ist, um den Kapitalstock je Beschäftigten aufrecht zu erhalten. Die strichlierte Kurve zeigt das tatsächliche Brutto-Investitionsniveau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K y_t} : Ist es höher als das erforderliche Investitionsniveau, wird der Kapitalstock je Beschäftigten steigen, und vice versa – so lange, bis beide exakt gleich hoch sind.
Aus dem Fundament des neoklassischen Wachstumsmodells können bereits zwei Hauptergebnisse des Modells formuliert werden:
- Eine Erhöhung der Sparquote wird für eine gewisse Zeit das Wachstum erhöhen, bis die Ökonomie beim neuen Gleichgewichtspunkt angelangt ist. Um das Wachstum ab diesem Zeitpunkt wieder zu erhöhen, muss abermals die Sparquote erhöht werden. Da die Sparquote jedoch nicht den Wert eins erreichen kann, kann eine fortwährende Erhöhung der Sparquote nicht auf Dauer aufrechterhalten werden. Bleibt die Sparquote konstant, so hat sie auf die langfristige Wachstumsrate der Produktion je Beschäftigten keinen Einfluss.
- Die Sparquote bestimmt jedoch die Höhe des Produktionsniveaus: Eine höhere Sparquote führt langfristig zu einem höheren Niveau der Produktion je Beschäftigten.
Zusammenfassend lässt sich festhalten, dass es nur zwei Möglichkeiten gibt, damit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y} , die Produktion je Beschäftigten, wächst: Entweder erhöht sich die Kapitalintensität, d.h. dem Faktor Arbeit steht pro Einheit mehr Kapital zur Verfügung – dieses Szenario wurde soeben durchleuchtet. Oder die Arbeit wird selbst produktiver – dieses Szenario steht im Mittelpunkt des folgenden Kapitels.
Das Solow-Modell und seine Erweiterungen
Einen häufig angewendeten, nichtsdestoweniger speziellen Fall einer Produktionsfunktion, die die geforderten Bedingungen erfüllt, ist jene vom Typ Cobb-Douglas: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{t}=K_{t}^{\alpha} L_{t}^{1-\alpha}, \quad 0<\alpha<1 } (1.15)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha } die Elastizität des Produktionsfaktors Kapital, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1-\alpha } die Elastizität des Produktionsfaktors Arbeit bezeichnet. Indem beide Seiten der Gleichung (1.15) durch den Faktor Arbeit dividiert werden, erhält man die Produktion je Beschäftigten (Arbeitsproduktivität oder einfach Produktivität): Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{t}=\frac{Y_{t}}{L_{t}} \Rightarrow y_{t}=k_{t}^{\alpha} } (1.16)
Aus Gleichung (1.16) geht bereits hervor, dass unter Abstraktion anderer Einflüsse die Produktivität mit steigendem Kapitaleinsatz grundsätzlich steigt. Anders ausgedrückt zeigt Gleichung (1.16) nichts anderes, als dass mehr Maschinen menschliche Arbeit produktiver machen. Im Folgenden wird die Produktionsfunktion vom Typ Cobb-Douglas angewendet, um den langfristigen Verlauf einer Volkswirtschaft zu beschreiben.
Technologischer Fortschritt
Das vorige Kapitel endete mit der Feststellung, dass zur langfristigen Produktionssteigerung die Produktivität des Faktors Arbeit erhöht werden muss. Um dies zu veranschaulichen, kann die Cobb-Douglas-Produktionsfunktion nun wie folgt angeschrieben werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{t}=K_{t}^{\alpha}\left(A_{t} L_{t}\right)^{1-\alpha}, \quad 0<\alpha<1 } (1.17)
Die zusätzliche Variable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_t} repräsentiert den technologischen Stand (das abstrakte Wissen) zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} . Diese allgemein verfügbare Technologie wächst mit konstanter Rate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} , daher gilt analog zum Bevölkerungswachstum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{A}_{t}=g A_{t} } (1.18)
und folglich zu jedem beliebigen Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{t}=A_{0} e^{g t} } (1.19)
Daraus folgt, dass die gesamte Produktion zum Zeitpunkt dargestellt werden kann als: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{t}=K_{t}^{\alpha}\left(A_{0} e^{g t} L_{0} e^{n t}\right)^{1-\alpha} \Rightarrow Y_{t}=K_{t}^{\alpha}\left(A_{0} L_{0}\right)^{(1-\alpha)} e^{(1-\alpha)(g+n) t} } (1.20)
[CHART]
Es gibt nun zwei Möglichkeiten, die Produktion je Beschäftigten in intensiver Form darzustellen: Erstens, beide Seiten aus Gleichung (1.17) werden durch den Faktor Arbeit dividiert, und man erhält die Produktion je Beschäftigten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{Y_{t}}{L_{t}}=K_{t}^{\alpha} L_{t}^{-\alpha} A_{t}^{1-\alpha} \Rightarrow y_{t}=k_{t}^{\alpha} A_{t}^{1-\alpha} } (1.21)
Aus Gleichung (1.21) folgt eine weiteres Hauptergebnis des Solow-Modells: Es wurde bereits festgehalten, dass die Sparquote nicht beliebig erhöht werden kann. Nimmt man nun an, dass die Sparquote langfristig konstant ist, sich die Ökonomie im Gleichgewichtszustand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K y_0=(n+\delta )k_0} befindet, und die allgemein verfügbare Technologie mit konstanter Rate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} wächst, so folgt daraus, dass die Produktion je Beschäftigten langfristig mit ebendieser Rate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} wächst. Dieses Wachstum wird als Steady-State-Wachstum oder Gleichgewichtswachstum bezeichnet.
Die zweite Möglichkeit zur Darstellung in intensiver Form besteht darin, beide Seiten aus Gleichung (1.17) durch die Variablen Arbeit und Technologie zu dividieren und auf diese Weise Produktion je Beschäftigten um den technologischen Fortschritt zu korrigieren. Es mag an dieser Stelle zunächst verwirren, die Technologie zuerst einzuführen, bloß um sie anschließend wieder herauszurechnen, doch wie noch zu sehen ist, vereinfacht es die folgenden Berechnungen; dargestellt wird die Produktion je effektiver Arbeitseinheit: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{Y_{t}}{A_{t} L_{t}}=K_{t}^{\alpha} L_{t}^{-\alpha} A_{t}^{-\alpha} \Rightarrow \hat{y}_{t}=\hat{k}_{t}^{\alpha} } (1.22)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y} =Y_t/A_t L_t } den Output je effektiver Arbeitseinheit darstellt, während Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}=K/AL} den Kapitalstock je effektiver Arbeitseinheit bezeichnet. Man sieht, dass
Gleichung (1.22) Gleichung (1.16) sehr ähnlich ist und kann nun festhalten, dass die Produktion je effektiver Arbeitseinheit in der langen Frist konstant bleibt. Dieser Zusammenhang wird in Abb. 1.4 veranschaulicht.
Kapital und Produktion im Zeitverlauf
Die Determinanten des Wachstums zeigen sich bei der weiteren Behandlung des Outputs je effektiver Arbeitseinheit. Analog zu Gleichung (1.12) gilt für die Gesamtwirtschaft unter Einbeziehung des technologischen Fortschritts: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{K}_{t}=s_{K} f\left(K_{t}, A_{t} L_{t}\right)-\delta K_{t} } (1.23)
da Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}_{t}=K_{t} /\left(A_{t} L_{t}\right)} folgen aus der Quotientenregel sowie der Produktregel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{k}}_{t}=\frac{\dot{K}_{t} A_{t} L_{t}-K_{t}\left(\dot{A}_{t} L_{t}+A_{t} \dot{L}_{t}\right)}{A_{t}^{2} L_{t}^{2}}=\frac{\dot{K}_{t}}{A_{t} L_{t}}-\frac{K_{t} \dot{A}_{t} L_{t}}{A_{t}^{2} L_{t}^{2}}-\frac{K_{t} A_{t} \dot{L}_{t}}{A_{t}^{2} L_{t}^{2}} } (1.24)
Es folgt daher aus den Gleichungen (1.12), (1.21) und (1.24) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{k}}_{t}=\frac{s_{K} f\left(K_{t}, A_{t} L_{t}\right)-\delta K_{t}}{A_{t} L_{t}}-\frac{K_{t} \dot{A}_{t} L_{t}}{A_{t}^{2} L_{t}^{2}}-\frac{K_{t} A_{t} \dot{L}_{t}}{A_{t}^{2} L_{t}^{2}}=s_{K} \hat{y}_{t}-\delta k_{t}-g k_{t}-n k_{t}=s_{K} \hat{y}_{t}-(n+g+\delta) \hat{k}_{t} } (1.25)
Gleichung (1.25) besagt, dass die Veränderung im Kapitalstock je effektiver Arbeitseinheit die Differenz aus zwei Termen ist: Der linke Term, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K \hat{y_t}} , entspricht den Bruttoinvestitionen je effektiver Arbeitseinheit; der rechte Term Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (n+g+\delta ) \hat{k_t}} , entspricht den Investitionen, die nötig sind, um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y_t}} konstant zu halten. Dies ist folglich dann der Fall, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K \hat{y_t}=(n+g+\delta ) \hat{k_t}} gilt. Wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K \hat{y_t}\neq (n+g+\delta ) \hat{k_t}} gilt, so steigt der Kapitalstock je effektiver Arbeitseinheit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k_t}} , wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K \hat{y_t}>(n+g+\delta ) \hat{k_t}} , und umgekehrt. Dieser Prozess verläuft analog zum in Abb. 1.3 dargestellten Mechanismus, als die Ökonomie immer zum Schnittpunkt der beiden Kurven tendiert: Wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K \hat{y_t}=(n+g+\delta ) \hat{k_t}} und somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}_{t}=0} gilt, befindet sich die Ökonomie im Steady-State.
Bei näherer Betrachtung der Produktionsfunktion je effektiver Arbeitseinheit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y}_{t}=\hat{k}_{t}^{\alpha}} , wird deutlich, dass der Output je effektiver Arbeitseinheit im Steady-State nicht wächst, sondern konstant bleibt. Was bedeutet das? Im Steady-State ist nicht die Produktion an sich, sondern die Produktion je effektiver Arbeitseinheit konstant. Aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y}_{t}=\hat{k}_{t}^{\alpha}} folgt als Bedingung für den Steady-State Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_{K} \hat{k}_{t}^{* \alpha}=(n+g+\delta) \hat{k}_{t}^{*} } (1.26)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k^*}} den Kapitalstock je effektiver Arbeitseinheit im Steady-State bezeichnet. Gleichung (1.26) lässt sich für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k^*}} ausdrücken und man erhält Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}^{*}=\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{1}{1-\alpha}} } (1.27)
Aus der Produktionsfunktion in Gleichung (1.22) folgt daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y}^{*}=\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{\alpha}{1-\alpha}} } (1.28)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y^*}} den Output je effektiver Arbeitseinheit im Steady-State bezeichnet. Da der technologische Fortschritt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} und die Bevölkerung (das Arbeitsangebot) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} mit den konstanten Raten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} wachsen, kann der Output im Steady-State zu jedem beliebigen Zeitpunkt dargestellt werden als Steady-State-Output je Beschäftigten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y^*} zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{t}^{*}=A_{t} \hat{y}^{*}=A_{0} e^{g t}\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{\alpha}{1-\alpha}} } (1.29)
und der gesamte Steady-State-Output Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y^*} zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{t}^{*}=A_{t} L_{t} \hat{y}^{*}=A_{0} L_{0} e^{(g+n) t}\left(\frac{s_{K}}{n+g+\delta}\right)^{\frac{\alpha}{1-\alpha}} } (1.30)
Die Gleichungen (1.28), (1.29) und (1.30) verdeutlichen die Hauptaussagen des Solow-Modells:
- Eine Erhöhung der Sparquote wirkt sich positiv auf das Outputniveau aus, hat aber langfristig keine Auswirkung auf das Wirtschaftswachstum.
- Eine höhere Bevölkerungswachstumsrate wirkt sich positiv auf den gesamten Output, aber negativ auf den Output je Beschäftigten aus.
- Die Rate des technologischen Fortschritts wirkt sich positiv auf den gesamten Output sowie den Output je Beschäftigten aus.
Das langfristige Wachstum je Beschäftigten ist letztlich identisch mit der Rate des technologischen Fortschritts – dies ist in Gleichung (1.29) zu erkennen. Tatsächlich erscheint es auch intuitiv einleuchtend, dass die Zunahme des allgemeinen Wissens dafür gesorgt hat, dass der Lebensstandard in unseren Breiten um ein Vielfaches höher ist als noch vor 100 Jahren. Vieles von dem, womit wir uns heute beruflich beschäftigen, war vor einigen Generationen noch unbekannt, oder zumindest in dieser Form noch nicht bekannt. Darüber hinaus bietet das Wissen als Determinante von Produktion und Wachstum auch eine Erklärung für die weltweiten Unterschiede im Lebensstandard: Wenn technologischer Fortschritt für die Erhöhung der Produktivität im Zeitverlauf innerhalb einer Ökonomie verantwortlich ist, so folgt daraus, dass Unterschiede hinsichtlich des Zugangs zu Technologie zwischen Ökonomien zwangsläufig zu unterschiedlich hoher Produktivität führen. Anders formuliert sind weltweite Disparitäten beim BIP zumindest auch eine Folge unterschiedlicher Bestände an Wissen und seiner Anwendung. Durch die Implementierung des Wissens als Produktionsfaktor bietet das Solow-Modell eine plausible Erklärung für weltweite Disparitäten der wirtschaftlichen Entwicklung.
Darüber hinaus ist das Solow-Modell in der Lage, einen langfristigen Wachstumspfad mit dem Phänomen temporärer Schwankungen zu verbinden. Wie in Abb. 1.1 am Beispiel Österreich veranschaulicht, kann das Wachstum in einzelnen Perioden zwar zum Teil recht erheblichen konjunkturellen Einfluss unterliegen, welche von der jeweiligen Wirtschaftspolitik oder äußeren Faktoren abhängig sind. Langfristig befindet sich die Wirtschaft jedoch offensichtlich auf einem bestimmten Wachstumspfad. Selbst wenn die Wirtschaft schwer erschüttert wird und ein großer Teil des Kapitalstocks etwa durch einen Krieg vernichtet wird, kehrt sie zum Gleichgewichtswachstum zurück. Wie in Abb. 1.3 zu sehen, gilt bei konstanter Sparquote während der Übergangsphase Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K y_t>(n+\delta )k_t} , und die Ökonomie weist in dieser Zeit ein relativ hohes Wachstum auf. Auf diese Weise ist das Solow-Modell auch in der Lage, das hohe Wirtschaftswachstum in Österreich nach dem Zweiten Weltkrieg zu erklären („Wirtschaftswunderjahre“).
Das Solow-Modell wird recht häufig dafür kritisiert, dass es zwar die Bedeutung des technologischen Fortschritts veranschaulicht, aber keine Antwort auf die Frage gibt, wie dieser technologische Fortschritt entsteht. [15] Ein weiteres Problem ergibt sich beim Versuch einer Quantifizierung des ursprünglichen Solow-Modells. Ein Unterschied um das Zehnfache beim BIP je Arbeitseinheit ist nicht ungewöhnlich bei Vergleichen sowohl im Raum wie über die Zeit. Ein zehnfacher Unterschied in Bezug auf Arbeitsproduktivität bedingt im Solow-Modell jedoch einen Unterschied von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10^{1 / \alpha} )} bei der Kapitalausstattung – bei der üblichen Annahme von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha \approx 1/3} ergibt sich daraus eine Kapitalausstattung je Arbeitseinheit um das Tausendfache. Das Verhältnis Kapital-Output mag sowohl über die Zeit wie in verschiedenen Ökonomien ganz erheblich variieren, derart gigantische Unterschiede sind jedoch empirisch nicht haltbar.
Ein zweites Problem der Quantifizierung ergibt sich bei Vergleichen um die Welt. Aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha \approx 1/3} ergibt sich weiter, dass eine Differenz beim Output je Arbeiter um das Zehnfache eine Differenz bei der Grenzproduktivität des Kapitals um das Hundertfache bedingt. Im Kontext ganzer Volkswirtschaften folgt, dass da, wo bereits viel Kapital vorhanden ist, der Grenzertrag einer weiteren Einheit die Gesamtproduktion relativ wenig erhöhen wird – und umgekehrt da, wo noch wenig Kapital vorhanden ist, eine weitere Einheit sehr viel Ertrag bringt. Folglich wäre eine rege Investitionstätigkeit in Entwicklungs- und Schwellenländern zu erwarten, während Industrieländer eher unattraktiv für Investoren wären: Aus Gleichung (1.7)
und der Cobb-Douglas-Produktionsfunktion aus Gleichung (1.15) ergibt sich als erwarteter Gewinn einer zusätzlichen Einheit Kapital zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} : Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial Y_{t}}{\partial K_{t}}=\alpha K_{t}^{\alpha-1} L_{t}^{1-\alpha}=\alpha\left(\frac{L_{t}}{K_{t}}\right)^{1-\alpha}>0 } (1.31)
Da Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha <1} gilt, ist die der erwartete Gewinn (rate of return) eindeutig positiv. Ein nochmaliges Ableiten der Produktionsfunktion zeigt, dass dieser zusätzliche Produktionsgewinn je Einheit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_t} umso kleiner wird, je größer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_t} ist: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial^{2} Y_{t}}{\partial K_{t}^{2}}=\alpha(\alpha-1) K_{t}^{\alpha-2} L_{t}^{1-\alpha}<0 } (1.32)
Aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha <1} folgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha -1<0} , somit ist die Beziehung eindeutig negativ. Anders gesagt: Unter sonst identischen Bedingungen ist es reizvoller dort zu investieren, wo es noch verhältnismäßig wenig Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_t} gibt. Es ist eines der Hauptmerkmale der neoklassischen Theorie, dass die Grenzproduktivität Kapitalströme lenken wird, und zwar dorthin, wo es am produktivsten tätig sein wird. Daraus folgt, dass neue Fabriken, Bürogebäude und andere Investitionsgüter tendenziell eher dort entstehen sollten, wo es noch verhältnismäßig wenig davon gibt. Kapital ist stets auf der Suche nach höheren Renditen und wird daher – wenn man es lässt – dorthin wandern, wo es diese erwartet. Folglich würde man eine Wanderung vom Zentrum in die Peripherie erwarten, d.h. von den wohlhabenden, reichlich mit Kapital ausgestatteten Industriestaaten in die Schwellen- und Entwicklungsländer; ein solcher Prozess lässt sich in der Realität bis zu einem gewissen Grad tatsächlich beobachten. Die meisten Investitionen finden jedoch in den Zentren statt, die meisten grenzüberschreitenden Kapitalströme haben ihr Ursprungs- wie Zielland innerhalb der Industriestaaten. Wie im Folgenden gezeigt wird, kann die Einführung einer zweiten Kapitalform – des Humankapitals – erklären, warum auch fortgeschrittene Ökonomien mit hohem Sachkapitalbestand attraktiv für weitere Sachkapitalinvestitionen sind.
Die Rolle des Humankapitals
Robert Lucas hat 1990 [16] mehrere mögliche Erklärungen diskutiert, warum Kapital nicht in jenem Ausmaß von Industrie- in Schwellenländer fließt, wie man es aus der neoklassischen Theorie erwarten würde. [17] Neben (damals weit verbreiteten) Einschränkungen und Verboten von Kapitalexporten und -importen sowie Unterschieden beim Zugang zu Technologie ist es insbesondere eine Neuinterpretation des Begriffs Kapital, die sich als Erklärung anbietet. Spätestens seit den 1970er-Jahren hat sich innerhalb der Industriestaaten die Ausbildung der Arbeitskräfte als bedeutender Wirtschaftsfaktor gezeigt – und seither in ihrer Bedeutung eher noch zugenommen. So gesehen bleibt die Ausstattung mit Kapital entscheidend für das Produktionsniveau, doch ist mit „Kapital“ nun nicht mehr ausschließlich Sachkapital in Form von Maschinen und Ausrüstung, sondern auch Humankapital in Form von Ausbildung, Erfahrung und Fertigkeiten des Faktors Arbeit gemeint.
N. Gregory Mankiw, David Romer und David N. Weil [18] haben kurz nach Lucas’ Beitrag Solows Modell erweitert, indem sie das Humankapital als zusätzlichen Faktor in die Produktionsfunktion aufnehmen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{t}=K_{t}^{\alpha} H_{t}^{\beta}\left(A_{t} L_{t}\right)^{1-\alpha-\beta}, \quad \alpha>0, \quad \beta>0, \quad \alpha+\beta<1 } (1.33)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_t} den Bestand an Humankapital zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} darstellt. Humankapital ist dabei definiert als die Gesamtheit der Fähigkeiten, der Erfahrung und des Wissens aller Arbeiter in einer Ökonomie. Alle anderen Variablen sind wie bisher definiert: Der aggregierte Output einer Ökonomie zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} ist folglich eine Funktion der Variablen Sachkapital Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_t} , Humankapital Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_t} und effektiver Arbeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_t \partial } . Die in Gleichung 1.16 ausgedrückten Bedingungen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta } stellen sicher, dass die Annahme konstanter Skalenerträge nach wie vor erfüllt ist.
Die Dynamik des Modells folgt für Arbeit und Technologie den in den Gleichungen (1.10) und (1.18) dargestellten Prozessen. Für Sachkapital gilt in Analogie zu Gleichung (1.23) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{K}_{t}=s_{K} f\left(K_{t}, H_{t}, A_{t} L_{t}\right)-\delta K_{t}=s_{K} Y_{t}-\delta K_{t} } (1.34)
Durch die Aufnahme einer zweiten Form von Kapital wird nun eine zweite Kapitalakkumulationsgleichung benötigt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{H}_{t}=s_{H} f\left(K_{t}, H_{t}, A_{t} L_{t}\right)-\delta H_{t}=s_{H} Y_{t}-\delta H_{t} } (1.35)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_H} jenen Anteil der Produktion darstellt, der für Neuinvestitionen in Humankapital aufgewendet wird; mit anderen Worten entspricht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_H Y_t} den Aufwendungen für das Ausbildungssystem zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} . Der Einfachheit zuliebe wird außerdem unterstellt, dass Humankapital mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta } dieselbe Abschreibungsrate aufweist wie das Sachkapital. Trotz dieser Gemeinsamkeiten bei der Modellierung ist Humankapital nicht einfach als zweite Form von Kapital zu verstehen, vielmehr nimmt es eine Doppelrolle ein: Einerseits folgt auf Investitionen in der Gegenwart ein höherer Output in der Zukunft, und wie beim Sachkapital muss zur Aufrechterhaltung des gegenwärtigen Niveaus permanent ein gewisser Anteil reinvestiert werden. Andererseits ist das Humankapital in den Arbeitern verkörpert: Der durchschnittliche Arbeiter stellt nun für die Produktion sowohl eine Einheit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} plus eine gewisse Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H} bereit. Somit wird zwar einerseits der Anteil des Einkommens, das an beide Arten Kapital geht, vergrößert. Andererseits ist das Humankapital Teil der Arbeit und wird folglich als Lohn ausbezahlt.
Das gesamte Lohnaufkommen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W} zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} beträgt somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_{t}=L_{t} w_{t}=L_{t} \frac{\partial Y_{t}}{\partial L_{t}}+H_{t} \frac{\partial Y_{t}}{\partial H_{t}} } (1.36)
während der Gewinnsatz zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} unverändert bleibt und der Beziehung in Gleichung (1.7) mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_t=\partial Y_t/\partial K_t} folgt. Analog zu Gleichung (1.22) können wiederum beide Seiten der Produktionsfunktion in Gleichung (1.35) durch effektive Arbeit dividiert werden, und man erhält so die Produktion je effektiver Arbeitseinheit: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y}_{t}=\frac{Y_{t}}{A_{t} L_{t}} \Rightarrow \hat{y}_{t}=\hat{k}_{t}^{\alpha} \hat{h}_{t}^{\beta} } (1.37)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}=K/AL} den Bestand an Sachkapital je effektiver Arbeitseinheit, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{h}=H/AL} den Bestand an Humankapital je effektiver Arbeitseinheit bezeichnet.
Die Entwicklung der Ökonomie lässt sich darstellen über die beiden Schlüsselgleichungen des Mankiw-Romer-Weil-Modells Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{k}}_{t}=s_{K} \hat{y}_{t}-(n+g+\delta) \hat{k}_{t} } (1.38)
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{h}}_{t}=s_{H} \hat{y}_{t}-(n+g+\delta) \hat{h}_{t} } (1.39)
die das Wachstum an Sachkapital je effektiver Arbeitseinheit, und das Wachstum an Humankapital je effektiver Arbeitseinheit darstellen. Setzt man jeweils die rechte Seite der beiden Gleichungen (1.38) und (1.39) gleich null und löst das entsprechende System aus zwei Gleichungen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{h}} , so erhält man den Steady-State-Wert des Sachkapitals je effektiver Arbeitseinheit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}^{*}=\left(\frac{s_{K}^{1-\beta} s_{H}^{\beta}}{n+g+\delta}\right)^{\frac{1}{1-\alpha-\beta}} } (1.40)
des Humankapitals je effektiver Arbeitseinheit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{h}^{*}=\left(\frac{s_{K}^{\alpha} s_{H}^{1-\alpha}}{n+g+\delta}\right)^{\frac{1}{1-\alpha-\beta}} } (1.41)
sowie, folgend aus Gleichung (1.37), Output im Steady-State je effektiver Arbeitseinheit: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y}^{*}=\hat{k}^{* a} \hat{h}^{* b}=\left(\frac{s_{K} s_{H}}{(n+g+\delta)^{\alpha+\beta}}\right)^{\frac{1}{1-\alpha-\beta}} } (1.42)
144.png|547x236px]]
Abb. 1.5: Die dynamische Stabilität des Mankiw-Romer-Weil-Modells – unabhängig
von der Ausgangslage strebt die Ökonomie stets zum Zustand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{k}}=0}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{h}}=0}
Die Ökonomie befindet sich im Steady-State-Wachstum, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{k}}=0} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\hat{h}}=0} : Sind beide Bedingungen erfüllt, beträgt wie im Solow-Modell das Wachstum je effektiver Einheit Null, und das Wachstum je Beschäftigten entspricht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g} . Dementsprechend werden positive oder negative Veränderung der Höhe von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_K} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_H} sich zwar entsprechend auf das langfristige Output-Niveau auswirken, nicht aber auf die langfristige Wachstumsrate. Die Auswirkungen auf das langfristige Outputniveau durch Veränderung von einer oder beiden Sparquoten (Sachkapital und/oder Humankapital) lassen sich aus Gleichung (1.42) ablesen.
Durch die Berücksichtigung eines zusätzlichen Faktors wird das Mankiw-Romer-Weil-Modell im Vergleich zum Solow-Modell zwar komplexer, bleibt aber stabil: Was immer auch der Ausgangspunkt der Ökonomie hinsichtlich der Werte für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{h}} sein mag, das System konvergiert zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}=0} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{ h}=0} [19] Dieser Zusammenhang wird im Phasendiagramm in Abb. 1.5 skizziert: Von einem beliebigen Ausgangspunkt strebt das System stets zum Schnittpunkt der beiden Kurven.
Die qualitativen Schlussfolgerungen des Mankiw-Romer-Weil-Modells sind ähnlich zu jenen des Solow-Modells, die Einbeziehung des Humankapital führt jedoch zu erheblichen quantitativen Unterschieden. Dazu zählt insbesondere die Grenzproduktivität des Kapitals, die im Cobb-Douglas-Fall folgende Form annimmt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial Y_{t}}{\partial K_{t}}=\alpha K_{t}^{\alpha-1} H_{t}^{\beta}\left(A_{t} L_{t}\right)^{1-\alpha-\beta} } (1.43)
Wie oben skizziert ist die Grenzproduktivität des Kapitals ausschlaggebend für den erwarteten Ertrag von Neuinvestitionen. Aus dem Zusammenhang, der sich in Gleichung (1.43) darstellt, ergibt sich ceteris paribus eine umso höhere Attraktivität für Investitionen, je mehr Humankapital in der betreffenden Ökonomie vorhanden ist. Wie sich überprüfen lässt, ist die Grenzproduktivität des Sachkapitals umso höher, je höher der Wert von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_t} ist. Auf diese Weise ist das Mankiw-Romer-Weil-Modell in der Lage, das Erklärungsvermögen des ursprünglichen Solow-Modells um Disparitäten in der Entwicklung sowie Investitionsströme in Ökonomien mit hohen Sachkapitalbeständen entscheidend zu verbessern.
Disparitäten der Entwicklung
Bis ins 18. Jahrhundert hinein waren die weltweiten Unterschiede im Lebensstandard relativ gering. Erst die Industrielle Revolution hat einerseits das stetige Wirtschaftswachstum ermöglicht, sorgte andererseits aber auch für unterschiedliche Wachstumsraten – die drastischen Unterschiede, die heute bestehen, sind hauptsächlich das Ergebnis unterschiedlichen Wirtschaftswachstums der letzten 100 bis 200 Jahre. Die Konsequenzen, die sich daraus ergeben, rechtfertigen für sich allein die Prüfung der Konvergenzhypothese, wonach Ökonomien mit einem heute geringeren Outputniveau in der Zukunft schneller wachsen. Anders formuliert: Werden jene, die heute zurückliegen, ihren Rückstand aufholen?
Die Konvergenz-Hypothese
Aus dem Solow-Modell (und seiner Erweiterung um Humankapital) lassen sich mindestens drei Kräfte ableiten, die Konvergenz zwischen Ökonomien erwarten lassen:
- Das Modell sagt eine Konvergenz zum eigenen Steady-State-Wachstum voraus. Daraus folgt, dass zwei Ökonomien mit vergleichbarem Steady-State, aber momentan unterschiedlichen aktuellen Niveaus, zueinander konvergieren werden.
- Die Grenzproduktivität des Kapitals ist dort höher, wo noch wenig vorhanden ist – bei freien Kapitalflüssen und unter sonst identischen Bedingungen wird dort investiert werden, wo noch wenig vorhanden ist, wodurch ein Aufholprozess hinsichtlich der Produktivität in Gang gesetzt wird.
- Output ist auch eine Funktion der Technologie. Daraus folgt, dass technologische Aufholprozesse zu einer Steigerung der Produktion führen.
Modellendogene Konvergenz
Der erste Punkt ergibt sich aus dem Modell selbst, wonach eine Ökonomie stets zu ihrem eigenen Steady-State konvergieren wird. [20] Die Stabilität des Modells gewährleistet eine Konvergenz der Produktionsfaktoren zu einem bestimmten Niveau – was auch immer die Ausgangslage sein mag. Dieser Zusammenhang wurde von Robert J. Barro und Xavier X. Sala-i-Martin [21] formal aus dem Solow-Modell abgeleitet und mündet in die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{T} \ln \left(\frac{y_{T}}{y_{0}}\right)=g+\frac{1-e^{-\tilde{\beta} T}}{T} \ln \left(\frac{y_{0}^{*}}{y_{0}}\right) } (1.44)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ln} den natürlichen Logarithmus bezeichnet und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\beta}=(1-\alpha )(n+g+\delta )} die Konvergenzgeschwindigkeit misst. [22] Die linke Seite in Gleichung (1.44) entspricht einer Approximation des Wachstums zwischen den Zeitpunkten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle =} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T} . Nach einigen Umformungen erhält man die ökonometrische Spezifikation Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\ln y_{T}-\ln y_{0}}{T}=\beta_{0}+\beta_{1} \ln y_{0} } (1.45)
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_{0}=g+\left[\left(1-e^{-\tilde{\beta} T}\right) / T\right] \ln y_{0}^{*}} der Konstanten und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_{1}=\left(e^{-\tilde{\beta} T}-1\right) / T} der Steigung der Regressionsgeraden entspricht, woraus sich schließlich als empirisch messbare Konvergenzgeschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\beta}=-\ln(1+Tb)/T} ergibt. In ökonometrischen Tests wird üblicherweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta _1} geschätzt: Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta _1} negativ, so liegt Konvergenz vor – ein höheres Ausgangsniveau des BIP je Einwohner, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_0} , führt der Hypothese zufolge zu einem langsameren Wachstum, daher besteht ein negativer Zusammenhang. Da Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta _1} der entscheidende Parameter ist, spricht man auch von Beta-Konvergenz.
Eine einfachere Methode, die Konvergenz-Hypothese zu prüfen, besteht darin, die Varianz des BIP je Einwohner für mehrere Zeitpunkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} zu messen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{t}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(\ln y_{i, t}-\frac{1}{n} \sum_{i=1}^{n} \ln y_{i, t}\right)^{2} } (1.46)
Um für allgemeine Wachstumsprozesse und Inflation zu kontrollieren, werden auch hier die Werte logarithmiert. Nimmt die Varianz im Zeitverlauf ab, so liegt Konvergenz vor. Da die Varianz üblicherweise durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma } symbolisiert wird, wird diese Art der Konvergenz auch Sigma-Konvergenz genannt.
Typen von Konvergenz
Ein Problem, das sich bei Prüfung der Konvergenz-Hypothesen auftritt, ist, dass ein Steady-State ein theoretisches Konstrukt darstellt, dessen wahre Höhe unbekannt ist – weshalb Annahmen darüber getroffen werden müssen, inwieweit sich die zu prüfenden Ökonomien hinsichtlich ihrer Steady-States voneinander unterscheiden. In empirischen Tests werden üblicherweise die Ausgangsdaten und die Wachstumsraten ausgewählter Ökonomien verglichen, gegebenenfalls ergänzt um weitere Variablen – d.h. es wird getestet, ob die Ökonomien zueinander konvergieren. Da das Solow-Modell als solches jedoch ein Modell für eine geschlossene Ökonomie ist, werden zwei Konzepte der Konvergenz unterschiedlicher Ökonomien unterschieden:
- Absolute Konvergenz bezeichnet den Prozess, wonach Ökonomien mit einem niedrigeren Output-Niveau auf jeden Fall schneller wachsen und folglich aufholen – es wird also unterstellt, dass alle Ökonomien zu einem identischen Steady-State-Niveau streben.
- Bedingte Konvergenz berücksichtigt Heterogenität zwischen Ökonomien und unterstellt, dass Ökonomien umso schneller wachsen, je weiter sie von ihrem eigenen Steady-State entfernt sind. Da das wahre Steady-State unbekannt ist, müssen Annahmen darüber getroffen werden, wodurch in der Realität die Höhe der Steady-States bestimmt wird.
Vergleichbare Steady-States
Als Beispiel für bedingte Konvergenz aufgrund vergleichbarer Steady-States kann der Aufholprozess Österreichs gegenüber der Schweiz nach dem Zweiten Weltkrieg genannt werden: Die beiden Länder sind sich hinsichtlich ihrer wichtigsten Parameter ähnlich, allerdings war das Sachkapital in Österreich vom Krieg weitgehend zerstört. Das führte zu einer erhöhten Grenzproduktivität von Sachkapitalinvestitionen in Österreich, was das Wachstum temporär beschleunigt hat: Ausgehend von einem niedrigeren Niveau hat Österreich über Jahrzehnte zur Schweiz aufgeholt, bis sich der Abstand auf relativ niedrigem Niveau eingependelt hat.
Kapitalflüsse
Das Modell von Mankiw, Romer und Weil bietet eine bessere Erklärung für die empirisch beobachtbaren Kapitalströme, ändert aber nichts an einer der Grundaussagen des Modells: Wo die Grenzproduktivität des Sachkapitals höher ist, ist der erwartete Ertrag einer Neuinvestition höher, also wird Kapital dorthin fließen. Die Attraktivität des Ziellands hängt nicht nur davon ab, wie viel Sachkapital dort bereits vorhanden ist, sondern insbesondere, wie produktiv es eingesetzt wird. Die Hypothese, wonach unter sonst gleichen Bedingungen Kapital in kapitalärmere Regionen fließen wird, bleibt unter der Annahme konstanter Skalenerträge aufrecht. Der Fall steigender Skalenerträge wird im folgenden Kapitel 1.3.2 diskutiert.
Technologische Aufholprozesse
Technologische Aufholprozesse als dritter Grund für Konvergenz können auf mannigfaltige Weise auftreten. Die Ausbreitung des Wissens ist bereits für die ältesten Hochkulturen kennzeichnend, ihre zum Teil jahrtausendealten Pfade wirken bis heute nach. Im Sinne ökonomischer Entwicklung kann Wissen dabei sehr umfassend begriffen werden und beschreibt sehr abstrakte Konzepte ebenso wie alltägliche Anwendungen.
Doch obwohl so unterschiedliche Dinge wie Integralrechnungen und Kochrezepte als verfügbares Wissen gelten, und obwohl ihre jeweilige Weiterentwicklung von sehr unterschiedlichen Faktoren abhängt, haben sie eine entscheidende Eigenschaft gemein: die Nichtrivalität. Das bedeutet, dass die Anwendung beliebigen verfügbaren Wissens – unabhängig davon, ob es sich um Integralrechnungen oder um Kochrezepte handelt – den Bestand ebendieses Wissens nicht verbraucht, sondern vielmehr beliebig oft angewendet werden kann. Diese Eigenschaft unterscheidet das Wissen von konventionellen privaten ökonomischen Gütern: Das Wissen nimmt die Charakteristik eines öffentlichen Guts an.
Ein Schluss, der aus diesen Überlegungen unmittelbar folgt ist, dass Produktion und Verteilung des Wissens nicht ausschließlich der Regulierung über Marktmechanismen überlassen werden können: Die Grenzkosten der Bereitstellung des Wissens, das bereits existiert, betragen null. Allerdings kann Wissen bis zu einem gewissen Grad auch geheim gehalten werden, wodurch es sich wiederum von öffentlichen Gütern unterscheidet: Es besteht also prinzipiell die Möglichkeit der Ausschließbarkeit. Der Grad der jeweiligen Ausschließbarkeit hängt von der Art des betreffenden Wissens ab.
Aus diesen Eigenschaften sowie der enormen Bedeutung, die das Wissen für die ökonomische Entwicklung hat, ergeben sich wichtige Schlussfolgerungen und neue Fragen hinsichtlich der Regulierung einzelner Ökonomien, von der Finanzierung der Universitäten bis zur idealen Dauer der exklusiven Anwendung patentierter Verfahren. Für die interregionale und internationale Entwicklung ist darüber hinaus von Bedeutung, wie leicht oder wie schwierig Wissen verfügbar ist.
Regionale Polarisation
Im Unterschied zur Konvergenz-Hypothese beobachten wir auf der ganzen Welt Zentrum-Peripherie-Gefälle, in denen das jeweilige Zentrum prosperiert, während das Hinterland zurückzufallen scheint. Im Folgenden werden die Grundlagen erläutert, wie ein solches Zentrum-Peripherie-Gefälle entsteht und sich möglicherweise vertieft. Diese Diskussion ist insbesondere für divergente Entwicklungen innerhalb einer Volkswirtschaft relevant: Die regionale Entwicklung kann vielfältige Muster zeigen und verläuft nur selten gleichmäßig. Ein besonders markanter Ausdruck ungleicher Entwicklung ist die historische Herausbildung von Städten.
Zwar ist es einerseits nahezu unmöglich, Verallgemeinerungen darüber aufzustellen, warum bestimmte ökonomische Entwicklungen an bestimmten Orten einsetzen und nicht an anderen. Es lässt sich allerdings beobachten, dass regionale Zentren wirtschaftlicher Entwicklung kumulativ als Folge eines gewissen Startvorteils entstehen. In weiterer Folge führen daraus entstandene Agglomerationsvorteile dazu, dass sich weitere Betriebe ansiedeln, die ihrerseits Arbeitskräfte anlocken, welche wiederum die Attraktivität des Standorts weiter erhöhen:
- Lokalisationsvorteile sind Kostenvorteile, die sich aus der räumlichen Ballung von Betrieben derselben Branche ergeben. Bestimmte Betriebe profitieren von der Ansiedlung an einem bestimmten Ort, indem sie auf einen gemeinsamen Pool qualifizierter Arbeitskräfte zurückgreifen, bzw. bereits vorhandene Verflechtungen zwischen Betrieben ausnützen.
- Verstädterungsvorteile bezeichnen Kostenvorteile, die durch Betriebe aus verschiedenen Branchen in unmittelbarer Nachbarschaft entstehen. Sie spiegeln externe Ersparnisse wider, die mit der räumlichen Ballung von Unternehmen und Sektoren zusammenhängen und deshalb in metropolitanen Regionen am stärksten ausgeprägt sind.
Die sich daraus ergebenden Vorteile und wirtschaftlichen Bindungen stellen den Anfangs- oder Startvorteil dar, der wirtschaftliche Entwicklung in Gang setzt. Im Sinne der Wachstumstheorie gilt die Annahme konstanter Skalenerträge hier nicht: Eine fortgesetzte Ansiedlung von Sach- und Humankapital führt aufgrund der Agglomerationsvorteile zu erhöhter Produktion, d.h. es bestehen steigende Skalenerträge. Allerdings können ab einer bestimmten Größe Agglomerationsvorteile zu -nachteilen werden, etwa durch überlastete Verkehrssysteme, Verwaltung oder Umweltbelastung. In diesem Fall liegen sinkende Skalenerträge vor.
In frühen Wachstumsphasen wirken häufig kumulative, sich selbst verstärkende Kräfte und beeinflussen über Größenersparnisse die wirtschaftliche Entwicklung im Raum: Wachstum in der Vergangenheit führt ab einer bestimmten Größe zu weiterem Wachstum. Ein solcher Prozess wird von Gunnar Myrdal [23] beschrieben, der bemerkt, dass eine gegenwärtige Anziehungskraft eines Zentrums ihren Ursprung hauptsächlich in einem historischen Zufall hat, der womöglich auch anderswo hätte stattfinden können.
Als Selbstverstärkung wird ein Prozess spiralförmiger Steigerung von Vorteilen in einem spezifischen geographischen Umfeld als Folge von Agglomerationseffekten und anderen externen Ersparnissen bezeichnet; umgekehrt kann jedoch auch eine Abwärtsspirale eintreten. In beiden Fällen werden dauerhafte oder zumindest längerfristig existente räumliche Disparitäten durch verschiedene soziale und ökonomische Prozesse im Zeitablauf sogar noch verstärkt. Durch die Wirkung auf die Ansiedlung der Faktoren und Kapital wird die Entwicklung entscheidend von anderen Ökonomien geprägt; deren Einfluss ist tendenziell umso stärker, je näher sie geographisch liegen. Dabei werden unterschieden:
- Zentripetale Entzugseffekte, welche die negativen Auswirkungen des Wachstums einer Region auf eine andere bezeichnen; bereits bestehende Disparitäten zwischen Zentrum und Peripherie werden verstärkt.
- Zentrifugale Ausbreitungseffekte, welche positive Auswirkungen des Wachstums einer Region auf eine andere bezeichnen; in weiterer Folge kann nun in der Peripherie ein kumulativer Wachstumsprozess entstehen.
Myrdal geht davon aus, dass in den meisten Fällen die Entzugseffekte stärker als die Ausbreitungseffekte wirken. Mechanismen dieser Art tragen dazu bei, dass sich ökonomische Zentren bilden und halten können – das Ergebnis ist ein räumlich ungleiches Muster der Entwicklung. Dieses Muster ist charakterisiert durch ein dominantes Zentrum (Kern) und eine subdominante Peripherie, wobei Zentrum und Peripherie gemeinsam ein interdependentes räumliches System bilden. Zentren verfügen dabei über eine hohe Kapazität zur Generierung und Absorption innovativen Wandels; die peripheren Regionen sind von den Zentren abhängig, ihr Entwicklungspfad wird hauptsächlich von den Institutionen der Zentren bestimmt. Das Zentrum dominiert zu jedem Zeitpunkt die Peripherie, was jedoch nicht unbedingt zum Nachteil der Peripherie sein muss:
- Das Zentrum fragt Güter aus der Peripherie nach, wodurch Geld in die Peripherie fließt.
- Arbeitskräfte wandern von der Peripherie ins Zentrum aufgrund neuer Beschäftigungsmöglichkeiten, eine mögliche Folge ist eine Verringerung der Arbeitslosigkeit in der Peripherie.
- Die Notwendigkeit von Inputs aus der Peripherie führt zu Investitionen, die durch Kapital aus dem Zentrum finanziert werden.
Die Folge solcher positiven Effekte kann sein, dass in der Peripherie nun selbst Auslösefaktoren für eine vorteilhafte Entwicklung überwiegen und eine solche in Gang setzen. Diese Schlussfolgerungen basieren im Wesentlichen auf dem neoklassischen Modell und seinen Grundannahmen, wonach die Produktionsfaktoren von Regionen geringer Erträge und Regionen hoher Erträge fließen und es in weiterer Folge zu einem Ausgleich bei der Faktorentlohnung kommt. Bei Nichterfüllung der Grundannahmen des Solow-Modells wie insbesondere jener konstanter Skalenerträge sind ausgleichende Kräfte jedoch nicht die zwangsläufige Folge. Anders formuliert führt Wachstum im Zentrum nicht zu einem parallelen Wachstum in der Peripherie, sondern kann zu einer Vertiefung der Disparitäten führen. Letzteres tritt auch dann auf, wenn die Peripherie zwar wächst, aber eben langsamer als das Zentrum.
Die Umkehrung der oben aufgezählten Ausbreitungseffekte beschreibt die Wirkung der Entzugseffekte:
- Der Erwerb von Gütern aus der Peripherie durch das Zentrum beschränkt sich möglicherweise auf primäre Güter, deren Nachfrageelastizität sehr gering ist; die Nachfrage bspw. nach Agrargütern oder Rohstoffen steigt nicht zwangsläufig, wenn das Zentrum hohe Wachstumsraten aufweist.
- Die Migration von Arbeitskräften aus der Peripherie ins Zentrum betrifft häufig eher die jungen und gut ausgebildeten Arbeitskräfte, die in weiterer Folge der Peripherie nicht mehr zur Verfügung stehen.
- Aufgrund von Agglomerationseffekten finden die meisten Investitionen nach wie vor in den Zentren statt, d.h. Kapitalströme gehen nicht zwangsläufig von Richtung Zentrum in Richtung Peripherie, sondern möglicherweise sogar umgekehrt.
Wenn es keine ausgleichenden Faktoren gibt, wie zum Beispiel ein Gegensteuern von Seiten der Politik, werden die Produktionsfaktoren Arbeit und Kapital beim Überwiegen zentripetaler Entzugseffekte von der Peripherie ins Zentrum wandern. Diese generieren wiederum Multiplikatoreffekte, die Disparitäten vertiefen sich weiter. Paul Krugman hat 1991 mit einem einflussreichen Modell gezeigt, [24] dass die Polarisationen sich umso mehr vertiefen, je günstiger Güter interregional gehandelt werden können. Der erste Grund hierfür ist, dass Produzenten bei sinkenden Handelskosten (dazu zählen Transportkosten, Zölle und regional differierende Präferenzen) den gesamten Markt von einem Standort aus bedienen können, während sie bei hohen Handelskosten die Standorte verteilen, um näher bei den Märkten zu sein. Der zweite Grund ist, dass bei sinkenden Handelskosten die Produzenten ihren bevorzugten Standort unter vielen möglichen wählen können. Aufgrund der oben beschriebenen Aggolmerationsvorteile werden das eher solche Standorte sein, die bereits über viel Sach- und Humankapital verfügen, wodurch sich die Disparitäten noch vertiefen.
Im Unterschied zum ursprünglichen Solow-Modell, das eine geschlossene Ökonomie beschreibt, berücksichtigen Polarisationsmodelle ihrem Wesen nach Interaktionen zwischen Ökonomien. Erweitert man das Solow-Modell um Kapitalflüsse und Migration, so zeigen sich auch im neoklassischen Wachstumsmodell Tendenzen zur Vertiefung bereits vorhandener Disparitäten, d.h. statt Konvergenz kommt es zu Divergenz: Neuinvestitionen finden eher dort statt, wo bereits viel Sach- und Humankapital vorhanden sind, ebenso wandern Humankapitalträger bevorzugt dorthin, wo das Lohnniveau höher ist.
Im Zuge der ökonomischen Integration sowohl der EU wie der Weltwirtschaft (Globalisierung) nehmen auch Volkswirtschaften immer mehr den Charakter von Regionalökonomien an, als sie ihre eigene Entwicklung immer mehr von der Entwicklung anderer Ökonomien abhängt, wodurch Polarisationsmodelle an Bedeutung gewinnen.
Empirie
Die Volkswirtschaftliche Gesamtrechnung (VGR) dient zur Beantwortung insbesondere zweier Fragestellungen: Erstens soll die Beschreibung der Entwicklung der wirtschaftlichen Aktivitäten und der gesamten Produktion eines Landes erreicht werden, zweitens sollen quantitative Aussagen über die Entwicklung des Wohlstands der Bürger eines Landes oder einer Region erreicht werden.
Welche Größen der VGR relevant sind, ist prinzipiell abhängig von theoretischen Überlegungen bzw. jeweiligen spezifischen Fragestellungen. Es gibt jedoch kaum eine Maßzahl der Sozial- und Wirtschaftswissenschaften, der in Politik und Öffentlichkeit so viel Bedeutung beigemessen wird wie dem Bruttoinlandsprodukt und seiner Entwicklung im Zeitverlauf. Das BIP dient als Indikator für internationale Vergleiche der Entwicklung und des Wohlstands wie für Erfolg oder Misserfolg einer Wirtschaftspolitik. Ob man den Blick nun auf die Welt, ein einzelnes Land oder eine Region wirft, es fällt schwer, die Bedeutung des Wirtschaftswachstums zu überschätzen: Die Schwierigkeiten, die man mit Regionen wie Süditalien oder Ostdeutschland assoziiert sind eng mit Fragen der wirtschaftlichen Entwicklung verknüpft. Das gilt ebenso für die Präferenzen über bestimmte Gesellschaftsordnungen bis hin zur Weltpolitik. Streitigkeiten wie etwa neoliberaler versus keynesianischer Wirtschaftspolitik innerhalb des kapitalistischen Systems lassen sich auf Fragen des wirtschaftlichen Erfolgs zurückführen und werden letztlich an diesem gemessen. Das BIP oder damit verwandte Größen der VGR hierbei als entscheidendes Kriterium heranzuziehen ist relativ unumstritten.
Je mehr das BIP jedoch als Maß für wirtschaftliche Leistungsfähigkeit angewendet wird, umso so mehr wird es auch kritisiert. Die wichtigsten Überlegungen sind dabei::
- Das Inlandsprinzip misst unter Umständen nicht das, was gemessen werden soll, d.h. produziertes und verfügbares Einkommen können erheblich voneinander abweichen.
- Im BIP ist enthalten, was neu produziert wird, nicht aber, was durch Abnutzung, Abbau, Zerstörung etc. verloren geht.
- Das BIP kann innerhalb einer Volkswirtschaft regional erheblich variieren.
- Die Höhe des BIP sagt nichts über die Einkommensverteilung innerhalb der Gesellschaft aus.
- Im BIP ist nur enthalten, was entgeltlich produziert wird, d.h. unbezahlte Arbeit (z.B. familiäre Erziehung, ehrenamtliche Tätigkeit) bleibt per definitionem unberücksichtigt. [25]
- Die Lebensqualität ist letztlich von vielen Faktoren abhängig, etwa dem Grad der Umweltverschmutzung, der sozialen Sicherheit etc.
Bezüglich der beiden ersten der Punkte finden sich in der VGR alternative, für bestimmte Fragestellungen besser geeignete Größen als das BIP, worauf im Folgenden näher eingegangen wird. Für Fragen der regionalen Entwicklung bietet sich das Bruttoregionalprodukt als analoges Maß an, Fragen der Verteilung innerhalb einer Ökonomie und ihrer Messung können teilweise ebenfalls mittels der VGR beantwortet werden, worauf im zweiten Hauptkapitel eingegangen wird. Der fünfte und sechste Punkt gehen über die Thematik dieses Skriptums hinaus: Festgehalten sei hier allerdings, dass komplexe, in diesen Fällen interdisziplinäre Fragen nur in den seltensten Fällen mittels eines einzigen Indikators beantwortet werden können, sondern vielmehr fast immer zusätzliche Methoden benötigen. Es sei jedoch hervorgehoben, dass das BIP kein Maß für den allgemeinen Wohlstand ist und auch nicht dafür konzipiert wurde. Es kann den Wohlstand bestenfalls schätzen (als Indikator), was das BIP misst, ist die Produktion. Seine Stärke liegt v.a. darin, dass es relativ einfach zu messen und daher als statistische Größe vergleichsweise zuverlässig ist: Grob vereinfacht fließt ins BIP ein, was in einer Periode für Geldeinheiten verkauft wird – nicht mehr und nicht weniger.
Messung von Größe und Wachstum
Bei der rein theoretischen Auseinandersetzung mit dem Wirtschaftswachstum genügte die Unterscheidung „gesamt“ versus „je Beschäftigten“ bzw. “je Einwohner“. In der Praxis gibt es jedoch verschiedene Größen, die je nach Fragestellung das geeignete Maß darstellen. Im Folgenden werden verschiedene Größen der Volkswirtschaftlichen Gesamtrechnung dargestellt; darüber hinaus werden einige Werte angegeben, um ein Gefühl für die Größenordnungen zu vermitteln. Zur Messung des gesamtwirtschaftlichen Geschehens ist eine ganze Reihe von Größen verbreitet, welche sich wiederum im Verhältnis zu verschiedenen, je nach Fragestellung adäquaten Bezugsgrößen (Einwohner, Beschäftigte etc.) darstellen lassen.
Bruttowertschöpfung (BWS): Sie ist die Grundlage der VGR und entspricht der Summe aller Produktionswerte abzüglich der Vorleistungen. In einer Welt ohne Ausland und ohne indirekte Steuern spiegelt sie das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} in den
Wachstumsmodellen wider. Die BWS entspricht der Produktion zu Herstellungspreisen oder Faktorkosten.Das Bruttoinlandsprodukt (BIP) ergibt sich durch Addition der indirekten Steuern abzüglich der Subventionen. Die Unterschiede zur BWS sind folglich die zusätzlichen Einnahmen und Ausgaben des Staates, der durch seine Politik in die Preissetzung am Markt eingreift. Das BIP entspricht daher der Produktion zu Marktpreisen.
Manchmal finden sich auch Ausdrücke wie „BIP zu Faktorkosten“, was daher der BWS entspricht.
minus Gütersubventionen:
Tab. 1.1: Schematischer Überblick über die wichtigsten Größen der VGR zur Erfassung der Gesamtwirtschaft und die entsprechenden Daten für Österreich 2015 (in Mrd. Euro, Differenzen in den Summen ergeben sich aus Rundungsfehlern); Quelle: Statistik Austria
Diese ab- und zufließenden Primäreinkommen setzen sich aus Einkommen aus Besitz und Unternehmung sowie aus Arbeitseinkommen zusammen. Erstere entstehen insbesondere durch Vermögensbestände von Inländern im Ausland wie Beteiligungen an Unternehmen, ausländische Staatsanleihen etc. Letztere entstehen aus Arbeitseinkommen von Inländern im Ausland wie jene von Auslandspendlern (und jeweils umgekehrt von Ausländern im Inland). Man beachte, dass gemäß dem Europäischen System Volkswirtschaftlicher Gesamtrechnungen (ESVG) das Inländer-Konzept nicht Inländer im staatsrechtlichen Sinn umfasst, sondern dass sämtliche Erwerbspersonen, die ihren wirtschaftlichen Schwerpunkt
| Bruttoinlandsprodukt: 339,90 | |
|---|---|
| - | Arbeitnehmerentgelte an die übrige Welt: 2,72 |
| - | Vermögenseinkommen an die übrige Welt: 28,50 |
| - | Produktions- und Importabgaben an die Institutionen der EU: 0,42 |
| + | Arbeitnehmerentgelte aus der übrigen Welt: 2,29 |
| + | Vermögenseinkommen aus der übrigen Welt: 27,24 |
| + | Subventionen aus der EU: 0,74 |
| = | Bruttonationaleinkommen: 338,52 |
- Tab. 1.2: Schematische Darstellung des Übergangs vom Bruttoinlandsprodukt zum Bruttonationaleinkommen mit den entsprechenden Daten für Österreich 2015 (in Mrd. Euro, Differenzen in den Summen ergeben sich aus Rundungsfehlern); Quelle: Statistik Austria
im Inland haben, in der VGR als Inländer erfasst werden – auch wenn sie im staatsrechtlichen Sinn Ausländer sind. [26] Nicht zuletzt deshalb machen den größten Anteil der zu- und abfließenden Primäreinkommen Vermögenseinkommen aus bzw. an die übrige Welt aus. Hinzu kommen gemäß ESVG schließlich noch Überweisungen aus bzw. an die EU. Eine detaillierte Darstellung des Übergangs vom BIP zum BNE mit Daten für Österreich findet sich in Tab. 1.2.
Insbesondere in Ländern, die einen hohen Zufluss an Auslandsdirektinvestitionen aufweisen, kommt es daher notwendigerweise mittelfristig zu einer erheblichen Diskrepanz zwischen Inlands- und Inländer-Produkt bzw -Einkommen. Während in Österreich das Verhältnis absolutes BNE/BIP bei 0,996 liegt, beträgt selbiges in der Republik Irland 0,792. [27] Auch bei Vernachlässigung einiger Feinheiten der Berechnung bleibt der Schluss zulässig, dass in Österreich 0,4% des entstehenden Einkommens, in Irland hingegen 20,8% des produzierten Einkommens netto an das Ausland fließen.
| Quelle | AT | HU | AT/HU |
|---|---|---|---|
| Der Spiegel Länderlexikon (BNE/EW in US-$) | 32.300 | 8.270 | 391% |
| OECD (BIP/EW zu KKP) | 31.944 | 15.946 | 200% |
| Weltbank (BNE/EW in US-$) | 32.280 | 8.370 | 386% |
| Der Fischer Weltalmanach online (BNE/EW in US-$) | 32.300 | 8.270 | 391% |
| Economist Intelligence Unit (BIP/EW zu KKP) | 31.930 | 15.184 | 210% |
| Cambridge Econometrics (BIP/EW in ECU, fixe Preise) | 26.209 | 4.720 | 555% |
| Eurostat (BIP/EW in Euro, jeweilige Preise) | 29.390 | 7.978 | 368% |
| Eurostat (BIP/EW in ECU, fixe Preise, Basisjahr 1995) | 27.413 | 4.770 | 575% |
| Eurostat (BIP/EW in ECU, Verkettung, Referenzjahr 1995) | 27.756 | 4.884 | 568% |
| Eurostat (BIP/EW zu KKP, EU-25 = 100) | 122,6 | 60,2 | 204% |
- Tab. 1.3:. Das BIP und BNE je Einwohner (EW) in Österreich und Ungarn sowie das Verhältnis im Jahr 2004 nach verschiedenen Quellen und Berechnungsmethoden
Bei der Interpretation der Daten kommt es daher darauf an, was gemessen wird. Das bei Wachstumsfragen relevante Problem nomineller versus realer Größen [28] ist dabei ebenso zu berücksichtigen wie die sinnvolle Wahl einer Bezugsgröße. Bei internationalen Vergleichen üblich ist, das BIP je Einwohner (Österreich im Jahr 2015: 39.390 Euro) anzugeben. Die Zahl der Erwerbstätigen kann sowohl im Zeitverlauf wie auch von Land zu Land schwanken, weshalb häufig die die Arbeitsproduktivität von Interesse ist: Sie ist definiert als Output je Arbeitseinheit und wird üblicherweise berechnet als BIP oder BWS je Erwerbstätigen oder je Arbeitsstunde (BWS je Erwerbstätigen in Österreich im Jahr 2015: 81.500 Euro). Nettolöhne und -gehälter (AT 2015: 92,17 Mrd. Euro) werden üblicherweise je Arbeitnehmer ausgewiesen (AT 2015: 28.800 Euro), zu beachten ist hier u.a., ob Erwerbstätige und Arbeitnehmer lediglich gezählt oder zu Vollzeitäquivalenten erfasst werden (hier: Vollzeitäquivalente), oder inwieweit sich die Gruppe der Erwerbstätigen mit jenen der Arbeitnehmer überschneidet (hier: 3.205.661 der 3.713.442 Erwerbstätigen waren 2015 Arbeitnehmer). Eine weitere Kennzahl stellt die Kapitalintensität dar, die das Verhältnis von BIP zum Bruttoanlagevermögen (Wert zu Wiederbeschaffungspreisen in Österreich 2015: 2,168 Billionen Euro)
darstellt und somit angibt, wie viel eine Kapitaleinheit im Durchschnitt zur Herstellung einer Einheit Bruttoinlandsprodukt beiträgt (Österreich 2015: 15,68 Cent).
Zur Illustration der beträchtlichen Unterschiede, die sich aus verschiedenen Berechnungsmethoden ergeben können, dient ein einfacher Vergleich verschiedener Angaben zum BIP bzw. BNE je Einwohner in Österreich und Ungarn für das Jahr 2004 in Tab. 1.3: Je nach Methode und Quelle wird die wirtschaftliche Leistung Österreichs als doppelt bis nahezu sechsmal so hoch eingestuft. Die Unterschiede ergeben sich v.a. daraus, ob unterschiedliche Preisniveaus berücksichtigt werden (Kaufkraftparitäten) und ob mit preisbereinigten („realen“) oder nominellen Werten gerechnet wird. Während das Rechnen zu Kaufkraftparitäten bei internationalen Vergleichen die Qualität des BIP als Indikator für Wohlstand verbessert, sind reale Werte eher bei Vergleichen einer Ökonomie mit sich selbst im Zeitverlauf geeignet (wie in Abb. 1.1). Wie in Tab. 1.3 ersichtlich, verringert das BIP zu Kaufkraftparitäten den Unterschied zwischen Österreich und Ungarn, da in Ungarn viele Güter billiger sind als in Österreich, während Preisbereinigungen innerhalb eines Landes die Unterschiede zwischen Ländern grob nach oben verzerren können.
Globale Konvergenz?
>Die in Kapitel 1.3.1 aus der neoklassischen Wachstumstheorie hergeleitete Konvergenz-Hypothese zählt zu den meistdiskutierten makroökonomischen Themen der vergangenen 25 Jahre. Zu den Hauptergebnissen zählt die von Sala-i-Martin geprägte Zwei-Prozent-Regel als Resultat zahlreicher Studien, wonach Ökonomien entsprechend einem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\beta}} aus Gleichung (1.44) mit einer Geschwindigkeit von 2% pro Jahr zueinander konvergieren [29] Die beiden prominentesten Beispiele zur Stützung der Konvergenz-Hypothese sind einerseits die Aufholprozesse der großen westeuropäischen Ökonomien Deutschland, Frankreich und Italien gegenüber Großbritannien in den letzten 200 Jahren, sowie der Aufholprozess innerhalb der OECD gegenüber den USA in den vergangenen 50 Jahren. Betrachtungen dieser Art haben jedoch die Schwachstelle, dass sie ex post erfolgen: Verglichen wird, was heute ähnlich ist, um dann festzustellen, dass ein Angleichungsprozess zu beobachten war. Demgegenüber steht die Feststellung von Gunnar Myrdal, der bereits 1957 bemerkte, dass es die Industriestaaten sind, die sich weiter industrialisieren und in denen alle Indikatoren nach oben zeigen. Tatsächlich stimmen die wohlhabenden Ökonomien von heute mit jenen von 1957 weitgehend überein. Temporäre Aufholprozesse wie zurzeit der VR China oder Indiens können nicht darüber hinwegtäuschen, dass mit Ausnahme der Republik Korea seit Myrdals Analyse kein einziges Land das BIP-je-Einwohner-Niveau der etablierten Industriestaaten erreichen konnte (abgesehen von Stadtstaaten wie Singapur und Rohstoff exportierenden Ländern wie Kuwait).
Wenn die gesamte Weltwirtschaft empirisch verglichen werden soll, stellt sich zunächst das Problem, dass es einige sehr, sehr große Länder und viele kleinere gibt. Ist es sinnvoll, eher kleinen Ländern wie Dänemark oder Guatemala bei einer Länder übergreifenden Studie denselben Stellenwert zuzuweisen wie etwa Russland oder Brasilien? Ein Lösungsansatz ist, statt einzelner Länder ökonomische Zonen und Blöcke zu betrachten: Abb. 1.6 zeigt das BIP als Anteil am Weltprodukt (= die Summe des absoluten BIP aller Länder = die Summe des absoluten BNE aller Länder) in den Jahren 1970 und 2015 für sieben Zonen bzw. Blöcke: Die USA, die EU innerhalb der Grenzen von 1995 bis 2004 („EU-15“), Japan, die UdSSR und ihre Nachfolgestaaten, die neun südamerikanischen Mitglied- und assoziierten Staaten des Mercosur, die Volksrepublik China (zu Grenzen von 2015) sowie Indien. Wie aus der Abbildung zu sehen ist, wurde 1970 rund 83%, und 2005 rund 76% des Weltprodukts in diesen sieben Zonen erwirtschaftet. Die Anteile der führenden Industriestaaten der USA, der EU-15 sowie Japans gingen im Beobachtungszeitraum zwar zurück, jedoch um weit weniger als der Anteil der betreffenden Länder an der Weltbevölkerung – was bedeutet, dass die Produktion je Einwohner in den führenden Industriestaaten im Vergleich zum Rest der Welt sogar noch zunahm.
Am auffälligsten ist der Rückgang des Anteils der UdSSR und ihrer Nachfolgerstaaten sowie der Ausbau Chinas. Zwar könnte man den Aufholprozess Chinas hier als Beleg für Konvergenz heranziehen – doch genauso gut könnte man den Rückgang des Anteils der UdSSR und ihrer Nachfolgerstaaten als Beleg für Divergenz sehen, zumal dieser Block 1970 technologisch den führenden Industriestaaten am nächsten war. Indien und die Mercosur-Staaten konnten ihre Anteile zwar leicht ausbauen, aber im selben Zeitraum wuchsen auch die jeweiligen Anteile an der Weltbevölkerung, was insbesondere das viel kommentierte Wachstum Indiens der letzten Jahre erheblich relativiert. Auf globaler Ebene lässt sich daher konstatieren, dass trotz temporär spektakulärer Wachstumsprozesse in einigen Ländern kein systematischer Aufholprozess ärmerer gegenüber wohlhabenderer Staaten zu beobachten ist.
174.png|244x227px]]175.png|245x204px]]
Innerhalb Europas ist die Persistenz der geographischen Disparitäten sogar noch stärker ausgeprägt als auf globaler Ebene: Jene Regionen, die sich bereits im 19. Jahrhundert industrialisierten, sind bis heute die produktivsten und wohlhabendsten Regionen Europas. Insbesondere die geographische Ausbreitung der Industrialisierung ist bis heute nachvollziehbar: Ausgehend von England über die Benelux-Staaten, Ostfrankreich und Deutschland bis nach Norditalien zieht sich ein geographischer Ausschnitt, in dem sich bis heute bevorzugt Hochtechnologie-Betriebe ansiedeln, in dem bis heute überproportional viele wissenschaftliche und kulturell bedeutende Einrichtungen zu finden sind und wo ein permanenter Zufluss von hochqualifizierten Arbeitskräften dafür sorgt, dass es auf absehbare Zeit auch so bleiben wird. Auch innerhalb Europas bedeuten gelegentliche temporäre Aufholprozesse wie jene Südeuropas in den 1980er- und 1990er-Jahren oder Mittelosteuropas seit den 1990er-Jahren noch lange kein Einholen oder gar Übberholen.
Regionales Wachstum innerhalb der Europäischen Union
Die bisherige Analyse hat gezeigt, dass es erstens Gesetzmäßigkeiten hinsichtlich der Entwicklung einer Ökonomie gibt, jedoch zweitens Ökonomien sich unterschiedlich entwickeln, wobei es keine automatische Angleichung gibt. Was für Europa gilt, gilt auch für die Europäische Union, die mittlerweile rund zwei Drittel der Bevölkerung Europas umfasst. Unterschiede hinsichtlich der Produktivität und des Wohlstands sind sowohl durch Nord-Süd-Gefälle wie durch Ost-West-Gefälle charakterisiert. Abb. 1.7 visualisiert diesen Sachverhalt durch eine Darstellung des Bruttoregionalprodukts (BRP) [30] für die EU: Es zeigt sich ein geographisches Muster, wobei die im Zentrum gelegenen Regionen jene mit dem höchsten BRP sind, während jene in Randlage benachteiligt scheinen. Die Regionen und Staaten innerhalb der Europäischen Union sind jedoch Teil desselben Wirtschaftsraums und unterliegen daher denselben Rahmenbedingungen, sie haben durch den Binnenmarkt prinzipiell Zugang zur selben Technologie und können bis zu einem gewissen Grad als ähnlich eingestuft werden. Deshalb folgt ein möglicher innereuropäischer Konvergenzprozess anderen Bedingungen als ein globaler. Als die Europäischen Gemeinschaften 1957/1958 gegründet wurden, bestanden sie aus sechs Ländern der produktivsten Industrieregionen der Welt, die sich auf vergleichbarem Niveau befanden; lediglich in Süditalien war die Produktivität deutlich niedriger. Nichtsdestoweniger wurde bereits mit dem Vertrag von Rom (1957) auch die Gründung der Europäischen Investitionsbank festgelegt, um Investitionen in weniger entwickelten Regionen zu unterstützen. Mit den verschiedenen Beitrittsrunden der heutigen Europäischen Union haben die regionalen Disparitäten jedoch zugenommen, zunächst durch den Beitritt der Republik Irland 1973, in den 1980er-Jahren durch die Süderweiterungen 1981 (Griechenland) und 1986 (Portugal und Spanien) und schließlich durch die Osterweiterungen seit 2004. Parallel zu dieser Entwicklung wurden die Bemühungen um eine Verringerung der Disparitäten erhöht, zunächst 1975 mit der Gründung des Europäischen Fonds für regionale Entwicklung.
Die Einheitliche Europäische Akte (1986) legte die Entwicklung hin zum Europäischen Binnenmarkt bis 1992 fest. Mit der unbeschränkten Niederlassung von Arbeit, Waren, Dienstleistungen und Kapital („vier Freiheiten“) wurde jedoch auch die Gefahr gesehen, dass einige Regionen und Länder Nachteile erfahren würden: Bei Liberalisierungen besteht grundsätzlich die Gefahr, dass bestimmte Ökonomien an Wettbewerbsfähigkeit einbüßen und eine Abwärtsspirale in Gang
gesetzt wird – einerseits, weil bei der Liberalisierung des Außenhandels ein in der Region produziertes Gut nun überlegener Konkurrenz von außen ausgesetzt wird,
176.png|495x423px|C:\Users\SES\Desktop\Abbildung 1_7 BMP.bmp]]
Abb. 1.7: Das BRP je Einwohner in den NUT2-Regionen der EU in Euro je Einwohner, 2013, Klasseneinteilung in Septilen [31]
andererseits, weil freier Verkehr von Arbeit und Kapital eine räumliche Konzentration der industriellen Produktion tendenziell noch verstärken. Um diese erwarteten negativen Auswirkungen abzufedern, wurde in der Einheitlichen Europäischen Akte explizit festgelegt, dass es Ziel der Gemeinschaft sei, die regionalen Disparitäten zu verringern. Die Regionalpolitik der Europäische Union wirkt demnach Entzugseffekten entgegen, indem über den Strukturfonds in benachteiligten Regionen insbesondere in die Infrastruktur investiert wird, wobei die Mittel aus dem EU-Haushalt stammen und somit überwiegend aus Steuern, die in den wohlhabenderen Regionen eingenommen werden.
Seit den 1980er-Jahren wurden die Mittel zur regionalen Förderung erheblich erhöht und erreichten 1993 bereits über 20 Mrd. ECU. Heute bilden die Mittel zur regionalen Förderung mittlerweile sogar den größten Ausgabeposten im EU-Haushaltsplan 2014-2020, das Budget beträgt im Durchschnitt 46,5 Mrd. Euro jährlich (zu Preisen von 2011), was rund einem Drittel des gesamten EU-Haushalts entspricht. Es stellt sich naturgemäß die Frage, ob diese Politik der Förderung rückständiger Gebiete erfolgreich ist. Einerseits wiesen die sogenannten Kohäsionsländer (d.h. von den EU-Förderungen besonders begünstigte Mitgliedstaaten) Griechenland, die Republik Irland, Portugal und Spanien seit den späten 1980er-Jahren relativ hohe Wachstumsraten des BIP auf und haben zum Mittelwert der EU aufgeschlossen oder ihn sogar übertroffen. Allerdings sind gerade diese Ökonomien von der 2008 ausgebrochenen Krise besonders betroffen und haben sich auch rund zehn Jahre danach noch nicht davon erholen können. Eine umfassende wissenschaftliche Analyse, inwieweit zwischen den hohen Wachstumsraten vor der Krise und der besonderen Betroffenheit von der Krise ein ursächlicher Zusammenhang besteht, steht bisher zwar noch aus. Die Krise macht jedoch deutlich, dass diese vier Länder, die bereits im 19. Jahrhundert im Verlauf der Industrialisierung den Anschluss verpassten, auf absehbare Zeit auch im 21. Jahrhundert ihre relativen Rückstande nicht wettmachen werden können.
Ähnliches wie für die Kohäsionsländer gilt im Prinzip auch für die seit 2004 der EU beigetretenen Staaten (neue Mitgliedstaaten, NMS): Diese weisen nach den durch die Transformation bedingten Rezessionen seit Mitte der 1990er-Jahre im Allgemeinen relativ hohe Wachstumsraten auf. Durch den Beitritt zum Binnenmarkt kam es zu einer regen Investitionstätigkeit von Unternehmen aus den EU-15, was nicht nur die industrielle Produktion, sondern durch den damit verbundenen Technologieschub auch die Produktivität erhöhte. Dieser Prozess kann jedoch nicht ewig fortgesetzt werden, auch wenn die NMS im Gegensatz zu den Kohäsionsländern seit Ausbruch der Krise weiterhin hohe Wachstumsraten aufweisen. Wie in Kapitel 1.2.3 gezeigt wurde, ist es bei hohem Sachkapitalbestand nötig, über einen hohen Humankapitalstand zu verfügen, um attraktiv für weitere Sachkapitalinvestitionen zu bleiben. Aufgrund der anhaltenden Abwanderung von Humankapitalträgern aus den NMS in Richtung EU-15 ist allerdings fraglich, ob die NMS ihren Aufholprozess fortsetzen werden können.
Von den 1980er-Jahren bis zum Ausbruch der Krise konnte für die Regionen der EU statistisch sowohl Beta- wie Sigma-Konvergenz gezeigt werden: Die Varianz nahm kontinuierlich ab, die Konvergenzgeschwindigkeit lag je nach ökonometrischer Spezifikation zwischen ein und zwei Prozent jährlich. Angesichts der vielen wirtschaftspolitischen Umwälzungen in dieser Zeit war der Konvergenzprozess bemerkenswert robust. Seit 2008 liegt jedoch weder Beta- noch Sigma-Konvergenz vor. Ein Grund für das Erliegen des Konvergenzprozesses ist, dass die ehemaligen Kohäsionsländer von der Krise besonders betroffen sind. Ein zweiter Grund ist jedoch innerhalb der NMS zu suchen; innerhalb dieser Länder sind Disparitäten stark ausgeprägt und verstärken sich tendenziell noch. So kommt es durch den Boom der Zentren innerhalb dieser Länder zwar einerseits zu einem Aufholprozess auf Ebene der Mitgliedstaaten, während sich innerhalb der Mitgliedstaaten die Disparitäten noch vergrößern.
Dieser Prozess ist nicht zuletzt deshalb problematisch, da die Persistenz der strukturellen Probleme größerer Regionen wie Süditalien oder Ostdeutschland zeigt, dass auch jahrzehntelange Förderungen nicht zwangsläufig erfolgreich sind.
Zusammenfassung
- Die Theorie langfristigen Wachstums unterscheidet sich grundlegend von Überlegungen zum kurz- bis mittelfristigen Wachstum, da Instrumente der Konjunkturpolitik unberücksichtigt bleiben. Stattdessen bestimmt in der neoklassischen Wachstumstheorie die Entwicklung der Produktionsfaktoren die langfristige Entwicklung. Hauptaussage der grundlegenden, auf Robert Solows Arbeiten basierenden Modelle ist, dass Kapitalakkumulation alleine nur in der mittleren Frist das Wachstum je Arbeitseinheit zu erhöhen in der Lage ist – langfristig tendiert die Ökonomie zu einem Gleichgewichtspfad, der der Rate des technologischen Fortschritts entspricht.
Aus der neoklassischen Theorie lassen sich drei wesentliche Kräfte identifizieren, die einen Ausgleich unterschiedlicher Produktionsniveaus unterschiedlicher Ökonomien bewirken können: Die Entwicklung zum eigenen Gleichgewichtspfad, die mit zunehmender Menge akkumulierten Kapitals abnehmende Grenzproduktivität des Kapitals, sowie technologische Aufholprozesse. Demgegenüber stehen Thesen zur regionalen Polarisation, die insbesondere für Regionalwirtschaften von Bedeutung sind: Sie beschrieben, wie ein Zentrum die Peripherie dominiert und sich die Disparitäten im Lauf der Zeit noch verstärken können.
Niveau und Wachstum einer Ökonomie werden über die Größen der Volkswirtschaftlichen Gesamtrechnung erfasst, in welcher für verschiedene Fragestellungen eine Auswahl an Größen erfasst sind. Ein weltweiter Vergleich des Bruttoinlandsprodukts seit 1970 zeigt, dass eine allgemeingültige Konvergenz-Hypothese durch die Empirie generell nicht gestützt wird, wiewohl temporäre Aufholprozesse beobachtet werden können. Innerhalb der EU ließ sich bis zum Ausbruch der Krise ein allgemeiner Trend der interregionaler Konvergenz beobachten, der seit 2008 jedoch zum Erliegen gekommen ist.
Übungen
|
- Der stationäre Zustand bezeichnet eine Entwicklung, in der die Ökonomie nicht mehr wächst, da landwirtschaftliche Produktion und Kapitalakkumulation ihre theoretischen Maxima erreicht haben.
- Der Steady-State bezeichnet eine Entwicklung, in der die Ökonomie mit konstanter Rate wächst. Diese Rate kann positiv, gleich null, oder theoretisch auch negativ sein. Eine positive Wachstumsrate der Gesamtwirtschaft kann mit einer negativen Wachstumsrate je Einwohner zusammenfallen.
- Ab einer hinreichenden Größe kann eine Ökonomie von einer Spezialisierung nicht weiter profitieren: Die Verdopplung aller Inputs führt zu einer Verdopplung des Outputs.
- Ist noch relativ wenig von einem Faktor vorhanden, so wird eine zusätzliche Einheit die Produktion erheblich erhöhen. Nimmt die Menge des Faktors weiter zu, während der oder die anderen konstant bleiben, so werden weitere Einheiten immer weniger zur Produktion beitragen.
- Die Entwicklung des Kapitalstocks je Arbeitseinheit über die Zeit ist in der Differentialgleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{k}_{t}=s_{K} y_{t}-(n+\delta) k_{t}} beschrieben. Daraus folgt, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{k}_{t}>0} wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_{K} y_{t}>(n+\delta) k_{t}} .
- Eine Senkung der Sparquote führt zu einem Rückgang des Wachstums, bis die Ökonomie beim neuen, niedrigeren Gleichgewichtspunkt angelangt ist.
- Der Output ist durch die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{y}_{t}=\hat{k}_{t}^{\alpha}} beschrieben. Die erste Ableitung ergibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \partial \hat{y}_{t} / \partial \hat{k}_{t}=\alpha \hat{k}_{t}^{\alpha-1}} und ist eindeutig positiv, da alle Variablen positiv sind.
- Aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c Y_{t}=f\left(c K_{t}, c L_{t}\right)} folgt im Cobb-Douglas-Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\left(c K_{t}, c L_{t}\right)=\left(c K_{t}\right)^{\alpha}\left(c L_{t}\right)^{1-\alpha}=c^{\alpha} c^{1-\alpha} K_{t}^{\alpha} L_{t}^{1-\alpha}=c f\left(K_{t}, L_{t}\right)}
- Die erste Ableitung ergibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \partial \hat{y}^{*} / \partial s_{K}=\alpha /\left[(1-\alpha) s_{K}^{1 /(1-\alpha)}(n+g+\delta)^{\alpha /(1-\alpha)}\right]} , da alle Variablen als positiv definiert sind und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha<1} gilt.
- Eine Verzehnfachung der Produktionsfunktion lässt sich anschreiben als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 y_{t}=10 k_{t}^{\alpha}} , woraus folgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 y_{t}=\left(10^{1 / \alpha} k_{t}\right)^{\alpha}} . Aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=1/3} ergibt sich eine Kapitalausstattung je Arbeitseinheit um das Tausendfache.
- Die erste Ableitung ergibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \partial \hat{y}^{*} / \partial s_{H}=[1 /(1-\alpha-\beta)]\left[s_{K} s_{H}^{-\alpha-\beta}(n+g+\delta)^{-\alpha-\beta}\right]^{1 /(1-\alpha-\beta)}} , da alle Variablen als positiv definiert sind und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha+\beta<1} gilt, ist die Ableitung positiv.
- Aus der Produktionsfunktion folgt für das gesamte Lohnaufkommen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_{t}=L_{t}\left(\partial Y_{t} / \partial L_{t}\right)+H_{t}\left(\partial Y_{t} / \partial H_{t}\right)=(1-\alpha-\beta) Y_{t}+\beta Y_{t}=(1-\alpha) Y_{t}} . Der Durchschnittslohn ergibt aus der Division des gesamten Lohnaufkommens durch das Arbeitsangebot: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_{t} / L_{t}=w_{t}=(1-\alpha) A_{t} \hat{k}_{t}^{\alpha} \hat{h}_{t}^{\beta}}
- Das Lucas-Paradoxon bezeichnet die empirische Beobachtung, dass Investitionen größtenteils in Ökonomien stattfinden, die bereits über eine hohe Kapitalausstattung je Arbeitseinheit verfügen.
- Nicht-Rivalität: Die Anwendung einer Einheit Wissens vermindert nicht den Bestand an vorhandenem Wissen.
- Lokalisationsvorteile sind Kostenvorteile, die sich aus der räumlichen Ballung von Unternehmen der selben Industriebranche ergeben.
- Zentripetale Entzugseffekte bezeichnen negative Auswirkungen des Wachstums einer Region auf eine andere, was zu einer Vertiefung bereits bestehender Disparitäten führt.
- Das BIP entspricht der Wertschöpfung zu Marktpreisen nach dem Inlands-Prinzip, das BNE entspricht der Wertschöpfung zu Marktpreisen nach dem Inländer-Prinzip. Die Größen unterscheiden sich um den Saldo der Primäreinkommen zwischen Inländern und übriger Welt.
- Hinweise: 1. Das BIP misst nicht das Vermögen, sondern das Einkommen. 2. Das BIP misst nicht das erhaltene, sondern das produzierte Einkommen.
- U.a. Deutschland, Frankreich und Italien gegenüber Großbritannien im 19. und teilweise 20. Jh., europäische OECD gegenüber den USA in der zweiten Hälfte des 20. Jh., außerdem ostasiatische Länder wie Singapur oder die Republik Korea in den vergangenen 30 bis 40 Jahren.
- Die Abstände zwischen den produktiven, wohlhabenden Ökonomien und den weniger produktiven Ökonomien blieben seit 1970 in den meisten Fällen konstant oder vergrößerten sich.
- 1. Liberalisierung des Außenhandels können zu überlegener Konkurrenz von außen führen.2. Freier Verkehr von Arbeit und Kapital führt zu einer tendenziellen Verstärkung räumlicher Konzentration der industriellen Produktion.
- Innerhalb der Regionen und Länder der EU und EFTA lässt sich eine Konvergenz beobachten. Gleichzeitig zeigt sich jedoch eine Zunahme der regionalen Disparitäten innerhalb vieler Länder.
- ↑ Siehe insbesondere Grundlagen der Volkswirtschaftslehre 3.
- ↑ Vgl. Grundlagen der Volkswirtschaftslehre 3, Tab. 1.1.
- ↑ Smith geht auf Wirtschaftswachstum im heutigen Sinne v.a. im ersten und zweiten Buch ein in: Adam Smith: An Inquiry into the Nature and Causes of the Wealth of Nations [1. Aufl. 1776], Deutscher Taschenbuch Verlag, 2003.
- ↑ Vgl. auch Grundlagen der Volkswirtschaftslehre 3, Kap. 1.2.2.
- ↑ Unter dem Eindruck der rasch voranschreitenden Industrialisierung hat Ricardo seine Werke mehrmals revidiert, 1821 mit der Einfügung des Kapitels „On Machinery“ des in der ersten Auflage 1817 erschienenen Werks: David Ricardo: On the Principles of Political Economy and Taxation [3. Aufl 1821], Prometheus, 1996.
- ↑ Die Analysen Marx’ zum Wirtschaftswachstum finden sich insbesondere im siebenten Abschnitt in: Karl Marx: Das Kapital – Kritik der politischen Ökonomie; Erster Band: Der Produktionsprozeß des Kapitals [2. Aufl. 1872], Parkland, 2003.
- ↑ Die ersten Ausführungen Solows finden sich unter: Robert M. Solow: A Contribution to the Theory of Economic Growth, Quarterly Journal of Economics 70, 1956
- ↑ Man beachte, dass in der Makroökonomik die Begriffe Kapital und Sachkapital zumeist synonym gebraucht werden, wiewohl es zahlreiche andere Kapitalformen gibt. Auch im vorliegenden Skriptum ist mit „Kapital“ ohne spezifische Bezeichnung stets das Sachkapital gemeint, d.h. die Begriffe Kapital und Sachkapital werden als Synonyme verwendet.
- ↑ In Abb. 1.1 wäre somit das BIP identisch mit dem BNE.
- ↑ In Österreich lag der Anteil der Land- und Forstwirtschaft inkl. Fischerei an der Bruttowertschöpfung (zu den Begriffen siehe Kapitel 1.4.1) im Jahr 2015 bei 1,29%, der Anteil des Bergbaus bei 0,39% (Berechnung nach Daten der Statistik Austria).
- ↑ Man kann sagen, dass das Modell nur anwendbar ist, wenn diese Annahmen erfüllt sind. Für Ökonomien, deren Realität von den Modellannahmen drastisch abweicht, hat das Modell folglich nur eingeschränkte Aussagekraft. Beispiele wären Ökonomien, die durch den Export von Rohstoffen sehr rasch wachsen wie etwa die OPEC-Länder in den 1970er- und 1980er-Jahren, oder Ökonomien, die die makroökonomischen Rahmenbedingungen wie Zinssatz, Inflation oder Staatsverschuldung nicht in den Griff bekommen, beispielsweise Japan oder die Ukraine in den 2000er- und 2010er-Jahren. Auch für die Ökonomien der Eurozone stellt sich angesichts der Euro-Dauerkrise zum Zeitpunkt der Drucklegung des vorliegenden Studienhefts schön langsam die Frage, ob die Modellannahmen noch zutreffen.
- ↑ Vgl. im Zusammenhang mit einzelnen Betrieben hierzu Grundlagen der Volkswirtschaftslehre 2 (Kapitel 1.1.4).
- ↑ Vgl. Grundlagen der Volkswirtschaftslehre 2 (Kapitel 1.1.1).
- ↑ Vgl. hierzu Grundlagen der Volkswirtschaftslehre 2, Gleichung (1.10).
- ↑ Die in den späten 1980er-Jahren entstandene endogene Wachstumstheorie (ausgehend von Arbeiten von Paul M. Romer sowie Robert E Lucas Jr.) versucht, die Determinanten der Höhe des technologischen Fortschritts zu modellieren und somit den technologischen Fortschritt als solchen zu bestimmen.
- ↑ Robert E. Lucas Jr.: Why Doesn’t Capital Flow from Rich to Poor Countries?, American Economic Review 80, 1990
- ↑ Dieses Phänomen wird auch Lucas-Paradoxon genannt.
- ↑ N. Gregory Mankiw, David Romer, David N. Weil: A Contribution to the Empirics of Economic Growth, Quarterly Journal of Economics 107, 1992
- ↑ Ausgenommen ist hier ein Ausgangspunkt mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{k}=0} oder ; ein solcher Ausgangspunkt entspricht jedoch einer nicht existierenden Ökonomie und ist daher für die weitere Betrachtung belanglos.
- ↑ Für das Mankiw-Romer-Weil-Modell ist dieser Zusammenhang in Abb. 1.5 dargestellt.
- ↑ Für eine ausführlichere Diskussion des Konzepts siehe: Robert J. Barro und Xavier X. Sala-i-Martin: Convergence, Journal of Political Economy 100, 1992
- ↑ Im Mankiw-Romer-Weil-Modell ergibt sich als Konvergenz-Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta \approx (1-\alpha -\beta )(n+g+\delta )}
- ↑ Gunnar Myrdal: Economic Theory and Under-Developed Regions [1. Aufl. 1957]. Duckworth, 1964
- ↑ Paul Krugman: Geography and Trade [1. Aufl. 1991]. Leuven University Press, 1992
- ↑ Dass Schwarzarbeit nicht erfasst würde, ist hingegen ein weit verbreiteter Irrtum. Als entgeltliche Arbeit ist sie definitionsgemäß Teil des Sozialprodukts; sie wird in Österreich auf ca. 4% des BIP geschätzt.
- ↑ Daher wird das Inländerkonzept treffender auch als „Wohnortkonzept“ bezeichnet.
- ↑ Angabe für Irland berechnet laut Central Statistics Office Ireland, nach Daten für 2015.
- ↑ Vgl. Grundlagen der Volkswirtschaftslehre 1, Kapitel 1.3.3.
- ↑ Siehe hierzu: Xavier X. Sala-i-Martin: The Classical Approach to Convergence Analysis, The Economic Journal 106, 1996
- ↑ Das Bruttoregionalprodukt ist konzeptionell identisch mit dem Bruttoinlandsprodukt.
- ↑ Quelle: Sascha Sardadvar: Vertiefen sich die räumlichen Wohlstandsgefälle innerhalb der Europäischen Union?, Wirtschaft und Gesellschaft 42, 2016