Kryptographie und Zugriffskontrolle - Asmmetrische Verfahren: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „<span id="asymmetrischeVerfahren"></span> = Asymmetrische Verfahren = Mitte der 1970er Jahre hatten Whitfield Diffie und Martin Hellman sowie Ralph Merkle unabhängig voneinander die Idee eines asymmetrischen Verfahrens beziehungsweise Public Key Systems . Das Prinzip beruht darauf, dass jeder Kommunikationspartner ein eigenes Schlüsselpaar besitzt, welches sich aus einem privaten und einem öffentlichen Schlüssel zusammensetzt. Der öffentliche Schlü…“) |
|||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
Der Diffie-Hellman Schlüsselaustausch (DH) (engl. Diffie Hellman Key Exchange, DHKE) ist ein Protokoll zum Austausch beziehungsweise zur Vereinbarung eines Secret Keys. Das Protokoll adressiert das Problem von symmetrischen Verfahren, dass zuerst ein gemeinsamer Schlüssel ausgetauscht werden muss, siehe Kapitel [[#symmetrischeVerfahren|[symmetrischeVerfahren]]]. Mit dem DH - Verfahren ist es möglich einen Secret Key zwischen zwei Kommunikationspartnern über einen unsicheren Kanal hinweg auszutauschen. Das Verfahren wurde von 1976 von Diffie und Hellman veröffentlicht. Da auch Ralph Merkle Vorarbeit geleistet hat, wird es auch manchmal als Diffie-Hellman-Merkle Schlüsselaustausch (DHM) bezeichnet | Der Diffie-Hellman Schlüsselaustausch (DH) (engl. Diffie Hellman Key Exchange, DHKE) ist ein Protokoll zum Austausch beziehungsweise zur Vereinbarung eines Secret Keys. Das Protokoll adressiert das Problem von symmetrischen Verfahren, dass zuerst ein gemeinsamer Schlüssel ausgetauscht werden muss, siehe Kapitel [[#symmetrischeVerfahren|[symmetrischeVerfahren]]]. Mit dem DH - Verfahren ist es möglich einen Secret Key zwischen zwei Kommunikationspartnern über einen unsicheren Kanal hinweg auszutauschen. Das Verfahren wurde von 1976 von Diffie und Hellman veröffentlicht. Da auch Ralph Merkle Vorarbeit geleistet hat, wird es auch manchmal als Diffie-Hellman-Merkle Schlüsselaustausch (DHM) bezeichnet | ||
'''Funktionsweise''':<br | '''Funktionsweise''':<br> | ||
Der Diffie-Hellman Schlüsselaustausch verwendet eine '''Einweg-Funktion''' (ohne Falltür), welche auf dem diskreter Exponentialfunktion basiert. Für eine Umkehrung ist der diskrete Logarithmus notwendig, der dieses Problem allerdings nicht in polynomialer Laufzeit (und damit schnell genug) lösen könnte. Die Funktionsweise wird anhand eines Beispiels in Tabelle [[#DH|1.1]] erläutert. | Der Diffie-Hellman Schlüsselaustausch verwendet eine '''Einweg-Funktion''' (ohne Falltür), welche auf dem diskreter Exponentialfunktion basiert. Für eine Umkehrung ist der diskrete Logarithmus notwendig, der dieses Problem allerdings nicht in polynomialer Laufzeit (und damit schnell genug) lösen könnte. Die Funktionsweise wird anhand eines Beispiels in Tabelle [[#DH|1.1]] erläutert. | ||
| Zeile 22: | Zeile 22: | ||
<div id="table: 9"> | <div id="table: 9"> | ||
{| | {| style="border-collapse: collapse;" border="1" | ||
|+ Diffie-Hellman Schlüsselaustausch anhand eines Beispiels | |+ Diffie-Hellman Schlüsselaustausch anhand eines Beispiels | ||
| | | | ||
<br> | |||
| Alice und Bob haben gemeinsames Wissen über eine Primzahl <math display="inline">p=23</math> | | Alice und Bob haben gemeinsames Wissen über eine Primzahl <math display="inline">p=23</math> | ||
| | | | ||
|- | <br> | ||
|- | |||
| | | | ||
<br> | |||
| und eine natürliche Zahl <math display="inline">g</math>, wobei <math display="inline">g<p</math> ist | | und eine natürliche Zahl <math display="inline">g</math>, wobei <math display="inline">g<p</math> ist | ||
| | | | ||
|- | <br> | ||
|- | |||
| | | | ||
<br> | |||
| | | | ||
<br> | |||
| | | | ||
|- | <br> | ||
|- | |||
| | | | ||
<br> | |||
| '''Alice''' | | '''Alice''' | ||
| '''Bob''' | | '''Bob''' | ||
|- | |- | ||
| | | | ||
<br> | |||
| | | | ||
<br> | |||
| | | | ||
|- | <br> | ||
|- | |||
| 1. | | 1. | ||
| Alice sucht sich eine geheime | | Alice sucht sich eine geheime | ||
| Bob sucht sich eine geheime | | Bob sucht sich eine geheime | ||
|- | |- | ||
| | | | ||
<br> | |||
| | | | ||
zufällige Zahl aus: | zufällige Zahl aus: | ||
| Zeile 57: | Zeile 69: | ||
<math display="inline">b=5</math> | <math display="inline">b=5</math> | ||
|- | |- | ||
| | | | ||
<br> | |||
| | | | ||
<br> | |||
| | | | ||
|- | <br> | ||
|- | |||
| 2. | | 2. | ||
| Alice berechnet A: | | Alice berechnet A: | ||
| Bob berechnet B: | | Bob berechnet B: | ||
|- | |- | ||
| | | | ||
<br> | |||
| <math display="inline">A = g^a \mod p</math> | | <math display="inline">A = g^a \mod p</math> | ||
| <math display="inline">B = g^b \mod p</math> | | <math display="inline">B = g^b \mod p</math> | ||
|- | |- | ||
| | | | ||
<br> | |||
| <math display="inline">A = 11^6 \mod 23 = 9</math> | | <math display="inline">A = 11^6 \mod 23 = 9</math> | ||
| <math display="inline">B = 11^5 \mod 23 = 5</math> | | <math display="inline">B = 11^5 \mod 23 = 5</math> | ||
|- | |- | ||
| | | | ||
<br> | |||
| | | | ||
<br> | |||
| | | | ||
|- | <br> | ||
|- | |||
| 3. | | 3. | ||
| Alice übermittelt <math display="inline">A = 9</math> an Bob | | Alice übermittelt <math display="inline">A = 9</math> an Bob | ||
| Bob übermittelt <math display="inline">B=5</math> an Alice | | Bob übermittelt <math display="inline">B=5</math> an Alice | ||
|- | |- | ||
| | | | ||
<br> | |||
| | | | ||
<br> | |||
| | | | ||
|- | <br> | ||
|- | |||
| 4. | | 4. | ||
| Alice berechnet den secret key: | | Alice berechnet den secret key: | ||
| Bob berechnet den secret key: | | Bob berechnet den secret key: | ||
|- | |- | ||
| | | | ||
<br> | |||
| <math display="inline">K = B^a \mod p</math> | | <math display="inline">K = B^a \mod p</math> | ||
| <math display="inline">K=A^b \mod p</math> | | <math display="inline">K=A^b \mod p</math> | ||
|- | |- | ||
| | | | ||
<br> | |||
| <math display="inline">K = 5^6 \mod 23 = 8</math> | | <math display="inline">K = 5^6 \mod 23 = 8</math> | ||
| <math display="inline">K = 9^5 \mod 23 = 8</math> | | <math display="inline">K = 9^5 \mod 23 = 8</math> | ||
| Zeile 101: | Zeile 126: | ||
</div> | </div> | ||
<span id="RSA"></span> | <span id="RSA"></span> | ||
== RSA-Verfahren == | == RSA-Verfahren == | ||
| Zeile 106: | Zeile 132: | ||
Nachdem das Konzept zu asymmetrischen Verfahren von Whitfield Diffie und Martin Hellman beziehungsweise Ralph Merkle veröffentlicht wurde, wurde RSA als erstes Verfahren dazu entwickelt. Es wurde von Ronald Rivest, Adi Shamir und Leonard Adleman im Jahr 1978 publiziert. RSA ist mittlerweile defacto Standard und weit verbreitet. | Nachdem das Konzept zu asymmetrischen Verfahren von Whitfield Diffie und Martin Hellman beziehungsweise Ralph Merkle veröffentlicht wurde, wurde RSA als erstes Verfahren dazu entwickelt. Es wurde von Ronald Rivest, Adi Shamir und Leonard Adleman im Jahr 1978 publiziert. RSA ist mittlerweile defacto Standard und weit verbreitet. | ||
RSA basiert auf dem Faktorisierungsproblem<ref>die Zerlegung einer Zahl in ihre Primfaktoren</ref> großer natürlicher Zahlen. Es gilt als mathematisch sehr schwierig das Produkt zweier Primzahlen zu faktorisieren. Genau diese Tatsache macht man sich bei RSA zum Vorteil. Ein solches Problem wird auch als '''Einweg-Funktion mit Falltür''' oder '''Falltür-Funktion''' bezeichnet (engl. '''Trapdoor One Way Function'''). Um die Funktionsweise von RSA zu verstehen werden folgende mathematische Grundlagen benötigt: | RSA basiert auf dem Faktorisierungsproblem <ref>die Zerlegung einer Zahl in ihre Primfaktoren</ref> großer natürlicher Zahlen. Es gilt als mathematisch sehr schwierig das Produkt zweier Primzahlen zu faktorisieren. Genau diese Tatsache macht man sich bei RSA zum Vorteil. Ein solches Problem wird auch als '''Einweg-Funktion mit Falltür''' oder '''Falltür-Funktion''' bezeichnet (engl. '''Trapdoor One Way Function'''). Um die Funktionsweise von RSA zu verstehen werden folgende mathematische Grundlagen benötigt: | ||
* Der Modulo Operator beziehungsweise das Rechnen mit Restklassen. | * Der Modulo Operator beziehungsweise das Rechnen mit Restklassen. | ||
* Die Eulersche <math display="inline">\varphi</math> - Funktion einer Zahl <math display="inline">N</math>, welche angibt wie viele natürliche es gibt die kleiner als <math display="inline">N</math> und teilerfremd zu <math display="inline">N</math> sind. | * Die Eulersche <math display="inline">\varphi</math> - Funktion einer Zahl <math display="inline">N</math>, welche angibt wie viele natürliche es gibt die kleiner als <math display="inline">N</math> und teilerfremd zu <math display="inline">N</math> sind. | ||
* Der Satz von Euler - Fermat, welcher besagt, dass <math display="inline">a^{\varphi(N)} \equiv 1 \mod N</math> | * Der Satz von Euler - Fermat, welcher besagt, dass <math display="inline">a^{\varphi(N)} \equiv 1 \mod N</math> | ||
'''Funktionsweise''':<br> | |||
'''Funktionsweise''':<br | |||
Die Funktionsweise wird anhand eines Beispiels mit kleinen Zahlen erklärt. Angenommen Bob will Alice eine Nachricht zukommen lassen, wird bei RSA vereinfacht wie folgt vorgegangen: | Die Funktionsweise wird anhand eines Beispiels mit kleinen Zahlen erklärt. Angenommen Bob will Alice eine Nachricht zukommen lassen, wird bei RSA vereinfacht wie folgt vorgegangen: | ||
<ol> | <ol> | ||
<li><p>Alice wählt zwei Primzahlen <math display="inline">p</math> und <math display="inline">q</math> aus und ermittelt deren Produkt <math display="inline">n</math>: <math display="block">n=p*q</math> Angenommen Alice wählt für <math display="inline">p=5</math> und für <math display="inline">q=13</math> aus, dann ist: | <li><p>Alice wählt zwei Primzahlen <math display="inline">p</math> und <math display="inline">q</math> aus und ermittelt deren Produkt <math display="inline">n</math>:</p> | ||
<math display="block">n=p*q</math>Angenommen Alice wählt für <math display="inline">p=5</math> und für <math display="inline">q=13</math> aus, dann ist: | |||
<math display="block">n=5*13=65</math> | |||
<p><math display="inline">n</math> wird auch als RSA-Modul bezeichnet. In der Praxis verwendet man natürlich möglichst große und unterschiedliche Primzahlen.</p></li> | <p><math display="inline">n</math> wird auch als RSA-Modul bezeichnet. In der Praxis verwendet man natürlich möglichst große und unterschiedliche Primzahlen.</p></li> | ||
<li><p>Alice berechnet für <math display="inline">n</math> die Eulersche <math display="inline">\varphi</math> - Funktion mit der Formel:</p> | <li><p>Alice berechnet für <math display="inline">n</math> die Eulersche <math display="inline">\varphi</math> - Funktion mit der Formel:</p> | ||
<math display="block">\varphi(n) = m = (p-1) * (q-1)</math><math display="block">m = (5-1) * (13-1) = 48</math></li> | |||
<li><p>Alice sucht sich nun eine zu <math display="inline">m</math> teilerfremde Zahl < | <li><p>Alice sucht sich nun eine zu <math display="inline">m</math> teilerfremde Zahl</p> | ||
<p>Daher der größte gemeinsame Teiler ist 1</p>a aus, welche größer als 1 ist, daher <math display="inline">1< a < m</math>. <math display="inline">a</math> wird auch als Verschlüsselungsexponent bezeichnet. In diesem Beispiel wählt Alice <math display="inline">a = 7</math></li> | |||
<li><p>Die Zahlen <math display="inline">n = 65</math> und <math display="inline">a = 7</math> stellen den öffentlichen Schlüssel von Alice dar. Diese kann sie nun Bob zur Verfügung stellen.</p></li> | <li><p>Die Zahlen <math display="inline">n = 65</math> und <math display="inline">a = 7</math> stellen den öffentlichen Schlüssel von Alice dar. Diese kann sie nun Bob zur Verfügung stellen.</p></li> | ||
<li><p>Bob möchte nun eine Nachricht an Alice schicken. Seine Nachricht ist eine Zahl kleiner als <math display="inline">n</math>, daher <math display="inline">x = 19</math>.</p></li> | <li><p>Bob möchte nun eine Nachricht an Alice schicken. Seine Nachricht ist eine Zahl kleiner als <math display="inline">n</math>, daher <math display="inline">x = 19</math>.</p></li> | ||
<li><p>Bob verschlüsselt seine Nachricht gemäß der Formel: <math display="block">y = x^a \mod n</math> <math display="block">y = 19^7 \mod 65</math> <math display="block">y = 59</math | <li><p>Bob verschlüsselt seine Nachricht gemäß der Formel:</p> | ||
<math display="block">y = x^a \mod n</math><math display="block">y = 19^7 \mod 65</math><math display="block">y = 59</math></li> | |||
<li><p>Bob sendet seinen ciphertext <math display="inline">y = 59</math> an Alice.</p></li> | <li><p>Bob sendet seinen ciphertext <math display="inline">y = 59</math> an Alice.</p></li> | ||
<li><p>Alice berechnet mit Hilfe des erweiterten euklidischen Algorithmus das modulare Inverse, die Zahl <math display="inline">b</math>:</p> | <li><p>Alice berechnet mit Hilfe des erweiterten euklidischen Algorithmus das modulare Inverse, die Zahl <math display="inline">b</math>:</p> | ||
<math display="block">b = a^{-1} \mod m</math><math display="block">b = 7^{-1} \mod 48</math><math display="block">b= 7</math></li> | |||
<li><p>Nun kann Alice die Nachricht von Bob mit dem Satz von Euler entschlüsseln:</p> | <li><p>Nun kann Alice die Nachricht von Bob mit dem Satz von Euler entschlüsseln:</p> | ||
<math display="block">x = y^b \mod n</math><math display="block">x = 59^7 \mod 65</math><math display="block">x = 19</math></li> | |||
</ol> | |||
Kennt ein Angreifer nur den öffentlichen Schlüssel bestehend aus den Zahlen <math display="inline">n</math> und <math display="inline">a</math>, müsste dieser aus diesen zwei Zahlen den privaten Schlüssel errechnen. Das einzig bekannte Verfahren zurzeit ist die Primfaktorenzerlegung, mit welchem dies prinzipiell machbar wäre, allerdings nicht in angemessener Zeit. Zu beachten sind bei einer RSA Implementierung allerdings 2 Punkte: | Kennt ein Angreifer nur den öffentlichen Schlüssel bestehend aus den Zahlen <math display="inline">n</math> und <math display="inline">a</math>, müsste dieser aus diesen zwei Zahlen den privaten Schlüssel errechnen. Das einzig bekannte Verfahren zurzeit ist die Primfaktorenzerlegung, mit welchem dies prinzipiell machbar wäre, allerdings nicht in angemessener Zeit. Zu beachten sind bei einer RSA Implementierung allerdings 2 Punkte: | ||
* die Wahl auf entsprechend große Primzahlen <math display="inline">p</math> und <math display="inline">q</math>. | * die Wahl auf entsprechend große Primzahlen <math display="inline">p</math> und <math display="inline">q</math>. | ||
* <math display="inline">p</math> und <math display="inline">q</math> sollen möglichst weit auseinander liegen. Eine sequentielle Suche nach Primzahlen kann auch bei hohen Primzahlen starten und rückwärts laufen. Ein klassischer Ausgangspunkt ist <math display="inline">\sqrt[]{n}</math>. Je näher sich die Zahlen <math display="inline">p</math> und <math display="inline">q</math> sind, desto näher befinden sie sich auch bei <math display="inline">\sqrt[]{n}</math> und desto kürzer wäre eine systematische Suche nach Primzahlen. | * <math display="inline">p</math> und <math display="inline">q</math> sollen möglichst weit auseinander liegen. Eine sequentielle Suche nach Primzahlen kann auch bei hohen Primzahlen starten und rückwärts laufen. Ein klassischer Ausgangspunkt ist <math display="inline">\sqrt[]{n}</math>. Je näher sich die Zahlen <math display="inline">p</math> und <math display="inline">q</math> sind, desto näher befinden sie sich auch bei <math display="inline">\sqrt[]{n}</math> und desto kürzer wäre eine systematische Suche nach Primzahlen. | ||
In der Praxis sollte auch sichergestellt werden, dass nach Generierung des RSA Moduls, die Variablen welche <math display="inline">p</math> und <math display="inline">q</math> enthalten, gelöscht werden. Sie werden in der weiteren Berechnung nicht mehr benötigt. | In der Praxis sollte auch sichergestellt werden, dass nach Generierung des RSA Moduls, die Variablen welche <math display="inline">p</math> und <math display="inline">q</math> enthalten, gelöscht werden. Sie werden in der weiteren Berechnung nicht mehr benötigt. | ||
| Zeile 145: | Zeile 173: | ||
Im Bereich der Primfaktorenzerlegung wurden bessere und schnellere Verfahren entwickelt und auch die Hardware wurde schneller. So wurde klar, dass nach alternativen Falltür-Funktionen gesucht werden musste, falls eines Tages eine effiziente Umkehrfunktion gefunden wird. Im Jahr 1985 wurden von Victor Miller und Neil Koblitz unabhängig voneinander Elliptische Kurven über endlichen Körpern vorgeschlagen. | Im Bereich der Primfaktorenzerlegung wurden bessere und schnellere Verfahren entwickelt und auch die Hardware wurde schneller. So wurde klar, dass nach alternativen Falltür-Funktionen gesucht werden musste, falls eines Tages eine effiziente Umkehrfunktion gefunden wird. Im Jahr 1985 wurden von Victor Miller und Neil Koblitz unabhängig voneinander Elliptische Kurven über endlichen Körpern vorgeschlagen. | ||
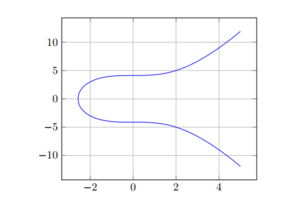
[[Datei:Kurve.png|300px|none|thumb|graphische Darstellung der elliptischen Kurve y2 = x3 + 17]] | |||
Eine elliptische Kurve ist ein Menge an Punkten die eine spezielle mathematische Funktion erfüllen. Über diese Punkte lässt sich eine additive zyklische Gruppe bilden <ref>wie über die Gruppe der Restklassen</ref> . Innerhalb dieser Gruppe gelten bestimmte Rechenregeln. Die Verfahren aus dem diskreten Logarithmus lassen sich auf die Punkte einer elliptischen Kurve übertragen. Hier ist die nicht umkehrbare Funktion allerdings die Division eines Punktes. | |||
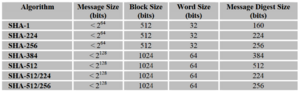
Bei wesentlich kürzeren Operanden und Schlüsseln bietet ECC die gleiche Sicherheit wie bei Verfahren welche auf dem diskreten Logarithmus oder RSA beruhen . Als Vergleich, ein Verfahren mit 1024 bis 3072-Bit basierend auf dem diskreten Logarithmus oder RSA ist äquivalent mit ECC von 160 bis 256-Bit.[[Datei:SHA-properties.png|300px|none|thumb|Vergleich des rechnerischen Aufwands von ECC, symmetrischen und asymmetrischen Verfahren aus [17]]] | |||
Aktuelle Version vom 28. September 2022, 08:28 Uhr
Asymmetrische Verfahren
Mitte der 1970er Jahre hatten Whitfield Diffie und Martin Hellman sowie Ralph Merkle unabhängig voneinander die Idee eines asymmetrischen Verfahrens beziehungsweise Public Key Systems . Das Prinzip beruht darauf, dass jeder Kommunikationspartner ein eigenes Schlüsselpaar besitzt, welches sich aus einem privaten und einem öffentlichen Schlüssel zusammensetzt. Der öffentliche Schlüssel kann natürlich öffentlich zugänglich gemacht werden. Der Plaintext wird vom Sender mit dem öffentlich zugänglichen Schlüssel des Empfängers verschlüsselt. Nur der Empfänger selbst ist mit seinem privaten Schlüssel in der Lage den Ciphertext wieder zu entschlüsseln. Die wesentlichen Vorteile und Nachteile von asymmetrischen Verfahren sind :
- Es ist kein aufwendiger Schlüsselaustausch über unsichere Kanäle notwendig. Der öffentliche Schlüssel ist ohnehin nicht geheim. Es muss nur sichergestellt werden, dass der öffentliche Schlüssel auch nur jenem zuzuordnen ist, der auch im Besitz des privaten Schlüssels ist. Siehe dazu auch Kapitel [PGP].
- Bei einem symmetrischen Verfahren musste mit jedem Kommunikationspartner ein eigener Schlüssel vereinbart beziehungsweise ausgetauscht werden. Mittels eines Public Key Verfahrens müssen keine geheimen Schlüssel verwaltet werden. Es ist ausreichend den öffentlichen Schlüssel des Kommunikationspartners zu kennen.
- Asymmetrische Verfahren bieten eine relativ hohe Stufe der Sicherheit. Sie basieren auf einer sogenannten Falltür-Funktion. Diese sind in angemessener Zeit nicht invertierbar, außer man kennt den geheimen Schlüssel. Da es allerdings keinen mathematischen Beweis für Falltür-Funktionen gibt, wäre es aber in der Zukunft theoretisch möglich, dass ein schnelles Verfahren gefunden wird, welches eine Umkehrung ermöglicht.
- Durch die Funktionsweise mit privaten und öffentlichen Schlüsseln bieten diese Verfahren auch die Möglichkeit für digitale Unterschriften beziehungsweise Signaturen, siehe dazu Kapitel [certificates].
- Asymmetrische Verfahren sind durch den hohen Aufwand beim Ver- beziehungsweise Entschlüsseln im Gegensatz zu symmetrischen Verfahren sehr langsam. In der Praxis wird daher oft ein hybrider Ansatz gewählt. Der Schlüsselaustausch erfolgt asymmetrisch, die weitere Kommunikation wird symmetrisch verschlüsselt.
Diffie-Hellman Schlüsselaustausch
Der Diffie-Hellman Schlüsselaustausch (DH) (engl. Diffie Hellman Key Exchange, DHKE) ist ein Protokoll zum Austausch beziehungsweise zur Vereinbarung eines Secret Keys. Das Protokoll adressiert das Problem von symmetrischen Verfahren, dass zuerst ein gemeinsamer Schlüssel ausgetauscht werden muss, siehe Kapitel [symmetrischeVerfahren]. Mit dem DH - Verfahren ist es möglich einen Secret Key zwischen zwei Kommunikationspartnern über einen unsicheren Kanal hinweg auszutauschen. Das Verfahren wurde von 1976 von Diffie und Hellman veröffentlicht. Da auch Ralph Merkle Vorarbeit geleistet hat, wird es auch manchmal als Diffie-Hellman-Merkle Schlüsselaustausch (DHM) bezeichnet
Funktionsweise:
Der Diffie-Hellman Schlüsselaustausch verwendet eine Einweg-Funktion (ohne Falltür), welche auf dem diskreter Exponentialfunktion basiert. Für eine Umkehrung ist der diskrete Logarithmus notwendig, der dieses Problem allerdings nicht in polynomialer Laufzeit (und damit schnell genug) lösen könnte. Die Funktionsweise wird anhand eines Beispiels in Tabelle 1.1 erläutert.
|
|
Alice und Bob haben gemeinsames Wissen über eine Primzahl |
|
|
|
und eine natürliche Zahl , wobei ist |
|
|
|
|
|
|
|
Alice | Bob |
|
|
|
|
| 1. | Alice sucht sich eine geheime | Bob sucht sich eine geheime |
|
|
zufällige Zahl aus:
|
zufällige Zahl aus:
|
|
|
|
|
| 2. | Alice berechnet A: | Bob berechnet B: |
|
|
||
|
|
||
|
|
|
|
| 3. | Alice übermittelt an Bob | Bob übermittelt an Alice |
|
|
|
|
| 4. | Alice berechnet den secret key: | Bob berechnet den secret key: |
|
|
||
|
|
RSA-Verfahren
Nachdem das Konzept zu asymmetrischen Verfahren von Whitfield Diffie und Martin Hellman beziehungsweise Ralph Merkle veröffentlicht wurde, wurde RSA als erstes Verfahren dazu entwickelt. Es wurde von Ronald Rivest, Adi Shamir und Leonard Adleman im Jahr 1978 publiziert. RSA ist mittlerweile defacto Standard und weit verbreitet.
RSA basiert auf dem Faktorisierungsproblem [1] großer natürlicher Zahlen. Es gilt als mathematisch sehr schwierig das Produkt zweier Primzahlen zu faktorisieren. Genau diese Tatsache macht man sich bei RSA zum Vorteil. Ein solches Problem wird auch als Einweg-Funktion mit Falltür oder Falltür-Funktion bezeichnet (engl. Trapdoor One Way Function). Um die Funktionsweise von RSA zu verstehen werden folgende mathematische Grundlagen benötigt:
- Der Modulo Operator beziehungsweise das Rechnen mit Restklassen.
- Die Eulersche - Funktion einer Zahl , welche angibt wie viele natürliche es gibt die kleiner als und teilerfremd zu sind.
- Der Satz von Euler - Fermat, welcher besagt, dass
Funktionsweise:
Die Funktionsweise wird anhand eines Beispiels mit kleinen Zahlen erklärt. Angenommen Bob will Alice eine Nachricht zukommen lassen, wird bei RSA vereinfacht wie folgt vorgegangen:
Alice wählt zwei Primzahlen und aus und ermittelt deren Produkt :
Angenommen Alice wählt für und für aus, dann ist:wird auch als RSA-Modul bezeichnet. In der Praxis verwendet man natürlich möglichst große und unterschiedliche Primzahlen.
Alice berechnet für die Eulersche - Funktion mit der Formel:
Alice sucht sich nun eine zu teilerfremde Zahl
Daher der größte gemeinsame Teiler ist 1
a aus, welche größer als 1 ist, daher . wird auch als Verschlüsselungsexponent bezeichnet. In diesem Beispiel wählt AliceDie Zahlen und stellen den öffentlichen Schlüssel von Alice dar. Diese kann sie nun Bob zur Verfügung stellen.
Bob möchte nun eine Nachricht an Alice schicken. Seine Nachricht ist eine Zahl kleiner als , daher .
Bob verschlüsselt seine Nachricht gemäß der Formel:
Bob sendet seinen ciphertext an Alice.
Alice berechnet mit Hilfe des erweiterten euklidischen Algorithmus das modulare Inverse, die Zahl :
Nun kann Alice die Nachricht von Bob mit dem Satz von Euler entschlüsseln:
Kennt ein Angreifer nur den öffentlichen Schlüssel bestehend aus den Zahlen und , müsste dieser aus diesen zwei Zahlen den privaten Schlüssel errechnen. Das einzig bekannte Verfahren zurzeit ist die Primfaktorenzerlegung, mit welchem dies prinzipiell machbar wäre, allerdings nicht in angemessener Zeit. Zu beachten sind bei einer RSA Implementierung allerdings 2 Punkte:
- die Wahl auf entsprechend große Primzahlen und .
- und sollen möglichst weit auseinander liegen. Eine sequentielle Suche nach Primzahlen kann auch bei hohen Primzahlen starten und rückwärts laufen. Ein klassischer Ausgangspunkt ist . Je näher sich die Zahlen und sind, desto näher befinden sie sich auch bei und desto kürzer wäre eine systematische Suche nach Primzahlen.
In der Praxis sollte auch sichergestellt werden, dass nach Generierung des RSA Moduls, die Variablen welche und enthalten, gelöscht werden. Sie werden in der weiteren Berechnung nicht mehr benötigt.
Für RSA beziehungsweise auch andere Verschlüsselungs-Verfahren, welche auf mathematischen Falltür-Funktionen basieren, ist zu beachten, dass es theoretisch auch Gefahren gibt. Zum einen könnte ein Algorithmus entwickelt werden, der ohne große Mühen das Problem der verwendeten Falltür-Funktion löst. Zum anderen auch technische Aspekte, wie die Entwicklung von Quantencomputern, für welche diese mathematischen Probleme wahrscheinlich weniger Aufwand bedeuten.
Elliptic Curve Cryptography
Im Bereich der Primfaktorenzerlegung wurden bessere und schnellere Verfahren entwickelt und auch die Hardware wurde schneller. So wurde klar, dass nach alternativen Falltür-Funktionen gesucht werden musste, falls eines Tages eine effiziente Umkehrfunktion gefunden wird. Im Jahr 1985 wurden von Victor Miller und Neil Koblitz unabhängig voneinander Elliptische Kurven über endlichen Körpern vorgeschlagen.
Eine elliptische Kurve ist ein Menge an Punkten die eine spezielle mathematische Funktion erfüllen. Über diese Punkte lässt sich eine additive zyklische Gruppe bilden [2] . Innerhalb dieser Gruppe gelten bestimmte Rechenregeln. Die Verfahren aus dem diskreten Logarithmus lassen sich auf die Punkte einer elliptischen Kurve übertragen. Hier ist die nicht umkehrbare Funktion allerdings die Division eines Punktes.
Bei wesentlich kürzeren Operanden und Schlüsseln bietet ECC die gleiche Sicherheit wie bei Verfahren welche auf dem diskreten Logarithmus oder RSA beruhen . Als Vergleich, ein Verfahren mit 1024 bis 3072-Bit basierend auf dem diskreten Logarithmus oder RSA ist äquivalent mit ECC von 160 bis 256-Bit.












































![{\textstyle {\sqrt[{}]{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec34534d4849a596ff853828867a0630c8fc93f)