Angewandte Mikroökonomik - Preisdiskriminierung: Unterschied zwischen den Versionen
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
=== Warum wenden Unternehmen Strategien der Preisdiskriminierung an? === | === Warum wenden Unternehmen Strategien der Preisdiskriminierung an? === | ||
Die Gesamtnachfragekurve auf einem Gütermarkt, welche die Nachfrage auf der x-Achse in Abhängigkeit vom Preis auf der y-Achse darstellt, hat üblicherweise eine negative Steigung, d.h. je höher der Preis, umso geringer der Absatz. Dies impliziert aber auch, dass Konsumenten für die erste Einheit des Gutes bereit sind mehr zu zahlen, als für die zweite Einheit. Die zweite Einheit ist ihnen wiederum mehr wert als die dritte, und so weiter. D.h. die Zahlungsbereitschaft sinkt, je mehr Einheiten des Gutes schon konsumiert wurden. Diese Tatsache lässt sich an vielen alltäglichen Beispielen verdeutlichen. Es ist es beispielsweise tendenziell so, dass uns der erste Schluck Wasser nach sportlicher Betätigung wichtiger ist (wir wären also bereit, mehr dafür zu zahlen), als der Schluck der folgen würde, nachdem wir bereits einen halben Liter Wasser getrunken haben. Die Tatsache einer Nachfragekurve mit negativer Steigung lässt sich also direkt von dem Konzept des abnehmenden Grenznutzens herleiten. | Die Gesamtnachfragekurve auf einem Gütermarkt, welche die Nachfrage auf der x-Achse in Abhängigkeit vom Preis auf der y-Achse darstellt, hat üblicherweise eine negative Steigung, d.h. je höher der Preis, umso geringer der Absatz. Dies impliziert aber auch, dass Konsumenten für die erste Einheit des Gutes bereit sind mehr zu zahlen, als für die zweite Einheit. Die zweite Einheit ist ihnen wiederum mehr wert als die dritte, und so weiter. D.h. die Zahlungsbereitschaft sinkt, je mehr Einheiten des Gutes schon konsumiert wurden. Diese Tatsache lässt sich an vielen alltäglichen Beispielen verdeutlichen. Es ist es beispielsweise tendenziell so, dass uns der erste Schluck Wasser nach sportlicher Betätigung wichtiger ist (wir wären also bereit, mehr dafür zu zahlen), als der Schluck, der folgen würde, nachdem wir bereits einen halben Liter Wasser getrunken haben. Die Tatsache einer Nachfragekurve mit negativer Steigung lässt sich also direkt von dem Konzept des abnehmenden Grenznutzens herleiten. | ||
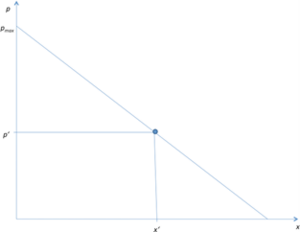
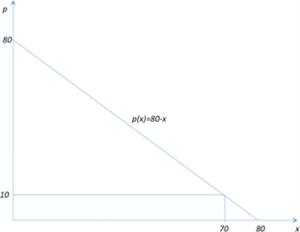
Ein Beispiel für eine typische indirekte Nachfragefunktion wird in Abbildung | Ein Beispiel für eine typische indirekte Nachfragefunktion wird in folgender Abbildung dargestellt. Wenn der Preis des Gutes ''p<sub>max</sub>'' oder höher liegt, so ist das Gut zu teuer und wird nicht nachgefragt (der Absatz ist null). Sinkt der Preis etwas unter ''p<sub>max</sub>'', so wird nur eine einzige Einheit nachgefragt. Soll mehr abgesetzt werden, muss der Preis weiter sinken. | ||
Angenommen, der Preis liegt bei ''p‘'' – hier werden ''q‘'' Einheiten des Gutes nachgefragt. Für alle Einheiten vor ''q‘'' wäre der Konsument allerdings bereit gewesen, einen höheren Preis als ''p‘'' zu zahlen, d.h. seine Zahlungsbereitschaft war höher. Trotzdem, wenn der Produzent einen einheitlichen Preis verlangen muss, so zahlt der Konsument für jede Einheit den einheitlichen Preis ''p‘''. Dadurch entsteht eine sogenannte Konsumentenrente. <ref>vgl. ''Grundlagen der Volkswirtschaftslehre 2''</ref> Diese ist durch das Dreieck gegeben, dass durch die Punkte ''p<sub>max</sub>'', ''p‘'' auf der y-Achse und den Schnittpunkt der Geraden ''q‘'' mit der Nachfragekurve gegeben ist. Die Fläche des Dreiecks entspricht jenem Geldbetrag, den die Konsumenten bereit gewesen wären, zu zahlen, aber dank einheitlicher Preissetzung nicht zahlen mussten. | Angenommen, der Preis liegt bei ''p‘'' – hier werden ''q‘'' Einheiten des Gutes nachgefragt. Für alle Einheiten vor ''q‘'' wäre der Konsument allerdings bereit gewesen, einen höheren Preis als ''p‘'' zu zahlen, d.h. seine Zahlungsbereitschaft war höher. Trotzdem, wenn der Produzent einen einheitlichen Preis verlangen muss, so zahlt der Konsument für jede Einheit den einheitlichen Preis ''p‘''. Dadurch entsteht eine sogenannte Konsumentenrente. <ref>vgl. ''Grundlagen der Volkswirtschaftslehre 2''</ref> Diese ist durch das Dreieck gegeben, dass durch die Punkte ''p<sub>max</sub>'', ''p‘'' auf der y-Achse und den Schnittpunkt der Geraden ''q‘'' mit der Nachfragekurve gegeben ist. Die Fläche des Dreiecks entspricht jenem Geldbetrag, den die Konsumenten bereit gewesen wären, zu zahlen, aber dank einheitlicher Preissetzung nicht zahlen mussten. | ||
[[Datei:Ec411 13.png|300px|none|thumb|Nachfragefunktion mit negativer Steigung]] | [[Datei:Ec411 13.png|300px|none|thumb|Nachfragefunktion mit negativer Steigung]] | ||
| Zeile 22: | Zeile 22: | ||
Kann der Produzent nur einen einheitlichen Stückpreis setzen, so gibt es in der Preissetzung einen trade-off (wie in Lektion 2 ausführlich diskutiert). In die Überlegung, ob ein niedrigerer Preis gesetzt werden soll, fließen in diesem Fall zwei Effekte ein. Einerseits bedeutet ein niedriger Preis, dass mehr Einheiten des Gutes gekauft werden, andererseits ist der Erlös pro Einheit niedriger. Diese zwei Effekte muss ein Produzent, der den optimalen Preis sucht, gegeneinander abwiegen. Dieser trade-off wird durch die Möglichkeit der Preisdiskriminierung (zumindest teilweise) umgangen. Der Produzent erzielt durch Preisdiskriminierung einen höheren Gewinn, da er einerseits einen Teil der Konsumentenrente abschöpfen kann und andererseits auch Konsumenten zum Kauf bewegen kann, denen der einheitliche Preis zu hoch wäre. Die Preisdiskriminierung erlaubt es dem Produzenten also, den Preis an die tatsächliche Zahlungsbereitschaft der Konsumenten anzupassen. | Kann der Produzent nur einen einheitlichen Stückpreis setzen, so gibt es in der Preissetzung einen trade-off (wie in Lektion 2 ausführlich diskutiert). In die Überlegung, ob ein niedrigerer Preis gesetzt werden soll, fließen in diesem Fall zwei Effekte ein. Einerseits bedeutet ein niedriger Preis, dass mehr Einheiten des Gutes gekauft werden, andererseits ist der Erlös pro Einheit niedriger. Diese zwei Effekte muss ein Produzent, der den optimalen Preis sucht, gegeneinander abwiegen. Dieser trade-off wird durch die Möglichkeit der Preisdiskriminierung (zumindest teilweise) umgangen. Der Produzent erzielt durch Preisdiskriminierung einen höheren Gewinn, da er einerseits einen Teil der Konsumentenrente abschöpfen kann und andererseits auch Konsumenten zum Kauf bewegen kann, denen der einheitliche Preis zu hoch wäre. Die Preisdiskriminierung erlaubt es dem Produzenten also, den Preis an die tatsächliche Zahlungsbereitschaft der Konsumenten anzupassen. | ||
Beispiele für Preisdiskriminierung im alltäglichen Leben sind etwa Ermäßigungen für Museen oder Schilifte für die lokale Bevölkerung oder Ermäßigungen im Theater oder bei Zeitungsabonnements für Studierende. <ref>Auch wenn Ermäßigungen für Einheimische von der EU eigentlich verboten wurden, begegnet man ihnen dennoch bei praktisch jeder Touristenattraktion, indem man vergünstigte Eintrittskarten mit dem Besitz einer Karte verbindet, die üblicherweise nur Einheimische besitzen, bspw. Jahreskarten für die örtlichen öffentlichen Verkehrsmittel, Mitgliedskarten der inländischen Autofahrerklubs, die Club-Ö1-Karte usw.</ref> In diesem Fall wird davon ausgegangen, dass die jeweilige Personengruppe eine niedrigere Zahlungsbereitschaft hat als andere Konsumenten. Diese Gruppen würden wohl im Fall eines einheitlichen gewinnmaximierenden Preises das Gut umso viel weniger konsumieren, dass es sich lohnt, nur für diese Gruppe den Preis zu reduzieren. Dadurch wird sichergestellt, dass auch diese Gruppen das Gut konsumieren, Absatz und Gewinn erhöhen sich. | Beispiele für Preisdiskriminierung im alltäglichen Leben sind etwa Ermäßigungen für Museen oder Schilifte für die lokale Bevölkerung oder Ermäßigungen im Theater oder bei Zeitungsabonnements für Studierende. <ref>Auch wenn Ermäßigungen für Einheimische von der EU eigentlich verboten wurden, begegnet man ihnen dennoch bei praktisch jeder Touristenattraktion, indem man vergünstigte Eintrittskarten mit dem Besitz einer Karte verbindet, die üblicherweise nur Einheimische besitzen, bspw. Jahreskarten für die örtlichen öffentlichen Verkehrsmittel, Mitgliedskarten der inländischen Autofahrerklubs, die Club-Ö1-Karte usw.</ref> In diesem Fall wird davon ausgegangen, dass die jeweilige Personengruppe eine niedrigere Zahlungsbereitschaft hat als andere Konsumenten. Diese Gruppen würden wohl im Fall eines einheitlichen gewinnmaximierenden Preises das Gut umso viel weniger konsumieren, dass es sich lohnt, nur für diese Gruppe den Preis zu reduzieren. Dadurch wird sichergestellt, dass auch diese Gruppen das Gut konsumieren, Absatz und Gewinn erhöhen sich. | ||
<span id="unter-welchen-bedingungen-kann-preisdiskriminierung-angewendet-werden"></span> | <span id="unter-welchen-bedingungen-kann-preisdiskriminierung-angewendet-werden"></span> | ||
=== Unter welchen Bedingungen kann Preisdiskriminierung angewendet werden? === | === Unter welchen Bedingungen kann Preisdiskriminierung angewendet werden? === | ||
Es gibt im Allgemeinen drei Bedingungen, die gelten müssen, damit Preisdiskriminierung als Strategie angewendet werden kann: | Es gibt im Allgemeinen drei Bedingungen, die gelten müssen, damit Preisdiskriminierung als Strategie angewendet werden kann: | ||
1) Die Anbieter müssen eine gewisse '''Marktmacht''' haben, d.h. sie müssen die Möglichkeit haben, als Preissetzer zu agieren. Dies ist der Fall in Monopolen, aber auch in oligopolistischen Märkten (vgl. Lektion 2). Es darf also in dem betrachteten Markt keinen freien Markteintritt geben, da in dem Fall Anbieter so lange in den Markt eindringen würden, solange es positive Gewinne zu erwarten gibt, d.h. so lange, bis der Preis den Grenzkosten entspricht. | 1) Die Anbieter müssen eine gewisse '''Marktmacht''' haben, d.h., sie müssen die Möglichkeit haben, als Preissetzer zu agieren. Dies ist der Fall in Monopolen, aber auch in oligopolistischen Märkten (vgl. Lektion 2). Es darf also in dem betrachteten Markt keinen freien Markteintritt geben, da in dem Fall Anbieter so lange in den Markt eindringen würden, solange es positive Gewinne zu erwarten gibt, d.h. so lange, bis der Preis den Grenzkosten entspricht. | ||
2) Die '''Nachfragekurve''' muss eine negative Steigung haben, d.h. die Zahlungsbereitschaft der Konsumenten muss variieren und mit zusätzlicher Menge abnehmen. Diese negative Steigung der (Gesamt-)<br> | 2) Die '''Nachfragekurve''' muss eine negative Steigung haben, d.h., die Zahlungsbereitschaft der Konsumenten muss variieren und mit zusätzlicher Menge abnehmen. Diese negative Steigung der (Gesamt-)<br> | ||
Nachfragekurve, der ein Produzent gegenübersteht, entsteht entweder, wenn (unter der Annahme identischer Konsumenten) die Zahlungsbereitschaft jedes einzelnen Konsumenten mit der konsumierten Menge abnimmt und/oder wenn sich Konsumenten in ihren Zahlungsbereitschaften unterscheiden (also unterschiedliche Nachfragefunktionen haben). In diesem Fall entsteht eine Gesamtnachfragekurve mit negativer Steigung, da manche Konsumenten eine höhere und andere eine niedrigere Zahlungsbereitschaft haben. Die negative Steigung der Nachfragekurve drückt sich durch eine negative Preiselastizität der Nachfrage aus: je höher der geforderte Preis umso geringer ist die Nachfrage nach dem Gut. | Nachfragekurve, der ein Produzent gegenübersteht, entsteht entweder, wenn (unter der Annahme identischer Konsumenten) die Zahlungsbereitschaft jedes einzelnen Konsumenten mit der konsumierten Menge abnimmt und/oder wenn sich Konsumenten in ihren Zahlungsbereitschaften unterscheiden (also unterschiedliche Nachfragefunktionen haben). In diesem Fall entsteht eine Gesamtnachfragekurve mit negativer Steigung, da manche Konsumenten eine höhere und andere eine niedrigere Zahlungsbereitschaft haben. Die negative Steigung der Nachfragekurve drückt sich durch eine negative Preiselastizität der Nachfrage aus: je höher der geforderte Preis, umso geringer ist die Nachfrage nach dem Gut. | ||
Weiters muss es den preisdiskriminierenden Anbieter möglich sein, die einzelnen Konsumenten beziehungsweise deren Preissensibilität (zumindest in gewissem Ausmaß) zu identifizieren, um Preise entsprechend zu setzen. | |||
3) Der '''Weiterverkauf''' des Gutes zwischen Konsumenten muss verhindert werden, da ansonsten ein Anreizproblem besteht: Gibt es die Möglichkeit des Weiterverkaufes, so haben Konsumenten mit dokumentiert niedriger Zahlungsbereitschaft einen Anreiz, das Gut zum niedrigeren Preis zu kaufen, um es danach zu einem höheren Preis an Konsumenten mit höherer Zahlungsbereitschaft weiterzuverkaufen. Die Konsumenten mit höherer Zahlungsbereitschaft würden dann also bei diesen Anbietern anstatt beim Produzenten kaufen. In diesem Fall würde Preisdiskriminierung also nicht funktionieren - nur die Konsumenten mit niedriger Zahlungsbereitschaft würden das Produkt direkt vom Produzenten kaufen. | 3) Der '''Weiterverkauf''' des Gutes zwischen Konsumenten muss verhindert werden, da ansonsten ein Anreizproblem besteht: Gibt es die Möglichkeit des Weiterverkaufes, so haben Konsumenten mit dokumentiert niedriger Zahlungsbereitschaft einen Anreiz, das Gut zum niedrigeren Preis zu kaufen, um es danach zu einem höheren Preis an Konsumenten mit höherer Zahlungsbereitschaft weiterzuverkaufen. Die Konsumenten mit höherer Zahlungsbereitschaft würden dann also bei diesen Anbietern anstatt beim Produzenten kaufen. In diesem Fall würde Preisdiskriminierung also nicht funktionieren - nur die Konsumenten mit niedriger Zahlungsbereitschaft würden das Produkt direkt vom Produzenten kaufen. | ||
Weiterkauf ist beispielsweise nicht möglich bei allen Arten von Dienstleistungen, ein Arzt kann bspw. Preisdiskriminierung betreiben, da sich eine Untersuchung nicht wiederverkaufen lässt. Weiters spielen in diesem Zusammenhang Transaktionskosten eine wichtige Rolle. Sind die Transaktionskosten hoch (ist es beispielsweise schwierig Kontakte zwischen Konsumenten mit niedriger und hoher Zahlungsbereitschaft herzustellen), so ist die Wahrscheinlichkeit von Wiederverkäufen geringer. Außerdem können Wiederverkäufe durch Regeln und Gesetze eingeschränkt werden. Diese Möglichkeit beinhaltet sowohl Maßnahmen wie zum Beispiel Ausweiskontrollen beim Kauf eines Theatertickets, als auch Zölle, die es unprofitabel machen, Waren aus Ländern, in denen Güter preiswerter sind, zu importieren, und in einem Land mit höheren Preisen weiterzuverkaufen. <ref>Allerdings stößt es bei Konsumenten nicht gerade auf Begeisterung, wenn sie mitbekommen, dass ein Produkt anderswo günstiger zu haben ist. Aus diesem Grund sah sich z.B. der deutsche Modekonzern Hugo Boss veranlasst, die Preise für Herrenanzüge global anzugleichen, nachdem chinesische Touristen regelmäßig feststellten, dass diese in gleicher Qualität in Mitteleuropa wesentlich günstiger waren als in ihrer Heimat (Handelsblatt, 2. August 2017).</ref> | |||
<span id="möglichkeiten-der-preisdiskriminierung"></span> | |||
== Möglichkeiten der Preisdiskriminierung == | == Möglichkeiten der Preisdiskriminierung == | ||
Je nach verfügbarer Information gibt es unterschiedliche Möglichkeiten der Preisdiskriminierung. | Je nach verfügbarer Information gibt es unterschiedliche Möglichkeiten der Preisdiskriminierung. | ||
* Hat der Produzent genaue Information zu der Zahlungsbereitschaft jedes einzelnen Konsumenten, so kann er perfekte Preisdiskriminierung ('''Preisdiskriminierung''' '''ersten Grades''') betreiben. Er kann in diesem Fall von jedem Konsumenten genau dessen Reservationspreis für die jeweilige Einheit verlangen. Die Stückpreise variieren also pro Einheit sowie pro Konsumenten und der Produzent ist in der Lage, die gesamte Konsumentenrente aus Abbildung 3-1 abzuschöpfen. Allerdings ist es in der Praxis nur in Ausnahmefällen möglich, die genaue Zahlungsbereitschaft der Konsumenten zu kennen. <ref>Man beachte, dass der Konsument nicht eine Person sein muss, sondern auch ein Unternehmen oder der Staat sein kann. Gerade wenn ein Produkt sehr differenziert, aus irgendeinem Grund sehr wichtig und die Stückzahl sehr niedrig ist, ist Preisdiskriminierung ersten Grades nicht unrealistisch, etwa bei bestimmten Rohstoffen oder Rüstungsgütern.</ref> | * Hat der Produzent genaue Information zu der Zahlungsbereitschaft jedes einzelnen Konsumenten, so kann er perfekte Preisdiskriminierung ('''Preisdiskriminierung''' '''ersten Grades''') betreiben. Er kann in diesem Fall von jedem Konsumenten genau dessen Reservationspreis für die jeweilige Einheit verlangen. Die Stückpreise variieren also pro Einheit sowie pro Konsumenten und der Produzent ist in der Lage, die gesamte Konsumentenrente aus Abbildung 3-1 abzuschöpfen. Allerdings ist es in der Praxis nur in Ausnahmefällen möglich, die genaue Zahlungsbereitschaft der Konsumenten zu kennen. <ref>Man beachte, dass der Konsument nicht eine Person sein muss, sondern auch ein Unternehmen oder der Staat sein kann. Gerade wenn ein Produkt sehr differenziert, aus irgendeinem Grund sehr wichtig und die Stückzahl sehr niedrig ist, ist Preisdiskriminierung ersten Grades nicht unrealistisch, etwa bei bestimmten Rohstoffen oder Rüstungsgütern.</ref> | ||
* Hat der Produzent weniger Information zur Verfügung, so kann er '''Preisdiskriminierung zweiten Grades''' betreiben. In diesem Fall weiß der Monopolist zwar, dass es Konsumenten(gruppen) mit unterschiedlichen Nachfragefunktionen gibt, kann allerdings die individuellen Konsumenten nicht den jeweiligen Nachfragefunktionen zuordnen. Um mit diesem Problem umzugehen, kann ein Preisschema erstellt werden, das dazu führt, dass sich die Konsumenten selbst bestimmten Gruppen zuordnen. Durch diese Selbstselektion der Konsumenten ist es nicht nötig, dass der Anbieter weiß, welcher Konsument welcher Gruppe zuzuordnen ist. Auch mit dieser Art der Preisdiskriminierung wird die Zahlungsbereitschaft der Konsumenten (zumindest teilweise) ausgereizt. Eine Möglichkeit ein solches System zu gestalten ist, dass man den Stückpreis eines Gutes von der nachgefragten Menge abhängig macht. In diesem Fall variiert der Stückpreis mit der gekauften Menge, ist allerdings für unterschiedliche Konsumenten (solange sie sich für dieselbe Menge entscheiden) konstant. | * Hat der Produzent weniger Information zur Verfügung, so kann er '''Preisdiskriminierung zweiten Grades''' betreiben. In diesem Fall weiß der Monopolist zwar, dass es Konsumenten(gruppen) mit unterschiedlichen Nachfragefunktionen gibt, kann allerdings die individuellen Konsumenten nicht den jeweiligen Nachfragefunktionen zuordnen. Um mit diesem Problem umzugehen, kann ein Preisschema erstellt werden, das dazu führt, dass sich die Konsumenten selbst bestimmten Gruppen zuordnen. Durch diese Selbstselektion der Konsumenten ist es nicht nötig, dass der Anbieter weiß, welcher Konsument welcher Gruppe zuzuordnen ist. Auch mit dieser Art der Preisdiskriminierung wird die Zahlungsbereitschaft der Konsumenten (zumindest teilweise) ausgereizt. Eine Möglichkeit ein solches System zu gestalten ist, dass man den Stückpreis eines Gutes von der nachgefragten Menge abhängig macht. In diesem Fall variiert der Stückpreis mit der gekauften Menge, ist allerdings für unterschiedliche Konsumenten (solange sie sich für dieselbe Menge entscheiden) konstant. | ||
* Die '''Preisdiskriminierung dritten Grades''' stellt eine weitere Möglichkeit dar, bei beschränkter Information Preisdiskriminierung durchzuführen. Hier zahlen unterschiedliche Gruppen von Konsumenten unterschiedliche Preise, allerdings ist der Stückpreis konstant (also unabhängig von der vom einzelnen Konsumenten nachgefragten Menge). Die Diskriminierung findet demnach zwischen, aber nicht innerhalb der einzelnen Gruppen statt. Diese Form der Preisdiskriminierung wird besonders gern eingesetzt, wenn sich Konsumenten nach bestimmten Merkmalen (Kinder, Studenten, Pensionisten, …) oder Räumen (Stadt/Land, strukturschwache/-starke Regionen, …) unterscheiden lassen. | * Die '''Preisdiskriminierung dritten Grades''' stellt eine weitere Möglichkeit dar, bei beschränkter Information Preisdiskriminierung durchzuführen. Hier zahlen unterschiedliche Gruppen von Konsumenten unterschiedliche Preise, allerdings ist der Stückpreis konstant (also unabhängig von der vom einzelnen Konsumenten nachgefragten Menge). Die Diskriminierung findet demnach zwischen, aber nicht innerhalb der einzelnen Gruppen statt. Diese Form der Preisdiskriminierung wird besonders gern eingesetzt, wenn sich Konsumenten nach bestimmten Merkmalen (Kinder, Studenten, Pensionisten, …) oder Räumen (Stadt/Land, strukturschwache/-starke Regionen, …) unterscheiden lassen. | ||
<span id="preisdiskriminierung-ersten-grades"></span> | <span id="preisdiskriminierung-ersten-grades"></span> | ||
== Preisdiskriminierung ersten Grades == | == Preisdiskriminierung ersten Grades == | ||
| Zeile 54: | Zeile 57: | ||
=== Preissetzung === | === Preissetzung === | ||
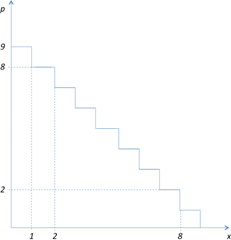
Angenommen der Produzent weiß, dass die indirekte Nachfragefunktion eines Konsumenten wie in Abbildung 3-3 aussieht. Für die erste Einheit des Gutes ist der Konsument bereit, 9 Geldeinheiten (GE) zu zahlen und bei perfekter Preisdiskriminierung werden für diese Einheit ebendiese 9 GE verlangt. Für die zweite Einheit ist die Zahlungsbereitschaft des Konsumenten niedriger, er ist nur noch bereit 8 GE zu zahlen. Daher verlangt der Anbieter für die zweite Einheit auch nur mehr diesen niedrigeren Preis, usw. Die Nachfragefunktion entspricht in diesem Fall also genau der Grenzertragsfunktion des Monopolisten: Sie zeigt an jedem Punkt an, wie viel zusätzlichen Erlös der Verkauf einer weiteren Einheit bringt. Gemäß der Optimalitätsregel des Monopolisten, die besagt, dass im Optimum Grenzerlös = Grenzkosten gelten muss, wird der Monopolist also so lange Einheiten verkaufen, so lange die Zahlungsbereitschaft des Konsumenten über den Grenzkosten liegt. Dies entspricht derselben verkauften Menge, die auch im perfekten Wettbewerb angeboten wird und ist damit höher als die Menge, die ein Monopolist, der einen einheitlichen Preis setzen muss, anbieten würde. Der Monopolist wählt unter perfekter Preisdiskriminierung dieselbe Menge wie ein Produzent unter perfektem Wettbewerb, da er von der Beschränkung entbunden ist, nur einen einheitlichen Preis zu verlangen. Dementsprechend ist der Trade-off, den er zuvor im Auge behalten musste (ein niedrigerer Preis bedeutete, dass ''jedes'' verkaufte Stück zu diesem niedrigeren Preis verkauft wird) nicht mehr relevant. Es ist nun optimal für ihn bis zu dem Punkt zu verkaufen, an dem die Zahlungsbereitschaft des Konsumenten gleich den Grenzkosten ist; darüber hinaus verkaufte Einheiten würden einen Verlust bedeuten. Unter der Annahme konstanter Grenzkosten von 2 GE, würden in dem Beispiel, welches in Abbildung 3-3 dargestellt wird, von dem Monopolisten also genau 8 Einheiten angeboten werden. | Angenommen der Produzent weiß, dass die indirekte Nachfragefunktion eines Konsumenten wie in Abbildung 3-3 aussieht. Für die erste Einheit des Gutes ist der Konsument bereit, 9 Geldeinheiten (GE) zu zahlen und bei perfekter Preisdiskriminierung werden für diese Einheit ebendiese 9 GE verlangt. Für die zweite Einheit ist die Zahlungsbereitschaft des Konsumenten niedriger, er ist nur noch bereit 8 GE zu zahlen. Daher verlangt der Anbieter für die zweite Einheit auch nur mehr diesen niedrigeren Preis, usw. Die Nachfragefunktion entspricht in diesem Fall also genau der Grenzertragsfunktion des Monopolisten: Sie zeigt an jedem Punkt an, wie viel zusätzlichen Erlös der Verkauf einer weiteren Einheit bringt. Gemäß der Optimalitätsregel des Monopolisten, die besagt, dass im Optimum Grenzerlös = Grenzkosten gelten muss, wird der Monopolist also so lange Einheiten verkaufen, so lange die Zahlungsbereitschaft des Konsumenten über den Grenzkosten liegt. Dies entspricht derselben verkauften Menge, die auch im perfekten Wettbewerb angeboten wird und ist damit höher als die Menge, die ein Monopolist, der einen einheitlichen Preis setzen muss, anbieten würde. Der Monopolist wählt unter perfekter Preisdiskriminierung dieselbe Menge wie ein Produzent unter perfektem Wettbewerb, da er von der Beschränkung entbunden ist, nur einen einheitlichen Preis zu verlangen. Dementsprechend ist der Trade-off, den er zuvor im Auge behalten musste (ein niedrigerer Preis bedeutete, dass ''jedes'' verkaufte Stück zu diesem niedrigeren Preis verkauft wird), nicht mehr relevant. Es ist nun optimal für ihn bis zu dem Punkt zu verkaufen, an dem die Zahlungsbereitschaft des Konsumenten gleich den Grenzkosten ist; darüber hinaus verkaufte Einheiten würden einen Verlust bedeuten. Unter der Annahme konstanter Grenzkosten von 2 GE, würden in dem Beispiel, welches in Abbildung 3-3 dargestellt wird, von dem Monopolisten also genau 8 Einheiten angeboten werden. | ||
<span id="wohlfahrtseffekte"></span> | <span id="wohlfahrtseffekte"></span> | ||
=== Wohlfahrtseffekte === | === Wohlfahrtseffekte === | ||
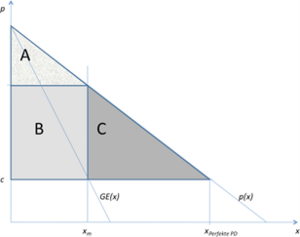
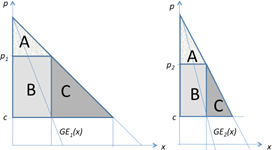
Im Monopol entspricht die Konsumentenrente der Fläche ''A'' in Abbildung 3-4, das Symbol ''M'' bezieht sich auf den Monopolpreis bei einheitlicher Preissetzung, ''PD'' auf Preisdiskriminierung wie soeben besprochen. Die Produzentenrente entspricht der Fläche ''B'' und der Nettowohlfahrtsverlust eines Monopols der Fläche ''C''. In einem Monopol mit Preisdiskriminierung ersten Grades ist die Konsumentenrente null (der Produzent verlangt immer genau die Zahlungsbereitschaft für jede Einheit) und die Produzentenrente der Fläche ''A+B+C''. Dies ist, im Gegensatz zu der Situation eines Monopols mit einheitlicher Preissetzung, ein paretoeffizientes Resultat. Keine der beiden Gruppen könnte bessergestellt werden, ohne eine andere schlechter zu stellen, da kein Nettowohlfahrtsverlust auftritt. Konsumenten, die eine sehr hohe Zahlungsbereitschaft haben, haben im Monopol mit einheitlicher Preissetzung eine höhere Wohlfahrt, da ihre Zahlungsbereitschaft höher als der Einheitspreis liegt. Konsumenten mit niedriger Zahlungsbereitschaft haben in beiden Fällen eine Konsumentenrente von null, da sie im Monopol mit einheitlicher Preissetzung nicht kaufen (der Preis liegt über ihrer Zahlungsbereitschaft), wohingegen sie im Monopol mit perfekter Preisdiskriminierung zwar kaufen, allerdings zu einem Preis, der genau ihrer Zahlungsbereitschaft entspricht. | Im Monopol entspricht die Konsumentenrente der Fläche ''A'' in Abbildung 3-4, das Symbol ''M'' bezieht sich auf den Monopolpreis bei einheitlicher Preissetzung, ''PD'' auf Preisdiskriminierung wie soeben besprochen. Die Produzentenrente entspricht der Fläche ''B'' und der Nettowohlfahrtsverlust eines Monopols der Fläche ''C''.<span style="background-color: rgb(241, 196, 15);"> In einem Monopol mit Preisdiskriminierung ersten Grades ist die Konsumentenrente null (der Produzent verlangt immer genau die Zahlungsbereitschaft für jede Einheit) und die Produzentenrente der Fläche ''A+B+C''. Dies ist, im Gegensatz zu der Situation eines Monopols mit einheitlicher Preissetzung,</span> ein paretoeffizientes Resultat. Keine der beiden Gruppen könnte bessergestellt werden, ohne eine andere schlechter zu stellen, da kein Nettowohlfahrtsverlust auftritt. Konsumenten, die eine sehr hohe Zahlungsbereitschaft haben, haben im Monopol mit einheitlicher Preissetzung eine höhere Wohlfahrt, da ihre Zahlungsbereitschaft höher als der Einheitspreis liegt. Konsumenten mit niedriger Zahlungsbereitschaft haben in beiden Fällen eine Konsumentenrente von null, da sie im Monopol mit einheitlicher Preissetzung nicht kaufen (der Preis liegt über ihrer Zahlungsbereitschaft), wohingegen sie im Monopol mit perfekter Preisdiskriminierung zwar kaufen, allerdings zu einem Preis, der genau ihrer Zahlungsbereitschaft entspricht. | ||
[[Datei:Ec411 14.png|300px|none|thumb|Eine diskrete indirekte Nachfragefunktion]][[Datei:Ec411 15.png|300px|none|thumb|Wohlfahrtseffekte bei Preisdiskriminierung ersten Grades]] | [[Datei:Ec411 14.png|300px|none|thumb|Eine diskrete indirekte Nachfragefunktion]][[Datei:Ec411 15.png|300px|none|thumb|Wohlfahrtseffekte bei Preisdiskriminierung ersten Grades]] | ||
Im perfekten Wettbewerb würde die gleiche Menge produziert werden. Die Konsumentenrente wäre in diesem Fall allerdings durch ''A+B+C'' gegeben, wohingegen die Produzentenrente gleich | Im perfekten Wettbewerb würde die gleiche Menge produziert werden. Die Konsumentenrente wäre in diesem Fall allerdings durch ''A+B+C'' gegeben, wohingegen die Produzentenrente gleich null wäre, da der einheitliche Preis in diesem Fall gleich den Grenzkosten wäre. Obwohl also die produzierte Menge die gleiche ist, unterschieden sich die Wohlfahrtsimplikationen stark. In Bezug auf die Wohlfahrt der Konsumenten wäre die Reihung daher perfekter Wettbewerb (größtmögliche Konsumentenrente), gefolgt von dem Monopol mit einheitlicher Preissetzung und abschließend Monopol mit Preisdiskriminierung ersten Grades (niedrigste Konsumentenrente). | ||
<span id="preisdiskriminierung-zweiten-grades"></span> | <span id="preisdiskriminierung-zweiten-grades"></span> | ||
== Preisdiskriminierung zweiten Grades == | == Preisdiskriminierung zweiten Grades == | ||
| Zeile 71: | Zeile 75: | ||
=== Staffelpreise === | === Staffelpreise === | ||
Bei der Preisdiskriminierung zweiten Grades selektieren sich Konsumenten durch ihre Konsumentscheidung selbst in die „richtige Gruppe“ | Bei der Preisdiskriminierung zweiten Grades selektieren sich Konsumenten durch ihre Konsumentscheidung selbst in die „richtige Gruppe“. Eine Art und Weise, dies zu erreichen, ist, den Stückpreis je nach gekaufter Menge anzupassen. Ein typisches Beispiel für eine solche Art der Preisdiskriminierung sind Mengenrabatte, die oft durch Staffelpreise umgesetzt werden. In diesem Schema wird für die ersten Einheiten (die erste Staffel) eines Gutes der Preis ''p<sub>1</sub>'' verlangt, für weitere Einheiten allerdings der niedrigere Preis ''p<sub>2</sub>''. Je mehr unterschiedliche Staffeln ein Monopolist anbietet, umso näher kommt er mit dieser Methode der perfekten Preisdiskriminierung. Staffelpreise bedeuten eine Reduktion des Stückpreises, abhängig von der konsumierten Gesamtmenge – je mehr Stück gekauft werden, umso niedriger ist der Stückpreis. Jeder Konsument zahlt allerdings, anders als bei der Preisdiskriminierung ersten Grades, denselben Stückpreis (gegeben er kauft dieselbe Menge). <ref>In manchen Fällen ist eine Preisänderung bei dem Kauf höherer Stückzahlen durch niedrigere Stückkosten des Produzenten begründet (als Resultat von zum Beispiel hohen Fixkosten in der Produktion). In diesem Fall wäre ein niedrigerer Stückpreis bei steigender Menge nicht durch Preisdiskriminierung verursacht, sondern stellte lediglich die Weitergabe einer Kostenreduktion an den Konsumenten dar.</ref> | ||
Im Folgenden wird die Möglichkeit zu Staffelpreisen an einem Beispiel verdeutlicht. Angenommen die Nachfrage folgt der indirekten Nachfragefunktion <math display="inline">p = 90 - q</math>. Weiters seien die Grenzkosten konstant mit <math display="inline">c = 30</math>. Das Optimierungsproblem des Produzenten stellt sich wie folgt dar: | Im Folgenden wird die Möglichkeit zu Staffelpreisen an einem Beispiel verdeutlicht. Angenommen die Nachfrage folgt der indirekten Nachfragefunktion <math display="inline">p = 90 - q</math>. Weiters seien die Grenzkosten konstant mit <math display="inline">c = 30</math>. Das Optimierungsproblem des Produzenten stellt sich wie folgt dar: | ||
| Zeile 87: | Zeile 91: | ||
[[Datei:Ec411 16.png|300px|none|thumb|Grafische Darstellung der Staffelpreisung]] | [[Datei:Ec411 16.png|300px|none|thumb|Grafische Darstellung der Staffelpreisung]] | ||
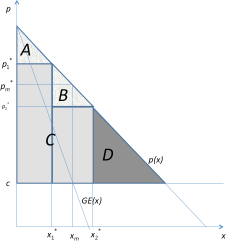
In Abbildung 3-5 zeigt eine grafische Darstellung dieses | In Abbildung 3-5 zeigt eine grafische Darstellung dieses Beispiel, die Konsumenten erhalten die Rente ''KR'' = ''A+B'', die Produzentenrente ''PR'' ist durch die Fläche ''C'' gegeben. Bei dieser Art der Preisdiskriminierung entsteht ein Nettowohlfahrtsverlust, welcher durch die Fläche ''D'' gegeben ist. Nummerisch sind in dem obigen Beispiel die Renten wie folgt gegeben: | ||
<math display="block">KR = A + B = \frac{20 \bullet 20}{2} + \frac{20 \bullet 20}{2}</math> | <math display="block">KR = A + B = \frac{20 \bullet 20}{2} + \frac{20 \bullet 20}{2}</math> | ||
<math display="block"> | |||
P R=C=(70-30) \cdot 20+(50-30) \cdot 20=1200 | |||
</math> | |||
Der Nettowohlfahrtsverlust beträgt: | Der Nettowohlfahrtsverlust beträgt: | ||
| Zeile 106: | Zeile 112: | ||
'''Identische Konsumenten''' | '''Identische Konsumenten''' | ||
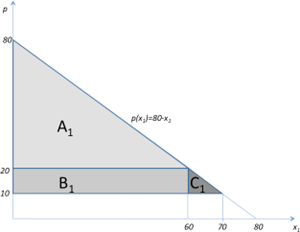
In diesem Fall haben alle Konsumenten die gleiche, dem Monopolisten bekannte | In diesem Fall haben alle Konsumenten die gleiche, dem Monopolisten bekannte (indirekte) Nachfragefunktion. Angenommen, diese ist durch <math display="inline">p = 80 - x</math> gegeben. Außerdem sind die konstanten Grenzkosten <math display="inline">c = 10\ GE</math>. In diesem Fall wird, wie in Abbildung 3-6 zu sehen, die potenzielle Konsumentenrente bei einem Preis von <math display="inline">p = c = 10</math> maximiert. | ||
[[Datei:Ec411 17.png|300px|none|thumb|Der Zwei-Komponenten-Tarif im Falle identischer Konsumenten]] | [[Datei:Ec411 17.png|300px|none|thumb|Der Zwei-Komponenten-Tarif im Falle identischer Konsumenten]] | ||
| Zeile 128: | Zeile 134: | ||
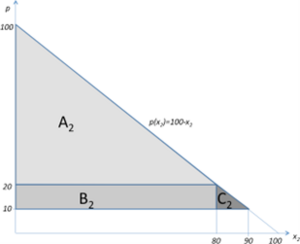
<math display="inline">q_{2} = 100 - p</math> folgt. Die beiden Nachfragefunktionen sind in Abbildungen 3-7 sowie 3-8 dargestellt. | <math display="inline">q_{2} = 100 - p</math> folgt. Die beiden Nachfragefunktionen sind in Abbildungen 3-7 sowie 3-8 dargestellt. | ||
Wie zuvor erörtert wurde, wird die Höhe des Pauschalbetrages durch die Konsumentenrente bestimmt, welche jeweils durch die Fläche A+B+C gegeben. Optimalerweise wird der Monopolist den Pauschalbetrag ''L'' entweder <math display="inline">L = {KR}_{1}</math> oder <math display="inline">L = {KR}_{2}</math> setzen, wobei im Falle <math display="inline">L = {KR}_{1}\ </math>beide Konsumenten das Gut nachfragen werden, im Falle <math display="inline">L = {KR}_{2}</math> allerdings nur Konsument 2 kaufen wird (da Konsument 1 eine niedrigere Zahlungsbereitschaft als Konsument 2 hat). Die Konsumentenrenten berechnen sich anhand der Formel für ein rechtwinkliges Dreieck, wobei eine Seite der Differenz zwischen Reservationspreis und tatsächlichem Preis und die andere der abgesetzten Menge entspricht. <ref>Der Reservationspreis berechnet sich durch <math display="inline">q = 0</math> in der Nachfragefunktion, daraus folgt für Konsument 1 <math display="inline">p_{r,1} = 80</math> und für Konsument 2 <math display="inline">p_{r,2} = 80</math></ref> | <span style="background-color: rgb(241, 196, 15);">Wie zuvor erörtert wurde, wird die Höhe des Pauschalbetrages durch die Konsumentenrente bestimmt, welche jeweils durch die Fläche A+B+C gegeben. Optimalerweise wird der Monopolist den Pauschalbetrag ''L'' entweder </span><math display="inline">L = {KR}_{1}</math><span style="background-color: rgb(241, 196, 15);"> oder</span> <math display="inline">L = {KR}_{2}</math> setzen, wobei im Falle <math display="inline">L = {KR}_{1}\ </math>beide Konsumenten das Gut nachfragen werden, im Falle <math display="inline">L = {KR}_{2}</math> allerdings nur Konsument 2 kaufen wird (da Konsument 1 eine niedrigere Zahlungsbereitschaft als Konsument 2 hat). Die Konsumentenrenten berechnen sich anhand der Formel für ein rechtwinkliges Dreieck, wobei eine Seite der Differenz zwischen Reservationspreis und tatsächlichem Preis und die andere der abgesetzten Menge entspricht. <ref>Der Reservationspreis berechnet sich durch <math display="inline">q = 0</math> in der Nachfragefunktion, daraus folgt für Konsument 1 <math display="inline">p_{r,1} = 80</math> und für Konsument 2 <math display="inline">p_{r,2} = 80</math></ref> | ||
<math display="block">{KR_{1} = \frac{1}{2}(80 - p)q_{1} = \frac{1}{2}(80 - p)^{2} | <math display="block">{KR_{1} = \frac{1}{2}(80 - p)q_{1} = \frac{1}{2}(80 - p)^{2} | ||
| Zeile 160: | Zeile 166: | ||
Der Monopolist sieht sich zwei Konsumenten mit unterschiedlichen Zahlungsbereitschaften gegenüber. Da Theaterstück 1 ein Publikumshit ist, sind die Zahlungsbereitschaften beider Konsumenten für Stück 1 höher als für Stück 2. Um herauszufinden, ob er in diesem Fall eine Strategie der Bündelung anwenden soll, vergleicht der Monopolist den Erlös mit beziehungsweise ohne Bündelung (Anmerkung: Da die Grenzkosten eines zusätzlichen Zuschauers im Theater gleich null sind, entspricht der zusätzliche Erlös dem zusätzlichen Bruttogewinn). | Der Monopolist sieht sich zwei Konsumenten mit unterschiedlichen Zahlungsbereitschaften gegenüber. Da Theaterstück 1 ein Publikumshit ist, sind die Zahlungsbereitschaften beider Konsumenten für Stück 1 höher als für Stück 2. Um herauszufinden, ob er in diesem Fall eine Strategie der Bündelung anwenden soll, vergleicht der Monopolist den Erlös mit beziehungsweise ohne Bündelung (Anmerkung: Da die Grenzkosten eines zusätzlichen Zuschauers im Theater gleich null sind, entspricht der zusätzliche Erlös dem zusätzlichen Bruttogewinn). | ||
{| | {| style="border-collapse: collapse; height: 173px;" border="1" | ||
! | ! style="width: 135.95px; height: 51px;" | | ||
! | ! style="width: 100.65px; height: 51px;" | Theaterstück 1 | ||
! | ! style="width: 104.65px; height: 51px;" | Theaterstück 2 | ||
! | ! style="width: 104.65px; height: 51px;" | Bündelung | ||
|- | |- style="height: 28px;" | ||
| Konsument 1 | | style="width: 135.95px; height: 28px;" | Konsument 1 | ||
| 20 | | style="width: 100.65px; height: 28px;" | 20 | ||
| 5 | | style="width: 104.65px; height: 28px;" | 5 | ||
| 25 | | style="width: 104.65px; height: 28px;" | 25 | ||
|- | |- style="height: 28px;" | ||
| Konsument 2 | | style="width: 135.95px; height: 28px;" | Konsument 2 | ||
| 14 | | style="width: 100.65px; height: 28px;" | 14 | ||
| 1 | | style="width: 104.65px; height: 28px;" | 1 | ||
| 15 | | style="width: 104.65px; height: 28px;" | 15 | ||
|- | |- style="height: 28px;" | ||
| Gesetzter Preis | | style="width: 135.95px; height: 28px;" | Gesetzter Preis | ||
| 14 | | style="width: 100.65px; height: 28px;" | 14 | ||
| 5 | | style="width: 104.65px; height: 28px;" | 5 | ||
| 15 | | style="width: 104.65px; height: 28px;" | 15 | ||
|- | |- style="height: 28px;" | ||
| Erlös | | style="width: 135.95px; height: 28px;" | Erlös | ||
| 2*14 = 28 | | style="width: 100.65px; height: 28px;" | 2*14 = 28 | ||
| 1*5 = 5 | | style="width: 104.65px; height: 28px;" | 1*5 = 5 | ||
| 2*15 = 30 | | style="width: 104.65px; height: 28px;" | 2*15 = 30 | ||
|- | |- style="height: 10px;" | ||
| Gesamterlös | | style="width: 135.95px; height: 10px;" | Gesamterlös | ||
| 28 + 5 = 33 | | style="width: 208.1px; height: 10px;" colspan="2" | 28 + 5 = 33 | ||
<br> | <br> | ||
| 30 | | style="width: 104.65px; height: 10px;" | 30 | ||
|} | |} | ||
Positiv korrelierte Zahlungsbereitschaften | |||
Im in Tabelle 3-1 dargestellten Beispiel ist Konsument 1 bereit, 20 GE für den Eintritt zu Stück 1 zu bezahlen, allerdings ist ihm der Besuch von Stück 2 nur 5 GE wert. Konsument 2 ist bereit 14 GE für Stück 1 und 1 GE für Stück 2 zu zahlen. Bietet der Monopolist die Tickets für die beiden Stücke einzeln an, so wird er optimalerweise für Stück 1 einen Eintrittspreis von 14 GE verlangen. Würde er den Preis mit 20 GE ansetzen, so würde nur Konsument 1 das Stück besuchen. Der Gesamterlös in dem Fall wäre dann 20 GE, während bei einem Eintrittspreis von 14 GE beide Konsumenten ins Theater gehen würden (und dem Monopolisten damit einen Erlös von insgesamt 28 GE bescheren würden). Für Stück 2 würde der Monopolist, derselben Logik folgend, einen Eintrittspreis von 5 GE verlangen. Sein Gesamterlös bei Nicht-Bündelung wäre demnach 33 GE. Bei einer Bündelung wäre die Zahlungsbereitschaft von Konsument 1 (für beide Stücke zusammen) durch 25 GE gegeben. Konsument 2 wäre bereit höchstens 15 GE zu zahlen, um in den Genuss des Besuches beider Stücke zu kommen. Optimalerweise würde der Monopolist also einen Preis von 15 GE setzen und damit bei Bündelung einen Erlös von insgesamt 30 GE erzielen. In diesem Beispiel brächte die Strategie der Bündelung also einen niedrigeren Erlös: Der Monopolist würde die Tickets einzeln anbieten. | Im in Tabelle 3-1 dargestellten Beispiel ist Konsument 1 bereit, 20 GE für den Eintritt zu Stück 1 zu bezahlen, allerdings ist ihm der Besuch von Stück 2 nur 5 GE wert. Konsument 2 ist bereit, 14 GE für Stück 1 und 1 GE für Stück 2 zu zahlen. Bietet der Monopolist die Tickets für die beiden Stücke einzeln an, so wird er optimalerweise für Stück 1 einen Eintrittspreis von 14 GE verlangen. Würde er den Preis mit 20 GE ansetzen, so würde nur Konsument 1 das Stück besuchen. Der Gesamterlös in dem Fall wäre dann 20 GE, während bei einem Eintrittspreis von 14 GE beide Konsumenten ins Theater gehen würden (und dem Monopolisten damit einen Erlös von insgesamt 28 GE bescheren würden). Für Stück 2 würde der Monopolist, derselben Logik folgend, einen Eintrittspreis von 5 GE verlangen. Sein Gesamterlös bei Nicht-Bündelung wäre demnach 33 GE. Bei einer Bündelung wäre die Zahlungsbereitschaft von Konsument 1 (für beide Stücke zusammen) durch 25 GE gegeben. Konsument 2 wäre bereit, höchstens 15 GE zu zahlen, um in den Genuss des Besuches beider Stücke zu kommen. Optimalerweise würde der Monopolist also einen Preis von 15 GE setzen und damit bei Bündelung einen Erlös von insgesamt 30 GE erzielen. In diesem Beispiel brächte die Strategie der Bündelung also einen niedrigeren Erlös: Der Monopolist würde die Tickets einzeln anbieten. | ||
{| | {| style="border-collapse: collapse; height: 150px;" border="1" | ||
! | ! style="width: 126.438px; height: 28px;" | | ||
! | ! style="width: 104.637px; height: 28px;" | Theaterstück 1 | ||
! | ! style="width: 104.637px; height: 28px;" | Theaterstück 2 | ||
! | ! style="width: 95.9125px; height: 28px;" | Bündelung | ||
|- | |- style="height: 29px;" | ||
| Konsument 1 | | style="width: 126.438px; height: 29px;" | Konsument 1 | ||
| 17 | | style="width: 104.637px; height: 29px;" | 17 | ||
| 3 | | style="width: 104.637px; height: 29px;" | 3 | ||
| 20 | | style="width: 95.9125px; height: 29px;" | 20 | ||
|- | |- style="height: 28px;" | ||
| Konsument 2 | | style="width: 126.438px; height: 28px;" | Konsument 2 | ||
| 15 | | style="width: 104.637px; height: 28px;" | 15 | ||
| 5 | | style="width: 104.637px; height: 28px;" | 5 | ||
| 20 | | style="width: 95.9125px; height: 28px;" | 20 | ||
|- | |- style="height: 28px;" | ||
| Gesetzter Preis | | style="width: 126.438px; height: 28px;" | Gesetzter Preis | ||
| 15 | | style="width: 104.637px; height: 28px;" | 15 | ||
| 3 | | style="width: 104.637px; height: 28px;" | 3 | ||
| 20 | | style="width: 95.9125px; height: 28px;" | 20 | ||
|- | |- style="height: 27px;" | ||
| Erlös | | style="width: 126.438px; height: 27px;" | Erlös | ||
| 2*15 = 30 | | style="width: 104.637px; height: 27px;" | 2*15 = 30 | ||
| 2*3 = 6 | | style="width: 104.637px; height: 27px;" | 2*3 = 6 | ||
| 2*20 = 40 | | style="width: 95.9125px; height: 27px;" | 2*20 = 40 | ||
|- | |- style="height: 10px;" | ||
| Gesamterlös | | style="width: 126.438px; height: 10px;" | Gesamterlös | ||
| 30 + 6 = 36 | | style="width: 212.075px; height: 10px;" colspan="2" | 30 + 6 = 36 | ||
<br> | <br> | ||
| 40 | | style="width: 95.9125px; height: 10px;" | 40 | ||
|} | |} | ||
Negativ korrelierte Zahlungsbereitschaften | |||
In dem in Tabelle 3-2 dargestellten Beispiel ist Konsument 1 bereit 17 GE für Theaterstück 1 auszugeben, wohingegen ihm der Besuch von Theaterstück 2 nur 3 GE wert ist. Auch Konsument 2 würde mehr zahlen, um Theaterstück 1 zu sehen, nämlich 15 GE; Theaterstück 2 ist ihm 5 GE wert. Man beachte, dass die Zahlungsbereitschaften hier negativ korreliert sind: Theaterstück 1 hat bei Konsument 1 eine höhere Zahlungsbereitschaft, Theaterstück 2 bei Konsument 2. Wiederum wird der Erlös, der erzielt würde, wenn die Tickets einzeln verkauft werden mit dem der Bündelung (analog zu dem vorhergehenden Beispiel). Wie aus Tabelle 3-2 ersichtlich ist, ist in diesem Fall der Erlös bei Bündelung höher. Der Monopolist wird sich also für eine Strategie der Bündelung entscheiden, da dies seinen Gewinn maximiert. | In dem in Tabelle 3-2 dargestellten Beispiel ist Konsument 1 bereit, 17 GE für Theaterstück 1 auszugeben, wohingegen ihm der Besuch von Theaterstück 2 nur 3 GE wert ist. Auch Konsument 2 würde mehr zahlen, um Theaterstück 1 zu sehen, nämlich 15 GE; Theaterstück 2 ist ihm 5 GE wert. Man beachte, dass die Zahlungsbereitschaften hier negativ korreliert sind: Theaterstück 1 hat bei Konsument 1 eine höhere Zahlungsbereitschaft, Theaterstück 2 bei Konsument 2. Wiederum wird der Erlös, der erzielt würde, wenn die Tickets einzeln verkauft werden, mit dem der Bündelung (analog zu dem vorhergehenden Beispiel) verglichen. Wie aus Tabelle 3-2 ersichtlich ist, ist in diesem Fall der Erlös bei Bündelung höher. Der Monopolist wird sich also für eine Strategie der Bündelung entscheiden, da dies seinen Gewinn maximiert. | ||
Warum liefern die beiden obigen Beispiele unterschiedliche optimale Verhaltensweisen des Monopolisten? Dies liegt darin begründet, dass im zweiten Fall die Zahlungsbereitschaften der Konsumenten ''negativ korreliert'' sind. Im konkreten Fall bedeutet dies, dass in Beispiel 2 Konsument 1 bereit ist für Stück 1 mehr zu zahlen als Konsument 2, während es sich bei Stück 2 genau umgekehrt verhält - hier ist Konsument 2 bereit mehr zu zahlen als Konsument 1. In Beispiel 1 ist dies nicht der Fall. Die Zahlungsbereitschaft von Konsument 1 ist für beide Theaterstücke höher als jene von Konsument 2. Daher zahlt sich in diesem Fall eine Bündelung nicht aus. | Warum liefern die beiden obigen Beispiele unterschiedliche optimale Verhaltensweisen des Monopolisten? Dies liegt darin begründet, dass im zweiten Fall die Zahlungsbereitschaften der Konsumenten ''negativ korreliert'' sind. Im konkreten Fall bedeutet dies, dass in Beispiel 2 Konsument 1 bereit ist für Stück 1 mehr zu zahlen als Konsument 2, während es sich bei Stück 2 genau umgekehrt verhält - hier ist Konsument 2 bereit mehr zu zahlen als Konsument 1. In Beispiel 1 ist dies nicht der Fall. Die Zahlungsbereitschaft von Konsument 1 ist für beide Theaterstücke höher als jene von Konsument 2. Daher zahlt sich in diesem Fall eine Bündelung nicht aus. | ||
| Zeile 237: | Zeile 241: | ||
<span id="preisdiskriminierung-dritten-grades"></span> | <span id="preisdiskriminierung-dritten-grades"></span> | ||
== Preisdiskriminierung dritten Grades == | == Preisdiskriminierung dritten Grades == | ||
| Zeile 250: | Zeile 255: | ||
Das Optimierungsproblem eines Monopolisten, der Preisdiskriminierung dritten Grades durchführen möchte, stellt sich wie folgt dar: Angenommen, er möchte sein Preisschema an die Existenz zweier unterschiedlicher Gruppen, Gruppe 1 und Gruppe 2, anpassen. Die Gruppen haben unterschiedliche Nachfragefunktionen. Wir wissen aus der Monopoltheorie, dass der Monopolist seinen Gewinn an dem Punkt maximiert, an dem ''Grenzertrag = Grenzkosten'' gilt. Da es sich um das gleiche Gut handelt, sind die Grenzkosten des Monopolisten, egal für welche Gruppe er produziert, gleich. Im Optimum gilt also | Das Optimierungsproblem eines Monopolisten, der Preisdiskriminierung dritten Grades durchführen möchte, stellt sich wie folgt dar: Angenommen, er möchte sein Preisschema an die Existenz zweier unterschiedlicher Gruppen, Gruppe 1 und Gruppe 2, anpassen. Die Gruppen haben unterschiedliche Nachfragefunktionen. Wir wissen aus der Monopoltheorie, dass der Monopolist seinen Gewinn an dem Punkt maximiert, an dem ''Grenzertrag = Grenzkosten'' gilt. Da es sich um das gleiche Gut handelt, sind die Grenzkosten des Monopolisten, egal für welche Gruppe er produziert, gleich. Im Optimum gilt also | ||
<math display="block"> | |||
G E_1=c=G E_2 | |||
</math> | |||
wobei <math display="inline">{GE}_{1}\ </math>den Grenzertrag, der sich aus der Nachfragefunktion von Gruppe <math display="inline">i</math>ergibt, darstellt. Diese Bedingung kann mit Hilfe der Amoroso-Robinson-Formel wie folgt angeschrieben werden: | wobei <math display="inline">{GE}_{1}\ </math>den Grenzertrag, der sich aus der Nachfragefunktion von Gruppe <math display="inline">i</math>ergibt, darstellt. Diese Bedingung kann mit Hilfe der Amoroso-Robinson-Formel wie folgt angeschrieben werden: | ||
<math display="block"> | |||
p_1\left(1+\frac{1}{\varepsilon_1}\right)=c=p_2\left(1+\frac{1}{\varepsilon_2}\right) | |||
</math> | |||
Wobei <math display="inline">\varepsilon</math> die Preiselastizität bezeichnet <math display="inline">\frac{\frac{\partial q_{i}}{\partial p}}{\frac{p}{q_{i}}}</math>: Je höher die Elastizität, umso sensibler reagiert die Gruppe auf Preisänderungen. Durch Umformen des Ausdrucks erhält man | Wobei <math display="inline">\varepsilon</math> die Preiselastizität bezeichnet <math display="inline">\frac{\frac{\partial q_{i}}{\partial p}}{\frac{p}{q_{i}}}</math>: Je höher die Elastizität, umso sensibler reagiert die Gruppe auf Preisänderungen. Durch Umformen des Ausdrucks erhält man | ||
<math display="block"> | |||
\frac{p_1}{p_2}=\frac{1-\frac{1}{\left|\varepsilon_2\right|}}{1-\frac{1}{|\varepsilon|}} | |||
</math> | |||
unter den Bedingungen <math display="inline">\left| \varepsilon_{1} \right| < 1</math> und <math display="inline">\left| \varepsilon_{2} \right| < 1</math>. Angenommen, Gruppe 1 hat die preiselastischere Nachfrage, d.h.<math display="inline">\ \left| \varepsilon_{1} \right| > \left| \varepsilon_{2} \right|</math>. Die Konsumenten in Gruppe 1 reagieren also stärker auf eine Preisänderung, d.h. im Speziellen bei einer Preiserhöhung ginge ihre Nachfrage stärker zurück als die von Gruppe 2. <math display="inline">\left| \varepsilon_{1} \right| > \left| \varepsilon_{2} \right|</math> bedeutet, dass | unter den Bedingungen <math display="inline">\left| \varepsilon_{1} \right| < 1</math> und <math display="inline">\left| \varepsilon_{2} \right| < 1</math>. Angenommen, Gruppe 1 hat die preiselastischere Nachfrage, d.h.<math display="inline">\ \left| \varepsilon_{1} \right| > \left| \varepsilon_{2} \right|</math>. Die Konsumenten in Gruppe 1 reagieren also stärker auf eine Preisänderung, d.h. im Speziellen bei einer Preiserhöhung ginge ihre Nachfrage stärker zurück als die von Gruppe 2. <math display="inline">\left| \varepsilon_{1} \right| > \left| \varepsilon_{2} \right|</math> bedeutet, dass | ||
<math display="block"> | |||
\frac{1-\frac{1}{\left|\varepsilon_2\right|}}{1-\frac{1}{\left|\varepsilon_1\right|}}<1 \Leftrightarrow \frac{p_1}{p_2}<1 \Leftrightarrow p_1<p_2 | |||
</math> | |||
Der Preis, den Gruppe 1 für das Gut bezahlt, ist also kleiner als jener, den Gruppe 2 zahlt. Das allgemeine Resultat ist also, dass optimalerweise die Gruppe mit der höheren Preiselastizität den niedrigeren Preis zahlen sollte. Intuitiv ist dies klar nachvollziehbar, da der Monopolist bei einer Preiserhöhung umso mehr verliert, je elastischer die Nachfrage ist. Man kann zum Beispiel davon ausgehen, dass Konsumenten, die bereit sind, viel Zeit für den Kauf eines Gutes aufzuwenden, eine wesentlich elastischere Nachfrage nach dem jeweiligen Gut haben | Der Preis, den Gruppe 1 für das Gut bezahlt, ist also kleiner als jener, den Gruppe 2 zahlt. Das allgemeine Resultat ist also, dass optimalerweise die Gruppe mit der höheren Preiselastizität den niedrigeren Preis zahlen sollte. Intuitiv ist dies klar nachvollziehbar, da der Monopolist bei einer Preiserhöhung umso mehr verliert, je elastischer die Nachfrage ist. Man kann zum Beispiel davon ausgehen, dass Konsumenten, die bereit sind, viel Zeit für den Kauf eines Gutes aufzuwenden, eine wesentlich elastischere Nachfrage nach dem jeweiligen Gut haben als der Durchschnittsbürger. Wenn der Preis hoch ist, werden diese Gruppen den Konsum des jeweiligen Gutes verhältnismäßig stark einschränken. Das kann zum Beispiel erklären, warum im Outlet-Center Parndorf sogar Kosmetika aus dem Standard-Angebot der jeweiligen Anbieter preisreduziert sind: Das Kalkül ist offensichtlich, dass Konsumenten, die extra nach Parndorf fahren, sensibel auf Preisunterschiede reagieren. | ||
<span id="wohlfahrtseffekte-der-preisdiskriminierung-dritten-grades"></span> | <span id="wohlfahrtseffekte-der-preisdiskriminierung-dritten-grades"></span> | ||
| Zeile 278: | Zeile 292: | ||
<span id="übungsbeispiele-1"></span> | <span id="übungsbeispiele-1"></span> | ||
== Übungsbeispiele == | == Übungsbeispiele == | ||
Übungsbeispiel 3.1 | '''Übungsbeispiel 3.1''' | ||
Ein Monopolist verkauft sein Gut in zwei Ländern und wendet Preisdiskriminierung an, indem er in jedem Land einen unterschiedlichen Preis verlangt. Der Monopolist hat konstante Grenzkosten von <math display="inline">c = 10</math>. Die Nachfrage in Land 1 ist gegeben durch <math display="inline">q_{1} = 50 - p_{1}</math>, die in Land 2 durch <math display="inline">q_{2} = 200/3 - 2p_{2}/3</math> . Welcher Preis wird in den einzelnen Ländern verlangt? Angenommen, ein weiterer Anbieter tritt in den Markt ein, der nicht als Produzent, sondern als Wiederverkäufer agiert. Er kann Güter wiederverkaufen, nachdem er sie von einem Land in das andere gebracht hat, mit Transportkosten von 4 GE pro Stück. Welchen Effekt hat dies auf den Monopolisten? | Ein Monopolist verkauft sein Gut in zwei Ländern und wendet Preisdiskriminierung an, indem er in jedem Land einen unterschiedlichen Preis verlangt. Der Monopolist hat konstante Grenzkosten von <math display="inline">c = 10</math>. Die Nachfrage in Land 1 ist gegeben durch <math display="inline">q_{1} = 50 - p_{1}</math>, die in Land 2 durch <math display="inline">q_{2} = 200/3 - 2p_{2}/3</math> . Welcher Preis wird in den einzelnen Ländern verlangt? Angenommen, ein weiterer Anbieter tritt in den Markt ein, der nicht als Produzent, sondern als Wiederverkäufer agiert. Er kann Güter wiederverkaufen, nachdem er sie von einem Land in das andere gebracht hat, mit Transportkosten von 4 GE pro Stück. Welchen Effekt hat dies auf den Monopolisten? | ||
Übungsbeispiel 3.2 | |||
'''Übungsbeispiel 3.2''' | |||
Eine Firma mit konstanten Grenzkosten von <math display="inline">c = 20</math> ist mit zwei unterschiedlichen Arten von Konsumenten konfrontiert. Die Nachfragefunktionen sind durch <math display="inline">q_{1} = 200 - p</math> für Konsument 1 und <math display="inline">q_{2} = 100 - 0,5p</math> für Konsument 2 gegeben. Berechnen Sie den jeweils Gewinn maximierenden Preis. Welchen Preis wird der Monopolist wählen? Welche Menge wird er produzieren, wie ist sein Gewinn? | Eine Firma mit konstanten Grenzkosten von <math display="inline">c = 20</math> ist mit zwei unterschiedlichen Arten von Konsumenten konfrontiert. Die Nachfragefunktionen sind durch <math display="inline">q_{1} = 200 - p</math> für Konsument 1 und <math display="inline">q_{2} = 100 - 0,5p</math> für Konsument 2 gegeben. Berechnen Sie den jeweils Gewinn maximierenden Preis. Welchen Preis wird der Monopolist wählen? Welche Menge wird er produzieren, wie ist sein Gewinn? | ||
Übungsbeispiel 3.3 | |||
'''Übungsbeispiel 3.3''' | |||
Manche Lokale verlangen niedrigere Preise bei Selbstabholung der Speisen als bei Lieferung. Erklären Sie inwiefern dies ein Beispiel für Preisdiskriminierung dritten Grades sein könnte. Geben Sie außerdem eine Erklärung, warum dieser Preisunterschied nicht unbedingt auf Preisdiskriminierung zurückzuführen sein muss. | Manche Lokale verlangen niedrigere Preise bei Selbstabholung der Speisen als bei Lieferung. Erklären Sie inwiefern dies ein Beispiel für Preisdiskriminierung dritten Grades sein könnte. Geben Sie außerdem eine Erklärung, warum dieser Preisunterschied nicht unbedingt auf Preisdiskriminierung zurückzuführen sein muss. | ||
Übungsbeispiel 3.4 | |||
'''Übungsbeispiel 3.4''' | |||
Ein Monopol hat zwei Arten von Kund*innen, kennt ihre Nachfragekurven und möchte einen Zwei-Komponenten-Tarif verlangen. Die Nachfragefunktion von Konsument 1 ist durch <math display="inline">q_{1} = a_{1} - bp</math>, jene von Konsument 2 durch <math display="inline">q_{2} = a_{2} - bp</math>, mit <math display="inline">a_{2} > a_{1}</math>. Leiten Sie allgemeine Ausdrücke für den optimalen Stückpreis <math display="inline">p</math>, sowie den Pauschalbetrag <math display="inline">L</math> ab, unter der Annahme, dass das Monopol konstante Grenzkosten von <math display="inline">c</math> hat und dass es für das Monopol optimal ist, | Ein Monopol hat zwei Arten von Kund*innen, kennt ihre Nachfragekurven und möchte einen Zwei-Komponenten-Tarif verlangen. Die Nachfragefunktion von Konsument 1 ist durch <math display="inline">q_{1} = a_{1} - bp</math>, jene von Konsument 2 durch <math display="inline">q_{2} = a_{2} - bp</math>, mit <math display="inline">a_{2} > a_{1}</math>. Leiten Sie allgemeine Ausdrücke für den optimalen Stückpreis <math display="inline">p</math>, sowie den Pauschalbetrag <math display="inline">L</math> ab, unter der Annahme, dass das Monopol konstante Grenzkosten von <math display="inline">c</math> hat und dass es für das Monopol optimal ist, | ||
| Zeile 302: | Zeile 323: | ||
(c) Setzen Sie anschließend für <math display="inline">a_{1}</math>, <math display="inline">a_{2}</math>, <math display="inline">b</math> und <math display="inline">c</math> beliebige Zahlen ein und berechnen Sie, ob der Monopolist beide oder nur einen Konsumenten bedienen soll. | (c) Setzen Sie anschließend für <math display="inline">a_{1}</math>, <math display="inline">a_{2}</math>, <math display="inline">b</math> und <math display="inline">c</math> beliebige Zahlen ein und berechnen Sie, ob der Monopolist beide oder nur einen Konsumenten bedienen soll. | ||
Übungsbeispiel 3 | |||
'''Übungsbeispiel 3.5''' | |||
Fassen Sie für die folgenden Typen von Preisdiskriminierung das Grundprinzip in ein bis zwei Sätzen zusammen und bringen Sie jeweils ein Beispiel. | Fassen Sie für die folgenden Typen von Preisdiskriminierung das Grundprinzip in ein bis zwei Sätzen zusammen und bringen Sie jeweils ein Beispiel. | ||
| Zeile 316: | Zeile 339: | ||
<br>'''Lösungen ''' | <br>'''Lösungen ''' | ||
<br> | <br>'''Übungsbeispiel 3.1''' | ||
Übungsbeispiel 3.1 | |||
Um den gewinnmaximierenden Output und Preis zu bestimmen, geht der Monopolist wie gehabt vor, diesmal nach Ländern getrennt (indirekte Nachfragefunktion anschreiben, diese in Gewinnfunktion einsetzen, nach Menge ableiten, diese Funktion nullsetzen und für Menge auflösen, Menge in Preisfunktion einsetzen, Preis und Menge in Gewinnfunktion einsetzen: | Um den gewinnmaximierenden Output und Preis zu bestimmen, geht der Monopolist wie gehabt vor, diesmal nach Ländern getrennt (indirekte Nachfragefunktion anschreiben, diese in Gewinnfunktion einsetzen, nach Menge ableiten, diese Funktion nullsetzen und für Menge auflösen, Menge in Preisfunktion einsetzen, Preis und Menge in Gewinnfunktion einsetzen: | ||
| Zeile 334: | Zeile 356: | ||
Die für Land 2 produzierte Menge steigt damit auf 49 Stück, der Gewinn des Monopolisten sinkt in Land 2 sinkt von 1350 auf 1176, also um 174 GE. | Die für Land 2 produzierte Menge steigt damit auf 49 Stück, der Gewinn des Monopolisten sinkt in Land 2 sinkt von 1350 auf 1176, also um 174 GE. | ||
Übungsbeispiel 3.2 | |||
'''Übungsbeispiel 3.2''' | |||
Man beachte, dass die Preiselastizitäten beider Konsumentengruppen identisch sind: | Man beachte, dass die Preiselastizitäten beider Konsumentengruppen identisch sind: | ||
| Zeile 349: | Zeile 373: | ||
Führt man die Gewinnmaximierung des Produzenten für beide Gruppen getrennt durch, so ergibt sich <math display="inline">p_{1} = p_{2} = 110</math> und folglich dieselbe Gesamtmenge und derselbe Gewinn. | Führt man die Gewinnmaximierung des Produzenten für beide Gruppen getrennt durch, so ergibt sich <math display="inline">p_{1} = p_{2} = 110</math> und folglich dieselbe Gesamtmenge und derselbe Gewinn. | ||
Übungsbeispiel 3.3 | |||
'''Übungsbeispiel 3.3''' | |||
Es könnte darin liegen, dass die Zahlungsbereitschaft einer Konsumentengruppe daraus abgeleitet wird, wie viel Zeit sie auf den Kauf einer Speise zu verwenden bereit sind. Das Lokal könnte demnach von Konsumenten, die selbst abholen, einen niedrigeren Preis verlangen, als von solchen, die sie sich zustellen lassen. Der Preisunterschied könnte allerdings auch auf Kostenunterschiede hindeuten und muss demnach nicht Preisdiskriminierung darstellen, da die Zustellung Kosten verursacht. In der Praxis besteht Preisdiskriminierung also dann, wenn der Preisunterschied über den Transportkosten liegt. | Es könnte darin liegen, dass die Zahlungsbereitschaft einer Konsumentengruppe daraus abgeleitet wird, wie viel Zeit sie auf den Kauf einer Speise zu verwenden bereit sind. Das Lokal könnte demnach von Konsumenten, die selbst abholen, einen niedrigeren Preis verlangen, als von solchen, die sie sich zustellen lassen. Der Preisunterschied könnte allerdings auch auf Kostenunterschiede hindeuten und muss demnach nicht Preisdiskriminierung darstellen, da die Zustellung Kosten verursacht. In der Praxis besteht Preisdiskriminierung also dann, wenn der Preisunterschied über den Transportkosten liegt. | ||
| Zeile 355: | Zeile 381: | ||
Im Fall der Produkte, die in Outlet-Centern wie in Parndorf angeboten werden, ist anzunehmen, dass die Preisdifferenz zu anderen Läden größer ist als die niedrigeren Kosten in Parndorf, so sie überhaupt niedriger sind (Miete, Gehälter u.a.). Das gilt auch umgekehrt: Auf Flughäfen zahlt man üblicherweise höhere Preise für Güter wie Parfum, Spirituosen oder Schokoladen. Wem es die Zeitersparnis wert ist (der Grenzaufwand für den Konsumenten ist null, wenn er sich ohnehin am Flughafen aufhalten muss), der wird die höheren Preise am Flughafen buchstäblich in Kauf nehmen. (Die Bezeichnung „duty free“ ist innerhalb der EU irreführend.) Allerdings kann auch hier allein aus den Preisen nicht auf Preisdiskriminierung geschlossen werden, da es sein kann, dass die Kosten, insbes. die Miete, am Flughafen höher sind als anderswo. | Im Fall der Produkte, die in Outlet-Centern wie in Parndorf angeboten werden, ist anzunehmen, dass die Preisdifferenz zu anderen Läden größer ist als die niedrigeren Kosten in Parndorf, so sie überhaupt niedriger sind (Miete, Gehälter u.a.). Das gilt auch umgekehrt: Auf Flughäfen zahlt man üblicherweise höhere Preise für Güter wie Parfum, Spirituosen oder Schokoladen. Wem es die Zeitersparnis wert ist (der Grenzaufwand für den Konsumenten ist null, wenn er sich ohnehin am Flughafen aufhalten muss), der wird die höheren Preise am Flughafen buchstäblich in Kauf nehmen. (Die Bezeichnung „duty free“ ist innerhalb der EU irreführend.) Allerdings kann auch hier allein aus den Preisen nicht auf Preisdiskriminierung geschlossen werden, da es sein kann, dass die Kosten, insbes. die Miete, am Flughafen höher sind als anderswo. | ||
Übungsbeispiel 3.4 | |||
'''Übungsbeispiel 3.4''' | |||
<ol style="list-style-type: lower-alpha;"> | <ol style="list-style-type: lower-alpha;"> | ||
<li><p>Wenn beide Konsumenten optimalerweise bedient werden, so ist der höchste Pauschalbetrag, den der Monopolist setzen kann wegen <math display="inline">a_{2} > a_{1}</math>gleich der Konsumentenrente von Konsument 1.</p></li> | <li><p>Wenn beide Konsumenten optimalerweise bedient werden, so ist der höchste Pauschalbetrag, den der Monopolist setzen kann, wegen <math display="inline">a_{2} > a_{1}</math>gleich der Konsumentenrente von Konsument 1.</p></li> | ||
</ol> | </ol> | ||
<math display="block">L = \frac{a_{1} - bp}{2}L = \frac{1}{2}\left( \frac{a_{1}}{b} - p \right)q_{1}</math> | <math display="block">L = \frac{a_{1} - bp}{2}L = \frac{1}{2}\left( \frac{a_{1}}{b} - p \right)q_{1}</math> | ||
| Zeile 373: | Zeile 401: | ||
<blockquote>Der optimale Pauschalbetrag ist also | <blockquote>Der optimale Pauschalbetrag ist also | ||
<math display="block"> | |||
L=\frac{\left(3 a_1-a_2-2 b c\right)^2}{2 b} | |||
</math></blockquote> | |||
<ol style="list-style-type: lower-alpha;" start="2"> | <ol style="list-style-type: lower-alpha;" start="2"> | ||
<li><p>Ist es optimal für den Monopolisten nur an Konsument 2 zu verkaufen, so ist sein Gesamtgewinn gegeben durch</p></li> | <li><p>Ist es optimal für den Monopolisten nur an Konsument 2 zu verkaufen, so ist sein Gesamtgewinn gegeben durch</p></li> | ||
| Zeile 387: | Zeile 417: | ||
<blockquote>Daher ist der optimale Pauschalbetrag | <blockquote>Daher ist der optimale Pauschalbetrag | ||
<math display="block"> | |||
L=\frac{\left(a_2-b c\right)^2}{2 b} | |||
</math></blockquote> | |||
<ol style="list-style-type: lower-alpha;" start="3"> | <ol style="list-style-type: lower-alpha;" start="3"> | ||
<li><p>…nach eigener Entscheidung…</p></li> | <li><p>…nach eigener Entscheidung…</p></li> | ||
</ol> | </ol> | ||
<span id="übungsbeispiel-3.5"></span> | <span id="übungsbeispiel-3.5"></span>'''Übungsbeispiel 3.5''' | ||
Kurzbeschreibung nach Belieben, Beispiele für Preisdiskriminierung: | Kurzbeschreibung nach Belieben, Beispiele für Preisdiskriminierung: | ||
| Zeile 404: | Zeile 434: | ||
* Preisdiskriminierung zweiten Grades: Bündelung: Tickets für die Fußballspiele der österreichischen Herren-Nationalmannschaft gegen Nordirland und Bosnien-Herzegowina im Herbst 2018 im Rahmen der Nations League konnten nur als Bündel erworben werden. | * Preisdiskriminierung zweiten Grades: Bündelung: Tickets für die Fußballspiele der österreichischen Herren-Nationalmannschaft gegen Nordirland und Bosnien-Herzegowina im Herbst 2018 im Rahmen der Nations League konnten nur als Bündel erworben werden. | ||
* Preisdiskriminierung dritten Grades nach Konsumentenmerkmalen: Tarife nach Geschlecht bei Frisören, Fußballspielen… | * Preisdiskriminierung dritten Grades nach Konsumentenmerkmalen: Tarife nach Geschlecht bei Frisören, Fußballspielen… | ||
* Preisdiskriminierung dritten Grades nach Räumen: Die Praxis Volkswagens und anderer Autohersteller, in ihren Heimatmärkten höhere Preise zu verlangen. <ref>Siehe hierzu Der Spiegel 5/1998 oder Auto-Revue 2/2002; Volkswagen verbat damals seinen italienischen Händlern, an deutschsprachige Kunden zu verkaufen, weil diese eine höhere Zahlungsbereitschaft für die Marken Audi und VW zeigten, was vom Volkswagen-Konzern durch höhere Preise in Deutschland und Österreich ausgenützt wurde. Volkswagen musste schließlich eine Strafe von 90 Millionen Euro Strafe an die EU zahlen (Manager Magazin Online am 18. September 2003).</ref> | * Preisdiskriminierung dritten Grades nach Räumen: Die Praxis Volkswagens und anderer Autohersteller, in ihren Heimatmärkten höhere Preise zu verlangen. <ref>Siehe hierzu Der Spiegel 5/1998 oder Auto-Revue 2/2002; Volkswagen verbat damals seinen italienischen Händlern, an deutschsprachige Kunden zu verkaufen, weil diese eine höhere Zahlungsbereitschaft für die Marken Audi und VW zeigten, was vom Volkswagen-Konzern durch höhere Preise in Deutschland und Österreich ausgenützt wurde. Volkswagen musste schließlich eine Strafe von 90 Millionen Euro Strafe an die EU zahlen (Manager Magazin Online am 18. September 2003).</ref> | ||
Aktuelle Version vom 14. Juli 2023, 11:37 Uhr
Preisdiskriminierung
Allgemeines
Unter Preisdiskriminierung versteht man die Strategie eines Unternehmens, mit Marktmacht unterschiedliche Preise für unterschiedliche Konsumenten zu setzen und damit mehr Gewinn zu lukrieren, als dies in einem Regime, das einen einheitlichen Preis vorsieht, möglich wäre. In Lektion 2 sind wir von einem solchen Regime ausgegangen – der Stückpreis eines Gutes war konstant. Diese Annahme wird im Folgenden aufgehoben.
Warum wenden Unternehmen Strategien der Preisdiskriminierung an?
Die Gesamtnachfragekurve auf einem Gütermarkt, welche die Nachfrage auf der x-Achse in Abhängigkeit vom Preis auf der y-Achse darstellt, hat üblicherweise eine negative Steigung, d.h. je höher der Preis, umso geringer der Absatz. Dies impliziert aber auch, dass Konsumenten für die erste Einheit des Gutes bereit sind mehr zu zahlen, als für die zweite Einheit. Die zweite Einheit ist ihnen wiederum mehr wert als die dritte, und so weiter. D.h. die Zahlungsbereitschaft sinkt, je mehr Einheiten des Gutes schon konsumiert wurden. Diese Tatsache lässt sich an vielen alltäglichen Beispielen verdeutlichen. Es ist es beispielsweise tendenziell so, dass uns der erste Schluck Wasser nach sportlicher Betätigung wichtiger ist (wir wären also bereit, mehr dafür zu zahlen), als der Schluck, der folgen würde, nachdem wir bereits einen halben Liter Wasser getrunken haben. Die Tatsache einer Nachfragekurve mit negativer Steigung lässt sich also direkt von dem Konzept des abnehmenden Grenznutzens herleiten.
Ein Beispiel für eine typische indirekte Nachfragefunktion wird in folgender Abbildung dargestellt. Wenn der Preis des Gutes pmax oder höher liegt, so ist das Gut zu teuer und wird nicht nachgefragt (der Absatz ist null). Sinkt der Preis etwas unter pmax, so wird nur eine einzige Einheit nachgefragt. Soll mehr abgesetzt werden, muss der Preis weiter sinken.
Angenommen, der Preis liegt bei p‘ – hier werden q‘ Einheiten des Gutes nachgefragt. Für alle Einheiten vor q‘ wäre der Konsument allerdings bereit gewesen, einen höheren Preis als p‘ zu zahlen, d.h. seine Zahlungsbereitschaft war höher. Trotzdem, wenn der Produzent einen einheitlichen Preis verlangen muss, so zahlt der Konsument für jede Einheit den einheitlichen Preis p‘. Dadurch entsteht eine sogenannte Konsumentenrente. [1] Diese ist durch das Dreieck gegeben, dass durch die Punkte pmax, p‘ auf der y-Achse und den Schnittpunkt der Geraden q‘ mit der Nachfragekurve gegeben ist. Die Fläche des Dreiecks entspricht jenem Geldbetrag, den die Konsumenten bereit gewesen wären, zu zahlen, aber dank einheitlicher Preissetzung nicht zahlen mussten.
Daraus folgt, dass der Produzent überlegen wird, die Konsumentenrente zu seinem Vorteil zu reduzieren. Im Idealfall würde von jedem Konsumenten so viel verlangt, wie er gerade noch bereit ist, zu zahlen. Mit Hilfe von Preisdiskriminierung könnte also ein höherer Gewinn erzielt werden, da diese Methode es dem Produzenten ermöglicht, einen nicht-konstanten Stückpreis zu verlangen und damit den Stückpreis der tatsächlichen Zahlungsbereitschaft des Konsumenten für die jeweilige Einheit anzupassen. So ist es dem Produzenten möglich, einen Teil der Konsumentenrente abzuschöpfen und damit einen höheren Gewinn zu erzielen.
Kann der Produzent nur einen einheitlichen Stückpreis setzen, so gibt es in der Preissetzung einen trade-off (wie in Lektion 2 ausführlich diskutiert). In die Überlegung, ob ein niedrigerer Preis gesetzt werden soll, fließen in diesem Fall zwei Effekte ein. Einerseits bedeutet ein niedriger Preis, dass mehr Einheiten des Gutes gekauft werden, andererseits ist der Erlös pro Einheit niedriger. Diese zwei Effekte muss ein Produzent, der den optimalen Preis sucht, gegeneinander abwiegen. Dieser trade-off wird durch die Möglichkeit der Preisdiskriminierung (zumindest teilweise) umgangen. Der Produzent erzielt durch Preisdiskriminierung einen höheren Gewinn, da er einerseits einen Teil der Konsumentenrente abschöpfen kann und andererseits auch Konsumenten zum Kauf bewegen kann, denen der einheitliche Preis zu hoch wäre. Die Preisdiskriminierung erlaubt es dem Produzenten also, den Preis an die tatsächliche Zahlungsbereitschaft der Konsumenten anzupassen.
Beispiele für Preisdiskriminierung im alltäglichen Leben sind etwa Ermäßigungen für Museen oder Schilifte für die lokale Bevölkerung oder Ermäßigungen im Theater oder bei Zeitungsabonnements für Studierende. [2] In diesem Fall wird davon ausgegangen, dass die jeweilige Personengruppe eine niedrigere Zahlungsbereitschaft hat als andere Konsumenten. Diese Gruppen würden wohl im Fall eines einheitlichen gewinnmaximierenden Preises das Gut umso viel weniger konsumieren, dass es sich lohnt, nur für diese Gruppe den Preis zu reduzieren. Dadurch wird sichergestellt, dass auch diese Gruppen das Gut konsumieren, Absatz und Gewinn erhöhen sich.
Unter welchen Bedingungen kann Preisdiskriminierung angewendet werden?
Es gibt im Allgemeinen drei Bedingungen, die gelten müssen, damit Preisdiskriminierung als Strategie angewendet werden kann:
1) Die Anbieter müssen eine gewisse Marktmacht haben, d.h., sie müssen die Möglichkeit haben, als Preissetzer zu agieren. Dies ist der Fall in Monopolen, aber auch in oligopolistischen Märkten (vgl. Lektion 2). Es darf also in dem betrachteten Markt keinen freien Markteintritt geben, da in dem Fall Anbieter so lange in den Markt eindringen würden, solange es positive Gewinne zu erwarten gibt, d.h. so lange, bis der Preis den Grenzkosten entspricht.
2) Die Nachfragekurve muss eine negative Steigung haben, d.h., die Zahlungsbereitschaft der Konsumenten muss variieren und mit zusätzlicher Menge abnehmen. Diese negative Steigung der (Gesamt-)
Nachfragekurve, der ein Produzent gegenübersteht, entsteht entweder, wenn (unter der Annahme identischer Konsumenten) die Zahlungsbereitschaft jedes einzelnen Konsumenten mit der konsumierten Menge abnimmt und/oder wenn sich Konsumenten in ihren Zahlungsbereitschaften unterscheiden (also unterschiedliche Nachfragefunktionen haben). In diesem Fall entsteht eine Gesamtnachfragekurve mit negativer Steigung, da manche Konsumenten eine höhere und andere eine niedrigere Zahlungsbereitschaft haben. Die negative Steigung der Nachfragekurve drückt sich durch eine negative Preiselastizität der Nachfrage aus: je höher der geforderte Preis, umso geringer ist die Nachfrage nach dem Gut.
Weiters muss es den preisdiskriminierenden Anbieter möglich sein, die einzelnen Konsumenten beziehungsweise deren Preissensibilität (zumindest in gewissem Ausmaß) zu identifizieren, um Preise entsprechend zu setzen.
3) Der Weiterverkauf des Gutes zwischen Konsumenten muss verhindert werden, da ansonsten ein Anreizproblem besteht: Gibt es die Möglichkeit des Weiterverkaufes, so haben Konsumenten mit dokumentiert niedriger Zahlungsbereitschaft einen Anreiz, das Gut zum niedrigeren Preis zu kaufen, um es danach zu einem höheren Preis an Konsumenten mit höherer Zahlungsbereitschaft weiterzuverkaufen. Die Konsumenten mit höherer Zahlungsbereitschaft würden dann also bei diesen Anbietern anstatt beim Produzenten kaufen. In diesem Fall würde Preisdiskriminierung also nicht funktionieren - nur die Konsumenten mit niedriger Zahlungsbereitschaft würden das Produkt direkt vom Produzenten kaufen.
Weiterkauf ist beispielsweise nicht möglich bei allen Arten von Dienstleistungen, ein Arzt kann bspw. Preisdiskriminierung betreiben, da sich eine Untersuchung nicht wiederverkaufen lässt. Weiters spielen in diesem Zusammenhang Transaktionskosten eine wichtige Rolle. Sind die Transaktionskosten hoch (ist es beispielsweise schwierig Kontakte zwischen Konsumenten mit niedriger und hoher Zahlungsbereitschaft herzustellen), so ist die Wahrscheinlichkeit von Wiederverkäufen geringer. Außerdem können Wiederverkäufe durch Regeln und Gesetze eingeschränkt werden. Diese Möglichkeit beinhaltet sowohl Maßnahmen wie zum Beispiel Ausweiskontrollen beim Kauf eines Theatertickets, als auch Zölle, die es unprofitabel machen, Waren aus Ländern, in denen Güter preiswerter sind, zu importieren, und in einem Land mit höheren Preisen weiterzuverkaufen. [3]
Möglichkeiten der Preisdiskriminierung
Je nach verfügbarer Information gibt es unterschiedliche Möglichkeiten der Preisdiskriminierung.
- Hat der Produzent genaue Information zu der Zahlungsbereitschaft jedes einzelnen Konsumenten, so kann er perfekte Preisdiskriminierung (Preisdiskriminierung ersten Grades) betreiben. Er kann in diesem Fall von jedem Konsumenten genau dessen Reservationspreis für die jeweilige Einheit verlangen. Die Stückpreise variieren also pro Einheit sowie pro Konsumenten und der Produzent ist in der Lage, die gesamte Konsumentenrente aus Abbildung 3-1 abzuschöpfen. Allerdings ist es in der Praxis nur in Ausnahmefällen möglich, die genaue Zahlungsbereitschaft der Konsumenten zu kennen. [4]
- Hat der Produzent weniger Information zur Verfügung, so kann er Preisdiskriminierung zweiten Grades betreiben. In diesem Fall weiß der Monopolist zwar, dass es Konsumenten(gruppen) mit unterschiedlichen Nachfragefunktionen gibt, kann allerdings die individuellen Konsumenten nicht den jeweiligen Nachfragefunktionen zuordnen. Um mit diesem Problem umzugehen, kann ein Preisschema erstellt werden, das dazu führt, dass sich die Konsumenten selbst bestimmten Gruppen zuordnen. Durch diese Selbstselektion der Konsumenten ist es nicht nötig, dass der Anbieter weiß, welcher Konsument welcher Gruppe zuzuordnen ist. Auch mit dieser Art der Preisdiskriminierung wird die Zahlungsbereitschaft der Konsumenten (zumindest teilweise) ausgereizt. Eine Möglichkeit ein solches System zu gestalten ist, dass man den Stückpreis eines Gutes von der nachgefragten Menge abhängig macht. In diesem Fall variiert der Stückpreis mit der gekauften Menge, ist allerdings für unterschiedliche Konsumenten (solange sie sich für dieselbe Menge entscheiden) konstant.
- Die Preisdiskriminierung dritten Grades stellt eine weitere Möglichkeit dar, bei beschränkter Information Preisdiskriminierung durchzuführen. Hier zahlen unterschiedliche Gruppen von Konsumenten unterschiedliche Preise, allerdings ist der Stückpreis konstant (also unabhängig von der vom einzelnen Konsumenten nachgefragten Menge). Die Diskriminierung findet demnach zwischen, aber nicht innerhalb der einzelnen Gruppen statt. Diese Form der Preisdiskriminierung wird besonders gern eingesetzt, wenn sich Konsumenten nach bestimmten Merkmalen (Kinder, Studenten, Pensionisten, …) oder Räumen (Stadt/Land, strukturschwache/-starke Regionen, …) unterscheiden lassen.
Preisdiskriminierung ersten Grades
Preissetzung
Angenommen der Produzent weiß, dass die indirekte Nachfragefunktion eines Konsumenten wie in Abbildung 3-3 aussieht. Für die erste Einheit des Gutes ist der Konsument bereit, 9 Geldeinheiten (GE) zu zahlen und bei perfekter Preisdiskriminierung werden für diese Einheit ebendiese 9 GE verlangt. Für die zweite Einheit ist die Zahlungsbereitschaft des Konsumenten niedriger, er ist nur noch bereit 8 GE zu zahlen. Daher verlangt der Anbieter für die zweite Einheit auch nur mehr diesen niedrigeren Preis, usw. Die Nachfragefunktion entspricht in diesem Fall also genau der Grenzertragsfunktion des Monopolisten: Sie zeigt an jedem Punkt an, wie viel zusätzlichen Erlös der Verkauf einer weiteren Einheit bringt. Gemäß der Optimalitätsregel des Monopolisten, die besagt, dass im Optimum Grenzerlös = Grenzkosten gelten muss, wird der Monopolist also so lange Einheiten verkaufen, so lange die Zahlungsbereitschaft des Konsumenten über den Grenzkosten liegt. Dies entspricht derselben verkauften Menge, die auch im perfekten Wettbewerb angeboten wird und ist damit höher als die Menge, die ein Monopolist, der einen einheitlichen Preis setzen muss, anbieten würde. Der Monopolist wählt unter perfekter Preisdiskriminierung dieselbe Menge wie ein Produzent unter perfektem Wettbewerb, da er von der Beschränkung entbunden ist, nur einen einheitlichen Preis zu verlangen. Dementsprechend ist der Trade-off, den er zuvor im Auge behalten musste (ein niedrigerer Preis bedeutete, dass jedes verkaufte Stück zu diesem niedrigeren Preis verkauft wird), nicht mehr relevant. Es ist nun optimal für ihn bis zu dem Punkt zu verkaufen, an dem die Zahlungsbereitschaft des Konsumenten gleich den Grenzkosten ist; darüber hinaus verkaufte Einheiten würden einen Verlust bedeuten. Unter der Annahme konstanter Grenzkosten von 2 GE, würden in dem Beispiel, welches in Abbildung 3-3 dargestellt wird, von dem Monopolisten also genau 8 Einheiten angeboten werden.
Wohlfahrtseffekte
Im Monopol entspricht die Konsumentenrente der Fläche A in Abbildung 3-4, das Symbol M bezieht sich auf den Monopolpreis bei einheitlicher Preissetzung, PD auf Preisdiskriminierung wie soeben besprochen. Die Produzentenrente entspricht der Fläche B und der Nettowohlfahrtsverlust eines Monopols der Fläche C. In einem Monopol mit Preisdiskriminierung ersten Grades ist die Konsumentenrente null (der Produzent verlangt immer genau die Zahlungsbereitschaft für jede Einheit) und die Produzentenrente der Fläche A+B+C. Dies ist, im Gegensatz zu der Situation eines Monopols mit einheitlicher Preissetzung, ein paretoeffizientes Resultat. Keine der beiden Gruppen könnte bessergestellt werden, ohne eine andere schlechter zu stellen, da kein Nettowohlfahrtsverlust auftritt. Konsumenten, die eine sehr hohe Zahlungsbereitschaft haben, haben im Monopol mit einheitlicher Preissetzung eine höhere Wohlfahrt, da ihre Zahlungsbereitschaft höher als der Einheitspreis liegt. Konsumenten mit niedriger Zahlungsbereitschaft haben in beiden Fällen eine Konsumentenrente von null, da sie im Monopol mit einheitlicher Preissetzung nicht kaufen (der Preis liegt über ihrer Zahlungsbereitschaft), wohingegen sie im Monopol mit perfekter Preisdiskriminierung zwar kaufen, allerdings zu einem Preis, der genau ihrer Zahlungsbereitschaft entspricht.
Im perfekten Wettbewerb würde die gleiche Menge produziert werden. Die Konsumentenrente wäre in diesem Fall allerdings durch A+B+C gegeben, wohingegen die Produzentenrente gleich null wäre, da der einheitliche Preis in diesem Fall gleich den Grenzkosten wäre. Obwohl also die produzierte Menge die gleiche ist, unterschieden sich die Wohlfahrtsimplikationen stark. In Bezug auf die Wohlfahrt der Konsumenten wäre die Reihung daher perfekter Wettbewerb (größtmögliche Konsumentenrente), gefolgt von dem Monopol mit einheitlicher Preissetzung und abschließend Monopol mit Preisdiskriminierung ersten Grades (niedrigste Konsumentenrente).
Preisdiskriminierung zweiten Grades
Staffelpreise
Bei der Preisdiskriminierung zweiten Grades selektieren sich Konsumenten durch ihre Konsumentscheidung selbst in die „richtige Gruppe“. Eine Art und Weise, dies zu erreichen, ist, den Stückpreis je nach gekaufter Menge anzupassen. Ein typisches Beispiel für eine solche Art der Preisdiskriminierung sind Mengenrabatte, die oft durch Staffelpreise umgesetzt werden. In diesem Schema wird für die ersten Einheiten (die erste Staffel) eines Gutes der Preis p1 verlangt, für weitere Einheiten allerdings der niedrigere Preis p2. Je mehr unterschiedliche Staffeln ein Monopolist anbietet, umso näher kommt er mit dieser Methode der perfekten Preisdiskriminierung. Staffelpreise bedeuten eine Reduktion des Stückpreises, abhängig von der konsumierten Gesamtmenge – je mehr Stück gekauft werden, umso niedriger ist der Stückpreis. Jeder Konsument zahlt allerdings, anders als bei der Preisdiskriminierung ersten Grades, denselben Stückpreis (gegeben er kauft dieselbe Menge). [5]
Im Folgenden wird die Möglichkeit zu Staffelpreisen an einem Beispiel verdeutlicht. Angenommen die Nachfrage folgt der indirekten Nachfragefunktion . Weiters seien die Grenzkosten konstant mit . Das Optimierungsproblem des Produzenten stellt sich wie folgt dar:
Der Monopolist maximiert seinen Gewinn, der sich aus dem Erlös des Verkaufs der ersten Stufe mit Stück sowie der zweiten Stufe mit Stück zusammensetzt, wobei die gesamte produzierte Menge bezeichnet. Daraus folgen die Optimalitätsbedingungen:
Für ein Optimum müssen beide Gleichungen simultan gelten. Durch Nullsetzen und Einsetzen einer Gleichung in die andere erhalten wir die optimalen Mengen und sowie Preise und .
In Abbildung 3-5 zeigt eine grafische Darstellung dieses Beispiel, die Konsumenten erhalten die Rente KR = A+B, die Produzentenrente PR ist durch die Fläche C gegeben. Bei dieser Art der Preisdiskriminierung entsteht ein Nettowohlfahrtsverlust, welcher durch die Fläche D gegeben ist. Nummerisch sind in dem obigen Beispiel die Renten wie folgt gegeben:
Der Nettowohlfahrtsverlust beträgt:
Vergleicht man dieses Ergebnis mit den Renten in einem Monopol mit einheitlicher Preissetzung, so können wir zeigen, dass in diesem konkreten Beispiel die Konsumentenrente mit Preisdiskriminierung niedriger ist, die Produzentenrente allerdings höher. Weiters ist der Nettowohlfahrtsverlust durch das Monopol niedriger bei Preisdiskriminierung als bei einem einheitlichen Preis. Je mehr Staffeln von dem Monopol gesetzt werden, umso ähnlicher wird die Situation der Preisdiskriminierung ersten Grades und umso kleiner wird dementsprechend der Nettowohlfahrtsverlust.
Der Zwei-Komponenten-Tarif
Bei diesem Preisschema verlangt der Produzent einen Pauschalbetrag, sowie einen zusätzlichen konstanten Preis pro Stück. Auch hier wird also der durchschnittliche Stückpreis immer geringer, je mehr Einheiten konsumiert werden. Um den Gewinn in dieser Situation zu maximieren, wird ein Produzent versuchen, die potenzielle Konsumentenrente zu maximieren und diese dann mittels Pauschalbetrags möglichst gesamt abzuschöpfen. Typische Beispiele für ein solches Preisschema sind Preise für Telefonnutzung, wo dem Benutzer meist eine monatliche Grundgebühr sowie eine Gesprächsgebühr pro telefonierte Minute verrechnet wird. Um diese Art der Preissetzung zu analysieren, müssen wir unterscheiden, ob in dem Markt lauter identische Konsumenten (mit identischen Nachfragefunktionen) oder unterschiedliche Konsumenten vertreten sind.
Identische Konsumenten
In diesem Fall haben alle Konsumenten die gleiche, dem Monopolisten bekannte (indirekte) Nachfragefunktion. Angenommen, diese ist durch gegeben. Außerdem sind die konstanten Grenzkosten . In diesem Fall wird, wie in Abbildung 3-6 zu sehen, die potenzielle Konsumentenrente bei einem Preis von maximiert.
Die indirekte Nachfragefunktion stellt dar, dass ein Konsument bei einem Preis von p=10 70 Einheiten des Gutes kauft. Er wäre allerdings bereit gewesen, für alle Einheiten vor der 70ten einen höheren Preis als 10 GE zu bezahlen. Dies macht sich der Monopolist zu Nutze und verlangt als Pauschale die gesamte Konsumentenrente, also . Selbst wenn der Konsument für die 70 Einheiten, zusätzlich zu dem Stückpreis von 10 GE, noch ebendiese Pauschale bezahlen müsste, so würde er immer noch dieselben 70 Einheiten nachfragen. Der Monopolist schöpft mit dieser Preissetzungsstrategie die gesamte Konsumentenrente ab.
Würde der Monopolist einen höheren Stückpreis verlangen (und damit nicht die potenzielle Konsumentenrente maximieren), so wäre sein Gewinn niedriger. Die Konsumenten würden eine geringere Menge des Gutes nachfragen und es gäbe einen Nettowohlfahrtsverlust durch die reduzierte Produzentenrente. Es ist nicht verwunderlich, dass dieses Ergebnis jenem der Preisdiskriminierung ersten Grades ähnelt, da die benötigte Information die gleiche ist – der Monopolist muss die Nachfragekurve der (identischen) Konsumenten genau kennen. Sollte diese Information nicht (oder nur teilweise) vorhanden sein, so kann der Zwei-Komponenten-Tarif trotzdem angewandt werden. In diesem Fall muss die Zahlungsbereitschaft der Konsumenten geschätzt werden, um den Pauschaltarif festzulegen. Diese wird damit vermutlich nicht maximiert, da im Zweifelsfall eine niedrigere Pauschalrate, als für den Monopolisten optimal wäre, gewählt wird.
Nichtidentische Konsumenten
Was passiert nun, wenn das Monopol mit unterschiedlichen Konsumenten (deren Nachfragefunktionen sich unterscheiden) konfrontiert ist, und er dabei nicht unterscheiden kann, welcher Konsument in welche Gruppe fällt? Im Falle, dass das Monopol die Möglichkeit hat, die beiden Konsumentengruppen zu identifizieren, in der Folge unterschiedlich zu behandeln und Weiterverkäufe zu verhindern, ist die Antwort einfach: Er wird die Pauschalbeträge für jeden Konsumenten unterschiedlich festsetzen und zwar genau so, dass (wie im zuvor behandelten Fall) die gesamte Konsumentenrente abgeschöpft wird. Der Stückpreis ist in allen Fällen konstant, da sich dieser nach den Grenzkosten des Monopolisten richtet.
Sollte es allerdings (durch rechtliche Bestimmungen oder Fehlen an Information über individuelle Konsumenten) nicht möglich sein, unterschiedlichen Konsumenten unterschiedliche Angebote zu unterbreiten, so hat der Monopolist zwei Möglichkeiten. Er kann einerseits ein einziges Preisschema festsetzen, welches so gewählt sein muss, dass es den Gewinn aus dem Verkauf an beide Konsumenten maximiert. Eine andere Möglichkeit ist, unterschiedliche Preispakete für unterschiedliche Konsumenten anzubieten und diese so festzusetzen, dass sich die Konsumenten in die jeweils für sie vorgesehene Gruppe selektieren, also genau das Preispaket in Anspruch nehmen, welches für sie vorgesehen ist.
Ein einheitliches Preisschema bei nichtidentischen Konsumenten
Angenommen, im Markt sind zwei unterschiedliche Konsumenten vertreten, Konsument 1 und Konsument 2. Die Nachfrage von Konsument 1 ist durch die Funktion gegeben, während die von Konsument 2 der Funktion
folgt. Die beiden Nachfragefunktionen sind in Abbildungen 3-7 sowie 3-8 dargestellt.
Wie zuvor erörtert wurde, wird die Höhe des Pauschalbetrages durch die Konsumentenrente bestimmt, welche jeweils durch die Fläche A+B+C gegeben. Optimalerweise wird der Monopolist den Pauschalbetrag L entweder oder setzen, wobei im Falle beide Konsumenten das Gut nachfragen werden, im Falle allerdings nur Konsument 2 kaufen wird (da Konsument 1 eine niedrigere Zahlungsbereitschaft als Konsument 2 hat). Die Konsumentenrenten berechnen sich anhand der Formel für ein rechtwinkliges Dreieck, wobei eine Seite der Differenz zwischen Reservationspreis und tatsächlichem Preis und die andere der abgesetzten Menge entspricht. [6]
was jeweils den Flächeninhalten A+B+C entspricht. Für das Monopol wäre es nicht optimal, eine andere Pauschalrate als eine dieser beiden zu setzen. Wäre zum Beispiel , dann würde keiner der beiden Konsumenten kaufen - eine Situation, die nicht optimal sein kann, da der Produzent durch den Verkauf einiger Einheiten des Gutes immer die Möglichkeit hätte, einen positiven Gewinn zu machen. Würde der Monopolist setzen, würden beide Konsumenten das Gut kaufen, allerdings wäre dies auch bei der Fall gewesen. Mit dieser Strategie verliert der Monopolist also an Gewinn. Die dritte Möglichkeit, nämlich den Pauschalbetrag zwischen und festzusetzen (), kann auch nicht optimal sein, da in diesem Fall nur Konsument 2 kaufen würde, dies allerdings auch bei dem höheren Pauschalbetrag eintreten würde. Der Gewinn, wenn der Pauschalbetrag gesetzt wird, ist gegeben durch:
Wobei sich der erste Term aus der Formel für die Fläche eines rechtwinkligen Dreiecks ergibt und im zweiten Term die unterschiedlichen Nachfragefunktionen berücksichtigt sind. In diesem Fall würden beide Konsumenten das Gut kaufen, d.h. der Monopolist bekäme zwei Mal die Pauschalrate sowie den Stückpreis für die verkauften Einheiten abzüglich der Produktionskosten. Angenommen, ,
so wird der optimale Preis durch Arbeiten und Nullsetzen bestimmt:
woraus sich der gewinnmaximierende Preis als ergibt, was einem Gewinn von entspricht.
Vergleichen wir diesen Gewinn mit jenem, der sich durch Setzen des der Pauschalbetrag L= KR2 ergibt:
Hier würde nur Konsument 2 das Gut kaufen, daher erhält der Monopolist nur einmal die Pauschalrate LKR2. Für jede Einheit des Gutes, welche verkauft wird, erhält der Produzent weiters den Stückpreis abzüglich der Produktionskosten. Bei Wiederholung des Rechengangs (ableiten – nullsetzen – für den Preis auflösen – den Preis in Gewinnfunktion einsetzen) ergeben sich als , was einem Gewinn von entspricht. Es wird also der höhere Preis gesetzt. Dieses Resultat unterscheidet sich von dem zuvor besprochenen (mit identischen Konsumenten), da der Monopolist unter diesen Umständen (einheitliche Pauschalratensetzung bei unterschiedlichen Konsumenten) in keinem Fall die gesamte Konsumentenrente abschöpfen kann. Daher ist es in obigem Beispiel optimal, den Preis höher als die Grenzkosten zu setzen.
Bündelung
Bei der Bündelung wird der Kauf eines Produktes an den Kauf eines anderen Produktes gebunden. Diese Strategie macht es für den Konsumenten unmöglich, ein Gut ohne das andere zu kaufen. Beispiele einer solchen Bündelung reichen von Hemden, die immer mit Knöpfen verkauft werden, über Computer, die beim Kauf bereits mit einem Betriebssystem ausgestattet sind, bis zu Kabelfernsehangeboten, in denen immer ein Bündel von Programmen gemeinsam bestellt werden muss. Oft, wie offensichtlich im Fall von Hemden, reduziert Bündelung die Transaktionskosten. Mitunter, wie bei Paketen von Fernsehsendern, sind die Grenzkosten nahe null. Im vereinfachten Beispiel von zwei Konsumenten mit unterschiedlichen Nachfragefunktionen macht eine Strategie der Bündelung für den Monopolisten nur dann Sinn, wenn die Nachfrage der beiden Konsumenten negativ korreliert ist. Der Grund dafür wird im Folgenden anhand eines nummerischen Beispiels verdeutlicht.
Angenommen, ein Monopolist möchte Theatertickets für zwei verschiedene Vorstellungen verkaufen. Soll er diese einzeln oder als nur als Bündel anbieten? Auch hier gilt wiederum die Annahme, dass der Monopolist zwar weiß, dass es zwei unterschiedliche Konsument-Typen gibt, die individuellen Konsumenten allerdings nicht der jeweiligen Nachfragefunktion zuordnen kann. Verkauft er die Theatertickets als Bündel, so wird eine Unterscheidung der individuellen Konsumenten unnötig, da beiden das gleiche Bündel angeboten wird.
Der Monopolist sieht sich zwei Konsumenten mit unterschiedlichen Zahlungsbereitschaften gegenüber. Da Theaterstück 1 ein Publikumshit ist, sind die Zahlungsbereitschaften beider Konsumenten für Stück 1 höher als für Stück 2. Um herauszufinden, ob er in diesem Fall eine Strategie der Bündelung anwenden soll, vergleicht der Monopolist den Erlös mit beziehungsweise ohne Bündelung (Anmerkung: Da die Grenzkosten eines zusätzlichen Zuschauers im Theater gleich null sind, entspricht der zusätzliche Erlös dem zusätzlichen Bruttogewinn).
| Theaterstück 1 | Theaterstück 2 | Bündelung | |
|---|---|---|---|
| Konsument 1 | 20 | 5 | 25 |
| Konsument 2 | 14 | 1 | 15 |
| Gesetzter Preis | 14 | 5 | 15 |
| Erlös | 2*14 = 28 | 1*5 = 5 | 2*15 = 30 |
| Gesamterlös | 28 + 5 = 33
|
30 | |
Positiv korrelierte Zahlungsbereitschaften
Im in Tabelle 3-1 dargestellten Beispiel ist Konsument 1 bereit, 20 GE für den Eintritt zu Stück 1 zu bezahlen, allerdings ist ihm der Besuch von Stück 2 nur 5 GE wert. Konsument 2 ist bereit, 14 GE für Stück 1 und 1 GE für Stück 2 zu zahlen. Bietet der Monopolist die Tickets für die beiden Stücke einzeln an, so wird er optimalerweise für Stück 1 einen Eintrittspreis von 14 GE verlangen. Würde er den Preis mit 20 GE ansetzen, so würde nur Konsument 1 das Stück besuchen. Der Gesamterlös in dem Fall wäre dann 20 GE, während bei einem Eintrittspreis von 14 GE beide Konsumenten ins Theater gehen würden (und dem Monopolisten damit einen Erlös von insgesamt 28 GE bescheren würden). Für Stück 2 würde der Monopolist, derselben Logik folgend, einen Eintrittspreis von 5 GE verlangen. Sein Gesamterlös bei Nicht-Bündelung wäre demnach 33 GE. Bei einer Bündelung wäre die Zahlungsbereitschaft von Konsument 1 (für beide Stücke zusammen) durch 25 GE gegeben. Konsument 2 wäre bereit, höchstens 15 GE zu zahlen, um in den Genuss des Besuches beider Stücke zu kommen. Optimalerweise würde der Monopolist also einen Preis von 15 GE setzen und damit bei Bündelung einen Erlös von insgesamt 30 GE erzielen. In diesem Beispiel brächte die Strategie der Bündelung also einen niedrigeren Erlös: Der Monopolist würde die Tickets einzeln anbieten.
| Theaterstück 1 | Theaterstück 2 | Bündelung | |
|---|---|---|---|
| Konsument 1 | 17 | 3 | 20 |
| Konsument 2 | 15 | 5 | 20 |
| Gesetzter Preis | 15 | 3 | 20 |
| Erlös | 2*15 = 30 | 2*3 = 6 | 2*20 = 40 |
| Gesamterlös | 30 + 6 = 36
|
40 | |
Negativ korrelierte Zahlungsbereitschaften
In dem in Tabelle 3-2 dargestellten Beispiel ist Konsument 1 bereit, 17 GE für Theaterstück 1 auszugeben, wohingegen ihm der Besuch von Theaterstück 2 nur 3 GE wert ist. Auch Konsument 2 würde mehr zahlen, um Theaterstück 1 zu sehen, nämlich 15 GE; Theaterstück 2 ist ihm 5 GE wert. Man beachte, dass die Zahlungsbereitschaften hier negativ korreliert sind: Theaterstück 1 hat bei Konsument 1 eine höhere Zahlungsbereitschaft, Theaterstück 2 bei Konsument 2. Wiederum wird der Erlös, der erzielt würde, wenn die Tickets einzeln verkauft werden, mit dem der Bündelung (analog zu dem vorhergehenden Beispiel) verglichen. Wie aus Tabelle 3-2 ersichtlich ist, ist in diesem Fall der Erlös bei Bündelung höher. Der Monopolist wird sich also für eine Strategie der Bündelung entscheiden, da dies seinen Gewinn maximiert.
Warum liefern die beiden obigen Beispiele unterschiedliche optimale Verhaltensweisen des Monopolisten? Dies liegt darin begründet, dass im zweiten Fall die Zahlungsbereitschaften der Konsumenten negativ korreliert sind. Im konkreten Fall bedeutet dies, dass in Beispiel 2 Konsument 1 bereit ist für Stück 1 mehr zu zahlen als Konsument 2, während es sich bei Stück 2 genau umgekehrt verhält - hier ist Konsument 2 bereit mehr zu zahlen als Konsument 1. In Beispiel 1 ist dies nicht der Fall. Die Zahlungsbereitschaft von Konsument 1 ist für beide Theaterstücke höher als jene von Konsument 2. Daher zahlt sich in diesem Fall eine Bündelung nicht aus.
Intuitiv liegt dieses Ergebnis darin begründet, dass ein einheitlicher Preis oft vom Konsumenten mit der niedrigeren Zahlungsbereitschaft bestimmt ist. Setzt man den einheitlichen Preis gemäß dessen Reservationspreis, ist sichergestellt, dass beide Konsumenten kaufen. Dies entspricht oft dem gewinnoptimierenden Verhalten. Unterscheiden sich die Zahlungsbereitschaften relativ stark, so muss das Monopol einen relativ niedrigen Preis verlangen, um eine möglichst große Menge zu verkaufen. Sind die Zahlungsbereitschaften negativ korreliert, so kann mit Hilfe der Strategie der Bündelung das Monopol die Varianz der Zahlungsbereitschaften reduzieren. Dies wird in Tabelle 3-2 deutlich, in der sich die Zahlungsbereitschaft der beiden Konsumenten für das Bündel nicht unterscheidet. Dadurch kann das Monopol bei Bündelung einen höheren Preis verlangen und trotzdem sicherstellen, dass beide Konsumenten das Produkt kaufen.
Preisdiskriminierung dritten Grades
Wenn der Monopolist die Nachfragekurve der einzelnen Konsumenten nicht kennt, er allerdings Konsumentengruppen unterscheiden kann, so kann er auch Preisdiskriminierung dritten Grades durchführen. Diese Art der Preisdiskriminierung wird in der Realität am häufigsten angewandt. Typische Beispiele sind Ermäßigungen bei Eintrittspreisen für Studierende oder Senioren. Diese Personengruppen haben traditionell für zum Beispiel Theaterbesuche eine niedrigere Zahlungsbereitschaft als die Durchschnittsbevölkerung und würden zu großen Teilen das Gut Theaterbesuch bei einheitlicher Preissetzung (die sich nach der Zahlungsbereitschaft der Durchschnittsbevölkerung richtet) nicht konsumieren. Wenn der Monopolist Preisdiskriminierung dritten Grades anwendet, so kann er auch diese Gruppen bedienen, ihre Konsumentenrente (zumindest zum Teil) abschöpfen und damit einen höheren Gewinn erzielen.
Preissetzung
Wie identifiziert der Monopolist, welcher individuelle Konsument welcher Gruppe zugeordnet werden sollte? Oft kann die Zuordnung anhand äußerer Merkmale erfolgen, wie dem Alter (Ermäßigungen für Kinder), dem Aufenthaltsort (Preisdiskriminierung nach Ländern) oder dem Beruf (Ermäßigungen für Studierende, Senioren oder Arbeitslose). In diesem Fall erfolgt eine Einteilung in Gruppen auf direkte Art und Weise.
Weiters gibt es auch die Möglichkeit, ähnlich wie bei der Preisdiskriminierung zweiten Grades, Konsumenten auf Basis ihres Verhaltens einzuteilen. Dafür wird ein Preisschema angeboten, welches zur Folge hat, dass Konsumenten sich selbst selektieren, also der Gruppe zuordnen, zu der sie gehören. Eine Möglichkeit, Konsumenten nach ihrer Zahlungsbereitschaft (beziehungsweise der Preiselastizität ihrer Nachfrage) zu unterscheiden, ist mit Hilfe der Zeit, die sie bereit sind, in den Kauf eines Gutes zu investieren. Wenn Konsumenten bereit sind, viel Zeit aufzuwenden (um beispielsweise ein Gut direkt vom Hersteller abzuholen oder lange Wartezeiten in Kauf zu nehmen), so bedeutet dies meist, dass sie eine niedrigere Zahlungsbereitschaft beziehungsweise eine höhere Preiselastizität haben. Der Monopolist kann also aus dem Verhalten der Konsumenten Rückschlüsse auf die Form ihrer Nachfragefunktion ziehen.
Das Optimierungsproblem eines Monopolisten, der Preisdiskriminierung dritten Grades durchführen möchte, stellt sich wie folgt dar: Angenommen, er möchte sein Preisschema an die Existenz zweier unterschiedlicher Gruppen, Gruppe 1 und Gruppe 2, anpassen. Die Gruppen haben unterschiedliche Nachfragefunktionen. Wir wissen aus der Monopoltheorie, dass der Monopolist seinen Gewinn an dem Punkt maximiert, an dem Grenzertrag = Grenzkosten gilt. Da es sich um das gleiche Gut handelt, sind die Grenzkosten des Monopolisten, egal für welche Gruppe er produziert, gleich. Im Optimum gilt also
wobei den Grenzertrag, der sich aus der Nachfragefunktion von Gruppe ergibt, darstellt. Diese Bedingung kann mit Hilfe der Amoroso-Robinson-Formel wie folgt angeschrieben werden:
Wobei die Preiselastizität bezeichnet : Je höher die Elastizität, umso sensibler reagiert die Gruppe auf Preisänderungen. Durch Umformen des Ausdrucks erhält man
unter den Bedingungen und . Angenommen, Gruppe 1 hat die preiselastischere Nachfrage, d.h.. Die Konsumenten in Gruppe 1 reagieren also stärker auf eine Preisänderung, d.h. im Speziellen bei einer Preiserhöhung ginge ihre Nachfrage stärker zurück als die von Gruppe 2. bedeutet, dass
Der Preis, den Gruppe 1 für das Gut bezahlt, ist also kleiner als jener, den Gruppe 2 zahlt. Das allgemeine Resultat ist also, dass optimalerweise die Gruppe mit der höheren Preiselastizität den niedrigeren Preis zahlen sollte. Intuitiv ist dies klar nachvollziehbar, da der Monopolist bei einer Preiserhöhung umso mehr verliert, je elastischer die Nachfrage ist. Man kann zum Beispiel davon ausgehen, dass Konsumenten, die bereit sind, viel Zeit für den Kauf eines Gutes aufzuwenden, eine wesentlich elastischere Nachfrage nach dem jeweiligen Gut haben als der Durchschnittsbürger. Wenn der Preis hoch ist, werden diese Gruppen den Konsum des jeweiligen Gutes verhältnismäßig stark einschränken. Das kann zum Beispiel erklären, warum im Outlet-Center Parndorf sogar Kosmetika aus dem Standard-Angebot der jeweiligen Anbieter preisreduziert sind: Das Kalkül ist offensichtlich, dass Konsumenten, die extra nach Parndorf fahren, sensibel auf Preisunterschiede reagieren.
Wohlfahrtseffekte der Preisdiskriminierung dritten Grades
In Abbildung 3-10 ist das zuvor besprochene Resultat dargestellt: Der Preis, den die Gruppe mit der weniger elastischen Nachfrage zahlt, ist höher als jener der Gruppe mit der elastischeren Nachfrage.
Unter perfektem Wettbewerb ist, analog zu obigen Beispielen, die Produzentenrente und die Konsumentenrente . Im Vergleich dazu ist bei Preisdiskriminierung dritten Grades die Produzentenrente durch und die Konsumentenrente durch gegeben. Der Nettowohlfahrtsverlust entspricht der Fläche C in der Abbildung.
Auch im Monopol mit einheitlicher Preissetzung tritt ein Nettowohlfahrtsverlust ein. Ob dieser größer oder kleiner als bei der Preisdiskriminierung dritten Grades ist, kann generell nicht bestimmt werden. Der Produzent allerdings hat insgesamt eine höhere Produzentenrente als in einem Monopol mit einheitlicher Preissetzung, da er sein Preisschema den unterschiedlichen Nachfragefunktionen anpassen kann.
Übungsbeispiele
Übungsbeispiel 3.1
Ein Monopolist verkauft sein Gut in zwei Ländern und wendet Preisdiskriminierung an, indem er in jedem Land einen unterschiedlichen Preis verlangt. Der Monopolist hat konstante Grenzkosten von . Die Nachfrage in Land 1 ist gegeben durch , die in Land 2 durch . Welcher Preis wird in den einzelnen Ländern verlangt? Angenommen, ein weiterer Anbieter tritt in den Markt ein, der nicht als Produzent, sondern als Wiederverkäufer agiert. Er kann Güter wiederverkaufen, nachdem er sie von einem Land in das andere gebracht hat, mit Transportkosten von 4 GE pro Stück. Welchen Effekt hat dies auf den Monopolisten?
Übungsbeispiel 3.2
Eine Firma mit konstanten Grenzkosten von ist mit zwei unterschiedlichen Arten von Konsumenten konfrontiert. Die Nachfragefunktionen sind durch für Konsument 1 und für Konsument 2 gegeben. Berechnen Sie den jeweils Gewinn maximierenden Preis. Welchen Preis wird der Monopolist wählen? Welche Menge wird er produzieren, wie ist sein Gewinn?
Übungsbeispiel 3.3
Manche Lokale verlangen niedrigere Preise bei Selbstabholung der Speisen als bei Lieferung. Erklären Sie inwiefern dies ein Beispiel für Preisdiskriminierung dritten Grades sein könnte. Geben Sie außerdem eine Erklärung, warum dieser Preisunterschied nicht unbedingt auf Preisdiskriminierung zurückzuführen sein muss.
Übungsbeispiel 3.4
Ein Monopol hat zwei Arten von Kund*innen, kennt ihre Nachfragekurven und möchte einen Zwei-Komponenten-Tarif verlangen. Die Nachfragefunktion von Konsument 1 ist durch , jene von Konsument 2 durch , mit . Leiten Sie allgemeine Ausdrücke für den optimalen Stückpreis , sowie den Pauschalbetrag ab, unter der Annahme, dass das Monopol konstante Grenzkosten von hat und dass es für das Monopol optimal ist,
(a) beide Konsumenten zu bedienen,
(b) nur Konsument 2 zu bedienen.
(c) Setzen Sie anschließend für , , und beliebige Zahlen ein und berechnen Sie, ob der Monopolist beide oder nur einen Konsumenten bedienen soll.
Übungsbeispiel 3.5
Fassen Sie für die folgenden Typen von Preisdiskriminierung das Grundprinzip in ein bis zwei Sätzen zusammen und bringen Sie jeweils ein Beispiel.
- Preisdiskriminierung ersten Grades
- Preisdiskriminierung zweiten Grades: Staffelung
- Preisdiskriminierung zweiten Grades: Zwei-Komponenten-Tarif
- Preisdiskriminierung zweiten Grades: Bündelung
- Preisdiskriminierung dritten Grades nach Konsumentenmerkmalen
- Preisdiskriminierung dritten Grades nach Räumen
Lösungen
Übungsbeispiel 3.1
Um den gewinnmaximierenden Output und Preis zu bestimmen, geht der Monopolist wie gehabt vor, diesmal nach Ländern getrennt (indirekte Nachfragefunktion anschreiben, diese in Gewinnfunktion einsetzen, nach Menge ableiten, diese Funktion nullsetzen und für Menge auflösen, Menge in Preisfunktion einsetzen, Preis und Menge in Gewinnfunktion einsetzen:
Nachdem der Wiederverkäufer Einheiten des Gutes von einem Markt zu dem anderen um 4 GE pro Stück transportieren kann, kann dieser den Monopolisten in Land 2 um >4 GE unterbieten, d.h. . Dies zwingt den Monopolisten dazu, den Preis des Gutes in Markt 2 so zu reduzieren, dass es sich nicht lohnt, als unabhängiger Importeurer tätig zu werden. Rechnerisch ist der Gewinn in Land 2 damit gegeben als
Die für Land 2 produzierte Menge steigt damit auf 49 Stück, der Gewinn des Monopolisten sinkt in Land 2 sinkt von 1350 auf 1176, also um 174 GE.
Übungsbeispiel 3.2
Man beachte, dass die Preiselastizitäten beider Konsumentengruppen identisch sind:
Aus diesem Grund lohnt es sich nicht, Preisdiskriminierung zu betreiben und gesetzter Preis, produzierte Menge und erzielter Gewinn können nach dem üblichen Schema berechnet werden:
Führt man die Gewinnmaximierung des Produzenten für beide Gruppen getrennt durch, so ergibt sich und folglich dieselbe Gesamtmenge und derselbe Gewinn.
Übungsbeispiel 3.3
Es könnte darin liegen, dass die Zahlungsbereitschaft einer Konsumentengruppe daraus abgeleitet wird, wie viel Zeit sie auf den Kauf einer Speise zu verwenden bereit sind. Das Lokal könnte demnach von Konsumenten, die selbst abholen, einen niedrigeren Preis verlangen, als von solchen, die sie sich zustellen lassen. Der Preisunterschied könnte allerdings auch auf Kostenunterschiede hindeuten und muss demnach nicht Preisdiskriminierung darstellen, da die Zustellung Kosten verursacht. In der Praxis besteht Preisdiskriminierung also dann, wenn der Preisunterschied über den Transportkosten liegt.
Im Fall der Produkte, die in Outlet-Centern wie in Parndorf angeboten werden, ist anzunehmen, dass die Preisdifferenz zu anderen Läden größer ist als die niedrigeren Kosten in Parndorf, so sie überhaupt niedriger sind (Miete, Gehälter u.a.). Das gilt auch umgekehrt: Auf Flughäfen zahlt man üblicherweise höhere Preise für Güter wie Parfum, Spirituosen oder Schokoladen. Wem es die Zeitersparnis wert ist (der Grenzaufwand für den Konsumenten ist null, wenn er sich ohnehin am Flughafen aufhalten muss), der wird die höheren Preise am Flughafen buchstäblich in Kauf nehmen. (Die Bezeichnung „duty free“ ist innerhalb der EU irreführend.) Allerdings kann auch hier allein aus den Preisen nicht auf Preisdiskriminierung geschlossen werden, da es sein kann, dass die Kosten, insbes. die Miete, am Flughafen höher sind als anderswo.
Übungsbeispiel 3.4
Wenn beide Konsumenten optimalerweise bedient werden, so ist der höchste Pauschalbetrag, den der Monopolist setzen kann, wegen gleich der Konsumentenrente von Konsument 1.
wobei dem Reservationpreis entspricht, der sich aus der Nachfragefunktion bei ergibt und der tatsächlich gesetzte Preis ist. Dieser ergibt sich aus dem Üblichen Formulieren der Gewinnfunktion, diese abzuleiten und nullzusetzen:
und somit
Der optimale Pauschalbetrag ist also
Ist es optimal für den Monopolisten nur an Konsument 2 zu verkaufen, so ist sein Gesamtgewinn gegeben durch
daher
und somit
Daher ist der optimale Pauschalbetrag
…nach eigener Entscheidung…
Übungsbeispiel 3.5
Kurzbeschreibung nach Belieben, Beispiele für Preisdiskriminierung:
- Preisdiskriminierung ersten Grades: Raketenabwehrsystem, Flugzeugträger, …
- Preisdiskriminierung zweiten Grades: Staffelung: Kugeln Eis im Gassenverkauf
- Preisdiskriminierung zweiten Grades: Zwei-Komponenten-Tarif: Mietauto, wenn sich der Gesamtpreis aus einer pauschalen Mietgebühr sowie einer Gebühr pro gefahrenem Kilometer zusammensetzt.
- Preisdiskriminierung zweiten Grades: Bündelung: Tickets für die Fußballspiele der österreichischen Herren-Nationalmannschaft gegen Nordirland und Bosnien-Herzegowina im Herbst 2018 im Rahmen der Nations League konnten nur als Bündel erworben werden.
- Preisdiskriminierung dritten Grades nach Konsumentenmerkmalen: Tarife nach Geschlecht bei Frisören, Fußballspielen…
- Preisdiskriminierung dritten Grades nach Räumen: Die Praxis Volkswagens und anderer Autohersteller, in ihren Heimatmärkten höhere Preise zu verlangen. [7]
- ↑ vgl. Grundlagen der Volkswirtschaftslehre 2
- ↑ Auch wenn Ermäßigungen für Einheimische von der EU eigentlich verboten wurden, begegnet man ihnen dennoch bei praktisch jeder Touristenattraktion, indem man vergünstigte Eintrittskarten mit dem Besitz einer Karte verbindet, die üblicherweise nur Einheimische besitzen, bspw. Jahreskarten für die örtlichen öffentlichen Verkehrsmittel, Mitgliedskarten der inländischen Autofahrerklubs, die Club-Ö1-Karte usw.
- ↑ Allerdings stößt es bei Konsumenten nicht gerade auf Begeisterung, wenn sie mitbekommen, dass ein Produkt anderswo günstiger zu haben ist. Aus diesem Grund sah sich z.B. der deutsche Modekonzern Hugo Boss veranlasst, die Preise für Herrenanzüge global anzugleichen, nachdem chinesische Touristen regelmäßig feststellten, dass diese in gleicher Qualität in Mitteleuropa wesentlich günstiger waren als in ihrer Heimat (Handelsblatt, 2. August 2017).
- ↑ Man beachte, dass der Konsument nicht eine Person sein muss, sondern auch ein Unternehmen oder der Staat sein kann. Gerade wenn ein Produkt sehr differenziert, aus irgendeinem Grund sehr wichtig und die Stückzahl sehr niedrig ist, ist Preisdiskriminierung ersten Grades nicht unrealistisch, etwa bei bestimmten Rohstoffen oder Rüstungsgütern.
- ↑ In manchen Fällen ist eine Preisänderung bei dem Kauf höherer Stückzahlen durch niedrigere Stückkosten des Produzenten begründet (als Resultat von zum Beispiel hohen Fixkosten in der Produktion). In diesem Fall wäre ein niedrigerer Stückpreis bei steigender Menge nicht durch Preisdiskriminierung verursacht, sondern stellte lediglich die Weitergabe einer Kostenreduktion an den Konsumenten dar.
- ↑ Der Reservationspreis berechnet sich durch in der Nachfragefunktion, daraus folgt für Konsument 1 und für Konsument 2
- ↑ Siehe hierzu Der Spiegel 5/1998 oder Auto-Revue 2/2002; Volkswagen verbat damals seinen italienischen Händlern, an deutschsprachige Kunden zu verkaufen, weil diese eine höhere Zahlungsbereitschaft für die Marken Audi und VW zeigten, was vom Volkswagen-Konzern durch höhere Preise in Deutschland und Österreich ausgenützt wurde. Volkswagen musste schließlich eine Strafe von 90 Millionen Euro Strafe an die EU zahlen (Manager Magazin Online am 18. September 2003).