Number Theory

Number Theory and its Application to Cryptography, Combinatorics, Relations

For a comprehensive subject on number theory the reader is referred to the book [Hardy and Wright(1975)].

Elementary number theory

Prime factorisation

${\textstyle \mathrm {\ \ \ \ } }$ Fundamental theorem of arithmetic

Fundamental theorem of arithmetic - in number theory
Every integer ${\textstyle a>1}$ is either prime itself or the product of prime numbers, where this product is unique, up to the order of the factors. In other words

$$a=\prod _{i=1}^{n}p_{i}^{e_{i}}$$

where ${\textstyle p_{i}}$ is the ${\textstyle i}$-th prime number arising in the product generating ${\textstyle a}$ and ${\textstyle e_{i}}$ is its multiplicity.

${\textstyle \mathrm {\ \ \ \ } }$ Prime factorisation algorithm
The prime factorisation is an iterative algorithm to determine the prime factors of a given number. The algorithm is based on the Fundamental theorem of arithmetic. The prime factors are determined by performing iterative division by prime numbers in increasing order.
Example Prime factorisation of ${\textstyle 2520}$

$${\begin{aligned}2520|2&\\1260|2&\\630|2&\\315|3&\\105|3&\\35|5&\\7|7&\\1|\mathrm {\ } &\\\end{aligned}}$$

Prime factorisation is believed to be difficult to perform practically for large number since its time complexity is NP, i.e. superpolynomial (= not bounded above by any polynomial).

Congruence

${\textstyle \mathrm {\ \ \ \ } }$ Modulo operator

Definition - modulo operator
The ${\textstyle a\mod m=}$ the remainder after dividing ${\textstyle a}$ by ${\textstyle m}$.
It follows

$$a\mod m=r\equiv a=k*m+r,\mathrm {~where~} 0<=r<m.$$

Operator identities of modulo operator are given as

1. Distributivity - addition
   $$(a+b)\mod n=[(a\mod n)+(b\mod n)]\mod n$$
2. Distributivity - multiplication
   $$ab\mod n=[(a\mod n)*(b\mod n)]\mod n$$
3. Distributivity - power
   $$a^{c}\mod m=(a\mod m)^{c}\mod m$$

These identities can be proved directly from the definition of the modulo operator. Due to these three identities one can think in modular arithmetic including only addition, multiplication and power, like in regular integer arithmetic without modulo.

${\textstyle \mathrm {\ \ \ \ } }$ Greatest common divisor

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Divisability

Definition - divisability
${\textstyle n}$ is dividable by a if and only if there exists an integer ${\textstyle k}$ for which ${\textstyle n=a*k}$. This is denoted by ${\textstyle a|n}$. The number ${\textstyle a}$ is called the divisor of ${\textstyle n}$.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Greatest common divisor operator

Definition - greatest common divisor, gcd() operator The greatest common division of the integers ${\textstyle a}$ and ${\textstyle b}$, ${\textstyle gcd(a,b)}$ is defined by

$$gcd(a,b)=\max _{i}\{d_{i}\mathrm {~such~that~} d_{i}|a\mathrm {~and~} d_{i}|b\}.$$

An alternative notation of ${\textstyle gcd(a,b)}$ is ${\textstyle (a,b)}$.

The operator characteristics of the ${\textstyle gcd()}$ operator are given by

1. Reflexivity:
   $$(a,b)=(b,a).$$
2. ${\textstyle 0}$ is neutral element with respect to the operator ${\textstyle gcd()}$. In other words
   $$(a,0)=a.$$
3. The following relation holds
   $$(a,b)=(b,a\mod b).$$
   Proof.
   

${\textstyle (a,b)=d\Rightarrow a=de,b=df\mathrm {~and~} (e,f)=1}$.
Let ${\textstyle e=gf+h}$ be, where ${\textstyle h<f}$. It follows that ${\textstyle (f,h)=1}$, since otherwise ${\textstyle f}$ and due to expression of ${\textstyle e}$ also ${\textstyle e}$ were dividable by ${\textstyle (f,h)}$ which would lead to ${\textstyle (e,f)>1}$. Then ${\textstyle a=de=dgf+dh=gb+dh\Rightarrow a\mod b=dh\mod df=dh}$, where the last step comes from ${\textstyle h<f}$. Thus ${\textstyle (b,a\mod b)=(b,dh)=(df,dh)=d}$, due to ${\textstyle (f,h)=1}$.

${\textstyle \mathrm {\ \ \ \ } }$ Congruence

Definition - relatively prime (also called as coprime)
The integers ${\textstyle a}$ and ${\textstyle b}$ are relatively prime if and only if ${\textstyle (a,b)=1}$.
Definition - congruence
The congruence is a relation and refers to a base number ${\textstyle m}$. The integers ${\textstyle a}$ and ${\textstyle b}$ are in congruence relation if and only if ${\textstyle (a\mod m)=(b\mod m)}$ . The congruence id denoted by ${\textstyle a\equiv b\mod m}$.

Note that ${\textstyle a\equiv b\mod m}$ implies ${\textstyle m|(b-a)}$. Congruence is an equivalence relation - partitioning the set ${\textstyle \mathbb {Z} }$ to ${\textstyle m}$ disjunct subsets.

Being an equivalence relation, congruence have the following properties:

$${\begin{aligned}&\mathrm {CP1.~} \mathrm {~reflexivity~} a\equiv a\mod m\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {CP2.~} \mathrm {~symmetry~} a\equiv b\mod ~m\Rightarrow b\equiv a\mod m\\&\mathrm {CP3.~} \mathrm {~transitivity~} a\equiv b\mod m\mathrm {~and~} b\equiv c\mod m\Rightarrow a\equiv c\mod m\\\end{aligned}}$$

The operator identities of the congruence refer to given ${\textstyle a\equiv b\mod m}$ and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c \equiv d \mod m} and can be given as
CO1. Adding a constant Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \alpha}

$$a+\alpha \equiv b+\alpha \mod m.$$

CO2. Multiplication by constant ${\textstyle \alpha }$

$${\begin{aligned}&\alpha *a\equiv \alpha *b\mod m.\\&\Rightarrow -a\equiv -b\mod m.\end{aligned}}$$

CO3. Addition of congruences

$$a+c\equiv b+d\mod m.$$

CO4. Multiplication of congruences

$$a*c\equiv b*d\mod m.$$

CO5. Division by constant ${\textstyle \alpha }$

$$\alpha *a\equiv \alpha *b\mod m\Rightarrow a\equiv b\mod m.$$

The first three identities can be proved directly from the definitions of the modulo and congruence operators. The last identity follows from the general identity for division by constant:

$$\alpha *a\equiv \alpha *b\mod m\Leftrightarrow a\equiv b\mod (m/d),$$

where ${\textstyle (\alpha ,m)=d}$.
Proof:

$${\begin{aligned}&\alpha *a\equiv \alpha *b\mod m\Leftrightarrow m|[\alpha *(b-a)]\Leftrightarrow \\&[m/d]|[\alpha /d*(b-a)]\Leftrightarrow [m/d]|[(b-a)],\end{aligned}}$$

since ${\textstyle (m/d,\alpha /d)=1}$. Then ${\textstyle [m/d]|[(b-a)]\Leftrightarrow a\equiv b\mod (m/d)}$.

${\textstyle \mathrm {\ \ \ \ } }$ Congruence class

Definition - Congruence class modulo ${\textstyle m}$ (also called residue class modulo ${\textstyle m}$)
Congruence class modulo ${\textstyle m}$ is any of the disjunct subsets resulted by partitioning the set ${\textstyle \mathbb {Z} }$ by congruence as equivalence relation. In other words congruence class modulo ${\textstyle m}$ is a set ${\textstyle {k\in Z\mathrm {~such~that~} k\equiv a\mod m}}$ for any ${\textstyle a=0,\ldots ,(m-1)}$. For a specific ${\textstyle a}$ the congruence class modulo ${\textstyle m}$ is denoted by ${\textstyle a+m\mathbb {Z} }$.

The set of all congruence classes modulo ${\textstyle m}$ is denoted by ${\textstyle \mathbb {Z} /m\mathbb {Z} }$. Thus the number of elements in this set is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} , and this set can be given as

$$\mathbb {Z} /m\mathbb {Z} =\{0+m\mathbb {Z} ,1+m\mathbb {Z} ,...,(m-1)+m\mathbb {Z} \}.$$

The set of congruence classes relative prime to ${\textstyle m}$ is denoted by ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$. For any ${\textstyle a}$ representing an element of ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$ holds ${\textstyle (a,m)=1}$.
Example

$$(\mathbb {Z} /10\mathbb {Z} )^{*}=\{1+10\mathbb {Z} ,3+10\mathbb {Z} ,7+10\mathbb {Z} ,9+10\mathbb {Z} \}.$$

If m is prime then number of elements in ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$ = Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} .

Diophantic equations

Euclidean algorithm

The Euclidean algorithm is the standard way of solving the equation of the form

$$ax+by=(a,b),$$

where ${\textstyle a,b,x,y\in \mathbb {Z} }$

${\textstyle \mathrm {\ \ \ \ } }$ Theoretic basics

Bézout’s identity
The greatest common divisor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} of two integers ${\textstyle a}$ and ${\textstyle b}$ can be represented as a linear sum of the original two numbers ${\textstyle a}$ and ${\textstyle b}$. In other words

$$\exists x,y\in \mathbb {Z} ,\mathrm {~for~which~} g=(a,b)=ax+by.$$

Theorem
The set of all integer linear combinations of the nonzero integer ${\textstyle a}$ and ${\textstyle b}$ equals the set of integer muliples of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (a,b)} , i.e:

$$a\mathbb {Z} +b\mathbb {Z} =(a,b)\mathbb {Z} ,$$

Proof:

• Step 1: direction ${\textstyle \Rightarrow }$ ${\textstyle a\mathbb {Z} +b\mathbb {Z} \in (a,b)\mathbb {Z} }$ - follows from definition of ${\textstyle (a,b)}$
• Step 2: direction ${\textstyle \Leftarrow }$ ${\textstyle (a,b)\mathbb {Z} \in a\mathbb {Z} +b\mathbb {Z} }$ - follows from Bézout’s identity ${\textstyle (a,b)=ax+by,\mathrm {~where~} x,y\in \mathbb {Z} \Rightarrow (a,b)\mathbb {Z} =ax\mathbb {Z} +by\mathbb {Z} }$

Corollary 1
The equation

$$ax+by=n,\mathrm {~where~} a,b,x,y,n\in \mathbb {Z} \mathrm {~and~} a\neq 0,b\neq 0$$

has a solution if and only if ${\textstyle (a,b)|n}$.
Proof: It follows directly from the above theorem.
Notes:

• Case 1: If ${\textstyle (a,b)=1}$ then the equation has always a solution.
• Case 2: If ${\textstyle (a,b)=d\neq 1}$ then this case can be fallbacked to Case 1:
  $${\begin{aligned}&a=de,b=df\mathrm {~and~} (e,f)=1~(\mathrm {otherwise~} (a,b)>d)\\&dex+dfy=dg,\mathrm {~then~dividing~by~} d\\&ex+fy=g,\mathrm {~where~} (e,f)=1.\end{aligned}}$$

Corollary 2
The equation Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ax+by = (a,b), \mathrm{~where~} a,b,x,y \in \mathbb{Z}\mathrm{~and~}a\neq0, b\neq0} has always a solution.
Proof: It follows directly from Corollary 1.

${\textstyle \mathrm {\ \ \ \ } }$ Solution of equation ${\textstyle ax+by=(a,b)}$

The solution of the equation

$$ax+by=(a,b)$$

consists of two steps as

1. determination of ${\textstyle (a,b)}$ - by means of base variant of Euclidean algorithms and
2. determination of ${\textstyle x}$ and ${\textstyle y}$ - by means of the extended variant of the algorithm.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Euclidean algorithm - base variant

The idea of the base variant of Euclidean algorithms is the recursive application of ${\textstyle (a,b)=(b,a\mod b)}$ until ${\textstyle (h,0)=h}$.
Example - determination of ${\textstyle (a,b)}$:

$${\begin{aligned}&455x+135y=(455,135)\\&\\&455=3*135+50\\&135=2*50+35\\&50=1*35+15\\&35=2*15+5\\&15=3*5+0\\&\\&\Rightarrow (455,135)=5\\\end{aligned}}$$

The Pseudo code of determination gcd(a,b) (as well as storing the coefficients q[i]-s) by means of the base variant of the Euclidean algorithm can be given as

$${\begin{aligned}&h=a;\mathrm {~the~higher~value~} \\&s=b\mathrm {~the~smaller~value~} \\&i=0;\\&while(s>0)\mathrm {~until~} s\mathrm {~reaches~} 0\\&\{\\&\mathrm {\ \ } q[i++]=h\div s;\\&\mathrm {\ \ } t=s;\\&\mathrm {\ \ } s=h\%s;\mathrm {~next~} s\\&\mathrm {\ \ } h=t;\mathrm {~next~} h\\&\}\\&n=i-1;\\&gcd=h;\\\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Euclidean algorithm - extended variant

The extended Euclidean algorithm is used to determine the unknowns ${\textstyle x}$ and ${\textstyle y}$ after carrying out the base variant of the Euclidean algorithm. This is a necessary previous step, since the extended Euclidean algorithm uses the quotient and remainders computed in the course of executing the steps of the base variant of Euclidean algorithms. The idea of extended Euclidean algorithm is a recursive application of backward substitution based on the steps of the base variant of Euclidean algorithms. This is shown in the next example.
Example - determination of ${\textstyle x}$ and ${\textstyle y}$:

$${\begin{aligned}&455x+135y=5\\&\\&\mathrm {~Starting~with~last~but~one~line~of~the~solution~by~the~base~variant~we~get~} \\5&=35-2*15=\\&=35-2*(50-1*35)=-2*50+3*35=\\&=-2*50+3*(135-2*50)=3*135-8*50=\\&=3*135-8*(455-3*135)=-8*455+27*135&\\&\Rightarrow x=-8,y=27\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ \ \ } }$ The time complexity

The time complexity of both the base and extended variant of Euclidean algorithm is ${\textstyle O((\log h)^{2})}$, where ${\textstyle h}$ is the number of digits in the smaller number among ${\textstyle a}$ and ${\textstyle b}$.

Fermat–Euler theorem and little Fermat theorem)

${\textstyle \mathrm {\ \ \ \ } }$ Euler’s phi function

Definition - ${\textstyle \phi (n)}$
Euler’s phi function, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \phi(n)} , also called as Euler’s totient function, is defined as the number of integers ${\textstyle k}$ in the range ${\textstyle 1\leq k\leq n}$, for which ${\textstyle k}$ and ${\textstyle n}$ are relatively primes. In other words

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi(n) = |{1<=k<=n \mathrm{~such~that~} (k,n)=1}|,} where ${\textstyle |A|}$ stands for the cardinality of the set ${\textstyle A}$. Note that ${\textstyle \phi (n)}$ never includes ${\textstyle n}$, since${\textstyle (n,n)=n\neq 1}$.

$$\Rightarrow \phi (n)<=n-1.$$

Example - Computation of ${\textstyle \phi (10)}$

$${\begin{aligned}&\{{1<=k<=10\mathrm {~such~that~} (k,10)=1}\}=\{1,3,7,9\}\\&\Rightarrow \phi (10)=|{1,3,7,9}|=4.\end{aligned}}$$

The properties of ${\textstyle \phi (n)}$ can be given as

1. If p is prime then ${\textstyle \phi (p)=p-1}$.
2. If (m,n)=1 then ${\textstyle \phi (m*n)=\phi (m)*\phi (n)}$.
3. If p and q are prime then ${\textstyle \phi (p*q)=(p-1)*(q-1)}$
   

Proof. This property follows from properties 2. and 1.

1. In general ${\textstyle \phi (n)}$ can be expressed by the prime factorisation of ${\textstyle n}$ as ${\textstyle \phi (n)=n*\prod _{i=1}^{k}(1-1/p_{i})}$, where ${\textstyle n=\prod _{i=1}^{k}p_{i}^{e_{i}}}$.

The order of congruence classes relative prime to ${\textstyle m}$, ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$ is exactly Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \phi(m)} . If m prime then this order is ${\textstyle m-1}$.

${\textstyle \mathrm {\ \ \ \ } }$ Fermat–Euler theorem

Fermat–Euler theorem - also called as Euler’s theorem.
If ${\textstyle a}$ and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} are relatively prime then

$$a^{\phi (n)}\equiv 1\mod n.$$

${\textstyle \mathrm {\ \ \ \ } }$ Fermat’s little theorem

Fermat’s little theorem - If ${\textstyle n}$ is prime and ${\textstyle a}$ and ${\textstyle n}$ are relatively prime then

$$a^{p-1}\equiv 1\mod n.$$

Fermat’s little theorem is a special case Fermat–Euler theorem for the case where ${\textstyle n}$ is prime.

Modular multiplicative inverse and its computation

${\textstyle \mathrm {\ \ \ \ } }$ Residue systems modulo ${\textstyle m}$
Definition - Complete system of residues modulo m
The complete system of residues modulo ${\textstyle m}$ is any set of ${\textstyle m}$ integers so that each element comes from a different congruence class modulo ${\textstyle m}$.
Definition - Least residue system modulo Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m}
Least residue system modulo ${\textstyle m}$ is the set 0,1,..., m-1.
Definition - Reduced residue system modulo ${\textstyle m}$
Reduced residue system modulo ${\textstyle m}$ is a set obtained from complete system of residues modulo ${\textstyle m}$ by deleting all elements being not coprime with ${\textstyle m}$.

${\textstyle \mathrm {\ \ \ \ } }$ Modular multiplicative inverse of an integer

Definition - Modular multiplicative inverse of an integer ${\textstyle a}$
The modular multiplicative inverse of an integer ${\textstyle a}$, is the integer x that is given by

$$ax\equiv 1\mod m.$$

Observe, that not every elements of a complete system of residues modulo ${\textstyle m}$ has modular multiplicative inverse !
Theorem
An integer ${\textstyle a}$ element of complete system of residues modulo ${\textstyle m}$ has modular multiplicative inverse if and only if ${\textstyle a}$ and ${\textstyle m}$ are relatively prime, in other words if ${\textstyle (a,m)=1}$.
Proof:

$${\begin{aligned}&ax\equiv 1\mod m\Leftrightarrow ax+bm=1\\&\mathrm {~The~equation~} ax+my=1\mathrm {~has~solution~if~and~only~if~} (a,m)=1.\end{aligned}}$$

The modular multiplicative inverse of integer ${\textstyle a}$ is denoted by ${\textstyle a^{-1}}$. This can be explained by dividing the relation the relation ${\textstyle ax\equiv 1\mod m}$ formally by ${\textstyle a}$. With this notation holds the relation

$$a^{-1}\equiv x\mod m\Leftrightarrow ax\equiv 1\mod m.$$

If exists, the modular multiplicative inverse of an integer ${\textstyle a}$ is determined uniquely
Corollary
If ${\textstyle m}$ is prime then each of the elements ${\textstyle {1,...,m-1}}$ of the least residue system modulo ${\textstyle m}$ has modular multiplicative inverse.
Proof: Each element of ${\textstyle {1,...,m-1}}$ and ${\textstyle m}$ are relatively primes.

${\textstyle \mathrm {\ \ \ \ } }$ Computation of the modular multiplicative inverse

The modular multiplicative inverse of an integer ${\textstyle a\mod m,(a,m)=1}$ can be computed on the following ways.

• Computation way 1. - by using the extended Euclidean algorithm

  $$ax\equiv 1\mod m\Leftrightarrow ax+bm=1.$$

  Due to ${\textstyle (a,m)=1}$ the equation ${\textstyle ax+bm=1}$ has solution. ${\textstyle \Rightarrow }$ Solving the equation ${\textstyle ax+bm=1}$ by the extended Euclidean algorithm, ${\textstyle x}$ gives the modular multiplicative inverse of an integer ${\textstyle a\mod m}$.

• Computation way 2. - by means of efficient computation of raising an integer to a higher power, using a formula based on Euler’s theorem

  $$a^{\phi (n)-1}*a\equiv 1\mod n\Rightarrow a^{-1}\equiv a^{\phi (n)-1}\mod n$$
  ${\textstyle \Rightarrow }$ The the modular multiplicative inverse of an integer ${\textstyle a\mod m}$ are given by Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a^{\phi(n)-1} \mod n} , which can be determined by efficient computation of a modular multiplicative inverse - by using exponentiation by squaring.

${\textstyle \mathrm {\ \ \ \ } }$ Modular exponentiation by squaring

Modular exponentiation is raising an integer to a higher power modulo ${\textstyle n}$, in other words computing ${\textstyle g^{e}\mod n}$. Exponentiation by squaring is an efficient computation of modular exponentiation. The idea of exponentiation by squaring is to compute ${\textstyle g^{e}\mod n}$ by the help of successive squares of ${\textstyle g}$. This can be implemented as follows.

• Rearrange ${\textstyle g^{e}}$ by using the binary representation of ${\textstyle e}$
  $$g^{e}=g^{(\sum _{i=0}^{k}e_{i}*2^{i})}=\prod _{i=0}^{k}g^{e_{i}*2^{i}}.$$
  ${\textstyle \Rightarrow }$ Only those terms of the product must be computed, for which ${\textstyle e_{i}=1}$, since for ${\textstyle e_{i}=0}$ the term ${\textstyle g^{e_{i}*2^{i}}}$ becomes ${\textstyle g^{0*2^{i}}=1}$. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow} The terms with ${\textstyle e_{i}=1}$ becomes powers of ${\textstyle g}$ as ${\textstyle g^{2^{i}}}$.
• Computation of the powers ${\textstyle g^{2^{i}}}$ successively by applying
  $$g^{2^{l+1}}=(g^{2^{l}})^{2}\mathrm {~for~} l>=0$$
• Computate each term with mod ${\textstyle n}$.

Example - Exponentiation by squaring

$${\begin{aligned}&3^{52}\mod 100\\&\\&52=110100=2^{2}+2^{4}+2^{5}\\&3^{(2^{0})}=3\\&3^{(2^{1})}=3^{2}=9\\&3^{(2^{2})}=9^{2}=81\\&3^{(2^{3})}=81^{2}\mod 100=61\\&3^{(2^{4})}=61^{2}\mod 100=21\\&3^{(2^{5})}=21^{2}\mod 100=41\\&\\&3^{52}\mod 100=81*21*41\mod 100=41.\end{aligned}}$$

${\textstyle \Rightarrow }$ Conclude that instead of 52 multiplications only 5 squaring and 3 multiplications were needed.

Discrete logarithm

${\textstyle \mathrm {\ \ \ \ } }$ Primitive root modulo m

Definition - primitive root modulo ${\textstyle m}$
The number Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} is primitive root modulo ${\textstyle m}$ if for every integer ${\textstyle a}$ being coprime to ${\textstyle m}$ (i.e. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (a,m)=1} ) there is an integer ${\textstyle k}$ for which ${\textstyle g^{k}\equiv a\mod n}$.
Interpretation
All elements of the set of congruence classes coprime to ${\textstyle n}$, ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$ can be generated by power of ${\textstyle g}$ modulo ${\textstyle m}$. Therefore

• ${\textstyle g}$ is also called as generator of the set of congruence classes coprime to ${\textstyle m}$ and
• ${\textstyle g}$ must be coprime to ${\textstyle m}$.

Definition - Multiplicative order of primitive root modulo Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m}
The multiplicative order of primitive root modulo ${\textstyle m}$ is the lowest power of a which is congruent to ${\textstyle 1}$ modulo ${\textstyle m}$.
Statement The multiplicative order of primitive root modulo ${\textstyle m}$ is ${\textstyle \phi (m)}$.

This is because

• this power of a is congruent to ${\textstyle 1}$ modulo ${\textstyle n}$, since ${\textstyle a^{\phi (m)}\equiv 1\mod n}$ due to Euler’s theorem and
• this is the lowest power as the other lower powers are needed to generate the other elements of the set ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$.

It follows that if ${\textstyle m}$ is prime then the multiplicative order ${\textstyle \phi (m)=m-1}$.

Note that not all elements of ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$ are primitive root modulo m ! However the non-primitive root modulo ${\textstyle m}$ elements are cyclic generator of a subset of ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$. The non-primitive root elements of ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$ have also multiplicative order, which is can be however less then ${\textstyle \phi (m)}$.
Example - ${\textstyle m=7}$ prime

$${\begin{aligned}&(\mathbb {Z} /7\mathbb {Z} )^{*}-\mathrm {~least~residue~system~modulo~} 7={0,1,...,6}\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {~~The~elements~} 3\mathrm {~and~} 4\mathrm {~are~primitive~root~modulo~} m.\\&\mathrm {~~For~example~the~element~} 2\mathrm {~is~not~primitive~root~modulo~} m!\\&\mathrm {~~} \Rightarrow \mathrm {~~Multiplicative~order~of~} 2\mathrm {~is~} 3<\phi (7)=6,\mathrm {~since~} 2^{3}\equiv 1\mod 7.\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ } }$ Discrete logarithm to the base ${\textstyle g}$ modulo Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m}
Definition - Discrete logarithm (also called index)
Discrete logarithm, also called index When ${\textstyle a=g^{k}\equiv a\mod m}$ then the ${\textstyle k}$ is called as discrete logarithm of the integer ${\textstyle a}$ to the base ${\textstyle g}$ modulo ${\textstyle m}$. Here ${\textstyle g}$ is primitive root modulo ${\textstyle m}$, and ${\textstyle a}$ is an element of ${\textstyle (\mathbb {Z} /m\mathbb {Z} )^{*}}$, i.e. ${\textstyle a}$ coprime to ${\textstyle m}$.

The practical importance of the discrete logarithm lies in its property that computation of discrete logarithm is believed to be difficult to perform, especially for some specific groups.

Application to cryptography

${\textstyle \mathrm {\ \ \ \ } }$ RSA cryptography

RSA is a cryptosystem, called after its developers: Rivest, Shamir and Adleman. The principle of the key generation can be described by means of the following steps.

• Step 1. Select large primes ${\textstyle p}$ and ${\textstyle q}$, e.g. each of them with size ${\textstyle 512}$ bits.
• Step 2. Compute ${\textstyle n=p*q}$
• Step 3. Compute Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \phi(n)= (p-1)*(q-1)}
• Step 4. Select a random integer ${\textstyle 1<e<\phi (n)}$, such that ${\textstyle e}$ is coprime to ${\textstyle \phi (n)}$
• Step 5. Determine an integer ${\textstyle 1<d<\phi (n)}$, such that ${\textstyle e*d\mod \phi (n)=1}$, i.e. ${\textstyle d}$ is modular multiplicative inverse of ${\textstyle e}$.
  

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow} The integer ${\textstyle d}$ can be computed

• • either by using the extended Euclidean algorithm
  • or by the help of Euler’s theorem and using exponentiation by squaring.

The keys are called as

• private key = d
• public keys = e, n

Secret parameters of the key generation: ${\textstyle p,q,\phi (n)}$.

The usage of RSA for encryption can be explained as

• Notation: ${\textstyle m}$ = message, ${\textstyle c}$ = chipertext - both in form natural numbers
• Condition: ${\textstyle m<n}$ - needed for the correct decryption, see below.
• The encryption end decryption processes
  • The encryption
    $$c=m^{e}\mod n,$$
  • The decryption
    $$m'=c^{d}\mod n$$

The correctness of the RSA cryptographic algorithm can be shows by showing

$$m'=m$$

Proof: Using the way of generation of ${\textstyle d}$ we have

$$e*d\mod \phi (n)=1\Rightarrow e*d=1+k*\phi (n)$$

By using it, the decrypted chipertext ${\textstyle m'}$ can be rearranged as

$${\begin{aligned}m'&=c^{d}\mod n=(m^{e})^{d}\mod n=m^{e*d}\mod n=m^{1+k*\phi (n)}\mod n=\\&=[(m^{1}\mod n)*((m^{\phi (n)})^{k}\mod n)]\mod n=\\&\mathrm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \uparrow \mathrm {~condition~} m<n\\&=[m*((m^{\phi (n)}\mod n)^{k})\mod n]\mod n=\\&\mathrm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \uparrow \mathrm {~Euler's~theorem~} \\&=(m*1)\mod n=m\\&\mathrm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \uparrow \mathrm {~condition~} m<n.\end{aligned}}$$

Note, that proof of correctness is also possible by using Fermat’s little theorem utilizing the fact that ${\textstyle n=p*q}$, i.e. multiplication of two primes.

RSA can be used both for

• encryption and
• authentication,

in both cases including key distribution. Proof of correctness for using RSA for authentication can be shown similar to that one provided for the case of using it for encryption.

The secrecy of RSA is based on the computational difficulty of prime factorization.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow} If n could be factorized on efficient way then the secrecy of RSA would be broken !!

${\textstyle \mathrm {\ \ \ \ } }$ Diffie–Hellman key exchange

Diffie–Hellman key exchange is a protocol for secure key distribution. The principle of the solution is to generate the common secret key without exchanging the key itself. This is achieved on the way that each party shares only a partial info on the key to be generated.

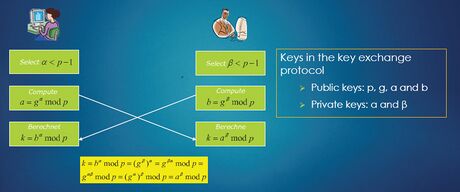
The Diffie-Hellman key establishment protocol can be described by the following steps.

• Step 1. The parties A and B agree on a prime ${\textstyle p}$ and a natural number ${\textstyle 1<g<p}$, which is a primitive root modulo ${\textstyle p}$.
• Step 2. Each party selects a secret number ${\textstyle \alpha <p-1}$ and ${\textstyle \beta <p-1}$, and computes the power ${\textstyle a=g^{\alpha }\mod p}$ and ${\textstyle b=g^{\beta }\mod p}$, respectively.
• Step 3. Each party sends ${\textstyle a}$ and ${\textstyle b}$ to the other party.
• Each party computes the common secret key Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k} based on the received numbers ${\textstyle a}$ and ${\textstyle b}$ as ${\textstyle k=a^{\beta }\mod p}$ and ${\textstyle k=b^{\alpha }\mod p}$.

Keys arising in the key exchange protocol are classified as

• Public keys: ${\textstyle p,g,a}$ and ${\textstyle b}$
• Private keys: ${\textstyle \alpha }$ and ${\textstyle \beta }$

The operation way of the Diffie-Hellman key exchange protocol is shown in Figure 1.

Figure 1: Diffie-Hellman key exchange protocol

The equality of the keys generated on the different sides can be shown as follows.

$${\begin{aligned}a^{\beta }\mod p&=(g^{\alpha })^{\beta }\mod p=g^{\alpha *\beta }\mod p=\\&=(g^{\beta })^{\alpha }\mod p=b^{\alpha }\mod p\\\end{aligned}}$$

The secrecy of Diffie-Hellman key exchange protocol is based on the computational difficulty of the discrete logarithms, more precisely on determining ${\textstyle \alpha }$ from ${\textstyle a=g^{\alpha }\mod p}$ or ${\textstyle \beta }$ from ${\textstyle b=g^{\beta }\mod p}$ in the knowledge of ${\textstyle g}$ and ${\textstyle a}$ or ${\textstyle b}$ and ${\textstyle p}$.

Combinatorics

For an introduction to basics of combinatorics see Permutation and Combination.

Relations

For an introduction and overview on mathematical relations see Relation.