Linear Algebra and Algorithms

Linear Algebra and Algorithms

For a comprehensive subject on linear algebra the reader is referred to the book [Lang(1987)].

Linear Algebra

Basic terms and definitions

A vector is a one-dimensional array of scalars, i.e. real or complex numbers. We will denote a vector by lowercase bold letters, like e.g. ${\textstyle {\bf {v}}}$. In linear algebra two forms of vectors are distinguished: row vector and column vector. For example

$$\left({\begin{array}{llllll}2&1&4&5&3\end{array}}\right)$$

is a row vector and

$$\left({\begin{array}{l}2\\1\\5\end{array}}\right)$$

is a column vector.

An ${\textstyle n\times m}$ matrix is a two-dimensional array of scalars having ${\textstyle n}$ rows an ${\textstyle m}$ columns. The scalar elements of matrix can be real or complex numbers. We consider only real matrices, i.e. matrices with real elements. Matrices will be denoted by uppercase bold letters. For example matrix ${\textstyle {\bf {F}}}$

$${\bf {F}}=\left({\begin{array}{llll}2&3&6&1\\1&4&10&5\\4&8&2&4\end{array}}\right)$$

is a ${\textstyle 3\times 4}$ matrix. Matrices can be seen as generalization of vectors, and thus vectors as special cases of matrices, where either the number of columns or rows is one. So the ${\textstyle n}$-element row vector is an ${\textstyle 1\times n}$ matrix and the ${\textstyle n}$-element column vector is an ${\textstyle n\times 1}$ matrix.

A square matrix has the same number of rows and columns, i.e. is of type ${\textstyle n\times n}$, and ${\textstyle n}$ is called as the order of the square matrix. An example of a ${\textstyle 3\times 3}$ square matrix ${\textstyle {\bf {S}}}$ is given below.

$${\bf {S}}=\left({\begin{array}{lll}1&1&3\\7&2&10\\4&5&3\end{array}}\right)$$

A diagonal matrix is a special square matrix, in which only the diagonal elements can differ from ${\textstyle 0}$. An example for the diagonal matrix ${\textstyle {\bf {D}}}$ is given as

$${\bf {D}}=\left({\begin{array}{llll}3&0&0&0\\0&4&0&0\\0&0&0&0\\0&0&0&4\end{array}}\right)$$

The diagonal matrix can be given also by means of a diag() operation by listing only the diagonal elements of the matrix as its arguments. For example the diagonal matrix ${\textstyle {\bf {D}}}$ can be given on such a way as

$${\bf {D}}=diag(3,4,0,4).$$

The element in the ${\textstyle i}$-th row and ${\textstyle j}$-th column of a matrix is referred as the ${\textstyle (i,j)}$-th element of that matrix and is denoted by ${\textstyle {\bf {A}}_{i,j}}$. It is usual to construct a matrix by the help of the group operator ${\textstyle [\ ]\ }$ . If ${\textstyle a_{ij}}$ denotes a defining formula of double indexed scalars for some range of indices ${\textstyle i}$ and ${\textstyle j}$ then matrix ${\textstyle {\bf {A}}}$ can be given by

$${\bf {A}}=[\ a_{ij}]\,$$

which means matrix ${\textstyle {\bf {A}}}$ is composed as grouping the scalars ${\textstyle a_{ij}}$ by two dimensions, where ${\textstyle i}$ describes the row index and ${\textstyle j}$ the column index. Therefore the ${\textstyle (i,j)}$-th element of matrix ${\textstyle {\bf {A}}}$ is set to ${\textstyle a_{ij}}$ for every values of ${\textstyle i}$ and ${\textstyle j}$ in their given ranges. For example if the double indexed scalars ${\textstyle z_{ij}}$ are defined as

$$z_{ij}=\left\{{\begin{aligned}1,\mathrm {\ \ } \mathrm {~if~} i==j~~\\0,\mathrm {\ \ } \mathrm {~otherwise~} \end{aligned}}\right\}~i,j=1,2,3.$$

then defining matrix ${\textstyle {\bf {I}}}$ as

$${\bf {I}}=[\ z_{ij}]\$$

leads to

$${\bf {I}}=\left({\begin{array}{lll}1&0&0\\0&1&0\\0&0&1\end{array}}\right).$$

Matrix ${\textstyle {\bf {I}}}$ is called ${\textstyle 3\times 3}$ identity matrix. The ${\textstyle n\times n}$ identity matrix for any ${\textstyle n\in \mathbb {N} ^{+}}$ is characterized by having the value ${\textstyle 1}$ in its every diagonal positions and all its other elements are ${\textstyle 0}$. Therefore the identity matrix is a special diagonal matrix. Let ${\textstyle {\bf {e}}_{\bf {i}}}$ stands for the column vector having the value ${\textstyle 1}$ on its ${\textstyle i}$-th position, while its every other elements are ${\textstyle 0}$. In an ${\textstyle n}$-dimensional Euclidean space the ${\textstyle n\times 1}$ vector ${\textstyle {\bf {e}}_{\bf {i}}}$ for ${\textstyle i=1,\ldots ,n}$ represents the unit vector in the ${\textstyle i}$-th dimension. For example for ${\textstyle n=3}$ the unit vectors ${\textstyle {\bf {e}}_{\bf {i}}}$ are given as

$${\begin{aligned}&{\bf {e}}_{\bf {1}}=\left({\begin{array}{l}1\\0\\0\end{array}}\right)\\&{\bf {e}}_{\bf {2}}=\left({\begin{array}{l}0\\1\\0\end{array}}\right)\\&{\bf {e}}_{\bf {3}}=\left({\begin{array}{l}0\\0\\1\end{array}}\right)\end{aligned}}$$

Then the ${\textstyle 3\times 3}$ identity matrix can be also expressed as row vector of the unit vectors as

$${\bf {I}}=\left({\begin{array}{lll}{\bf {e}}_{\bf {1}}&{\bf {e}}_{\bf {2}}&{\bf {e}}_{\bf {3}}\end{array}}\right).$$

Elementary matrix operations

An elementary univariate operation on matrices is the transpose operation. The transpose of matrix ${\textstyle {\bf {A}}}$ is defined by exchanging its ${\textstyle (i,j)}$-th element by its ${\textstyle (j,i)}$-th element for each pair of ${\textstyle i}$ and ${\textstyle j}$ in their given ranges. The transpose of a matrix is called transposed matrix and transpose of a given matrix ${\textstyle {\bf {A}}}$ is denoted by ${\textstyle {\bf {A}}^{T}}$. For example the transpose of the above defined matrix ${\textstyle {\bf {F}}}$ is given by

$${\bf {F}}^{T}=\left({\begin{array}{llll}2&1&4\\3&4&8\\6&10&2\\1&5&4\end{array}}\right)$$

The transpose of the ${\textstyle n\times m}$ matrix is an ${\textstyle m\times n}$ matrix and thus the transpose operation changes the dimensionality of the matrix for ${\textstyle n\neq m}$. The transpose of square matrix remains a square matrix. The transpose of the ${\textstyle 1\times n}$ row matrix is an ${\textstyle n\times 1}$ column matrix and vice versa.

The multiplication of matrix by a scalar is defined elementwise, i.e.by multiplying each element of the matrix by the given scalar. For example matrix ${\textstyle {\bf {F}}}$ multiplied by ${\textstyle c=3}$ gives

$$c{\bf {F}}=3\left({\begin{array}{llll}2&3&6&1\\1&4&10&5\\4&8&2&4\end{array}}\right)=\left({\begin{array}{llll}6&9&18&3\\3&12&30&15\\12&24&6&12\end{array}}\right)$$

Two matrix can be added if they are of same type, i.e. both are ${\textstyle n\times m}$. Similarly a matrix can be substracted form another one if they are of same type. For example if ${\textstyle 3\times 4}$ matrix ${\textstyle {\bf {G}}}$ is given as

$${\bf {G}}=\left({\begin{array}{llll}7&-2&5&-4\\2&3&-1&3\\-4&1&4&2\end{array}}\right)$$

then the matrix ${\textstyle {\bf {T}}}$ as the sum ${\textstyle {\bf {G}}+{\bf {F}}}$ are given by

$${\begin{aligned}{\bf {T}}={\bf {G}}+{\bf {F}}&=\left({\begin{array}{llll}7&-2&5&-4\\2&3&-1&3\\-4&1&4&2\end{array}}\right)+\left({\begin{array}{llll}2&3&6&1\\1&4&10&5\\4&8&2&4\end{array}}\right)\\&=\left({\begin{array}{llll}9&1&11&-3\\3&7&9&8\\0&9&6&6\end{array}}\right)\end{aligned}}$$

Two matrix can be multiplied if the number of columns of the first matrix and the number of rows of the second one are the same. The multiplication of the ${\textstyle n\times m}$ matrix ${\textstyle {\bf {A}}}$ by the ${\textstyle m\times k}$ matrix ${\textstyle {\bf {B}}}$, gives an ${\textstyle n\times k}$ times product matrix ${\textstyle {\bf {P}}}$. Let the ${\textstyle i,j}$-th, ${\textstyle j,k}$-th and ${\textstyle i,k}$-th elements of matrix ${\textstyle {\bf {A}}}$, ${\textstyle {\bf {B}}}$ and ${\textstyle {\bf {P}}}$ be ${\textstyle a_{ij}}$, ${\textstyle b_{jk}}$ and ${\textstyle p_{ik}}$, respectively. Then the matrix multiplication

$${\bf {P}}={\bf {A}}{\bf {B}}$$

is defined by the elements of ${\textstyle {\bf {A}}}$, ${\textstyle {\bf {B}}}$ and ${\textstyle {\bf {P}}}$ as

$$p_{ik}=\sum _{j=1}^{m}a_{ij}b_{jk}~~\mathrm {~for~} i=1,\ldots ,n,~~k=1,\ldots ,k.$$

Hence the ${\textstyle (i,k)}$-th element of the product matrix ${\textstyle {\bf {P}}}$ is the (scalar) product of the ${\textstyle i}$-th row of matrix ${\textstyle {\bf {A}}}$ and the ${\textstyle k}$-th column of matrix ${\textstyle {\bf {B}}}$ both consisting of ${\textstyle m}$ elements. In order to illustrate the matrix multiplication we define the ${\textstyle 4\times 3}$ times matrix ${\textstyle {\bf {H}}}$ as

$${\bf {H}}=\left({\begin{array}{llll}1&-2&3\\-1&1&2\\3&1&0\\5&3&2\end{array}}\right).$$

Then the matrix product ${\textstyle {\bf {F}}{\bf {H}}}$ results in a ${\textstyle 3\times 3}$ times matrix ${\textstyle T}$, which is given by

$${\begin{aligned}{\bf {R}}={\bf {F}}{\bf {H}}&=\left({\begin{array}{llll}2&3&6&1\\1&4&10&5\\4&8&2&4\end{array}}\right)\left({\begin{array}{llll}1&-2&3\\-1&1&2\\3&1&0\\5&3&2\end{array}}\right)\\&=\left({\begin{array}{lll}22&8&14\\52&27&21\\22&14&36\end{array}}\right)\end{aligned}}$$

Let ${\textstyle {\bf {e}}}$ stands for the column vector having every element set to value ${\textstyle 1}$. It is called unit vector. Multiplying a matrix from right by ${\textstyle {\bf {e}}}$ gives the row sums of that matrix in a column vector form. For example

$${\begin{aligned}{\bf {H}}{\bf {e}}=\left({\begin{array}{llll}1&-2&3\\-1&1&2\\3&1&0\\5&3&2\end{array}}\right)\left({\begin{array}{l}1\\1\\1\end{array}}\right)=\left({\begin{array}{l}2\\2\\4\\10\end{array}}\right)\end{aligned}}$$

gives the row sum of matrix ${\textstyle {\bf {H}}}$.

The addition of matrices is commutative and associative, i.e. the following relations hold for any ${\textstyle n\times m}$ matrices ${\textstyle {\bf {A}}}$, ${\textstyle {\bf {B}}}$ and ${\textstyle {\bf {C}}}$:

$${\begin{aligned}&\mathrm {O1.~} {\bf {A}}+{\bf {B}}={\bf {B}}+{\bf {A}},~~~~~~~~~~~~~~~~~~\mathrm {~commutativity~of~} +\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {O2.~} {\bf {A}}+\left({\bf {B}}+{\bf {C}}\right)=\left({\bf {A}}+{\bf {B}}\right)+{\bf {C}}~~\mathrm {~associativity~of~} +\end{aligned}}$$

The matrix multiplication is distributive with respect to the matrix addition and matrix multiplication is associative, i.e. the following relations hold for any ${\textstyle n\times m}$ matrix ${\textstyle {\bf {A}}}$, ${\textstyle m\times k}$ matrices ${\textstyle {\bf {B}}}$ and ${\textstyle {\bf {D}}}$ and ${\textstyle k\times l}$ matrix ${\textstyle {\bf {C}}}$:

$${\begin{aligned}&\mathrm {O3.~} {\bf {A}}\left({\bf {B}}+{\bf {D}}\right)={\bf {A}}{\bf {B}}+{\bf {A}}{\bf {D}},~~\mathrm {~distributivity~of~} *\mathrm {~with~respect~to~} +\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {O4.~} {\bf {A}}\left({\bf {B}}{\bf {C}}\right)=\left({\bf {A}}{\bf {B}}\right){\bf {C}}~~~~~~~~~~~\mathrm {~associativity~of~} *\end{aligned}}$$

However matrix multiplication is in general, except from some special cases, NOT commutative, i.e. for ${\textstyle n\times n}$ matrices ${\textstyle {\bf {A}}}$ and ${\textstyle {\bf {B}}}$

$$\mathrm {O5.~} {\bf {A}}{\bf {B}}\neq {\bf {B}}{\bf {A}}\mathrm {~in~general~} \mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} .$$

Therefore multiplication/product of matrix ${\textstyle {\bf {A}}}$ and ${\textstyle {\bf {B}}}$ is not specified. Instead one should speak about multiplying matrix ${\textstyle {\bf {A}}}$ by ${\textstyle {\bf {B}}}$ from right (by default) or from left.

The special classes of matrices, for which commutativity holds includes

• multiplication by identity matrix ${\textstyle {\bf {I}}}$: ${\textstyle {\bf {A}}{\bf {I}}={\bf {I}}{\bf {A}}}$,
• multiplication of diagonal matrices ${\textstyle {\bf {D}}_{\bf {1}}}$ and ${\textstyle {\bf {D}}_{\bf {2}}}$ with each other: ${\textstyle {\bf {D}}_{\bf {1}}{\bf {D}}_{\bf {2}}={\bf {D}}_{\bf {2}}{\bf {D}}_{\bf {1}}}$,
• multiplication of two powers of the same matrix ${\textstyle {\bf {A}}}$: ${\textstyle {\bf {A}}^{n}{\bf {A}}^{m}={\bf {A}}^{m}{\bf {A}}^{n}}$ and
• multiplication of two polynomials of the same matrix ${\textstyle {\bf {A}}}$, ${\textstyle P_{1}({\bf {A}})}$ and ${\textstyle P_{2}({\bf {A}})}$: ${\textstyle P_{1}({\bf {A}})P_{2}({\bf {A}})=P_{2}({\bf {A}})P_{1}({\bf {A}})}$, which follows from the commutativity of two powers of the same matrix by repetitive application of distributivity of the matrix multiplication.

Further useful relations are

$${\begin{aligned}&\left({\bf {A}}+{\bf {B}}\right)^{T}={\bf {A}}^{T}+{\bf {B}}^{T}\\&\left({\bf {A}}{\bf {B}}\right)^{T}={\bf {B}}^{T}{\bf {A}}^{T}.\end{aligned}}$$

The major difference of the elementary matrix operations comparing to their scalar counterparts is that matrix multiplication is not commutative in general. This has far-reaching consequences for the matrix theory.

Linear independence of vectors

The expression

$$c_{1}{\bf {v}}_{\bf {1}}+\ldots c_{n}{\bf {v}}_{\bf {n}}$$

is called as a linear combination of the vectors ${\textstyle {\bf {v}}_{\bf {1}},\ldots ,{\bf {v}}_{\bf {n}}}$ and the scalars ${\textstyle c_{1},\ldots ,c_{n}}$ are weights. Linear, since the used operations ${\textstyle +}$ and constant multiplication are linear.

For example each vector ${\textstyle {\bf {w}}}$ pointing to a point in the ${\textstyle 3}$-dimensional Euclidean space can be given as a linear combinations of the vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {e}}_{\bf {3}}}$ as

$${\bf {w}}=x{\bf {e}}_{\bf {1}}+y{\bf {e}}_{\bf {2}}+z{\bf {e}}_{\bf {3}}$$

We say that the vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {e}}_{\bf {3}}}$ span the ${\textstyle 3}$-dimensional Euclidean space and hence generate the whole ${\textstyle 3}$-dimensional space. There are infinite many other vector combinations, which span the ${\textstyle 3}$-dimensional Euclidean space, the vector are not necessarily be perpendicular to each other, like e.g. ${\textstyle {\bf {v}}_{\bf {1}}=(1,2,3)}$, ${\textstyle {\bf {v}}_{\bf {2}}=(-1,1,2)}$ and ${\textstyle {\bf {v}}_{\bf {3}}=(0,0,1)}$.

However if we consider the vectors ${\textstyle {\bf {e}}_{\bf {1}}=(1,0,0)}$, ${\textstyle {\bf {e}}_{\bf {2}}=(0,1,0)}$ and ${\textstyle {\bf {v}}_{\bf {0}}=(2,3,0)}$ then we can only cover the vectors at the plane with ${\textstyle z=0}$ by the linear combinations of ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {v}}_{\bf {0}}}$. In this case we say that the vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {v}}_{\bf {0}}}$ generate (or span) only a (${\textstyle 2}$-dimensional) sub-space of the whole ${\textstyle 3}$-dimensional Euclidean space. This is because the 3rd vector ${\textstyle {\bf {v}}_{\bf {0}}}$ can be given as the linear combination of the other two as

$${\bf {v}}_{\bf {0}}=2{\bf {e}}_{\bf {1}}+3{\bf {e}}_{\bf {2}}.$$

This phenomena is characterised by saying that the vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {v}}_{\bf {0}}}$ are not linear independent of each other. In fact not only ${\textstyle {\bf {v}}_{\bf {0}}}$ can be given as linear combination of the other two, but any of the three vectors can be given as a linear combination of the other two. The vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {v}}_{\bf {0}}}$ are linear dependent.

However the ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {e}}_{\bf {3}}}$ behave on another way, none of them can be given as linear combination of the other two. We say the vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {e}}_{\bf {3}}}$ are linear independent. Among the vectors ${\textstyle {\bf {e}}_{\bf {1}}}$, ${\textstyle {\bf {e}}_{\bf {2}}}$ and ${\textstyle {\bf {v}}_{\bf {0}}}$ only any two of them are linear independent of each other.

It can be seen that a given ${\textstyle n}$ number of ${\textstyle n}$-dimensional vectors determine the whole ${\textstyle n}$-dimensional space if and only if they are linear independent. If they are linear dependent and only ${\textstyle k<n}$ of them are linear independent, then they generate (or span) only a ${\textstyle k}$-dimensional sub-space of the whole ${\textstyle n}$-dimensional space.

If the ${\textstyle n}$ vectors are collected in a matrix, for example each vector put in a different row of the matrix, then the maximum number number of linear independent row vectors of the matrix is called as the rank of that matrix. The vectors can be put also in the different columns of a matrix, in which case the the maximum number of linear independent column vectors of the matrix is the rank of that matrix. It can be seen that the maximum number of linear independent rows and the maximum number of linear independent columns of a matrix are the same, so each matrix has a unique rank. The rank of the matrix ${\textstyle {\bf {A}}}$ is denoted by ${\textstyle rank({\bf {A}})}$. Based on the above the rank of a matrix is the dimension of the subspace generated by its columns or rows as vectors.

It follows that the the statements below hold for the rank of a matrix.

• The rank of an ${\textstyle n\times m}$ matrix ${\textstyle {\bf {A}}}$ is at most the smaller of ${\textstyle n}$ and ${\textstyle m}$, in other words
  $$rank({\bf {A}})\leq \min(n,m).$$
• The rank of the ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$ is at most its order, in other words
  $$rank({\bf {A}})\leq n.$$

Determinant

The determinant is a scalar assigned to a square matrix. It depends on every elements of the matrix, hence determinant is a scalar function of the square matrix. The determinant of the ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ is denoted as ${\textstyle det({\bf {A}})}$ (or ${\textstyle det{\bf {A}}}$) and ${\textstyle |{\bf {A}}|}$.

${\textstyle \mathrm {\ \ \ \ } }$ Expression of determinant - Leibniz formula

The determinant is a sum of signed products, where each product is composed as a multiplication of elements taken from each row of the square matrix, each of them at different column positions and every such products are included in the sum. In other words the determinant of ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}=[\ a_{ij}]\ }$ is given by

$$det({\bf {A}})=\sum _{p}sgn(p)a_{1p(1)}\ldots a_{np(n)}=\sum _{p}sgn(p)\left(\prod _{i=1}^{n}a_{ip(i)}\right),$$

where ${\textstyle p=p(1)\ldots p(n)}$ is a permutation of the column indices ${\textstyle 1\ldots n}$ and the sign function ${\textstyle sgn(p)}$ assigns ${\textstyle +1}$ to a permutation ${\textstyle p}$ if it can be created by even number of exchanges of two numbers starting from ${\textstyle 1\ldots n}$ and otherwise it gives ${\textstyle -1}$. The number of products in the sum equals to the number of possible permutations, which is ${\textstyle n!}$. This expression of the determinant is called Leibniz formula.

${\textstyle \mathrm {\ \ \ \ } }$ Determinant of a ${\textstyle 2\times 2}$ matrix

Let the ${\textstyle 2\times 2}$ matrix ${\textstyle {\bf {A}}}$ given as

$${\bf {A}}=\left({\begin{array}{ll}a&b\\c&d\\\end{array}}\right).$$

For ${\textstyle n=2}$ there are only two permutations, therefore the expression of ${\textstyle det({\bf {A}})}$ can be given as

$$det({\bf {A}})=ad-bc.$$

${\textstyle \mathrm {\ \ \ \ } }$ Determinant of a ${\textstyle 3\times 3}$ matrix - Sarrus rule

Let the ${\textstyle 3\times 3}$ matrix ${\textstyle {\bf {A}}}$ given as ${\textstyle {\bf {A}}=[\ a_{ij}]\ }$, in other words

$${\bf {A}}=\left({\begin{array}{lll}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}}\right).$$

For ${\textstyle n=3}$ there are ${\textstyle 3!=6}$ permutations, three of them are encountered with sign ${\textstyle +}$ and the other three with ${\textstyle -}$. The expression of ${\textstyle det({\bf {A}})}$ can be given as

$${\begin{aligned}det({\bf {A}})&=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\&-a_{31}a_{22}a_{13}-a_{32}a_{23}a_{11}-a_{33}a_{21}a_{12}.\end{aligned}}$$

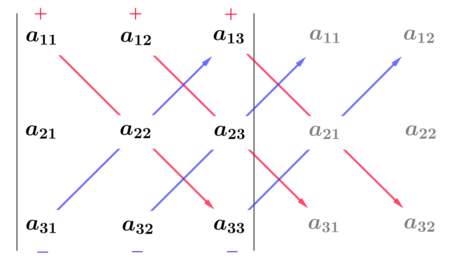
This expression can be easily memorized by the help of the Sarrus rule, see in Figure 12. Copying the first two columns of the matrix right to it, the products with positive sign can be obtained along the diagonals from top to down and right, while the products with negative sign are the ones from down to top and right.

Figure 12: Illustration of Sarrus rule for computing the determinant of $3 \times 3$ matrix (Source: By Kmhkmh - Own work, CC BY 4.0, \url{https://commons.wikimedia.org/w/index.php?curid=127614131})

Unfortunately the schema of Sarrus can not be generalized for higher dimensions.

${\textstyle \mathrm {\ \ \ \ } }$ Geometric interpretation

The columns of the ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ can be interpreted as vectors in the ${\textstyle n}$-dimensional Euclidean space. For ${\textstyle n=2}$ these vectors span a parallelogram, and the determinant is exactly the signed value of the area of this parallelogram. This is shown in Figure 13.

Figure 13: Geometric interpretation of determinant of 2D square matrix as area of parallelogram (Source: By TheWanderingTraders - This SVG diagram includes elements that have been taken or adapted from this diagram:, CC BY-SA 4.0, \url{https://commons.wikimedia.org/w/index.php?curid=158528546})

For ${\textstyle n=3}$ the column vectors of ${\textstyle {\bf {A}}}$, denoted by ${\textstyle {\bf {r}}_{1}}$, ${\textstyle {\bf {r}}_{2}}$ and ${\textstyle {\bf {r}}_{3}}$, form a parallelepiped and the determinant gives the signed volume of this parallelepiped, see in Figure 14.

Figure 14: Geometric interpretation of determinant of 3D square matrix as area of parallelepiped (By Claudio Rocchini - Own work, CC BY 3.0, \url{https://commons.wikimedia.org/w/index.php?curid=2788190})

This interpretation holds also for higher dimensions. So the column vectors of ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ span a parallelotope in the ${\textstyle n}$-dimensional space and the determinant of ${\textstyle {\bf {A}}}$ gives its signed ${\textstyle n}$-dimensional volume.

${\textstyle \mathrm {\ \ \ \ } }$ Properties of determinant

Determinant of several special matrices

• Determinant of identity matrix ${\textstyle {\bf {I}}}$ is ${\textstyle det({\bf {I}})=1}$.
• Determinant of diagonal matrix ${\textstyle {\bf {D}}=diag(d_{1},\ldots ,d_{n})}$ is ${\textstyle det({\bf {D}})=d_{1}\ldots d_{n}=\prod _{i=1}^{n}d_{i}}$.

The determinant of ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ has the following properties regarding row and column manipulations.

1. Multiplying matrix ${\textstyle {\bf {A}}}$ by constant ${\textstyle c}$ results in multiplication of the determinant by ${\textstyle c^{n}}$, in other words
   $$.$$
2. Multiplying any row or any column of ${\textstyle {\bf {A}}}$ by constant ${\textstyle c}$ leads to a multiplication of the determinant of ${\textstyle {\bf {A}}}$ by ${\textstyle c}$. In other words the determinant of the modified matrix is ${\textstyle c~det({\bf {A}})}$.
3. Exchanging two rows or two columns of ${\textstyle {\bf {A}}}$ leads to a multiplication of the determinant by ${\textstyle -1}$.
4. Adding a scalar multiplication of another row to a row of ${\textstyle {\bf {A}}}$ or adding a scalar multiplication of another column to a column of ${\textstyle {\bf {A}}}$ does not change the value of the determinant.

Further useful properties of the determinant are

$${\begin{aligned}&\mathrm {D1.~} det({\bf {A}}^{T})=det({\bf {A}})\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {D2.~} det(c{\bf {A}})=c^{n}det({\bf {A}})~~c\in \mathbb {R} \\&\mathrm {D3.~} det({\bf {A}}{\bf {B}})=det({\bf {A}})det({\bf {B}})\\\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ } }$ Laplace expansion

The minor ${\textstyle M_{i,j}}$ of of the ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}=[\ a_{ij}]\ }$ is defined as the determinant of the ${\textstyle (n-1)\times (n-1)}$ submatrix of ${\textstyle {\bf {A}}}$, which is obtained by omitting the ${\textstyle i}$-th row and ${\textstyle j}$-th column of the matrix ${\textstyle {\bf {A}}}$, for ${\textstyle i,j=1,\ldots ,n}$. The determinant of the matrix ${\textstyle {\bf {A}}}$ can be expressed by expanding it along its ${\textstyle i}$-th row. This gives a sum of signed product of each element of the ${\textstyle i}$-th row by its corresponding minor. In other words

$$det({\bf {A}})=\sum _{j=1}^{n}(-1)^{(i+j)}a_{ij}M_{i,j}.$$

This is called as Laplace expansion along the ${\textstyle i}$-th row of matrix ${\textstyle {\bf {A}}}$.

As an example we show the Laplace expansion of the ${\textstyle 3}$-dimensional square matrix ${\textstyle {\bf {A}}}$ with general notations along its 1st row, which leads to

$${\begin{aligned}det({\bf {A}})&=\left|\left({\begin{array}{lll}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}}\right)\right|\\&=a_{11}\left|\left({\begin{array}{lll}a_{22}&a_{23}\\a_{32}&a_{33}\end{array}}\right)\right|-a_{12}\left|\left({\begin{array}{lll}a_{21}&a_{23}\\a_{31}&a_{33}\end{array}}\right)\right|+a_{13}\left|\left({\begin{array}{lll}a_{21}&a_{22}\\a_{31}&a_{32}\end{array}}\right)\right|.\end{aligned}}$$

The Laplace expansion along the ${\textstyle j}$-th column of matrix ${\textstyle {\bf {A}}}$ can be also defined on similar way.

${\textstyle \mathrm {\ \ \ \ } }$ Determinant and linear independence

One of the most important use of the determinant is its relation to linear independence. The determinant of the ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ is non-zero if and only if the rows (and columns) of matrix ${\textstyle {\bf {A}}}$ are linear independent.

This can be seen e.g. by the help of the geometric interpretation of the determinant. If the column vectors of matrix ${\textstyle {\bf {A}}}$ are linear independent then they generate the whole ${\textstyle n}$-dimensional space and thus the ${\textstyle n}$-volume of the parallelotope spanned by them must be non-zero and therefore also the determinant is non-zero. However if the column vectors of matrix ${\textstyle {\bf {A}}}$ are linear dependent then ${\textstyle n}$ column vectors of matrix ${\textstyle {\bf {A}}}$ generate only a ${\textstyle k<n}$-dimensional subspace of the whole ${\textstyle n}$-dimensional space, which implies that the ${\textstyle n}$-volume of the parallelotope spanned by them must be zero and hence also the determinant is zero.

Inverse matrix

We consider the question whether a matrix does exist, which multiplied by the square matrix ${\textstyle {\bf {A}}}$ results in the identity matrix. It would be an analogue of the reciprocal number in the set of real (or complex) numbers. Immediately the following questions arise

• What is the condition of the existence of an such matrix ? Not every number has reciprocal also in the set of real numbers (i.e. the number zero).
• If such matrices exist for multiplying by ${\textstyle {\bf {A}}}$ both from left and right, then they are the same ?, This question is due to the general non-commutativity of the matrices.

${\textstyle \mathrm {\ \ \ \ } }$ The adjugate matrix

The adjugate matrix of the ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ is denoted by ${\textstyle adj({\bf {A}})}$, and it is defined as the transpose of the matrix of the signed minors. More precisely ${\textstyle adj({\bf {A}})}$ is given by its elements as

$$\left(adj({\bf {A}})\right)_{i,j}=(-1)^{(i+j)}M_{j,i}~~i,j=1,\ldots ,n.$$

The importance of the adjugate matrix lies in the following relation, which holds for every square matrix ${\textstyle {\bf {A}}}$:

$${\bf {A}}adj({\bf {A}})=adj({\bf {A}}){\bf {A}}=det({\bf {A}}){\bf {I}}.$$

${\textstyle \mathrm {\ \ \ \ } }$ The inverse matrix

The ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ is an invertable matrix if there exist a matrix, which is multiplied by ${\textstyle {\bf {A}}}$ from left gives the identity matrix and multiplied by ${\textstyle {\bf {A}}}$ from right also gives the identity matrix. This matrix is called the inverse matrix of ${\textstyle {\bf {A}}}$ and denoted by ${\textstyle {\bf {A}}^{-1}}$. Thus for the inverse matrix ${\textstyle {\bf {A}}^{-1}}$ holds the following defining relation:

$${\bf {A}}{\bf {A}}^{-1}={\bf {A}}^{-1}{\bf {A}}={\bf {I}}.$$

Dividing the above relation for ${\textstyle adj({\bf {A}})}$ by ${\textstyle det({\bf {A}})}$, it leads to expression of the inverse matrix ${\textstyle {\bf {A}}^{-}1}$ as

$${\bf {A}}^{-1}={\frac {adj({\bf {A}})}{det({\bf {A}})}}.$$

Since the adjugate matrix always exists, the inverse matrix ${\textstyle {\bf {A}}^{-}1}$ exists if and only the determinant of ${\textstyle {\bf {A}}}$ is non-zero. The square matrix which is not invertable is also called as singular matrix. Similarly the invertable matrix is also called as non-singular. Therefore

• The square matrix is singular if and only if its determinant is zero.
• The square matrix is non-singular if and only if its determinant is non-zero.

${\textstyle \mathrm {\ \ \ \ } }$ Inverse of a ${\textstyle 2\times 2}$ matrix

Let the ${\textstyle 2\times 2}$ matrix ${\textstyle {\bf {A}}}$ given as

$${\bf {A}}=\left({\begin{array}{ll}a&b\\c&d\\\end{array}}\right).$$

The determinant of ${\textstyle {\bf {A}}}$ can be given as ${\textstyle det({\bf {A}})=ad-bc}$ Due to ${\textstyle n=2}$ all the minors are scalars. Hence the inverse matrix ${\textstyle {\bf {A}}^{-1}}$ can be expressed as

$${\bf {A}}^{-1}={\frac {adj({\bf {A}})}{det({\bf {A}})}}={\frac {\left({\begin{array}{ll}d&-b\\-c&a\\\end{array}}\right)}{ad-bc}}$$

This can be checked by multiplying ${\textstyle {\bf {A}}}$ by ${\textstyle {\bf {A}}^{-1}}$

$${\bf {A}}{\bf {A}}^{-1}=\left({\begin{array}{ll}a&b\\c&d\\\end{array}}\right){\frac {\left({\begin{array}{ll}d&-b\\-c&a\\\end{array}}\right)}{ad-bc}}={\frac {\left({\begin{array}{ll}ad-bc&-ab+ab\\cd-cd&-cb+da\\\end{array}}\right)}{ad-bc}}=\left({\begin{array}{ll}1&0\\0&1\\\end{array}}\right)$$

which is ${\textstyle {\bf {I}}}$ as expected. It is easy to remember the nominator of the inverse of ${\textstyle 2\times 2}$ matrix: the values in the main diagonal (a and d) are exchanged and the values in the secondary diagonal (b and c) are multiplied by ${\textstyle (-1)}$.

${\textstyle \mathrm {\ \ \ \ } }$ Inverse of a ${\textstyle 3\times 3}$ matrix

Let the ${\textstyle 3\times 3}$ matrix ${\textstyle {\bf {A}}}$ given as ${\textstyle {\bf {A}}=[\ a_{ij}]\ }$, in other words

$${\bf {A}}=\left({\begin{array}{lll}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}}\right).$$

Due to ${\textstyle n=3}$ all the minors are determinants of ${\textstyle 2}$-dimensional matrix. Hence the inverse matrix ${\textstyle {\bf {A}}^{-}1}$ can be expressed as

$${\begin{aligned}{\bf {A}}^{-1}&={\frac {adj({\bf {A}})}{det({\bf {A}})}}={\frac {\left({\begin{array}{lll}M_{11}&-M_{21}&M_{31}\\-M_{12}&M_{22}&-M_{32}\\M_{13}&-M_{23}&M_{33}\end{array}}\right)}{det({\bf {A}})}}\\&={\frac {\left({\begin{array}{lll}\left|{\begin{array}{ll}a_{22}&a_{23}\\a_{32}&a_{33}\end{array}}\right|&-\left|{\begin{array}{ll}a_{12}&a_{13}\\a_{32}&a_{33}\end{array}}\right|&\left|{\begin{array}{ll}a_{12}&a_{13}\\a_{22}&a_{23}\end{array}}\right|\\-\left|{\begin{array}{ll}a_{21}&a_{23}\\a_{31}&a_{33}\end{array}}\right|&\left|{\begin{array}{ll}a_{11}&a_{13}\\a_{31}&a_{33}\end{array}}\right|&-\left|{\begin{array}{ll}a_{11}&a_{13}\\a_{21}&a_{23}\end{array}}\right|\\\left|{\begin{array}{ll}a_{21}&a_{22}\\a_{31}&a_{32}\end{array}}\right|&-\left|{\begin{array}{ll}a_{11}&a_{12}\\a_{31}&a_{32}\end{array}}\right|&\left|{\begin{array}{ll}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}}\right|\end{array}}\right)}{det({\bf {A}})}}\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ } }$ Properties of the inverse matrix

Inverse matrix of several special matrices

• Inverse matrix of identity matrix is itself. ${\textstyle {\bf {I}}}$ is ${\textstyle {\bf {I}}^{-1}={\bf {I}}}$.
• Inverse matrix of diagonal matrix is also diagonal.
  

${\textstyle {\bf {D}}=diag(d_{1},\ldots ,d_{n})}$, ${\textstyle d_{i}\neq 0}$ ${\textstyle i=1,\ldots ,n}$:
${\textstyle {\bf {D}}^{-1}=diag({\frac {1}{d_{1}}},\ldots ,{\frac {1}{d_{n}}})}$.

Further useful properties of the inverse matrix are

$${\begin{aligned}&\mathrm {I1.~} ({\bf {A}}^{-1})^{-1}={\bf {A}}\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {I2.~} ({\bf {A}}^{T})^{-1}=({\bf {A}}^{-1})^{T}\\&\mathrm {I3.~} (c{\bf {A}})^{-1}=c^{-1}{\bf {A}}^{-1}~~c\in \mathbb {R} \\&\mathrm {I4.~} ({\bf {A}}{\bf {B}})^{-1}={\bf {B}}^{-1}{\bf {A}}^{-1}\\&\mathrm {I5.~} det({\bf {A}}^{-1})=det({\bf {A}})^{-1}\end{aligned}}$$

Linear systems of equations

The linear system of equations consisting of ${\textstyle n}$ unknowns ${\textstyle x_{1},\ldots ,x_{n}}$ and ${\textstyle m}$ equations can be given as

$${\begin{aligned}&a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\&a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\&\vdots \\&a_{m1}x_{1}+a_{m2}x_{2}+\ldots +a_{mn}x_{n}=b_{m}.\end{aligned}}$$

This can be also called as ${\textstyle m\times n}$ linear system of equations. By introducing the ${\textstyle m\times n}$ matrix ${\textstyle {\bf {A}}}$ and the ${\textstyle n\times 1}$ column vector ${\textstyle {\bf {x}}}$ and the ${\textstyle m\times 1}$ column vector ${\textstyle {\bf {b}}}$ as

$${\bf {A}}=[\ a_{ij}]\,$$

$${\bf {x}}=\left({\begin{array}{l}x_{1}\\x_{2}\\\vdots \\x_{n}\\\end{array}}\right)$$

$${\bf {b}}=\left({\begin{array}{l}b_{1}\\b_{2}\\\vdots \\b_{m}\\\end{array}}\right)$$

the system of linear equations can be rewritten in matrix vector form as

$${\bf {A}}{\bf {x}}={\bf {b}}.$$

Here ${\textstyle {\bf {A}}}$ is the coefficient matrix, ${\textstyle {\bf {x}}}$ is a column vector of unknowns or unknown column vector and ${\textstyle {\bf {b}}}$ is given column vector.

${\textstyle \mathrm {\ \ \ \ } }$ Reformulation - linear combination of column vectors of matrix ${\textstyle {\bf {A}}}$

The above system of linear equations can be rewritten by the help of the group operator ${\textstyle [\ ]\ }$ on index ${\textstyle i}$ as

$$\ =[\ b_{i}]\,$$

where ${\textstyle [\ b_{i}]\ }$ is a vector ${\textstyle {\bf {b}}}$ due to the application of the group operator ${\textstyle [\ ]\ }$. The order of grouping on index ${\textstyle i}$ and summing can be exchanged on the left hand side of the equation, which gives

$$\sum _{j=1}^{n}[\ a_{ij}]\ x_{j}=[\ b_{i}]\,$$

Introducing the column vectors composed from the columns of ${\textstyle {\bf {A}}}$ as

$${\bf {a}}_{\bf {j}}=\left({\begin{array}{l}a_{1j}\\a_{2j}\\\vdots \\a_{nj}\\\end{array}}\right)~~j=1,\ldots ,n,$$

the relation can be further rearranged as

$$\sum _{j=1}^{n}{\bf {a}}_{\bf {j}}x_{j}={\bf {b}},$$

Based on this formulation, the problem of solving the above ${\textstyle m\times n}$ linear system of equations can be seen as finding the weights ${\textstyle x_{j}}$-s, ${\textstyle j=1,\ldots n}$ with which the given vector ${\textstyle {\bf {b}}}$ can be composed as the linear combination of the ${\textstyle m}$- dimensional vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$.

This interpretation enables to establish criteria for solvability for different cases of the ${\textstyle m\times n}$ linear system of equations depending on the relation between ${\textstyle n}$ and ${\textstyle m}$ as well as the linear independence of the vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$ and ${\textstyle {\bf {b}}}$.

${\textstyle \mathrm {\ \ \ \ } }$ Solvability - general case

The following statements follow from the above linear combination interpretation for the solvability of the ${\textstyle m\times n}$ linear system of equations.

1. The linear system of equations is solvable if and only if vector ${\textstyle {\bf {b}}}$ can be composed as linear combination of the vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$, in other words if the vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$ and vector ${\textstyle {\bf {b}}}$ are linear dependent. This means that adding vector ${\textstyle {\bf {b}}}$ to the set of vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$ does not increase the number of linear independent vectors in the set. This is equivalent to the statement that the extended matrix ${\textstyle {\bf {A}}^{*}}$ obtained as adding column vector ${\textstyle {\bf {b}}}$ as ${\textstyle (n+1)}$ column to matrix ${\textstyle {\bf {A}}}$, has the same rank as matrix ${\textstyle {\bf {A}}}$.
2. If ${\textstyle rank({\bf {A}}^{*})=rank({\bf {A}})}$ then two cases must be distinguished according to the relation between ${\textstyle rank({\bf {A}})}$ and ${\textstyle n}$.
   • If ${\textstyle rank({\bf {A}})=n}$ then the vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$ generate the ${\textstyle n}$-dimensional space, in which the weights of the ${\textstyle n}$-dimensional vector ${\textstyle {\bf {b}}}$ is unique, therefore the system has a unique solution. Note that in this case ${\textstyle m\geq n}$ must be, since ${\textstyle rank({\bf {A}})}$ can not be greater than ${\textstyle \min(m,n)}$.
   • If ${\textstyle k=rank({\bf {A}})<n}$ then the vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$ generate a ${\textstyle k}$-dimensional space, in which only ${\textstyle k<n}$ components of the the ${\textstyle n}$-dimensional vector ${\textstyle {\bf {b}}}$ can be composed by linear combination of the the vectors ${\textstyle {\bf {a}}_{\bf {j}}}$, ${\textstyle j=1,\ldots n}$. Therefore in this case ${\textstyle n-k}$ unknowns can be freely selected and the system has infinite many solutions. Note that in this case ${\textstyle m\geq rank({\bf {A}})}$, so it can be also smaller than ${\textstyle n}$.

The different cases of solvability and their criteria are summarized in Table 1.

Solvability criteria of ${\textstyle m\times n}$ linear system of equations

Rank criterion	General case	Special case
	${\textstyle {\bf {A}}{\bf {x}}={\bf {b}}}$	${\textstyle {\bf {A}}{\bf {x}}={\bf {0}}}$
		Homogeneous system
${\textstyle rank({\bf {A}}^{*})\neq rank({\bf {A}})}$	No solution	- Not possible -
${\textstyle rank({\bf {A}}^{*})=rank({\bf {A}})}$	Unique solution	Only trivial solution
and ${\textstyle rank({\bf {A}})=n}$		${\textstyle {\bf {x}}={\bf {0}}}$
${\textstyle rank({\bf {A}}^{*})=rank({\bf {A}})}$	Infinite many	Also non-trivial
and ${\textstyle rank({\bf {A}})<n}$	solutions	solutions,
	${\textstyle (n-rank({\bf {A}}))}$	infinite many
	unknowns can be	${\textstyle (n-rank({\bf {A}}))}$
	chosen freely	free parameters

${\textstyle \mathrm {\ \ \ \ } }$ Solvability - square matrix ${\textstyle {\bf {A}}}$

Several further findings can be obtained for the special case of ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$. If ${\textstyle rank({\bf {A}})=n}$ then matrix ${\textstyle {\bf {A}}}$ is non-singular and ${\textstyle det({\bf {A}})\neq 0}$. Otherwise matrix ${\textstyle {\bf {A}}}$ is singular and ${\textstyle det({\bf {A}})=0}$

Taking all these into account the solvability conditions for the square matrix ${\textstyle {\bf {A}}}$ can be summarized in a slightly simplified form, which is shown in Table 2.

Solvability criteria of ${\textstyle n\times n}$ linear system of equations

Rank criterion	Inhomogeneous system	Homogeneous system
	${\textstyle {\bf {A}}{\bf {x}}={\bf {b}}}$	${\textstyle {\bf {A}}{\bf {x}}={\bf {0}}}$
${\textstyle det({\bf {A}})\neq 0}$	Unique solution	Only trivial solution
(${\textstyle \Leftrightarrow }$ ${\textstyle rank({\bf {A}})=n}$)	${\textstyle {\bf {x}}={\bf {A}}^{-1}{\bf {b}}}$	${\textstyle {\bf {x}}={\bf {0}}}$
${\textstyle det({\bf {A}})=0}$	Infinite many	Also non-trivial
(${\textstyle \Leftrightarrow }$ ${\textstyle rank({\bf {A}})<n}$) and	solutions	solutions,
${\textstyle rank({\bf {A}}^{*})=rank({\bf {A}})}$	${\textstyle (n-rank({\bf {A}}))}$	infinite many
	unknowns can be	${\textstyle (n-rank({\bf {A}}))}$
	chosen freely	free parameters
${\textstyle det({\bf {A}})=0}$	No solution	- Not possible -
(${\textstyle \Leftrightarrow }$ ${\textstyle rank({\bf {A}})<n}$) and
${\textstyle rank({\bf {A}}^{*})\neq rank({\bf {A}})}$

Eigenvectors, eigenvalues, spectral decomposition

For a given ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$ finding the scalars ${\textstyle \lambda }$ and ${\textstyle n\times 1}$ column vectors ${\textstyle {\bf {u}}}$ satisfying the equation

$${\bf {A}}{\bf {u}}=\lambda {\bf {u}}$$

called as eigenvalue problem of matrix ${\textstyle {\bf {A}}}$. The scalars ${\textstyle \lambda }$ satisfying the equation are called eigenvalues of matrix ${\textstyle {\bf {A}}}$ and the vectors ${\textstyle {\bf {u}}}$ satisfying the equation are called eigenvectors of matrix ${\textstyle {\bf {A}}}$. Transforming an eigenvector by multiplying it by ${\textstyle {\bf {A}}}$ gives a vector ${\textstyle \lambda {\bf {u}}}$ being parallel to the considered eigenvector. Hence the transformation by ${\textstyle {\bf {A}}}$ does not change the direction of the eigenvectors and their length will be multiplied by the eigenvalue. This explains the names eigenvectors and eigenvalues.

${\textstyle \mathrm {\ \ \ \ } }$ Characteristic polynomial

Rearranging the above relation gives

$$\left({\bf {A}}-\lambda {\bf {I}}\right){\bf {u}}={\bf {0}}.$$

This is homogeneous system of linear equations, which has non-trivial solution only if the determinant of the coefficient matrix ${\textstyle \left({\bf {A}}-\lambda {\bf {I}}\right)}$ is zero, in other words, if

$$det\left({\bf {A}}-\lambda {\bf {I}}\right)=0.$$

Observe that ${\textstyle \lambda }$ arises in each element of the main diagonal of matrix ${\textstyle \left({\bf {A}}-\lambda {\bf {I}}\right)}$. It follows that the permutation giving the products of the main diagonal and therefore also the determinant of this matrix is an ${\textstyle n}$-order polynomial of ${\textstyle \lambda }$. This ${\textstyle n}$-order polynomial of ${\textstyle \lambda }$ is called the characteristic polynomial of matrix ${\textstyle {\bf {A}}}$. Its solutions give the eigenvalues. According to the fundamental theory of algebra, an ${\textstyle n}$-order polynomial has exactly ${\textstyle n}$ solutions in the set of complex numbers. It follows that there exist ${\textstyle n}$ complex eigenvalues implying at most ${\textstyle n}$ real eigenvalues, from which some of them can arise more times.

${\textstyle \mathrm {\ \ \ \ } }$ Algebraic multiplicity and geometric multiplicity

Let ${\textstyle \lambda _{i}}$, ${\textstyle i=1,\ldots ,s}$, ${\textstyle s\leq n}$ denote the eigenvalues of matrix ${\textstyle {\bf {A}}}$. The number of arising of the eigenvalue ${\textstyle \lambda _{i}}$ in the solution of the characteristic polynomial is called the algebraic multiplicity ${\textstyle \lambda _{i}}$. For each ${\textstyle \lambda _{i}}$ the homogeneous system

$$\left({\bf {A}}-\lambda _{i}{\bf {I}}\right){\bf {u}}={\bf {0}}.$$

determines the eigenvectors belonging to the eigenvalue ${\textstyle \lambda _{i}}$. Due to the homogeneous character of the system, its solution must have at least one free parameter. This is manifested in the fact that any constant multiplication of an eigenvector is also a solution of a system. Hence an eigenvector is determined only up to a constant multiplication, i.e. only the direction (in the ${\textstyle n}$-dimensional Euclidean system) of the eigenvector is determined, but its length not. The number of linearly independent eigenvectors belonging to the eigenvalue ${\textstyle \lambda _{i}}$ can be one or more depending on the rank of matrix ${\textstyle \left({\bf {A}}-\lambda _{i}{\bf {I}}\right)}$. In fact linearly independent eigenvectors belonging to the eigenvalue ${\textstyle \lambda _{i}}$ is the number of freely selectable parameter, which is ${\textstyle n-rank({\bf {A}}-\lambda _{i}{\bf {I}})}$, which is called the geometric multiplicity of ${\textstyle \lambda _{i}}$.

${\textstyle \mathrm {\ \ \ \ } }$ An example for determining eigenvalues an eigenvectors

Matrix ${\textstyle {\bf {A}}}$ is given as

$${\bf {A}}=\left({\begin{array}{ll}1-a&a\\b&1-b\end{array}}\right),~~a,b\geq 0.$$

1. Computing the eigenvalues of the matrix ${\textstyle {\bf {A}}}$
   

${\textstyle |\lambda {\bf {I}}-{\bf {A}}|=\left(\lambda -(1-a)\right)\left(\lambda -(1-b)\right)-ab=0}$
${\textstyle \lambda ^{2}-\lambda (1-a+1-b)+(1-a)(1-b)-ab=0}$
${\textstyle \lambda ^{2}-\lambda (2-a-b)+1-a-b=0}$

$${\begin{aligned}\lambda _{1,2}&={\frac {(2-a-b)\pm {\sqrt {(2-a-b)^{2}-4(1-a-b)}}}{2}}\\&={\frac {(2-a-b)\pm {\sqrt {4-4(a+b)+(a+b)^{2}-4+4(a+b)}}}{2}}\\&={\frac {(2-a-b)\pm (a+b)}{2}}\\&\Rightarrow ~~\lambda _{1}=1,~\mathrm {(since~the~matrix~} {\bf {A}}\mathrm {~stochastic~is,)~and} \\&~~~\lambda _{2}=1-a-b.\end{aligned}}$$

1. Determining the eigenvectors of the matrix ${\textstyle {\bf {A}}}$
   • The eigenvector belonging to ${\textstyle \lambda _{1}=1}$
     

${\textstyle ({\bf {A}}-{\bf {I}}){\bf {u}}_{\bf {1}}={\bf {0}}}$
${\textstyle \left({\begin{array}{ll}-a&a\\b&-b\end{array}}\right)\left({\begin{array}{l}u_{1}\\u_{2}\end{array}}\right)=\left({\begin{array}{l}0\\0\end{array}}\right)}$
${\textstyle -au_{1}+au_{2}=0}$
${\textstyle bu_{1}-bu_{2}=0}$
${\textstyle \Rightarrow }$  ${\textstyle {\bf {u}}_{\bf {1}}=\left({\begin{array}{l}1\\1\end{array}}\right)}$

1. • The eigenvector corresponding to ${\textstyle \lambda _{2}=1-a-b}$
     

${\textstyle ({\bf {A}}-(1-a-b){\bf {I}}){\bf {u}}_{\bf {2}}={\bf {0}}}$
${\textstyle \left({\begin{array}{ll}b&a\\b&a\end{array}}\right)\left({\begin{array}{l}u_{1}\\u_{2}\end{array}}\right)=\left({\begin{array}{l}0\\0\end{array}}\right)}$
${\textstyle bu_{1}+au_{2}=0}$
${\textstyle \Rightarrow }$  ${\textstyle {\bf {u}}_{\bf {2}}=\left({\begin{array}{l}1\\{\frac {-b}{a}}\end{array}}\right)}$    or    ${\textstyle {\bf {u}}_{\bf {2}}=\left({\begin{array}{l}a\\-b\end{array}}\right)}$,  since the eigenvectors are only determined up to a multiplicative constant.

${\textstyle \mathrm {\ \ \ \ } }$ Left and right eigenvalues and eigenvectors

So far we considered the form of the eigenvalue problem, in which the vector ${\textstyle {\bf {u}}}$ being a column vector and hence locates on the right side of matrix ${\textstyle {\bf {A}}}$. From this reason this eigenvalue problem is also called as right eigenvalue problem, and the ${\textstyle \lambda }$-s and ${\textstyle {\bf {u}}}$-s are also called as right eigenvalues and right eigenvectors of matrix ${\textstyle {\bf {A}}}$, respectively.

There is a similar eigenvalue problem, in which the vector ${\textstyle v}$ is a row vector and arises on the left hand side of the matrix ${\textstyle {\bf {A}}}$ as

$${\bf {v}}{\bf {A}}={\bf {v}}\lambda ,$$

and it called as left eigenvalue problem. The solution ${\textstyle \lambda }$-s and ${\textstyle {\bf {v}}}$-s are also called as left eigenvalues and left eigenvectors of matrix ${\textstyle {\bf {A}}}$, respectively.

The two kind of eigenvalue problem can be related by transposing them into each other. For example transposing the right eigenvalue problem gives

$${\bf {u}}^{T}{\bf {A}}^{T}={\bf {u}}^{T}\lambda .$$

This shows the relation between the two kind of eigenvalue problem, which can be formulated as follows. The right side eigenvalues and eigenvectors of square matrix ${\textstyle {\bf {A}}}$ are the left side eigenvalues and eigenvectors of the transpose of matrix ${\textstyle {\bf {A}}}$, respectively. It follows that for a symmetric matrix ${\textstyle {\bf {S}}}$ the right and the left side eigenvalues and eigenvectors are the same, respectively, due to ${\textstyle {\bf {S}}=}$S${\textstyle ^{T}}$.

${\textstyle \mathrm {\ \ \ \ } }$ Properties of eigenvalues

Let ${\textstyle \lambda ({\bf {A}})}$ and ${\textstyle \lambda ({\bf {A}})_{i}}$ stands for the eigenvalues and the ${\textstyle i}$-th eigenvalue, ${\textstyle i=1,\ldots ,n}$ of ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$, respectively. Useful properties of the eigenvalues are given as

$${\begin{aligned}&\mathrm {E1.~} \lambda (c{\bf {A}})=c\lambda ({\bf {A}})~~c\in \mathbb {R} \mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {E2.~} \lambda ({\bf {A}}^{-1})=\left(\lambda {\bf {A}}\right)^{-1}\\&\mathrm {E3.~} \prod _{i=1}^{n}\lambda ({\bf {A}})_{i}=det({\bf {A}})\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ } }$ Spectral decomposition

The spectral decomposition of ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$ is a factorization into the canonical form as

$${\bf {A}}={\bf {U}}{\bf {\Lambda }}{\bf {U}}^{-1},$$

where ${\textstyle {\bf {\Lambda }}}$ is a diagonal matrix. The spectral decomposition is also called eigendecomposition or diagonalisation.

The matrices arising in the factorization can be interpreted as follows. The diagonal elements of the diagonal matrix ${\textstyle {\bf {\Lambda }}}$ are the right eigenvalues of matrix ${\textstyle {\bf {A}}}$. Note that each eigenvalue arises in the diagonal as many times as its algebraic multiplicity. The column vectors of matrix ${\textstyle {\bf {U}}}$ are the right eigenvectors ${\textstyle {\bf {u}}_{\bf {k}}}$ belonging to the ${\textstyle \lambda _{k}}$ eigenvalues, ${\textstyle k=1,\ldots ,n}$. Thus ${\textstyle \lambda _{k}}$ and ${\textstyle {\bf {u}}_{\bf {k}}}$ satisfies

$${\bf {A}}{\bf {u}}_{\bf {k}}={\bf {u}}_{\bf {k}}\lambda _{k},~~k=1,\ldots ,n,$$

which can be arranged in matrix form as

$${\bf {A}}{\bf {U}}={\bf {U}}{\bf {\Lambda }}.$$

Note that the fact that ${\textstyle {\bf {u}}_{\bf {k}}}$ is determined only up to a constant, does not influence the canonical form of the spectral decomposition. This can be seen by replacing ${\textstyle {\bf {u}}_{\bf {k}}}$ by ${\textstyle c_{k}{\bf {u}}_{\bf {k}}}$, in matrix form ${\textstyle {\bf {U}}}$ by ${\textstyle {\bf {U}}{\bf {C}}}$ with ${\textstyle {\bf {C}}=diag(c_{1},\ldots ,c_{n}}$, in the canonical form, which leads to

$${\bf {U}}{\bf {C}}{\bf {\Lambda }}\left({\bf {U}}{\bf {C}}\right)^{-1}={\bf {U}}{\bf {C}}{\bf {\Lambda }}{\bf {C}}^{-1}{\bf {U}}^{-1}={\bf {U}}{\bf {C}}{\bf {C}}^{-1}{\bf {\Lambda }}{\bf {U}}^{-1}={\bf {U}}{\bf {\Lambda }}{\bf {U}}^{-1},$$

where we utilized the commutativity of the diagonal matrices ${\textstyle {\bf {\Lambda }}{\bf {C}}^{-1}}$.

${\textstyle \mathrm {\ \ \ \ } }$ An example for spectral decomposition

Continuing the the example for determining eigenvalues an eigenvectors of the matrix ${\textstyle {\bf {A}}}$

$${\bf {A}}=\left({\begin{array}{ll}1-a&a\\b&1-b\end{array}}\right),~~a,b\geq 0,$$

now we show the spectral decomposition of matrix ${\textstyle {\bf {A}}}$.

So far we have determined the right eigenvalues ${\textstyle \lambda _{1}=1}$ and ${\textstyle \lambda _{2}=1-a-b}$, and the right eigenvectors ${\textstyle {\bf {u}}_{\bf {1}}=\left({\begin{array}{l}1\\1\end{array}}\right)}$ and ${\textstyle {\bf {u}}_{\bf {2}}=\left({\begin{array}{l}a\\-b\end{array}}\right)}$ belonging to them.

1. Composition of diagonal matrix ${\textstyle \Lambda }$ The diagonal elements of matrix ${\textstyle \Lambda }$ are the eigenvalues ${\textstyle \lambda _{1}}$ and ${\textstyle \lambda _{2}}$. Thus matrix ${\textstyle \Lambda }$ is given by
   ${\textstyle \Lambda =\left({\begin{array}{ll}1&0\\0&1-a-b\end{array}}\right)}$

2. Composition of matrix ${\textstyle {\bf {U}}}$ The columns of matrix ${\textstyle {\bf {U}}}$ are the eigenvectors ${\textstyle {\bf {u}}_{\bf {1}}}$ and ${\textstyle {\bf {u}}_{\bf {2}}}$. Thus matrix ${\textstyle {\bf {U}}}$ is given as
   ${\textstyle {\bf {U}}=\left({\begin{array}{ll}1&a\\1&-b\end{array}}\right)}$

3. Determination of the inverse of matrix ${\textstyle {\bf {U}}}$
   ${\textstyle {\bf {U}}=\left({\begin{array}{ll}1&a\\1&-b\end{array}}\right)}$
   ${\textstyle \Rightarrow }$  ${\textstyle {\bf {U}}^{-1}={\frac {1}{\det {\bf {U}}}}\left({\begin{array}{ll}-b&-a\\-1&1\end{array}}\right)={\frac {1}{-(a+b)}}\left({\begin{array}{ll}-b&-a\\-1&1\end{array}}\right)=\left({\begin{array}{ll}{\frac {b}{a+b}}&{\frac {a}{a+b}}\\{\frac {1}{a+b}}&{\frac {-1}{a+b}}\end{array}}\right)}$

4. The spectral decomposition of matrix ${\textstyle {\bf {A}}}$

   ${\textstyle {\bf {A}}=\left({\begin{array}{ll}1&a\\1&-b\end{array}}\right)\left({\begin{array}{ll}1&0\\0&1-a-b\end{array}}\right)\left({\begin{array}{ll}{\frac {b}{a+b}}&{\frac {a}{a+b}}\\{\frac {1}{a+b}}&{\frac {-1}{a+b}}\end{array}}\right)}$

${\textstyle \mathrm {\ \ \ \ } }$ Conditions for the existence of spectral decomposition

Note that not every square matrix is diagonalisable. Two useful conditions for ${\textstyle n\times n}$ matrix ${\textstyle {\bf {A}}}$ to be diagonalisable can be given as

1. The spectral decomposition of matrix ${\textstyle {\bf {A}}}$ exists if and only if the number of linearly independent right eigenvectors of ${\textstyle {\bf {A}}}$ equals to ${\textstyle n}$.
2. A sufficient condition for the existence of spectral decomposition of matrix ${\textstyle {\bf {A}}}$ is that its characteristic polynomial has no repeated roots.

Based on the first condition, the canonical form of the spectral decomposition can be derived. The column vectors of ${\textstyle {\bf {U}}}$ are linear independent, so it is non-singular and hence exists the inverse matrix ${\textstyle {\bf {U}}^{-1}}$. Multiplying the matrix form relation ${\textstyle {\bf {A}}{\bf {U}}={\bf {U}}{\bf {\Lambda }}}$ by ${\textstyle {\bf {U}}^{-1}}$ from right gives

$${\bf {A}}{\bf {U}}{\bf {U}}^{-1}={\bf {U}}{\bf {\Lambda }}{\bf {U}}^{-1},$$

from which ${\textstyle {\bf {U}}{\bf {U}}^{-1}={\bf {I}}}$ falls out resulting the canonical form of the spectral decomposition.

${\textstyle \mathrm {\ \ \ \ } }$ Application of spectral decomposition

Spectral decomposition is used im many area of the natural sciences. Below we list several typical example for using spectral decomposition.

1. Calculating a power of matrix ${\textstyle {\bf {A}}}$
   $${\bf {A}}^{k}=\left({\bf {U}}{\bf {\Lambda }}{\bf {U}}^{-1}\right)^{k}={\bf {U}}{\bf {\Lambda }}^{k}{\bf {U}}^{-1},~~k\in \mathbb {N^{+}} .$$
2. Expressing the inverse of matrix ${\textstyle {\bf {A}}}$
   $${\bf {A}}^{-1}={\bf {U}}{\bf {\Lambda }}^{-1}{\bf {U}}^{-1},~~\mathrm {~which~can~be~obtained~by~taking~inverse~of~canonical~form~} .$$
   Such expression of the inverse of matrix ${\textstyle {\bf {A}}}$ exists if and only if ${\textstyle \lambda _{i}\neq 0}$ for every ${\textstyle i=1,\ldots ,n}$.
3. Expressing matrix function ${\textstyle f({\bf {A}})}$ of matrix ${\textstyle {\bf {A}}}$.
   

Here ${\textstyle f({\bf {A}})}$ defined by the help of power series of f()

$${\begin{aligned}f({\bf {A}})={\bf {U}}f({\bf {\Lambda }}){\bf {U}}^{-1},~~&\mathrm {~which~can~be~shown~by~using~power~series~form~of~} f({\bf {A}})\\&\mathrm {~and~above~relation~for~} {\bf {A}}^{k}.\end{aligned}}$$

1. Showing the convergence of ${\textstyle \sum _{n}^{\infty }{\bf {A}}^{n}}$
   $${\begin{aligned}\sum _{n}^{\infty }{\bf {A}}^{n},~~&\mathrm {~convergent~is,~when~} |\lambda _{i}|<1,\mathrm {~for~} i=1,\ldots ,n.\end{aligned}}$$

Matrix norms

Eigenvalues can be considered to be a set of numbers characterizing the magnitude of a square matrix. Often the eigenvalue with the highest magnitude has outstanding importance. Besides of it, there is a need for characterising the magnitude of a square matrix only by one number, analogously to the absolute value of a real or complex number.

The matrix norm is a measure characterizing the magnitude of a square matrix by one number. The matrix norm is denoted by ${\textstyle \left\|~~\right\|}$, e.g. the norm of the square matrix ${\textstyle {\bf {A}}}$ is ${\textstyle \left\|{\bf {A}}\right\|}$.

${\textstyle \mathrm {\ \ \ \ } }$ Definition of several matrix norms

On the contrary to the uniqueness of the absolute value, more matrix norms can be defined. Let ${\textstyle a_{ij}}$ be the ${\textstyle i,j}$-th element of the ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$. Then several martix norms can be given as

1. Max norm
   $$\left\|{\bf {A}}\right\|=n\max _{i,j}|a_{ij}|.$$
   Note that there is another, similar norm which is also called as max norm.
2. Max row sum
   $$\left\|{\bf {A}}\right\|=\max _{i}\sum _{j}|a_{ij}|.$$
3. ${\textstyle L1}$ norm
   $$\left\|{\bf {A}}\right\|=\sum _{i}\sum _{j}|a_{ij}|.$$

${\textstyle \mathrm {\ \ \ \ } }$ General properties of matrix norms

Matrix norms are useful tools e.g. in theoretical derivations, like e.g. to prove the existence of an upper limit. In fact in most of the cases the concrete form of the matrix norm is not interesting. Instead some properties of the matrix norm are utilized. These important general properties of matrix norm are listed for ${\textstyle n\times n}$ square matrices ${\textstyle {\bf {A}}}$ and ${\textstyle {\bf {B}}}$ as

$${\begin{aligned}&\mathrm {N1.~} \left\|{\bf {A}}\right\|\geq 0.\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\&\mathrm {N2.~} \left\|c{\bf {A}}\right\|=c\left\|{\bf {A}}\right\|~~~~c\in \mathbb {R} .\\&\mathrm {N3.~} \left\|{\bf {A}}\right\|+\left\|{\bf {B}}\right\|\geq \left\|{\bf {A}}+{\bf {B}}\right\|\mathrm {~-~triangle~inequality~} .\\&\mathrm {N4.~} \left\|{\bf {0}}\right\|=0.\end{aligned}}$$

Useful matrix norms also have the following additional property

$${\begin{aligned}&\mathrm {N5.~} \left\|{\bf {A}}{\bf {B}}\right\|\leq \left\|{\bf {A}}\right\|\left\|{\bf {B}}\right\|\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} .\end{aligned}}$$

.

All the three above defined matrix norms have this additional property. Let ${\textstyle a_{ij}}$ and ${\textstyle b_{jk}}$ be the ${\textstyle i,j}$-th and ${\textstyle j,k}$-th element of the ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$ and ${\textstyle {\bf {B}}}$, respectively . Then the additional property can be shown for these matrix norms as follows.

1. Max norm
   $${\begin{aligned}\left\|{\bf {A}}|{\bf {B}}\right\|&=n\max _{i,k}|\sum _{j}a_{ij}b_{jk}|\leq n\max _{i,k}\sum _{j}|a_{ij}||b_{jk}|\\&\leq n^{2}\max _{i,j}|a_{ij}|\max _{j,k}|b_{jk}|=n\max _{i,j}|a_{ij}|n\max _{j,k}|b_{jk}|=\left\|{\bf {A}}\right\|\left\|{\bf {B}}\right\|.\end{aligned}}$$
2. Max row sum
   $${\begin{aligned}\left\|{\bf {A}}|{\bf {B}}\right\|&=\max _{i}\sum _{k}|\sum _{j}a_{ij}b_{jk}|\leq \max _{i}\sum _{j}|a_{ij}|\sum _{k}|b_{jk}|\\&\leq \max _{i}\sum _{j}|a_{ij}|\left(\max _{j}\sum _{k}|b_{jk}|\right)=\left\|{\bf {A}}\right\|\left\|{\bf {B}}\right\|.\end{aligned}}$$
3. ${\textstyle L1}$ norm
   $${\begin{aligned}\left\|{\bf {A}}|{\bf {B}}\right\|&==\sum _{i}\sum _{k}|\sum _{j}a_{ij}b_{jk}|\leq \sum _{i}\sum _{k}\sum _{j}|a_{ij}||b_{jk}|\\&=\sum _{i}\sum _{j}|a_{ij}|\sum _{k}|b_{jk}|\leq \sum _{i}\sum _{j}|a_{ij}|\left\|{\bf {B}}\right\|=\left\|{\bf {A}}\right\|\left\|{\bf {B}}\right\|.\end{aligned}}$$

Several typical applications of matrix norms are given below.

• To show that a norm of a matrix expression is upper limited.
• To show that ${\textstyle \lim _{n\rightarrow \infty }{\bf {A}}^{n}={\bf {0}}}$, when ${\textstyle \left\|{\bf {A}}\right\|<1}$.
• To show that ${\textstyle \sum _{n=0}^{\infty }{\bf {A}}^{n}}$ convergent is, when ${\textstyle \left\|{\bf {A}}\right\|<1}$.

Application of linear algebra

Solving system of equations

${\textstyle \mathrm {\ \ \ \ } }$ System of linear equations

Let us consider the system of linear equations with ${\textstyle n}$ unknowns and ${\textstyle n}$ equations, i.e. with ${\textstyle n\times n}$ square matrix ${\textstyle {\bf {A}}}$. This system of linear equations can be written in matrix vector form as

$${\bf {A}}{\bf {x}}={\bf {b}}$$

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Inhomogeneous system with ${\textstyle rank({\bf {A}})=n}$

Let us consider the case with ${\textstyle rank({\bf {A}})=n}$, which is an important subclass of system of linear equations. Then there is always a unique solution, since the rank can not be changed via extending ${\textstyle {\bf {A}}}$ to ${\textstyle {\bf {A}}^{*}}$, due to ${\textstyle rank({\bf {A}}^{*})=\min(n,n+1)=n}$. The solution can be given in closed form by multiplying the matrix vector equation by ${\textstyle {\bf {A}}^{-1}}$ from left, which gives the closed form solution as

$${\bf {x}}={\bf {A}}^{-1}{\bf {b}}.$$

Note that the inverse matrix exists in this case, since matrix ${\textstyle {\bf {A}}}$ is non-singular due to ${\textstyle rank({\bf {A}})=n}$.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Homogeneous system with ${\textstyle rank({\bf {A}})=(n-1)}$

Recall that the equation

$${\bf {A}}adj({\bf {A}})=det({\bf {A}}){\bf {I}}$$

holds for the matrix ${\textstyle adj({\bf {A}})}$. If ${\textstyle det({\bf {A}})=0}$ then this leads to

$${\bf {A}}adj({\bf {A}})={\bf {0}}$$

Let ${\textstyle \left(adj({\bf {A}})\right)_{i}}$ denotes the ${\textstyle i}$-th column vector of ${\textstyle adj({\bf {A}})}$, ${\textstyle i=1,\ldots ,n}$. It follows that any column vector ${\textstyle \left(adj({\bf {A}})\right)_{i}}$ is a solution of the homogeneous equation ${\textstyle {\bf {A}}{\bf {x}}={\bf {0}}}$ with ${\textstyle det({\bf {A}})=0}$. If additionally ${\textstyle rank({\bf {A}})=(n-1)}$, then there is only one free parameter. Since any constant multiplication of a column vector ${\textstyle \left(adj({\bf {A}})\right)_{i}}$ is also a solution, it follows that

• ${\textstyle c\left(adj({\bf {A}})\right)_{1}}$, ${\textstyle c\in \mathbb {R} }$ gives every solution of the homogeneous equation ${\textstyle {\bf {A}}{\bf {x}}={\bf {0}}}$ with ${\textstyle rank({\bf {A}})=(n-1)}$ and
• the columns of ${\textstyle adj({\bf {A}})}$ are constant multiplications of each other if ${\textstyle rank({\bf {A}})=(n-1)}$.

${\textstyle \mathrm {\ \ \ \ } }$ System of non-linear equations

Let us consider the following system of non-linear equations with ${\textstyle n}$ unknowns and ${\textstyle n}$ equations:

$${\begin{aligned}&f_{1}(x_{1},\ldots ,x_{n})=0\\\vdots \\&f_{n}(x_{1},\ldots ,x_{n})=0\\\end{aligned}}$$

Introducing the notations

$${\bf {x}}=\left({\begin{array}{l}x_{1}\\\vdots \\x_{n}\end{array}}\right)$$

$${\bf {g}}({\bf {x}})=\left({\begin{array}{l}f_{1}(x_{1},\ldots ,x_{n})\\\vdots \\f_{n}(x_{1},\ldots ,x_{n})=0\end{array}}\right)$$

this can be rewritten as

$${\bf {g}}({\bf {x}})={\bf {0}}.$$

Solving of this system of non-linear equations is equivalent with minimization problem

$$\arg \min _{\bf {x}}{\bf {F}}({\bf {x}})=\arg \min _{\bf {x}}{\frac {1}{2}}{\bf {g}}^{T}({\bf {x}}){\bf {g}}({\bf {x}}),$$

since the square of each element in ${\textstyle {\bf {g}}({\bf {x}})}$ is non-negative. The gradient of ${\textstyle {\bf {F}}({\bf {x}}}$ can be expressed as

$$\nabla _{\bf {x}}{\bf {F}}({\bf {x}})=\nabla _{\bf {x}}\left({\frac {1}{2}}{\bf {g}}^{T}({\bf {x}}){\bf {g}}({\bf {x}})\right)={\bf {J}}_{\bf {g}}^{T}({\bf {x}}){\bf {g}}({\bf {x}}),$$

where ${\textstyle {\bf {J}}_{\bf {g}}^{T}({\bf {x}})}$ is the Jacobian matrix of ${\textstyle {\bf {g}}({\bf {x}})}$. Then the minimization problem can be solved numerically by applying the gradient descent algorithm. This can be executed by initializing ${\textstyle {\bf {x}}}$ as

$${\bf {x}}_{0}={\bf {0}}$$

and performing the iterative steps

$${\bf {x}}_{k+1}={\bf {x}}_{k}-\gamma _{k}{\bf {J}}_{\bf {g}}^{T}({\bf {x}}_{k}){\bf {g}}({\bf {x}}_{k}),$$

where ${\textstyle \gamma _{k}}$ is the step size and can be determined by any of the line search methods (see in 3.2.3).

Gradient methods

The gradient methods are numeric methods for unconstrained mathematical optimization. They can be applied to differentiable multivariate functions. They are usually formulated as finding the minimum of a multivariate function. All of them use the gradient of the multivariate function, this explains the name.

The basic idea of gradient methods is to decrease the function value in each step of the algorithm. It is well known that at the given point ${\textstyle {\bf {x_{0}}}\in \mathbb {R} ^{N}}$ of the multivariate function, ${\textstyle f(}$x${\textstyle ):\mathbb {R} ^{N}\rightarrow \mathbb {R} }$, the infinitesimal difference in the function value is the highest in the direction of the gradient at that point, ${\textstyle \nabla _{\bf {x}}f({\bf {x}}_{0})}$. Therefore the steepest decent is in the opposite direction of the gradient. The iterative step of any gradient methods takes a step in a direction ${\textstyle {\bf {d}}}$ which is related to the negative gradient at the current point, ${\textstyle -\nabla _{\bf {x}}f({\bf {x}}_{0})}$. The step size is denoted by ${\textstyle \gamma }$. Hence the iterative step of any gradient methods can be given as

$${\bf {x}}_{k+1}={\bf {x}}_{k}+\gamma _{k}{\bf {d}}_{k}.$$

Note that both the step size ${\textstyle \gamma }$ and the vector ${\textstyle {\bf {d}}}$ can depend on the iteration step.

${\textstyle \mathrm {\ \ \ \ } }$ Requirements and conditions to decrease the function value in each iteration

In order to decrease the function value in each step, two requirements must be made.

• ${\textstyle {\bf {R.1}}}$ It must be ensured that the ${\textstyle {\bf {d}}_{k}}$ infinitesimally shows into a descent direction.
• ${\textstyle {\bf {R.2}}}$ The step size ${\textstyle \gamma _{k}}$ must be enough small to avoid overshooting the nearest local minimum and thus to avoid leading to divergence.

The first requirement is equivalent with showing that the negative gradient ${\textstyle -\nabla _{\bf {x}}f({\bf {x}}_{0})}$ and ${\textstyle {\bf {d}}_{k}}$ and vector ${\textstyle {\bf {d}}_{k}}$ lie on the same side of the hyperplane being perpendicular to the gradient. In this case their scalar product is positive. This leads to the condition ${\textstyle {\bf {C.1}}}$ ensuring ${\textstyle {\bf {R.1}}}$ as

$${\bf {C.1}}\mathrm {~~~~} \nabla _{\bf {x}}f({\bf {x}}_{k})^{T}{\bf {d}}_{k}<0\mathrm {~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} .$$

The second requirement can be fulfilled by formalising "enough small" by specifying a demanded amount of decrease in function value. This is done by the Armijo condition demanding that the decrease in function value should be at least proportional to the product of the step size ${\textstyle \gamma _{k}}$ and the directional derivative ${\textstyle \nabla _{\bf {x}}f({\bf {x}}_{k})^{T}{\bf {d}}_{k}}$. Hence the ${\textstyle {\bf {R.2}}}$ can be fulfilled by condition ${\textstyle {\bf {C.2}}}$, which is the Armijo condition and given as

$${\bf {C.2}}\mathrm {~~} \mathrm {~~Armijo~condition~~} f({\bf {x}}_{k}+\gamma _{k}{\bf {d}}_{k})-f({\bf {x}}_{k})\leq \delta \gamma _{k}\nabla _{\bf {x}}f({\bf {x}}_{k})^{T}{\bf {d}}_{k}\mathrm {~~~~~~~~~~~~~~~} ,$$

where ${\textstyle \delta }$ is the constant of proportionality. In the practice usually ${\textstyle \delta }$ is set to small values, like e.g. ${\textstyle 10^{-4}}$. Observe that on both sides of this inequality there are negative values.

${\textstyle \mathrm {\ \ \ \ } }$ Determination of the step size ${\textstyle \gamma }$

If the step size were set to too small then the convergence would become too slow. This leads to a third requirement as
${\textstyle {\bf {R.3}}}$ The step size ${\textstyle \gamma _{k}}$ must be enough large to avoid slowing the convergence. The requirements ${\textstyle {\bf {R.2}}}$ and ${\textstyle {\bf {R.3}}}$ together ensure an optimal step size.

The three most important search methods for determining the optimal step size are

• Exact line search
• Inexact line search
• Backtracing line search

The exact line search determines the optimal step size ${\textstyle \gamma _{k}}$ by minimizing the function value after taking the next step. This leads to a one-dimensional minimization problem as

$$\arg \min _{\gamma _{k}}g(\gamma _{k})=\arg \min _{\gamma _{k}}f({\bf {x}}_{k}+\gamma _{k}{\bf {d}}_{k}).$$

The exact line search are used only seldom in practice due to its high computing effort.

In the inexact line search the step size, starting from an initial value, like e.g. ${\textstyle 1}$, is iteratively decreased until the function value after the step will be less than the current one, in other words until

$$f({\bf {x}}_{k+1})=f({\bf {x}}_{k}+\gamma _{k}{\bf {d}}_{k})<f({\bf {x}}_{k}).$$

The backtracing line search searches for "enough small" step size by utilizing the Armijo condition. Starting from an initial step size, the step size is iteratively multiplied by a properly selected constant of proportionality, ${\textstyle \delta }$ until the Armijo condition fulfils.

While exact line search fulfils both requirements ${\textstyle {\bf {R.2}}}$ and ${\textstyle {\bf {R.3}}}$, inexact line search fulfils only ${\textstyle {\bf {R.2}}}$ and backtracing line search lies somewhere in between. Because of this and its simplicity, it is often used in the practice.

The pseudo-code of an algorithm for gradient method with backtracing line search can be seen in Algorithm 9.

Algorithm 9 Gradient method - with backtracing line search
—————————————————————————————
Inputs: - multivariate function ${\textstyle f({\bf {x}})}$
- initial value ${\textstyle {\bf {x}}_{0}}$
- precision value ${\textstyle \epsilon }$
Outputs:
- found local minimum place ${\textstyle {\bf {x}}_{m}}$
- local minimum ${\textstyle f({\bf {x}}_{m})}$
—————————————————————————————
1 Initialisation ${\textstyle k=-1}$, ${\textstyle f({\bf {x}}_{-1})=\infty )}$
2 while ${\textstyle |f({\bf {x}}_{k})-f({\bf {x}}_{k+1})|>\epsilon }$
3 ${\textstyle \mathrm {\ \ } }$ ${\textstyle k=k+1}$
4    Compute gradient ${\textstyle \nabla _{\bf {x}}f({\bf {x}}_{k})}$
5    Compute vector ${\textstyle {\bf {d}}_{k}}$
   —– Backtracing line search - begin —
6    Init backtracing line search ${\textstyle \gamma _{k}=1}$, set ${\textstyle 0<\delta <1}$
7    while ${\textstyle f({\bf {x}}_{k}+\gamma _{k}{\bf {d}}_{k})-f({\bf {x}}_{k})>\delta \gamma _{k}\nabla _{\bf {x}}f({\bf {x}}_{k})^{T}{\bf {d}}_{k}}$
8 ${\textstyle \mathrm {\ \ \ } }$ ${\textstyle \gamma _{k}=\delta \gamma _{k}}$
9    end
   —– Backtracing line search - end —-
10   Update ${\textstyle {\bf {x}}_{k+1}}$ as ${\textstyle {\bf {x}}_{k+1}={\bf {x}}_{k}+\gamma _{k}{\bf {d}}_{k}}$
11   end
12   return ${\textstyle {\bf {x}}_{k+1}}$ and ${\textstyle f({\bf {x}}_{k+1})}$
—————————————————————————————

${\textstyle \mathrm {\ \ \ \ } }$ The gradient descent

The gradient descent algorithm is a special case of the gradient methods by setting ${\textstyle {\bf {d}}}$ to be the steepest descent, in other words ${\textstyle {\bf {d}}=-\nabla _{\bf {x}}f({\bf {x}})}$. Thus gradient descent is a first-order method and its iterative step can be given as

$${\bf {x}}_{k+1}={\bf {x}}_{k}-\gamma _{k}\nabla _{\bf {x}}f({\bf {x}}_{k}).$$

In the context of deep learning the step size ${\textstyle \gamma }$ is also called as learning rate. The pseudo-code of the gradient descent algorithm is given in Algorithm 10.

Algorithm 10 Gradient descent algorithm
—————————————————————————————
Inputs: - multivariate function ${\textstyle f({\bf {x}})}$
- initial value ${\textstyle {\bf {x}}_{0}}$
- precision value ${\textstyle \epsilon }$
Outputs:
- found local minimum place ${\textstyle {\bf {x}}_{m}}$
- local minimum ${\textstyle f({\bf {x}}_{m})}$
—————————————————————————————
1 Initialisation ${\textstyle k=-1}$, ${\textstyle f({\bf {x}}_{-1})=\infty )}$
2 while ${\textstyle |f({\bf {x}}_{k})-f({\bf {x}}_{k+1})|>\epsilon }$
3 ${\textstyle \mathrm {\ \ } }$ ${\textstyle k=k+1}$
4    Compute gradient ${\textstyle \nabla _{\bf {x}}f({\bf {x}}_{k})}$
5    Update learning rate by setting ${\textstyle \gamma _{k}}$
6    Update ${\textstyle {\bf {x}}_{k+1}}$ as ${\textstyle {\bf {x}}_{k+1}={\bf {x}}_{k}-\gamma _{k}\nabla _{\bf {x}}f({\bf {x}}_{k})}$
7    end
8    return ${\textstyle {\bf {x}}_{k+1}}$ and ${\textstyle f({\bf {x}}_{k+1})}$
—————————————————————————————

The convergence to local minimum can be guaranteed under certain assumptions on function ${\textstyle f({\bf {x}})}$ and specific choice s of the dependency of learning rate ${\textstyle \gamma _{k}}$ on ${\textstyle {\bf {x}}_{k}}$, ${\textstyle {\bf {x}}_{k-1}}$, ${\textstyle f({\bf {x}}_{k})}$ and ${\textstyle f({\bf {x}}_{k-1})}$. If function ${\textstyle f({\bf {x}})}$ is convex, then local minimum is also the global minimum.

The extension of gradient descent, the stochastic gradient descent algorithm and its improved variants are the most commonly used numeric optimization algorithms for training deep neural networks.

${\textstyle \mathrm {\ \ \ \ } }$ Further special cases of gradient methods

Several further algorithm can be obtained as special cases of gradient methods by setting vector ${\textstyle {\bf {d}}}$ specially. These includes

• Diagonal scaled gradient descent and
• Newton’s method.

The diagonal scaled gradient descent algorithm is obtained by setting
${\textstyle {\bf {d}}=-{\bf {D}}\nabla _{\bf {x}}f({\bf {x}})}$, where ${\textstyle ={\bf {D}}=diag(d_{1},\ldots ,d_{L})}$ is a diagonal matrix. Note that just like vector ${\textstyle {\bf {d}}}$, matrix ${\textstyle {\bf {D}}}$ can also depend on the iteration step.

The Newton’s method, also called as Newton–Raphson method applied to optimization can be also obtained by setting ${\textstyle {\bf {d}}=-{\bf {D}}\nabla _{\bf {x}}f({\bf {x}})}$ with ${\textstyle {\bf {D}}={\bf {H}}_{f}^{-1}}$, where ${\textstyle {\bf {H}}_{f}^{-1}=\nabla _{\bf {x}}^{2}f({\bf {x}})}$ is the Hessian matrix. Since the Hessian matrix includes second order derivatives of function ${\textstyle f({\bf {x}})}$, Newton’s method is a second order optimization method. For the class of convex functions the Newton’s method converges to the minimum quadratically fast.

Second-order algorithms

The second-order algorithms use the second order information in their original formulation from the Hessian matrix. The following second-order methods are considered

• Newton’s method
• Quasi-Newton methods
• Non-linear conjugate gradient algorithm

${\textstyle \mathrm {\ \ \ \ } }$ Newton methods

Newton’s method for local optimization is based on the second order Taylor-expansion of the function to be optimized. We apply it to minimize the function ${\textstyle f({\bf {x}})}$. The second order Taylor-expansion of ${\textstyle f({\bf {x}})}$ around ${\textstyle {\bf {x}}_{k}}$ is given as

$$f({\boldsymbol {x}})\approx f({\bf {x}}_{k})+({\bf {x}}-{\bf {x}}_{k})^{T}\nabla _{\bf {x}}f({\bf {x}}_{k})+{\frac {1}{2}}({\bf {x}}-{\bf {x}}_{k})^{T}{\bf {H}}_{f}({\bf {x}}_{k})({\bf {x}}-{\bf {x}}_{k}).$$

The method chooses the next value of the parameter vector ${\textstyle {\bf {x}}}$ as the minimum of the above Taylor-expansion form. It is well known that the necessary condition of ${\textstyle {\bf {x}}}$ being the minimum is that the gradient of ${\textstyle f({\bf {x}})}$ must be ${\textstyle {\bf {0}}}$. Computing the gradient of ${\textstyle f({\bf {x}})}$ with respect to ${\textstyle {\bf {x}}}$ and setting it to ${\textstyle {\bf {0}}}$ gives

$$\nabla _{\bf {x}}f({\bf {x}})=\nabla _{\bf {x}}f({\bf {x}}_{k})+{\bf {H}}_{f}({\bf {x}}_{k})({\bf {x}}-{\bf {x}}_{k})={\bf {0}},$$

from which the next value of the parameter vector ${\textstyle {\bf {x}}_{k+1}}$ can be expressed by setting ${\textstyle {\bf {x}}={\bf {x}}_{k+1}}$ as

$${\bf {x}}_{k+1}={\bf {x}}_{k}-{\bf {H}}_{f}^{-1}({\bf {x}}_{k})\nabla _{\bf {x}}f({\bf {x}}_{k}),$$

which is the same formula as we got by setting ${\textstyle {\bf {D}}={\bf {H}}_{f}^{-1}}$ in the general iteration relation of the gradient methods. This recursive computational rule utilizes also the second order information in Hessian matrix. If the function to be minimized is locally quadratic then the method jumps in one step to the minimum. Otherwise it iterates in quadratic steps and hence faster than the gradient descent. There are two major issues with the Newton’s method as

1. Limitation - The convergence of the method is ensured only for locally convex regions. It can move in wrong direction near a saddle point.
2. Drawback - The numerical complexity of the method is ${\textstyle {\mathcal {O}}(N^{3})}$, that is higher than that of the first-order methods. Here ${\textstyle N}$ is the number of parameters, i.e. the size of vector ${\textstyle {\bf {x}}}$. This is due to the computation of the inverse Hessian in each iteration step.

${\textstyle \mathrm {\ \ \ \ } }$ Quasi-Newton methods

In many applications, like e.g. in machine learning and in deep learning trainings, the the number of parameters, ${\textstyle N}$ is usually in magnitude of thousands and millions. Therefore Newton’s method can not be applied directly due to its numerical complexity in such applications.

Instead the quasi-Newton methods can be applied, in which the Hessian matrix is approximated by the matrix ${\textstyle {\bf {B}}}$, which needs much less computation effort. The matrix ${\textstyle {\bf {B}}}$ is chosen to satisfy the so called secant equation

$$\nabla _{\bf {x}}f({\bf {x}})=\nabla _{\bf {x}}f({\bf {x}}_{k})+{\bf {B}}({\bf {x}}_{k})({\bf {x}}-{\bf {x}}_{k}),$$

This leads to a significant reduction in the computational complexity.

The most prominent quasi-Newton method is the
Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm. It uses the matrix ${\textstyle B}$ only for determining the search direction, but it does not apply the quadratic step size like in the original Newton’s method. Instead a line search is performed. If the function is not convex then the step size is determined by finding a point satisfying the Wolfe conditions. The numerical complexity of the BFGS algorithm is ${\textstyle {\mathcal {O}}(N^{2})}$. However the algorithm stores the matrix ${\textstyle {\bf {B}}}$ in each iteration step leading to the memory need ${\textstyle {\mathcal {O}}(N^{2})}$. This makes it not appropriate for using in DL.

A further improvement of BFGS is the Limited Memory BFGS (L-BFGS), whose memory need is ${\textstyle {\mathcal {O}}(1)}$ to ${\textstyle {\mathcal {O}}(N)}$ depending on the amount of information used from previous iteration at updating matrix ${\textstyle {\bf {B}}}$. The method converges faster in locally convex environment than in a non-convex one.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Non-linear conjugate gradient algorithm

One potential problem of gradient descent algorithm, that in narrow valley it takes a zig-zag route, which slows the convergence. This is because the consecutive gradients are orthogonal and therefore some part of progress already achieved in the previous gradient direction will be undo.
The conjugate gradient algorithm overcomes this problem by selecting the consecutive directions being so called conjugate gradient directions. In case of N-dimensional quadratic function it reaches the minimum exactly after ${\textstyle N}$ steps, since it does not undo progress made in previous directions. The next direction is determined as the linear combination of the actual gradient and the actual direction, in which the previous direction is weighted by ${\textstyle \beta }$. Since the next and actual directions are conjugate gradients, the next direction can be determined on straightforward way by the help of the eigenvectors of the Hessian of the multivariate function to be minimized. The conjugate gradient algorithm was intended to solve a quadratic minimization problem, which is equivalent with solving a system of linear equations.

The non-linear conjugate gradient algorithm is a generalization of the conjugate gradient algorithm to find a minimum of any non-linear multivariate function. In this case the algorithm does not stop after ${\textstyle N}$ steps, so a small modification is required in order to restart search eventually in the direction of unaltered gradient. This is performed by periodic reset of ${\textstyle \beta }$ to ${\textstyle 0}$. In case of large ${\textstyle N}$, which is the case of e.g. in training deep learning models, the computation of the Hessian matrix requires a high computational effort. Therefore computationally more efficient ways were proposed to compute parameter ${\textstyle \beta }$. Two of the best known formulas for computing ${\textstyle \beta }$ are given as follows:

• Fletcher-Reeves formula:
  $$\beta _{k}^{FR}={\frac {\nabla _{\bf {x}}^{T}f({\bf {x}}_{k})\nabla _{\bf {x}}f({\bf {x}}_{k})}{\nabla _{\bf {x}}^{T}f({\bf {x}}_{k-1})\nabla _{\bf {x}}f({\bf {x}}_{k-1})}}.$$
• Polak-Ribiere formula:
  $$\beta _{k}^{PR}={\frac {\nabla _{\bf {x}}^{T}f({\bf {x}}_{k})\left(\nabla _{\bf {x}}f({\bf {x}}_{k})-\nabla _{\bf {x}}f({\bf {x}}_{k-1})\right)}{\nabla _{\bf {x}}^{T}f({\bf {x}}_{k-1})\nabla _{\bf {x}}f({\bf {x}}_{k-1})}}.$$

The pseudo-code of the algorithm is given in Algorithm 11.

Algorithm 11 Non-linear conjugate gradient algorithm
—————————————————————————————
Inputs: - multivariate function ${\textstyle f({\bf {x}})}$
- initial value ${\textstyle {\bf {x}}_{0}}$
- precision value ${\textstyle \epsilon }$
Outputs:
- found local minimum place ${\textstyle {\bf {x}}_{m}}$
- local minimum ${\textstyle f({\bf {x}}_{m})}$
—————————————————————————————
1 Initialisation ${\textstyle k=-1}$, ${\textstyle f({\bf {x}}_{-1})=\infty )}$
2 Initialize conjugate direction ${\textstyle {\bf {s}}_{-1}={\bf {0}}}$
3 while ${\textstyle |f({\bf {x}}_{k})-f({\bf {x}}_{k+1})|>\epsilon }$
4 ${\textstyle \mathrm {\ \ } }$ ${\textstyle k=k+1}$
5    Compute gradient ${\textstyle \nabla _{\bf {x}}f({\bf {x}}_{k})}$
6    Update conjugate direction ${\textstyle {\bf {s}}_{k}=-\nabla _{\bf {x}}f({\bf {x}}_{k})+\beta _{k}{\bf {s}}_{k-1}}$
7    Perform line search ${\textstyle \gamma _{k}=\arg \min _{\gamma }f({\bf {x}}_{k}+\gamma {\bf {s}}_{k})}$
8    Update ${\textstyle {\bf {x}}_{k+1}}$ as ${\textstyle {\bf {x}}_{k+1}={\bf {x}}_{k}+\gamma _{k}{\bf {s}}_{k}}$
9 end
10 return ${\textstyle {\bf {x}}_{k+1}}$ and ${\textstyle f({\bf {x}}_{k+1})}$
—————————————————————————————

The Quasi-Newton methods converge potentially much faster than the non-linear conjugate gradient algorithm.