Methoden der Datenanalyse - Faktorenanalyse: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „= Multidimensionale Skalierung = ''Die multidimensionale Skalierung bedient sich ähnlicher Techniken und Ideen wie die Clusteranalyse und die Faktorenanalyse. Ziel der Lektion ist es, Unterschiede und Gemeinsamkeiten herauszuarbeiten sowie exemplarisch in eine Analyse in R einzuführen.'' Wir verlassen nun jene statistischen Analyseverfahren, die primär das Ziel haben, über die beobachteten Daten Voraussagen zu treffen und wechseln zu solchen, die au…“) |
|||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
= | = Faktorenanalyse = | ||
''Die | ''Wichtiges Ziel der Lektion ist die Erkenntnis, welche Aussagen über nichtbeobachtbare Merkmale aufgrund der Korrelationsstruktur eines Satzes von vorhandenen Variablen abgeleitet werden können. Die Grundlagen der Faktorenanalyse als Basis von Strukturmodellen und die Darstellung der subjektiven Entscheidungen, die im Zuge einer Faktorenanalyse getroffen werden müssen sind ebenso Schwerpunkte, wie die Analyse der Daten in R.'' | ||
== Einführung == | |||
Die | Die in den ersten beiden Lektionen besprochenen Verfahren der Regressions- bzw. Varianzanalyse eignen sich, um den Zusammenhang zwischen einem Satz an ausgewählten Variablen und einer davon abhängigen Variable zu testen. Oft kommt es allerdings vor, dass die Menge an potentiellen Variablen relativ groß ist, einzelne Variablen hoch miteinander korrelieren, oder man nicht am Einfluss der Variablen auf eine abhängige Variable, sondern an der Korrelationsstruktur bzw. an latenten (=nicht beobachtbaren), den Daten zugrundeliegenden Faktoren interessiert ist. Den zweiten Fall haben wir bei Beispiel 1 gehabt. Hier waren Spritverbrauch in der Stadt bzw. auf der Autobahn klarerweise hoch korreliert und damit war schwer abzuschätzen, wie groß der Anteil jeder der beiden Variablen an der Erklärung des Preises ist (im gewählten Modell kam dann jedoch ohnehin keine der beiden Variablen vor). Für den Fall, dass man an latenten Faktoren interessiert ist, gibt es folgende Beispiele: | ||
* Menschliches Verhalten ist beispielsweise von einer Vielzahl an Einflussfaktoren abhängig. In Fragebögen, die das Verhalten in bestimmten Situationen abfragen, werden oft viele ähnliche Fragen, die miteinander hoch korrelieren, gestellt. Letztendlich will man dabei aber latente Konstrukte, wie z.B. „Aggresionspotential“ oder „Verlässlichkeit“ erheben. | |||
* Erhebung von Prädiktoren für die Kreditwürdigkeit von Kunden einer Bank. Bekannt sind zahlreiche Kundenvariablen, die hoch korreltiert sind und verdichtet werden können. | |||
* Welche Fähigkeiten liegen Leistungen in Intelligenztests zugrunde? Es existieren viele verschiedene (ähnliche Tests), bei denen hochkorrelierte Leistungen zu beobachten sind. Welche (nicht beobachtbaren) Faktoren liegen diesen Leistungen zugrunde? | |||
<p>Die Faktorenanalyse bedient sich nun mathematischer Verfahren, die es ermöglichen, viele, miteinander hoch korrelierende Variablen auf einige wenige, nicht korrelierenden Faktoren umzurechnen, sodass die Information (Varianz) der Daten aber weitgehend vorhanden bleibt.</p> | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Beispiel 10 (Extrembeispiel)''' | |||
Angenommen Sie wollen den Umsatz von Speiseeis in Wien in Abhängigkeit von der jeweils um 12h in der Wiener Innenstadt gemessenen Temperatur vorhersagen. Sie messen die Temperatur in Grad Celsius, in Fahrenheit und in Kelvin. Anschließend führen Sie eine multiple lineare Regression des Speiseeisumsatzes, die alle drei Variablen als Erklärung enthält, durch. | |||
Aufgrund der Tatsache, dass zwischen den drei Skalen mittels Lineartransformation umgerechnet werden kann <ref>Kelvin= Celsius+273,15 bzw. Fahrenheit=32+9/5*Celsius.</ref> (exakte Multikollinearität), ergeben sich für die Koeffizientenschätzungen unendlich große Varianzen und beliebige Werte. Die Information, die in allen drei Variablen steckt, kann ohne Verlust mit einer der drei Temperaturvariablen dargestellt werden. | |||
|} | |||
Die im folgenden dargestellten Methoden betreffen die explorative Faktorenanalyse. Mit ihrer Hilfe können keine Wirkzusammenhänge inferenzstatistisch geprüft werden, sondern es können nur Zusammenhangsstrukturen exploriert werden. Demgegenüber steht die konfirmatorische Faktorenanalyse, bei der hypothesenprüfend vorgegangen wird. Diese ist ein Spezialfall der in der folgenden Lektion vorgestellten Strukturgleichungsmodelle und wird dort betrachtet. | |||
Für die explorative Faktorenanalyse gilt weiters, dass hier einige subjektive Entscheidungen des Anwenders im Analyseprozess erforderlich sind. Man ist mehr als bei anderen statistischen Verfahren auf Vermutungen angewiesen. Die Faktorenanalyse versteht sich eher als mathematisches Hilfsmittel, welches logisch begründeten Strukturtheorien zur Seite gestellt wird. | |||
Die Faktorenanalyse geht zurück auf Spearman, der diese ursprünglich 1904 zum Zwecke der Intelligenzmessung verwendet hat. Das einleitende Beispiel im folgenden Abschnitt widmet sich daher diesem Thema. | |||
== Modellvorstellung == | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Beispiel 11''' | |||
Schulnoten sind Indikatoren für den unbekannten Faktor Intelligenz. Es werden aus Gründen der Einfachheit zwei voneinander unabhängige Intelligenzen (quantitative Intelligenz, Q, und verbale Intelligenz, V) postuliert. | |||
Folgende beispielhafte Annahme über das Zustandekommen der Noten in sechs verschiedenen Fächern werden getroffen: | |||
= | <math>\text { Math }=0,80 * Q+0,20 * V+A_{m}</math> | ||
<math>\text { Phys }=0,70 * Q+0,30 * V+A_{p}</math> | |||
{ | <math>\text { Chem }=0,60 * Q+0,30 * V+A_{c}</math> | ||
<math>\text { Eng }=0,20 * Q+0,80 * V+A_{e}</math> | |||
<math>\text { Hist }=0,15 * Q+0,82 * V+A_{h}</math> | |||
<math>\text { Fran }=0,25 * Q+0,85 * V+A_{f}</math> | |||
Die Noten setzen sich also mittels Linearkombination aus den beiden Intelligenzen plus einem spezifischen Faktor für das jeweilige Fach zusammen. | |||
|} | |} | ||
Die Koeffizienten der Regressiongleichungen aus Beispiel 11 heißen „Ladungen“. <math>Q</math> und <math>V</math> heißen „gemeinsame Faktoren“. | |||
Wird nun ein derartiger Zusammenhang unterstellt, können auch die paarweisen Korrelationen zwischen je zwei Schulnoten (Fächern) daraus abgeleitet werden. | |||
Bei der Faktorenanalyse kennt man die in Beispiel 11 getroffene Annahme nicht. Man beschreitet hier den umgekehrten Weg. Gegeben sind alle paarweisen Korrelationen (im Beispiel die Korrelationen zwischen den Schulnoten) und gesucht sind die (in Beispiel 11) gegebenen Ladungen. | |||
Es werden dann einige mathematisch-statistische Restriktionen gemacht, um das Schätzproblem bei der Faktorenanalyse etwas genauer zu spezifizieren. Beispielsweise muss gefordert werden, dass die gemeinsamen Faktoren untereinander unabhängig sind. Das heißt, wenn jemand eine hohe quantitative Intelligenz hat, dann kann daraus keine Tendenz über die verbale Intelligenz geschlossen werden. Außerdem wir gefordert, dass die gemeinsamen Faktoren von den spezifischen Faktoren unabhängig sind. | |||
Notiert wird das Modell der Faktorenanalyse in den gängigen Lehrbüchern in Matrixschreibweise (analog zu Beispiel 11): | |||
<math display="block"> | |||
Y=F L^{t}+E | |||
</math> | |||
wobei <math>Y</math> die bereits spaltenweise auf Mittelwert Null zentrierte Datenmatrix (<math>n \times p, n</math> Versuchseinheiten und <math>p</math> Variablen), <math>F</math> die Matrix (<math>(n \times k)</math>), die die gemeinsamen Faktoren enthält, <math>L</math> die Ladungsmatrix (<math>p \times k</math>) und <math>E</math> die (<math>n \times p</math>)- Matrix der Einzelrestwerte ist. In Beispiel 11 ist <math>P=6</math> und <math>K=2</math>. | |||
Aufgrund der vielen Unbekannten in diesem Modell ist dieses nicht empirisch überprüfbar bzw. uneindeutig. Durch die erwähnten mathematischen Annahmen lässt sich aber die für die Faktorenanalyse zentrale, unter bestimmten Umständen eindeutige Zerlegung bilden: <math>\boldsymbol{\Sigma}=\mathbf{L} \mathbf{L}^{\mathrm{t}}+\mathbf{V}</math> | |||
<math>\Sigma</math> ist die sogenannte „Varianz-Kovarianzmatrix“ der Daten. Sie enthält in der Hauptdiagonale alle Varianzen der <math>p</math> Variablen und abseits davon alle Kovarianzen. Die Varianz-Kovarianz-Matrix (bzw. bei standardisierten Variablen die Korrelationsmatrix) ist der wesentliche Input bei einer Faktorenanalyse, den es zu analysieren gilt. <math>L</math> ist eine Diagonalmatrix mit den Varianzen der spezifischen Faktoren. Das wesentliche Ziel bei der Faktorenanalyse ist es nun, eine jener Matrizen <math>L</math> zu finden, für die diese Zerlegung möglich ist, und zwar für eine minimale Anzahl an <math>k</math>zugrundeliegenden gemeinsamen Faktoren. | |||
== Faktorextraktion == | |||
Es gibt nun verschiedene Schätzmethoden, um die Ladungsmatrix <math>L</math> zu schätzen. | |||
=== Die Maximum-Likelihood-Methode === | |||
Diese bedient sich einem in der Statistik weit verbreiteten Konzept zur Konstruktion von Schätzern. Es wird hier eine multivariate Normalverteilung der beobachteten Daten unterstellt. Als Folge davon kann analytisch jener Schätzer für die Ladungsmatrix <math>L</math>] ermittelt werden, der unter dieser Annahme am plausibelsten ist. Hier wird also stochastisch durch Verteilungsannahmen argumentiert. Die Wahl, wieviele Faktoren (<math>k</math>) gewählt werden, kann unter anderem durch statistische Hypothesentests erfolgen. | |||
=== Die Hauptkomponentenanalyse === | |||
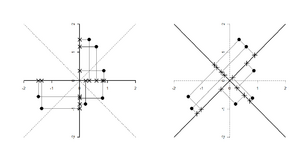
Die Ergebnisse der Hauptkomponentenanalyse erhält man ebenfalls durch Optimierung. Kriterium ist, dass die (zentrierte) Datenmatrix <math>Z</math> durch Multiplikation mit einer <math>k \times k-</math>-Matrix (mit orthonormalen Spalten) derart transformiert wird, dass die Spalten der so transformierten Matrix jeweils schrittweise die höchste Varianz erzeugen. Dieser Vorgang wird Hauptachsentransformation genannt. Diese sehr theoretisch beschriebene Vorgehensweise soll anhand eines Beispieles skizziert werden (Abbildung 32). | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Beispiel 12''' | |||
[[file:img1642203546153.png|300px|none|thumb|Sieben Datenpunkte im zweidimensionalen Raum, vor und nach der Achsendrehung]] | |||
Abbildung 32 zeigt sieben Datenpunkte in zwei Variablen. In der linken Abbildung kann die Varianz in X- bzw. Y-Richtung durch Normalprojektion an die jeweiligen Achsen geschätzt werden. Die Daten sind so gewählt, dass sowohl die Varianz in X- als auch in Y-Richtung gleich 1 ist. Geometrisch gesehen wird bei der Hauptachsentransformation das Koordinatensystem solange gedreht, bis die größte der Varianzen der projizierten Datenpunkte auf die neuen Achsen maximal wird. Diese Drehung entspricht in diesem Beispiel 45 Grad und führt dazu, dass die Varianz der Daten auf der Achse von links unten nach rechts oben 1,501 beträgt. Dies ist die größte erzielbare Varianz auf einer Achse. Die Werte auf der zweiten Achse weisen eine Varianz von 0,499 auf. Nachdem die Daten nur zwei Dimensionen haben, bleibt für die zweite Achse nur mehr eine Richtung. Im allgemeinen wird jedoch für die zweite Achse jene Richtung gewählt, die ihrerseits wieder die maximale Varianz liefert. | |||
In Summe sind die Varianzen in beiden Richtungen sowohl in der Grafik links als auch rechts gleich 2. Sie teilen sich nur anders auf. Um wieder zu obigen Text zurückzukehren: Die hier angewandte Transformation bedeutet rechnerisch eine Multiplikation der Datenmatrix mit der Matrix | |||
<math display="block"> | |||
\mathbf{L}=\left(\begin{array}{cc} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right) | |||
</math> | |||
|} | |} | ||
{| | Wird <math>k=p</math> gewählt, heißt das, dass die volle Varianz erklärt wird (d.h. die volle Information erhalten bleibt). Die (bei hoher Korrelation in den Daten stark) ungleiche Varianzzerlegung macht man sich aber zunutze um nun die ersten <math>k</math> interessierenden Achsen zu wählen und die anderen zu eliminieren. Damit erzielt man einen Kompromiss zwischen Datenreduktion und Informationsverlust. Der Anteil der Summe aller bis zur <math>k</math>-ten Achse erklärten Varianzen an der Gesamtzahl <math>p</math>der Variablen im Originaldatensatz ist der erklärte Varianzanteil. Dieser ist ein Kriterium zur Bestimmung, auf wieviele Achsen die Daten reduziert werden sollen. | ||
! width="100%" | ''' | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Fortsetzung Beispiel 12''' | |||
Die Varianz der Daten an der ersten transformierten Achse beträgt 1,501. Die Anzahl der Originalvariablen bzw. die Summe derer Varianzen beträgt 2. Daher beträgt der erklärte Varianzanteil bei alleiniger Datenreduktion auf eine Achse <math>\frac{1.501}{2}=75 \%</math>. | |||
|} | |} | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Aufgabe 15''' | |||
Angenommen es liegt ein Satz von acht (auf Varianz gleich Eins) standardisierten, korrelierten Variablen vor, der mittels Hauptkomponentenmethode reduziert werden soll. | |||
== | <ol style="list-style-type: lower-alpha;"> | ||
<li style="text-align: left;"><p>Sie entschließen sich, die Daten auf drei Achsen zu reduzieren. Wie groß sollte die Summe der drei erklärten Varianzen jedenfalls sein?</p></li> | |||
<li style="text-align: left;"><p>Wie groß sollte der erklärte Varianzanteil dann jedenfalls sein?</p></li> | |||
<li><p style="text-align: left;">Angenommen Sie erzielen eine Varianzerklärung von 74%. Wieviele Achsen haben Sie dabei maximal gewählt?</p></li> | |||
</ol> | |||
|} | |||
Die eben diskutierte Vorgehensweise nur <math>k<p</math> Achsen aus der transformierten Matrix zur Erklärung der Originaldaten auszuwählen, wird „Hauptkomponentenmethode“ genannt. Während bei <math>k=p</math> nur eine Lösung existiert, den gesamt erklärten Varianzanteil zu maximieren, ist die Lösung bei <math>1<k<p</math> gewählten Achsen nicht eindeutig. Darauf wird in Abschnitt 5.6 eingegangen. | |||
Die Lösung der Hauptkomponentenanalyse wird im Normalfall nicht graphisch durchgeführt, sondern reduziert sich – mathematisch gesehen – auf das Finden der Eigenwerte der Korrelations- bzw. Kovarianzmatrix der Daten. Deshalb liest man statt erklärten Varianzanteilen in Software-Outputs von Faktorenanalysen auch immer wieder von Eigenwerten. Die Varianzen der Daten in den einzelnen Richtungen sind gerade durch diese Eigenwerte gegeben. | |||
Die Hauptkomponentenmethode ist die am häufigsten angewandte Methode zur Extraktion von Faktoren. Der Grund ist auch, dass hier im Gegensatz zu anderen Berechnungsmethoden kein iteratives Vorgehen benötigt wird. Im Hinblick zur eigentlichen Faktorenanalyse wird hier kein Modell zugrundegelegt, sondern es wird lediglich eine technische Optimierungsaufgabe zur Datenreduktion durchgeführt. Eine Methode, die die Hauptkomponentenmethode verwendet um in einem iterativen Prozess (wie vorher erwünscht) statt den Varianzen die Anpassung an die Korrelationsmatrix optimiert, ist die Hauptfaktorenanalyse. Auf diese wird aber aus Platzgründen nicht weiter eingegangen. | |||
== Bestimmung der Anzahl an Faktoren == | |||
Die | Die wesentlichste Frage, wenn mittels Hauptkomponentenanalyse versucht wird, einen Satz von <math>k<p</math> Dimensionen – die „gemeinsamen Faktoren“ – zu ermitteln, ist, wie groß <math>k</math> nun sein soll. Dazu gibt es drei häufig verwendete Kriterien. | ||
=== Die erklärte Varianz === | |||
Ein mögliches Kriterium kann sein, dass man einen gewissen Anteil an erklärter Varianz nicht unterschreiten will, da man sonst nicht mehr das Gefühl hat, die ursprünglichen Daten mit dem reduzierten Datensatz gut zu beschreiben. | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Beispiel 13''' | |||
Im diesem Beispiel (Backhaus et al., 2003) sind die mittels Fragebogen von mehreren Personen erhobenen Eigenschaften von sechs Margarinesorten erhoben. Die Daten beschreiben die Mittelwerte der Stichprobe, die auf einer Ratingskala zwischen 1 und 7 bewertet wurden. | |||
{| style="border-collapse: collapse; height: 196px; background-color: rgb(149, 165, 166);" border="1" | |||
! style="height: 28px; width: 284.468px;" | | |||
! style="height: 28px; width: 219.352px;" | Anteil ungesättigter Fettsäuren | |||
! style="height: 28px; width: 232.373px;" | Kaloriengehalt | |||
! style="height: 28px; width: 219.352px;" | Vitamingehalt | |||
! style="height: 28px; width: 180.278px;" | Haltbarkeit | |||
! style="height: 28px; width: 115.22px;" | Preis | |||
|- style="height: 28px;" | |||
| style="height: 28px; width: 284.468px;" | Rama | |||
| style="height: 28px; width: 219.352px;" | 1 | |||
| style="height: 28px; width: 232.373px;" | 1 | |||
| style="height: 28px; width: 219.352px;" | 2 | |||
| style="height: 28px; width: 180.278px;" | 1 | |||
| style="height: 28px; width: 115.22px;" | 2 | |||
|- style="height: 28px;" | |||
| style="height: 28px; width: 284.468px;" | Sanella | |||
| style="height: 28px; width: 219.352px;" | 2 | |||
| style="height: 28px; width: 232.373px;" | 6 | |||
| style="height: 28px; width: 219.352px;" | 3 | |||
| style="height: 28px; width: 180.278px;" | 3 | |||
| style="height: 28px; width: 115.22px;" | 4 | |||
|- style="height: 28px;" | |||
| style="height: 28px; width: 284.468px;" | Becel | |||
| style="height: 28px; width: 219.352px;" | 4 | |||
| style="height: 28px; width: 232.373px;" | 5 | |||
| style="height: 28px; width: 219.352px;" | 4 | |||
| style="height: 28px; width: 180.278px;" | 4 | |||
| style="height: 28px; width: 115.22px;" | 5 | |||
|- style="height: 28px;" | |||
| style="height: 28px; width: 284.468px;" | Du darfst | |||
| style="height: 28px; width: 219.352px;" | 5 | |||
| style="height: 28px; width: 232.373px;" | 6 | |||
| style="height: 28px; width: 219.352px;" | 6 | |||
| style="text-align: left; height: 28px; width: 180.278px;" | 2 | |||
| style="text-align: left; height: 28px; width: 115.22px;" | 3 | |||
|- style="text-align: left; height: 28px;" | |||
| style="height: 28px; width: 284.468px;" | Holländische Butter | |||
| style="height: 28px; width: 219.352px;" | 2 | |||
| style="height: 28px; width: 232.373px;" | 3 | |||
| style="height: 28px; width: 219.352px;" | 3 | |||
| style="height: 28px; width: 180.278px;" | 5 | |||
| style="height: 28px; width: 115.22px;" | 7 | |||
|- style="text-align: left; height: 28px;" | |||
| style="height: 28px; width: 284.468px;" | Weihnachtsbutter | |||
| style="height: 28px; width: 219.352px;" | 3 | |||
| style="height: 28px; width: 232.373px;" | 4 | |||
| style="height: 28px; width: 219.352px;" | 4 | |||
| style="height: 28px; width: 180.278px;" | 6 | |||
| style="height: 28px; width: 115.22px;" | 7 | |||
|}Es soll nun untersucht werden, ob sich die fünf beobachteten Variablen auf wenige latente Faktoren reduzieren lassen.Ausgangspunkt ist die Korrelations-Matrix der Daten: | |||
* '''Margarine<-read.csv("C:\\...\\...\\Margarine.csv",header=TRUE,dec=",",sep=";")''' | |||
* '''Marke<-Margarine[,1]''' | |||
* '''Margarine<-Margarine[,-1]''' | |||
In der ersten Spalte des Datensatzes sind die Markennamen. Diese werden gespeichert. Weitergerechnet wird dann ohne die erste Spalte. | |||
* '''cor(Margarine)''' | |||
{| | {| style="border-collapse: collapse; height: 168px; background-color: rgb(149, 165, 166); float: left;" border="1" | ||
! width=" | ! style="height: 28px; width: 179.236px;" | | ||
! width=" | ! style="height: 28px; width: 169.167px;" | Anteil unge-sättigter FS | ||
! width=" | ! style="height: 28px; width: 179.236px;" | Kaloriengehalt | ||
! style="height: 28px; width: 169.167px;" | Vitamingehalt | |||
! style="height: 28px; width: 138.958px;" | Haltbarkeit | |||
| | ! style="height: 28px; width: 118.854px;" | Preis | ||
| | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 179.236px;" | Anteil unge-sättigter FS | ||
| | | style="height: 28px; width: 169.167px;" | 1 | ||
| style="height: 28px; width: 179.236px;" | ,712 | |||
| | | style="height: 28px; width: 169.167px;" | ,961 | ||
| style="height: 28px; width: 138.958px;" | ,109 | |||
| | | style="height: 28px; width: 118.854px;" | ,044 | ||
|- style="height: 28px;" | |||
|- | | style="height: 28px; width: 179.236px;" | Kaloriengehalt | ||
| | | style="height: 28px; width: 169.167px;" | ,712 | ||
| | | style="height: 28px; width: 179.236px;" | 1 | ||
| | | style="height: 28px; width: 169.167px;" | ,704 | ||
| | | style="height: 28px; width: 138.958px;" | ,138 | ||
| style="height: 28px; width: 118.854px;" | ,067 | |||
| | |- style="height: 28px;" | ||
| style="height: 28px; width: 179.236px;" | Vitamingehalt | |||
|- | | style="height: 28px; width: 169.167px;" | ,961 | ||
| | | style="height: 28px; width: 179.236px;" | ,704 | ||
| | | style="height: 28px; width: 169.167px;" | 1 | ||
| | | style="height: 28px; width: 138.958px;" | ,078 | ||
| | | style="height: 28px; width: 118.854px;" | ,024 | ||
| | |- style="height: 28px;" | ||
| style="height: 28px; width: 179.236px;" | Haltbarkeit | |||
|- | | style="height: 28px; width: 169.167px;" | ,109 | ||
| | | style="height: 28px; width: 179.236px;" | ,138 | ||
| | | style="height: 28px; width: 169.167px;" | ,078 | ||
| | | style="height: 28px; width: 138.958px;" | 1 | ||
| | | style="height: 28px; width: 118.854px;" | ,983 | ||
| | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 179.236px;" | Preis | ||
| style="height: 28px; width: 169.167px;" | ,044 | |||
| style="height: 28px; width: 179.236px;" | ,067 | |||
| style="height: 28px; width: 169.167px;" | ,024 | |||
| style="height: 28px; width: 138.958px;" | ,983 | |||
| style="height: 28px; width: 118.854px;" | 1 | |||
|} | |} | ||
Die | Es zeigen sich hier sehr schön zwei untereinander jeweils hoch korrelierte Blöcke von Variablen. Auf Basis der Korrelationsmatrix könnte ein Faktor für die ersten drei und ein Faktor für die letzten zwei Variablen gewählt werden. Aufgrund der niedrigen Korrelationen abseits dieser Blöcke wäre die Unkorreliertheit der beiden Faktoren wohl auch einigermaßen sichergestellt. | ||
* '''Margarine<-scale(Margarine)''' | |||
# bewirkt, dass die Variablen auf Mittelwert 0 und Varianz 1 standardisiert werden. | |||
Bei der Faktorenanalyse ist dieses Vorgehen durchaus üblich, da man im wesentlichen an der Korrelationsstruktur (statt an den Kovarianzen) interessiert ist. | |||
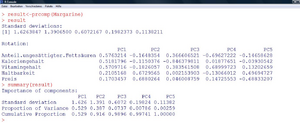
Die eigentliche Analyse geschieht nun mit der Funktion „prcomp“ (Abbildung 33). Der Output der Funktion liefert einerseits die Standardabweichungen der extrahierten Faktoren und andererseits die Hauptachsentransformation (unter „Rotation“). Dass die Methode schrittweise jene Richtungen extrahiert, die größtmögliche Varianz erklären, sieht man auch an der absteigenden Folge der Standardabweichungen. Die erste Komponente hat Standardabweichung 1,6264 und damit Varianz 1,6264<sup>2</sup>=2,645. Nachdem eine Gesamtvarianz von 5 aufzuteilen ist, bedeutet das, dass die erste Komponente bereits 2,645/5=52,9% an Varianz erklärt. Die zweite Komponente hat eine Varianz von 1,3907<sup>2</sup>=1,934 und liefert damit weitere 1,934/5=38,7% an Erklärung. Zusammen sind das bereits 91,6%. Mit dem Befehl „summary“ (siehe weiter Abbildung 33) bekommt man diese Varianzzerlegung ausgegeben. | |||
|} | |||
[[file:img1642217907396.png|300px|none|thumb|Faktorenanalyse in R - Teil 1]] | |||
Hat man für sich selbst z.B. im Vorhinein bestimmt, dass jene Faktorenzahl gewählt wird, dass zumindest 80% der Varianz erklärt werden, würde man sich mittels dieses Kriteriums für zwei Variablen entscheiden. | |||
=== Das Kaiser-Kriterium === | |||
Das Kaiser-Kriterium (Kaiser & Dickman, 1959, zitiert in Fahrmeir et al., 1996, S. 669) wählt jene Komponenten aus, die überdurchschnittlich an Varianz beitragen. Bei auf Varianz 1 skalierten Daten ist bei<math></math> Variablen eine Varianz von <math></math> aufzuteilen. Es werden daher jene Komponenten gewählt, deren Varianz größer als 1 ist. | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Fortsetzung Beispiel 13''' | |||
Nur die ersten beiden Standardabweichungen/Varianzen (Eigenwerte) sind größer 1. Daher werden nach diesem Kriterium ebenfalls zwei Komponenten gewählt. | |||
|} | |} | ||
=== | === Der Scree-Plot === | ||
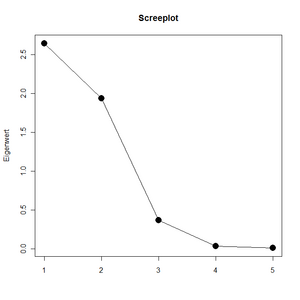
Ein visuelles Kriterium stellt der Screeplot dar, der die einzelnen Varianzen absteigend nebeneinander aufträgt und mit Linien verbindet (Abbildung 34). Gewählt werden nun (von links) alle Komponenten bis zu jenem Punkt (exklusive), an dem der weitere Linienverlauf nach rechts im wesentlichen einer Gerade entspricht. | |||
[[file:img1642160505806.png|300px|none|thumb|Screeplot Beispiel 13]] | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Fortsetzung Beispiel 13''' | |||
In Abbildung 34 ist ersichtlich, dass der größte Abfall von Komponente 2 auf Komponente 3 passiert. Dann fällt die Linie relativ flach weiter. Nach diesem Kriterium können zwei, eventuell auch drei Komponenten gewählt werden. | |||
|} | |||
== Weitere Analyse und Interpretation == | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! style="text-align: left;" width="100%" | '''Fortsetzung Beispiel 13''' | |||
Laut der Analyse im letzten Abschnitt empfiehlt sich die Wahl von zwei Hauptkomponenten. Das heißt, dass in Abbildung 33 die ersten beiden Spalten der Transformationsmatrix gewählt und interpretiert werden müssen. Die Koeffizienten geben die relative Bedeutung an. | |||
Faktor 1 berechnet sich als | |||
0,576 * Anteil ungesättigter Fettsäuren + 0,518 * Kaloriengehalt | |||
+0,571 * Vit.-Gehalt + 0,211 * Haltbarkeit + 0,170 * Preis. | |||
|- | |- | ||
| | | style="text-align: left;" | | ||
| | Demnach sind im ersten extrahierten Faktor eher die ersten drei Variablen in etwa gleicher Stärke ausgedrückt. Inhaltlich könnte dieser Faktor mit „Gesundheit“ bezeichnet werden. | ||
In Komponente 2 sind die letzten beiden Variablen stärker gewichtet. Daher kann Komponente 2 als „Wirtschaftlichkeit“ interpretiert werden. | |||
|} | |} | ||
Der Zweck der Faktorenanalyse ist Datenreduktion. Daher ist das nächste Ziel, die (standardisierten) Originaldaten nun in den neuen gemeinsamen Faktoren darzustellen. Dazu wird die Datenmatrix mit den ersten <math></math> Spalten der Transformationsmatrix multipliziert. | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! style="text-align: left;" width="100%" | '''Fortsetzung Beispiel 13''' | |||
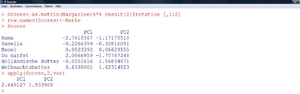
Die Werte der ursprünglichen Variablen in den neuen gemeinsamen Faktoren werden in der Matrix „Scores“ zusammengefasst (Abbildung 35). Hohe Werte stehen für gute Gesundheitswerte bzw. hohe Wirtschaftlichkeit. Man kann so die Datenpunkte im neuen Datenraum veranschaulichen und auch in einem XY-Scatterplot darstellen. Beispielsweise ist „Du darfst“ am „gesündesten“, und hat den niedrigsten Wert bzgl. Wirtschaftlichkeit, was geringem Preis und geringer Haltbarkeit entspricht. | |||
|- | |||
| style="text-align: left;" | | |||
[[file:img1642166365426.png|300px|none|thumb|Faktorenanalyse in R - Teil 2]] | |||
Berechnet man nun von beiden Faktoren die Varianzen, erhält man wieder die bekannten Werte von vorhin. | |||
|} | |} | ||
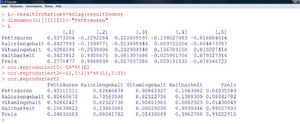
Multipliziert man die Spalten der Transformationsmatrix mit der jeweiligen Standardabweichung (Abbildung 33), erhält man die Ladungsmatrix mit den Einträgen <math>l_{i j}</math>. Diese ist insofern interessant, als hier die Korrelationen der einzelnen Variablen mit den einzelnen Faktoren abgelesen werden können. Außerdem kann dort für jede Variable die sogenannte „Kommunalität“ <math>h_{i}^{2}</math> ermittelt werden. Diese gibt jeweils an, wieviel Prozent der Varianz der Variable durch den gewählten Satz gemeinsamer Faktoren erklärt wird. Die Formel lautet | |||
<math display="block"> | |||
h_{i}^{2}=\sum_{j=1}^{k} l_{i j}^{2} | |||
</math> | |||
== | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Fortsetzung Beispiel 13''' | |||
Abbildung 36 zeigt die Erzeugung der Ladungsmatrix <math>L</math> aus der Transformationsmatrix in R. Wir sehen, dass die ersten drei Variablen eine sehr hohe Korrelation mit dem ersten Faktor aufweisen. Haltbarkeit und Preis hingegen korrelieren mit dem zweiten gewählten Faktor zu 0,94 bzw. 0,96. Auch hier sieht man, dass ein dritter Faktor nicht mehr erforderlich ist, da hier kaum noch hohe Korrelationen zu den Variablen zu beobachten sind. | |||
Welche Variablen werden nun durch die ersten beiden Komponenten gut erklärt? | |||
{ | Die Kommunalität des „Anteils ungesättigter Fettsäuren“ beträgt z.B. <math>h_{1}^{2}=0,937^{2}+(-0,229)^{2}=93,1 \%</math>. Also werden 93,1% der Varianz der Variable „Anteil ungesättigter Fettsäuren“ durch die beiden Komponenten erklärt. | ||
[[file:img1642174987811.png|300px|none|thumb|Faktorenanalyse in R - Teil 3]] | |||
Der Kreis schließt sich nun wieder, da unser ursprüngliches Ziel war, die Korrelationsstruktur der Daten zu erklären. Wie gut das gelingt, kann durch die Matrix der durch die zwei gemeinsamen Faktoren reproduzierten Korrelationen ermittelt werden. Diese ist nun mit der ursprünglichen Korrelationsmatrix zu vergleichen. | |||
Beispielsweise beträgt die Korrelation zwischen Kalorien- und Vitamingehalt ursprünglich 0,704. Aufgrund der beiden gewählten Faktoren kommt man auf eine Korrelation von 0,823. Für diese Korrelation ergibt sich daher ein Residuum von <math>0,704-0,823=-0,119</math>. Die Residuen der Hauptdiagonalelemente (<math>\left(1-h_{i}^{2}\right)</math>) sind die durch die Faktoren nicht erklärten Varianzanteile der Variablen. | |||
|} | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
< | ! width="100%" | '''Aufgabe 16''' | ||
Berechnen Sie die Kommunalitäten für die restlichen vier Variablen aus Beispiel 13 und vergleichen Sie ihre Werte mit den Hauptdiagonalelementen der reproduzierten Korrelationsmatrix. | |||
|} | |||
== Faktorrotation == | |||
Wie bereits erwähnt, gibt es für <math>1<k<p</math> mehrere (unendlich viele) Lösungen für <math>L</math>, die allesamt die maximale Varianz erklären. Diese unterscheiden sich wieder durch „Drehungen“ im Raum. Das heißt, die gefundene Matrix <math>L</math> kann durch Multiplikation einer beliebigen <math>k \times k</math>-Matrix mit orthonormalen Spalten transformiert werden, sodass die neue Matrix <math>L^t</math> den gleichen maximal erklärten Varianzanteil liefert. Dies macht man sich zunutze, um jene Lösungen für<math>L</math> auszuwählen, die besonders leicht zu interpretieren sind. Das ist dann möglich, wenn die Ladungen entweder nahe bei 1 oder nahe bei 0 sind. Mit anderen Worten heißt das, dass die Varianz der Koeffizienten maximiert werden soll. Die Faktorrotationsmethoden, die die Varianz der Ladungen spalten- bzw. zeilenweise maximieren, heißen Varimax bzw. Quartimax. | |||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | |||
! width="100%" | '''Fortsetzung Beispiel 13''' | |||
Die Ladungskoeffizienten in Beispiel 13 enthalten bereits inhaltlich gut interpretierbare Werte und müssen nicht weiter transformiert werden. Wird dennoch eine Transformation durchgeführt, heißt das, dass sich an der erklärten Varianz von 91,6% nichts ändert. Lediglich die Aufteilung 52,9%:38,7% ändert sich zugunsten des zweiten Faktors, da nicht mehr erforderlich ist, dass die erste Komponente die maximale Varianz erklärt. | |||
|} | |} | ||
== Wiederholungsaufgaben und Zusammenfassung == | == Wiederholungsaufgaben und Zusammenfassung == | ||
# | # Berechnen Sie die Residuen der reproduzierten Korrelationen in Beispiel 13 und geben Sie an, welche Korrelation am schlechtesten durch die gefundene Faktorlösung dargestellt wird. | ||
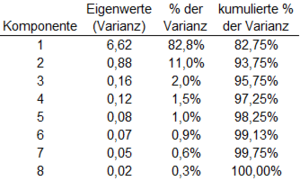
# | # Sie erhalten als Ergebnis einer Faktorenanalyse folgende erklärte Varianzen: | ||
<blockquote>[[Datei:Mt422 a1.png|300px|none|thumb]]</blockquote> | |||
* Wieviele Faktoren müssen Sie nehmen, wenn Sie zumindest 90% der Varianz erklären wollen? | |||
* Wieviele Faktoren müssen Sie nach dem Kaiser-Kriterium wählen? | |||
* Für wieviele Faktoren würden Sie sich mittels zugehörigem Scree-Plot entscheiden? | |||
<ol style="list-style-type: decimal;" start="3"> | |||
<li><p>Zeichnen Sie für die ersten beiden Spalten der Matrix <math>L</math> (Abbildung 36) einen XY-Scatterplot (in R: „'''plot(x,y)'''“) und beschreiben Sie verbal das Ergebnis der Analyse.</p></li> | |||
</ol> | |||
==== Zusammenfassung ==== | |||
Im Gegensatz zu den vorangegangenen Lektionen wird bei den Verfahren der Faktorenanalyse die (Korrelations-)Struktur eines Satzes von Variablen untersucht. Die Fragestellung ist, ob und wie diese Struktur durch einige wenige Variablen erklärt werden kann. Der Input bei diesen Verfahren ist daher die Kovarianz- bzw. Korrelationsmatrix, der Output im wesentlichen die Ladungsmatrix, die bestimmt, in welcher Art und Weise die gefundenen Faktoren durch die Originalvariablen bestimmt werden. | |||
Es existieren viele Methoden, Faktoren zu bestimmen. Neben der Maximum-Likelihood-Faktorenanalyse hat sich die Hauptkomponentenanalyse als beliebtes und häufig verwendetes Verfahren herausgestellt. In deren Rahmen wird zunächst eine Hauptachsentransformation in Komponenten, die schrittweise maximale Varianz an den Originaldaten erklären, durchgeführt. Setzt man dieses Verfahren dazu ein, um einen guten Satz an Variablen zu bekommen, wird dies die „Hauptkomponentenmethode“ genannt. Eine weitere sich aus dem Verfahren ableitende, iterative Vorgehensweise, bei der das Gewicht stärker auf der Erklärung der Kovarianzen anstelle der Varianzen liegt, ist die Hauptfaktorenanalyse. | |||
Die Anzahl an ausgewählten Faktoren wird zumeist durch einen vorgegebenen minimal erforderlichen, erklärten Varianzanteil, durch das Kaiser-Kriterium oder den Scree-Plot ermittelt und sind daher teilweise subjektiv. Die vollständige Darstellung der Faktorenanalyse umfasst schließlich noch eine Darstellung der Beobachtungseinheiten im neu transformierten Raum sowie weiteren, die Güte der Analyse beschreibenden Darstellungen, wie z.B. der Matrix der reproduzierten Korrelationen. | |||
Wichtig ist nochmals zu erwähnen, dass die Verfahren der (exploratorischen) Faktorenanalyse praktisch keine Hypothesenprüfungen zulassen. Die Ergebnisse sind auch nicht „richtig“ oder „falsch“, sondern bieten eine mathematische Unterstützung zur Dokumentation von Zusammenhangsstrukturen. | |||
Aktuelle Version vom 9. März 2023, 08:12 Uhr
Faktorenanalyse
Wichtiges Ziel der Lektion ist die Erkenntnis, welche Aussagen über nichtbeobachtbare Merkmale aufgrund der Korrelationsstruktur eines Satzes von vorhandenen Variablen abgeleitet werden können. Die Grundlagen der Faktorenanalyse als Basis von Strukturmodellen und die Darstellung der subjektiven Entscheidungen, die im Zuge einer Faktorenanalyse getroffen werden müssen sind ebenso Schwerpunkte, wie die Analyse der Daten in R.
Einführung
Die in den ersten beiden Lektionen besprochenen Verfahren der Regressions- bzw. Varianzanalyse eignen sich, um den Zusammenhang zwischen einem Satz an ausgewählten Variablen und einer davon abhängigen Variable zu testen. Oft kommt es allerdings vor, dass die Menge an potentiellen Variablen relativ groß ist, einzelne Variablen hoch miteinander korrelieren, oder man nicht am Einfluss der Variablen auf eine abhängige Variable, sondern an der Korrelationsstruktur bzw. an latenten (=nicht beobachtbaren), den Daten zugrundeliegenden Faktoren interessiert ist. Den zweiten Fall haben wir bei Beispiel 1 gehabt. Hier waren Spritverbrauch in der Stadt bzw. auf der Autobahn klarerweise hoch korreliert und damit war schwer abzuschätzen, wie groß der Anteil jeder der beiden Variablen an der Erklärung des Preises ist (im gewählten Modell kam dann jedoch ohnehin keine der beiden Variablen vor). Für den Fall, dass man an latenten Faktoren interessiert ist, gibt es folgende Beispiele:
- Menschliches Verhalten ist beispielsweise von einer Vielzahl an Einflussfaktoren abhängig. In Fragebögen, die das Verhalten in bestimmten Situationen abfragen, werden oft viele ähnliche Fragen, die miteinander hoch korrelieren, gestellt. Letztendlich will man dabei aber latente Konstrukte, wie z.B. „Aggresionspotential“ oder „Verlässlichkeit“ erheben.
- Erhebung von Prädiktoren für die Kreditwürdigkeit von Kunden einer Bank. Bekannt sind zahlreiche Kundenvariablen, die hoch korreltiert sind und verdichtet werden können.
- Welche Fähigkeiten liegen Leistungen in Intelligenztests zugrunde? Es existieren viele verschiedene (ähnliche Tests), bei denen hochkorrelierte Leistungen zu beobachten sind. Welche (nicht beobachtbaren) Faktoren liegen diesen Leistungen zugrunde?
Die Faktorenanalyse bedient sich nun mathematischer Verfahren, die es ermöglichen, viele, miteinander hoch korrelierende Variablen auf einige wenige, nicht korrelierenden Faktoren umzurechnen, sodass die Information (Varianz) der Daten aber weitgehend vorhanden bleibt.
| Beispiel 10 (Extrembeispiel)
Angenommen Sie wollen den Umsatz von Speiseeis in Wien in Abhängigkeit von der jeweils um 12h in der Wiener Innenstadt gemessenen Temperatur vorhersagen. Sie messen die Temperatur in Grad Celsius, in Fahrenheit und in Kelvin. Anschließend führen Sie eine multiple lineare Regression des Speiseeisumsatzes, die alle drei Variablen als Erklärung enthält, durch. Aufgrund der Tatsache, dass zwischen den drei Skalen mittels Lineartransformation umgerechnet werden kann [1] (exakte Multikollinearität), ergeben sich für die Koeffizientenschätzungen unendlich große Varianzen und beliebige Werte. Die Information, die in allen drei Variablen steckt, kann ohne Verlust mit einer der drei Temperaturvariablen dargestellt werden. |
|---|
Die im folgenden dargestellten Methoden betreffen die explorative Faktorenanalyse. Mit ihrer Hilfe können keine Wirkzusammenhänge inferenzstatistisch geprüft werden, sondern es können nur Zusammenhangsstrukturen exploriert werden. Demgegenüber steht die konfirmatorische Faktorenanalyse, bei der hypothesenprüfend vorgegangen wird. Diese ist ein Spezialfall der in der folgenden Lektion vorgestellten Strukturgleichungsmodelle und wird dort betrachtet.
Für die explorative Faktorenanalyse gilt weiters, dass hier einige subjektive Entscheidungen des Anwenders im Analyseprozess erforderlich sind. Man ist mehr als bei anderen statistischen Verfahren auf Vermutungen angewiesen. Die Faktorenanalyse versteht sich eher als mathematisches Hilfsmittel, welches logisch begründeten Strukturtheorien zur Seite gestellt wird.
Die Faktorenanalyse geht zurück auf Spearman, der diese ursprünglich 1904 zum Zwecke der Intelligenzmessung verwendet hat. Das einleitende Beispiel im folgenden Abschnitt widmet sich daher diesem Thema.
Modellvorstellung
| Beispiel 11
Schulnoten sind Indikatoren für den unbekannten Faktor Intelligenz. Es werden aus Gründen der Einfachheit zwei voneinander unabhängige Intelligenzen (quantitative Intelligenz, Q, und verbale Intelligenz, V) postuliert. Folgende beispielhafte Annahme über das Zustandekommen der Noten in sechs verschiedenen Fächern werden getroffen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Math }=0,80 * Q+0,20 * V+A_{m}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Phys }=0,70 * Q+0,30 * V+A_{p}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Chem }=0,60 * Q+0,30 * V+A_{c}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Eng }=0,20 * Q+0,80 * V+A_{e}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Hist }=0,15 * Q+0,82 * V+A_{h}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Fran }=0,25 * Q+0,85 * V+A_{f}} Die Noten setzen sich also mittels Linearkombination aus den beiden Intelligenzen plus einem spezifischen Faktor für das jeweilige Fach zusammen. |
|---|
Die Koeffizienten der Regressiongleichungen aus Beispiel 11 heißen „Ladungen“. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V} heißen „gemeinsame Faktoren“.
Wird nun ein derartiger Zusammenhang unterstellt, können auch die paarweisen Korrelationen zwischen je zwei Schulnoten (Fächern) daraus abgeleitet werden.
Bei der Faktorenanalyse kennt man die in Beispiel 11 getroffene Annahme nicht. Man beschreitet hier den umgekehrten Weg. Gegeben sind alle paarweisen Korrelationen (im Beispiel die Korrelationen zwischen den Schulnoten) und gesucht sind die (in Beispiel 11) gegebenen Ladungen.
Es werden dann einige mathematisch-statistische Restriktionen gemacht, um das Schätzproblem bei der Faktorenanalyse etwas genauer zu spezifizieren. Beispielsweise muss gefordert werden, dass die gemeinsamen Faktoren untereinander unabhängig sind. Das heißt, wenn jemand eine hohe quantitative Intelligenz hat, dann kann daraus keine Tendenz über die verbale Intelligenz geschlossen werden. Außerdem wir gefordert, dass die gemeinsamen Faktoren von den spezifischen Faktoren unabhängig sind.
Notiert wird das Modell der Faktorenanalyse in den gängigen Lehrbüchern in Matrixschreibweise (analog zu Beispiel 11):
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y=F L^{t}+E }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y}
die bereits spaltenweise auf Mittelwert Null zentrierte Datenmatrix (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n \times p, n}
Versuchseinheiten und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p}
Variablen), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F}
die Matrix (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (n \times k)}
), die die gemeinsamen Faktoren enthält, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L}
die Ladungsmatrix (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p \times k}
) und die ()- Matrix der Einzelrestwerte ist. In Beispiel 11 ist und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K=2}
.
Aufgrund der vielen Unbekannten in diesem Modell ist dieses nicht empirisch überprüfbar bzw. uneindeutig. Durch die erwähnten mathematischen Annahmen lässt sich aber die für die Faktorenanalyse zentrale, unter bestimmten Umständen eindeutige Zerlegung bilden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\Sigma}=\mathbf{L} \mathbf{L}^{\mathrm{t}}+\mathbf{V}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Sigma} ist die sogenannte „Varianz-Kovarianzmatrix“ der Daten. Sie enthält in der Hauptdiagonale alle Varianzen der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} Variablen und abseits davon alle Kovarianzen. Die Varianz-Kovarianz-Matrix (bzw. bei standardisierten Variablen die Korrelationsmatrix) ist der wesentliche Input bei einer Faktorenanalyse, den es zu analysieren gilt. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} ist eine Diagonalmatrix mit den Varianzen der spezifischen Faktoren. Das wesentliche Ziel bei der Faktorenanalyse ist es nun, eine jener Matrizen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} zu finden, für die diese Zerlegung möglich ist, und zwar für eine minimale Anzahl an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} zugrundeliegenden gemeinsamen Faktoren.
Faktorextraktion
Es gibt nun verschiedene Schätzmethoden, um die Ladungsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} zu schätzen.
Die Maximum-Likelihood-Methode
Diese bedient sich einem in der Statistik weit verbreiteten Konzept zur Konstruktion von Schätzern. Es wird hier eine multivariate Normalverteilung der beobachteten Daten unterstellt. Als Folge davon kann analytisch jener Schätzer für die Ladungsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} ] ermittelt werden, der unter dieser Annahme am plausibelsten ist. Hier wird also stochastisch durch Verteilungsannahmen argumentiert. Die Wahl, wieviele Faktoren (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} ) gewählt werden, kann unter anderem durch statistische Hypothesentests erfolgen.
Die Hauptkomponentenanalyse
Die Ergebnisse der Hauptkomponentenanalyse erhält man ebenfalls durch Optimierung. Kriterium ist, dass die (zentrierte) Datenmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} durch Multiplikation mit einer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k \times k-} -Matrix (mit orthonormalen Spalten) derart transformiert wird, dass die Spalten der so transformierten Matrix jeweils schrittweise die höchste Varianz erzeugen. Dieser Vorgang wird Hauptachsentransformation genannt. Diese sehr theoretisch beschriebene Vorgehensweise soll anhand eines Beispieles skizziert werden (Abbildung 32).
| Beispiel 12
Abbildung 32 zeigt sieben Datenpunkte in zwei Variablen. In der linken Abbildung kann die Varianz in X- bzw. Y-Richtung durch Normalprojektion an die jeweiligen Achsen geschätzt werden. Die Daten sind so gewählt, dass sowohl die Varianz in X- als auch in Y-Richtung gleich 1 ist. Geometrisch gesehen wird bei der Hauptachsentransformation das Koordinatensystem solange gedreht, bis die größte der Varianzen der projizierten Datenpunkte auf die neuen Achsen maximal wird. Diese Drehung entspricht in diesem Beispiel 45 Grad und führt dazu, dass die Varianz der Daten auf der Achse von links unten nach rechts oben 1,501 beträgt. Dies ist die größte erzielbare Varianz auf einer Achse. Die Werte auf der zweiten Achse weisen eine Varianz von 0,499 auf. Nachdem die Daten nur zwei Dimensionen haben, bleibt für die zweite Achse nur mehr eine Richtung. Im allgemeinen wird jedoch für die zweite Achse jene Richtung gewählt, die ihrerseits wieder die maximale Varianz liefert. In Summe sind die Varianzen in beiden Richtungen sowohl in der Grafik links als auch rechts gleich 2. Sie teilen sich nur anders auf. Um wieder zu obigen Text zurückzukehren: Die hier angewandte Transformation bedeutet rechnerisch eine Multiplikation der Datenmatrix mit der Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{L}=\left(\begin{array}{cc} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right) } |
|---|
Wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=p} gewählt, heißt das, dass die volle Varianz erklärt wird (d.h. die volle Information erhalten bleibt). Die (bei hoher Korrelation in den Daten stark) ungleiche Varianzzerlegung macht man sich aber zunutze um nun die ersten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} interessierenden Achsen zu wählen und die anderen zu eliminieren. Damit erzielt man einen Kompromiss zwischen Datenreduktion und Informationsverlust. Der Anteil der Summe aller bis zur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} -ten Achse erklärten Varianzen an der Gesamtzahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} der Variablen im Originaldatensatz ist der erklärte Varianzanteil. Dieser ist ein Kriterium zur Bestimmung, auf wieviele Achsen die Daten reduziert werden sollen.
| Fortsetzung Beispiel 12
Die Varianz der Daten an der ersten transformierten Achse beträgt 1,501. Die Anzahl der Originalvariablen bzw. die Summe derer Varianzen beträgt 2. Daher beträgt der erklärte Varianzanteil bei alleiniger Datenreduktion auf eine Achse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1.501}{2}=75 \%} . |
|---|
| Aufgabe 15
Angenommen es liegt ein Satz von acht (auf Varianz gleich Eins) standardisierten, korrelierten Variablen vor, der mittels Hauptkomponentenmethode reduziert werden soll.
|
|---|
Die eben diskutierte Vorgehensweise nur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k<p} Achsen aus der transformierten Matrix zur Erklärung der Originaldaten auszuwählen, wird „Hauptkomponentenmethode“ genannt. Während bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=p} nur eine Lösung existiert, den gesamt erklärten Varianzanteil zu maximieren, ist die Lösung bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1<k<p} gewählten Achsen nicht eindeutig. Darauf wird in Abschnitt 5.6 eingegangen.
Die Lösung der Hauptkomponentenanalyse wird im Normalfall nicht graphisch durchgeführt, sondern reduziert sich – mathematisch gesehen – auf das Finden der Eigenwerte der Korrelations- bzw. Kovarianzmatrix der Daten. Deshalb liest man statt erklärten Varianzanteilen in Software-Outputs von Faktorenanalysen auch immer wieder von Eigenwerten. Die Varianzen der Daten in den einzelnen Richtungen sind gerade durch diese Eigenwerte gegeben.
Die Hauptkomponentenmethode ist die am häufigsten angewandte Methode zur Extraktion von Faktoren. Der Grund ist auch, dass hier im Gegensatz zu anderen Berechnungsmethoden kein iteratives Vorgehen benötigt wird. Im Hinblick zur eigentlichen Faktorenanalyse wird hier kein Modell zugrundegelegt, sondern es wird lediglich eine technische Optimierungsaufgabe zur Datenreduktion durchgeführt. Eine Methode, die die Hauptkomponentenmethode verwendet um in einem iterativen Prozess (wie vorher erwünscht) statt den Varianzen die Anpassung an die Korrelationsmatrix optimiert, ist die Hauptfaktorenanalyse. Auf diese wird aber aus Platzgründen nicht weiter eingegangen.
Bestimmung der Anzahl an Faktoren
Die wesentlichste Frage, wenn mittels Hauptkomponentenanalyse versucht wird, einen Satz von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k<p} Dimensionen – die „gemeinsamen Faktoren“ – zu ermitteln, ist, wie groß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} nun sein soll. Dazu gibt es drei häufig verwendete Kriterien.
Die erklärte Varianz
Ein mögliches Kriterium kann sein, dass man einen gewissen Anteil an erklärter Varianz nicht unterschreiten will, da man sonst nicht mehr das Gefühl hat, die ursprünglichen Daten mit dem reduzierten Datensatz gut zu beschreiben.
| Beispiel 13
Im diesem Beispiel (Backhaus et al., 2003) sind die mittels Fragebogen von mehreren Personen erhobenen Eigenschaften von sechs Margarinesorten erhoben. Die Daten beschreiben die Mittelwerte der Stichprobe, die auf einer Ratingskala zwischen 1 und 7 bewertet wurden.
In der ersten Spalte des Datensatzes sind die Markennamen. Diese werden gespeichert. Weitergerechnet wird dann ohne die erste Spalte.
Es zeigen sich hier sehr schön zwei untereinander jeweils hoch korrelierte Blöcke von Variablen. Auf Basis der Korrelationsmatrix könnte ein Faktor für die ersten drei und ein Faktor für die letzten zwei Variablen gewählt werden. Aufgrund der niedrigen Korrelationen abseits dieser Blöcke wäre die Unkorreliertheit der beiden Faktoren wohl auch einigermaßen sichergestellt.
Bei der Faktorenanalyse ist dieses Vorgehen durchaus üblich, da man im wesentlichen an der Korrelationsstruktur (statt an den Kovarianzen) interessiert ist. Die eigentliche Analyse geschieht nun mit der Funktion „prcomp“ (Abbildung 33). Der Output der Funktion liefert einerseits die Standardabweichungen der extrahierten Faktoren und andererseits die Hauptachsentransformation (unter „Rotation“). Dass die Methode schrittweise jene Richtungen extrahiert, die größtmögliche Varianz erklären, sieht man auch an der absteigenden Folge der Standardabweichungen. Die erste Komponente hat Standardabweichung 1,6264 und damit Varianz 1,62642=2,645. Nachdem eine Gesamtvarianz von 5 aufzuteilen ist, bedeutet das, dass die erste Komponente bereits 2,645/5=52,9% an Varianz erklärt. Die zweite Komponente hat eine Varianz von 1,39072=1,934 und liefert damit weitere 1,934/5=38,7% an Erklärung. Zusammen sind das bereits 91,6%. Mit dem Befehl „summary“ (siehe weiter Abbildung 33) bekommt man diese Varianzzerlegung ausgegeben. |
|---|
Hat man für sich selbst z.B. im Vorhinein bestimmt, dass jene Faktorenzahl gewählt wird, dass zumindest 80% der Varianz erklärt werden, würde man sich mittels dieses Kriteriums für zwei Variablen entscheiden.
Das Kaiser-Kriterium
Das Kaiser-Kriterium (Kaiser & Dickman, 1959, zitiert in Fahrmeir et al., 1996, S. 669) wählt jene Komponenten aus, die überdurchschnittlich an Varianz beitragen. Bei auf Varianz 1 skalierten Daten ist bei Variablen eine Varianz von aufzuteilen. Es werden daher jene Komponenten gewählt, deren Varianz größer als 1 ist.
| Fortsetzung Beispiel 13
Nur die ersten beiden Standardabweichungen/Varianzen (Eigenwerte) sind größer 1. Daher werden nach diesem Kriterium ebenfalls zwei Komponenten gewählt. |
|---|
Der Scree-Plot
Ein visuelles Kriterium stellt der Screeplot dar, der die einzelnen Varianzen absteigend nebeneinander aufträgt und mit Linien verbindet (Abbildung 34). Gewählt werden nun (von links) alle Komponenten bis zu jenem Punkt (exklusive), an dem der weitere Linienverlauf nach rechts im wesentlichen einer Gerade entspricht.
| Fortsetzung Beispiel 13
In Abbildung 34 ist ersichtlich, dass der größte Abfall von Komponente 2 auf Komponente 3 passiert. Dann fällt die Linie relativ flach weiter. Nach diesem Kriterium können zwei, eventuell auch drei Komponenten gewählt werden. |
|---|
Weitere Analyse und Interpretation
| Fortsetzung Beispiel 13
Laut der Analyse im letzten Abschnitt empfiehlt sich die Wahl von zwei Hauptkomponenten. Das heißt, dass in Abbildung 33 die ersten beiden Spalten der Transformationsmatrix gewählt und interpretiert werden müssen. Die Koeffizienten geben die relative Bedeutung an. Faktor 1 berechnet sich als 0,576 * Anteil ungesättigter Fettsäuren + 0,518 * Kaloriengehalt +0,571 * Vit.-Gehalt + 0,211 * Haltbarkeit + 0,170 * Preis. |
|---|
|
Demnach sind im ersten extrahierten Faktor eher die ersten drei Variablen in etwa gleicher Stärke ausgedrückt. Inhaltlich könnte dieser Faktor mit „Gesundheit“ bezeichnet werden. In Komponente 2 sind die letzten beiden Variablen stärker gewichtet. Daher kann Komponente 2 als „Wirtschaftlichkeit“ interpretiert werden. |
Der Zweck der Faktorenanalyse ist Datenreduktion. Daher ist das nächste Ziel, die (standardisierten) Originaldaten nun in den neuen gemeinsamen Faktoren darzustellen. Dazu wird die Datenmatrix mit den ersten Spalten der Transformationsmatrix multipliziert.
| Fortsetzung Beispiel 13
Die Werte der ursprünglichen Variablen in den neuen gemeinsamen Faktoren werden in der Matrix „Scores“ zusammengefasst (Abbildung 35). Hohe Werte stehen für gute Gesundheitswerte bzw. hohe Wirtschaftlichkeit. Man kann so die Datenpunkte im neuen Datenraum veranschaulichen und auch in einem XY-Scatterplot darstellen. Beispielsweise ist „Du darfst“ am „gesündesten“, und hat den niedrigsten Wert bzgl. Wirtschaftlichkeit, was geringem Preis und geringer Haltbarkeit entspricht. |
|---|
|
Berechnet man nun von beiden Faktoren die Varianzen, erhält man wieder die bekannten Werte von vorhin. |
Multipliziert man die Spalten der Transformationsmatrix mit der jeweiligen Standardabweichung (Abbildung 33), erhält man die Ladungsmatrix mit den Einträgen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{i j}} . Diese ist insofern interessant, als hier die Korrelationen der einzelnen Variablen mit den einzelnen Faktoren abgelesen werden können. Außerdem kann dort für jede Variable die sogenannte „Kommunalität“ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{i}^{2}} ermittelt werden. Diese gibt jeweils an, wieviel Prozent der Varianz der Variable durch den gewählten Satz gemeinsamer Faktoren erklärt wird. Die Formel lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{i}^{2}=\sum_{j=1}^{k} l_{i j}^{2} }
| Fortsetzung Beispiel 13
Abbildung 36 zeigt die Erzeugung der Ladungsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} aus der Transformationsmatrix in R. Wir sehen, dass die ersten drei Variablen eine sehr hohe Korrelation mit dem ersten Faktor aufweisen. Haltbarkeit und Preis hingegen korrelieren mit dem zweiten gewählten Faktor zu 0,94 bzw. 0,96. Auch hier sieht man, dass ein dritter Faktor nicht mehr erforderlich ist, da hier kaum noch hohe Korrelationen zu den Variablen zu beobachten sind. Welche Variablen werden nun durch die ersten beiden Komponenten gut erklärt? Die Kommunalität des „Anteils ungesättigter Fettsäuren“ beträgt z.B. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{1}^{2}=0,937^{2}+(-0,229)^{2}=93,1 \%} . Also werden 93,1% der Varianz der Variable „Anteil ungesättigter Fettsäuren“ durch die beiden Komponenten erklärt. Der Kreis schließt sich nun wieder, da unser ursprüngliches Ziel war, die Korrelationsstruktur der Daten zu erklären. Wie gut das gelingt, kann durch die Matrix der durch die zwei gemeinsamen Faktoren reproduzierten Korrelationen ermittelt werden. Diese ist nun mit der ursprünglichen Korrelationsmatrix zu vergleichen. Beispielsweise beträgt die Korrelation zwischen Kalorien- und Vitamingehalt ursprünglich 0,704. Aufgrund der beiden gewählten Faktoren kommt man auf eine Korrelation von 0,823. Für diese Korrelation ergibt sich daher ein Residuum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,704-0,823=-0,119} . Die Residuen der Hauptdiagonalelemente (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(1-h_{i}^{2}\right)} ) sind die durch die Faktoren nicht erklärten Varianzanteile der Variablen. |
|---|
| Aufgabe 16
Berechnen Sie die Kommunalitäten für die restlichen vier Variablen aus Beispiel 13 und vergleichen Sie ihre Werte mit den Hauptdiagonalelementen der reproduzierten Korrelationsmatrix. |
|---|
Faktorrotation
Wie bereits erwähnt, gibt es für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1<k<p} mehrere (unendlich viele) Lösungen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} , die allesamt die maximale Varianz erklären. Diese unterscheiden sich wieder durch „Drehungen“ im Raum. Das heißt, die gefundene Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} kann durch Multiplikation einer beliebigen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k \times k} -Matrix mit orthonormalen Spalten transformiert werden, sodass die neue Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L^t} den gleichen maximal erklärten Varianzanteil liefert. Dies macht man sich zunutze, um jene Lösungen fürFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} auszuwählen, die besonders leicht zu interpretieren sind. Das ist dann möglich, wenn die Ladungen entweder nahe bei 1 oder nahe bei 0 sind. Mit anderen Worten heißt das, dass die Varianz der Koeffizienten maximiert werden soll. Die Faktorrotationsmethoden, die die Varianz der Ladungen spalten- bzw. zeilenweise maximieren, heißen Varimax bzw. Quartimax.
| Fortsetzung Beispiel 13
Die Ladungskoeffizienten in Beispiel 13 enthalten bereits inhaltlich gut interpretierbare Werte und müssen nicht weiter transformiert werden. Wird dennoch eine Transformation durchgeführt, heißt das, dass sich an der erklärten Varianz von 91,6% nichts ändert. Lediglich die Aufteilung 52,9%:38,7% ändert sich zugunsten des zweiten Faktors, da nicht mehr erforderlich ist, dass die erste Komponente die maximale Varianz erklärt. |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Berechnen Sie die Residuen der reproduzierten Korrelationen in Beispiel 13 und geben Sie an, welche Korrelation am schlechtesten durch die gefundene Faktorlösung dargestellt wird.
- Sie erhalten als Ergebnis einer Faktorenanalyse folgende erklärte Varianzen:
- Wieviele Faktoren müssen Sie nehmen, wenn Sie zumindest 90% der Varianz erklären wollen?
- Wieviele Faktoren müssen Sie nach dem Kaiser-Kriterium wählen?
- Für wieviele Faktoren würden Sie sich mittels zugehörigem Scree-Plot entscheiden?
Zeichnen Sie für die ersten beiden Spalten der Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} (Abbildung 36) einen XY-Scatterplot (in R: „plot(x,y)“) und beschreiben Sie verbal das Ergebnis der Analyse.
Zusammenfassung
Im Gegensatz zu den vorangegangenen Lektionen wird bei den Verfahren der Faktorenanalyse die (Korrelations-)Struktur eines Satzes von Variablen untersucht. Die Fragestellung ist, ob und wie diese Struktur durch einige wenige Variablen erklärt werden kann. Der Input bei diesen Verfahren ist daher die Kovarianz- bzw. Korrelationsmatrix, der Output im wesentlichen die Ladungsmatrix, die bestimmt, in welcher Art und Weise die gefundenen Faktoren durch die Originalvariablen bestimmt werden.
Es existieren viele Methoden, Faktoren zu bestimmen. Neben der Maximum-Likelihood-Faktorenanalyse hat sich die Hauptkomponentenanalyse als beliebtes und häufig verwendetes Verfahren herausgestellt. In deren Rahmen wird zunächst eine Hauptachsentransformation in Komponenten, die schrittweise maximale Varianz an den Originaldaten erklären, durchgeführt. Setzt man dieses Verfahren dazu ein, um einen guten Satz an Variablen zu bekommen, wird dies die „Hauptkomponentenmethode“ genannt. Eine weitere sich aus dem Verfahren ableitende, iterative Vorgehensweise, bei der das Gewicht stärker auf der Erklärung der Kovarianzen anstelle der Varianzen liegt, ist die Hauptfaktorenanalyse.
Die Anzahl an ausgewählten Faktoren wird zumeist durch einen vorgegebenen minimal erforderlichen, erklärten Varianzanteil, durch das Kaiser-Kriterium oder den Scree-Plot ermittelt und sind daher teilweise subjektiv. Die vollständige Darstellung der Faktorenanalyse umfasst schließlich noch eine Darstellung der Beobachtungseinheiten im neu transformierten Raum sowie weiteren, die Güte der Analyse beschreibenden Darstellungen, wie z.B. der Matrix der reproduzierten Korrelationen.
Wichtig ist nochmals zu erwähnen, dass die Verfahren der (exploratorischen) Faktorenanalyse praktisch keine Hypothesenprüfungen zulassen. Die Ergebnisse sind auch nicht „richtig“ oder „falsch“, sondern bieten eine mathematische Unterstützung zur Dokumentation von Zusammenhangsstrukturen.
- ↑ Kelvin= Celsius+273,15 bzw. Fahrenheit=32+9/5*Celsius.