Methoden der Datenanalyse - Multidimensionale Skalierung: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
Die Grundannahme besteht darin, dass ein Raum existiert, der durch orthogonale Achsen gebildet wird und die <math>N</math> Objekte so darstellt, dass einander ähnliche Objekte beisammen liegen (eine niedrige Distanz aufweisen) und einander unähnliche Objekte weit voneinander entfernt sind. Idealerweise gilt für alle Paare von je zwei Objekten zueinander <math>d_{i j} \leq d_{k l}</math>, falls die Objekte <math>i</math> und <math>j</math> als einander ähnlicher eingestuft werden als die Objekte <math>k</math> und <math>l</math> (<math>d_{i j} </math> und <math>d_{k l} </math> sind die im gewählten Raum ersichtlichen Distanzen der Objekte <math>i</math> und <math>j</math> bzw. und <math>k</math> und <math>l</math> zueinander). | Die Grundannahme besteht darin, dass ein Raum existiert, der durch orthogonale Achsen gebildet wird und die <math>N</math> Objekte so darstellt, dass einander ähnliche Objekte beisammen liegen (eine niedrige Distanz aufweisen) und einander unähnliche Objekte weit voneinander entfernt sind. Idealerweise gilt für alle Paare von je zwei Objekten zueinander <math>d_{i j} \leq d_{k l}</math>, falls die Objekte <math>i</math> und <math>j</math> als einander ähnlicher eingestuft werden als die Objekte <math>k</math> und <math>l</math> (<math>d_{i j} </math> und <math>d_{k l} </math> sind die im gewählten Raum ersichtlichen Distanzen der Objekte <math>i</math> und <math>j</math> bzw. und <math>k</math> und <math>l</math> zueinander). | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 5''' | ! width="100%" | '''Beispiel 5''' | ||
Die beliebte Einordnung von politischen Parteien in Links- und Rechtsparteien könnte als eindimensionales Ergebnis einer MDS gesehen werden. Ergibt sich für eine Person z.B. die Einteilung „Grüne“ – „SPÖ“ – „ÖVP“ – „FPÖ“, so heißt dies, dass die „FPÖ“ der „ÖVP“ jedenfalls näher steht als der „SPÖ“. Wahlanalysen zeigen jedoch oft, dass gerade „SPÖ“ und „FPÖ“ oft ähnliche Wählerschichten ansprechen, was eine derartige Einteilung unzureichend machen würde. | Die beliebte Einordnung von politischen Parteien in Links- und Rechtsparteien könnte als eindimensionales Ergebnis einer MDS gesehen werden. Ergibt sich für eine Person z.B. die Einteilung „Grüne“ – „SPÖ“ – „ÖVP“ – „FPÖ“, so heißt dies, dass die „FPÖ“ der „ÖVP“ jedenfalls näher steht als der „SPÖ“. Wahlanalysen zeigen jedoch oft, dass gerade „SPÖ“ und „FPÖ“ oft ähnliche Wählerschichten ansprechen, was eine derartige Einteilung unzureichend machen würde. | ||
|} | |} | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 6''' | ! width="100%" | '''Beispiel 6''' | ||
| Zeile 40: | Zeile 40: | ||
* Die Ankerpunktmethode: Es werden einzelne Objekte herausgegriffen und die Ähnlichkeiten zu zumindest zwei anderen Objekten miteinander verglichen. | * Die Ankerpunktmethode: Es werden einzelne Objekte herausgegriffen und die Ähnlichkeiten zu zumindest zwei anderen Objekten miteinander verglichen. | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 7''' | ! width="100%" | '''Beispiel 7''' | ||
| Zeile 59: | Zeile 59: | ||
'''2'''3 vs. '''2'''4, '''3'''2 vs. '''3'''4, '''4'''2 vs. '''4'''3 | '''2'''3 vs. '''2'''4, '''3'''2 vs. '''3'''4, '''4'''2 vs. '''4'''3 | ||
|} | |} | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Aufgabe 12''' | ! width="100%" | '''Aufgabe 12''' | ||
| Zeile 70: | Zeile 70: | ||
== Konkretes Vorgehen bei der MDS == | == Konkretes Vorgehen bei der MDS == | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Beispiel 8''' | ! width="100%" | '''Beispiel 8''' | ||
| Zeile 81: | Zeile 81: | ||
Die Angabe bedeutet, dass sich die Objekte A und D am ähnlichsten und die Objekte B und D am unähnlichsten sind. | Die Angabe bedeutet, dass sich die Objekte A und D am ähnlichsten und die Objekte B und D am unähnlichsten sind. | ||
|} | |} | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Aufgabe 13''' | ! width="100%" | '''Aufgabe 13''' | ||
| Zeile 91: | Zeile 91: | ||
Zu Beginn der Analyse wird die Dimension der Lösung, sowie die Metrik festgelegt. Wir entscheiden uns aufgrund der sehr geringen Anzahl an Objekten für eine zweidimensionale Lösung und für die euklidische Distanz. Es kann nun eine beliebige Positionierung der Punkte im zweidimensionalen Raum als Startlösung gewählt werden. | Zu Beginn der Analyse wird die Dimension der Lösung, sowie die Metrik festgelegt. Wir entscheiden uns aufgrund der sehr geringen Anzahl an Objekten für eine zweidimensionale Lösung und für die euklidische Distanz. Es kann nun eine beliebige Positionierung der Punkte im zweidimensionalen Raum als Startlösung gewählt werden. | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Fortsetzung Beispiel 8''' | ! width="100%" | '''Fortsetzung Beispiel 8''' | ||
Wir wählen folgende Startkonfiguration: | Wir wählen folgende Startkonfiguration: | ||
{| style="border-collapse: collapse; height: 84px; background-color: rgb(149, 165, 166); float: left;" border="1" | {| style="border-collapse: collapse; height: 84px; background-color: rgb(149, 165, 166); float: left;" border="1" | ||
! style="height: 28px; width: 88.287px;" | | ! style="height: 28px; width: 88.287px;" | | ||
! style="height: 28px; width: 30.6019px;" | A | ! style="height: 28px; width: 30.6019px;" | A | ||
| Zeile 103: | Zeile 103: | ||
! style="height: 28px; width: 25.5787px;" | D | ! style="height: 28px; width: 25.5787px;" | D | ||
! style="height: 28px; width: 25.625px;" | E | ! style="height: 28px; width: 25.625px;" | E | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 88.287px;" | Dimension 1 | | style="height: 28px; width: 88.287px;" | Dimension 1 | ||
| style="height: 28px; width: 30.6019px;" | 7 | | style="height: 28px; width: 30.6019px;" | 7 | ||
| Zeile 110: | Zeile 110: | ||
| style="height: 28px; width: 25.5787px;" | 9 | | style="height: 28px; width: 25.5787px;" | 9 | ||
| style="height: 28px; width: 25.625px;" | 1 | | style="height: 28px; width: 25.625px;" | 1 | ||
|- style="height: 28px;" | |- style="height: 28px;" | ||
| style="height: 28px; width: 88.287px;" | Dimension 2 | | style="height: 28px; width: 88.287px;" | Dimension 2 | ||
| style="height: 28px; width: 30.6019px;" | 1 | | style="height: 28px; width: 30.6019px;" | 1 | ||
| Zeile 126: | Zeile 126: | ||
Die sich daraus ergebenden quadrierten <ref>Da nur die Reihenfolge der Distanzen eine Rolle spielt, können auch – um „Wurzel“-Zahlen zu vermeiden – quadrierte euklidische Distanzen verwendet werden.</ref> euklidischen Distanzen lauten (vgl. Minkowski-Metrik in Abschnitt 3.2.1): | Die sich daraus ergebenden quadrierten <ref>Da nur die Reihenfolge der Distanzen eine Rolle spielt, können auch – um „Wurzel“-Zahlen zu vermeiden – quadrierte euklidische Distanzen verwendet werden.</ref> euklidischen Distanzen lauten (vgl. Minkowski-Metrik in Abschnitt 3.2.1): | ||
{| style="border-collapse: collapse; background-color: rgb(149, 165, 166); float: left;" border="1" | {| style="border-collapse: collapse; background-color: rgb(149, 165, 166); float: left;" border="1" | ||
! width="12%" | | ! width="12%" | | ||
! width="28%" | A | ! width="28%" | A | ||
| Zeile 167: | Zeile 167: | ||
=== Monotoniebedingung und Disparitäten === | === Monotoniebedingung und Disparitäten === | ||
Vergleicht man die Größenordnung der Distanzen mit der geforderten Größenordnung sorgfältig, erkennt man beispielsweise, dass die Distanz zwischen A und D – wie gefordert – die kleinste ist. Wir würden diese Tatsache mit <math>u_{A D}=d_{A D}=1</math> notieren. Die Distanz zwischen B und E hingegen sollte die zweitkleinste sein (<math>u_{D | Vergleicht man die Größenordnung der Distanzen mit der geforderten Größenordnung sorgfältig, erkennt man beispielsweise, dass die Distanz zwischen A und D – wie gefordert – die kleinste ist. Wir würden diese Tatsache mit <math>u_{A D}=d_{A D}=1</math> notieren. Die Distanz zwischen B und E hingegen sollte die zweitkleinste sein (<math>u_{D E}=2</math>), ist aber die größte <math>d_{B E}=2</math>. Einen Eindruck über die Gesamtanpassung bekommt man, wenn man die <math>u</math>- und <math>d</math>-Werte einander im sogenannten „Shepard-Diagramm“ gegenüberstellt. Im Idealfall würden wir nun eine monoton nichtfallende Funktion in <math>u</math> sehen, was offensichtlich nicht der Fall ist. | ||
<span id="_Ref249874007" class="anchor"></span>Die Disparitäten sind mit „x“ gekennzeichnet | <span id="_Ref249874007" class="anchor"></span>Die Disparitäten sind mit „x“ gekennzeichnet | ||
Die Disparitäten finden nun auf zweierlei Art Verwendung. Erstens kann aus ihnen eine Maßzahl für die Güte der Anpassung – ein Stressmaß – generiert werden. Ein weit verbreitetes Stressmaß ist folgendes: | Die Disparitäten finden nun auf zweierlei Art Verwendung. Erstens kann aus ihnen eine Maßzahl für die Güte der Anpassung – ein Stressmaß – generiert werden. Ein weit verbreitetes Stressmaß ist folgendes: | ||
| Zeile 187: | Zeile 186: | ||
<math display="block"> | <math display="block"> | ||
x_{k r}^{+}=x_{k r}+\frac{a}{K-1} \sum_{l=1, l \neq k}^{N}\left(1-\frac{\widehat{d}_{k l}}{d_{k l}}\right) *\left(x_{l r}-x_{k r}\right) \quad(r=1, \ldots R) | x_{k r}^{+}=x_{k r}+\frac{a}{K-1} \sum_{l=1, l \neq k}^{N}\left(1-\frac{\widehat{d}_{k l}}{d_{k l}}\right) *\left(x_{l r}-x_{k r}\right) \quad(r=1, \ldots R) | ||
</math> | </math> | ||
Hier ist <math></math> die Anzahl der Objekte, <math></math> das Objekt, dass verschoben werden soll, <math></math> jene Koordinate, die neu berechnet wird und <math></math> das Ausmaß in dem der Punkt entlang der Richtung verschoben wird. | Hier ist <math>K</math> die Anzahl der Objekte, <math>k</math> das Objekt, dass verschoben werden soll, <math>r</math> jene Koordinate, die neu berechnet wird und <math>\alpha</math> das Ausmaß in dem der Punkt entlang der Richtung verschoben wird. | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! style="text-align: left;" width="100%" | '''Fortsetzung Beispiel 8''' | ! style="text-align: left;" width="100%" | '''Fortsetzung Beispiel 8''' | ||
Im folgenden sind die nach dem Kleinste-Quadrate-Kriterium berechneten Disparitäten, sowie das resultierende Stressmaß angegeben: | Im folgenden sind die nach dem Kleinste-Quadrate-Kriterium berechneten Disparitäten, sowie das resultierende Stressmaß angegeben: | ||
{| style="border-collapse: collapse; background-color: rgb(149, 165, 166); float: left;" border="1" | {| style="border-collapse: collapse; background-color: rgb(149, 165, 166); float: left;" border="1" | ||
! style="width: 97.2338px;" | Objektpaar k,l | ! style="width: 97.2338px;" | Objektpaar k,l | ||
! style="width: 31.4583px;" | [<math>u_{k l}</math> | ! style="width: 31.4583px;" | [<math>u_{k l}</math> | ||
| Zeile 312: | Zeile 311: | ||
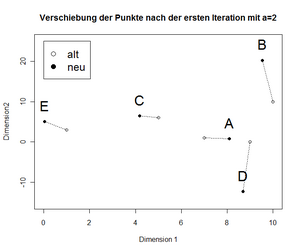
Die Monotonie ist noch lange nicht erreicht. Eine neue, bessere Positionierung wird mittels obiger Formel für a=2 berechnet. An dieser Stelle wird dies beispielhaft für die erste Koordinate von Punkt C skizziert: | |||
<math display="block"> | <math display="block"> | ||
x_{31}^{+}=x_{31}+\frac{2}{5-1} \sum_{l=1, l=3}^{5}\left(1-\frac{\widehat{d}_{3 l}}{d_{31}}\right) *\left(x_{l 1}-x_{31}\right) | x_{31}^{+}=x_{31}+\frac{2}{5-1} \sum_{l=1, l=3}^{5}\left(1-\frac{\widehat{d}_{3 l}}{d_{31}}\right) *\left(x_{l 1}-x_{31}\right)= 5+0,5\left[\left(1-\frac{5,4}{3}\right) *(7-5)+\left(1-\frac{5,4}{5}\right) *(10-5)+\left(1-\frac{5,4}{7}\right) *(9-5)+\left(1-\frac{7}{9}\right)\right. *(1-5)]=4,01 | ||
</math> | </math> | ||
| Zeile 337: | Zeile 340: | ||
<span id="_Ref249874155" class="anchor"></span>Tabelle 5: Klassifikation des Stressmaßes | <span id="_Ref249874155" class="anchor"></span>Tabelle 5: Klassifikation des Stressmaßes | ||
{| | {| style="border-collapse: collapse;" border="1" | ||
! | ! style="width: 155.949px;" | Anpassung | ||
! | ! style="width: 61.2616px;" | Perfekt | ||
! | ! style="width: 82.5463px;" | Sehr gut | ||
! | ! style="width: 62.2685px;" | Gut | ||
! | ! style="width: 89.1088px;" | Ausreichend | ||
! | ! style="width: 83.5417px;" | Gering | ||
|- | |- | ||
| Wert des Stressmaßes | | style="width: 155.949px;" | Wert des Stressmaßes | ||
| <0,025 | | style="width: 61.2616px;" | <0,025 | ||
| 0,025-0,05 | | style="width: 82.5463px;" | 0,025-0,05 | ||
| 0,05-0,1 | | style="width: 62.2685px;" | 0,05-0,1 | ||
| 0,1-0,2 | | style="width: 89.1088px;" | 0,1-0,2 | ||
| >0,2 | | style="width: 83.5417px;" | >0,2 | ||
|} | |} | ||
Beurteilung nach einem Datenverdichtungskoeffizient | Beurteilung nach einem Datenverdichtungskoeffizient | ||
| Zeile 356: | Zeile 359: | ||
Der Datenverdichtungskoeffizient setzt die Anzahl der Ähnlichkeiten zur Anzahl der Koordinaten im Output in Bezug. Im Beispiel 8 waren zehn Ähnlichkeiten in eine Reihenfolge zu bringen und zehn Koordinaten (5 mal 2) zu errechnen, was einen Koeffizient von 1 ergibt. Nach einer Faustregel sollte der Koeffizient größer oder gleich 2 sein. | Der Datenverdichtungskoeffizient setzt die Anzahl der Ähnlichkeiten zur Anzahl der Koordinaten im Output in Bezug. Im Beispiel 8 waren zehn Ähnlichkeiten in eine Reihenfolge zu bringen und zehn Koordinaten (5 mal 2) zu errechnen, was einen Koeffizient von 1 ergibt. Nach einer Faustregel sollte der Koeffizient größer oder gleich 2 sein. | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! width="100%" | '''Aufgabe 14''' | ! width="100%" | '''Aufgabe 14''' | ||
| Zeile 372: | Zeile 375: | ||
<li><p>Aggregation der Urteile auf bekannte statistische Maßzahlen (Median, Mittelwert) – hier ist wichtig, dass die Personengruppen homogen sind</p></li> | <li><p>Aggregation der Urteile auf bekannte statistische Maßzahlen (Median, Mittelwert) – hier ist wichtig, dass die Personengruppen homogen sind</p></li> | ||
<li><p>Getrennte MDs für jede einzelne Person und Aggregation der Ergebnisse</p></li> | <li><p>Getrennte MDs für jede einzelne Person und Aggregation der Ergebnisse</p></li> | ||
<li><p>Eine gemeinsame Analyse der Ähnlichkeitsdaten (Replicated MDS)</p | <li><p>Eine gemeinsame Analyse der Ähnlichkeitsdaten (Replicated MDS)</p></li> | ||
</ul> | </ul> | ||
== Multidimensionale Skalierung in R == | |||
Die MDS kann beispielsweise in SPSS durchgeführt werden, oder auch mit Software, die auf MDS spezialisiert ist (MDSCAL, KYST, POLYCON). Wir verwenden aus Kontinuitätsgründen für unsere Analyse wieder R. | Die MDS kann beispielsweise in SPSS durchgeführt werden, oder auch mit Software, die auf MDS spezialisiert ist (MDSCAL, KYST, POLYCON). Wir verwenden aus Kontinuitätsgründen für unsere Analyse wieder R. | ||
{| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | {| style="border-collapse: collapse; background-color: rgb(206, 212, 217);" | ||
! style="text-align: left;" width="100%" | '''Beispiel 9''' | ! style="text-align: left;" width="100%" | '''Beispiel 9''' | ||
| Zeile 420: | Zeile 422: | ||
# Gegeben sei ein nichtlineares MDS-Problem mit vier Objekten. Bestimmen Sie, ob (1) oder (2) die richtigen Disparitäten sind und berechnen Sie das Stressmaß. | # Gegeben sei ein nichtlineares MDS-Problem mit vier Objekten. Bestimmen Sie, ob (1) oder (2) die richtigen Disparitäten sind und berechnen Sie das Stressmaß. | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
! width="25%" | Paare k,l | ! width="25%" | Paare k,l | ||
! width="13%" | 1,2 | ! width="13%" | 1,2 | ||
| Zeile 446: | Zeile 448: | ||
|- | |- | ||
| | | | ||
<math>(1) \widehat{u_{k l}}</math> | |||
| 2 | | 2 | ||
| 2 | | 2 | ||
| Zeile 455: | Zeile 457: | ||
|- | |- | ||
| | | | ||
<math>(2) \widehat{u_{k l}}</math> | |||
| 3 | | 3 | ||
| 1,5 | | 1,5 | ||
Aktuelle Version vom 9. März 2023, 08:11 Uhr
Multidimensionale Skalierung
Die multidimensionale Skalierung bedient sich ähnlicher Techniken und Ideen wie die Clusteranalyse und die Faktorenanalyse. Ziel der Lektion ist es, Unterschiede und Gemeinsamkeiten herauszuarbeiten sowie exemplarisch in eine Analyse in R einzuführen.
Wir verlassen nun jene statistischen Analyseverfahren, die primär das Ziel haben, über die beobachteten Daten Voraussagen zu treffen und wechseln zu solchen, die auch latente (nicht messbare) Dimensionen („Faktoren“) zur Erklärung der beobachteten Daten zulassen.
Die Analyse mittels „multidimensionaler Skalierung“ (MDS) wird in diesem Skriptum nicht zufällig zwischen Clusteranalyse und Faktorenanalyse behandelt, sondern vereint auch Elemente aus beiden Analysemethoden in sich und nimmt damit eine Zwischenstellung ein.
Ziel des Verfahrens ist es, eine Anzahl von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} Objekten hinsichtlich ihrer Ähnlichkeit in der subjektiven Wahrnehmung durch eine oder mehrere Personen in einem für den Anwender übersichtlichen „Raum“ zu positionieren und abzubilden.
Merkmale, die einen Raum aufspannen, können hier nicht abgefragt werden, weil sie oft nicht bewusst sind und nur assoziativ angesprochen werden. Personen sollen lediglich Ähnlichkeits- und Distanzaussagen machen.
Die Gemeinsamkeit zur in der vorigen Lektion besprochenen Clusteranalyse besteht darin, dass Distanzen zwischen verschiedenen Objekten die zentrale Rolle in diesem Verfahren spielen. Der Unterschied ist jedoch, dass diese Distanzen oft nicht – wie in der Clusteranalyse – aufgrund von beobachtbaren Merkmalsausprägungen in verschiedenen Variablen objektiv berechnet werden können, sondern diese Distanzen nur in der Vorstellung der Personen existieren. Als Ergebnis einer MDS ist daher nicht nur die Darstellung von Objekten im Raum zu nennen, sondern ggf. auch die Interpretation der diesen Raum aufspannenden Dimensionen. Diese latenten Dimensionen bilden die Verbindung zur Faktorenanalyse, die im nächsten Abschnitt besprochen wird. Den Aspekt der Datenreduktion ist den beiden Verfahren ebenfalls gemein.
Grundlagen und Annahmen
Die Grundannahme besteht darin, dass ein Raum existiert, der durch orthogonale Achsen gebildet wird und die Objekte so darstellt, dass einander ähnliche Objekte beisammen liegen (eine niedrige Distanz aufweisen) und einander unähnliche Objekte weit voneinander entfernt sind. Idealerweise gilt für alle Paare von je zwei Objekten zueinander , falls die Objekte und als einander ähnlicher eingestuft werden als die Objekte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{i j} } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{k l} } sind die im gewählten Raum ersichtlichen Distanzen der Objekte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j} bzw. und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} zueinander).
| Beispiel 5
Die beliebte Einordnung von politischen Parteien in Links- und Rechtsparteien könnte als eindimensionales Ergebnis einer MDS gesehen werden. Ergibt sich für eine Person z.B. die Einteilung „Grüne“ – „SPÖ“ – „ÖVP“ – „FPÖ“, so heißt dies, dass die „FPÖ“ der „ÖVP“ jedenfalls näher steht als der „SPÖ“. Wahlanalysen zeigen jedoch oft, dass gerade „SPÖ“ und „FPÖ“ oft ähnliche Wählerschichten ansprechen, was eine derartige Einteilung unzureichend machen würde. |
|---|
| Beispiel 6
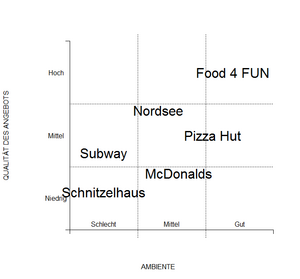
Die MDS kann auch verwendet werden, um Marktlücken ausfindig zu machen. Hat man beispielsweise die in Abbildung 25 dargestellte Vorstellung über den Fast-Food-Markt in Österreich, können hier „freie Flecken“ identifiziert werden (z.B. rechts oben für eine neue Fastfood-Kette „Food 4 FUN“). |
|---|
Der Input bei dieser Analyse ist jeweils eine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N x N} Matrix, die entweder metrische Distanzen zwischen je zwei Objekten enthält (beispielsweise aufgrund des Ratings einer Person, die alle Paare von Objekten hinsichtlich ihrer Distanzen bewertet) – man spricht hier von metrischer MDS – oder schlichtweg die Reihenfolge der Ähnlichkeiten zwischen je zwei Objekten. Im letzten Fall spricht man von „nichtmetrischer MDS“. Ein Beispiel für eine metrische MDS könnte die örtliche Positionierung von Städten zueinander auf Basis der angegebenen Entfernungen der Städte zueinander sein (wie in einem Autoatlas ersichtlich). Die Verfahren, die metrische MDS durchführen, reduzieren sich im wesentlichen auf Fragestellungen, die in der Faktorenanalyse in der nächsten Lektion behandelt werden. In weiterer Folge wird hier daher auf die nichtmetrische MDS, die als Ziel die Optimierung der Ordnungsstruktur der Distanzen hat, eingegangen.
Etwas verkürzt kann man also sagen, dass eine Ordnung der Objektpaare als Input in diesem Verfahren übergeben wird und eine metrische Information das Ergebnis ist. Es findet damit eine Transformation auf eine Skala höherer Ordnung statt (metrisch statt ordinal). Bis jetzt ist noch unzureichend geklärt, ob es gerechtfertigt ist, aus empirisch ermittelten Ähnlichkeiten auf die Lage der Objekte im mehrdimensionalen Raum zu schließen.
Um die ordinale Information über die Ähnlichkeitsbeziehungen abzufragen, wird häufig eine der folgenden drei Methoden angewandt:
- Eine vollständige Rangordnung aller möglichen Paare. Die Person muss alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{c} N 2 \end{array}\right)} Paare von Beziehungen hinsichtlich ihrer Ähnlichkeit ordnen.
- Die Tetradenmethode: Bei allen Paaren von Objektpaaren muss bestimmt werden, welche einander ähnlicher sind.
- Die Ankerpunktmethode: Es werden einzelne Objekte herausgegriffen und die Ähnlichkeiten zu zumindest zwei anderen Objekten miteinander verglichen.
| Beispiel 7
Bei vier Objekten müssten folgende Kombinationen bewertet werden Vollständige Rangordnung: 12, 13, 14, 23, 24, 34 Tetradenmethode: 12 vs. 13, 12 vs. 14, 12 vs 23, 12 vs. 24, 12 vs. 34, 13 vs. 14, 13 vs. 23, 13 vs. 24, 13 vs. 34, 14 vs. 23, 14 vs. 24, 14 vs. 34, 23 vs. 24, 23 vs. 34, 24 vs. 34 Ankerpunktmethode mit drei Objekten: 12 vs. 13, 21 vs. 23, 31 vs. 32 12 vs. 14, 21 vs. 24, 41 vs. 42 13 vs. 14, 31 vs. 34, 41 vs. 43 23 vs. 24, 32 vs. 34, 42 vs. 43 |
|---|
| Aufgabe 12
Wieviele Relationen müssen bei 15 Objekten verglichen werden (nach der Methode der vollständigen Rangordnung bzw. der Tetradenmethode)? |
|---|
Sieht man von möglichen Problemen ab, die durch solche Bewertungen auftreten können – z.B. nicht transitive bzw. nicht symmetrische Ordnungen, die ein Hinweis sein können, dass Objekte nicht in einem metrischen Raum wahrgenommen werden – gestaltet sich die Aufgabe, aus einer solcherart gefundenen Ordnung die Lage der Punkte zueinander abzuleiten, relativ eindeutig.
Weiters zu entscheiden ist nun einerseits, in welcher Metrik das Ergebnis (die sogenannte „Konfiguration“) berechnet werden soll. Hier werden üblicherweise die schon erwähnten Minkowski-q-Metriken gewählt und unter diesen jene für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=2} (euklidische Distanz). Dies vor allem wegen der auch in der Faktorenanalyse wichtigen Invarianz der Lösung bezüglich Drehungen oder Spiegelungen [1] . Andererseits ist die Dimensionalität des zu erzeugenden Raumes zu wählen. Hier hat man zunächst keine Anhaltspunkte, da das finden von Dimensionen gerade die Aufgabe der MDS ist. Jedoch kommen die meisten Autoren aufgrund der Tatsache, dass die menschliche Vorstellung bei dreidimensionalen Räumen endet zu der Auffassung, dass zwei oder drei Dimensionen ausreichend sind. Hinweise, ob zwei oder drei Dimensionen besser sind, folgen noch. Das Vorgehen bei einer nichtlinearen MDS wird im folgenden Abschnitt beispielhaft demonstriert.
Konkretes Vorgehen bei der MDS
| Beispiel 8
Gegeben seien fünf Objekte A-E. Anhand folgender Ordnungsrelation der Ähnlichkeiten von je zwei Objekten soll eine MDS durchgeführt werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \overline{A D}<\overline{B E}<\overline{A C}<\overline{C D}<\overline{B C}<\overline{D E}<\overline{A E}<\overline{C E}<\overline{A B}<\overline{B D} } Die Angabe bedeutet, dass sich die Objekte A und D am ähnlichsten und die Objekte B und D am unähnlichsten sind. |
|---|
| Aufgabe 13
Zeigen Sie, dass die Objekte A bis E aus Beispiel 8 nicht in einer Dimension positioniert werden können, ohne zumindest eine der beschriebenen Ungleichungen zu verletzen. |
|---|
Wahl einer Startkonfiguration
Zu Beginn der Analyse wird die Dimension der Lösung, sowie die Metrik festgelegt. Wir entscheiden uns aufgrund der sehr geringen Anzahl an Objekten für eine zweidimensionale Lösung und für die euklidische Distanz. Es kann nun eine beliebige Positionierung der Punkte im zweidimensionalen Raum als Startlösung gewählt werden.
| Fortsetzung Beispiel 8
Wir wählen folgende Startkonfiguration:
Die sich daraus ergebenden quadrierten [2] euklidischen Distanzen lauten (vgl. Minkowski-Metrik in Abschnitt 3.2.1):
|
|---|
Monotoniebedingung und Disparitäten
Vergleicht man die Größenordnung der Distanzen mit der geforderten Größenordnung sorgfältig, erkennt man beispielsweise, dass die Distanz zwischen A und D – wie gefordert – die kleinste ist. Wir würden diese Tatsache mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{A D}=d_{A D}=1} notieren. Die Distanz zwischen B und E hingegen sollte die zweitkleinste sein (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{D E}=2} ), ist aber die größte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{B E}=2} . Einen Eindruck über die Gesamtanpassung bekommt man, wenn man die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u} - und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} -Werte einander im sogenannten „Shepard-Diagramm“ gegenüberstellt. Im Idealfall würden wir nun eine monoton nichtfallende Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u} sehen, was offensichtlich nicht der Fall ist.
Die Disparitäten sind mit „x“ gekennzeichnet
Die Disparitäten finden nun auf zweierlei Art Verwendung. Erstens kann aus ihnen eine Maßzahl für die Güte der Anpassung – ein Stressmaß – generiert werden. Ein weit verbreitetes Stressmaß ist folgendes:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{STRESS}_{1}=\sqrt{\frac{\sum_{k} \sum_{l}\left(d_{k l}-\widetilde{d_{k l}}\right)^{2}}{\sum_{k} \sum_{l} d_{k l}^{2}}} }
Die Anpassung ist umso besser, je kleiner das Stressmaß ist.
Zweitens hat Kruskal (1964, zitiert in Backhaus et al., 2003) einen Algorithmus vorgeschlagen, wie auf Basis der Disparitäten Richtungen ermittelt werden können, in die die Datenpunkte im Raum verschoben werden müssen, um das Stressmaß zu verbessern.
Die neuen Koordinaten berechnen sich folgendermaßen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{k r}^{+}=x_{k r}+\frac{a}{K-1} \sum_{l=1, l \neq k}^{N}\left(1-\frac{\widehat{d}_{k l}}{d_{k l}}\right) *\left(x_{l r}-x_{k r}\right) \quad(r=1, \ldots R) }
Hier ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K} die Anzahl der Objekte, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} das Objekt, dass verschoben werden soll, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} jene Koordinate, die neu berechnet wird und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} das Ausmaß in dem der Punkt entlang der Richtung verschoben wird.
| Fortsetzung Beispiel 8
Im folgenden sind die nach dem Kleinste-Quadrate-Kriterium berechneten Disparitäten, sowie das resultierende Stressmaß angegeben:
Die Monotonie ist noch lange nicht erreicht. Eine neue, bessere Positionierung wird mittels obiger Formel für a=2 berechnet. An dieser Stelle wird dies beispielhaft für die erste Koordinate von Punkt C skizziert: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{31}^{+}=x_{31}+\frac{2}{5-1} \sum_{l=1, l=3}^{5}\left(1-\frac{\widehat{d}_{3 l}}{d_{31}}\right) *\left(x_{l 1}-x_{31}\right)= 5+0,5\left[\left(1-\frac{5,4}{3}\right) *(7-5)+\left(1-\frac{5,4}{5}\right) *(10-5)+\left(1-\frac{5,4}{7}\right) *(9-5)+\left(1-\frac{7}{9}\right)\right. *(1-5)]=4,01 }
|
|---|
und der Ergebnisse nach der ersten Iteration
Beurteilung der Lösung
Die in Beispiel 8 schlussendlich erhaltene Lösung ist invariant gegenüber Drehungen von oder Spiegelungen an den Achsen.
Im konkreten Fall sind zwei Dimensionen mehr als ausreichend. In einer Analyse mit deutlich mehr Objekten gibt es folgende Kriterien, um die Frage der Dimensionszahl zu beantworten:
Beurteilung nach dem Stressmaß
Ein errechnetes Stressmaß kann laut Tabelle 5 klassifiziert werden. Zu beachten ist, dass sich das Stressmaß bei Hinzunahme einer weiteren Dimension nur verbessern kann. Dimensionen sollen nur dann hinzugefügt werden, wenn diese Verbesserung deutlich ausfällt.
Tabelle 5: Klassifikation des Stressmaßes
| Anpassung | Perfekt | Sehr gut | Gut | Ausreichend | Gering |
|---|---|---|---|---|---|
| Wert des Stressmaßes | <0,025 | 0,025-0,05 | 0,05-0,1 | 0,1-0,2 | >0,2 |
Beurteilung nach einem Datenverdichtungskoeffizient
Der Datenverdichtungskoeffizient setzt die Anzahl der Ähnlichkeiten zur Anzahl der Koordinaten im Output in Bezug. Im Beispiel 8 waren zehn Ähnlichkeiten in eine Reihenfolge zu bringen und zehn Koordinaten (5 mal 2) zu errechnen, was einen Koeffizient von 1 ergibt. Nach einer Faustregel sollte der Koeffizient größer oder gleich 2 sein.
| Aufgabe 14
Bestimmen Sie, ab welcher Anzahl an Objekten erst nach diesem Kriterium zwei, bzw. drei Dimensionen verwendet werden dürfen. |
|---|
Beurteilung nach Interpretierbarkeit der Dimensionen
Nachdem ein optionales Ziel der MDS darin besteht, die Dimensionen, die den Raum aufspannen, zu interpretieren, kann auch dies als Kriterium benutzt werden. Ermöglicht eine zwei- oder dreidimensionale Lösung eine bessere Interpretation der jeweiligen Konfiguration? Die Interpretierbarkeit der Dimensionen erhöht Anschaulichkeit und bestärkt jedenfalls die Validität der gefundenen Lösung.
Vorgehensweise bei Vorliegen der Daten von mehreren Personen
Die bisherige Vorgehensweise, bei der nur eine Person ein Ranking abgibt, wird auch „klassische MDs“ genannt. Fließen Urteile von mehreren Personen ein, bestehen grundsätzlich drei Möglichkeiten:
Aggregation der Urteile auf bekannte statistische Maßzahlen (Median, Mittelwert) – hier ist wichtig, dass die Personengruppen homogen sind
Getrennte MDs für jede einzelne Person und Aggregation der Ergebnisse
Eine gemeinsame Analyse der Ähnlichkeitsdaten (Replicated MDS)
Multidimensionale Skalierung in R
Die MDS kann beispielsweise in SPSS durchgeführt werden, oder auch mit Software, die auf MDS spezialisiert ist (MDSCAL, KYST, POLYCON). Wir verwenden aus Kontinuitätsgründen für unsere Analyse wieder R.
| Beispiel 9
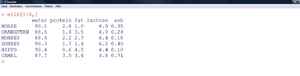
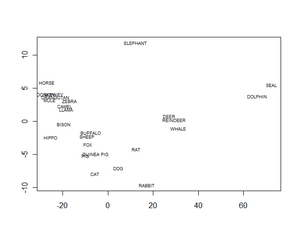
Der vorliegende Datensatz ist im package „flexclust“ in R zu finden und beinhaltet die Daten über die Bestandteile der Milch von 25 verschiedenen Säugetieren („water“, „protein“, „fat“, „lactose“, „ash“) in Prozent. Ziel ist es, die Daten in zwei Dimensionen darzustellen, sodass Tiere, deren Milch ähnlich ist auch im XY-Scatterplot umso näher beisammen sind. Wir wählen die Funktion „isoMDS“ aus dem Package „MASS“, die eine nichtmetrische MDS durchführt, also die Rangordnung der Input-Distanzen zueinander verarbeitet.
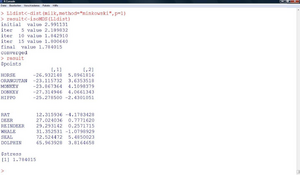
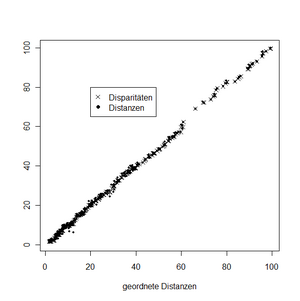
Zuerst wird eine Distanzmatrix der L1-Distanzen („L1dist“) erzeugt. Diese ist Input für die nichtmetrische MDS, die in R mit der Funktion „isoMDS“ durchgeführt werden kann. Das Ergebnis wird im Objekt „result“ gespeichert. Ergebnis sind die Koordinaten in den gewünschten zwei Dimensionen. Der Stress-Wert wird in Prozent angegeben. Das Ergebnis ist lt. Tabelle 5 daher „ausgezeichnet“. Schließlich soll das Ergebnis noch mittels zweier Plots veranschaulicht werden:
Abbildung 30 zeigt also die Lage der Objekte zueinander im Raum. Beachtet werden muss hier, dass die X- und Y-Achse (aus Platzgründen) nicht gleich skaliert sind (um einen Faktor 4), was gerade bei der MDS wichtig wäre, da die Distanzen sonst verzerren. In diesem Fall ist die X-Achse viel bedeutender als die Y-Achse (Seehund und Delphin sind in Wirklichkeit viel weiter vom Rest entfernt, als der Elefant). Entweder Abbildung 30 müsste viermal so breit gezeichnet werden, oder man zieht die inhaltliche Konsequenz, dass möglicherweise sogar eine Dimension ausreichend ist. In der Tat ergibt sich mit einem Stress-Wert von 4,1% auch bei einer Dimension ein „sehr gutes“ Ergebnis. Der perfekte Zusammenhang zwischen Distanzen und Disparitäten ist ebenfalls ein Hinweis, dass eine Reduktion auf eine Dimension in Betracht kommen könnte. |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Wiederholen Sie die Begriffe Konfiguration, Distanzen und Disparitäten im Zusammenhang mit der MDS.
- Beschreiben Sie Unterschiede und Gemeinsamkeiten zwischen Clusteranalyse und MDS.
- Berechnen Sie für die in Abbildung 27 dargestellten Datenpunkte „D“ und „E“ die neuen Koordinaten (jeweils a=2).
- Gegeben sei ein nichtlineares MDS-Problem mit vier Objekten. Bestimmen Sie, ob (1) oder (2) die richtigen Disparitäten sind und berechnen Sie das Stressmaß.
| Paare k,l | 1,2 | 1,4 | 3,4 | 2,3 | 2,4 | 1,3 |
|---|---|---|---|---|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{k l}} | 1 | 2 | 3 | 4 | 5 | 6 |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{k l}} | 3 | 1 | 2 | 4 | 6 | 5 |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1) \widehat{u_{k l}}}
|
2 | 2 | 2 | 4 | 5,5 | 5,5 |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (2) \widehat{u_{k l}}}
|
3 | 1,5 | 1,5 | 5 | 5 | 5 |
Zusammenfassung
Die multidimensionale Skalierung erweitert die Idee der Clusteranalyse dahingehend, dass anstelle von Distanzen zwischen beobachtbaren Merkmalen von Objekten hier Distanzen der Objekte in latenten Dimensionen die zentrale Rolle spielen. Diese bilden hier im Gegensatz zur Clusteranalyse den Output der Analyse. Die Vorstellung, dass Beurteilungen von Ähnlichkeit zwischen Objekten oft nicht durch objektive, beobachtbare Messungen ermittelt werden können, sondern teilweise unbewusst existieren, bildet das Grundgerüst dieser vor allem in der Psychologie, aber auch in der Ökologie unter dem Begriff „Ordination“ verbreiteten Methode.
Datengrundlage bildet bei den nichtmetrischen MDS-Verfahren eine Ordnung von Ähnlichkeiten zwischen den interessierenden Objekten. Mittels iterativer Optimierungsverfahren kann – ausgehend von einer Startlösung – eine bezüglich eines Stressmaßes optimale Lösung erzielt werden.
Bei der gefundenen Lösung ist die Lage der Punkte zueinander bei Wahl der euklidischen Distanz eindeutig. Die orthogonalen Achsen können schließlich beliebig gedreht werden, auch mit dem Ziel möglichst gut interpretierbare Dimensionen zu erhalten.