Angewandte Mikroökonomik - Grundzüge der Spieltheorie: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
Die Entscheidungssituation wird in einem „Spiel“ dargestellt. Elemente eines Spiels umfassen (1) die Spieler, (2) den Strategienraum, aus dem die Spieler eine Aktion wählen können, und (3) die Auszahlungsstruktur, d.h. der „Gewinn“, den jeder Spieler zu erwarten hat, gegeben eine bestimmte Kombination aus Strategien wird gewählt. Außerdem von Bedeutung ist die zeitliche Abfolge der Entscheidungen der Spieler. Spieler können entweder simultan (dann spricht man von einem „statischen Spiel“) oder nacheinander („dynamisches Spiel“) entscheiden. Im Fall eines dynamischen Spiels entscheidet Spieler 2 sich erst dann für eine Aktion, nachdem er die Strategie von Spieler 1 beobachtet hat. Im Folgenden werden wir uns sowohl mit statischen als auch mit dynamischen Spielen auseinandersetzen und unterschiedliche Lösungskonzepte kennenlernen. | Die Entscheidungssituation wird in einem „Spiel“ dargestellt. Elemente eines Spiels umfassen (1) die Spieler, (2) den Strategienraum, aus dem die Spieler eine Aktion wählen können, und (3) die Auszahlungsstruktur, d.h. der „Gewinn“, den jeder Spieler zu erwarten hat, gegeben eine bestimmte Kombination aus Strategien wird gewählt. Außerdem von Bedeutung ist die zeitliche Abfolge der Entscheidungen der Spieler. Spieler können entweder simultan (dann spricht man von einem „statischen Spiel“) oder nacheinander („dynamisches Spiel“) entscheiden. Im Fall eines dynamischen Spiels entscheidet Spieler 2 sich erst dann für eine Aktion, nachdem er die Strategie von Spieler 1 beobachtet hat. Im Folgenden werden wir uns sowohl mit statischen als auch mit dynamischen Spielen auseinandersetzen und unterschiedliche Lösungskonzepte kennenlernen. | ||
< | <br> | ||
== Statische Spiele == | == Statische Spiele == | ||
Ein statisches Spiel zeichnet sich dadurch aus, dass sich die Spieler simultan für eine Aktion entscheiden. D.h., wenn Spieler 2 seine Entscheidung trifft, weiß er nicht, welche Entscheidung sein Gegenspieler, Spieler 1, trifft. Ein solches Spiel wird oft in der „Normalform“ dargestellt. Angenommen, das Spiel hat zwei Spieler, welche aus zwei möglichen Strategien wählen können. Ein solches Spiel wird wie in Tabelle | Ein statisches Spiel zeichnet sich dadurch aus, dass sich die Spieler simultan für eine Aktion entscheiden. D.h., wenn Spieler 2 seine Entscheidung trifft, weiß er nicht, welche Entscheidung sein Gegenspieler, Spieler 1, trifft. Ein solches Spiel wird oft in der „Normalform“ dargestellt. Angenommen, das Spiel hat zwei Spieler, welche aus zwei möglichen Strategien wählen können. Ein solches Spiel wird wie in jener Tabelle dargestellt: | ||
{| style="border-collapse: collapse; height: 112px;" border="1" | |||
{| | ! style="height: 28px; width: 66.6094px;" | | ||
! | ! style="height: 28px; width: 52.875px;" | | ||
! | ! style="height: 28px; width: 69.3438px;" | '''Spieler 2''' | ||
! | ! style="height: 28px; width: 69.3906px;" | | ||
! | |- style="height: 28px;" | ||
|- | | style="height: 28px; width: 66.6094px;" | | ||
| | |||
<br> | <br> | ||
| | | style="height: 28px; width: 52.875px;" | | ||
<br> | <br> | ||
| Links | | style="height: 28px; width: 69.3438px;" | '''Links''' | ||
| Rechts | | style="height: 28px; width: 69.3906px;" | '''Rechts''' | ||
|- | |- style="height: 28px;" | ||
| Spieler 1 | | style="height: 28px; width: 66.6094px;" | '''Spieler 1''' | ||
| Oben | | style="height: 28px; width: 52.875px;" | '''Oben''' | ||
| OL1, OL2 | | style="height: 28px; width: 69.3438px;" | OL1, OL2 | ||
| OR1, OR2 | | style="height: 28px; width: 69.3906px;" | OR1, OR2 | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 66.6094px;" | | ||
<br> | <br> | ||
| Unten | | style="height: 28px; width: 52.875px;" | '''Unten''' | ||
| UL1, UL2 | | style="height: 28px; width: 69.3438px;" | UL1, UL2 | ||
| UR1, UR2 | | style="height: 28px; width: 69.3906px;" | UR1, UR2 | ||
|} | |} | ||
Die Normalform eines Spieles | |||
In diesem Spiel gibt es zwei Spieler, Spieler 1 und Spieler 2. Spieler 1 hat zwei Strategien zur Auswahl. Er kann entweder die Aktion „oben“ oder die Aktion „unten“ wählen. Spieler 2 auf der anderen Seite kann sich für „rechts“ oder „links“ entscheiden. Die Auszahlungsmatrix stellt außerdem die Auszahlungen (meist wird dies durch Zahlen dargestellt, die Auszahlung bezieht sich also zum Beispiel auf den monetären Nutzen) der Spieler bei jeder möglichen Kombination von gewählten Aktionen dar. Wenn zum Beispiel Spieler 1 „oben“ und Spieler 2 „links“ wählt, so bekommt Spieler 1 die Auszahlung „OL1“ und Spieler 2 „OL2“. | In diesem Spiel gibt es zwei Spieler, Spieler 1 und Spieler 2. Spieler 1 hat zwei Strategien zur Auswahl. Er kann entweder die Aktion „oben“ oder die Aktion „unten“ wählen. Spieler 2 auf der anderen Seite kann sich für „rechts“ oder „links“ entscheiden. Die Auszahlungsmatrix stellt außerdem die Auszahlungen (meist wird dies durch Zahlen dargestellt, die Auszahlung bezieht sich also zum Beispiel auf den monetären Nutzen) der Spieler bei jeder möglichen Kombination von gewählten Aktionen dar. Wenn zum Beispiel Spieler 1 „oben“ und Spieler 2 „links“ wählt, so bekommt Spieler 1 die Auszahlung „OL1“ und Spieler 2 „OL2“. | ||
| Zeile 49: | Zeile 48: | ||
* Wenn beide gestehen, so können sie des Überfalls überführt werden und müssen im Anschluss eine Haftstrafe von jeweils 6 Jahren verbüßen. Gesteht nur einer der Räuber die Tat, so kann mit diesem Geständnis dem anderen Räuber die Tat nachgewiesen werden, der gestehende Räuber kommt – als Belohnung für seine Kooperationswilligkeit – frei (0 Jahre). Der von seinem Kollegen belastete Räuber muss dann, da er nicht kooperationswillig war, 12 Jahre in Haft verbringen. Sollten beide Räuber Stillschweigen bewahren, so kann ihnen nur ein geringfügiges Vergehen angelastet werden (z.B. unerlaubtes Tragen einer Feuerwaffe) und sie bekommen eine Gefängnisstrafe von je 1 Jahr. | * Wenn beide gestehen, so können sie des Überfalls überführt werden und müssen im Anschluss eine Haftstrafe von jeweils 6 Jahren verbüßen. Gesteht nur einer der Räuber die Tat, so kann mit diesem Geständnis dem anderen Räuber die Tat nachgewiesen werden, der gestehende Räuber kommt – als Belohnung für seine Kooperationswilligkeit – frei (0 Jahre). Der von seinem Kollegen belastete Räuber muss dann, da er nicht kooperationswillig war, 12 Jahre in Haft verbringen. Sollten beide Räuber Stillschweigen bewahren, so kann ihnen nur ein geringfügiges Vergehen angelastet werden (z.B. unerlaubtes Tragen einer Feuerwaffe) und sie bekommen eine Gefängnisstrafe von je 1 Jahr. | ||
{| | {| style="border-collapse: collapse; height: 113px;" border="1" | ||
! | ! style="width: 78px; height: 29px;" | | ||
! | ! style="width: 117px; height: 29px;" | | ||
! | ! style="width: 98px; height: 29px;" | '''Räuber 2''' | ||
! | ! style="width: 106px; height: 29px;" | | ||
|- | |- style="height: 28px;" | ||
| | | style="width: 78px; height: 28px;" | | ||
<br> | <br> | ||
| | | style="width: 117px; height: 28px;" | | ||
<br> | <br> | ||
| Gestehen | | style="width: 98px; height: 28px;" | '''Gestehen''' | ||
| Nicht gestehen | | style="width: 106px; height: 28px;" | '''Nicht gestehen''' | ||
|- | |- style="height: 28px;" | ||
| Räuber 1 | | style="width: 78px; height: 28px;" | '''Räuber 1''' | ||
| Gestehen | | style="width: 117px; height: 28px;" | '''Gestehen''' | ||
| -6, -6 | | style="width: 98px; height: 28px;" | -6, -6 | ||
| 0, -12 | | style="width: 106px; height: 28px;" | 0, -12 | ||
|- | |- style="height: 28px;" | ||
| | | style="width: 78px; height: 28px;" | | ||
<br> | <br> | ||
| Nicht gestehen | | style="width: 117px; height: 28px;" | '''Nicht gestehen''' | ||
| -12, 0 | | style="width: 98px; height: 28px;" | -12, 0 | ||
| -1, -1 | | style="width: 106px; height: 28px;" | -1, -1 | ||
|} | |} | ||
Das Gefangenendilemma | |||
Die Darstellung des Gefangenendilemma in der Normalform ist in Tabelle | Die Darstellung des Gefangenendilemma in der Normalform ist in oberer Tabelle zu sehen. Da die Jahre, die ein Räuber im Gefängnis verbringen muss, eine negative Auszahlung darstellen (Jahre in Freiheit), werden sie als negative Zahlen dargestellt. | ||
<span id="lösungskonzept-iteratives-eliminieren-dominierter-strategien"></span> | <span id="lösungskonzept-iteratives-eliminieren-dominierter-strategien"></span> | ||
=== Lösungskonzept: iteratives Eliminieren dominierter Strategien === | === Lösungskonzept: iteratives Eliminieren dominierter Strategien === | ||
In der Spieltheorie untersucht man das Entscheidungsverhalten von Individuen, d.h. man möchte herausfinden, wie sich Individuen beziehungsweise Entscheidungsträger in gewissen Situationen, in denen strategische Entscheidungen vonnöten sind, rational verhalten. Im Folgenden werden wir uns mit Lösungskonzepten auseinandersetzen, mittels derer wir die Frage „Welche Aktionen werden die Entscheidungsträger wählen?“ beantworten können. | In der Spieltheorie untersucht man das Entscheidungsverhalten von Individuen, d.h., man möchte herausfinden, wie sich Individuen beziehungsweise Entscheidungsträger in gewissen Situationen, in denen strategische Entscheidungen vonnöten sind, rational verhalten. Im Folgenden werden wir uns mit Lösungskonzepten auseinandersetzen, mittels derer wir die Frage „Welche Aktionen werden die Entscheidungsträger wählen?“ beantworten können. | ||
Eine erste Möglichkeit herauszufinden, wie sich die Entscheidungsträger verhalten, liegt in der Betrachtung dominanter beziehungsweise dominierter Strategien. Eine stark (= strikt) dominante Strategie ist eine Strategie, die immer bevorzugt wird, egal welche Aktion der andere Spieler wählt. Demgegenüber ist eine stark (= strikt) dominierte Strategie eine, die unter keinen Umständen gewählt wird. Von schwach dominanten Strategien spricht man, wenn die Strategie eine zumindest gleich hohe Auszahlung bringt (bzw. schwach dominiert bei maximal gleich hoher Auszahlung). Der Unterschied zwischen stark und schwach dominant/dominiert ist v.a. bei gleich hohen Auszahlungen relevant, in diesem Fall ist ein Spieler indifferent. | Eine erste Möglichkeit herauszufinden, wie sich die Entscheidungsträger verhalten, liegt in der Betrachtung dominanter beziehungsweise dominierter Strategien. Eine stark (= strikt) dominante Strategie ist eine Strategie, die immer bevorzugt wird, egal welche Aktion der andere Spieler wählt. Demgegenüber ist eine stark (= strikt) dominierte Strategie eine, die unter keinen Umständen gewählt wird. Von schwach dominanten Strategien spricht man, wenn die Strategie eine zumindest gleich hohe Auszahlung bringt (bzw. schwach dominiert bei maximal gleich hoher Auszahlung). Der Unterschied zwischen stark und schwach dominant/dominiert ist v.a. bei gleich hohen Auszahlungen relevant, in diesem Fall ist ein Spieler indifferent. | ||
| Zeile 86: | Zeile 85: | ||
Um dieses Konzept zu veranschaulichen, betrachten wir noch einmal das Gefangenendilemma aus Sicht von Räuber 1: | Um dieses Konzept zu veranschaulichen, betrachten wir noch einmal das Gefangenendilemma aus Sicht von Räuber 1: | ||
* Er hat die Möglichkeit, aus zwei Strategien zu wählen, „gestehen“ oder „nicht gestehen“. Angenommen, Räuber 2 wählt die Aktion „gestehen“. In diesem Fall würde Räuber 1, wählte er „gestehen“, 6 Jahre im Gefängnis verbringen, während er, sollte er sich für „nicht gestehen“ entscheiden, 12 Jahre verbüßen | * Er hat die Möglichkeit, aus zwei Strategien zu wählen, „gestehen“ oder „nicht gestehen“. Angenommen, Räuber 2 wählt die Aktion „gestehen“. In diesem Fall würde Räuber 1, wählte er „gestehen“, 6 Jahre im Gefängnis verbringen, während er, sollte er sich für „nicht gestehen“ entscheiden, 12 Jahre verbüßen müsste - wählt Räuber 2 „gestehen“, so ist es für Räuber 1 am besten, ebenfalls zu gestehen (da er dann nur 6 statt von 12 Jahren im Gefängnis verbringen muss). | ||
* Wie stellt sich die Situation nun dar, wenn Räuber 2 sich für die Aktion „nicht gestehen“ entscheidet? In diesem Fall würde Räuber 1, sollte er sich für „gestehen“ entscheiden, 0 Jahre Gefängnis erhalten. Sollte er sich hingegen für „nicht gestehen“ entscheiden, müsste er 1 Jahr in Gefangenschaft verbringen. Auch in diesem Fall ist es also im Interesse von Räuber 1 die Aktion „gestehen“ zu wählen. | * Wie stellt sich die Situation nun dar, wenn Räuber 2 sich für die Aktion „nicht gestehen“ entscheidet? In diesem Fall würde Räuber 1, sollte er sich für „gestehen“ entscheiden, 0 Jahre Gefängnis erhalten. Sollte er sich hingegen für „nicht gestehen“ entscheiden, müsste er 1 Jahr in Gefangenschaft verbringen. Auch in diesem Fall ist es also im Interesse von Räuber 1 die Aktion „gestehen“ zu wählen. | ||
Da Räuber 2 mit denselben Auszahlungen konfrontiert ist, gilt für ihn das gleiche Ergebnis. Im Gefangenendilemma ist also „gestehen“ für beide Seiten die dominante Strategie. Das ist das relevante Ergebnis des Gefangenendilemmas: ''Wofür auch immer sich der andere Spieler entscheidet, der Entscheidungsträger wählt „gestehen“.'' Obwohl offensichtlich ist, dass das kollektiv beste Ergebnis erzielt würde, wenn beide Spieler „nicht gestehen“ wählen, kommt dieses Ergebnis nicht zustande: Jeder Spieler ist für sich besser daran, wenn er „gestehen“ wählt. <ref>Man beachte, dass das Spiel nur eine Runde gespielt wird und es keine Kommunikationsmöglichkeit gibt.</ref> | Da Räuber 2 mit denselben Auszahlungen konfrontiert ist, gilt für ihn das gleiche Ergebnis. Im Gefangenendilemma ist also „gestehen“ für beide Seiten die dominante Strategie. Das ist das relevante Ergebnis des Gefangenendilemmas: ''Wofür auch immer sich der andere Spieler entscheidet, der Entscheidungsträger wählt „gestehen“.'' Obwohl offensichtlich ist, dass das kollektiv beste Ergebnis erzielt würde, wenn beide Spieler „nicht gestehen“ wählen, kommt dieses Ergebnis nicht zustande: Jeder Spieler ist für sich besser daran, wenn er „gestehen“ wählt. <ref>Man beachte, dass das Spiel nur eine Runde gespielt wird und es keine Kommunikationsmöglichkeit gibt.</ref> | ||
Wir haben nun mit der Theorie dominanter Strategien dieses Spiel gelöst. Da „gestehen“ für beide Räuber die dominante Strategie ist, werden sie beide diese wählen. Der Spielausgang ist also durch („gestehen“, „gestehen“) gegeben, und beide Räuber werden jeweils 6 Jahre im Gefängnis verbringen. | Wir haben nun mit der Theorie dominanter Strategien dieses Spiel gelöst. Da „gestehen“ für beide Räuber die dominante Strategie ist, werden sie beide diese wählen. Der Spielausgang ist also durch („gestehen“, „gestehen“) gegeben, und beide Räuber werden jeweils 6 Jahre im Gefängnis verbringen. | ||
{| | {| style="border-collapse: collapse; height: 112px; width: 318px;" border="1" | ||
| style="width: 63.9062px; height: 28px;" | | |||
| | |||
| | |||
<br> | <br> | ||
| | | style="width: 40.7969px; height: 28px;" | | ||
<br> | <br> | ||
| | | style="width: 37.625px; height: 28px;" | | ||
<br> | <br> | ||
| | | style="width: 66.7188px; height: 28px;" | '''Spieler 2''' | ||
| style="width: 92.9531px; height: 28px;" | | |||
<br> | <br> | ||
|- | |- style="height: 28px;" | ||
| | | style="width: 63.9062px; height: 28px;" | | ||
<br> | <br> | ||
| | | style="width: 40.7969px; height: 28px;" | | ||
| | |||
<br> | <br> | ||
| | | style="width: 37.625px; height: 28px;" | '''Links''' | ||
| style="width: 66.7188px; height: 28px;" | '''Mitte''' | |||
| style="width: 92.9531px; height: 28px;" | '''Rechts''' | |||
|- style="height: 28px;" | |||
| style="width: 63.9062px; height: 28px;" | '''Spieler 1''' | |||
| style="width: 40.7969px; height: 28px;" | '''Oben''' | |||
| style="width: 37.625px; height: 28px;" | 3, 2 | |||
| style="width: 66.7188px; height: 28px;" | 3, 4 | |||
| style="width: 92.9531px; height: 28px;" | 2, 3 | |||
|- style="height: 28px;" | |||
| style="width: 63.9062px; height: 28px;" | | |||
<br> | <br> | ||
| style="width: 40.7969px; height: 28px;" | '''Unten''' | |||
| style="width: 37.625px; height: 28px;" | 2, 5 | |||
| style="width: 66.7188px; height: 28px;" | 2, 3 | |||
| style="width: 92.9531px; height: 28px;" | 4, 2 | |||
|} | |} | ||
Beispiel zum iterativen Eliminieren dominierter Strategien | |||
Tabelle | Die obere Tabelle veranschaulicht ein weiteres Spiel, in dem dieses Lösungskonzept zur Anwendung kommt. Das besprochene Lösungskonzept schlägt zur Lösung eines solchen Spieles vor, die dominierten Strategien zu eliminieren, da diese bei rationalem Verhalten nie gewählt werden würden. Betrachten wir Spieler 2. Wenn Spieler 1 „oben“ wählt, so ist es für Spieler 2 am besten, „Mitte“ zu wählen. Wählt Spieler 1 „unten“, so ist es optimal für Spieler 2, „links“ zu wählen. Dementsprechend wird Spieler 2 nie die Strategie „rechts“ wählen, egal welche Aktion Spieler 1 wählt - sie ist durch die beiden anderen Strategien dominiert. | ||
{| | {| style="border-collapse: collapse;" border="1" | ||
| width="26%" | | | width="26%" | | ||
<br> | <br> | ||
| width="23%" | | | width="23%" | | ||
<br> | <br> | ||
| width="23%" | Spieler 2 | | width="23%" | '''Spieler 2''' | ||
| width="26%" | | | width="26%" | | ||
<br> | <br> | ||
| Zeile 173: | Zeile 140: | ||
| | | | ||
<br> | <br> | ||
| Links | | '''Links''' | ||
| Mitte | | '''Mitte''' | ||
|- | |- | ||
| Spieler 1 | | '''Spieler 1''' | ||
| Oben | | '''Oben''' | ||
| 3, 2 | | 3, 2 | ||
| 3, 4 | | 3, 4 | ||
| Zeile 183: | Zeile 150: | ||
| | | | ||
<br> | <br> | ||
| Unten | | '''Unten''' | ||
| 2, 5 | | 2, 5 | ||
| 2, 3 | | 2, 3 | ||
|} | |} | ||
Beispiel nach erster Eliminierung | |||
Da Spieler 1 bekannt ist, dass Spieler 2 niemals „rechts“ wählen wird, verkürzt sich nach Eliminierung dieser irrelevanten Alternative wie in Tabelle | Da Spieler 1 bekannt ist, dass Spieler 2 niemals „rechts“ wählen wird, verkürzt sich nach Eliminierung dieser irrelevanten Alternative wie in der oberen Tabelle dargestellt. Betrachten wir nun das Entscheidungsproblem von Spieler 1. Wenn Spieler 2 „links“ wählt, so ist es für Spieler 1 am besten „oben“ zu wählen. Auch wenn Spieler 2 „Mitte“ wählt, ist „oben“ die bessere Alternative für Spieler 1. Demnach ist „unten“ also eine dominierte Strategie für Spieler 1. Da Spieler 2 dies voraussieht, stellt sich das Spiel wie in folgender Tabelle dar (die Strategie „unten“ wird eliminiert): | ||
{| | {| style="border-collapse: collapse; height: 84px;" border="1" | ||
| | | style="height: 28px; width: 65px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 58px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 74px;" | '''Spieler 2''' | ||
| | | style="height: 28px; width: 49px;" | | ||
<br> | <br> | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 65px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 58px;" | | ||
<br> | <br> | ||
| Links | | style="height: 28px; width: 74px;" | '''Links''' | ||
| Mitte | | style="height: 28px; width: 49px;" | '''Mitte''' | ||
|- | |- style="height: 28px;" | ||
| Spieler 1 | | style="height: 28px; width: 65px;" | '''Spieler 1''' | ||
| Oben | | style="height: 28px; width: 58px;" | '''Oben''' | ||
| 3, 2 | | style="height: 28px; width: 74px;" | 3, 2 | ||
| 3, 4 | | style="height: 28px; width: 49px;" | 3, 4 | ||
|} | |} | ||
Beispiel nach zweiter Eliminierung | |||
Spieler 2 hat nun die Wahl zwischen einer Auszahlung von 2 beziehungsweise 4 und wird demnach die Aktion „Mitte“ wählen. Das Gleichgewicht in dem Spiel ist also durch („oben“, „Mitte“) gegeben. Die Spieler erhalten die Auszahlungen (3, 4). So wird durch das iterative Eliminieren, | Spieler 2 hat nun die Wahl zwischen einer Auszahlung von 2 beziehungsweise 4 und wird demnach die Aktion „Mitte“ wählen. Das Gleichgewicht in dem Spiel ist also durch („oben“, „Mitte“) gegeben. Die Spieler erhalten die Auszahlungen (3, 4). So wird durch das iterative Eliminieren möglich, den Ausgang eines strategischen Spiels vorauszusagen. | ||
<span id="diskussion"></span> | <span id="diskussion"></span> | ||
=== Diskussion === | === Diskussion === | ||
Spiele, die dem Gefangenendilemma gleichen und mit diesem gelöst werden können, treten in vielen Situationen auf. Ein besonders markantes Beispiel dafür ist das atomare Wettrüsten, welches während des Kalten Krieges zwischen der UdSSR und den USA stattfand. Die Angst angegriffen zu werden, führte zur ständigen Aufrüstung. Das wünschenswerte Gleichgewicht in dieser Situation wäre beidseitige Abrüstung und damit einhergehend das Einsparen vieler Ressourcen und nuklearer Unfälle gewesen. Ein Atomkrieg hätte jedoch eine noch größere negative Auszahlung mit sich gebracht (gewissermaßen unendlich). Zwar war das Spiel nicht statisch, aber so lange nicht völlig abgerüstet würde, war man selbst stets besser daran, aufzurüsten. Nur die Pattstellung durch maximale atomare Abschreckung minimierte die Wahrscheinlichkeit, dass die jeweils andere Seite den atomaren Erstschlag durchführen würde. <ref>Das rationale Kalkül hinter dem scheinbaren Wahnsinn wird hervorragend im Film-Klassiker „Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb“ (dt. Titel „Dr. Seltsam oder: Wie ich lernte, die Bombe zu lieben“) von Stanley Kubrick dargestellt.</ref> | Spiele, die dem Gefangenendilemma gleichen und mit diesem gelöst werden können, treten in vielen Situationen auf. Ein besonders markantes Beispiel dafür ist das atomare Wettrüsten, welches während des Kalten Krieges zwischen der UdSSR und den USA stattfand. Die Angst angegriffen zu werden, führte zur ständigen Aufrüstung. Das wünschenswerte Gleichgewicht in dieser Situation wäre beidseitige Abrüstung und damit einhergehend das Einsparen vieler Ressourcen und nuklearer Unfälle gewesen. Ein Atomkrieg hätte jedoch eine noch größere negative Auszahlung mit sich gebracht (gewissermaßen unendlich). Zwar war das Spiel nicht statisch, aber so lange nicht völlig abgerüstet würde, war man selbst stets besser daran, aufzurüsten. Nur die Pattstellung durch maximale atomare Abschreckung minimierte die Wahrscheinlichkeit, dass die jeweils andere Seite den atomaren Erstschlag durchführen würde. <ref>Das rationale Kalkül hinter dem scheinbaren Wahnsinn wird hervorragend im Film-Klassiker „Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb“ (dt. Titel „Dr. Seltsam oder: Wie ich lernte, die Bombe zu lieben“) von Stanley Kubrick dargestellt.</ref> | ||
Somit können Gleichgewichte, die aus Gefangenendilemma-ähnlichen Situationen resultieren, ineffizient insofern sein, dass mindestens ein Spieler bessergestellt werden könnte, ohne den anderen schlechter zu stellen. Im Falle der oben beschriebenen Situationen wären sogar alle Spieler bei einem Ausgang des Spieles („nicht gestehen“, „nicht gestehen“), bessergestellt. Das Ergebnis sieht jedoch möglicherweise anders aus, wenn dasselbe Spiel wiederholt gespielt wird, die Räuber also immer wieder aufeinandertreffen. | Somit können Gleichgewichte, die aus Gefangenendilemma-ähnlichen Situationen resultieren, ineffizient insofern sein, dass mindestens ein Spieler bessergestellt werden könnte, ohne den anderen schlechter zu stellen. Im Falle der oben beschriebenen Situationen wären sogar alle Spieler bei einem Ausgang des Spieles („nicht gestehen“, „nicht gestehen“), bessergestellt. Das Ergebnis sieht jedoch möglicherweise anders aus, wenn dasselbe Spiel wiederholt gespielt wird, die Räuber also immer wieder aufeinandertreffen. | ||
| Zeile 228: | Zeile 196: | ||
Das obige Lösungskonzept ist zwar sehr hilfreich, allerdings werden wir oft auf Situationen stoßen, in denen keine Strategie dominiert ist und die optimale Strategie damit von der Aktion des Gegenübers abhängt. Können wir auch in einem solchen Fall eine Vorhersage über den Ausgang eines Spieles treffen? Dies ist möglich mit einem weiteren Lösungskonzept, dem Konzept des Nash-Gleichgewichtes. | Das obige Lösungskonzept ist zwar sehr hilfreich, allerdings werden wir oft auf Situationen stoßen, in denen keine Strategie dominiert ist und die optimale Strategie damit von der Aktion des Gegenübers abhängt. Können wir auch in einem solchen Fall eine Vorhersage über den Ausgang eines Spieles treffen? Dies ist möglich mit einem weiteren Lösungskonzept, dem Konzept des Nash-Gleichgewichtes. | ||
{| | {| style="border-collapse: collapse; height: 112px;" border="1" | ||
| | | style="height: 28px; width: 62.9531px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 55.4531px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 55.4531px;" | '''Ehefrau''' | ||
| | | style="height: 28px; width: 62.9688px;" | | ||
<br> | <br> | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 62.9531px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 55.4531px;" | | ||
<br> | <br> | ||
| Fußball | | style="height: 28px; width: 55.4531px;" | '''Fußball''' | ||
| Theater | | style="height: 28px; width: 62.9688px;" | '''Theater''' | ||
|- | |- style="height: 28px;" | ||
| Ehemann | | style="height: 28px; width: 62.9531px;" | '''Ehemann''' | ||
| Fußball | | style="height: 28px; width: 55.4531px;" | '''Fußball''' | ||
| 2, 1 | | style="height: 28px; width: 55.4531px;" | 2, 1 | ||
| 0,0 | | style="height: 28px; width: 62.9688px;" | 0,0 | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 62.9531px;" | | ||
<br> | <br> | ||
| Theater | | style="height: 28px; width: 55.4531px;" | '''Theater''' | ||
| 0,0 | | style="height: 28px; width: 55.4531px;" | 0,0 | ||
| 1,2 | | style="height: 28px; width: 62.9688px;" | 1,2 | ||
|} | |} | ||
Der Kampf der Geschlechter | |||
Tabelle | Die obere Tabelle zeigt das Spiel „Kampf der Geschlechter“, das auf einer alltäglichen Konfliktsituation basiert. Ein Ehepaar möchte etwas gemeinsam unternehmen, hat aber verschiedene Präferenzen: Er geht lieber zu einem Fußballspiel, sie ins Theater. Beide Ehepartner begleiten jedoch lieber ihren Gatten / ihre Gattin, als gar nichts zu unternehmen. In diesem Fall gibt es keine dominierte Strategie. Im Falle, dass die Frau „Theater“ wählt, bevorzugt auch der Mann „Theater“, und vice versa beim Fußballspiel. | ||
Um in diesem Spiel ein Gleichgewicht zu identifizieren, arbeitet man mit dem Konzept der Methode der Besten-Antwort-Korrespondenz. Dabei findet man die „beste Antwort“ beider Spieler auf die möglichen Strategien des jeweils anderen und markiert diese; in Tabelle | Um in diesem Spiel ein Gleichgewicht zu identifizieren, arbeitet man mit dem Konzept der Methode der Besten-Antwort-Korrespondenz. Dabei findet man die „beste Antwort“ beider Spieler auf die möglichen Strategien des jeweils anderen und markiert diese; in nachfolgender Tabelle wird dies durch Unterstreichen durchgeführt. | ||
{| | {| style="border-collapse: collapse; height: 112px;" border="1" | ||
| | | style="height: 28px; width: 62.9531px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 55.4531px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 55.4531px;" | '''Ehefrau''' | ||
| | | style="height: 28px; width: 62.9688px;" | | ||
<br> | <br> | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 62.9531px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 55.4531px;" | | ||
<br> | <br> | ||
| Fußball | | style="height: 28px; width: 55.4531px;" | '''Fußball''' | ||
| Theater | | style="height: 28px; width: 62.9688px;" | '''Theater''' | ||
|- | |- style="height: 28px;" | ||
| Ehemann | | style="height: 28px; width: 62.9531px;" | '''Ehemann''' | ||
| Fußball | | style="height: 28px; width: 55.4531px;" | '''Fußball''' | ||
| | | style="height: 28px; width: 55.4531px;" | <u>2</u>, <u>1</u> | ||
| 0,0 | | style="height: 28px; width: 62.9688px;" | 0,0 | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 62.9531px;" | | ||
<br> | <br> | ||
| Theater | | style="height: 28px; width: 55.4531px;" | '''Theater''' | ||
| 0,0 | | style="height: 28px; width: 55.4531px;" | 0,0 | ||
| | | style="height: 28px; width: 62.9688px;" | <u>1</u>,<u>2</u> | ||
|} | |} | ||
Nash-Gleichgewichte im Kampf der Geschlechter | |||
Ein Nash-Gleichgewicht tritt dann auf, wenn beide Spieler beste Antworten auf die Strategie des jeweils anderen wählen, also in dem Punkt, an dem zwei unterstrichene Auszahlungen in einem Matrixelement aufeinandertreffen. In dem Kampf der Geschlechter sind also die beiden Strategiepaare (Fußball, Fußball) und (Theater, Theater) Nash-Gleichgewichte. Ein Nash-Gleichgewicht wird als Gleichgewicht bezeichnet, da in einem solchen beide Spieler keinen Anreiz haben, (einseitig) abzuweichen, d.h. einseitig eine andere als die Gleichgewichtsstrategie zu wählen. Anders formuliert kann sich kein Spieler, gegeben der Aktion seines Gegenübers, verbessern, indem er eine andere Strategie wählte. Wenn im konkreten Fall die Ehefrau zuerst den Vorschlag macht besteht das Gleichgewicht (Theater, Theater). Keiner der Ehepartner hat ein Interesse daran, abzuweichen, da dann die Auszahlung niedriger wäre, indem das Ehepaar gar nichts unternehmen würde. | Ein Nash-Gleichgewicht tritt dann auf, wenn beide Spieler beste Antworten auf die Strategie des jeweils anderen wählen, also in dem Punkt, an dem zwei unterstrichene Auszahlungen in einem Matrixelement aufeinandertreffen. In dem Kampf der Geschlechter sind also die beiden Strategiepaare (Fußball, Fußball) und (Theater, Theater) Nash-Gleichgewichte. Ein Nash-Gleichgewicht wird als Gleichgewicht bezeichnet, da in einem solchen beide Spieler keinen Anreiz haben, (einseitig) abzuweichen, d.h., einseitig eine andere als die Gleichgewichtsstrategie zu wählen. Anders formuliert kann sich kein Spieler, gegeben der Aktion seines Gegenübers, verbessern, indem er eine andere Strategie wählte. Wenn im konkreten Fall die Ehefrau zuerst den Vorschlag macht, besteht das Gleichgewicht (Theater, Theater). Keiner der Ehepartner hat ein Interesse daran, abzuweichen, da dann die Auszahlung niedriger wäre, indem das Ehepaar gar nichts unternehmen würde. | ||
Zu beachten ist in diesem Zusammenhang, dass ein Gleichgewicht in dominanten Strategien immer ein Nash-Gleichgewicht ist, dies allerdings umgekehrt nicht gilt. Das Konzept des Nash-Gleichgewichtes ist also ein „schwächeres“ als das des Gleichgewichtes in dominanten Strategien. Es ermöglicht, Gleichgewichte auch in Spielen zu finden, in denen keine Strategien dominiert sind, und damit gewisse Vorhersagen über den Ausgang in einer solchen Situation abzugeben. | Zu beachten ist in diesem Zusammenhang, dass ein Gleichgewicht in dominanten Strategien immer ein Nash-Gleichgewicht ist, dies allerdings umgekehrt nicht gilt. Das Konzept des Nash-Gleichgewichtes ist also ein „schwächeres“ als das des Gleichgewichtes in dominanten Strategien. Es ermöglicht, Gleichgewichte auch in Spielen zu finden, in denen keine Strategien dominiert sind, und damit gewisse Vorhersagen über den Ausgang in einer solchen Situation abzugeben. | ||
| Zeile 297: | Zeile 265: | ||
<span id="dynamische-spiele"></span> | <span id="dynamische-spiele"></span> | ||
== Dynamische Spiele == | == Dynamische Spiele == | ||
Bis jetzt wurden nur statische Spiele betrachtet – eine Möglichkeit, die Dimension Zeit in ein Spiel zu inkorporieren ist es, die Spieler nacheinander (nicht: simultan) entscheiden zu lassen. Hierbei handelt es sich um sequenzielle Spiele. Eine weitere Möglichkeit ist es, die Spieler ein simultanes Spiel mehrere Male hintereinander spielen zu lassen. In diesem Fall handelt es sich um wiederholte Spiele. | Bis jetzt wurden nur statische Spiele betrachtet – eine Möglichkeit, die Dimension Zeit in ein Spiel zu inkorporieren, ist es, die Spieler nacheinander (nicht: simultan) entscheiden zu lassen. Hierbei handelt es sich um sequenzielle Spiele. Eine weitere Möglichkeit ist es, die Spieler ein simultanes Spiel mehrere Male hintereinander spielen zu lassen. In diesem Fall handelt es sich um wiederholte Spiele. | ||
<span id="der-zusammenhang-zwischen-sequenziellen-und-simultanen-spielen-das-lösungskonzept-der-rückwärtsinduktion"></span> | <span id="der-zusammenhang-zwischen-sequenziellen-und-simultanen-spielen-das-lösungskonzept-der-rückwärtsinduktion"></span> | ||
=== Der Zusammenhang zwischen sequenziellen und simultanen Spielen: Das Lösungskonzept der Rückwärtsinduktion === | === Der Zusammenhang zwischen sequenziellen und simultanen Spielen: Das Lösungskonzept der Rückwärtsinduktion === | ||
In einem sequenziellen Spiel ist die zeitliche Abfolge von großer Bedeutung. Betrachten wir dafür ein Spiel, welches zuerst als simultanes Spiel und darauffolgend als sequenzielles Spiel gespielt wird. Die Spielmatrix, welche sich auf das simultane Spiel bezieht, stellt sich wie in Tabelle | In einem sequenziellen Spiel ist die zeitliche Abfolge von großer Bedeutung. Betrachten wir dafür ein Spiel, welches zuerst als simultanes Spiel und darauffolgend als sequenzielles Spiel gespielt wird. Die Spielmatrix, welche sich auf das simultane Spiel bezieht, stellt sich wie in nachfolgender Tabelle dar: | ||
{| | {| style="border-collapse: collapse; height: 112px;" border="1" | ||
| | | style="height: 28px; width: 65px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 58px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 65px;" | '''Spieler 2''' | ||
| | | style="height: 28px; width: 58px;" | | ||
<br> | <br> | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 65px;" | | ||
<br> | <br> | ||
| | | style="height: 28px; width: 58px;" | | ||
<br> | <br> | ||
| Links | | style="height: 28px; width: 65px;" | '''Links''' | ||
| Rechts | | style="height: 28px; width: 58px;" | '''Rechts''' | ||
|- | |- style="height: 28px;" | ||
| Spieler 1 | | style="height: 28px; width: 65px;" | '''Spieler 1''' | ||
| Oben | | style="height: 28px; width: 58px;" | '''Oben''' | ||
| | | style="height: 28px; width: 65px;" | <u>1</u>, <u>9</u> | ||
| 1,<u>9</u> | | style="height: 28px; width: 58px;" | 1,<u>9</u> | ||
|- | |- style="height: 28px;" | ||
| | | style="height: 28px; width: 65px;" | | ||
<br> | <br> | ||
| Unten | | style="height: 28px; width: 58px;" | '''Unten''' | ||
| 0,0 | | style="height: 28px; width: 65px;" | 0,0 | ||
| | | style="height: 28px; width: 58px;" | <u>2</u>,<u>1</u> | ||
|} | |} | ||
Beispiel für ein simultanes Spiel | |||
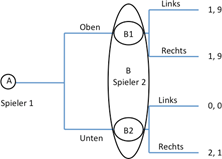
In obigem Spiel sind die Beste-Antwort-Strategien analog zum vorigen Abschnitt markiert. Wie man sehen kann, gibt es in diesem simultanen Spiel zwei Nash-Gleichgewichte: (oben, links) und (unten, rechts). Wie ändert sich die Voraussage für den Spielausgang, wenn das gleiche Spiel sequenziell gespielt wird? Angenommen Spieler 1 entscheidet sich zuerst für eine Aktion. Spieler 2 reagiert danach. Diese Situation lässt sich in einem Spielbaum wie in Abbildung | In obigem Spiel sind die Beste-Antwort-Strategien analog zum vorigen Abschnitt markiert. Wie man sehen kann, gibt es in diesem simultanen Spiel zwei Nash-Gleichgewichte: (oben, links) und (unten, rechts). Wie ändert sich die Voraussage für den Spielausgang, wenn das gleiche Spiel sequenziell gespielt wird? Angenommen, Spieler 1 entscheidet sich zuerst für eine Aktion. Spieler 2 reagiert danach. Diese Situation lässt sich in einem Spielbaum wie in nachfolgender Abbildung darstellen: | ||
[[Datei:Ec411 1.png|300px|none|thumb|Beispiel für ein sequenzielles Spiel]] | [[Datei:Ec411 1.png|300px|none|thumb|Beispiel für ein sequenzielles Spiel]] | ||
Im abgebildeten Spielbaum ist jeder Punkt, an dem ein Spieler eine Entscheidung trifft (Entscheidungspunkte), markiert. Als Lösungskonzept kommt die Rückwärtsinduktion zur Anwendung. Dabei wird das Spiel von hinten aufgerollt, d.h. man betrachtet zuerst die letzte Entscheidung des Spieles und arbeitet sich dann nach vorne. | Im abgebildeten Spielbaum ist jeder Punkt, an dem ein Spieler eine Entscheidung trifft (Entscheidungspunkte), markiert. Als Lösungskonzept kommt die Rückwärtsinduktion zur Anwendung. Dabei wird das Spiel von hinten aufgerollt, d.h., man betrachtet zuerst die letzte Entscheidung des Spieles und arbeitet sich dann nach vorne. | ||
Der letzte Entscheidungspunkt in Abbildung | Der letzte Entscheidungspunkt in der oberen Abbildung ist Punkt B. In diesem Punkt entscheidet sich Spieler 2 zwischen den beiden potenziellen Aktionen „links“ und „rechts“. Sollte er sich an Punkt B1 befinden – was dann der Fall ist, wenn sich Spieler 1 in der Runde davor für „oben“ entschieden hat – dann ist für Spieler 2 irrelevant, ob er links oder rechts wählt – er erhält in beiden Fällen eine Auszahlung im Wert von 9. Sollte er sich an dem Punkt B2 befinden, so wird er rechts wählen, da 1 größer ist als 0. Somit ist klar, dass Spieler 2 in jedem Fall rechts wählen wird, da die Auszahlung entweder gleich oder größer ist als bei der Wahl „links“. | ||
Mit diesem Wissen gehen wir nun nach vorne im Spielablauf, zur Entscheidung von Spieler 1 im Entscheidungspunkt A. Er weiß, wie Spieler B auf seine Entscheidung reagieren wird und trifft mit diesem Wissen seine eigene Entscheidung. D.h., Spieler 1 hat die Wahl zwischen einer Auszahlung von 1, wenn er „oben“ wählt und 2, wenn er „unten“ wählt. Somit ist klar, dass Spieler 1 „unten“ wählen wird und der Spielausgang durch das Aktionenpaar (unten, rechts) gegeben und die damit einhergehenden Auszahlungen sind (2, 1). | Mit diesem Wissen gehen wir nun nach vorne im Spielablauf, zur Entscheidung von Spieler 1 im Entscheidungspunkt A. Er weiß, wie Spieler B auf seine Entscheidung reagieren wird und trifft mit diesem Wissen seine eigene Entscheidung. D.h., Spieler 1 hat die Wahl zwischen einer Auszahlung von 1, wenn er „oben“ wählt und 2, wenn er „unten“ wählt. Somit ist klar, dass Spieler 1 „unten“ wählen wird und der Spielausgang durch das Aktionenpaar (unten, rechts) gegeben und die damit einhergehenden Auszahlungen sind (2, 1). | ||
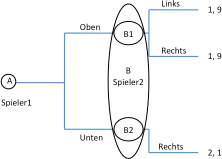
Bei dem Lösungskonzept der Rückwärtsinduktion geht man von dem Konzept der „common rationality“ aus, d.h., man nimmt an, dass alle Spieler rational handeln und dies auch voneinander wissen. Im obigen Beispiel handelt Spieler B rational, in dem er an Entscheidungspunkt B1 indifferent zwischen „links“ und „rechts“ ist und an Entscheidungspunkt B2 „rechts“ wählt. Spieler A wiederum weiß, dass Spieler B rational handelt und baut darauf seine eigene Entscheidung auf. D.h., er betrachtet das verkürzte Spiel, welches für ihn tatsächlich relevant ist, wie in Abbildung | Bei dem Lösungskonzept der Rückwärtsinduktion geht man von dem Konzept der „common rationality“ aus, d.h., man nimmt an, dass alle Spieler rational handeln und dies auch voneinander wissen. Im obigen Beispiel handelt Spieler B rational, in dem er an Entscheidungspunkt B1 indifferent zwischen „links“ und „rechts“ ist und an Entscheidungspunkt B2 „rechts“ wählt. Spieler A wiederum weiß, dass Spieler B rational handelt und baut darauf seine eigene Entscheidung auf. D.h., er betrachtet das verkürzte Spiel, welches für ihn tatsächlich relevant ist, wie in folgender Abbildung dargestellt. | ||
[[Datei:Ec411 2.png|300px|none|thumb|Lösung eines sequenziellen Spieles]] | [[Datei:Ec411 2.png|300px|none|thumb|Lösung eines sequenziellen Spieles]] | ||
| Zeile 354: | Zeile 323: | ||
=== Das Ultimatum-Spiel === | === Das Ultimatum-Spiel === | ||
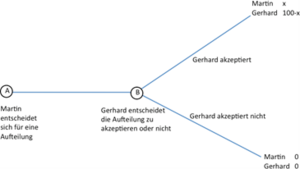
Ein oft zitiertes Beispiel für ein sequenzielles Spiel ist das sogenannte Ultimatum-Spiel. Martin soll 100 Euro zwischen sich selbst und einem zweiten Spieler, Gerhard, aufteilen. Der Spielverlauf gibt vor, dass Martin zuerst über die Aufteilung der 100 Euro entscheidet. Er macht damit ein Angebot an Gerhard, welcher dieses Angebot im nächsten Schritt annehmen oder ablehnen kann. Nimmt er es an, so werden die 100 Euro gemäß Martins Angebot aufgeteilt. Lehnt er es ab, so bekommen beide Spieler kein Geld und die 100 Euro gehen verloren (oder zurück an den Spielleiter). Der Spielbaum des Ultimatum-Spiels ist in Abbildung | Ein oft zitiertes Beispiel für ein sequenzielles Spiel ist das sogenannte Ultimatum-Spiel. Martin soll 100 Euro zwischen sich selbst und einem zweiten Spieler, Gerhard, aufteilen. Der Spielverlauf gibt vor, dass Martin zuerst über die Aufteilung der 100 Euro entscheidet. Er macht damit ein Angebot an Gerhard, welcher dieses Angebot im nächsten Schritt annehmen oder ablehnen kann. Nimmt er es an, so werden die 100 Euro gemäß Martins Angebot aufgeteilt. Lehnt er es ab, so bekommen beide Spieler kein Geld und die 100 Euro gehen verloren (oder zurück an den Spielleiter). Der Spielbaum des Ultimatum-Spiels ist in nachfolgender Abbildung dargestellt. | ||
[[Datei:Ec411 3.png|300px|none|thumb|Das Ultimatum Spiel]] | [[Datei:Ec411 3.png|300px|none|thumb|Das Ultimatum Spiel]] | ||
| Zeile 362: | Zeile 331: | ||
Auch dieses Spiel lösen wir wieder mit Hilfe der Rückwärtsinduktion. In der letzten Entscheidungsstufe entscheidet Gerhard zwischen 0 Euro, wenn er Martins Angebot ablehnt, und (100 - x) Euro, wenn er es annimmt, wobei x dem Anteil entspricht, den Martin vorgeschlagen haben wird, selbst zu behalten. Demnach wird er in dieser Stufe jedes Angebot von Martin akzeptieren, welches ihm eine Auszahlung von mehr als 0 Euro sichert, da jede dieser Auszahlungen größer ist, als gar nichts zu bekommen. Martin, als rationaler Spieler, antizipiert dieses Verhalten und wird – nachdem er, um seine eigene Auszahlung zu maximieren, Gerhards Anteil möglichst klein halten muss – Gerhard nur 1 Euro anbieten und demnach 99 Euro für sich selbst behalten. Dies ist also der Ausgang des Ultimatum-Spiels: In der ersten Stufe bietet Martin Gerhard 1 Euro an und behält damit 99 Euro für sich. In der zweiten Stufe akzeptiert Gerhard dieses Angebot, da 1 Euro größer ist als 0 Euro. Die Auszahlungen im Gleichgewicht sind demnach (99,1). | Auch dieses Spiel lösen wir wieder mit Hilfe der Rückwärtsinduktion. In der letzten Entscheidungsstufe entscheidet Gerhard zwischen 0 Euro, wenn er Martins Angebot ablehnt, und (100 - x) Euro, wenn er es annimmt, wobei x dem Anteil entspricht, den Martin vorgeschlagen haben wird, selbst zu behalten. Demnach wird er in dieser Stufe jedes Angebot von Martin akzeptieren, welches ihm eine Auszahlung von mehr als 0 Euro sichert, da jede dieser Auszahlungen größer ist, als gar nichts zu bekommen. Martin, als rationaler Spieler, antizipiert dieses Verhalten und wird – nachdem er, um seine eigene Auszahlung zu maximieren, Gerhards Anteil möglichst klein halten muss – Gerhard nur 1 Euro anbieten und demnach 99 Euro für sich selbst behalten. Dies ist also der Ausgang des Ultimatum-Spiels: In der ersten Stufe bietet Martin Gerhard 1 Euro an und behält damit 99 Euro für sich. In der zweiten Stufe akzeptiert Gerhard dieses Angebot, da 1 Euro größer ist als 0 Euro. Die Auszahlungen im Gleichgewicht sind demnach (99,1). | ||
Aus eigenen Beobachtungen würden wohl viele Menschen diesem Ausgang des Spieles nicht glauben. Sie selbst würden ein Angebot wie jenes von Martin als unfair empfinden und es demnach – auch wenn eine solche Handlungsweise nicht rational (im Sinne von: Gewinn maximierend) ist – ablehnen. Zu dem Erstaunen von vielen Spieltheoretikern stellte sich bei Experimenten heraus, dass dies tatsächlich zutrifft: circa 40% bis 60% der Teilnehmer lehnten ein niedriges Angebot ab, obwohl dies zur Folge hatte, dass sie am Ende des Spieles eine Auszahlung von 0 erhielten. Nach ihren Motiven befragt, gaben viele an, dass sie eine so ungleiche Aufteilung unfair empfanden und es daher vorzogen leer auszugehen, wenn dies hieße, dass der Gegenspieler ebenfalls eine Auszahlung von Null erhielt. <ref>Fehr, Ernst und Simon Gächter (2000): Fairness and retaliation: the economics of reciprocity, Journal of Economic Perspectives 14: 159-181</ref> Man wollte also das Gegenüber, welches das unfaire Angebot unterbreitet hatte, bestrafen. | Aus eigenen Beobachtungen würden wohl viele Menschen diesem Ausgang des Spieles nicht glauben. Sie selbst würden ein Angebot wie jenes von Martin als unfair empfinden und es demnach – auch wenn eine solche Handlungsweise nicht rational (im Sinne von: Gewinn maximierend) ist – ablehnen. Zu dem Erstaunen von vielen Spieltheoretikern stellte sich bei Experimenten heraus, dass dies tatsächlich zutrifft: circa 40% bis 60% der Teilnehmer lehnten ein niedriges Angebot ab, obwohl dies zur Folge hatte, dass sie am Ende des Spieles eine Auszahlung von 0 erhielten. Nach ihren Motiven befragt, gaben viele an, dass sie eine so ungleiche Aufteilung unfair empfanden und es daher vorzogen leer auszugehen, wenn dies hieße, dass der Gegenspieler ebenfalls eine Auszahlung von Null erhielt. <ref>Fehr, Ernst und Simon Gächter (2000): Fairness and retaliation: the economics of reciprocity, Journal of Economic Perspectives 14: 159-181</ref> Man wollte also das Gegenüber, welches das unfaire Angebot unterbreitet hatte, bestrafen. | ||
<span id="glaubwürdige-drohungen-und-versprechen"></span> | <span id="glaubwürdige-drohungen-und-versprechen"></span> | ||
| Zeile 372: | Zeile 341: | ||
=== Das Problem der Verbindlichkeit === | === Das Problem der Verbindlichkeit === | ||
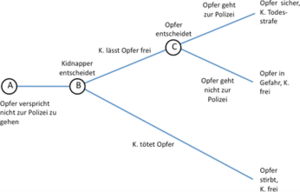
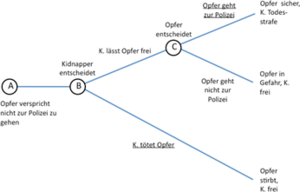
Betrachten wir ein weiteres Spiel, welches obiges Problem deutlich darstellt. Ein Kidnapper überlegt, ob er sein Opfer laufen lassen soll oder nicht. Der Spielbaum sieht wie in Abbildung | Betrachten wir ein weiteres Spiel, welches obiges Problem deutlich darstellt. Ein Kidnapper überlegt, ob er sein Opfer laufen lassen soll oder nicht. Der Spielbaum sieht wie in folgender Abbildung dargestellt aus. | ||
Ein Kidnapper, der sein Opfer entführt hat, ändert plötzlich seinen Plan und möchte das Opfer am liebsten wieder frei lassen. Er ist allerdings besorgt, dass das Opfer, sobald es frei ist, zur Polizei gehen könnte und er als Folge ins Gefängnis müsste. Die andere mögliche Aktion des Kidnappers ist, dass er das Opfer umbringt und sich damit von seiner Verantwortung befreit. Das Opfer auf der anderen Seite realisiert, dass es, selbst wenn es freikommen sollte, immer noch in Gefahr schweben würde, da der Kidnapper es sich zu einem späteren Zeitpunkt noch einmal anders überlegen könnte. Das Opfer hat also, sollte es freikommen, einen Anreiz, zur Polizei zu gehen. | Ein Kidnapper, der sein Opfer entführt hat, ändert plötzlich seinen Plan und möchte das Opfer am liebsten wieder frei lassen. Er ist allerdings besorgt, dass das Opfer, sobald es frei ist, zur Polizei gehen könnte und er als Folge ins Gefängnis müsste. Die andere mögliche Aktion des Kidnappers ist, dass er das Opfer umbringt und sich damit von seiner Verantwortung befreit. Das Opfer auf der anderen Seite realisiert, dass es, selbst wenn es freikommen sollte, immer noch in Gefahr schweben würde, da der Kidnapper es sich zu einem späteren Zeitpunkt noch einmal anders überlegen könnte. Das Opfer hat also, sollte es freikommen, einen Anreiz, zur Polizei zu gehen. | ||
| Zeile 378: | Zeile 347: | ||
[[Datei:Ec411 4.png|300px|none|thumb|Das Kidnapper-Opfer-Spiel]] | [[Datei:Ec411 4.png|300px|none|thumb|Das Kidnapper-Opfer-Spiel]] | ||
In dem vorliegenden Spiel wenden wir wieder das Lösungskonzept Rückwärtsinduktion an. Die erste Überlegung gilt also der Entscheidung an Punkt C - wie würde sich das Opfer an diesem Punkt entscheiden? Es hat die Wahl zwischen der Auszahlung (in einem erweiterten Sinn) „Opfer ist sicher“ und „Opfer schwebt weiter in Gefahr“. In dieser Situation würde das Opfer natürlich ersteres präferieren und wird sich dementsprechend dafür entschließen, zur Polizei zu gehen. Betrachten wir nun den Entscheidungspunkt davor, Punkt B. In Punkt B trifft der Kidnapper eine Entscheidung, wissend, wie sich das Opfer danach (an Punkt C) verhalten wird. Der Kidnapper kann das Opfer entweder frei lassen oder es umbringen. Wenn er das Opfer frei lässt, weiß er, dass dieses danach zur Polizei gehen würde. In diesem Fall würde der Kidnapper zur Todesstrafe verurteilt werden. Sollte er sich dafür entscheiden, das Opfer zu töten, so wird er überleben. Der Kidnapper wird sich also an Punkt B dafür entscheiden, sein Opfer zu töten. Der Spielbaum mit den eingezeichneten optimalen Strategien an jedem Entscheidungspunkt sieht also wie in Abbildung | In dem vorliegenden Spiel wenden wir wieder das Lösungskonzept Rückwärtsinduktion an. Die erste Überlegung gilt also der Entscheidung an Punkt C - wie würde sich das Opfer an diesem Punkt entscheiden? Es hat die Wahl zwischen der Auszahlung (in einem erweiterten Sinn) „Opfer ist sicher“ und „Opfer schwebt weiter in Gefahr“. In dieser Situation würde das Opfer natürlich ersteres präferieren und wird sich dementsprechend dafür entschließen, zur Polizei zu gehen. Betrachten wir nun den Entscheidungspunkt davor, Punkt B. In Punkt B trifft der Kidnapper eine Entscheidung, wissend, wie sich das Opfer danach (an Punkt C) verhalten wird. Der Kidnapper kann das Opfer entweder frei lassen oder es umbringen. Wenn er das Opfer frei lässt, weiß er, dass dieses danach zur Polizei gehen würde. In diesem Fall würde der Kidnapper zur Todesstrafe verurteilt werden. Sollte er sich dafür entscheiden, das Opfer zu töten, so wird er überleben. Der Kidnapper wird sich also an Punkt B dafür entscheiden, sein Opfer zu töten. Der Spielbaum mit den eingezeichneten optimalen Strategien an jedem Entscheidungspunkt sieht also wie in der unteren Abbildung aus. | ||
Wir kennen nun also den Ausgang des obigen strategischen Spiels. An Punkt A wird das Opfer versprechen, nicht zur Polizei zu gehen und an Punkt B wird sich der Kidnapper dafür entscheiden, das Opfer zu töten. Die „Auszahlungen” bestehen also darin, dass das Opfer getötet wird und der Kidnapper überlebt. | Wir kennen nun also den Ausgang des obigen strategischen Spiels. An Punkt A wird das Opfer versprechen, nicht zur Polizei zu gehen und an Punkt B wird sich der Kidnapper dafür entscheiden, das Opfer zu töten. Die „Auszahlungen” bestehen also darin, dass das Opfer getötet wird und der Kidnapper überlebt. | ||
| Zeile 404: | Zeile 373: | ||
== Übungen == | == Übungen == | ||
Übungsbeispiel 1.1 | '''Übungsbeispiel 1.1''' | ||
Betrachten Sie eine Tit-For-Tat-Strategie in einem wiederholten Gefangenendilemma. Nehmen Sie an, ein Spieler macht einen Fehler und wählt „gestehen“ (also das nicht-kooperative Verhalten), obwohl er eigentlich kooperieren wollte (also eigentlich „nicht gestehen“ wählen wollte). Wenn danach beide Spieler weiterhin die Tit-For-Tat-Strategie spielen, wie entwickelt sich der Spielverlauf? Welche Aktionen werden gewählt? | Betrachten Sie eine Tit-For-Tat-Strategie in einem wiederholten Gefangenendilemma. Nehmen Sie an, ein Spieler macht einen Fehler und wählt „gestehen“ (also das nicht-kooperative Verhalten), obwohl er eigentlich kooperieren wollte (also eigentlich „nicht gestehen“ wählen wollte). Wenn danach beide Spieler weiterhin die Tit-For-Tat-Strategie spielen, wie entwickelt sich der Spielverlauf? Welche Aktionen werden gewählt? | ||
Übungsbeispiel 1.2 | |||
'''Übungsbeispiel 1.2''' | |||
Nehmen Sie an, im Gefangenendilemma wird beiden Räubern erlaubt, sich aneinander zu rächen, nachdem sie ihre jeweiligen Gefängnisstrafen hinter sich gebracht haben. Wie würde sich das Spiel formal ändern? Könnte ein effizienteres Ergebnis erreicht werden? | Nehmen Sie an, im Gefangenendilemma wird beiden Räubern erlaubt, sich aneinander zu rächen, nachdem sie ihre jeweiligen Gefängnisstrafen hinter sich gebracht haben. Wie würde sich das Spiel formal ändern? Könnte ein effizienteres Ergebnis erreicht werden? | ||
Übungsbeispiel 1.3 | |||
'''Übungsbeispiel 1.3''' | |||
Angenommen, in dem in Tabelle 1-8 dargestellten Spiel würde Spieler 2 zuerst die Entscheidung treffen und Spieler 1 würde erst danach reagieren. Die zeitliche Abfolge wäre also genau umgekehrt als sie in Abbildung 1-1 dargestellt ist. Zeichnen Sie den Spielbaum, der dieses sequenzielle Spiel darstellt. Wodurch ist das Gleichgewicht in diesem Spiel gegeben? Welche zeitliche Abfolge würde Spieler 2 bevorzugen? Würde er lieber zuerst oder lieber nach Spieler 1 entscheiden? | Angenommen, in dem in Tabelle 1-8 dargestellten Spiel würde Spieler 2 zuerst die Entscheidung treffen und Spieler 1 würde erst danach reagieren. Die zeitliche Abfolge wäre also genau umgekehrt als sie in Abbildung 1-1 dargestellt ist. Zeichnen Sie den Spielbaum, der dieses sequenzielle Spiel darstellt. Wodurch ist das Gleichgewicht in diesem Spiel gegeben? Welche zeitliche Abfolge würde Spieler 2 bevorzugen? Würde er lieber zuerst oder lieber nach Spieler 1 entscheiden? | ||
Übungsbeispiel 1.4 | |||
'''Übungsbeispiel 1.4''' | |||
Ein Unternehmer überlegt, ob er eine neue Dependance in einer anderen Stadt eröffnen soll. Er müsste dazu einen neuen Manager anstellen, der sich um die neue Filiale kümmern würde. Findet er einen Manager, der diese Aufgabe ehrlich erledigen würde, so könnte er ihm ein Gehalt von monatlich 5000 Euro zahlen. Dies wäre ein sehr gutes Gehalt für den Manager, da er anderswo nur 2500 Euro verdienen könnte. Wäre der Manager ehrlich, könnte der Unternehmer, trotz des hohen Gehalts, immer noch einen Gewinn von 1600 Euro im Monat machen. Da sich die Filiale in einer anderen Stadt befindet, wäre es unmöglich für den Unternehmer, den Manager zu überwachen. Dieser hätte also die Möglichkeit, sich unehrlich zu verhalten und dem Unternehmen Geld zu stehlen. In dem Fall könnte der Manager sein Gehalt um 2200 Euro aufbessern (insgesamt also 7200 Euro in seiner Position „verdienen“), während der Unternehmer Verluste mit der neuen Filiale machen würde. Diese würden sich auf 1200 Euro belaufen. Der Unternehmer gibt eine Annonce auf, mehrere Bewerber melden sich. | Ein Unternehmer überlegt, ob er eine neue Dependance in einer anderen Stadt eröffnen soll. Er müsste dazu einen neuen Manager anstellen, der sich um die neue Filiale kümmern würde. Findet er einen Manager, der diese Aufgabe ehrlich erledigen würde, so könnte er ihm ein Gehalt von monatlich 5000 Euro zahlen. Dies wäre ein sehr gutes Gehalt für den Manager, da er anderswo nur 2500 Euro verdienen könnte. Wäre der Manager ehrlich, könnte der Unternehmer, trotz des hohen Gehalts, immer noch einen Gewinn von 1600 Euro im Monat machen. Da sich die Filiale in einer anderen Stadt befindet, wäre es unmöglich für den Unternehmer, den Manager zu überwachen. Dieser hätte also die Möglichkeit, sich unehrlich zu verhalten und dem Unternehmen Geld zu stehlen. In dem Fall könnte der Manager sein Gehalt um 2200 Euro aufbessern (insgesamt also 7200 Euro in seiner Position „verdienen“), während der Unternehmer Verluste mit der neuen Filiale machen würde. Diese würden sich auf 1200 Euro belaufen. Der Unternehmer gibt eine Annonce auf, mehrere Bewerber melden sich. | ||
(a) Angenommen, der Unternehmer geht davon aus, dass alle Manager, die er anstellen könnte, nur daran interessiert sind, ihr Einkommen zu | (a) Angenommen, der Unternehmer geht davon aus, dass alle Manager, die er anstellen könnte, nur daran interessiert sind, ihr Einkommen zu maximieren – wird er sich dafür entscheiden, die Filiale eröffnen? Stellen Sie das Spiel in Normalform dar und begründen Sie Ihre Antwort. | ||
maximieren – wird er sich dafür entscheiden, die Filiale eröffnen? Stellen Sie das Spiel in Normalform dar und begründen Sie Ihre Antwort. | |||
(b) Angenommen, der Unternehmer weiß, dass einer seiner Kandidaten für die Stelle des Managers unehrliches Verhalten aus religiösen Gründen ablehnt. Er nimmt an, dass dieser Kandidat bereit wäre, bis zu 20.000 Euro zu zahlen, damit er nicht mit dem Gefühl der Schuld leben muss (anders formuliert: die Sünde des Diebstahls kostete den Manager 20.000 Euro). Würde der Unternehmer in diesem Fall die Filiale eröffnen? Wie ändert sich in diesem Fall die Spielmatrix? Stellen Sie das Spiel dar und begründen Sie Ihre Antwort. | (b) Angenommen, der Unternehmer weiß, dass einer seiner Kandidaten für die Stelle des Managers unehrliches Verhalten aus religiösen Gründen ablehnt. Er nimmt an, dass dieser Kandidat bereit wäre, bis zu 20.000 Euro zu zahlen, damit er nicht mit dem Gefühl der Schuld leben muss (anders formuliert: die Sünde des Diebstahls kostete den Manager 20.000 Euro). Würde der Unternehmer in diesem Fall die Filiale eröffnen? Wie ändert sich in diesem Fall die Spielmatrix? Stellen Sie das Spiel dar und begründen Sie Ihre Antwort. | ||
Übungsbeispiel 1.5 | |||
'''Übungsbeispiel 1.5''' | |||
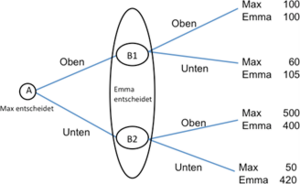
Max und Emma spielen ein Spiel, in dem Max als erster eine Entscheidung trifft (siehe Abbildung unten). Nachdem Max sich entweder für „oben“ oder „unten“ entschieden hat, kann sich Emma ihrerseits für „oben“ oder „unten“ entscheiden. | Max und Emma spielen ein Spiel, in dem Max als erster eine Entscheidung trifft (siehe Abbildung unten). Nachdem Max sich entweder für „oben“ oder „unten“ entschieden hat, kann sich Emma ihrerseits für „oben“ oder „unten“ entscheiden. | ||
| Zeile 436: | Zeile 412: | ||
<hr> | <hr> | ||
<br>'''Lösungen ''' | <br>'''Lösungen''' | ||
<br> | '''Übungsbeispiel 1.1''' | ||
<br>Der zweite Spieler wird, nachdem der erste Spieler (unbeabsichtigt) auf eine nichtkooperative Strategie abgewichen ist, selbst auch abweichen (als Resultat der Tit-For-Tat-Strategie). In der nächsten Runde wird allerdings der erste Spieler, als Antwort auf das Abweichen des zweiten Spielers in der Vorrunde, selbst wieder abweichen und jeder der Spieler wird danach die nichtkooperative Strategie wählen. Dieses Beispiel macht deutlich, dass eine Tit-For-Tat-Strategie nicht die optimale Strategie ist, wenn die Möglichkeit besteht, dass Spieler Fehler begehen. | |||
Übungsbeispiel 1.2 | '''Übungsbeispiel 1.2''' | ||
Wenn die beiden Spieler die Möglichkeit haben, sich aneinander zu rächen, würde sich formal die Auszahlungsstruktur des Spieles ändern. Dies könnte zu einem effizienten Ausgang des Spieles führen – zum Beispiel könnten die Spieler sich einigen, einander umzubringen, sollte der jeweils andere gestehen. Wenn Sie nun annehmen, dass die Auszahlung „Tod“ einen unendlich negativen Nutzen hat, kann sich die Spielmatrix so ändern, dass das Gleichgewicht, in dem beide Spieler „nicht gestehen“ wählen, auftritt. Dazu jedoch zwei Anmerkungen: | Wenn die beiden Spieler die Möglichkeit haben, sich aneinander zu rächen, würde sich formal die Auszahlungsstruktur des Spieles ändern. Dies könnte zu einem effizienten Ausgang des Spieles führen – zum Beispiel könnten die Spieler sich einigen, einander umzubringen, sollte der jeweils andere gestehen. Wenn Sie nun annehmen, dass die Auszahlung „Tod“ einen unendlich negativen Nutzen hat, kann sich die Spielmatrix so ändern, dass das Gleichgewicht, in dem beide Spieler „nicht gestehen“ wählen, auftritt. Dazu jedoch zwei Anmerkungen: | ||
| Zeile 450: | Zeile 427: | ||
* Erstens kann einer der Räuber immer noch „gestehen“ wählen und den anderen, nachdem dieser freigekommen ist, zuerst umbringen. Es müsste also sichergestellt werden, dass die Drohung hinreichend realistisch ist, um zum Ergebnis „nicht gestehen“ zu kommen. | * Erstens kann einer der Räuber immer noch „gestehen“ wählen und den anderen, nachdem dieser freigekommen ist, zuerst umbringen. Es müsste also sichergestellt werden, dass die Drohung hinreichend realistisch ist, um zum Ergebnis „nicht gestehen“ zu kommen. | ||
* Man beachte die Analogie zur atomaren Abschreckung: Die Drohung, die strategische Atomwaffen implizieren, ist, das Land des Feindes völlig zu zerstören, nachdem dieser den Erstschlag ausgeführt hat. Die Lösung des „Spiels“ der atomaren Abschreckung ist daher für beide Seiten „nicht angreifen“. Dazu gehört auch, sich als Atommacht stets so zu verhalten, dass die Angst vor der völligen Zerstörung für den Feind realistisch ist. Strategische Atomwaffen nur zu besitzen reicht daher nicht aus, es muss der Zweitschlag jederzeit – auch dann, wenn das eigene Land durch den Erstschlag bereits zerstört sein sollte – durchgeführt werden können, um beim Feind glaubwürdig zu sein. Aus diesem Grund sind bspw. mit strategischen Atomwaffen bestückte U-Boote permanent irgendwo in den Meeren unterwegs und selbst für befreundete Staaten nicht zu orten (d.h. der Feind muss einerseits wissen, dass es diese jederzeit einsatzfähigen Waffen gibt, er darf aber gleichzeitig nicht wissen, wo sie sich befinden, da er sie sonst außer Gefecht setzen könnte). | * Man beachte die Analogie zur atomaren Abschreckung: Die Drohung, die strategische Atomwaffen implizieren, ist, das Land des Feindes völlig zu zerstören, nachdem dieser den Erstschlag ausgeführt hat. Die Lösung des „Spiels“ der atomaren Abschreckung ist daher für beide Seiten „nicht angreifen“. Dazu gehört auch, sich als Atommacht stets so zu verhalten, dass die Angst vor der völligen Zerstörung für den Feind realistisch ist. Strategische Atomwaffen nur zu besitzen reicht daher nicht aus, es muss der Zweitschlag jederzeit – auch dann, wenn das eigene Land durch den Erstschlag bereits zerstört sein sollte – durchgeführt werden können, um beim Feind glaubwürdig zu sein. Aus diesem Grund sind bspw. mit strategischen Atomwaffen bestückte U-Boote permanent irgendwo in den Meeren unterwegs und selbst für befreundete Staaten nicht zu orten (d.h. der Feind muss einerseits wissen, dass es diese jederzeit einsatzfähigen Waffen gibt, er darf aber gleichzeitig nicht wissen, wo sie sich befinden, da er sie sonst außer Gefecht setzen könnte). | ||
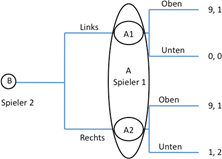
Übungsbeispiel 1.3 | '''Übungsbeispiel 1.3''' | ||
Der neue Spielbaum sieht wie folgt aus: | Der neue Spielbaum sieht wie folgt aus: | ||
| Zeile 458: | Zeile 435: | ||
Im neuen Gleichgewicht wählt Spieler 2 entweder „links“ oder „rechts“, da keine Strategie stark dominant ist. Spieler 1 wählt danach „oben“, die Auszahlung ist (9, 1). Man beachte, dass Spieler 2 indifferent ist, ob Spieler 1 „oben“ oder „unten“ wählen wird, der Ausgang des Spiels somit als Auszahlung bekannt ist, aber nicht, welches Ergebnis als solches vorliegen wird. Nichtsdestoweniger bevorzugt Spieler 2 zuerst zu entscheiden, da er in diesem Fall eine Auszahlung von 9 erhält (im Gegensatz zu einer Auszahlung von 1 bei der umgekehrten Abfolge der Spielzüge). | Im neuen Gleichgewicht wählt Spieler 2 entweder „links“ oder „rechts“, da keine Strategie stark dominant ist. Spieler 1 wählt danach „oben“, die Auszahlung ist (9, 1). Man beachte, dass Spieler 2 indifferent ist, ob Spieler 1 „oben“ oder „unten“ wählen wird, der Ausgang des Spiels somit als Auszahlung bekannt ist, aber nicht, welches Ergebnis als solches vorliegen wird. Nichtsdestoweniger bevorzugt Spieler 2 zuerst zu entscheiden, da er in diesem Fall eine Auszahlung von 9 erhält (im Gegensatz zu einer Auszahlung von 1 bei der umgekehrten Abfolge der Spielzüge). | ||
Übungsbeispiel 1.4 | |||
'''Übungsbeispiel 1.4''' | |||
<ol style="list-style-type: lower-alpha;"> | <ol style="list-style-type: lower-alpha;"> | ||
| Zeile 464: | Zeile 443: | ||
</ol> | </ol> | ||
{| | {| style="border-collapse: collapse;" border="1" | ||
| width="25%" | | | width="25%" | | ||
<br> | <br> | ||
| Zeile 497: | Zeile 476: | ||
</ol> | </ol> | ||
{| | {| style="border-collapse: collapse;" border="1" | ||
| width="26%" | | | width="26%" | | ||
<br> | <br> | ||
| Zeile 526: | Zeile 505: | ||
<blockquote>Die stark dominante Strategie des Managers ist „ehrlich“. Das Nash-Gleichgewicht ist somit durch (eröffnen, ehrlich) gegeben.</blockquote> | <blockquote>Die stark dominante Strategie des Managers ist „ehrlich“. Das Nash-Gleichgewicht ist somit durch (eröffnen, ehrlich) gegeben.</blockquote> | ||
Übungsbeispiel 1.5 | '''Übungsbeispiel 1.5''' | ||
<ol style="list-style-type: lower-alpha;"> | <ol style="list-style-type: lower-alpha;"> | ||
Aktuelle Version vom 18. Juli 2023, 07:46 Uhr
Grundzüge der Spieltheorie
Was ist ein Spiel?
Spieltheorie ist eine Möglichkeit, strategische Interaktionen formal darzustellen und damit Informationen zu den Handlungen einzelner Individuen, die mit strategischen Entscheidungen konfrontiert sind, abzuleiten. Strategische Entscheidungen sind solche, die die Aktionen anderer beeinflussen beziehungsweise durch diese selbst beeinflusst werden. Ist dies der Fall, so findet zwischen den Agenten strategische Interaktion statt.
Die Entscheidungssituation wird in einem „Spiel“ dargestellt. Elemente eines Spiels umfassen (1) die Spieler, (2) den Strategienraum, aus dem die Spieler eine Aktion wählen können, und (3) die Auszahlungsstruktur, d.h. der „Gewinn“, den jeder Spieler zu erwarten hat, gegeben eine bestimmte Kombination aus Strategien wird gewählt. Außerdem von Bedeutung ist die zeitliche Abfolge der Entscheidungen der Spieler. Spieler können entweder simultan (dann spricht man von einem „statischen Spiel“) oder nacheinander („dynamisches Spiel“) entscheiden. Im Fall eines dynamischen Spiels entscheidet Spieler 2 sich erst dann für eine Aktion, nachdem er die Strategie von Spieler 1 beobachtet hat. Im Folgenden werden wir uns sowohl mit statischen als auch mit dynamischen Spielen auseinandersetzen und unterschiedliche Lösungskonzepte kennenlernen.
Statische Spiele
Ein statisches Spiel zeichnet sich dadurch aus, dass sich die Spieler simultan für eine Aktion entscheiden. D.h., wenn Spieler 2 seine Entscheidung trifft, weiß er nicht, welche Entscheidung sein Gegenspieler, Spieler 1, trifft. Ein solches Spiel wird oft in der „Normalform“ dargestellt. Angenommen, das Spiel hat zwei Spieler, welche aus zwei möglichen Strategien wählen können. Ein solches Spiel wird wie in jener Tabelle dargestellt:
| Spieler 2 | |||
|---|---|---|---|
|
|
|
Links | Rechts |
| Spieler 1 | Oben | OL1, OL2 | OR1, OR2 |
|
|
Unten | UL1, UL2 | UR1, UR2 |
Die Normalform eines Spieles
In diesem Spiel gibt es zwei Spieler, Spieler 1 und Spieler 2. Spieler 1 hat zwei Strategien zur Auswahl. Er kann entweder die Aktion „oben“ oder die Aktion „unten“ wählen. Spieler 2 auf der anderen Seite kann sich für „rechts“ oder „links“ entscheiden. Die Auszahlungsmatrix stellt außerdem die Auszahlungen (meist wird dies durch Zahlen dargestellt, die Auszahlung bezieht sich also zum Beispiel auf den monetären Nutzen) der Spieler bei jeder möglichen Kombination von gewählten Aktionen dar. Wenn zum Beispiel Spieler 1 „oben“ und Spieler 2 „links“ wählt, so bekommt Spieler 1 die Auszahlung „OL1“ und Spieler 2 „OL2“.
Das Gefangenendilemma
Das „Gefangenendilemma“ ist eines der bekanntesten Probleme aus der Spieltheorie. In diesem Spiel werden zwei Räuber von der Polizei festgenommen. Allerdings liegen zu wenige Beweise vor, die Räuber des Vergehens zu überführen, daher werden sie – getrennt voneinander – verhört. Beide Räuber haben entweder die Möglichkeit zu gestehen oder nichts zu sagen; diese zwei Möglichkeiten entsprechen dem Strategienraum der Räuber. Dieser sieht wie folgt aus:
- Wenn beide gestehen, so können sie des Überfalls überführt werden und müssen im Anschluss eine Haftstrafe von jeweils 6 Jahren verbüßen. Gesteht nur einer der Räuber die Tat, so kann mit diesem Geständnis dem anderen Räuber die Tat nachgewiesen werden, der gestehende Räuber kommt – als Belohnung für seine Kooperationswilligkeit – frei (0 Jahre). Der von seinem Kollegen belastete Räuber muss dann, da er nicht kooperationswillig war, 12 Jahre in Haft verbringen. Sollten beide Räuber Stillschweigen bewahren, so kann ihnen nur ein geringfügiges Vergehen angelastet werden (z.B. unerlaubtes Tragen einer Feuerwaffe) und sie bekommen eine Gefängnisstrafe von je 1 Jahr.
| Räuber 2 | |||
|---|---|---|---|
|
|
|
Gestehen | Nicht gestehen |
| Räuber 1 | Gestehen | -6, -6 | 0, -12 |
|
|
Nicht gestehen | -12, 0 | -1, -1 |
Das Gefangenendilemma
Die Darstellung des Gefangenendilemma in der Normalform ist in oberer Tabelle zu sehen. Da die Jahre, die ein Räuber im Gefängnis verbringen muss, eine negative Auszahlung darstellen (Jahre in Freiheit), werden sie als negative Zahlen dargestellt.
Lösungskonzept: iteratives Eliminieren dominierter Strategien
In der Spieltheorie untersucht man das Entscheidungsverhalten von Individuen, d.h., man möchte herausfinden, wie sich Individuen beziehungsweise Entscheidungsträger in gewissen Situationen, in denen strategische Entscheidungen vonnöten sind, rational verhalten. Im Folgenden werden wir uns mit Lösungskonzepten auseinandersetzen, mittels derer wir die Frage „Welche Aktionen werden die Entscheidungsträger wählen?“ beantworten können.
Eine erste Möglichkeit herauszufinden, wie sich die Entscheidungsträger verhalten, liegt in der Betrachtung dominanter beziehungsweise dominierter Strategien. Eine stark (= strikt) dominante Strategie ist eine Strategie, die immer bevorzugt wird, egal welche Aktion der andere Spieler wählt. Demgegenüber ist eine stark (= strikt) dominierte Strategie eine, die unter keinen Umständen gewählt wird. Von schwach dominanten Strategien spricht man, wenn die Strategie eine zumindest gleich hohe Auszahlung bringt (bzw. schwach dominiert bei maximal gleich hoher Auszahlung). Der Unterschied zwischen stark und schwach dominant/dominiert ist v.a. bei gleich hohen Auszahlungen relevant, in diesem Fall ist ein Spieler indifferent.
Um dieses Konzept zu veranschaulichen, betrachten wir noch einmal das Gefangenendilemma aus Sicht von Räuber 1:
- Er hat die Möglichkeit, aus zwei Strategien zu wählen, „gestehen“ oder „nicht gestehen“. Angenommen, Räuber 2 wählt die Aktion „gestehen“. In diesem Fall würde Räuber 1, wählte er „gestehen“, 6 Jahre im Gefängnis verbringen, während er, sollte er sich für „nicht gestehen“ entscheiden, 12 Jahre verbüßen müsste - wählt Räuber 2 „gestehen“, so ist es für Räuber 1 am besten, ebenfalls zu gestehen (da er dann nur 6 statt von 12 Jahren im Gefängnis verbringen muss).
- Wie stellt sich die Situation nun dar, wenn Räuber 2 sich für die Aktion „nicht gestehen“ entscheidet? In diesem Fall würde Räuber 1, sollte er sich für „gestehen“ entscheiden, 0 Jahre Gefängnis erhalten. Sollte er sich hingegen für „nicht gestehen“ entscheiden, müsste er 1 Jahr in Gefangenschaft verbringen. Auch in diesem Fall ist es also im Interesse von Räuber 1 die Aktion „gestehen“ zu wählen.
Da Räuber 2 mit denselben Auszahlungen konfrontiert ist, gilt für ihn das gleiche Ergebnis. Im Gefangenendilemma ist also „gestehen“ für beide Seiten die dominante Strategie. Das ist das relevante Ergebnis des Gefangenendilemmas: Wofür auch immer sich der andere Spieler entscheidet, der Entscheidungsträger wählt „gestehen“. Obwohl offensichtlich ist, dass das kollektiv beste Ergebnis erzielt würde, wenn beide Spieler „nicht gestehen“ wählen, kommt dieses Ergebnis nicht zustande: Jeder Spieler ist für sich besser daran, wenn er „gestehen“ wählt. [1]
Wir haben nun mit der Theorie dominanter Strategien dieses Spiel gelöst. Da „gestehen“ für beide Räuber die dominante Strategie ist, werden sie beide diese wählen. Der Spielausgang ist also durch („gestehen“, „gestehen“) gegeben, und beide Räuber werden jeweils 6 Jahre im Gefängnis verbringen.
|
|
|
|
Spieler 2 |
|
|
|
|
Links | Mitte | Rechts |
| Spieler 1 | Oben | 3, 2 | 3, 4 | 2, 3 |
|
|
Unten | 2, 5 | 2, 3 | 4, 2 |
Beispiel zum iterativen Eliminieren dominierter Strategien
Die obere Tabelle veranschaulicht ein weiteres Spiel, in dem dieses Lösungskonzept zur Anwendung kommt. Das besprochene Lösungskonzept schlägt zur Lösung eines solchen Spieles vor, die dominierten Strategien zu eliminieren, da diese bei rationalem Verhalten nie gewählt werden würden. Betrachten wir Spieler 2. Wenn Spieler 1 „oben“ wählt, so ist es für Spieler 2 am besten, „Mitte“ zu wählen. Wählt Spieler 1 „unten“, so ist es optimal für Spieler 2, „links“ zu wählen. Dementsprechend wird Spieler 2 nie die Strategie „rechts“ wählen, egal welche Aktion Spieler 1 wählt - sie ist durch die beiden anderen Strategien dominiert.
|
|
|
Spieler 2 |
|
|
|
|
Links | Mitte |
| Spieler 1 | Oben | 3, 2 | 3, 4 |
|
|
Unten | 2, 5 | 2, 3 |
Beispiel nach erster Eliminierung
Da Spieler 1 bekannt ist, dass Spieler 2 niemals „rechts“ wählen wird, verkürzt sich nach Eliminierung dieser irrelevanten Alternative wie in der oberen Tabelle dargestellt. Betrachten wir nun das Entscheidungsproblem von Spieler 1. Wenn Spieler 2 „links“ wählt, so ist es für Spieler 1 am besten „oben“ zu wählen. Auch wenn Spieler 2 „Mitte“ wählt, ist „oben“ die bessere Alternative für Spieler 1. Demnach ist „unten“ also eine dominierte Strategie für Spieler 1. Da Spieler 2 dies voraussieht, stellt sich das Spiel wie in folgender Tabelle dar (die Strategie „unten“ wird eliminiert):
|
|
|
Spieler 2 |
|
|
|
|
Links | Mitte |
| Spieler 1 | Oben | 3, 2 | 3, 4 |
Beispiel nach zweiter Eliminierung
Spieler 2 hat nun die Wahl zwischen einer Auszahlung von 2 beziehungsweise 4 und wird demnach die Aktion „Mitte“ wählen. Das Gleichgewicht in dem Spiel ist also durch („oben“, „Mitte“) gegeben. Die Spieler erhalten die Auszahlungen (3, 4). So wird durch das iterative Eliminieren möglich, den Ausgang eines strategischen Spiels vorauszusagen.
Diskussion
Spiele, die dem Gefangenendilemma gleichen und mit diesem gelöst werden können, treten in vielen Situationen auf. Ein besonders markantes Beispiel dafür ist das atomare Wettrüsten, welches während des Kalten Krieges zwischen der UdSSR und den USA stattfand. Die Angst angegriffen zu werden, führte zur ständigen Aufrüstung. Das wünschenswerte Gleichgewicht in dieser Situation wäre beidseitige Abrüstung und damit einhergehend das Einsparen vieler Ressourcen und nuklearer Unfälle gewesen. Ein Atomkrieg hätte jedoch eine noch größere negative Auszahlung mit sich gebracht (gewissermaßen unendlich). Zwar war das Spiel nicht statisch, aber so lange nicht völlig abgerüstet würde, war man selbst stets besser daran, aufzurüsten. Nur die Pattstellung durch maximale atomare Abschreckung minimierte die Wahrscheinlichkeit, dass die jeweils andere Seite den atomaren Erstschlag durchführen würde. [2]
Somit können Gleichgewichte, die aus Gefangenendilemma-ähnlichen Situationen resultieren, ineffizient insofern sein, dass mindestens ein Spieler bessergestellt werden könnte, ohne den anderen schlechter zu stellen. Im Falle der oben beschriebenen Situationen wären sogar alle Spieler bei einem Ausgang des Spieles („nicht gestehen“, „nicht gestehen“), bessergestellt. Das Ergebnis sieht jedoch möglicherweise anders aus, wenn dasselbe Spiel wiederholt gespielt wird, die Räuber also immer wieder aufeinandertreffen.
Lösungskonzept: Nash-Gleichgewicht
Das obige Lösungskonzept ist zwar sehr hilfreich, allerdings werden wir oft auf Situationen stoßen, in denen keine Strategie dominiert ist und die optimale Strategie damit von der Aktion des Gegenübers abhängt. Können wir auch in einem solchen Fall eine Vorhersage über den Ausgang eines Spieles treffen? Dies ist möglich mit einem weiteren Lösungskonzept, dem Konzept des Nash-Gleichgewichtes.
|
|
|
Ehefrau |
|
|
|
|
Fußball | Theater |
| Ehemann | Fußball | 2, 1 | 0,0 |
|
|
Theater | 0,0 | 1,2 |
Der Kampf der Geschlechter
Die obere Tabelle zeigt das Spiel „Kampf der Geschlechter“, das auf einer alltäglichen Konfliktsituation basiert. Ein Ehepaar möchte etwas gemeinsam unternehmen, hat aber verschiedene Präferenzen: Er geht lieber zu einem Fußballspiel, sie ins Theater. Beide Ehepartner begleiten jedoch lieber ihren Gatten / ihre Gattin, als gar nichts zu unternehmen. In diesem Fall gibt es keine dominierte Strategie. Im Falle, dass die Frau „Theater“ wählt, bevorzugt auch der Mann „Theater“, und vice versa beim Fußballspiel.
Um in diesem Spiel ein Gleichgewicht zu identifizieren, arbeitet man mit dem Konzept der Methode der Besten-Antwort-Korrespondenz. Dabei findet man die „beste Antwort“ beider Spieler auf die möglichen Strategien des jeweils anderen und markiert diese; in nachfolgender Tabelle wird dies durch Unterstreichen durchgeführt.
|
|
|
Ehefrau |
|
|
|
|
Fußball | Theater |
| Ehemann | Fußball | 2, 1 | 0,0 |
|
|
Theater | 0,0 | 1,2 |
Nash-Gleichgewichte im Kampf der Geschlechter
Ein Nash-Gleichgewicht tritt dann auf, wenn beide Spieler beste Antworten auf die Strategie des jeweils anderen wählen, also in dem Punkt, an dem zwei unterstrichene Auszahlungen in einem Matrixelement aufeinandertreffen. In dem Kampf der Geschlechter sind also die beiden Strategiepaare (Fußball, Fußball) und (Theater, Theater) Nash-Gleichgewichte. Ein Nash-Gleichgewicht wird als Gleichgewicht bezeichnet, da in einem solchen beide Spieler keinen Anreiz haben, (einseitig) abzuweichen, d.h., einseitig eine andere als die Gleichgewichtsstrategie zu wählen. Anders formuliert kann sich kein Spieler, gegeben der Aktion seines Gegenübers, verbessern, indem er eine andere Strategie wählte. Wenn im konkreten Fall die Ehefrau zuerst den Vorschlag macht, besteht das Gleichgewicht (Theater, Theater). Keiner der Ehepartner hat ein Interesse daran, abzuweichen, da dann die Auszahlung niedriger wäre, indem das Ehepaar gar nichts unternehmen würde.
Zu beachten ist in diesem Zusammenhang, dass ein Gleichgewicht in dominanten Strategien immer ein Nash-Gleichgewicht ist, dies allerdings umgekehrt nicht gilt. Das Konzept des Nash-Gleichgewichtes ist also ein „schwächeres“ als das des Gleichgewichtes in dominanten Strategien. Es ermöglicht, Gleichgewichte auch in Spielen zu finden, in denen keine Strategien dominiert sind, und damit gewisse Vorhersagen über den Ausgang in einer solchen Situation abzugeben.
Somit gibt es nicht immer ein eindeutiges Nash-Gleichgewicht. Im obigen Beispiel des Kampfes der Geschlechter etwa sind beide Strategiepaare (Fußball, Fußball) und (Theater, Theater) Nash-Gleichgewichte. In einem solchen Fall können wir mit Hilfe der Spieltheorie nur eine Aussage darüber treffen, dass eines dieser Gleichgewichte auftreten wird; welches der beiden gewählt wird, kann jedoch nicht vorausgesagt werden. D.h., im Falle des Nash-Gleichgewichts-Konzeptes kann keine Aussage darüber getroffen werden, wie die Spieler zu einem Gleichgewicht kommen, nur dass, sobald die Spieler sich im Gleichgewicht befinden, dieses stabil ist (da keiner der Spieler einen Anreiz hat, einseitig abzuweichen). Um das Gleichgewicht zu erreichen, werden häufig Koordinationsmechanismen benötigt (zum Beispiel ein Telefonanruf im Kampf der Geschlechter). Wenn bspw. internationale Abkommen geschlossen werden, so müssen diese, um stabil zu sein, Nash-Gleichgewichte darstellen. Der Koordinationsmechanismus ist in diesem Fall durch internationale Konferenzen, auf welchen die Details der Abkommen ausgehandelt werden, gegeben. Sobald ein solches Abkommen in Kraft tritt, d.h. alle Teilnehmer auf das Nash-Gleichgewicht koordiniert sind, hat kein einzelner Teilnehmer mehr einen Anreiz, abzuweichen – das Abkommen ist also stabil.
Dynamische Spiele
Bis jetzt wurden nur statische Spiele betrachtet – eine Möglichkeit, die Dimension Zeit in ein Spiel zu inkorporieren, ist es, die Spieler nacheinander (nicht: simultan) entscheiden zu lassen. Hierbei handelt es sich um sequenzielle Spiele. Eine weitere Möglichkeit ist es, die Spieler ein simultanes Spiel mehrere Male hintereinander spielen zu lassen. In diesem Fall handelt es sich um wiederholte Spiele.
Der Zusammenhang zwischen sequenziellen und simultanen Spielen: Das Lösungskonzept der Rückwärtsinduktion
In einem sequenziellen Spiel ist die zeitliche Abfolge von großer Bedeutung. Betrachten wir dafür ein Spiel, welches zuerst als simultanes Spiel und darauffolgend als sequenzielles Spiel gespielt wird. Die Spielmatrix, welche sich auf das simultane Spiel bezieht, stellt sich wie in nachfolgender Tabelle dar:
|
|
|
Spieler 2 |
|
|
|
|
Links | Rechts |
| Spieler 1 | Oben | 1, 9 | 1,9 |
|
|
Unten | 0,0 | 2,1 |
Beispiel für ein simultanes Spiel
In obigem Spiel sind die Beste-Antwort-Strategien analog zum vorigen Abschnitt markiert. Wie man sehen kann, gibt es in diesem simultanen Spiel zwei Nash-Gleichgewichte: (oben, links) und (unten, rechts). Wie ändert sich die Voraussage für den Spielausgang, wenn das gleiche Spiel sequenziell gespielt wird? Angenommen, Spieler 1 entscheidet sich zuerst für eine Aktion. Spieler 2 reagiert danach. Diese Situation lässt sich in einem Spielbaum wie in nachfolgender Abbildung darstellen:
Im abgebildeten Spielbaum ist jeder Punkt, an dem ein Spieler eine Entscheidung trifft (Entscheidungspunkte), markiert. Als Lösungskonzept kommt die Rückwärtsinduktion zur Anwendung. Dabei wird das Spiel von hinten aufgerollt, d.h., man betrachtet zuerst die letzte Entscheidung des Spieles und arbeitet sich dann nach vorne.
Der letzte Entscheidungspunkt in der oberen Abbildung ist Punkt B. In diesem Punkt entscheidet sich Spieler 2 zwischen den beiden potenziellen Aktionen „links“ und „rechts“. Sollte er sich an Punkt B1 befinden – was dann der Fall ist, wenn sich Spieler 1 in der Runde davor für „oben“ entschieden hat – dann ist für Spieler 2 irrelevant, ob er links oder rechts wählt – er erhält in beiden Fällen eine Auszahlung im Wert von 9. Sollte er sich an dem Punkt B2 befinden, so wird er rechts wählen, da 1 größer ist als 0. Somit ist klar, dass Spieler 2 in jedem Fall rechts wählen wird, da die Auszahlung entweder gleich oder größer ist als bei der Wahl „links“.
Mit diesem Wissen gehen wir nun nach vorne im Spielablauf, zur Entscheidung von Spieler 1 im Entscheidungspunkt A. Er weiß, wie Spieler B auf seine Entscheidung reagieren wird und trifft mit diesem Wissen seine eigene Entscheidung. D.h., Spieler 1 hat die Wahl zwischen einer Auszahlung von 1, wenn er „oben“ wählt und 2, wenn er „unten“ wählt. Somit ist klar, dass Spieler 1 „unten“ wählen wird und der Spielausgang durch das Aktionenpaar (unten, rechts) gegeben und die damit einhergehenden Auszahlungen sind (2, 1).
Bei dem Lösungskonzept der Rückwärtsinduktion geht man von dem Konzept der „common rationality“ aus, d.h., man nimmt an, dass alle Spieler rational handeln und dies auch voneinander wissen. Im obigen Beispiel handelt Spieler B rational, in dem er an Entscheidungspunkt B1 indifferent zwischen „links“ und „rechts“ ist und an Entscheidungspunkt B2 „rechts“ wählt. Spieler A wiederum weiß, dass Spieler B rational handelt und baut darauf seine eigene Entscheidung auf. D.h., er betrachtet das verkürzte Spiel, welches für ihn tatsächlich relevant ist, wie in folgender Abbildung dargestellt.
Gegeben, Spieler 1 ist tatsächlich mit diesem Spiel konfrontiert, ist es offensichtlich, dass er sich für die Aktion „unten“ entscheiden wird, da diese ihm eine höhere Auszahlung sichert. Durch die Integration einer Zeitdimension gelangen wir nun also zu einer konkreten Vorhersage für den Ausgang dieses Spieles.
Das Ultimatum-Spiel
Ein oft zitiertes Beispiel für ein sequenzielles Spiel ist das sogenannte Ultimatum-Spiel. Martin soll 100 Euro zwischen sich selbst und einem zweiten Spieler, Gerhard, aufteilen. Der Spielverlauf gibt vor, dass Martin zuerst über die Aufteilung der 100 Euro entscheidet. Er macht damit ein Angebot an Gerhard, welcher dieses Angebot im nächsten Schritt annehmen oder ablehnen kann. Nimmt er es an, so werden die 100 Euro gemäß Martins Angebot aufgeteilt. Lehnt er es ab, so bekommen beide Spieler kein Geld und die 100 Euro gehen verloren (oder zurück an den Spielleiter). Der Spielbaum des Ultimatum-Spiels ist in nachfolgender Abbildung dargestellt.
Dieses Spiel lässt sich nicht in simultaner Form darstellen, da Martins Strategienraum sehr groß ist. Er kann sich in dem Spiel nicht nur zwischen zwei alternativen Aktionen entscheiden, sondern kann eine Aufteilung von 0 bis 100 wählen. Er hat also, wenn man annimmt, dass er runde Beträge angeben muss, die Auswahl aus 101 möglichen Aktionen.
Auch dieses Spiel lösen wir wieder mit Hilfe der Rückwärtsinduktion. In der letzten Entscheidungsstufe entscheidet Gerhard zwischen 0 Euro, wenn er Martins Angebot ablehnt, und (100 - x) Euro, wenn er es annimmt, wobei x dem Anteil entspricht, den Martin vorgeschlagen haben wird, selbst zu behalten. Demnach wird er in dieser Stufe jedes Angebot von Martin akzeptieren, welches ihm eine Auszahlung von mehr als 0 Euro sichert, da jede dieser Auszahlungen größer ist, als gar nichts zu bekommen. Martin, als rationaler Spieler, antizipiert dieses Verhalten und wird – nachdem er, um seine eigene Auszahlung zu maximieren, Gerhards Anteil möglichst klein halten muss – Gerhard nur 1 Euro anbieten und demnach 99 Euro für sich selbst behalten. Dies ist also der Ausgang des Ultimatum-Spiels: In der ersten Stufe bietet Martin Gerhard 1 Euro an und behält damit 99 Euro für sich. In der zweiten Stufe akzeptiert Gerhard dieses Angebot, da 1 Euro größer ist als 0 Euro. Die Auszahlungen im Gleichgewicht sind demnach (99,1).
Aus eigenen Beobachtungen würden wohl viele Menschen diesem Ausgang des Spieles nicht glauben. Sie selbst würden ein Angebot wie jenes von Martin als unfair empfinden und es demnach – auch wenn eine solche Handlungsweise nicht rational (im Sinne von: Gewinn maximierend) ist – ablehnen. Zu dem Erstaunen von vielen Spieltheoretikern stellte sich bei Experimenten heraus, dass dies tatsächlich zutrifft: circa 40% bis 60% der Teilnehmer lehnten ein niedriges Angebot ab, obwohl dies zur Folge hatte, dass sie am Ende des Spieles eine Auszahlung von 0 erhielten. Nach ihren Motiven befragt, gaben viele an, dass sie eine so ungleiche Aufteilung unfair empfanden und es daher vorzogen leer auszugehen, wenn dies hieße, dass der Gegenspieler ebenfalls eine Auszahlung von Null erhielt. [3] Man wollte also das Gegenüber, welches das unfaire Angebot unterbreitet hatte, bestrafen.
Glaubwürdige Drohungen und Versprechen
In der obigen Variante wäre eine Drohung Gerhards bei rationalen Spielern nicht glaubwürdig. Der Grund dafür ist, dass es für Gerhard nicht rational ist, ein Angebot von 1 Euro abzulehnen, da er sonst 0 Euro erhielte und Martin seine Entscheidung nicht mehr ändern kann. Wenn man also von rationalen Spielern ausgeht, dann sind Drohungen oder Versprechen, die sich bei Rückwärtsinduktion als nicht rational herausstellen, nicht glaubwürdig. Eine glaubhafte Drohung (oder Versprechen) ist eine, deren Ausführung im Interesse des Spielers liegt, wenn er an der Reihe ist, seine Entscheidung zu treffen. Aus dieser Logik stammt das Konzept der Rückwärtsinduktion.
Das Problem der Verbindlichkeit
Betrachten wir ein weiteres Spiel, welches obiges Problem deutlich darstellt. Ein Kidnapper überlegt, ob er sein Opfer laufen lassen soll oder nicht. Der Spielbaum sieht wie in folgender Abbildung dargestellt aus.
Ein Kidnapper, der sein Opfer entführt hat, ändert plötzlich seinen Plan und möchte das Opfer am liebsten wieder frei lassen. Er ist allerdings besorgt, dass das Opfer, sobald es frei ist, zur Polizei gehen könnte und er als Folge ins Gefängnis müsste. Die andere mögliche Aktion des Kidnappers ist, dass er das Opfer umbringt und sich damit von seiner Verantwortung befreit. Das Opfer auf der anderen Seite realisiert, dass es, selbst wenn es freikommen sollte, immer noch in Gefahr schweben würde, da der Kidnapper es sich zu einem späteren Zeitpunkt noch einmal anders überlegen könnte. Das Opfer hat also, sollte es freikommen, einen Anreiz, zur Polizei zu gehen.
In dem vorliegenden Spiel wenden wir wieder das Lösungskonzept Rückwärtsinduktion an. Die erste Überlegung gilt also der Entscheidung an Punkt C - wie würde sich das Opfer an diesem Punkt entscheiden? Es hat die Wahl zwischen der Auszahlung (in einem erweiterten Sinn) „Opfer ist sicher“ und „Opfer schwebt weiter in Gefahr“. In dieser Situation würde das Opfer natürlich ersteres präferieren und wird sich dementsprechend dafür entschließen, zur Polizei zu gehen. Betrachten wir nun den Entscheidungspunkt davor, Punkt B. In Punkt B trifft der Kidnapper eine Entscheidung, wissend, wie sich das Opfer danach (an Punkt C) verhalten wird. Der Kidnapper kann das Opfer entweder frei lassen oder es umbringen. Wenn er das Opfer frei lässt, weiß er, dass dieses danach zur Polizei gehen würde. In diesem Fall würde der Kidnapper zur Todesstrafe verurteilt werden. Sollte er sich dafür entscheiden, das Opfer zu töten, so wird er überleben. Der Kidnapper wird sich also an Punkt B dafür entscheiden, sein Opfer zu töten. Der Spielbaum mit den eingezeichneten optimalen Strategien an jedem Entscheidungspunkt sieht also wie in der unteren Abbildung aus.
Wir kennen nun also den Ausgang des obigen strategischen Spiels. An Punkt A wird das Opfer versprechen, nicht zur Polizei zu gehen und an Punkt B wird sich der Kidnapper dafür entscheiden, das Opfer zu töten. Die „Auszahlungen” bestehen also darin, dass das Opfer getötet wird und der Kidnapper überlebt.
Hier sehen wir, welch ein großes Problem es darstellen kann, wenn in bestimmten Situationen Versprechen nicht glaubwürdig gegeben werden können. Beide, sowohl das Opfer als auch der Kidnapper, möchten eigentlich, dass das Opfer frei gehen kann, doch kann dies nicht das Resultat des Spieles sein, da das Versprechen des Opfers, den Kidnapper nicht zu verraten, nicht glaubwürdig ist.
Dieses “commitment problem” tritt in strategischen Situationen oft auf (wir haben ähnliche Situationen wie im Kidnapper-Opfer-Spiel auch im Gefangenendilemma oder Ultimatum-Spiel beobachtet). Ein „commitment problem“ ist in solchen Situationen gegeben, in welchen ein erwünschter Spielausgang (also ein Spielausgang, in dem beide Spieler bessergestellt wären) nicht erreicht werden kann, da keine glaubhaften Versprechen beziehungsweise Drohungen von Seiten der Spieler ausgesprochen werden können. In einem solchen Fall wird ein sogenannter „commitment device“ gebraucht, um doch noch den erwünschten Spielausgang zu erreichen. Dies gibt dem jeweiligen Spieler einen Anreiz, das Versprechen beziehungsweise die Drohung im Fall des Falles auch einzuhalten und macht diese damit glaubwürdig.
Im Kidnapper-Spiel könnte das Opfer ein Verbrechen begehen, welches es den Kidnapper beobachten lässt. Der Kidnapper könnte dann selbst zur Polizei gehen, sollte das Opfer sich nicht an sein Versprechen den Kidnapper nicht anzuzeigen halten. Damit hat das Opfer einen Anreiz sich an sein Versprechen zu halten - es wird also glaubwürdig. In dem Fall wäre der Ausgang des Spieles (Opfer in Gefahr, Kidnapper frei) ein Ausgang, den beide Spieler zu dem oben besprochenen Gleichgewicht bevorzugen.
Wiederholte Spiele
Eine spezielle Form sequenzieller Spiele ist die Klasse der wiederholten Spiele. Hier wird ein simultanes Spiel mehrere Male wiederholt. Wenn ein Spiel mehrere Male wiederholt wird, so eröffnet dies die Möglichkeit den Gegenspieler in der zweiten Runde für unerwünschtes Verhalten in der ersten Runde zu bestrafen. Durch diese Strategie kann kooperatives Verhalten attraktiver gemacht werden.
Im Gefangenendilemma wird das Spiel nun in dem Sinn wiederholt, dass dieselben zwei Räuber mehrere Mal aufeinandertreffen. Somit gibt es die Möglichkeit, dass ein Räuber dem anderen droht, sollte dieser sich in der ersten Runde nicht kooperativ verhalten. Dies stellt eine Möglichkeit dar, die für das Kollektiv optimale Situation zu erreichen, in diesem Fall („nicht gestehen“, „nicht gestehen“). Man spricht hier von einer Tit-For-Tat-Strategie, d.h., Räuber 1 wird in der ersten Runde (beim ersten Aufeinandertreffen) kooperieren (also „nicht gestehen“ wählen), in jeder weiteren Runde allerdings die Aktion wählen, die Räuber 2 in der Runde davor gewählt hatte. Wenn bspw. Räuber 2 in der ersten Runde „gestehen“ wählt und damit Räuber 1 für 12 Jahre ins Gefängnis schickt (der schlechteste Ausgang für Räuber 1), so wird Räuber 1 Räuber 2 in der nächsten Runde, wenn das Spiel ein weiteres Mal gespielt wird, dafür bestrafen, indem er selbst nun „gestehen“ spielt. Ob diese Strategie funktionieren kann mit einem Gleichgewicht („nicht gestehen“, „nicht gestehen“), wird dadurch bestimmt, ob das Spiel endlich oder unendlich viele Male wiederholt wird.
Dies wird klar, wenn man auch in diesem Fall mit dem Konzept der Rückwärtsinduktion arbeitet. Nehmen wir an, das Gefangenendilemma wird endlich oft wiederholt, die Räuber treffen zum Beispiel fünf Mal aufeinander. Beginnen wir also bei dem letzten Entscheidungspunkt, an dem das Spiel zum fünften Mal gespielt wird. Von diesem Punkt aus gesehen stellt sich die Entscheidungssituation also genau so dar, wie in dem einfachen, nicht wiederholten simultanen Spiel: „Gestehen“ ist die dominante Strategie und wird daher auch von beiden Räubern gewählt. Die Vorhersage für den Ausgang des Spieles ist somit („gestehen“, „gestehen“). Mit diesem Wissen beginnen die Räuber die vorletzte Wiederholung des Spieles (Runde 4). Beide wissen, dass sich in der darauffolgenden Runde der jeweils andere Räuber für „gestehen“ entscheiden wird. Damit verliert die oben zitierte Tit-For-Tat-Strategie an Glaubwürdigkeit, da der Ausgang der jeweils nächsten Runde feststeht, egal, wie in der Runde davor entschieden wurde. Die Tit-For-Tat-Strategie ist also in der vierten Runde nicht glaubwürdig und damit ist der Ausgang in Runde 4 auch („gestehen“, „gestehen“) – usw. bis zur ersten Runde. Damit ist die Tit-For-Tat-Strategie jedoch bereits in der ersten Runde nicht glaubwürdig und bietet keine Möglichkeit, Kooperation unter den Räubern zu etablieren.
Der Ausgang endlich wiederholter simultaner Spiele entspricht also dem Ausgang des einmaligen simultanen Spiels. Durch die endliche Wiederholung kann keine Verhaltensänderung induziert werden. Wird das Spiel allerdings unendlich oft wiederholt (beziehungsweise ist das Ende der Wiederholungen nicht bekannt), funktioniert eine Tit-For-Tat-Stratgie und bietet damit eine Möglichkeit, das kollektive Optimum zu etablieren oder diesem zumindest näherzukommen. Die Spieler kooperieren, da sie sich dadurch Kooperation des Gegenspielers in der Zukunft erwarten. Die Tit-For-Tat-Strategie im Speziellen funktioniert nach dem Prinzip: „Behandle andere, wie du selbst behandelt werden möchtest“. Die in diesem Prinzip inhärente Drohung der Vergeltung dient beiden Spielern, indem ein Gleichgewicht, das von beiden bevorzugt wird, erreicht werden kann.
Übungen
Übungsbeispiel 1.1
Betrachten Sie eine Tit-For-Tat-Strategie in einem wiederholten Gefangenendilemma. Nehmen Sie an, ein Spieler macht einen Fehler und wählt „gestehen“ (also das nicht-kooperative Verhalten), obwohl er eigentlich kooperieren wollte (also eigentlich „nicht gestehen“ wählen wollte). Wenn danach beide Spieler weiterhin die Tit-For-Tat-Strategie spielen, wie entwickelt sich der Spielverlauf? Welche Aktionen werden gewählt?
Übungsbeispiel 1.2
Nehmen Sie an, im Gefangenendilemma wird beiden Räubern erlaubt, sich aneinander zu rächen, nachdem sie ihre jeweiligen Gefängnisstrafen hinter sich gebracht haben. Wie würde sich das Spiel formal ändern? Könnte ein effizienteres Ergebnis erreicht werden?
Übungsbeispiel 1.3
Angenommen, in dem in Tabelle 1-8 dargestellten Spiel würde Spieler 2 zuerst die Entscheidung treffen und Spieler 1 würde erst danach reagieren. Die zeitliche Abfolge wäre also genau umgekehrt als sie in Abbildung 1-1 dargestellt ist. Zeichnen Sie den Spielbaum, der dieses sequenzielle Spiel darstellt. Wodurch ist das Gleichgewicht in diesem Spiel gegeben? Welche zeitliche Abfolge würde Spieler 2 bevorzugen? Würde er lieber zuerst oder lieber nach Spieler 1 entscheiden?
Übungsbeispiel 1.4
Ein Unternehmer überlegt, ob er eine neue Dependance in einer anderen Stadt eröffnen soll. Er müsste dazu einen neuen Manager anstellen, der sich um die neue Filiale kümmern würde. Findet er einen Manager, der diese Aufgabe ehrlich erledigen würde, so könnte er ihm ein Gehalt von monatlich 5000 Euro zahlen. Dies wäre ein sehr gutes Gehalt für den Manager, da er anderswo nur 2500 Euro verdienen könnte. Wäre der Manager ehrlich, könnte der Unternehmer, trotz des hohen Gehalts, immer noch einen Gewinn von 1600 Euro im Monat machen. Da sich die Filiale in einer anderen Stadt befindet, wäre es unmöglich für den Unternehmer, den Manager zu überwachen. Dieser hätte also die Möglichkeit, sich unehrlich zu verhalten und dem Unternehmen Geld zu stehlen. In dem Fall könnte der Manager sein Gehalt um 2200 Euro aufbessern (insgesamt also 7200 Euro in seiner Position „verdienen“), während der Unternehmer Verluste mit der neuen Filiale machen würde. Diese würden sich auf 1200 Euro belaufen. Der Unternehmer gibt eine Annonce auf, mehrere Bewerber melden sich.
(a) Angenommen, der Unternehmer geht davon aus, dass alle Manager, die er anstellen könnte, nur daran interessiert sind, ihr Einkommen zu maximieren – wird er sich dafür entscheiden, die Filiale eröffnen? Stellen Sie das Spiel in Normalform dar und begründen Sie Ihre Antwort.
(b) Angenommen, der Unternehmer weiß, dass einer seiner Kandidaten für die Stelle des Managers unehrliches Verhalten aus religiösen Gründen ablehnt. Er nimmt an, dass dieser Kandidat bereit wäre, bis zu 20.000 Euro zu zahlen, damit er nicht mit dem Gefühl der Schuld leben muss (anders formuliert: die Sünde des Diebstahls kostete den Manager 20.000 Euro). Würde der Unternehmer in diesem Fall die Filiale eröffnen? Wie ändert sich in diesem Fall die Spielmatrix? Stellen Sie das Spiel dar und begründen Sie Ihre Antwort.
Übungsbeispiel 1.5
Max und Emma spielen ein Spiel, in dem Max als erster eine Entscheidung trifft (siehe Abbildung unten). Nachdem Max sich entweder für „oben“ oder „unten“ entschieden hat, kann sich Emma ihrerseits für „oben“ oder „unten“ entscheiden.
Wo liegt das Gleichgewicht in diesem Spiel, welche Strategien werden gewählt und welche Auszahlungen erhalten Max und Emma?
Nehmen Sie an, Emma kann, bevor Max sich entscheidet, eine verbindliche Aussage darüber treffen, entweder „oben“ oder „unten“ zu wählen – was würde sie wählen? Wie würde das Gleichgewicht in diesem Fall aussehen?
Lösungen
Übungsbeispiel 1.1
Der zweite Spieler wird, nachdem der erste Spieler (unbeabsichtigt) auf eine nichtkooperative Strategie abgewichen ist, selbst auch abweichen (als Resultat der Tit-For-Tat-Strategie). In der nächsten Runde wird allerdings der erste Spieler, als Antwort auf das Abweichen des zweiten Spielers in der Vorrunde, selbst wieder abweichen und jeder der Spieler wird danach die nichtkooperative Strategie wählen. Dieses Beispiel macht deutlich, dass eine Tit-For-Tat-Strategie nicht die optimale Strategie ist, wenn die Möglichkeit besteht, dass Spieler Fehler begehen.
Übungsbeispiel 1.2
Wenn die beiden Spieler die Möglichkeit haben, sich aneinander zu rächen, würde sich formal die Auszahlungsstruktur des Spieles ändern. Dies könnte zu einem effizienten Ausgang des Spieles führen – zum Beispiel könnten die Spieler sich einigen, einander umzubringen, sollte der jeweils andere gestehen. Wenn Sie nun annehmen, dass die Auszahlung „Tod“ einen unendlich negativen Nutzen hat, kann sich die Spielmatrix so ändern, dass das Gleichgewicht, in dem beide Spieler „nicht gestehen“ wählen, auftritt. Dazu jedoch zwei Anmerkungen:
- Erstens kann einer der Räuber immer noch „gestehen“ wählen und den anderen, nachdem dieser freigekommen ist, zuerst umbringen. Es müsste also sichergestellt werden, dass die Drohung hinreichend realistisch ist, um zum Ergebnis „nicht gestehen“ zu kommen.
- Man beachte die Analogie zur atomaren Abschreckung: Die Drohung, die strategische Atomwaffen implizieren, ist, das Land des Feindes völlig zu zerstören, nachdem dieser den Erstschlag ausgeführt hat. Die Lösung des „Spiels“ der atomaren Abschreckung ist daher für beide Seiten „nicht angreifen“. Dazu gehört auch, sich als Atommacht stets so zu verhalten, dass die Angst vor der völligen Zerstörung für den Feind realistisch ist. Strategische Atomwaffen nur zu besitzen reicht daher nicht aus, es muss der Zweitschlag jederzeit – auch dann, wenn das eigene Land durch den Erstschlag bereits zerstört sein sollte – durchgeführt werden können, um beim Feind glaubwürdig zu sein. Aus diesem Grund sind bspw. mit strategischen Atomwaffen bestückte U-Boote permanent irgendwo in den Meeren unterwegs und selbst für befreundete Staaten nicht zu orten (d.h. der Feind muss einerseits wissen, dass es diese jederzeit einsatzfähigen Waffen gibt, er darf aber gleichzeitig nicht wissen, wo sie sich befinden, da er sie sonst außer Gefecht setzen könnte).
Übungsbeispiel 1.3
Der neue Spielbaum sieht wie folgt aus:
Im neuen Gleichgewicht wählt Spieler 2 entweder „links“ oder „rechts“, da keine Strategie stark dominant ist. Spieler 1 wählt danach „oben“, die Auszahlung ist (9, 1). Man beachte, dass Spieler 2 indifferent ist, ob Spieler 1 „oben“ oder „unten“ wählen wird, der Ausgang des Spiels somit als Auszahlung bekannt ist, aber nicht, welches Ergebnis als solches vorliegen wird. Nichtsdestoweniger bevorzugt Spieler 2 zuerst zu entscheiden, da er in diesem Fall eine Auszahlung von 9 erhält (im Gegensatz zu einer Auszahlung von 1 bei der umgekehrten Abfolge der Spielzüge).
Übungsbeispiel 1.4
Der Strategienraum der Spieler „Unternehmer“ und „Manager“ ist in Normalform wie folgt gegeben:
|
|
|
Manager |
|
|
|
|
Ehrlich | Unehrlich |
| Unternehmer | Eröffnen | 1600, 5000 | -1200, 7200 |
|
|
Nicht eröffnen | 0, 2500 | 0, 2500 |
Aus Sicht des Managers ist die Strategie „unehrlich“ schwach dominant. Die beste Antwort des Unternehmers ist daher „nicht eröffnen“ und das Nash-Gleichgewicht ist durch („nicht eröffnen“, „unehrlich“) gegeben.
In diesem Fall hat der Manager, sollte er sich unehrlich verhalten, einen negativen Nutzen. Dieser macht jede monetäre Auszahlung einer unehrlichen Strategie bis zu 15000 Euro zunichte. Daher sieht die neue Normalform des Spieles so aus:
|
|
|
Manager |
|
|
|
|
Ehrlich | Unehrlich |
| Unternehmer | Eröffnen | 1600, 5000 | -1200, 0 |
|
|
Nicht eröffnen | 0, 2500 | 0, 2500 |
Die stark dominante Strategie des Managers ist „ehrlich“. Das Nash-Gleichgewicht ist somit durch (eröffnen, ehrlich) gegeben.
Übungsbeispiel 1.5
Max nimmt an, dass Emma, wenn sie an der Reihe ist, die Strategie wählt, die ihre Auszahlung maximiert, also „unten“. Somit kann Max seine Auszahlung maximieren, indem er „oben“ wählt. Das Gleichgewicht in diesem Spiel ist also durch („oben“, „unten“) gegeben, Max bekommt eine Auszahlung von 60 und Emma von 105.
Könnte Emma ein glaubwürdiges Versprechen abgeben, dass sie immer „oben“ wählte, egal, was Max entscheidet, würde sich ein für beide Spieler besseres Resultat ergeben. Max würde in diesem Fall „unten“ wählen und Emma „oben“, sodass die Gleichgewichtsauszahlungen durch (500, 400) gegeben wären.
- ↑ Man beachte, dass das Spiel nur eine Runde gespielt wird und es keine Kommunikationsmöglichkeit gibt.
- ↑ Das rationale Kalkül hinter dem scheinbaren Wahnsinn wird hervorragend im Film-Klassiker „Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb“ (dt. Titel „Dr. Seltsam oder: Wie ich lernte, die Bombe zu lieben“) von Stanley Kubrick dargestellt.
- ↑ Fehr, Ernst und Simon Gächter (2000): Fairness and retaliation: the economics of reciprocity, Journal of Economic Perspectives 14: 159-181