Unternehmensanalyse und -planung - Unternehmensbewertung: Unterschied zwischen den Versionen
| (41 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
<span id="anwendung-des-shareholder-value-ansatzes"></span> | <span id="anwendung-des-shareholder-value-ansatzes"></span> | ||
== Anwendung des Shareholder-Value-Ansatzes <ref>vgl. Mandl/Rabl, 1997, S. 285</ref> | == Anwendung des Shareholder-Value-Ansatzes <ref>vgl. Mandl/Rabl, 1997, S. 285</ref> == | ||
Der Shareholder-Value-Ansatz ist eines von vielen bekannten DCF-Verfahren (Discounted-Cashflow-Methods). Im Rahmen von DCF-Verfahren wird der Unternehmenswert durch Diskontierung von Cashflows ermittelt. Der Diskontierungssatz ergibt sich dabei aus den Renditeforderungen der Kapitalgeber. Die DCF-Verfahren wurden in den USA zur Bewertung von Kapitalgesellschaften entwickelt und sind durch eine konzeptionelle Orientierung am Kapitalmarkt gekennzeichnet. | Der Shareholder-Value-Ansatz ist eines von vielen bekannten DCF-Verfahren (Discounted-Cashflow-Methods). Im Rahmen von DCF-Verfahren wird der Unternehmenswert durch Diskontierung von Cashflows ermittelt. Der Diskontierungssatz ergibt sich dabei aus den Renditeforderungen der Kapitalgeber. Die DCF-Verfahren wurden in den USA zur Bewertung von Kapitalgesellschaften entwickelt und sind durch eine konzeptionelle Orientierung am Kapitalmarkt gekennzeichnet. | ||
| Zeile 36: | Zeile 36: | ||
<span id="das-value-driver-modell-nach-rappaport"></span> | <span id="das-value-driver-modell-nach-rappaport"></span> | ||
=== Das Value-Driver-Modell nach Rappaport <ref>vgl. Rappaport, 1986, S. 50 ff.</ref> | === Das Value-Driver-Modell nach Rappaport <ref>vgl. Rappaport, 1986, S. 50 ff.</ref> === | ||
Rappaport definiert die folgenden Value Drivers: | Rappaport definiert die folgenden Value Drivers: | ||
| Zeile 98: | Zeile 98: | ||
<ul> | <ul> | ||
<li><p>Fremdkapitalkostensatz'':'' Der Fremdkapitalkostensatz wird als gewichteter durchschnittlicher Zinssatz aller bestehenden Fremdfinanzierungen berechnet. Hierbei ist jedoch zu beachten, dass Fremdkapitalzinsen die Steuerlast reduzieren, sodass für die Berechnung des WACC der Fremdkapitalzinssatz mit dem Faktor (1 – Steuersatz) anzupassen ist.</p></li> | <li><p>Fremdkapitalkostensatz'':'' Der Fremdkapitalkostensatz wird als gewichteter durchschnittlicher Zinssatz aller bestehenden Fremdfinanzierungen berechnet. Hierbei ist jedoch zu beachten, dass Fremdkapitalzinsen die Steuerlast reduzieren, sodass für die Berechnung des WACC der Fremdkapitalzinssatz mit dem Faktor (1 – Steuersatz) anzupassen ist.</p></li> | ||
<li><p>Eigenkapitalkostensatz: Der Eigenkapitalkostensatz wird zumeist mit dem CAPM <ref>vgl. Franke/Hax, 1994, S. 345 ff.</ref> | <li><p>Eigenkapitalkostensatz: Der Eigenkapitalkostensatz wird zumeist mit dem CAPM <ref>vgl. Franke/Hax, 1994, S. 345 ff.</ref> (Capital-Asset-Pricing-Model) bestimmt und setzt sich zusammen aus:</p></li> | ||
</ul> | </ul> | ||
::- einem Zins für risikolose Investitionen, | ::- einem Zins für risikolose Investitionen, | ||
::- einer marktüblichen Risikoprämie für den Aktienmarkt und | |||
::- einem unternehmensspezifischen Risikomaß, welches mit der Risikoprämie multipliziert wird. | |||
: | <span style="font-size: 10pt;">Als Risikomaß wird das sogenannte Beta (Maß für den statistischen Zusammenhang zwischen Unternehmens- und Marktrendite) verwendet.</span> <ref>Eine detaillierte Beschreibung des CAPM-Modells würde den Rahmen dieses Heftes | ||
sprengen und ist für die hier verfolgten Lernziele auch nicht notwendig.</ref> | |||
Jedenfalls wird der Eigenkapitalkostensatz aufgrund des höheren Risikos, welches der Eigenkapital- im Vergleich zum Fremdkapitalgeber trägt, immer höher sein als der Fremdkapitalkostensatz. | Jedenfalls wird der Eigenkapitalkostensatz aufgrund des höheren Risikos, welches der Eigenkapital- im Vergleich zum Fremdkapitalgeber trägt, immer höher sein als der Fremdkapitalkostensatz. | ||
| Zeile 114: | Zeile 115: | ||
Wir betrachten ein Unternehmen mit folgenden Parametern: | Wir betrachten ein Unternehmen mit folgenden Parametern: | ||
Eigenkapitalquote 50 % | :Eigenkapitalquote 50 % | ||
:Körperschaftssteuersatz 25 % | |||
:Fremdkapitalkostensatz 10 % | |||
:Eigenkapitalkostensatz 12 % | |||
:'''WACC = 0,5 * 12 + 0,5 * 10 * (1 - 0,25 ) = 9,75 %''' | |||
:<br> | |||
Nun könnte man meinen, dass es möglich wäre, den WACC durch eine Veränderung der Kapitalstruktur in Richtung eines höheren Fremdkapitalanteils zu senken und dadurch den Unternehmenswert zu erhöhen, denn bei einer Verringerung der Eigenkapitalquote auf 40 % ergäbe sich ein WACC von | |||
:'''WACC = 0,4 * 12 + 0,6 * 10 * (1 - 0,25) = 9,3 %''' | |||
Dies ist jedoch nicht möglich, da durch eine Senkung der Eigenkapitalquote das Risiko (Kapitalstrukturrisiko) sowohl für die Eigen- als auch für die Fremdkapitalgeber steigen würde, worauf diese sofort mit einer Erhöhung ihrer Renditeforderung (Eigen- und Fremdkapitalkostensätze würden steigen) reagieren würden. Dieser Zusammenhang wurde durch das Irrelevanztheorem von Modigliani/Miller bewiesen. | Dies ist jedoch nicht möglich, da durch eine Senkung der Eigenkapitalquote das Risiko (Kapitalstrukturrisiko) sowohl für die Eigen- als auch für die Fremdkapitalgeber steigen würde, worauf diese sofort mit einer Erhöhung ihrer Renditeforderung (Eigen- und Fremdkapitalkostensätze würden steigen) reagieren würden. Dieser Zusammenhang wurde durch das Irrelevanztheorem von Modigliani/Miller bewiesen. | ||
<span id="exkurs-irrelevanztheorem-nach-modiglianimiller"></span> | <span id="exkurs-irrelevanztheorem-nach-modiglianimiller"></span> | ||
=== Exkurs: Irrelevanztheorem nach Modigliani/Miller === | === Exkurs: Irrelevanztheorem nach Modigliani/Miller === | ||
| Zeile 144: | Zeile 144: | ||
<span id="modellkonforme-finanzierung"></span> | <span id="modellkonforme-finanzierung"></span> | ||
=== Modellkonforme Finanzierung <ref>vgl. Mandl/Rabl, 1997, S. 346 f.</ref> | === Modellkonforme Finanzierung <ref>vgl. Mandl/Rabl, 1997, S. 346 f.</ref> === | ||
Erfolgt die Diskontierung der erwarteten FCF mit einem konstanten gewogenen Kapitalkostensatz, wird eine in Zukunft gleichbleibende Kapitalstruktur auf Marktwertbasis unterstellt. Durch die Vorgabe einer Zielkapitalstruktur wird der Anteil des Eigen- bzw. Fremdkapitals am Marktwert der Unternehmung für die künftigen Perioden festgelegt. Damit wird die Finanzierungspolitik des Unternehmens determiniert und als in Zukunft gleichbleibend erachtet. | Erfolgt die Diskontierung der erwarteten FCF mit einem konstanten gewogenen Kapitalkostensatz, wird eine in Zukunft gleichbleibende Kapitalstruktur auf Marktwertbasis unterstellt. Durch die Vorgabe einer Zielkapitalstruktur wird der Anteil des Eigen- bzw. Fremdkapitals am Marktwert der Unternehmung für die künftigen Perioden festgelegt. Damit wird die Finanzierungspolitik des Unternehmens determiniert und als in Zukunft gleichbleibend erachtet. | ||
| Zeile 159: | Zeile 159: | ||
Für die Planung der FCF stehen folgende Informationen zur Verfügung: | Für die Planung der FCF stehen folgende Informationen zur Verfügung: | ||
Umsatz letztes Geschäftsjahr: 500.000,00 | {| style="border-collapse: collapse; width: 30%;" fcf="" ermittlung="" | ||
|- | |||
Umsatzwachstumsrate jährlich: 10 % | | style="width: 25%;" | Umsatz letztes Geschäftsjahr: | ||
| style="width: 15%;" | 500.000,00 | |||
|- | |||
| style="width: 25%;" | Umsatzwachstumsrate jährlich: | |||
| style="width: 15%;" | 10 % | |||
|- | |||
| style="width: 25%;" | Umsatzüberschussrate: | |||
| style="width: 15%;" | 5 % | |||
|- | |||
| style="width: 25%;" | KöSt-Satz: | |||
| style="width: 15%;" | 25 % | |||
|- | |||
| style="width: 25%;" | Nettoinvestitionen ins WC: | |||
| style="width: 15%;" | 10 % | |||
|- | |||
| style="width: 25%;" | Nettoinvestitionen ins AV: | |||
| style="width: 15%;" | 15 % | |||
|- | |||
| style="width: 25%;" | Detailprognosezeitraum: | |||
| style="width: 15%;" | 5 Jahre | |||
|} | |||
<br>Innerhalb des Planungshorizonts bleiben alle Daten unverändert. Für die Zeit danach wird von einem nominell konstanten „Perpetuity Cashflow“ in Höhe des NOPAT der Periode t<sub>5</sub> ausgegangen. | |||
{| style="border-collapse: collapse; margin-left: auto; margin-right: auto;" border="1" | |||
|+ FCF Ermittlung | |||
{| style="border-collapse: collapse; margin-left: auto; margin-right: auto;" border="1" | |||
| width="13%" | | | width="13%" | | ||
<br> | <br> | ||
| Zeile 265: | Zeile 276: | ||
|} | |} | ||
Bis zum Planungshorizont wachsen die FCF jährlich in Höhe der konstanten Umsatzwachstumsrate von 10 %. Ab t<sub>6</sub> fällt annahmegemäß ein Perioden-CF in Höhe des NOPAT der Periode t<sub>5</sub> an. Unter der Annahme eines gewogenen Kapitalkostensatzes (WACC) von 10 % errechnet sich der Unternehmenswert als Marktwert des Gesamtkapitals wie folgt: | Bis zum Planungshorizont wachsen die FCF jährlich in Höhe der konstanten Umsatzwachstumsrate von 10 %. Ab t<sub>6</sub> fällt annahmegemäß ein Perioden-CF in Höhe des NOPAT der Periode t<sub>5</sub> an. Unter der Annahme eines gewogenen Kapitalkostensatzes (WACC) von 10 % errechnet sich der Unternehmenswert als Marktwert des Gesamtkapitals wie folgt: | ||
Residual-Value (als Barwert zu t<sub>5</sub>): 301.970,60 | {| style="border-collapse: collapse; width: 55%;" | ||
|- | |||
| style="width: 25%;" | Residual-Value (als Barwert zu t<sub>5</sub>): | |||
| style="width: 15%;" | 301.970,60 | |||
|- | |||
| style="width: 25%;" | Barwert des Residual-Value zu t<sub>0</sub>: | |||
| style="width: 15%;" | 187.500,00 | |||
|- | |||
| style="width: 25%;" | Barwert der FCF bis zum Planungshorizont zu t<sub>0</sub>: | |||
| style="width: 15%;" | 36.931,82 | |||
|- | |||
| style="width: 25%;" | '''Marktwert des Unternehmens (GK):''' | |||
| style="width: 15%;" | '''224.431,82''' | |||
|} | |||
<br>Bei im Zeitablauf konstanten Werten für die Value Drivers können die künftigen FCF nach dem Modell von Rappaport sehr einfach ermittelt werden: Unter dieser Annahme wachsen die FCF innerhalb des Detailprognosezeitraumes in jeder Periode mit der Wachstumsrate des Umsatzes. Um die FCF der späteren Perioden zu bestimmen, braucht daher grundsätzlich nur der FCF der ersten Planungsperiode errechnet werden. Der zu erwartende PCF kann ebenfalls aus dem hochgerechneten Umsatz zum Ende des Detailprognosezeitraumes ermittelt werden. | |||
<span id="abschließende-beurteilung-der-value-driver-modelle"></span> | |||
=== Abschließende Beurteilung der Value-Driver-Modelle === | === Abschließende Beurteilung der Value-Driver-Modelle === | ||
| Zeile 315: | Zeile 333: | ||
'''Unternehmenswert Belgien:''' | '''Unternehmenswert Belgien:''' | ||
Umsatz t'''<sub>0</sub>''': 571.100,00 | {| style="border-collapse: collapse; width: 100%;" | ||
|- | |||
Umsatzwachstumsrate jährlich: 14 % | | style="width: 15%;" | Umsatz t'''<sub>0</sub>''': | ||
| style="width: 15%;" | 571.100,00 | |||
Umsatzüberschussrate: 9 % | |- | ||
| style="width: 15%;" | Umsatzwachstumsrate jährlich: | |||
KöSt-Satz: 34 % | | style="width: 15%;" | 14 % | ||
|- | |||
Nettoinvestitionen ins WC: 15 % | | style="width: 15%;" | Umsatzüberschussrate: | ||
| style="width: 15%;" | 9 % | |||
Nettoinvestitionen ins AV: 10 % | |- | ||
| style="width: 15%;" | KöSt-Satz: | |||
WACC: 7,43 % | | style="width: 15%;" | 34 % | ||
|- | |||
| style="width: 15%;" | Nettoinvestitionen ins WC: | |||
| style="width: 15%;" | 15 % | |||
|- | |||
| style="width: 15%;" | Nettoinvestitionen ins AV: | |||
| style="width: 15%;" | 10 % | |||
|- | |||
| style="width: 15%;" | WACC: | |||
| style="width: 50%;" | 7,43 % | |||
|- | |||
| style="width: 15%;" | Detailprognosezeitraum: | |||
| style="width: 15%;" | 5 Jahre | |||
|} | |||
[[Datei:Bw411 7.jpg| | [[Datei:Bw411 7.jpg|600px|center|frameless|Ermittlung FCF Belgien]] | ||
<span id="_Toc268090448" class="anchor"></span> | <span id="_Toc268090448" class="anchor"></span><br> | ||
| Zeile 338: | Zeile 368: | ||
'''Unternehmenswert Österreich:''' | '''Unternehmenswert Österreich:''' | ||
Umsatz t'''<sub>0</sub>''': 562.050,00 | {| style="border-collapse: collapse; width: 100%;" | ||
|- | |||
Umsatzwachstumsrate jährlich: 12 % | | style="width: 15%;" | Umsatz t'''<sub>0</sub>''': | ||
| style="width: 15%;" | 562.050,00 | |||
Umsatzüberschussrate: 10 % | |- | ||
| style="width: 15%;" | Umsatzwachstumsrate jährlich: | |||
KöSt-Satz: 25 % | | style="width: 15%;" | 12 % | ||
|- | |||
Nettoinvestitionen ins WC: 15 % | | style="width: 15%;" | Umsatzüberschussrate: | ||
| style="width: 15%;" | 10 % | |||
Nettoinvestitionen ins AV: 10 % | |- | ||
| style="width: 15%;" | KöSt-Satz: | |||
WACC: 7,92 % | | style="width: 15%;" | 25 % | ||
|- | |||
| style="width: 15%;" | Nettoinvestitionen ins WC: | |||
| style="width: 15%;" | 15 % | |||
|- | |||
| style="width: 15%;" | Nettoinvestitionen ins AV: | |||
| style="width: 15%;" | 10 % | |||
|- | |||
| style="width: 15%;" | WACC: | |||
| style="width: 50%;" | 7,92 % | |||
|- | |||
| style="width: 15%;" | Detailprognosezeitraum: | |||
| style="width: 15%;" | 5 Jahre | |||
|} | |||
[[Datei:Bw411 8.jpg| | [[Datei:Bw411 8.jpg|600px|center|thumb|Ermittlung FCF Österreich]] | ||
<span id="_Toc268090449" class="anchor"></span> | <span id="_Toc268090449" class="anchor"></span> | ||
Aufgrund der Ergebnisse der Unternehmensbewertung steht nun fest, dass Österreich als Standort zu wählen ist. | Aufgrund der Ergebnisse der Unternehmensbewertung steht nun fest, dass Österreich als Standort zu wählen ist. | ||
| Zeile 391: | Zeile 433: | ||
Innerhalb des Planungshorizonts bleiben alle Daten bis auf die Umsatzwachstumsrate unverändert. Für die Zeit danach wird von einem nominell konstanten „Perpetuity Cashflow“ in Höhe des NOPAT der Periode t<sub>5</sub> ausgegangen. | Innerhalb des Planungshorizonts bleiben alle Daten bis auf die Umsatzwachstumsrate unverändert. Für die Zeit danach wird von einem nominell konstanten „Perpetuity Cashflow“ in Höhe des NOPAT der Periode t<sub>5</sub> ausgegangen. | ||
Eigenkapitalquote: 45 % | |||
Eigenkapitalkostensatz 12 % | Eigenkapitalkostensatz 12 % | ||
| Zeile 423: | Zeile 465: | ||
'''Wiederholungsaufgabe 3-2:''' | '''Wiederholungsaufgabe 3-2:''' | ||
Es soll der Börsenwert des eigenen Unternehmens und damit die Rendite des von den | Es soll der Börsenwert des eigenen Unternehmens und damit die Rendite des von den Aktionär*innen zur Verfügung gestellten Kapitals gesteigert werden. | ||
'''Wiederholungsaufgabe 3-3:''' | '''Wiederholungsaufgabe 3-3:''' | ||
Im Zusammenhang mit dem „Value-Based-Management“ wurde untersucht, durch welche Komponenten der Shareholder-Value und damit insbesondere die künftig für die Kapitalgeber verfügbaren FCF beeinflusst werden können. Diese Komponenten werden als Value Drivers (Wertgeneratoren) bezeichnet. | Im Zusammenhang mit dem „Value-Based-Management“ wurde untersucht, durch welche Komponenten der Shareholder-Value und damit insbesondere die künftig für die Kapitalgeber*innen verfügbaren FCF beeinflusst werden können. Diese Komponenten werden als Value Drivers (Wertgeneratoren) bezeichnet. | ||
* Umsatzwachstumsrate | * Umsatzwachstumsrate | ||
Aktuelle Version vom 4. Juli 2023, 13:39 Uhr
Unternehmensbewertung
Das Konzept und seine Herkunft
Die Aufgabe des Managements kann beschrieben werden als Versuch, die Interessen der verschiedenen Anspruchsgruppen (Stakeholder, z.B. Mitarbeiter*innen, Zulieferer, Kund*innen) eines Unternehmens auszubalancieren bzw. zu befriedigen. Wenn eine oder mehrere dieser Anspruchsgruppen der Unternehmung die Zusammenarbeit versagt, ist das Überleben des Unternehmens bedroht.
Besondere Bedeutung ist aus der Sicht des Managements jedoch den Interessen der Eigenkapitalgeber*innen oder Aktionär*innen beizumessen. Direkt oder indirekt bestimmen sie zumindest zu einem großen Teil die Besetzung des Managements. Ferner können unbefriedigende Entwicklungen des Aktienkurses dazu führen, dass sie ihr finanzielles Engagement beenden und so den finanziellen Spielraum massiv einschränken. Dadurch werden Unternehmen auch anfällig für feindliche Übernahmen, was u.a. für das Management mit dem Verlust des Arbeitsplatzes verbunden sein kann.
Entsprechend verfolgt das Shareholder-Value-Konzept das Ziel, den Wert des Eigenkapitals zu maximieren. Vor dem Hintergrund des einleitend Gesagten kann dies dauerhaft jedoch nicht ohne ausreichende Beachtung der legitimen Interessen aller übrigen Anspruchsgruppen geschehen. Eine Maximierung des Wertes der Unternehmung schafft zudem erst den nötigen Spielraum, um auch diese Interessen angemessen zu berücksichtigen. Insofern bedingt sich die Zufriedenstellung aller Anspruchsgruppen gegenseitig.
Der US-amerikanische Finanzprofessor Alfred Rappaport begründete 1986 das Shareholder-Value-Konzept.
Es besagt, dass Unternehmen ihre Geschäftsstrategie stark an den Interessen der Aktionär*innen ausrichten. Durch ein wertorientiertes Unternehmensmanagement (Value-Based-Management) soll der Börsenwert des eigenen Unternehmens und damit die Rendite des von den Aktionär*innen zur Verfügung gestellten Kapitals gesteigert werden. Im Zuge der Globalisierung der Märkte verlangt die Konkurrenz um knappe Finanzressourcen von den Unternehmen zunehmend eine Erwirtschaftung zufriedenstellender Renditen auf das zur Verfügung gestellte Kapital. Diese Rendite auf das eingesetzte Kapital besteht – neben Dividendenzahlungen, Bezugsrechten und Sonderausschüttungen – insbesondere aus der Kurswertsteigerung der Unternehmensaktie.
Die Kursentwicklung einer Aktie und damit der Börsenwert eines Unternehmens hängen langfristig eng mit der kontinuierlichen Schaffung von neuen Unternehmenswerten zusammen. Wertorientiertes Management zielt dementsprechend darauf ab, den inneren Wert des Unternehmens zu steigern, sprich neue Werte zu schaffen. Dies geschieht dann, wenn die Rendite die Kapitalkosten übersteigt. Zur Umsetzung des Shareholder-Value-Gedankens bedienen sich die Unternehmen anderer Steuerungsinstrumente als GuV und Bilanz.
Der Shareholder-Value-Ansatz ist eines von vielen bekannten DCF-Verfahren (Discounted-Cashflow-Methods). Im Rahmen von DCF-Verfahren wird der Unternehmenswert durch Diskontierung von Cashflows ermittelt. Der Diskontierungssatz ergibt sich dabei aus den Renditeforderungen der Kapitalgeber. Die DCF-Verfahren wurden in den USA zur Bewertung von Kapitalgesellschaften entwickelt und sind durch eine konzeptionelle Orientierung am Kapitalmarkt gekennzeichnet.
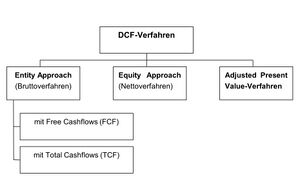
Im Laufe der Zeit haben sich unterschiedliche DCF-Verfahren herausgebildet. Unterschiede bestehen vor allem in Art und Umfang der Einbeziehung der Fremdfinanzierung, der aus der Fremdfinanzierung resultierenden Steuerwirkungen sowie von Änderungen der Kapitalstruktur im Zeitablauf in das Bewertungskalkül. Dabei können die in folgender Abbildung dargestellten Verfahrenstypen unterschieden werden.
Im Shareholder-Value-Ansatz wird der Unternehmenswert mittels der zukünftigen freien Cashflows (FCF) ermittelt, damit gehört er zum Entity Approach (Bruttoverfahren – siehe obige Abbildung).
Value-Driver-Modelle
Für die Planung der zukünftigen FCF ist es erforderlich, das Unternehmen in einen operativen und einen nicht-operativen Bereich zu trennen. Für den nicht-operativen Bereich müssen spezifische Prognoseüberlegungen, die von der Art der dort entfalteten Tätigkeiten abhängen, angestellt werden. Zur Abschätzung der in Zukunft aus dem operativen Bereich bzw. der eigentlichen Betriebstätigkeit des Unternehmens zu erwartenden FCF wird als Spezifikum der Einsatz von Value- Driver-Modellen empfohlen.
Im Zusammenhang mit dem „Value-Based-Management“ wurde untersucht, durch welche Komponenten der Shareholder-Value und damit insbesondere die künftig für die Kapitalgeber verfügbaren FCF beeinflusst werden können. Diese Komponenten werden als Value Drivers (Wertgeneratoren) bezeichnet. In der Literatur wurden unterschiedliche Value-Driver-Modelle vorgestellt, von denen jenes von Rappaport (1986) das bekannteste ist. Andere Autoren, die ihrerseits solche Modelle hervorbrachten, waren Stern/Stewart [2] (1990), Copeland/Koller/Murrin [3] (1994) und Lewis [4] (1994).
Das Value-Driver-Modell nach Rappaport [5]
Rappaport definiert die folgenden Value Drivers:
- Umsatzwachstumsrate (UW)
- Umsatzrentabilität oder Umsatzüberschussrate (UÜ)
- Nettoinvestitionsrate ins Working Capital (IRWC)
- Nettoinvestitionsrate ins Anlagevermögen (IRAV)
- Gewogene Kapitalkosten (WACC)*
- Länge der Detailprognoseperiode bzw. Planungshorizont (T)
- Ertragssteuersatz auf Unternehmensebene (S)
WACC = Weighted Average Capital Cost
Zur Ermittlung des operativen FCF einer Periode t geht Rappaport von folgendem Zusammenhang aus:
FCFt = NOPATt – NIAV t – NIWC t
Dabei bezeichnet NOPAT (Net Operating Profit After Taxes) den operativen Gewinn vor Zinsen und nach Steuern einer Periode. Um den FCF der Periode zu erhalten, wird dieser Gewinn um die Nettoinvestitionen in das Anlagevermögen (NIAV) und in das Working Capital (NIWC) vermindert. Die Nettoinvestitionen in das Working Capital geben den Kapitalbindungseffekt an, der aus der Erhöhung des Working Capitals in einer Periode resultiert. Die Nettoinvestitionen in das Anlagevermögen sind definiert als jene Investitionsauszahlungen einer Periode, die über die (bereits im NOPAT berücksichtigten) Abschreibungen hinausgehen. Dabei wird implizit unterstellt, dass keine Desinvestitionen anfallen werden.
Die Umsatzüberschussrate (UÜ) gibt das Verhältnis zwischen dem operativen Gewinn vor Steuern und Zinsen (EBIT: Earnings Before Interest And Taxes) und dem Umsatz (U) an:
Im EBIT sind neben den Herstellungskosten für die verkauften Produkte auch die Verwaltungs- und Vertriebsaufwendungen abgezogen. Auch die Abschreibungen auf das Anlagevermögen haben das EBIT gemindert. Wird das EBIT einer Periode um die darauf entfallende Gewinnsteuer vermindert, erhält man den NOPAT der Periode.
Die Nettoinvestitionen in das Working Capital und in das Anlagevermögen werden im Modell jeweils als Produkt aus der Umsatzerhöhung der Periode und der Nettoinvestitionsrate berechnet. Die im Rahmen der Planung festzulegenden Nettoinvestitionsraten sind demgemäß jeweils als Quotient aus Nettoinvestitionen (NI) und Umsatzerhöhung (∆U) definiert.
Sie geben die zusätzliche Kapitalbindung im Anlagevermögen und Working Capital an, die bei einer Erhöhung des Umsatzes um eine Geldeinheit erforderlich ist.
Bezeichnet Ut-1 den Umsatz der Vorperiode, kann der operative FCFt der künftigen Periode t nach Rappaport unter Verwendung der oben definierten Value-Drivers wie folgt berechnet werden:
FCFt = Ut-1 * (1 + UW) * UÜ * (1 – S) – Ut-1 * UW * IRAV – Ut-1 * UW * IRWC
Ab dem Planungshorizont (T) geht Rappaport davon aus, dass zusätzliche Investitionen im Durchschnitt nur mehr eine Rendite erbringen, die den gewogenen Kapitalkosten entspricht. Der Kapitalwert der durch diese Investitionen verursachten Cashflows ist damit aber gleich Null, sodass sie bei der Ermittlung des Unternehmenswertes unberücksichtigt bleiben können. Auf dieser Grundlage geht Rappaport für die Zeit nach dem Planungshorizont von einem (nominell) konstanten FCF aus, den er als „Perpetuity Cashflow“ (PCF) bezeichnet. Der PCF entspricht dabei dem NOPAT der letzten Detailprognoseperiode. Der Barwert der konstanten PCF nach dem Planungshorizont wird von Rappaport als „Residual Value“ (RV) bezeichnet:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{R} V=\frac{\mathrm{PCF}}{W A C C} }
WACC (Weighted Average Capital Cost)
Der WACC stellt, wie bereits oben erwähnt, den gewichteten durchschnittlichen Zinssatz von Fremd- und Eigenkapital dar, mit welchem die FCF und der RV auf den Gegenwartswert zu diskontieren sind, um den Marktwert des Unternehmens (Wert des Gesamtkapitals) zu erhalten. Zieht man vom Unternehmenswert noch den Marktwert des Fremdkapitals ab, so erhält man den Marktwert des Eigenkapitals oder Shareholder Value.
Bei Unterstellung von vollkommen effizienten Märkten würde sich der faire Wert einer Aktie durch Division des Shareholder Value durch die Anzahl der emittierten Aktien errechnen.
Der WACC wird folgendermaßen ermittelt:
Fremdkapitalkostensatz: Der Fremdkapitalkostensatz wird als gewichteter durchschnittlicher Zinssatz aller bestehenden Fremdfinanzierungen berechnet. Hierbei ist jedoch zu beachten, dass Fremdkapitalzinsen die Steuerlast reduzieren, sodass für die Berechnung des WACC der Fremdkapitalzinssatz mit dem Faktor (1 – Steuersatz) anzupassen ist.
Eigenkapitalkostensatz: Der Eigenkapitalkostensatz wird zumeist mit dem CAPM [6] (Capital-Asset-Pricing-Model) bestimmt und setzt sich zusammen aus:
- - einem Zins für risikolose Investitionen,
- - einer marktüblichen Risikoprämie für den Aktienmarkt und
- - einem unternehmensspezifischen Risikomaß, welches mit der Risikoprämie multipliziert wird.
Als Risikomaß wird das sogenannte Beta (Maß für den statistischen Zusammenhang zwischen Unternehmens- und Marktrendite) verwendet. [7]
Jedenfalls wird der Eigenkapitalkostensatz aufgrund des höheren Risikos, welches der Eigenkapital- im Vergleich zum Fremdkapitalgeber trägt, immer höher sein als der Fremdkapitalkostensatz.
Beispiel: WACC-Berechnung:
Wir betrachten ein Unternehmen mit folgenden Parametern:
- Eigenkapitalquote 50 %
- Körperschaftssteuersatz 25 %
- Fremdkapitalkostensatz 10 %
- Eigenkapitalkostensatz 12 %
- WACC = 0,5 * 12 + 0,5 * 10 * (1 - 0,25 ) = 9,75 %
Nun könnte man meinen, dass es möglich wäre, den WACC durch eine Veränderung der Kapitalstruktur in Richtung eines höheren Fremdkapitalanteils zu senken und dadurch den Unternehmenswert zu erhöhen, denn bei einer Verringerung der Eigenkapitalquote auf 40 % ergäbe sich ein WACC von
- WACC = 0,4 * 12 + 0,6 * 10 * (1 - 0,25) = 9,3 %
Dies ist jedoch nicht möglich, da durch eine Senkung der Eigenkapitalquote das Risiko (Kapitalstrukturrisiko) sowohl für die Eigen- als auch für die Fremdkapitalgeber steigen würde, worauf diese sofort mit einer Erhöhung ihrer Renditeforderung (Eigen- und Fremdkapitalkostensätze würden steigen) reagieren würden. Dieser Zusammenhang wurde durch das Irrelevanztheorem von Modigliani/Miller bewiesen.
Exkurs: Irrelevanztheorem nach Modigliani/Miller
Franco Modigliani [8] und Merton H. Miller [9] publizierten im Jahre 1958 in der Zeitschrift „American Economic Review“ [10] einen Aufsatz über „Kapitalkosten, Unternehmensfinanzierung und Investitionstheorie“, mit dem sie die Finanzierungstheorie grundlegend beeinflussten.
Die zentrale Behauptung, die sie in diesem Aufsatz aufstellten und auch bewiesen, lautete:
„Die Art der Finanzierung eines Unternehmens ist für den Erfolg eines Unternehmens genauso wichtig wie das fünfte Rad am Wagen. Jedenfalls könne man durch eine Veränderung des Verhältnisses von Fremd- und Eigenkapital weder den Marktwert des Unternehmens noch die durchschnittlichen Kapitalkosten beeinflussen“. [11]
In der deutschsprachigen Finanzierungsliteratur werden die von Modigliani und Miller aufgestellten Thesen als „Irrelevanztheorem nach Modigliani/Miller“ bezeichnet. Den Beweis für die Richtigkeit ihrer Thesen erbrachten Modigliani/Miller in Form eines Arbitragearguments (Arbitragebeweis von Modigliani/Miller 1958). Sie zeigten, dass man durch Kauf und Verkauf von Wertpapieren risikolos beliebig reich werden kann, falls die durchschnittlichen Kapitalkosten zweier Firmen, die sich nur in Bezug auf ihren Verschuldungsgrad voneinander unterscheiden, nicht übereinstimmen.
Auch mit Hilfe des Capital-Asset-Pricing-Modells lässt sich die Irrelevanz der Kapitalstruktur eines Unternehmens für seinen Marktwert beweisen.
Modellkonforme Finanzierung [12]
Erfolgt die Diskontierung der erwarteten FCF mit einem konstanten gewogenen Kapitalkostensatz, wird eine in Zukunft gleichbleibende Kapitalstruktur auf Marktwertbasis unterstellt. Durch die Vorgabe einer Zielkapitalstruktur wird der Anteil des Eigen- bzw. Fremdkapitals am Marktwert der Unternehmung für die künftigen Perioden festgelegt. Damit wird die Finanzierungspolitik des Unternehmens determiniert und als in Zukunft gleichbleibend erachtet.
Will man Schwankungen der Kapitalstruktur im Zeitablauf durch periodenspezifisch gewogene Kapitalkostensätze berücksichtigen, ergeben sich für die WACC-Ermittlung komplexe Probleme: Es ändern sich nicht nur die Gewichtungsfaktoren zwischen den einzelnen Finanzierungsquellen, sondern auch die Höhe der Eigenkapitalkosten, wenn unterstellt wird, dass die Renditeforderung der Eigenkapitalgeber mit zunehmender Verschuldung steigt. Eine unmittelbare Berücksichtigung dieser Problematik ist im Rahmen des WACC-Ansatzes nicht möglich, weshalb dessen Anwendung nur bei in Zukunft konstanter Kapitalstruktur sinnvoll ist. Die Annahme einer konstanten Kapitalstruktur ist nur im Fall künftig konstanter FCF unproblematisch. Dort impliziert diese Annahme, dass zu t0+ eine Anpassung des Fremdkapitalvolumens vorgenommen wird und in weiterer Folge der Marktwert des Fremdkapitals konstant bleibt, da auch der Marktanteil des Eigenkapitals durch die konstante Höhe der FCF konstant bleibt.
Im praktisch relevanten Fall schwankender FCF im Zeitablauf ändert sich jedoch der Marktwertanteil des Eigenkapitals und damit die Kapitalstruktur von Periode zu Periode. Das heißt, dass der Ansatz, um die Kapitalstruktur konstant zu halten, eine periodenspezifische Anpassung des Fremdkapitalvolumens impliziert. Man spricht von „modellkonformer Finanzierung“.
Beispiel Value-Driver-Modell
Zum besseren Verständnis des bisher zum Value-Driver-Modell nach Rappaport Gesagten sei noch folgendes Beispiel angeführt:
Für die Planung der FCF stehen folgende Informationen zur Verfügung:
| Umsatz letztes Geschäftsjahr: | 500.000,00 |
| Umsatzwachstumsrate jährlich: | 10 % |
| Umsatzüberschussrate: | 5 % |
| KöSt-Satz: | 25 % |
| Nettoinvestitionen ins WC: | 10 % |
| Nettoinvestitionen ins AV: | 15 % |
| Detailprognosezeitraum: | 5 Jahre |
Innerhalb des Planungshorizonts bleiben alle Daten unverändert. Für die Zeit danach wird von einem nominell konstanten „Perpetuity Cashflow“ in Höhe des NOPAT der Periode t5 ausgegangen.
|
|
t1 | t2 | t3 | t4 | t5 | ab t6 |
|
Umsatz EBIT NOPAT - NI (WC) - NI (AV) |
550.000,0 27.500,0 20.625,0 -5.000,0 -7.500,0 |
605.000,0 30.250,0 22.687,5 -5.500,0 -8.250,0 |
665.500,0 33.275,0 24.956,3 -6.050,0 -9.075,0 |
732.050,0 36.602,5 27.451,9 -6.655,0 -9.982,5 |
805.255,0 40.262,8 30.197,1 -7.320,5 -10.980,8 |
805.255,0 40.262,8 30.197,1 0,0 0,0 |
| FCF | 8.125,00 | 8.937,50 | 9.831,25 | 10.814,38 | 11.895,81 | 30.197,06 |
Bis zum Planungshorizont wachsen die FCF jährlich in Höhe der konstanten Umsatzwachstumsrate von 10 %. Ab t6 fällt annahmegemäß ein Perioden-CF in Höhe des NOPAT der Periode t5 an. Unter der Annahme eines gewogenen Kapitalkostensatzes (WACC) von 10 % errechnet sich der Unternehmenswert als Marktwert des Gesamtkapitals wie folgt:
| Residual-Value (als Barwert zu t5): | 301.970,60 |
| Barwert des Residual-Value zu t0: | 187.500,00 |
| Barwert der FCF bis zum Planungshorizont zu t0: | 36.931,82 |
| Marktwert des Unternehmens (GK): | 224.431,82 |
Bei im Zeitablauf konstanten Werten für die Value Drivers können die künftigen FCF nach dem Modell von Rappaport sehr einfach ermittelt werden: Unter dieser Annahme wachsen die FCF innerhalb des Detailprognosezeitraumes in jeder Periode mit der Wachstumsrate des Umsatzes. Um die FCF der späteren Perioden zu bestimmen, braucht daher grundsätzlich nur der FCF der ersten Planungsperiode errechnet werden. Der zu erwartende PCF kann ebenfalls aus dem hochgerechneten Umsatz zum Ende des Detailprognosezeitraumes ermittelt werden.
Abschließende Beurteilung der Value-Driver-Modelle
Der große Vorteil der Value-Driver-Modelle liegt in ihrer Einfachheit und Anschaulichkeit. Mit wenigen, jedoch sehr pauschalen Annahmen kann der Unternehmenswert unmittelbar berechnet werden bzw. kann gezeigt werden, wie sich eine Veränderung der für die Value Drivers angesetzten Werte auf den Unternehmenswert auswirkt.
Die Anforderungen, die an eine Planungsrechnung im Rahmen von Unternehmensbewertungen zu stellen sind, können jedoch durch die Value-Driver-Modelle nicht erfüllt werden, zumal die ihnen zugrundeliegenden pauschalen Annahmen meist nicht realitätsgerecht sind.
Einsatzmöglichkeiten für Value-Driver-Modelle sind im Rahmen grober Schätzungen von Wert-Bandbreiten oder in Form von Plausibilitätskontrollen denkbar.
Stewart beschrieb den Anwendungsbereich für sein Value-Driver-Modell wie folgt:
„As a conceptual simplification of discounted cash flow, the value-driver-model is useful for explaining the fundamentals of valuation to senior managers and key operating people more than as a practical procedure for valuation.“ [13]
Fortsetzung Beispiel
Um nun eine endgültige Standortentscheidung treffen zu können, sind in der Folge für beide Standorte die Unternehmenswerte zu ermitteln:
Standortunabhängig ist geplant, während des gesamten Prognosezeitraums die Eigenkapitalquote konstant bei 35 % zu halten. Die geschätzten Durchschnittskosten für das Fremdkapital betragen 8,5 % für das Eigenkapital 10,8 %
Daraus resultieren folgende WACC´s:
Belgien: 0,35 * 10,8 + 0,65 * 8,5 * (1 - 0,34) = 7,43 %
Österreich: 0,35 * 10,8 + 0,65 * 8,5 * (1 - 0,25) = 7,92 %
Innerhalb des Planungshorizonts bleiben alle Daten unverändert. Für die Zeit danach wird von einem nominell konstanten „Perpetuity Cashflow“ in Höhe des NOPAT der Periode t5 ausgegangen.
Aufgrund der leicht niedrigeren Preise in Belgien ist davon auszugehen, dass hier die Umsatzüberschussrate um 1 % tiefer als in Österreich liegen wird. Jedoch ist laut Marktforschungsbericht [14] mit einem um 2 % höheren Marktwachstum zu rechnen. Die Investoren planen jedenfalls den Umsatz mindestens gleich stark wie das prognostizierte Marktwachstum zu steigern. Die geschätzten Umsatzüberschussraten für Belgien und Österreich betragen 9 bzw. 10 %.
Standortunabhängig sind jährlich Investitionen ins Working-Capital und ins Anlagevermögen von 15 bzw. 10 % geplant.
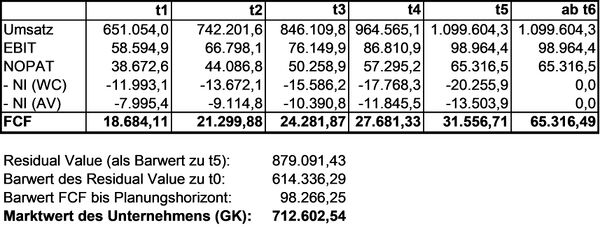
Unternehmenswert Belgien:
| Umsatz t0: | 571.100,00 |
| Umsatzwachstumsrate jährlich: | 14 % |
| Umsatzüberschussrate: | 9 % |
| KöSt-Satz: | 34 % |
| Nettoinvestitionen ins WC: | 15 % |
| Nettoinvestitionen ins AV: | 10 % |
| WACC: | 7,43 % |
| Detailprognosezeitraum: | 5 Jahre |
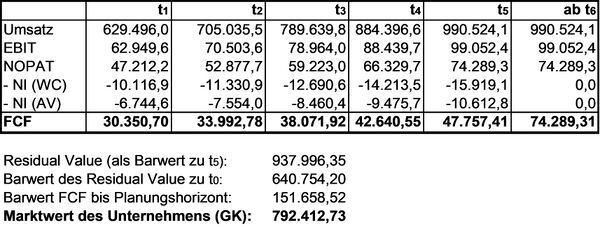
Unternehmenswert Österreich:
| Umsatz t0: | 562.050,00 |
| Umsatzwachstumsrate jährlich: | 12 % |
| Umsatzüberschussrate: | 10 % |
| KöSt-Satz: | 25 % |
| Nettoinvestitionen ins WC: | 15 % |
| Nettoinvestitionen ins AV: | 10 % |
| WACC: | 7,92 % |
| Detailprognosezeitraum: | 5 Jahre |
Aufgrund der Ergebnisse der Unternehmensbewertung steht nun fest, dass Österreich als Standort zu wählen ist.
Wiederholungsaufgaben/Übungen
|
Wiederholungsaufgabe 3‑1: Wer begründete das Shareholder-Value-Konzept und wann ca. war das? Wiederholungsaufgabe 3‑2: Welche Ziele verfolgt das Value-Based-Management? Wiederholungsaufgabe 3‑3: Was versteht man unter Value-Drivern und welche Value-Driver kennen Sie? Wiederholungsaufgabe 3‑4: Was versteht man unter WACC und wie wird dieser errechnet? Wiederholungsaufgabe 3‑5: Kann der WACC durch Kapitalstrukturveränderungen beeinflusst werden? |
Übungsbeispiel 1:
Ermitteln Sie den Unternehmenswert für folgendes Unternehmen:
Innerhalb des Planungshorizonts bleiben alle Daten bis auf die Umsatzwachstumsrate unverändert. Für die Zeit danach wird von einem nominell konstanten „Perpetuity Cashflow“ in Höhe des NOPAT der Periode t5 ausgegangen.
Eigenkapitalquote: 45 %
Eigenkapitalkostensatz 12 %
Fremdkapitalkostensatz: 10 %
Umsatz letztes Geschäftsjahr: 200.000,00
Umsatzwachstumsrate bis Ende t3: 6 %
Umsatzwachstumsrate ab t4 10 %
Umsatzüberschussrate: 14 %
KöSt-Satz: 19 %
Nettoinvestitionen ins WC: 10 %
Nettoinvestitionen ins AV: 15 %
Detailprognosezeitraum: 5 Jahre
Lösungen
Wiederholungsaufgabe 3-1:
Alfred Rappaport. 1986
Wiederholungsaufgabe 3-2:
Es soll der Börsenwert des eigenen Unternehmens und damit die Rendite des von den Aktionär*innen zur Verfügung gestellten Kapitals gesteigert werden.
Wiederholungsaufgabe 3-3:
Im Zusammenhang mit dem „Value-Based-Management“ wurde untersucht, durch welche Komponenten der Shareholder-Value und damit insbesondere die künftig für die Kapitalgeber*innen verfügbaren FCF beeinflusst werden können. Diese Komponenten werden als Value Drivers (Wertgeneratoren) bezeichnet.
- Umsatzwachstumsrate
- Umsatzrentabilität oder Umsatzüberschussrate
- Nettoinvestitionsrate ins Working Capital
- Nettoinvestitionsrate ins Anlagevermögen
- Gewogene Kapitalkosten
- Länge der Detailprognoseperiode bzw. Planungshorizont
- Ertragssteuersatz auf Unternehmensebene
Wiederholungsaufgabe 3-4:
Der WACC (weighted average capital cost) stellt den gewichteten durchschnittlichen Zinssatz von Fremd- und Eigenkapital dar. Zu seiner Berechnung siehe Punkt 3.3.2
Wiederholungsaufgabe 3-5:
Kann der WACC durch Kapitalstrukturveränderungen beeinflusst werden?
Dies ist nicht möglich, da durch eine Senkung der Eigenkapitalquote das Risiko (Kapitalstrukturrisiko) sowohl für die Eigen- als auch für die Fremdkapitalgeber steigen würde, worauf diese sofort mit einer Erhöhung ihrer Renditeforderung (Eigen- und Fremdkapitalkostensätze würden steigen) reagieren würden.
- ↑ vgl. Mandl/Rabl, 1997, S. 285
- ↑ vgl. Stewart, 1991, S. 291 ff.
- ↑ vgl. Copeland/Koller/Murrin, 1994, S. 137 ff.
- ↑ vgl. Lewis, 1994, S. 154 ff.
- ↑ vgl. Rappaport, 1986, S. 50 ff.
- ↑ vgl. Franke/Hax, 1994, S. 345 ff.
- ↑ Eine detaillierte Beschreibung des CAPM-Modells würde den Rahmen dieses Heftes sprengen und ist für die hier verfolgten Lernziele auch nicht notwendig.
- ↑ Franco Modigliani erhielt 1985 den Wirtschaftsnobelpreis
- ↑ Merton H. Miller erhielt den Wirtschaftsnobelpreis 1990
- ↑ vgl. American Economic Review, 1958, S. 261 ff.
- ↑ Kruschwitz, 1995, S. 217
- ↑ vgl. Mandl/Rabl, 1997, S. 346 f.
- ↑ Stewart, 1991, S. 254
- ↑ siehe Marktforschungsergebnisse in Ausgangssituation