Optimierung - Optimierung: Unterschied zwischen den Versionen
| Zeile 520: | Zeile 520: | ||
Die Gleichung <math display="inline">x^2 = y</math> hat natürlich zwei Lösungen:<br> | Die Gleichung <math display="inline">x^2 = y</math> hat natürlich zwei Lösungen:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
\(\mathbit{x}_\mathbf{1}=\sqrt\mathbit{y}\) und \(\mathbit{x}_\mathbf{2}=-\sqrt\mathbit{y}\) | \(\mathbit{x}_\mathbf{1}=\sqrt\mathbit{y}\) und \(\mathbit{x}_\mathbf{2}=-\sqrt\mathbit{y}\) | ||
\end{ | \end{aligned}</math> Dementsprechend ist die Umkehrabbildung über ganz <math display="inline">\mathbb{R}</math> nicht eindeutig definierbar, sehr wohl aber für <math display="inline">\mathbit{x}\in\mathbb{R}^+</math> (strichpunktiert) bzw. <math display="inline">\mathbit{x}\in\mathbb{R}^-</math> (strichliert). Aufgabe 3:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
f_1^\prime(x)=-2x\mathbit{exp}{(}-x^2) | f_1^\prime(x)=-2x\mathbit{exp}{(}-x^2) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
f_2^\prime(x)=\left(\frac{\mathbit{sin}{x}}{\mathbit{cos}{x}}\right)^\prime=1+{\mathbit{tan}}^2{(}x)=\frac{1}{{\mathbit{cos}}^2{(}x)} | f_2^\prime(x)=\left(\frac{\mathbit{sin}{x}}{\mathbit{cos}{x}}\right)^\prime=1+{\mathbit{tan}}^2{(}x)=\frac{1}{{\mathbit{cos}}^2{(}x)} | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
f_3^\prime\left(x\right)=\frac{3x^2}{2\sqrt{1+x^3}} | f_3^\prime\left(x\right)=\frac{3x^2}{2\sqrt{1+x^3}} | ||
\end{ | \end{aligned}</math> Aufgabe 4:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
\int_{\mathbit{x}=1}^{2}\lambda\mathrm{\ exp}\left(-\lambda\mathbit{x}\right)\ dx=\mathrm{\ \ }-\left.\mathrm{\ exp}\left(-\lambda\mathbit{x}\right)\right|_1^2=\ e^{-\lambda}-e^{\mathrm{-2}\lambda} | \int_{\mathbit{x}=1}^{2}\lambda\mathrm{\ exp}\left(-\lambda\mathbit{x}\right)\ dx=\mathrm{\ \ }-\left.\mathrm{\ exp}\left(-\lambda\mathbit{x}\right)\right|_1^2=\ e^{-\lambda}-e^{\mathrm{-2}\lambda} | ||
\end{ | \end{aligned}</math> | ||
Aufgabe 5:<br> | Aufgabe 5:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
x_2=0-\frac{p^\prime(0)}{p^\pprime(0)} \\\ | x_2=0-\frac{p^\prime(0)}{p^\pprime(0)} \\\ | ||
x_3=\frac{1}{2}-\frac{p^\prime\left(1/2\right)}{p^\prime\left(1/2\right)}= | x_3=\frac{1}{2}-\frac{p^\prime\left(1/2\right)}{p^\prime\left(1/2\right)}= | ||
\frac{1}{2}-\frac{1}{32}=\mathrm{0.4688} | \frac{1}{2}-\frac{1}{32}=\mathrm{0.4688} | ||
\end{ | \end{aligned}</math> Vergleicht man diesen Wert mit der tatsächlichen Stelle des lokalen Minimums <math display="inline">x = 0.4691</math>, so erkennt man, wie nahe das Newton Verfahren bereits nach zwei Iterationen gekommen ist. | ||
Aufgabe 6:<br> | Aufgabe 6:<br> | ||
| Zeile 553: | Zeile 553: | ||
Eigenvektoren: (1,2,-3)T , (-4,3,1)T und (2,4,3) T<br> | Eigenvektoren: (1,2,-3)T , (-4,3,1)T und (2,4,3) T<br> | ||
Aufgabe 7:<br> | Aufgabe 7:<br> | ||
a) <math display="block">\begin{ | a) <math display="block">\begin{aligned} | ||
\nabla f_1\left(x,y,z\right)=\left(\begin{matrix}4-4x\\6-2y\\-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) | \nabla f_1\left(x,y,z\right)=\left(\begin{matrix}4-4x\\6-2y\\-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> Kandidat für Extremum: <math display="inline">x=1, y=3, z=0</math> <math display="block">\begin{aligned} | ||
H_{f_1}\left(x,y,z\right)=\left(\begin{matrix}-4&0&0\\0&-2&0\\0&0&-2\\\end{matrix}\right) | H_{f_1}\left(x,y,z\right)=\left(\begin{matrix}-4&0&0\\0&-2&0\\0&0&-2\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> negativ definit ⇒ (1,3,0)T ist ein lokales Maximum | ||
b) <math display="block">\begin{ | b) <math display="block">\begin{aligned} | ||
\nabla f_2\left(x,y,z\right)=\left(\begin{matrix}6x-4y\\6y-4x\\10-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) | \nabla f_2\left(x,y,z\right)=\left(\begin{matrix}6x-4y\\6y-4x\\10-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> Kandidat für Extremum: <math display="inline">x=0, y=0, z=5</math><br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
H_{f_2}\left(x,y,z\right)=\left(\begin{matrix}6&-4&0\\-4&6&0\\0&0&-2\\\end{matrix}\right) | H_{f_2}\left(x,y,z\right)=\left(\begin{matrix}6&-4&0\\-4&6&0\\0&0&-2\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> ist indefinit (Eigenwerte -2, 2 und 10) (0,0,5)T ist ein Sattelpunkt und kein lokaler Extremwert | ||
Aufgabe 8:<br> | Aufgabe 8:<br> | ||
Die Lagrange Funktion lautet: <math display="block">\begin{ | Die Lagrange Funktion lautet: <math display="block">\begin{aligned} | ||
L\left(x,y\right)=x^2+y^2+\lambda\left(x^2+xy+y^2-3\right) | L\left(x,y\right)=x^2+y^2+\lambda\left(x^2+xy+y^2-3\right) | ||
\end{ | \end{aligned}</math> | ||
Null setzen der partiellen Ableitungen gibt <math display="block">\begin{ | Null setzen der partiellen Ableitungen gibt <math display="block">\begin{aligned} | ||
\frac{\partial}{\partial x}L\left(x,y\right)=2x+\lambda\left(2x+y\right)=0 \\\ | \frac{\partial}{\partial x}L\left(x,y\right)=2x+\lambda\left(2x+y\right)=0 \\\ | ||
\frac{\partial}{\partial y}L\left(x,y\right)=2y+\lambda\left(2y+x\right)=0 | \frac{\partial}{\partial y}L\left(x,y\right)=2y+\lambda\left(2y+x\right)=0 | ||
\end{ | \end{aligned}</math> | ||
Addieren wir diese beiden Gleichungen so erhalten wir <math display="block">\begin{ | Addieren wir diese beiden Gleichungen so erhalten wir <math display="block">\begin{aligned} | ||
2\left(x+y\right)+\lambda\left(3x+3y\right)=0 | 2\left(x+y\right)+\lambda\left(3x+3y\right)=0 | ||
\end{ | \end{aligned}</math> oder äquivalent dazu <math display="block">\begin{aligned} | ||
\left(x+y\right)\left(2+3\lambda\right)=0 | \left(x+y\right)\left(2+3\lambda\right)=0 | ||
\end{ | \end{aligned}</math> Das bedeutet entweder der erste Faktor oder der zweite Faktor verschwindet. | ||
Fall1: <math display="inline">x+y=0, d.h. y = -x</math>.<br> | Fall1: <math display="inline">x+y=0, d.h. y = -x</math>.<br> | ||
Die Nebenbedingung lautet dann <math display="block">\begin{ | Die Nebenbedingung lautet dann <math display="block">\begin{aligned} | ||
g\left(x,-x\right)=x^2=3 | g\left(x,-x\right)=x^2=3 | ||
\end{ | \end{aligned}</math> Und wir erhalten die beiden Lösungen <math display="inline">x=\sqrt3,y=-\sqrt3 \: x=-\sqrt3,y=\sqrt3</math><br> | ||
Fall2: <math display="inline">2+3\lambda = 0, d.h. \lambda = -2/3</math>.<br> | Fall2: <math display="inline">2+3\lambda = 0, d.h. \lambda = -2/3</math>.<br> | ||
Die erste Gleichung lautet <math display="block">\begin{ | Die erste Gleichung lautet <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial x}=2x-\frac{2}{3}\left(2x+y\right)=0 | \frac{\partial L}{\partial x}=2x-\frac{2}{3}\left(2x+y\right)=0 | ||
\end{ | \end{aligned}</math> und daher <math display="inline">x = y</math>. Die Nebenbedingung wird zu <math display="block">\begin{aligned} | ||
g\left(x,x\right)=3x^2=3 | g\left(x,x\right)=3x^2=3 | ||
\end{ | \end{aligned}</math> und wir erhalten die beiden Lösungen <math display="inline">x=-\sqrt3,y=\sqrt3 \: x=-1,y=-1</math> | ||
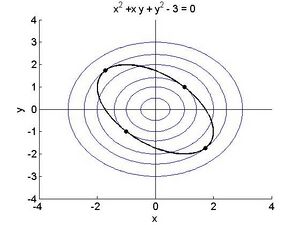
Vergleichen wir die Funktionswerte: <math display="inline">f\left(\sqrt3,-\sqrt3\right)=f\left(-\sqrt3,\sqrt3\right)=6 \: f\left(1,1\right)=f\left(-1,-1\right)=2</math> Die ersten beiden Punkte liefern jeweils ein Maximum, die zweiten Punkte ein Minimum unter der Nebenbedingung. Die folgende Abbildung veranschaulicht die Zusammenhänge. | Vergleichen wir die Funktionswerte: <math display="inline">f\left(\sqrt3,-\sqrt3\right)=f\left(-\sqrt3,\sqrt3\right)=6 \: f\left(1,1\right)=f\left(-1,-1\right)=2</math> Die ersten beiden Punkte liefern jeweils ein Maximum, die zweiten Punkte ein Minimum unter der Nebenbedingung. Die folgende Abbildung veranschaulicht die Zusammenhänge. | ||
| Zeile 599: | Zeile 599: | ||
Die konzentrischen Kreise geben einige Niveaulinien der Zielfunktion <math display="inline">f\left(x,y\right)=x^2+y^2</math> . Beachte wiederum wie an den 4 extremalen Punkten die Kurve der Nebenbedingungen dazu tangential liegt. | Die konzentrischen Kreise geben einige Niveaulinien der Zielfunktion <math display="inline">f\left(x,y\right)=x^2+y^2</math> . Beachte wiederum wie an den 4 extremalen Punkten die Kurve der Nebenbedingungen dazu tangential liegt. | ||
Aufgabe 9: Die Lagrange Funktion lautet <math display="block">\begin{ | Aufgabe 9: Die Lagrange Funktion lautet <math display="block">\begin{aligned} | ||
L\left(x,y\right)=x^2+y+1+\lambda\left(x+y-4\right) | L\left(x,y\right)=x^2+y+1+\lambda\left(x+y-4\right) | ||
\end{ | \end{aligned}</math> Null setzen der partiellen Ableitungen gibt <math display="block">\begin{aligned} | ||
\frac{\partial}{\partial x}L\left(x,y\right)=2x+\lambda=0 \\\ | \frac{\partial}{\partial x}L\left(x,y\right)=2x+\lambda=0 \\\ | ||
\frac{\partial}{\partial y}L\left(x,y\right)=1+\lambda=0 | \frac{\partial}{\partial y}L\left(x,y\right)=1+\lambda=0 | ||
\end{ | \end{aligned}</math> und von den KKT Bedingungen <math display="block">\begin{aligned} | ||
\lambda\left(x+y-4\right)=0 | \lambda\left(x+y-4\right)=0 | ||
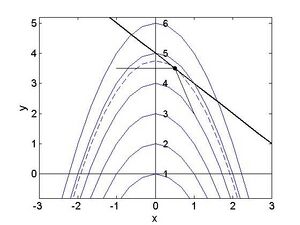
\end{ | \end{aligned}</math> Im Inneren des zulässigen Bereiches muss gelten <math display="inline">\lambda=0</math>, und daher wird die zweite Gleichung oben zu <math display="inline">1=0</math>, offensichtlich ein Widerspruch, Für <math display="inline">\lambda<0</math> muss gelten liefert die zweite Gleichung <math display="inline">\lambda=-1</math>, und daher die erste Gleichung <math display="inline">\lambda\left(x+y-4\right)=0</math>. Die KKT Bedingung gibt <math display="inline">\left(x+y-4\right)=0</math>, und daher <math display="inline">\left(x+y-4\right)=0</math>. Der Punkt <math display="inline">(1/2, 7/2)</math> ist somit eine potentielle lokale Extremstelle, um zu erkennen worum es sich tatsächlich handelt betrachte folgende Abbildung, die wiederum die Niveaulinien der Zielfunktion sowie den Rand des zulässigen Bereichs zeigt. | ||
[[Datei:A9.jpg|300px|none|thumb]] | [[Datei:A9.jpg|300px|none|thumb]] | ||
| Zeile 617: | Zeile 617: | ||
Aufgabe 1.1:<br> | Aufgabe 1.1:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
f\left(x\right)=x^{\mathrm{exp}\left(x\right)}=\mathrm{exp}\left[\mathrm{log}\left(x\right)e^x\right] \\\ | f\left(x\right)=x^{\mathrm{exp}\left(x\right)}=\mathrm{exp}\left[\mathrm{log}\left(x\right)e^x\right] \\\ | ||
f^\prime\left(x\right)=\mathrm{exp}\left[\mathrm{log}\left(x\right)e^x\right]. \left[\frac{1}{x}e^x+\mathrm{log} \left(x\right)e^x\right] = \\\ | f^\prime\left(x\right)=\mathrm{exp}\left[\mathrm{log}\left(x\right)e^x\right]. \left[\frac{1}{x}e^x+\mathrm{log} \left(x\right)e^x\right] = \\\ | ||
x^{\mathrm{exp}\left(x\right)}\left[\frac{1}{x}e^x+\mathrm{log} \left(x\right)e^x\right] | x^{\mathrm{exp}\left(x\right)}\left[\frac{1}{x}e^x+\mathrm{log} \left(x\right)e^x\right] | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
f^\prime\left(x\right)=\frac{\left(3x-2\right)\left(2x+\frac{1}{2\sqrt x}\right)-3\left(x^2+\sqrt x\right)}{(3x-2)^2} | f^\prime\left(x\right)=\frac{\left(3x-2\right)\left(2x+\frac{1}{2\sqrt x}\right)-3\left(x^2+\sqrt x\right)}{(3x-2)^2} | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
f^\prime\left(x\right)=\frac{1}{\sqrt{2x}}\mathrm{cos}\left(x^2\right)-\sqrt x\mathrm{sin}x^22x | f^\prime\left(x\right)=\frac{1}{\sqrt{2x}}\mathrm{cos}\left(x^2\right)-\sqrt x\mathrm{sin}x^22x | ||
\end{ | \end{aligned}</math> | ||
Aufgabe 1.2:<br> | Aufgabe 1.2:<br> | ||
| Zeile 637: | Zeile 637: | ||
Aufgabe 1.3<br> | Aufgabe 1.3<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
f\left(x\right)=\frac{1}{3}e^{3x+4} \: (Substitution\: y = 3x+4) | f\left(x\right)=\frac{1}{3}e^{3x+4} \: (Substitution\: y = 3x+4) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
f(x)=(x^2\mathrm{log}(x^2)-x^2)/2 \: (Substitution\: y = x^2\: und \: partielle \:Integration) | f(x)=(x^2\mathrm{log}(x^2)-x^2)/2 \: (Substitution\: y = x^2\: und \: partielle \:Integration) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
f\left(x\right)=-\frac{1}{4}\mathrm{cos}\left(4x-3\right) \: (Substitution\: y = 4x-3) | f\left(x\right)=-\frac{1}{4}\mathrm{cos}\left(4x-3\right) \: (Substitution\: y = 4x-3) | ||
\end{ | \end{aligned}</math> | ||
Aufgabe 1.4<br> | Aufgabe 1.4<br> | ||
Berechnung der Integrale <math display="block">\begin{ | Berechnung der Integrale <math display="block">\begin{aligned} | ||
-\left(x^2+2x+2\right)e^{-x}|_0^1=2-5e^{-1} | -\left(x^2+2x+2\right)e^{-x}|_0^1=2-5e^{-1} | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
x\left(\mathrm{log}\left(\sfrac{x}{2}\right)-1\right)|_1^2=\mathrm{log}2-1 | x\left(\mathrm{log}\left(\sfrac{x}{2}\right)-1\right)|_1^2=\mathrm{log}2-1 | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
\int_{x=2}^{3}\left(3-x\right)+\int_{x=3}^{4}\left(x-3\right)\mathrm{dx}=1 | \int_{x=2}^{3}\left(3-x\right)+\int_{x=3}^{4}\left(x-3\right)\mathrm{dx}=1 | ||
\end{ | \end{aligned}</math> | ||
Aufgabe 1.5<br> | Aufgabe 1.5<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
D=\left\{\left(x,y\right)\in R^2:x^2>y^2\right\}=\left\{\left(x,y\right):\left|x\right|>\left|y\right|\right\} \\\ | D=\left\{\left(x,y\right)\in R^2:x^2>y^2\right\}=\left\{\left(x,y\right):\left|x\right|>\left|y\right|\right\} \\\ | ||
\mathrm{\nabla f}=\frac{1}{x^2-y^2}\left(\begin{matrix}2x\\-2y\\\end{matrix}\right) , H_f=\frac{1}{\left(x^2-y^2\right)^2}\left(\begin{matrix}-2\left(x^2+y^2\right)&4\mathrm{xy}\\4\mathrm{xy}&-2\left(x^2+y^2\right)\\\end{matrix}\right) | \mathrm{\nabla f}=\frac{1}{x^2-y^2}\left(\begin{matrix}2x\\-2y\\\end{matrix}\right) , H_f=\frac{1}{\left(x^2-y^2\right)^2}\left(\begin{matrix}-2\left(x^2+y^2\right)&4\mathrm{xy}\\4\mathrm{xy}&-2\left(x^2+y^2\right)\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
D=\left\{\left(x,y\right)\in\mathbb{R}^2:x\neq y\right\} | D=\left\{\left(x,y\right)\in\mathbb{R}^2:x\neq y\right\} | ||
\mathrm{\nabla f}=\frac{1}{(x-y)^2}\left(\begin{matrix}-y^2\\x^2\\\end{matrix}\right), H_f=\frac{1}{(x-y)^3}\left(\begin{matrix}2y^2&-2\mathrm{xy}\\-2\mathrm{xy}&2x^2\\\end{matrix}\right) | \mathrm{\nabla f}=\frac{1}{(x-y)^2}\left(\begin{matrix}-y^2\\x^2\\\end{matrix}\right), H_f=\frac{1}{(x-y)^3}\left(\begin{matrix}2y^2&-2\mathrm{xy}\\-2\mathrm{xy}&2x^2\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
D=R^3 (keine Einschränkungen) \\\ | D=R^3 (keine Einschränkungen) \\\ | ||
\mathrm{\nabla f}=\left(\begin{matrix}\mathrm{yz}+2\mathrm{xy}+z^2\\\mathrm{xz}+x^2+2\mathrm{yz} \\\mathrm{xy}+y^2+2\mathrm{xz} \\\end{matrix}\right), H_f=\left(\begin{matrix}2y&2x+z&y+2z\\2x+z&2z&x+2z\\y+2z&x+2z&2x\\\end{matrix}\right) | \mathrm{\nabla f}=\left(\begin{matrix}\mathrm{yz}+2\mathrm{xy}+z^2\\\mathrm{xz}+x^2+2\mathrm{yz} \\\mathrm{xy}+y^2+2\mathrm{xz} \\\end{matrix}\right), H_f=\left(\begin{matrix}2y&2x+z&y+2z\\2x+z&2z&x+2z\\y+2z&x+2z&2x\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> | ||
Aufgabe 2.1:<br>=( | Aufgabe 2.1:<br>=( | ||
| Zeile 929: | Zeile 929: | ||
<br> | <br> | ||
Aufgabe 2.3:<br> | Aufgabe 2.3:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
\mathrm{\nabla f}=\left(\begin{matrix}4x^3\\4y^3\\\end{matrix}\right), H_f=\left(\begin{matrix}\mathrm{12}x^2&0\\0&\mathrm{12}y^2\\\end{matrix}\right) , {\vec{x}}_1=\left(\begin{matrix}1\\1\\\end{matrix}\right) \\ | \mathrm{\nabla f}=\left(\begin{matrix}4x^3\\4y^3\\\end{matrix}\right), H_f=\left(\begin{matrix}\mathrm{12}x^2&0\\0&\mathrm{12}y^2\\\end{matrix}\right) , {\vec{x}}_1=\left(\begin{matrix}1\\1\\\end{matrix}\right) \\ | ||
\end{ | \end{aligned}</math> 1. Schritt: <math display="block">\begin{aligned} | ||
\mathrm{\nabla f}\left({\vec{x}}_1\right)=\left(\begin{matrix}4\\4\\\end{matrix}\right), H_f\left({\vec{x}}_1\right)=\left(\begin{matrix}\mathrm{12}&0\\0&\mathrm{12}\\\end{matrix}\right) | \mathrm{\nabla f}\left({\vec{x}}_1\right)=\left(\begin{matrix}4\\4\\\end{matrix}\right), H_f\left({\vec{x}}_1\right)=\left(\begin{matrix}\mathrm{12}&0\\0&\mathrm{12}\\\end{matrix}\right) | ||
{\vec{x}}_2=\left(\begin{matrix}1\\1\\\end{matrix}\right)-\left(\begin{matrix}\sfrac{1}{\mathrm{12}}&0\\0&\sfrac{1}{\mathrm{12}}\\\end{matrix}\right)\left(\begin{matrix}4\\4\\\end{matrix}\right)=\left(\begin{matrix}\sfrac{2}{3}\\\sfrac{2}{3}\\\end{matrix}\right) | {\vec{x}}_2=\left(\begin{matrix}1\\1\\\end{matrix}\right)-\left(\begin{matrix}\sfrac{1}{\mathrm{12}}&0\\0&\sfrac{1}{\mathrm{12}}\\\end{matrix}\right)\left(\begin{matrix}4\\4\\\end{matrix}\right)=\left(\begin{matrix}\sfrac{2}{3}\\\sfrac{2}{3}\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> 2. Schritt: <math display="block">\begin{aligned} | ||
\mathrm{\nabla f}\left({\vec{x}}_2\right)=\left(\begin{matrix}\sfrac{\mathrm{32}}{\mathrm{27}}\\\sfrac{\mathrm{32}}{\mathrm{27}}\\\end{matrix}\right), H_f\left({\vec{x}}_1\right)=\left(\begin{matrix}\sfrac{\mathrm{16}}{3}&0\\0&\sfrac{\mathrm{16}}{3}\\\end{matrix}\right) | \mathrm{\nabla f}\left({\vec{x}}_2\right)=\left(\begin{matrix}\sfrac{\mathrm{32}}{\mathrm{27}}\\\sfrac{\mathrm{32}}{\mathrm{27}}\\\end{matrix}\right), H_f\left({\vec{x}}_1\right)=\left(\begin{matrix}\sfrac{\mathrm{16}}{3}&0\\0&\sfrac{\mathrm{16}}{3}\\\end{matrix}\right) | ||
{\vec{x}}_3=\left(\begin{matrix}\sfrac{2}{3}\\\sfrac{2}{3}\\\end{matrix}\right)-\left(\begin{matrix}\sfrac{3}{\mathrm{16}}&0\\0&\sfrac{3}{\mathrm{16}}\\\end{matrix}\right)\left(\begin{matrix}\sfrac{\mathrm{32}}{\mathrm{27}}\\\sfrac{\mathrm{32}}{\mathrm{27}}\\\end{matrix}\right)=\left(\begin{matrix}\sfrac{4}{9}\\\sfrac{4}{9}\\\end{matrix}\right) | {\vec{x}}_3=\left(\begin{matrix}\sfrac{2}{3}\\\sfrac{2}{3}\\\end{matrix}\right)-\left(\begin{matrix}\sfrac{3}{\mathrm{16}}&0\\0&\sfrac{3}{\mathrm{16}}\\\end{matrix}\right)\left(\begin{matrix}\sfrac{\mathrm{32}}{\mathrm{27}}\\\sfrac{\mathrm{32}}{\mathrm{27}}\\\end{matrix}\right)=\left(\begin{matrix}\sfrac{4}{9}\\\sfrac{4}{9}\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> 3. Schritt: <math display="block">\begin{aligned} | ||
\mathrm{\nabla f}\left({\vec{x}}_3\right)=\left(\begin{matrix}\sfrac{4^4}{9^3}\\\sfrac{4^4}{9^3}\\\end{matrix}\right), H_f\left({\vec{x}}_1\right)=\left(\begin{matrix}\sfrac{4^3}{3^3}&0\\0&\sfrac{4^3}{3^3}\\\end{matrix}\right) | \mathrm{\nabla f}\left({\vec{x}}_3\right)=\left(\begin{matrix}\sfrac{4^4}{9^3}\\\sfrac{4^4}{9^3}\\\end{matrix}\right), H_f\left({\vec{x}}_1\right)=\left(\begin{matrix}\sfrac{4^3}{3^3}&0\\0&\sfrac{4^3}{3^3}\\\end{matrix}\right) | ||
{\vec{x}}_4=\left(\begin{matrix}\sfrac{4}{9}\\\sfrac{4}{9}\\\end{matrix}\right)-\left(\begin{matrix}\sfrac{3^3}{4^3}&0\\0&\sfrac{3^3}{4^3}\\\end{matrix}\right)\left(\begin{matrix}\sfrac{4^4}{9^3}\\\sfrac{4^4}{9^3}\\\end{matrix}\right)=\left(\begin{matrix}\sfrac{8}{\mathrm{27}}\\\sfrac{8}{\mathrm{27}}\\\end{matrix}\right) | {\vec{x}}_4=\left(\begin{matrix}\sfrac{4}{9}\\\sfrac{4}{9}\\\end{matrix}\right)-\left(\begin{matrix}\sfrac{3^3}{4^3}&0\\0&\sfrac{3^3}{4^3}\\\end{matrix}\right)\left(\begin{matrix}\sfrac{4^4}{9^3}\\\sfrac{4^4}{9^3}\\\end{matrix}\right)=\left(\begin{matrix}\sfrac{8}{\mathrm{27}}\\\sfrac{8}{\mathrm{27}}\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math> Das globale Minimum ist offensichtlich der Punkt <math display="inline">(0,0)</math>, und man erkennt bereits nach drei Schritten, dass das Newton-Verfahren in diese Richtung konvergiert. Man kann weiters vermuten, dass allgemein gelten wird <math display="block">\begin{aligned} | ||
{\vec{x}}_{k+1}=\left(\begin{matrix}\sfrac{2^k}{3^k}\\\sfrac{2^k}{3^k}\\\end{matrix}\right) | {\vec{x}}_{k+1}=\left(\begin{matrix}\sfrac{2^k}{3^k}\\\sfrac{2^k}{3^k}\\\end{matrix}\right) | ||
\end{ | \end{aligned}</math><br> | ||
<br> | <br> | ||
<br> | <br> | ||
Aufgabe 2.4:<br> | Aufgabe 2.4:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
L=4x+3y+\lambda\left(x^2+y^2-1\right) | L=4x+3y+\lambda\left(x^2+y^2-1\right) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial x}=4+2x\lambda=0 | \frac{\partial L}{\partial x}=4+2x\lambda=0 | ||
\end{ | \end{aligned}</math> Multipliziere mit -x <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial y}=3+2y\lambda=0 | \frac{\partial L}{\partial y}=3+2y\lambda=0 | ||
\end{ | \end{aligned}</math> Multipliziere mit y <math display="block">\begin{aligned} | ||
4y-3x = 0, \: oder\: y=\frac{3}{4}x | 4y-3x = 0, \: oder\: y=\frac{3}{4}x | ||
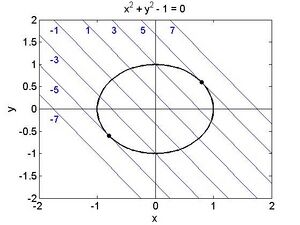
\end{ | \end{aligned}</math> Nebenbedingung: <math display="inline">x^2+y^2=1</math> Zwei Lösungen<br> | ||
<math display="inline">(4/5, 3/5)</math> ist Maximum (Funktionswert 5)<br> | <math display="inline">(4/5, 3/5)</math> ist Maximum (Funktionswert 5)<br> | ||
<math display="inline">(-4/5, -3/5)</math> ist Minimum (Funktionswert -5) | <math display="inline">(-4/5, -3/5)</math> ist Minimum (Funktionswert -5) | ||
| Zeile 960: | Zeile 960: | ||
[[Datei:W2 4.jpg|300px|none|thumb]] | [[Datei:W2 4.jpg|300px|none|thumb]] | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
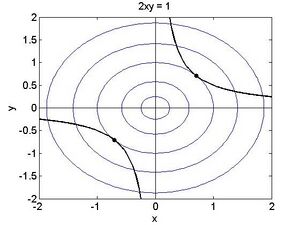
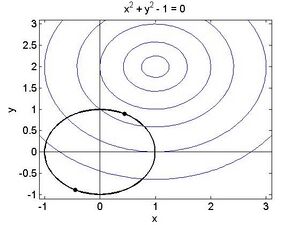
L=x^2+y^2+\lambda\left(2\mathrm{xy}-1\right) | L=x^2+y^2+\lambda\left(2\mathrm{xy}-1\right) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial x}=2x+2y\lambda=0 | \frac{\partial L}{\partial x}=2x+2y\lambda=0 | ||
\end{ | \end{aligned}</math> Multipliziere mit x <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial y}=2y+2x\lambda=0 | \frac{\partial L}{\partial y}=2y+2x\lambda=0 | ||
\end{ | \end{aligned}</math> Multipliziere mit -y <math display="block">\begin{aligned} | ||
2x^2-2y^2=0 | 2x^2-2y^2=0 | ||
\end{ | \end{aligned}</math> Nebenbedingung: <math display="inline">y=\frac{1}{2x}</math> <math display="block">\begin{aligned} | ||
x^4=\frac{1}{4} | x^4=\frac{1}{4} | ||
\end{ | \end{aligned}</math> | ||
Zwei reelle Lösungen:<br> | Zwei reelle Lösungen:<br> | ||
| Zeile 978: | Zeile 978: | ||
[[Datei:W2 4a.jpg|300px|none|thumb]] | [[Datei:W2 4a.jpg|300px|none|thumb]] | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
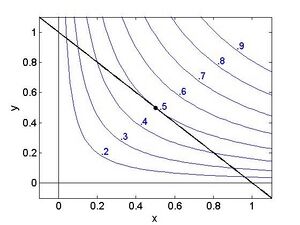
L=\mathrm{exp}(xy)+\lambda(x+y-1) | L=\mathrm{exp}(xy)+\lambda(x+y-1) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial x}=y\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 | \frac{\partial L}{\partial x}=y\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
\frac{\partial L}{\partial y}=x\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 | \frac{\partial L}{\partial y}=x\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 | ||
\end{ | \end{aligned}</math> Bilde Differenz der beiden <math display="block">\begin{aligned} | ||
\left(x-y\right)\mathrm{exp}xy=0 | \left(x-y\right)\mathrm{exp}xy=0 | ||
\end{ | \end{aligned}</math> also <math display="inline">x = y</math> Nebenbedingung: <math display="inline">x+y=1</math><br> | ||
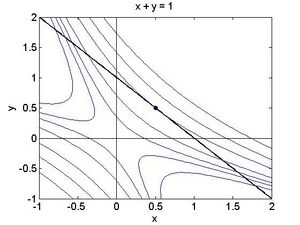
Eindeutige Lösung <math display="inline">x = y = 1/2</math> mit Funktionswert <math display="block">\begin{ | Eindeutige Lösung <math display="inline">x = y = 1/2</math> mit Funktionswert <math display="block">\begin{aligned} | ||
\mathrm{exp}\left(\frac{1}{4}\right) | \mathrm{exp}\left(\frac{1}{4}\right) | ||
\end{ | \end{aligned}</math> | ||
Die Zeichnung zeigt, dass es sich wiederum um ein Minimum handelt: | Die Zeichnung zeigt, dass es sich wiederum um ein Minimum handelt: | ||
| Zeile 995: | Zeile 995: | ||
[[Datei:W2 4b.jpg|300px|none|thumb]] | [[Datei:W2 4b.jpg|300px|none|thumb]] | ||
Die Werte in der Zeichnung geben den Logarithmus der Wurzel der entsprechende Wertes der Funktion an. Z. Bsp ist das Minimum der Funktion unter der Nebenbedingung gegeben durch <math display="block">\begin{ | Die Werte in der Zeichnung geben den Logarithmus der Wurzel der entsprechende Wertes der Funktion an. Z. Bsp ist das Minimum der Funktion unter der Nebenbedingung gegeben durch <math display="block">\begin{aligned} | ||
f\left(0\mathrm{.}5,0\mathrm{.}5\right)=\mathrm{exp}(0.5^2) | f\left(0\mathrm{.}5,0\mathrm{.}5\right)=\mathrm{exp}(0.5^2) | ||
\end{ | \end{aligned}</math> | ||
Aufgabe 2.5:<br> | Aufgabe 2.5:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
L=(x-1)^2+(y-2)^2-1+\lambda(x^2+y^2-1) | L=(x-1)^2+(y-2)^2-1+\lambda(x^2+y^2-1) | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
KKT: \frac{\partial L}{\partial x}=2\left(x-1\right)+2x\lambda=0 \\\ \frac{\partial L}{\partial y}=2\left(y-2\right)+2y\lambda=0 \\\ | KKT: \frac{\partial L}{\partial x}=2\left(x-1\right)+2x\lambda=0 \\\ \frac{\partial L}{\partial y}=2\left(y-2\right)+2y\lambda=0 \\\ | ||
\lambda\left(x^2+y^2-1\right)=0 \:(Comp.\: Slack.) | \lambda\left(x^2+y^2-1\right)=0 \:(Comp.\: Slack.) | ||
\end{ | \end{aligned}</math> Fall 1:<br> | ||
<math display="inline">\lambda=0</math> (Lösung im inneren des zulässigen Bereichs)<br> | <math display="inline">\lambda=0</math> (Lösung im inneren des zulässigen Bereichs)<br> | ||
<math display="inline">x = 1</math> und <math display="inline">y = 2</math> einzige formale Lösung, liegt nicht im zulässigen Bereich!<br> | <math display="inline">x = 1</math> und <math display="inline">y = 2</math> einzige formale Lösung, liegt nicht im zulässigen Bereich!<br> | ||
| Zeile 1.011: | Zeile 1.011: | ||
<math display="inline">x^2+y^2-1=0</math> (Lösung am Rand)<br> | <math display="inline">x^2+y^2-1=0</math> (Lösung am Rand)<br> | ||
<math display="inline">\left(x-1\right)y-\left(y-2\right)x=2x-y=0</math>, also <math display="inline">2x = y</math> (ähnlich wie in Aufgabe 2.4)<br> | <math display="inline">\left(x-1\right)y-\left(y-2\right)x=2x-y=0</math>, also <math display="inline">2x = y</math> (ähnlich wie in Aufgabe 2.4)<br> | ||
Einsetzen in NB liefert zwei Lösungen: <math display="block">\begin{ | Einsetzen in NB liefert zwei Lösungen: <math display="block">\begin{aligned} | ||
\left(\frac{1}{\sqrt5},\frac{2}{\sqrt5}\right) \:mit\: Funktionswert \: 5 - \frac{\mathrm{10}}{\sqrt5} \: (Minimum\: unter\: NB) \\\ | \left(\frac{1}{\sqrt5},\frac{2}{\sqrt5}\right) \:mit\: Funktionswert \: 5 - \frac{\mathrm{10}}{\sqrt5} \: (Minimum\: unter\: NB) \\\ | ||
\left(-\frac{1}{\sqrt5},-\frac{2}{\sqrt5}\right) \:mit \:Funktionswert \: 5 + \frac{\mathrm{10}}{\sqrt5} \: (Maximum \:unter\: NB) | \left(-\frac{1}{\sqrt5},-\frac{2}{\sqrt5}\right) \:mit \:Funktionswert \: 5 + \frac{\mathrm{10}}{\sqrt5} \: (Maximum \:unter\: NB) | ||
\end{ | \end{aligned}</math> | ||
[[Datei:W2 5.jpg|300px|none|thumb]] | [[Datei:W2 5.jpg|300px|none|thumb]] | ||
| Zeile 1.020: | Zeile 1.020: | ||
<br> | <br> | ||
<br> | <br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
L=x^2+3\mathrm{xy}++�2+\lambdax+y-1 | L=x^2+3\mathrm{xy}++�2+\lambdax+y-1 | ||
\end{ | \end{aligned}</math> <math display="block">\begin{aligned} | ||
KKT: \frac{\partial L}{\partial x}=2x+3y+\lambda=0 \\\ | KKT: \frac{\partial L}{\partial x}=2x+3y+\lambda=0 \\\ | ||
\frac{\partial L}{\partial y}=3x+2y+\lambda=0\\\ | \frac{\partial L}{\partial y}=3x+2y+\lambda=0\\\ | ||
\lambda\left(x+y-1\right)=0 \:(Comp. \:Slack.) | \lambda\left(x+y-1\right)=0 \:(Comp. \:Slack.) | ||
\end{ | \end{aligned}</math> Fall 1:<br> | ||
<math display="inline">\lambda=0</math> (Lösung im inneren des zulässigen Bereichs)<br> | <math display="inline">\lambda=0</math> (Lösung im inneren des zulässigen Bereichs)<br> | ||
<math display="inline">x = 0</math> und <math display="inline">y = 0</math> einzige formale Lösung, Hessematrix indefinit<br> | <math display="inline">x = 0</math> und <math display="inline">y = 0</math> einzige formale Lösung, Hessematrix indefinit<br> | ||
| Zeile 1.036: | Zeile 1.036: | ||
<math display="inline">x-y=0</math>, also <math display="inline">x = y</math> (ähnlich wie in Aufgabe 2.4)<br> | <math display="inline">x-y=0</math>, also <math display="inline">x = y</math> (ähnlich wie in Aufgabe 2.4)<br> | ||
Einsetzen in NB liefert eindeutige Lösung:<br> | Einsetzen in NB liefert eindeutige Lösung:<br> | ||
<math display="block">\begin{ | <math display="block">\begin{aligned} | ||
x = y = 1/2 | x = y = 1/2 | ||
\end{ | \end{aligned}</math> mit Funktionswert <math display="inline">5/4</math> Die Grafik zeigt, dass es sich um ein Maximum handelt: | ||
[[Datei:W2 5 a.jpg|300px|none|thumb]] | [[Datei:W2 5 a.jpg|300px|none|thumb]] | ||
Die Niveaulinien entsprechen Hyperbeln: <math display="inline">x^2+3\mathrm{xy}+2=const.</math> Je weiter man sich vom Ursprung nach rechts oben bewegt, desto größer sind die Werte die die Funktion entlang der Niveaulinie annimmt. Je weiter man sich vom Ursprung nach links oben (bzw. rechts unten) bewegt, desto kleiner sind die entsprechenden Funktionswerte. | Die Niveaulinien entsprechen Hyperbeln: <math display="inline">x^2+3\mathrm{xy}+2=const.</math> Je weiter man sich vom Ursprung nach rechts oben bewegt, desto größer sind die Werte die die Funktion entlang der Niveaulinie annimmt. Je weiter man sich vom Ursprung nach links oben (bzw. rechts unten) bewegt, desto kleiner sind die entsprechenden Funktionswerte. | ||
Version vom 23. September 2022, 16:28 Uhr
Optimierung
Ziel dieser Lektion ist es die nichtlineare Optimierung auf Funktionen mit mehreren Variablen zu erweitern. Dazu wird die Theorie der Eigenwerte aus der linearen Algebra benötigt. Neben der theoretischen Abhandlung sollen hier auch algorithmische Ansätze besprochen werden. Ein wesentlicher Punkt ist die Suche nach Extremwerten unter der Einhaltung von gewissen Nebenbedingungen. Als notwendige Kriterien werden die Lagrange–Methode sowie die Karush–Kuhn–Tucker Bedingungen besprochen.
Lokale Extrema von reellen Funktionen
Wir erinnern uns, dass für Funktionen mit einer Veränderlichen eine notwendige Bedingung für lokale Extrema darin besteht, dass die erste Ableitung verschwindet, i.e. durch Lösen der Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^\prime\left(x\right)=0}
erhält man mögliche Kandidaten für ein Maximum bzw. ein Minimum einer Funktion.
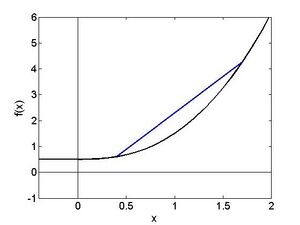
Beispiel 6: Betrachte das Polynom aus Beispiel 4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(x) = -x^4+x^3+4x^2-4x+2}
Ableitung liefert
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p^{\prime}(x)=-4 x^3+3 x^2+8 x-4}
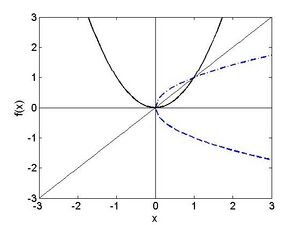
Die Suche nach Nullstellen von liefert potenzielle Kandidaten für lokale Maxima und Minima. Für ein Polynom dritten Grades gibt es geschlossene Formeln, um die Nullstellen zu bestimmen, man erhält näherungsweise
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1 = -1.3263, x_2 = 1.6073, x_3 = 0.4691}
Der Vergleich mit Abbildung [bild4 ] lässt erkennen, dass an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1}
das absolute Maximum der Funktion liegt, während es sich bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_2}
um ein lokales Minimum und bei um ein lokales Maximum handelt.
Bereits für eine solch einfache Funktion wie ein Polynom dritten Grades ist die Bestimmung der Nullstellen nicht ganz trivial. Für die meisten Funktionen ist eine explizite Lösung überhaupt nicht möglich, und man ist auf numerische Methoden angewiesen. Die wichtigste wird im folgenden Abschnitt vorgestellt:
Das Newton Verfahren
Wir wollen die Nullstelle einer Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(x)} finden. (In Zusammenhang mit den Optimierungsaufgaben dieses Kapitels ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x\right)=f^\prime\left(x\right)} die Ableitung der Funktion, deren Extremwerte gesucht werden; das Verfahren kann aber selbstverständlich für beliebige einmal differenzierbare Funktionen angewandt werden.) Das Newton-Verfahren ist ein Iterationsverfahren. Wir beginnen mit einer Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1} , die hoffentlich bereits in der Nähe der Nullstelle liegt. Grundidee ist nun die Funktion durch ihre Tangente an der Stelle zu ersetzen, und anschließend die Nullstelle der Tangente zu suchen. Die Lösung liefert den nächsten Punkt der Iteration:
Anschließend wird diese Prozedur so lange wiederholt, bis das Verfahren konvergiert, d.h. (bis auf numerische Genauigkeit) eine Nullstelle gefunden wurde. Es kann gezeigt werden, dass das Newton Verfahren extrem rasch (quadratisch) konvergiert, sobald man sich in der Nähe einer Nullstelle befindet. Die deutsche Wikipedia Seite bietet eine sehr schöne Animation, die verdeutlich wie das Newton Verfahren in der Praxis funktioniert. Um Kandidaten für lokale Extrema von zu erhalten sucht man Nullstellen der Ableitung von f, und das Iterationsverfahren hat daher die Gestalt
Das bedeutet eine Funktion muss mindestens zweimal differenzierbar sein, damit diese Methode verwendet werden kann. In der Literatur findet man eine Unzahl an weiteren Methoden zur numerischen Bestimmung von Nullstellen.
Aufgabe 5:
Berechne für das Polynom aus Beispiel 6 die ersten beiden Newtonschritte mit Startwert . Schreib ein kleines Programm in der Programmiersprache deiner Wahl. Versuche auch andere Startwerte und beobachte wie sich das Verfahren verhält.
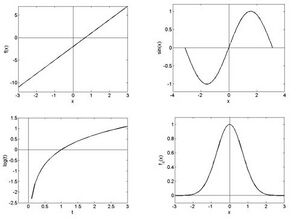
Die Bestimmung von globalen Extrema ist typischerweise wesentlich komplizierter als die Suche nach lokalen Extrema. Auch müssen diese nicht zwangsläufig existieren; die Funktion besitzt unendlich lokale Minima und Maxima, die gleichzeitig globale Extremwerte sind, die Funktion besitzt unendlich viele lokale Extremwerte, aber keinen globalen. Plotten Sie die beiden Funktionen, um sich diese Tatsache vor Augen zu führen! Für eine gewisse Klasse von Funktionen kann man jedoch von lokaler Optimalität auf globale Optimalität schließen. Speziell nennt man eine Funktion f konvex (konkav), falls die Funktionswerte zwischen zwei Werten x und y jeweils unterhalb der Verbindungsgeraden der beiden Funktionswerte an x und y – der sogenannten Sekante - liegen. D.h. für jede Zahl t zwischen 0 und 1 gilt
Abbildung 1.1 zeigt eine konvexe Funktion und deren Sekante für zwei ausgewählte Werte und . Die Sekante liegt oberhalb des Graphen der Funktion. Falls die zweite Ableitung existiert so gilt für eine konvexe Funktion
und für eine konkave Funktion
Für eine konvexe (konkave) Funktion gibt es höchstens ein lokales Extremum, und dies ist dann das globale Minimum (Maximum).
Funktionen mehrerer Veränderlicher
Um Extremwerte von Funktionen in mehreren freien Variablen zu finden ist es erforderlich, die Kriterien für Extremwerten für höherdimensionale Definitionsbereiche zu verallgemeinern. Hier werden Gradient und Hessematrix die gleichen Rollen spielen wie 1. und 2. Ableitung im Eindimensionalen. Während die Bedingung an den Gradienten – er muss gleich dem Nullvektor sein, d.h., die Richtungsableitung muss in jeder Richtung verschwinden, sich ganz unmittelbar übertragen lässt, brauchen wir für die 2. Ableitungen etwas lineare Algebra – schließlich wollen wir der Matrix ansehen, ob die 2. Richtungsableitungen in jeder Richtung positiv oder negativ sind, oder ob das Krümmungsverhalten in den verschiedenen Richtungen unterschiedlich ist.
Determinante einer Matrix
Eine nxn-Matrix A entspricht einer linearen Abbildung:
D.h., jeder Vektor aus dem wird durch die Abbildung gedreht und/oder gestreckt oder gestaucht, so dass sein Bild wieder ein Vektor aus dem ist. Nun sprengt eine ausführliche Abhandlung der linearen Funktionen den Rahmen dieses Kurses; eine Größe, die wir aber im Weiteren brauchen werden, ist die Determinante der Matrix. Sie errechnet sich für eine 2x2 Matrix
nach der Formel
für eine 3x3 Matrix
nach der Formel
(Regel von Sarrus), für höherdimensionale Matrizen mithilfe des Entwicklungssatzes und in der Praxis mit einem Algebra-Programm; Spezialfälle von Matrizen mit leicht ermittelbaren Determinanten sind Matrizen, die nur in der Diagonale Einträge ungleich 0 haben, sowie Matrizen, die entweder oberhalb oder unterhalb der Diagonale nur Nullen stehen haben; in beiden Fällen ist die Determinante das Produkt der Diagonal-Elemente. Ist die Determinante einer Matrix 0, so heißt das, dass zumindest eine Gerade von der Matrix auf den Nullvektor abgebildet wird; d.h., die Ebene wird auf eine Gerade abgebildet, der dreidimensionale Raum auf eine Ebene (oder eine Gerade) usw. Diese Eigenschaft macht man sich zunutze, um die sogenannten Eigenwerte der Matrix zu finden.
Eigenwerte und Eigenvektoren einer Matrix
Für eine Matrix A nennt man einen Vektor einen Eigenvektor zum Eigenwert , falls die sogenannte Eigenwertgleichung
erfüllt ist. Dies bedeutet, dass der Eigenvektor x durch Multiplikation mit A einfach um den Faktor gestreckt (oder gestaucht) wird, ohne dabei gedreht zu werden; ist negativ, so wird der Vektor zusätzlich noch am Koordinaten-Ursprung gespiegelt – d.h., er zeigt nun in die entgegengesetzte Richtung.
Beispiel 7:
Gegeben sei die Matrix
Es gilt
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}3&2\\-3&-4\\\end{matrix}\right)\left(\begin{matrix}2\\-1\\\end{matrix}\right)=\left(\begin{matrix}4\\-2\\\end{matrix}\right)\end{aligned}}
Somit ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}1\\-3\\\end{matrix}\right) \end{aligned}}
ein Eigenvektor zum Eigenwert -3,
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}\mathrm{\ \ }2\\-1\\\end{matrix}\right) \end{aligned}}
Eigenvektor zum Eigenwert 2.
Wie kann man Eigenwerte und Eigenvektoren berechnen? Die Eigenwertgleichung bei bekanntem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda} ist ein lineares Gleichungssystem mit Gleichungen in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} Variablen. Allerdings sind auch die Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_i} zunächst unbekannt, und müssen erst bestimmt werden: wenn ein Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}} Lösung Lösung der Eigenwertgleichung ist, so können wir diese Gleichung umformen zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(A-\lambda I\right)\vec{x}=\vec{o}} , (Hier ist I die Einheitsmatrix und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{o}} der Nullvektor.) Daher ist die Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle A-\lambda I} singulär und hat die Determinante 0 – schließlich wird ja nicht nur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}} auf den Nullvektor abgebildet, sondern auch jedes Vielfache, also die ganze Gerade, die durch diesen Vektor läuft. Es gilt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} det(A-\lambda I)=(-\lambda)^n+a_{n-1}\lambda^{n-1}+\cdots+a_1\lambda+a_0=0 \end{aligned}}
(Die Koeffizienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a_i} ergeben sich dabei aus der Berechnung der Determinante, wie weiter unten ausgeführt.) Man bezeichnet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle det\left(A-\lambda I\right)} als das charakteristische Polynom von A, die Eigenwerte sind die Nullstellen dieses Polynom. Die Suche nach allen Nullstellen erfolgt für großes n im Normalfall durch die im vorigen Abschnitt besprochenen numerischen Methoden. Für n=2 können Nullstellen sogar als Lösung einer quadratischen Gleichung unmittelbar gefunden werden, für n=3 häufig durch Erraten einer Nullstelle und anschließendes Aufspalten des Polynoms in Linearfaktoren (s. Beispiel 10).
Fortsetzung Beispiel 7:
Die charakteristische Gleichung lautetFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left|A-\lambda I\right|=\left|\begin{matrix}3-\lambda&2\\-3&-4-\lambda\\\end{matrix}\right|=\lambda^2+\lambda-6=0 \end{aligned}}
Lösen der quadratischen GleichungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda=-\frac{1}{2}\pm\sqrt{\frac{1}{4}+6}=-\frac{1}{2}\pm\frac{5}{2} \end{aligned}}
liefert die Nullstellen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_1=-3} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_2=2} .
Die zugehörigen Eigenvektoren erhält man durch Lösen der jeweiligen Eigenwertgleichungen. Beachte, dass die Eigenvektoren nur bis auf einen multiplikativen Faktor festgelegt sind.
Aufgabe 6:
Berechne alle Eigenwerte und Eigenvektoren für folgende Matrizen:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}\mathrm{\ 8}&7\\1&2\\\end{matrix}\right) \\\ B=\left(\begin{matrix}1&-1\\-1&1\\\end{matrix}\right) \\\ C=\left(\begin{matrix}1&-2&2\\-2&-2&4\\1&4&-6\\\end{matrix}\right) \end{aligned}}
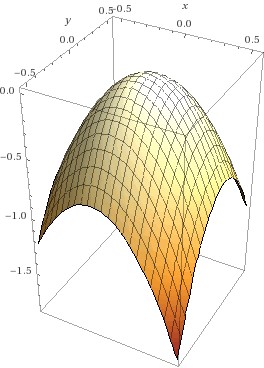
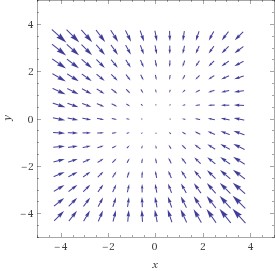
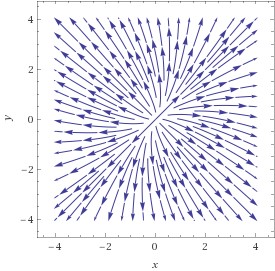
Die Theorie der Eigenwerte und Eigenvektoren spielt in vielen Anwendungsbereichen eine wesentliche Rolle . Ein Polynom n-ten Grades hat genau n Null-stellen, allerdings müssen diese nicht unbedingt verschieden sein – das Polynom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2-2x+1} hat die beiden Nullstellen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1=x_2=1} Man sagt: 1 ist eine Nullstelle mit Vielfachheit 2. Nullstellen können auch komplexe Zahlen sein. Für symmetrische Matrizen (d.h. AT = A), kann man zeigen, dass alle Eigenwerte reell sind. Zu den Eigenwerten mit Vielfachheit n gehören dann n linear unabhängige Eigenvektoren. Um uns die Bedeutung dieser Größen im Zusammenhang mit mehrdimensionalen Funktionen vor Augen zu führen, betrachten wir die AbbildungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\left(x+y\right)^2+1.5\left(x-y\right)^2 \end{aligned}}
Die linke Graphik zeigt den (ziemlich faden …) Funktionsgraphen – ein Paraboloid; die mittlere Graphik zeigt das Gradientenfeld – in jedem Punkt zeigt der Vektorpfeil in die Richtung des steilsten Anstiegs; die rechte Graphik zeigt nun die möglichen Wege einer Kugel, die wir am Scheitelpunkt absetzen: genau am Scheitelpunkt ist der Gradient null, d.h., die Richtungsableitung in jeder Richtung ist 0 und die Kugel bleibt einfach liegen. Geben wir ihr aber einen winzig kleinen Schubs, so ist der Gradient ungleich 0 und sie rollt sie nun in jedem Punkt dem Gradienten entgegen – schließlich will sie so schnell wie möglich nach unten und der Gradient zeigt den schnellsten Weg nach oben; die meisten möglichen Bahnen sind daher gekrümmt, d.h., der Gradient ändert ständig seine Richtung; es gibt allerdings zwei Richtungen, in denen die Bahnen Geraden sind – und das sind nun genau die Richtungen der Eigenvektoren der Hessematrix: in jedem Punkt auf dieser Geraden ändert sich der Gradient genau in der Richtung der Verbindung des Punktes mit dem Koordinaten-Ursprung; in unserem Fall zeigen die Pfeile auf diesen Trajektorien-Geraden jeweils vom Ursprung weg – damit ist klar: der Punkt ist ein Maximum – d.h., die Kugel wird in jeder Richtung vom Scheitel wegrollen. Das wiederum bedeutet für die Funktion, die die Höhe des Paraboloids für jeden Punkt der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x,y}
– Ebene angibt, dass ihre 2. Richtungsableitung im Scheitelpunkt in jeder Richtung negativ sein muss.
Daraus ergibt sich folgendes Kriterium für Extremalstellen: der Gradient muss dort verschwinden; sind alle Eigenwerte der Hessematrix negativ, so ist der Punkt ein Maximum, sind sie positiv, ein Minimum, gibt es sowohl positive als auch negative, so haben wir einen Sattelpunkt. Die Vorzeichen der Eigenwerte bestimmt man mit den Definitheitskriterien:
Definitheit
Wir werden in diesem Abschnitt immer davon ausgehen, dass A eine symmetrische Matrix ist. Für die Anwendung, die wir letztendlich betrachten wollen, nämlich für die Hessematrix, ist dies natürlich der Fall, da ja gilt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial^2f}{\partial x_i\partial x_j}=\frac{\partial^2f}{\partial x_j\partial x_i}. \end{aligned}}
Im Zusammenhang mit symmetrischen Matrizen sind quadratische Formen von besonderem Interesse, dabei handelt es sich um die zur Matrix A gehörende FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{matrix}q:&\mathbb{R}^n\rightarrow\mathbb{R}\\\ &\vec{x}\mapsto{\vec{x}}^TA\vec{x}\\\end{matrix} \end{aligned}}
Beispiel 8:
Gegeben sei die symmetrische MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}1&2\\2&-4\\\end{matrix}\right) \end{aligned}}
Die zu A gehörende quadratische Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q} ordnet jedem zweidimensionalen Vektor den Wert zu.
Eine quadratische Form heißt
positiv definit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} > \vec{0} }
für alle x 0
positiv semidefinit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} \geq \vec{0} }
für alle x 0
negativ definit, falls für alle x 0
negativ semidefinit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} \leq \vec{0} }
für alle x 0
indefinit, falls für einige x und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{y}}^TA\vec{y} < 0 }
für einige y.
Diese Definitheitseigenschaften stehen in unmittelbarem Zusammenhang mit den Eigenwerten der Matrix A. Man kann zeigen, eine quadratische Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}^TA\vec{x}}
ist
positiv definit, falls alle Eigenwerte > 0
positiv semidefinit, falls alle Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \geq}
0
negativ definit, falls alle Eigenwerte < 0
negativ semidefinit, falls alle Eigenwerte 0
indefinit, falls einige Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle >}
0 und einige Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle <}
0 sind.
Die dazugehörigen Matrizen werden dann ebenfalls als positiv (semi-) definit usw. bezeichnet. In der Praxis kann die Definitheit von Matrizen oft mit dem Hauptminorenkriterium bestimmt werden. Als i-ten führenden Hauptminor einer Matrix bezeichnet man die Determinante der Matrix, die man gewinnt, wenn man nur die ersten i Zeilen und Spalten betrachtet; für eine MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}a_{1,1}&\cdots&a_{1,n}\\\vdots&\ddots&\vdots\\a_{n,1}&\cdots&a_{n,n}\\\end{matrix}\right) \end{aligned}}
lauten sie also (die senkrechten Striche sind eine alternative Schreibweise für die Berechnung der Determinante der Matrix zwischen den Strichen): Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\Delta}_1(A)=a_{1,1}, \quad \tilde{\Delta}_2(A)=\left(\begin{array}{cc} a_{1,1} & a_{1,2} \\ a_{2,1} a_{2,2} \end{array}\right), \ldots, \tilde{\Delta}_n=\operatorname{det} A }
Es gilt nun: sind alle führenden Hauptminoren positiv, so ist die Matrix positiv definit; sind die Vorzeichen der führenden Hauptminoren abwechselnd positiv und negativ – beginnend mit negativ – so ist die Matrix negativ definit. Weiters ist die Determinante der Matrix das Produkt der Eigenwerte - ist also die Determinante 0, so ist die Matrix indefinit, ist sie ungleich 0, sind alle Eigenwerte ungleich 0. Viele Fälle können mit diesen Kriterien durch Ausschluss bestimmt werden; nur wenn einer oder mehrere führende Hauptminoren 0 sind, ist keine eindeutige Aussage möglich. Wir können nun allgemeine Kriterien dafür aufstellen, wann eine zweimal differenzierbare mehrdimensionale nichtlineare Funktion ein lokales Extremum aufweist. Eine notwendige Bedingung ist wie bereits erwähnt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla f}=0} .Für Funktionen in einer Variablen bedeutet das: die Ableitung verschwindet. Ist die zweite Ableitung positiv, so findet sich dort ein Minimum. Diese Bedingung für Minima lässt sich auf Funktionen in mehreren Variablen erweitern: Wenn der Gradient in einem Punkt verschwindet und die zweite Ableitung in jeder Richtung negativ ist, so handelt es sich um ein lokales Minimum. Dafür genügt es, dass die zweite Ableitung in Richtung der Eigenvektoren der Hessematrix negativ ist, d.h., dass alle Eigenwerte der Hessematrix negativ sind und diese daher negativ definit ist; analoges gilt für die Maxima.
Achtung! Ein naheliegender Irrtum: man könnte glauben, dass es reicht, wenn wir uns das Krümmungsverhalten in x und y Richtung anschaun – also die zweiten partiellen Ableitungen; das ist aber nicht der Fall: die Abbildung zeigt eine Funktion, die entlang x und der y-Achse konkav ist; trotzdem ist der Nullpunkt – in dem der Gradient verschwindet – ein Sattelpunkt – es gibt nämlich auch Richtungen, in denen die Funktion konvex ist - die Diagonalen.
Basierend auf den Definitheitseigenschaften der Hessematrix Hf gelten folgende hinreichenden Bedingungen für Extremwerte: SeiFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{\nabla f}\left({\vec{x}}_0\right)=0. \end{aligned}}
Falls Hf an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_0}
positiv definit, so hat f dort ein lokales Minimum.
Falls Hf an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_0}
negativ definit, so hat f dort ein lokales Maximum.
Falls Hf an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_0}
indefinit, so handelt es sich an der Stelle weder um ein lokales Maximum noch um ein Minimum, sondern um einen sogenannten Sattelpunkt.
Im Falle von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle H_f}
positiv semidefinit oder negativ semidefinit kann keine Aussage getroffen werden (vgl. die Situation im eindimensionalen, wenn die zweite Ableitung verschwindet).
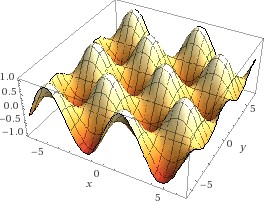
Die folgende Eierkarton-Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \sin{x\cos{y\ }}} hat Bereiche, in denen sie in jeder Richtung kokav ist – dort finden sich die Maxima, also die Gipfel - andere, in denen sie in jeder Richtung konvex ist – dort sind die Minima, also die Gruben, und weitere Beriche, in denen sie in einer Richtung konvex ist, in einer anderen konkav – dort finden sich die Sattelpunkte. Stellen sie sich einen Bewohner einer dieser Gruben vor, der eine Freundin in der benachbarten Grube besuchen möchte; dabei muss er über einen Pass wandern – und dieser Pass ist dann der Sattelpunkt.
Beispiel 9:
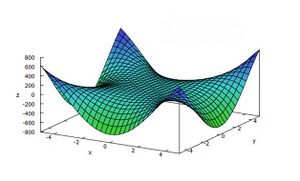
Der linke Graph in Abbildung 1.3 zeigt einen Oberflächenplot der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2-y^2}
:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{matrix}f:&\mathbb{R}^2\rightarrow\mathbb{R}\\\ &\left(x,y\right)\mapsto x^2-y^2\\\end{matrix}. \end{aligned}}
Es giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{\nabla f}\left(x,y\right)=\left(\begin{matrix}\mathrm{\ \ }2x\\-2y\\\end{matrix}\right) \end{aligned}}
und daher ist der Ursprung x=0, y=0 Kandidat für eine Extremstelle. Allerdings giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_f\left(x,y\right)=\left(\begin{matrix}2&0\\0&-2\\\end{matrix}\right) \end{aligned}}
mit den offensichtlichen Eigenwerten -2 und 2. Die Hessematrix ist indefinit, und der Ursprung ist keine Extremstelle, sondern ein Sattelpunkt. Abbildung 1.2 veranschaulicht, woher dieser Name kommt: die zweite Ableitung der Funktion in Richtung der x-Achse ist überall positiv, daher insbesondere im Punkt (0,0); ebenso ist die zweite Ableitung in Richtung der y – Achse überall negativ, d.h. der Punkt (0,0) ist ein lokales Minimum, wenn wir ihn in Richtung der x-Achse queren und ein lokales Maximum, wenn wir ihn in Richtung y – Achse überqueren. Ein lokales Minimum müsste aber in jeder Richtung Minimum sein, daher kann (0,0) keines sein, und aus dem analogen Grund ebenso wenig ein Maximum.
Aufgabe 7:
Untersuche die folgenden beiden Funktionen auf lokale Extrema:
\begin{array}{r}
f_1(x, y, z)=4 x-2 x^2+6 y-y^2-z^2+3 \\
f_2(x, y, z)=3 x^2-4 x y+3 y^2+10 z-z^2
\end{array}
Algorithmen zur Optimierung
Bisher haben wir nur notwendige und hinreichende Bedingungen für lokale Extremstellen kennen gelernt. Bereits im Eindimensionalen war die aktuelle Berechnung der Stelle nicht immer einfach. Für die in der Praxis so wichtigen Funktionen mehrerer Veränderlicher ist dieses Problem häufig um ein Vielfaches komplizierter – schließlich muss in der Iteration in jedem Schritt die Richtung, in der weitergesucht wird, neu bestimmt werden. Man ist oft auf numerische Lösungsmethoden angewiesen. Dieses Gebiet ist ein aktiver Forschungszweig, und nach wie vor sind bei weitem nicht alle Fragestellungen gelöst. Wir wollen an dieser Stelle nur zwei grundlegende Verfahren besprechen. Eine Umsetzung dieser Verfahren mithilfe von R finden Sie in den Videos auf der Homepage erläutert.
Das Newton Verfahren in mehreren Dimensionen
Das in Abschnitt davor bereits erwähnte Newton-Verfahren kann recht einfach auf mehrere Dimensionen verallgemeinert werden. Die Grundidee bleibt dabei gleich, man sucht nach Nullstellen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla f}\left(\vec{x}\right)} und ersetzt mit Hilfe dieses Gradienten die Funktion durch eine lineare Approximation. Man erhält das IterationsverfahrenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}_{k+1}={\vec{x}}_k-\left[H_f\left({\vec{x}}_k\right)\right]^{-1}\mathrm{\nabla f}\left({\vec{x}}_k\right) \end{aligned}}
Verfolgen wir die Analogie zum bekannten eindimensionalen Fall: sucht man dort einen Extremwert, so kann mithilfe des eindimensionalen Newton-Verfahrens die Nullstellen der Ableitung bestimmen; dazu wird der Wert der ersten Ableitung an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_i} durch die zweite Ableitung dividiert, dieser Quotient gibt dann an, wie weit auf der x-Achse weitergegangen werden muss. Ist die Funktion, deren Extremwert gesucht wird, eine quadratische Funktion, dann ist das Verfahren nach einem Schritt am Ziel – dann ist nämlich die Ableitung eine lineare Funktion, deren Nullstelle in einem Schritt gefunden wird; für jede andere Funktion entspricht das Newton-Verfahren dann der Approximation durch quadratische Funktionen. Formal sieht die Iterationsvorschrift im Mehrdimensionalen genauso aus wie im eindimensionalen. Allerdings approximieren wir jetzt den Gradienten durch eine lineare Funktion, und die Division durch die zweite Ableitung im eindimensionalen entspricht der Multiplikation mit der Inversen der Hessematrix. Wenn die zu optimierende Funktion eine quadratische Funktion ist, so führt das Verfahren bereits in einem Schritt zum Ziel – wie im eindimensionalen. Die Hesse-Matrix muss im Allgemeinen nach jedem Iterationsschritt für jedes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_k} neu berechnet und invertiert werden, was bei großer Dimension n recht zeitaufwendig ist. In der Praxis wird dieses Update der Hesse-Matrix daher nicht in jedem Schritt durchgeführt, dies führt zu sogenannten Quasi-Newton Verfahren . Das Newtonverfahren konvergiert äußerst rasch, sobald man sich in der Nähe eines lokalen Minimums befindet. Allerdings ist es noch schwieriger als in einer Dimension, überhaupt in die Nähe eines Minimums zu kommen. Oft werden dazu Verfahren wie das folgende verwendet, die zwar nicht so rasch konvergieren, sich dafür aber mit Sicherheit in Richtung Minimum bewegen.
Das Gradientenverfahren
Die Idee hier ist, dass zunächst eine Suchrichtung festgelegt wird, und dann in diese Richtung ein eindimensionales Optimierungsverfahren angewendet wird. Bei der Suche nach einem Minimum ist es natürlich, dass man eine Richtung sucht, in der die Werte der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} kleiner werden, eine sogenannte Abstiegsrichtung. Mathematisch gesprochen verringern sich die Werte der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(\vec{x}\right)} in Richtung des Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{d}} , fallsFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(\vec{x}+c\vec{d}\right)<f\left(\vec{x}\right) \end{aligned}}
für kleine Werte von c > 0. Dies hat zur Folge, dassFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left[\mathrm{\nabla f}\left(\vec{x}\right)\right]^T\vec{d}<0 \end{aligned}}
Das heißt wenn das innere Produkt des Gradienten mit einem Richtungsvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{d}} negativ ist, so handelt es sich um eine Abstiegsrichtung. Wie man leicht zeigen kann erfolgt der steilste Abstieg gerade in die entgegengesetzte Richtung des Gradientenvektors, d.h.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \vec{d}=-\frac{{\nabla f}(\vec{x})}{||{{\nabla f}(\vec{x})}||} \end{aligned}}
ist der normierte Vektor, der die Richtung des optimalen Abstiegs angibt. Die Idee des Gradientenverfahrens besteht nun darin, dass man wieder mit einem beliebigen Startvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_1} beginnt und die SuchtrichtungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \vec{d_1}=-\frac{{\nabla f}(\vec{x_1})}{||{{\nabla f}(\vec{x_1})}||} \end{aligned}}
festlegt. (Für die Rechnung einfacher und im Ergebnis äquivalent ist es, wenn der Vektor nicht normiert wird; es ist zwar dann kein Richtungsvektor mehr – aber der nächste Iterationspunkt ist genau derselbe.) Definiere die eindimensionale FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(y\right)=f\left({\vec{x}}_1+y{\vec{d}}_1\right) \end{aligned}}
deren Minimum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1} nun zum Beispiel mit dem eindimensionalen Newtonverfahren bestimmt werden kann. Dieses liefert den nächsten IterationspunktFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}_2={\vec{x}}_1+y_1{\vec{d}}_1 \end{aligned}}
Bestimme an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_2} eine neue Suchrichtung, und wiederhole das Verfahren so lange, bis ein lokales Minimum gefunden wurde. Dies ist dann der Fall, wenn der Gradient von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_k} sich kaum mehr vom Nullvektor unterscheidet. Das Gradientenverfahren konvergiert zwangsläufig gegen einen kritischen Punkt, d.h. gegen einen Punkt mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla f}\left(\vec{x}\right)= 0} . Allerdings kann es in der Nähe eines Minimums zum sogenannten Zickzackphänomen kommen. Dabei ändert sich die Suchrichtung in jedem Iterationsschritt in drastischer Weise, während kaum mehr eine Verminderung des Wertes der Zielfunktion zu beobachten ist. Es empfiehlt sich häufig in der Nähe des Minimums zu anderen Verfahren überzugehen, etwa zu einem Quasi-Newton Verfahren. Für weitere Details sei hier wiederum auf die Literatur verwiesen (Bomze, Grossmann 1993, Nocedal, Wright 1999, etc.)
Optimierung unter Nebenbedingungen
Häufig treten in ökonomischen Anwendungen Optimierungsprobleme auf, bei denen gewisse Nebenbedingungen erfüllt werden müssen. Das bedeutet, das nicht mehr der ganze Definitionsbereich einer Funktion betrachtet wird, sondern nur eine Teilmenge; deren genaue Gestalt hängt von den Nebenbedingungen ab; maximieren wir etwa eine Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} unter der Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=x^2+y^2=4} , so wird das Maximum auf dem Kreis mit Radius 2 gesucht. Dieser ist die Höhenschichtline der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)} zum Niveau 4. Wenn wir statt der Gleichung die Ungleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=x^2+y^2\le1} als Nebenbedingung vorgeben, so wird das Maximum auf der ganzen Kreisscheibe gesucht (also auch im Inneren des Kreises). Für den Spezialfall der Optimierung von linearen Funktionen unter linearen Nebenbedingungen gibt es das sogenannte Simplex-Verfahren, das hier nicht behandelt wird; es gibt dafür inzwischen leicht auffindbare Internetresourcen (z.B. www.phpsimplex.com oder LINDO); wir behandeln die weitaus schwierigere Fragestellung der nichtlinearen Optimierung unter Nebenbedingungen, die selbst linear oder nichtlinear sein können. Die wichtigste Methode zur Behandlung von Optimierungsaufgaben unter Nebenbedingungen besteht darin, diese auf Optimierungsprobleme ohne Nebenbedingungen zurückzuführen. Der Einfachheit halber werden wir diese Theorie hier nur für Funktionen in zwei Veränderlichen vorstellen, die Verallgemeinerung auf mehrere Veränderliche erfordert zwar mehr Rechenaufwand, jedoch keine neuen Konzepte. Wir beschreiben nur die Suche nach einem lokalen Minimum, für Maxima läuft alles völlig analog, bzw. kann man das Minimum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -f\left(x,y\right)} suchen um das Maximum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} zu erhalten.
Lagrange – Multiplikatoren – Gleichungen als Nebenbedingung
Wir wollen folgende Aufgabe lösen:FindeFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{min\ }f\left(x,y\right) \end{aligned}}
unterFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=c \end{aligned}}
d.h., wir suchen das Minimum der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} über der Höhenschichtline zum Niveau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)} , wobei wir voraussetzen, dass sowohl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} als auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} differenzierbar sind. Im ersten Schritt der Methode wird ein Lagrange-Multiplikator, zumeist mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda} bezeichnet (hat nichts mit den Eigenwerten einer Matrix zu tun!), eingeführt. Man definiert die Lagrange-Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L} als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y,\lambda\right)=f\left(x,y\right)+\lambda\left(g\left(x,y\right)-c\right) \end{aligned}}
und sucht jene Paare , für das es ein Lambda gibt, mit dem die Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x_0,y_0,\lambda(x_0,y_0\right))}
ein Minimum annimmt. Die Nebenbedingung steckt nun implizit in der Lagrange-Funktion. Falls die Nebenbedingung erfüllt ist so gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L\left(x,y,\lambda\right)=f\left(x,y\right)}
. Falls die Nebenbedingung nicht erfüllt ist und zum Beispiel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x_0,y_0\right)>c}
, so wird die Lagrange-Funktion für diesen Punkt für hinreichen kleines Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
beliebig klein, und und die Lagrangefunktion kann in diesem Punkt für kein ein Minimum annehmen. Beachten Sie auch: das Kriterium ist etwas anderes als die Suche nach Tripeln Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x,y,\ \lambda\right)}
, welche die Lagrangefunktion minimieren – solche wird man im Allgemeinen nicht finden: gilt nämlich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(g\left(x,y\right)-c\right)\neq0}
, dann gibt es aus den genannten Gründen kein optimales Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
!
Das Lagrange-Theorem besagt nun folgendes: falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x_0,y_0\right)}
ein lokales Minimum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)}
unter der Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c}
ist, und falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla g}(x_0,y_0)\neq(0,0)^T }
so gibt es eine eindeutige Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
, für welche die Lagrange-Funktion einen stationären Punkt in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x_0,y_0\right)}
hat, d.h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla L}(x_0,y_0)=(0,0)^T}
unter Beibehaltung der Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c}
. Um Kandidaten zur Lösung der ursprünglichen Aufgabe zu erhalten, muss also das folgende System von Gleichungen gelöst werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\frac{\partial}{\partial x} L(x, y, \lambda)=\frac{\partial}{\partial x} f(x, y)+\lambda \frac{\partial}{\partial x} g(x, y)=0\\ &\frac{\partial}{\partial y} L(x, y, \lambda)=\frac{\partial}{\partial y} f(x, y)+\lambda \frac{\partial}{\partial y} g(x, y)=0\\ &\frac{\partial}{\partial \lambda} L(x, y, \lambda)=g(x, y)-c=0 \end{aligned} }
d.h., der Gradient der Zielfunktion ist ein lineares Vielfaches des Gradienten der Funktion, die die Nebenbedingung angibt. Nun zeigt uns der Gradient die Richtung des stärksten Anstiegs an und steht normal auf die Höhenschichtlinie. Stellen wir uns den Graphen der Zielfunktion als hügelige Landschaft vor, so wird durch die Nebenbedingung ein Weg durch diese Landschaft gelegt, und gesucht werden die höchsten bzw. tiefsten Punkte auf diesem Weg. An diesen fällt das Gelände senkrecht zum Weg am steilsten ab (s. Abbildung 1.3).
Beispiel 11:
Ein Verbraucher habe die NutzenfunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\mathrm{xy}. \end{aligned}}
Maximiere die Nutzenfunktion unter der BudgetbeschränkungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=x+2y=\mathrm{10}. \end{aligned}}
Die Lagrange Funktion lautet:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y,\lambda\right)=\mathrm{xy}+\left(x+2y-\mathrm{10}\right) \end{aligned}}
Null setzen der partiellen Ableitungen gibtFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x}L\left(x,y,\lambda\right)=y+\lambda=0 \\\ \frac{\partial}{\partial y}L\left(x,y,\lambda\right)=x+2\lambda=0 \end{aligned}}
Elimination von aus diese beiden Gleichungen liefert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x-2y=0} Und wir haben die NebenbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x+2y=\mathrm{10} \end{aligned}}
Dieses lineare Gleichungssystem mit zwei Variablen hat eine eindeutige Lösung:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x = 5, y = 2.5 \end{aligned}}
und schließlichFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda=-y=-2\mathrm{.}5 \end{aligned}}
An sich haben wir bisher nur eine notwendige Bedingung für ein lokales Extremum und es sollte noch gezeigt werden, dass es sich tatsächlich um ein Maximum handelt. Ähnlich wie im Falle der Optimierung ohne Nebenbedingung gibt es entsprechende Kriterien an die zweiten Ableitungen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} , anhand derer man entscheiden kann ob es sich um ein Maximum oder ein Minimum handelt. Wir wollen uns zunächst auf eine graphische Darstellung des Sachverhalts beschränken:
Abbildung 1.4 zeigt einerseits ausgewählte Niveaulinien der Zielfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=\mathrm{xy}}
, anderseits die Gerade Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=5-\frac{x}{2}}
welche gerade die Budget-beschränkung beschreibt. Sinnvoller weise sind beide Investitionen x und y positiv. Entsprechende Ungleichungs-Nebenbedingungen werden im nächsten Abschnitt besprochen. Am Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (x_0 = 5, y_0 = 2.5)}
berührt die Gerade die Niveaulinie zum Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle xy = 12.5}
. Es ist klar ersichtlich, dass an allen anderen Punkten die Gerade jene Niveaulinien schneidet, die einem geringeren Wert der Zielfunktion entsprechen. Daher handelt es sich bei dem Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (x_0, y_0)}
um ein lokales Maximum der Zielfunktion unter der gegebenen Budgetbeschränkung. Dass an dieser Stelle die Nebenbedingungsgerade tangential an die Niveaulinie liegt ist typisch, und der geometrische Grund dafür, dass die Lagrange-Methode funktioniert. Abbildung 1.5 ist eine dreidimensionale Veranschaulichung des Sachverhaltes; die stark ausgezogene Kurve ist der Graph der Funktion unter der Nebenbedingung (der „Weg durch das hügelige Gelände“, um beim Bild zu bleiben). An seinem höchsten Punkt ist er tangential zum Graphen der Höhenschichtlinien, d.h., das Gelände fällt dort senkrecht zum Weg am steilsten ab.
Für eine allgemeine Klassifizierung von Punkten, die mithilfe der Lagrage Funktion gefunden wurden, steht die Methode der berandeten Hessematrizen zur Verfügung; im zweidimensionalen Fall: Sei
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(x, y, \lambda)=f(x, y)+\lambda g(x, y-c) }
die Lagrangefunktion eines Optimierungsproblems; dann bilden wir die Hessematrix nach allen drei Variablen – allerdings beginnend mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{H}=\left(\begin{array}{c} \frac{\partial^2 L}{\partial \lambda^2} \frac{\partial^2 L}{\partial \lambda \partial x} \frac{\partial^2 L}{\partial \lambda \partial y} \\ \frac{\partial^2 L}{\partial \lambda \partial x} \frac{\partial^2 L}{\partial x^2} \frac{\partial^2 L}{\partial x \partial y} \\ \frac{\partial^2 L}{\partial \lambda \partial y} \frac{\partial^2 L}{\partial x \partial y} \frac{\partial^2 L}{\partial y^2} \end{array}\right) }
(der linke obere Eintrag – die zweite Ableitung nach – ist immer 0.)
Ist die Determinante dieser Matrix positiv, so haben wir ein lokales Maximum, ist sie negativ, ein Minimum, ist die Determinante Null, so ist die Frage nicht entscheidbar.
Einen Sonderfall stellen Nebenbedingungen dar, die eine beschränkte Menge beschreiben – z.B. einen geschlossenen Kreis, eine Ellipse oder ein Streckenstück; auf einer solchen Menge können wir einfach alle kritischen Punkte der Reihe nach betrachten – der mit dem größten Funktionswert ist das Maximum, der mit dem kleinsten das Minimum.
Aufgabe 8:
Finde die beiden Extremstellen vonFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y^2 \end{aligned}}
unter der NebenbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=x^2+\mathrm{xy}+2=3 \end{aligned}}
Die vorgestellte Theorie lässt sich weitgehend unverändert auf Funktionen mit mehr als zwei unabhängigen Variablen erweitern. Häufig gibt es in der Anwendung mehr als eine Nebenbedingung, und die Lagrange-Methode besteht dann darin, dass für jede Nebenbedingung ein eigener Lagrange-Multiplikator hinzugefügt wird. Bei einem Optimierungsproblem in n Variablen mit m Nebenbedingungen erhält man demnach eine Lagrange-Funktion L in n+m Variablen. Kandidaten für lokale Extrema erhält man wiederum indem man nach stationären Punkten von L sucht, wobei es nun gilt n+m Gleichungen in n+m Variablen zu lösen.
Karush Kuhn Tucker Bedingungen
Häufig tauchen Nebenbedingungen nicht in Gleichungsform, sondern in Ungleichungsform auf, z.B., dass eine Variable x nur positive Werte annehmen kann, also die Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\geq0} erfüllen muss. Das allgemeine Problem in zwei Variablen mit einer Nebenbedingung hat die Form: FindeFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{max\ (}f(x,y)) \end{aligned}}
unterFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)\le c \end{aligned}}
D.h., wir suchen das Minimum der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} über einem Bereich, der von der Höhenschichtline zum Niveau c der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)} begrenzt wird, wobei wir wieder voraussetzen, dass sowohl f als auch g differenzierbar sind. Die Menge aller Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x,y\right)} welche die Nebenbedingung erfüllen, wird als zulässige Menge bezeichnet. Im Prinzip kann dieses Problem mit den bereits gelernten Methoden behandelt werden, indem man einerseits nach lokalen Extremstellen im Inneren des zulässigen Bereichs sucht (Optimierung ohne Nebenbedingung), und andererseits den Rand des zulässigen Bereichs Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c} mit Hilfe der Lagrange-Methode untersucht. Unter gewissen Voraussetzungen an die Randbedingungen (den sogenannten constraint qualifications ) lassen sich allerdings notwendige Bedingungen für lokale Extremwerte im gesamten zulässigen Bereich angeben. Dazu wird wiederum die Lagrange-FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y,\lambda\right)=f\left(x,y\right)+\lambda\left(g\left(x,y\right)-c\right) \end{aligned}}
definiert, allerdings gilt hier für die Lagrange Multiplikatoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda\le0} . Entscheidend ist nun die sogenannte komplementäre Schlaffheitsbedingung (complementary slackness). Man fordert, dass entweder die Nebenbedingung exakt erfüllt ist (d.h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c} ), oder aber der Lagrange MultiplikatorFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0} . Diese Bedingung ist erfüllt fallsFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda\left(g\left(x,y\right)-c\right)=0 \end{aligned}}
Die complementary slackness Bedingung beinhaltet in sehr eleganter Form dass ein lokaler Extremwert direkt am Rande des zulässigen Bereiches andere Bedingungen erfüllen muss als im Inneren: für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
erhält man die lokalen Maxima im Inneren, diese sind die gleichen, die wir auch ohne Nebenbedingung gefunden hätte. Am Rand hingegen müssen die Gradienten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)}
(anti-) parallel sein, d.h., wenn wir der Richtung des steilsten Angstiegs der Zielfunktion folgen würden, würden wir den von der Nebenbedingung erlaubten Bereich verlassen. Zusammenfassend liefert dies die sogenannten Karush Kuhn Tucker (KKT) Bedingungen als notwendige Bedingungen für lokale Extrema unter Ungleichheits-Nebenbedingungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x} L(x, y, \lambda)=\frac{\partial}{\partial x} f(x, y)+\lambda \frac{\partial}{\partial x} g(x, y) &=0 \\ \frac{\partial}{\partial y} L(x, y, \lambda)=\frac{\partial}{\partial y} f(x, y)+\lambda \frac{\partial}{\partial y} g(x, y) &=0 \\ g(x, y) \leq c \lambda & \leq 0 \\ \lambda(g(x, y)-c) &=0 \end{aligned} }
Beispiel 12:
Ein Unternehmen hat die Möglichkeit zwei Güter zu produzieren. Bei beiden Produkten ist der erzielbare Preis jeweils proportional zur Qualität x bzw. y, während der Aufwand zur Qualitätssteigerung quadratisch wächst. D.h.:
Produkt 1: Für Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ax}
bedarf es Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Ax^2}
Arbeitseinheiten
Produkt 2: Für Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle by}
bedarf es Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle By^2}
Arbeitseinheiten
wobei alle Konstanten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (a,b, A,B)}
größer als 0 sein sollen.
Das Unternehmen hat insgesamt höchstens L Einheiten an Arbeit pro Woche zur Verfügung, die es der Produktion der beiden Güter zuordnen kann. Bestimme welche Qualität Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x}
bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y}
den Erlös maximiert, wenn der wöchentliche Absatz auf jeden Fall gewährleistet ist. Lösung: Der erzielbare Erlös beträgtFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\mathrm{ax}+b \end{aligned}}
Die Gesamtarbeitsleitung ist beschränkt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)={\mathrm{Ax}}^2+{\mathrm{By}}^2\le L \end{aligned}}
Die KKT Bedingungen lauten also: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x} L(x, y) &=a+2 \lambda \mathrm{Ax}=0 \\ \frac{\partial}{\partial y} L(x, y)=b+2 \lambda \mathrm{By}=0 &=\\ \lambda\left(\mathrm{Ax}^2+\mathrm{By}^2-L\right) &=0 \end{aligned} } wobeiFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda\le0 {\mathrm{Ax}}^2+{\mathrm{By}}^2\le L \end{aligned}}
Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0} folgt aus den ersten beiden Gleichungen unmittelbar Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a=b=0} , im Widerspruch zur Angabe. Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda<0} folgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x>0,y>0} , und daherFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda=\frac{-a}{2Ax}=\frac{-b}{2By} \end{aligned}}
Somit gilt auch
Andererseits muss gelten (complementary slackness)Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{Ax}^2+\mathrm{By}^2=L \end{aligned}}
und wir folgern, dass insgesamt die optimale Lösung erreicht wird fürFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x=\sqrt{\frac{L}{a^2B+b^2A}}\cdot\frac{a\sqrt{B}}{\sqrt{A}} y=\sqrt{\frac{L}{a^2B+b^2A}}\cdot\frac{b\sqrt{A}}{\sqrt{B}} \end{aligned}}
Aufgabe 9: Untersuche die FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y+1 \end{aligned}}
auf Extremwerte unter der NebenbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=x+y\le4 \end{aligned}}
Zusammenfassung
Wir haben einige Aspekte der nichtlinearen Optimierung kennen gelernt. Speziell wurden zur Lösung von mehrdimensionalen Optimierungsaufgaben als hinreichende Bedingungen für lokale Maxima und Minima die Definitheitseigenschaften der Hessematrix angegeben. Für Optimierungsaufgaben mit Nebenbedingungen wurden nur notwendige Bedingungen zum Finden von lokalen Extremstellen besprochen, und zwar die Lagrange-Methode im Falle von Gleichheits-nebenbedingungen, und die Karush-Kuhn-Tucker Bedingungen für Ungleichheits-nebenbedingungen. Als einfache Algorithmen zum Lösen von nichtlinearen Optimierungsaufgaben wurden das Newton-Verfahren und das Gradientenverfahren kurz diskutiert.
Optimierung ist ein weites Feld, und viele interessante Gebiete konnten hier nicht einmal kurz angerissen werden. Eine Liste von gängigen Fragestellungen umfasst Transportprobleme, Zuordnungsprobleme, Netzplantechnik oder das weitläufige Gebiet der ganzzahligen und kombinatorischen Optimierung. Die dort benötigten Techniken unterscheiden sich oft wesentlich von denen die in diesem Kapitel erwähnt wurden, und oftmals finden Konzepte der Graphentheorie Verwendung. Für eine elementare deutschsprachige Einführung sei etwa auf das Buch von Domschke und Drexl (1995) verwiesen.
Wiederholungsaufgaben/Übungen
Aufgabe 1
Untersuche folgende Funktionen auf Extremwerte bzw. Sattelstellen (verwende die Definitheit der Hessematrix, um Entscheidung zu treffen).Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y^2 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f(x,y)=(1+x)^2-(1-y)^2 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\mathrm{xy} \end{aligned}}
Aufgabe 2
Führe zu den Funktionen aus Aufgabe 1 jeweils die erste Iteration des Gradientenverfahrens aus, wobei im Punkt (1,1) gestartet wird. Für welche der drei Aufgaben ist die Suche nach einem (lokalen oder globalen) Minimum überhaupt sinnvoll?
Aufgabe 3
Führe für die FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^4+y^4 \end{aligned}}
die ersten beiden Schritte des Newtonverfahrens aus, wenn im Punkt (1,1) gestartet wird.
Aufgabe 4
Finde die Extremwerte der folgenden Funktionen unter den angegebenen Nebenbedingungen:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=4x+3y\\\ NB:g\left(x,y\right)=x^2+y^2=1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y^2\\\ NB:g\left(x,y\right)=2\mathrm{xy}=1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} f(x, y)=e^{x y} \\ N B: g(x, y)=x+y=1 \end{array} }
(Gib jeweils Skizzen mit den Niveaulinien an um zu klären, ob es sich um ein Maximum oder ein Minimum handelt).
Aufgabe 5
Ermittle mit Hilfe der KKT-Bedingungen alle Extremstellen der folgenden Funktionen unter den gegebenen NebenbedingungenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f(x,y)=(x-1)^2+(y-2)^2-1\\\ NB:g\left(x,y\right)=x^2+y^2\le1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+3\mathrm{xy}+y^2 \\\ NB: g\left(x,y\right)=x+y\le1 \end{aligned}}
Stelle die Lösungen wiederum graphisch dar!
Lösungen der Aufgaben
Aufgabe 1:
Aufgabe 2:
Die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2 = y}
hat natürlich zwei Lösungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \(\mathbit{x}_\mathbf{1}=\sqrt\mathbit{y}\) und \(\mathbit{x}_\mathbf{2}=-\sqrt\mathbit{y}\) \end{aligned}}
Dementsprechend ist die Umkehrabbildung über ganz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}}
nicht eindeutig definierbar, sehr wohl aber für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbit{x}\in\mathbb{R}^+}
(strichpunktiert) bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbit{x}\in\mathbb{R}^-}
(strichliert). Aufgabe 3:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_1^\prime(x)=-2x\mathbit{exp}{(}-x^2) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_2^\prime(x)=\left(\frac{\mathbit{sin}{x}}{\mathbit{cos}{x}}\right)^\prime=1+{\mathbit{tan}}^2{(}x)=\frac{1}{{\mathbit{cos}}^2{(}x)} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_3^\prime\left(x\right)=\frac{3x^2}{2\sqrt{1+x^3}} \end{aligned}}
Aufgabe 4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{\mathbit{x}=1}^{2}\lambda\mathrm{\ exp}\left(-\lambda\mathbit{x}\right)\ dx=\mathrm{\ \ }-\left.\mathrm{\ exp}\left(-\lambda\mathbit{x}\right)\right|_1^2=\ e^{-\lambda}-e^{\mathrm{-2}\lambda} \end{aligned}}
Aufgabe 5:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x_2=0-\frac{p^\prime(0)}{p^\pprime(0)} \\\ x_3=\frac{1}{2}-\frac{p^\prime\left(1/2\right)}{p^\prime\left(1/2\right)}= \frac{1}{2}-\frac{1}{32}=\mathrm{0.4688} \end{aligned}}
Vergleicht man diesen Wert mit der tatsächlichen Stelle des lokalen Minimums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 0.4691}
, so erkennt man, wie nahe das Newton Verfahren bereits nach zwei Iterationen gekommen ist.
Aufgabe 6:
Matrix A – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-10\lambda+9=0}
Eigenwerte: 1 und 9 (positiv definit)
Eigenvektoren: (1,-1)T und (7,1)T
Matrix B – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-2\lambda=0}
Eigenwerte: 2 und 0 (positiv semidefinit)
Eigenvektoren: (1,-1)T und (1,1)T
Matrix C – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^3+7\lambda^2-18\lambda=0}
Eigenwerte: -9, 2 und 0 (indefinit)
Eigenvektoren: (1,2,-3)T , (-4,3,1)T und (2,4,3) T
Aufgabe 7:
a) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f_1\left(x,y,z\right)=\left(\begin{matrix}4-4x\\6-2y\\-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) \end{aligned}}
Kandidat für Extremum: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=1, y=3, z=0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_{f_1}\left(x,y,z\right)=\left(\begin{matrix}-4&0&0\\0&-2&0\\0&0&-2\\\end{matrix}\right) \end{aligned}}
negativ definit ⇒ (1,3,0)T ist ein lokales Maximum
b) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f_2\left(x,y,z\right)=\left(\begin{matrix}6x-4y\\6y-4x\\10-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) \end{aligned}}
Kandidat für Extremum: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=0, y=0, z=5}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_{f_2}\left(x,y,z\right)=\left(\begin{matrix}6&-4&0\\-4&6&0\\0&0&-2\\\end{matrix}\right) \end{aligned}}
ist indefinit (Eigenwerte -2, 2 und 10) (0,0,5)T ist ein Sattelpunkt und kein lokaler Extremwert
Aufgabe 8:
Die Lagrange Funktion lautet:
Null setzen der partiellen Ableitungen gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x}L\left(x,y\right)=2x+\lambda\left(2x+y\right)=0 \\\ \frac{\partial}{\partial y}L\left(x,y\right)=2y+\lambda\left(2y+x\right)=0 \end{aligned}}
Addieren wir diese beiden Gleichungen so erhalten wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 2\left(x+y\right)+\lambda\left(3x+3y\right)=0 \end{aligned}} oder äquivalent dazu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(x+y\right)\left(2+3\lambda\right)=0 \end{aligned}} Das bedeutet entweder der erste Faktor oder der zweite Faktor verschwindet.
Fall1: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y=0, d.h. y = -x}
.
Die Nebenbedingung lautet dann Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,-x\right)=x^2=3 \end{aligned}}
Und wir erhalten die beiden Lösungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=\sqrt3,y=-\sqrt3 \: x=-\sqrt3,y=\sqrt3}
Fall2: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2+3\lambda = 0, d.h. \lambda = -2/3}
.
Die erste Gleichung lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=2x-\frac{2}{3}\left(2x+y\right)=0 \end{aligned}}
und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
. Die Nebenbedingung wird zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,x\right)=3x^2=3 \end{aligned}}
und wir erhalten die beiden Lösungen Fehler beim Parsen (Syntaxfehler): {\textstyle x=-\sqrt3,y=\sqrt3 \: x=-1,y=-1}
Vergleichen wir die Funktionswerte: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(\sqrt3,-\sqrt3\right)=f\left(-\sqrt3,\sqrt3\right)=6 \: f\left(1,1\right)=f\left(-1,-1\right)=2} Die ersten beiden Punkte liefern jeweils ein Maximum, die zweiten Punkte ein Minimum unter der Nebenbedingung. Die folgende Abbildung veranschaulicht die Zusammenhänge.
Die konzentrischen Kreise geben einige Niveaulinien der Zielfunktion . Beachte wiederum wie an den 4 extremalen Punkten die Kurve der Nebenbedingungen dazu tangential liegt.
Aufgabe 9: Die Lagrange Funktion lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y\right)=x^2+y+1+\lambda\left(x+y-4\right) \end{aligned}} Null setzen der partiellen Ableitungen gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x}L\left(x,y\right)=2x+\lambda=0 \\\ \frac{\partial}{\partial y}L\left(x,y\right)=1+\lambda=0 \end{aligned}} und von den KKT Bedingungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda\left(x+y-4\right)=0 \end{aligned}} Im Inneren des zulässigen Bereiches muss gelten , und daher wird die zweite Gleichung oben zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1=0} , offensichtlich ein Widerspruch, Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda<0} muss gelten liefert die zweite Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=-1} , und daher die erste Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda\left(x+y-4\right)=0} . Die KKT Bedingung gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x+y-4\right)=0} , und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x+y-4\right)=0} . Der Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} ist somit eine potentielle lokale Extremstelle, um zu erkennen worum es sich tatsächlich handelt betrachte folgende Abbildung, die wiederum die Niveaulinien der Zielfunktion sowie den Rand des zulässigen Bereichs zeigt.
Der zulässige Bereich befindet sich unterhalb der Geraden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=4-x} . Am kritischen Punkt nimmt die Funktion den Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 19/4} an, in unmittelbarer Umgebung davon gibt es sowohl Punkte mit größeren als auch mit kleineren Funktionswerten. Es handelt sich bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} also um kein lokales Extremum, sondern um eine Art Sattelpunkt, allerdings nur wenn die Nebenbedingung in Betracht gezogen wird. Entlang der Geraden ist der Punkt ein Minimum. Für alle Werte die in einem zugespitzten Kegel mit Spitze bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} liegen (Siehe Abbildung) liegt ein Maximum vor.
Lösungen der Wiederholungsaufgaben
Aufgabe 1.1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x\right)=x^{\mathrm{exp}\left(x\right)}=\mathrm{exp}\left[\mathrm{log}\left(x\right)e^x\right] \\\ f^\prime\left(x\right)=\mathrm{exp}\left[\mathrm{log}\left(x\right)e^x\right]. \left[\frac{1}{x}e^x+\mathrm{log} \left(x\right)e^x\right] = \\\ x^{\mathrm{exp}\left(x\right)}\left[\frac{1}{x}e^x+\mathrm{log} \left(x\right)e^x\right] \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^\prime\left(x\right)=\frac{\left(3x-2\right)\left(2x+\frac{1}{2\sqrt x}\right)-3\left(x^2+\sqrt x\right)}{(3x-2)^2} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^\prime\left(x\right)=\frac{1}{\sqrt{2x}}\mathrm{cos}\left(x^2\right)-\sqrt x\mathrm{sin}x^22x \end{aligned}}
Aufgabe 1.2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{\mathrm{exp} \left(x\right)}{x-1}}
an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 1}
nicht definiert. Linksseitiger Limes ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -\infty}
, rechtsseitiger Limes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle +\infty}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)}
hat keine Nullstellen, allerdings konvergiert es gegen 0 für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\rightarrow-\infty}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^\prime\left(x\right)=\frac{\left(x-2\right)\mathrm{exp} \left(x\right)}{(x-1)^2}}
, Nullstelle nur bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 2}
(potentielles lokales Extremum)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{\prime\prime}\left(x\right)=\frac{\left(x^2-4x+5\right)\mathrm{exp} \left(x\right)}{(x-1)^3}}
keine reellen Nullstellen, daher keine Wendepunkte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{\prime\prime}\left(2\right)=\mathrm{exp}2>0}
, daher ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 2}
ein lokales Minimum
Aufgabe 1.3
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x\right)=\frac{1}{3}e^{3x+4} \: (Substitution\: y = 3x+4) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f(x)=(x^2\mathrm{log}(x^2)-x^2)/2 \: (Substitution\: y = x^2\: und \: partielle \:Integration) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x\right)=-\frac{1}{4}\mathrm{cos}\left(4x-3\right) \: (Substitution\: y = 4x-3) \end{aligned}}
Aufgabe 1.4
Berechnung der Integrale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} -\left(x^2+2x+2\right)e^{-x}|_0^1=2-5e^{-1} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(\mathrm{log}\left(\sfrac{x}{2}\right)-1\right)|_1^2=\mathrm{log}2-1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{x=2}^{3}\left(3-x\right)+\int_{x=3}^{4}\left(x-3\right)\mathrm{dx}=1 \end{aligned}}
Aufgabe 1.5
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} D=\left\{\left(x,y\right)\in R^2:x^2>y^2\right\}=\left\{\left(x,y\right):\left|x\right|>\left|y\right|\right\} \\\ \mathrm{\nabla f}=\frac{1}{x^2-y^2}\left(\begin{matrix}2x\\-2y\\\end{matrix}\right) , H_f=\frac{1}{\left(x^2-y^2\right)^2}\left(\begin{matrix}-2\left(x^2+y^2\right)&4\mathrm{xy}\\4\mathrm{xy}&-2\left(x^2+y^2\right)\\\end{matrix}\right) \end{aligned}}
Aufgabe 2.1:
=(
2y
) kritischer Wert (x,y) = (0,0)
H_f=(
0&2
) positiv definit (konvex) (0,0) ist globales Minimum
=(
2(1-y)
) kritischer Wert (x,y) = (-1,1)
H_f=(
0&-2
) indefinit (-1,1) ist Sattelpunkt
=(
x
) kritischer Wert (x,y) = (0,0)
H_f=(
1&0
) indefinit (EW ) (0,0) ist Sattelpunkt
Aufgabe 2.2:
a) =(
2y
) , _1=(
1
) Abstiegsrichtung _1=-(
2
)
g(h)=f((
1
)-h(
2
))=2(1-2h)^2 g^(h)=-8(1-2h)=0 h= _2=(
1
)-(
2
)=(
0
)
=(
2(1-y)
) , _1=(
1
) Abstiegsrichtung _1=-(
0
)
g(h)=f((
1
)-h(
0
))=(2-4h)^2 g^(h)=-8(2-4h)=0 h= _2=(
1
)-(
0
)=(
1
)
=(
x
) , _1=(
1
) Abstiegsrichtung _1=-(
1
)
g(h)=f((
1
)-h(
1
))=(1-h)^2 g^(h)=-2(1-h)=0 h=1, _2=(
1
)-(
1
)=(
0
)
In allen 3 Fällen landet man bereits nach einem Iterationsschritt im kritischen Punkt. Dies ist für allgemeine Funktionen nicht der Fall, sondern stammt daher, dass wir es hier jeweils mit quadratischen Funktionen zu tun haben. Im Beispiel a) haben wir somit nach einer Iteration bereits das globale Minimum gefunden. Aber Achtung! In Beispiel b) und c) sind wir jeweils in einem Sattelpunkt gelandet, und das Gradientenverfahren würde hier einfach abbrechen, weil der Gradient an einem kritischen Punkt natürlich gerade 0 ist. Würden wir in Beispiel b) etwa im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-1,-1)}
starten so erhält man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(h)=f\left(\left(\begin{matrix}-1\\-1\\\end{matrix}\right)-h\left(\begin{matrix}0\\4\\\end{matrix}\right)\right)=-(2+4h)^2}
und man erkennt, dass für wachsendes der Funktionswert gegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -\infty}
strebt.
Aufgabe 2.3:
Aufgabe 2.4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=4x+3y+\lambda\left(x^2+y^2-1\right) \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=4+2x\lambda=0 \end{aligned}} Multipliziere mit -x Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=3+2y\lambda=0 \end{aligned}} Multipliziere mit y Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 4y-3x = 0, \: oder\: y=\frac{3}{4}x \end{aligned}} Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+y^2=1} Zwei Lösungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (4/5, 3/5)} ist Maximum (Funktionswert 5)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-4/5, -3/5)} ist Minimum (Funktionswert -5)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=x^2+y^2+\lambda\left(2\mathrm{xy}-1\right) \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=2x+2y\lambda=0 \end{aligned}} Multipliziere mit x Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=2y+2x\lambda=0 \end{aligned}} Multipliziere mit -y Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 2x^2-2y^2=0 \end{aligned}} Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=\frac{1}{2x}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^4=\frac{1}{4} \end{aligned}}
Zwei reelle Lösungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(\frac{1}{\sqrt2},\frac{1}{\sqrt2}\right)}
sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(-\frac{1}{\sqrt2},-\frac{1}{\sqrt2}\right)}
jeweils mit Funktionswert 1.
Die Zeichnung zeigt, dass es sich jeweils um ein Minimum handelt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=\mathrm{exp}(xy)+\lambda(x+y-1) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=y\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=x\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 \end{aligned}}
Bilde Differenz der beiden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(x-y\right)\mathrm{exp}xy=0 \end{aligned}}
also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y=1}
Eindeutige Lösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y = 1/2}
mit Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{exp}\left(\frac{1}{4}\right) \end{aligned}}
Die Zeichnung zeigt, dass es sich wiederum um ein Minimum handelt:
Die Werte in der Zeichnung geben den Logarithmus der Wurzel der entsprechende Wertes der Funktion an. Z. Bsp ist das Minimum der Funktion unter der Nebenbedingung gegeben durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(0\mathrm{.}5,0\mathrm{.}5\right)=\mathrm{exp}(0.5^2) \end{aligned}}
Aufgabe 2.5:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=(x-1)^2+(y-2)^2-1+\lambda(x^2+y^2-1) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} KKT: \frac{\partial L}{\partial x}=2\left(x-1\right)+2x\lambda=0 \\\ \frac{\partial L}{\partial y}=2\left(y-2\right)+2y\lambda=0 \\\ \lambda\left(x^2+y^2-1\right)=0 \:(Comp.\: Slack.) \end{aligned}}
Fall 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
(Lösung im inneren des zulässigen Bereichs)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = 2}
einzige formale Lösung, liegt nicht im zulässigen Bereich!
Fall 2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+y^2-1=0}
(Lösung am Rand)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x-1\right)y-\left(y-2\right)x=2x-y=0}
, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2x = y}
(ähnlich wie in Aufgabe 2.4)
Einsetzen in NB liefert zwei Lösungen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\frac{1}{\sqrt5},\frac{2}{\sqrt5}\right) \:mit\: Funktionswert \: 5 - \frac{\mathrm{10}}{\sqrt5} \: (Minimum\: unter\: NB) \\\ \left(-\frac{1}{\sqrt5},-\frac{2}{\sqrt5}\right) \:mit \:Funktionswert \: 5 + \frac{\mathrm{10}}{\sqrt5} \: (Maximum \:unter\: NB) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=x^2+3\mathrm{xy}++�2+\lambdax+y-1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} KKT: \frac{\partial L}{\partial x}=2x+3y+\lambda=0 \\\ \frac{\partial L}{\partial y}=3x+2y+\lambda=0\\\ \lambda\left(x+y-1\right)=0 \:(Comp. \:Slack.) \end{aligned}}
Fall 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
(Lösung im inneren des zulässigen Bereichs)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 0}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = 0}
einzige formale Lösung, Hessematrix indefinit
Sattelpunkt
Fall 2:
(Lösung am Rand)
Eliminiere Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x-y=0}
, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
(ähnlich wie in Aufgabe 2.4)
Einsetzen in NB liefert eindeutige Lösung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x = y = 1/2 \end{aligned}}
mit Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 5/4}
Die Grafik zeigt, dass es sich um ein Maximum handelt:
Die Niveaulinien entsprechen Hyperbeln: Je weiter man sich vom Ursprung nach rechts oben bewegt, desto größer sind die Werte die die Funktion entlang der Niveaulinie annimmt. Je weiter man sich vom Ursprung nach links oben (bzw. rechts unten) bewegt, desto kleiner sind die entsprechenden Funktionswerte.