Methoden der Datenanalyse - Varianzanalyse

Varianzanalyse

Die Varianzanalyse stellt nicht nur ein spezielles Analyseverfahren, sondern eine generelle Methode dar, um Zusammenhänge zwischen verschiedenen Merkmalen inferenzstatistisch zu beurteilen. Ziel der Lektion ist das Grundmodell der Varianzanalyse sowie die wichtige Idee der Quadratsummenzerlegung darzustellen. Die Durchführung der Analysen der Modelle mit einem bzw. zwei Faktoren sowie die Umsetzung in der Software R sind die weiteren zentralen Punkte.

Begriffsabgrenzung

Die (univariate) Varianzanalyse („ANOVA“ = „analysis of variance“) wird ebenfalls dazu verwendet, den Einfluss einer oder mehrerer unabhängiger Variablen auf eine zumindest intervallskalierte (metrische) Zielvariable zu untersuchen. Im Gegensatz zur Regression sind die hier vorkommenden unabhängigen Variablen kategoriell. Es wird daher nicht eine lineare Funktion als Zusammenhang unterstellt, sondern die Varianzanalyse stellt eine Methode zur Analyse von Mittelwertsunterschieden in ver­schiedenen Versuchsgruppen dar. Der Name „Varianzanalyse“ kommt daher, dass zur Beurteilung der Signifikanz solcher Mittelwertsunterschiede Varianzen berechnet werden.

Liegt eine erklärende Gruppenvariable (ein „Faktor“) vor, spricht man von einer „ein­fachen“ bzw. „einfaktoriellen“ Varianzanalyse, ansonsten von zwei- oder mehr­faktoriellen Varianzanalysen. Im Gegensatz zur Regressionsanalyse werden üblicher­weise auch Interaktionen zwischen (zwei oder mehreren) erklärenden Variablen im Modell berücksichtigt.

Die verschiedenen Ausprägungen eines jeden Faktors werden „Faktorstufen“ ge­nannt. Hat man in jeder Faktorstufe gleich viele Daten zur Verfügung, spricht man von einem „balancierten Design“, sonst von einem „unbalancierten Design“. Gibt es (bei zumindest zwei vorhandenen Faktoren) nicht in jeder Kombination von Faktoren Beobachtungen, heißt die Versuchsanordnung „unvollständiges Design“.

Hat man als erklärende Variablen sowohl metrische, als auch kategorielle Variablen, wird eine Kovarianzanalyse durchgeführt, die aber hier nicht weiter behandelt wird. Ebenfalls nicht behandelt wird der Fall der multivariaten Varianzanalyse („MANOVA“) bei der mehrere abhängige, korrelierte Variablen vorkommen.

Typische Fragestellungen der ANOVA können sein:

• Ob und wie unterscheiden sich Mietkosten einer Wohnung in Bezug auf die Lage (Innen- vs. Außenbezirke) bzw. in Bezug auf die Zimmeranzahl?
• Gibt es Unterschiede im Ertrag bei verschiedenen Getreidesorten?
• Hängt der Absatz eines Produktes von der Platzierung im Supermarkt ab?
• Ist ein bestimmtes Training für eine Leistung förderlich?
• Ist eine Therapie in Bezug auf ein Kriterium erfolgreich?

Hinweis: Die einfaktorielle Varianzanalyse kann auch als die Verallgemeinerung des schon bekannten t-Tests (zum Vergleich zweier Erwartungswerte aus normal­verteilten Grundgesamtheiten) für eine beliebige Anzahl an Erwartungswerten (Gruppen) gesehen werden.

Die einfache Varianzanalyse für unabhängige Stichproben

Modell der einfachen Varianzanalyse für unabhängige Stichproben

Formal lautet das Modell der einfachen Varianzanalyse:

$$y_{ij}=\mu +\alpha _{1}+\epsilon _{ij},\qquad \left(i=1,\ldots ,k;j=1,\ldots ,n_{i}\right);$$

wobei $y_{ij}$ die Werte der metrischen Variable sind (j-ter Wert in Gruppe i), $\mu$ der unbedingte Erwartungswert (ohne Kenntnis der Gruppe), $\alpha _{i}$der „Effekt“ von Gruppe $i$ ist (also der Unterschied des jeweiligen Gruppenerwartungswerts $\mu _{i}$ zu $\mu$ und $\epsilon _{ij}$ der durch die Gruppenvariable nicht erklärte Teil der abhängigen Variable – analog zur Regression, der Fehler – ist. Die $n_{i}$ sind die Stichprobenumfänge der $k$ Gruppen.

Wie bei der Regression ist auch hier die Annahme, dass die Fehler $\epsilon _{ij}$ normalverteilt mit Erwartungswert Null und Varianz $\sigma ^{2}$ und voneinander unabhängig sind (Varianzhomogenität und Unkorreliertheit der Fehler).

Schätzen und Testen bei der einfachen Varianzanalyse

Beispiel 2 Es soll die Zugfestigkeit von drei Drahtsorten verglichen werden. Dazu werden von Sorte 1 sieben Proben, von Sorte 2 fünf Proben und von Sorte 3 sechs Proben auf ihre Zugfestigkeit überprüft. Es ergaben sich folgende Werte (in Newton/mm2): Versuch 1 2 3 4 5 6 7 Sorte 1 9 15,4 8,2 3,9 7,3 10,8 6,8 Sorte 2 7,3 15,6 14,2 13 9,7 - - Sorte 3 18 9,6 11,5 19,4 17,1 14,1 - Es soll die Frage untersucht werden, ob sich die einzelnen Drahtsorten hinsichtlich ihrer Festigkeit unterscheiden.

Da in Beispiel 2 nur eine gruppierende Variable (in drei Ausprägungen) existiert, liegt eine einfache Varianzanalyse vor. Da nicht in jeder Gruppe gleich viele Beobachtungen sind, ist das Design unbalanciert.

Gemäß des Modells der einfachen Varianzanalyse haben wir also die Vorstellung: Die Zugfestigkeit einer Drahtsorte bei einem bestimmten Versuch setzt sich additiv zusammen aus

• einer mittleren Zugfestigkeit, die ein „durchschnittlicher“ Draht hat,
• einem Wert, um die die Zugfestigkeit einer speziellen Drahtsorte besser oder schlechter ist, als ein „durchschnittlicher“ Draht und
• einer Abweichung von der durchschnittlichen Zugfestigkeit dieser Drahtsorte, die in dem bestimmten Versuch beobachtet wurde und mangels anderer Erklärungsmöglichkeiten dem Zufall zugeordnet wird.

Dementsprechend werden auch die Parameter in diesem Modell geschätzt.

Schätzung der Zugfestigkeit $\mu$ eines durchschnittlichen Drahts durch

$${\hat {\mu }}={\frac {1}{\sum _{i=1}^{k}n_{i}}}\sum _{i=1}^{k}\sum _{j=1}^{n_{i}}y_{ij}$$

Schätzung des Effekts von Drahtsorte $i$, $\alpha _{i}$, durch

$${\hat {\alpha }}_{i}={\hat {\mu }}_{i}-{\hat {\mu }}={\frac {1}{n_{i}}}\sum _{j=1}^{n_{i}}y_{ij}-{\hat {\mu }}$$

Schätzung des Fehlers $\epsilon _{ij}$ durch das Residuum

$${\widehat {\epsilon _{ij}}}=y_{ij}-{\widehat {y_{ij}}}=y_{ij}-\left({\hat {\mu }}+{\hat {a_{i}}}\right)$$

Fortsetzung Beispiel 2 Fehler beim Parsen (Unbekannte Funktion „\math“): {\displaystyle \hat{\mu}=\frac{1}{7+5+6}(9+15,4+\cdots+6,8+7,3+\cdots+9,7+18+\cdots+14,1)=11,717 <\math> <math>\widehat{\alpha_{1}}=\widehat{\mu_{1}}-\hat{\mu}=\frac{1}{7}(9+15,4+\cdots+6,8)-11,717=8,771-11,717=-2,945 <\math> <math>\widehat{\alpha_{2}}=\widehat{\mu_{2}}-\hat{\mu}=\frac{1}{5}(7,3+15,6+\cdots+9,7)-11,717=11,960-11,717=0,243 <\math> <math>\widehat{\alpha_{3}}=\widehat{\mu_{3}}-\hat{\mu}=\frac{1}{6}(18+9,6+\cdots+14,1)-11,717=14,950-11,717=3,233 <\math> Kontrolle: <math>n_{1} \widehat{\alpha_{1}}+n_{2} \widehat{\alpha_{2}}+n_{3} \widehat{\alpha_{3}}=0 ? \rightarrow 7 *(-2,945)+5 * 0,243+6 * 3,233=0} Residuum exemplarisch: ${\widehat {\varepsilon _{15}}}=y_{15}-{\widehat {\mu _{1}}}=7,3-8,771=-1,471$

Aufgabe 3 Berechnen Sie für alle Beobachtungen aus Beispiel 2 die Residuen und bestimmen Sie jene Beobachtung, die durch das Modell am schlechtesten erklärt wird (d.h. das betragsmäßig größte Residuum aufweist).

Die Schätzungen der einzelnen Parameter beschränken sich also immer nur auf die Berechnung von Mittelwerten und deren Differenzen. Aus den Berechnungen von Beispiel 2 wissen wir nun beispielsweise, dass Drahtsorte 3 eine um 3,233 Newton/mm² größere Zugfestigkeit als der Durchschnitt aufweist. Das bezieht sich jedoch nur auf die beobachtete Stichprobe. Damit haben wir auf die ursprüngliche Frage „Unterscheiden sich die 3 Drahtsorten bezüglich der Zugfestigkeit“ nur eine deskriptivstatistische Antwort gegeben.

In der Regel ist aber von Interesse, ob wir durch die Daten genügend Evidenz dafür haben, dass sich auch die Mittelwerte der Grundgesamtheit (die Erwartungswerte) unter­scheiden. Hier ist es nun wieder erforderlich, einen statistischen Test zu berechnen.

Das Hypothesenpaar bei der einfaktoriellen Varianzanalyse lautet folgendermaßen:

Getestet wird also, ob alle Erwartungswerte gleich sind, oder zumindest zwei Erwartungswerte existieren, die ungleich sind.

Beim t-Test (Anzur, 2007, S. 71) wurde als relevante Prüfgröße die Differenz der Mittel­werte der beiden Gruppen bezogen auf den Standardfehler der Mittelwerts­differenz berechnet. Dieses Konzept ist nun nicht mehr möglich, da die Differenzen von mehr als zwei Gruppen berechnet werden müssten (die „mittlere“, die „maximale“, die „minimale“?). Anstelle der Differenz kommt nun das Konzept mit den Varianzen ins Spiel.

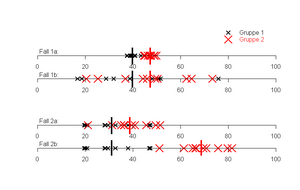
Abbildung 11 zeigt anhand von zwei Gruppen das Problem aber auch gleichzeitig die Lösung. Ziel der Varianzanalyse ist es, herauszufinden, ob die (durch­schnittliche) Lage der Beobachtungen auf dem Zahlenstrahl in beiden Gruppen gleich ist. In Fall 1 besteht zwischen Gruppe 1 und Gruppe 2 bei a und b dieselbe Mittelwertsdifferenz. Es ist aber mit freiem Auge ersichtlich, dass in Fall 1a besser zwischen den beiden Gruppen getrennt werden kann, als in Fall 1b. Grund sind die größeren Varianzen innerhalb der beiden Gruppen im Fall 1b. Bei Fall 2 streuen nun die Werte aller Gruppen gleich um ihren Mittelwert. Demnach sind die Varianzen innerhalb der Gruppen jeweils gleich. Nun kann besser zwischen jenen Gruppen getrennt werden, die den größeren Mittelwertsunterschied haben. Zusammen­gefasst heißt das, dass umso mehr Evidenz für eine unterschiedliche Lage der Gruppen gegeben ist, je größer die Mittelwertsdifferenz ist und je kleiner die Streuung der Werte um ihren eigenen Mittelwert ist. Im Fall von mehr als zwei Gruppen wird die Mittelwertsdifferenz einfach durch die Streuung (Varianz) der Gruppenmittelwerte ersetzt.

Gegenübergestellt werden in der Varianzanalyse also die Varianzen (Quadrat­summen ) „innerhalb“ der Gruppen und „zwischen“ den Gruppen. Die Hilfsgrößen, um einen Test für oben genanntes Hypothesenpaar durchzuführen sind solche Quadrat­summen. In der einfachen Varianzanalyse gilt immer folgende Quadratsummenzerlegung:

QT QI QZ

QT…Quadratsumme „Total“

QI…Quadratsumme „Innerhalb“

QZ…Quadratsumme „Zwischen“

Die Gesamtvariabilität der Daten QT kann also in zwei additive Teile gespalten werden. Dadurch bietet sich als weitere deskriptive Größe analog zur Regressions­analyse das Bestimmtheitsmaß an, welches als Quotient aus QZ und QT berechnet wird und wieder den Anteil an der durch das Modell erklärten Varianz an der Zielgröße angibt.

Aufgabe 4 Denken Sie sich zwei Datensätze aus (je drei Gruppen mit je fünf Beobachtungen pro Gruppe). Einen, bei dem das Bestimmtheitsmaß 100% beträgt und einen, bei dem das Bestimmtheitsmaß 0% beträgt. Welche Charakteristik haben die Daten jeweils.

Vier Datenreihen mit je zwei Gruppen,
 die gut bzw. schlecht getrennt werden können

Um nun inferenzstatistische Aussagen zu machen, wird nun die Quadratsumme „Zwischen“ nicht zur totalen Quadratsumme, sondern zur Quadratsumme „Innerhalb“ in Beziehung gesetzt. Dies liefert auch dann die Prüfgröße F für unsere Hypothese:

Es kann gezeigt werden, dass Datei:Media/image62.pngDatei:Media/image62.png unter Gültigkeit der Nullhypothese (die Erwar­tungswerte aller Gruppen sind gleich) und den anderen vorher erwähnten Modell­annahmen (Normalverteilung der Fehler) nach einer F-Verteilung mit Datei:Media/image63.pngDatei:Media/image63.png und Datei:Media/image64.pngDatei:Media/image64.png Freiheitsgraden verteilt ist. Dadurch werden Schranken definiert, bis zu wel­chen Werten von Datei:Media/image62.pngDatei:Media/image62.png eine Entscheidung für die Nullhypothese und ab wann eine Ent­scheidung für die Alternativhypothese erfolgt. Was man weiters wie bei jedem statistischen Test benötigt, ist Datei:Media/image65.pngDatei:Media/image65.png, die “Irrtumswahrscheinlichkeit“ (=die Wahr­scheinlichkeit, die Datei:Media/image66.pngDatei:Media/image66.png zu verwerfen, obwohl sie zutrifft).

Fortsetzung Beispiel 2

Aufgabe 5 Berechnen Sie für die Daten aus Beispiel 2 das Bestimmtheitsmaß.

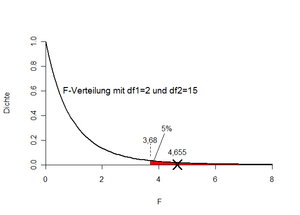
Soll bei Datei:Media/image71.pngDatei:Media/image71.png nun für die H₀ oder für die H₁ entschieden werden? Bei kleinen Werten von F beobachten wir entweder kleine Werte für QZ und/oder große Werte für QI. Beides spricht eher für die H₀. Umgekehrt sind große Werte für F eher Evidenz für H₁. Um die Frage zu beantworten, wird nun der „kritische Wert“ in der Tabelle der F-Verteilung (oder z.B. in Excel) nachgeschlagen. Bei Datei:Media/image72.pngDatei:Media/image72.png am oberen Ende der Verteilung suchen wir de facto das Datei:Media/image73.pngDatei:Media/image73.png-Quantil der F-Verteilung mit Datei:Media/image74.pngDatei:Media/image74.png und Datei:Media/image75.pngDatei:Media/image75.png Freiheitsgraden. In Excel kann dies mit der Funktion „FINV“ berechnet werden („=FINV(0,05;2;15)“). Dies liefert als maximal zulässigen F-Wert 3,68. Unser aus den Daten beobachtete F-Wert beträgt 4,655. Diese ist größer als der kritische Wert und daher wird die Nullhypothese verworfen. Ergebnis: Die drei Drahtsorten unterscheiden sich (bei Datei:Media/image72.pngDatei:Media/image72.png) signifikant voneinander bezüglich ihrer Zugfestigkeit. Abbildung 12 veranschaulicht die Entscheidungssituation nochmals.

In der Praxis rechnet man die Varianzanalyse natürlich wieder mit Software. In R kann wieder die Funktion „lm“ verwendet werden. Die unabhängige Variable muss aber als „Faktor“ spezifiziert werden, da sonst ein linearer Zusammenhang mit der Gruppennummer geschätzt wird.

Dichtefunktion von F unter Annahme der Nullhypothese

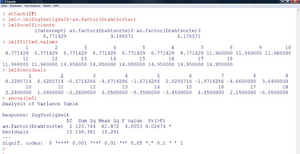
Abbildung 13 zeigt die Vorgehensweise in R, nachdem das csv-File eingelesen wurde (Name in R: „ZF“). Die geschätzten Koeffizienten sind hier nicht in der Effektkodierung angegeben (Datei:Media/image77.pngDatei:Media/image77.png in Abschnitt 2.2.1), sondern in der sogenannten „Dummykodierung“. Die Mittelwerte der einzelnen Gruppen werden folgendermaßen reproduziert:

Da die Zugehörigkeit zu einer der drei Drahtsorten die einzige Information ist, die zur Prognose der Zugfestigkeit verwendet werden kann, entsprechen die geschätzten Werte für die einzelnen Daten („fitted values“) genau diesen Mittelwerten. Die „Tafel der Varianzanalyse“ liefert nun aus inferenzstatistischer Sicht die Kerninformation. Der p-Wert des Tests (siehe „Pr(>F); die Wahrscheinlichkeit, unter Gültigkeit der Nullhypothese den aus den Daten berechneten Wert für F oder einen noch größeren zu erhalten) ist kleiner als das üblicherweise gewählte Niveau des Datei:Media/image65.pngDatei:Media/image65.png-Fehlers (5%). Daher erfolgt auch mittels Software die Entscheidung für H₁.

Einfaktorielle ANOVA - Parameterschätzung in R

Aufgabe 6 Abbildung 13 (unten) zeigt die typische „Tafel der Varianzanalyse“. Vergleichen Sie die darin vorkommenden Werte mit den bereits vorher berechneten, um die Berechnung nachzuvollziehen. In der Tafel ist statt des kritischen Wertes aus der F-Verteilung (3,68) der p-Wert ersichtlich. Versuchen Sie, die Berechnung des p-Werts in Excel mit der Funktion „FVERT“ nachzuvollziehen. Betrachten Sie dazu auch nochmals Abbildung 12. Argumentieren Sie, warum der p-Wert ausreichend ist, um für oder gegen H0 zu entscheiden und setzen Sie die Kriterien für die Testentscheidung, die in diesem Abschnitt auf zwei Wegen ermittelt wurde, zueinander in Beziehung.
Aufgabe 7 Zu welcher Entscheidung würde man in Beispiel 2 bei Datei:Media/image82.pngDatei:Media/image82.png kommen?
Aufgabe 8 In welchem Verhältnis müssten in Beispiel 2 (bei Datei:Media/image72.pngDatei:Media/image72.png bzw.Datei:Media/image83.pngDatei:Media/image83.png) die Quadratsummen „Zwischen“ und „Innerhalb“ stehen, damit gerade noch für die H0 entschieden wird. Wie groß wäre dann jeweils das zugehörige Bestimmtheitsmaß?

Prüfung der Modellvoraussetzungen, Residuenanalyse

Bei der Varianzanalyse beschränken sich die Prüfungen auf

• Ausreißer,
• Heteroskedastizität und
• Normalverteilung.

Diese werden gleich wie bei der Regressionsanalyse durchgeführt. Die Voraussetzung der Heteroskedastizität kann hier aber auch relativ einfach zusätzlich mit einem Test durchgeführt werden. Üblicherweise werden der Bartlett-Test (in R: Funktion „bartlett.test“) oder der Cochran-Test verwendet.

Multiple Mittelwertsvergleiche, Multiples Testen

Die Methode der einfaktoriellen Varianzanalyse liefert nur eine Antwort auf die Frage, ob es Unterschiede zwischen irgendwelchen zwei Gruppen gibt, aber nicht, zwischen welchen beiden Gruppen es diese Unterschiede gibt.

Um einzelne Unterschiede herauszufinden, müsste man theoretisch zwischen allen Gruppen paarweise t-Tests machen. Wie schon erwähnt, ist die einfaktorielle Varianzanalyse ja eine Verallgemeinerung des t-Tests. Man müsste dann allerdings Datei:Media/image84.pngDatei:Media/image84.png solche t-Tests berechnen. Bei Datei:Media/image85.pngDatei:Media/image85.png Gruppen wären das schon 10 t-Tests.

Die (neben der Notwendigkeit der zehnmaligen Durchführung eines Tests) auftretende Problematik ist, dass wenn bei jedem einzelnen Test eine 5%-Wahrscheinlichkeit besteht, einen Datei:Media/image65.pngDatei:Media/image65.png-Fehler zu begehen (d.h. die Nullhypothese fälschlicherweise zu verwerfen), die Wahrscheinlichkeit, bei 10 Tests zumindest einmal einen Datei:Media/image65.pngDatei:Media/image65.png-Fehler zu begehen, viel höher ist. Formal wäre diese Wahrscheinlichkeit

Man kann sich das auch so vorstellen: Spielt man einmal eine Runde im Lotto mit, besteht nur eine sehr kleine Chance, einen Gewinn zu erzielen. Jedoch ist die Wahrscheinlichkeit, in 100 Lottorunden zumindest einmal zu gewinnen schon relativ hoch (wenngleich das zumeist auch die entstandenen Einsätze nicht ausgleicht…).

Die Lösung zum Testproblem ist nun, entweder den Datei:Media/image65.pngDatei:Media/image65.png-Fehler jedes einzelnen Tests derart zu reduzieren, dass Datei:Media/image87.pngDatei:Media/image87.png dem ursprünglich beabsichtigten Datei:Media/image65.pngDatei:Media/image65.png entspricht, oder die Methode der Varianzanalyse zu verwenden, bei der nur ein Test durchgeführt wird.

In der Praxis berechnet man bei derartigen Fragestellungen zuerst eine Varianz­ana­lyse. Fällt diese signifikant aus, werden anschließend sogenannte Post-Hoc-Tests gerechnet, die herausfinden sollen, zwischen welchen Gruppen die Unterschiede bestehen. In diesen Prozeduren werden die Datei:Media/image65.pngDatei:Media/image65.png-Fehler dann automatisch korrigiert.

Die zweifache Varianzanalyse für unabhängige Stichproben

Beispiel 3 Der Marketingleiter eines Lebensmittelkonzerns steht vor der Frage, zu welchem empfohlenen Richtpreis eine neue Margarinemarke auf den Markt gebracht werden soll. Grundsätzlich stehen ihm drei Strategien zur Verfügung: „Niedrigpreispolitik“, d.h. das Produkt wird unter dem Preis vergleichbarer Konkurrenzprodukte angeboten; „Normalpreispolitik“; „Hochpreispolitik“, d.h. das Produkt wird über dem Preis vergleichbarer Konkurrenzprodukte angeboten. Neben der Preisstrategie (Faktor A) ist die Kommunikationsstrategie (Faktor B) von Interesse, und zwar in den alternativen Formen „Postwurfsendungen“, „Anzeigenwerbung in regionalen Zeitungen“. Um die Wirkungen der Faktoren auf das Kaufverhalten zu untersuchen, wählt der Marketingleiter einen (3 x 2)-Versuchsplan, wobei auf die Kunden der ausgewählten Supermärkte jeweils eine unterschiedliche Kombination von Preis- und Kommunikationsstrategie wirken. An jeweils 10 zufällig ausgewählten Tagen werden die abgesetzten Mengeneinheiten der Margarine registriert. Die Resultate sind in der folgenden Tabelle wiedergegeben. Niedrigpreispolitik Postwurfsendungen 68 65 63 59 67 64 66 59 64 63 Anzeigenwerbung 59 57 54 56 53 51 52 55 54 52 Normalpreispolitik Postwurfsendungen 59 50 51 48 53 49 50 52 53 50 Anzeigenwerbung 51 45 46 48 49 50 47 46 45 47 Hochpreispolitik Postwurfsendungen 40 39 35 36 37 35 34 38 39 36 Anzeigenwerbung 47 39 40 46 45 49 44 48 47 44

Modell der zweifachen Varianzanalyse für unabhängige Stichproben

Bei Vorliegen eines zweiten Faktors erweitert sich das einfaktorielle Modell zu

wobei Datei:Media/image90.pngDatei:Media/image90.png die Werte der metrischen Variable sind (Datei:Media/image91.pngDatei:Media/image91.png-ter Wert bei Preispolitik Datei:Media/image42.pngDatei:Media/image42.png und Kommunikationsstrategie Datei:Media/image92.pngDatei:Media/image92.png), Datei:Media/image40.pngDatei:Media/image40.png der unbedingte Erwartungswert (ohne Kenntnis der Gruppe), Datei:Media/image41.pngDatei:Media/image41.png der Effekt der jeweiligen Preispolitik, Datei:Media/image10.pngDatei:Media/image10.png der Effekt der jeweiligen Kommunikationsstrategie, Datei:Media/image93.pngDatei:Media/image93.png jener Effekt ist, der sich aus der Kombination der Preispolitik Datei:Media/image42.pngDatei:Media/image42.png mit der Kommunikationsstrategie Datei:Media/image92.pngDatei:Media/image92.png zusätzlich ergeben könnte und Datei:Media/image94.pngDatei:Media/image94.png der durch die drei Effektgruppen nicht erklärte Teil der abhängigen Variable ist. Die Annahmen für Datei:Media/image94.pngDatei:Media/image94.png sind analog zum einfaktoriellen Modell.

Es kommen bei zwei erklärenden Faktoren also nicht zwei sondern drei Parameter­gruppen vor, weil es möglich ist, dass Kombinationen von Effekten andere Mittelwerte in der abhängigen Variable liefern. Dies wird im weiteren Verlauf der Analyse klarer.

Schätzen und Testen bei der zweifachen Varianzanalyse

Wie bei der einfachen Varianzanalyse können die einzelnen „Anteile“ an der Messung nun geschätzt werden.

Schätzung der durchschnittlichen Kaufmenge Datei:Media/image40.pngDatei:Media/image40.png durch

Schätzung des Effekts der Preispolitik i, Datei:Media/image41.pngDatei:Media/image41.png, durch

Schätzung des Effekts der Kommunikationsstrategie j, Datei:Media/image10.pngDatei:Media/image10.png, durch

Schätzung des Interaktionseffektes (Preispolitik vs. Kommunikationsstrategie) durch

Schätzung des Fehlers Datei:Media/image94.pngDatei:Media/image94.png durch das Residuum

Aufgabe 9 Berechnen Sie die Schätzungen für Datei:Media/image100.pngDatei:Media/image100.png (1), Datei:Media/image101.pngDatei:Media/image101.png (3) Datei:Media/image102.pngDatei:Media/image102.png (2) und Datei:Media/image103.pngDatei:Media/image103.png (3*2=6)

Ob die in Aufgabe 9 berechneten deskriptiven Effekte signifikant sind, kann wieder analog obiger Vorgehensweise berechnet werden. Geprüft werden können nun drei Hypothesenpaare:

Datei:Media/image104.pngDatei:Media/image104.png Kein Einfluss der Preispolitik auf den Absatz

Datei:Media/image105.pngDatei:Media/image105.png Einfluss der Preispolitik auf die Absatz

Datei:Media/image106.pngDatei:Media/image106.png Kein Einfluss der Komm.-Strategie auf den Absatz

Datei:Media/image107.pngDatei:Media/image107.png Einfluss der Komm.-Strategie auf den Absatz

Interaktionen (Datei:Media/image110.pngDatei:Media/image110.png) bzw. keine Interaktionen (Datei:Media/image111.pngDatei:Media/image111.png) zwischen Preispolitik und Komm.-Strategie in Bezug auf den Absatz.

Für jede Hypothese kann nun wieder eine Quadratsumme, eine daraus abgeleitete, unter H₀ F-verteilte Prüfgröße Datei:Media/image62.pngDatei:Media/image62.png, sowie zur Bestimmung der Signifikanz ein p-Wert berechnet werden.

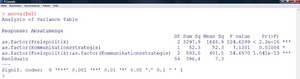
Fortsetzung Beispiel 3 In R wird das lineare Modell nun so spezifiziert: Marketing<-read.csv("C:\\...\\...\\Marketing.csv",header=TRUE,dec=",",sep=";") attach(Marketing) lm1<-lm(Absatzmenge~as.factor(Preispolitik)+as.factor(Kommunikationsstrategie)+ as.factor(Preispolitik):as.factor(Kommunikationsstrategie)) anova(lm1) Man erhält dann folgende Tabelle (Abbildung 14): Zweifaktorielle ANOVA - Tafel der Varianzanalyse in R Alle p-Werte (Spalte rechts) sind kleiner als 5%. Daher wird in allen drei Fällen die Nullhypothese verworfen. Das Ergebnis ist (in Zusammenhang mit Aufgabe 9): Die Preispolitik hat einen signifikanten Einfluss auf die Absatzmenge des Produktes. Erwartungsgemäß wird bei höheren Preisen im Mittel weniger abgesetzt. Die Kommunikationsstrategie hat ebenfalls einen Einfluss auf die Absatzmenge. Bei Postwurfsendungen ist die durchschnittlich abgesetzte Menge größer. Es gibt signifikante Interaktionen zwischen Preispolitik und Kommunikations­strategie: Die Postwurfsendungen liefern nicht bei jeder Preispolitik die höhere Absatzmenge. Bei Hochpreispolitik ist Anzeigenwerbung erfolg­reicher. Die einzelnen Effekte (jene, die ausreichen, um das lineare Modell vollständig zu schätzen) können auch wieder mittels „lm1$coefficients“ ausgegeben werden. Folgender Befehl visualisiert diese Zusammenhänge schließlich noch in einem einfachen Liniendiagramm der Mittelwerte: interaction.plot(Preispolitik,Kommunikationsstrategie,Absatzmenge)

Ist ein balanciertes Design vorhanden (wie im Beispiel), macht es keinen Unterschied, in welcher Reihenfolge die Faktoren in die Gleichung eingegeben werden. Bei unbalancierten Designs ist die Interpretation der Signifikanzen schwieriger, da die Reihenfolge, in der die einzelnen Faktoren in die Gleichung eingehen, entscheidend ist.

Weitere Beispiele für varianzanalytische Designs

Varianzanalyse bei abhängigen Stichproben

Einfache Varianzanalyse für abhängige Stichproben

Wie beim t-Test für abhängige Stichproben kann auch eine Varianzanalyse für abhängige Stichproben berechnet werden. Beispielsweise, wenn Messung von Personen zu drei oder mehr Zeitpunkten vorliegen. In diesem Design können zwei Effekte geprüft werden: Unterschiede in der Versuchsbedingung (hier: Messzeitpunkt) und Unterschiede in den Versuchseinheiten (hier Personen).

Zweifache Varianzanalyse mit Messwiederholung

Hier können die Daten zum Beispiel zwei Gruppen von Personen (z.B. Männer und Frauen) sein, an denen je drei Messungen durchgeführt werden.

Unvollständige varianzanalytische Designs

Wenn nicht in allen Faktorkombinationen Daten erhoben werden, heißt das varianzanalytische Design „unvollständig“. Im folgenden werden zwei Beispiele für unvollständige Designs erwähnt.

Hierarchisches Design

Ein hierarchisches Design könnte sich beispielsweise dann ergeben, wenn man an der Wirkung eines Medikamentes, sowie am Behandlungserfolg verschiedener Spitäler interessiert ist. Sollen acht Medikamente und zwei Spitäler untersucht werden, ergibt sich ein Versuchsplan mit 2*8=12 Faktorkombinationen. Falls nun die Medikamente 1-4 nur in Spital 1 verwendet werden und die Medikamente 5-8 nur in Spital 2, dann können nicht wie in Beispiel 3 auch Wechselwirkungen auf Signifikanz getestet werden. Man sagt, dass der Faktor Medikament im Faktor Spital geschachtelt ist (auch „nested“). Dementsprechend müssen die Formeln der zweifaktoriellen ANOVA im vollständigen Design adaptiert werden.

Lateinisches Quadrat

Ein unvollständiges Design, das nicht durch mangelnde Verfügbarkeit der Daten, sondern vom Versuchsplaner selbst erzeugt wird, ist das „lateinische Quadrat“. Als Beispiel sei eine dreifaktorielle Varianzanalyse mit je drei Faktorstufen gegeben. Bei 10 Versuchseinheiten in jeder Kombination müsste man insgesamt 3*3*3*n Versuchseinheiten zur Verfügung haben. Stattdessen wird das Design auf z.B. 3*3 Faktorkombinationen gekürzt, sodass allerdings immer noch jede Faktorstufe und jede Kombination aus zwei Faktorstufen gleich oft vorkommt (Tabelle 1 und Tabelle 2). Der Vorteil dieses Designs liegt in der Kostenersparnis der Erhebung. Der Nachteil ist, dass nicht alle Hypothesen des vollständigen Designs prüfbar sind. Ist man ohnehin nur an den Einzelwirkungen der drei Faktoren und nicht an Interaktionen interessiert, fällt dieser Nachteil weg.

Tabelle 1: Übersicht über die gewählten Faktorkombinationen bei einer Kürzung
auf ein lateinisches Quadrat. Die Marker (X) geben an, welche Kombinationen tatsächlich gewählt werden

	B1			B2			B3
	C1	C2	C3	C1	C2	C3	C1	C2	C3
A1	X					X		X
A2		X		X					X
A3			X		X		X

Tabelle 2: Lateinisches Quadrat aus Tabelle 1 in Kurzschreibweise

	C1	C2	C3
A1	B1	B3	B2
A2	B2	B1	B3
A3	B3	B2	B1

Wiederholungsaufgaben und Zusammenfassung

1. Welche Bedeutung kommt der Quadratsummenzerlegung in der Varianzanalyse zu?
2. Warum ist es wichtig, dass die Fehler normalverteilt sind?
3. Sie erhalten bei einer einfaktoriellen Varianzanalyse mit Datei:Media/image72.pngDatei:Media/image72.png ein signifikantes Ergebnis. Wäre das Ergebnis auch signifikant, wenn Sie

• einen gleichgroßen Effekt (gleich große Mittelwertsdifferenzen) bei einem doppelt so großen Stichprobenumfang beobachten würden?
• einen gleichgroßen Effekt (gleich große Mittelwertsdifferenzen) bei einem halb so großen Stichprobenumfang beobachten würden?
• auf Datei:Media/image82.pngDatei:Media/image82.png testen?

4. Wie verändert sich der kritische Wert der F-Verteilung bei der Varianzanalyse, wenn Datei:Media/image65.pngDatei:Media/image65.png von 5% auf 1% gesenkt wird?

Zusammenfassung

Der Begriff „Varianzanalyse“ steht für eine große Zahl an Verfahren, bei denen mithilfe der Berechnung von Varianzen bzw. Quadratsummen inferenzstatistische Aussagen über Beziehungen verschiedener Variablen gemacht werden können („Quadratsummenzerlegung“). Dabei ist die Modellvorstellung immer, dass es eine oder mehrere gruppierende Variablen gibt, die auf eine metrische Variable einwirken (univariate ANOVA). Die Gruppeneinteilung kann „randomisiert“ erfolgen (indem die Versuchseinheiten zu verschiedenen Gruppen zugeordnet werden “Experiment“; Kausalschluss möglich) oder schon vorgegeben sein („Kranke vs. Gesunde“, „Männer vs. Frauen“, „Raucher vs. Nichtraucher“ „Beobachtungsstudie“; Kausalschluss nicht möglich).

Die Rechenschritte im Zuge einer Varianzanalyse betreffen einerseits die Parameterschätzungen des Modells welche auf die Berechnung von Gruppenmittelwerten und deren Differenzen hinauslaufen. Andererseits geschieht die Beurteilung, ob die in der Stichprobe gefundenen Unterschiede für die Grundgesmtheit verallgemeinert werden können, erst jeweils mittels des F-Tests, mittels Verteilungsannahmen, die sich aus der Forderung von normalverteilten Daten ableiten. Grundsätzlich gilt, dass soviele Hypothesen wie Effektgruppen vorhanden sind, getestet werden können.

Die Ergebnisse der Hypothesenprüfung werden jeweils in einer „Tafel der Varianzanalyse“ übersichtlich zusammengefasst.