Methoden der Datenanalyse - Varianzanalyse: Unterschied zwischen den Versionen

Version vom 17. Jänner 2022, 13:45 Uhr

\underbrace {\sum _{i=1}^{k}\sum _{j=1}^{n_{1}}\left(y_{ij}-{\hat {\mu }}\right)^{2}} _{\mathrm {QT} }=\underbrace {\sum _{i=1}^{k}\sum _{j=1}^{n_{1}}\left(y_{ij}-{\hat {\mu }}_{i}\right)^{2}} _{\mathrm {QI} }+\underbrace {\sum _{i=1}^{k}n_{i}\left({\hat {\mu }}_{i}-{\hat {\mu }}\right)^{2}} _{\mathrm {QZ} }

QT…Quadratsumme „Total“

QI…Quadratsumme „Innerhalb“

QZ…Quadratsumme „Zwischen“

Die Gesamtvariabilität der Daten QT kann also in zwei additive Teile gespalten werden. Dadurch bietet sich als weitere deskriptive Größe analog zur Regressionsanalyse das Bestimmtheitsmaß an, welches als Quotient aus QZ und QT berechnet wird und wieder den Anteil an der durch das Modell erklärten Varianz an der Zielgröße angibt.

Aufgabe 4 Denken Sie sich zwei Datensätze aus (je drei Gruppen mit je fünf Beobachtungen pro Gruppe). Einen, bei dem das Bestimmtheitsmaß 100% beträgt und einen, bei dem das Bestimmtheitsmaß 0% beträgt. Welche Charakteristik haben die Daten jeweils.

Vier Datenreihen mit je zwei Gruppen,
die gut bzw. schlecht getrennt werden können

Um nun inferenzstatistische Aussagen zu machen, wird nun die Quadratsumme „Zwischen“ nicht zur totalen Quadratsumme, sondern zur Quadratsumme „Innerhalb“ in Beziehung gesetzt. Dies liefert auch dann die Prüfgröße F ^[1] für unsere Hypothese:

F={\frac {MQZ}{MQI}}={\frac {{\frac {1}{k-1}}QZ}{{\frac {1}{N-k}}QI}}={\frac {(N-k)QZ}{(k-1)QI}}\qquad {\left[N=n_{1}+n_{2}+n_{3}\right]}

Es kann gezeigt werden, dass $F$ unter Gültigkeit der Nullhypothese (die Erwartungswerte aller Gruppen sind gleich) und den anderen vorher erwähnten Modellannahmen (Normalverteilung der Fehler) nach einer F-Verteilung mit $k-1$ und $N-k$ Freiheitsgraden verteilt ist. Dadurch werden Schranken definiert, bis zu welchen Werten von eine Entscheidung für die Nullhypothese und ab wann eine Entscheidung für die Alternativhypothese erfolgt. Was man weiters wie bei jedem statistischen Test benötigt, ist $\alpha$ , die “Irrtumswahrscheinlichkeit“ (=die Wahrscheinlichkeit, die $H_{0}$ zu verwerfen, obwohl sie zutrifft).

Fortsetzung Beispiel 2

QT=(9-11,717)^{2}+\cdots (14,1-11,717)^{2}=323,105

QI=(9-8,771)^{2}+\cdots +(6,8-8,771)^{2}+\cdots +(14,1-14,950)^{2}=199,361

QZ=QT-QI=323,105-199,361=123,744

F={\frac {{\frac {1}{3-1}}*123,744}{{\frac {1}{18-3}}*199,361}}={\frac {61,872}{13,291}}=4,655

Aufgabe 5

↑ Die Prüfgröße F bzw. die Prüfverteilung ist benannt nach Sir Ronald A. Fisher, der erstmals im Jahre 1935 mit Erscheinen seines Buches „The Design of Experiments“ eine ausführliche Darstellung von Varianzanalyse und Versuchsplanung veröffentlichte (Hartung, 1998, S.12).

[1] Die Prüfgröße F bzw. die Prüfverteilung ist benannt nach Sir Ronald A. Fisher, der erstmals im Jahre 1935 mit Erscheinen seines Buches „The Design of Experiments“ eine ausführliche Darstellung von Varianzanalyse und Versuchsplanung veröffentlichte (Hartung, 1998, S.12).

[1]

@@ Zeile 1: / Zeile 1: @@
-{|
+<math display="block">
-! width="100%" | '''Fortsetzung Beispiel 2'''
+\underbrace{\sum_{i=1}^{k} \sum_{j=1}^{n_{1}}\left(y_{i j}-\hat{\mu}\right)^{2}}_{\mathrm{QT}}=\underbrace{\sum_{i=1}^{k} \sum_{j=1}^{n_{1}}\left(y_{i j}-\hat{\mu}_{i}\right)^{2}}_{\mathrm{QI}}+\underbrace{\sum_{i=1}^{k} n_{i}\left(\hat{\mu}_{i}-\hat{\mu}\right)^{2}}_{\mathrm{QZ}}
+</math>
+QT…Quadratsumme „Total“
+QI…Quadratsumme „Innerhalb“
+QZ…Quadratsumme „Zwischen“
+Die Gesamtvariabilität der Daten QT kann also in zwei additive Teile gespalten werden. Dadurch bietet sich als weitere deskriptive Größe analog zur Regressionsanalyse das Bestimmtheitsmaß an, welches als Quotient aus QZ und QT berechnet wird und wieder den Anteil an der durch das Modell erklärten Varianz an der Zielgröße angibt.
-<math display="block">\hat{\mu}=\frac{1}{7+5+6}(9+15,4+\cdots+6,8+7,3+\cdots+9,7+18+\cdots+14,1)=11,717 </math>
-<math display="block">\widehat{\alpha_{1}}=\widehat{\mu_{1}}-\hat{\mu}=\frac{1}{7}(9+15,4+\cdots+6,8)-11,717=8,771-11,717=-2,945 </math>
-<math display="block">\widehat{\alpha_{2}}=\widehat{\mu_{2}}-\hat{\mu}=\frac{1}{5}(7,3+15,6+\cdots+9,7)-11,717=11,960-11,717=0,243 </math>
-<math display="block">\widehat{\alpha_{3}}=\widehat{\mu_{3}}-\hat{\mu}=\frac{1}{6}(18+9,6+\cdots+14,1)-11,717=14,950-11,717=3,233 </math>
-Kontrolle: <math display="block">n_{1} \widehat{\alpha_{1}}+n_{2} \widehat{\alpha_{2}}+n_{3} \widehat{\alpha_{3}}=0 ? \rightarrow 7 *(-2,945)+5 * 0,243+6 * 3,233=0</math>
-Residuum exemplarisch: <math display="block">\widehat{\varepsilon_{15}}=y_{15}-\widehat{\mu_{1}}=7,3-8,771=-1,471</math>
-|}
 {|
-! width="100%" | '''Aufgabe 3'''
+! width="100%" | '''Aufgabe 4'''
-Berechnen Sie für alle Beobachtungen aus Beispiel 2 die Residuen und bestimmen Sie jene Beobachtung, die durch das Modell am schlechtesten erklärt wird (d.h. das betragsmäßig größte Residuum aufweist).
+Denken Sie sich zwei Datensätze aus (je drei Gruppen mit je fünf Beobachtungen pro Gruppe). Einen, bei dem das Bestimmtheitsmaß 100% beträgt und einen, bei dem das Bestimmtheitsmaß 0% beträgt. Welche Charakteristik haben die Daten jeweils.
 |}
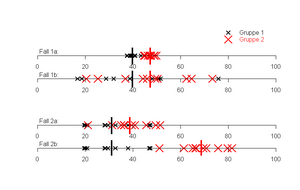
-Die Schätzungen der einzelnen Parameter beschränken sich also immer nur auf die Berechnung von Mittelwerten und deren Differenzen. Aus den Berechnungen von Beispiel 2 wissen wir nun beispielsweise, dass Drahtsorte 3 eine um 3,233 Newton/mm<sup>2</sup> größere Zugfestigkeit als der Durchschnitt aufweist. Das bezieht sich jedoch nur auf die beobachtete Stichprobe. Damit haben wir auf die ursprüngliche Frage „Unterscheiden sich die 3 Drahtsorten bezüglich der Zugfestigkeit“ nur eine deskriptivstatistische Antwort gegeben.
+[[file:img1642169593358.png|300px|none|thumb|Vier Datenreihen mit je zwei Gruppen,<br class="mwt-preserveHtml" data-mwt-sameline="true" data-mwt-spaces="" /><span class="mwt-placeHolder mwt-singleLinebreak mwt-slbltr mwt-hidePlaceholder" title="Non-displayed single linebreak" contenteditable="false" draggable="true"> </span>die gut bzw. schlecht getrennt werden können]]
-In der Regel ist aber von Interesse, ob wir durch die Daten genügend Evidenz dafür haben, dass sich auch die Mittelwerte der Grundgesamtheit (die Erwartungswerte) unterscheiden. Hier ist es nun wieder erforderlich, einen statistischen Test zu berechnen.
-Das Hypothesenpaar bei der einfaktoriellen Varianzanalyse lautet folgendermaßen:
+Um nun inferenzstatistische Aussagen zu machen, wird nun die Quadratsumme „Zwischen“ nicht zur totalen Quadratsumme, sondern zur Quadratsumme „Innerhalb“ in Beziehung gesetzt. Dies liefert auch dann die Prüfgröße F <ref>Die Prüfgröße F bzw. die Prüfverteilung ist benannt nach Sir Ronald A. Fisher, der erstmals im Jahre 1935 mit Erscheinen seines Buches „The Design of Experiments“ eine ausführliche Darstellung von Varianzanalyse und Versuchsplanung veröffentlichte (Hartung, 1998, S.12).</ref>  für unsere Hypothese:
 <math display="block">
-H_{0}: \mu_{1}=\mu_{2}=\cdots=\mu_{k} \Leftrightarrow \alpha_{1}=\alpha_{2}=\cdots=\alpha_{k}=0
+F=\frac{M Q Z}{M Q I}=\frac{\frac{1}{k-1} Q Z}{\frac{1}{N-k} Q I}=\frac{(N-k) Q Z}{(k-1) Q I}  \qquad
-</math>
+{\left[N=n_{1}+n_{2}+n_{3}\right]}
-<math display="block">
-H_{1}: \exists(i, j): \mu_{i} \neq \mu_{j} \Leftrightarrow \exists \alpha_{i} \neq 0
 </math>
-Getestet wird also, ob alle Erwartungswerte gleich sind, oder zumindest zwei Erwartungswerte existieren, die ungleich sind.
+Es kann gezeigt werden, dass <math>F</math> unter Gültigkeit der Nullhypothese (die Erwartungswerte aller Gruppen sind gleich) und den anderen vorher erwähnten Modellannahmen (Normalverteilung der Fehler) nach einer F-Verteilung mit <math>k-1</math> und <math>N-k</math> Freiheitsgraden verteilt ist. Dadurch werden Schranken definiert, bis zu welchen Werten von <math></math> eine Entscheidung für die Nullhypothese und ab wann eine Entscheidung für die Alternativhypothese erfolgt. Was man weiters wie bei jedem statistischen Test benötigt, ist <math>\alpha</math>, die “Irrtumswahrscheinlichkeit“ (=die Wahrscheinlichkeit, die <math>H_0</math> zu verwerfen, obwohl sie zutrifft).
-Beim t-Test (Anzur, 2007, S. 71) wurde als relevante Prüfgröße die Differenz der Mittelwerte der beiden Gruppen bezogen auf den Standardfehler der Mittelwertsdifferenz berechnet. Dieses Konzept ist nun nicht mehr möglich, da die Differenzen von mehr als zwei Gruppen berechnet werden müssten (die „mittlere“, die „maximale“, die „minimale“?). Anstelle der Differenz kommt nun das Konzept mit den Varianzen ins Spiel.
+{|
+! width="100%" | '''Fortsetzung Beispiel 2'''
-Abbildung 11 zeigt anhand von zwei Gruppen das Problem aber auch gleichzeitig die Lösung. Ziel der Varianzanalyse ist es, herauszufinden, ob die (durchschnittliche) Lage der Beobachtungen auf dem Zahlenstrahl in beiden Gruppen gleich ist. In Fall 1 besteht zwischen Gruppe 1 und Gruppe 2 bei a und b dieselbe Mittelwertsdifferenz. Es ist aber mit freiem Auge ersichtlich, dass in Fall 1a besser zwischen den beiden Gruppen getrennt werden kann, als in Fall 1b. Grund sind die größeren Varianzen innerhalb der beiden Gruppen im Fall 1b. Bei Fall 2 streuen nun die Werte aller Gruppen gleich um ihren Mittelwert. Demnach sind die Varianzen innerhalb der Gruppen jeweils gleich. Nun kann besser zwischen jenen Gruppen getrennt werden, die den größeren Mittelwertsunterschied haben. Zusammengefasst heißt das, dass umso mehr Evidenz für eine unterschiedliche Lage der Gruppen gegeben ist, je größer die Mittelwertsdifferenz ist und je kleiner die Streuung der Werte um ihren eigenen Mittelwert ist. Im Fall von mehr als zwei Gruppen wird die Mittelwertsdifferenz einfach durch die Streuung (Varianz) der Gruppenmittelwerte ersetzt.
+<math display="block">
+Q T=(9-11,717)^{2}+\cdots(14,1-11,717)^{2}=323,105
+</math>
+<math display="block">
+Q I=(9-8,771)^{2}+\cdots+(6,8-8,771)^{2}+\cdots+(14,1-14,950)^{2}=199,361
+</math>
+<math display="block">
+Q Z=Q T-Q I=323,105-199,361=123,744
+</math>
+<math display="block">
+F=\frac{\frac{1}{3-1} * 123,744}{\frac{1}{18-3} * 199,361}=\frac{61,872}{13,291}=4,655
+</math>
-Gegenübergestellt werden in der Varianzanalyse also die Varianzen (Quadratsummen <ref>Unter Quadratsumme wird die Summe von quadrierten Zahlen verstanden. In der Varianzanalyse geht es immer um die Summe von quadrierten Abweichungen von Mittelwerten. Im Prinzip ist eine Quadratsumme eine Varianz, die nicht durch den Stichprobenumfang dividiert wurde.</ref> ) „innerhalb“ der Gruppen und „zwischen“ den Gruppen. Die Hilfsgrößen, um einen Test für oben genanntes Hypothesenpaar durchzuführen sind solche Quadratsummen. In der einfachen Varianzanalyse gilt immer folgende Quadratsummenzerlegung:
+|-
+|
+<br>
+|}
+{|
+! width="100%" | '''Aufgabe 5'''

Methoden der Datenanalyse - Varianzanalyse: Unterschied zwischen den Versionen

Version vom 17. Jänner 2022, 13:45 Uhr

Navigationsmenü

Suche