Computer- und Netzwerksicherheit - Kryptograhpie: Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
Der Schlüssel wird für die gesamte Länge der Nachricht immer wieder wiederholt. Im Beispiel befindet sich der Buchstabe D bei seinem ersten vorkommen im Text unter dem Buchstaben K des Schlüssels und wird daher um 10 Zeichen verschoben und somit zu einem N. Bei seinem zweiten Vorkommen befindet sich das D der Nachricht jedoch unter dem Y des Schlüssels und wird daher zu einem B. | Der Schlüssel wird für die gesamte Länge der Nachricht immer wieder wiederholt. Im Beispiel befindet sich der Buchstabe D bei seinem ersten vorkommen im Text unter dem Buchstaben K des Schlüssels und wird daher um 10 Zeichen verschoben und somit zu einem N. Bei seinem zweiten Vorkommen befindet sich das D der Nachricht jedoch unter dem Y des Schlüssels und wird daher zu einem B. | ||
Um den Abstand zwischen dem Zeichen der Nachricht und dem Zeichen des Schlüssels schneller manuell ermitteln zu können wird oft eine Tabelle eingesetzt, in der alle möglichen Abstandskombinationen aufgelistet sind. Diese wird als Vigenere-Tabelle bezeichnet und ist in Abbildung | Um den Abstand zwischen dem Zeichen der Nachricht und dem Zeichen des Schlüssels schneller manuell ermitteln zu können wird oft eine Tabelle eingesetzt, in der alle möglichen Abstandskombinationen aufgelistet sind. Diese wird als Vigenere-Tabelle bezeichnet und ist in Abbildung "Vigenere-Tabelle" zu sehen. | ||
[[Datei:IT244 7.png|300px|none|thumb|Vigenere-Tabelle]] | [[Datei:IT244 7.png|300px|none|thumb|Vigenere-Tabelle]] | ||
| Zeile 72: | Zeile 72: | ||
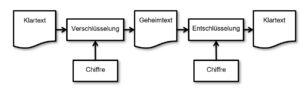
Bei der '''Verschlüsselung''' handelt es sich um die Umwandlung von Klartext in Geheimtext mittels zugehöriger Chiffre und Schlüssel und bei der '''Entschlüsselung''' um die Umwandlung des Geheimtextes zurück in den Klartext. | Bei der '''Verschlüsselung''' handelt es sich um die Umwandlung von Klartext in Geheimtext mittels zugehöriger Chiffre und Schlüssel und bei der '''Entschlüsselung''' um die Umwandlung des Geheimtextes zurück in den Klartext. | ||
Der Ablauf eines Weges vom Klartext über den Geheimtext zurück zum Klartext ist in Abbildung | Der Ablauf eines Weges vom Klartext über den Geheimtext zurück zum Klartext ist in Abbildung "Zusammenhang der Kryptographie Begriffe" noch einmal grafisch dargestellt. | ||
[[Datei:IT244 8.png|300px|none|thumb|Zusammenhang der Kryptographie Begriffe]] | [[Datei:IT244 8.png|300px|none|thumb|Zusammenhang der Kryptographie Begriffe]] | ||
| Zeile 89: | Zeile 89: | ||
== Symmetrische Verfahren == | == Symmetrische Verfahren == | ||
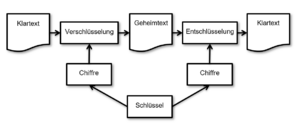
Bei einem symmetrischen kryptographischen Verfahren (Chiffre) wird ein Klartext mit ein und '''demselben Schlüssel''' verschlüsselt und auch wieder entschlüsselt (siehe Abbildung | Bei einem symmetrischen kryptographischen Verfahren (Chiffre) wird ein Klartext mit ein und '''demselben Schlüssel''' verschlüsselt und auch wieder entschlüsselt (siehe Abbildung "Symmetrische Verfahren mit einem Schlüssel"). Bei symmetrischen Verfahren werden '''Substitutions-Methoden''' und '''Transpositions-Methoden''' angewendet, um den Klartext unkenntlich zu machen. Diese können innerhalb der Chiffre natürlich auch beliebig kombiniert werden. | ||
[[Datei:IT244 9.png|300px|none|thumb|Symmetrische Verfahren mit einem Schlüssel]] | [[Datei:IT244 9.png|300px|none|thumb|Symmetrische Verfahren mit einem Schlüssel]] | ||
| Zeile 119: | Zeile 119: | ||
Bei der Transposition werden einzelne Teile des Textes mit anderen Teilen vertauscht. Der Schlüssel gibt dabei an, welcher Teil mit welchem vertauscht werden soll. | Bei der Transposition werden einzelne Teile des Textes mit anderen Teilen vertauscht. Der Schlüssel gibt dabei an, welcher Teil mit welchem vertauscht werden soll. | ||
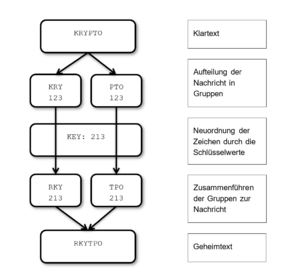
Ein Beispiel für eine einfache Transpositions-Methode ist in Abbildung | Ein Beispiel für eine einfache Transpositions-Methode ist in Abbildung "Transpositions-Cipher" dargestellt. Dabei wird der Plaintext zuerst in Gruppen zerlegt. Diese Gruppen werden nun gemäß dem Schlüsselwert intern neu angeordnet und ergeben dann in Summe wiederum den Ausgabetext. Auch diese Methode ist in beide Richtungen – sowohl zur Ver-, als auch zur Entschlüsselung – anwendbar. | ||
[[Datei:IT244 10.png|300px|none|thumb|Transpositions-Cipher]] | [[Datei:IT244 10.png|300px|none|thumb|Transpositions-Cipher]] | ||
| Zeile 126: | Zeile 126: | ||
=== Aktuelle Kryptographie-Standards mit symmetrischen Methoden === | === Aktuelle Kryptographie-Standards mit symmetrischen Methoden === | ||
In der nachfolgenden Tabelle | In der nachfolgenden Tabelle "Gängige Standards mit symmetrischen Algorithmen" sind die aktuell gängigsten symmetrischen Chiffren und ihre Eckpunkte aufgelistet. | ||
<span id="_Ref414288799" class="anchor"></span>Tabelle : Gängige Standards mit symmetrischen Algorithmen | <span id="_Ref414288799" class="anchor"></span>Tabelle: Gängige Standards mit symmetrischen Algorithmen | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
| Zeile 168: | Zeile 168: | ||
== Asymmetrische Verfahren == | == Asymmetrische Verfahren == | ||
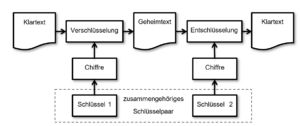
Bei asymmetrischen Verfahren werden zur Verschlüsselung und Entschlüsselung einer Nachricht '''zwei unterschiedliche Schlüssel''' verwendet. Die beiden Schlüssel gehören dabei immer zusammen und bilden ein '''Schlüsselpaar''' (siehe Abbildung | Bei asymmetrischen Verfahren werden zur Verschlüsselung und Entschlüsselung einer Nachricht '''zwei unterschiedliche Schlüssel''' verwendet. Die beiden Schlüssel gehören dabei immer zusammen und bilden ein '''Schlüsselpaar''' (siehe Abbildung "Asymmetrische Verfahren mit zwei unterschiedlichen Schlüsseln"). Es ist somit nicht möglich eine Nachricht mit demselben Schlüssel zu entschlüsseln, mit dem sie verschlüsselt wurde. Es kann dabei jeder der beiden Schlüssel zur Verschlüsselung einer Nachricht eingesetzt werden. Zur Entschlüsselung wird dabei immer der jeweils andere Schlüssel benötigt. | ||
[[Datei:IT244 11.png|300px|none|thumb|Asymmetrische Verfahren mit zwei unterschiedlichen Schlüsseln]] | [[Datei:IT244 11.png|300px|none|thumb|Asymmetrische Verfahren mit zwei unterschiedlichen Schlüsseln]] | ||
| Zeile 187: | Zeile 187: | ||
Eine weit verbreitete asymmetrische Methode wurde 1977 von Ronald L. '''R'''ivest, Adi '''S'''hamir und Leonard '''A'''dleman entwickelt und trägt daher den Namen '''RSA'''. Sie ist eine Weiterentwicklung des Diffie-Hellmann Schlüsseltauschverfahrens (siehe Lektion 3.5). Genauso wie dieses basiert sie auf dem Einsatz von '''Einwegfunktionen''' (Einwegfunktionen ist in der nachfolgenden Lektion 3.5 genauer beschrieben). Das Schlüsselpaar wird bei RSA durch den Einsatz sehr großer Primzahlen generiert, wobei die Anwendung des ersten Schlüssels die Nachricht unkenntlich macht und die zusätzliche Anwendung des zweiten Schlüssels die Anwendung des ersten Schlüssels wieder aufhebt. Der zugehörige zweite Schlüssel der Einwegfunktion ist nur durch Primfaktorzerlegungen sehr großer Primzahlen berechenbar. Dies ist jedoch ein sehr rechen- und damit zeitaufwändiger Vorgang. | Eine weit verbreitete asymmetrische Methode wurde 1977 von Ronald L. '''R'''ivest, Adi '''S'''hamir und Leonard '''A'''dleman entwickelt und trägt daher den Namen '''RSA'''. Sie ist eine Weiterentwicklung des Diffie-Hellmann Schlüsseltauschverfahrens (siehe Lektion 3.5). Genauso wie dieses basiert sie auf dem Einsatz von '''Einwegfunktionen''' (Einwegfunktionen ist in der nachfolgenden Lektion 3.5 genauer beschrieben). Das Schlüsselpaar wird bei RSA durch den Einsatz sehr großer Primzahlen generiert, wobei die Anwendung des ersten Schlüssels die Nachricht unkenntlich macht und die zusätzliche Anwendung des zweiten Schlüssels die Anwendung des ersten Schlüssels wieder aufhebt. Der zugehörige zweite Schlüssel der Einwegfunktion ist nur durch Primfaktorzerlegungen sehr großer Primzahlen berechenbar. Dies ist jedoch ein sehr rechen- und damit zeitaufwändiger Vorgang. | ||
Eine weiter asymmetrische Methode ist die der '''E'''lliptic '''C'''urve '''C'''ryptographie ('''ECC'''). Sie basiert auf der Berechnung von Punkten entlang einer elliptischen Kurve in einem zweidimensionalen Koordinatensystem. Dabei werden eine bestimmte Kurve und ein Startpunkt angegeben. Das Schlüsselpaar ergibt sich dann durch die Koordinaten eines Zielpunkts und der Anzahl der nötigen Schritte, die nötig sind, um vom Startpunkt aus zu ihm zu gelangen. Ähnlich der Berechnung der Multiplikation zweier Primzahlen ist und der Schwierigkeit einer Rückrechnung mittels Primfaktorzerlegung ist es einfach einen Punkt auf der Kurve zu berechnen, jedoch schwierig die Anzahl der nötigen Schritte zu ermitteln, die nötig sind um zu diesem Punkt zu gelangen. Ein Beispiel einer solchen Elliptic Curve ist in Abbildung | Eine weiter asymmetrische Methode ist die der '''E'''lliptic '''C'''urve '''C'''ryptographie ('''ECC'''). Sie basiert auf der Berechnung von Punkten entlang einer elliptischen Kurve in einem zweidimensionalen Koordinatensystem. Dabei werden eine bestimmte Kurve und ein Startpunkt angegeben. Das Schlüsselpaar ergibt sich dann durch die Koordinaten eines Zielpunkts und der Anzahl der nötigen Schritte, die nötig sind, um vom Startpunkt aus zu ihm zu gelangen. Ähnlich der Berechnung der Multiplikation zweier Primzahlen ist und der Schwierigkeit einer Rückrechnung mittels Primfaktorzerlegung ist es einfach einen Punkt auf der Kurve zu berechnen, jedoch schwierig die Anzahl der nötigen Schritte zu ermitteln, die nötig sind um zu diesem Punkt zu gelangen. Ein Beispiel einer solchen Elliptic Curve ist in Abbildung "Elliptic Curve" dargestellt. | ||
Die ECC Methoden sind stärker als die herkömmlichen asymmetrischen Methoden. Sie können sehr gut als performante Hardwarekomponenten implementiert werden und eignen sich daher besonders für den Einsatz in mobilen Endgeräten mit geringer Rechenleistung. | Die ECC Methoden sind stärker als die herkömmlichen asymmetrischen Methoden. Sie können sehr gut als performante Hardwarekomponenten implementiert werden und eignen sich daher besonders für den Einsatz in mobilen Endgeräten mit geringer Rechenleistung. | ||
| Zeile 200: | Zeile 200: | ||
Um dieses Problem zu lösen gibt es einige Methoden, die daher auch als Schlüsseltauschverfahren bezeichnet werden. | Um dieses Problem zu lösen gibt es einige Methoden, die daher auch als Schlüsseltauschverfahren bezeichnet werden. | ||
Die erste veröffentlichte mögliche Schlüsseltausch-Methode wurde 1976 von Diffie und Hellmann entwickelt. Sie basiert auf dem Einsatz von mathematischen Einwegfunktionen. Eine '''Einwegfunktion''' ist eine Funktion, welche leicht berechnet werden kann, deren Rückrechnung jedoch sehr schwierig ist. Dies lässt sich mit dem Mischen zweier Farbkübel zu vergleichen: Es ist zwar leicht zwei Farben zu mischen, jedoch enorm aufwändig sie wieder in ihre ursprünglichen Farbtöne aufzuteilen (vgl. Abbildung | Die erste veröffentlichte mögliche Schlüsseltausch-Methode wurde 1976 von Diffie und Hellmann entwickelt. Sie basiert auf dem Einsatz von mathematischen Einwegfunktionen. Eine '''Einwegfunktion''' ist eine Funktion, welche leicht berechnet werden kann, deren Rückrechnung jedoch sehr schwierig ist. Dies lässt sich mit dem Mischen zweier Farbkübel zu vergleichen: Es ist zwar leicht zwei Farben zu mischen, jedoch enorm aufwändig sie wieder in ihre ursprünglichen Farbtöne aufzuteilen (vgl. Abbildung "Einwegfunktion der Farbmischung") und manuell nur durch ausprobieren möglich. | ||
[[Datei:IT244 13.png|300px|none|thumb|Einwegfunktion der Farbmischung]] | [[Datei:IT244 13.png|300px|none|thumb|Einwegfunktion der Farbmischung]] | ||
| Zeile 215: | Zeile 215: | ||
# Jeder Teilnehmer mischt seine '''eigene geheime Farbe zur empfangenen Mischung''' des anderen. Damit haben nun beide einen Farbkübel mit derselben Mischung aus: '''gemeinsame Farbe + eigene geheime Farbe + geheime Farbe des anderen'''. | # Jeder Teilnehmer mischt seine '''eigene geheime Farbe zur empfangenen Mischung''' des anderen. Damit haben nun beide einen Farbkübel mit derselben Mischung aus: '''gemeinsame Farbe + eigene geheime Farbe + geheime Farbe des anderen'''. | ||
# Die gemeinsame Mischung kann nun als Schlüssel für den geheimen Nachrichtenaustausch verwendet werden. | # Die gemeinsame Mischung kann nun als Schlüssel für den geheimen Nachrichtenaustausch verwendet werden. | ||
Die einzelnen Schritte des Schlüsseltauschs sind in Abbildung | Die einzelnen Schritte des Schlüsseltauschs sind in Abbildung "Ablauf des Diffie-Hellmann Schlüsseltausches" noch einmal bildlich dargestellt. In der rechten Spalte ist ersichtlich welche Informationen ein möglicher Angreifer mithören kann. Er gelangt zwar an die gemeinsame Farbe und an die beiden Mischungen. Es ist ihm jedoch nicht möglich die geheimen Farben zu ermitteln. Damit fehlt ihm auch die Möglichkeit den gemeinsamen Schlüssel herauszufinden. | ||
[[Datei:IT244 14.png|300px|none|thumb|Ablauf des Diffie-Hellmann Schlüsseltausches]] | [[Datei:IT244 14.png|300px|none|thumb|Ablauf des Diffie-Hellmann Schlüsseltausches]] | ||
| Zeile 259: | Zeile 259: | ||
Ein guter Hash-Algorithmus hat möglichst wenige '''Kollisionen'''. Das bedeutet, dass die Wahrscheinlichkeit bei unterschiedlichen Eingangswerten denselben Ausgangswert zu bekommen sehr gering ist. | Ein guter Hash-Algorithmus hat möglichst wenige '''Kollisionen'''. Das bedeutet, dass die Wahrscheinlichkeit bei unterschiedlichen Eingangswerten denselben Ausgangswert zu bekommen sehr gering ist. | ||
Das nachfolgende Beispiel in Tabelle | Das nachfolgende Beispiel in Tabelle "Beispiel Hashfunktion HashMe()" zeigt mögliche Hashwerte einer fiktiven Hashfunktion HashMe(). Die letzten beiden Zeilen sind ein Beispiel einer Kollision. | ||
<span id="_Ref414362664" class="anchor"></span>Tabelle : Beispiel Hashfunktion HashMe() | <span id="_Ref414362664" class="anchor"></span>Tabelle: Beispiel Hashfunktion HashMe() | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
| Zeile 292: | Zeile 292: | ||
| | | | ||
ae4692a6f28a03cd | ae4692a6f28a03cd | ||
| | | <br> | ||
|} | |} | ||
Da ein Hashwert einer bestimmten Nachricht immer gleich ist, eignet er sich sehr gut zur '''Integritätsprüfung'''. Sobald sich ein Teil der Nachricht ändert, ändert sich auch der Hashwert. Das Vorhandensein einer Änderung der Nachricht kann somit einfach durch den Vergleich des Original-Hashwertes und des aktuellen Hashwertes aufgezeigt werden. | Da ein Hashwert einer bestimmten Nachricht immer gleich ist, eignet er sich sehr gut zur '''Integritätsprüfung'''. Sobald sich ein Teil der Nachricht ändert, ändert sich auch der Hashwert. Das Vorhandensein einer Änderung der Nachricht kann somit einfach durch den Vergleich des Original-Hashwertes und des aktuellen Hashwertes aufgezeigt werden. | ||
| Zeile 302: | Zeile 302: | ||
Da mit Hash-Werten die Integrität von Nachrichten geprüft werden kann, werden diese auch oft als '''Fingerprint''' oder '''Message-Digest''' bezeichnet. | Da mit Hash-Werten die Integrität von Nachrichten geprüft werden kann, werden diese auch oft als '''Fingerprint''' oder '''Message-Digest''' bezeichnet. | ||
Einige derzeit gängige Hash-Algorithmen sind in Tabelle | Einige derzeit gängige Hash-Algorithmen sind in Tabelle "Gängige Hash-Algorithmen" aufgelistet. | ||
<span id="_Ref414365977" class="anchor"></span>Tabelle : Gängige Hash-Algorithmen | <span id="_Ref414365977" class="anchor"></span>Tabelle: Gängige Hash-Algorithmen | ||
{| style="border-collapse: collapse;" border="1" | {| style="border-collapse: collapse;" border="1" | ||
Version vom 25. Jänner 2022, 15:52 Uhr
Kryptographie
Bei der Kryptographie handelt es sich um Methoden, Daten in eine Form zu bringen, in der Sie nur von denen gelesen werden können, die dazu berechtigt sind. Für alle anderen sollen die Daten während ihrer Übermittlung und Speicherung unlesbar sein.
Die Kryptographie hat ihren bekannten Ursprung in den Jahren um 2000 v. Chr. Die Ägypter nutzten Hieroglyphen um Grabkammern zu dekorieren und die Lebensgeschichte des Verstorbenen zu erzählen. Das Augenmerk lag dabei jedoch nicht in der Unkenntlichmachung der Informationen sondern darin, sie durch die bildhafte Darstellungsform zeremoniell und majestätisch wirken zu lassen. [Ha13, 760]
Eine der ersten Methoden mit der Absicht einen Text unkenntlich zu machen, war die hebräische Atbash Methode. Dabei wurde als Schlüssel jedem Buchstaben im Alphabet ein anderer Buchstabe zugewiesen. Ein Beispiel für einen Schlüssel wären demnach die folgenden beiden Zeilen [Ha13, 760]:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
ZYXWVUTSRQPONMLKJIHGFEDCBA
Damit könnte nun beispielsweise der Text „KRYPTO“ zum Text „PIBKGL“ verschlüsselt werden, indem der Buchstabe des ursprünglichen Textes in der ersten Zeile des Schlüssels nachgesehen und dann durch den jeweiligen Buchstaben der zweiten Zeile ersetzt wird. Zur Entschlüsselung wird dieselbe Technik umgekehrt angewendet, indem der Buchstabe des verschlüsselten Textes in der zweiten Zeile gesucht und dann durch den jeweiligen Eintrag der ersten Zeile ersetzt wird.
Ein weiterer historisch erfolgreicher Algorithmus ist der Cäsar-Algorithmus. Er wurde in der Zeit der gallischen Kriege von Julius Cäsar entwickelt und eingesetzt um vertrauliche Nachrichten zu übermitteln, ohne dem Nachrichtenboten vertrauen zu müssen. Das Prinzip des Cäsar- Algorithmus ist simpel. Jeder Buchstabe der Nachricht wird um eine bestimmte Anzahl an Stellen im Alphabet nach hinten verschoben, wobei beim Erreichen des letzten Buchstaben Z wieder mit dem ersten Buchstaben A weitergezählt wird. Die Anzahl der Buchstaben, um die die Nachricht verschoben wird, wird dabei meist als Teil des Algorithmus Namens angegeben. So sind bei einer Cäsar 5 Verschlüsselung die Buchstaben der Nachricht um 5 Stellen verschoben und bei einer Cäsar 15 Verschlüsselung um 15 Stellen.
Der Text „KRYPTO“ wird durch Anwendung einer Cäsar 5 Verschlüsselung zu „PWDUYT“. Dabei wird auch deutlich, dass beim Verschieben des Buchstaben Y zum Buchstaben D, nach Erreichen von Z wieder mit A begonnen wird.
Der Cäsar-Algorithmus ist aus heutiger Sicht auch von Nicht-Kryptographen leicht zu knacken. Aus damaliger Sicht war es jedoch ein sehr sicheres Verfahren, da der Bildungsgrad der Bevölkerung nicht sehr hoch war und viele nicht schreiben und lesen konnten.
Eine deutliche Verbesserung des Cäsar-Algorithmus würde im 16. Jahrhundert von Blaise de Vigenere entwickelt und deshalb auch als Vigenere-Algorithmus bezeichnet. Dabei wird nicht mehr jeder Buchstabe um eine bestimmte Anzahl von Zeichen verschoben, sondern ein Schlüssel definiert, der die jeweilige Verschiebung der einzelnen Buchstaben bestimmt. Im nachfolgenden Beispiel wird ein Text mit Hilfe des Schlüssels „KRYPTO“ verschlüsselt.
Klartext: DIETAUBEISTAUFDEMDACH
Schlüssel: KRYPTOKRYPTOKRYPTOKRY
Verschlüsselt: NZCITILVGHMOEWBTFRKTF
Der Schlüssel wird für die gesamte Länge der Nachricht immer wieder wiederholt. Im Beispiel befindet sich der Buchstabe D bei seinem ersten vorkommen im Text unter dem Buchstaben K des Schlüssels und wird daher um 10 Zeichen verschoben und somit zu einem N. Bei seinem zweiten Vorkommen befindet sich das D der Nachricht jedoch unter dem Y des Schlüssels und wird daher zu einem B.
Um den Abstand zwischen dem Zeichen der Nachricht und dem Zeichen des Schlüssels schneller manuell ermitteln zu können wird oft eine Tabelle eingesetzt, in der alle möglichen Abstandskombinationen aufgelistet sind. Diese wird als Vigenere-Tabelle bezeichnet und ist in Abbildung "Vigenere-Tabelle" zu sehen.
In dieser Lektion werden nun weiter die Grundbegriffe der Kryptographie, ihre wesentlichen Methoden und mögliche Angriffsvektoren genauer behandelt.
Wesentliche Begriffe der Kryptographie
In der Kryptographie gibt es einige wichtige Grundbegriffe. Sie dienen der Beschreibung der Methoden und den unterschiedlichen Stadien von Ver- und Entschlüsselung. Diese Begriffe sind nun nachfolgend beschrieben.
Klartext (Plaintext)
Beim Klartext handelt es sich um die unverschlüsselte Nachricht, die übertragen werden soll. Solange sich die Nachricht in diesem Zustand befindet kann sie von jedem gelesen werden, der Zugriff auf sie hat.
Geheimtext (Ciphertext)
Dabei handelt es sich um eine verschlüsselte Klartext Nachricht. Sie ist in diesem Zustand nicht lesbar. Jeder, der in den Besitz des Geheimtextes kommt muss den zugehörigen Algorithmus und Schlüssel kennen um die Nachricht wieder in den Klartext umwandeln zu können.
Chiffre (Cipher / Algorithmus)
Die zur Ver- und Entschlüsselung eingesetzte Methode und der zugehörige Algorithmus werden als Chiffre (Cipher) bezeichnet. Sie verarbeitet einen Plaintext mit Hilfe des Keys zu Ciphertext und umgekehrt. Dabei handelt es sich um eine Ansammlung von Umwandlungen der Zeichen (oder Bits) des Textes.
Es gibt bekannte und unbekannte Chiffren. Alle gängig eingesetzten Chiffren sind hinlänglich ihrer genauen Funktionsweise bekannt. Die Stärke der Chiffre ist von wesentlicher Bedeutung für die Sicherheit. Die Unbekannte ist dabei immer der Schlüssel. Ein wesentlicher Vorteil von bekannten Chiffren ist die große Anzahl an Nutzern und der Möglichkeit sie öffentlich zu analysieren und zu testen. Damit werden gefundene Schwachstellen meist schnell veröffentlicht und behoben. Dass die Sicherheit eines kryptographischen Verfahrens im Wesentlichen in der Geheimhaltung des Schüssels und nicht in der des Ciphers liegt, ist die wesentliche Aussage von Kerckhoff‘s Prinzip (siehe auch Lektion 3.2).
Unbekannte Chiffren werden meist von Nachrichtendiensten eingesetzt. Ihr Vorteil liegt darin, dass ein möglicher Angreifer nicht nur den Schlüssel, sondern auch die Chiffre herausfinden muss, um die Nachricht lesen zu können. Der wesentliche Nachteil ist das Fehlen einer breiten Anwenderschicht und die damit verbundenen Reviews und Tests. Es muss daher sehr viel Aufwand in die Entwicklung und Testung der Chiffre gesteckt werden, um mögliche Sicherheitslücken identifizieren zu können.
Bei den Chiffren wird zwischen symmetrischen und asymmetrischen Algorithmen unterschieden. Diese sind weiter in Lektion 3.3 und 3.4 genauer beschrieben.
Schlüssel (Key) und Keyspace
Der Schlüssel wird von der Chiffre verwendet um Variabilität und Unregelmäßigkeiten in den Algorithmus zu bringen. Damit soll sichergestellt werden, dass dieselbe Chiffre, angewendet auf denselben Klartext, durch den Einsatz unterschiedlicher Schlüssel zu unterschiedlichen Geheimtexten führt. Somit ist der Schlüssel das wesentliche, geheim zuhaltende, Element.
Welche möglichen Schlüssel für eine Chiffre angewendet werden können, wird durch den Keyspace definiert. Dieser enthält alle möglichen Schlüssel. Je größer der Keyspace ist, desto mehr unterschiedliche Schlüssel existieren. Je mehr mögliche Schlüssel auf eine Chiffre anwendbar sind, desto aufwändiger wird es für einen Angreifer eine Nachricht durch bloßes Ausprobieren unterschiedlicher Schlüssel zu entschlüsseln.
Der Cäsar Algorithmus hat beispielsweise einen Keyspace von 26 möglichen Schlüsseln, da es genauso viele Buchstaben im lateinischen Alphabet gibt. Ein Angreifer würde durch einfaches durchprobieren daher maximal 26 Versuche benötigen, wobei die Verwendung des Schlüssels A sehr unwahrscheinlich ist, da der Text damit gleich bleiben würde.
Aktuelle Cipher haben hingegen wesentlich größere Keyspaces. Beispielsweise hat AES256 (siehe Lektion 3.3) eine Schlüssellänge von 256 Bit. Daraus ergibt sich ein Keyspace von 2256 möglichen Schlüsseln. Da ein Angreifer durch zufälliges durchprobieren einen Schlüssel in der Regel nach der Hälfte der möglichen Kombinationen errät, muss er hier ca. (2256)/2 = 2255 Versuche durchführen.
Verschlüsselung (Encryption) / Entschlüsselung (Decryption)
Bei der Verschlüsselung handelt es sich um die Umwandlung von Klartext in Geheimtext mittels zugehöriger Chiffre und Schlüssel und bei der Entschlüsselung um die Umwandlung des Geheimtextes zurück in den Klartext.
Der Ablauf eines Weges vom Klartext über den Geheimtext zurück zum Klartext ist in Abbildung "Zusammenhang der Kryptographie Begriffe" noch einmal grafisch dargestellt.
Security by Obscurity und das Kerckhoffs’sche Prinzip
Ein kryptographisches System lässt sich durch die bloße Geheimhaltung der zugehörigen Chiffre nicht gewährleisten. Dieser Versuch wird auch als Security by Obscurity bezeichnet, da hier davon ausgegangen würde, dass alleine die Unwissenheit über die Methodik der Chiffre zu mehr Sicherheit führt. Dadurch ergeben sich jedoch einige wesentliche Probleme. Die geringe Anzahl an eingeweihten Anwendern entdeckt Fehler des Ciphers spät bis überhaupt nicht. Sobald die geheime Chiffre jedoch bekannt wird, ist jede durch ihre Geheimhaltung erreichte Sicherheit gebrochen. Wurde dann nicht auf eine ausreichende Geheimhaltung und Komplexität der Schlüssel geachtet hat wird das gesamte System unbrauchbar.
Kerkhoff entwickelte 1883 die Grundprinzipien sicherer Verschlüsselung, welche bis heute Bestand haben. Einer dieser Grundsätze wird heute als das Kerhoffs‘sche Prinzip bezeichnet. Es besagt, dass nicht das System selbst, sondern der Schlüssel geheim sein muss, um eine maximale Sicherheit zu erreichen. Der Algorithmus soll immer öffentlich bekannt sein. Der Schlüssel muss dabei unbedingt geheim gehalten werden. Je mehr unterschiedliche Geheimnisse rund um ein kryptographisches System nötig sind, umso verwundbarer ist es gegenüber möglichen Angriffen, welche Teile der Geheimnisse herausfinden. [Ha13, 767]
Auch wenn das Kerhoffs‘sche Prinzip besagt, dass die Sicherheit alleinig in der Geheimhaltung des Schlüssels liegt, so hat Security by Obscurity doch auch manchmal ihre Berechtigung. So kann beispielsweise durch die Kombination mehrerer bekannter Verfahren eine Unregelmäßigkeit hergestellt werden, welche möglichen Angreifern eine Analyse erschwert und damit eine erste Hürde darstellt, die überwunden werden muss.
Eine bekannte Anwendung ist das sogenannte „Salzen“ von Hashwerten. Dabei wird dem Plaintext vor der Hashwertberechnung ein zusätzlicher Teil („Salt“) hinzugefügt. Gelingt es einem Angreifer nun anhand der Hashwerte mögliche Ausgangswerte zu konstruieren, kann er den Ursprungswert nur durch das zusätzliche Wissen des „Salts“ rekonstruieren. Die berechneten Werte sind somit unbrauchbar.
Symmetrische Verfahren
Bei einem symmetrischen kryptographischen Verfahren (Chiffre) wird ein Klartext mit ein und demselben Schlüssel verschlüsselt und auch wieder entschlüsselt (siehe Abbildung "Symmetrische Verfahren mit einem Schlüssel"). Bei symmetrischen Verfahren werden Substitutions-Methoden und Transpositions-Methoden angewendet, um den Klartext unkenntlich zu machen. Diese können innerhalb der Chiffre natürlich auch beliebig kombiniert werden.
Substitutions-Methoden
Bei der Substitution handelt es sich um die Umwandlung eines Zeichens (oder Bits) durch ein anderes. Dies wären beispielsweise bei einem Cäsar 5 Algorithmus das Ersetzen des Zeichen K durch das Zeichen P zur Verschlüsselung und das Ersetzen des Zeichens P durch das Zeichen K zur Entschlüsselung. Der Schlüssel ist hierbei der Wert 5, welcher die Zuordnung des jeweiligen Zielzeichens ermöglicht.
Ein Beispiel auf Bit-Ebene ist die einfache XOR Verknüpfung des Schlüssels mit dem Text, welche ebenfalls in beide Richtungen anwendbar ist:
Klartext: 010010110101001001011001
Schlüssel: 010000010100001001000011
Geheimtext: 000010100001000000011010
Die Berechnung des Geheimtextes und des Klartextes ist dabei in beide Richtungen über die Verknüpfung mit dem Schlüssel möglich.
Ist der mittels XOR verknüpfte Schlüssel:
- gleich lang wie die Nachricht,
- zufällig generiert und
- wird dieser nur ein einziges Mal verwendet,
wird dies als One-Time-Pad bezeichnet. Diese Methode ist, ohne den Schlüssel in Besitz zu bekommen, definitiv unknackbar und damit die sicherste kryptographische Methode. Die Herausforderung besteht hierbei darin den Schlüssel sicher zu übermitteln, da dieser gleich lang wie die Nachricht sein muss. Dies ist meist nur sehr umständlich machbar und mit einem ähnlichen Aufwand verbunden, wie die Übermittlung der Nachricht selbst. One-Time-Pads werden daher eher zur Übermittlung kleinerer, hoch sensibler, Datenmengen eingesetzt. Sie könnten jedoch an Bedeutung gewinnen, da eine sichere Übermittlung von größeren Schlüsseln mittels Quantentechnologien immer praxistauglicher wird.
Transpositions-Methode
Bei der Transposition werden einzelne Teile des Textes mit anderen Teilen vertauscht. Der Schlüssel gibt dabei an, welcher Teil mit welchem vertauscht werden soll.
Ein Beispiel für eine einfache Transpositions-Methode ist in Abbildung "Transpositions-Cipher" dargestellt. Dabei wird der Plaintext zuerst in Gruppen zerlegt. Diese Gruppen werden nun gemäß dem Schlüsselwert intern neu angeordnet und ergeben dann in Summe wiederum den Ausgabetext. Auch diese Methode ist in beide Richtungen – sowohl zur Ver-, als auch zur Entschlüsselung – anwendbar.
Aktuelle Kryptographie-Standards mit symmetrischen Methoden
In der nachfolgenden Tabelle "Gängige Standards mit symmetrischen Algorithmen" sind die aktuell gängigsten symmetrischen Chiffren und ihre Eckpunkte aufgelistet.
Tabelle: Gängige Standards mit symmetrischen Algorithmen
| Standard Name | Algorithmus | Schlüssellängen |
|---|---|---|
| Data Encryption Standard (DES) | Data Encryption Algorithm (DEA) | 56 Bit Schlüssel (+8 Bit Parität = 64Bit) |
| Triple-DES (3DES) | Triple Data Encryption Algorithm (TDEA) | 112 Bit |
| Advanced Encryption Standard (AES) | Rijndael |
128 Bit 192 Bit 256 Bit |
| International Data Encryption Algorithm (IDEA) | International Data Encryption Algorithm (IDEA) | 128 Bit |
| Blowfish | Blowfish | Variable Länge zwischen 32 und 448 Bit |
| RC4 | RC4 | Variable Länge |
Asymmetrische Verfahren
Bei asymmetrischen Verfahren werden zur Verschlüsselung und Entschlüsselung einer Nachricht zwei unterschiedliche Schlüssel verwendet. Die beiden Schlüssel gehören dabei immer zusammen und bilden ein Schlüsselpaar (siehe Abbildung "Asymmetrische Verfahren mit zwei unterschiedlichen Schlüsseln"). Es ist somit nicht möglich eine Nachricht mit demselben Schlüssel zu entschlüsseln, mit dem sie verschlüsselt wurde. Es kann dabei jeder der beiden Schlüssel zur Verschlüsselung einer Nachricht eingesetzt werden. Zur Entschlüsselung wird dabei immer der jeweils andere Schlüssel benötigt.
Dies ist auch vergleichbar mit einem Vorhängeschloss und einem Schlüssel. Das Schloss kann eingesetzt werden um eine Kiste zu versperren. Ohne den zugehörigen Schlüssel kann das Schloss jedoch nicht mehr geöffnet werden. Im Fall der asymmetrischen Verschlüsselung ist jeder der beiden Schlüssel gleichzeitig das Schloss des jeweils anderen Schlüssels:
- Key 1 = Schloss 2 (kann von Key 2 geöffnet werden)
- Key 2 = Schloss 1 (kann von Key 1 geöffnet werden)
Die beiden Schlüssel werden als Public-Key und Private-Key bezeichnet. Diese Bezeichnungen beruhen darauf, dass einer der beiden Schlüssel immer privat – also nur einer bestimmten Person bekannt – sein sollte. Der andere Schlüssel kann dann öffentlich an alle weitergegeben werden, die Nachrichten an den Besitzer des Private-Keys schicken wollen. Er ist somit public.
Will nun jemand eine Nachricht an den Besitzer des Private-Keys übermitteln kann er nun den dazu den Public-Key für die Verschlüsselung verwenden. Da die Nachricht nur mit dem zugehörigen Private-Key entschlüsselt werden kann, kann sie auch nur von dessen Besitzer gelesen werden. Der Public-Key ist zwar öffentlich verfügbar, jedoch zur Entschlüsselung der Nachricht nicht verwendbar.
Diese Methode kann nun auch umgekehrt verwendet werden um eine Nachricht durch den Besitzer des Private-Keys zu signieren. Dabei wird meist ein Hashwert (siehe Lektion 3.6) der Nachricht generiert, die signiert werden soll. Dieser Hashwert wird nun mit dem Private-Key verschlüsselt und an die Nachricht angehängt. Will nun ein Empfänger prüfen, ob die Nachricht tatsächlich vom Besitzer des Private-Keys stammt, muss er nur den Hashwert mit dem öffentlich verfügbaren Public-Key entschlüsseln und mit dem aktuellen Hashwert der empfangenen Nachricht vergleichen. Sind die beiden Hashwerte ident, ist somit sichergestellt, dass die Nachricht vom Besitzer des Private-Keys stammen muss, da nur er den Hashwert korrekt verschlüsseln konnte. Würde sie auf dem Weg zum Empfänger verändert worden sein, wären die Hashwerte unterschiedlich.
Asymmetrische Methoden basieren auf komplexen mathematischen Berechnungen und sind vergleichsweise langsam. Sie werden daher meist nicht für die Verschlüsselung der Nachricht, sondern nur für die Verschlüsselung eines Schlüssels für die Anwendung einer symmetrischen Methode verwendet. Damit ist sichergestellt, dass der Schlüssel sicher übertragen wird und gleichzeitig eine schnellere Ver- und Entschlüsselung der übrigen Nachricht, mittels symmetrischer Methoden, erfolgen kann.
Eine weit verbreitete asymmetrische Methode wurde 1977 von Ronald L. Rivest, Adi Shamir und Leonard Adleman entwickelt und trägt daher den Namen RSA. Sie ist eine Weiterentwicklung des Diffie-Hellmann Schlüsseltauschverfahrens (siehe Lektion 3.5). Genauso wie dieses basiert sie auf dem Einsatz von Einwegfunktionen (Einwegfunktionen ist in der nachfolgenden Lektion 3.5 genauer beschrieben). Das Schlüsselpaar wird bei RSA durch den Einsatz sehr großer Primzahlen generiert, wobei die Anwendung des ersten Schlüssels die Nachricht unkenntlich macht und die zusätzliche Anwendung des zweiten Schlüssels die Anwendung des ersten Schlüssels wieder aufhebt. Der zugehörige zweite Schlüssel der Einwegfunktion ist nur durch Primfaktorzerlegungen sehr großer Primzahlen berechenbar. Dies ist jedoch ein sehr rechen- und damit zeitaufwändiger Vorgang.
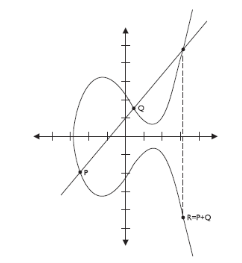
Eine weiter asymmetrische Methode ist die der Elliptic Curve Cryptographie (ECC). Sie basiert auf der Berechnung von Punkten entlang einer elliptischen Kurve in einem zweidimensionalen Koordinatensystem. Dabei werden eine bestimmte Kurve und ein Startpunkt angegeben. Das Schlüsselpaar ergibt sich dann durch die Koordinaten eines Zielpunkts und der Anzahl der nötigen Schritte, die nötig sind, um vom Startpunkt aus zu ihm zu gelangen. Ähnlich der Berechnung der Multiplikation zweier Primzahlen ist und der Schwierigkeit einer Rückrechnung mittels Primfaktorzerlegung ist es einfach einen Punkt auf der Kurve zu berechnen, jedoch schwierig die Anzahl der nötigen Schritte zu ermitteln, die nötig sind um zu diesem Punkt zu gelangen. Ein Beispiel einer solchen Elliptic Curve ist in Abbildung "Elliptic Curve" dargestellt.
Die ECC Methoden sind stärker als die herkömmlichen asymmetrischen Methoden. Sie können sehr gut als performante Hardwarekomponenten implementiert werden und eignen sich daher besonders für den Einsatz in mobilen Endgeräten mit geringer Rechenleistung.
Schlüsseltauschverfahren
Eine wesentliche Herausforderung der verschlüsselten Datenübertragung ist der Schlüsseltausch. Es muss daher eine Methode gefunden werden den nötigen Schlüssel zur Entschlüsselung der Nachricht an den Empfänger zu übermitteln, ohne dass dieser abgefangen werden kann. Würde der Schlüssel einfach vor der Übermittlung einer Nachricht übertragen werden, dann könnte ein möglicher Angreifer sowohl den Schlüssel, als auch den verschlüsselte Nachricht abfangen und dann beides gemeinsam einsetzen und die Nachricht einfach entschlüsseln.
Um dieses Problem zu lösen gibt es einige Methoden, die daher auch als Schlüsseltauschverfahren bezeichnet werden.
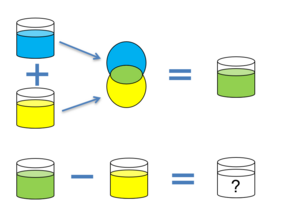
Die erste veröffentlichte mögliche Schlüsseltausch-Methode wurde 1976 von Diffie und Hellmann entwickelt. Sie basiert auf dem Einsatz von mathematischen Einwegfunktionen. Eine Einwegfunktion ist eine Funktion, welche leicht berechnet werden kann, deren Rückrechnung jedoch sehr schwierig ist. Dies lässt sich mit dem Mischen zweier Farbkübel zu vergleichen: Es ist zwar leicht zwei Farben zu mischen, jedoch enorm aufwändig sie wieder in ihre ursprünglichen Farbtöne aufzuteilen (vgl. Abbildung "Einwegfunktion der Farbmischung") und manuell nur durch ausprobieren möglich.
Dies macht sich der Diffie-Hellmann Schlüsseltausch nun zu Nutze, indem er mathematische Einwegfunktionen verwendet um einen gemeinsamen und geheimen Schlüssel über eine unsichere Leitung auszutauschen. Die Vorgehensweise ist nachfolgend durch ein Beispiel mit Farbkübeln beschrieben und dann anschließend mathematisch erklärt.
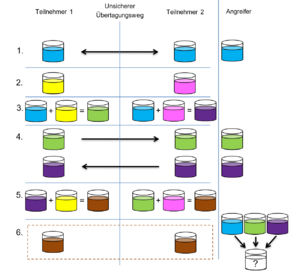
Der Ablauf ist dabei folgendermaßen:
- Beide Teilnehmer vereinbaren eine gemeinsame (nicht geheime) Farbe.
- Jeder Teilnehmer generiert eine eigene geheime Farbe, nur er selbst kennt.
- Nun mischen sie jeweils die geheime Farbe zur gemeinsamen Farbe.
- Danach übermitteln sie sich gegenseitig die Mischungen.
- Jeder Teilnehmer mischt seine eigene geheime Farbe zur empfangenen Mischung des anderen. Damit haben nun beide einen Farbkübel mit derselben Mischung aus: gemeinsame Farbe + eigene geheime Farbe + geheime Farbe des anderen.
- Die gemeinsame Mischung kann nun als Schlüssel für den geheimen Nachrichtenaustausch verwendet werden.
Die einzelnen Schritte des Schlüsseltauschs sind in Abbildung "Ablauf des Diffie-Hellmann Schlüsseltausches" noch einmal bildlich dargestellt. In der rechten Spalte ist ersichtlich welche Informationen ein möglicher Angreifer mithören kann. Er gelangt zwar an die gemeinsame Farbe und an die beiden Mischungen. Es ist ihm jedoch nicht möglich die geheimen Farben zu ermitteln. Damit fehlt ihm auch die Möglichkeit den gemeinsamen Schlüssel herauszufinden.
Mathematisch betrachtet basiert der Diffie-Hellmann Schlüsseltausch auf dem diskreten Logarithmus-Problem und wird mit Hilfe folgender Formel abgebildet:
n = gk mod p
Das diskrete Logarithmus-Problem beschreibt die Schwierigkeit für gegebene Werte der Variablen n, g und der Primzahl p den Wert der Variablen k zu finden. Bei kleinen Werten ist eine Berechnung von k noch machbar. Je größer sie jedoch werden, desto länger wird die dafür benötigte Zeit, da ein Rückrechnen nur durch Ausprobieren möglich ist. Für jedes zusätzliche Bit des Wertes müssen doppelt so viele Versuche angewendet werden.
Beim Schlüsseltausch sind g und p nun die gemeinsamen Werte (gemeinsame Farbe), welche öffentlich übermittelt werden und n das jeweilige Mischergebnis. k ist dabei der jeweils geheime Wert (eigene geheime Farbe), welcher niemals übermittelt wird.
Um zur gemeinsamen Farbmischung zu kommen macht sich der Schlüsseltausch nun zu Nutze, dass (x a) b gleich (x a) b und damit x a b ist. Sind a und b nun die beiden geheimen Zahlen können sie zum jeweils anderen Ergebnis hinzugefügt werden, ohne den jeweiligen Exponenten der anderen Seite zu kennen. Übermittelt wird hierbei immer nur das Ergebnis.
Angewendet auf die oben genannte Formel des diskreten Logarithmus-Problems ergibt sich nun folgender Ablauf des Schlüsseltauschs:
- Die gemeinsamen Werte für g und p werden übermittelt
- Beide Teilnehmer generieren eine geheime Zahl (Teilnehmer A: a; Teilnehmer B: b)
- Sie berechnen nun jeweils aus q, p und ihrer eigenen geheimen Zahl (a bzw. b) den Wert zur Übermittlung:
Teilnehmer A: A = ga mod p
Teilnehmer B: B = gb mod p
- Teilnehmer A übermittelt nun den Wert A an Teilnehmer B und Teilnehmer B den Wert B an Teilnehmer A.
- Nun können beide Teilnehmer mit ihrer eigenen geheimen Zahl den gemeinsamen Schlüssel K berechnen:
Teilnehmer A: K = Ba mod p
Teilnehmer B: K = Ab mod p
- Beide Teilnehmer können nun K zur Verschlüsselung ihrer geheimen Nachrichten verwenden.
Das Ba mod p gleich Ab mod p ist, kann mittels gegenseitigem Einsetzen bewiesen werden:
K = Ba mod p = (gb mod p)a mod p = gb a mod p
K = Ab mod p = (ga mod p)b mod p = ga b mod p
K = gb a mod p = ga b mod p
Da ein möglicher Angreifer jedoch nur in Besitz der Werte g, p, A und B kommt, kann er den Schlüssel K nur mit enorm hohem Aufwand ermitteln.
Auf dem Grundprinzip von Diffie-Hellmann wurde später mit RSA (siehe Lektion 3.4) die asymmetrischen Verschlüsselungsmethoden entwickelt. Die Diffie-Hellmann Methode wurde inzwischen auch um die verstärkte Sicherheit von Elliptic Curves erweitert und findet ihre diesbezügliche Verbreitung unter dem Namen Elliptic Curve Diffie-Helman (ECDH).
Hashing
Beim Hashing handelt es sich um die Anwendung einer nicht reversiblen Funktion, auf einen bestimmten Wert. Das Ergebnis einer Hash-Funktion ist somit nicht auf den Ausgangswert umkehrbar. Dabei wird meist ein Wert variabler Länge zu einem Wert fixer Länge umgewandelt, der dem Ursprungswert nicht mehr ähnelt.
Ein guter Hash-Algorithmus hat möglichst wenige Kollisionen. Das bedeutet, dass die Wahrscheinlichkeit bei unterschiedlichen Eingangswerten denselben Ausgangswert zu bekommen sehr gering ist.
Das nachfolgende Beispiel in Tabelle "Beispiel Hashfunktion HashMe()" zeigt mögliche Hashwerte einer fiktiven Hashfunktion HashMe(). Die letzten beiden Zeilen sind ein Beispiel einer Kollision.
Tabelle: Beispiel Hashfunktion HashMe()
| Eingangswert | Hashwert = HashMe(Eingangswert) | |
|---|---|---|
| Peter | 0c74c6051287c95d |
|
|
Guten Tag! Hiermit nehme ich Ihr Angebot mit der Nummer 12334 an. Mit freundlichen Grüßen, Miriam Muster |
878b87429ff50296 |
|
| Mich gibt es hoffentlich nur einmal! | ae4692a6f28a03cd | Kollision |
| 45667533423233467885354 |
ae4692a6f28a03cd |
Da ein Hashwert einer bestimmten Nachricht immer gleich ist, eignet er sich sehr gut zur Integritätsprüfung. Sobald sich ein Teil der Nachricht ändert, ändert sich auch der Hashwert. Das Vorhandensein einer Änderung der Nachricht kann somit einfach durch den Vergleich des Original-Hashwertes und des aktuellen Hashwertes aufgezeigt werden.
Dieses Prinzip wird auch bei digitalen Signaturen verwendet. Dabei wird ein Hashwert der zu signierenden Nachricht generiert und mit dem Private-Key (Siehe Lektion 3.4) des Absenders verschlüsselt. Dieser wird der Nachricht dann als Signatur beigefügt. Der Empfänger kann nun den Hashwert mit dem Public-Key entschlüsseln und mit dem aktuellen Hashwert der empfangenen Nachricht vergleichen. Sind die beiden Werte gleich ist sichergestellt, dass:
- sich der Inhalt der Nachricht nicht verändert hat und
- der Besitzer des Private-Key ist auch der Absender der Nachricht ist, da nur er eine Verschlüsselung durchführen kann, welche mit dem zugehörigen Public-Key korrekt entschlüsselt wird.
Da mit Hash-Werten die Integrität von Nachrichten geprüft werden kann, werden diese auch oft als Fingerprint oder Message-Digest bezeichnet.
Einige derzeit gängige Hash-Algorithmen sind in Tabelle "Gängige Hash-Algorithmen" aufgelistet.
Tabelle: Gängige Hash-Algorithmen
| Standard Name | Länge des Hash-Wertes | Anmerkung |
|---|---|---|
| MD4 | 128 Bit | Optimiert für schnelle Berechnung |
| MD5 | 128 Bit | Komplexerer Algorithmus als MD4 und daher langsamere Berechnung |
| SHA | 160 Bit | Ähnlich wie MD4 |
| HAVAL | Variable Länge | Ähnlich wie MD5 |
| Tiger | 192 Bit |
Ähnlich wie MD4 Optimiert für 64 Bit Systeme |
Angriffsvektoren der Kryptographie
Die möglichen direkten Angriffsvektoren der Kryptographie teilen sich in die, nachfolgend beschriebenen, Kategorien:
- Brute-Force Angriffe,
- Kryptoanalyse und
- Angriffe gegen Hashwerte.
Um die genannten Angriffe ausführen zu können, ist es meist erforderlich den zugehörigen Datenverkehr abzuhören und gegebenenfalls auch zu manipulieren. Dazu werden oft Sniffing- und Man-in-the-Middle-Attacken genutzt, welche später in Lektion 5.6 genauer beschrieben werden.
Brute-Force Angriffe
Bei Brute-Force Angriffen wird versucht eine Verschlüsselung zu knacken, indem eine Vielzahl möglicher Schlüssel ausprobiert wird. Dabei steigt mit der Länge der Schlüssel auch die Anzahl der dazu nötigen Versuche (siehe auch Lektion 3.1.4).
Die Stärke einer Chiffre wird daher auch dadurch angegeben, wie lange es dauern würde, durch einen Brute-Force Angriff einen möglichen Schlüssel zu finden.
Um die Möglichkeiten einzuschränken wird daher oft die Methode des Wörterbuchangriffs eingesetzt. Dabei werden keine beliebigen Schlüssel generiert, sondern stattdessen Einträge eines Wörterbuches bzw. einer Liste häufig eingesetzter Schlüssel (bzw. Passwörter) verwendet. Diese Listen werden meist auch nach der statistischen Häufigkeit der Verwendung der Begriffe gereiht, um die am häufigsten genutzten Passwörter auch zuerst zu versuchen. Die zugehörigen Statistiken werden dabei aus bereits im Internet veröffentlichten oder gestohlenen Passwortlisten generiert.
Da der Aufwand eines Angriffes mit der Länge der verwendeten Schlüssel zunimmt, kann ihm besonders durch den Einsatz langer Schlüssel begegnet werden. Auch ist es wichtig Passwörter zu verwenden, welche nicht durch Wörterbücher und Passwortlisten generiert werden können.
Kryptoanalyse
Bei der Kryptoanalyse handelt es sich um ein Teilgebiet der Kryptographie. Sie hat zum Gegenstand aus möglichen bekannten Teilen eines kryptographischen Systems (Klartext, Geheimtext, Chiffre) nicht bekannte Teile herauszufinden.
Da der Algorithmus einer Chiffre in der Regel bekannt ist, kann die Kryptoanalyse diesen als Basis verwenden. Um nun den Schlüssel oder den Klartext rekonstruieren zu können, stehen dem Analytiker folgende Analysemethoden zur Verfügung:
- Ciphertext-Only (der Analyse steht nur der Geheimtext zur Verfügung),
- Known-Plaintext (der Analyse steht der Geheimtext und der Klartext zur Verfügung),
- Chosen-Plaintext (der Analyse steht der Geheimtext zur Verfügung und der Klartext kann für die Analyse frei gewählt werden) und
- Chosen-Ciphertext (der Analyse steht der Klartext zur Verfügung und der Geheimtext kann für die Analyse frei gewählt werden).
Angriffe gegen Hashwerte
Angriffe gegen Hashwerte haben das Ziel Kollisionen zu finden, die zu einem gesuchten Hashwert führen. Werden beispielsweise Passwörter als Hash gespeichert und kommt ein Angreifender in den Besitz dieser Daten, kann er die Passwörter nicht einfach aus den Werten berechnen, da Hashwerte nicht reversibel sind.
Es ist jedoch möglich (ähnlich wie einem Brute-Force Angriff 3.7.1) aus einer Liste von Passwörtern mögliche Hashwerte zu berechnen und diese dann mit den Hashwerten zu vergleichen.
Da diese Listen sehr groß (einige Terrabyte und mehr) werden können und damit auch nur sehr schwer zu durchsuchen sind, wurde die Methode der Rainbow-Tables entwickelt. Dabei handelt es sich um eine näherungsweise Suche, die mögliche Teilstücke des Hashwerts berechnet. Die Suche erfolgt damit in mehreren Schritten verknüpften Tabellen, ist jedoch wesentlich schneller als die Suche in einer enorm großen Liste. Der Name Rainbow-Tables kommt dabei von einer der ersten grafischen Darstellungen der zugehörigen Methode. Dabei wurden die einzelnen Schritte (Tabellen) in unterschiedlichen Farben dargestellt.
Diesem Angriff kann entgegengewirkt werden, indem die Passwortlänge erhöht wird und indem der Hashwert bei der Berechnung zusätzlich „gesalzen“ wird. Durch die Erhöhung der Länge wird die nötige Menge der vorausberechnenden Werte entsprechend höher, was einen Angriff auf lange Passwörter entsprechend erschwert. Beim Salzen wird dem Passwort vor der Hashwertberechnung ein zusätzlicher Wert hinzugefügt. Dieser Wert wird als „Salt“ bezeichnet. Kann dieser Ausgangswert nun mittels Rainbow-Tables ermittelt werden, handelt es sich um den gesalzenen Wert und nicht um das tatsächliche Passwort. Die Angreifenden müssten daher einerseits den Salt kennen und dann sehr aufwändig eine eigene Rainbow-Table generieren, die ebenfalls diesen Salt anhält.
Wiederholungsaufgaben/Übungen
1 Erklären Sie den Cäsar-Algorithmus anhand der Verschlüsselung des Wortes "WIBA" durch Cäsar 5.
2 Erklären Sie die Begriffe Klartext, Geheimtext, und Chiffre. Stellen Sie Ihre Zusammenhänge bei der Verschlüsselung und Entschlüsselung grafisch dar.
3 Erklären Sie den Begriff “Security by Obscurity“? Welches Prinzip spricht dagegen?
4 Wodurch unterscheiden sich symmetrische und asymmetrische Kryptographie-Verfahren?
5 Wie läuft der Diffie-Hellmann Schlüsseltausch ab. Erklären Sie ihn anhand eines einfachen Beispiels mit Farbkübeln ODER mathematisch.
6 Was ist Hashing und wozu wird es eingesetzt?
7 Was ist ein Brute-Force Angriff?