Methoden der Datenanalyse - Varianzanalyse

Modell der zweifachen Varianzanalyse für unabhängige Stichproben

Bei Vorliegen eines zweiten Faktors erweitert sich das einfaktorielle Modell zu

$$y_{ijl}=\mu +\alpha _{i}+\beta _{j}+\alpha \beta _{ij}+\varepsilon _{ijl}\qquad (i=1,\ldots ,k;j=1,\ldots ,m;l=1,\ldots n)$$

wobei $\varepsilon _{ijl}$ die Werte der metrischen Variable sind ($l$-ter Wert bei Preispolitik $i$ und Kommunikationsstrategie $j$), [$\mu$ der unbedingte Erwartungswert (ohne Kenntnis der Gruppe), $\alpha$ der Effekt der jeweiligen Preispolitik, $\beta _{j}$ der Effekt der jeweiligen Kommunikationsstrategie, $\alpha \beta _{j}$ jener Effekt ist, der sich aus der Kombination der Preispolitik $i$ mit der Kommunikationsstrategie $j$ zusätzlich ergeben könnte und $\varepsilon _{ijl}$ der durch die drei Effektgruppen nicht erklärte Teil der abhängigen Variable ist. Die Annahmen für $\varepsilon _{ijl}$ sind analog zum einfaktoriellen Modell.

Es kommen bei zwei erklärenden Faktoren also nicht zwei sondern drei Parameter­gruppen vor, weil es möglich ist, dass Kombinationen von Effekten andere Mittelwerte in der abhängigen Variable liefern. Dies wird im weiteren Verlauf der Analyse klarer.

Schätzen und Testen bei der zweifachen Varianzanalyse

Wie bei der einfachen Varianzanalyse können die einzelnen „Anteile“ an der Messung nun geschätzt werden.

Schätzung der durchschnittlichen Kaufmenge $\mu$ durch

$${\hat {\mu }}={\frac {1}{k*m*n}}\sum _{i=1}^{k}\sum _{j=1}^{m}\sum _{l=1}^{n}y_{ijl}$$

Schätzung des Effekts der Preispolitik i, $i,\alpha _{i}$, durch

$${\widehat {\alpha _{i}}}={\widehat {\mu _{l}}}-{\hat {\mu }}={\frac {1}{m*n}}\sum _{i=1}^{m}\sum _{l=1}^{n}y_{ijl}-{\hat {\mu }}$$

Schätzung des Effekts der Kommunikationsstrategie j, $j,\beta _{j}$, durch

$${\widehat {\beta _{j}}}={\widehat {\mu _{j}}}-{\hat {\mu }}={\frac {1}{k*n}}\sum _{i=1}^{k}\sum _{l=1}^{n}y_{ijl}-{\hat {\mu }}$$

Schätzung des Interaktionseffektes (Preispolitik vs. Kommunikationsstrategie) durch

$${\widehat {\alpha \beta _{\imath \jmath }}}={\widehat {\mu _{\imath j}}}-\left({\hat {\mu }}+{\widehat {\alpha _{\imath }}}+{\widehat {\beta _{j}}}\right)={\frac {1}{n}}\sum _{l=1}^{n}y_{ijl}-\left({\hat {\mu }}+{\widehat {\alpha _{\imath }}}+{\widehat {\beta _{j}}}\right)$$

Schätzung des Fehlers $\varepsilon _{ijl}$ durch das Residuum

$${\widehat {\varepsilon _{ijl}}}=y_{ijl}-{\widehat {y_{ijl}}}=y_{ijl}-\left({\hat {\mu }}+{\widehat {\alpha _{l}}}+{\widehat {\beta _{j}}}+{\widehat {\alpha \beta _{lj}}}\right)$$

Aufgabe 9 Berechnen Sie die Schätzungen für ${\hat {\mu }}(1),{\widehat {\alpha }}_{i}(3){\widehat {\beta }}_{j}(2){\text{ und }}{\widehat {\alpha \beta _{ij}}}\left(3^{*}2=6\right)$

Ob die in Aufgabe 9 berechneten deskriptiven Effekte signifikant sind, kann wieder analog obiger Vorgehensweise berechnet werden. Geprüft werden können nun drei Hypothesenpaare:

$${\begin{array}{ll}H_{0}^{(1)}:\alpha _{1}=\alpha _{2}=\alpha _{3}=0&\rightarrow {\text{ Kein Einfluss der Preispolitik auf den Absatz }}\\H_{1}^{(1)}:\exists \alpha _{i}\neq 0&\rightarrow {\text{ Einfluss der Preispolitik auf die Absatz }}\\H_{0}^{(2)}:\beta _{1}=\beta _{2}=0&\rightarrow {\text{ Kein Einfluss der Komm.-Strategie auf den Absatz }}\\H_{1}^{(2)}:\exists \beta _{j}\neq 0&\rightarrow {\text{ Einfluss der Komm.-Strategie auf den Absatz }}\\H_{0}^{(3)}:\alpha \beta _{11}=\alpha \beta _{12}=\alpha \beta _{21}=\alpha \beta _{22}=\alpha \beta _{31}=\alpha \beta _{32}=0\\H_{1}^{(3)}:\exists \alpha \beta _{ij}\neq 0&\end{array}}$$

Interaktionen ($\left(H_{1}^{(3)}\right)$) bzw. keine Interaktionen ($\left(H_{0}^{(3)}\right)$) zwischen Preispolitik und Komm.-Strategie in Bezug auf den Absatz.

Für jede Hypothese kann nun wieder eine Quadratsumme, eine daraus abgeleitete, unter H₀ F-verteilte Prüfgröße $F$, sowie zur Bestimmung der Signifikanz ein p-Wert berechnet werden.

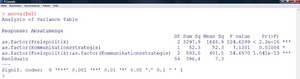
Fortsetzung Beispiel 3 In R wird das lineare Modell nun so spezifiziert: Marketing<-read.csv("C:\\...\\...\\Marketing.csv",header=TRUE,dec=",",sep=";") attach(Marketing) lm1<-lm(Absatzmenge~as.factor(Preispolitik)+as.factor(Kommunikationsstrategie)+ as.factor(Preispolitik):as.factor(Kommunikationsstrategie)) anova(lm1) Man erhält dann folgende Tabelle (Abbildung 14): Zweifaktorielle ANOVA - Tafel der Varianzanalyse in R Alle p-Werte (Spalte rechts) sind kleiner als 5%. Daher wird in allen drei Fällen die Nullhypothese verworfen. Das Ergebnis ist (in Zusammenhang mit Aufgabe 9): Die Preispolitik hat einen signifikanten Einfluss auf die Absatzmenge des Produktes. Erwartungsgemäß wird bei höheren Preisen im Mittel weniger abgesetzt. Die Kommunikationsstrategie hat ebenfalls einen Einfluss auf die Absatzmenge. Bei Postwurfsendungen ist die durchschnittlich abgesetzte Menge größer. Es gibt signifikante Interaktionen zwischen Preispolitik und Kommunikations­strategie: Die Postwurfsendungen liefern nicht bei jeder Preispolitik die höhere Absatzmenge. Bei Hochpreispolitik ist Anzeigenwerbung erfolg­reicher. Die einzelnen Effekte (jene, die ausreichen, um das lineare Modell vollständig zu schätzen) können auch wieder mittels „lm1$coefficients“ ausgegeben werden. Folgender Befehl visualisiert diese Zusammenhänge schließlich noch in einem einfachen Liniendiagramm der Mittelwerte: interaction.plot(Preispolitik,Kommunikationsstrategie,Absatzmenge)

Ist ein balanciertes Design vorhanden (wie im Beispiel), macht es keinen Unterschied, in welcher Reihenfolge die Faktoren in die Gleichung eingegeben werden. Bei unbalancierten Designs ist die Interpretation der Signifikanzen schwieriger, da die Reihenfolge, in der die einzelnen Faktoren in die Gleichung eingehen, entscheidend ist.

Weitere Beispiele für varianzanalytische Designs

Varianzanalyse bei abhängigen Stichproben

Einfache Varianzanalyse für abhängige Stichproben

Wie beim t-Test für abhängige Stichproben kann auch eine Varianzanalyse für abhängige Stichproben berechnet werden. Beispielsweise, wenn Messung von Personen zu drei oder mehr Zeitpunkten vorliegen. In diesem Design können zwei Effekte geprüft werden: Unterschiede in der Versuchsbedingung (hier: Messzeitpunkt) und Unterschiede in den Versuchseinheiten (hier Personen).

Zweifache Varianzanalyse mit Messwiederholung

Hier können die Daten zum Beispiel zwei Gruppen von Personen (z.B. Männer und Frauen) sein, an denen je drei Messungen durchgeführt werden.

Unvollständige varianzanalytische Designs

Wenn nicht in allen Faktorkombinationen Daten erhoben werden, heißt das varianzanalytische Design „unvollständig“. Im folgenden werden zwei Beispiele für unvollständige Designs erwähnt.

Hierarchisches Design

Ein hierarchisches Design könnte sich beispielsweise dann ergeben, wenn man an der Wirkung eines Medikamentes, sowie am Behandlungserfolg verschiedener Spitäler interessiert ist. Sollen acht Medikamente und zwei Spitäler untersucht werden, ergibt sich ein Versuchsplan mit 2*8=12 Faktorkombinationen. Falls nun die Medikamente 1-4 nur in Spital 1 verwendet werden und die Medikamente 5-8 nur in Spital 2, dann können nicht wie in Beispiel 3 auch Wechselwirkungen auf Signifikanz getestet werden. Man sagt, dass der Faktor Medikament im Faktor Spital geschachtelt ist (auch „nested“). Dementsprechend müssen die Formeln der zweifaktoriellen ANOVA im vollständigen Design adaptiert werden.

Lateinisches Quadrat

Ein unvollständiges Design, das nicht durch mangelnde Verfügbarkeit der Daten, sondern vom Versuchsplaner selbst erzeugt wird, ist das „lateinische Quadrat“. Als Beispiel sei eine dreifaktorielle Varianzanalyse mit je drei Faktorstufen gegeben. Bei 10 Versuchseinheiten in jeder Kombination müsste man insgesamt 3*3*3*n Versuchseinheiten zur Verfügung haben. Stattdessen wird das Design auf z.B. 3*3 Faktorkombinationen gekürzt, sodass allerdings immer noch jede Faktorstufe und jede Kombination aus zwei Faktorstufen gleich oft vorkommt (Tabelle 1 und Tabelle 2). Der Vorteil dieses Designs liegt in der Kostenersparnis der Erhebung. Der Nachteil ist, dass nicht alle Hypothesen des vollständigen Designs prüfbar sind. Ist man ohnehin nur an den Einzelwirkungen der drei Faktoren und nicht an Interaktionen interessiert, fällt dieser Nachteil weg.

Tabelle 1: Übersicht über die gewählten Faktorkombinationen bei einer Kürzung
auf ein lateinisches Quadrat. Die Marker (X) geben an, welche Kombinationen tatsächlich gewählt werden

	B1			B2			B3
	C1	C2	C3	C1	C2	C3	C1	C2	C3
A1	X					X		X
A2		X		X					X
A3			X		X		X

Tabelle 2: Lateinisches Quadrat aus Tabelle 1 in Kurzschreibweise

	C1	C2	C3
A1	B1	B3	B2
A2	B2	B1	B3
A3	B3	B2	B1

Wiederholungsaufgaben und Zusammenfassung

1. Welche Bedeutung kommt der Quadratsummenzerlegung in der Varianzanalyse zu?
2. Warum ist es wichtig, dass die Fehler normalverteilt sind?
3. Sie erhalten bei einer einfaktoriellen Varianzanalyse mit $\alpha =5\%$ ein signifikantes Ergebnis. Wäre das Ergebnis auch signifikant, wenn Sie

• einen gleichgroßen Effekt (gleich große Mittelwertsdifferenzen) bei einem doppelt so großen Stichprobenumfang beobachten würden?
• einen gleichgroßen Effekt (gleich große Mittelwertsdifferenzen) bei einem halb so großen Stichprobenumfang beobachten würden?
• auf $\alpha =1\%$ testen?

4. Wie verändert sich der kritische Wert der F-Verteilung bei der Varianzanalyse, wenn $\alpha$ von 5% auf 1% gesenkt wird?

Zusammenfassung

Der Begriff „Varianzanalyse“ steht für eine große Zahl an Verfahren, bei denen mithilfe der Berechnung von Varianzen bzw. Quadratsummen inferenzstatistische Aussagen über Beziehungen verschiedener Variablen gemacht werden können („Quadratsummenzerlegung“). Dabei ist die Modellvorstellung immer, dass es eine oder mehrere gruppierende Variablen gibt, die auf eine metrische Variable einwirken (univariate ANOVA). Die Gruppeneinteilung kann „randomisiert“ erfolgen (indem die Versuchseinheiten zu verschiedenen Gruppen zugeordnet werden “Experiment“; Kausalschluss möglich) oder schon vorgegeben sein („Kranke vs. Gesunde“, „Männer vs. Frauen“, „Raucher vs. Nichtraucher“ „Beobachtungsstudie“; Kausalschluss nicht möglich).

Die Rechenschritte im Zuge einer Varianzanalyse betreffen einerseits die Parameterschätzungen des Modells welche auf die Berechnung von Gruppenmittelwerten und deren Differenzen hinauslaufen. Andererseits geschieht die Beurteilung, ob die in der Stichprobe gefundenen Unterschiede für die Grundgesmtheit verallgemeinert werden können, erst jeweils mittels des F-Tests, mittels Verteilungsannahmen, die sich aus der Forderung von normalverteilten Daten ableiten. Grundsätzlich gilt, dass soviele Hypothesen wie Effektgruppen vorhanden sind, getestet werden können.

Die Ergebnisse der Hypothesenprüfung werden jeweils in einer „Tafel der Varianzanalyse“ übersichtlich zusammengefasst.