Kryptographie und Zugriffskontrolle - Digitale Signaturen und Zertifikate

Digitale Signaturen und Zertifikate

Digitale Signaturen sind neben der Übertragung von geheimen Schlüsseln über unsichere Kanäle, die wichtigste Anwendung von asymmetrischen Verfahren (siehe Kapitel [asymmetrischeVerfahren]). Mittels digitaler Signaturen werden Webbrowser Sitzungen abgesichert, rechtlich bindende Verträge signiert oder Software sicher aktualisiert . An digitale Signaturen werden je nach Anwendung folgende Sicherheitsziele gestellt:

• Vertraulichkeit (engl. Confidentiality)
• Integrität (engl. Integrity)
• Authentizität (engl. Message Authentication)
• Nicht-Abstreitbarkeit (engl. Non-Repudiation)

Welche Sicherheitsziele erforderlich sind, hängt von der Art der Anwendung ab. So schreiben Paar und Pelzl:

"Different applications call for different sets of security services. For instance, for private e-mail the first three functions are desireable, whereas a corporate e-mail system might also require nonrepudiation. As another example, if we want to secure software updates for a cell phone, the chief objectives might be integrity and message authentication because the manufacturer primarily wants to assure that only orginal updates are loaded into the handheld device."

Außerdem gibt es neben den oben genannten Sicherheitszielen noch einige andere, abhängig von der Anwendung :

• Identifikation (engl. Identification): eindeutige Ermittlung der Person oder des Gerätes.
• Zugriffskontrolle (engl. Access Control): Zugriff auf Ressourcen wird nur für entsprechende Personen erlaubt.
• Verfügbarkeit (engl. Availability): Sicherstellung das ein System verfügbar ist.
• Physikalische Sicherheit (engl. Physical Security): Schutz gegen physikalische Manipulation.
• Anonymität (engl. Anonymity): Schutz gegen die Offenlegung der Identität oder der Missbrauch einer solchen.

Funktionsweise:
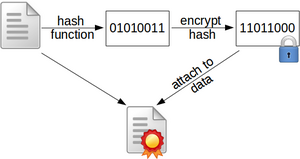
Die Erstellung einer digitalen Signaturen erfolgt nicht durch das Signieren der Daten direkt. Stattdessen wird ein Hashwert des Dokuments signiert, siehe auch Abbildung 1.1.

Signieren eines Dokuments

Der Vorgang des Signierens ist allerdings nichts anderes als die (asymmetrische) Verschlüsslung des Hashwertes mit dem private Keys des Unterzeichners. Der verschlüsselte Hashwert stellt sodann die Signatur des Dokuments dar und wird diesem beigefügt.

Verifikation des signierten Dokuments

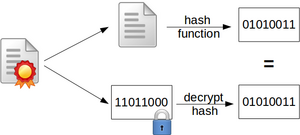
Erhält der Empfänger das signierte Dokument, muss dieser zwei Dinge tun, um die Signatur zu überprüfen, siehe dazu Abbildung 1.2. Erstens wird ebenfalls der Hashwert des Dokuments generiert. Zweitens wird mit Hilfe des Public Keys des Absenders der verschlüsselte Hashwert wieder entschlüsselt. Durch die Entschlüsselung erhält der Empfänger den durch den Absender berechneten Hashwert des Dokuments. Sind der entschlüsselte und der selbst berechnete Hashwert ident, handelt es sich um eine gültige Signatur.

Signatur mit RSA

Eine Signatur mit RSA wird nach den selben Prinzipien wie bei der Verschlüsselung mit RSA durchgeführt, siehe dazu auch Kapitel [RSA] .

Funktionsweise:

1. Bob möchte eine signierte Nachricht an Alice senden. Bob generiert ein RSA-Schlüsselpärchen. Er hat sodann einen privaten Schlüssel ${\textstyle k_{prv}=(d)}$ und einen öffentlichen Schlüssel bestehend aus ${\textstyle n}$ und ${\textstyle e}$, daher ${\textstyle k_{pub}=(n,e)}$
2. Bob stellt Alice seinen öffentlichen Schlüssel ${\textstyle k_{pub}=(n,e)}$ zur Verfügung.
3. Bob berechnet die Signatur von ${\textstyle x}$ wie folgt: ${\textstyle s=sig_{k_{prv}}(x)\equiv x^{d}\mod n}$
4. Bob sendet die signierte Nachricht ${\textstyle x}$ sowie die Signatur ${\textstyle s}$ an Alice.
5. Alice kann die Signatur wie folgt verifizieren: ${\textstyle verify_{k_{pub}}(x,s)=x'\equiv s^{e}\mod n}$. Falls ${\textstyle x'\equiv x\mod n}$, dann sind ${\textstyle x}$ und ${\textstyle x'}$ ident und handelt es sich um eine gültige Signatur. Falls ${\textstyle x'\not \equiv x\mod n}$ ist die Signatur nicht gültig.

Digital Signature Algorithm

Der Digital Signature Algorithm (DSA) ist ein durch die NSA entwickelter und durch die NIST erstmals 1994 eingeführtes Signaturverfahren . Er wird im FIPS 186-4 spezifiziert und wird als Digital Signature Standard (DSS) bezeichnet. DSA stellt dabei den verwendeten Algorithmus dar.

Unterstützte Bitlängen beim Digital Signature Algorithmus in Abhängigkeit der Parameter ${\textstyle L}$ und ${\textstyle N}$ nach

${\textstyle L}$	${\textstyle N}$
1024	160
2048	224
2048	256
3072	256

Der DSA basiert wie RSA ebenfalls auf dem Problem des diskreten Logarithmus, daher der Schwierigkeit ein Produkt zweier Primzahlen zu faktorisieren. Der DSA unterstützt unterschiedliche Bitlängen (siehe Tabelle 1.1) und besteht aus mehreren Komponenten beziehungsweise Parametern, die nachfolgend beschrieben sind .

• Eine öffentlich bekannte Primzahl ${\textstyle p}$, welche ${\textstyle L}$ Bit lang ist.
• Ein öffentlich bekannter Primfaktor ${\textstyle q}$ von ${\textstyle p-1}$, wobei ${\textstyle q}$ eine unterstützte Länge ${\textstyle N}$ haben.
• Gibt die Länge von ${\textstyle q}$ an und muss ein Vielfaches von 64 sein, sowie ${\textstyle 512\leq L\leq 3072}$
• Ein öffentlich bekannter Generator dessen Ordnung ${\textstyle q}$ ist, nach dem Satz von Lagrange
• ein Secret Key mit ${\textstyle 0<x<q}$
• ein Public Key mit ${\textstyle y=g^{x}\mod p}$
• eine Hash - Funktion, zumeist wird SHA-1 oder auch SHA-2 verwendet

Funktionsweise:

1. Die Werte ${\textstyle p,q}$ und ${\textstyle g}$ sind öffentlich bekannt. Daher können sie in einer Gruppe von Personen benutzt werden.
2. Alice möchte ein Dokument ${\textstyle M}$ signieren. Sie besitzt dazu ein Schlüsselpaar, wobei ${\textstyle x_{A}}$ ihren privaten Schlüssel und ${\textstyle y_{A}}$ ihren öffentlichen Schlüssel darstellt.
3. Alice generiert eine zufällige Zahl ${\textstyle k}$ als ihren Secret Key, wobei ${\textstyle 0<k<q}$.
4. Alice berechnet sodann die Signatur, welche sich aus ${\textstyle r}$ und ${\textstyle s}$ zusammensetzt:
   $$r=(g^{k}\mod p)\mod q$$
   $$s=(k^{-1}(H(M)+x_{A}*r))\mod q$$
5. Alice schickt Dokument ${\textstyle M}$ und Signatur ${\textstyle (r,s)}$ an Bob.
6. Bob kann die Signatur nun wie folgt überprüfen. Er berechnet sich 3 Hilfswerte ${\textstyle w,u_{1}}$ und ${\textstyle u_{2}}$. Mit Hilfe dieser Hilfswerte kann sich Bob dann ${\textstyle v}$ berechnen.
   $$w=s^{-1}\mod q$$
   $$u_{1}=w*H(M)\mod q$$
   $$u_{2}=w*r\mod q$$
   $$v=((g^{u_{1}}*y_{A}^{u_{2}})\mod p)\mod q$$
7. Entspricht ${\textstyle v\equiv r}$, dann ist die Signatur gültig.

X.509 und Public Key Infrastructure

X.509 spezifiziert das Format eines Public Key Zertifikates nach RFC 5280. . Public Key Zertifikate kommen vor allem im SSL/TLS Protokoll (siehe Kapitel [SSL] und zum Beispiel bei der E-Mail Verschlüsselung S/MIME (siehe Kapitel [SMIME]) zum Einsatz.

Zertifikat von onlinecampus.fernfh.ac.at

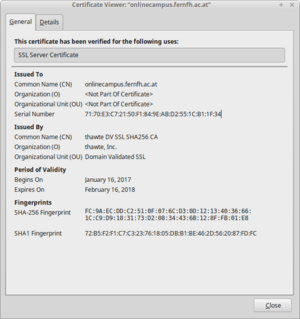
Der RFC 5280 spezifiziert folgende Attribute eines X.509 Zertifikats:

• Version
• Seriennummer
• Algorithmus
• Aussteller des Zertifikats
• Gültigkeit (von Datum bis Datum)
• Inhaber
• Schlüsselinformation des Inhabers
• Erweiterungen
• Signaturalgorithmus
• Signatur
• optional eine eindeutige ID des Ausstellers und des Inhabers

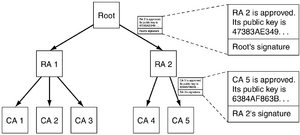
Für die Verwaltung und Erzeugung von X.509 Zertifikaten wird eine sogenannte Public Key Infrastructure (PKI) verwendet. Eine PKI Umgebung ist hierarchisch aufgebaut. Diese besteht aus mehreren Komponenten  :

hierarchischer Aufbau einer PKI aus

• Certificate Authority (CA): Die Zertifizierungsstelle hat die Aufgabe Zertifikate auszustellen und auch wieder zurückzurufen (Revoke). CAs können hierarchisch aufgebaut werden und sodann in eine Root-CA und ihre Intermediate CAs unterteilt. Zwei oder mehrere CAs können sich gegenseitig vertrauen (Trust) und in einer Mesh Struktur aufgebaut sein. Näheres dazu ist in RFC 4158 zu finden
• Registration Authority (RA): Die Registrierungsstelle hat die Aufgabe Zertifikatsanträge entgegenzunehmen (Certificate Signing Requests). Nach der eindeutigen Identifikation des Antragstellers wird der CSR an die CA zur Ausstellung weiterzugeben.
• Trust Center: CA und RA arbeiten eng zusammen und werden als Trust Center zusammengefasst.
• Certificate Revocation List (CRL): Werden Zertifikate vor Ablauf ihrer Gültigkeit von der CA zurückgerufen, werden diese in die CRL eingetragen. Diese wird in definierten Zeitabständen aktualisiert. Um gesperrte Zertifikate auszutauschen kann auch ein Protokoll wie das Online Certificate Status Protocol (OCSP) verwendet werden, siehe dazu den RFC 2560
• Directory Service: Das Directory Service oder Verzeichnisdienst bietet eine Möglichkeit nach ausgestellten Zertifikaten zu suchen.

Hardware Security Module

Ein Hardware Security Module (HSM) ist eine Hardware, die speziell für den Schutz und der Berechnung von Schlüsselmaterial ausgelegt ist . Diese werden schon lange im Banken eingesetzt um die dort notwendigen kryptografischen Transaktionen sicherzustellen. Ein HSM muss folgende Anforderungen erfüllen:

• Berechnung von echten Zufallszahlen.
• Zur Verfügung Stellung aller benötigten kryptographischen Operationen, wie Signatur-, Verschlüsselungs- und Hashalgorithmen.
• Es muss Schutz vor Seitenkanalangriffen vorhanden sein.
• Es muss ein Schutz gegen Angriffe und Manipulation der Hardware vorhanden sein (engl. tamper resistant)

Um die Qualität und den Funktionsumfang von HSMs zu vergleichen hat das NIST den FIPS 140 entworfen. Dieser Standard zertifiziert eine HSM in vier unterschiedliche Sicherheitslevel, siehe dazu .