Optimierung - Wiederholungsaufgaben Übungen
Wiederholungsaufgaben/Übungen
Aufgabe 1
Untersuche folgende Funktionen auf Extremwerte bzw. Sattelstellen (verwende die Definitheit der Hessematrix, um Entscheidung zu treffen).Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y^2 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f(x,y)=(1+x)^2-(1-y)^2 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\mathrm{xy} \end{aligned}}
Aufgabe 2
Führe zu den Funktionen aus Aufgabe 1 jeweils die erste Iteration des Gradientenverfahrens aus, wobei im Punkt (1,1) gestartet wird. Für welche der drei Aufgaben ist die Suche nach einem (lokalen oder globalen) Minimum überhaupt sinnvoll?
Aufgabe 3
Führe für die FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^4+y^4 \end{aligned}}
die ersten beiden Schritte des Newtonverfahrens aus, wenn im Punkt (1,1) gestartet wird.
Aufgabe 4
Finde die Extremwerte der folgenden Funktionen unter den angegebenen Nebenbedingungen:
(Gib jeweils Skizzen mit den Niveaulinien an um zu klären, ob es sich um ein Maximum oder ein Minimum handelt).
Aufgabe 5
Ermittle mit Hilfe der KKT-Bedingungen alle Extremstellen der folgenden Funktionen unter den gegebenen Nebenbedingungen
Stelle die Lösungen wiederum graphisch dar!
Lösungen der Aufgaben
Aufgabe 1:
Aufgabe 2:
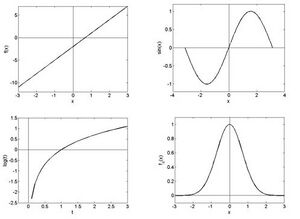
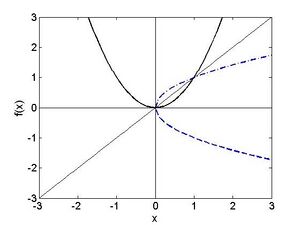
Die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2 = y}
hat natürlich zwei Lösungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1=\sqrt{y} \text { und } x_2=-\sqrt{y}}
Dementsprechend ist die Umkehrabbildung über ganz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}}
nicht eindeutig definierbar, sehr wohl aber für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x \in \mathbb{R}^{+}}
(strichpunktiert) bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{x}\in\mathbb{R}^-}
(strichliert). Aufgabe 3:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_1^\prime(x)=-2x\mathbb{exp}{(}-x^2) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_2^\prime(x)=\left(\frac{\mathbb{sin}{x}}{\mathbb{cos}{x}}\right)^\prime=1+{\mathbb{tan}}^2{(}x)=\frac{1}{{\mathbb{cos}}^2{(}x)} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_3^\prime\left(x\right)=\frac{3x^2}{2\sqrt{1+x^3}} \end{aligned}}
Aufgabe 4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{\mathbb{x}=1}^{2}\lambda\mathrm{\ exp}\left(-\lambda\mathbb{x}\right)\ dx=\mathrm{\ \ }-\left.\mathrm{\ exp}\left(-\lambda\mathbb{x}\right)\right|_1^2=\ e^{-\lambda}-e^{\mathrm{-2}\lambda} \end{aligned}}
Aufgabe 5:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} x_2=0-\frac{p^{\prime}(0)}{p^{(0)}} \\ x_3=\frac{1}{2}-\frac{p^{\prime}(1 / 2)}{p^{\prime}(1 / 2)}=\frac{1}{2}-\frac{1}{32}=0.4688 \end{array}}
Vergleicht man diesen Wert mit der tatsächlichen Stelle des lokalen Minimums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 0.4691} , so erkennt man, wie nahe das Newton Verfahren bereits nach zwei Iterationen gekommen ist.
Aufgabe 6:
Matrix A – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-10\lambda+9=0}
Eigenwerte: 1 und 9 (positiv definit)
Eigenvektoren: (1,-1)T und (7,1)T
Matrix B – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-2\lambda=0}
Eigenwerte: 2 und 0 (positiv semidefinit)
Eigenvektoren: (1,-1)T und (1,1)T
Matrix C – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^3+7\lambda^2-18\lambda=0}
Eigenwerte: -9, 2 und 0 (indefinit)
Eigenvektoren: (1,2,-3)T , (-4,3,1)T und (2,4,3) T
Aufgabe 7:
a)Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f_1\left(x,y,z\right)=\left(\begin{matrix}4-4x\\6-2y\\-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) \end{aligned}}
Kandidat für Extremum: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=1, y=3, z=0} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_{f_1}\left(x,y,z\right)=\left(\begin{matrix}-4&0&0\\0&-2&0\\0&0&-2\\\end{matrix}\right) \end{aligned}}
negativ definit ⇒ (1,3,0)T ist ein lokales Maximum
b)Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f_2\left(x,y,z\right)=\left(\begin{matrix}6x-4y\\6y-4x\\10-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) \end{aligned}}
Kandidat für Extremum: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=0, y=0, z=5}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_{f_2}\left(x,y,z\right)=\left(\begin{matrix}6&-4&0\\-4&6&0\\0&0&-2\\\end{matrix}\right) \end{aligned}}
ist indefinit (Eigenwerte -2, 2 und 10) (0,0,5)T ist ein Sattelpunkt und kein lokaler Extremwert
Aufgabe 8:
Die Lagrange Funktion lautet:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y\right)=x^2+y^2+\lambda\left(x^2+xy+y^2-3\right) \end{aligned}}
Null setzen der partiellen Ableitungen gibtFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\frac{\partial}{\partial x} L(x, y)=2 x+\lambda(2 x+y)=0 \\ &\frac{\partial}{\partial y} L(x, y)=2 y+\lambda(2 y+x)=0 \end{aligned}}
Addieren wir diese beiden Gleichungen so erhalten wirFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 2\left(x+y\right)+\lambda\left(3x+3y\right)=0 \end{aligned}}
oder äquivalent dazuFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(x+y\right)\left(2+3\lambda\right)=0 \end{aligned}}
Das bedeutet entweder der erste Faktor oder der zweite Faktor verschwindet.
Fall1: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y=0, d.h. y = -x}
.
Die Nebenbedingung lautet dannFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,-x\right)=x^2=3 \end{aligned}}
Und wir erhalten die beiden Lösungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=\sqrt{3}, y=-\sqrt{3} x=-\sqrt{3}, y=\sqrt{3}}
Fall2: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2+3\lambda = 0, d.h. \lambda = -2/3}
.
Die erste Gleichung lautetFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=2x-\frac{2}{3}\left(2x+y\right)=0 \end{aligned}}
und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y} . Die Nebenbedingung wird zuFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,x\right)=3x^2=3 \end{aligned}}
und wir erhalten die beiden Lösungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=-\sqrt{3}, y=\sqrt{3} x=-1, y=-1}
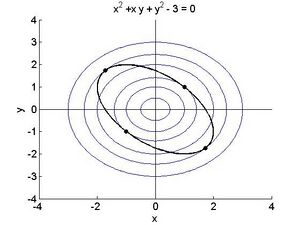
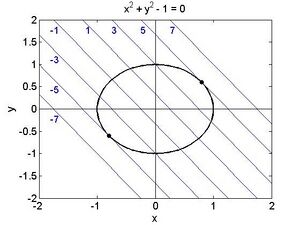
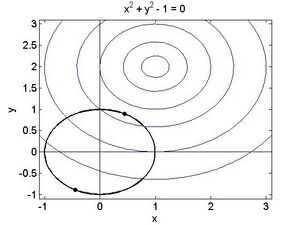
Vergleichen wir die Funktionswerte: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(\sqrt{3},-\sqrt{3})=f(-\sqrt{3}, \sqrt{3})=6 f(1,1) = f(-1,-1)=2} Die ersten beiden Punkte liefern jeweils ein Maximum, die zweiten Punkte ein Minimum unter der Nebenbedingung. Die folgende Abbildung veranschaulicht die Zusammenhänge.
Die konzentrischen Kreise geben einige Niveaulinien der Zielfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=x^2+y^2} . Beachte wiederum wie an den 4 extremalen Punkten die Kurve der Nebenbedingungen dazu tangential liegt.
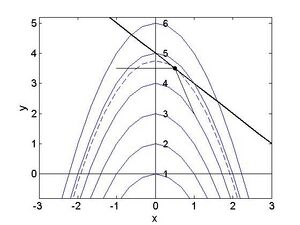
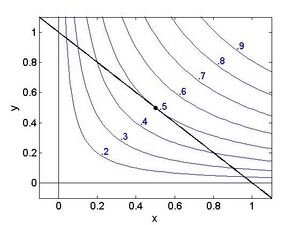
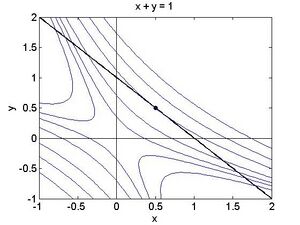
Aufgabe 9: Die Lagrange Funktion lautetFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(x, y)=x^2+y+1+\lambda(x+y-4) } Null setzen der partiellen Ableitungen gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial x} L(x, y)=2 x+\lambda=0 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial y} L(x, y)=1+\lambda=0 } und von den KKT Bedingungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda(x+y-4)=0 } Im Inneren des zulässigen Bereiches muss gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0} , und daher wird die zweite Gleichung oben zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1=0} , offensichtlich ein Widerspruch, Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda<0} muss gelten liefert die zweite Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=-1} , und daher die erste Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda\left(x+y-4\right)=0} . Die KKT Bedingung gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x+y-4\right)=0} , und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x+y-4\right)=0} . Der Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} ist somit eine potentielle lokale Extremstelle, um zu erkennen worum es sich tatsächlich handelt betrachte folgende Abbildung, die wiederum die Niveaulinien der Zielfunktion sowie den Rand des zulässigen Bereichs zeigt.
Der zulässige Bereich befindet sich unterhalb der Geraden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=4-x} . Am kritischen Punkt nimmt die Funktion den Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 19/4} an, in unmittelbarer Umgebung davon gibt es sowohl Punkte mit größeren als auch mit kleineren Funktionswerten. Es handelt sich bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} also um kein lokales Extremum, sondern um eine Art Sattelpunkt, allerdings nur wenn die Nebenbedingung in Betracht gezogen wird. Entlang der Geraden ist der Punkt ein Minimum. Für alle Werte die in einem zugespitzten Kegel mit Spitze bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} liegen (Siehe Abbildung) liegt ein Maximum vor.
Lösungen der Wiederholungsaufgaben
Aufgabe 1.1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{array}{r} f(x)=x^{\exp (x)}=\exp \left[\log (x) e^x\right] \\ f^{\prime}(x)=\exp \left[\log (x) e^x\right] \cdot\left[\frac{1}{x} e^x+\log (x) e^x\right]= \\ x^{\exp (x)}\left[\frac{1}{x} e^x+\log (x) e^x\right] \end{array} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^\prime\left(x\right)=\frac{\left(3x-2\right)\left(2x+\frac{1}{2\sqrt x}\right)-3\left(x^2+\sqrt x\right)}{(3x-2)^2} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^\prime\left(x\right)=\frac{1}{\sqrt{2x}}\mathrm{cos}\left(x^2\right)-\sqrt x\mathrm{sin}x^22x \end{aligned}}
Aufgabe 1.2:
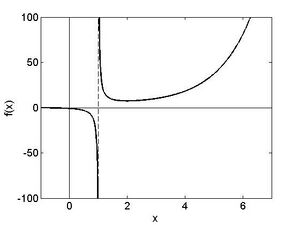
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{\mathrm{exp} \left(x\right)}{x-1}}
an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 1}
nicht definiert. Linksseitiger Limes ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -\infty}
, rechtsseitiger Limes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle +\infty}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)}
hat keine Nullstellen, allerdings konvergiert es gegen 0 für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\rightarrow-\infty}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^\prime\left(x\right)=\frac{\left(x-2\right)\mathrm{exp} \left(x\right)}{(x-1)^2}}
, Nullstelle nur bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 2}
(potentielles lokales Extremum)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{\prime\prime}\left(x\right)=\frac{\left(x^2-4x+5\right)\mathrm{exp} \left(x\right)}{(x-1)^3}}
keine reellen Nullstellen, daher keine Wendepunkte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{\prime\prime}\left(2\right)=\mathrm{exp}2>0}
, daher ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 2}
ein lokales Minimum
Aufgabe 1.3
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=\frac{1}{3} e^{3 x+4}(\text { Substitution } y=3 x+4) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=\left(x^2 \log \left(x^2\right)-x^2\right) / 2\left(\right. Substitution y=x^2 und partielle Integration ) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=-\frac{1}{4} \cos (4 x-3)(\text { Substitution } y=4 x-3) }
Aufgabe 1.4
Berechnung der Integrale
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} -\left(x^2+2x+2\right)e^{-x}|_0^1=2-5e^{-1} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left.x(\log (x 2)-1)\right|_1 ^2=\log 2-1}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{x=2}^{3}\left(3-x\right)+\int_{x=3}^{4}\left(x-3\right)\mathrm{dx}=1 \end{aligned}}
Aufgabe 1.5
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D=\left\{(x, y) \in R^2: x^2>y^2\right\}=\{(x, y):|x|>|y|\}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla \mathrm{f}=\frac{1}{x^2-y^2}\left(\begin{array}{c} 2 x \\ -2 y \end{array}\right), H_f=\frac{1}{\left(x^2-y^2\right)^2}\left(\begin{array}{cc} -2\left(x^2+y^2\right) & 4 \mathrm{xy} \\ 4 \mathrm{xy} & -2\left(x^2+y^2\right) \end{array}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D=\left\{(x, y) \in \mathbb{R}^2: x \neq y\right\} \nabla f=\frac{1}{(x-y)^2}\left(\begin{array}{c} -y^2 \\ x^2 \end{array}\right), H_f=\frac{1}{(x-y)^3}\left(\begin{array}{cc} 2 y^2 & -2 \mathrm{xy} \\ -2 \mathrm{xy} & 2 x^2 \end{array}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\nabla f=\left(\begin{array}{l} 2 x \\ 2 y \end{array}\right) \text { kritischerWert }(x, y)=(0,0) \\ &H_f=\left(\begin{array}{ll} 2 & 0 \\ 0 & 2 \end{array}\right) \text { positivde finit }(\text { konvex })(0,0) \text { ist globales Minimum } \\ &\nabla \mathrm{f}=\left(\begin{array}{cc} 2(x+1) \\ 2(1-y) \end{array}\right) \text { kritischer Wert }(x, y)=(-1,1) \\ &H_f=\left(\begin{array}{cc} 2 & 0 \\ 0 & -2 \end{array}\right) \text { indefinit }(-1,1) \text { ist Sattelpunkt } \\ &\nabla \mathrm{f}=\left(\begin{array}{l} y \\ x \end{array}\right) \text { kritischerWert }(x, y)=(0,0) \\ &H_f=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right) \text { indefinit }(E W \pm 1)(0,0) \text { ist Sattelpunkt } \end{aligned} }
Aufgabe 2.2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a) \nabla \mathrm{f}=\left(\begin{array}{l}2 x \\ 2 y\end{array}\right), \vec{x}_1=\left(\begin{array}{l}1 \\ 1\end{array}\right) }
Abstiegsrichtung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{d}_1=-\left(\begin{array}{l} 2 \\ 2 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(h)=f\left(\begin{array}{l} 1 \\ 1 \end{array}\right) -h\left(\begin{array}{l} 2 \\ 2 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle =2(1-2 h)^2 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g^{\prime}(h)=-8(1-2 h)=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h=12 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}_2=\left(\begin{array}{l} 1 \\ 1 \end{array}\right)- }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2}\left(\begin{array}{l} 2 \\ 2 \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla \mathrm{f}=\left(\begin{array}{l} 2(x+1) \\ 2(1-y) \end{array}\right), \vec{x}_1=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) }
Abstiegsrichtung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{d}_1=-\left(\begin{array}{l} 4 \\ 0 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(h)=f\left(\left(\begin{array}{l} 1 \\ 1 \end{array}\right)-h\left(\begin{array}{l} 4 \\ 0 \end{array}\right)\right)=(2-4 h)^2 g^{\prime}(h)=-8(2-4 h)=0 h=12 \vec{x}_2=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) }
In allen 3 Fällen landet man bereits nach einem Iterationsschritt im kritischen Punkt. Dies ist für allgemeine Funktionen nicht der Fall, sondern stammt daher, dass wir es hier jeweils mit quadratischen Funktionen zu tun haben. Im Beispiel a) haben wir somit nach einer Iteration bereits das globale Minimum gefunden. Aber Achtung! In Beispiel b) und c) sind wir jeweils in einem Sattelpunkt gelandet, und das Gradientenverfahren würde hier einfach abbrechen, weil der Gradient an einem kritischen Punkt natürlich gerade 0 ist. Würden wir in Beispiel b) etwa im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-1,-1)}
starten so erhält man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(h)=f\left(\left(\begin{matrix}-1\\-1\\\end{matrix}\right)-h\left(\begin{matrix}0\\4\\\end{matrix}\right)\right)=-(2+4h)^2}
und man erkennt, dass für wachsendes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h}
der Funktionswert gegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -\infty}
strebt.
Aufgabe 2.3:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla \mathrm{f}=\left(\begin{array}{c} 4 x^3 \\ 4 y^3 \end{array}\right), H_f=\left(\begin{array}{cc} 12 x^2 & 0 \\ 0 & 12 y^2 \end{array}\right), \vec{x}_1=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) }
1. Schritt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla f\left(\vec{x}_1\right)=\left(\begin{array}{l} 4 \\ 4 \end{array}\right), H_f\left(\vec{x}_1\right)=\left(\begin{array}{cc} 12 & 0 \\ 0 & 12 \end{array}\right) \vec{x}_2=\left(\begin{array}{l} 1 \\ 1 \end{array}\right)-\left(\begin{array}{cc} 112 & 0 \\ 0 & 112 \end{array}\right)\left(\begin{array}{l} 4 \\ 4 \end{array}\right)=\left(\begin{array}{l} 23 \\ 23 \end{array}\right) }
2. Schritt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla f\left(\vec{x}_2\right)=\left(\begin{array}{l} 3227 \\ 3227 \end{array}\right), H_f\left(\vec{x}_1\right)=\left(\begin{array}{cc} 163 & 0 \\ 0 & 163 \end{array}\right) \vec{x}_3=\left(\begin{array}{l} 23 \\ 23 \end{array}\right)-\left(\begin{array}{cc} 316 & 0 \\ 0 & 316 \end{array}\right)\left(\begin{array}{l} 3227 \\ 3227 \end{array}\right)=\left(\begin{array}{l} 49 \\ 49 \end{array}\right) }
Aufgabe 2.4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=4 x+3 y+\lambda\left(x^2+y^2-1\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial x}=4+2 x \lambda=0 }
Multipliziere mit -x
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial y}=3+2 y \lambda=0 }
Multipliziere mit y
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 4 y-3 x=0, \text { oder } y=\frac{3}{4} x }
Nebenbedingung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+y^2=1}
Zwei Lösungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (4/5, 3/5)}
ist Maximum (Funktionswert 5)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-4/5, -3/5)}
ist Minimum (Funktionswert -5)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=x^2+y^2+\lambda\left(2\mathrm{xy}-1\right) \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=2x+2y\lambda=0 \end{aligned}}
Multipliziere mit xFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=2y+2x\lambda=0 \end{aligned}}
Multipliziere mit -yFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 2x^2-2y^2=0 \end{aligned}}
Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=\frac{1}{2x}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^4=\frac{1}{4} \end{aligned}}
Zwei reelle Lösungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(\frac{1}{\sqrt2},\frac{1}{\sqrt2}\right)}
sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(-\frac{1}{\sqrt2},-\frac{1}{\sqrt2}\right)}
jeweils mit Funktionswert 1.
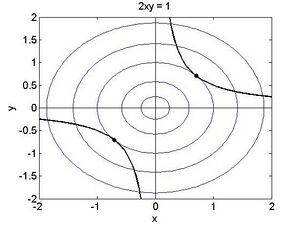
Die Zeichnung zeigt, dass es sich jeweils um ein Minimum handelt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=\mathrm{exp}(xy)+\lambda(x+y-1) \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=y\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=x\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 \end{aligned}}
Bilde Differenz der beidenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(x-y\right)\mathrm{exp}xy=0 \end{aligned}}
also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y=1}
Eindeutige Lösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y = 1/2}
mit FunktionswertFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{exp}\left(\frac{1}{4}\right) \end{aligned}}
Die Zeichnung zeigt, dass es sich wiederum um ein Minimum handelt:
Die Werte in der Zeichnung geben den Logarithmus der Wurzel der entsprechende Wertes der Funktion an. Z. Bsp ist das Minimum der Funktion unter der Nebenbedingung gegeben durchFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(0\mathrm{.}5,0\mathrm{.}5\right)=\mathrm{exp}(0.5^2) \end{aligned}}
Aufgabe 2.5:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=(x-1)^2+(y-2)^2-1+\lambda\left(x^2+y^2-1\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K K T: \frac{\partial L}{\partial x}=2(x-1)+2 x \lambda=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial y}=2(y-2)+2 y \lambda=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda\left(x^2+y^2-1\right)=0(\text { Comp. Slack. }) }
Fall 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
(Lösung im inneren des zulässigen Bereichs)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = 2}
einzige formale Lösung, liegt nicht im zulässigen Bereich!
Fall 2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+y^2-1=0}
(Lösung am Rand)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x-1\right)y-\left(y-2\right)x=2x-y=0}
, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2x = y}
(ähnlich wie in Aufgabe 2.4)
Einsetzen in NB liefert zwei Lösungen:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right) \text { mit Funktionswert } 5-\frac{10}{\sqrt{5}}(\text { Minimum unter } N B) \\ \left(-\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}}\right) \text { mit Funktionswert } 5+\frac{10}{\sqrt{5}}(\text { Maximum unter } N B) \end{array}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} L=x^2+3 x y++2++y-1 \\ K K T: \frac{\partial L}{\partial x}=2 x+3 y+\lambda=0 \\ \frac{\partial L}{\partial y}=3 x+2 y+\lambda=0 \\ \lambda(x+y-1)=0(\text { Comp. Slack. }) \end{array}}
Fall 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
(Lösung im inneren des zulässigen Bereichs)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 0}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = 0}
einzige formale Lösung, Hessematrix indefinit
Sattelpunkt
Fall 2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y-1=0}
(Lösung am Rand)
Eliminiere Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x-y=0}
, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
(ähnlich wie in Aufgabe 2.4)
Einsetzen in NB liefert eindeutige Lösung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x = y = 1/2 \end{aligned}}
mit Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 5/4} Die Grafik zeigt, dass es sich um ein Maximum handelt:
Die Niveaulinien entsprechen Hyperbeln: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+3\mathrm{xy}+2=const.} Je weiter man sich vom Ursprung nach rechts oben bewegt, desto größer sind die Werte die die Funktion entlang der Niveaulinie annimmt. Je weiter man sich vom Ursprung nach links oben (bzw. rechts unten) bewegt, desto kleiner sind die entsprechenden Funktionswerte.