Grundlagen der Modellierung - Prozess- und Ablaufmodellierung
Prozess- und Ablaufmodellierung
Um die Prozesse und Abläufe von IT-Systemen zu modellieren gibt es eine Vielzahl möglicher Modellformen. Drei der wichtigsten Modelle werden nun nachfolgend genauer beschrieben. Jede davon hat ihre speziellen Anwendungsbereiche. Es ist daher nicht möglich sich allein auf eine einzelne Form zu beschränken, sondern notwendig das jeweils beste Modell für das betreffende System auszuwählen. Die Modellierung von Geschäftsprozessen ist thematisch damit natürlich eng verwandt und wird in der nächsten Lektion erläutert.
Struktogramm (Nassi-Shneiderman-Diagramm)
Bei Struktogrammen handelt es sich um Modelle von logischen Programmabläufen. Sie finden meist im Bereich der Softwareentwicklung Anwendung und ermöglichen eine grafische, pseudocodeartige, Modellierung. Entwickelt wurden sie von Isaac Nassi und Ben Shneidermann (Nassi & Shneiderman, 1973). Struktogramme werden daher auch als Nassi-Shneiderman-Diagramme bezeichnet. Heute ist die Modellierungsform der Struktogramme offiziell in der DIN 66261:1985 „Informationsverarbeitung; Sinnbilder für Struktogramme nach Nassi-Shneiderman“ genormt.
Den Einsatz von Struktogrammen haben Sie bereits in der Lehrveranstaltung „Programmiersprachen und angewandte Programmierung“ kurz kennengelernt.
Aufbau eines Struktogramms
Struktogramme werden von oben nach unten aufgebaut. Der Programmfluss beginnt demnach beim obersten und endet beim letzten unteren Element. Das gesamte Diagramm ist immer so breit, wie sein breitestes Element.
Es gibt vier mögliche Elementarten (Nassi & Shneiderman, 1973):
- Prozess-Elemente,
- Entscheidungs-Elemente,
- Iterations-Elemente (Schleifen) und
- Begin-End-Elemente.
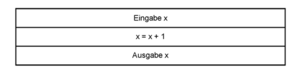
Bei den Prozess-Elementen handelt es sich um Elemente, welche einen einzelnen Programmbefehl beinhalten. Sie repräsentieren damit eine Codezeile und können Variablendefinitionen, Variablenzuordnungen, Berechnungen und Funktionsaufrufe beinhalten. Ein simples Programm mit drei Prozesselementen ist in der Abbildung "Prozess-Elemente eines Struktogramms" dargestellt. Es handelt sich dabei um ein minimales Beispiel von Eingabe, Verarbeitung und Ausgabe. Dabei wird ein Wert in die Variable x eingelesen, um den Wert 1 erhöht und wieder ausgegeben.
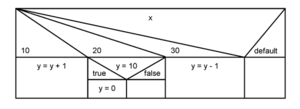
Entscheidungs-Elemente ermöglichen den Ablauf, gemäß bestimmter Bedingungen, zu verzweigen. Sie können beliebig viele Verzweigungen beinhalten, welche selbst wiederum beliebig viele Unterelemente enthalten dürfen. Haben sie nur zwei Verzweigungen mit den Bedingungswerten true und false, repräsentieren sie programmiertechnisch eine If-Then-Else Bedingung, haben sie mehrere Werte, handelt es sich um eine Select-Case Bedingung. Eine Select-Case Bedingung sollte dabei auch immer einen Default-Verzweigung haben, welche zur Anwendung kommt, wenn keine der anderen Bedingungen zutrifft. Die Verzweigungsbedingung befindet sich in der Kopfzeile des Elements. Die möglichen Verzweigungen werden dann mittels Trennlinien darunter dargestellt. Unter der Verzweigungsbedingung teilt sich das Diagramm dann in mehrere, entsprechend schmälere, Bereiche, welche selbst wiederum Elemente enthalten können. Nach der Abarbeitung des Entscheidungs-Elements wird der Ablauf beim nächsten, darunter befindlichen, Element fortgesetzt. Ein Beispiel für ein Entscheidungs-Element ist in der Abbildung "Entscheidungs-Elemente eines Struktogramms" dargestellt. Es überprüft, ob eine Variable x einen Wert gleich 10, gleich 20 oder gleich 30 hat. Ist der Wert gleich 10 wird die Variable y um 1 erhöht. Ist er gleich 20 wird überprüft ob die Variable y gleich 10 ist und in diesem Fall auf 0 gesetzt. Wenn x größer 30 ist, wird die Variable y um 1 vermindert.
Iterations-Elemente repräsentieren Schleifen. Sie können kopf- oder fußgesteuert sein, was wiederum bedeutet ob die Abbruchbedingung der Schleife an ihrem Beginn, und damit vor jedem Durchlauf, oder an ihrem Ende, und damit nach jedem Durchlauf geprüft wird. Die Elemente innerhalb der Schleife, werden solange immer wieder durchlaufen, bis entweder der Ausdruck der Schleifenbedingung nicht mehr wahr ist, oder in einem Prozesselement der Befehl break ausgeführt wird. Nach dem Abbruch der Schleife wird der Ablauf beim nächsten, darunter befindlichen, Element fortgesetzt. Eine Schleifenbedingung kann auch durch ein beschreibendes Wort wie „Solange“ oder im englischen „Do“ eingeleitet werden.
Eine Sonderform sind die Zählerschleifen. Dabei wird die Abbruchbedingung in Form einer Zählbedingung geschrieben, welche eine Variable, einen Startwert, einen Endwert und eine Schrittweite enthält. Wird keine Schrittweite angegeben entspricht sie dem Wert 1.
Ein Beispiel einer kopfgesteuerten Zählerschleife und einer fußgesteuerten Schleife findet sich in der Abbildung "Iterations-Element eines Struktogramms". Dabei wird zuerst eine Variable x mit dem Wert 0 initialisiert, danach von der ersten Schleife bis 10 hochgezählt und von der zweiten Schleife wieder bis 0 heruntergezählt. In jedem Durchlauf der Schleife wird die Variable zusätzlich ausgegeben. Die fußgesteuerte Schleife wurde hierbei nicht als Zählerschleife, sondern als Schleife mit einfacher Abbruchbedingung, modelliert. Die Zähloperation befindet sich daher innerhalb der Schleife als Prozess-Element.
Bei Beginn-End-Elementen handelt es sich um die Möglichkeit mehrere Elemente zu einem gemeinsamen Ausführungsblock zu gruppieren. Sie dienen der besseren Lesbarkeit für den Entwickler, da durch sie die Zusammengehörigkeit der Elemente eines bestimmten Ablaufs deutlich gemacht wird. Im nachfolgenden Beispiel, in der Abbildung "Begin-End-Element eines Struktogramms", wird der Ablauf aus Abbildung 22 in einem Begin-End-Element zusammengefasst.
Auslagerung von Abläufen in Funktionen
Es ist oft sinnvoll einzelne, mehrmals benötigte, Abläufe in Funktionen und Prozeduren auszulagern. Dies ist in der Norm nicht vorgesehen und wird in der Praxis meist durch ein Prozess-Element mit einem entsprechenden Aufrufbefehl der Funktion oder Prozedur realisiert. Dadurch wird ebenfalls sichergestellt, dass die Programmausführung nach dem aufrufenden Prozess-Element wieder fortgesetzt wird. Die ausgelagerte Funktion oder Prozedur selbst, wird dann wiederum getrennt in einem eigenen Struktogramm abgebildet.
Zusätzlich ist es üblich das aufrufende Prozess-Element mittels zweier einschließender vertikaler Linien zu kennzeichnen. Ein Beispiel für einen Aufruf der Funktion Verschlüssele mit dem Parameter x und der anschließenden Speicherung des Rückgabewertes in y ist in Abbildung 26 dargestellt.
Beispiel eines Struktogramms
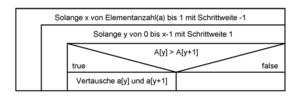
Es soll das Struktogramm eines Bubble-Sortieralgorithmus für die aufsteigende Sortierung eines Arrays erstellt werden. Dieser durchläuft die zu sortierende Menge von Anfang bis Ende und überprüft jeweils, ob das aktuelle Element kleiner ist als das nachfolgende Element. Trifft dies nicht zu, werden die Elemente vertauscht und das nächste Element betrachtet. Durch diesen Vorgang steigt das größte Element immer weiter auf, bis zum Ende der Liste [1] . Der Durchgang wird nun kontinuierlich von vorne weg wiederholt. Das jeweils letzte Element jedes Durchgangs muss beim nächsten Durchgang nicht mehr beachtet werden, da es sich um das größte Element des Durchganges handelt. Die zu sortierende Menge ist somit im hinteren Teil bereits korrekt sortiert. Die Liste ist sortiert, wenn der letzte Durchgang nur noch aus einem einzelnen Element bestehen würde.
Die Realisierung erfolgt über zwei verschachtelte Schleifen und ist in der Abbildung "Struktogramms für einen Bubble-Sort" als Struktogramm zur Sortierung eines Arrays a dargestellt.
Zustandsautomaten (endliche Automaten)
Bei einem Zustandsautomaten handelt es sich um ein System, welches eine genau definierbare, endliche, Anzahl von Zuständen annehmen und durchlaufen kann. Zustandsautomaten werden daher auch als endliche Automaten bezeichnet. Zustandsautomaten werden meist für den Entwurf von elektronischen Schaltungen, jedoch auch für das Design von Programmabläufen, verwendet.
Bei der Modellierung eines Zustandsautomaten wird von einer fiktiven Maschine ausgegangen, welche selbst über einen definierten Zustand verfügt. Dieser Zustand kann sich, durch bestimmte Ereignisse, welche wiederum Bedingungen unterliegen, ändern. Die zugehörigen Bedingungen können von externen Einflüssen und von bestimmten Zuständen des Automaten abhängen. Ihre Vorteile sind die einfache grafische Abbildbarkeit von zustandsbasierten Abläufen und die Möglichkeit einer tabellarischen Darstellung. Diese können dann wiederum einfach in entsprechende Programmlogiken übersetzt werden.
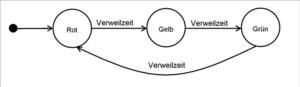
In der Abbildung "Zustandsautomat Ampel" ist das Beispiel eines einfachen Zustandsautomaten einer Ampel dargestellt.
Ein Zustandsautomat besteht aus (Oesterreich, 2006, S. 317):
- einer endlichen, nicht-leeren Menge von Zuständen,
- einer endlichen, nicht-leeren Menge von Ereignissen,
- Zustandsübergängen,
- einem Anfangszustand und
- einer Menge von Endzuständen.
Die zwei unterschiedlichen Formen von Zustandsautomaten sind:
- Moor Zustandsautomaten und
- Mealy Zustandsautomaten.
Ein Moore Zustandsautomat verwendet sowohl externe Inputs als auch den eigenen aktiven Zustand zur Ermittlung des neuen Zustandes. Beim Mealy Zustandsautomat wird zusätzlich auch der ursprüngliche Input der vorangegangenen Zustandsänderung als Bedingung verwendet. Somit kann Folgezustand nicht nur vom aktuellen, sondern auch von jener Funktion abhängig gemacht werden, die zur Änderung zum aktuellen Zustand geführt hatte. Die beiden Darstellungsformen sind gleichwertig und ineinander überführbar. So ist der Moore Zustandsautomat komplexer in seiner Darstellung, aber leichter zu lesen und der Mealy Zustandsautomat einfacher in seiner Darstellung, jedoch komplexer zu lesen.
Die Modellierung eines Zustandsautomaten geschieht meist in vier Schritten (Wang, 2014, S. 157):
- Erstellung des Zustandsdiagramms,
- Erstellung der Übergangstabelle,
- Finden der booleschen Ausdrucke und
- Implementierung der Ablauflogik.
Diese vier Schritte werden nun nachfolgend genauer erläutert. Vorab ist hierbei jedoch zu erwähnen, dass Schritt 3 bei einfacheren Zustandsautomaten im Bereich der Softwareentwicklung übersprungen werden kann. Bei komplexen Automaten und im Bereich der Entwicklung elektronischer Schaltungen ist er jedoch erforderlich.
Zustandsdiagramme
Der erste Schritt bei der Modellierung eines Zustandsautomaten ist die Erstellung eines Zustandsdiagramms. Dabei werden alle möglichen Zustände des modellierten Systems in Form von Kreisen gezeichnet. Die Bezeichnung des Zustandes befindet sich dabei innerhalb des Kreises. Jeder mögliche Übergang eines Zustandes in einen anderen wird durch einen Pfeil, vom Beginnzustand zum Folgezustand, dargestellt, welcher mit der jeweiligen Übergangsbedingung beschriftet ist. Weiter sollte der jeweilige Anfangszustand immer gekennzeichnet werden. Dies geschieht durch einen kleinen schwarz ausgefüllten Kreis als Startpunkt, welcher mit einem Pfeil auf den Startzustand verweist. Die Definition eines Startzustandes wird im Bereich der Erstellung elektronischer Schaltungen oft weggelassen oder vergessen, da in diesem Fall der Startzustand automatisch der Zustand mit dem Eingangswert 0 ist, welcher bei der erstmaligen Aktivierung der Schaltung anliegt. Im Bereich der IT-Systementwicklung ist es jedoch erforderlich, immer auch einen Startzustand zu definieren, da dieser für die korrekte Modellierung des Programmcodes benötigt wird.
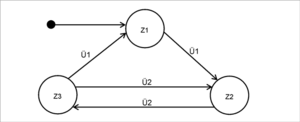
Die einzelnen Elemente sind in der Abbildung "Zustandsdiagramm", in Form eines einfachen Zustandsautomaten mit den Zuständen Z1, Z2 und Z3, sowie den Übergangsbedingungen Ü1 und Ü2, grafisch dargestellt. Ein Wechsel zwischen den Zuständen Z2 und Z3 ist hier in beide Richtungen durch die Übergangsbedingung Ü2 möglich. Ein Wechsel von Z1 zu Z2 und von Z3 zu Z1 ist, durch Ü1, nur in jeweils eine Richtung erlaubt. Als Startzustand wurde Z1 definiert.
Übergangstabellen
Nach der grafischen Modellierung des Zustandsautomaten wird dieser in eine Übergangstabelle überführt. Ziel der Übergangstabelle ist es, jeden möglichen Zustandsübergang als logisch abbildbaren Ausdruck zu erhalten, um diese dann später in eine Programmstruktur für die Implementierung des Zustandsautomaten übersetzen zu können. Die Übergangstabelle enthält dabei alle möglichen Eingangswerte, die Übergangsbedingungen und die möglichen Ausgangswerte. Es werden dabei nur mögliche Kombinationen betrachtet. So ist im Beispiel aus Abbildung 29 nur die Übergangsbedingung Ü1 relevant, wenn sich der Automat im Zustand Z1 oder Z3 befindet. Tritt in diesem Zustand die Übergangsbedingung Ü2 ein, hat dies aktuell keine Auswirkung.
Ein Beispiel einer möglichen Übergangstabelle für das Zustandsdiagramm in Abbildung 29 ist in Tabelle 2 dargestellt.
Tabelle 2 – Übergangstabelle
| Ist-Zustand | Übergangsbedingung | Neuer-Zustand |
|---|---|---|
| Z1 | Ü1 | Z2 |
| Z2 | Ü2 | Z3 |
| Z3 | Ü2 | Z2 |
| Z3 | Ü1 | Z1 |
Die Anzahl der Spalten kann, bei komplexeren Automaten, natürlich auch größer sein. So ist es manchmal sinnvoll die einzelnen Übergangsbedingungen in eigenen Spalten darzustellen, wenn eine Kombination mehrerer Bedingungen möglich ist. In der nachfolgenden Tabelle 3 wird die Anforderung des Automaten um eine kombinierte Übergangsbedingung erweitert. Hier ist ein Übergang von Z2 zu Z3 nur möglich, wenn gleichzeitig auch Z1 eintritt.
Tabelle 3 – Übergangstabelle mit Kombination von Zuständen
| Ist-Zustand | Übergangsbedingung Ü1 | Übergangsbedingung Ü2 | Neuer-Zustand |
|---|---|---|---|
| Z1 | Ja | Nein | Z2 |
| Z2 | Ja | Ja | Z3 |
| Z3 | Nein | Ja | Z2 |
| Z3 | Ja | Nein | Z1 |
Finden der booleschen Ausdrucke
Dieser Schritt kann bei einfacheren Zustandstabellen übersprungen werden, da die weitere Implementierung dort auch direkt mit den Werten der Tabelle erfolgen kann. Bei komplexeren Systemen macht es jedoch Sinn eine Darstellung mittels boolescher Ausdrücke durchzuführen, da dadurch die Komplexität der Implementierung sinkt. Weiter ist durch die Darstellung in booleschen Ausdrücken eine Unordnung und Optimierung der Logik möglich, was gerade bei komplexen Systemen zu einer Performancesteigerung der späteren Implementierung führt.
Um boolesche Ausdrucke zu erhalten muss die im vorherigen Schritt erstellte Zustandstabelle in eine binäre Darstellung umgewandelt werden. Das erfordert zuerst eine Umwandlung der unterschiedlichen Status und Übergangsbedingungen in eine binäre Zahl:
- Z1 00
- Z2 01
- Z3 10
- Ü1 00
- Ü2 01
Die dadurch entstandene Tabelle ist in Tabelle 4 dargestellt.
Tabelle 4 – Übergangstabelle in binärer Form
| Ist-Zustand | Übergangsbedingung | Neuer-Zustand |
|---|---|---|
| 00 | 0 | 01 |
| 01 | 1 | 10 |
| 10 | 1 | 01 |
| 10 | 0 | 00 |
Um nun daraus nun boolesche Ausdrucke erhalten zu können müssen alle binären Zahlen, welche mehr als einer Ziffer haben, als eigene Variable je Ziffer abgebildet werden. In Tabelle 5 ist diese Umwandlung bereits durchgeführt. Die Variablen des Ist-Zustandes sind hierbei I1 und I2 und die Variablen des neuen Zustandes N1 und N2. Für die Übergangsbedingung wird B1 verwendet. Hier genügt eine Variable, da sich die Bedingungen nur in einer Ziffer unterscheiden.
Tabelle 5 – Übergangstabelle in boolescher Form
| Ist-Zustand | Übergangsbedingung | Neuer-Zustand | ||
|---|---|---|---|---|
| I1 | I2 | B1 | N1 | N2 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
Daraus ergeben sich mehrere Logik-Gleichungen, die nun nach den Regeln der booleschen Logik optimiert werden können. Für die Tabelle wäre das nun die Formeln:
- (nicht N1) und N2 = (nicht I1) und (nicht I2) und (nicht B1)
- N1 und (nicht N2) = (nicht I1) und I2 und B1
- (nicht N1) und N2 = I1 und (nicht I2) und B1
- (nicht N1) und (nicht N2) = I1 und (nicht I2) und (nicht B2)
Die nötigen Verfahren zur Optimierung von Logik-Gleichungssystemen sind nicht Teil dieser Lehrveranstaltung und werden daher auch nicht näher erläutert [2] . Eine einfache Möglichkeit der Optimierung wäre die Zusammenfassung von Formeln mit gleichem Output durch eine Oder-Verknüpfung und das Vereinfachen der entstandenen Formel:
- (nicht N1) und N2 = ( B1 und (nicht I1) ) und (nicht I2) und ( I1 und (nicht B1) )
- N1 und (nicht N2) = (nicht I1) und I2 und B1
- (nicht N1) und (nicht N2) = I1 und (nicht I2) und (nicht B2)
Überführung von Zustandsautomaten in Programmcode
Je nach dem zu implementierenden System, wird die Zustandstabelle nun in Programmcode oder eine elektrische Schaltung überführt. Für die Überführung in Programmcode gibt es mehrere Möglichkeiten:
- Implementierung als Select-Case Anweisung oder
- Implementierung als Tabellenabfrage.
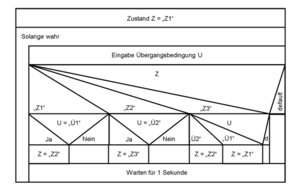
Für die Implementierung als Select-Case Anweisung werden alle Eingangs- und Ausgangsparameter als Variablen angelegt und gemäß dem Startzustand vorinitialisiert. Der Zustandsautomat selbst wird dann als Select-Case Anweisung implementiert, welche regelmäßig ausgeführt wird und gegebenenfalls den Zustand ändert. Oft handelt es sich dabei um eine Endlosschleife welche am Ende mit einem Wartebefehl versehen ist. Die Übergangstabelle aus Tabelle 3 wurde im Struktogramm in der Abbildung "Ablauflogik eines Zustandsautomaten mit Case Anweisung" durch eine Select-Case Anweisung implementiert.
Bei der Implementierung als Tabellenabfrage wird die Übergangstabelle in ein mehrdimensionales Feld geschrieben, welche dann bei jedem Durchlauf zeilenweise überprüft wird. Eine vereinfachte Darstellung dieser Implementierungsform ist als Struktogramm in der Abbildung "Ablauflogik eines Zustandsautomaten mit Tabellenabfrage" gargestellt. Die eigentliche Implementierung ist dann in den verschiedenen Programmiersprachen sehr unterschiedlich, je nachdem wie einfach Zugriffe auf mehrdimensionale Arrays, und die Suche nach bestimmten Zeilen, möglich sind. So ist beispielsweise in C ein Durchsuchen über eine Schleife erforderlich, hingegen in Perl eine direkte Abfrage über den Spaltenindex, der wiederum dem Zustandsnamen entsprechen kann möglich.
Beispiel eines Zustandsautomaten
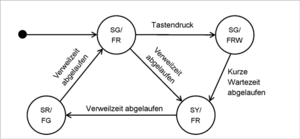
In der Abbildung "Zustandsdiagramm Verkehrsampel mit Fußgängerübergang" ist der Zustandsautomat einer Verkehrsampel mit Fußgängerübergang dargestellt. Anders als bei der einfachen Ampel in der Abbildung "Zustandsautomat Ampel", hat diese Ampelanlage eigene Farben für den Verkehr und die Fußgängerseite. Weiter ist sie mit einem Schalter ausgestattet, der von den Fußgängern gedrückt wird, wenn sie die Straße überqueren wollen. Dadurch wird, nach einer kurzen Wartezeit, eine Zustandsänderung der Ampel ausgelöst. Anderenfalls ändert sich der Status die Fahrbahnampel regelmäßig in einem längeren Intervall. Die Umsetzung soll später in Form eines Programmes und nicht direkt als elektronische Schaltung erfolgen.
Schritt 1: Erstellung des Zustandsdiagramms
Die möglichen Status sind nun:
- SG/FR für Straßenampel grün und Fußgängerampel rot,
- SG/FRW für Straßenampel grün, Fußgängerampel rot und Taste gedrückt,
- SY/FR für Straßenampel gelb und Fußgängerampel rot, sowie
- SR/FG für Straßenampel rot und Fußgängerampel grün.
Daraus wurde nun in der Abbildung "Zustandsdiagramm Verkehrsampel mit Fußgängerübergang" ein Zustandsdiagramm der Ampelanlage erstellt.
Schritt 2: Erstellung der Übergangstabelle
Nun wird aus dem Zustandsdiagramm eine Übergangstabelle erstellt, welche nachfolgend in Tabelle 6 ersichtlich ist.
Tabelle 6 – Übergangstabelle "Verkehrsampel mit Fußgängerübergang"
| Ist-Zustand | Übergangsbedingung | Neuer-Zustand |
|---|---|---|
| SGFR | Tastendruck (T) | SGFRW |
| SGFR | Verweilzeit abgelaufen (V) | SYFR |
| SGFRW | Kurze Wartezeit abgelaufen (W) | SYFR |
| SYFR | Verweilzeit abgelaufen (V) | SRFG |
| SRFG | Verweilzeit abgelaufen (V) | SGFR |
Schritt 3: Finden der booleschen Ausdrucke
Dieser Schritt wird übersprungen, da der Zustandsautomat nicht komplex ist und als Softwareprogramm umgesetzt werden soll. Es wird daher direkt zu Schritt 4 übergegangen.
Schritt 4: Implementierung der Ablauflogik
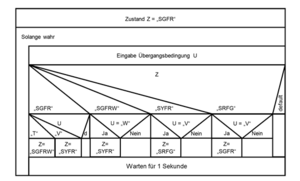
Als Implementierungsform wurde die des Select-Case-Statements gewählt. Die Ablauflogik wird in Form eines Struktogramms in der Abbildung "Ablauflogik Verkehrsampel mit Fußgängerübergang" dargestellt.
Petri-Netze
Im Jahr 1939 wurden von Carl Adam Petri die Petri-Netze Entwickelt um seine Kenntnisse chemischer Prozesse anschaulich zu machen. Im Jahr 1941 begann er dann damit seine neue Modellierungsform zu erweitern, um ein strukturiertes Modell zur Formulierung und Lösung der spezifischen Problemstellungen von Computersystemen zur Verfügung zu stellen. Als Entwicklungsgrundlage der Petri-Netze dienten auch die Zustandsautomaten. (Reisig, 2010, S. IX)
Mit einem Petri-Netz werden diskrete Systeme abgebildet. Das bedeutet, dass das System und seine Abläufe und Zustände von einem bestimmten Zeitpunkt abhängig sind. Weiter ermöglichen sie die Modellierung und Abbildung verteilter Systeme.
Aufbau eines Petri-Netzes
Ein Petri-Netz besteht aus einem oder mehreren Abläufen, welche immer eine zeitliche Abhängigkeit und einen bestimmten Zustand haben. Der Zustand wird hierbei jedoch in Form von Token abgebildet, welche immer von einem Platz zum nächsten weitergereicht werden können. Die grundlegenden Elemente eines Petri-Netzes sind (Reisig, 2010, S. 22ff):
- Plätze, welche als Kreis oder Ellipse dargestellt werden,
- Transitionen, welche als Quadrate oder Rechtecke dargestellt werden,
- Kanten, die als Pfeile dargestellt werden, und
- Token, welche entweder als ausgefüllter Punkt, oder als bestimmtes Element, abgebildet werden.
Ein wesentliches Element sind die Token. Sie befinden sich an bestimmten Plätzen und werden an verarbeitende Stellen, die Transitionen, weitergeben. Diese erzeugen wiederum neue Token und legen diese wiederum an Plätzen ab. In manchen Modellteilen kann es daher so aussehen, als würden die Transitionen Token „weitergeben“, sofern derselbe Token-Typ, in gleicher Anzahl in die Transition eingeht und sie wieder verlässt. Tatsächlich handelt es sich jedoch immer um eigene eingehende und ausgehende Token.
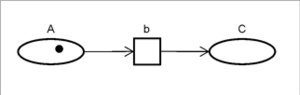
In Abbildung 34 ist ein einfaches Petri-Netz dargestellt, welches einen einfachen Token vom Platz A über die Transition b zum Platz C weiterreicht.
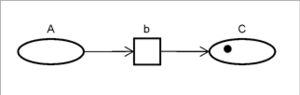
Nach einem Ablaufschritt wurde der Token dann „weitergereicht“ und befindet sich am Platz C. Konkret hat jedoch die Kante zwischen A und b zu einer Entnahme des Tokens aus A geführt. Die Transition b wurde nun dadurch ausgelöst und hat, angeleitet durch die Kante zwischen b und C einen neuen Token am Platz C abgelegt. Dies ist nachfolgend in Abbildung 35 wieder grafisch dargestellt.
Diese ersten beiden Beispiele nutzen die einfachste Form von Token, ohne spezielle Ausprägung. Dieser Form eines Petri-Netzes wird als elementares Netz bezeichnet.
Es ist auch möglich die Token selbst mit einem bestimmten Typ zu versehen. Damit können die verarbeitenden Transitionen von ganz bestimmten Token abhängig gemacht werden. Wenn es beispielsweise einen Token-Typ „Kaffeetasse“ und einen Token-Typ „Kaffeebohne“ gibt, kann eine Transition auch von der Existenz beider bestimmter Typen im vorhergehenden Platz abhängig gemacht werden, um dann wiederum einen Token vom Typ „volle Kaffeetasse“ im nachfolgenden Platz abzulegen. Wenn mehrere Token-Typen unterschieden werden, dann muss die zuständige Kante auch mit den weiterzugebenden Token beschriftet werden. Im nachfolgenden Beispiel, in Abbildung 36, ist ein simpler Ablauf einer Kaffeezubereitung in Form eines sehr einfachen Petri-Netzes abgebildet. Grundvoraussetzung ist hierbei, dass sich genügend Kaffeebohnen und leere Tassen im Platz „Küchenschrank“ befinden. Erst wenn die Token der Kante vorhanden sind, wird die Transition „Kaffeezubereitung“ gestartet, welche wiederum eine „volle Kaffeetasse“ im Platz „Küchentisch“ ablegt. Die Token sind, der Einfachheit halber, in Form von Piktogrammen dargestellt.
In diesem Modell wird nun eine Bohne und eine Tasse aus dem Platz „Küchenschrank“ durch die Bedingung der Kante entnommen und an die Transition „Kaffeezubereitung“ übergeben. Diese wiederum generiert eine volle Kaffeetasse und legt sie in den Platz „Küchentisch“. Nach der Abarbeitung befindet sich damit im Platz „Küchenschrank“ eine Kaffeebohne und im Platz Küchentisch eine „volle Kaffeetasse“.
Eine Transition kann sowohl mehrere eingehende, als auch mehrere ausgehende Kanten haben. Um die Aktion der Transition auszulösen, müssen immer alle eingehenden Kanten erfüllt sein. Erst wenn alle nötigen Kanten erfüllt werden, werden auch die vorausgesetzten Token der vorangehenden Plätze entnommen. Wird nur ein Teil der eingehenden Kanten erfüllt, bleiben somit alle Token in den Plätzen liegen, bis sie dann gemeinsam entnommen werden können. In Abbildung 37 wurde das Beispiel der Kaffeezubereitung nun um einen zweiten eingehenden Platz „Kaffeedose“ erweitert, welcher nun die Bohnen enthält.
Damit ein Nachfüllen der Tassen und Bohnen, sowie die Entnahme des fertigen Kaffees möglich sind, werden nun eigene eingehende Transition eingeführt, welche eine Interaktion des Systems mit äußeren Einflüssen erlauben. Diese Transitionen nennt man kalte Transitionen. Es wird generell zwischen heißen und kalten Transitionen unterschieden. Eine heiße Transition wird einem System immer automatisch aktiv, sobald ihre Vorbedingungen erfüllt sind. Eine kalte Transition ist zusätzlich noch von äußeren Bedingungen abhängig und wird somit nicht automatisch aktiv. Zur besseren Kennzeichnung werden kalte Transitionen mit dem Zeichen „ε“ [3] gekennzeichnet, was wiederum auf ihren externen Charakter hinweisen soll.
Nachfolgend, in Abbildung 38, wurde das Modell der Kaffeezubereitung nun um das Nachfüllen der Kaffeebohnen und Kaffeetassen, sowie um die Entnahme des fertigen Kaffees vom Küchentisch erweitert.
In dem Beispiel würde immer so viel Kaffee gekocht wie, aufgrund der verfügbaren Kaffeetassen und Kaffeebohnen möglich ist. Die Entnahme der fertigen Kaffees aus dem Platz „Küchentisch“ ist möglich, tritt jedoch nicht sicher ein. Wird die Transition „Kaffee trinken“ nicht von außen abgerufen, so füllt sich der Küchentisch immer weiter an.
Eine weitere mögliche Anwendung von Transitionen und Kanten ist die Angabe einer zusätzlichen Bedingung. Diese kann den Inhalt eines übergebenen Token prüfen und verhält sich damit wie eine Variablenabfrage, wobei der Token die Variable darstellt. Damit lassen sich beispielsweise auch Zähler abbilden. Die Bedingung wird dazu in das Transition-Symbol geschrieben und muss zusätzlich zu den eingehenden Kanten erfüllt werden.
Um die Anwendung von Bedingungen in Transitionen zu erläutern wurde das Kaffeezubereitungsbeispiel nun um einen Hinweis zu Entkalkung der Kaffeemaschine erweitert, der nach 100 zubereiteten Kaffees auftreten, und dann nach der Bestätigung des Hinweises durch die Serviceperson wieder auf 0 gesetzt werden, soll.
Da die Geschwindigkeit der Ausführung der Transitionen nicht einheitlich ist, wird im aktuellen Beispiel die asynchrone Abarbeitung des Petri-Netzes deutlich. So kann die Transition „Kaffeezubereitung“ natürlich auch mehr Zeit in Anspruch nehmen, als die simple Transition „Zähler ausführen“. Durch das Auslösen der Transitionen mittels Token, wird eine Verteilung der Aufgaben erreicht, welche zwar parallel jedoch nicht unbedingt synchron abgearbeitet werden. Da es sich bei Transitionen immer um Aktionen handelt, welche asynchron laufen, darf eine Transition nie direkt eine Kante zu einer anderen Transition haben, da dadurch eine direkte Abhängigkeit entstehen würde. Auch darf im Gegenzug kein Platz eine direkte Kante zu einem anderen Platz haben, da ohne Transition nicht klar wäre, in welchem Platz sich ein Token dann befinden würde.
Berechnungen und Plätze mit Zahlenwerten
Zusätzlich zur einfachen Entnahme und Generierung von Token können Kanten auch Berechnungen mit der Token Anzahl des zugehörigen Platzes durchführen. Die Funktionsweise und Darstellung dieser Rechenmöglichkeiten sind nun nachfolgend, anhand eines einfachen Modells mit zwei Plätzen, einer Transition und den zugehörigen Kanten, genauer beschrieben.
Den Plätzen A und B in Abbildung 40 können durch ihre zugehörigen Kanten und die Transition b Token entnommen und hinzugefügt werden. Dies geschieht normalerweise in Richtung der Pfeile. Eine Kante mit einem Pfeil in Richtung des Platzes legt einen Token in dem Platz ab und eine Kante mit einem vom Platz wegzeigenden Pfeil entnimmt einen Token aus dem Platz.
Wenn ein Platz nur einen Standardtyp von Token enthält, kann er auch als Wert geschrieben werden. In Abbildung 41 noch einmal das vorherige Beispiel in der Schreibweise als Werte.
Es ist nicht relevant, ob ein Platz als Oval, oder als Kreis gezeichnet wird. Bei der Darstellung der Token Anzahl als Zahl ist ein runder Platz ausreichend und platzsparender. In Abbildung 42 ist noch einmal dasselbe Modell mit runden Plätzen dargestellt.
Durch die Angabe einer Formel mit einer Variable, können Berechnungen mit dem
Wert (der Token Anzahl) des Platzes durchgeführt werden. Die Variable (z.B. x) steht dabei für den aktuellen Wert des zugehörigen Platzes. In Abbildung 43 wird durch die Ausführung der Transition b die Token Anzahl von A um zwei Reduziert und die Token Anzahl von C um 5 erhöht. Die Kante zwischen A und c ist dabei die Vorbedingung zur Ausführung der Transition. Sind nicht genügend Token in A um die Berechnung durchzuführen, wird sie auch nicht ausgeführt. Nach der Ausführung des Beispiels hat der Platz A den Wert 0 und der Platz C den Wert 5.
Diese Berechnungen müssen jedoch nicht zwingend der Pfeilrichtung entsprechen. Die Pfeilrichtung bezieht sich bei einer Formel nur auf die Auslösung der Transition (Pfeil zur Transition löst sie aus. Pfeil weg von der Transition geschieht durch die Auslösung). Ein Beispiel einer Token Entnahme entgegen der Pfeilrichtung ist in Abbildung 44 dargestellt. Dabei werden bei Erfüllung der Kante zwischen A und b jeweils fünf Token von C abgezogen. Nach Ausführung des Beispiels hat somit A den Wert 0 und C den Wert 5.
Der Wert (=Token Anzahl) eines Platzes darf nicht negativ sein. Wäre der Wert des Platzes C hier nicht 10, sondern kleiner als 5, dann wäre das ein Fehler. Dieser kann jedoch, wie nachfolgend beschrieben, durch eine zusätzliche Bedingung in der Transition verhindert werden.
Soll der Wert eines Platzes an eine Bedingung übergeben werden, erfolgt dies durch eine eigene Kante die nur den Variablennamen (z.B. x) enthält. Diese Kante führt keine Änderung an dem Wert des Platzes durch, sondern übergibt nur den Wert an die Transition. Das Modell aus Abbildung 44 wurde in Abbildung 45 um eine Bedingung erweitert, welche überprüft, ob der Wert des Platzes C größer oder gleich 5 ist, um einen möglichen Fehler bei der Ausführung der Transition zu verhindern. Der Wert des Platzes C wird dazu durch eine eigene Kante mit der Variable y an die Bedingung der Transition b übergeben.
Abbildung verteilter Systeme
Durch die Anwendung von kalten und warmen Transitionen können Systemgrenzen und Schnittstellen definiert werden. Im Fall eines verteilten Systems können damit nun asynchrone Abhängigkeiten zwischen einzelnen Systemen modelliert werden. Um ein Beispiel für eine solche Schnittstelle zu schaffen wird nachfolgend, in Abbildung 46, ein einfaches Modell eines Geschirrspülers entwickelt, welches dann mit dem Petri-Netz der Kaffee Zubereitung kombiniert wird.
Nun wird das Petri-Netz des Geschirrspülens mit dem der Kaffeezubereitung kombiniert. Die Nahtstellen sind dabei die kalte Transition „Schmutzige Tasse einfüllen“ und „Kaffee trinken“, sowie „Tasse nachfüllen“ und „Saubere Tasse entnehmen“. Da eine Transition nicht direkt in eine andere Transition übergehen kann, sonst wären die Vorgänge synchron und damit nur eine einzige Transition, muss dazwischen jeweils ein eigener Platz definiert werden, an dem sich die Tassen befinden, solange die „abholende“ Transition noch nicht bereit ist. Die Kombination der beiden Systeme ist nun nachfolgend in Abbildung 47 dargestellt.