Maschinelles Lernen und Deep Learning
Maschinelles Lernen und Deep Learning
Ansätze des maschinellen Lernens
Einführung in Maschinelles Lernen
Das maschinelles Lernen (Machine Learning - ML) hat die Grundidee, Wissen aus Beispielen aufzubauen und zu verallgemeinern.
Definition von maschinellem Lernen
Beim maschinellen Lernen geht es um die Entwicklung und Untersuchung statistischer Algorithmen zum Erlernen von Wissen aus Beispielen und deren Verallgemeinerung für die automatische Ausführung von Aufgaben.
Interpretation des Prozesses des maschinellen Lernens
Ein ML-Verfahren baut das Wissen auf durch das Training eines statistischen Modells anhand von Beispielen auf sollche Art auf, was ermöglicht die korrekte Auswertung zumindest der Teilmenge ungesehener Daten. Dies wird als Lerntransfer bezeichnet. Ein anderer Teil der unsichtbaren Daten konnte jedoch normalerweise nicht korrekt ausgewertet werden, weil entweder nicht genügend Trainingsdaten vorhanden waren oder die zugrunde liegenden statistischen Daten nicht richtig parametrisiert waren.
Positionierung und angewandte Methoden des maschinellen Lernens
Der Begriff maschinelles Lernen wurde 1959 von Arthur Samuel vorgeschlagen. In den Anfängen wurden auch Begriffe wie selbstlernende Computer (self-teaching computers) und Rechenmaschinen (computing machinery) verwendet. Maschinelles Lernen ist ein Teilgebiet der KI. In der Frühzeit verfolgte man das Ziel, künstliche Intelligenz zu verwirklichen. ML wurde in den 1990er Jahren zu einem eigenen Fachgebiet, als es sich praktischen Problemen zuwandte und von der Anwendung symbolischer Methoden (wie Logische Programmierung) zu Fuzzy-Logik, Computational Statistics, Wahrscheinlichkeitstheorie, Mustererkennung und Information Retrieval überging. Die auf einem statistischen Ansatz basierende Mustererkennung erzielte in den 1990er Jahren einen großen kommerziellen Erfolg in praktischen Anwendungen wie Spracherkennungssystemen mit großem Vokabular. ML wird im bestimmten Geschäftskontext auch als Predictive Analytics bezeichnet. Verwandte Bereiche sind IE, Data Mining und statistisches Lernen, in denen einige ML-Methoden übernommen wurden.
Aufgaben von ML-Algorithmen
Die ML-Algorithmen realisieren im mathematischen Sinne folgende Aufgaben:
- Regression,
- Klassifizierung,
- Representation Learning (Repräsentationslernen) und
- optimale Kontrolle.
Regression und Klassifizierung können zur Vorhersage der Ausgabe basierend auf den trainierten ML-Modellen verwendet werden.
In ML verwendete Methoden
Im ML kommen zahlreiche Methoden zum Einsatz. Neben der linearen Regression werden für Regressionsaufgaben auch die Polynomregression und die Kernelregression verwendet. Zu den Klassifizierungsmethoden gehören die Anwendung statistischer Modelle, die Lokalisierung der Klassen in einem beobachtbaren Raum, die Suche nach dynamischer Programmierung und Entscheidungsbäume. Zu den leistungsstarken Methoden zur Realisierung von Diskriminanzfunktionen für beliebige Klassifizierungsprobleme gehören Support-Vektor-Maschinen und multilayer NNs mit speziellen Strukturen (special structure multilayer NNs). Weitere Einzelheiten zu diesen Methoden befinden sich in Abschnitt 4.
Learning Ansätze
Die klassischen Lernansätze (auch Paradigmen genannt) von ML werden in der Regel als
- überwachtes (maschinelles) Lernen (supervised learning - SL)
- unüberwachtes Lernen (unsupervised learning)
- Verstärkungslernen (Reinforcement learning - RL)
kategorisiert. Die Kombination der klassischen Lernansätzen ergeben auch andere Lernansätze, wie z. B. Halb-überwachtes Lernen (semi-supervised learning - SSL) oder Multi-Instanz-Lernen (multi-instance learning).
Beim überwachten Lernen lernt die Maschine aus einem Dataset, der aus beschrifteten (labeled) Beispielen besteht. Die typischen Aufgaben des überwachten Lernens im mathematischen Sinne sind Klassifikation und Regression. Die Beispiele stellen die Eingabe normalerweise als Folge von Vektoren dar. Jedes Beispiel ist beschriftet und die Labels stellen die richtige Antwort dar, z. B. die richtige Klasse im Falle einer Klassifizierung, die zu diesem Beispiel gehört. Die Vektoren in den Beispielen repräsentieren entweder die gesamte Eingabe oder es handelt sich um Feature Vektoren, die wesentliche, aus der Eingabe extrahierte Informationen darstellen. Ein Beispiel für Eingabevektoren, die die gesamte Eingabe darstellen, ist die Bildklassifizierung (image classification), bei der jedes Beispiel ein Bild ist, das als Folge (oder Matrix) von Vektoren dargestellt wird, von denen jeder ein Pixel beschreibt. Eine andere Art von Beispiel ist die Spracherkennung, bei der jedes Beispiel besteht aus einer Folge wesentlicher Features, die aus den Audiodaten extrahiert werden. Extrahierte Feature Vektoren stellen nicht nur nur die wesentlichen Informationen dar, die für die betrachtete Aufgabe benötigt werden, sondern sind in der Regel auch eine viel kompaktere Darstellung der Eingabe als die gesamten Eingabedaten.
Beim unüberwachten Lernen lernt die Maschine aus Beispielen ohne Labels. Die Beispiele stellen die Eingabe normalerweise als Folge von Feature Vektoren dar. Im Allgemeinen ist die Aufgabe des unüberwachten Lernens das Representation Learning. Durch Repräsentationslernen werden die Eingabedaten in eine Darstellung umgewandelt, wobei der wesentliche Teil der Informationen über die Eingabedaten erhalten bleibt, während die Darstellung einfacher, weniger dimensional und in vielen Fällen spärlicher bleibt. Konkreter sind die typischen Aufgaben des unüberwachten Lernens die Wahrscheinlichkeitsschätzung (likelihood estimation) und das Erlernen der Struktur der Eingabedaten, wie z.B. im Falle der Clusteranalyse (cluster analysis). Die Aufgabe der Wahrscheinlichkeitsschätzung zielt auf das Lernen der Wahrscheinlichkeitsfunktion der Eingabedaten ab, während im stetigen Fall die Wahrscheinlichkeitsdichtefunktion der Eingabedaten geschätzt wird, wobei diese in beiden Fällen durch weniger Parameter als die Größe der Eingabedaten dargestellt wird. Clustering kann auch als Klassifikation mit automatisch ermittelten Klassen aufgefasst werden.
Reinforcement Learning (RL) unterscheidet sich vom überwachten und unüberwachten Lernen in dem Sinne, dass für das Lernen kein Dataset erforderlich ist. Stattdessen wechselwirkt die Maschine iterativ mit ihrer Umgebung und lernt aus den Rückmeldungen der Umgebung zu ihren Aktionen. Die durch Verstärkungslernen realisierte Aufgabe ist die optimale Steuerung, die auch in biologischen Systemen auftritt und einen Bezug zu Neurowissenschaften und Psychologie hat.
Alle drei Grundparadigmen des ML (überwachtes Lernen, unüberwachtes Lernen und verstärkendes Lernen) können als Optimierungsaufgabe formuliert werden.
Der Dataset wird normalerweise, aber nicht immer, in Form einer Designmatrix dargestellt. In dieser Matrix speichert jede Zeile ein anderes Beispiel. Jede Spalte stellt ein anderes Feature dar. Zum Beispiel der Iris-Dataset [Fisher(1936)], Iris-Datensatz, einer der ältesten in ML untersuchten Dataset, enthält vier Features in jeder Zeile. Diese Features beschreiben unterschiedliche Größen der Pflanzen, wie Kelchblattbreite, Kelchblattlänge usw. Eine solche Matrixdarstellung des Datasets ist nur möglich, wenn die Beispiele als Vektoren die gleiche Größe haben. Im Falle von Beispielvektoren unterschiedlicher Größe kann der Dataset als Satz von Beispielvektoren dargestellt werden.
Die typischen Aufgaben des überwachten und unüberwachten Lernens können mathematisch beschrieben werden, indem typische Annahmen der statistischen Lerntheorie (statistical learning theory assumptions) auf den Prozess von der Datenerstellung angewendet werden. Ihnen zufolge wird angenommen, dass jedes durch einen Zufallsvektor dargestellte Beispiel aus einer zugrunde liegenden Population (background population) generiert wird und diese Zufallsvektoren unabhängig und identisch verteilt sind (independent and identically distributed - i.i.d.).
Die Aufgabe der Wahrscheinlichkeitsschätzung des unüberwachten Lernens kann als Beobachtung von Stichproben eines Zufallsvektors im Dataset und Erlernen der Wahrscheinlichkeitsfunktion (oder Wahrscheinlichkeitsdichtefunktion) beschrieben werden. Andererseits können die Klassifizierungs- oder Regressionsaufgaben des überwachten Lernens als das Beobachten der Stichproben eines Zufallsvektorpaars und und das Erlernen der Vorhersage von aus beschrieben werden, in den meisten Fällen durch Erlernen der bedingten Wahrscheinlichkeitsfunktion (oder Wahrscheinlichkeitsdichtefunktion) . Dabei stellt ein Label dar, das auch aus mehreren Komponenten bestehen kann. Im Falle der Klassifikation sind die Vektoren Werte eines diskreten Raums, während sie im Falle der Regression Vektoren aus dem stetigen Raum sind. Der Begriff „überwachtes Lernen“ geht auf die Ansicht zurück, dass ein Lehrer der Eingabe das richtige Ziel zur Verfügung stellt, um der Maschine zu zeigen, was vorhergesagt werden soll. Das überwachte Lernen und das unüberwachte Lernen sind nicht formal definiert und getrennt. Dies lässt sich erkennen, indem man das Lernen von in das Lernen mehrerer bedingter Verteilungen umwandelt und indem man das Lernen von in das Lernen mehrerer Verteilungen umwandelt . Ersteres kann durch Anwendung des Multiplikationssatzes der Wahrscheinlichkeit als
Es gibt viele Aufgaben, die auf die Klassifizierung oder eine der typischen Aufgaben des überwachten oder unüberwachten Lernens zurückgeführt werden können oder auf dieser basieren. Nachfolgend geben wir eine Liste und eine kurze Diskussion einiger solcher Aufgaben.
- Klassifizierung mit fehlender Eingabe (classification with missing input). Diese Aufgabe wird gelöst, indem mehr Funktionszuordnungen von der Eingabe auf Klassen angewendet werden, anstatt nur eine zu verwenden. Jede Funktionszuordnung realisiert eine Klassifizierung mit unterschiedlichen Teilmengen fehlender Eingaben. Auf diese Weise wird diese Aufgabe auf weitere Klassifizierungsaufgaben zurückgeführt.
- Anomalieerkennung (anomaly detection). Diese Aufgabe lernt neben vielen üblichen Eingabemustern auch einige ungewöhnliche. Es handelt sich also im Wesentlichen auch um eine Klassifikation. Diese Aufgabe hat sehr wichtige Anwendungen wie z.B. Erkennung von Kreditkartenbetrug (credit card fraud detection).
- Transkription (transcription). Diese Aufgabe wandelt unstrukturierte Eingabedaten in Text um. Es umfasst z.B. Spracherkennung oder optische Zeichenerkennung. Text besteht aus einer endlichen Anzahl von Einheiten (Buchstaben, Wörter) und daher handelt es sich bei dieser Aufgabe letztlich auch um eine Klassifikation.
- Maschinelle Übersetzung (machine translation). Diese Aufgabe führt eine Konvertierung von der Eingabesequenz von Einheiten (z. B. Wörtern) in die Ausgabesequenz von Einheiten aus anderer Menge durch, wie etwa die Übersetzung einer natürlichen Sprache in eine andere. Übersetzer verwenden üblicherweise eine abstrakte Ebene, um Verbindungen zwischen den Einheiten der Eingabe und Ausgabe herzustellen. Die Vorhersage von Ausgabeeinheiten aus der Eingabesequenz wird ebenfalls durch Klassifizierung realisiert.
- Probenahme (sampling). Diese Aufgabe generiert neue Beispiele, die den Beispielen des Datasets ähneln, die zum Lernen verwendet werden. Dies kann durch eine Kombination aus Klassifizierung, Repräsentationslernen und Zufallszahlengenerierung realisiert werden.
- Rauschunterdrückung (denoising). Bei dieser Aufgabe muss die Maschine das saubere Beispiel aus dem verrauschten Beispiel vorhersagen. Daher wäre dies ein klassisches überwachtes Lernen. Allerdings sind die sauberen Beispiele nicht verfügbar und daher wird diese Aufgabe indirekt durch unüberwachtes Lernen gelöst.
- Synthese (synthesis). Diese Aufgabe generiert aus der Eingabe eine neue Art von Ausgabe. Ein typisches Beispiel ist die Sprachsynthese, bei der aus der Texteingabe eine synthetisierte Sprache generiert wird. Im Grunde handelt es sich auch um eine Mustererkennung, wie bei der Transkription, aber es werden mehr Varianten der Ausgabe erzeugt als nur eine, um die Auswahl natürlicherer und realistischerer Varianten zu unterstützen. Im Prinzip handelt es sich bei der Synthese um ein überwachtes Lernen. Allerdings können in der Regel keine synthetisierte Sprachmustern angegeben werden und daher wird die Synthese indirekt durch unüberwachtes Lernen realisiert.
- Erstellung einer strukturierten Ausgabe (generating structured output). Bei dieser Aufgabe stehen die Komponenten des Ausgabevektors in Wechselbeziehungen oder/und passen zu einer Struktur. Ein typisches Beispiel ist das Parsen (parsing), d.h. Strukturieren der Einheiten des eingegebenen Satzes in natürlicher Sprache in einem Baum, der die grammatikalische Struktur des Satzes in Form von Substantiven, Verben, Adverbien usw. beschreibt. Dies kann mithilfe von Grammatikregeln realisiert werden, wodurch überwachtes Lernen realisiert wird. Die Synthese generiert auch eine strukturierte Ausgabe.
Es gibt auch andere ML-Lernansätze, die als eine Mischung aus überwachtem und unüberwachtem Lernen angesehen werden können.
Beim halbüberwachten Lernen verfügt nur eine Teilmenge der Beispiele über Labels.
Beim Multi-Instanz-Lernen wird der Dataset in disjunkte Gruppen von Beispielen unterteilt und die Gruppen werden beschriftet, die einzelnen Beispiele jedoch nicht. Beispielsweise können solche Labels bei der binären Klassifizierung die Information zuweisen, ob die Gruppe ein Beispiel einer Klasse enthält oder nicht.
Selbstüberwachtes Lernen (self-supervised learning - SSL) ist ein Ergebnis der Kombination künstlicher neuronaler Netze mit klassischen ML-Ansätzen. Es nutzt die Fähigkeit von KNN, um die Extraktion einer internen Struktur aus einem unstrukturierten Text zu ermöglichen. SSL besteht aus einer unüberwachten Lernphase, gefolgt von einer überwachten. In der ersten Phase werden einige in der Eingabe vorhandene Strukturinformationen, wie eingebettete Metadaten, Domänenwissen oder Korrelationen, durch unüberwachtes Lernen extrahiert. Anschließend werden diese Informationen zur automatischen Beschriftung der Eingabe verwendet. In der zweiten Phase wird überwachtes Lernen an dieser beschrifteten Eingabe durchgeführt.
Typical ML Modelle
Drei charakteristische Beispiele für ML-Modelle sind
- Lineares Regressionsmodell (linear regression model),
- Hidden-Markov-Modell und
- Künstliche neuronale Netzwerkmodelle.
Lineares Regressionsmodell und HMM sind statistische Modelle. Sie lernen die bedingte Wahrscheinlichkeitsverteilung . Im Gegensatz dazu lernen KNN-Modelle Diskriminanzfunktionen, um Klassifizierungsaufgaben durchzuführen.
Linear regression model
Wie schon gezeigt wurde, die ML-Schätzung des Mittelwerts der normalverteilten Zufallsvariablen mit pdf entspricht der MSE-Schätzung der Parameter , unter der Annahme der linearen Beziehung . Dabei ist der Mittelwert und die gegebene feste Varianz der normalverteilten Zufallsvariablen. Auf dieser Grundlage kann die bedingte Wahrscheinlichkeitsdichte des linearen Regressionsmodells, das das eindimensionale aus dem Eingabevektor vorhersagt, als die normalverteilte Zufallsvariable mit pdf angesehen werden. Mit anderen Worten
Das Training des Modells implementiert die ML-Schätzung der Parameter als
Dieses ML-Modell bestimmt über die deterministische Abhängigkeit des Mittelwerts von der Eingabe als .
Hidden-Markov-Modell
Hidden-Markov-Modells werden zur Realisierung eines Klassifikators verwendet. Bei der Klassifizierung werden die Wahrscheinlichkeiten der möglichen Ausgaben berechnet und die wahrscheinlichste Ausgabe wird bestimmt. Auf diese Weise lokalisieren die trainierten Parameter des statistischen Modells die Klassen implizit in einem beobachtbaren Klassenraum.
In HMM gibt es eine Reihe möglicher Ausgabesymbole, das Ausgabealphabet . In jeder diskreten Zeitepoche gibt das HMM ein Ausgabesymbol aus und so erzeugt eine Folge von Ausgaben, , , wobei bezeichnet die diskrete Zeit. Darüber hinaus liegt eine zeitdiskrete Markov-Kette mit dem Zustandsraum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle S} und der Übergangswahrscheinlichkeitsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}} zugrunde. Die Zustandsfolge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \overrightarrow{\bf y}=(y_1,\ldots,y_T)} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_i \in S} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i=1,\ldots,T} kann nicht direkt beobachtet werden. Stattdessen kann die Reihenfolge der Ausgabesymbole beobachtet werden. Wenn ein probabilistischer Zusammenhang zwischen dem ausgegebenen Ausgabesymbol zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_t} und der Zustandsfolge des zugrunde liegenden DTMC Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (y_1,...,y_T)} besteht, dann ist dieser Zusammenhang zusammen mit dem DTMC bestimmt die Folge der Ausgabesymbole Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (x_1,...,x_T)} im stochastischen Sinne. Im einfachsten Fall werden die Ausgabesymbole unabhängig voneinander emittiert und somit kann der Emissionsprozess durch die bedingten Wahrscheinlichkeiten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b_{j,k} = p(x_t = v_j|y_t = s_k)} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v_j \in V} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle s_k \in S} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t=1,...,T} , charakterisiert werden. Somit wird das ausgegebene Ausgabesymbol zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t} im stochastischen Sinne durch den Zustand des zugrunde liegenden DTMC zu diesem Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t} vollständig bestimmt. Diese bedingten Wahrscheinlichkeiten können in einer Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf B} = [b_{j,k}]} organisiert werden. Dann sind die Matrizen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf B}} die Parameter des HMM. Wenn HMM als Klassifikator verwendet wird, dient die gegebene Folge von Beobachtungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \overrightarrow{\bf x}} als Eingabe und die zugrunde liegende Folge von Zuständen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \overrightarrow{\bf y}} entspricht der Klasse. Die bedingte Wahrscheinlichkeitsdichte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(\overrightarrow{\bf y}|\overrightarrow{\bf x})} des HMM-Modells ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p(\overrightarrow{\bf y}|\overrightarrow{\bf x}) = \frac{p(\overrightarrow{\bf y},\overrightarrow{\bf x})}{\sum_{\overrightarrow{\boldsymbol{\upsilon}}}p(\overrightarrow{\boldsymbol{\upsilon}},\overrightarrow{\bf x})}= \frac{\prod_{t=1}^{T} {\bf A}_{y_{t-1},y_{t}} \prod_{t=1}^{T} {\bf B}_{y_{t},x_{t}} }{\sum_{\overrightarrow{\boldsymbol{\upsilon}}}\prod_{t=1}^{T} {\bf A}_{\upsilon_{t-1},\upsilon_{t}} \prod_{t=1}^{T} {\bf B}_{\upsilon_{t},x_{t}} }} gegeben, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}_{y_{0},y_{1}} = p(y_1)} per Definition.
Eine gegebene Ausgabefolge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \overrightarrow{\bf x}}
kann durch viele Folgen von Zuständen des zugrunde liegenden DTMC erstellt werden, jede davon mit bestimmten Wahrscheinlichkeiten. Daher wird bei der Klassifizierung diejenige Folge von Zuständen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \overrightarrow{\bf y}^*}
, ausgewählt, die mit der höchsten Wahrscheinlichkeit die gegebene Ausgabefolge, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \overrightarrow{\bf x}}
, erzeugt. Diese Folge von Zuständen wird die entsprechende Klasse sein und wird auch als bester Pfad (best path) bezeichnet. Mit anderen Worten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \overrightarrow{\bf y}^* = \arg\max_{\overrightarrow{\bf y}} p(\overrightarrow{\bf y}|\overrightarrow{\bf x}) .}
In der Praxis wird der beste Pfad üblicherweise mittels Viterbi-Algorithmus
(Viterbi-Algorithmus) berechnet, der eine recheneffiziente Lösung der oben genannten Optimierungsaufgabe implementiert.
Das Training des HMM-Modells bedeutet das Erlernen der Parametermatrizen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf B}} . Dies erfolgt durch die ML-Schätzung dieser Parameter als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ({\bf A},{\bf B}) = \arg\max_{{\bf A},{\bf B}} p(\overrightarrow{\bf y}|\overrightarrow{\bf x}, {\bf A},{\bf B}).}
Eine rechnerisch effiziente Realisierung der oben genannten Optimierungsaufgabe kann durch Verwendung des EM-Algorithmus (EM-Algorithmus) entwickelt werden. Daraus ergibt sich der Baum-Welch-Algorithmus (Baum-Welch-Algorithmus), der in der Praxis der Standardalgorithmus zum Trainieren eines HMM-Modells ist. Ein solches HMM-Modell kann z. B. zur Wettervorhersage oder zur Umsetzung des akustischen Teils einer Spracherkennungsaufgabe verwendet werden.
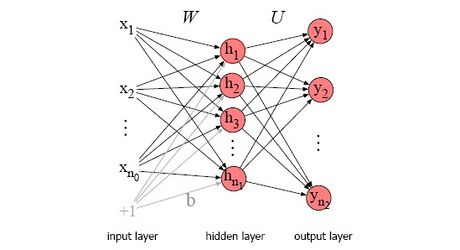
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Künstliche neuronale Netze
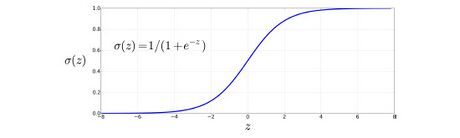
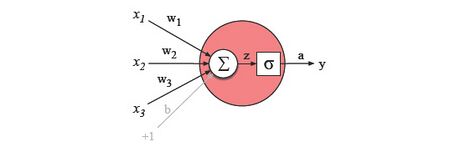
Ein künstliches neuronales Netzwerk kann diskriminierende Funktionen realisieren, die nicht unbedingt einer probabilistischen Interpretation haben. Hierzu zählen vor allem nichtlineare Funktionen. Die realisierten Funktionen können als Näherungen angesehen werden, die durch die Gewichtsparameter des KNN bestimmt werden. Auf diese Weise können KNNs als eine Verallgemeinerung der herkömmlichen ML-Modelle betrachtet werden, was ihre Verwendung für Klassifizierungsaufgaben motiviert. KNN ist ein Netzwerk künstlicher Neuronen, das auf den Prinzipien biologischer neuronaler Netzwerke basiert. KNNs, die aus mindestens drei Schichten bestehen, können auch für nichtlinear trennbare Klassifizierungsaufgaben (non-linear separable classification tasks) verwendet werden.
Grundkonzepte von ML
In diesem Unterabschnitt diskutieren wir die Grundkonzepte von ML und mehrere verwandte Teile der statistischen Lerntheorie (statistical learning theory). Diese gelten für das Lernen aus Datensets, also werden die Konzepte des überwachten und unüberwachten Lernens aufgeführt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Generalisierungsfähigkeit
Das übergeordnete Ziel des maschinellen Lernens aus Datensets ist, dass der ML-Algorithmus seine Aufgabe auch bei unbekannten Eingabebeispielen gut durchführen muss. Konkreter bedeutet dies, dass die Verteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p({\bf x})} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p({\bf y}|{\bf x})} gut genug gelernt werden muss, um auch für unbekannte Beispiele, d. h. Sequenzen von Vektoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}} , gültig zu sein. Da die Herausforderung jedes ML-Algorithmus besteht in Herstellung einer Generalisierungsfähigkeit.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Trainings- und Generalisierungsfehler
Um eine Generalisierungsfähigkeit zu etablieren, muss der ML-Algorithmus die betrachtete Aufgabe zumindest für den zum Lernen verwendeten Dataset gut genug durchführen. Um diese Fähigkeiten zu kontrollieren, muss man sie zunächst durch die Berechnung einiger Maße quantifizieren können. Der zum Lernen verwendete Dataset wird als Trainingsdaten (training data) bezeichnet. Der Dataset, der zur Messung der Leistung des ML-Algorithmus an anderen, bisher unbekannte Beispiele enthaltenden Daten verwendet wird, wird als Testdaten (test set) bezeichnet. Die Leistung des ML-Algorithmus bei den Trainingsdaten kann anhand des Trainingsfehlers (training error) gemessen werden, bei dem es sich um den erwarteten Wert des Fehlers im Trainingsdaten handelt. Ebenso ist der Testfehler (test error) der erwartete Wert des Fehlers in Testdaten. Es ist in der Lage, die Leistung des ML-Algorithmus an unbekannten Beispielen und damit auch die Generalisierungsfähigkeit des ML-Algorithmus zu messen. Aus diesem Grund wird der Generalisierungsfehler (generalization error) als Testfehler definiert. In der Praxis wird der Erwartungswert des Fehlers durch den statistischen Mittelwert der Fehler der einzelnen Beispiele angenähert. Beispielsweise wurden im linearen Regressionsmodell mit eindimensionaler Ausgabe die Gewichtsparameter des Regressionsmodells durch Minimierung von MSE trainiert, was dem Trainingsfehler entspricht:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{MSE} = \frac{1}{K} \lVert {\bf X}^{(train)}{\bf w} - {\bf y}^{(train)} \rVert_2^2,}
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} die Anzahl von Eingabevektoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}} (= Anzahl von Zeilen der Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf X}^{(train)}} ist. Es wird erwartet, dass der Testfehler größer oder gleich dem Trainingsfehler ist. Somit kann der Generalisierungsfehler als Summe von [Trainingsfehler] und [die Lücke zwischen Trainings- und Generalisierungsfehler] zerlegt werden. Daher kann ein ML-Algorithmus mit hoher Generalisierungsfähigkeit durch
- Verminderung des Trainingsfehlers und
- Verminderung der Lücke zwischen Trainings- und Generalisierungsfehler
erreicht werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Overfitting, Underfitting und Kapazität
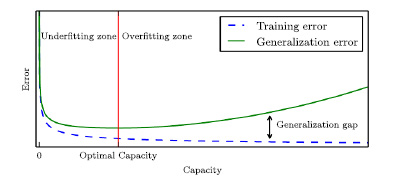
Zwei potenzielle Trainingsprobleme im Zusammenhang mit den oben genannten Trainingsfehler und Lücke zwischen Training und Generalisierungsfehler, sind Overfitting und Underfitting. Overfitting tritt auf, wenn das Modell der Maschine nicht nur an die zugrunde liegenden Verteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p({\bf x})} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p({\bf y}|{\bf x})} der Beispiele angepasst wird, sondern auch an der Entwicklung der zufälligen Rauschen zwischen den Beispielen, die sich von der zugrunde liegenden Verteilung unterscheiden. Dies führt zu einem geringen Trainingsfehler, aber zu einem hohen Testfehler, da die Testdaten wahrscheinlich auch andere zufällige Rauschinhalte enthälen, die zwischen den Trainingsbeispielen liegen. Daher ist im Falle einer Overfitting die Lücke zwischen Trainings- und Generalisierungsfehler groß. Eine Underfitting tritt auf, wenn das Modell der Maschine nicht an alle angezeigten Trainingsbeispiele angepasst werden kann. Dies führt dazu, dass der Trainingsfehler nicht ausreichend niedrig sein kann. Overfitting, Underfitting hängen mit der Kapazität (representation capacity oder capacity) des Modells zusammen und können daher durch diese gesteuert werden. Grob gesagt, die Kapazität bestimmt durch die Darstellungsfähigkeit des Modells die Modellierungsfähigkeit des ML-Modells an, z.B. in Bezug auf den Funktionsumfang seiner Eingabe.
Den Zusammenhang zwischen Kapazität und Overfitting, Underfitting wird anhand eines anschaulichen Beispiels näher erläutert. Nehmen wir an, dass sich für eindimensionale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf y}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}} das zugrunde liegende Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(y|x)} um eine parabolische Funktion seines Eingangwertes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} konzentriert. In diesem Fall wird das Maschinenmodell eine lineare Regression als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y = wx + b.} Diese lineare Funktion von x mit den beiden Parametern w und b kann nicht alle Beispiele abdecken, da Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} parabolisch sind. Dies führt zu einer Underfitting. Nimmt man eine Funktion höherer Ordnung als Maschinenmodell, z.B. die Polynomfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} mit Grad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 7} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y = \sum_{i=1}^7 w_i x^i + b,} ergibt ein Modell mit acht Parametern (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle w_1,\ldots,w_7} und b) und einer erweiterten Menge der Funktionen zur Beschreibung des Maschinenmodells. Die Menge von Funktionen, die die Modellierungsfähigkeit der Maschine spezifizieren, wird auch als Hypothesenraum (hypothesis space) bezeichnet. Dieses Modell ist trotz der Tatsache, dass es sich um ein Polynom vom Grad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 7} in x handelt, immer noch eine lineare Funktion der Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle w_1,\ldots,w_7} und b und daher der theoretische Rahmen von MSE immer noch gelten. Dadurch kann das Modell weiterhin mithilfe der Normalgleichungen in geschlossener Form trainiert werden. Die Anwendung dieses Modells als Maschinenmodell kann alle gegebenen (weniger als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 7} ) Beispiele aus der parabolischen Population abdecken, aber zwischen den Beispiel-x-Punkten folgt es einer Kurve, die nicht parabolisch, sondern polynomisch vom Grad 7 ist. Dies führt zu einer Overfitting, d.h. geringer Trainingsfehler, aber hoher Testfehler. Das optimale Modell eines ML-Algorithmus ist grob gesagt dasjenige, dessen Kapazität mit der Kapazität der zugrunde liegenden Verteilung der Trainingsdaten übereinstimmt. Allgemeiner gesagt, das Modell mit der Kapazität, die für die tatsächliche Komplexität der Aufgabe und der verfügbaren Menge an Trainingsdaten geeignet ist. Zur Lösung komplexer Aufgaben sind Modelle mit hoher Kapazität erforderlich. Wenn die tatsächlich benötigte Kapazität jedoch geringer ist als die des Maschinenmodells, kann es zu einer Overfitting kommen. In unserem anschaulichen Beispiel ist das optimale Maschinenmodell die quadratische Funktion der Eingabe. Mit anderen Worten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y = w_2 x^2 + w_1 x + b.}
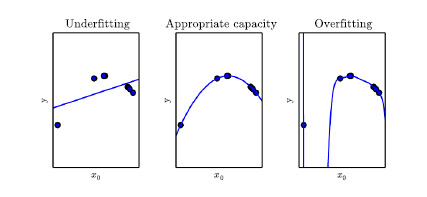
Abbildung 13 zeigt alle drei Fälle für 5 Trainingsbeispiele aus der zugrunde liegenden parabolischen Verteilung der Trainingsdaten, aber mit Polynomfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x}
mit Grad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 9}
. Es ist ersichtlich, dass das lineare Modell zu einer Underfitting führt, da die lineare Funktion nicht zur parabolischen Funktion passen kann. Das Modell vom Grad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 7}
kann alle Beispiele abdecken, aber es kann unendlich viele Funktionen (nicht nur die parabolische) darstellen, die durch die Trainingspunkte laufen, da es mehr Parameter hat als die Anzahl der verfügbaren Trainingsbeispiele. Daher kann es zu einer Overfitting kommen.
Das Finden der besten Funktion aus der Menge der durch die Kapazität spezifizierten Funktionen ergibt ein Optimierungsproblem, das in den meisten Fällen nur numerisch gelöst werden kann. In der Praxis bedeutet dies, dass das ML-Training nicht die theoretisch beste, global optimale Funktion liefert, sondern eine Funktion, die den Trainingsfehler erheblich reduziert. Diese zusätzliche Einschränkung des numerischen Optimierungsalgorithmus führt dazu, dass die erfahrene, sogenannte effektive Kapazität des Modells in der Regel geringer ist als die Darstellungsfähigkeit des Modells.
Die Ideen zur Ermittlung der besten Generalisierungsfähigkeit der ML-Modelle können als Anwendung allgemeinerer Gedanken von Philosophen auf die statistische Lerntheorie angesehen werden. Das Prinzip der Sparsamkeit (principle of parsimony), heute weithin als Occam’s razor bekannt, besagt, dass unter den potenziellen Hypothesenräumen, die die Beobachtungen abdecken können, der einfachste ausgewählt werden sollte. Dieses Prinzip aus dem 13.-14. Jahrhundert wurde im 20. Jahrhundert von mehreren Wissenschaftlern, die die Begründer der statistischen Lerntheorie waren, wie Vapnik, Chervonenkis oder Blumer, präzisiert ([Vapnik and Chervonenkis(1971)], [Blumer et al.(1989)] und [Vapnik(1995)]).
Es gibt einen Kompromiss zwischen Trainingsfehlern und der Lücke zwischen Trainings- und Generalisierungsfehlern als Funktion der Kapazität. Typischerweise nimmt der Trainingsfehler mit zunehmender Kapazität ab und konvergiert zu einem asymptotischen minimalen Trainingsfehler. Andererseits ist der Generalisierungsfehler immer größer oder gleich dem Trainingsfehler und die Lücke zwischen ihnen nimmt im Bereich der Overfitting mit zunehmender Kapazität zu. Daraus ergibt sich ein U-förmiger Verlauf des Generalisierungsfehlers als Funktion der Kapazität. Die optimale Kapazität sollte hoch genug sein, um ausreichend komplexen Hypothesenraum zu ermöglichen, der zu geringen Trainingsfehlern führt (d. h. um eine Underfitting so weit wie möglich zu vermeiden) und niedrig genug sein, um eine Overfitting so weit wie möglich zu vermeiden, was zu einer geringen Lücke zwischen Training und Generalisierung führt Fehler. Die Situation ist in Abbildung 14 dargestellt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }}
Abhängigkeit von der Trainingsdatengröße
Wenn die Maschine die wahre zugrunde liegende Verteilung der Trainingsdaten kennen würde, würde man keinen Trainingsfehler erwarten. Allerdings gab es auch in diesem Fall einen kleinen Fehler aufgrund von Rauschen in der Verteilung, z. B. wegen der Abhängigkeit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf y}} auch von anderen Variablen außer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}} . Dieser verbleibende Fehler, der das theoretische Minimum des Testfehlers darstellt, wird Bayes-Fehler genannt.
Wenn die Modellkapazität optimal ist, bedeutet eine Erhöhung der Trainingsdatengröße, dass der Testfehler asymptotisch den Bayes-Fehler erreicht, der Trainingsfehler kann jedoch unter den Bayes-Fehler fallen. Dies liegt daran, dass der Trainingsfehler an den trainierten Beispielen gemessen wird und daher das Rauschen, das den Bayes-Fehler verursacht, nicht unbedingt auftritt. Wenn die Kapazität des Modells im Bereich von Underfitting liegt, führt eine Erhöhung der Trainingsdatengröße zu einem Anstieg des Trainingsfehlers und gleichzeitig zu einer Verringerung des Testfehlers. Der Grund für die erste liegt darin, dass ein größerer Dataset im Bereich von Underfitting schwieriger anzupassen ist. In diesem Fall muss der Trainingsfehler mindestens bis zum Bayes-Fehler ansteigen. Der Grund für die zweite ist darauf zurückzuführen, dass weniger Hypothesen stimmen mit den Trainingsdaten überein. Aufgrund der Underfitting geht der Testfehler asymptotisch mit zunehmender Trainingsdatengröße zu einem Fehler, der höher als der Bayes-Fehler ist.
Die wichtigsten Trends zum Generalisierungsfehler sowie dessen Zusammenhang mit Trainingsfehlern und Kapazität lassen sich wie folgt zusammenfassen:
- Der erwartete Generalisierungsfehler ist größer oder gleich dem erwarteten Trainingsfehler.
- Die optimale Kapazität liegt am minimalen Punkt des Generalisierungsfehlers als Funktion der Kapazität.
- Der erwartete Generalisierungsfehler nimmt mit zunehmender Trainingsdatengröße monoton ab.
- Mit zunehmender Trainingsdatengröße geht der Generalisierungsfehler asymptotisch zu
- Bayes-Fehler, wenn die Modellkapazität optimal ist und
- einen Fehlerwert, der den Bayes-Fehler überschreitet, wenn die Kapazität im Bereich von Underfitting liegt.
Daraus folgt, dass es bei einem Modell mit optimaler Kapazität immer noch möglich ist, dass die Lücke zwischen der Trainings- und der Generalisierungslücke groß ist. In diesem Fall kann die große Lücke und damit auch der Generalisierungsfehler durch Erhöhen der Trainingsdatengröße verringert werden.
Andererseits kommt es bei der Verwendung großer Trainingsdaten nicht zu einer Overfitting. Dies kann durch das Modell von Abbildung 13 veranschaulicht werden. Wenn die Anzahl der Trainingsbeispiele Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 9} erreicht, ermitteln sie genau eine Kurve, die zu allen Trainingsbeispielen passt. Daher handelt es sich um die echte quadratische Funktion, was bedeutet, dass einige der Gewichte zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} werden. Somit kommt es zu keiner Overfitting. Wenn also extrem große Trainingsdaten verwendet werden, besteht das Hauptproblem in der Underfitting.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} ML-Training relevanter Eigenschaften der statistischen Punktschätzung
In vielen Maschinenmodellen wird die statistische Punktschätzung verwendet, um die optimalen Werte der ML-Parameter zu berechnen. Dies ist z.B. der Fall. im linearen Regressionsmodell oder im HMM. Es seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{\boldsymbol{\theta}}_{(n)}} die wahren Werte und die geschätzten Werte über Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} Beispiele (d. h. die Eingabevektoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}_{i}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i= 1,\ldots,n} ) von der ML-Parameter. Die Schätzung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{\boldsymbol{\theta}}_{(n)}} ist eine Statistik von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} Stichproben, die aus der zugrunde liegenden datengenerierenden Verteilung (Population) entnommen wurden, und daher auch als Wahrscheinlichkeitsverteilung angesehen werden kann, die durch die Verteilung der zugrunde liegenden datengenerierenden Verteilung bestimmt wird. Zu den relevanten Eigenschaften der Punktschätzung gehören:
- Bias (Verzerrung),
- Varianz und
- Konsistenz.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Bias, Varianz and MSE
Der Bias des Schätzers Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{\boldsymbol{\theta}}} ist mit anderen Worten die Differenz zwischen seiner Erwartungswert über einen Dataset und seinem wahren Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Bias(\hat{\boldsymbol{\theta}}_{(n)}) = E[\hat{\boldsymbol{\theta}}]- {\boldsymbol{\theta}},}
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle E[]}
für den Erwartungswert steht. Ein Schätzer ist erwartungstreu (unbiased), wenn sein Bias gleich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0}
ist, und asymptotisch erwartungstreu, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lim_{n \rightarrow \infty }Bias(\hat{\boldsymbol{\theta}}_{(n)}) = 0}
. Zum Beispiel der Stichprobenmittelwert (sample mean) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{1}{n}\sum_{i=1}^n {\bf x}_{i}}
der Beispiele Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}_{i}}
, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i= 1,\ldots,n}
ist ein unverzerrter (unbiased) Schätzer des Mittelwerts. Allerdings ist die Stichprobenvarianz (sample variance)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{1}{n}\sum_{i=1}^n \left({\bf x}_{i} - \hat{\boldsymbol{\mu}}_{(n)}\right)^2}
, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{\boldsymbol{\mu}}_{(n)}}
der Stichprobenmittelwert ist, weist einen Bias ungleich Null auf. Es bedarf einer leichten Modifikation, um die unverzerrte Stichprobenvarianz (unbiased sample variance) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{1}{n-1}\sum_{i=1}^n \left({\bf x}_{i} - \hat{\boldsymbol{\mu}}_{(n)}\right)^2}
mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0}
Bias zu bilden.
Die Varianz des Schätzers Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{\boldsymbol{\theta}}} ist einfach seine Varianz als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Var(\hat{\boldsymbol{\theta}}_{(n)}).} Die Varianz des Schätzers drückt die Unsicherheit der Schätzung aus. Der Standardfehler (standard error, standard deviation) des Schätzers ist die Quadratwurzel seiner Varianz und wird mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle SE(\hat{\boldsymbol{\theta}}_{(n)})} bezeichnet. Der Standardfehler des Stichprobenmittelwerts kann angegeben werden als:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle SE(\frac{1}{n}\sum_{i=1}^n {\bf x}_{i}) = \sqrt{Var(\frac{1}{n}\sum_{i=1}^n {\bf x}_{i})} = \sqrt{\frac{1}{n^2}\sum_{i=1}^n Var({\bf x}_{i})} = \sqrt{(\frac{\sigma^2}{n})} = \frac{\sigma}{\sqrt{(n)}},} wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \sigma^2} die wahre Varianz der zugrunde liegenden Verteilung ist. Das bedeutet, dass die Varianz des Stichprobenmittelwerts proportional mit der Anzahl der Stichproben abnimmt. Entsprechend nimmt der Standardfehler des Stichprobenmittelwerts mit der Quadratwurzel der Anzahl der Stichproben ab, d. h. weniger als linear. In der Praxis hat der Standardfehler meist eine höhere Relevanz als die Varianz.
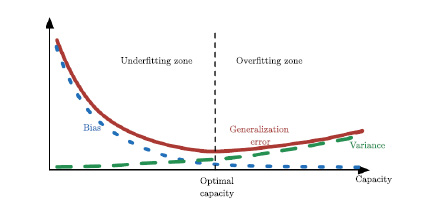
Der MSE einer Schätzung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{\boldsymbol{\theta}}_{(n)}} ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle MSE(\hat{\boldsymbol{\theta}}_{(n)}) = E[(\hat{\boldsymbol{\theta}}_{(n)} - {\boldsymbol{\theta}})^2]} gegeben. Es besteht ein sinnvoller Zusammenhang zwischen der Bias, der Varianz und dem MSE einer Schätzung als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle MSE(\hat{\boldsymbol{\theta}}_{(n)}) = Bias^2(\hat{\boldsymbol{\theta}}_{(n)}) + Var(\hat{\boldsymbol{\theta}}_{(n)}).}
Dies lässt sich einfach aus den Definitionen, wie folgt, ableiten, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} MSE(\hat{\boldsymbol{\theta}}_{(n)}) &= E[(\hat{\boldsymbol{\theta}}_{(n)} - {\boldsymbol{\theta}})^2] = E[(\hat{\boldsymbol{\theta}}_{(n)})^2]-2 E[\hat{\boldsymbol{\theta}}_{(n)}] {\boldsymbol{\theta}} + {\boldsymbol{\theta}}^2 \\ &= \left(E[(\hat{\boldsymbol{\theta}}_{(n)})^2] - E^2[\hat{\boldsymbol{\theta}}_{(n)}]\right) + \left(E^2[(\hat{\boldsymbol{\theta}}_{(n)}] -2 E[\hat{\boldsymbol{\theta}}_{(n)}] {\boldsymbol{\theta}} + {\boldsymbol{\theta}}^2\right) \\ &= Var(\hat{\boldsymbol{\theta}}_{(n)}) + \left(E[\hat{\boldsymbol{\theta}}_{(n)}] - {\boldsymbol{\theta}}\right)^2 = Var(\hat{\boldsymbol{\theta}}_{(n)}) + Bias^2(\hat{\boldsymbol{\theta}}_{(n)}). \end{aligned}} Wenn der Generalisierungsfehler nicht als Fehler in der Ausgabe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf y}} , sondern als MSE der ML-Parameter gemessen wird, weist die Abhängigkeit des Generalisierungsfehlers von der Kapazität immer noch die gleiche U-förmige Kurve auf, da der Fehler von ML-Training spiegelt sich auf allen Fehlerebenen (Fehler in der Ausgabe, Fehler in ML-Parametern, MSE von ML-Parametern usw.) auf ähnliche Weise wider. Dann sind Bias und Varianz die Komponenten des Generalisierungsfehlers. Die Erhöhung der Kapazität führt auch zu einer Erhöhung der Varianz (neben der gleichen Anzahl von Trainingsbeispielen nimmt auch die Anzahl der passenden Polynome vom Grad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} zu). Daher muss der Bias mit zunehmender Kapazität abnehmen. Aus diesem Grund geht die gleichzeitige Reduktion des Bias und der Varianz nicht. Dies kann als Bias-Varianz-Kompromiss (bias-variance tradeoff) beschrieben werden. Die Beziehungen zwischen Bias, Varianz, MSE und Kapazität sind in Abbildung 15 dargestellt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }}
Konsistenz
Ein Schätzer ist konsistent, wenn der geschätzte Wert, mit der ansteigenden Anzahl der Stichproben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} , gegen der wahre Parameterwert geht. Mit anderen Worten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim_{n \rightarrow \infty } \hat{\boldsymbol{\theta}}_{(n)} = {\boldsymbol{\theta}}.}
Wenn die Konvergenz in Wahrscheinlichkeit zu interpretiern ist, dann wird diese Konsistenz als schwache Konsistenz bezeichnet.
Die ML-Schätzung hat die schöne Eigenschaft, dass sie unter bestimmten Bedingungen konsistent ist. Aus diesem Grund wird die ML-Schätzung häufig im ML-Training verwendet, wie z.B. im Fall des linearen Regressionsmodells oder des HMM.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Über Spezifitätsebene von ML-Algorithmen
Aus Sicht der statistischen Lerntheorie kann ein ML-Algorithmus das Wissen aus einer endlichen Anzahl gesehener Trainingsbeispiele verallgemeinern. Es stellt sich die Frage, ob ein ML-Algorithmus etabliert werden kann, der für alle möglichen ML-Aufgaben das entsprechenden Wissen generalisieren kann.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} No-free-Lunch-Theorem
Die Antwort auf diese Frage liefert das No-Free-Lunch-Theorem
([Wolpert9(1996)]). Es sagt aus, dass jeder Klassifizierungsalgorithmus, gemittelt über alle möglichen zugrunde liegenden datengenerierenden Verteilungen, den gleichen Testfehler aufweist. Daher gibt es erwartungsgemäß keinen universellen besten Klassifikator.
Für eine reale Aufgabe können wir die mögliche datengenerierenden Verteilungen einschränken, indem wir einige Annahmen treffen. Solche Informationen können z.B. sein: einige Kenntnisse über die Form der zugrunde liegenden Verteilung (z. B. ihre Verteilungsfamilie oder die wahre Kapazität, die die Menge von Funktionen beschreibt, die zur vollständigen Erfassung der zugrunde liegenden Verteilung erforderlich sind).
Zusammenfassend lässt sich sagen, dass der richtige Ansatz zum Entwerfen eines ML-Algorithmus nicht darin besteht, nach einem universell besten Algorithmus zu suchen, sondern darin, einen spezifischen ML-Algorithmus zu planen, indem einige Präferenzen erstellt werden, um seinen Anwendungsbereich auf die aufgabenrelevanten zugrunde liegenden Verteilungen einzugrenzen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Hyperparameter
Das übliche direkte Ziel des Lernens besteht darin, mehrere Parameter des ML-Modells zu bestimmen, indem der Trainingsfehler basierend auf dem Maschinenmodell minimiert wird. Beispielsweise werden im Fall der linearen Regression die Parameter im Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf w}} durch Minimierung des quadratischen Fehlers der Trainingsdaten bestimmt. Allerdings führt das Modell mit den so ermittelten Parametern, wie wir gesehen haben, nicht unbedingt zum besten Generalisierungsfehler, da dieser auch von der Darstellungsfähigkeit des Modells abhängt. Daher muss auch die optimale Kapazität ermittelt werden, in der Regel durch iteratives Wiederholen des Trainings mit unterschiedlichen Kapazitätseinstellungen. Folglich wird die Kapazität als Parameter nicht durch den ML-Algorithmus selbst bestimmt.
Solche Parameter, die zur Steuerung des ML-Algorithmus dienen, aber nicht vom ML-Algorithmus selbst bestimmt werden, werden Hyperparameter genannt. Die Kapazität ist ein Beispiel für Hyperparameter, aber ML-Algorithmen können viele andere Hyperparameter haben. Eine Parameter des Modells ist ein Hyperparameter, wenn ihre Bestimmung durch das Lernen auf dem Trainingsdaten nicht der geeignete Weg ist, weil
- entweder die daraus resultierende Optimierung wäre schwierig,
- oder, häufiger, diese Parameter vom ML-Algorithmus anhand der Trainingsdaten nicht gelernt werden kann.
Ein Beispiel für den zweiten Fall ist die Kapazität. Wenn der ML-Algorithmus versuchen würde, die Kapazität anhand der Trainingsdaten zu erlernen, wurde immer die maximal verfügbare Kapazität gewählt, da der Trainingsfehler mit zunehmender Kapazität abnimmt. Es würde also zu einer Overfitting kommen.
Um dieses Problem zu beheben, wird ein anderer Dataset verwendet, der während des Trainings nicht beobachtet wurde und sich auch nicht mit dem Testdaten überschneidet. Dieser Dataset wird als Validierungsdaten bezeichnet. Normalerweise wird der Validierungsdaten vom Trainingsdaten getrennt. Der verbleibende Teil des Trainingsdaten wird zum Erlernen der Parameter verwendet und der Validierungsdaten wird verwendet, um den Generalisierungsfehler nach dem Training darauf zu messen (und daher ist diese auch als Validierungsfehler genannt) und auf iterative Weise die optimale Hyperparameter zu bestimen.
Die Validierung ist auch Teil des „Trainings“ des gesamten Modells einschließlich der Hyperparameter und der Validierungsfehler daher typischerweise den am Testdaten gemessenen Generalisierungsfehler unterschätzt.
Optimierungsframework für das Training von ML-Modellen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Von der mathematischen Optimierung bis zu ML-Problemen
Das Ziel von ML kann als Minimierung des Fehlers zwischen den vorhergesagten Werten, die vom trainierten ML-Modell erzeugt werden, und den wahren Werten der Testdaten beschrieben werden. Dies kann zu einem allgemeinen Optimierungsrahmen (optimization frameworks) formalisiert werden. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{y}({\bf x},{\boldsymbol{\theta}})} die vorhergesagte univariate Ausgabe als Funktion des Eingabevektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}} und des Parametervektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}} . Der allgemeine Optimierungsrahmen für den Fall einer univariaten Ausgabe kann, anstelle eines Fehlermaßes, durch die allgemeinere beispielbasierte (per-example) Loss Funktion (Verlustfunktion) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)} wie folgt ausgedrückt werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R^*({\boldsymbol{\theta}}) = E_{({\bf x},y)\sim p } [L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)],}
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle E_{({\bf x},y)\sim p }} für den Erwartungswert über die wahre zugrunde liegende datengenerierende Verteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} steht. Die Größe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle R^*({\boldsymbol{\theta}})} wird als Risk genannt. Somit kann die Optimierungsaufgabe, die das Ziel von ML formalisiert, wie folgt angegeben werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\boldsymbol{\theta}} = \arg\min_{{\boldsymbol{\theta}}} R^*({\boldsymbol{\theta}}) = \arg\min_{{\boldsymbol{\theta}}} E_{({\bf x},y)\sim p } [L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)].}
Bei ML-Problemen ist jedoch die wahre zugrunde liegende datengenerierende Verteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} nicht bekannt. Stattdessen können wir den erwarteten Loss für die Trainingsdaten berechnen, was zum empirischen Risk Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle R({\boldsymbol{\theta}})} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R({\boldsymbol{\theta}}) = E_{({\bf x},y) \sim \hat{p} } [L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)] \approx \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}({\bf x}_{i},{\boldsymbol{\theta}}),y_{i})} führt, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{p}} die Trainingsdatengenerierende Verteilung, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} die Anzahl der Trainingsbeispiele sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}_{i}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{i}} die Eingabe und Ausgabe im Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} -ten Beispiel, jeweils Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i=1,\ldots,m} sind. Daher kann das ML-Training auch als eine Optimierungsaufgabe (optimization task) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\boldsymbol{\theta}} &= \arg\min_{{\boldsymbol{\theta}}} R({\boldsymbol{\theta}}) = \arg\min_{{\boldsymbol{\theta}}} E_{({\bf x},y) \sim \hat{p} } [L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)] \\ &\approx \arg\min_{{\boldsymbol{\theta}}} \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}({\bf x}_{i},{\boldsymbol{\theta}}),y_{i}) = \arg\min_{{\boldsymbol{\theta}}} \sum_{i=1}^{m} L(\hat{y}({\bf x}_{i},{\boldsymbol{\theta}}),y_{i}) \end{aligned}} formuliert werden.
Wenn die ML-Schätzung im Training des Machine Modells verwendet wird, ist die Formalisierung ihrer Optimierungsaufgabe durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\boldsymbol{\theta}} &= \arg\max_{{\boldsymbol{\theta}}} \sum_{i=1}^{m} \log~ p(y_{i}|\hat{y}({\bf x}_{i},{\boldsymbol{\theta}})) \\ &= \arg\min_{{\boldsymbol{\theta}}} \frac{1}{m}\sum_{i=1}^{m} \left(-\log~ p(y_{i}|\hat{y}({\bf x}_{i},{\boldsymbol{\theta}}))\right) \\ &\approx \arg\min_{{\boldsymbol{\theta}}} E_{({\bf x},y)~ \hat{p} } \left(-\log~ p(y,\hat{y}({\bf x},{\boldsymbol{\theta}})))\right) \end{aligned}} gegeben. Daher entspricht die Loss Funktion der negativen logarithmischen Wahrscheinlichkeit in der ML-Schätzung. Einige weitere typische Optionen für die Wahl der Loss Funktion umfassen
- quadratischer Fehler der Ausgabe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle = E[(\hat{y}({\bf x},{\boldsymbol{\theta}})-y)^2]} z.B. in der MSE-Minimierung für die lineare Regression,
- Fehler als Differenz zwischen vorhergesagter und wahrer Ausgabe, d. h Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(\hat{y}({\bf x},{\boldsymbol{\theta}})-y\right)} , wie z.B. in den meisten Klassifikationsaufgaben.
Beim HMM-Training wird die empirische Risk-Minimierung implizit durch die Iterationsschritte des EM-Algorithmus realisiert, die im Baum-Welch-Algorithmus integriert sind.
Wenn das Problem des maschinellen Lernens eine rein mathematische Optimierungsaufgabe wäre, könnte es durch die Anwendung eines mathematischen Optimierungsalgorithmus gelöst werden. Das Problem des maschinellen Lernens unterscheidet sich jedoch in folgenden Aspekten von der rein mathematischen Optimierung:
- Die wahre zugrunde liegende datengenerierende Verteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p}
ist nicht bekannt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow} Anstelle des Risk wird das empirische Risk verwendet.
- Im ML-Problem können Loss Funktion auftreten, die durch numerische Optimierungsverfahren nicht effizient optimiert werden können.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow} In solchen Fällen wird anstelle der ursprünglichen Loss Funktion eine Ersatz-Loss Funktion (surrogate loss function) verwendet
- ML-Training stoppt nach dem Kriterium des „Early Stopping“, anstatt wirklich ein Minimum zu erreichen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow}
Frühzeitiges Stoppen basiert normalerweise auf der Erkennung des Beginns einer Overfitting.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow}
Die Loss Funktion (oder Ersatz-Loss Funktion) kann beim Stoppen immer noch große Ableitungen haben.
- Die Zielfunktion der Optimierung (= die zu optimierende Funktion) bei ML-Problemen ist normalerweise eine Erwartung des Loss über die Trainingsdaten.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow} Die (Approximation der) Zielfunktion hat normalerweise eine Form, die die Summe über Trainingsbeispiele enthält.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Organisieren des Trainingsprozesses
Die Optimierung im ML-Training erfolgt mittels numerischer Optimierungstechniken. Methoden erster Ordnung (first-order methods) müssen lediglich den Gradienten der Zielfunktion in jeder Iteration berechnen. Die Methoden zweiter Ordnung (second-order methods) berechnen zusätzlich auch die Hesse-Matrix oder eine Näherung davon in jeder Iteration. In jedem Fall wird der Gradient in jeder Iteration berechnet.
Mehrere Argumente zeigen, dass es ratsam ist, die folgenden Empfehlungen bei der Organisation des Trainingssprozesses zu berücksichtigen.
- Jede Iteration in einem Trainingsprozess sollte über eine kleinere Anzahl von Trainingsbeispielen, sogenannte Minibatches, statt über große Trainingssätze organisiert werden.
- Es wird empfohlen, die Beispiele im Trainingsdaten vor dem Training des ML-Modells zu randomisieren (d.h. zu mischen).
Optimierungsalgorithmen in ML werden entsprechend der Art der Verwendung des Trainingsdaten wie folgt klassifiziert.
- Batch- oder deterministische (Gradienten-)Methoden – Sie verarbeiten alle Trainingsbeispiele in jeder Iteration.
- Minibatch oder stochastische Minibatch-Methoden – Sie verwenden eine kleinere Anzahl von Trainingsbeispielen, die sogennante Minibatches in jeder Iteration.
- Stochastische Methoden – verwenden nur ein Trainingsbeispiel in jeder Iteration.
- Online-Methoden – beziehen sich auf die Art und Weise, die Beispiele eines Streams zu übernehmen und Beispiele ständig zu erstellen.
Heutzutage ist es üblich, die stochastischen Minibatch-Methoden auch einfach als stochastische Methoden zu nennen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Stochastischer Gradientenabstieg
Stochastischer Gradientenabstieg (stochastic gradient descent - SGD) ist die am weitesten verbreitete numerische Optimierungsmethode im Bereich Machinelles Lernen. Die Hauptidee von SGD besteht darin, für jede Iteration im Training einen Minibatch kleinerer Größe zusammenzustellen, indem der Trainingsbeispiele zufällig ausgewählt werden. Aufgrund der Zufallsstichprobe ergibt die Berechnung des Gradienten der Zielfunktion als Durchschnitt der Gradienten der Loss solcher Stichprobenbeispiele, welcher eine Schätzung des Gradienten des mittleren Loss über die wahre datengenerierende Verteilung darstellt, und dies wiederum entspricht dem Gradienten der Generalisierungsfehler, wenn die ausgewählte Loss Funktion der Fehler ist. Mit anderen Worten:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{m}\sum_{i=1}^{m}\nabla_{{\boldsymbol{\theta}}} L(\hat{y}({\bf x}_{i},{\boldsymbol{\theta}}),y_{i}) \approx E_{({\bf x},y)\sim p } \nabla_{{\boldsymbol{\theta}}}[L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)] = \nabla_{{\boldsymbol{\theta}}} E_{({\bf x},y)\sim p } [L(\hat{y}({\bf x},{\boldsymbol{\theta}}),y)].}
Dies gilt nur, wenn in jedem Minibatch noch ungenutzte Beispiele verwendet werden. Wenn derselbe Trainingsdaten mehrmals durchlaufen wird, werden die einzelnen Durchläufe über den Trainingsdaten als Epochen bezeichnet. In diesem Fall schätzt nur die erste Epoche den Gradienten des Generalisierungsfehlers, die weiteren Epochen tendieren dazu, den Trainingsfehler zu schätzen. Normalerweise verringern zusätzliche Epochen den Trainingsfehler jedoch stärker als die Vergrößerung der Lücke zwischen Trainings- und Generalisierungsfehler, welche durch den Verstoß gegen Unäbhängigkeit der Beispiele in den aufeinanderfolgenden Epochen verursacht wird. Daher randomisieren die meisten SGD-Implementierungen den Trainingssatz zunächst einmal und durchlaufen ihn dann mehrmals.
Ähnlich wie beim Batch-Gradientenabstieg (batch gradient descent) verfügt SGD auch über ein Parameter Namens Lernrate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon} . Während Batch-Gradienten mit festen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon} arbeiten können, erfordert die richtige Verwendung von SGD jedoch eine schrittweise Verringerung der Lernrate im Laufe der Zeit. Dies ist notwendig, da die in SGD verwendete Zufallsstichprobe (random sampling) bei jeder Iteration etwas Rauschen verursacht. Eine nicht abnehmende Lernrate würde verhindern, dass der Gradient mit zunehmender Anzahl von Iterationen kleiner wird. Die schematische Funktionsweise des SGD-Algorithmus ist in Algorithmus dargestellt.
Algorithm Stochastischer Gradientenabstieg
—————————————————————————————
Eingabe:
- Lernratenparameter, die die Reihenfolge der Lernraten beschreiben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_1,\epsilon_2,\ldots}
- Anfangsparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}_{( \mathrm{init})}}
Ausgabe: die geschätzten Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}}
.
—————————————————————————————
1 Initialisierung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k=1}
, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}_{(1)} = {\boldsymbol{\theta}}_{( \mathrm{init})}}
and set Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_1}
2 while Stoppkriterium ist NICHT erfüllt
3 Beispiele aus Trainingsdaten nehmen um
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ }}
Minibatch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ({\bf x}_{1}, {\bf y}_{1}) \ldots, ({\bf x}_{m},{\bf y}_{m})}
zusammenzustellen
4 Berechnen den Gradienten der Loss Funktion als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf g} = \frac{1}{m} \sum_{i=1}^{m} \nabla_{{\boldsymbol{\theta}}} L(\hat{y}({\bf x}_{i},{\boldsymbol{\theta}}_{(k)}),y_{i})}
5 Update: Berechnen den nächsten Wert von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}}
as Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}_{(k+1)} = {\boldsymbol{\theta}}_{(k)} - \epsilon_k {\bf g}}
6 Inkrementieren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k}
as und einstellen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_k}
7 end
—————————————————————————————
Die einzige verbleibende Frage besteht darin, die abnehmende Reihenfolge der Lernraten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_1,\epsilon_2,\ldots}
anzugeben. Um die Konvergenz des SGD sicherzustellen, muss zunächst die folgende hinreichende Bedingung berücksichtigt werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\sum_{k=1}^{\infty}\epsilon_k = \infty, \mathrm{~and~} \\ & \sum_{k=1}^{\infty}\epsilon_k^2 < \infty. \end{aligned}}
In der Praxis ist die häufig verwendete Methode, die die Lernrate in den ersten -Iterationen linear abnehmen lässt und sie dann konstant zu hält Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon_k = \left\{ \begin{aligned} (1- \frac{k}{T}) \epsilon_0 + \frac{k}{T} \epsilon_T, \mathrm{\ \ } \mathrm{~wenn~} k=1,\ldots,T \\ \epsilon_T, \mathrm{\ \ }\mathrm{~wenn~} k > T \mathrm{\ \ \ \ \ \ \ \ }\\ \end{aligned} \right\}.}
Best Practices zum Festlegen der Werte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle T} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_0} und werden wie folgt angegeben.
- normalerweise ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle T} so eingestellt, dass es bis zum Stoppen mehrere Hundert Iterationen ergibt,
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_0 \approx \frac{1}{100}} und
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_T} wird höher als die Lernrate eingestellt, welche nach den ersten 100 Iterationen zur besten Leistung führen würde, aber nicht zu hoch, um starke Schwankungen in der Zielfunktion zu vermeiden.
Eine zu kleine Einstellung von sollte vermieden werden, da dies zu einer Verlangsamung des Lernprozesses führen würde.
Die Konvergenz von SGD kann durch den sogenannten Excess Error charakterisiert werden, der die Differenz zwischen dem Wert der Zielfunktion nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k} -Iterationen und ihrem Minimalwert bei der Konvergenz des Algorithmus darstellt. SGD macht zunächst schnelle Fortschritte im Excess Error, der dann asymptotisch langsam wird. Bei konvexen Problemen geht der Exzessfehler mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(\frac{1}{\sqrt(k)})} zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(\frac{1}{k})} .
Die wichtigsten Vorteile von SGD lassen sich wie folgt zusammenfassen:
- SGD-Training minimiert den Generalisierungsfehler anstelle des Trainingsfehlers, solange Trainingsbeispiele nicht wiederverwendet werden.
- In SGD wächst die Rechenzeit eines Updates, d. h. eines Durchlaufs auf einem Minibatch, nicht mit der Größe der Trainingsdaten, da sie nicht davon abhängt. Dies gewährleistet eine Konvergenz in praktisch angemessener Zeitspanne, auch wenn die Trainingsdatengröße sehr groß wird.
- SGD macht nach einer kleinen Anzahl von Schritten schnelle Fortschritte, da der Gradient anhand sehr weniger Beispiele ausgewertet wird.
Zum Design des ML-Algorithmus
Ein ML-Algorithmus besteht aus den Elementen
- Modell,
- Loss Funktion,
- numerische Optimierungsmethode und
- Dataset.
Das Maschinenmodell und die Loss Funktion müssen passend zur jeweiligen Aufgabe ausgewählt werden. Traditionell sind die Zielfunktion und die Einschränkungen des ML-Problems (ohne ANNs) so konzipiert, dass sie zu einem konvexen Optimierungsproblem führen. Somit treten die Schwierigkeiten eines allgemeinen Optimierungsproblems nicht auf und daher können sowohl numerische Optimierungsverfahren erster als auch zweiter Ordnung angewendet werden.
Einige Best Practices zur Partitionierung und zur Bestimmung der erforderlichen Größen des einzelnen Datasets werden wie folgt bereitgestellt.
Partitionieren des Datasets
Typischerweise werden % des Datasets als Trainingsbeispiele und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 20} % als Testbeispiele verwendet.
Typischerweise werden etwa Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 80} % der Trainingsbeispiele für das Training und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 20} % als Validierungsdaten verwendet
Daraus ergibt sich eine Partition: ca. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 65} % Trainingsdaten, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 15} % Validierungsdaten und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 20} % Testdaten.
Die erforderliche Minibatch-Größe im Training:
ca. – im Falle der Verwendung numerischer Optimierungsmethoden erster Ordnung, wie der (stochastische) Gradientenabstieg,
ca. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 10000} – bei Verwendung numerischer Optimierungsverfahren zweiter Ordnung.
Tipp für die Verwendung eines kleinen Testdaten: Wenn der Dataset nicht groß genug ist, dann ist die Kreuzvalidierungstechnik (cross-validation technique) (Kreuzvalidierung) empfohlen. Es besteht aus der Durchführung mehrerer Testrunden, wobei in jeder Testrunde der Dataset zufällig oder rotierend in einen Trainingsdaten und einen Testdaten aufgeteilt wird.
Der schematische Algorithmus zur Bestimmung der Parameter des Maschinenmodells ist in Algorithmus angegeben.
Algorithm schematische Algorithmus zur Bestimmung der Parameter
des Maschinenmodells
—————————————————————————————
Eingabe:
- Maschinenmodell,
- Loss Funktion,
- numerische Optimierungsmethode ,
- Trainingsdaten, Validierungsdaten, Testdaten.
Ausgabe: optimale Modellparameter.
—————————————————————————————
1 Initialisierung hyperparameter
2 while Stoppkriterium basierend auf Pass-Through-Over-Validierungsdaten
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ }}
NICHT erfüllt
3 Update hyperparameter
4 initialisieren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}}
5 while Stoppkriterium basierend auf Trainingsfehler NICHT erfüllt
6 Update mittels Iterationsschritt Pass-Through-Over-Trainingsdaten
7 end
8 Pass-Through-Over-Validierungsdaten unter Verwendung des Aktualwerts
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }}
von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\theta}}}
9 end
10 Berechnen von Testfehler mittels Pass-Through-Over-Testdaten
—————————————————————————————
Unterschiede zwischen maschinellem Lernen und Deep Learning
Deep Learning (DL) ist maschinelles Lernen, bei dem KNN zum Einsatz kommt und mindestens eine Hidden Layer (verdeckten Schicht) aufweist. Dieser zusätzliche Teil führt jedoch zu vielen Unterschieden in der Funktionsweise und dem Design der DL-Algorithmen im Vergleich zu den herkömmlichen ML-Algorithmen.
Deep Learning versus konventionelles maschinelles Lernen
Obwohl herkömmliches ML und DL die gleichen Lernansätze anwenden, wie z.B. überwachtes oder überwachtes Lernen, ihre mathematischen Modelle sind unterschiedlich. Während herkömmliches ML hauptsächlich statistische oder deterministische Modelle verwendet, die Diskriminanzfunktionen als Wahrscheinlichkeitsfunktionen über den Hypothesenraum implementieren, realisiert DL KNNs mit Hidden Layer Approximationen von jeglicher Art, auch nichtlinearen Diskriminanzfunktionen. Dementsprechend ist die Feature Extraktion (Merkmalsextraktion) in DL-Modellen implizit und die Funktionsweise kann nur teilweise mathematisch nachvollziehbar beschrieben werden. Als Konsequenz daraus wird DL für viele Menschen als eine Black Box angesehen, deren interne Funktionsweise höchtens nur teilweise nachvollziehbar ist. Andererseits wurden die in DL verwendeten KNNs ursprünglich durch die Beobachtung der menschlichen Gehirnstruktur inspiriert, während die konventionellen ML-Modelle auf von Menschen erstellten mathematischen Abstraktionen basieren. Die wichtigsten Gemeinsamkeiten und Unterschiede zwischen DL und konventionellen ML sind hinsichtlich ihrer Eigenschaften in der Tabelle 3 zusammengefasst.
| Eigenschaften | DL | konventionelle ML |
|---|---|---|
| Ansatz zum Lernen | überwachtes/ | überwachtes/unüberwachtes |
| unüberwachtes | und durch Verstärkung | |
| Modell | KNN | statistisches or |
| deterministisches | ||
| Diskriminanzfunktion | beliebige Funktionen | Wahrscheinlichkeitsfunktion/ |
| realized | einschließlich | Wahrscheinlichkeitsdichte |
| nichtlineare | ||
| Feature Extraction | implicit | explicit |
| Mathematisch | nein | ja |
| behandelbar | ||
| Verständlich | nur teilweise | völlig |
| Basierend auf | Beobachten der | von Menschen geschaffenen |
| menschlichen | mathematischen | |
| Gehirnstruktur | Abstraktionen | |
| Optimierungsaufgabe | allgemein | in der Regel |
| für Parameter Lernen | nicht konvex | konvex |
DL-Algorithmen sind für komplexere ML-Aufgaben gedacht, die für herkömmliche ML-Algorithmen zu schwierig sein können. Dementsprechend ist die entsprechende Optimierungsaufgabe für das Lernen von Parameter im DL-Modellen allgemein nicht konvex. Dies hat weitreichende Konsequenzen für den Entwurf solcher DL-Algorithmen hinsichtlich auf Optimierung.
Im Folgenden untersuchen wir die potenziellen Probleme bei der Optimierung aufgrund ihrer allgemeinen nicht-konvexen Natur und geben einen kurzen Überblick über die etablierten und vielversprechenden algorithmischen Strategien, die die identifizierten Herausforderungen zumindest teilweise bewältigen können.
Mögliche Probleme bei der DL-Optimierung
Da die meisten Optimierungsaufgaben für das Anpassen von Parameter bei DL-Problemen im Allgemeinen nicht konvex sind, sind die meisten verwendeten numerischen Optimierungsmethoden nur erster Ordnung. Eine Liste der wichtigsten potenziellen Probleme bei der numerischen Optimierung allgemeiner nichtkonvexer Probleme kann wie folgt angegeben werden:
- Schlecht konditionierte Hesse-Matrix (poorly conditioned/ ill-conditioning Hessian matrix).
- Lokales Mininum anstelle des globalen finden.
- Sattelpunkte und flache Regionen (saddle points and flat regions)
- Steile Regionen (steep regions)
Algorithmische Strategien für DL
Um die Herausforderungen aufgrund der oben gelisteten Probleme bei der DL-Optimierung zu bewältigen, wurden mehrere Modifikationen des stochastischen Gradientenabstiegsalgorithmus, mehrere Algorithmen zweiter Ordnung und auch mehrere Parameterinitialisierungen vorgeschlagen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Modifikationen des Gradientenabstiegsalgorithmus
Wir listen einige modifizierte Varianten des Algorithmus für den stochastischen Gradientenabstieg auf, die am häufigsten zum Training von Dl-Modellen verwendet werden. Diese beinhalten
- Momentum und Nesterov Momentum,
- AdaGrad-Algorithmus und RMSProp-Algorithmus ohne/mit Nesterov Momentum und
- Adam-Algorithmus.
Optimierungsmethoden zweiter Ordnung
Methoden zweiter Ordnung erfordern einige Anpassungen, um für das Lernen der Parameter in neuronalen Netzen geeignet zu sein. Die Methoden zweiter Ordnung, die für das Training von Dl-Modellen relevant sind, sind:
- Quasi-Newton-Methoden (quasi-Newton methods)
- Nichtlinearer konjugierter Gradientenalgorithmus (non-linear conjugate gradient algorithm)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Methode zum Initialisieren der Parameter
Die Auswahl der Anfangsparameter ist wichtig, da sie
- die Konvergenz,
- die Konvergenzgeschwindigkeit und
- den Generalisierungsfehler und damit die Generalisierungsfähigkeit
des Modells beeinflussen.
Die Wahl der Anfangsparameter des NN-Modells ist jedoch eine schwierige Aufgabe, da die NN-Optimierung nicht gut genug verstanden ist. Daher ist eine echte Gestaltung der Anfangsparameter nicht möglich. Stattdessen werden einige ziemlich einfache heuristische Strategien verwendet, die auf eine bestimmte erforderliche Eigenschaft abzielen. Das einzige verstandene Prinzip ist, dass richtig gewählte Anfangsparameter die „Symmetrie“ zwischen verschiedenen Einheiten „brechen“ müssen. Dies bedeutet, dass mehrere versteckte Einheiten, die mit demselben Eingang verbunden sind und dieselbe Aktivierungsfunktion haben, mit unterschiedlichen Werten initialisiert werden müssen, damit sie unterschiedliche Gewichte lernen können.
Die am häufigsten etablierten Initialisierungsstrategien können wie folgt angegeben werden.
- Typische Initialisierungsstrategie mit zufälligen Gewichten und konstantem Bias
- Initialisierungsstrategie unter Ausnutzung von ML-Techniken
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Typische Initialisierungsstrategie mit zufälligen Gewichten und konstantem Bias
Die Gewichte werden zufällig initialisiert, entweder aus einer Gaußschen oder einer Gleichverteilung. Tatsächlich hat die Art der Verteilung nur einen geringen Einfluss auf das Training. Der Maßstab der anfänglichen Verteilung (initial scale) ist jedoch wichtig, da er den Generalisierungsfehler beeinflusst.
Häufig verwendete Heuristiken zur Bestimmung des Maßstabs der anfänglichen Verteilung sind:
- Dichte Initialisierung (dense initialization)
- Spärliche Initialisierung (sparse initialization)
- Als Hyperparameter initialisieren (initialize as hyperparameter)
- Faustregel (rule of thumb)
Dichte Initialisierung gibt den Maßstab für vollständig verbundene Layer mit n Input Units und m Output Unit als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ~U(-\frac{1}{\sqrt(n)}, \frac{1}{\sqrt(n)})} oder als normalisierte Initialisierung als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ~U(-\sqrt(\frac{6}{(n+m)}), \sqrt(\frac{6}{(n+m)}))} an. Eine andere Möglichkeit der dichten Initialisierung besteht darin, die Gewichte als zufällige orthogonale Matrizen mit Skalierungs- oder Verstärkungsfaktor (gain factor) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} anzugeben. Dies hat den Vorteil, dass die Konvergenz unabhängig von der Tiefe wird, d. h. von der Anzahl der Layers.
Bei spärlicher Initialisierung wird jede neurale Einheit so initialisiert, dass nur genau k Gewichte ungleich Null sind. Auf diese Weise hängt die Anzahl der effektiven Eingabewerten in die Einheit (= mit Gewichten ungleich Null) nicht von der Gesamtzahl der Eingabewerten in diese Einheit ab.
Der Maßstab der anfänglichen Verteilung kann auch als Hyperparameter betrachtet und bestimmt werden. Diese Methode kann sowohl für dichte als auch für spärliche Initialisierung verwendet werden.
Die Faustregel besagt, dass der Maßstab der anfänglichen Verteilung in der Größenordnung des Bereichs der Standardabweichung von Gradienten liegen sollte, die bei einem einzelnen Minibatch auftreten.
Das Bias wird normalerweise auf heuristisch ausgewählte Konstanten eingestellt. In den meisten Fällen funktioniert die Einstellung auf Null. Es gibt jedoch mehrere Fälle, in denen die Einstellung auf einen Wert ungleich Null erforderlich ist. Diese Fälle werden nachfolgend aufgeführt.
- Bias für Output Unit. In diesem Fall wird der Bias auf die rechten Randstatistiken (right marginal statistics) der Output Unit eingestellt, indem die Umkehrung der Aktivierungsfunktion der Output Unit (inverse of the activation function of the output unit) angewendet wird.
- Bias für Aktivierungsfunktionen, um eine Sättigung zu vermeiden. In solchen Fällen, wie z. B. bei ReLU, wird der Wert auf 0.1 statt auf 0 eingestellt. Dies kann jedoch nicht zusammen mit einigen Initialisierungsstrategien für Gewichte angewendet werden, wie z. B. der Initialisierungsstrategie mit zufälligen Gewichten.
- Bias für die Einheit, die die Rolle des Gates spielt. Hier wird der Bias auf 1 eingestellt, wie z. B. für das Forget-Gate des LSTM-Modells (siehe Unterabschnitt 4.4.4).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Initialisierungsstrategie unter Ausnutzung von ML-Techniken
Das überwachte Lernmodell wird durch Parameter initialisiert, die vom unüberwachten Lernmodell gelernt werden, wobei beide mit denselben Trainingsdaten trainiert werden.
Grundlagen neuronaler Netze
Neuronale Netzwerke (neural network) sind ein grundlegendes Rechensystem und ein wichtiger integraler Bestandteil der KI.
Künstliches Neuron
Ein künstliches Neuron (artificial neuron) ist eine Recheneinheit, die eine mathematische Funktion realisiert, die von biologischen Neuronen inspiriert ist. Es wird Neuron genannt, da sein Ursprung auf das McCulloch-Pitts-Neuron
([McCulloch and Pitts(1943)]) zurückgeht, das ein Rechenelement war, das Aussagenlogik nutzte, um ein vereinfachtes Modell für das biologische Neuron bereitzustellen. Anders als frühere Realisierungen haben moderne künstliche Neuronen nicht mehr die Absicht, neurophysiologische Beobachtungen widerzuspiegeln. Ein künstliches Neuron ist eine kleine Recheneinheit, die in der Regel mehrere Eingabewerte aufnimmt, daraus eine gewichtete Summe bildet, darauf eine nichtlineare Übertragungsfunktion anwendet und einen Ausgabewert erzeugt. Daher realisiert es eine mathematische Funktion, die aus einem Eingabevektor einen einzelnen Ausgabewert erzeugt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Neuronale Einheit
Eine neuronale Einheit (neural unit) ist ein künstliches Neuron mit einer nichtlinearen Übertragungsfunktion, die als Aktivierungsfunktion (activation function) bezeichnet wird. Es handelt sich um eine einzelne Recheneinheit, die reale Eingabewerte annimmt, einige Berechnungen an ihnen durchführt und einen einzelnen Ausgabewert erzeugt.
Die von einer neuronalen Einheit realisierten Kernfunktionen bestehen darin, eine gewichtete Summe der Eingaben zu bilden und darauf eine nichtlineare Aktivierungsfunktion anzuwenden. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1,\ldots,x_n} die Menge der realen Eingabewerte (input values) und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle w_1,\ldots,w_n} die Menge der entsprechenden Gewichte (weights) sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b} ein Bias-Term (bias). Dann kann die gewichtete Summe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle z} mathematisch als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z = \sum_{i=1}^n w_i x_i + b} beschrieben werden. Durch Einführung der Vektornotationen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x} = (x_1,\ldots,x_n)^T} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf w} = (w_1,\ldots,w_n)} kann die gewichtete Summe als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z = {\bf w}{\bf x} + b} ausgedrückt werden. Der Ausgabewert (output value) der neuronalen Einheit wird durch Anwenden der nichtlinearen Aktivierungsfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f()} auf die gewichtete Summe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle z} erhalten. Somit kann die gesamte Funktionalität der neuronalen Einheit mathematisch als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y = f(z) = f\left({\bf w}{\bf x} + b\right)} gegeben werden.
Ein Beispiel für eine Aktivierungsfunktion ist die Sigmoidfunktion (sigmoid function) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \sigma(z)} , die als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma(z) = \frac{1}{1+e^{-z}}} angegeben werden kann. Die Sigmoidfunktion wandelt eine reale Eingabe in einen Wert zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} um, was als Normalisierung (normalization) angesehen werden kann, aber auch eine Interpretation als Wahrscheinlichkeit zulässt. Die Werte um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} werden in Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} verschoben. Ein weiterer Vorteil der Sigmoidfunktion ist, dass sie differenzierbar ist, was beim Lernen der Gewichtsparameter der neuronalen Einheit während des Trainings benötigt wird (siehe unten bei Training einzelner Neuronen). Die Sigmoidfunktion ist in Abbildung 16 dargestellt.
Die Ausgabe der Aktivierungsfunktion wird Aktivierungswert (activation value) genannt und mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a}
bezeichnet. Die mathematische Funktionalität der neuronalen Einheit, die die Sigmoidfunktion anwendet, ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y = a = \sigma({\bf w}{\bf x} + b) = \frac{1}{1+e^{-({\bf w}{\bf x} + b)}}}
gegeben. Der obige Ausdruck zeigt, dass die mathematische Funktionalität einer neuronalen Einheit im Allgemeinen durch den Unterschied zur Step-Function allgemeiner ist als nur eine binäre Klassifizierung (binary classification). Dies gilt für die neuronalen Einheiten mit den am häufigsten verwendeten Aktivierungsfunktionen, mit Ausnahme des Perzeptrons (siehe unten).
Das schematische Diagramm einer grundlegenden neuronalen Einheit ist in Abbildung 17 zu sehen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }}
Perzeptron
Eine der frühen neuronalen Einheiten ist ein Perzeptron (perceptron), das im Jahr 1957 von Rosenblatt vorgeschlagen wurde ([Rosenblatt(1958)]). Es wendet die Heaviside Step-Function Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h(z)} an, die durch gegeben ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h(z) = \left\{ \begin{aligned} 1, \mathrm{\ \ } \mathrm{~wenn~} z > 0 \\ 0, \mathrm{\ \ } \mathrm{~wenn~} z \leq 0\\ \end{aligned} \right\}.}
Auf diese Weise wird die mathematische Funktionalität des Perzeptrons Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y = h(z) = h\left({\bf w}{\bf x} + b\right) = \left\{ \begin{aligned} 1, \mathrm{\ \ } \mathrm{~wenn~} {\bf w}{\bf x} + b > 0 \\ 0, \mathrm{\ \ } \mathrm{~wenn~} {\bf w}{\bf x} + b \leq 0 \\ \end{aligned} \right\}} realisiert eine lineare Diskriminanzfunktion für zwei Klassen, also mit binärer Ausgabe (binary output). Daher ist das Perzeptron nur ein binärer Klassifikator (binary classifier).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Übliche Aktivierungsfunktionen
Neben der Sigmoidfunktion gibt es auch andere häufig verwendete Aktivierungsfunktionen.
Eine Sigmoid-ähnliche Funktion ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \tanh(z)} , die ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tanh(z) = \frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}} gegeben. Die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \tanh(z)} hat die vorteilhafte Eigenschaft, dass sie differenzierbar ist. Darüber hinaus „wirft“ es die Werte um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} in Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -1} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle +1} .
Eine weitere einfache, aber übliche Aktivierungsfunktion ist die Rectified Linear Unit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ReLU(z)} . Diese Funktion ist als positiver Teil ihres Arguments definiert. Anders ausgedrückt sie nimmt den Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle z} für positive Werte an und andernfalls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} : Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ReLU(z) = \max(z,0) = \left\{ \begin{aligned} z, \mathrm{\ \ } \mathrm{~wenn~} z > 0 \\ 0, \mathrm{\ \ } \mathrm{~wenn~} z \leq 0. \\ \end{aligned} \right\} = = \frac{z+|z|}{2}.}
Die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ReLU(z)} hat die schönen Eigenschaften
- es ist nahezu linear,
- seine Ableitung ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} (anstatt fast Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} zu sein, wie es bei den anderen Aktivierungsfunktionen der Fall ist) für höhere Werte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle z} und hat daher nicht das Vanishing Gradient Problem [vanishing_grad].
Die Aktivierungsfunktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \tanh(z)} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ReLU(z)} sind in Abbildung 18 dargestellt.
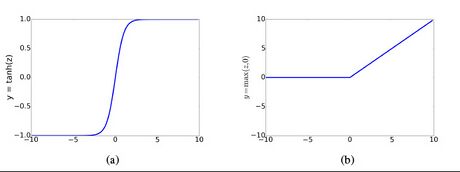
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }}
Das Training eines einzelnen Neurons verstehen
Das Ziel des Trainings eines einzelnen Neurons besteht darin, die Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf w}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b} zu lernen. Dies geschieht durch Minimierung der Per-Example Loss Function Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L(\hat{y}({\bf x},{\boldsymbol{w}}, b),y)} , wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \hat{y}({\bf x},{\boldsymbol{w}}, b)} ist die von der neuronalen Einheit erzeugte Ausgabe in Abhängigkeit von Parametern Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf w}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b} , und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} ist die richtige erwartete Ausgabe. Die Minimierung erfolgt üblicherweise durch Anwendung einer Variante des Gradientenabstiegsalgorithmus, dessen Iterationsschritt durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ({\boldsymbol{w}}, b)_{k+1} = ({\boldsymbol{w}}, b)_{k}-\epsilon_k \nabla_{({\boldsymbol{w}}, b)}L(\hat{y}({\bf x},({\boldsymbol{w}}, b)),y)} gegeben ist, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon_k} die Lernrate (learning rate) in der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k} -ten Iteration ist. Der Kern dieses Iterationsschritts (iteration step) ist die Berechnung des Gradienten von Loss. Mit der Kettenregel (chain rule) kann das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} -te Element dieses Gradienten als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial w_i} = \frac{\partial L}{\partial \hat{y}} \frac{\partial f\left({\bf w}{\bf x} + b\right)}{\partial w_i} = \frac{\partial L}{\partial \hat{y}} f^{(1)}\left({\bf w}{\bf x} + b\right) x_i} angegeben werden, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{(1)}} für die erste Ableitung der Aktivierungsfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(z)} steht.
Notwendigkeit eines neuronalen Netzwerks
Schon in der Frühzeit hat sich herausgestellt, dass auch relativ einfache Aufgaben nicht von einer neuronalen Einheit gelöst werden können. Durch die Kombination neuronaler Einheiten kann jedoch die Rechenleistung (computational capability) des so erstellten neuronalen Netzwerks drastisch erhöht werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Neuronale Einheit für logisches UND und ODER
Jede der logischen UND- und ODER-Operatoren kann durch ein einzelnes Perzeptron realisiert werden. Dies liegt daran, dass jede dieser Operatoren zu einem linear trennbaren binären Klassifizierungsproblem (linearly separable binary classification problem) führt. Abbildung 19 zeigt die lineare Trennbarkeit (linear separability) dieser logischen Operatoren im zweidimensionalen Raum (two-dimensional space) der logischen Eingaben (logical inputs).
Die resultierenden Gewichte und Bias sind in Abbildung 20 dargestellt. Der Bias wird als Gewicht für eine dritte Eingabe mit der Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle +1}
angezeigt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }}
Das XOR-Problem
Die Wahrheitstabelle des logischen XOR-Operator ist in der Tabelle angegeben 4.
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_2} | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nach dem Ausprobieren mehrerer Möglichkeiten stellt sich heraus, dass es nicht möglich ist, den logischen XOR-Operator mit einem Perzeptron zu realisieren. Dies liegt daran, dass das Perzeptron eine lineare Diskriminierungsfunktion realisiert, d. h. es kann nur eine Linie (= 2-D-Hyperebene) als Entscheidungsgrenze zwischen den Klassen realisieren, die Funktionalität des logischen XOR-Operator darstellt jedoch eine linear nicht trennbare Aufgabe. Dies ist in Abbildung 21 dargestellt.
Die Lösung für das XOR-Problem ist ein neuronales Netzwerk. Das logische XOR kann durch die Verwendung von zwei Layers (Schichten) mit ReLU-basierten neuronalen Einheiten realisiert werden (siehe in [Goodfellow et al.(2016)]). Dieses aus zwei Schichten bestehende neuronale Netz ([Goodfellow et al.(2016)]) ist in Abbildung 22 dargestellt.
Es gibt eine mittlere Layer, die aus zwei neuronalen Einheiten mit den Ausgaben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h_1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h_2}
besteht, und eine Output Layer, die aus einer einzelnen neuronalen Einheit mit der Ausgabe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y}
besteht. Die Hidden Layer (verborgene Schicht = die Schicht zwischen der Input- und Output Layers) transformiert den ursprünglichen zweidimensionalen Raum der Eingaben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_2}
(im Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x}
-Raum) in einen neuen zweidimensionalen Raum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h_1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h_2}
(der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h}
-Raum). Wie in Abbildung 23 zu sehen ist, fallen die Eingabepunkte (input points) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (0,1)}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1,0)}
in einem Punkt im neuen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h}
-Raum zusammen, wodurch die beiden möglichen Ausgaben des logischen XOR im neuen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h}
-Raum linear trennbar werden.
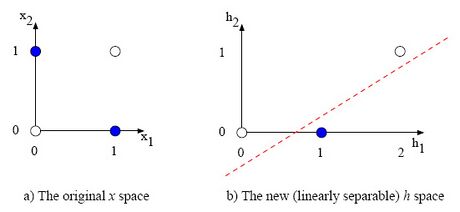
Feedforward Neural Network
Das Feedforward Neural Network - FNN (Feedforward-Neuronales Netzwerk) ist die einfachste Art eines neuronalen Netzwerks. Es handelt sich um ein Multilayer Network (mehrschichtiges Netzwerk) ohne Zyklen, was bedeutet, dass keine Ausgaben einer tatsächlichen Layer an die tatsächliche oder niedrigere Layers zurückgegeben werden. FNNs werden manchmal als Multilayer Perzeptron - MLP (mehrschichtige Perzeptrone) bezeichnet, da die verwendeten neuronalen Einheiten in früheren Zeiten Perzeptrone waren, die rein lineare Diskriminanzfunktionen realisierten. Moderne Multilayer Neural Network verfügen jedoch über neuronale Einheiten mit nichtlinearen Aktivierungsfunktionen.
Das FNN besteht aus drei Arten von Layer: einer Input Layer (Eingabeschicht), einer oder mehreren Hidden Layers (verborgenen Schichten) und einer Output Layer (Ausgabeschicht). Wenn es mehr Hidden Layers gibt, wird das Netzwerk als Deep Feedforward Neural Network (Deep-Feedforward-Neuronales Netzwerk) bezeichnet. Jede Layer ist Fully-Connected Layer (vollständig verbunden), was bedeutet, dass jede Einheit in jeder Layer die Ausgaben aller Einheiten der vorherigen Layer als Eingabe erhält. Im Folgenden werden wir ein FNN mit einer Hidden Layer erklären.
Die Parameter jeder Einheit der Hidden Layer (Hidden Unit) werden als einzelne Zeilen einer Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}} zusammengefügt und die einzelne Bias Elemente werden als ein Spaltenvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf b}} dargestellt. Somit stellt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle W_{ji}} als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j,i} -tes Element von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}} das Gewicht der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} -ten Input Unit (Eingabeeinheit) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_i} gegenüber der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} -ten Hidden Unit (verborgenen Einheit) dar. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h_j} die Ausgabe der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} -ten Hidden Unit. Die Organisation der Ausgaben der Hidden Units in einem Spaltenvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf h}} ermöglicht es, die Funktionalität der gesamten Hidden Layer in Vektor-Matrix-Notation als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf h} = f_h\left({\bf W}{\bf x} + {\bf b}\right)} zu beschreiben, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f_h({\bf z})} eine Vektorwertige Aktivierungsfunktion ist, die normalerweise durch eine gemeinsame Skalarfunktion realisiert wird, die elementweise für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}{\bf x}} , also für die Ausgaben aller Hidden Units angewendet wird.
In ähnlicher Weise repräsentiert die Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf U}} die Gewichte der Einheiten der Output Layer (Output Units - Ausgabeeinheiten). Somit repräsentiert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U_{kj}} , das das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k,j} -te Element von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf U}} ist, das Gewicht der Ausgabe der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} -ten Hidden Unit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h_j} an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k} -te Output Unit. Die Ausgabe der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k} -ten Output Unit sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_k} . Die Organisation der Ausgaben der Output Units in einem Spaltenvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf y}} ermöglicht es, die Funktionalität der gesamten Output Layer in Vektor-Matrix-Notation als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf y} = f_o\left({\bf U}{\bf h} \right)} zu beschreiben, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f_o({\bf z})} eine Vektorwertige Aktivierungsfunktion ist. Ein Feedforward Neural Network mit einer Hidden Layer wird in Abbildung 24 dargestellt.
Alle diese Faktoren zusammen bewirken, dass die Berechnung des FFN mathematisch in Vektor-Matrix-Notation als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf y} = f_o\left({\bf U}\left(f_h\left({\bf W}{\bf x} + {\bf b}\right)\right) \right)} beschrieben werden kann.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Die Notwendigkeit nichtlinearer Aktivierungsfunktionen
Es gibt mindestens zwei Gründe, nichtlineare Aktivierungsfunktionen zu verwenden:
- eine allgemeinere Raumtransformation zu ermöglichen (wie z. B. im Fall der Realisierung eines logischen XOR) und
- ein Sinn für die Verwendung mehrerer Ebenen zu geben.
Ohne Verwendung nichtlinearer Aktivierungsfunktionen ist die Funktionalität zweier aufeinanderfolgender linearer Layers Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\bf z}_1 &= {\bf W}_1{\bf x} + {\bf b}_1, \\ {\bf z}_2 &= {\bf W}_2{\bf z}_1 + {\bf b}_2 \end{aligned}} könnte durch die Verwendung nur einer linearen Layer realisiert werden. Dies kann wie folgt gezeigt werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf z}_2 = {\bf W}_2{\bf z}_1 + {\bf b}_2 = {\bf W}_2\left({\bf W}_1{\bf x} + {\bf b}_1 \right) + {\bf b}_2 = {\bf W}_2 {\bf W}_1{\bf x} + {\bf W}_2 {\bf b}_1 + {\bf b}_2 = {\bf W}_{*}{\bf x} + {\bf b}_{*}.}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Die Softmax Funktion
Wenn das FNN als Klassifikator verwendet wird, dürften die Ausgabewerte der Output Layer keine einfachen reellen Zahlen sein, sondern müssen Wahrscheinlichkeiten sein. Dann kann entschieden werden, dass die von der Output Unit mit der höchsten Wahrscheinlichkeit repräsentierte Klasse die vorhergesagte Klasse ist. Auf diese Weise realisieren die Ausgabewahrscheinlichkeiten der Output Units Diskriminanzfunktionen.
Es gibt eine Vektorwertige Aktivierungsfunktion, die die realwertigen Ausgabewerte der Output Units in eine Wahrscheinlichkeitsverteilung normiert. Sie heißt Softmax Funktion und ist auf dem Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf z}=(z_1, \ldots, z_d)} als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle softmax(z_i) = \frac{e^{z_i}}{\sum_{i=j}^{d} e^{z_j}}, \mathrm{\ \ } 1 \leq i \leq d} definiert.
Unter Verwendung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle softmax({\bf z})} als Aktivierungsfunktion für die Output Layer kann die Funktionalität des FNN mathematisch wie folgt angegeben werden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf y} = softmax\left({\bf U}\left(f_h\left({\bf W}{\bf x} + {\bf b}\right)\right) \right).}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Einbeziehung von Bias in die Gewichte
Der Bias kann als Gewichtung einer virtuellen Input Unit mit einem konstanten Eingabewert von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} angesehen werden. Auf diese Weise kann die Bias in die Gewichte eingearbeitet werden. Dies ist in Abbildung 25 dargestellt.
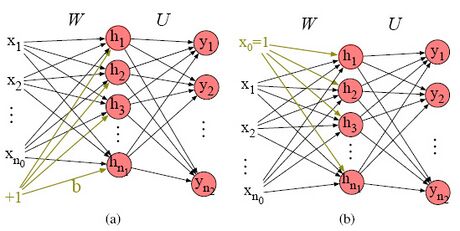
Diese Einbeziehung des Bias in die Gewichte führt zu einer Erweiterung der Gewichtsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}}
, indem an jeder Position am Spaltenindex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0}
eine Spalte mit dem Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b}
eingefügt wird. Der erweiterte Eingabevektor und die Gewichtsmatrix werden mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}^*}
bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}^*}
bezeichnet. Die Verwendung dieser Notation vereinfacht die Beschreibung der Funktionalitäten der Hidden Layer und des gesamten FNN als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &{\bf h} = f_h\left({\bf W}^*{\bf x}^*\right), \\ &{\bf y} = softmax\left({\bf U}\left(f_h\left({\bf W}^*{\bf x}^*\right)\right) \right). \end{aligned}}
Training neuronaler Netze
Ziel des Trainings ist das Erlernen der Modellparameter, also der Elemente von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf b}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf U}} . Dies geschieht durch die Minimierung des Loss im gesamten Trainingsdaten, die auf der Loss Funktion pro Beispiel beruht. Die Minimierung selbst wird durch einen numerischen Optimierungsalgorithmus erster Ordnung durchgeführt, normalerweise eine Variante des Gradientenabstiegs, der in jeder Iteration die Berechnung des Gradienten des Loss pro Beispiel nach den zu erlernenden Modellparameter erfordert.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Loss Funktion
Im Falle einer binären Klassifizierung mit Sigmoid auf der letzten Layer (d. h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} kann die Werte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} haben) verwenden die neuronalen Netze den Cross-Entropy Loss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L_{CE}} als Loss Funktion, die wie folgt angegeben ist.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{CE}(\hat{y},y) = -\left(y~log~\hat{y} + (1-y)~log(1-\hat{y}) \right).}
Die wahre Ausgabe für Klassifizierungsaufgaben mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle C} -Klassen kann durch den One-Hot-Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf y} = (y_1,\ldots,y_C)} beschrieben werden. Ein One-Hot-Vektor ist ein Vektor, bei dem ein Element Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} und der Rest Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} ist. Die geschätzte Ausgabe wird durch den Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf \hat{y}}= (\hat{y}_1,\ldots,\hat{y}_C)} beschrieben, der die geschätzte Wahrscheinlichkeitsverteilung über die möglichen Klassen angibt. Für Klassifizierungsaufgaben mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle C} -Klassen kann der Cross-Entropy Loss wie folgt angegeben werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{CE}({\bf \hat{y}},{\bf y}) = -\sum_{c=1}^C y_c~ log~\hat{y}_c = -\sum_{c=1}^C \mathbf{1}_{\{y_c = 1\}} log~\hat{y}_c = - log~\hat{y}_t,} wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t} die wahre Klasse ist.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Der Backpropagation-Algorithmus
Der Loss des FNN pro Beispiel kann als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{CE}({\bf \hat{y}},{\bf y}) = - log~\hat{y}_t} angegeben werden, wobei die geschätzte Ausgabewahrscheinlichkeitsverteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf \hat{y}}} als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf \hat{y}} = f_o\left({\bf U}\left(f_h\left({\bf W}^*{\bf x}^*\right)\right) \right)} gegeben ist.
Dies kann für ein FNN mit mehr Hidden Layer verallgemeinert werden. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L} die Anzahl der Hidden Layer plus der Output Layer und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}^{[i]}} die Gewichtsmatrix der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} -ten Layer, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i=1,\ldots, L} . Somit ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}^{[1]}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}^{[L-1]}} die Gewichtsmatrix der ersten und der letzten Hidden Layer, während Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W} ^{[L]}} ist die Gewichtsmatrix der Output Layer. Außerdem sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f_i(z)} die Aktivierungsfunktion der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} -ten Layer. Jede übliche Aktivierungsfunktion für die Hidden Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i=1,\ldots,L-1} , wie z.B. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ReLU(z)} wird elementweise angewendet und kann daher als Skalarfunktion beschrieben werden. Allerdings Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle softmax(z)} , die übliche Aktivierungsfunktion der Output Layer, hängt von allen Einheiten der Output Layer ab und kann daher als Vektorwertige Funktion beschrieben werden. Daher wird es mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf F}_{L}} bezeichnet. Dann kann die geschätzte Ausgabewahrscheinlichkeitsverteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf \hat{y}}} wie folgt angegeben werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\bf \hat{y}} = {\bf F}_{L}\left({\bf W}_L f_{L-1}\left({\bf W}_{L-1} \ldots f_2\left({\bf W}_2 f_1\left({\bf W}_1{\bf x}\right)\right) \ldots \right)\right).}
Mit der Kettenregel kann die Ableitung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L_{CE}} nach dem Eingabevektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf x}} als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L_{CE}}{\partial {\bf x}} = \frac{\partial L_{CE}}{\partial {\bf \hat{y}}} \frac{\partial {\bf \hat{y}}}{\partial {\bf x}} = \frac{\partial L_{CE}}{\partial {\bf \hat{y}}} {\bf F}_{L}^{(1)} {\bf W}_L f_{L-1}^{(1)}{\bf W}_{L-1} \ldots f_{1}^{(1)}{\bf W}_{1}} angegeben werden, wobei jeder Term eine totale Ableitung ist, d. h. der Term Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{\partial L_{CE}}{\partial {\bf \hat{y}}}} ist ein Zeilenvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf F}_{L }^{(1)}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf W}_i} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i=1,\ldots,L} sind Matrizen und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f_{j}^{(1)}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j=1,\ldots,L-1} sind Skalarterme.
Üblicherweise wird die obige Ableitung als Gradient Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \nabla_{{\bf x}}L_{CE}} ausgedrückt, der ein Spaltenvektor ist und daher gleich der Transponierten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{\partial L_{CE}}{\partial {\bf x}}} ist. So, indem wir die obige Beziehung transponieren, erhalten wir
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla_{{\bf x}}L_{CE} = {\bf W}_{1}^T f_{1}^{(1)} \ldots {\bf W}_{L-1}^T f_{L-1}^{(1)} {\bf W}_L^T {\bf F}_{L}^{(1)} \nabla_{{\bf \hat{y}}}L_{CE}.}
Um die Ableitung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L_{CE}} nach den Gewichten der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} -ten Layer zu betrachten, müssen wir den „Fehler bei Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} “ einführen, der ein Teil des obigen Produkts ist, dass den Gradienten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L_{CE}} nach der Eingabe der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} -ten Aktivierungsfunktion als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\boldsymbol{\varsigma}}_{m} = f_{m}^{(1)} {\bf W}_{m+1}^T f_{m+1}^{(1)} \ldots {\bf W}_{L-1}^T f_{L-1}^{(1)} {\bf W}_L^T {\bf F}_{L}^{(1)} \nabla_{{\bf \hat{y}}}L_{CE}} und der Ausgabewert der Aktivierungsfunktion auf der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m-1} -ten Layer als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{m-1} = f_{m-1}\left({\bf W}_{m-1} \ldots f_2\left({\bf W}_2 f_1\left({\bf W}_1{\bf x}\right)\right) \ldots \right)} beschreibt.
Aufgrund der linearen Verwendung der Gewichte an den Inputs in der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} -ten Layer kann der Gradient der Gewichte in der Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \nabla_{{\bf W}_{m}}} mithilfe der oben eingeführten Quantitäten als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla_{{\bf W}_{m}}L_{CE} = {\boldsymbol{\varsigma}}_{m} a_{m-1}^T} ausgedrückt werden.
Die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\varsigma}}_{m}} Quantitäten können rekursiv als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\boldsymbol{\varsigma}}_{m-1} = f_{m-1}^{(1)} {\bf W}_{m}^T {\boldsymbol{\varsigma}}_{m}, \mathrm{\ \ } m = L, L-1,\ldots,2} berechnet werden, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\boldsymbol{\varsigma}}_{L} = {\bf F}_{L}^{(1)} \nabla_{{\bf \hat{y}}}L_{CE}.}
Dies ist eine Rückwärtsberechnung (backward computation), die den „Fehler auf Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} “ von Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L} rekursiv bis zur Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} zurückpropagiert. Dies erklärt den Namen „Backpropagation-Algorithmus“ ("backpropagation algorithm").
Aufgrund der Rückwärtsrekursion erfordert jeder Schritt nur eine Matrixmultiplikation, was rechnerisch viel billiger ist als die Berechnung der Mengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\boldsymbol{\varsigma}}_{m}} basierend auf ihren Definitionen auf dem Vorwärtsweg.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Das Vanishing Gradient Problem
In FNNs, die Backpropagation-Algorithmus anwenden, wird erwartet, dass der „Fehler auf Layer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle m} “ in vielen Fällen mit zunehmender Anzahl von Layer abnimmt. Dies führt dazu, dass sich der Trainingsprozess verlangsamt, im schlimmsten Fall verhindert es das weitere Training des neuronalen Netzwerks. Dieses Problem wird als „Vanishing Gradient Problem“ bezeichnet. Das Problem wurde 1991 in Hochreiters Diplomarbeit [Hochreiter(1991)] identifiziert.
Eine mögliche Ursache für dieses Problem ist, dass die Ableitung älterer Aktivierungsfunktionen im Bereich von [-1,+1] fallen. Im Backpropagation-Algorithmus der Gradient ist proportional mit dem Produkt von so vielen solcher Ableitungen, wie die Anzahl der Layer. Daher nimmt der Gradient des Loss mit der Anzahl der Layer exponentiell ab, was dazu führt, dass das Training der ersten Layer sehr langsam wird.
Wenn die Ableitungen der verwendeten Aktivierungsfunktionen größer als eins sein können, besteht die Gefahr, dass der Gradient unkontrolliert wächst, was zu einem verwandten Problem namens „Exploding Gradient Problem“ führt.
Sowohl das „Vanishing Gradient Problem“ als auch das „Exploding Gradient Problem“ können auch beim Recurrent Neuronal Network auftreten (siehe Unterabschnitt 4.4), da ihr Training auf entsprechenden tiefen FNNS durchgeführt wird, die durch Entrollen des ursprünglichen Recurrent Neuronal Network entworfen werden kann.
Das „Vanishing Gradient Problem“ tritt typischerweise in neuronalen Netzen mit einer Anzahl von Layer in der Größenordnung von 100 auf. Eine mögliche Lösung besteht darin, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ReLU(z)} als Aktivierungsfunktion zu verwenden, da sie nur auf der linken Seite einen kleinen Gradienten aufweist, während ihr Gradient auf der rechten Seite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle +1} beträgt. Eine andere Lösung besteht darin, eine ordnungsgemäße Gewichtsinitialisierung anzuwenden, die zu einem nicht verschwindenden Gradienten führt. Weitere Lösungsmöglichkeiten befinden sich unter Vanishing_gradient_problem.