Verschiedene Techniken für maschinelles Lernen und Deep Learning

Verschiedene Techniken für maschinelles Lernen und Deep Learning

Support-Vektor-Maschinen

Support-Vektor-Maschinen (support vector machines - SVMs) sind moderne Klassifikatoren. In ihrer ursprünglichen Form können sie auf die Klassifizierung mit zwei Klassen angewendet werden (binären Klassifikator - binary classifier). Die gute Klassifizierungsfähigkeit von SVMs basiert auf der Idee, dass eine Erhöhung der Dimensionalität der Eingabedaten eine bessere Trennbarkeit der Klassen ermöglicht. Je höher die Dimension der Projektion der Eingabedaten, desto größer ist die Wahrscheinlichkeit einer besseren Trennfähigkeit der entsprechenden Hyperebenen. Der Name SVM kommt von den Support-Vektoren, den Feature Vektoren des Trainingssatzes, die am Rand der Klassen im hochdimensionalen Raum liegen. Es stellt sich heraus, dass sie die optimale Entscheidungsfläche vollständig bestimmen.

SVMs werden für verschiedene reale Probleme eingesetzt, darunter unter anderem die Erkennung handschriftlicher Zeichen (hand-written character recognition), die Bildklassifizierung, die Klassifizierung von Satellitendaten (satellite data classification) und Klassifizierungsaufgaben in den Biowissenschaften (classification tasks in biological sciences).

Lineare SVM mit linear trennbaren Klassen

Eine SVM ist linear, wenn ihre Entscheidungsfläche im Raum der Eingabevektoren linear ist, also eine Hyperebene ist. Angenommen, der Eingabedaten ist durch die ${\textstyle L}$-dimensionalen Vektoren ${\textstyle {\bf {x}}_{1},\ldots ,{\bf {x}}_{N}}$ und ihre entsprechenden Klassenbezeichnungen ${\textstyle y_{1},\ldots ,y_{N}}$ gegeben. Die beste Trennfähigkeit kann durch ${\textstyle L-1}$-dimensionale Hyperebenen erreicht werden. Die Klassen sind linear trennbar, wenn zwischen den Klassen Hyperebenen liegen. In diesem Unterabschnitt diskutieren wir lineare SVM mit linear trennbaren Klassen.

${\textstyle \mathrm {\ \ \ \ } }$ Optimale Hyperebene als Entscheidungsflächen

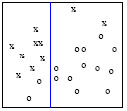
Im Allgemeinen gibt es bei linear trennbaren Klassen viele Hyperebenen, die die Klassen trennen können. Ihre Trennfähigkeit hängt jedoch von ihrer Positionierung zu den Klassen der Eingabedaten ab, siehe Abbildung 26.

Abbildung 26: Abhängigkeit der Trennfähigkeit von Hyperebenen von ihrer Position zu den Klassen der Eingabedaten (Quelle: Wikipedia_SVM).

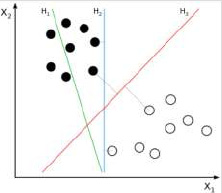
Intuitiv ergibt die Hyperebene mit dem größten Abstand zu den Klassen die größte Trennungsfähigkeit. Der Abstand einer Hyperebene zu den Klassen entspricht dem Abstand zu ihren nächstgelegenen Punkten. Die Summe der Abstände von einer Hyperebene zu den Klassen wird als Margin bezeichnet. Z. B. in Abbildung 26 H1 trennt die Klassen gar nicht. H2 und H3 schon, aber H2 nur mit einer kleinen Margin. H3 ist die Hyperebene, die die Klassen mit der maximalen Margin trennt.

Tatsächlich kann gezeigt werden, dass die Hyperebene mit dem größten Margin als Entscheidungsfläche die optimale ist, in dem Sinne, dass sie bei der Klassifizierung den geringeren Generalisierungsfehler verursacht. Die optimale Hyperebene wird als Hyperebene mit maximalem Margin bezeichnet.

${\textstyle \mathrm {\ \ \ \ } }$ Optimierungsaufgabe zum Finden der Maximum-Margin Hyperebene

Jede Hyperebene kann durch eine lineare Gleichung in Normalform beschrieben werden als

$${\bf {w}}^{T}{\bf {x}}+c=0.$$

Hier ist ${\textstyle {\bf {w}}}$ ein ${\textstyle N}$-dimensionaler Normalenvektor, d. h. er ist rechtwinklig zur Hyperebene und die Konstante ${\textstyle c}$ hängt von der Größe von ${\textstyle {\bf {w}}}$ ab (Multiplikation der obigen Gleichung mit einer beliebigen Konstante ${\textstyle k}$ bleibt die Richtung von ${\textstyle {\bf {w}}}$ gleich, aber sowohl seine Größe als auch ${\textstyle c}$ ändern sich). Die Projektion eines beliebigen Punktes ${\textstyle {\bf {x}}}$ als Vektor auf die Richtung von ${\textstyle {\bf {w}}}$ ist ${\textstyle {\frac {{\bf {w}}^{T}{\bf {x}}}{\lVert {\bf {w}}\rVert }}}$. Andererseits impliziert die Gleichung der Hyperebene, dass für jeden auf der Hyperebene liegenden Punkt ${\textstyle {\bf {w}}^{T}{\bf {x}}=-c}$ gilt. Somit ist die Projektion eines beliebigen Punktes ${\textstyle {\bf {x}}}$, der auf der Hyperebene liegt, als Vektor auf die Richtung von ${\textstyle {\bf {w}}}$ kann durch

$${\frac {-c}{\lVert {\bf {w}}\rVert }}$$

gegeben werden. Wählen wir die Konstante ${\textstyle c}$ in den Gleichungen der an den Klassengrenzen liegenden Hyperebenen als ${\textstyle b-1}$ und ${\textstyle b+1}$, was für diese Hyperebenen zu den Gleichungen als

$${\begin{aligned}&{\bf {w}}^{T}{\bf {x}}+b=1,\\&{\bf {w}}^{T}{\bf {x}}+b=-1\end{aligned}}$$

führt. Dann entspricht der Margin für eine Hyperebene, die auf halber Strecke zwischen den oben genannten Hyperebenen liegt, ${\textstyle \rho ({\bf {w}},b)}$ dem Abstand zwischen diesen Hyperebenen. Der kann als Differenz der Projektionen jedes auf diesen Hyperebenen liegenden Punktes auf ihren Normalenvektor berechnet werden, der durch

$$\rho ({\bf {w}},b)={\frac {(1-b)}{\lVert {\bf {w}}\rVert }}-{\frac {(-b-1)}{\lVert {\bf {w}}\rVert }}={\frac {2}{\lVert {\bf {w}}\rVert }}$$

gegeben ist.

Daraus folgt, dass die Maximierung der Margin gleichwertig mit der Minimierung von ${\textstyle \lVert {\bf {w}}\rVert ^{2}}$ ist.

Somit beträgt der Abstand zwischen der Hyperebene, die auf halbem Weg zwischen den obigen Hyperebenen liegt, und einer von ihnen ${\textstyle {\frac {1}{\lVert {\bf {w}}\rVert }}}$, was impliziert, dass für die Gleichung der Hyperebene, die auf halbem Weg zwischen die obigen Hyperebenen liegt, ${\textstyle {\frac {(1-b)}{\lVert {\bf {w}}\rVert }}-{\frac {(-c)}{\lVert {\bf {w}}\rVert }}={\frac {1}{\lVert {\bf {w}}\rVert }}}$ gilt, woraus ${\textstyle c=b}$ und somit ist diese Gleichung durch

$${\bf {w}}^{T}{\bf {x}}+b=0$$

gegeben. Diese Hyperebenen und die oben genannten Abstände sind in Abbildung 27 dargestellt.

Abbildung 27: Hyperebene, die auf halber Strecke zwischen den Klassen liegt, deren Abstände und Margin (Quelle: Wikipedia_SVM).

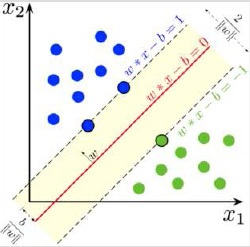
Wählen wir die Bezeichnungen ${\textstyle y_{i}=1}$ und ${\textstyle y_{i}=-1}$ für die erste bzw. zweite Klasse. Dann erfüllen alle Vektoren der Eingabedaten, die zur ersten und zweiten Klasse gehören, jeweils die Ungleichungen

$${\begin{aligned}&{\bf {w}}^{T}{\bf {x}}_{i}+b\geq 1,\mathrm {~wenn~} y_{i}=1\mathrm {~and~} \\&{\bf {w}}^{T}{\bf {x}}_{i}+b\leq -1.\mathrm {~wenn~} y_{i}=-1.\end{aligned}}$$

Diese beiden Ungleichungen können in einer äquivalenten kompakten Form als

$$y_{i}({\bf {w}}^{T}{\bf {x}}_{i}+b)\geq 1$$

geschrieben werden. Wenn man all dies zusammenfügt, ergibt sich die Optimierungsaufgabe mit Nebenbedingungen (constrained optimization task) zum Finden der Maximum-Margin Hyperebene als

$${\begin{aligned}&({\bf {w}},b)=\arg \min _{{\bf {w}},b}\lVert {\bf {w}}\rVert ^{2},~\mathrm {~unter~den~Bedingungen~} ~\\&y_{i}({\bf {w}}^{T}{\bf {x}}_{i}+b)\geq 1,~~i=1,\ldots ,N.\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ } }$ Quadratisches Programm (quadratic programming problem) für die Lagrange-Multiplikatoren

Um das Optimierungsproblem mit Nebenbedingungen zu lösen, die Lagrange-Funktion wird konstruiert als

$$L({\bf {w}},b,{\boldsymbol {\Lambda }})={\frac {1}{2}}{\bf {w}}^{T}{\bf {w}}-\sum _{i=1}^{N}\lambda _{i}\left(y_{i}({\bf {w}}^{T}{\bf {x}}_{i}+b)-1\right),$$

wobei die Elemente von ${\textstyle {\boldsymbol {\Lambda }}^{T}=(\lambda _{1},\ldots ,\lambda _{N})}$ aufgrund der Nebenbedingungen die nicht negativen Lagrange-Multiplikatoren sind. Berechnen die ersten Ableitungen nach ${\textstyle {\bf {w}}}$ und ${\textstyle b}$ bei Minimum ${\textstyle {\bf {w}}^{*}}$ und ${\textstyle b^{*}}$ ergibt

$$\left.{\frac {\partial L({\bf {w}},b,{\boldsymbol {\Lambda }})}{\partial {\bf {w}}}}\right|_{{\bf {w}}={\bf {w}}^{*}}=\left({\bf {w}}^{*}-\sum _{i=1}^{N}\lambda _{i}y_{i}{\bf {x}}_{i}\right)=0,$$

und

$$\left.{\frac {\partial L({\bf {w}},b,{\boldsymbol {\Lambda }})}{\partial b}}\right|_{b=b^{*}}=\sum _{i=1}^{N}\lambda _{i}y_{i}=0.$$

Wenn man sie in die Lagrange-Funktion bei ${\textstyle {\bf {w}}={\bf {w}}^{*}}$ und ${\textstyle b=b^{*}}$ einsetzt, erhält man

$${\begin{aligned}L({\bf {w}}^{*},b^{*},{\boldsymbol {\Lambda }})&={\frac {1}{2}}{{\bf {w}}^{*}}^{T}{\bf {w}}^{*}-\sum _{i=1}^{N}\lambda _{i}y_{i}{{\bf {w}}^{*}}^{T}{\bf {x}}_{i}-\sum _{i=1}^{N}\lambda _{i}y_{i}b^{*}+\sum _{i=1}^{N}\lambda _{i}\\&={\frac {1}{2}}{{\bf {w}}^{*}}^{T}{\bf {w}}^{*}-{{\bf {w}}^{*}}^{T}{\bf {w}}^{*}+\sum _{i=1}^{N}\lambda _{i}\\&=\sum _{i=1}^{N}\lambda _{i}-{\frac {1}{2}}{{\bf {w}}^{*}}^{T}{\bf {w}}^{*}\\&=\sum _{i=1}^{N}\lambda _{i}-{\frac {1}{2}}\sum _{i=1}^{N}\sum _{j=1}^{N}\lambda _{i}\lambda _{j}y_{i}y_{j}{\bf {x}}_{i}{\bf {x}}_{j}.\end{aligned}}$$

Einführung des Label Vektors ${\textstyle {\bf {y}}}$ und der symmetrischen Matrix ${\textstyle N\times N}$ ${\textstyle {\bf {D}}}$ als

$${\begin{aligned}&{\bf {y}}^{T}=(y_{1},\ldots ,y_{N}),\\&{\bf {D}}=[{\bf {D}}_{ij}]=[y_{i}y_{j}{\bf {x}}_{i}{\bf {x}}_{j}]\end{aligned}}$$

ermöglicht die Erstellung eines quadratischen Programms in Vektor-Matrix-Notation für die Lagrange-Multiplikatoren as

$${\begin{aligned}&\arg \max _{\boldsymbol {\Lambda }}L({\boldsymbol {\Lambda }})=\arg \max _{\boldsymbol {\Lambda }}{\boldsymbol {\Lambda }}^{T}{\bf {e}}-{\frac {1}{2}}{\boldsymbol {\Lambda }}^{T}{\bf {D}}{\boldsymbol {\Lambda }},~\mathrm {~unter~den~Bedingungen~} ~\\&{\boldsymbol {\Lambda }}^{T}{\bf {y}}=0,~\mathrm {~fuer~} ~{\boldsymbol {\Lambda }}\geq {\bf {0}},\end{aligned}}$$

wobei ${\textstyle {\bf {e}}}$ für den ${\textstyle N}$-dimensionalen Einheitsvektor steht.

Bemerkung 1. Die Nebenbedingung ${\textstyle {\boldsymbol {\Lambda }}^{T}{\bf {y}}=0}$ ist dieselbe wie die partielle Ableitung der Lagrange-Funktion nach ${\textstyle b}$ in Vektorform. Die andere partielle Ableitung und die ursprünglichen Nebenbedingungen sind hier nicht notwendig, da die Zielfunktion im obigen quadratischen Programmierproblem nicht von ${\textstyle {\bf {w}}}$ abhängt.

${\textstyle \mathrm {\ \ \ \ } }$ Die Eigenschaften der optimalen Hyperebene

Nach dem Kuhn-Tucker-Theorem

$${\begin{aligned}\lambda _{i}^{*}\left(y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})\right)=0,~~i=1,\ldots ,N\end{aligned}}$$

gilt für die optimalen Parameter der Lagrange-Funktion. Daraus folgt, dass ${\textstyle \lambda _{i}^{*}\neq 0}$ nur für die Fälle gilt, in denen die Ungleichung-Constraint zu einer Gleichheit wird, d. h. wenn

$${\begin{aligned}y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})-1=0~\Leftrightarrow ~y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})=1\end{aligned}}$$

gilt. Die Vektoren ${\textstyle {\bf {x}}_{i}}$ der Eingabedaten, die die obige Gleichheit erfüllen, werden Support-Vektoren genannt. Dies sind die Vektoren, die zu den an den Klassengrenzen liegenden Hyperebenen passen.

Für die optimale Hyperebene gelten folgende Eigenschaften:

• P.1 Der Parametervektor ${\textstyle {\bf {w}}^{*}}$ der optimalen Hyperebene kann als lineare Kombination der Support-Vektoren als
  $${\bf {w}}^{*}=\sum _{i=1}^{N}\lambda _{i}^{*}y_{i}{\bf {x}}_{i}.$$
  ausgedrückt werden.
• P.2 Die Support-Vektoren bestimmen vollständig die optimale Hyperebene, also sowohl ${\textstyle {\bf {w}}^{*}}$ als auch ${\textstyle b^{*}}$.
• P.3 Zwischen dem Wert der Lagrange-Funktion im Optimum und dem Margin für die optimale Hyperebene, ${\textstyle \rho ^{*}}$ gilt die Relation,
  $$L({\bf {w}}^{*},b^{*},{\boldsymbol {\Lambda }}^{*})={\frac {2}{{\rho ^{*}}^{2}}}.$$

Die Gleichung von P.1 kann durch Umstellen der Gleichung erhalten werden, die als erste Ableitung der Lagrange-Funktion nach ${\textstyle {\bf {w}}}$ erhalten wurde. Die ${\textstyle {\bf {x}}_{i}}$-s für jedes ${\textstyle \lambda _{i}^{*}\neq 0}$ erfüllen die Gleichheit ${\textstyle y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})=1}$ und somit sind sie Support-Vektoren. Daher wird ${\textstyle {\bf {w}}^{*}}$ in der Expression in P.1 als Linearkombination der Support-Vektoren angegeben. Dies legt nahe, dass nur diese Vektoren des Eingabedaten einen effektiven Beitrag zum Parametervektor ${\textstyle {\bf {w}}^{*}}$ leisten, was den Namen „Support-Vektor“ erklärt.

Nachdem ${\textstyle {\bf {w}}^{*}}$ bestimmt wurde, kann ${\textstyle b^{*}}$ durch Einsetzen eines beliebigen Support-Vektoren in die Gleichung ${\textstyle y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})=1}$ berechnet werden. Damit ist P.2 gezeigt.

Um P.3 zu zeigen, stellen wir eine Beziehung zwischen ${\textstyle {{\bf {w}}^{*}}^{T}{\bf {w}}^{*}}$ und ${\textstyle \sum _{i=1}^{N}\lambda _{i}^{*}}$ her als

$${{\bf {w}}^{*}}^{T}{\bf {w}}^{*}=\sum _{i=1}^{N}\lambda _{i}^{*}y_{i}{{\bf {w}}^{*}}^{T}{\bf {x}}_{i}=\sum _{i=1}^{N}\lambda _{i}^{*}(1-y_{i}b^{*})=\sum _{i=1}^{N}\lambda _{i}^{*},$$

wobei P.1, die Gleichheit ${\textstyle y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})=1}$ für die Support-Vektoren und die Beziehung ${\textstyle \sum _{i=1}^{N}\lambda _{i}y_{i}=0}$ bei ${\textstyle \lambda _{i}=\lambda _{i}^{*}}$ verwendet wurden. Die Anwendung dieser Beziehung auf die Lagrange-Funktion im Optimum führt zu

$$L({\bf {w}}^{*},b^{*},{\boldsymbol {\Lambda }}^{*})=\sum _{i=1}^{N}\lambda _{i}^{*}-{\frac {1}{2}}{{\bf {w}}^{*}}^{T}{\bf {w}}^{*}={\frac {1}{2}}{{\bf {w}}^{*}}^{T}{\bf {w}}^{*}$$

Kombiniert man es mit dem Ausdruck der Margin ${\textstyle \rho ({\bf {w}},b)={\frac {2}{\lVert {\bf {w}}\rVert }}}$ bei ${\textstyle {\bf {w}}={\bf {w}}^{*}}$ und ${\textstyle b=b^{*}}$ ergibt

$${\rho ^{*}}^{2}={\frac {4}{2L({\bf {w}}^{*},b^{*},{\boldsymbol {\Lambda }}^{*})}}={\frac {2}{L({\bf {w}}^{*},b^{*},{\boldsymbol {\Lambda }}^{*})}},$$

woraus P.3 direkt folgt.

${\textstyle \mathrm {\ \ \ \ } }$ Optimaler Hyperebenen-Algorithmus

Basierend auf den obigen Unterkapiteln kann ein Algorithmus zur Bestimmung des linearen SVM-Klassifikators mit linear trennbaren Klassen erstellt werden, d. h. um die Parameter ${\textstyle {\bf {w}}}$ und ${\textstyle b}$ zu berechnen. Dieser optimale Hyperebenen-Algorithmus besteht aus den folgenden Schritten:

1. Berechnen das optimale ${\textstyle {{\boldsymbol {\Lambda }}^{*}}^{T}=(\lambda _{1}^{*},\ldots ,\lambda _{N}^{*})}$, durch Löung des quadratischen Programms
   $${\begin{aligned}&\arg \max _{\boldsymbol {\Lambda }}L({\boldsymbol {\Lambda }})=\arg \max _{\boldsymbol {\Lambda }}{\boldsymbol {\Lambda }}^{T}{\bf {e}}-{\frac {1}{2}}{\boldsymbol {\Lambda }}^{T}{\bf {D}}{\boldsymbol {\Lambda }},~\mathrm {~unter~den~Bedingungen~} ~\\&{\boldsymbol {\Lambda }}^{T}{\bf {y}}=0,~\mathrm {~fuer~} ~{\boldsymbol {\Lambda }}\geq {\bf {0}},\end{aligned}}$$
2. Berechnen die optimalen Parametergewichte ${\textstyle {\bf {w}}^{*}}$ basierend auf der Eigenschaft P.1, d. h. aus ${\textstyle \lambda _{i}}$-s und aus den Support-Vektoren unter Verwendung der Gleichung
   $${\bf {w}}^{*}=\sum _{i=1}^{N}\lambda _{i}^{*}y_{i}{\bf {x}}_{i}.$$
3. Berechnen den Parameter ${\textstyle b^{*}}$, indem einen Support-Vektor in die Gleichung ${\textstyle y_{i}({{\bf {w}}^{*}}^{T}{\bf {x}}_{i}+b^{*})=1}$ eingesetzt wird.

Lineare SVM mit linear nicht trennbaren Klassen

Wenn die Klassen linear nicht trennbar sind, gibt es keine Hyperebene, die alle Trainingsbeispiele korrekt trennen kann. In diesem Fall kann man nach der Hyperebene suchen, die die meisten Trainingsbeispiele trennen kann, d. h. was den geringsten Fehler bei der Trennung macht. Daher muss der Fehler bei der Trennung in die Formulierung der Optimierungsaufgabe zum Finden der optimalen Hyperebene einbezogen werden.

Abbildung 28: Hyperebene für linear nicht trennbare Klassen mit fehlerhaft getrennten Trainingsbeispielen (Quelle: cmu_edu).

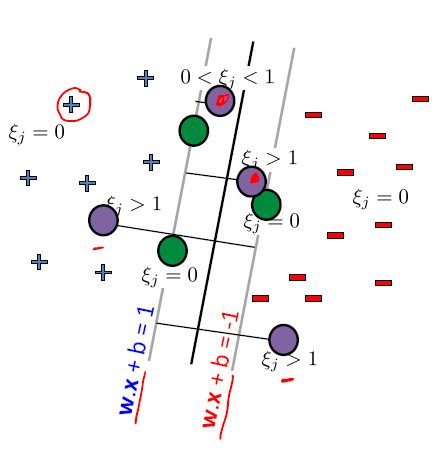
${\textstyle \mathrm {\ \ \ \ } }$ Optimierungsaufgabe zum Finden der optimalen Hyperebene

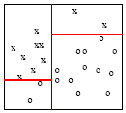
Sei ${\textstyle \xi _{i}}$ der Fehler des fälschlicherweise getrennten Trainingsbeispiels ${\textstyle {\bf {x}}_{i}}$, der im der ausgewählten Hyperebene zugeordneten Margin liegt, siehe Abbildung 28. Die Trainingsbeispiele mit ${\textstyle \xi _{i}=0}$ (grüne Kreise) sind Support-Vektoren. Die Trainingsbeispiele mit ${\textstyle 0<\xi _{i}<1}$ (lila Kreise) sind richtig klassifiziert, liegen aber innerhalb des Margins. Die Trainingsbeispiele mit ${\textstyle 1<\xi _{i}}$ (lila Kreise) sind falsch klassifiziert. Die zuvor für die linear separierbaren Klassen festgelegte Nebenbedingungen müssen geändert werden, da die fehlerhaft separierten Trainingsbeispiele innerhalb des Margins liegen. Die richtige Nebenbedingung, die den Fehler des fälschlicherweise getrennten Trainingsbeispiele berücksichtigt, kann wie folgt formuliert werden:

$$y_{i}({\bf {w}}^{T}{\bf {x}}_{i}+b)\geq 1-\xi _{i},~~\mathrm {~wobeie~} ~~\xi _{i}\geq 0,~~i=1,\ldots ,N.$$

Jetzt wollen wir nicht nur ${\textstyle \lVert {\bf {w}}\rVert ^{2}}$ sondern auch den Gesamtfehler bei der Trennung minimieren, um einen großen Margin zu haben. Hier den Gesamtfehler kann als

$$\sum _{i=1}^{N}\xi _{i}$$

ausgedrückt werden.

Je kleiner der Wert ${\textstyle \lVert {\bf {w}}\rVert ^{2}}$, desto größer der Margin, was zu einem größeren Gesamtfehler bei der Trennung führt. Somit stehen der Wert ${\textstyle \lVert {\bf {w}}\rVert ^{2}}$ und der Gesamtfehler bei der Trennung im Kompromiss zueinander. Daher ist die Optimierungsaufgabe mit Nebenbedingungen zum Finden der optimalen Hyperebene für linear nicht trennbare Klassen wird durch

$${\begin{aligned}&({\bf {w}},b)=\arg \min _{{\bf {w}},b}{\frac {1}{2}}\lVert {\bf {w}}\rVert ^{2}+G\sum _{i=1}^{N}\xi _{i},~\mathrm {~unter~den~Bedingungen~} ~\\&y_{i}({\bf {w}}^{T}{\bf {x}}_{i}+b)\geq 1-\xi _{i},~~\mathrm {~und~} ~~\xi _{i}\geq 0,~~i=1,\ldots ,N\end{aligned}}$$

gegeben, wobei ${\textstyle G}$ eine Konstante ist, die die Gewichtung der beiden zu minimierenden Ziele festlegt. Die optimale Hyperebene wird Soft-Margin-Hyperebene genannt. Der Name kommt von der Art dieses Margin, der das Überhängen mehrerer Trainingsbeispiele ermöglicht. Es kann gezeigt werden, dass alle Eigenschaften P.1 - P.3 auch für diesen nicht trennbaren Fall gelten.

Bemerkung 2. Wenn diese Optimierung mit einem hohen Wert von ${\textstyle G}$ angewendet wird, dann verhält sie sich ähnlich wie die Optimierung für trennbare Klassen.

SVM mit nichtlinearem Kernel

Im Fall linear nicht trennbarer Klassen kann eine bessere Trennbarkeit durch die Verwendung einer nichtlinearen Entscheidungsfläche anstelle einer Hyperebene erreicht werden. Dies wird in Abbildung 29 veranschaulicht.

Abbildung 29: Nichtlineare Entscheidungsfläche für nicht trennbare Klassen (Quelle: Wikipedia_SVM).

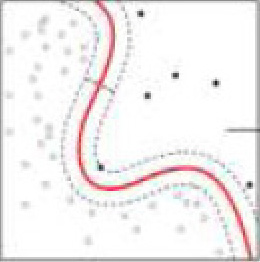
${\textstyle \mathrm {\ \ \ \ } }$ Die Idee der nichtlinearen SVM

Aus diesem Grund wird die Theorie der Support Vector Machine auf nichtlineare Entscheidungsflächen erweitert. Die Idee dieser Erweiterung besteht darin, die Eingabevektoren ${\textstyle {\bf {x}}_{i}}$ in ${\textstyle M}$-dimensionale Vektoren umzuwandeln, indem eine ${\textstyle M}$-dimensionale Vektorfunktion ${\textstyle \phi ()}$ auf sie angewendet und dann eine optimale Hyperebene im ${\textstyle M}$-dimensionalen Raum der transformierten Vektoren konstruiert wird. Durch richtig ausgewählte Vektorfunktion ${\textstyle \phi ()}$ werden die transformierten Klassen im ${\textstyle M}$-dimensionalen Raum wieder durch eine optimale Hyperebene linear trennbar ! Dies ist in Abbildung 30 illustriert.

Abbildung 30: Nichtlineare Entscheidungsfläche für nicht trennbare Klassen (Quelle: Wikipedia_SVM).

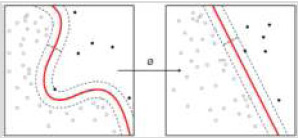
Dann ist die potentielle Entscheidungsgrenze eine ${\textstyle M}$-dimensionale Hyperebene für die transformierten Vektoren ${\textstyle {\boldsymbol {\phi }}({\bf {x}}_{i})=(\phi _{1}({\bf {x}}_{i}),\ldots ,\phi _{M}({\bf {x}}_{i})}$, für ${\textstyle i=1,\ldots ,N}$ mit den Parametern ${\textstyle {\bf {w}}}$ und ${\textstyle b}$, welche die Form

$$f({\bf {x}})={\bf {w}}^{T}{\boldsymbol {\phi }}({\bf {x}})+b$$

hat.

Unter Anwendung der Eigenschaft P.1 der Soft-Margin-Hyperebene im ${\textstyle M}$-dimensionalen Raum der transformierten Vektoren kann der optimale Parametervektor ${\textstyle {\bf {w}}^{*}}$ als Linearkombination von der Support-Vektoren im transformierten Raum als

$${\bf {w}}^{*}=\sum _{i=1}^{N}\lambda _{i}^{*}y_{i}{\boldsymbol {\phi }}({\bf {x}}_{i})$$

bestimmt werden. Wenn man es in die Expression der Entscheidungsgrenze einsetzt, kann man die Entscheidungsfläche ${\textstyle f^{*}({\bf {x}})}$ als

$$f^{*}({\bf {x}})=\sum _{i=1}^{N}\lambda _{i}^{*}y_{i}{\boldsymbol {\phi }}({\bf {x}})^{T}{\boldsymbol {\phi }}({\bf {x}}_{i})+b^{*}.$$

ausdrücken.

${\textstyle \mathrm {\ \ \ \ } }$ Der Kernel-Trick

Das einzige Rechenproblem besteht darin, potenzielle hochdimensionale Räume zu behandeln, die in ${\textstyle {\boldsymbol {\phi }}({\bf {x}})}$ für große Werte von ${\textstyle M}$ entstehen. Tatsächlich ist es jedoch nicht erforderlich. Die Entscheidungsfunktion (decision function) ${\textstyle f^{*}({\bf {x}})}$ hängt nur vom Skalarprodukt ${\textstyle {\boldsymbol {\phi }}({\bf {x}})^{T}{\boldsymbol {\phi }}({\bf {x}}_{i})}$ und nicht von den einzelnen Vektoren ${\textstyle {\boldsymbol {\phi }}({\bf {x}})}$ und ${\textstyle {\boldsymbol {\phi }}({\bf {x}}_{i})}$ ab. Unter bestimmten Bedingungen gibt es Funktionen K(u, v), die wie folgt faktorisiert werden können.

$$K({\bf {u}},{\bf {v}})={\boldsymbol {\phi }}({\bf {u}}){\boldsymbol {\phi }}({\bf {v}}).$$

Mit einer solchen Funktion ${\textstyle K({\bf {u}},{\bf {v}})}$ kann die Entscheidungsgrenze ${\textstyle f^{*}({\bf {x}})}$ in der Form

$$f^{*}({\bf {x}})=\sum _{i=1}^{N}\lambda _{i}^{*}y_{i}K({\bf {x}},{\bf {x}}_{i})+b^{*}$$

geschrieben werden. Die Funktion ${\textstyle K({\bf {u}},{\bf {v}})}$ eine Skalarfunktion ist. Dies bedeutet, dass es ausreicht, statt potenziell hochdimensionalen Vektorfunktionen ${\textstyle {\boldsymbol {\phi }}}$ zunächst einen von interner Form von ${\textstyle K(,)}$ abhängigen Operator, wie z.B. Skalarprodukt oder eine beliebige Distanz, auf die Vektoren ${\textstyle {\bf {x}}}$, ${\textstyle {\bf {x}}_{i}}$ anzuwenden, und das Ergebnis dann in die Skalarfunktion ${\textstyle K()}$ einzusetzen, die dann rechnerisch leicht berechenbar ist.

Die Funktion ${\textstyle K({\bf {u}},{\bf {v}})}$ wird Kernel genannt und die Idee, sie zu verwenden, anstatt die Vektorenfunktion ${\textstyle {\boldsymbol {\phi }}()}$ zu behandeln, was die Berechnung leicht berechenbar macht, nennt man Kernel-Trick. Maschinen, die den Kernel-Trick anwenden, werden Kernel-Maschinen benannt.

${\textstyle \mathrm {\ \ \ \ } }$ Eigenschaften von SVM mit nichtlinearem Kernel

Die Hauptmerkmale von SVM mit nichtlinearem Kernel kann wie folgt zusammengefasst werden.

1. Seine Entscheidungsfunktion ${\textstyle f^{*}({\bf {x}})}$ kann mit der Hilfe Kernel ${\textstyle K({\bf {x}},{\bf {x}}_{i})}$ ausgedrückt werden.
2. Seine Entscheidungsfunktion ist nichtlinear im Raum des Eingabevektors.
3. Der nichtlinear transformierte Vektorraum kann hochdimensional sein.
4. Die nichtlineare Entscheidungsfläche ist eine Soft-Margin-Hyperebene im transformierten Vektorraum.
5. Die Entscheidungsfläche wird mit dem Soft-Margin-Hyperplane-Algorithmus berechnet, mit der einzigen Unterschied zur Einstellung der Matrix ${\textstyle {\bf {D}}}$ als
   $${\bf {D}}=[{\bf {D}}_{ij}]=[y_{i}y_{j}K({\bf {x}}_{i},{\bf {x}}_{j})].$$

${\textstyle \mathrm {\ \ \ \ } }$ Ausgewählte nichtlineare Kernel

Nachfolgend sind einige häufig verwendete nichtlineare Kernel aufgeführt.

• Polynomkernel – für Klassifikator vom Grad ${\textstyle d}$
  $$K({\bf {u}},{\bf {v}})=({\bf {u}}{\bf {v}}+a)^{d}$$
  Für ${\textstyle a=0}$ und ${\textstyle d=1}$ wird es zum linearen Kernel.
• Potentialfunktion
  $$K({\bf {u}},{\bf {v}})=exp\left(-{\frac {\lVert {\bf {u}}-{\bf {v}}\rVert )}{\sigma }}\right)$$
• Gaußsche Radialfunktion als Kernel (Gaussian radial function)
  $$K({\bf {u}},{\bf {v}})=exp\left(-{\frac {\lVert {\bf {u}}-{\bf {v}}\rVert ^{2})}{2\sigma ^{2}}}\right)$$
• Sigmoid- oder hyperbolische Tangensfunktion
  $$K({\bf {u}},{\bf {v}})=\tanh \left(\alpha {\bf {u}}{\bf {v}}+\beta \right),\mathrm {~fuer~einige~} \alpha >0\mathrm {~und~} \beta <0$$

Erweiterungen

SVM verfügt über mehrere Erweiterungen. Nachfolgend befindet sich eine kurze Zusammenfassung der wichtigsten von denen.

• Multiklassen-SVM. Multiclass SVM ist ein Klassifikator, der für mehr als zwei Klassen entwickelt wurde. Der vorherrschende Realisierungsansatz führt auf Klassifikatoren mit zwei Klassen zurück. Eine dieser Methoden ist die Eins-gegen-Alle-Methode (one-versus-all), bei der für jede Klasse ein Klassifikator angewendet wird, um sie vom Rest zu trennen, und der Klassifikator mit der höchsten Ausgabe gewinnt.
• Transduktive SVM. Transduktive SVM realisiert halbüberwachtes Lernen. Neben dem beschrifteten Trainingdaten wird ein unbeschriftet Daten von Vektoren ${\textstyle {\bf {x}}_{j}^{'}}$, ${\textstyle j=1,\ldots ,U}$ bereitgestellt. Die Optimierungsaufgabe wird modifiziert, indem neben den Parametern ${\textstyle {\bf {w}}}$ und ${\textstyle b}$ auch nach den vorherzusagenden Labels ${\textstyle y_{j}^{'}}$ gesucht wird und die Nebenbedingungen durch ${\textstyle y_{i}^{'}({\bf {w}}^{T}{\bf {x}}_{i}+b)\geq 1}$ und ${\textstyle y_{i}^{'}\in {-1,1}}$ ergänzt werden.
• Support-Vektor-Clustering (SVC). SVC ist eine Maschine, die unüberwachtes Lernen realisiert.
• Strukturierte SVM (structured SVM). Strukturierte SVM ist eine Verallgemeinerung von SVM, die strukturierte und unendlich viele Labels ermöglicht.
• Support-Vector-Regression (SVR). SVR basiert auf der an die Regression angepassten SVM-Theorie. Jetzt ist ${\textstyle {\bf {w}}^{T}{\bf {x}}_{i}+b}$ der vorhergesagte Wert und ${\textstyle y_{i}}$ die richtige Ausgabe, wobei beide stetige Werte annehmen. Dann wird die Regression durch die Optimierungsaufgabe mit der Nebenbedingung ${\textstyle |y_{i}-({\bf {w}}^{T}{\bf {x}}_{i}+b)|\leq \epsilon }$ bestimmt, wobei ${\textstyle \epsilon }$ ein freier Schwellenwert für Fehler (error threshold) ist.

${\textstyle \mathrm {\ \ \ \ } }$ Implementierung

Normalerweise ist vor der Berechnung von SVM eine Vorverarbeitung der Trainingsdaten erforderlich. Zu den notwendigen Vorverarbeitungsschritten gehören:

• Skalierung mit Methoden wie Min-Max, Dezimalskalierung (decimal scaling) oder Z-Score.
• Mittelwertnormalisierung (mean normalization), d. h. Subtrahieren des Mittelwerts von den Vektoren.
• Varianznormalisierung (variance normalization), d. h. Division jeder Vektorkomponente durch ihre Varianz.

Kernel SVM ist in vielen ML Softwarepaketen implementiert, darunter unter anderem

• P-Pack SVM mit Subgradienten-Verfahren,
• MATLAB, SAS,
• LIBSVM, SVMlight,kernlab, JKernelMachines und
• scikit-learn Python-Bibliothek.

Entscheidungsbäume und Random Forests

Klassifikations- und Regressionsbäume (Classification and Regression Trees - CART) sind Entscheidungsbäume, die für Klassifikations- und Regressionsaufgaben verwendet werden können. In diesem Unterabschnitt diskutieren wir den Ansatz von Entscheidungsbäume für Klassifikationsaufgaben.

Klassifikationsbäume realisieren eine hierarchische Partitionierung des Raumes der Eingabevektoren. Die Eingabevektoren werden auch als Featurevektoren genannt, da jede einzelne Komponente der Eingabevektoren ein Merkmal (also Feature) darstellt. Die Partitionierung führt zu einzelnen disjunkten Bereichen des Raumes der Eingabevektoren, von denen jeder einer Klasse zugeordnet ist. Die Grundidee des Klassifikationsbaums ist also die Zuordnung disjunkter Bereiche des Raumes der Eingabevektoren zu Klassen, was sich wesentlich von den Ideen anderer Klassifikationsmethoden unterscheidet, wie z. B. neuronalen Netzen, die Diskriminanzfunktionen realisieren, oder Support Vector Machines, die Entscheidungsgrenzen als Hyperebene realisieren.

Ein medizinisches Beispiel

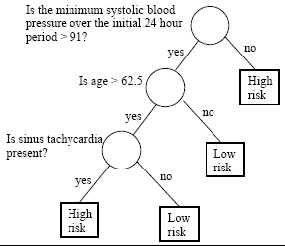
In einem medizinischen Beispiel werden die Patienten in Hochrisiko- und Niedrigrisiko-Patienten eingeteilt. Die Einteilung erfolgt durch Fragen an die Patienten. Die Fragen können in einem binären Baum organisiert werden, siehe Abbildung 31.

Abbildung 31: Ein medizinisches Beispiel für einen Klassifikationsbaum (Quelle: [CARTPennStateCourse(2024)]).

Jede Frage bezieht sich auf ein Merkmal (Feature), das eine Variable im Raum der Eingabevektoren darstellt. Solche Variablen sind systolischer Blutdruck, Alter und das Vorhandensein einer Sinustachykardie. Somit verwendet die Aufgabe einen dreidimensionalen Raum der Eingabevektoren, wobei zwei Dimensionen sind kontinuierlich, während die letzte diskret ist (kann nur den Wert logisch wahr oder falsch aufnehmen). Auf diese Weise entspricht jedes Blatt des Binärbaums einem disjunkten Bereich des Raums der Eingabevektoren.

Erstellen eines Entscheidungsbaums

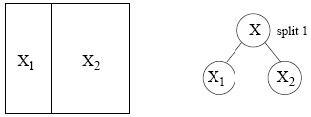
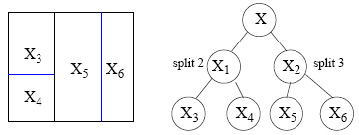
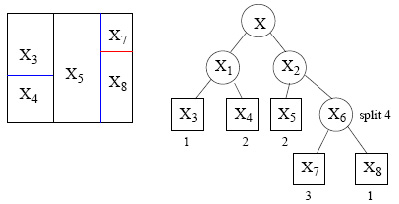
Der Entscheidungsbaum wird iterativ aufgebaut, wobei in jeder Iteration eine der resultierenden Regionen der vorherigen Iteration in zwei weitere disjunkte Regionen aufgeteilt wird. Jede Region wird normalerweise entlang einer Komponente des Eingabevektors aufgeteilt. Dies entspricht einer Frage wie „Ist ${\textstyle x_{j}\leq k}$, wobei die Aufteilung entlang der ${\textstyle j}$-ten Komponente der Eingabevektoren durchgeführt wird und ${\textstyle k}$ eine mögliche Position für die Aufteilung ist. Dies wird in Abbildung 32 veranschaulicht.

Abbildung 32: Veranschaulichung der iterativen Aufteilung des Raums der Eingabevektoren in jedem Schritt entlang einer Komponente des Eingabevektors (Quelle: [CARTPennStateCourse(2024)]).

Dabei ist ${\textstyle X}$ der gesamte Raum der Eingabevektoren und ${\textstyle X_{i}}$-s, ${\textstyle i=1,\ldots }$ stehen für die einzelnen Regionen des Raums der Eingabevektoren als Ergebnis der aktuellen Aufteilung. Aufgrund der binären Baumdarstellung wächst der Baum in jeder Iteration und jede Region kann auch als Knoten im binären Baum dargestellt werden.

Um den Entscheidungsbaum mittels der oben beschriebenen iterativen Aufteilung zu konstruieren, müssen die Teilaufgaben im Voraus festgelegt werden.

• Auswahl der nächsten Aufteilung (split), d. h. Entscheidung, welcher Knoten (d. h. Region) und wie aufgeteilt werden soll.
• Bereitstellung eines Abbruchkriteriums (stopping criterion) für das Wachstum des Baums.
• Zuweisen einer Klasse zu jedem Blatt des endgültigen Baums.

${\textstyle \mathrm {\ \ \ \ } }$ Auswahl der nächsten Aufteilung

Es besteht der Bedarf an einem Maß, mit deren Hilfe aus allen Kandidaten-Aufteilungen die nächstbeste Aufteilung ausgewählt werden kann. Jeder
Kandidaten-Aufteilung kann durch den aufzuteilenden Knoten ${\textstyle t}$ und eine Aufteilung ${\textstyle s}$ angegeben werden, der die für die Aufteilung zu verwendende Komponente des Eingabevektors und seine Position angibt.

Ein häufig verwendetes Maß zur Auswahl der nächstbesten Aufteilung ist das Maß „Goodness of split“ („Güte der Aufteilung“). Die "Goodness of split" einer Kandidaten-Aufteilung kann jedoch berechnet werden, indem die Impurity-Funktion (Unreinheitsfunktion) auf einige Knoten angewendet wird. Daher führen wir zunächst die Impurity-Funktion ein.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Die Impurity-Funktion

Intuitiv ist eine Region „rein“, wenn die meisten Punkte (d. h. Beispiele der Trainingsdaten) zur selben Klasse gehören. Dazu muss gemessen werden, wie unrein (impure) eine Region ist. Ein Beispiel zum Erstellen reiner Regionen in zwei Aufteilungsschritten ist in Abbildung 33 dargestellt.

Abbildung 33: Ein Beispiel zum Erstellen reiner Regionen in zwei Aufteilungsschritten (Quelle: [CARTPennStateCourse(2024)]).

Nach der ersten Aufteilung gehören nur zwei Punkte auf der linken Seite zur durch Kreise gekennzeichneten Klasse. Durch Anwenden der zweiten Teilung ist es möglich, einen Baum mit 100 % reinen Knoten zu erhalten. Man kann beobachten, dass nach jedem Aufteilungsschritt die Reinheit zunimmt oder gleichwertig die Impurity abnimmt.

Seien ${\textstyle p_{1},\ldots ,p_{C}}$ die Wahrscheinlichkeiten, dass ein markierter Datenpunkt in der Region zur Klasse ${\textstyle 1,\ldots ,C}$ gehört. Dann ist die Impurity-Funktion ${\textstyle \phi ()}$ auf ${\textstyle p_{1},\ldots ,p_{C}}$, ${\textstyle p_{c}\geq 0}$ für ${\textstyle c=1,\ldots ,C}$ und ${\textstyle \sum _{c=1}^{C}p_{c}=1}$ durch ihre folgenden Eigenschaften definiert:

1. Die Funktion ${\textstyle \phi ()}$ hat ein Maximum nur bei gleichmäßig verteilten ${\textstyle p_{c}}$-s, d. h. wenn alle ${\textstyle p_{c}}$-s gleich sind.
2. Die Funktion ${\textstyle \phi ()}$ hat ein Minimum an Punkten, wenn einer der ${\textstyle p_{c}}$-Werte ${\textstyle 1}$ und alle anderen ${\textstyle 0}$ sind.
3. Die Funktion ${\textstyle \phi ()}$ ist symmetrisch in ${\textstyle p_{1},\ldots ,p_{C}}$
   

${\textstyle \Rightarrow }$ ${\textstyle \phi ()}$ hat für jede Permutation von ${\textstyle p_{1},\ldots ,p_{C}}$ den gleichen Wert.

Sei ${\textstyle p(t)}$ die Wahrscheinlichkeit, dass ein Punkt (= Featurevektor eines Beispiels einer Trainingsdata) im Knoten ${\textstyle t}$ liegt. Ähnlich sei ${\textstyle p(c,t)}$ die Wahrscheinlichkeit, dass ein Punkt im Knoten ${\textstyle t}$ liegt und zur Klasse ${\textstyle c}$ gehört. Darüber hinaus sei ${\textstyle p(c|t)}$, ${\textstyle c=1,\ldots ,C}$ die bedingte Wahrscheinlichkeit, dass ein Punkt zur Klasse ${\textstyle c}$ gehört, vorausgesetzt, dass er im Knoten ${\textstyle t}$ liegt. Diese bedingten Wahrscheinlichkeiten können basierend auf ihren Definitionen als ${\textstyle p(c|t)={\frac {p(c,t)}{p(t)}}}$ berechnet werden. Dann ist das Impurity-Measure (Unreinheitsmaß) des Knotens ${\textstyle t}$, ${\textstyle i(t)}$ als

$$i(t)=\phi \left(p(1|t),p(2|t),\ldots ,p(C|t)\right)$$

gegeben.

Die am häufigsten verwendeten Impurity-Funktionen sind

1. Entropie (entropy): ${\textstyle \sum _{c=1}^{C}p_{c}log{\frac {1}{p_{c}}}}$ (For ${\textstyle p_{c}=0}$ apply ${\textstyle \lim _{p_{c}\rightarrow 0}p_{c}log{\frac {1}{p_{c}}}=0}$.)
2. Fehlklassifizierungsrate (missclassification rate): ${\textstyle 1-\max _{c}p_{c}}$.
3. Gini-Index (Gini index): ${\textstyle \sum _{c=1}^{C}p_{c}(1-p_{c})=1-\sum _{c=1}^{C}p_{c}^{2}}$.

Es ist wichtig zu verstehen, dass es egal ist, welche Impurity-Funktion angewendet wird, da ihre Fähigkeit zur Messung der Impurity durch ihre Eigenschaften gewährleistet wird, die für alle Impurity-Funktionen gelten.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Auswahl basierend auf dem Maß „Goodness of split“

Der linke und rechte Kindknoten des Knotens ${\textstyle t}$ werden jeweils als ${\textstyle t_{L}}$ und ${\textstyle t_{R}}$ bezeichnet. ${\textstyle p(t_{L})}$ und ${\textstyle p(t_{R})}$ bezeichnen die Wahrscheinlichkeit, dass sich ein Punkt im Knoten ${\textstyle t_{L}}$ bzw. ${\textstyle t_{R}}$ befindet. Dann sind die bedingten Wahrscheinlichkeiten, dass sich ein Punkt im Knoten ${\textstyle t_{L}}$ und ${\textstyle t_{R}}$ befindet, wenn der Punkt im Knoten ${\textstyle t}$ ist, durch

$${\begin{aligned}&p_{L}={\frac {p(t_{L})}{p(t)}}\\&p_{R}={\frac {p(t_{R})}{p(t)}}\end{aligned}}$$

gegeben.

Basierend auf der Definition von ${\textstyle i(t)}$ kann die „Goodness of split“ einer
Kandidaten-Aufteilung ${\textstyle s,t}$ als die Differenz der Impurity des Knotens ${\textstyle t}$ und der gewichteten Summe der Impurity der linken und rechten untergeordneten Knoten angegeben werden. Mit anderen Worten

$$\phi (s,t)=\Delta i(s,t)=i(t)-p_{L}i(t_{L})-p_{R}i(t_{R}).$$

Somit drückt die oben definierte „Goodness of split“ den Gewinn aus, wenn der Kandidaten-Aufteilung ${\textstyle (s,t)}$ angewendet wird, d. h. wenn die durch ${\textstyle s}$ angegebene Aufteilung auf Knoten ${\textstyle t}$ angewendet wird. Hier sind ${\textstyle p_{L}}$ und ${\textstyle p_{R}}$ Gewichte oder Anteile von Punkten, die zu linken und rechten Knoten gehen.

Die gewichtete Impurity (weighted impurity) des Knotens ${\textstyle t}$ wird definiert als

$$I(t)=p(t)i(i).$$

Dies kann als die Impurity des Knotens ${\textstyle t}$ interpretiert werden, gewichtet mit dem Anteil seiner Punkte im Baum.

Dann wird die Differenz des gewichteten Impurity-Mass des übergeordneten Knotens ${\textstyle t}$ und der linken und rechten untergeordneten Knoten definiert als

$${\begin{aligned}\Phi (s,t)&=\Delta I(s,t)=I(t)-I(t_{L})-I(t_{R})=p(t)i(t)-p(t_{L})i(t_{L})-p(t_{R})i(t_{R})\\&=p(t)i(t)-p(t)p_{L}i(t_{L})-p(t)p_{R}i(t_{R})=p(t)\Delta i(s,t).\end{aligned}}$$

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Auswahl basierend auf der Twoing Rule

Eine andere Möglichkeit, die nächste Aufteilung auszuwählen, ist die Anwendung der Twoing Rule. Diese Regel wählt die nächste Aufteilung aus, die den Gesamtunterschied der Posterior-Wahrscheinlichkeiten der Klassen maximiert und die Anteile der Punkte ausgleicht, die auf die untergeordneten Knoten fallen. Mit anderen Worten wählt die Twoing Rule am Knoten ${\textstyle t}$ die Aufteilung aus, die das Optimierungskriterium

$$\max _{s}{\frac {p_{L}p_{R}}{4}}\left(\sum _{c}|p(c|t_{L})-p(c|t_{R})|\right)^{2}$$

erfüllt.

Der Term in der Klammer stellt die Gesamtdifferenz der
Posterior-Wahrscheinlichkeiten der Klassen dar, während der Multiplikationsfaktor ${\textstyle {\frac {p_{L}p_{R}}{4}}}$ im Maximumkriterium das Ausgleichsziel umsetzt.

${\textstyle \mathrm {\ \ \ \ } }$ Das Problem des guten Abbruchkriterium

Wenn man die "Goodness of split" zur Auswahl der nächsten Aufteilung anwendet, ist zu erwarten, dass die gewichtete Impurity mit jedem Schritt abnimmt. Der Baum, der durch iterative Auswahl der nächstbesten Aufteilung wächst, ist jedoch ein Greedy Algorithmus. Daher kann auf eine schlechte Aufteilung mit niedrigem ${\textstyle \Delta I(s,t)}$ eine gute Aufteilung mit höherem ${\textstyle \Delta I(s,t)}$ folgen. Daher wäre ein Abbruchkriterium wie das Abbrechen des Wachstums des Entscheidungsbaums, wenn ${\textstyle \Delta I(s,t)}$ unter einen bestimmten Schwellenwert fällt, kein zufriedenstellendes Abbruchkriterium. Ebenso würde ein „Vorausblick“ auf weitere Schritte in der Entwicklung von ${\textstyle \Delta I(s,t)}$ dieses Problem nicht lösen, da die weitere Entwicklung von ${\textstyle \Delta I(s,t)}$ nach diesen Schritten unbekannt ist, d. h. eine gute Aufteilung mit höherem ${\textstyle \Delta I(s,t)}$ könnte auch nach diesen Schritten folgen.

Daher kann auf diese Weise kein gutes Abbruchkriterium festgelegt werden. Deshalb lässt sich die richtige Strategie wie folgt feststellen.

• Lassen den Baum zunächst wachsen, bis er ausreichend groß ist, und
• Prune (beschneiden) ihn dann gemäß einem zufriedenstellenden Kriterium, siehe Unterabschnitt 4.2.3.

Das Erreichen einer ausreichend großen Größe kann beispielsweise anhand eines der folgenden Kriterien entschieden werden.

• Lassen den Baum wachsen, bis alle Knoten rein sind (= nur noch eine Klasse enthalten).
• Lassen den Baum wachsen, bis die Anzahl der Datenpunkte unter eine vordefinierte Grenze fällt, z. B. 6.

${\textstyle \mathrm {\ \ \ \ } }$ Zuweisen eine Klasse jedem Blatt

Nachdem der Entscheidungsbaum fertig ist, wird jedem Blatt eine Klasse zugewiesen. Die angewandte Regel ist unkompliziert: Jedem Blatt wird die Klasse mit der höchsten Wahrscheinlichkeit zugewiesen. Mit anderen Worten: Die dem Blattknoten ${\textstyle t}$ zugewiesene Klasse ${\textstyle c^{*}(t)}$ kann als

$$c^{*}(t)=\arg \max _{c}p(c|t)$$

gegeben werden.

Pruning

Die Beschreibung des Pruning (Beschneidung) bedarf einiger Vorüberlegungen (preliminary considerations).

${\textstyle \mathrm {\ \ \ \ } }$ Vorüberlegungen

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Optimale Teilbäume

Das Finden eines optimalen Teilbaums mittels erschöpfender Suche ist keine praktikable Strategie, da die Anzahl der Teilbäume auch bei einem mittelgroßen Baum beträchtlich groß sein kann. Stattdessen wird eine effizientere Methode benötigt, die die folgenden Voraussetzungen erfüllt.

• Der Teilbaum nach dem Pruning sollte in einem vordefinierten Sinne optimal sein.
• Die Methode zur Bestimmung dieses optimalen Teilbaums sollte rechnerisch handhabbar sein.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Fehlklassifizierungsrate

Die Fehlklassifizierungsrate ist die Wahrscheinlichkeit der Fehlklassifizierung (misclassification) in einem bestimmten Blattknoten, welche durch die Resubstitutionsschätzung (resubstitution estimate) ${\textstyle r(t)}$ charakterisiert wird. Aufgrund der Klassenzuweisungsregel (class assign rule), dass jedem Blatt die Klasse mit der höchsten Wahrscheinlichkeit zugewiesen wird, ist ${\textstyle r(t)}$ gegeben als

$$r(t)=1-p(c^{*}(t)|t)=1-\max _{c}p(c|t).$$

Wir definieren ${\textstyle R(t)=r(t)p(t)}$. Seien ${\textstyle T}$ und ${\textstyle {\tilde {T}}}$ die Bezeichnungen des gesamten Baums bzw. der Menge der Blattknote. Der Klassifizierungsfehler für den gesamten Baum, ${\textstyle R(T)}$, ist definiert als die Summe der gewichteten Resubstitutionsschätzung über die Menge der Blattknoten, ${\textstyle {\tilde {T}}}$, mit anderen Worten

$$R(T)=\sum _{t\in {\tilde {T}}}R(t)=\sum _{t\in {\tilde {T}}}r(t)p(t).$$

Eine wesentliche Aussage ist, dass die Aufteilung eines Knotens in zwei Kindknoten immer den Klassifizierungsfehler für den gesamten Baum verringert. Dies folgt aus

$$R(t)\geq R(t_{L})+R(t_{L}R),$$

welches eine Folge der Klassenzuweisungsregel ist und kann wie folgt nachgewiesen werden.

$${\begin{aligned}p(c^{*}(t)|t)&=p(c^{*}(t),t_{L}|t)+p(c^{*}(t),t_{R}|t)=p(c^{*}(t)|t_{L})p(t_{L}|t)+p(c^{*}(t)|t_{R})p(t_{R}|t)\\&=p(c^{*}(t)|t_{L})p(t_{L}|t)+p(c^{*}(t)|t_{R})p(t_{R}|t)=p_{L}p(c^{*}(t)|t_{L})+p_{R}p(c^{*}(t)|t_{R})\\&\leq p_{L}\max _{c}p(c|t_{L})+p_{R}\max _{c}p(c|t_{R}).\end{aligned}}$$

Daher gilt

$${\begin{aligned}r(t)&=1-p(c^{*}(t)|t)\geq 1-\left(p_{L}\max _{c}p(c|t_{L})+p_{R}\max _{c}p(c|t_{R})\right)\\&=p_{L}\left(1-\max _{c}p(c|t_{L})\right)+p_{R}\left(1-\max _{c}p(c|t_{R})\right)=p_{L}r(t_{L})+p_{R}r(t_{R}),\end{aligned}}$$

aus denen

$${\begin{aligned}R(t)&=p(t)r(t)\geq p(t)p_{L}r(t_{L})+p(t)p_{R}r(t_{R})\\&=p(t_{L})r(t_{L})+p(t_{R})r(t_{R})=R(t_{L})+R(t_{R})\end{aligned}}$$

folgt.

${\textstyle \mathrm {\ \ \ \ } }$ Minimal Cost-Complexity Pruning

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Begriffe und Notationen

Zur Beschreibung des Prunings werden verschiedene Begriffe und Notationen eingeführt.

• Descendant (Nachkomme): Ein Knoten ${\textstyle t_{2}}$ ist ein Descendant von Knoten ${\textstyle t_{1}}$, wenn es einen Pfad von ${\textstyle t_{1}}$ nach unten im Baum zu Knoten ${\textstyle t_{2}}$ gibt.
• Ancestor (Vorfahr): ${\textstyle t_{1}}$ ist Ancestor von ${\textstyle t_{2}}$, wenn ${\textstyle t_{2}}$ ein Descendant von ${\textstyle t_{1}}$ ist.
• Branch (Zweig) ${\textstyle T_{t}}$ des Baums ${\textstyle T}$ mit Wurzelknoten ${\textstyle t\in T}$: besteht aus Knoten ${\textstyle t}$ und allen seinen Descendants.
• Pruning a branch (Das Beschneiden eines Zweigs) ${\textstyle T_{t}}$ aus einem Baum ${\textstyle T}$ bedeutet das Löschen aller Knoten des Zweigs ${\textstyle T_{t}}$, außer dem Wurzelknoten.

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Kosten-Komplexität-Kriterium (cost-complexity criterion) zum Finden des optimalen Teilbaums

Der Klassifizierungsfehler ${\textstyle R(T)}$ ist kein geeignetes Maß, um den optimalen Teilbaum (optimal subtree) zu finden, da er mit zunehmendem Baum monoton abnimmt und somit den größten Baum bevorzugt. Das Hinzufügen eines Strafterms (penalty term), der kleinere Bäume bevorzugt, führt jedoch zu einem ausgewogenen Maß (balanced measure), dessen Minimierung zum Finden des optimalen Teilbaums geeignet ist.

Sei ${\textstyle |{\tilde {T}}|}$ die Anzahl der Blattknoten in der Menge ${\textstyle {\tilde {T}}}$ und ${\textstyle \eta }$ ein Komplexitätsparameter (complexity parameter). Die Kosten-Komplexität (cost-complexity) eines Baums ${\textstyle T}$ ist durch

$$R_{\eta }(T)=R(T)+\eta |{\tilde {T}}|$$

definiert.

Weiterhin sei ${\textstyle T_{0}}$ der initiale Baum (initial tree), der durch Wachstum auf eine ausreichend große Größe erhalten wird, und ${\textstyle {\hat {T}}}$ die Menge der Teilbäume des Baums ${\textstyle T}$. Dann soll der optimale Teilbaum eine minimale Kosten-Komplexität aufweisen

$$\arg \min _{T\in {\hat {(}}T_{0})}R_{\eta }(T)=\min _{T\in {\hat {(}}T_{0})}\left(R(T)+\eta |{\tilde {T}}|\right).$$

Hier begünstigt der Strafterm ${\textstyle \eta |{\tilde {T}}|}$ in der Zielfunktion (objective function) kleinere Bäume und der Komplexitätsparameter ${\textstyle \eta }$ gibt die Wichtigkeitsgewichtung (importance weight) der Größe des Baums an.

Es kann vorkommen, dass mehrere Teilbäume dieselbe minimale
Kosten-Komplexität aufweisen, z. B. einer mit kleinerer Größe, aber höherem Klassifizierungsfehler. In diesem Fall wird der Teilbaum mit der kleinsten Größe bevorzugt. Daher kann der optimale Teilbaum ${\textstyle T^{*}(\eta )}$ als der mit der minimalen Größe unter der Teilbäume mit minimaler Kosten-Komplexität angegeben werden. Es kann wie folgt als Optimierungsproblem formuliert werden.

$${\begin{aligned}T^{*}(\eta )&=\arg \min _{T\in {\hat {T}}_{0}}R_{\eta }(T)=\arg \min _{T\in {\hat {T}}_{0}}\left(R(T)+\eta |{\tilde {T}}|\right),\\|T^{*}(\eta )|&\leq T(\eta )\mathrm {\ \ } \mathrm {~fuer~alle~} \mathrm {\ \ } T(\eta )\mathrm {~mit~} T(\eta )=T^{*}(\eta ).\end{aligned}}$$

Da es nur endlich viele Teilbäume des Baums ${\textstyle T_{0}}$ gibt, ergibt ${\textstyle R_{\eta }(T^{*}(\eta ))}$ nur für endlich viele ${\textstyle \eta }$-s unterschiedliche Werte. Daher ist ${\textstyle R_{\eta }(T^{*}(\eta ))}$ als Funktion von ${\textstyle \eta }$ eine stückweise Treppenfunktion mit Sprüngen (piecewise step function with jumps).

${\textstyle \mathrm {\ \ \ \ \ \ } }$ Weakest-Link-Cutting

Wir erweitern die Definition der Kosten-Komplexität vom Baum auch auf Knoten. Für den Knoten ${\textstyle t\in T}$ ist seine Kosten-Komplexität als

$$R_{\eta }(t)=R(t)+\eta$$

definiert.

Die Weakest-Link-Cutting-Methode bestimmt den optimalen Teilbaum durch Durchlaufen der optimalen Teilbäume ${\textstyle R_{\eta }(T^{*}(\eta ))}$ als Funktion von ${\textstyle \eta }$ von ${\textstyle \eta =0}$ bis ${\textstyle \eta =1}$, indem sie den nächsten Sprungpunkt (jump point) in ${\textstyle \eta }$ rekursiv bestimmt. Das Durchlaufen der optimalen Teilbäume erfordert für jeden Knoten ${\textstyle t}$ den Vergleich von

$${\begin{aligned}R_{\eta }(t)&=R(t)+\eta \mathrm {\ \ } \mathrm {~und~} \\R_{\eta }(T_{t})&=R(T_{t})+\eta |{\tilde {T}}_{t}|.\end{aligned}}$$

Beginnend mit ${\textstyle \eta =0}$ wissen wir bereits, dass ${\textstyle R_{0}(T_{t})<R_{0}(t)}$ für jedes ${\textstyle t\in T_{0}}$, d.h. der optimale Teilbaum für ${\textstyle \eta =0}$ ist der initiale Baum ${\textstyle T_{0}}$ selbst. Diese Ungleichung gilt auch für einige kleine ${\textstyle \eta }$. Durch schrittweises Erhöhen von ${\textstyle \eta }$ wird der Punkt erreicht, an dem ${\textstyle R_{\eta }(T_{t})=R_{\eta }(t)}$, da der Koeffizient von ${\textstyle \eta }$ in ${\textstyle R_{\eta }(T_{t})}$ größer als in ${\textstyle R_{\eta }(t)}$ ist. Der Wert von ${\textstyle \eta }$ an diesem Punkt kann aus der Gleichheit bestimmt werden, was zum Wert

$${\frac {R(t)-R(T_{t})}{|{\tilde {T}}_{t}|-1}}.$$

an diesem Gleichheitspunkt (equality point) führt.

Direkt über diesem ${\textstyle \eta }$ ist der Wert ${\textstyle R_{\eta }(T_{t})>R_{\eta }(t)}$, was bedeutet, dass das Pruning des Zweigs ${\textstyle T_{t}}$ zu einem Teilbaum mit geringerer Kosten-Komplexität führt. Es kann jedoch vorkommen, dass dieser Gleichheitspunkt für einen anderen Knoten früher erreicht wird, d. h. bei geringerem ${\textstyle \eta }$. Daher tritt der erste Sprung in minimaler Kosten-Komplexität, ${\textstyle R_{\eta }(T^{*}(\eta ))}$, am Gleichheitspunkt mit dem kleinsten ${\textstyle \eta }$ unter den Gleichheitspunkten aller Nicht-Blattknoten (non-leaf nodes) des Baums ${\textstyle T_{0}}$ auf. Der Wert von ${\textstyle \eta }$ an diesem Sprungpunkt von ${\textstyle R_{\eta }(T^{*}(\eta ))}$ wird mit ${\textstyle \eta _{1}}$ bezeichnet und kann wie folgt berechnet werden.

$$\eta _{1}=\min _{t\in T_{0}\ {\tilde {T}}_{0}}{\frac {R(t)-R(T_{t})}{|{\tilde {T}}_{t}|-1}}.$$

Sei ${\textstyle t_{1}}$ der Knoten, an dem diese erste Gleichheit auftritt, mit anderen Worten

$$t_{1}=\arg \min _{t\in T_{0}\ {\tilde {T}}_{0}}{\frac {R(t)-R(T_{t})}{|{\tilde {T}}_{t}|-1}}.$$

Then just above ${\textstyle \eta _{1}}$ the optimal subtree, i.e. the subtree with the smallest cost-complexity is the one, which is obtained by pruning the branch ${\textstyle T_{t_{1}}}$ from ${\textstyle T_{0}}$, which is denoted as ${\textstyle T_{1}=T_{0}\ T_{t_{1}}}$. Repeating the gradually increase of ${\textstyle \eta }$ and the computation of the next jump point based on the cost-complexity of the actual optimal subtree, a recursive algorithm can be defined to obtain the jump points ${\textstyle \eta _{i}}$ and the optimal subtrees in the individual ${\textstyle \eta }$ regions. In each step the algorithm prunes the branch, whose cost-complexity becomes larger than the one of its root node at earliest in ${\textstyle \eta }$, which can be seen as the weakest-link. That is why the algorithm is called weakest-link cutting algorithm. Its schematic operation is given in Algorithm .

Dann ist knapp über ${\textstyle \eta _{1}}$ der optimale Teilbaum, d. h. der Teilbaum mit der geringsten Kosten-Komplexität, derjenige, der durch Pruning den Zweig ${\textstyle T_{t_{1}}}$ von ${\textstyle T_{0}}$ erhalten wird, was als ${\textstyle T_{1}=T_{0}\ T_{t_{1}}}$ bezeichnet wird. Durch Wiederholen der schrittweisen Erhöhung von ${\textstyle \eta }$ und der Berechnung des nächsten Sprungpunkts basierend auf der Kosten-Komplexität des aktuell optimalen Teilbaums kann ein rekursiver Algorithmus definiert werden, um die Sprungpunkte ${\textstyle \eta _{i}}$ und die optimalen Teilbäume in den einzelnen ${\textstyle \eta }$-Regionen zu erhalten. In jedem Schritt führt der Algorithmus das Pruning den Zweig durch, dessen Kostenkomplexität in ${\textstyle \eta }$ am frühesten größer wird als die seines Wurzelknotens, der als Weakest-Link (schwächstes Glied) angesehen werden kann. Aus diesem Grund wird der Algorithmus als Weakest-Link-Cutting-Algorithmus (Algorithmus zum Beschneiden des schwächsten Glieds) bezeichnet. Seine schematische Funktionsweise ist im Algorithmus  angegeben.

Algorithm  Weakest-Link-Cutting-Algorithmus
—————————————————————————————
Eingabe:
- der initiale Baum ${\textstyle T_{0}}$ Ausgabe:
- Folge von Sprungpunkten ${\textstyle \eta _{i}}$, ${\textstyle i\geq 1}$, - Folge von optimalen Teilbäumen ${\textstyle T_{i}}$ in den einzelnen Regionen ${\textstyle [\eta _{i}-\eta _{i+1})}$, ${\textstyle i\geq 0}$ und ${\textstyle \eta _{0}=0}$.
—————————————————————————————
1 Initialisierung: ${\textstyle T_{act}=T_{0}}$, ${\textstyle \eta _{act}=0}$, ${\textstyle \eta _{next}=0}$, ${\textstyle \mathrm {\ \ \ \ \ } }$ ${\textstyle \eta []=0}$, ${\textstyle t[]=0}$, ${\textstyle T[]=0}$, ${\textstyle \eta [0]=0}$, ${\textstyle T[0]=T_{0}}$, ${\textstyle i=1}$
2 while ${\textstyle \eta _{next}<1}$
3    ${\textstyle \Delta \eta =\min _{t\in T_{act}\ {\tilde {T}}_{act}}{\frac {R(t)-R(T_{t})}{|{\tilde {T}}_{t}|-1}}}$
4    ${\textstyle \eta _{next}=\eta _{act}+\Delta \eta }$
5    ${\textstyle \eta [i]=\eta _{next}}$
6    ${\textstyle t[i]=\arg \min _{t\in T_{act}}\ {\tilde {T}}_{act}{\frac {R(t)-R(T_{t})}{|{\tilde {T}}_{t}|-1}}}$
7    ${\textstyle T[i]=T_{act}\ T_{t[i]}}$
8    Update ${\textstyle T_{act}=T[i]}$, ${\textstyle \eta _{act}=\eta _{next}}$
9    Inkrement ${\textstyle i}$ as ${\textstyle i=i+1}$
10 end
—————————————————————————————

Eigenschaften des Entscheidungsbaums

Ein wesentliches Merkmal des Entscheidungsbaumansatzes (decision tree approach) ist, dass der Raum seiner Eingabevektoren explizit vorgegeben ist, d. h. die Dimensionen der Eingabevektoren sind explizit bekannt. Dies ist ein wesentlicher Unterschied zu HMMs oder neuronalen Netzwerken, deren Eingabevektoren (=Featurevektoren) implizit bestimmt werden.

Nachfolgend wird eine Liste über die Vorteile des Entscheidungsbaumansatzes angeführt.

• Der Entscheidungsbaumansatz verarbeitet nicht nur Ordinalvariablen (Ordinalskala), sondern auch kategorische Variablen (Nominalskala).
• Der Entscheidungsbaumansatz ist invariant gegenüber monotonen Transformationen der Featurekomponenten als Ordinalvariablen.
• Der Entscheidungsbaumansatz liefert eine Schätzung der Fehlklassifizierungsrate für jede Klasse.
• Der Entscheidungsbaum ist robust gegenüber fehlklassifizierten Punkten (misclassified points) im Trainingsdaten und Ausreißern (outliers).
• Der Entscheidungsbaum ist leicht zu interpretieren, was ihn insbesondere in medizinischen Anwendungsszenarien attraktiv macht.

Random Forest

${\textstyle \mathrm {\ \ \ \ } }$ Bootstrap-Aggregation - Bagging

Das bisher besprochene Training ist ein deterministischer Prozess, der dieselben Parameter aus demselben Trainingsdaten ergibt. Ein anderer Ansatz besteht darin, eine zufällige Komponente in den Trainingsprozess einzuführen und mehrere Durchläufe desselben Trainingsdaten mit dem zufällig modifizierten Trainingsprozess durchzuführen. Eine solche zufällige Modifikation kann beispielsweise darin bestehen, in jedem Durchgang eine zufällig ausgewählte Teilmenge der Trainingsdaten zu nehmen und nur diese Teilmenge für das Training in diesem Durchgang zu verwenden. Die Ergebnisse nach jedem Durchgang werden angesammelt und das Endergebnis wird aus der Sammlung der Ergebnisse durch eine zweckmäßige Kombination erstellt. Hier sind die Ergebnisse beispielsweise die Parameter des Modells. Die Kombination der angesammelten Ergebnisse kann beispielweise durch Mittelwertbildung (by averaging), gewichtete Mittelwertbildung (by weighted averaging), Berechnung des Medians (computing the median) oder durch Anwendung einer Mehrheitswahl (majority voting) erfolgen. Dieser Ansatz wird als Bootstrap-Aggregation genannt oder mit dem Akronym Bagging bezeichnet.

Das Ziel von Bagging ist normalerweise, die Varianz im Ergebnis zu verringern. Die Varianz des Stichprobenmittelwerts nimmt proportional zur Anzahl der Stichproben ab und daher das Ansammlung und Mittelwertbildung mehrerer Ergebnisse eine reduzierende Wirkung auf die Varianz hat.

Bootstrap-Aggregation hat mehrere Vorteile.

• Die Mittelung über eine Sammlung trainierter Parameter reduziert Overfitting, da sie die erfasste Entwicklung zwischen den Trainingsbeispielen, die von der zugrunde liegenden Verteilung abweichen, teilweise aufhebt.
• Die Mittelung über eine Sammlung trainierter Parameter führt zu einem stabileren Endergebnis.
• Modelle mit hoher Kapazität können aufgrund der reduzierten Overfitting eine flexiblere Anpassung (fitting) erreichen.
• Die Mittelung über eine Sammlung trainierter Parameter führt zum Aufbrechen des Bias-Varianz-Kompromisses (siehe in Absatz [subsec:bias_variance]), indem die Varianz neben dem gleichen Bias reduziert wird.

Bootstrap-Aggregation wurde von Leo Breiman [Breiman(1996)] entwickelt.

${\textstyle \mathrm {\ \ \ \ } }$ Random Forest

Random Forest ist eine Bootstrap-Aggregation, die auf Klassifizierungs- und Regressionsbäume angewendet wird. In Random Forest werden mehrere Bäume trainiert. Während des Trainings jedes Baums wird nur eine zufällig ausgewählte Teilmenge von Komponenten des Eingabevektoren berücksichtigt, die für die Aufteilung verwendet wird.

Leo Breiman hat umfangreiche Experimente mit Random Forest durchgeführt. Er fand heraus, dass es insgesamt etwas besser abschneidet als Support Vector Machines.

Convolutional Neural Networks für Bildverarbeitung

Convolutional Neural Networks (CNNs) sind eine Subklasse von KNNs, die sich für die Verarbeitung von Eingaben in Gridform, insbesondere von Bildern, eignen. Die Convolutional im Namen von CNN ergibt sich aus der Convolution Layer, die den Kernbaustein von CNN ist. Der Convolution Layer realisiert einen mathematischen Convolution (= Faltungsoperation). CNNs eignen sich besonders zum Extrahieren lokales Features und komplexerer Muster wie Texturen (textures). Hier lokal bedeutet, dass diese Features nur von den Pixeln abhängen, die sich um das betrachtete Pixel herum befinden.

Als Beispiel nehmen wir ein Feature, das durch Subtrahieren des Werts des linken Nachbarpixels vom Wert jedes einzelnen Pixels erstellt wird. Diese Funktion eignet sich zur Erkennung von Konturen, genauer gesagt von Kanten mit vertikalen Komponenten, was eine mögliche Teilaufgabe der Objekterkennung darstellt. Dies ist in Abbildung 34 dargestellt.

Abbildung 34: Vertikale Kantenerkennung (Quelle: [Goodfellow et al.(2016)]).

Das Bild auf der rechten Seite zeigt die Anwendung des Feature zur Konturerkennung auf das Originalbild auf der linken Seite.

Die mathematische Convolution

Die stetige Version des Faltungsoperators ist ein Integral einer Multiplikation zweier Funktionen ${\textstyle x(\tau )}$ und ${\textstyle w(t-\tau )}$, über die reellwertige Variable ${\textstyle \tau }$ als

$$s(t)=\int x(\tau )w(t-\tau )d\tau .$$

Das resultierende Integral hängt nur von ${\textstyle t}$ ab. Solche Operatoren kommen in vielen technischen Teilgebieten vor, wie z.B. Beschreiben der Wahrscheinlichkeitsdichtefunktion der Summe zweier unabhängiger Zufallsvariablen mit den Wahrscheinlichkeitsdichtefunktionen ${\textstyle x(t)}$ und ${\textstyle w(t)}$ oder Entrauschen des Signals ${\textstyle x(t)}$ durch Bildung seines gewichteten Durchschnitts durch Anwendung von ${\textstyle t}$ abhängige Gewichte ${\textstyle w(t)}$.

Das Argument des Integrals reicht in seiner allgemeinsten Form von ${\textstyle -\infty }$ bis ${\textstyle \infty }$, hängt aber normalerweise vom Kontext ab. Im Beispiel pdf der Summe unabhängiger nicht negativer Zufallsvariablen geht das Integral von ${\textstyle 0}$ bis unendlich, während im zweiten Beispiel ${\textstyle t}$ die Zeit darstellen kann und das Integral von ${\textstyle 0}$ bis ${\textstyle t}$ geht. Werte für ${\textstyle \tau >t}$ zu haben, würde bedeuten, auch zukünftige Werte des Signals ${\textstyle x(\tau )}$ in die Berechnung des entrauschten Werts bei ${\textstyle t}$, ${\textstyle s(t)}$, einzubeziehen, was normalerweise im realen Kontext nicht möglich ist.

Die Convolution wird in der Regel mit einem Sternchen bezeichnet.

$$s(t)=(x*w)(t)~\mathrm {~oder~vereinfacht~} s=x*w.$$

Die erste und die zweite Funktion, ${\textstyle x(t)}$ und ${\textstyle w(t)}$ werden als Eingabe und Kernel bezeichnet. Die Ausgabefunktion, ${\textstyle s(t)}$, wird im neuronalen Netzwerkkontext auch als Feature-Map genannt.

${\textstyle \mathrm {\ \ \ \ } }$ Die diskrete Convolution

Die diskrete Convolution ist analog definiert und kann als

$$s(n)=\sum _{m=-\infty }^{\infty }x(m)w(n-m)$$

angegeben werden.

${\textstyle \mathrm {\ \ \ \ } }$ Die zweidimensionale Convolution

Convolution kann auch als mehrdimensionaler Operator definiert werden. Die zweidimensionale diskrete Convolution kann wie folgt angegeben werden:

$$S(n,m)=(I*K)(n,m)=\sum _{i}\sum _{j}I(i,j)K(n-i,m-j).$$

Bei Anwenden auf ein Bild, beschreibt ${\textstyle I}$ das zweidimensionale Bild und ${\textstyle K}$ ist ein zweidimensionaler Kernel. Beide werden als zweidimensionales endliches Array dargestellt und die resultierende Matrix, ${\textstyle S(n,m)}$ wird als Ausgabematrix genannt. In diesem Fall können die Funktionen ${\textstyle I(n,m)}$ und ${\textstyle K(n,m)}$ in der oben angeführten Formel mit Ausnahme einer endlichen Menge von Punkten als Null angenommen werden. Auf diese Weise kann die unendliche Summe in der Convolution tatsächlich eine endliche Summe auch darstellen. Mehrdimensionale Arrays werden auch als Tensoren bezeichnet.

Die Convolution ist ein kommutativer Operator, was bedeutet, dass ${\textstyle S(n,m)}$ auch als

$$S(n,m)=(K*I)(n,m)=\sum _{i}\sum _{j}I(n-i,m-j)K(i,j)$$

angegeben werden kann. Dies kann gezeigt werden, wenn den Umtausch ${\textstyle (n-i)\rightarrow i}$ und ${\textstyle (m-j)\rightarrow j}$ im Expression von ${\textstyle (I*K)(n,m)}$ mit Summierung über ${\textstyle -\infty }$ zu ${\textstyle \infty }$ durchgeführt werden. Dieser Ausdruck von ${\textstyle S(n,m)}$ wird auch als Form mit Kernel-Flipping bezeichnet. Normalerweise ist dies die Form, die im ML-Kontext implementiert wird.

${\textstyle \mathrm {\ \ \ \ } }$ Illustration der Convolution

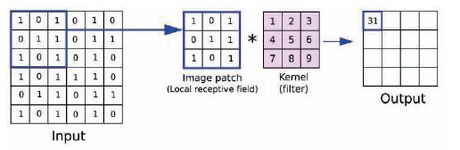
Die Anwendung der zweidimensionalen Convolution lässt sich anhand der Form mit Kernel-Flipping veranschaulichen. Die Gewichte werden in einem Kernelfenster angeordnet (d.h. die Elemente von K()) und auf das Bildfeld des Pixels angewendet, über denen das Kernelfenster positioniert ist. Dies ergibt einen Wert der Ausgabe. Durch horizontales und vertikales Verschieben des Kernelfensters über alle möglichen Positionen ergeben sich alle Werte des Ausgabetensors. Dies wird in Abbildung 35 dargestellt.

Abbildung 35: Illustration der 2D-Convolution anhand des Kernelfensters basierend auf der Form mit Kernel-Flipping (Quelle: [Reynolds(2021)]).

Beispielsweise kann die Convolution der vertikalen Kantenerkennung, die in Abbildung 34 illustriert wurde, mit dem in Abbildung 36 dargestellten Kernelfenster realisiert werden.

Abbildung 36: Kernelfenster der vertikalen Kantenerkennung.

Motivation aus rechnerischer Sicht

Die Anwendung der Convolution in NN ist auch aus rechnerischer Sicht vorteilhaft. Die rechnerischen Vorteile der Verwendung der Convolution in NNs zum Extrahieren lokaler Features können wie folgt aufgeführt werden:

• Sparse Connectivity (dünn besetzte Konnektivität),
• Parameter-Sharing und
• Äquivarianz zu verschieben (eqivariance to shift).

${\textstyle \mathrm {\ \ \ \ } }$ Sparse Connectivity

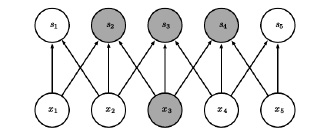
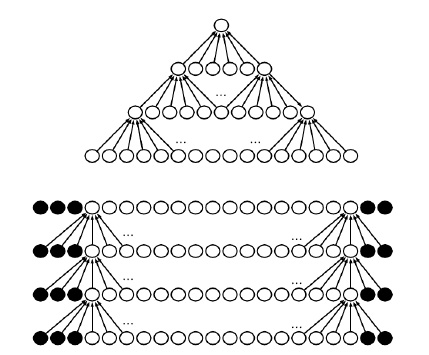
Lokale Features werden nur durch eine begrenzte Anzahl benachbarter Pixel beeinflusst. Bei seiner Realisierung ist jede Einheit der nächsten Layer nur mit einigen Einheiten der tatsächlichen Layer verbunden. Wenn jede Einheit der nächsten Layer nur mit ${\textstyle k}$ der ${\textstyle n}$ Einheiten der tatsächlichen Layer verbunden ist, verringert sich die erforderliche Anzahl von Operationen an jeder Einheit der nächsten Layer ebenfalls um ${\textstyle {\mathcal {O}}(n)}$ zu ${\textstyle {\mathcal {O}}(k)}$. Dies ist eine große Errungenschaft, da ${\textstyle k}$ normalerweise mehrere Größenordnungen kleiner als ${\textstyle n}$ sein kann. Diese Sparse Connectivity, sowohl von unten als auch von oben betrachtet, ist in Abbildung 37 dargestellt.

Abbildung 37: Sparse Connectivity von unten (Links) und von oben (Rechts) (Quelle: [Goodfellow et al.(2016)]).

In einem tiefen CNN mit mehr Hidden Layer können die tieferen Hidden Layer jedoch indirekt mit mehr Eingabeeinheiten interagieren. Dies ist in Abbildung 38 dargestellt.

Abbildung 38: Der rezeptive Bereich der Einheiten in tieferen Hidden Layer (Quelle: [Goodfellow et al.(2016)]).

${\textstyle \mathrm {\ \ \ \ } }$ Parameter-Sharing

Die Verwendung der Convolution in NN bedeutet, dass auch für Bildfelder von mehreren Pixels dieselben Gewichte angewendet werden, siehe Abbildung 35 im Falle von 2-D-Convolution. Dies wird als Parameter-Sharing bezeichnet. In einem Fully-Connected neuronalen Netzwerkmodell wird jeder Gewichtungsparameter nur einmal verwendet, um genau eine Eingabeeinheit zu gewichten und nur einen Ausgabewert zu berechnen. Im Convolutional Neuronalen Netzen wird jedes Gewicht im Kernel für jede Eingabeeinheit verwendet.

${\textstyle \mathrm {\ \ \ \ } }$ Äquivarianz zu verschieben

Die Äquivarianz von Convolution und Verschiebung bedeutet, dass der Umtausch der Reihenfolge von Convolution und Verschiebung das Ergebnis nicht ändert. Daraus folgt, dass die Anwendung desselben Convolution Kernel auf ein verschobenes Bild zur gleichen Ausgabe führt, jedoch verschoben. Daher können Teilaufgaben wie z.B. die Konturerkennung mit den gleichen Gewichtsparametern (d. h. mit den gleichen lokalen Features) im gesamten Bild unabhängig von der verschobenen Position des Objekts durchgeführt werden. Somit die Einführung eines neuen lokalen Features wegen der Verschiebung des Bildes ist nicht erforderlich. Aber die Convolution hat keine Äquivarianz zu anderen Transformationen wie der Drehung oder Skalierung eines Bildes.

Pooling

Jedes Element des Ausgabetensors der Convolution liefert einen Wert über das lokale Feature, das der Kernel an dieser Position realisiert. Pooling reduziert die Dimensionen der Ausgabe, indem die Ausgaben von Clustern neuronaler Einheiten zu einer Ausgabe kombiniert werden. Dies kann auch als eine zusammenfassende Statistik gesehen werden.

${\textstyle \mathrm {\ \ \ \ } }$ Typische Pooling Operationen

Zu den typischen Pooling Operationen gehören Max-Pooling, Average-Pooling, ${\textstyle L^{2}}$-Norm-Pooling oder Weighted-Average-Pooling. Max-Pooling liefert die maximale Ausgabe unter den benachbarten Positionen innerhalb eines rechteckigen Bereichs. Dies ist beispielsweise bei der Konturerkennung sinnvoll, um den schärfsten Unterschied zwischen den benachbarten Pixelwerten extrahieren, der die wahrscheinlichste Position der Kontur darstellt. Das Average-Pooling gibt den Durchschnitt der Ausgaben innerhalb eines rechteckigen Bereichs um die betrachtete Position zurück. Dies ist sinnvoll, z.B. bei Teilaufgaben wie der Einstufung eines bestimmten lokalen Feature, bei dem die räumliche Dichte der größeren Ausgabewerte dieses lokalen Feature proportional zum ausgabenden Wert ist. Ebenso bezieht sich die Norm ${\textstyle L^{2}}$ auch auf die Ausgaben innerhalb eines rechteckigen Bereichs um die betrachtete Position. Das Weighted-Average-Pooling berechnet gewichtete Summen unter Anwendung von Gewichtungen basierend auf der Entfernung von der betrachteten Position.

${\textstyle \mathrm {\ \ \ \ } }$ Lerninvarianz

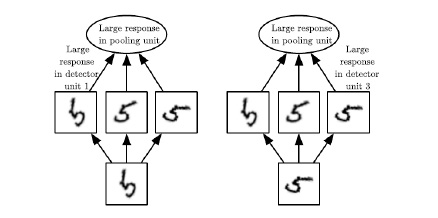
Pooling kann zum Lernen der skaleninvarianten und/oder orientierungsinvarianten Detektion von Features verwendet werden. Dies wird dadurch realisiert, dass Pooling auf separat parametrisierte Convolutionen angewendet wird. Dies ist für den Fall der Zeichenerkennung von Zahlen mit unterschiedlichen Orientierungen in Abbildung 39 dargestellt.

Abbildung 39: Erlernen des Erkennens des Zahlzeichens ,5“ invariant zu seiner Position (Quelle: [Goodfellow et al.(2016)]).

Jede Einheit der Convolution Layer (Convolution Unit) ist parametrisiert, um eine große Ausgabe für unterschiedlich positionierte Zahlenzeichen „5“ zu liefern. Die Versorgung einer Max-Pooling-Einheit mit diesen Ausgaben führt zu einer großen Ausgabe für jedes der unterschiedlich positionierten Zahlenzeichen „5“. Basierend auf das Label „5“ kann das Modell darauf trainiert werden, das Zahlenzeichen „5“ zu erkennen, das von seiner Position abhängt.

Convolution Block

${\textstyle \mathrm {\ \ \ \ } }$ Nichtlineare Aktivierungsfunktion

Die Ausgabe jeder Convolution Unit durchläuft normalerweise eine nichtlineare Aktivierungsfunktion (nonlinear activation function), bevor sie zur Einheit der Pooling Layer (Pooling Unit) gelangt. Die nichtlineare Aktivierungsfunktion führt zumindest annähernd eine Abbildung eines bestimmten Eingabebereichs auf einen Ausgabewert (z.B. 0 oder 1) durch. Dies kann so gesehen werden, dass einige Eingabewerte gezwungen werden, sich einem vordefinierten Ausgabewert anzunähern, wodurch im Wesentlichen eine Polarisierung oder Detektorfunktionalität (detection functionality) realisiert wird. Eine der am häufigsten verwendeten nichtlinearen Aktivierungsfunktionen in CNN ist die Rectified Linear Unit, ${\textstyle ReLU(z)}$.

${\textstyle \mathrm {\ \ \ \ } }$ Zusammensetzung eines Convolution Blocks

Ein typischer Convolution Block besteht aus drei Komponenten, in der folgenden Reihenfolge.

1. Convolutional Layer
2. Detektor Layer (=Nichtlineare Aktivierungsfunktion)
3. Pooling Layer

In Diagrammen von CNN-Architekturen werden die Nichtlineare Aktivierungsfunktion oft mit Convolutional Layer zusammen in einem gemeinsamen rechteckigen Box dargestellt. In der sogenannten komplexen Layer-Terminologie werden die drei Komponenten als „Stages“ genannt und die Komponente zusammen als Convolutional Layer.

Weitere typische Layers eines CNNs

${\textstyle \mathrm {\ \ \ \ } }$ Flatten Layer

Die Flatten Layer wird benötigt, um die Ausgabenwerten in 2D-Matrixform in einen Vektor umzuwandeln, der die Einspeisung in die Dense Layer ermöglicht. Diese Layer hat keine Parameter zu trainieren.

${\textstyle \mathrm {\ \ \ \ } }$ Dense Layer

Die Dense Layer (dichte Schicht) ist eine Fully-Connected Layer (vollständig verbundene Schicht), also jede ihrer Einheiten mit der Ausgaben aller Einheiten der vorherigen Layer verbunden ist. Die Dense Layer lernt, die Features auf hohem Abstraktionsniveau aus den Convolution Blocks zu kombinieren, um die Klassifizierungsaufgabe zu erfüllen.

${\textstyle \mathrm {\ \ \ \ } }$ Dropout layer

Die Dropout Layer realisiert eine so genannte Regularisierungstechnik (regularization technique), um die Overfitting zu reduzieren. Sie wendet Dropout an, bei dem die Ausgabe zufällig ausgewählter Einheiten in jeder Trainingsphase auf Null gesetzt wird. Dies führt zu einem zufällig unterschiedlichen Menge aktiver Neuralen Einheiten in jeder Trainingsphase, was das Netzwerk dazu anregt, weniger empfindlich auf die Gewichte bestimmter Neuralen Einheiten zu reagieren und so zu einer höheren Generalisierungsfähigkeit führt.

${\textstyle \mathrm {\ \ \ \ } }$ Output layer

Die Output Layer hat so viele Einheiten wie die Anzahl der Klassen in der Klassifizierungsaufgabe. Bei Klassifizierungsaufgaben mit mehreren Klassen besteht sie nur aus einer Softmax Funktion, die die Ausgabe der vorherigen Ebene in Wahrscheinlichkeiten der einzelnen Klassen umwandelt. Das Ergebnis der Klassifizierungsaufgabe, d. h. die vorhergesagte Klasse, ist dann derjenige mit der höchsten Wahrscheinlichkeit.

Convolution in der Praxis

Normalerweise wendet ein CNN viele Convolution an, um mehr Features extrahieren zu können. Um die Effizienz des Trainings zu erhalten, wird dieses als Parallelrechnung (parallel computation), z.B. durch Ausnützung der Parallelrechner-Fähigkeiten einer Grafikkarte implementiert.

${\textstyle \mathrm {\ \ \ \ } }$ Convolution on grid of vectors

Bisher wurde das Eingabebild (input image) als Raster realer Werte behandelt. In der Praxis handelt es sich bei der Eingabe eines CNN jedoch eher um ein Gitter von Vektoren (grid of vectors). Beispielsweise wird jedes Pixel eines Farbbildes durch ein Vektor der Dimension 3 beschrieben, die die Intensitäten von Rot, Grün und Blau beschreiben.

${\textstyle \mathrm {\ \ \ \ } }$ Zero Padding

Die Darstellung der Convolution durch Verschieben des Kernelfensters zeigt sofort, dass die Convolution mit der Kernelbreite (kernel width) ${\textstyle k}$ dazu führt, dass die Ausgabebreite(output width) mit ${\textstyle (k-1)}$ schrumpft. Dies kann vermieden werden, indem vor und nach jeder Eingabezeile einige Nullen hinzugefügt werden. Dies wird als Zero Padding (Nullauffüllung) bezeichnet. Zero Padding ermöglicht die unabhängige Steuerung der Ausgabegröße und Kernelbreite. Hier betrachten wir drei Sonderfälle der Zero Padding. Sie werden in der MATLAB-Terminologie als

• gültige Convolution (valid convolution),
• gleiche Convolution (same convolution) und
• vollständige Convolution (full convolution)

bezeichnet.

Bei einer gültigen Convolution gibt es keine Zero Padding. Es sind nur die Positionen des Kernelfensters erlaubt, an denen es vollständig im Bild enthalten ist. Somit schrumpft die Ausgabebreite bei Anwenden von jedem Convolution Layer, was die Anzahl der anwendbaren Convolution Layer begrenzt. Bei gleicher Convolution werden der Eingabe so viele Nullen hinzugefügt, womit die Ausgabe die gleiche Breite wie die Breite der Eingabe kommt. Dies bedeutet, dass zu jeder Zeile der Eingabe genau ${\textstyle (k-1)}$ Nullen hinzugefügt werden. Normalerweise werden diese Nullen vor dem linken und nach dem rechten Rand des Eingabegitters geteilt, was bedeutet, dass die Pixel am Rand des Eingabegitters Einfluss auf weniger Ausgabepixel haben als diejenigen, die sich innerhalb des Eingabegitters befinden. Die Vermeidung dieses Unterschieds motiviert die vollständige Convolution, bei der der Eingabe so viele Nullen hinzugefügt werden, dass ausreicht, um auch die Pixel am Rand des Eingabegitters ${\textstyle k}$-mal zu besuchen. Dies wird erreicht, indem ${\textstyle (k-1)}$ Nullen sowohl vor dem linken als auch nach dem rechten Rand des Eingabegitters hinzugefügt werden. Dies führt jedoch dazu, dass die Ausgabe breiter wird, d. h. die Ausgabegröße wird um ${\textstyle (k-1)}$ größer als die Eingabegröße. Die verschiedenen Sonderfälle des Zero Padding sind in Abbildung 40 dargestellt.

Abbildung 40: Zero Padding für gültige (Oberes) und gleiche (Unteres) Convolution (Quelle: [Goodfellow et al.(2016)]).

CNN Beispielarchitekturen für die Bildklassifizierung

${\textstyle \mathrm {\ \ \ \ } }$ Eine einfache Musterarchitektur

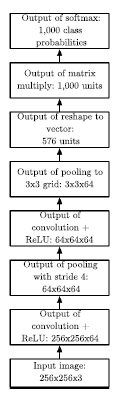
Eine einfache Beispielarchitektur für die Bildklassifizierung ist in Abbildung 41 dargestellt.

Abbildung 41: Beispielarchitektur für die Bildklassifizierung 256 x 256 x 3 (Quelle: [Goodfellow et al.(2016)]).

In der ersten Convolution Stage wird 16 parallele Convolution angewendet, um die Extraktion komplexerer lokaler Features und/oder das Erlernen von Invarianzen zu ermöglichen. Diese Beispielarchitektur zeigt die Positionierung der typische Layers in einer CNN-Architektur.

${\textstyle \mathrm {\ \ \ \ } }$ Einige bekannte CNN-Architekturen

Nachstehed sind einige bekannte CNN-Architekturen mit Links zu ihren Beschreibungen aufgeführt.

• LeNet-5
• AlexNet
• VGG-16
• Inception-v3
• ResNet-50

Recurrent Neural Network

Feedforward Neural Network werden durch gleichzeitige Eingabe (Input) gespeist. Im Gegensatz dazu sind Recurrent Neural Networks - RNN (rekurrentes neuronales Netzwerk) in der Lage, sequentielle Eingaben zu verarbeiten. Es eignet sich für Aufgaben, bei denen es um Eingaben mit sequentiellem Charakter geht, wie z.B. Text, gesprochene Sprache. Die sequentielle Natur der Eingabe spiegelt sich oft in ihrer zeitlichen Natur wider.

Ein Recurrent Neural Network ist ein neuronales Netzwerk, dessen Netzwerkarchitektur einen Zyklus aufweist, d. h. der Wert einer Unit in einer Layer des Netzwerks hängt von ihrer eigenen vorherigen Ausgabe als Eingabe ab. Diese Abhängigkeit ermöglicht, dass die Ausgabe des Recurrent Neural Network aufgrund seiner wiederkehrenden Verbindungen von Hunderten (theoretisch unendlich vielen) vorherigen Input Units abhängt. Diese langfristige Abhängigkeit von der Zeit ist das Novum des RNN, das neue Möglichkeiten für das Recurrent Neural Network eröffnet, beispielsweise wenn es zur Sprachmodellierung verwendet wird.

Der Zyklus in der Netzwerkarchitektur eines Recurrent Neural Network macht es leistungsstark, erschwert jedoch die Schlussfolgerung seiner Ausgabe aus seinen Eingaben und macht auch das Training des Netzwerks komplizierter.

Einfaches Recurrent Neural Network

Wir wollen uns nur mit einer eingeschränkten Unterklasse der allgemeinen Klasse Recurrent Neural Network befassen, den sogenannten Elman Networks (Elman-Netzwerken) [Elman(1990)] oder einfachen Recurrent Neural Network. Diese dient auch als Basis für weitere Architekturen von Recurrent Neural Network, wie z.B. das LSTM (siehe Unterabschnitt 4.4.4). Von nun an werden wir dieses einfache Recurrent Neural Network als Recurrent Neural Network oder RNN bezeichnen.

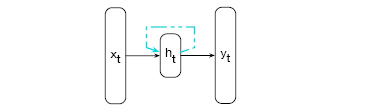
Wir werden den Index ${\textstyle t}$ verwenden, um die Zeit des gegebenen Vektors darzustellen, wie z.B. ${\textstyle {\bf {x}}_{t}}$ repräsentiert den Eingabevektor zum Zeitpunkt ${\textstyle t}$ oder ${\textstyle {\bf {h}}_{t}}$ repräsentiert den Ausgabevektor der einzigen Hidden Layer zum Zeitpunkt ${\textstyle t}$. Die Architektur des RNN ist in Abbildung 42 dargestellt ([Elman(1990)]).

Abbildung 42: Die Architektur des einfachen Recurrent Neural Network (Quelle: [JurafskyMartin(2023)]).

Wie in Abb. 9.1 zu sehen ist, liegt das Wesentliche des RNN in der wiederkehrenden Verknüpfung vom Ausgang der Hidden Layer mit dem Eingang der Hidden Layer, der in der gestrichelten Linie dargestellt ist. Die Ausgabe der Hidden Layer zum vorherigen Zeitpunkt realisiert einen Speicher und kann als Kontext angesehen werden, der Informationen über die Verarbeitung früherer Eingaben kodiert. Noch wichtiger ist, dass im RNN keine Längenbeschränkung für diesen Kontext auferlegt wird. Im Prinzip kann dieser Kontext Informationen bis zum Anfang der Eingabesequenz (input sequence) erfassen.

${\textstyle \mathrm {\ \ \ \ } }$ Vorwärtsinferenz (Forward Inference)

Der Ausgabewert der Hidden Layer zum Zeitpunkt ${\textstyle t-1}$ wird bei der Berechnung des Ausgabewerts der Hidden Layer zum Zeitpunkt ${\textstyle t}$ einbezieht, indem ein neuer Satz von Gewichten darauf angewendet wird, die durch die Matrix ${\textstyle {\bf {U}}}$ dargestellt werden. Somit kann die zeitabhängige Berechnung des RNN wie folgt angegeben werden:

$${\begin{aligned}&{\bf {h}}_{t}=f_{h}({\bf {U}}{\bf {h}}_{t-1}+{\bf {W}}{\bf {x}}_{t})\\&{\bf {y}}_{t}={\bf {F}}_{o}({\bf {V}}{\bf {h}}_{t}).\end{aligned}}$$

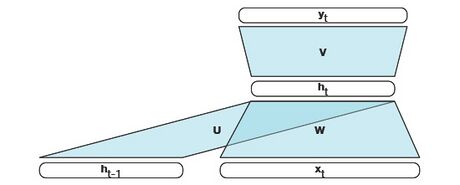
Die Aktivierungsfunktion der Output Layer ${\textstyle {\bf {F}}_{o}({\bf {z}}_{t})}$ ist normalerweise eine Softmax Funktion, also eine Vektorwertige Funktion. Das Hinzufügen der Zeitabhängigkeit zur Beschreibung von RNN scheint dieses Netzwerk komplexer zu machen, aber tatsächlich kann seine Berechnung durch die Einführung des Vektors ${\textstyle {\bf {h}}_{t-1}}$ auf eine Berechnung eines entprechenden Feedforward Network zurückgeführt werden. Dies ist in Abbildung 43 dargestellt.

Abbildung 43: Die Einfaches Recurrent Neural Network, dargestellt als entsprechendes Feedforward Network (Quelle: [JurafskyMartin(2023)]).

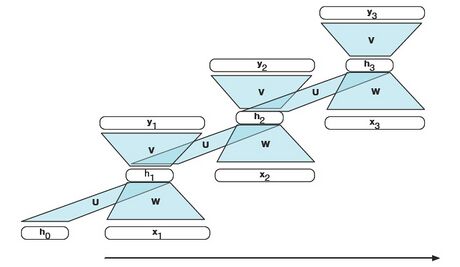
Der sequentielle Charakter des RNN kann durch zeitliches Ausrollen hervorgehoben werden. Dies ist in Abbildung 44 dargestellt.

Abbildung 44: Die Einfaches Recurrent Neural Network, dargestellt im zeitlichen Ablauf (Quelle: [JurafskyMartin(2023)]).

${\textstyle \mathrm {\ \ \ \ } }$ Training

RNN zu trainieren bedeutet, die Parameter der Gewichtsmatrizen ${\textstyle {\bf {W}}}$, ${\textstyle {\bf {U}}}$ und ${\textstyle {\bf {V}}}$ zu lernen. Aufgrund der wiederkehrenden Struktur des Netzwerks sind vor der Gestaltung des Trainings folgende Überlegungen notwendig.

• Die Berechnung des Loss zum Zeitpunkt ${\textstyle t}$ erfordert die Ausgabe der Hidden Layer zum Zeitpunkt ${\textstyle t-1}$.
• Die Ausgabe der Hidden Layer zum Zeitpunkt ${\textstyle t}$ beeinflusst nicht nur die Ausgabe des Netzwerks zum Zeitpunkt ${\textstyle t}$, sondern auch die Ausgabe der Hidden Layer zum Zeitpunkt ${\textstyle t+1}$.
  

${\textstyle \Leftrightarrow }$ Die Berechnung des Fehlers am Ausgang der Hidden Layer zum Zeitpunkt ${\textstyle t}$ erfordert die Kenntnis seiner Auswirkung auf ${\textstyle {\bf {y}}_{t}}$ und alle ${\textstyle {\bf {y}}_{t+i}}$ und ${\textstyle {\bf {h}}_{t+i}}$, ${\textstyle i\geq 1}$.

Daraus folgt, dass das Training von RNN das Ausrollen des Recurrent Neural Network in ein Feedforward Network erfordert und das Training dann auf diesem Feedforward Network auf übliche Weise durchgeführt werden kann, einschließlich der folgenden zwei Durchgänge:

• Vorwärtsinferenz, Berechnung von ${\textstyle {\bf {h}}_{t}}$ und ${\textstyle {\bf {y}}_{t}}$ und Speichern von ${\textstyle {\bf {h}}_{t}}$ für die Verwendung des nächsten Zeitschritts ${\textstyle t\geq 1}$ sowie die Akkumulation des Loss bei jedem Zeitschritt.
• Rückwärtsdurchlauf (backward pass), um den Fehler der Ausgabe der Hidden Layer für jeden rekursiven Rückschritt zu berechnen und zu speichern sowie den Gradient zu berechnen.

Dieser Ansatz zum Training von RNN wird als Backpropagation Through Time [Werbos(1974)] bezeichnet.

Bei Anwendungen mit längeren Eingabesequenzen, wie z.B. Streaming, Spracherkennung, muss das Ausrollen auf Segmente mit fester Länge beschränkt werden, da das Ausrollen der gesamten Eingabesequenz praktisch nicht möglich ist.

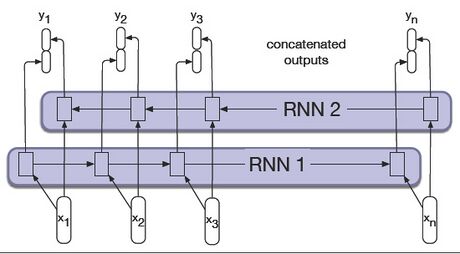
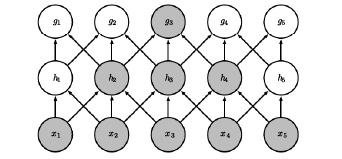
Stacked RNN

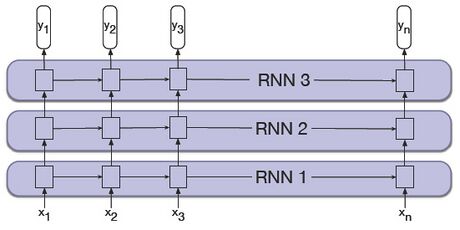
Stacked RNN (gestapeltes RNN) ist eine Erweiterung von RNN, bei der die gesamte Ausgabesequenz eines RNN als Eingabesequenz für ein nächstes RNN verwendet wird. Die Architektur des Stacked RNN ist in Abbildung 45 dargestellt.

Abbildung 45: Architektur des Stacked RNN (Quelle: [JurafskyMartin(2023)]).

Stacked RNNs haben im Allgemeinen höhere Fähigkeiten als ein RNN. Dies liegt daran, dass allgemein davon ausgegangen wird, dass jede Layer eine andere Abstraktionsebene einführt. Allerdings steigt der Zeit- und Ressourcenbedarf des Trainings mit der Anzahl der Layer schnell an. Die optimale Anzahl der Layer hängt von den Anforderungen der Anwendung ab.

Bidirektionales RNN

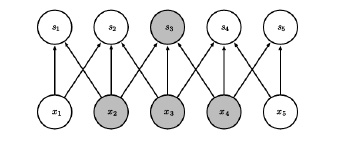
Die Idee des bidirektionalen RNN [SchusterPaliwal(1997)] besteht darin, nicht nur die Kontextinformationen aus dem linken Teil der Folge von Eingabevektoren (linker Kontext), sondern auch aus dem rechten Teil davon zu verwenden. In Anwendungen, in denen die Sequenz keine Zeit darstellt und die gesamte Eingabesequenz verfügbar ist, ist diese Architektur sinnvoll. Es stellt sicher, dass Kontokontextinformationen nicht nur von links, sondern auch von rechts genutzt werden, was z. B. die Leistung der Klassifizierungsaufgabe verbessert.

Im RNN repräsentiert die Ausgabe der Hidden Layer zum Zeitpunkt ${\textstyle t}$ die Kontextinformationen aus dem linken Teil der Folge von Eingabevektoren. Dies kann als Vorwärts-RNN angesehen werden, da die Hidden Layer die Informationen über die Eingabevektoren von links nach rechts weitergibt. Ein ähnlicher Rückwärts-RNN kann eingerichtet werden, dessen Hidden Layer die Informationen über die Eingabevektoren von rechts nach links weitergibt. Somit können die Ausgabevektoren der Vorwärts- und Rückwärts-RNNs, als Hidden Layers, zum Zeitpunkt ${\textstyle t}$, ${\textstyle {\bf {h}}_{t}^{f}}$ und ${\textstyle {\bf {h}}_{t}^{b}}$ als

$${\begin{aligned}&{\bf {h}}_{t}^{f}=RNN_{forward}({\bf {x}}_{1},\ldots ,{\bf {x}}_{t})\\&{\bf {h}}_{t}^{b}=RNN_{backward}({\bf {x}}_{t},\ldots ,{\bf {x}}_{n})\end{aligned}}$$

beschrieben werden, wobei ${\textstyle n}$ ist die Anzahl der Eingabevektoren in der Eingabesequenz. Die Parametergewichte des Rückwärts-RNN können durch das Training eines RNN auf einer umgekehrten Eingabesequenz erlernt werden.

Dann werden die gesamten Zustands- oder Kontextinformationen zum Zeitpunkt ${\textstyle t}$ zusammengestellt, indem sowohl die linken als auch die rechten Kontextinformationen kombiniert werden. Dies geschieht durch die Kombination der Vektoren ${\textstyle {\bf {h}}_{t}^{f}}$ und ${\textstyle {\bf {h}}_{t}^{b}}$, die die linken und die rechten Kontextinformationen darstellen. Mögliche Kombinationsvarianten sind Verkettung (concatenation), Multiplikation oder elementweise Addition. Beispielsweise kann durch Anwenden der Verkettung der Vektor ${\textstyle {\bf {h}}_{t}}$, der die gesamten Kontextinformationen darstellt, als

$${\bf {h}}_{t}=[{\bf {h}}_{t}^{f}{\bf {h}}_{t}^{b}],$$

angegeben werden, wobei ${\textstyle [{\bf {a}}{\bf {b}}]}$ für die Verkettung der Vektoren ${\textstyle {\bf {a}}}$ und ${\textstyle {\bf {b}}}$ steht. Ein solches bidirektionales RNN mit Verkettung ist in Abbildung 46 dargestellt.

Abbildung 46: Bidirektionales RNN mit separat trainierten Modellen in Vorwärts- und Rückwärtsrichtung (Quelle: [JurafskyMartin(2023)]).

Das LSTM

Eine Einschränkung von RNN besteht darin, dass es für Aufgaben, bei denen Informationen berücksichtigt werden müssen, die weit vom aktuellen Index ${\textstyle t}$ entfernt sind, nicht effektiv ist. Der Grund dafür ist, dass die in ${\textstyle {\bf {h}}_{t}}$ kodierten Informationen eher lokal sind und somit den Einfluss näherer Teile der Eingabesequenz widerspiegeln.

Um dieses Problem zu lösen, wurden kompliziertere RNN-Architekturen entworfen, die explizit diejenige Informationsteile steuern, die vergessen beziehungsweise für die zukünftige Verwendung gespeichert werden sollen, und diese Steuerung dynamisch über die Zeit durchführen. Eine solche RNN-Architektur ist das neuronale Netzwerk Long Short-Term Memory (LSTM)
Das LSTM wird als Hidden Unit realisiert. Es führt zu jedem Zeitpunkt ${\textstyle t}$, einen Kontextvektor, ${\textstyle {\bf {c}}_{t}}$, ein. Der Kontextvektor wird zur Maskierung bei der Berechnung der tatsächlichen Ausgabe der Hidden Unit zum Zeitpunkt ${\textstyle t}$, ${\textstyle {\bf {h}}_{t}}$ verwendet. Andererseits wird der Kontextvektor bei jedem Zeitschritt aktualisiert, d. h. ${\textstyle {\bf {c}}_{t}}$ wird aus ${\textstyle {\bf {c}}_{t-1}}$ berechnet. Während dieses Updates wird

• ein Teil des Kontextvektors ${\textstyle {\bf {c}}_{t-1}}$ durch Maskierung mit dem Forget Gate ${\textstyle {\bf {f}}_{t}}$ gelöscht (welches Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf k}_{ t}} resultiert) und
• ein Teil der eigentlichen Information ${\textstyle {\bf {g}}_{t}}$, die aus ${\textstyle {\bf {h}}_{t-1}}$ und ${\textstyle {\bf {x}}_{t}}$ wie üblich extrahiert, wird durch Maskierung mit dem Add Gate ${\textstyle {\bf {i}}_{t}}$ bewahrt (welches ${\textstyle {\bf {j}}_{t}}$ resultiert) und
• die Summe von ${\textstyle {\bf {k}}_{t}}$ und ${\textstyle {\bf {j}}_{t}}$ gebildet um den aktualisierten Kontextvektor ${\textstyle {\bf {c}}_{t}}$ anzugeben.

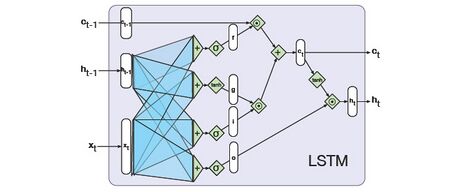
Die elementweise Multiplikation (auch als Hadamard-Produkt von Vektoren bezeichnet) wird mit ${\textstyle \odot }$ bezeichnet, und die Sigmoid Aktivierungsfunktionen werden zur Realisierung der Funktionalität der Maskierung verwendet. Das Sigmoid wird aufgrund seiner Eigenschaft ausgewählt, indem seine Eingabe entweder in Richtung ${\textstyle 0}$ oder ${\textstyle 1}$ zu werfen. Genauer gesagt werden die oben genannten Vektoren, wie folgt, berechnet.

1. Löschen eines Teils von ${\textstyle {\bf {c}}_{t-1}}$ durch Maskieren mit dem Forget Gate ${\textstyle {\bf {f}}_{t}}$ ${\textstyle \Rightarrow }$ ${\textstyle {\bf {k}}_{t}}$
   $${\begin{aligned}&{\bf {f}}_{t}=\sigma ({\bf {U}}_{f}{\bf {h}}_{t-1}+{\bf {W}}_{f}{\bf {x}}_{t})\\&{\bf {k}}_{t}={\bf {c}}_{t-1}\odot {\bf {f}}_{t}.\end{aligned}}$$
2. Extrahieren der tatsächlichen Informationen ${\textstyle {\bf {g}}_{t}}$ aus ${\textstyle {\bf {h}}_{t-1}}$ und ${\textstyle {\bf {x}}_{t}}$ sowie Bewahren eines Teils davon durch Maskieren mit das Add Gate ${\textstyle {\bf {i}}_{t}}$ ${\textstyle \Rightarrow }$ ${\textstyle {\bf {j}}_{t}}$
   $${\begin{aligned}&{\bf {g}}_{t}=tanh(({\bf {U}}_{g}{\bf {h}}_{t-1}+{\bf {W}}_{g}{\bf {x}}_{t})&{\bf {i}}_{t}=\sigma ({\bf {U}}_{i}{\bf {h}}_{t-1}+{\bf {W}}_{i}{\bf {x}}_{t})\\&{\bf {j}}_{t}={\bf {g}}_{t}\odot {\bf {i}}_{t}.\end{aligned}}$$
3. Zusammenstellen des aktualisierten Kontextvektors durch Summieren von ${\textstyle {\bf {k}}_{t}}$ und ${\textstyle {\bf {j}}_{t}}$ ${\textstyle \Rightarrow }$ ${\textstyle {\bf {c}}_{t}}$
   $${\begin{aligned}&{\bf {c}}_{t}={\bf {k}}_{t}+{\bf {j}}_{t}.\end{aligned}}$$
4. Berechnen von ${\textstyle {\bf {o}}_{t}}$ auf übliche Weise aus ${\textstyle {\bf {h}}_{t-1}}$ und ${\textstyle {\bf {x}}_{t}}$ sowie erstellen den Ausgabevektor der Hidden Unit durch Maskieren von ${\textstyle {\bf {o}}_{t}}$ mit dem tatsächlichen Kontextvektor ${\textstyle {\bf {c}}_{t}}$ ${\textstyle \Rightarrow }$ ${\textstyle {\bf {h}}_{t}}$
   $${\begin{aligned}&{\bf {o}}_{t}=\sigma ({\bf {U}}_{o}{\bf {h}}_{t-1}+{\bf {W}}_{o}{\bf {x}}_{t})\\&{\bf {h}}_{t}={\bf {o}}_{t}\odot tanh({\bf {c}}_{t}).\end{aligned}}$$

Die gesamte Berechnung der neuronalen LSTM-Einheit ist in Abbildung 47 dargestellt.

Abbildung 47: Die Berechnungsarchitektur einer neuronalen LSTM-Einheit (Quelle: [JurafskyMartin(2023)]).

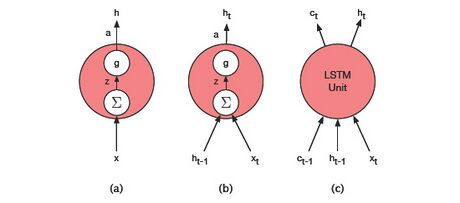
Der Vergleich der Eingabe- und Ausgabeschnittstellen der neuronalen Einheiten FNN, RNN und LSTM ist in Abbildung 48 zu sehen.

Abbildung 48: Neuronale Einheiten von (a) FNN, (b) RNN und (c) LSTM (Quelle: [JurafskyMartin(2023)]).