Graph Theory and Algorithms
Graph Theory and Algorithms
For a comprehensive subject on graph theory the reader is referred to the book [Gross and Yellen(1998)].
Seven Bridges of Königsberg
Seven Bridges of Königsberg is a problem of mathematics formulated by Leonhard Euler after a walk in Königsberg in Prussia (now Kaliningrad, Russia). The islands were connected to each other and the mainlands on the two sides of the Pregel River via seven bridges (see Figure 2).
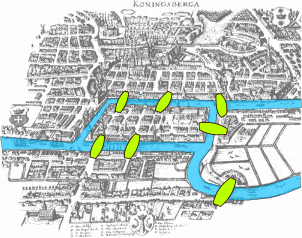
The problem is to find a walk path that would cross each of the seven bridges only once.
Leonhard Euler has resolved the problem in 1736 by showing that such a walk path does not exist. His solution founded the graph theory and therefore the Seven Bridges of Königsberg problem is considered to be the first problem of graph theory.
Graphs theory basics
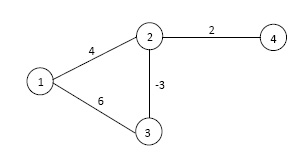
A graph is a mathematical object consisting of vertices (nodes) and edges connecting pairs of vertices, see example in Figure 3.
Graph theory studies properties of graphs and problems which can be described by means of graphs. Graph theoretical algorithms and results are applied in many areas, like e.g. transport networks, computer science or biology.
Basics
Basic terms
A graph is composed of vertices (nodes) and edges connecting pairs of vertices. Vertex and edge are the two basic units of the graph. The set of vertices and edges is denoted by and , respectively. In undirected graph the edges have no direction, they simple connect two vertices. The graph shown in Figure 3 is an example of an undirected graph.
The degree of a vertex is the number of edges connected to it. A path is an uninterrupted line connecting two vertices over sequence of edges and vertices. For example the path in Figure 3 connects the vertices and . This way a path is specified by an ordered list of all vertices locating on the uninterrupted line going from the starting vertex of the path to the end vertex of it. A cycle is a path, whose start vertex and end vertex is the same. For example in Figure 3 is a cycle. A graph is called connected graph, if there is a path between any two vertices of the graph. For example the graph in Figure 3 is a connected graph.
In the weighted graph each edge has a weight (or cost) associated to them. This weight can represent different physical properties, like e.g. distance between two nodes, capacity of a network link, transport cost of a way between two nodes, etc. An example of a weighted graph can be seen in Figure 4.
Types of graphs
The classification of graphs into various types is based on the properties of the considered subclass of graphs. The most important types of graphs together with their definitions are given as follows.
- Undirected graph - A graph with edges having no direction.
- Directed graph - A graph with edges having direction.
- Unweighted graph - A graph with edges having no weights associated to them.
- Weighted graph - A graph with edges having weights associated to them.
- Connected graph - A graph having path between any two of its vertices.
- Disconnected graph - A graph containing at least one pair of vertices having no path between them.
- Cyclic graph - A graph containing at least one cycle.
- Acyclic graph - A graph does not containing any cycles.
- Tree - A connected acyclic graph.
- Multi-graph - A graph containing at least one pair of vertices having multiple edges between them.
- Simple graph - A graph without cycles and multiple edges between the same pair of vertices.
- Complete graph - A graph in which each pair of vertices is connected by edge.
Graph descriptions
The most often used graph representations in algorithms are
- adjacency matrix and
- adjacency list,
because they enable the mathematical description of graphs by means of programming variables, like matrix, array and list.
Adjacency matrix
Adjacency matrix is suitable to describe unweighted graphs, both undirected and directed ones. Adjacency matrix is a matrix, whose -th element describes the existence of the connection from vertex to vertex as a binary value. If there is a connection then this value equals , otherwise . For example the adjacency matrix of the undirected, unweighted graph example in Figure 3 looks like
The construction of the adjacency matrix implies that the adjacency matrix of an undirected graph is always a symmetric matrix. The idea of describing an unweighted graph by constructing an adjacency matrix as 2-dimensional array can be theoretically extended to describe a weighted graph by constructing a 3-dimensional array, in which the third dimension represents the weight assigned to the edge specified by the first two dimensions. Such a 3-dimensional could be called as adjacency tensor.
Adjacency list
Another way of mathematical representation of a graph is the adjacency list. Adjacency list is an array of lists, in which each list specifies a set of neighbours of a vertex assigned to the actual list as index of the array. In describing a weighted graph, the list consists of the comma separated sequence of "ending vertex: weight" pairs, where each such pair specifies an edge to the given ending vertex with the given weight starting from the vertex to which the considered list belongs to. In case of an unweighted graph the list is a comma separated sequence of neighbour vertexes of the vertex to which the considered list belongs to. Therefore this type of representation is suitable to describe both unweighted and weighted graphs. For example the adjacency list of the unweighted graph example in Figure 3 is given as
Similarly the adjacency list of the weighted graph example in Figure 4 can be given as
Edge list
Still another way of mathematically describing a graph is to specify it as edge list. Each edge is specified by a sequence in the form starting vertex, ending vertex, weight (optional) . Thus the edge list can be given as a two/three column matrix for unweighted/weighted graphs. Hence this type of representation is suitable to describe both unweighted and weighted graphs. The unweighted graph in Figure 3 and the weighted graph in Figure 4 can be described by edge list, respectively, as
Graph problems
Graph theory can be applied for solving different problems in many areas. Without claim for completeness we list several well-known graph problems with their brief description.
- Graph coloring - Graph coloring is a group of problems all of them having something to do with coloring of graphs. Usually they are specified by means of a restriction on the way of coloring, like e.g no adjacent vertices may have the same color. One of the famous result in graph coloring is the so called Four-color theorem
- Network flow problems - Network flow problems deal with question related to Flow networks.
- Covering problems - Covering problems are set cover problems dealing with covering some subsets of vertices/subgraphs. Vertex cover problem is a special case of set cover problems, in which for every edge its starting or end vertex is in the vertex cover.
- Route problems - Route problems are graph problems, which are all related to find a route specified by various constraints on the graph.
Route problems
Route problems form an important class of graph problems, since they have applications in many areas. Here is a list of several selected Route problems, which will be discussed in more details in the rest of this section.
- Hamiltonian path and Eulerian path
- Traveling salesman problem
- Chinese postman problem (Route inspection problem)
- Minimum spanning tree
- Shortest path problem
Minimum Vertex Cover Problem
Vertex cover problem is a kind of set cover problems, in which a set of vertices are searched, which includes at least one endpoint of every edge of the graph. The Minimum Vertex Cover Problem (MIN-VC) is a vertex cover problem on undirected graph, in which a set of minimum number of vertices are searched, which includes at least one endpoint of every edge of the graph.
For example the minimum vertex cover of the example graph in Figure 5 is or or or .
The MIN-VC is an optimization problem and it can be reformulated to a decision problem, which is also called as "vertex cover problem". It is known to be NP-complete (nondeterministic polynomial-time complete), so usually so it cannot be solved by a polynomial-time algorithm.
There is an approximate algorithm for determining the minimum vertex cover of an undirected graph. Its schematic representation is shown in Algorithm 1.
Algorithm 1 Approximate algorithm for MIN-VC
—————————————————————————————
Input: Undirected graph given by an edge list (= set ).
Output : Found set of vertex cover .
—————————————————————————————
1 Initialise set of vertex cover: =
2 while is not empty
3 Take an arbitrary edge from set
4 Add and to
5 Remove all edges from set having endpoint either or
6 end
—————————————————————————————
It can be proven that the above approximate algorithm for MIN-VC always finds a vertex cover whose size is not more than twice of the size of the minimum vertex cover. The computational complexity of the algorithm is . The memory need of the algorithm is The memory is needed to store the visited vertices, i.e. the set .
Eulerian path and Hamiltonian path
Eulerian path and cycle
Eulerian path
Eulerian path in an undirected graph is a path that visits every edges of exactly once. Note that the undirected graph can be unweighted or weighted. However this does not affect the mathematical treatment of Eulerian path, therefore we treat these cases commonly by simple omitting unweighted or weighted characterization of .
The necessary and sufficient conditions for for the existence of Eulerian path in the undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} can be given as
- Every vertices with non-zero degree of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} form a connected graph.
- Either none of the vertices or exactly two vertices of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} have odd degree and all its other vertices have even degree.
Along the Euler path, each time walking through a vertex we walking through two previously unseen edges: one at approaching the vertex and the other at leaving it. On this way the number of edges at each middle vertex (i.e. the vertices except the starting and ending vertices of the path) must be even. The starting and ending vertices of the path are enabled to have odd degree, as the start or finish of the walk goes through on only one edge connected to that vertices. This argument proves the necessity of the condition. It turns out that the condition is also sufficient.
For example the example graph in Figure 6 has an Euler path , since only vertices Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 4} have odd degree.
An Euler path can be determined by going through the graph starting from a vertex with odd degree and selecting always previously unseen edges at each vertices. The conditions ensure that this always leads to an Euler path. This process requires the logging of the already visited edges at each vertex. It follows that the computational complexity of finding an Euler path is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|^2}
The Seven Bridges of Königsberg is a problem of finding an Euler path. In fact Leonard Euler solved it in 1736 by showing that there is no path that visits every of the seven bridges exactly once. His solution applies the above argument for necessary condition. Euler’s solution of the Königsberg bridge problem is the first theorem of graph theory and laid the foundations of graph theory.
Eulerian cycle
Eulerian cycle in an undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} is a closed path that visits every edges of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} exactly once and returns to the starting vertex. Similarly to Eulerian path, the undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} can be unweighted or weighted, which does not affect of the mathematical treatment of Eulerian cycle. Hence these cases are treated commonly by simple omitting unweighted or weighted characterization of . A graph containing a Eulerian cycle is a Eulerian graph.
The necessary and sufficient conditions for the existence of Eulerian cycle in the undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} can be formulated as
- Every vertices with non-zero degree of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} form a connected graph.
- Every vertices of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} have even degree.
This can be argumented similarly as in case of Eulerian path. Because in case of Eulerian cycle the path returns to the starting vertex, no odd degree is allowed yet for that vertex.
The example graph in Figure 6 has no Eulerian cycle, since not every vertices have even degree (vertices and have odd degree).
However the in the graph in Figure 7 every vertices have even degree, therefore it has a Eulerian cycle, e.g. (1,3,5,6,7,5,4,3,2,1).
Finding a Eulerian cycle can be completed on the same way as described for Eulerian path, but the visit can start at any vertex, since all vertices have even degree. Like in case of finding an Eulerian path, finding a Eulerian cycle has a computational complexity of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|^2} .
Hamiltonian path and cycle
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Hamiltonian path
Hamiltonian path in an undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} is a path that goes through every vertex of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} exactly once. The path have not to return to the starting vertex, i.e. Hamiltonian path is an open path. Finding a Hamiltonian path is in general an NP-complete problem.
For example the example graph in Figure 3 has more Hamiltonian paths: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (3,2,1,4,5,6)} or Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1,4,3,2,5,6)} .
Hamiltonian path has applications in many fields including
- transportation networks (finding optimal routes),
- circuit design and
- graph theory research.
Hamiltonian cycle
Hamiltonian cycle (or Hamiltonian circuit) in an undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} is a closed path that goes through every vertex of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} exactly once and returns to the starting vertex. A graph containing a Hamiltonian cycle is a Hamiltonian graph, otherwise it is non-Hamiltonian graph. Like in case of finding a Hamiltonian path, finding a Hamiltonian cycle is also an NP-complete problem. Finding a Hamiltonian path is often easier than finding a Hamiltonian cycle.
The example graph in Figure 3 has no Hamiltonian cycle.
However a slightly different graph in Figure 8 has a Hamiltonian cycle: (5,2,1,4,3,5).
Hamiltonian cycle has applications in many fields including
- computer science,
- logistics and
- network design.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Algorithms for finding Hamiltonian cycle
In the next we give a brief description of the following two algorithms for finding Hamiltonian cycle:
- Brute-force search and
- Backtracing algorithm
Brute-force search - for finding Hamiltonian cycle
The brute-force search (also called exhaustive search) follows a naive approach and tries all the possible permutations of all the Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |V|} vertices. This results in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |V|!} different sequences of the Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |V|} vertices, so the computational complexity of this algorithm is .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Backtracing algorithm - for finding Hamiltonian cycle
The idea of Backtracing algorithm is to add iteratively a new vertex to the actual path of subsequence of vertices, which is an adjacent to the last vertex of the actual path and not yet included in that path. After having the path with Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |\mathcal{V}|} vertices, it is checked whether it composes a cycle or not. If not then change the path by trying systematically all the adjacent vertices at every position in the path backwards, which is called backtracking.
The algorithm can be implemented on elegant way by applying a recursive function call. The pseudo code of the algorithm is given in Algorithm 2.
Algorithm 2 Backtracing algorithm - for finding Hamiltonian cycle
—————————————————————————————
Input: Undirected graph.
Output:
- true, if Hamiltonian cycle found,
- false, if Hamiltonian cycle exist
—————————————————————————————
1 Initialise path (=sequence of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |\mathcal{V}|}
vertices)
2 Set = first vertex
3 if Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle try\_next\_vertex\_and\_check\_cycle(1)}
4 return Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle true}
(cycle found)
5 else
6 return Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle false}
(cycle not exists)
7 end
—————————————————————————————
Recursive function
bool try_next_vertex_and_check_cycle(path_index k)
Input: next index in the path (=sequence of vertices)
Output:
- true, if cycle found,
- false, if backtracking or cycle not exists
—————————————————————————————
1 if Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k == |\mathcal{V}|}
2 if exists edge between last and first vertices of path
3 return Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle true}
(cycle found)
4 else
5 return Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle false}
(backtracking or cycle not exists)
6 end
7 for
8 if Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
is adjacent to Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path[k-1]}
(=last vertex in path)
9 and
10 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
is not yet in
11 path[k]=v
12 if Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle try\_next\_vertex\_and\_check\_cycle(k+1)}
13 return Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle true}
14 end
15 (Backtracking - remove v from path)
16 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path[k] = -1}
17 end
18 end
19 return false (backtracking or cycle not exists)
—————————————————————————————
In the course of backtracking every neighbours of every vertices can be tried by the algorithm. Therefore its computational complexity is .
Chinese postman problem (Route inspection problem)
The Chinese postman problem (also called as route inspection problem) is an extension of finding Eulerian cycle in connected and (unweighted or weighted) undirected graphs. The Chinese postman problem is to find shortest path that visits every edge of the connected and undirected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} at least once and return to the starting vertex. So the problem is defined on connected graph. The shortest path is defined as the one with minimum number of edges for unweighted graph and as the path with minimum accumulated weights for weighted graph. The solution path of Chinese postman problem is called Chinese postman tour. The Chinese postman problem can be solved in polynomial time.
Solution for Eulerian graph
If the graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} contains an Eulerian cycle, then it is also the solution for the Chinese postman problem, since Eulerian cycle has the shortest path (minimum number of edges in unweighted graph and minimum accumulated weights in weighted graph) due to the necessity of visiting all edges at least once.
Therefore the necessary and sufficient condition for the solution for the Chinese postman problem to be the Eulerian cycle is the existence of Eulerian cycle, which can be given as
- Every vertices of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} have even degree.
For example graph in Figure 7 the solution, i.e the Chinese postman tour is the Eulerian cycle, e.g. (1,3,5,6,7,5,4,3,2,1).
Solution for Non-Eulerian graph
If the graph has no Eulerian cycle, then the graph must be extended to become Eulerian. This is done by duplicating some edges of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} connected to vertices with odd degree in order to change the degree of all these vertices become to even. The edges to be duplicated must be selected from the relevant ones (i.e. connected to vertices with odd degree) on that way, that the increase of the path length due to edge duplication must be the possible smallest. Therefore those pairing of the vertices with odd degree are selected, which have the shortest path connecting them.
The example unweighted graph in Figure 9 shows a Non-Eulerian graph and the Chinese postman tour obtained by duplicating the edges [2,4] and [3,1].
Similarly the example Non-Eulerian weighted graph in Figure 10 illustrates the construction of the Chinese postman by duplicating the edges [2,4], [4,6] and [5,1]. Here duplicating [2,4] together with [4,6] instead of [2,6] inserts shorter path (i.e. accumulated weight 2+1= 3 instead of 5). Similarly duplicating [5,1] instead of [5,3] together with [3,1] inserts shorter path (i.e. accumulated weight 1 instead of 1+2=3).
Algorithm for Chinese postman problem
Based on the above considerations the algorithm for finding the Chinese postman route can be given schematically by means of its steps in Algorithm 3.
Algorithm 3 Algorithm for Chinese postman problem
—————————————————————————————
Input: Undirected graph .
Output: Chinese postman route.
—————————————————————————————
1 if grap is Eulerian
2 Find an Eulerian cycle in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}}
3 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle totalWeight}
= sum of all edge weights of
4 return Eulerian cycle and
5 else
6 Determine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N}
from graph, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N =|\mathcal{V}|}
7 Find all vertices with odd degree and store in array Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle oddVertices}
8 Construct the complete graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{C}}
from odd vertices together with edges
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ }}
representing shortest paths among any pairs of odd vertices
9 Find minimum weight perfect matching in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{C}}
, i.e the set of edges
reaching every odd vertices and together having smallest sum of weights.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ }}
This set of edges is called minimum T-join.
10 Extend the graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}}
by adding all edges from minimum T-join
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ }}
resulting in extended graph
12 Find an Eulerian cycle in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{H}}
13 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle totalWeight}
= sum of all edge weights of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{H}}
14 return Eulerian cycle of and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle totalWeight}
15 end
—————————————————————————————
The numerical complexity of the above minimum T-join based algorithm for solving the Chinese postman problem is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|^3)}
, since both setting up the complete graph, and finding minimum weight perfect matching in it takes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|^3)}
computational steps.
Minimum spanning tree - Kruskal’s algorithm
A spanning tree of a graph is a tree including every vertices of the graph. The number of edges of a spanning tree is , since the Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |\mathcal{V}|} -th edge would introduce a cycle and it were not any more a tree.
The minimum spanning tree (MST) is defined for a weighted, undirected, connected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} , as a spanning tree with the minimal accumulated weights.
Kruskal’s algorithm can be used to determine the MST of graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}} . In the Kruskal’s algorithm all edges of are sorted according to their weights in increasing order. Then the algorithm iteratively adds the next edge from the sorted list, i.e. the edge with the smallest weight, together with their vertexes to MST, if the newly added edge does not induce a cycle. The algorithm proceeds until every edge on the list is checked. On this way the resulted graph will have Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |\mathcal{V}|-1} edge, so it will be a spanning tree and the way of constructing implies that it will have the least accumulated weights.
The algorithm takes in each step the locally optimal decision due to adding the edge with the smallest weight among the still available ones. Therefore Kruskal’s algorithm is a greedy algorithm.
The algorithm is shown schematically in Algorithm 4.
Algorithm 4 Kruskal’s algorithm for detrmining MST
—————————————————————————————
Input: Undirected weighted connected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}}
.
Output: MST of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}}
.
—————————————————————————————
1 Initialise graph MST to be set empty.
2 Sort every edges of in increasing weight order and insert them,
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ }}
together with their vertexes into array Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle sortedListEdges[]}
3 for Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v=0,\ldots size(sortedListEdges)-1}
4 if inserting into MST does not induce a cycle
5 Add Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle sortedListEdges[v]}
into MST
6 end
7 end
8 return MST
—————————————————————————————
The computational complexity of the algorithm is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{E}|*log(|\mathcal{E}|))}
, since sorting the edges has Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{E}|*log(|\mathcal{E}|))}
complexity, iterating through every edges and checking cycle has and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(log(|\mathcal{V}|) =\mathcal{O}(log(|\mathcal{E}|)}
due to Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |\mathcal{E}|}
is at most Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |\mathcal{V}|^2}
.
The memory need of the algorithm is , which is needed to store edges together with their vertexes.
Traveling salesman problem
The Traveling Salesman Problem (TSP) originates from a context of cities and given distances among them. TSP is to look for the shortest path that goes through each city exactly once and returns to the starting city. Usually there exists a route between any pair of cities with some given distance. In graph theory context an equivalent formulation of TSP can be given as looking for a path with the least accumulated weights in a weighted, often complete graph, that goes through each vertex exactly once and returns to the starting vertex. This is equivalent with finding the Hamiltonian cycle with the minimum accumulated weight in a weighted, often complete graph. Thus the TSP is more general than Hamilton cycle problem and hence Hamilton cycle problem is a special case of TSP. The resulted path can be also called as TSP path.
The TSP was formulated mathematically in the 19th century and was first studied mathematically in the 1930s. The decision problem version of TSP is an NP-complete problem, so TSP is NP-hard. TSP is one of the most intensively investigated problem in combinatorial optimization, since it is used as benchmark for other optimization methods in terms of computational complexity.
Some properties of TSP can be provided as
- Symmetric and asymmetric TSP. In symmetric TSP the distance between two cities is the same in both direction, which leads to a formulation in graph theory context to a TSP on undirected graph. In asymmetric TSP either do not exist a path between two cities in both direction or the distances are different excluding the higher one from the TSP formulation. In these cases the formulation in graph theory context yileds a TSP on directed graph.
- Completing the graph by adding edges with sufficiently long distances will not affect the optimal path.
- The path to be a cycle or an open path does not make difference in the computational complexity of TSP (like in case of Hamilton path problem).
The TSP has applications in numerous fields, like logistics, route planning in transport networks, manufacturing of microchips and DNA sequencing. One-way streets, airfares with different departure and arrival fees are real-world scenarios for applying asymmetric TSP.
Generalizations of TSP
Several generalizations of TSP are listed below.
- The travelling politician problem (also called as "generalized travelling salesman problem") has a context with states having one or more cities and the travelling man must visit exactly one city from each state. It has been shown that travelling politician problem can be led back to standard TSP with modified distance matrix.
- The travelling purchaser problem has a purchaser, who has to buy a set of products, which can be bought in more cities but at different prices. The optimization objective is to find a path among a subset of cities that enables to buy all the products with minimal total cost (=taveling cost + purchasing cost).
- Vehicle routing problem.
- Ring star problem ([Labbé et al.(2004)]).
Integer linear programming formulation
In order to form the TSP as Integer Linear Programming (ILP) optimization, several variables must be introduced. Let Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N} denote the number of cities (vertices), i.e. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N = |\mathcal{V}|} . Let Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{ij}} stand for the distances (weights) between the cities (vertices) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} , for Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i,j = 1, \ldots, N} . Let Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_{ij}} be a decision variable describing whether the path goes from city (vertix) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} to Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} , or not for Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i,j = 1, \ldots, N} . In other words Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{ij} = \left\{ \begin{aligned} 1, \mathrm{\ \ } \mathrm{~if~path~goes~i \rightarrow j} \\ 0, \mathrm{\ \ } \mathrm{~otherwise~~~~~~~~~~~} \end{aligned} \right\}.} The integer nature of the values Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0} and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} makes this optimization problem an ILP. The objective function of the optimization task is to minimize the path length (= accumulated weights), in other word
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \arg \min_{x_{ij}} \sum_{i=1}^{N} \sum_{j=1,~j \neq i}^{N} c_{ij} x_{ij} ~j = 1, \ldots, N.}
However without further constraints this optimization considers not only paths, which are characterized by also leaving each reached vertex, but all set of edges enabling the minimum being at Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_{ij}=0} for every Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i,j \in \mathcal{V}} . Therefore further constraints are necessary to ensure that paths are considered and each vertex is visited exactly once. These requirements can be forced by formulating the following further two constraints, which force that the path reaches each vertex exactly once and leaves each vertex exactly once Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \sum_{i=1,~i \neq j}^{N} x_{ij} = 1, ~~ j = 1, \ldots, N, \\ \sum_{j=1,~j \neq i}^{N} x_{ij} = 1, ~~ i = 1, \ldots, N. \end{aligned}}
These constraints ensure that the selected way looks locally as path and all vertices are visited, but still allow that the selected set of edges comprises several local paths each of them visiting only a disjunct subset of vertices instead of one global path visiting every vertices. This global path requirement makes TSP a difficult problem. There are more ways to formulate this global path requirement as a linear constraint. The Miller-Tucker-Zemlin formulation introduces dummy variables Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_i} for keeping track the order of visit the city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} , for Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i = 1, \ldots, N} . The path starts with visiting city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} . The global path requirement is ensured by forcing Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_j} being higher than Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_i} when city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} is visited before city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} , for Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i = 2, \ldots, N} . More precisely Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_j} must be higher than Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_i} at least by one when city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} locates on the path after city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} , and otherwise by a values less than Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N} to ensure that Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_{ij}=0} does not force an unwanted relation between Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_i} and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_j} . Since city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} is left out from these constraint, it ensures that the optimal path must return to city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} , otherwise the value of the dummy variable of the city visited after city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N-1} would be less that Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u_{N-1}} , which would violate the constraint. The city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} is the only one for which a decrease in value of the dummy variable allowed when the path reaches city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1} . These considerations lead to the formulation of the global path requirement as a linear constraint as Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_i -u_j + 1 \leq (N-1)(1-x_{ij}) ~~ i,j \in \{2, \ldots, N \} \mathrm{~and~} i \leq j.}
Putting all these together gives the Miller-Tucker-Zemlin ILP formulation of the TSP as Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \arg \min_{x_{ij}} \sum_{i=1}^{N} \sum_{j=1,~j \neq i}^{N} c_{ij} x_{ij},~\ldots, N, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \mathrm{~subject~to} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \mathrm{~constraint~}1.~~~ \sum_{i=1,~i \neq j}^{N} x_{ij} = 1, ~~ j = 1, \ldots, N, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \mathrm{~constraint~}2.~~~ \sum_{j=1,~j \neq i}^{N} x_{ij} = 1, ~~ i = 1, \ldots, N, \mathrm{~and~} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \mathrm{~constraint~}3.~~~ u_i -u_j + 1 \leq (N-1)(1-x_{ij}) ~~ i,j \in \{2, \ldots, N \} \mathrm{~and~} i \leq j. \end{aligned}}
Algorithms for TSP
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Exact algorithm - Brute-force search
The brute-force search tries all the possible permutations of all the Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |V|} vertices and selects the one with the lowest accumulated weights. This results in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |V|!} different sequence of vertices the Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle |V|} vertices, so the computational complexity of this algorithm is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|!)} . Hence this approach becomes intractable already for number of cities in the magnitude of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 20} .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ }} Approximate algorithms
Due to the NP-completeness of the TSP the exact solution becomes intractable very fast as the number of cities increases. Therefore there is a need for establishing approximate algorithms for the TSP.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Nearest neighbour algorithm
The Nearest Neighbour (NN) algorithm selects the nearest not yet visited neighbour city at each step. Thus its decision is locally optimal in each step, therefore it is a greedy algorithm. Its schematic representation is shown in Algorithm 5.
Algorithm 5 Nearest neighbour approximate algorithm for TSP
—————————————————————————————
Input: Undirected weighted graph.
Output: Hamiltonian cycle with minimum accumulated weights.
—————————————————————————————
1 Determine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N}
from graph, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N =|\mathcal{V}|}
2 Initialize Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path}
array, set Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path[0]=1}
and set Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle totalWeight = 0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ }}
( array =sequence of vertices)
3 for Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v=1,\ldots N-1}
4 Select nearest not yet visited city among neighbours of city Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path[v-1]}
, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
5 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path[v]=u}
6 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle totalWeight += weight(path[v-1], u)}
7 end
8 return Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle path}
,
—————————————————————————————
The computational complexity of the NN algorithm is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|)}
. For city arrangement distributed randomly on the plane, the NN algorithms gives a path which is only 25% longer than the shortest one. However for specific city arrangements the NN algorithm can produce also the worst route.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ \ \ \ }} Christofides algorithm
The heuristic approach of Christofides is based on using graph theoretical results to compose an approximate algorithm. It utilizes that a TSP path can not be longer than an Eulerian path over all cities of the graph. Therefore first a subgraph including all cities must be found, than it is extended to be an Eulerian graph, afterwards the Eulerian path is determined in the Eulerian graph and finally it is converted to a TSP path (i.e. to visit each city only once). If the minimum spanning tree of the original graph is selected as first graph and it is made to be an Eulerian graph by doubling every edge in it, then the total length of an Eulerian path can not be more than twice the one of the TSP path. Note that the length of the path changes also at converting the Eulerian path to a TSP path. During this step, shortcut is created for each city visited twice by inserting an edge from the city before this to a city after this. On this way one can approximate a solution for the TSP. The steps of the Christofides algorithm are shown schematically in Algorithm 6.
Algorithm 6 Christofides approximate algorithm for TSP
—————————————————————————————
Input: Undirected weighted graph.
Output: Approximate TSP path.
—————————————————————————————
1 Find a minimum spanning tree Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{T}}
of the graph.
2 Duplicate every edges of to create an Eulerian graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{M}}
3 Find an Eulerian path in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{M}}
4 Convert Eulerian path to approximate TSP path by using shortcuts
5 return approximate TSP path
—————————————————————————————
The Christofides algorithm was one of the first approximation algorithm, which shown that establishing an approximation algorithms can be practically usable approach for solving exactly intractable problems.
An improved version of the algorithm is the algorithm of Christofides and Serdyukov, in whic a better way of creating an Eulerian graph is applied. This is done by applying the so called minimum weight matching. The steps of the algorithm of Christofides and Serdyukov can be seen schematically in Algorithm 7.
Algorithm 7 Approximate algorithm of Christofides and Serdyukov for TSP
—————————————————————————————
Input: Undirected weighted graph.
Output: Approximate TSP path.
—————————————————————————————
1 Find a minimum spanning tree Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{T}}
of the graph.
2 Apply minimum weight matching to odd-degree vertices of giving graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{W}}
3 Find optimal Eulerian path in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{W}}
4 Convert Eulerian path to approximate TSP path by using shortcuts
5 return approximate TSP path
—————————————————————————————
Approximate algorithm of Christofides and Serdyukov gives an approximate TSP path with accumulated weights, which is at most 1,5 times higher than the one of the optimal TSP path. The computational complexity of the approximate algorithm of Christofides and Serdyukov is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{V}|^3)}
, which is mainly caused by minimum weight matching algorithm part.
Shortest path problem
The shortest path in a weighted graph between two vertices is the path connecting them with the smallest accumulated weight. There are more algorithm for finding shortest path, each with a slightly different applicability scope.
Besides of Diskstra’s algoritm another common algorithms are the Bellman-Ford and the Floyd Warshall algorithms.
Dijkstra-Algorithmus
Diskstra’s algorithm finds the shortest path from a given source vertex to every vertices in a weighted graph . The graph must not contain negative edge, since in that case the algorithm fails.
The idea of Diskstra’s algorithm is an iterative extension of shortest path tree (SPT) containing a subtree with vertices, for which the shortest paths from the a given source have already been found. The vertices outside of SPT have also minimum distance values assigned during the intermediate steps of the processing. The minimum distance values of vertices being neighbour of any vertices of SPT and locating outside of SPT represent the minimum distance from source vertex to the considered vertex via every possible routes over the vertices of the actual SPT. The iterative extension of SPT is performed by selecting the vertex with the shortest minimum distance among the vertices locating outside of SPT, adding this vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u} together with its minimum distance to SPT and reevaluating the minimum distances of each vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v} locating outside of the updated SPT and being the neighbour of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u} . During the reevaluation the minimum distance of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v} is compared to the sum (minimum distance of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v} + weight of (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v} - )) and if the later is smaller then the minimum distance of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v} will be updated.
The schematical representation of the algorithm can be seen in Algorithm 8.
Algorithm 8 Dijkstra-Algorithmus for determining SPT
—————————————————————————————
Inputs:
- Undirected weighted connected graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}}
.
- Source vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle s}
.
Output: Array of minimum distances to every vertices .
—————————————————————————————
1 Create an adjacenty matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf S}}
for maintaining SPT with vertices (subtree),
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ }}
for which the shortest paths from the a given source have already been found
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ }}
and initialize it to empty.
Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf S}}
stores already found minimum distance values for its vertices.
2 Create and adjacency matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}}
for representing the graph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{R}}
being a
subgraph of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{G}}
containing vertices locating outside of SPT
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ }}
and every edges of them. Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}}
stores also actual values of
minimum distance to every vertices of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{R}}
.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\ \ \ }}
Initialize all these distance values to Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \infty}
, and for the source vertex
set the minimum distance to the value Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 0}
.
3 while matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}}
is not empty (=not all vertices are moved from it)
4 take a vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
from subgraph matrix with the smallest minimum distance
5 add vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
with its minimum distance and its edge connecting it to SPT
6 matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf S}}
7 for each vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
of graph being neighbour of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
8 (update minimum distance of vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
in matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}}
: )
9 if minimum distance of + weight of (- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
) < minimum distance of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
10 minimum distance of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
= minimum distance of Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
+ weight of (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle v}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
)
11 mark edge of to Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
as edge connecting to SPT
12 end
13 end
14 remove the row of vertex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u}
from subgraph matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf A}}
15 (that means also removing vertex from subgraph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{R}}
)
16 end
17 Build up array Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle minDist[]}
from SPT matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\bf S}}
18 return array
—————————————————————————————
The computational complexity of the algorithm is , since finding the vertex in the subgraph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{R}}
takes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(log(|\mathcal{V}|))}
operations, which must be done for every vertices. Note that it is the same as Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(|\mathcal{E}|*log(|\mathcal{E}|))}
due to Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathcal{O}(log(|\mathcal{V}|))= \mathcal{O}(log(|\mathcal{E}|))}
.
The finding the vertex of subgraph Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \boldsymbol{R}} with the smallest minimum distance can be implemented by the help of priority queue (or Heap). The standard usage of priority queue would overwrite minimum distance in the inserted pair (minimum distance - vertex) for the same vertex always by the minimum distance of the lastly checked edge to that vertex, which is not necessarily the smallest one among every edges. This can be resolved by inserting more copies of the pair (minimum distance - vertex) for the same vertex, since priority queue will take only the one of them with the smallest value of minimum distance.
Dijkstra’s algorithm assumes that in each intermediate step, the minimum distances of the vertices in SPT, are already the final ones, i.e. the shortest paths from the a given source to the vertices of SPT have already been found. This holds with non- negative weight, since in this case a new path to a vertex in SPT via any vertices of outside of SPT would increase the distance by a sum of non-negative weights which then can not be smaller then the distance marked in SPT as the minimum one. However this is not true in case of existence of negative weight, and thus for graphs with negative weights Dijkstra’s algorithm can return higher distance than than the real minimal one, i.e. wrong result. This is illustrated on the graph in Figure 11.
For this graph Dijkstra’s algorithm would give minimum distance for node Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2} and the value Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 4} and Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 6} , which is wrong, since the right value is Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 3} and , respectively
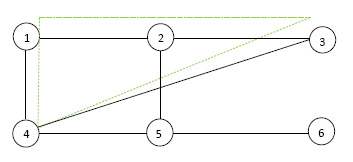







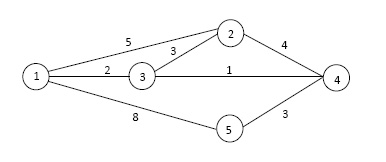










![{\textstyle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b83673fcebf53d7a6e92b09eed049d3704f53516)
![{\displaystyle {\begin{aligned}&&[[1,2],[2,3],[1,4],[4,5],[2,5],[3,4],[5,6]]\\&&[[1,2,5],[2,3,3],[3,1,2],[2,4,4],[4,3,1],[1,5,8],[4,5,3]].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbc713e92d587035a19deab2d46dd6d160848b9b)
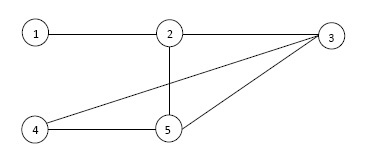












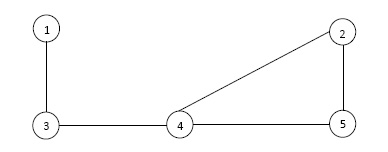


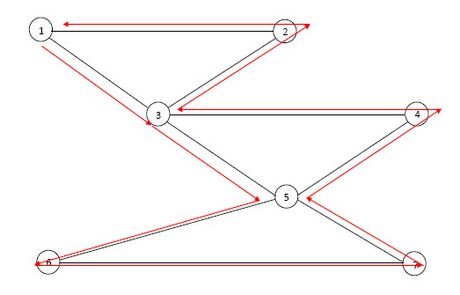
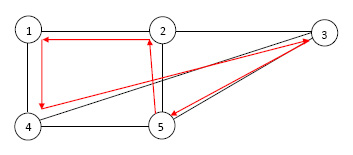

![{\textstyle path[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f87848eb098c4838c03875101e6589b37fb87946)


![{\textstyle path[]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82b38d173ef4e0ecc6a1d37d341d0675010207ba)
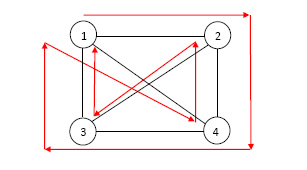
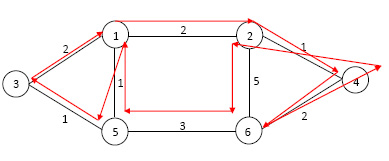




![{\textstyle sortedListEdges[v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2ab293c8e4c8444301da3a7de4ea19b6fb85429)




![{\textstyle minDist[]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6230bad8111a06627bee255aff3b7d1b7072a4c)