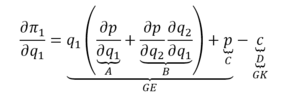Angewandte Mikroökonomik - Gesamt
Sascha Sardadvar studierte Volkswirtschaft an der Universität Wien, der FU Berlin und der Wirtschaftsuniversität Wien. Er hat zahlreiche Artikel in regional- und wirtschaftswissenschaftlichen Fachzeitschriften veröffentlicht und habilitierte sich im Sommer 2015 im Fach Economic Geography and Regional Science. Zu seinen Forschungsschwerpunkten zählen Theorie und Empirie regionalen Wirtschaftswachstums, Ursachen und Auswirkungen interregionaler Arbeitsmigration sowie Fragen der Innovationsökonomik.
Grundzüge der Spieltheorie
Was ist ein Spiel?
Spieltheorie ist eine Möglichkeit, strategische Interaktionen formal darzustellen und damit Informationen zu den Handlungen einzelner Individuen, die mit strategischen Entscheidungen konfrontiert sind, abzuleiten. Strategische Entscheidungen sind solche, die die Aktionen anderer beeinflussen beziehungsweise durch diese selbst beeinflusst werden. Ist dies der Fall, so findet zwischen den Agenten strategische Interaktion statt.
Die Entscheidungssituation wird in einem „Spiel“ dargestellt. Elemente eines Spiels umfassen (1) die Spieler, (2) den Strategienraum, aus dem die Spieler eine Aktion wählen können, und (3) die Auszahlungsstruktur, d.h. der „Gewinn“, den jeder Spieler zu erwarten hat, gegeben eine bestimmte Kombination aus Strategien wird gewählt. Außerdem von Bedeutung ist die zeitliche Abfolge der Entscheidungen der Spieler. Spieler können entweder simultan (dann spricht man von einem „statischen Spiel“) oder nacheinander („dynamisches Spiel“) entscheiden. Im Fall eines dynamischen Spiels entscheidet Spieler 2 sich erst dann für eine Aktion, nachdem er die Strategie von Spieler 1 beobachtet hat. Im Folgenden werden wir uns sowohl mit statischen als auch mit dynamischen Spielen auseinandersetzen und unterschiedliche Lösungskonzepte kennenlernen.
Statische Spiele
Ein statisches Spiel zeichnet sich dadurch aus, dass sich die Spieler simultan für eine Aktion entscheiden. D.h., wenn Spieler 2 seine Entscheidung trifft, weiß er nicht, welche Entscheidung sein Gegenspieler, Spieler 1, trifft. Ein solches Spiel wird oft in der „Normalform“ dargestellt. Angenommen, das Spiel hat zwei Spieler, welche aus zwei möglichen Strategien wählen können. Ein solches Spiel wird wie in jener Tabelle dargestellt:
| Spieler 2 | |||
|---|---|---|---|
|
|
|
Links | Rechts |
| Spieler 1 | Oben | OL1, OL2 | OR1, OR2 |
|
|
Unten | UL1, UL2 | UR1, UR2 |
Die Normalform eines Spieles
In diesem Spiel gibt es zwei Spieler, Spieler 1 und Spieler 2. Spieler 1 hat zwei Strategien zur Auswahl. Er kann entweder die Aktion „oben“ oder die Aktion „unten“ wählen. Spieler 2 auf der anderen Seite kann sich für „rechts“ oder „links“ entscheiden. Die Auszahlungsmatrix stellt außerdem die Auszahlungen (meist wird dies durch Zahlen dargestellt, die Auszahlung bezieht sich also zum Beispiel auf den monetären Nutzen) der Spieler bei jeder möglichen Kombination von gewählten Aktionen dar. Wenn zum Beispiel Spieler 1 „oben“ und Spieler 2 „links“ wählt, so bekommt Spieler 1 die Auszahlung „OL1“ und Spieler 2 „OL2“.
Das Gefangenendilemma
Das „Gefangenendilemma“ ist eines der bekanntesten Probleme aus der Spieltheorie. In diesem Spiel werden zwei Räuber von der Polizei festgenommen. Allerdings liegen zu wenige Beweise vor, die Räuber des Vergehens zu überführen, daher werden sie – getrennt voneinander – verhört. Beide Räuber haben entweder die Möglichkeit zu gestehen oder nichts zu sagen; diese zwei Möglichkeiten entsprechen dem Strategienraum der Räuber. Dieser sieht wie folgt aus:
- Wenn beide gestehen, so können sie des Überfalls überführt werden und müssen im Anschluss eine Haftstrafe von jeweils 6 Jahren verbüßen. Gesteht nur einer der Räuber die Tat, so kann mit diesem Geständnis dem anderen Räuber die Tat nachgewiesen werden, der gestehende Räuber kommt – als Belohnung für seine Kooperationswilligkeit – frei (0 Jahre). Der von seinem Kollegen belastete Räuber muss dann, da er nicht kooperationswillig war, 12 Jahre in Haft verbringen. Sollten beide Räuber Stillschweigen bewahren, so kann ihnen nur ein geringfügiges Vergehen angelastet werden (z.B. unerlaubtes Tragen einer Feuerwaffe) und sie bekommen eine Gefängnisstrafe von je 1 Jahr.
| Räuber 2 | |||
|---|---|---|---|
|
|
|
Gestehen | Nicht gestehen |
| Räuber 1 | Gestehen | -6, -6 | 0, -12 |
|
|
Nicht gestehen | -12, 0 | -1, -1 |
Das Gefangenendilemma
Die Darstellung des Gefangenendilemma in der Normalform ist in oberer Tabelle zu sehen. Da die Jahre, die ein Räuber im Gefängnis verbringen muss, eine negative Auszahlung darstellen (Jahre in Freiheit), werden sie als negative Zahlen dargestellt.
Lösungskonzept: iteratives Eliminieren dominierter Strategien
In der Spieltheorie untersucht man das Entscheidungsverhalten von Individuen, d.h., man möchte herausfinden, wie sich Individuen beziehungsweise Entscheidungsträger in gewissen Situationen, in denen strategische Entscheidungen vonnöten sind, rational verhalten. Im Folgenden werden wir uns mit Lösungskonzepten auseinandersetzen, mittels derer wir die Frage „Welche Aktionen werden die Entscheidungsträger wählen?“ beantworten können.
Eine erste Möglichkeit herauszufinden, wie sich die Entscheidungsträger verhalten, liegt in der Betrachtung dominanter beziehungsweise dominierter Strategien. Eine stark (= strikt) dominante Strategie ist eine Strategie, die immer bevorzugt wird, egal welche Aktion der andere Spieler wählt. Demgegenüber ist eine stark (= strikt) dominierte Strategie eine, die unter keinen Umständen gewählt wird. Von schwach dominanten Strategien spricht man, wenn die Strategie eine zumindest gleich hohe Auszahlung bringt (bzw. schwach dominiert bei maximal gleich hoher Auszahlung). Der Unterschied zwischen stark und schwach dominant/dominiert ist v.a. bei gleich hohen Auszahlungen relevant, in diesem Fall ist ein Spieler indifferent.
Um dieses Konzept zu veranschaulichen, betrachten wir noch einmal das Gefangenendilemma aus Sicht von Räuber 1:
- Er hat die Möglichkeit, aus zwei Strategien zu wählen, „gestehen“ oder „nicht gestehen“. Angenommen, Räuber 2 wählt die Aktion „gestehen“. In diesem Fall würde Räuber 1, wählte er „gestehen“, 6 Jahre im Gefängnis verbringen, während er, sollte er sich für „nicht gestehen“ entscheiden, 12 Jahre verbüßen müsste - wählt Räuber 2 „gestehen“, so ist es für Räuber 1 am besten, ebenfalls zu gestehen (da er dann nur 6 statt von 12 Jahren im Gefängnis verbringen muss).
- Wie stellt sich die Situation nun dar, wenn Räuber 2 sich für die Aktion „nicht gestehen“ entscheidet? In diesem Fall würde Räuber 1, sollte er sich für „gestehen“ entscheiden, 0 Jahre Gefängnis erhalten. Sollte er sich hingegen für „nicht gestehen“ entscheiden, müsste er 1 Jahr in Gefangenschaft verbringen. Auch in diesem Fall ist es also im Interesse von Räuber 1 die Aktion „gestehen“ zu wählen.
Da Räuber 2 mit denselben Auszahlungen konfrontiert ist, gilt für ihn das gleiche Ergebnis. Im Gefangenendilemma ist also „gestehen“ für beide Seiten die dominante Strategie. Das ist das relevante Ergebnis des Gefangenendilemmas: Wofür auch immer sich der andere Spieler entscheidet, der Entscheidungsträger wählt „gestehen“. Obwohl offensichtlich ist, dass das kollektiv beste Ergebnis erzielt würde, wenn beide Spieler „nicht gestehen“ wählen, kommt dieses Ergebnis nicht zustande: Jeder Spieler ist für sich besser daran, wenn er „gestehen“ wählt. [1]
Wir haben nun mit der Theorie dominanter Strategien dieses Spiel gelöst. Da „gestehen“ für beide Räuber die dominante Strategie ist, werden sie beide diese wählen. Der Spielausgang ist also durch („gestehen“, „gestehen“) gegeben, und beide Räuber werden jeweils 6 Jahre im Gefängnis verbringen.
|
|
|
|
Spieler 2 |
|
|
|
|
Links | Mitte | Rechts |
| Spieler 1 | Oben | 3, 2 | 3, 4 | 2, 3 |
|
|
Unten | 2, 5 | 2, 3 | 4, 2 |
Beispiel zum iterativen Eliminieren dominierter Strategien
Die obere Tabelle veranschaulicht ein weiteres Spiel, in dem dieses Lösungskonzept zur Anwendung kommt. Das besprochene Lösungskonzept schlägt zur Lösung eines solchen Spieles vor, die dominierten Strategien zu eliminieren, da diese bei rationalem Verhalten nie gewählt werden würden. Betrachten wir Spieler 2. Wenn Spieler 1 „oben“ wählt, so ist es für Spieler 2 am besten, „Mitte“ zu wählen. Wählt Spieler 1 „unten“, so ist es optimal für Spieler 2, „links“ zu wählen. Dementsprechend wird Spieler 2 nie die Strategie „rechts“ wählen, egal welche Aktion Spieler 1 wählt - sie ist durch die beiden anderen Strategien dominiert.
|
|
|
Spieler 2 |
|
|
|
|
Links | Mitte |
| Spieler 1 | Oben | 3, 2 | 3, 4 |
|
|
Unten | 2, 5 | 2, 3 |
Beispiel nach erster Eliminierung
Da Spieler 1 bekannt ist, dass Spieler 2 niemals „rechts“ wählen wird, verkürzt sich nach Eliminierung dieser irrelevanten Alternative wie in der oberen Tabelle dargestellt. Betrachten wir nun das Entscheidungsproblem von Spieler 1. Wenn Spieler 2 „links“ wählt, so ist es für Spieler 1 am besten „oben“ zu wählen. Auch wenn Spieler 2 „Mitte“ wählt, ist „oben“ die bessere Alternative für Spieler 1. Demnach ist „unten“ also eine dominierte Strategie für Spieler 1. Da Spieler 2 dies voraussieht, stellt sich das Spiel wie in folgender Tabelle dar (die Strategie „unten“ wird eliminiert):
|
|
|
Spieler 2 |
|
|
|
|
Links | Mitte |
| Spieler 1 | Oben | 3, 2 | 3, 4 |
Beispiel nach zweiter Eliminierung
Spieler 2 hat nun die Wahl zwischen einer Auszahlung von 2 beziehungsweise 4 und wird demnach die Aktion „Mitte“ wählen. Das Gleichgewicht in dem Spiel ist also durch („oben“, „Mitte“) gegeben. Die Spieler erhalten die Auszahlungen (3, 4). So wird durch das iterative Eliminieren möglich, den Ausgang eines strategischen Spiels vorauszusagen.
Diskussion
Spiele, die dem Gefangenendilemma gleichen und mit diesem gelöst werden können, treten in vielen Situationen auf. Ein besonders markantes Beispiel dafür ist das atomare Wettrüsten, welches während des Kalten Krieges zwischen der UdSSR und den USA stattfand. Die Angst angegriffen zu werden, führte zur ständigen Aufrüstung. Das wünschenswerte Gleichgewicht in dieser Situation wäre beidseitige Abrüstung und damit einhergehend das Einsparen vieler Ressourcen und nuklearer Unfälle gewesen. Ein Atomkrieg hätte jedoch eine noch größere negative Auszahlung mit sich gebracht (gewissermaßen unendlich). Zwar war das Spiel nicht statisch, aber so lange nicht völlig abgerüstet würde, war man selbst stets besser daran, aufzurüsten. Nur die Pattstellung durch maximale atomare Abschreckung minimierte die Wahrscheinlichkeit, dass die jeweils andere Seite den atomaren Erstschlag durchführen würde. [2]
Somit können Gleichgewichte, die aus Gefangenendilemma-ähnlichen Situationen resultieren, ineffizient insofern sein, dass mindestens ein Spieler bessergestellt werden könnte, ohne den anderen schlechter zu stellen. Im Falle der oben beschriebenen Situationen wären sogar alle Spieler bei einem Ausgang des Spieles („nicht gestehen“, „nicht gestehen“), bessergestellt. Das Ergebnis sieht jedoch möglicherweise anders aus, wenn dasselbe Spiel wiederholt gespielt wird, die Räuber also immer wieder aufeinandertreffen.
Lösungskonzept: Nash-Gleichgewicht
Das obige Lösungskonzept ist zwar sehr hilfreich, allerdings werden wir oft auf Situationen stoßen, in denen keine Strategie dominiert ist und die optimale Strategie damit von der Aktion des Gegenübers abhängt. Können wir auch in einem solchen Fall eine Vorhersage über den Ausgang eines Spieles treffen? Dies ist möglich mit einem weiteren Lösungskonzept, dem Konzept des Nash-Gleichgewichtes.
|
|
|
Ehefrau |
|
|
|
|
Fußball | Theater |
| Ehemann | Fußball | 2, 1 | 0,0 |
|
|
Theater | 0,0 | 1,2 |
Der Kampf der Geschlechter
Die obere Tabelle zeigt das Spiel „Kampf der Geschlechter“, das auf einer alltäglichen Konfliktsituation basiert. Ein Ehepaar möchte etwas gemeinsam unternehmen, hat aber verschiedene Präferenzen: Er geht lieber zu einem Fußballspiel, sie ins Theater. Beide Ehepartner begleiten jedoch lieber ihren Gatten / ihre Gattin, als gar nichts zu unternehmen. In diesem Fall gibt es keine dominierte Strategie. Im Falle, dass die Frau „Theater“ wählt, bevorzugt auch der Mann „Theater“, und vice versa beim Fußballspiel.
Um in diesem Spiel ein Gleichgewicht zu identifizieren, arbeitet man mit dem Konzept der Methode der Besten-Antwort-Korrespondenz. Dabei findet man die „beste Antwort“ beider Spieler auf die möglichen Strategien des jeweils anderen und markiert diese; in nachfolgender Tabelle wird dies durch Unterstreichen durchgeführt.
|
|
|
Ehefrau |
|
|
|
|
Fußball | Theater |
| Ehemann | Fußball | 2, 1 | 0,0 |
|
|
Theater | 0,0 | 1,2 |
Nash-Gleichgewichte im Kampf der Geschlechter
Ein Nash-Gleichgewicht tritt dann auf, wenn beide Spieler beste Antworten auf die Strategie des jeweils anderen wählen, also in dem Punkt, an dem zwei unterstrichene Auszahlungen in einem Matrixelement aufeinandertreffen. In dem Kampf der Geschlechter sind also die beiden Strategiepaare (Fußball, Fußball) und (Theater, Theater) Nash-Gleichgewichte. Ein Nash-Gleichgewicht wird als Gleichgewicht bezeichnet, da in einem solchen beide Spieler keinen Anreiz haben, (einseitig) abzuweichen, d.h., einseitig eine andere als die Gleichgewichtsstrategie zu wählen. Anders formuliert kann sich kein Spieler, gegeben der Aktion seines Gegenübers, verbessern, indem er eine andere Strategie wählte. Wenn im konkreten Fall die Ehefrau zuerst den Vorschlag macht, besteht das Gleichgewicht (Theater, Theater). Keiner der Ehepartner hat ein Interesse daran, abzuweichen, da dann die Auszahlung niedriger wäre, indem das Ehepaar gar nichts unternehmen würde.
Zu beachten ist in diesem Zusammenhang, dass ein Gleichgewicht in dominanten Strategien immer ein Nash-Gleichgewicht ist, dies allerdings umgekehrt nicht gilt. Das Konzept des Nash-Gleichgewichtes ist also ein „schwächeres“ als das des Gleichgewichtes in dominanten Strategien. Es ermöglicht, Gleichgewichte auch in Spielen zu finden, in denen keine Strategien dominiert sind, und damit gewisse Vorhersagen über den Ausgang in einer solchen Situation abzugeben.
Somit gibt es nicht immer ein eindeutiges Nash-Gleichgewicht. Im obigen Beispiel des Kampfes der Geschlechter etwa sind beide Strategiepaare (Fußball, Fußball) und (Theater, Theater) Nash-Gleichgewichte. In einem solchen Fall können wir mit Hilfe der Spieltheorie nur eine Aussage darüber treffen, dass eines dieser Gleichgewichte auftreten wird; welches der beiden gewählt wird, kann jedoch nicht vorausgesagt werden. D.h., im Falle des Nash-Gleichgewichts-Konzeptes kann keine Aussage darüber getroffen werden, wie die Spieler zu einem Gleichgewicht kommen, nur dass, sobald die Spieler sich im Gleichgewicht befinden, dieses stabil ist (da keiner der Spieler einen Anreiz hat, einseitig abzuweichen). Um das Gleichgewicht zu erreichen, werden häufig Koordinationsmechanismen benötigt (zum Beispiel ein Telefonanruf im Kampf der Geschlechter). Wenn bspw. internationale Abkommen geschlossen werden, so müssen diese, um stabil zu sein, Nash-Gleichgewichte darstellen. Der Koordinationsmechanismus ist in diesem Fall durch internationale Konferenzen, auf welchen die Details der Abkommen ausgehandelt werden, gegeben. Sobald ein solches Abkommen in Kraft tritt, d.h. alle Teilnehmer auf das Nash-Gleichgewicht koordiniert sind, hat kein einzelner Teilnehmer mehr einen Anreiz, abzuweichen – das Abkommen ist also stabil.
Dynamische Spiele
Bis jetzt wurden nur statische Spiele betrachtet – eine Möglichkeit, die Dimension Zeit in ein Spiel zu inkorporieren, ist es, die Spieler nacheinander (nicht: simultan) entscheiden zu lassen. Hierbei handelt es sich um sequenzielle Spiele. Eine weitere Möglichkeit ist es, die Spieler ein simultanes Spiel mehrere Male hintereinander spielen zu lassen. In diesem Fall handelt es sich um wiederholte Spiele.
Der Zusammenhang zwischen sequenziellen und simultanen Spielen: Das Lösungskonzept der Rückwärtsinduktion
In einem sequenziellen Spiel ist die zeitliche Abfolge von großer Bedeutung. Betrachten wir dafür ein Spiel, welches zuerst als simultanes Spiel und darauffolgend als sequenzielles Spiel gespielt wird. Die Spielmatrix, welche sich auf das simultane Spiel bezieht, stellt sich wie in nachfolgender Tabelle dar:
|
|
|
Spieler 2 |
|
|
|
|
Links | Rechts |
| Spieler 1 | Oben | 1, 9 | 1,9 |
|
|
Unten | 0,0 | 2,1 |
Beispiel für ein simultanes Spiel
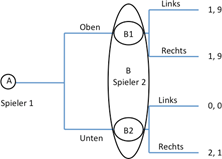
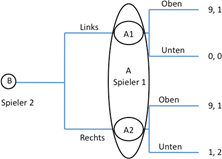
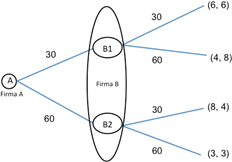
In obigem Spiel sind die Beste-Antwort-Strategien analog zum vorigen Abschnitt markiert. Wie man sehen kann, gibt es in diesem simultanen Spiel zwei Nash-Gleichgewichte: (oben, links) und (unten, rechts). Wie ändert sich die Voraussage für den Spielausgang, wenn das gleiche Spiel sequenziell gespielt wird? Angenommen, Spieler 1 entscheidet sich zuerst für eine Aktion. Spieler 2 reagiert danach. Diese Situation lässt sich in einem Spielbaum wie in nachfolgender Abbildung darstellen:
Im abgebildeten Spielbaum ist jeder Punkt, an dem ein Spieler eine Entscheidung trifft (Entscheidungspunkte), markiert. Als Lösungskonzept kommt die Rückwärtsinduktion zur Anwendung. Dabei wird das Spiel von hinten aufgerollt, d.h., man betrachtet zuerst die letzte Entscheidung des Spieles und arbeitet sich dann nach vorne.
Der letzte Entscheidungspunkt in der oberen Abbildung ist Punkt B. In diesem Punkt entscheidet sich Spieler 2 zwischen den beiden potenziellen Aktionen „links“ und „rechts“. Sollte er sich an Punkt B1 befinden – was dann der Fall ist, wenn sich Spieler 1 in der Runde davor für „oben“ entschieden hat – dann ist für Spieler 2 irrelevant, ob er links oder rechts wählt – er erhält in beiden Fällen eine Auszahlung im Wert von 9. Sollte er sich an dem Punkt B2 befinden, so wird er rechts wählen, da 1 größer ist als 0. Somit ist klar, dass Spieler 2 in jedem Fall rechts wählen wird, da die Auszahlung entweder gleich oder größer ist als bei der Wahl „links“.
Mit diesem Wissen gehen wir nun nach vorne im Spielablauf, zur Entscheidung von Spieler 1 im Entscheidungspunkt A. Er weiß, wie Spieler B auf seine Entscheidung reagieren wird und trifft mit diesem Wissen seine eigene Entscheidung. D.h., Spieler 1 hat die Wahl zwischen einer Auszahlung von 1, wenn er „oben“ wählt und 2, wenn er „unten“ wählt. Somit ist klar, dass Spieler 1 „unten“ wählen wird und der Spielausgang durch das Aktionenpaar (unten, rechts) gegeben und die damit einhergehenden Auszahlungen sind (2, 1).
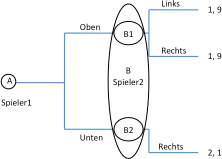
Bei dem Lösungskonzept der Rückwärtsinduktion geht man von dem Konzept der „common rationality“ aus, d.h., man nimmt an, dass alle Spieler rational handeln und dies auch voneinander wissen. Im obigen Beispiel handelt Spieler B rational, in dem er an Entscheidungspunkt B1 indifferent zwischen „links“ und „rechts“ ist und an Entscheidungspunkt B2 „rechts“ wählt. Spieler A wiederum weiß, dass Spieler B rational handelt und baut darauf seine eigene Entscheidung auf. D.h., er betrachtet das verkürzte Spiel, welches für ihn tatsächlich relevant ist, wie in folgender Abbildung dargestellt.
Gegeben, Spieler 1 ist tatsächlich mit diesem Spiel konfrontiert, ist es offensichtlich, dass er sich für die Aktion „unten“ entscheiden wird, da diese ihm eine höhere Auszahlung sichert. Durch die Integration einer Zeitdimension gelangen wir nun also zu einer konkreten Vorhersage für den Ausgang dieses Spieles.
Das Ultimatum-Spiel
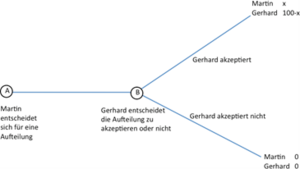
Ein oft zitiertes Beispiel für ein sequenzielles Spiel ist das sogenannte Ultimatum-Spiel. Martin soll 100 Euro zwischen sich selbst und einem zweiten Spieler, Gerhard, aufteilen. Der Spielverlauf gibt vor, dass Martin zuerst über die Aufteilung der 100 Euro entscheidet. Er macht damit ein Angebot an Gerhard, welcher dieses Angebot im nächsten Schritt annehmen oder ablehnen kann. Nimmt er es an, so werden die 100 Euro gemäß Martins Angebot aufgeteilt. Lehnt er es ab, so bekommen beide Spieler kein Geld und die 100 Euro gehen verloren (oder zurück an den Spielleiter). Der Spielbaum des Ultimatum-Spiels ist in nachfolgender Abbildung dargestellt.
Dieses Spiel lässt sich nicht in simultaner Form darstellen, da Martins Strategienraum sehr groß ist. Er kann sich in dem Spiel nicht nur zwischen zwei alternativen Aktionen entscheiden, sondern kann eine Aufteilung von 0 bis 100 wählen. Er hat also, wenn man annimmt, dass er runde Beträge angeben muss, die Auswahl aus 101 möglichen Aktionen.
Auch dieses Spiel lösen wir wieder mit Hilfe der Rückwärtsinduktion. In der letzten Entscheidungsstufe entscheidet Gerhard zwischen 0 Euro, wenn er Martins Angebot ablehnt, und (100 - x) Euro, wenn er es annimmt, wobei x dem Anteil entspricht, den Martin vorgeschlagen haben wird, selbst zu behalten. Demnach wird er in dieser Stufe jedes Angebot von Martin akzeptieren, welches ihm eine Auszahlung von mehr als 0 Euro sichert, da jede dieser Auszahlungen größer ist, als gar nichts zu bekommen. Martin, als rationaler Spieler, antizipiert dieses Verhalten und wird – nachdem er, um seine eigene Auszahlung zu maximieren, Gerhards Anteil möglichst klein halten muss – Gerhard nur 1 Euro anbieten und demnach 99 Euro für sich selbst behalten. Dies ist also der Ausgang des Ultimatum-Spiels: In der ersten Stufe bietet Martin Gerhard 1 Euro an und behält damit 99 Euro für sich. In der zweiten Stufe akzeptiert Gerhard dieses Angebot, da 1 Euro größer ist als 0 Euro. Die Auszahlungen im Gleichgewicht sind demnach (99,1).
Aus eigenen Beobachtungen würden wohl viele Menschen diesem Ausgang des Spieles nicht glauben. Sie selbst würden ein Angebot wie jenes von Martin als unfair empfinden und es demnach – auch wenn eine solche Handlungsweise nicht rational (im Sinne von: Gewinn maximierend) ist – ablehnen. Zu dem Erstaunen von vielen Spieltheoretikern stellte sich bei Experimenten heraus, dass dies tatsächlich zutrifft: circa 40% bis 60% der Teilnehmer lehnten ein niedriges Angebot ab, obwohl dies zur Folge hatte, dass sie am Ende des Spieles eine Auszahlung von 0 erhielten. Nach ihren Motiven befragt, gaben viele an, dass sie eine so ungleiche Aufteilung unfair empfanden und es daher vorzogen leer auszugehen, wenn dies hieße, dass der Gegenspieler ebenfalls eine Auszahlung von Null erhielt. [3] Man wollte also das Gegenüber, welches das unfaire Angebot unterbreitet hatte, bestrafen.
Glaubwürdige Drohungen und Versprechen
In der obigen Variante wäre eine Drohung Gerhards bei rationalen Spielern nicht glaubwürdig. Der Grund dafür ist, dass es für Gerhard nicht rational ist, ein Angebot von 1 Euro abzulehnen, da er sonst 0 Euro erhielte und Martin seine Entscheidung nicht mehr ändern kann. Wenn man also von rationalen Spielern ausgeht, dann sind Drohungen oder Versprechen, die sich bei Rückwärtsinduktion als nicht rational herausstellen, nicht glaubwürdig. Eine glaubhafte Drohung (oder Versprechen) ist eine, deren Ausführung im Interesse des Spielers liegt, wenn er an der Reihe ist, seine Entscheidung zu treffen. Aus dieser Logik stammt das Konzept der Rückwärtsinduktion.
Das Problem der Verbindlichkeit
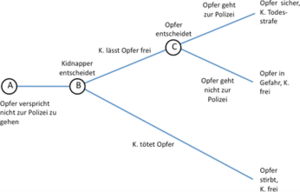
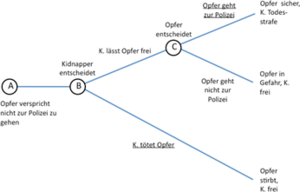
Betrachten wir ein weiteres Spiel, welches obiges Problem deutlich darstellt. Ein Kidnapper überlegt, ob er sein Opfer laufen lassen soll oder nicht. Der Spielbaum sieht wie in folgender Abbildung dargestellt aus.
Ein Kidnapper, der sein Opfer entführt hat, ändert plötzlich seinen Plan und möchte das Opfer am liebsten wieder frei lassen. Er ist allerdings besorgt, dass das Opfer, sobald es frei ist, zur Polizei gehen könnte und er als Folge ins Gefängnis müsste. Die andere mögliche Aktion des Kidnappers ist, dass er das Opfer umbringt und sich damit von seiner Verantwortung befreit. Das Opfer auf der anderen Seite realisiert, dass es, selbst wenn es freikommen sollte, immer noch in Gefahr schweben würde, da der Kidnapper es sich zu einem späteren Zeitpunkt noch einmal anders überlegen könnte. Das Opfer hat also, sollte es freikommen, einen Anreiz, zur Polizei zu gehen.
In dem vorliegenden Spiel wenden wir wieder das Lösungskonzept Rückwärtsinduktion an. Die erste Überlegung gilt also der Entscheidung an Punkt C - wie würde sich das Opfer an diesem Punkt entscheiden? Es hat die Wahl zwischen der Auszahlung (in einem erweiterten Sinn) „Opfer ist sicher“ und „Opfer schwebt weiter in Gefahr“. In dieser Situation würde das Opfer natürlich ersteres präferieren und wird sich dementsprechend dafür entschließen, zur Polizei zu gehen. Betrachten wir nun den Entscheidungspunkt davor, Punkt B. In Punkt B trifft der Kidnapper eine Entscheidung, wissend, wie sich das Opfer danach (an Punkt C) verhalten wird. Der Kidnapper kann das Opfer entweder frei lassen oder es umbringen. Wenn er das Opfer frei lässt, weiß er, dass dieses danach zur Polizei gehen würde. In diesem Fall würde der Kidnapper zur Todesstrafe verurteilt werden. Sollte er sich dafür entscheiden, das Opfer zu töten, so wird er überleben. Der Kidnapper wird sich also an Punkt B dafür entscheiden, sein Opfer zu töten. Der Spielbaum mit den eingezeichneten optimalen Strategien an jedem Entscheidungspunkt sieht also wie in der unteren Abbildung aus.
Wir kennen nun also den Ausgang des obigen strategischen Spiels. An Punkt A wird das Opfer versprechen, nicht zur Polizei zu gehen und an Punkt B wird sich der Kidnapper dafür entscheiden, das Opfer zu töten. Die „Auszahlungen” bestehen also darin, dass das Opfer getötet wird und der Kidnapper überlebt.
Hier sehen wir, welch ein großes Problem es darstellen kann, wenn in bestimmten Situationen Versprechen nicht glaubwürdig gegeben werden können. Beide, sowohl das Opfer als auch der Kidnapper, möchten eigentlich, dass das Opfer frei gehen kann, doch kann dies nicht das Resultat des Spieles sein, da das Versprechen des Opfers, den Kidnapper nicht zu verraten, nicht glaubwürdig ist.
Dieses “commitment problem” tritt in strategischen Situationen oft auf (wir haben ähnliche Situationen wie im Kidnapper-Opfer-Spiel auch im Gefangenendilemma oder Ultimatum-Spiel beobachtet). Ein „commitment problem“ ist in solchen Situationen gegeben, in welchen ein erwünschter Spielausgang (also ein Spielausgang, in dem beide Spieler bessergestellt wären) nicht erreicht werden kann, da keine glaubhaften Versprechen beziehungsweise Drohungen von Seiten der Spieler ausgesprochen werden können. In einem solchen Fall wird ein sogenannter „commitment device“ gebraucht, um doch noch den erwünschten Spielausgang zu erreichen. Dies gibt dem jeweiligen Spieler einen Anreiz, das Versprechen beziehungsweise die Drohung im Fall des Falles auch einzuhalten und macht diese damit glaubwürdig.
Im Kidnapper-Spiel könnte das Opfer ein Verbrechen begehen, welches es den Kidnapper beobachten lässt. Der Kidnapper könnte dann selbst zur Polizei gehen, sollte das Opfer sich nicht an sein Versprechen den Kidnapper nicht anzuzeigen halten. Damit hat das Opfer einen Anreiz sich an sein Versprechen zu halten - es wird also glaubwürdig. In dem Fall wäre der Ausgang des Spieles (Opfer in Gefahr, Kidnapper frei) ein Ausgang, den beide Spieler zu dem oben besprochenen Gleichgewicht bevorzugen.
Wiederholte Spiele
Eine spezielle Form sequenzieller Spiele ist die Klasse der wiederholten Spiele. Hier wird ein simultanes Spiel mehrere Male wiederholt. Wenn ein Spiel mehrere Male wiederholt wird, so eröffnet dies die Möglichkeit den Gegenspieler in der zweiten Runde für unerwünschtes Verhalten in der ersten Runde zu bestrafen. Durch diese Strategie kann kooperatives Verhalten attraktiver gemacht werden.
Im Gefangenendilemma wird das Spiel nun in dem Sinn wiederholt, dass dieselben zwei Räuber mehrere Mal aufeinandertreffen. Somit gibt es die Möglichkeit, dass ein Räuber dem anderen droht, sollte dieser sich in der ersten Runde nicht kooperativ verhalten. Dies stellt eine Möglichkeit dar, die für das Kollektiv optimale Situation zu erreichen, in diesem Fall („nicht gestehen“, „nicht gestehen“). Man spricht hier von einer Tit-For-Tat-Strategie, d.h., Räuber 1 wird in der ersten Runde (beim ersten Aufeinandertreffen) kooperieren (also „nicht gestehen“ wählen), in jeder weiteren Runde allerdings die Aktion wählen, die Räuber 2 in der Runde davor gewählt hatte. Wenn bspw. Räuber 2 in der ersten Runde „gestehen“ wählt und damit Räuber 1 für 12 Jahre ins Gefängnis schickt (der schlechteste Ausgang für Räuber 1), so wird Räuber 1 Räuber 2 in der nächsten Runde, wenn das Spiel ein weiteres Mal gespielt wird, dafür bestrafen, indem er selbst nun „gestehen“ spielt. Ob diese Strategie funktionieren kann mit einem Gleichgewicht („nicht gestehen“, „nicht gestehen“), wird dadurch bestimmt, ob das Spiel endlich oder unendlich viele Male wiederholt wird.
Dies wird klar, wenn man auch in diesem Fall mit dem Konzept der Rückwärtsinduktion arbeitet. Nehmen wir an, das Gefangenendilemma wird endlich oft wiederholt, die Räuber treffen zum Beispiel fünf Mal aufeinander. Beginnen wir also bei dem letzten Entscheidungspunkt, an dem das Spiel zum fünften Mal gespielt wird. Von diesem Punkt aus gesehen stellt sich die Entscheidungssituation also genau so dar, wie in dem einfachen, nicht wiederholten simultanen Spiel: „Gestehen“ ist die dominante Strategie und wird daher auch von beiden Räubern gewählt. Die Vorhersage für den Ausgang des Spieles ist somit („gestehen“, „gestehen“). Mit diesem Wissen beginnen die Räuber die vorletzte Wiederholung des Spieles (Runde 4). Beide wissen, dass sich in der darauffolgenden Runde der jeweils andere Räuber für „gestehen“ entscheiden wird. Damit verliert die oben zitierte Tit-For-Tat-Strategie an Glaubwürdigkeit, da der Ausgang der jeweils nächsten Runde feststeht, egal, wie in der Runde davor entschieden wurde. Die Tit-For-Tat-Strategie ist also in der vierten Runde nicht glaubwürdig und damit ist der Ausgang in Runde 4 auch („gestehen“, „gestehen“) – usw. bis zur ersten Runde. Damit ist die Tit-For-Tat-Strategie jedoch bereits in der ersten Runde nicht glaubwürdig und bietet keine Möglichkeit, Kooperation unter den Räubern zu etablieren.
Der Ausgang endlich wiederholter simultaner Spiele entspricht also dem Ausgang des einmaligen simultanen Spiels. Durch die endliche Wiederholung kann keine Verhaltensänderung induziert werden. Wird das Spiel allerdings unendlich oft wiederholt (beziehungsweise ist das Ende der Wiederholungen nicht bekannt), funktioniert eine Tit-For-Tat-Stratgie und bietet damit eine Möglichkeit, das kollektive Optimum zu etablieren oder diesem zumindest näherzukommen. Die Spieler kooperieren, da sie sich dadurch Kooperation des Gegenspielers in der Zukunft erwarten. Die Tit-For-Tat-Strategie im Speziellen funktioniert nach dem Prinzip: „Behandle andere, wie du selbst behandelt werden möchtest“. Die in diesem Prinzip inhärente Drohung der Vergeltung dient beiden Spielern, indem ein Gleichgewicht, das von beiden bevorzugt wird, erreicht werden kann.
Übungen
Übungsbeispiel 1.1
Betrachten Sie eine Tit-For-Tat-Strategie in einem wiederholten Gefangenendilemma. Nehmen Sie an, ein Spieler macht einen Fehler und wählt „gestehen“ (also das nicht-kooperative Verhalten), obwohl er eigentlich kooperieren wollte (also eigentlich „nicht gestehen“ wählen wollte). Wenn danach beide Spieler weiterhin die Tit-For-Tat-Strategie spielen, wie entwickelt sich der Spielverlauf? Welche Aktionen werden gewählt?
Übungsbeispiel 1.2
Nehmen Sie an, im Gefangenendilemma wird beiden Räubern erlaubt, sich aneinander zu rächen, nachdem sie ihre jeweiligen Gefängnisstrafen hinter sich gebracht haben. Wie würde sich das Spiel formal ändern? Könnte ein effizienteres Ergebnis erreicht werden?
Übungsbeispiel 1.3
Angenommen, in dem in Tabelle 1-8 dargestellten Spiel würde Spieler 2 zuerst die Entscheidung treffen und Spieler 1 würde erst danach reagieren. Die zeitliche Abfolge wäre also genau umgekehrt als sie in Abbildung 1-1 dargestellt ist. Zeichnen Sie den Spielbaum, der dieses sequenzielle Spiel darstellt. Wodurch ist das Gleichgewicht in diesem Spiel gegeben? Welche zeitliche Abfolge würde Spieler 2 bevorzugen? Würde er lieber zuerst oder lieber nach Spieler 1 entscheiden?
Übungsbeispiel 1.4
Ein Unternehmer überlegt, ob er eine neue Dependance in einer anderen Stadt eröffnen soll. Er müsste dazu einen neuen Manager anstellen, der sich um die neue Filiale kümmern würde. Findet er einen Manager, der diese Aufgabe ehrlich erledigen würde, so könnte er ihm ein Gehalt von monatlich 5000 Euro zahlen. Dies wäre ein sehr gutes Gehalt für den Manager, da er anderswo nur 2500 Euro verdienen könnte. Wäre der Manager ehrlich, könnte der Unternehmer, trotz des hohen Gehalts, immer noch einen Gewinn von 1600 Euro im Monat machen. Da sich die Filiale in einer anderen Stadt befindet, wäre es unmöglich für den Unternehmer, den Manager zu überwachen. Dieser hätte also die Möglichkeit, sich unehrlich zu verhalten und dem Unternehmen Geld zu stehlen. In dem Fall könnte der Manager sein Gehalt um 2200 Euro aufbessern (insgesamt also 7200 Euro in seiner Position „verdienen“), während der Unternehmer Verluste mit der neuen Filiale machen würde. Diese würden sich auf 1200 Euro belaufen. Der Unternehmer gibt eine Annonce auf, mehrere Bewerber melden sich.
(a) Angenommen, der Unternehmer geht davon aus, dass alle Manager, die er anstellen könnte, nur daran interessiert sind, ihr Einkommen zu maximieren – wird er sich dafür entscheiden, die Filiale eröffnen? Stellen Sie das Spiel in Normalform dar und begründen Sie Ihre Antwort.
(b) Angenommen, der Unternehmer weiß, dass einer seiner Kandidaten für die Stelle des Managers unehrliches Verhalten aus religiösen Gründen ablehnt. Er nimmt an, dass dieser Kandidat bereit wäre, bis zu 20.000 Euro zu zahlen, damit er nicht mit dem Gefühl der Schuld leben muss (anders formuliert: die Sünde des Diebstahls kostete den Manager 20.000 Euro). Würde der Unternehmer in diesem Fall die Filiale eröffnen? Wie ändert sich in diesem Fall die Spielmatrix? Stellen Sie das Spiel dar und begründen Sie Ihre Antwort.
Übungsbeispiel 1.5
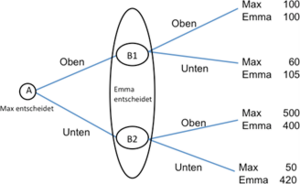
Max und Emma spielen ein Spiel, in dem Max als erster eine Entscheidung trifft (siehe Abbildung unten). Nachdem Max sich entweder für „oben“ oder „unten“ entschieden hat, kann sich Emma ihrerseits für „oben“ oder „unten“ entscheiden.
Wo liegt das Gleichgewicht in diesem Spiel, welche Strategien werden gewählt und welche Auszahlungen erhalten Max und Emma?
Nehmen Sie an, Emma kann, bevor Max sich entscheidet, eine verbindliche Aussage darüber treffen, entweder „oben“ oder „unten“ zu wählen – was würde sie wählen? Wie würde das Gleichgewicht in diesem Fall aussehen?
Lösungen
Übungsbeispiel 1.1
Der zweite Spieler wird, nachdem der erste Spieler (unbeabsichtigt) auf eine nichtkooperative Strategie abgewichen ist, selbst auch abweichen (als Resultat der Tit-For-Tat-Strategie). In der nächsten Runde wird allerdings der erste Spieler, als Antwort auf das Abweichen des zweiten Spielers in der Vorrunde, selbst wieder abweichen und jeder der Spieler wird danach die nichtkooperative Strategie wählen. Dieses Beispiel macht deutlich, dass eine Tit-For-Tat-Strategie nicht die optimale Strategie ist, wenn die Möglichkeit besteht, dass Spieler Fehler begehen.
Übungsbeispiel 1.2
Wenn die beiden Spieler die Möglichkeit haben, sich aneinander zu rächen, würde sich formal die Auszahlungsstruktur des Spieles ändern. Dies könnte zu einem effizienten Ausgang des Spieles führen – zum Beispiel könnten die Spieler sich einigen, einander umzubringen, sollte der jeweils andere gestehen. Wenn Sie nun annehmen, dass die Auszahlung „Tod“ einen unendlich negativen Nutzen hat, kann sich die Spielmatrix so ändern, dass das Gleichgewicht, in dem beide Spieler „nicht gestehen“ wählen, auftritt. Dazu jedoch zwei Anmerkungen:
- Erstens kann einer der Räuber immer noch „gestehen“ wählen und den anderen, nachdem dieser freigekommen ist, zuerst umbringen. Es müsste also sichergestellt werden, dass die Drohung hinreichend realistisch ist, um zum Ergebnis „nicht gestehen“ zu kommen.
- Man beachte die Analogie zur atomaren Abschreckung: Die Drohung, die strategische Atomwaffen implizieren, ist, das Land des Feindes völlig zu zerstören, nachdem dieser den Erstschlag ausgeführt hat. Die Lösung des „Spiels“ der atomaren Abschreckung ist daher für beide Seiten „nicht angreifen“. Dazu gehört auch, sich als Atommacht stets so zu verhalten, dass die Angst vor der völligen Zerstörung für den Feind realistisch ist. Strategische Atomwaffen nur zu besitzen reicht daher nicht aus, es muss der Zweitschlag jederzeit – auch dann, wenn das eigene Land durch den Erstschlag bereits zerstört sein sollte – durchgeführt werden können, um beim Feind glaubwürdig zu sein. Aus diesem Grund sind bspw. mit strategischen Atomwaffen bestückte U-Boote permanent irgendwo in den Meeren unterwegs und selbst für befreundete Staaten nicht zu orten (d.h. der Feind muss einerseits wissen, dass es diese jederzeit einsatzfähigen Waffen gibt, er darf aber gleichzeitig nicht wissen, wo sie sich befinden, da er sie sonst außer Gefecht setzen könnte).
Übungsbeispiel 1.3
Der neue Spielbaum sieht wie folgt aus:
Im neuen Gleichgewicht wählt Spieler 2 entweder „links“ oder „rechts“, da keine Strategie stark dominant ist. Spieler 1 wählt danach „oben“, die Auszahlung ist (9, 1). Man beachte, dass Spieler 2 indifferent ist, ob Spieler 1 „oben“ oder „unten“ wählen wird, der Ausgang des Spiels somit als Auszahlung bekannt ist, aber nicht, welches Ergebnis als solches vorliegen wird. Nichtsdestoweniger bevorzugt Spieler 2 zuerst zu entscheiden, da er in diesem Fall eine Auszahlung von 9 erhält (im Gegensatz zu einer Auszahlung von 1 bei der umgekehrten Abfolge der Spielzüge).
Übungsbeispiel 1.4
Der Strategienraum der Spieler „Unternehmer“ und „Manager“ ist in Normalform wie folgt gegeben:
|
|
|
Manager |
|
|
|
|
Ehrlich | Unehrlich |
| Unternehmer | Eröffnen | 1600, 5000 | -1200, 7200 |
|
|
Nicht eröffnen | 0, 2500 | 0, 2500 |
Aus Sicht des Managers ist die Strategie „unehrlich“ schwach dominant. Die beste Antwort des Unternehmers ist daher „nicht eröffnen“ und das Nash-Gleichgewicht ist durch („nicht eröffnen“, „unehrlich“) gegeben.
In diesem Fall hat der Manager, sollte er sich unehrlich verhalten, einen negativen Nutzen. Dieser macht jede monetäre Auszahlung einer unehrlichen Strategie bis zu 15000 Euro zunichte. Daher sieht die neue Normalform des Spieles so aus:
|
|
|
Manager |
|
|
|
|
Ehrlich | Unehrlich |
| Unternehmer | Eröffnen | 1600, 5000 | -1200, 0 |
|
|
Nicht eröffnen | 0, 2500 | 0, 2500 |
Die stark dominante Strategie des Managers ist „ehrlich“. Das Nash-Gleichgewicht ist somit durch (eröffnen, ehrlich) gegeben.
Übungsbeispiel 1.5
Max nimmt an, dass Emma, wenn sie an der Reihe ist, die Strategie wählt, die ihre Auszahlung maximiert, also „unten“. Somit kann Max seine Auszahlung maximieren, indem er „oben“ wählt. Das Gleichgewicht in diesem Spiel ist also durch („oben“, „unten“) gegeben, Max bekommt eine Auszahlung von 60 und Emma von 105.
Könnte Emma ein glaubwürdiges Versprechen abgeben, dass sie immer „oben“ wählte, egal, was Max entscheidet, würde sich ein für beide Spieler besseres Resultat ergeben. Max würde in diesem Fall „unten“ wählen und Emma „oben“, sodass die Gleichgewichtsauszahlungen durch (500, 400) gegeben wären.
Oligopoltheorie
Nichtperfekte Märkte: Monopole und Oligopole
Märkte können unterschiedliche Strukturen aufweisen. Es gibt zum Beispiel Märkte, auf denen sich nur ein Anbieter befindet, man spricht hier von einem Monopol. Das Gegenteil davon ist ein Markt, auf dem sich so viele Anbieter befinden, dass diese den Marktpreis als gegeben annehmen, d.h. davon ausgehen, dass sie sowohl bei unilateraler Preiserhöhung (durch verminderten Absatz) wie Preissenkung (der Preis deckt die Kosten nicht) Verluste machen werden; hier spricht man von perfektem Wettbewerb (Polypol). Die Situation dazwischen, ein Markt mit einigen wenigen Anbietern, heißt Oligopol: Hier haben die Anbieter einen gewissen Spielraum bei der Preissetzung. Eine Sonderform ist das Duopol, in dem nur zwei Anbieter präsent sind. In dieser Lektion werden strategische Interaktionen, die auf nichtperfekten Märkten zwischen den einzelnen Unternehmen stattfinden, mit Hilfe der spieltheoretischen Grundlagen der vorigen Lektion erklärt.
Monopole
Da ein Monopolist alleiniger Anbieter auf dem Markt ist, kann er auch die angebotene Gesamtmenge eines Produktes bestimmen. Mit dieser Mengenentscheidung setzt der Monopolist gleichzeitig einen Preis fest, er ist also ein „Preissetzer“. Erhöht er das Angebot, so muss er den Preis senken, um alles abzusetzen. Reduziert er das Angebot, wird sich zwar der Preis erhöhen, zu dem er alles absetzen kann, aber der Absatz als solcher wird fallen. Der Monopolist muss also die Menge (oder, nach derselben Logik, den Preis) derart setzen, dass sein Gewinn maximiert wird. In einem solchen Markt gibt es typischerweise erhebliche Eintrittsschranken, da ansonsten Anbieter in den Markt eindringen würden, um ihrerseits einen Teil des positiven Profits zu lukrieren. Wenn es in einem Markt keine Eintrittsschranken gibt, strömen zusätzliche Anbieter so lange in den Markt, bis die Profite null betragen. [4] Eintrittsschranken sind zum Beispiel durch staatliche Regelungen gegeben. Eintrittsschranken können jedoch auch Folge hoher Fixkosten sein, die nötig sind, um überhaupt produzieren zu können.
Oligopole
In diesem Fall befinden sich nur einige wenige Anbieter am Markt - es gibt also auch hier Eintrittsschranken, die ein Eindringen anderer Anbieter in den Markt verhindern. Die wenigen Anbieter können (ähnlich wie ein Monopolist) durch ihre Mengenentscheidung den Marktpreis beeinflussen, sie sind also Preissetzer. Da es nicht nur einen Anbieter am Markt gibt, der den Preis allein setzen kann, werden strategische Interaktionen zwischen den Oligopolisten stattfinden. Die Anbieter beeinflussen einander durch ihre Mengen- oder Preisentscheidungen zwangsläufig. Die untere Tabelle fasst die unterschiedlichen Marktstrukturen zusammen. [5]
| Monopol | Oligopol | Polypol | |
|---|---|---|---|
|
Optimalitätsbedingung (= Gewinnmaximierung) |
Grenzertrag (GE) =Grenzkosten (GK) |
Grenzertrag (GE) =Grenzkosten (GK) |
Grenzertrag (GE) =Grenzkosten (GK) =Preis (p) |
| Möglichkeit Preise zu setzen | Preissetzer | Preissetzer | Preisnehmer |
| Marktmacht | Ja, Preis>Grenzkosten | Ja, Preis>Grenzkosten | Nein, Preis=Grenzkosten |
| Markteintritt | Nein | begrenzt, Markteintrittsschranken | Ja, freier Markteintritt |
| Anzahl der Anbieter im Markt | 1 | wenige | viele |
| Gewinn | ≥0 | ≥0 | 0 |
| Optimale Strategie durch andere Anbieter beeinflusst | Nein (keine anderen Anbieter im Markt) | Ja | Nein (Preis=Grenzkosten gilt in jedem Fall) |
Charakteristika unterschiedlicher Marktstrukturen
Alle Anbieter, in jeder Marktstruktur, haben das Ziel, ihren Gewinn zu maximieren. Dies geschieht, indem der Anbieter seinen Grenzertrag gleich den Grenzkosten setzt. Im Fall von perfektem Wettbewerb dringen so viele Anbieter in den Markt ein, dass der Marktpreis auf die Grenzkosten gedrückt wird, und dadurch keine Profite mehr möglich sind. Im Fall von Oligopol beziehungsweise Monopolstrukturen haben die Anbieter Marktmacht, setzen den Marktpreis also höher als die Grenzkosten, und können damit einen positiven Gewinn verbuchen.
Zur Vereinfachung wird im Folgenden zumeist ein Duopol betrachtet, wobei die Analyse sich auf Fälle mit mehreren Anbieter ausdehnen lässt. Prinzipiell gibt es unterschiedliche Möglichkeiten, wie Anbieter in einem Oligopol interagieren können. Wie oben diskutiert, haben die Anbieter eine gewisse Marktmacht, d.h. sie können entweder durch eine Mengenentscheidung den Preis setzen oder durch eine Preisentscheidung die Menge, die verkauft wird, bestimmen. Das klassische Beispiel für einen Mengensetzer ist die OPEC. Bei regelmäßigen Treffen wird über die Höhe der Erdölförderung während einer gewissen Periode beraten und damit das Angebot an Erdöl bestimmt.
Um die in Lektion 1 eingeführten Termini zu verwenden, kann man also sagen, die beiden Anbieter (Spieler) wählen in einem Oligopol-Spiel aus einer Strategiemenge, die durch die möglichen Preise beziehungsweise Mengen gegeben ist. Als Resultat der eigenen Mengen- beziehungsweise Preisentscheidung sowie der der Gegenspieler erhalten die Anbieter nach Spielende einen Gewinn durch den Verkauf ihres Gutes (= eine Auszahlung). Analog zu den zuvor besprochenen unterschiedlichen Spielvarianten treffen die Anbieter entweder in einem simultanen oder sequenziellen Spiel aufeinander. Es ergeben sich also verschiedene mögliche Interaktionen, welche im Folgenden betrachtet werden. Die Interaktion kann simultan geschehen und Anbieter können dabei entweder Preise oder Mengen setzen. Weiters wird die Situation betrachtet, in der Anbieter in einem sequenziellen Spiel nacheinander reagieren und dabei Mengen setzen. Dabei geht es nicht darum, den realen Oligopol-Prozess exakt zu modellieren, sondern gewisse Regelmäßigkeiten im Verhalten von Oligopolisten abzuleiten und herauszufinden, welche Faktoren einen entscheidenden Einfluss haben. Außerdem gibt es natürlich auch die Möglichkeit, dass die Anbieter in einem Oligopol kooperieren, d.h. ihre Mengenentscheidungen abstimmen, um gemeinsam den größtmöglichen Gewinn zu erwirtschaften. In diesem Fall bilden die Anbieter ein Kartell, auch diese Möglichkeit wird im Folgenden analysiert.
Simultane Mengensetzung: Cournot-Wettbewerb
Allgemeine Lösung
In einem Duopol produzieren Anbieter 1 und Anbieter 2 dasselbe Gut und stehen vor dem Problem, welche Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}}
beziehungsweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}}
des Guts sie anbieten sollen, um ihren jeweiligen Gewinn zu maximieren. Die auf dem Markt angebotene Gesamtmenge, die den Gleichgewichtspreis bestimmt, ist im Duopol durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = q_{1} + q_{2}}
gegeben. Damit hängt die optimale Wahl von Anbieter 1 von der Mengenentscheidung von Anbieter 2 ab und umgekehrt.
Der Strategienraum beinhaltet alle möglichen Mengenentscheidungen und ist damit sehr groß, weshalb sich dieses Spiel nicht in Normalform wie in Lektion 1 darstellen lässt. Die Aktionen der beiden Anbieter sind durch ihre Mengenentscheidungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} gegeben. Im Cournot-Wettbewerb wird ein statisches Spiel behandelt. Die Anbieter treffen nur in dieser einen Runde aufeinander und müssen in dieser Runde all ihre Güter verkaufen (es kann also nichts gelagert werden). Daher gilt in dem Modell, dass die produzierte gleich der verkauften Menge ist.
Wir beginnen damit, die allgemeine Situation zu betrachten, in welcher die Oligopolisten mit einer allgemeinen (indirekten) Nachfragefunktion konfrontiert sind. Diese beschreibt, welcher Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} sich bei einer angebotenen Gesamtmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} einstellt. [6] Der Preis sinkt mit der auf dem Markt angebotenen Menge. Es gilt also
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial p}{\partial Q} < 0}
d.h., wird die die Menge erhöht, ist die Veränderung der Menge negativ (das Ergebnis der ersten Ableitung der Preisfunktion ist kleiner null). Wie in Lektion 1 gezeigt wurde, müssen zur Lösung des Spiels Beste-Antwort-Korrespondenzen (= Reaktionsfunktionen) beider Spieler gefunden werden. Mit Hilfe dieser kann das Nash-Gleichgewicht identifiziert werden, welches die Lösung des Spieles darstellt.
Die Reaktionsfunktion von Anbieter 1 beschreibt, welche Menge er optimal setzen sollte, gegeben Anbieter 2 produziert eine bestimmte Outputmenge. Die Reaktionsfunktion bestimmt sich also als Resultat des Gewinnmaximierungsproblems von Anbieter 1. Dabei nehmen wir der Einfachheit halber konstante Grenzkosten in der Höhe von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} an. Welche Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} maximiert den Profit von Anbieter 1, gegeben Anbieter 2 produziert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} ? Formal wird das Optimierungsproblem von Anbieter 1 wie folgt angeschrieben:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \max\left( \pi_{1} \right) = pq_{1} - cq_{1}}
Anbieter 1 möchte also seinen Gewinn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1}} , der sich aus dem Erlös durch die verkaufte Menge minus die Kosten der Produktion zusammensetzt, maximieren. Die Bedingung für ein Optimum wird durch Nullsetzen der ersten Ableitung der Zielfunktion gefunden. In diesem Fall ist also die Bedingung für ein Optimum gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial \pi_1}{\partial q_1}=\underbrace{\frac{\partial p}{\partial q_1} q_1}_{G E}+\underbrace{p}_B-\underbrace{c}_{G K}=0 }
Diese Bedingung stellt den Effekt einer zusätzlich angebotenen Einheit auf den Gewinn von Anbieter 1 dar. Zwei Effekte (A+B) beziehen sich dabei auf den Ertrag von Anbieter 1, indem Effekte A und B als Summe den Grenzertrag (GE) einer zusätzlich produzierten Einheit ausmachen. Einerseits kann Anbieter 1 eine zusätzliche Einheit des Gutes verkaufen (Effekt B). Daher erhöht sich der Ertrag um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} (die zusätzliche Einheit wird zum Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} verkauft). Andererseits verringert sich der Gewinn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi} , der aus dem Verkauf aller anderen Einheiten des Gutes erzielt wird, da der Preis, zu dem die Einheiten verkauft werden können, nun geringer ist (Effekt A). Die zusätzlichen Kosten, die durch die Produktion der zusätzlichen Einheit anfallen, sind durch die konstanten Grenzkosten (GK) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} gegeben (Effekt C). Wie in Tabelle 2-1 dargestellt, befindet sich der Anbieter im Optimum, wenn die zusätzlichen Kosten gleich dem zusätzlichen Ertrag. Der Anbieter wird daher jene Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q} produzieren, bei der gilt: GE = GK. Eine Situation, in der die Grenzkosten größer als der Grenzertrag sind, kann nicht optimal sein, da der Anbieter durch die letzte verkaufte Einheit Verlust machen würde – die zusätzliche Einheit kostet dem Anbieter mehr, als sie ihm an zusätzlichem Gewinn bringt. Andererseits kann auch eine Situation, in der die Grenzkosten kleiner als der Grenzertrag sind, nicht optimal sein, da der Anbieter in einer solchen Situation durch einen größeren Output einen positiven Gewinn erzielen könnte. Nur wenn GE = GK gilt, kann der Gewinn durch Veränderung des Outputs nicht mehr erhöht werden.
Unter der Annahme, dass beide Anbieter die gleichen Grenzkosten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} haben, ist das Maximierungsproblem von Anbieter 2 symmetrisch. Die Optimalitätsbedingung lautet also spiegelgleich zu Anbieter 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial \pi_2}{\partial q_2}=\underbrace{\frac{\partial p}{\partial q_2} q_2}_{G E}+\underbrace{p}_B-\underbrace{c}_{G K}=0 }
Aus obigen Optimalitätsausdrücken können wir nun die Reaktionsfunktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}\left( q_{2} \right)} aus Sicht von Anbieter 1 sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}\left( q_{1} \right)} aus Sicht von Anbieter 2 ableiten. Um das Nash-Gleichgewicht dieses Spieles zu identifizieren, muss der Schnittpunkt beider Kurven gefunden werden. Da die Reaktionsfunktionen die Menge des jeweiligen Gegenspielers enthalten, benötigt man zur Lösung ein Gleichungssystem. Die Lösung wird im Folgenden anhand eines Beispiels mit einer linearen indirekten Nachfragefunktion demonstriert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = a - b\left( q_{1} + q_{2} \right)}
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b} Konstante sind. Es ist deutlich zu sehen, dass der Preis mit Erhöhung des Angebots fällt. Man erhält die Lösung, indem man zuerst obige Nachfragefunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = a - b\left( q_{i} + q_{j} \right)} in die Gewinnfunktion von Anbieter 1, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{i} = pq_{i} - cq_{j}} , wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} beliebige Anbieter repräsentiert, einsetzt. Im vorliegenden Fall erhält man für Anbieter 1:
Da die Fragestellung lautet: „Wie viel muss ich produzieren, um meinen Gewinn zu maximieren?“ wird diese Funktion nach der eigenen Outputmenge abgeleitet:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi_{1}}{\partial q_{1}} = a - 2bq_{1} - bq_{2} - c}
Der rechte Teil der Gleichung wird nun null gesetzt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a - 2bq_{1} - bq_{2} - c = 0}
und anschließend für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} explizit ausgedrückt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = \frac{a - bq_{2} - c}{2b}}
Das ist die Reaktionsfunktion von Anbieter 1: Welche Menge immer auch Anbieter 2 produzieren wird, Anbieter 1 erhält den maximalen Gewinn durch die angegebene Menge als Funktion der Menge von Anbieter 2. Die Reaktionsfunktion von Anbieter 2 ist symmetrisch:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{2} = \frac{a - bq_{1} - c}{2b}}
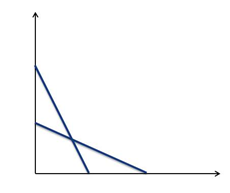
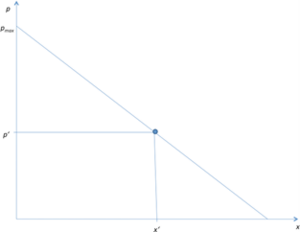
Das Problem kann wie in nachfolgender Abbildung grafisch veranschaulicht und gelöst werden: Der Schnittpunkt der beiden dargestellten Reaktionsfunktionen stellt das Gleichgewicht dar.
Mathematisch erhält man das Nash-Gleichgewicht, indem eine Reaktionsfunktion in die andere eingesetzt wird:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = \frac{a - b\frac{a - bq_{1} - c}{2b} - c}{2b}}
Diese Gleichung wird für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} explizit ausgedrückt und ergibt daher für Anbieter 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = \frac{a - c}{3b}}
Und analog für Anbieter 2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{2} = \frac{a - c}{3b}}
Da die beiden Anbieter perfekt symmetrisch sind, setzen beide im Gleichgewicht dieselbe optimale Menge. Der produzierte Gesamtoutput Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} ist gegeben durch:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q = q_{1} + q_{2} = 2\frac{a - c}{3b}}
Die produzierte Gesamtmenge impliziert einen sich materialisierenden Preis. Dieser ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = a - bQ = \frac{a + 2c}{3}}
Man beachte, dass diese Lösung nicht der Lösung eines Monopolisten entspricht. Analog zum Gefangenendilemma wird die den kollektiven Gewinn maximierende gesamte Auszahlung nicht erreicht, da die beiden Anbieter nicht miteinander kommunizieren. Vielmehr ergibt sich die Lösung aus der Unterstellung rationalen Verhaltens des jeweiligen Gegenspielers.
Nummerische Lösung
Setzt man für die Konstanten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b} beliebige Zahlen ein, so kann das Cournot-Gleichgewicht mittels eines nummerischen Beispiels veranschaulicht werden. Angenommen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a = 1} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b = \frac{1}{1000}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{1} = c_{2} = 0,28} so ist die indirekte Nachfragefunktion
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = 1 - \frac{q_{1} + q_{2}}{1000}}
und die Gewinnfunktionen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\pi_{1} = 1 - \frac{q_{1} + q_{2}}{1000}q_{1} - cq_{1} }{\pi_{2} = 1 - \frac{q_{1} + q_{2}}{1000}q_{2} - cq_{2}}}
Diese Gleichungen werden nun nach der jeweils eigenen Menge abgeleitet, die resultierende Funktion null gesetzt. Daraus ergeben sich die Reaktionsfunktionen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {q_{1} = \frac{1 - 0,001q_{2} - 0,28}{0,002} }{q_{2} = \frac{1 - 0,001q_{1} - 0,28}{0,002}}}
Durch Schneiden dieser beiden Funktionen oder durch Auflösen der Gleichung erhält man das Nash-Gleichgewicht als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = q_{2} = 240} . Produziert Anbieter 1240 Stück, so ist die beste Antwort von Anbieter 2 auf diese Aktion ebenfalls 240 Stück zu produzieren und vice versa. Gegeben, die Anbieter befinden sich in diesem Gleichgewicht, hat kein Anbieter einen Anreiz individuell abzuweichen (also eine andere Menge als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 240} zu wählen), da jede Abweichung einen niedrigeren Profit bedeuten würde.
In diesem nummerischen Beispiel erhält man als weitere Resultate
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = q_{1} + q_{2} = 480}
, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 1 - \left( \frac{Q}{1000} \right)0,52}
sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1} = pq_{1} - cq_{1} = 57,6}
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{2} = pq_{2} - cq_{2} = 57,6}
, der gesamte Profit ist somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Pi = \pi_{1} + \pi_{2} = 115,2}
.
Allgemeine Lösung bei mehr als zwei Anbietern
Das Cournot-Gleichgewicht lässt sich auch für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N > 2} Anbieter berechnen. Die indirekte Nachfragefunktion der Konsumenten sei wiederum linear:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = a - b\left( q_{1} + q_{2} + ... + q_{N} \right)}
Auch hier bestimmt sich also der Preis durch die angebotene Gesamtmenge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = \left( q_{1} + q_{2} + ... + q_{N} \right) = \sum_{i = 1}^{N}q_{1}}
. Das Optimierungsproblem von Anbieter 1 ist demnach gegeben durch die Gewinnfunktion
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{1} = \left( a - b\left( q_{1} + q_{2} + ... + q_{N} \right) \right)q_{1} - cq_{1}}
die analog zum vorigen Abschnitt maximiert werden muss.
Die Optimalitätsbedingung für Anbieter 1 ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi_{1}}{\partial q_{1}} = a - 2bq_{1} - bq_{2} - ... - bq_{N} - c}
Haben alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N} Anbieter dieselben Kosten, so gilt im Gleichgewicht
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = q_{2} = ... = q_{N}} . Die abgeleitete Gewinnfunktion wird wiederum null gesetzt, was explizit für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} ausgedrückt ergibt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = \frac{a - c}{2b} - \frac{q_{2} + ... + q_{N}}{2} = \frac{a - c}{2b} - \frac{(N - 1)q_{j}}{2}}
Die Reaktionsfunktionen der anderen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (N - 1)} Anbieter ergeben sich analog. Ein Cournot-Gleichgewicht tritt dort auf, wo sich die Reaktionsfunktionen im mehrdimensionalen Raum schneiden. Da alle Anbieter identisch sind ergibt und somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{i} = q_{j} = \frac{Q}{N}} gilt, ergibt sich die Lösung durch explizites Ausdrücken der Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{i} = \frac{a - c}{2b} - \frac{(N - 1)q_{i}}{2}}
was
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{i} = \frac{a - c}{b(N + 1)}}
ergibt. Die allgemeine Gültigkeit dieses Ergebnisses lässt sich veranschaulichen, indem man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N = 2} für den Fall von zwei Anbietern einsetzt. Das Ergebnis ist zwangsläufig dasselbe wie in Abschnitt 2.2.1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{i} = \frac{a - c}{b(2 + 1)} = \frac{a - c}{3b}}
und für das nummerische Beispiel aus Abschnitt 2.2.2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{i} = \frac{1 - 0,28}{\left( \frac{1}{1000} \right)(2 + 1)} = 240}
Nimmt man nun einen Markt mit drei Anbietern, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N = 3} , an, so ergibt sich als Menge eines einzelnen Anbieters
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{i} = \frac{a - c}{b(3 + 1)} = \frac{a - c}{4b} = 180}
als Gesamtmenge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q = Nq_{i} = 540}
als Preis
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = 1 - \frac{Q}{1000} = 0,46}
und als jeweiliger Gewinn
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{i} = pq_{i} - cq_{i} = 32,4}
Die angebotene Gesamtmenge ist größer, der Preis und der Gewinn je Anbieter sind kleiner. Man beachte, dass nicht nur der Preis und die produzierende Menge mit einer größeren Zahl an Anbietern sinkt, sondern neben dem individuellen Gewinn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{i}} auch der kollektive Gewinn:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Pi = \sum_{i = 1}^{N}\pi_{i} = Nq_{i}(p - c) = 97,2}
Somit werden bei Markteintritten zusätzlicher Anbieter sowohl der individuelle wie der kollektive Gewinn stets sinken, ebenso aber auch der Preis. Daraus ergibt sich in der Praxis auf oligopolistischen Märkten ein permanenter Konflikt zwischen großen Anbietern (Konzernen) und der Gesellschaft: Während die Konsumenten und die Gesamtwirtschaft von zusätzlichen Anbietern profitieren, sind die Konzerne bestrebt, die Zahl ihrer Mitbewerber zu minimieren. Da die meisten Personen an den produzierenden Anbietern nicht beteiligt sind, ist es in der Regel im allgemeinen Interesse, die Zahl der Anbieter möglichst groß zu halten.
Sequenzielle Mengensetzung: Stackelberg-Wettbewerb
Wie realistisch das Cournot-Modell ist, hängt davon ab, welchen Markt man betrachtet. Häufig haben Anbieter jedoch die Möglichkeit, die Entscheidungsstruktur sequenziell statt simultan wie im Cournot-Wettbewerb zu modellieren. Im Stackelberg-Wettbewerb betrachten wir daher ein sequenzielles Spiel, analog zur Spieltheorie in Lektion 1. Zur Vereinfachung betrachten wir auch hier den Fall eines Duopols. Anbieter 1 trifft zuerst eine Mengenentscheidung, Anbieter 2 beobachtet diese und setzt die für ihn optimale Menge.
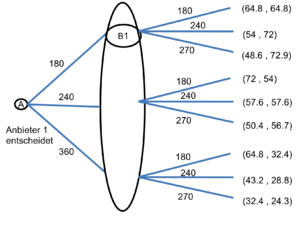
Allgemeines Spiel
Die untere Abbildung zeigt den Entscheidungsbaum im sequenziellen Spiel, der Gewinn eines Anbieters ist jeweils eine Funktion der Mengen beider Anbieter:
In der ersten Runde (Entscheidungspunkt A) wählt Anbieter 1 eine bestimmte Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} . Anbieter 2 beobachtet diese und trifft danach seinerseits eine Mengenentscheidung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} (Entscheidungspunkt B). Daraus resultieren die Gewinne Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{2}} .
Auch in diesem Fall ist es nicht möglich, den gesamten Strategienraum der beiden Anbieter grafisch darzustellen, da es sehr viele verschiedene mögliche Mengenkombinationen gibt. Später werden wir die Strategienmengen beider Anbieter künstlich beschränken und annehmen, sie könnten nur bestimmte Mengen produzieren, damit wir die einzelnen Strategien explizit darstellen können und damit einen direkten Vergleich zu den Entscheidungsbäumen in Kapitel 1 herstellen. Für den Moment halten wir das Spiel allerdings so allgemein wie möglich.
Für eine analytische Lösung des Spieles wenden wir das Konzept der Rückwärtsinduktion an. Dementsprechend beginnen wir am Ende des Spieles und betrachten zuerst das Entscheidungsproblem von Anbieter 2. Anbieter 2 wird jene Menge setzen, die den Gewinn, gegeben eine gewisse Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} , maximiert. Anbieter 1 weiß, dass Anbieter 2 sich rational, also gemäß seiner Reaktionsfunktion, verhalten wird. Wenn man davon ausgeht, dass der Preis mit steigender Menge fällt, so muss Anbieter 1 die gesetzte Menge von Anbieter 2 für sein eigenes Gewinnmaximierungsproblem berücksichtigen. Das Optimierungsproblem für Anbieter 1 stellt sich wie folgt dar:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \max\left( \pi_{1} \right) = p\left( q_{1},q_{2}\left( q_{1} \right) \right)q_{1} - cq_{1}}
Der Anbieter berücksichtigt also die Reaktionsfunktion von Anbieter 2, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}\left( q_{1} \right)}
, die ihrerseits eine Reaktionsfunktion auf die Menge von Anbieter 1 ist. Demzufolge muss Anbieter 1 die Reaktion von Anbieter 2 berücksichtigen, um die für sich selbst Gewinn maximierende Menge zu produzieren. Die Optimalitätsbedingung von Anbieter 1 ergibt sich wiederum aus der ersten Ableitung nach der eigenen Menge. Beim Ableiten muss berücksichtigt werden, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p}
selbst eine Funktion von
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = q_{1} + q_{2}}
ist und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}}
wiederum eine Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}}
, was in der Gewinnfunktion durch die Darstellung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p\left( q_{1},q_{2}\left( q_{1} \right) \right)}
zum Ausdruck kommt. Zur Anwendung kommen die Produkt- und die Kettenregel:
Würde Anbieter 1 eine zusätzliche Einheit produzieren, so hätte dies vier Effekte auf seinen Gewinn. Die Effekte auf den Ertrag sind gegeben durch
1) Anbieter 1 verkauft eine Einheit mehr des Gutes und hat dadurch einen zusätzlichen Ertrag von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} (Effekt C).
2) Wenn Anbieter 1 eine zusätzliche Einheit anbietet, so steigt das Gesamtangebot des Gutes, was ein Sinken des Preises zur Folge hätte (Effekt A).
3) Wenn Anbieter 1 eine Einheit zusätzlich anbietet, so wird der Wettbewerber, Anbieter 2, weniger anbieten als zuvor. Dadurch sinkt das Gesamtangebot des Gutes, was ein Steigen des Preises zur Folge hätte (Effekt B).
Außerdem hat eine zusätzlich produzierte Einheit einen Effekt auf die Kosten der Anbieter 1:
4) Anbieter 1 muss die zusätzliche Einheit des Gutes produzieren und hat dadurch zusätzliche Kosten c (Effekt D).
Im Optimum ist (wie zuvor besprochen) der zusätzliche Ertrag gleich den zusätzlichen Kosten der zuletzt produzierten Einheit.
Effekt 2) und 3) wirken in entgegengesetzter Richtung auf das Gesamtangebot des Gutes. Hier wird der Unterschied zu dem Cournot-Wettbewerb offensichtlich. Im Stackelberg-Wettbewerb ist durch die sequenzielle Struktur ein Effekt vorhanden, der im Cournot-Wettbewerb nicht zum Tragen kam, nämlich dass Anbieter 1 seinen Mitbewerber Anbieter 2 durch die eigene Mengenentscheidung beeinflussen kann. Dies hat zur Folge, dass der Ertrag einer zusätzlichen Einheit im Stackelberg-Wettbewerb größer ist, da der Rückgang der Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} der Zunahme von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} entgegenwirkt, die Gesamtmenge also weniger stark ansteigt als im Cournot-Wettbewerb und als Resultat der Preis weniger stark sinkt. Intuitiv ist nun also schon offensichtlich, dass Anbieter 1 in einem Stackelberg-Wettbewerb eine höhere und dementsprechend Anbieter 2 eine niedrigere, Menge wählt als im Cournot-Spiel.
Beispielrechnung
Betrachten wir nun zum direkten Vergleich der beiden Spielstrukturen Cournot und Stackelberg auch hier den Fall einer linearen indirekten Nachfragefunktion
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = a - b\left( q_{1} + q_{2} \right)}
. Anbieter 2 sieht sich mit derselben Situation wie im Cournot-Spiel konfrontiert, nämlich seine Menge in Abhängigkeit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}}
so zu wählen, dass sein Gewinn in Abhängigkeit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}}
maximiert wird, folglich ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{2} = \frac{a - bq_{1} - c}{2b}}
Anbieter 1 wird diese Reaktion nun antizipieren, da er den ersten Zug hat. Rechnerisch ist der einzige Unterschied zum Cournot-Spiel, dass Anbieter 1 das Verhalten von Anbieter 2 direkt in seine eigene Gewinnfunktion integrieren kann, weshalb sich sein Optimierungsproblem wie folgt darstellt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{1} = pq_{1} - cq_{1} = \left( a - b\left( q_{1} + q_{2} \right) \right)q_{1} - cq_{1} = \left( a - b\left( q_{1} + \frac{a - bq_{1} - c}{2b} \right) \right)q_{1} - cq_{1}}
Nach einigem Umformen erhält man
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{1} = \frac{aq_{1} - bq_{1}^{2} - cq_{1}}{2}}
und somit als erste Ableitung nach dem eigenen Output
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi_{1}}{\partial q_{1}} = \frac{a - 2bq_{1} - c}{2}}
Nullsetzen dieser Funktion und für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} explizit ausgedrückt ergibt die optimale Mengensetzung für Anbieter 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = \frac{a - c}{2b}}
Dieses Resultat erhält man naturgemäß auch durch Einsetzen in obige Ableitung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi_{1}}{\partial q_{1}} = q_{1}\left( \frac{\partial p}{\partial q_{1}} + \frac{\partial p}{\partial q_{2}}\frac{\partial q_{2}}{\partial q_{1}} \right) + p - c = q_{1}\left( - b + \left( - b( - 0,5) \right) \right) + a - b\left( q_{1} + \frac{a - bq_{1} - c}{2b} \right) - c = \frac{a - bq_{1} - c}{2} }
und anschließendem Nullsetzen und Auflösen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} . Die von Anbieter 2 produzierte Menge, die gesamte Menge sowie der sich materialisierende Preis sind gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{2} = \frac{a - b\frac{a - c}{2b} - c}{2b} = \frac{a - c}{4b}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q = q_{1} + q_{2} = \frac{a - c}{2b} + \frac{a - c}{4b} = \frac{3}{4}\frac{a - c}{b}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = a - b\frac{3}{4}\frac{a - c}{b} = \frac{a + 3c}{4}}
Als konkretes Beispiel kann ein Beispiel mit Zahlen betrachtet werden. Die indirekte Nachfragefunktion sei in diesem Fall, wie im vorigen Beispiel zum Cournot-Spiel, durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a = 1} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b = \frac{1}{1000}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{1} = c_{2} = 0,28} gegeben, woraus sich indirekte Nachfragefunktion
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = 1 - \frac{q_{1} + q_{2}}{1000}}
ergibt. Zur Veranschaulichung beschränken wir die theoretisch unendlich große Strategienmengen der beiden Anbieter so, dass der Spielbaum einfach und wir diese explizit darstellen können. In diesem Sinne nehmen wir an, dass Anbieter 1 nur die Mengen {180, 240, 360}, Anbieter 2 nur die Mengen {180, 240, 270} setzen kann. Der Spielbaum stellt sich wie in unterer Abbildung dar.
Das Spiel kann nun, analog zu Lektion 1, durch Rückwärtsinduktion gelöst werden: Anbieter 2 trifft die letzte Entscheidung in dem Spiel, wobei er am Entscheidungspunkt B1 270 Einheiten produziert, weil hier der Gewinn 72,9 betragen wird, und analog für die anderen Entscheidungspunkte. Man braucht also bloß zu prüfen, was für Anbieter 1 den höchsten Gewinn in Abhängigkeit der Entscheidung von Anbieter 2 abwerfen wird. Das ist die Menge 360, weil sich Anbieter 2 im Punkt B3 für 180 entscheiden wird.
Der Spielbaum beinhaltet die tatsächliche Lösung, wie durch Einsetzen der Zahlen in obige Gleichungen überprüft werden kann:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = \frac{a - c}{2b} = \frac{1 - 0,28}{2 \cdot \frac{1}{1000}} = 360}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{2} = \frac{a - c}{4b} = \frac{1 - 0,28}{4 \cdot \frac{1}{1000}} = 180}
Gegenüber dem Cournot-Spiel sind die Mengen also unterschiedlich und somit auch der Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 0,46} . Das hat naturgemäß Auswirkungen auf die Gewinne, sie betragen nun Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1} = 64,8} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{2} = 32,4} . Spieler 1 profitiert vom ersten Zug, da sein Gewinn höher ist als im Cournot-Spiel, jener von Anbieter 2 ist niedriger.
In der Realität wird meistens der größte Anbieter den ersten Zug setzen, aber das muss nicht immer der Fall sein. Entscheidend ist weniger die Größe, sondern der Informationsvorsprung über das Verhalten der Konsumenten oder ihre Loyalität zu einem bestimmten Anbieter. So zeigt bspw. eine Untersuchung des österreichischen Markts für Tageszeitungen für den Beobachtungszeitraum 1979-2003, dass nicht die scheinbar übermächtige Mediaprint (Kronen-Zeitung, Kurier) die Einzelverkaufspreise zuerst setzte, sondern fast immer die jeweiligen regionalen Konkurrenten (Kleine Zeitung, Oberösterreichische Nachrichten, Salzburger Nachrichten, Tiroler Tageszeitung, Vorarlberger Nachrichten) den ersten Zug in den jeweiligen Preiserhöhungsrunden spielten. [7]
Preissetzung: Bertrand-Wettbewerb
In den vorangegangenen Modellen haben wir uns mit Mengensetzung in einem Oligopol beschäftigt. Der Preis in diesen Modellen wurde demnach endogen im Modell (als Resultat der Mengenentscheidungen) bestimmt. Eine andere Möglichkeit in einem Oligopol ist, dass Anbieter Preise statt Mengen wählen und sich daraus simultan die angebotene Menge ergibt. Ein Beispiel zur Erklärung des Verhaltens ist das Bertrand-Modell.
Der Wettbewerb stellt sich dabei wie folgt dar: Jeder Oligopolist wählt einen Preis, zu dem er das Produkt anbietet. Die Produkte beider Oligopolisten sind perfekt substituierbar, d.h. dem Konsumenten ist es egal, ob er das Produkt von Anbieter 1 oder Anbieter 2 kauft. Dies bedeutet wiederum für die Anbieter, dass (gegeben es gibt keine Kapazitätsbeschränkungen) nur der Anbieter mit dem niedrigeren Preis Produkte verkaufen wird. Daraus ergibt die in der folgenden Tabelle dargestellte Spielmatrix.
Im in der unteren Tabelle dargestellten Beispiel ist die Gesamtnachfrage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} abhängig vom gesetzten Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} . Die Grenzkosten der Produktion sind für beide Anbieter konstant und betragen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} .
|
|
|
Anbieter 2 |
|
|
|
|
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p=\bar{p} } | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p=\bar{p}-\varepsilon } |
| Anbieter 1 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p=\bar{p} } | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left( \bar{p} - c \right)\frac{Q}{2},\left( \bar{p} - c \right)\frac{Q}{2}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,\left( \left( \bar{p} - \varepsilon \right) - c \right)Q} |
|
|
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p=\bar{p}-\varepsilon } | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left( \left( \bar{p} - \varepsilon \right) - c \right)Q,0} |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left( \left( \bar{p} - \varepsilon \right) - c \right)\frac{Q}{2},} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left( \left( \bar{p} - \varepsilon \right) - c \right)\frac{Q}{2}} |
Spielmatrix Bertrand-Wettbewerb
Das Szenario entspricht dem Gefangenendilemma: Beide Anbieter haben die Möglichkeit, entweder den höheren Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \bar{p}}
zu setzen oder diesen um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \varepsilon}
zu unterbieten, der gesetzte Preis beträgt dann Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( \bar{p} - \varepsilon \right)}
. Wenn beide Anbieter den hohen Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \bar{p}}
setzen, erhält jeder Anbieter die halbe Gesamtnachfrage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{Q}{2}}
und erhält die Auszahlung, die sich aus Multiplikation der halben Gesamtnachfrage mit der Differenz von Preis und Kosten je Einheit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( \bar{p} - c \right)}
, ergibt, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( \bar{p} - c \right)\frac{Q}{2}}
. Wenn ein Anbieter einseitig abweicht und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \bar{p}}
um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \varepsilon}
unterbietet, so erhält er die gesamte Nachfrage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q}
und folglich die Auszahlung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( \left( \bar{p} - \varepsilon \right) - c \right)Q}
, während der andere Anbieter leer ausgeht. Der Preis, zu dem der Anbieter die Güter verkauft, ist dann zwar niedriger, allerdings wird dies mehr als kompensiert durch die höhere Nachfrage, die der Anbieter in diesem Fall befriedigen kann. Wenn beide Anbieter sich dazu entschließen, den niedrigeren Preis anzubieten, so hat dies zur Folge, dass sie sich wieder die Gesamtnachfrage teilen, diese allerdings zu einem niedrigeren Preis bedient wird, die jeweilige Auszahlung beträgt dann
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( \left( \bar{p} - \varepsilon \right) - c \right)\frac{Q}{2}}
.
Löst man das Spiel wie das Gefangenendilemma, so ist die dominante Strategie, den Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = \bar{p} - \varepsilon} zu setzen, d.h. den anderen Anbieter zu unterbieten: Was immer auch der andere Anbieter als Preis setzen wird, die eigene Auszahlung ist höher, wenn dessen Preis unterboten wird. Die Anbieter auf dem Markt werden sich dieser Logik folgend so lange unterbieten, bis kein zusätzlicher Gewinn durch die Strategie des Unterbietens möglich ist. Dies ist der Fall, wenn der Preis gleich den Grenzkosten, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = c} , ist. Bei diesem Preis wird nicht weiter unterboten, da die Anbieter sich damit zwar den gesamten Markt sichern würden, allerdings mit jedem verkauften Stück Verluste machten.
Das Nash-Gleichgewicht in diesem Spiel ist also durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = c} gegeben und der Gewinn beider Anbieter beträgt null. Wie im Gefangenendilemma wird der kollektive Gewinn dadurch minimiert, da es für beide besser wäre, einen höheren Preis zu setzen. Jeder einzelne Anbieter hat allerdings einen Anreiz, individuell von dieser Strategie abzuweichen (d.h., den anderen Anbieter mit dem Setzen eines marginal niedrigeren Preises zu unterbieten).
Das Marktergebnis von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = c} entspricht dem des Polypols, die Anbieter setzen den niedrigstmöglichen Preis. Man beachte, dass im Beispiel aus Abbildung 2-4 dieser Fall bereits bei zwei Anbietern eintritt – es ist also nicht nötig, dass sehr viele Anbieter am Markt tätig sind. Somit materialisiert sich ein Ausgang des Spieles, welcher dem des perfekten Wettbewerbes entspricht.
In der Praxis lässt sich dieses Verhalten recht häufig beobachten, es ist zugleich auch das stärkste Argument für die freie Marktwirtschaft als Wirtschaftssystem: Wenn die Anbieter nicht kommunizieren können und einander nicht vertrauen, bleibt ihnen keine andere Wahl, als den niedrigsten Preis zu setzen und somit die dem gesamtwirtschaftlichen Optimum entsprechende Menge bereitzustellen.
Das Bertrand-Modell entspricht der Praxis umso mehr, je mehr die angebotenen Güter substituierbar oder sogar homogen sind, Beispiele sind der Wettbewerb zwischen Mobilfunkanbietern oder Tankstellen. Je mehr jedoch die Güter durch Produktdifferenzierung charakterisiert sind, umso eher kann man einen höheren Preis setzen, wenn es gelingt, bestimmte Verbrauchervorlieben zu bedienen, Beispiele hierfür sind der Pkw-Markt oder Märkte für Luxusgüter. Das ist auch ein Grund, warum auf den meisten Märkten zwar eine oligopolistische Marktstruktur mit nur wenigen Anbietern herrscht, aber gleichzeitig eine enorme Produktvielfalt gegeben ist. Diese Produktvielfalt, wie sie für unser Wirtschaftssystem charakteristisch ist, ist nicht mit einer besonderen Leistungsfähigkeit des Systems gleichzusetzen, da exzessive Produktdifferenzierung erstens Mittel bindet, die zur Bereitstellung nötig sind und zweitens eben den beschriebenen und von den Herstellern gewünschten Effekt hat, den Preiswettbewerb zu reduzieren.
Kooperatives Verhalten: Kartellbildung
Kartelle bilden den Ur-Konflikt ab, der in Wirtschaftssystemen mit privatem Unternehmertum permanent besteht. Auf der einen Seite basiert das marktwirtschaftliche System auf der Effizienz, die sich aus dem Wettbewerb ergibt. Auf der anderen Seite haben die Unternehmen den Anreiz, den Wettbewerb zu reduzieren, um den Gewinn zu maximieren. Das System basiert also auf dem Prinzip, dass Unternehmen ihre Gewinne maximieren dürfen und sollen, weil davon ausgegangen wird, dass sie das zu besserer Qualität und effizienterer Produktionsweise anspornt, was die gesamte Wohlfahrt erhöht. Viel bequemer und lukrativer aus Sicht der Unternehmen ist es jedoch, diesen Druck der permanenten Verbesserung von Produktion und Produkten zu reduzieren, indem man sich mit den Konkurrenten abspricht. Was gerade deshalb in allen modernen Marktwirtschaften verboten ist, weil es die Daseinsberechtigung des Systems an sich untergräbt.
Bereits Adam Smith, dessen Metapher der unsichtbaren Hand gerne als Beleg für die Überlegenheit des marktwirtschaftlichen Systems zitiert wird, hat dazu bemerkt, dass Geschäftsleute des gleichen Gewerbes selten, „selbst zu Festen und zur Zerstreuung, zusammen [kommen], ohne dass das Gespräch in einer Verschwörung gegen die Öffentlichkeit endet oder irgendein Plan ausgeheckt wird, wie man die Preise erhöhen kann“. [8] Man beachte, dass Smith explizit von Verschwörung spricht. Verschwörungstheorien haben in der Öffentlichkeit keinen besonders guten Ruf, da die bekanntesten unter ihnen (Mondlandung, Anschläge auf Einrichtungen der USA am 11. September 2001) an den Haaren herbeigezogen sind und einer kritischen Überprüfung nicht standhalten. Daraus kann man jedoch nicht den Schluss ziehen, dass es keine Verschwörungen gäbe. Ein Blick auf die Seite der Wettbewerbsbehörde der EU genügt, um sich davon zu überzeugen, dass Verschwörungen gegen die Öffentlichkeit in der Wirtschaft geradezu alltäglich sind. [9] Die Industrieökonomik als Disziplin der Angewandten Mikroökonomik ist in diesem Sinn über weite Strecken nichts anderes als eine Verschwörungstheorie: Gegenstand des Interesses ist zumeist, zu untersuchen, wie sich Unternehmen unter Umgehung der Gesetze darauf verständigen können, auf Kosten der Allgemeinheit ihren Gewinn zu erhöhen. Die meisten dieser Verschwörungen betreffen die Bildung von Kartellen.
Kartelle sind Zusammenschlüsse von Anbietern, die ihre Preis- oder Mengensetzung koordinieren, um einen höheren Gewinn zu erzielen. Im Optimalfall (aus Sicht der Unternehmen) verhält sich ein Kartell dabei wie ein einzelner Anbieter, der über ein Monopol verfügt. Ein erfolgreiches Kartell erzielt also gemeinsam den Gewinn, den ein Monopol erzielen würde, beziehungsweise unter nichtperfekten Umständen zumindest einen höheren Gewinn, als jedes Kartellmitglied bei nichtkooperativem Verhalten (also unter perfektem beziehungsweise oligopolistischem Wettbewerb wie in Abschnitt 2.4) erhalten würde.
Formale Darstellung des Kartellverhaltens
Anbieter können also durch Koordination ihres Verhaltens mit anderen einen höheren Gewinn erzielen. Um diesen Prozess nachvollziehen zu können, betrachten wir formal die optimale Mengensetzung eines Kartells. Angenommen, das Kartell besteht aus zwei Anbietern, Anbieter 1 und Anbieter 2, welche beide die gleichen konstanten Grenzkosten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} haben. In diesem Fall sieht das Optimierungsproblem des Kartells wie folgt aus:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \max\left( \pi_{1} + \pi_{2} \right) = p\left( q_{1} + q_{2} \right) - c\left( q_{1} + q_{2} \right)}
Die Optimalitätsbedingungen für die Bestimmung der Mengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} sind gegeben durch die Ableitungen nach den Mengen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial p}{\partial q_{1}}\left( q_{1} + q_{2} \right) + p - c}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial p}{\partial q_{2}}\left( q_{1} + q_{2} \right) + p - c}
Man beachte, dass auch hier die Kettenregel zur Anwendung kommt, da der Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} eine Funktion der Mengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} ist. Aus den Ableitungen ist der Unterschied des Kartellproblems zu nicht-kooperativem Cournot-Verhalten ersichtlich. Betrachten wir dafür die Überlegungen von Anbieter 1, wenn sie die Optimalität einer Mengenerhöhung überprüft. Eine Mengenerhöhung hat zwei Effekte auf ihren Gewinn: einerseits kann der Anbieter eine Einheit mehr verkaufen, dies steigert also ihren Gewinn. Andererseits sinkt der Preis, der für alle verkauften Einheiten verlangt werden kann, da nun eine größere Menge angeboten wird. Dieser niedrigere Preis gilt sowohl für die Einheiten, die Anbieter 1 verkauft, als auch für die von Anbieter 2 angebotenen. Es gibt also einen sogenannten externen Effekt der Mengenentscheidung von Anbieter 1 auf den Gewinn von Anbieter 2. In nicht-kooperativem Cournot-Verhalten ignoriert Anbieter 1 diesen Effekt – er ist einzig und allein daran interessiert, seinen Gewinn zu maximieren und hat daher kein Interesse an der Auswirkung seines Verhaltens auf den Gewinn von Anbieter 2. Wenn die Anbieter als Kartell agieren, ist das Ziel allerdings, den Gesamtgewinn zu maximieren. In diesem Fall bezieht Anbieter 1 also den Effekt seiner Entscheidung auf den Gewinn von Anbieter 2 ein. Dies sehen wir formal in obiger Gleichung, da hier der Effekt einer Preiserhöhung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{\partial p}{\partial q_{1}}} nicht nur auf den Erlös, der aus dem Verkauf von Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} erzielt werden kann, sondern auf den Gesamterlös aus der Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( q_{1} + q_{2} \right)} beachtet wird.
Zusammenfassend maximiert also bei nichtkooperativem Verhalten jeder Anbieter einzeln seinen Gewinn und achtet dabei nicht auf etwaige externe Effekte, die seine Entscheidung auf andere Marktteilnehmer hat. In einem Kartell, in dem die Zielsetzung die Maximierung des Gesamtgewinns ist, werden diese Externalitäten in die Entscheidung einbezogen. Alle Kartellmitglieder entscheiden sich daher für die Aktionen, die den Gesamtgewinn maximieren, d.h. sie agieren so, als handelten sie wie ein Unternehmen. Wenn es gelingt, im Kartell alle Marktteilnehmer zu integrieren, kann gemeinsam sogar der Monopolgewinn erzielt werden.
Um im Folgenden einen Vergleich aller Oligopol-Modelle anstellen zu können, betrachten wir auch hier den Fall eines Kartells in einem Markt mit linearen Nachfragefunktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = a - bQ} , mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = q_{1} + q_{2}} sowie identer, konstanter Grenzkosten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} beider Unternehmen.
Das Optimierungsproblem der Kartellmitglieder ist dementsprechend gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \max(\Pi) = \left( a - bq_{1} - bq_{2} \right)\left( q_{1} + q_{2} \right) - cq_{1} - cq_{2}}
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Pi = \pi_{1} + \pi_{2}} den Gewinn des Kartells bezeichnet. Die Bedingungen erster Ordnung, welche in einem Optimum erfüllt sein müssen, sind, da die Kartellmitglieder gleich Grenzkosten haben, für beide Unternehmen gleich und gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\Pi}{\partial q_{1}} = \frac{\partial\Pi}{\partial q_{2}} = a - 2b\left( q_{1} + q_{2} \right) - c}
Durch Nullsetzen der Funktion erhält man die optimalen Mengen, die aufgrund identischer Kostenfunktionen identisch sind. Die zu lösende Gleichung reduziert sich dadurch auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a - 2b \cdot 2q_{i} - c = 0} und man erhält als Lösung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{1} = q_{2} = \frac{a - c}{4b}}
und als Kartellpreis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = a - bQ = a - b \cdot 2\left( \frac{(a - c)}{4b} \right)} daher
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = \frac{a + c}{2}}
Die Kartellsituation stellt sich für die einzelnen Spieler (Anbieter) wie eine Gefangenendilemma-Situation dar. Jeder Spieler hat individuell einen Anreiz, von der kooperativen Strategie abzuweichen. Dies ist darin begründet, dass, solange sich alle anderen Kartellmitglieder an die Abmachung halten, eine einseitige Mengenerhöhung den Preis nicht stark ändert, allerdings ein wesentlich größerer Gewinn möglich ist. Trotzdem ist es für das Kartell als Ganzes besser, wenn sich alle Mitglieder an die Absprache halten, da der individuelle Gewinn, sollten alle Mitglieder abweichen, natürlich geringer ist als der, der in einem Kartell erzielt werden kann. Wie auch im Gefangenendilemma ist daher eine stabile Vereinbarung für kooperatives Verhalten nur dann möglich, wenn Vertrauen zwischen den Spielern herrscht, das durch gute Kontrollmechanismen hergestellt wird. Gibt es keine solchen Mechanismen, ist eine Kartellvereinbarung nicht stabil und es ist sehr wahrscheinlich, dass diese nicht erfolgreich umgesetzt werden kann.
Bedingungen, die Kartellformation und -erfolg begünstigen
Kartellverhalten ist indes nicht nur auf Preise und Mengen beschränkt, sondern kann auch die Umgebung von Umweltschutz-Vorgaben betreffen, wofür die Manipulation der Abgase durch deutsche Automobilhersteller ein gutes Beispiel ist. Wie die konkrete Verschwörung auch aussieht, bestimmte Märkte begünstigen die Bildung von Kartellen, andere erschweren sie. Die folgenden sechs Bedingungen sind dabei entscheidend:
1) Die Bildung von Kartellen wird begünstigt, wenn zu erwarten ist, dass das Kartellverhalten der Anbieter zu einer substanziellen Preiserhöhung gegenüber der Situation mit perfektem Wettbewerb führt. Da die Bildung von Kartellen in den meisten Ländern verboten ist und immer ein gewisses Risiko besteht, entdeckt und bestraft zu werden, müssen die potenziellen Gewinne dieses Risiko abdecken. Dies ist dann der Fall, wenn die Nachfrage relativ unelastisch ist, d.h. wenn eine Preissteigerung keine starke Reduktion der Nachfrage nach sich zieht. In diesem Fall kann durch den höheren Preis, den ein Kartellverhalten mit sich bringt, auch ein substantiell höherer Gewinn lukriert werden.
2) Die Wahrscheinlichkeit, dass ein Kartell erfolgreich ist, erhöht sich, wenn die Mitglieder des Kartells einen großen Teil des (beziehungsweise am besten den gesamten) Marktes beherrschen. D.h., ein Kartell muss eine gewisse Marktmacht haben. Dies ist der Grund, warum Kartelle fast immer in oligopolistischen Märkten beobachtet werden. In jedem Fall kann ein Kartell nur funktionieren, wenn der Zugang zum Markt reguliert (etwa durch den Staat) oder sehr teuer (durch hohe Fixkosten) ist, da ansonsten so lange neue Anbieter, die keine Kartellmitglieder sind, in den Markt eindringen werden, bis der Markt keine positiven Gewinne mehr bietet.
3) Weiters müssen, damit ein Kartell erfolgreich agieren kann, die Organisationskosten relativ niedrig sein. Dies ist der Fall, wenn die Industrie wenige Anbieter umfasst und relativ homogene (also gleichartige) Güter produziert werden. Beides erleichtert die Koordination und senkt so die Organisationskosten.
4) Da in einem Kartell stets ein Anreiz besteht, individuell von der kooperativen Strategie abzuweichen, ist ein Kartell dann mit höherer Wahrscheinlichkeit erfolgreich, wenn die Selbstkontrolle der Mitglieder untereinander einfach und kostengünstig möglich ist. Die Kontrollkosten sind niedriger, wenn das Kartell wenige Mitglieder hat, die Anbieter ein homogenes Produkt anbieten (da in diesem Fall die Preispolitik des Unternehmens leichter zu überprüfen ist) und die Verkäufe selten und in großen Mengen stattfinden. Die von vielen Unternehmen verwendete Strategie, Konsumenten die Differenz des Kaufpreises zurückzuerstatten, sollten diese dasselbe Produkt von einem anderen Anbieter billiger erhalten, ist in vielen Fällen ein solcher Kontrollmechanismus. Konsumenten werden in diesem Fall als Kontrolleure herangezogen, die aufdecken, sollten sich Kartellmitglieder nicht an die vereinbarten Preise halten. Diese Strategie von Unternehmen deutet also in manchen Fällen – gegenteilig zu der von ihnen suggerierten Idee – darauf hin, dass in dieser Branche Preisabsprachen stattgefunden haben.
5) Auch das Kartellrecht in der jeweiligen Ökonomie spielt eine wichtige Rolle. Die Höhe der potenziellen Strafen beeinflusst dabei den Anreiz ein Kartell zu bilden. Die Anbieter können die gesetzlichen Regelungen umgehen, indem sie sich nicht explizit auf Preise beziehungsweise Mengen einigen, sondern dies stillschweigend geschieht. In diesem Fall signalisieren sich die Anbieter ihre Preisstrategien durch gesetzte Aktionen, womit die Möglichkeit zu einer stillschweigenden, nie explizit ausgesprochenen Vereinbarung gegeben ist. Internationale Kartelle, wie zum Beispiel die OPEC, sind meist immun gegenüber länderspezifischem Kartellrecht, da sie nicht der Rechtsprechung eines einzelnen Landes unterliegen.
6) Abschließend ist auch der Zeitrahmen, in dem das Kartell agiert, von Bedeutung. Kartelle sind stabiler, wenn die Anbieter über mehrere Runden hinweg aufeinandertreffen. Der Grund dafür ist, dass die Kartellsituation der des Gefangenendilemmas gleicht. Wie in Lektion 1 gezeigt wurde, wird das kooperative Gleichgewicht dann wahrscheinlicher, wenn die Spieler in mehreren Runden hintereinander aufeinandertreffen. In so einem Fall kann beispielsweise eine Tit-For-Tat-Strategie kartellkonformes Verhalten unterstützen. Mehrere Runden sind konformem Verhalten nur dann zuträglich, wenn das Spiel entweder unendlich oft wiederholt wird, oder – gleichlautend, aber realistischer – das Ende nicht absehbar ist (d.h., es ist nicht klar, in welcher Runde die Spieler zum letzten Mal aufeinandertreffen werden).
Wie sehr das Gefangenendilemma der Situation auf oligopolistischen Märkten entspricht, ist auch daran zu erkennen, dass innerhalb der EU sowohl die EU-Wettbewerbsbehörde wie nationale Wettbewerbsbehörden – darunter auch die österreichische – die Kronzeugenregelung anwenden: Der Anbieter, der buchstäblich als erster gesteht, darf mit einem geringeren Strafmaß rechnen. Mitunter entsteht ein regelrechter Wettlauf zwischen den Anbietern, als erster zu gestehen, sobald klar ist, dass das Kartell auffliegen wird. So haben Daimler und Volkswagen 2017 in der Abgasmanipulations-Affäre ihre Selbstanzeigen innerhalb einer Stunde eingereicht und in der Folge darum gestritten, wer als erster gestanden hat. [10] Die Voestalpine, als österreichisches Beispiel, konnte ihre Strafe im Kartell um Eisenbahnschienen auf Kosten ThyssenKrupps reduzieren, indem sie sich als erstes Unternehmen meldete. [11] Man beachte, dass sich Kartelle wie jene für Eisenbahnschienen, Aufzüge [12] oder andere Produkte, die man nur selten für sich selbst kauft, oft auf wirklich jeden auswirken – ob man nun möchte oder nicht, man zahlt für die höheren Schienenpreise mit, indem man Bahn fährt oder als Steuerzahler die ÖBB, die die überteuerten Schienen bezahlen muss, subventioniert; indem man Miete zahlt für ein Haus, das einen überteuerten Aufzug hat oder auch nur der eigene Arbeitgeber Miete für das Büro oder die Fabrik mit überteuertem Aufzug zahlen muss, usw.
Die Wettbewerbsbehörden behandeln Konzerne also wie die Räuber im Gefangenendilemma und das mit Erfolg: Wer die Allgemeinheit jahrzehntelang durch höhere Preise betrügt, der hat vermutlich auch keine Skrupel, seine Komplizen zu verraten, wenn es einen finanziellen (Gewinn maximierenden) Vorteil bringt. Aus der betriebswirtschaftlichen Logik muss das erwartete Strafmaß berücksichtigt und natürlich minimiert werden. Wenn man es schafft, im Falle des Falles von der Kronzeugenregulierung zu profitieren, ist man als Gewinn maximierendes Unternehmen besonders „erfolgreich“.
Vergleich der Oligopolmodelle
In diesem Abschnitt sollen nun die Ergebnisse der unterschiedlichen Varianten oligopolistischen Wettbewerbs verglichen werden. In der folgenden Tabelle werden die produzierte Menge, der sich materialisierende Preis, sowie die Gewinne der Unternehmen gegenübergestellt. Alle diese Indikatoren werden unter Annahme linearer Nachfragefunktionen, sowie konstanter, identischer Grenzkosten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} bei oligopolistischem Wettbewerb zwischen zwei Anbietern errechnet.
Wir sehen, dass die Gesamtproduktion des Gutes im Bertrand-Wettbewerb am höchsten ist. Am zweitmeisten wird in einem Markt in dem Stackelberg-Wettbewerb herrscht produziert. Danach folgt ein Markt mit Cournot-Wettbewerb. Die angebotene Menge ist am geringsten, wenn die beiden Anbieter ein Kartell bilden, da ein Kartell sich wie ein Monopolist verhält.
| Produzierte Menge je Anbieter | Gesamt -
produktion |
Preis | Profit je Anbieter | |
|---|---|---|---|---|
| Cournot, alle Anbieter | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{3 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{2(a-c)}{3 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a+2 c}{3}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{(a-c)^2}{9 b}} |
| Stackelberg, Anbieter 1 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{2 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{3(a-c)}{4 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a+3 c}{4}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{(a-c)^2}{8 b}} |
| Stackelberg, Anbieter 2 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{4 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{3(a-c)}{4 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a+3 c}{4}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{(a-c)^2}{16 b}} |
| Bertrand, alle Anbieter | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{2 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} |
| Kartell, alle Anbieter | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{4 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a-c}{2 b}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{a+c}{2}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{(a-c)^2}{8 b}} |
Vergleich unterschiedlicher Oligopolmodelle
Der Preis ist ein klarer Indikator dafür wie stark die Konsumenten von dem oligopolistischen Wettbewerb beeinflusst werden. Je höher der Preis, umso mehr leiden die Konsumenten darunter, dass der Markt von nur wenigen Anbietern beherrscht wird. Nachdem der Bertrand-Wettbewerb das gleiche Ergebnis wie der perfekte Wettbewerb liefert, ist der Preis am niedrigsten. Den zweitniedrigsten Preis kann man beim Stackelberg-Wettbewerb beobachten. Der Cournot-Wettbewerb resultiert in einem relativ hohen Preis. Der höchste Preis und damit das schlechteste Ergebnis aus Sicht der Konsumenten ist im Kartell gegeben. Dementsprechend sind die Gewinne der Anbieter bei Kartellbildung am höchsten, im Bertrand-Wettbewerb am niedrigsten.
Übungsbeispiele
Übungsbeispiel 2.1
Ein Duopol ist mit einer indirekten Nachfragefunktion gegeben durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 120 - Q} konfrontiert. Anbieter 1 hat konstante Grenzkosten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{1} = 20} während Anbieter 2 zu den Kosten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{2} = 40} produziert. Berechnen Sie den Output jeder Anbieter, die angebotene Gesamtmenge, den Marktpreis und den Gewinn je Anbieter in einem
(a) kooperativen Gleichgewicht (Kartell), sowie
(b) in einem Cournot-Gleichgewicht.
Übungsbeispiel 2.2
Bestimmen Sie in jedem der unten dargestellten Spiele die optimale Strategie jedes Spielers, gegeben die Spieler handeln simultan. Würde die Möglichkeit zu Absprachen den vorhergesagten Ausgang des Spieles ändern? Warum beziehungsweise warum nicht?
(a)
| B | |||
|---|---|---|---|
|
|
|
B1 | B2 |
| A | A1 | 4,2 | 1,1 |
|
|
A2 | 2,1 | 0,0 |
(b)
| B | |||
|---|---|---|---|
|
|
|
B1 | B2 |
| A | A1 | -1,-2 | 1,-3 |
|
|
A2 | 2,3 | 2,2 |
(c)
| B | |||
|---|---|---|---|
|
|
|
B1 | B2 |
| A | A1 | 3,3 | 7,2 |
|
|
A2 | 1,7 | 6,6 |
Übungsbeispiel 2.3
Angenommen, die Nachfragefunktion, mit der drei Anbieter konfrontiert sind, ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = 500 - 2p}
gegeben. Jeder Anbieter hat konstante Grenzkosten von
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{i} = 5}
.
(a) Wie sieht die Kartelllösung aus? (b) Nehmen sie nun an, dass Anbieter 1 100 Stück des Gutes zu den Grenzkosten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{1} = 4} produzieren kann. Die anderen beiden Anbieter haben immer noch Grenzkosten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_{j} = 5} . Wie würden sich die angebotene Gesamtmenge, der Preis und die Gewinne ändern? Wird die Aufteilung der Gewinne aus dem Kartell durch die Tatsache unterschiedlicher Grenzkosten komplizierter? Begründen Sie Ihre Antwort.
'
Übungsbeispiel 2.4
„Wenn alle Anbieter den gleichen Preis verlangen, so müssen sie eine Absprache getroffen haben“ – Ist diese Aussage richtig oder falsch? Begründen Sie Ihre Antwort.
Übungsbeispiel 2.5
Nehmen Sie an, die Auszahlungen in der gegebenen Spielmatrix sind Gewinne, die sich aus unterschiedlichen Mengenentscheidungen in einem nicht-kooperativen sequenziellen Spiel, in dem Anbieter A als erstes entscheidet, ergeben. Die Anbieter müssen sich also entscheiden, entweder 30 oder 60 Stück des Guts zu produzieren.
| B | |||
|---|---|---|---|
|
|
|
60 | 30 |
| A | 60 | 3,3 | 8,4 |
|
|
30 | 4, 8 | 6,6 |
(a) Schreiben Sie den Spielbaum des Spieles an. Wie sieht das Stackelberg-Gleichgewicht in dem sequenziellen Spiel aus?
Wie würde sich Ihre Antwort ändern, würde Anbieter B zuerst wählen?
(b) Nun nehmen Sie an, es handle sich um ein simultanes Spiel. Gibt es ein eindeutiges Gleichgewicht? Wenn ja, welches?
Lösungen
Übungsbeispiel 2.1
In einem kooperativen Gleichgewicht sollte Anbieter 1 den gesamten Output produzieren, da er die niedrigeren Grenzkosten hat. Optimalerweise wird die Monopolmenge produziert. Um diese zu berechnen, formuliert man die Gewinnfunktion so, als ob es nur einen Anbieter gäbe: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Pi = (120 - Q)Q - 20Q} . Diese Funktion wird nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} abgeleitet, die daraus entstehende Funktion gleich null gesetzt und für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} explizit aufgelöst. Es ergeben sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = 50} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 70} . Der Profit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Pi = \left( p - c_{1} \right)Q = 2500} wird geteilt, daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1} = \pi_{2} = 1250} .
In der Praxis wäre es wohl zu auffällig, wenn ein Unternehmen ohne zu produzieren Gewinne erzielt. Ein Szenario, dass sich unter nichtperfektem Wettbewerb jedoch regelmäßig ergibt ist eines, in dem Anbieter mit höheren Grenzkosten durch die höheren Preise dennoch überleben können.
Hier werden zunächst die Gewinnfunktionen formuliert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{1} = \left( p - c_{1} \right)q_{1} = \left( 120 - \left( q_{1} + q_{2} \right) - c_{1} \right)q_{1} = 100q_{1} - q_{1}^{2} - q_{1}q_{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{2} = \left( p - c_{2} \right)q_{2} = \left( 120 - \left( q_{1} + q_{2} \right) - c_{2} \right)q_{2} = 80q_{2} - q_{2}^{2} - q_{1}q_{2}}
und jeweils nach der eigenen Menge abgleitet:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\pi_{1}}{\partial q_{1}} = 100 - 2q_{1} - q_{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\pi_{2}}{\partial q_{2}} = 80 - 2q_{2} - q_{1}}
Diese Ausdrücke werden nullgesetzt, woraus sich ein Gleichungssystem aus zwei Gleichungen mit zwei Unbekannten ergibt. Auflösen des Gleichungssystems ergibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 40} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2} = 20} und somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = 60} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 60} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1} = 1600} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{2} = 400} .
Übungsbeispiel 2.2
(a) Dominante Strategien sind A1 beziehungsweise B1. Kooperatives Verhalten würde den Ausgang des Spieles nicht ändern, nachdem es keine andere Kombination von Strategien gibt bei der beide Spieler mindestens gleich gut gestellt wären.
(b) Dominante Strategien sind A2 beziehungsweise B1. Auch hier würde die Möglichkeit zu kooperativem Verhalten den Ausgang des Spieles nicht ändern, nachdem es keine Kombination von Strategien gibt, bei der die Spieler mindestens gleich gut gestellt wären.
(c) Dies entspricht einer Gefangenendilemma-Situation – die dominanten Strategien sind A1 beziehungsweise B1. Könnten die Spieler sich absprechen, so würden sie sich auf die Strategien A2 beziehungsweise B2 verständigen, da dieser Ausgang beiden Spielern eine höhere Auszahlung bringt.
Übungsbeispiel 2.3
Die Kartelllösung ergibt sich analog zu Übungsbeispiel 2.1: Die Gewinnfunktion ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Pi = \left( 250 - \frac{Q}{2} \right)Q - 5Q} . Diese Funktion wird nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} abgeleitet, die daraus entstehende Funktion gleich null gesetzt und für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q} explizit aufgelöst. Es ergeben sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q = 245} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 127,5} . Da alle Kartellmitglieder dieselben Grenzkosten haben, ist es an sich egal, wer wie viel produziert, am einfachsten ist es aber, wenn jedes Mitglied ein Drittel produziert, daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1} = \left( p - c_{i} \right)\left( \frac{Q}{3} \right) = 10004,1\dot{6}} .
Wenn ein Anbieter die ersten 100 Stück des Gutes zu den Grenzkosten von 4 (anstatt 5) GE produzieren kann, so bleiben optimale Menge und Preis unverändert zu (a). Allerdings würde dies die Aufteilung der Kartellgewinne verkomplizieren, da Anbieter 1 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 100(5 - 4) = 100} mehr Gewinn erzielt.
Übungsbeispiel 2.4
Es ist unklar, ob diese Aussage richtig oder falsch ist. Die Antwort hängt von den Gegebenheiten in der Industrie ab. Haben zum Beispiel alle Anbieter in einer Industrie dieselben Kostenfunktionen, so würden sie optimalerweise alle den gleichen Preis verlangen, auch ohne ein Kartell zu bilden. Allein aus der Preissetzung kann Kartellverhalten nicht beweisen werden – mehr Ausschluss gibt da schon die Art der Preissetzung oder ob und wie diese angekündigt werden. Achten Sie auf Meldungen im Wirtschaftsteil der Tageszeitungen: Oft werden Preiserhöhungen angekündigt und man mag sich fragen, wieso eigentlich? Mitunter wird die Presse als Kommunikationsmittel benutzt, und man wartet ab, wie die anderen Mitbewerber reagieren (z.B. können sie ihre eigenen Preiserhöhungen ankündigen, oder fallweise auch nicht mitgehen, das erste Unternehmen zieht dann seine Preiserhöhung wieder zurück).
Übungsbeispiel 2.5
Der Spielbaum sieht wie folgt aus:
Nachdem Anbieter A weiß, dass Anbieter B sich bei Entscheidungspunkt B1 für die Menge 60 beziehungsweise bei Punkt B2 für die Menge 30 entscheiden wird, wird sie bei Punkt A die Menge 60 wählen. Nachdem die Spielmatrix symmetrisch ist, wäre der Ausgang der gleiche, wenn Anbieter B als erstes entscheidet. In diesem Fall würde allerdings Anbieter B 60 Stück und Anbieter A 30 Stück produzieren.
Würde es sich um ein simultanes Spiel handeln, so gibt es kein eindeutiges Gleichgewicht, da keiner der beiden Spieler eine dominante Strategie hat. Es ergibt sich eine Situation, die der des Kampfes der Geschlechter gleicht.
Preisdiskriminierung
Allgemeines
Unter Preisdiskriminierung versteht man die Strategie eines Unternehmens, mit Marktmacht unterschiedliche Preise für unterschiedliche Konsumenten zu setzen und damit mehr Gewinn zu lukrieren, als dies in einem Regime, das einen einheitlichen Preis vorsieht, möglich wäre. In Lektion 2 sind wir von einem solchen Regime ausgegangen – der Stückpreis eines Gutes war konstant. Diese Annahme wird im Folgenden aufgehoben.
Warum wenden Unternehmen Strategien der Preisdiskriminierung an?
Die Gesamtnachfragekurve auf einem Gütermarkt, welche die Nachfrage auf der x-Achse in Abhängigkeit vom Preis auf der y-Achse darstellt, hat üblicherweise eine negative Steigung, d.h. je höher der Preis, umso geringer der Absatz. Dies impliziert aber auch, dass Konsumenten für die erste Einheit des Gutes bereit sind mehr zu zahlen, als für die zweite Einheit. Die zweite Einheit ist ihnen wiederum mehr wert als die dritte, und so weiter. D.h. die Zahlungsbereitschaft sinkt, je mehr Einheiten des Gutes schon konsumiert wurden. Diese Tatsache lässt sich an vielen alltäglichen Beispielen verdeutlichen. Es ist es beispielsweise tendenziell so, dass uns der erste Schluck Wasser nach sportlicher Betätigung wichtiger ist (wir wären also bereit, mehr dafür zu zahlen), als der Schluck, der folgen würde, nachdem wir bereits einen halben Liter Wasser getrunken haben. Die Tatsache einer Nachfragekurve mit negativer Steigung lässt sich also direkt von dem Konzept des abnehmenden Grenznutzens herleiten.
Ein Beispiel für eine typische indirekte Nachfragefunktion wird in folgender Abbildung dargestellt. Wenn der Preis des Gutes pmax oder höher liegt, so ist das Gut zu teuer und wird nicht nachgefragt (der Absatz ist null). Sinkt der Preis etwas unter pmax, so wird nur eine einzige Einheit nachgefragt. Soll mehr abgesetzt werden, muss der Preis weiter sinken.
Angenommen, der Preis liegt bei p‘ – hier werden q‘ Einheiten des Gutes nachgefragt. Für alle Einheiten vor q‘ wäre der Konsument allerdings bereit gewesen, einen höheren Preis als p‘ zu zahlen, d.h. seine Zahlungsbereitschaft war höher. Trotzdem, wenn der Produzent einen einheitlichen Preis verlangen muss, so zahlt der Konsument für jede Einheit den einheitlichen Preis p‘. Dadurch entsteht eine sogenannte Konsumentenrente. [13] Diese ist durch das Dreieck gegeben, dass durch die Punkte pmax, p‘ auf der y-Achse und den Schnittpunkt der Geraden q‘ mit der Nachfragekurve gegeben ist. Die Fläche des Dreiecks entspricht jenem Geldbetrag, den die Konsumenten bereit gewesen wären, zu zahlen, aber dank einheitlicher Preissetzung nicht zahlen mussten.
Daraus folgt, dass der Produzent überlegen wird, die Konsumentenrente zu seinem Vorteil zu reduzieren. Im Idealfall würde von jedem Konsumenten so viel verlangt, wie er gerade noch bereit ist, zu zahlen. Mit Hilfe von Preisdiskriminierung könnte also ein höherer Gewinn erzielt werden, da diese Methode es dem Produzenten ermöglicht, einen nicht-konstanten Stückpreis zu verlangen und damit den Stückpreis der tatsächlichen Zahlungsbereitschaft des Konsumenten für die jeweilige Einheit anzupassen. So ist es dem Produzenten möglich, einen Teil der Konsumentenrente abzuschöpfen und damit einen höheren Gewinn zu erzielen.
Kann der Produzent nur einen einheitlichen Stückpreis setzen, so gibt es in der Preissetzung einen trade-off (wie in Lektion 2 ausführlich diskutiert). In die Überlegung, ob ein niedrigerer Preis gesetzt werden soll, fließen in diesem Fall zwei Effekte ein. Einerseits bedeutet ein niedriger Preis, dass mehr Einheiten des Gutes gekauft werden, andererseits ist der Erlös pro Einheit niedriger. Diese zwei Effekte muss ein Produzent, der den optimalen Preis sucht, gegeneinander abwiegen. Dieser trade-off wird durch die Möglichkeit der Preisdiskriminierung (zumindest teilweise) umgangen. Der Produzent erzielt durch Preisdiskriminierung einen höheren Gewinn, da er einerseits einen Teil der Konsumentenrente abschöpfen kann und andererseits auch Konsumenten zum Kauf bewegen kann, denen der einheitliche Preis zu hoch wäre. Die Preisdiskriminierung erlaubt es dem Produzenten also, den Preis an die tatsächliche Zahlungsbereitschaft der Konsumenten anzupassen.
Beispiele für Preisdiskriminierung im alltäglichen Leben sind etwa Ermäßigungen für Museen oder Schilifte für die lokale Bevölkerung oder Ermäßigungen im Theater oder bei Zeitungsabonnements für Studierende. [14] In diesem Fall wird davon ausgegangen, dass die jeweilige Personengruppe eine niedrigere Zahlungsbereitschaft hat als andere Konsumenten. Diese Gruppen würden wohl im Fall eines einheitlichen gewinnmaximierenden Preises das Gut umso viel weniger konsumieren, dass es sich lohnt, nur für diese Gruppe den Preis zu reduzieren. Dadurch wird sichergestellt, dass auch diese Gruppen das Gut konsumieren, Absatz und Gewinn erhöhen sich.
Unter welchen Bedingungen kann Preisdiskriminierung angewendet werden?
Es gibt im Allgemeinen drei Bedingungen, die gelten müssen, damit Preisdiskriminierung als Strategie angewendet werden kann:
1) Die Anbieter müssen eine gewisse Marktmacht haben, d.h., sie müssen die Möglichkeit haben, als Preissetzer zu agieren. Dies ist der Fall in Monopolen, aber auch in oligopolistischen Märkten (vgl. Lektion 2). Es darf also in dem betrachteten Markt keinen freien Markteintritt geben, da in dem Fall Anbieter so lange in den Markt eindringen würden, solange es positive Gewinne zu erwarten gibt, d.h. so lange, bis der Preis den Grenzkosten entspricht.
2) Die Nachfragekurve muss eine negative Steigung haben, d.h., die Zahlungsbereitschaft der Konsumenten muss variieren und mit zusätzlicher Menge abnehmen. Diese negative Steigung der (Gesamt-)
Nachfragekurve, der ein Produzent gegenübersteht, entsteht entweder, wenn (unter der Annahme identischer Konsumenten) die Zahlungsbereitschaft jedes einzelnen Konsumenten mit der konsumierten Menge abnimmt und/oder wenn sich Konsumenten in ihren Zahlungsbereitschaften unterscheiden (also unterschiedliche Nachfragefunktionen haben). In diesem Fall entsteht eine Gesamtnachfragekurve mit negativer Steigung, da manche Konsumenten eine höhere und andere eine niedrigere Zahlungsbereitschaft haben. Die negative Steigung der Nachfragekurve drückt sich durch eine negative Preiselastizität der Nachfrage aus: je höher der geforderte Preis, umso geringer ist die Nachfrage nach dem Gut.
Weiters muss es den preisdiskriminierenden Anbieter möglich sein, die einzelnen Konsumenten beziehungsweise deren Preissensibilität (zumindest in gewissem Ausmaß) zu identifizieren, um Preise entsprechend zu setzen.
3) Der Weiterverkauf des Gutes zwischen Konsumenten muss verhindert werden, da ansonsten ein Anreizproblem besteht: Gibt es die Möglichkeit des Weiterverkaufes, so haben Konsumenten mit dokumentiert niedriger Zahlungsbereitschaft einen Anreiz, das Gut zum niedrigeren Preis zu kaufen, um es danach zu einem höheren Preis an Konsumenten mit höherer Zahlungsbereitschaft weiterzuverkaufen. Die Konsumenten mit höherer Zahlungsbereitschaft würden dann also bei diesen Anbietern anstatt beim Produzenten kaufen. In diesem Fall würde Preisdiskriminierung also nicht funktionieren - nur die Konsumenten mit niedriger Zahlungsbereitschaft würden das Produkt direkt vom Produzenten kaufen.
Weiterkauf ist beispielsweise nicht möglich bei allen Arten von Dienstleistungen, ein Arzt kann bspw. Preisdiskriminierung betreiben, da sich eine Untersuchung nicht wiederverkaufen lässt. Weiters spielen in diesem Zusammenhang Transaktionskosten eine wichtige Rolle. Sind die Transaktionskosten hoch (ist es beispielsweise schwierig Kontakte zwischen Konsumenten mit niedriger und hoher Zahlungsbereitschaft herzustellen), so ist die Wahrscheinlichkeit von Wiederverkäufen geringer. Außerdem können Wiederverkäufe durch Regeln und Gesetze eingeschränkt werden. Diese Möglichkeit beinhaltet sowohl Maßnahmen wie zum Beispiel Ausweiskontrollen beim Kauf eines Theatertickets, als auch Zölle, die es unprofitabel machen, Waren aus Ländern, in denen Güter preiswerter sind, zu importieren, und in einem Land mit höheren Preisen weiterzuverkaufen. [15]
Möglichkeiten der Preisdiskriminierung
Je nach verfügbarer Information gibt es unterschiedliche Möglichkeiten der Preisdiskriminierung.
- Hat der Produzent genaue Information zu der Zahlungsbereitschaft jedes einzelnen Konsumenten, so kann er perfekte Preisdiskriminierung (Preisdiskriminierung ersten Grades) betreiben. Er kann in diesem Fall von jedem Konsumenten genau dessen Reservationspreis für die jeweilige Einheit verlangen. Die Stückpreise variieren also pro Einheit sowie pro Konsumenten und der Produzent ist in der Lage, die gesamte Konsumentenrente aus Abbildung 3-1 abzuschöpfen. Allerdings ist es in der Praxis nur in Ausnahmefällen möglich, die genaue Zahlungsbereitschaft der Konsumenten zu kennen. [16]
- Hat der Produzent weniger Information zur Verfügung, so kann er Preisdiskriminierung zweiten Grades betreiben. In diesem Fall weiß der Monopolist zwar, dass es Konsumenten(gruppen) mit unterschiedlichen Nachfragefunktionen gibt, kann allerdings die individuellen Konsumenten nicht den jeweiligen Nachfragefunktionen zuordnen. Um mit diesem Problem umzugehen, kann ein Preisschema erstellt werden, das dazu führt, dass sich die Konsumenten selbst bestimmten Gruppen zuordnen. Durch diese Selbstselektion der Konsumenten ist es nicht nötig, dass der Anbieter weiß, welcher Konsument welcher Gruppe zuzuordnen ist. Auch mit dieser Art der Preisdiskriminierung wird die Zahlungsbereitschaft der Konsumenten (zumindest teilweise) ausgereizt. Eine Möglichkeit ein solches System zu gestalten ist, dass man den Stückpreis eines Gutes von der nachgefragten Menge abhängig macht. In diesem Fall variiert der Stückpreis mit der gekauften Menge, ist allerdings für unterschiedliche Konsumenten (solange sie sich für dieselbe Menge entscheiden) konstant.
- Die Preisdiskriminierung dritten Grades stellt eine weitere Möglichkeit dar, bei beschränkter Information Preisdiskriminierung durchzuführen. Hier zahlen unterschiedliche Gruppen von Konsumenten unterschiedliche Preise, allerdings ist der Stückpreis konstant (also unabhängig von der vom einzelnen Konsumenten nachgefragten Menge). Die Diskriminierung findet demnach zwischen, aber nicht innerhalb der einzelnen Gruppen statt. Diese Form der Preisdiskriminierung wird besonders gern eingesetzt, wenn sich Konsumenten nach bestimmten Merkmalen (Kinder, Studenten, Pensionisten, …) oder Räumen (Stadt/Land, strukturschwache/-starke Regionen, …) unterscheiden lassen.
Preisdiskriminierung ersten Grades
Preissetzung
Angenommen der Produzent weiß, dass die indirekte Nachfragefunktion eines Konsumenten wie in Abbildung 3-3 aussieht. Für die erste Einheit des Gutes ist der Konsument bereit, 9 Geldeinheiten (GE) zu zahlen und bei perfekter Preisdiskriminierung werden für diese Einheit ebendiese 9 GE verlangt. Für die zweite Einheit ist die Zahlungsbereitschaft des Konsumenten niedriger, er ist nur noch bereit 8 GE zu zahlen. Daher verlangt der Anbieter für die zweite Einheit auch nur mehr diesen niedrigeren Preis, usw. Die Nachfragefunktion entspricht in diesem Fall also genau der Grenzertragsfunktion des Monopolisten: Sie zeigt an jedem Punkt an, wie viel zusätzlichen Erlös der Verkauf einer weiteren Einheit bringt. Gemäß der Optimalitätsregel des Monopolisten, die besagt, dass im Optimum Grenzerlös = Grenzkosten gelten muss, wird der Monopolist also so lange Einheiten verkaufen, so lange die Zahlungsbereitschaft des Konsumenten über den Grenzkosten liegt. Dies entspricht derselben verkauften Menge, die auch im perfekten Wettbewerb angeboten wird und ist damit höher als die Menge, die ein Monopolist, der einen einheitlichen Preis setzen muss, anbieten würde. Der Monopolist wählt unter perfekter Preisdiskriminierung dieselbe Menge wie ein Produzent unter perfektem Wettbewerb, da er von der Beschränkung entbunden ist, nur einen einheitlichen Preis zu verlangen. Dementsprechend ist der Trade-off, den er zuvor im Auge behalten musste (ein niedrigerer Preis bedeutete, dass jedes verkaufte Stück zu diesem niedrigeren Preis verkauft wird), nicht mehr relevant. Es ist nun optimal für ihn bis zu dem Punkt zu verkaufen, an dem die Zahlungsbereitschaft des Konsumenten gleich den Grenzkosten ist; darüber hinaus verkaufte Einheiten würden einen Verlust bedeuten. Unter der Annahme konstanter Grenzkosten von 2 GE, würden in dem Beispiel, welches in Abbildung 3-3 dargestellt wird, von dem Monopolisten also genau 8 Einheiten angeboten werden.
Wohlfahrtseffekte
Im Monopol entspricht die Konsumentenrente der Fläche A in Abbildung 3-4, das Symbol M bezieht sich auf den Monopolpreis bei einheitlicher Preissetzung, PD auf Preisdiskriminierung wie soeben besprochen. Die Produzentenrente entspricht der Fläche B und der Nettowohlfahrtsverlust eines Monopols der Fläche C. In einem Monopol mit Preisdiskriminierung ersten Grades ist die Konsumentenrente null (der Produzent verlangt immer genau die Zahlungsbereitschaft für jede Einheit) und die Produzentenrente der Fläche A+B+C. Dies ist, im Gegensatz zu der Situation eines Monopols mit einheitlicher Preissetzung, ein paretoeffizientes Resultat. Keine der beiden Gruppen könnte bessergestellt werden, ohne eine andere schlechter zu stellen, da kein Nettowohlfahrtsverlust auftritt. Konsumenten, die eine sehr hohe Zahlungsbereitschaft haben, haben im Monopol mit einheitlicher Preissetzung eine höhere Wohlfahrt, da ihre Zahlungsbereitschaft höher als der Einheitspreis liegt. Konsumenten mit niedriger Zahlungsbereitschaft haben in beiden Fällen eine Konsumentenrente von null, da sie im Monopol mit einheitlicher Preissetzung nicht kaufen (der Preis liegt über ihrer Zahlungsbereitschaft), wohingegen sie im Monopol mit perfekter Preisdiskriminierung zwar kaufen, allerdings zu einem Preis, der genau ihrer Zahlungsbereitschaft entspricht.
Im perfekten Wettbewerb würde die gleiche Menge produziert werden. Die Konsumentenrente wäre in diesem Fall allerdings durch A+B+C gegeben, wohingegen die Produzentenrente gleich null wäre, da der einheitliche Preis in diesem Fall gleich den Grenzkosten wäre. Obwohl also die produzierte Menge die gleiche ist, unterschieden sich die Wohlfahrtsimplikationen stark. In Bezug auf die Wohlfahrt der Konsumenten wäre die Reihung daher perfekter Wettbewerb (größtmögliche Konsumentenrente), gefolgt von dem Monopol mit einheitlicher Preissetzung und abschließend Monopol mit Preisdiskriminierung ersten Grades (niedrigste Konsumentenrente).
Preisdiskriminierung zweiten Grades
Staffelpreise
Bei der Preisdiskriminierung zweiten Grades selektieren sich Konsumenten durch ihre Konsumentscheidung selbst in die „richtige Gruppe“. Eine Art und Weise, dies zu erreichen, ist, den Stückpreis je nach gekaufter Menge anzupassen. Ein typisches Beispiel für eine solche Art der Preisdiskriminierung sind Mengenrabatte, die oft durch Staffelpreise umgesetzt werden. In diesem Schema wird für die ersten Einheiten (die erste Staffel) eines Gutes der Preis p1 verlangt, für weitere Einheiten allerdings der niedrigere Preis p2. Je mehr unterschiedliche Staffeln ein Monopolist anbietet, umso näher kommt er mit dieser Methode der perfekten Preisdiskriminierung. Staffelpreise bedeuten eine Reduktion des Stückpreises, abhängig von der konsumierten Gesamtmenge – je mehr Stück gekauft werden, umso niedriger ist der Stückpreis. Jeder Konsument zahlt allerdings, anders als bei der Preisdiskriminierung ersten Grades, denselben Stückpreis (gegeben er kauft dieselbe Menge). [17]
Im Folgenden wird die Möglichkeit zu Staffelpreisen an einem Beispiel verdeutlicht. Angenommen die Nachfrage folgt der indirekten Nachfragefunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 90 - q} . Weiters seien die Grenzkosten konstant mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c = 30} . Das Optimierungsproblem des Produzenten stellt sich wie folgt dar:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \max(\pi) = p_{1}q_{1} + p_{2}\left( q_{2} - q_{1} \right) - cq_{2} = \left( 90 - q_{1} \right)q_{1} + \left( 90 - q_{2} \right)\left( q_{2} - q_{1} \right) - 30q_{2}}
Der Monopolist maximiert seinen Gewinn, der sich aus dem Erlös des Verkaufs der ersten Stufe mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1}} Stück sowie der zweiten Stufe mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left( q_{2} - q_{1} \right)} Stück zusammensetzt, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2}} die gesamte produzierte Menge bezeichnet. Daraus folgen die Optimalitätsbedingungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi}{\partial q_{1}} = - 2q_{1} + q_{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi}{\partial q_{2}} = 60 - 2q_{2} + q_{1}}
Für ein Optimum müssen beide Gleichungen simultan gelten. Durch Nullsetzen und Einsetzen einer Gleichung in die andere erhalten wir die optimalen Mengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 20} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2} = 40} sowie Preise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{1} = 70} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{2} = 50} .
In Abbildung 3-5 zeigt eine grafische Darstellung dieses Beispiel, die Konsumenten erhalten die Rente KR = A+B, die Produzentenrente PR ist durch die Fläche C gegeben. Bei dieser Art der Preisdiskriminierung entsteht ein Nettowohlfahrtsverlust, welcher durch die Fläche D gegeben ist. Nummerisch sind in dem obigen Beispiel die Renten wie folgt gegeben:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle KR = A + B = \frac{20 \bullet 20}{2} + \frac{20 \bullet 20}{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P R=C=(70-30) \cdot 20+(50-30) \cdot 20=1200 }
Der Nettowohlfahrtsverlust beträgt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D = \frac{(50 - 30)20}{2} = 200}
Vergleicht man dieses Ergebnis mit den Renten in einem Monopol mit einheitlicher Preissetzung, so können wir zeigen, dass in diesem konkreten Beispiel die Konsumentenrente mit Preisdiskriminierung niedriger ist, die Produzentenrente allerdings höher. Weiters ist der Nettowohlfahrtsverlust durch das Monopol niedriger bei Preisdiskriminierung als bei einem einheitlichen Preis. Je mehr Staffeln von dem Monopol gesetzt werden, umso ähnlicher wird die Situation der Preisdiskriminierung ersten Grades und umso kleiner wird dementsprechend der Nettowohlfahrtsverlust.
Der Zwei-Komponenten-Tarif
Bei diesem Preisschema verlangt der Produzent einen Pauschalbetrag, sowie einen zusätzlichen konstanten Preis pro Stück. Auch hier wird also der durchschnittliche Stückpreis immer geringer, je mehr Einheiten konsumiert werden. Um den Gewinn in dieser Situation zu maximieren, wird ein Produzent versuchen, die potenzielle Konsumentenrente zu maximieren und diese dann mittels Pauschalbetrags möglichst gesamt abzuschöpfen. Typische Beispiele für ein solches Preisschema sind Preise für Telefonnutzung, wo dem Benutzer meist eine monatliche Grundgebühr sowie eine Gesprächsgebühr pro telefonierte Minute verrechnet wird. Um diese Art der Preissetzung zu analysieren, müssen wir unterscheiden, ob in dem Markt lauter identische Konsumenten (mit identischen Nachfragefunktionen) oder unterschiedliche Konsumenten vertreten sind.
Identische Konsumenten
In diesem Fall haben alle Konsumenten die gleiche, dem Monopolisten bekannte (indirekte) Nachfragefunktion. Angenommen, diese ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 80 - x} gegeben. Außerdem sind die konstanten Grenzkosten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c = 10\ GE} . In diesem Fall wird, wie in Abbildung 3-6 zu sehen, die potenzielle Konsumentenrente bei einem Preis von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = c = 10} maximiert.
Die indirekte Nachfragefunktion stellt dar, dass ein Konsument bei einem Preis von p=10 70 Einheiten des Gutes kauft. Er wäre allerdings bereit gewesen, für alle Einheiten vor der 70ten einen höheren Preis als 10 GE zu bezahlen. Dies macht sich der Monopolist zu Nutze und verlangt als Pauschale die gesamte Konsumentenrente, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle KR = \frac{\left( (80 - 10)70 \right)}{2} = 2450} . Selbst wenn der Konsument für die 70 Einheiten, zusätzlich zu dem Stückpreis von 10 GE, noch ebendiese Pauschale bezahlen müsste, so würde er immer noch dieselben 70 Einheiten nachfragen. Der Monopolist schöpft mit dieser Preissetzungsstrategie die gesamte Konsumentenrente ab.
Würde der Monopolist einen höheren Stückpreis verlangen (und damit nicht die potenzielle Konsumentenrente maximieren), so wäre sein Gewinn niedriger. Die Konsumenten würden eine geringere Menge des Gutes nachfragen und es gäbe einen Nettowohlfahrtsverlust durch die reduzierte Produzentenrente. Es ist nicht verwunderlich, dass dieses Ergebnis jenem der Preisdiskriminierung ersten Grades ähnelt, da die benötigte Information die gleiche ist – der Monopolist muss die Nachfragekurve der (identischen) Konsumenten genau kennen. Sollte diese Information nicht (oder nur teilweise) vorhanden sein, so kann der Zwei-Komponenten-Tarif trotzdem angewandt werden. In diesem Fall muss die Zahlungsbereitschaft der Konsumenten geschätzt werden, um den Pauschaltarif festzulegen. Diese wird damit vermutlich nicht maximiert, da im Zweifelsfall eine niedrigere Pauschalrate, als für den Monopolisten optimal wäre, gewählt wird.
Nichtidentische Konsumenten
Was passiert nun, wenn das Monopol mit unterschiedlichen Konsumenten (deren Nachfragefunktionen sich unterscheiden) konfrontiert ist, und er dabei nicht unterscheiden kann, welcher Konsument in welche Gruppe fällt? Im Falle, dass das Monopol die Möglichkeit hat, die beiden Konsumentengruppen zu identifizieren, in der Folge unterschiedlich zu behandeln und Weiterverkäufe zu verhindern, ist die Antwort einfach: Er wird die Pauschalbeträge für jeden Konsumenten unterschiedlich festsetzen und zwar genau so, dass (wie im zuvor behandelten Fall) die gesamte Konsumentenrente abgeschöpft wird. Der Stückpreis ist in allen Fällen konstant, da sich dieser nach den Grenzkosten des Monopolisten richtet.
Sollte es allerdings (durch rechtliche Bestimmungen oder Fehlen an Information über individuelle Konsumenten) nicht möglich sein, unterschiedlichen Konsumenten unterschiedliche Angebote zu unterbreiten, so hat der Monopolist zwei Möglichkeiten. Er kann einerseits ein einziges Preisschema festsetzen, welches so gewählt sein muss, dass es den Gewinn aus dem Verkauf an beide Konsumenten maximiert. Eine andere Möglichkeit ist, unterschiedliche Preispakete für unterschiedliche Konsumenten anzubieten und diese so festzusetzen, dass sich die Konsumenten in die jeweils für sie vorgesehene Gruppe selektieren, also genau das Preispaket in Anspruch nehmen, welches für sie vorgesehen ist.
Ein einheitliches Preisschema bei nichtidentischen Konsumenten
Angenommen, im Markt sind zwei unterschiedliche Konsumenten vertreten, Konsument 1 und Konsument 2. Die Nachfrage von Konsument 1 ist durch die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 80 - p}
gegeben, während die von Konsument 2 der Funktion
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2} = 100 - p}
folgt. Die beiden Nachfragefunktionen sind in Abbildungen 3-7 sowie 3-8 dargestellt.
Wie zuvor erörtert wurde, wird die Höhe des Pauschalbetrages durch die Konsumentenrente bestimmt, welche jeweils durch die Fläche A+B+C gegeben. Optimalerweise wird der Monopolist den Pauschalbetrag L entweder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = {KR}_{1}} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = {KR}_{2}} setzen, wobei im Falle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = {KR}_{1}\ } beide Konsumenten das Gut nachfragen werden, im Falle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = {KR}_{2}} allerdings nur Konsument 2 kaufen wird (da Konsument 1 eine niedrigere Zahlungsbereitschaft als Konsument 2 hat). Die Konsumentenrenten berechnen sich anhand der Formel für ein rechtwinkliges Dreieck, wobei eine Seite der Differenz zwischen Reservationspreis und tatsächlichem Preis und die andere der abgesetzten Menge entspricht. [18]
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {KR_{1} = \frac{1}{2}(80 - p)q_{1} = \frac{1}{2}(80 - p)^{2} }{KR_{2} = \frac{1}{2}(100 - p)q_{2} = \frac{1}{2}(100 - p)^{2}}}
was jeweils den Flächeninhalten A+B+C entspricht. Für das Monopol wäre es nicht optimal, eine andere Pauschalrate als eine dieser beiden zu setzen. Wäre zum Beispiel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L > {KR}_{2}} , dann würde keiner der beiden Konsumenten kaufen - eine Situation, die nicht optimal sein kann, da der Produzent durch den Verkauf einiger Einheiten des Gutes immer die Möglichkeit hätte, einen positiven Gewinn zu machen. Würde der Monopolist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L < {KR}_{1}} setzen, würden beide Konsumenten das Gut kaufen, allerdings wäre dies auch bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = \ {KR}_{1}} der Fall gewesen. Mit dieser Strategie verliert der Monopolist also an Gewinn. Die dritte Möglichkeit, nämlich den Pauschalbetrag zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {KR}_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {KR}_{2}} festzusetzen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {KR}_{1} < L < \ {KR}_{2}} ), kann auch nicht optimal sein, da in diesem Fall nur Konsument 2 kaufen würde, dies allerdings auch bei dem höheren Pauschalbetrag Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = \ {KR}_{2}} eintreten würde. Der Gewinn, wenn der Pauschalbetrag Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L = \ KR1_{1}\ } gesetzt wird, ist gegeben durch:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{KR1} = 2\frac{\left( 80 - p_{KR1} \right)^{2}}{2} + \left( p_{KR1} - c \right)\left( q_{1} + q_{2} \right) = \left( 80 - p_{KR1} \right)^{2} + \left( p_{KR1} - c \right)\left( 180 - 2p_{KR1} \right)}
Wobei sich der erste Term aus der Formel für die Fläche eines rechtwinkligen Dreiecks ergibt und im zweiten Term die unterschiedlichen Nachfragefunktionen berücksichtigt sind. In diesem Fall würden beide Konsumenten das Gut kaufen, d.h. der Monopolist bekäme zwei Mal die Pauschalrate sowie den Stückpreis für die verkauften Einheiten abzüglich der Produktionskosten. Angenommen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c = 10} ,
so wird der optimale Preis durch Arbeiten und Nullsetzen bestimmt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi_{KR1}}{\partial p_{KR1}} = 4600 - p_{KR1}^{2} + 40p_{KR1}}
woraus sich der gewinnmaximierende Preis als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{KR1} = 20} ergibt, was einem Gewinn von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{1} = 5000} entspricht.
Vergleichen wir diesen Gewinn mit jenem, der sich durch Setzen des der Pauschalbetrag L= KR2 ergibt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_{KR1} = \frac{\left( 100 - p_{KR2} \right)^{2}}{2} + \left( p_{KR2} - c \right)q_{2}}
Hier würde nur Konsument 2 das Gut kaufen, daher erhält der Monopolist nur einmal die Pauschalrate LKR2. Für jede Einheit des Gutes, welche verkauft wird, erhält der Produzent weiters den Stückpreis abzüglich der Produktionskosten. Bei Wiederholung des Rechengangs (ableiten – nullsetzen – für den Preis auflösen – den Preis in Gewinnfunktion einsetzen) ergeben sich als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{KR2} = 10} , was einem Gewinn von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \pi_{2} = 4050} entspricht. Es wird also der höhere Preis gesetzt. Dieses Resultat unterscheidet sich von dem zuvor besprochenen (mit identischen Konsumenten), da der Monopolist unter diesen Umständen (einheitliche Pauschalratensetzung bei unterschiedlichen Konsumenten) in keinem Fall die gesamte Konsumentenrente abschöpfen kann. Daher ist es in obigem Beispiel optimal, den Preis höher als die Grenzkosten zu setzen.
Bündelung
Bei der Bündelung wird der Kauf eines Produktes an den Kauf eines anderen Produktes gebunden. Diese Strategie macht es für den Konsumenten unmöglich, ein Gut ohne das andere zu kaufen. Beispiele einer solchen Bündelung reichen von Hemden, die immer mit Knöpfen verkauft werden, über Computer, die beim Kauf bereits mit einem Betriebssystem ausgestattet sind, bis zu Kabelfernsehangeboten, in denen immer ein Bündel von Programmen gemeinsam bestellt werden muss. Oft, wie offensichtlich im Fall von Hemden, reduziert Bündelung die Transaktionskosten. Mitunter, wie bei Paketen von Fernsehsendern, sind die Grenzkosten nahe null. Im vereinfachten Beispiel von zwei Konsumenten mit unterschiedlichen Nachfragefunktionen macht eine Strategie der Bündelung für den Monopolisten nur dann Sinn, wenn die Nachfrage der beiden Konsumenten negativ korreliert ist. Der Grund dafür wird im Folgenden anhand eines nummerischen Beispiels verdeutlicht.
Angenommen, ein Monopolist möchte Theatertickets für zwei verschiedene Vorstellungen verkaufen. Soll er diese einzeln oder als nur als Bündel anbieten? Auch hier gilt wiederum die Annahme, dass der Monopolist zwar weiß, dass es zwei unterschiedliche Konsument-Typen gibt, die individuellen Konsumenten allerdings nicht der jeweiligen Nachfragefunktion zuordnen kann. Verkauft er die Theatertickets als Bündel, so wird eine Unterscheidung der individuellen Konsumenten unnötig, da beiden das gleiche Bündel angeboten wird.
Der Monopolist sieht sich zwei Konsumenten mit unterschiedlichen Zahlungsbereitschaften gegenüber. Da Theaterstück 1 ein Publikumshit ist, sind die Zahlungsbereitschaften beider Konsumenten für Stück 1 höher als für Stück 2. Um herauszufinden, ob er in diesem Fall eine Strategie der Bündelung anwenden soll, vergleicht der Monopolist den Erlös mit beziehungsweise ohne Bündelung (Anmerkung: Da die Grenzkosten eines zusätzlichen Zuschauers im Theater gleich null sind, entspricht der zusätzliche Erlös dem zusätzlichen Bruttogewinn).
| Theaterstück 1 | Theaterstück 2 | Bündelung | |
|---|---|---|---|
| Konsument 1 | 20 | 5 | 25 |
| Konsument 2 | 14 | 1 | 15 |
| Gesetzter Preis | 14 | 5 | 15 |
| Erlös | 2*14 = 28 | 1*5 = 5 | 2*15 = 30 |
| Gesamterlös | 28 + 5 = 33
|
30 | |
Positiv korrelierte Zahlungsbereitschaften
Im in Tabelle 3-1 dargestellten Beispiel ist Konsument 1 bereit, 20 GE für den Eintritt zu Stück 1 zu bezahlen, allerdings ist ihm der Besuch von Stück 2 nur 5 GE wert. Konsument 2 ist bereit, 14 GE für Stück 1 und 1 GE für Stück 2 zu zahlen. Bietet der Monopolist die Tickets für die beiden Stücke einzeln an, so wird er optimalerweise für Stück 1 einen Eintrittspreis von 14 GE verlangen. Würde er den Preis mit 20 GE ansetzen, so würde nur Konsument 1 das Stück besuchen. Der Gesamterlös in dem Fall wäre dann 20 GE, während bei einem Eintrittspreis von 14 GE beide Konsumenten ins Theater gehen würden (und dem Monopolisten damit einen Erlös von insgesamt 28 GE bescheren würden). Für Stück 2 würde der Monopolist, derselben Logik folgend, einen Eintrittspreis von 5 GE verlangen. Sein Gesamterlös bei Nicht-Bündelung wäre demnach 33 GE. Bei einer Bündelung wäre die Zahlungsbereitschaft von Konsument 1 (für beide Stücke zusammen) durch 25 GE gegeben. Konsument 2 wäre bereit, höchstens 15 GE zu zahlen, um in den Genuss des Besuches beider Stücke zu kommen. Optimalerweise würde der Monopolist also einen Preis von 15 GE setzen und damit bei Bündelung einen Erlös von insgesamt 30 GE erzielen. In diesem Beispiel brächte die Strategie der Bündelung also einen niedrigeren Erlös: Der Monopolist würde die Tickets einzeln anbieten.
| Theaterstück 1 | Theaterstück 2 | Bündelung | |
|---|---|---|---|
| Konsument 1 | 17 | 3 | 20 |
| Konsument 2 | 15 | 5 | 20 |
| Gesetzter Preis | 15 | 3 | 20 |
| Erlös | 2*15 = 30 | 2*3 = 6 | 2*20 = 40 |
| Gesamterlös | 30 + 6 = 36
|
40 | |
Negativ korrelierte Zahlungsbereitschaften
In dem in Tabelle 3-2 dargestellten Beispiel ist Konsument 1 bereit, 17 GE für Theaterstück 1 auszugeben, wohingegen ihm der Besuch von Theaterstück 2 nur 3 GE wert ist. Auch Konsument 2 würde mehr zahlen, um Theaterstück 1 zu sehen, nämlich 15 GE; Theaterstück 2 ist ihm 5 GE wert. Man beachte, dass die Zahlungsbereitschaften hier negativ korreliert sind: Theaterstück 1 hat bei Konsument 1 eine höhere Zahlungsbereitschaft, Theaterstück 2 bei Konsument 2. Wiederum wird der Erlös, der erzielt würde, wenn die Tickets einzeln verkauft werden, mit dem der Bündelung (analog zu dem vorhergehenden Beispiel) verglichen. Wie aus Tabelle 3-2 ersichtlich ist, ist in diesem Fall der Erlös bei Bündelung höher. Der Monopolist wird sich also für eine Strategie der Bündelung entscheiden, da dies seinen Gewinn maximiert.
Warum liefern die beiden obigen Beispiele unterschiedliche optimale Verhaltensweisen des Monopolisten? Dies liegt darin begründet, dass im zweiten Fall die Zahlungsbereitschaften der Konsumenten negativ korreliert sind. Im konkreten Fall bedeutet dies, dass in Beispiel 2 Konsument 1 bereit ist für Stück 1 mehr zu zahlen als Konsument 2, während es sich bei Stück 2 genau umgekehrt verhält - hier ist Konsument 2 bereit mehr zu zahlen als Konsument 1. In Beispiel 1 ist dies nicht der Fall. Die Zahlungsbereitschaft von Konsument 1 ist für beide Theaterstücke höher als jene von Konsument 2. Daher zahlt sich in diesem Fall eine Bündelung nicht aus.
Intuitiv liegt dieses Ergebnis darin begründet, dass ein einheitlicher Preis oft vom Konsumenten mit der niedrigeren Zahlungsbereitschaft bestimmt ist. Setzt man den einheitlichen Preis gemäß dessen Reservationspreis, ist sichergestellt, dass beide Konsumenten kaufen. Dies entspricht oft dem gewinnoptimierenden Verhalten. Unterscheiden sich die Zahlungsbereitschaften relativ stark, so muss das Monopol einen relativ niedrigen Preis verlangen, um eine möglichst große Menge zu verkaufen. Sind die Zahlungsbereitschaften negativ korreliert, so kann mit Hilfe der Strategie der Bündelung das Monopol die Varianz der Zahlungsbereitschaften reduzieren. Dies wird in Tabelle 3-2 deutlich, in der sich die Zahlungsbereitschaft der beiden Konsumenten für das Bündel nicht unterscheidet. Dadurch kann das Monopol bei Bündelung einen höheren Preis verlangen und trotzdem sicherstellen, dass beide Konsumenten das Produkt kaufen.
Preisdiskriminierung dritten Grades
Wenn der Monopolist die Nachfragekurve der einzelnen Konsumenten nicht kennt, er allerdings Konsumentengruppen unterscheiden kann, so kann er auch Preisdiskriminierung dritten Grades durchführen. Diese Art der Preisdiskriminierung wird in der Realität am häufigsten angewandt. Typische Beispiele sind Ermäßigungen bei Eintrittspreisen für Studierende oder Senioren. Diese Personengruppen haben traditionell für zum Beispiel Theaterbesuche eine niedrigere Zahlungsbereitschaft als die Durchschnittsbevölkerung und würden zu großen Teilen das Gut Theaterbesuch bei einheitlicher Preissetzung (die sich nach der Zahlungsbereitschaft der Durchschnittsbevölkerung richtet) nicht konsumieren. Wenn der Monopolist Preisdiskriminierung dritten Grades anwendet, so kann er auch diese Gruppen bedienen, ihre Konsumentenrente (zumindest zum Teil) abschöpfen und damit einen höheren Gewinn erzielen.
Preissetzung
Wie identifiziert der Monopolist, welcher individuelle Konsument welcher Gruppe zugeordnet werden sollte? Oft kann die Zuordnung anhand äußerer Merkmale erfolgen, wie dem Alter (Ermäßigungen für Kinder), dem Aufenthaltsort (Preisdiskriminierung nach Ländern) oder dem Beruf (Ermäßigungen für Studierende, Senioren oder Arbeitslose). In diesem Fall erfolgt eine Einteilung in Gruppen auf direkte Art und Weise.
Weiters gibt es auch die Möglichkeit, ähnlich wie bei der Preisdiskriminierung zweiten Grades, Konsumenten auf Basis ihres Verhaltens einzuteilen. Dafür wird ein Preisschema angeboten, welches zur Folge hat, dass Konsumenten sich selbst selektieren, also der Gruppe zuordnen, zu der sie gehören. Eine Möglichkeit, Konsumenten nach ihrer Zahlungsbereitschaft (beziehungsweise der Preiselastizität ihrer Nachfrage) zu unterscheiden, ist mit Hilfe der Zeit, die sie bereit sind, in den Kauf eines Gutes zu investieren. Wenn Konsumenten bereit sind, viel Zeit aufzuwenden (um beispielsweise ein Gut direkt vom Hersteller abzuholen oder lange Wartezeiten in Kauf zu nehmen), so bedeutet dies meist, dass sie eine niedrigere Zahlungsbereitschaft beziehungsweise eine höhere Preiselastizität haben. Der Monopolist kann also aus dem Verhalten der Konsumenten Rückschlüsse auf die Form ihrer Nachfragefunktion ziehen.
Das Optimierungsproblem eines Monopolisten, der Preisdiskriminierung dritten Grades durchführen möchte, stellt sich wie folgt dar: Angenommen, er möchte sein Preisschema an die Existenz zweier unterschiedlicher Gruppen, Gruppe 1 und Gruppe 2, anpassen. Die Gruppen haben unterschiedliche Nachfragefunktionen. Wir wissen aus der Monopoltheorie, dass der Monopolist seinen Gewinn an dem Punkt maximiert, an dem Grenzertrag = Grenzkosten gilt. Da es sich um das gleiche Gut handelt, sind die Grenzkosten des Monopolisten, egal für welche Gruppe er produziert, gleich. Im Optimum gilt also
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G E_1=c=G E_2 }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {GE}_{1}\ } den Grenzertrag, der sich aus der Nachfragefunktion von Gruppe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i} ergibt, darstellt. Diese Bedingung kann mit Hilfe der Amoroso-Robinson-Formel wie folgt angeschrieben werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1\left(1+\frac{1}{\varepsilon_1}\right)=c=p_2\left(1+\frac{1}{\varepsilon_2}\right) }
Wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \varepsilon}
die Preiselastizität bezeichnet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{\frac{\partial q_{i}}{\partial p}}{\frac{p}{q_{i}}}}
: Je höher die Elastizität, umso sensibler reagiert die Gruppe auf Preisänderungen. Durch Umformen des Ausdrucks erhält man
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{p_1}{p_2}=\frac{1-\frac{1}{\left|\varepsilon_2\right|}}{1-\frac{1}{|\varepsilon|}} }
unter den Bedingungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left| \varepsilon_{1} \right| < 1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left| \varepsilon_{2} \right| < 1} . Angenommen, Gruppe 1 hat die preiselastischere Nachfrage, d.h.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ \left| \varepsilon_{1} \right| > \left| \varepsilon_{2} \right|} . Die Konsumenten in Gruppe 1 reagieren also stärker auf eine Preisänderung, d.h. im Speziellen bei einer Preiserhöhung ginge ihre Nachfrage stärker zurück als die von Gruppe 2. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left| \varepsilon_{1} \right| > \left| \varepsilon_{2} \right|} bedeutet, dass
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1-\frac{1}{\left|\varepsilon_2\right|}}{1-\frac{1}{\left|\varepsilon_1\right|}}<1 \Leftrightarrow \frac{p_1}{p_2}<1 \Leftrightarrow p_1<p_2 }
Der Preis, den Gruppe 1 für das Gut bezahlt, ist also kleiner als jener, den Gruppe 2 zahlt. Das allgemeine Resultat ist also, dass optimalerweise die Gruppe mit der höheren Preiselastizität den niedrigeren Preis zahlen sollte. Intuitiv ist dies klar nachvollziehbar, da der Monopolist bei einer Preiserhöhung umso mehr verliert, je elastischer die Nachfrage ist. Man kann zum Beispiel davon ausgehen, dass Konsumenten, die bereit sind, viel Zeit für den Kauf eines Gutes aufzuwenden, eine wesentlich elastischere Nachfrage nach dem jeweiligen Gut haben als der Durchschnittsbürger. Wenn der Preis hoch ist, werden diese Gruppen den Konsum des jeweiligen Gutes verhältnismäßig stark einschränken. Das kann zum Beispiel erklären, warum im Outlet-Center Parndorf sogar Kosmetika aus dem Standard-Angebot der jeweiligen Anbieter preisreduziert sind: Das Kalkül ist offensichtlich, dass Konsumenten, die extra nach Parndorf fahren, sensibel auf Preisunterschiede reagieren.
Wohlfahrtseffekte der Preisdiskriminierung dritten Grades
In Abbildung 3-10 ist das zuvor besprochene Resultat dargestellt: Der Preis, den die Gruppe mit der weniger elastischen Nachfrage zahlt, ist höher als jener der Gruppe mit der elastischeren Nachfrage.
Unter perfektem Wettbewerb ist, analog zu obigen Beispielen, die Produzentenrente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle PR = 0} und die Konsumentenrente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle KR = A + B + C} . Im Vergleich dazu ist bei Preisdiskriminierung dritten Grades die Produzentenrente durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle PR = B} und die Konsumentenrente durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle KR = A} gegeben. Der Nettowohlfahrtsverlust entspricht der Fläche C in der Abbildung.
Auch im Monopol mit einheitlicher Preissetzung tritt ein Nettowohlfahrtsverlust ein. Ob dieser größer oder kleiner als bei der Preisdiskriminierung dritten Grades ist, kann generell nicht bestimmt werden. Der Produzent allerdings hat insgesamt eine höhere Produzentenrente als in einem Monopol mit einheitlicher Preissetzung, da er sein Preisschema den unterschiedlichen Nachfragefunktionen anpassen kann.
Übungsbeispiele
Übungsbeispiel 3.1
Ein Monopolist verkauft sein Gut in zwei Ländern und wendet Preisdiskriminierung an, indem er in jedem Land einen unterschiedlichen Preis verlangt. Der Monopolist hat konstante Grenzkosten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c = 10} . Die Nachfrage in Land 1 ist gegeben durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 50 - p_{1}} , die in Land 2 durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2} = 200/3 - 2p_{2}/3} . Welcher Preis wird in den einzelnen Ländern verlangt? Angenommen, ein weiterer Anbieter tritt in den Markt ein, der nicht als Produzent, sondern als Wiederverkäufer agiert. Er kann Güter wiederverkaufen, nachdem er sie von einem Land in das andere gebracht hat, mit Transportkosten von 4 GE pro Stück. Welchen Effekt hat dies auf den Monopolisten?
Übungsbeispiel 3.2
Eine Firma mit konstanten Grenzkosten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c = 20} ist mit zwei unterschiedlichen Arten von Konsumenten konfrontiert. Die Nachfragefunktionen sind durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 200 - p} für Konsument 1 und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2} = 100 - 0,5p} für Konsument 2 gegeben. Berechnen Sie den jeweils Gewinn maximierenden Preis. Welchen Preis wird der Monopolist wählen? Welche Menge wird er produzieren, wie ist sein Gewinn?
Übungsbeispiel 3.3
Manche Lokale verlangen niedrigere Preise bei Selbstabholung der Speisen als bei Lieferung. Erklären Sie inwiefern dies ein Beispiel für Preisdiskriminierung dritten Grades sein könnte. Geben Sie außerdem eine Erklärung, warum dieser Preisunterschied nicht unbedingt auf Preisdiskriminierung zurückzuführen sein muss.
Übungsbeispiel 3.4
Ein Monopol hat zwei Arten von Kund*innen, kennt ihre Nachfragekurven und möchte einen Zwei-Komponenten-Tarif verlangen. Die Nachfragefunktion von Konsument 1 ist durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = a_{1} - bp} , jene von Konsument 2 durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{2} = a_{2} - bp} , mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a_{2} > a_{1}} . Leiten Sie allgemeine Ausdrücke für den optimalen Stückpreis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} , sowie den Pauschalbetrag Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L} ab, unter der Annahme, dass das Monopol konstante Grenzkosten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} hat und dass es für das Monopol optimal ist,
(a) beide Konsumenten zu bedienen,
(b) nur Konsument 2 zu bedienen.
(c) Setzen Sie anschließend für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a_{1}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a_{2}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} beliebige Zahlen ein und berechnen Sie, ob der Monopolist beide oder nur einen Konsumenten bedienen soll.
Übungsbeispiel 3.5
Fassen Sie für die folgenden Typen von Preisdiskriminierung das Grundprinzip in ein bis zwei Sätzen zusammen und bringen Sie jeweils ein Beispiel.
- Preisdiskriminierung ersten Grades
- Preisdiskriminierung zweiten Grades: Staffelung
- Preisdiskriminierung zweiten Grades: Zwei-Komponenten-Tarif
- Preisdiskriminierung zweiten Grades: Bündelung
- Preisdiskriminierung dritten Grades nach Konsumentenmerkmalen
- Preisdiskriminierung dritten Grades nach Räumen
Lösungen
Übungsbeispiel 3.1
Um den gewinnmaximierenden Output und Preis zu bestimmen, geht der Monopolist wie gehabt vor, diesmal nach Ländern getrennt (indirekte Nachfragefunktion anschreiben, diese in Gewinnfunktion einsetzen, nach Menge ableiten, diese Funktion nullsetzen und für Menge auflösen, Menge in Preisfunktion einsetzen, Preis und Menge in Gewinnfunktion einsetzen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {p_{1} = 50 - q_{1},p_{2} = 100 - 1,5q_{2} }{\pi_{1} = \left( 50 - q_{1} \right)q_{1} - 10q_{1},\pi_{2} = \left( 100 - 1,5q_{2} \right)q_{2} - 10q_{2} }{\frac{\partial\pi_{1}}{\partial q_{1}} = 40 - 2q_{1} = 0,\frac{\partial\pi_{2}}{\partial q_{2}} = 90 - 3q_{2} = 0 }{q_{1} = 20,p_{1} = 30,\pi_{1} = 400,q_{2} = 30,p_{2} = 55,\pi_{2} = 1350,\Pi = \pi_{1} + \pi_{2} = 1750}}
Nachdem der Wiederverkäufer Einheiten des Gutes von einem Markt zu dem anderen um 4 GE pro Stück transportieren kann, kann dieser den Monopolisten in Land 2 um >4 GE unterbieten, d.h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{2} < 51} . Dies zwingt den Monopolisten dazu, den Preis des Gutes in Markt 2 so zu reduzieren, dass es sich nicht lohnt, als unabhängiger Importeurer tätig zu werden. Rechnerisch ist der Gewinn in Land 2 damit gegeben als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {p_{2} = p_{1} + 4 }{q_{2} = 100 - 1,5p_{2} }{\pi_{2} = \left( p_{1} + 4 \right)\left( 100 - 1,5\left( p_{1} + 4 \right) \right) - 10\left( 100 - 1,5\left( p_{1} + 4 \right) \right) = 34 \cdot 49 - 10 \cdot 49 = 1176}}
Die für Land 2 produzierte Menge steigt damit auf 49 Stück, der Gewinn des Monopolisten sinkt in Land 2 sinkt von 1350 auf 1176, also um 174 GE.
Übungsbeispiel 3.2
Man beachte, dass die Preiselastizitäten beider Konsumentengruppen identisch sind:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\varepsilon_{1} = \frac{\partial q_{1}}{\partial p}\frac{p}{q_{1}} = ( - 1)\frac{p}{200 - p} = - \frac{p}{200 - p} }{\varepsilon_{2} = \frac{\partial q_{2}}{\partial p}\frac{p}{q_{2}} = ( - 0,5)\frac{p}{100 - 0,5p} = - \frac{p}{200 - p}}}
Aus diesem Grund lohnt es sich nicht, Preisdiskriminierung zu betreiben und gesetzter Preis, produzierte Menge und erzielter Gewinn können nach dem üblichen Schema berechnet werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\pi = \left( q_{1} + q_{2} \right)(p - c) = (200 - p + 100 - 0,5p)(p - 20) }{\frac{\partial\pi}{\partial p} = - 30p + 330 = 0 }{p = 110,q_{1} = 90,q_{2} = 45,\pi = 12150}}
Führt man die Gewinnmaximierung des Produzenten für beide Gruppen getrennt durch, so ergibt sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{1} = p_{2} = 110} und folglich dieselbe Gesamtmenge und derselbe Gewinn.
Übungsbeispiel 3.3
Es könnte darin liegen, dass die Zahlungsbereitschaft einer Konsumentengruppe daraus abgeleitet wird, wie viel Zeit sie auf den Kauf einer Speise zu verwenden bereit sind. Das Lokal könnte demnach von Konsumenten, die selbst abholen, einen niedrigeren Preis verlangen, als von solchen, die sie sich zustellen lassen. Der Preisunterschied könnte allerdings auch auf Kostenunterschiede hindeuten und muss demnach nicht Preisdiskriminierung darstellen, da die Zustellung Kosten verursacht. In der Praxis besteht Preisdiskriminierung also dann, wenn der Preisunterschied über den Transportkosten liegt.
Im Fall der Produkte, die in Outlet-Centern wie in Parndorf angeboten werden, ist anzunehmen, dass die Preisdifferenz zu anderen Läden größer ist als die niedrigeren Kosten in Parndorf, so sie überhaupt niedriger sind (Miete, Gehälter u.a.). Das gilt auch umgekehrt: Auf Flughäfen zahlt man üblicherweise höhere Preise für Güter wie Parfum, Spirituosen oder Schokoladen. Wem es die Zeitersparnis wert ist (der Grenzaufwand für den Konsumenten ist null, wenn er sich ohnehin am Flughafen aufhalten muss), der wird die höheren Preise am Flughafen buchstäblich in Kauf nehmen. (Die Bezeichnung „duty free“ ist innerhalb der EU irreführend.) Allerdings kann auch hier allein aus den Preisen nicht auf Preisdiskriminierung geschlossen werden, da es sein kann, dass die Kosten, insbes. die Miete, am Flughafen höher sind als anderswo.
Übungsbeispiel 3.4
Wenn beide Konsumenten optimalerweise bedient werden, so ist der höchste Pauschalbetrag, den der Monopolist setzen kann, wegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a_{2} > a_{1}} gleich der Konsumentenrente von Konsument 1.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L = \frac{a_{1} - bp}{2}L = \frac{1}{2}\left( \frac{a_{1}}{b} - p \right)q_{1}}
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{a_{1}}{b}} dem Reservationpreis entspricht, der sich aus der Nachfragefunktion bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} = 0} ergibt und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p} der tatsächlich gesetzte Preis ist. Dieser ergibt sich aus dem Üblichen Formulieren der Gewinnfunktion, diese abzuleiten und nullzusetzen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi = 2\frac{1}{2}\left( \frac{a_{1}}{b} - p \right)q_{1} + (p - c)\left( q_{1} + q_{2} \right) = \left( \frac{a_{1}}{b} - p \right)\left( a_{1} - bp \right) + (p - c)\left( a_{1} + a_{2} - 2bp \right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi}{\partial p} = - a_{1} + a_{2} - 2bp + 2bc}
und somit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = c - \frac{a_{1} - a_{2}}{2b}}
Der optimale Pauschalbetrag ist also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=\frac{\left(3 a_1-a_2-2 b c\right)^2}{2 b} }
Ist es optimal für den Monopolisten nur an Konsument 2 zu verkaufen, so ist sein Gesamtgewinn gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi = \frac{1}{2}\left( \frac{a_{2}}{b} - p \right)q_{1} + (p - c)q_{2} = \frac{1}{2}\left( \frac{a_{2}}{b} - p \right)\left( a_{2} - bp \right) + (p - c)\left( a_{2} - bp \right)}
daher
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial\pi}{\partial p} = - bp + bc}
und somit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p = c}
Daher ist der optimale Pauschalbetrag Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=\frac{\left(a_2-b c\right)^2}{2 b} }
…nach eigener Entscheidung…
Übungsbeispiel 3.5
Kurzbeschreibung nach Belieben, Beispiele für Preisdiskriminierung:
- Preisdiskriminierung ersten Grades: Raketenabwehrsystem, Flugzeugträger, …
- Preisdiskriminierung zweiten Grades: Staffelung: Kugeln Eis im Gassenverkauf
- Preisdiskriminierung zweiten Grades: Zwei-Komponenten-Tarif: Mietauto, wenn sich der Gesamtpreis aus einer pauschalen Mietgebühr sowie einer Gebühr pro gefahrenem Kilometer zusammensetzt.
- Preisdiskriminierung zweiten Grades: Bündelung: Tickets für die Fußballspiele der österreichischen Herren-Nationalmannschaft gegen Nordirland und Bosnien-Herzegowina im Herbst 2018 im Rahmen der Nations League konnten nur als Bündel erworben werden.
- Preisdiskriminierung dritten Grades nach Konsumentenmerkmalen: Tarife nach Geschlecht bei Frisören, Fußballspielen…
- Preisdiskriminierung dritten Grades nach Räumen: Die Praxis Volkswagens und anderer Autohersteller, in ihren Heimatmärkten höhere Preise zu verlangen. [19]
Literaturverzeichnis
Weiterführende und vertiefende Literatur
Bester, Helmut (2017): Theorie der Industrieökonomik [7. Aufl.]. Berlin: Springer Gabler
Hamilton, Jonathan H. und Valerie Y. Suslow (2013): Übungen zur Mikroökonomie [8. Aufl.]. München, Pearson
Pindyck, Robert S. und Daniel L. Rubinfeld (2013): Mikroökonomie [8. Aufl.]. München, Pearson
Samuelson, Paul A. und William D. Nordhaus (2016): Volkswirtschaftslehre. München: FinanzBuch
Sardadvar, Sascha (2013) Preissetzungsverhalten auf regionalen Märkten: Eine industrieökonomische Untersuchung des österreichischen Marktes für Tageszeitungen. Saarbrücken: AV
Varian, Hal R. (2006): Grundzüge der Mikroökonomik [9. Aufl.]. Berlin und Boston: De Gruyter
Internetquellen
Bundeswettbewerbsbehörde: https://www.bwb.gv.at/
Europäische Kommission Wettbewerb: http://ec.europa.eu/competition/index_en.html
- ↑ Man beachte, dass das Spiel nur eine Runde gespielt wird und es keine Kommunikationsmöglichkeit gibt.
- ↑ Das rationale Kalkül hinter dem scheinbaren Wahnsinn wird hervorragend im Film-Klassiker „Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb“ (dt. Titel „Dr. Seltsam oder: Wie ich lernte, die Bombe zu lieben“) von Stanley Kubrick dargestellt.
- ↑ Fehr, Ernst und Simon Gächter (2000): Fairness and retaliation: the economics of reciprocity, Journal of Economic Perspectives 14: 159-181
- ↑ „Profite in der Höhe null“ bzw. „positiver Gewinn“ ist hier und im Folgenden nicht wörtlich gemeint, sondern bezieht sich auf die Differenz zu einer Einlage mit identischem Risiko. Nur wenn ein Investor der Ansicht ist, dass der Profit eines Unternehmens mindestens so groß ist wie der einer alternativen Einlage bei identischem Risiko, wird in das Unternehmen investiert werden. Oligopole und Monopole ermöglichen im ökonomischen Sinn „exzessive Profite“.
- ↑ Für Details zu den Marktformen vgl. die Skripten aus dem Bachelor-Studium oder andere einführende Literatur (s. Liste am Ende des Skriptums).
- ↑ Typischerweise werden Nachfragefunktionen so angeschrieben, dass die gesamte Nachfragemenge explizit auf einer Seite der Gleichung (in Abhängigkeit des Preises und anderer Variablen) ausgedrückt wird. Formt man eine solche Nachfragefunktion um, sodass der Preis (nun in Abhängigkeit der produzierten Menge und anderer Variablen) explizit ausgedrückt wird, spricht man von einer „indirekten Nachfragefunktion“.
- ↑ Sardadvar, Sascha (2014): A model of price setting in regional duopolies based on consumer loyalty: theory and evidence from the Austrian newspaper industry, The Annals of Regional Science 53: 591-616
- ↑ Smith, Adam (1776): An Inquiry Into The Nature And Causes Of The Wealth Of Nations, dt. Aufl. 2003, München: Deutscher Taschenbuch Verlag,
- ↑ http://ec.europa.eu/competition/cartels/cases/cases.html
- ↑ Der Spiegel 30/2017.
- ↑ Wiener Zeitung, 5. Juli 2012
- ↑ zum Aufzugkartell s. Handelsblatt, 25. Februar 2007
- ↑ vgl. Grundlagen der Volkswirtschaftslehre 2
- ↑ Auch wenn Ermäßigungen für Einheimische von der EU eigentlich verboten wurden, begegnet man ihnen dennoch bei praktisch jeder Touristenattraktion, indem man vergünstigte Eintrittskarten mit dem Besitz einer Karte verbindet, die üblicherweise nur Einheimische besitzen, bspw. Jahreskarten für die örtlichen öffentlichen Verkehrsmittel, Mitgliedskarten der inländischen Autofahrerklubs, die Club-Ö1-Karte usw.
- ↑ Allerdings stößt es bei Konsumenten nicht gerade auf Begeisterung, wenn sie mitbekommen, dass ein Produkt anderswo günstiger zu haben ist. Aus diesem Grund sah sich z.B. der deutsche Modekonzern Hugo Boss veranlasst, die Preise für Herrenanzüge global anzugleichen, nachdem chinesische Touristen regelmäßig feststellten, dass diese in gleicher Qualität in Mitteleuropa wesentlich günstiger waren als in ihrer Heimat (Handelsblatt, 2. August 2017).
- ↑ Man beachte, dass der Konsument nicht eine Person sein muss, sondern auch ein Unternehmen oder der Staat sein kann. Gerade wenn ein Produkt sehr differenziert, aus irgendeinem Grund sehr wichtig und die Stückzahl sehr niedrig ist, ist Preisdiskriminierung ersten Grades nicht unrealistisch, etwa bei bestimmten Rohstoffen oder Rüstungsgütern.
- ↑ In manchen Fällen ist eine Preisänderung bei dem Kauf höherer Stückzahlen durch niedrigere Stückkosten des Produzenten begründet (als Resultat von zum Beispiel hohen Fixkosten in der Produktion). In diesem Fall wäre ein niedrigerer Stückpreis bei steigender Menge nicht durch Preisdiskriminierung verursacht, sondern stellte lediglich die Weitergabe einer Kostenreduktion an den Konsumenten dar.
- ↑ Der Reservationspreis berechnet sich durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q = 0} in der Nachfragefunktion, daraus folgt für Konsument 1 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{r,1} = 80} und für Konsument 2 Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{r,2} = 80}
- ↑ Siehe hierzu Der Spiegel 5/1998 oder Auto-Revue 2/2002; Volkswagen verbat damals seinen italienischen Händlern, an deutschsprachige Kunden zu verkaufen, weil diese eine höhere Zahlungsbereitschaft für die Marken Audi und VW zeigten, was vom Volkswagen-Konzern durch höhere Preise in Deutschland und Österreich ausgenützt wurde. Volkswagen musste schließlich eine Strafe von 90 Millionen Euro Strafe an die EU zahlen (Manager Magazin Online am 18. September 2003).