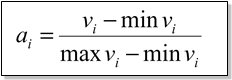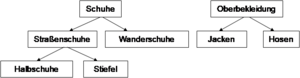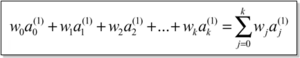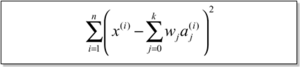Nachdruck – auch auszugsweise –, Weitergabe an Dritte und Benutzung für die Erteilung von Unterricht nur mit ausdrücklicher Zustimmung der Ferdinand Porsche Fernfachhochschule GmbH.

Es wird ausdrücklich erklärt, dass alle Angaben trotz sorgfältiger Bearbeitung ohne Gewähr erfolgen und eine Haftung des Autors/der Autorin oder des Verlegers/der Verlegerin ausgeschlossen ist.

Medieninhaberin (Verlegerin):

Ferdinand Porsche Fernfachhochschule GmbH

Ferdinand Porsche Ring 3

2700 Wiener Neustadt

Austria, Europe

Torsten Priebe

Torsten Priebe studierte Wirtschaftsinformatik an der Universität Essen (Abschluss 2000) und arbeitete in Folge als Wissenschaftlicher Mitarbeiter am dortigen Lehrstuhl für Wirtschaftsinformatik und Informationssysteme. Gemeinsam mit Prof. Günther Pernul wechselte er 2002 an die Universität Regensburg, wo im Jahr 2005 seine Promotion zum Doktor der Wirtschaftswissenschaften mit einer Doktorarbeit über die Integration von Business Intelligence und Wissensmanagementlösungen in Portalsystemen erfolgte. Aktuell ist Dr. Priebe als Senior Solution Architect bei Teradata in Wien tätig, einem der weltweit führenden Anbieter von Data-Warehouse- und Analyselösungen.
Zuvor verantwortete er als Managing Consultant den Bereich Business Intelligence bei Capgemini in Wien, mit Fokus auf Governance, Datenqualität und Metadatenmanagement, vornehmlich im Finanzdienstleistungssektor. Seit 2007 hat Dr. Priebe weiters einen Lehrauftrag für Business Intelligence an der Universität Regensburg.

Data Warehousing & OLAP

Einführung

Business Intelligence
’Business Intelligence is the use of information that enables organisations to best decide, measure, manage and optimize performance to achieve efficiency and financial benefit.’ ^[1]
Business Intelligence (BI) bezieht sich auf Anwendungen und Technologien, die eingesetzt werden, um Daten und Informationen innerhalb eines Unternehmens zu sammeln, zugänglich zu machen und zu analysieren. BI-Systeme können Unternehmen helfen, umfassenderes Wissen über die Faktoren zu gewinnen, die ihr Geschäft beeinflussen, z.B. Kennzahlen über Vertrieb, Produktion und interne Abläufe. Sie können helfen, bessere Entscheidungen zu treffen.
Während sich operative Informationssysteme mit der Unterstützung operativer Geschäftsprozesse (Auftragsabwicklung, Materialwirtschaft, …) beschäftigen, unterstützen BI-Systeme (auch Analytische Informationssysteme) Managementaufgaben und Wissensprozesse. Ziel ist die Nutzbarmachung der Datenbanken (und anderen Datenspeichern) verborgenen Informationen. Business Intelligence im weiteren Sinne beschäftigt sich sowohl mit strukturierten (in Datenbanken gespeicherte) Daten als auch mit unstrukturierten (z.B. textuellen) Dokumenten. Diese Vorlesung konzentriert sich auf Business Intelligence im engeren Sinne, sprich die Speicherung und Analyse von strukturierten Daten.

Data Warehouse
’Ein Data Warehouse ist eine physische Datenbank mit integrierter Sicht auf beliebige Daten zu Analysezwecken.’ ^[2]

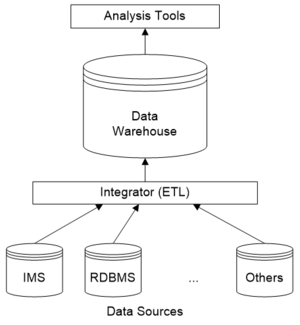
Als integrierte Datenbank für Business Intelligence dient ein Data Warehouse. Der Begriff Data Warehouse ist jedoch in der Literatur teils unterschiedlich definiert (z.B. reine Datenbank vs. komplette Systemarchitektur, Verwendung des multidimensionalen Modells).

Vereinfachte Architektur

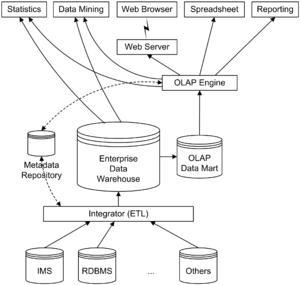
Daten werden von unterschiedlichen Datenquellen (IMS = hierarchisches Datenbanksystem aus der IBM Mainframe-Welt, RDBMS = relationales Datenbanksystem) über eine Integrationsschicht (ETL – Extract, Transform, Load) in das Data Warehouse kopiert.
Analysewerkzeuge greifen auf die Daten im Data Warehouse zu.

Charakteristika eines Data Warehouse:

Trennung von operationaler (transaktionsorientierter) und analytischer Datenverwaltung und -speicherung
Wenige Benutzer*innen (im Vergleich zu operativen Systemen) mit langen leseintensiven Transaktionen
Periodische (meist additive) Aktualisierungen (Ladevorgänge)
Sehr große Datenmengen (Gigabytes bis Terabytes); Einbindung von Daten aus unterschiedlichsten Quellen (ggf. auch Berücksichtigung externer Daten)
Extrahieren der relevanten Informationen aus den operationalen Rohdaten, normalerweise aggregiert; einfaches, verständliches Datenmodell

Zum letzten Punkt ist jedoch anzumerken, dass ein echtes Enterprise Data Warehouse gegen Veränderungen in der Analyseanforderung resistent sein sollte. Daher stellt sich die Frage, welche Informationen durch Aggregation verloren gehen. Oft hält man im Data Warehouse Detaildaten und verwendet für aggregierte Daten mit vereinfachtem Datenmodell einen abgeleiteten Data Mart.

Die klassische Definition für ein Data Warehouse stammt von William Harvey (ganannt Bill) Inmon:
’A Data Warehouse is a subject-oriented, integrated, non-volatile, time-variant collection of data organized to support management needs.’

Sie lässt sich wie folgt in ihre Bestandteile zerlegen:

Subject-oriented (themenorientiert): Das Datenmodell sollte sich an Analysethemen (Kundin, Produkt, etc.) orientieren und nicht an operativen Anwendungen
Integrated: Daten aus heterogenen Systemen sind in einer einzelnen integrierten Datenbank gespeichert, Inkonsistenzen sind entfernt
Non-volatile/time-variant (historisch/nicht flüchtig): Der Begriff “time-variant” ist missverständlich und wurde zu „..., where each unit of data is relevant to some moment in time“ umformuliert. Ein Data Warehouse speichert historische Daten (die üblicherweise 5-10 Jahre aufbewart bleiben) um Trendanalysen zu ermöglichen. Es wird grundsätzlich nichts, was einmal in das Data Warehouse aufgenommen worden ist, überschrieben, um Reproduzierbarkeit und Nachvollziehbarkeit der gemachten Auswertungen zu gewährleisten.

Grundlagen und Historie
Die Entwicklung von analytischen Systemen zur Management- und Entscheidungsunterstützung geht auf die 60er und 70er Jahre zurück. Ziel war und ist die Integration heterogener Datenbanken zur Entscheidungsunterstützung, einige Lösungen sind schon lange als verteilte und föderierte Datenbanken vorhanden.
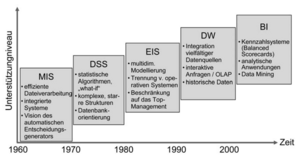
Zunächst existierten analytische Informationssysteme mit Direktzugriff auf Operativdaten. Begriffe wie MIS (Management Information System), DSS (Decision Support System), EIS (Executive Information System) kamen in den 70er Jahren auf.

Entscheidungsunterstützung im Zeitverlauf

In den 60er Jahren dominierten Berichte im Batch-Betrieb. Sie waren jedoch schwer zu verstehen und zu analysieren, unflexibel und teuer. Jede Abfrage/jeder Bericht musste neu programmiert werden.
Die 70er Jahre brachten terminalbasierte DSS/EIS. Sie waren jedoch immer noch unflexibel und individuell programmiert.
In den 80er Jahren dominierten dann Desktop-Datenzugriff und –Analyseprogramme. Anfragetools und Spreadsheets brachten eine leichtere Bedienung, aber noch immer keine a priori Integration (Direktzugriff auf operative Datenbanken).
Data Warehousing mit ETL- und OLAP-Werkzeugen entwickelte sich Mitte der 90er Jahre. Die Daten werden a priori integriert und zur Analyse im Data Warehouse gespeichert. DSS/EIS können nun auf Data Warehouses mit Hilfe von Standard-OLAP-Werkzeugen zugreifen. Aber es gehört mehr zur Entscheidungsunterstützung als nur OLAP, z.B. in die Zukunft gerichtete Analysen (Prognosesysteme, Data Mining) und Dokumente/unstrukturierte Daten.
In den letzten Jahren hat der Begriff ’Business Intelligence’ den Ausdruck OLAP weitestgehend abgelöst, er ist jedoch üblicherweise weiter gefasst (inkludiert Data Mining, fachliche Anwendungen, teils unstrukturierte Daten, Portale, …).
Die folgende Tabelle fasst die Abgrenzung zwischen operativen Systemen (OLTP – Online Transaction Processing) und Data Warehousing/OLAP (Online Analytical Processing) zusammen.

OLTP vs. DWH/OLAP
Charakteristik	OLTP	DWH/OLAP
Benutzertyp	Sachbearbeiter*in, operativ	Management, Planung
Benutzerzahl	Tausende	Tendenziell weniger
Antwortzeit	Sekunden	Sekunden bis Minuten, sogar Stunden bei komplexen Anfragen
Anwendung	Verwaltung, operatives Geschäft	Analyse, Entscheidungsunterstützung
Anfragetyp	Record/Tupelorientiert, vordefiniert	Multidimensional, aggregiert, ad-hoc
Transaktionstyp	Kurse Lese-/Schreiboperationen	Lange Leseoperationen
Datenverwaltungsziel	Transaktionskonsistenz (ACID)	Historisierung
Datenbankgröße	Megabytes bis Gigabytes	Gigabytes bis Terabytes
Optimierungsanforderung	Indexzugriff über Primärschlüssel	Full-table scans

OLTP vs. DWH/OLAP

Gründe für die Trennung von OLTP- und DWH/OLAP-Systemen:

OLTP optimiert für kurze Transaktionen und bekannte Lastprofile
Komplexe OLAP-Anfragen degradieren die Performance von Transaktionen des operationalen Betriebs
Spezieller physischer und logischer Datenbankentwurf für multidimensionale Anfragen notwendig
Transaktionseigenschaften (ACID) im DWH unwichtig, da nur Lesezugriff
Es werden historische Daten benötigt, die in OLTP-Systemen typischerweise nicht vorliegen
Konsolidierung (Integration, Bereinigung und Aggregation) von Daten aus verschiedenen heterogenen Datenquellen
Datenredundanz (Speicherung vorberechneter Aggregate auf verschiedenen Ebenen) kann aus Performance-Gründen notwendig sein; ist im DWH kontrollierbar
Sicherheit (z.B. Anonymisierung der Daten im DWH)

Online Analytical Processing (OLAP)
OLAP ist eine ’Anwendungsarchitektur’, die ein Data Warehouse als Datenquelle verwendet. Hauptcharakteristikum ist die Multidimensionalität als intuitiver Analyseansatz.
Typische Anfragen:

Wie haben sich die Verkaufszahlen in Bezug auf Verkaufskanäle und Produktgruppen dieses Jahr entwickelt (im Vergleich zum letzten Jahr)?
Welche Geschäfte machen 80 Prozent des Umsatzes einer bestimmten Marke?

Erweiterte Architektur

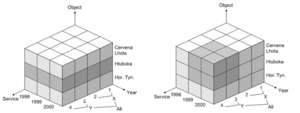
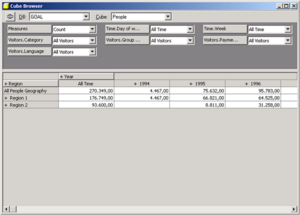
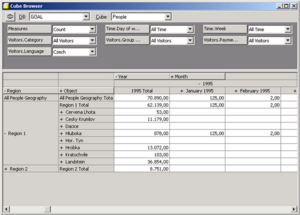
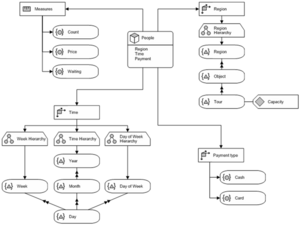
Das multidimensionale Modell von OLAP-Systemen basiert auf dem Hypercube-Paradigma. Analytische Kennzahlen/Fakten (quantifizierende Informationen, innerhalb des Würfels) orientieren sich an Dimensionen (qualifizierende Informationen, außerhalb des Würfels). Dimensionen sind meist hierarchisch strukturiert.

Hypercube-Paradigma

Typische OLAP-Operationen zur explorativen Navigation sind Slicing und Dicing zur Auswahl eines Teilwürfels (z.B. Beschränkung auf Objekt „Hluboka“).

Slice and Dice

Weitere Operationen sind Drill-down und Roll-up zur Auswahl des Detaillevels/Aggregierungsgrades. Split und Merge erhöht bzw. verringert die Dimensionalität des Ergebniswürfels, z.B. je Objekt -> je Objekt und Jahr. Drill-Across: weist betrachtete Kennzahlen in anderen Dimensionen aus. Drill-Through betrifft die Architektur des DWH, z.B. Wechsel der Datenquelle.

Illustration der OLAP-Operationen

Edgar Frank Codd hat 12 Regeln aufgestellt, die ein OLAP-System zu erfüllen hat ^[3] :

Mehrdimensionale Sicht
Transparenz für den Anwender*innen (Einbindung in Spreadsheets, etc.)
Flexible Zugriffsmöglichkeiten (Möglichkeit, auf unterschiedlichste Quellen zuzugreifen)
Konsistente Geschwindigkeit
Client-Server-Architektur
Gleichrangigkeit der Dimensionen
Dynamische Verwaltung dünn besetzter Matrizen (Sparse Data)
Mehrbenutzer*innenbetrieb
Unbeschränkte, dimensionsübergreifende Funktionen
Intuitive Datenmanipulation (Drill-down, Roll-up, etc.)
Flexibles Reporting
Unbegrenzte Dimensionen/Aggregationsebenen

Einen ähnlichen Kriterienkatalog hat Nigel Pendse mit dem FASMI-Test (Fast Analysis of Shared Multidimensional Information) im Rahmen der OLAP Report Marktstudie aufgestellt:

Fast: Hochgradig effiziente Analyse mit garantierter Antwortzeit von 5-20 Sek. unabhängig vom zugrundenliegenden Datenvolumen und der Komplexität der Abfrage
Analysis: Einfaches Benutzer*inneninterface, das dem „techn. Sachverstand der Zielgruppe“ gerecht wird, sinnvolle (inkl. graphische) Datenpräsentation
Shared: Mehrbenutzer*innenbetrieb
Multidimensional: Multidimensionale Sicht, hierarchisch strukturierte Dimensionen
Information: Für aussagekräftige Informationen muss das Produkt auf Daten verschiedenster Quellen zugreifen können

Architekturen

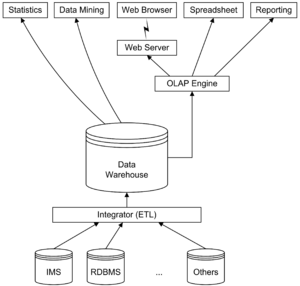
Die vorgestellte vereinfachte Architektur lässt sich um Metadaten und Data Marts ergänzen.

Erweiterte Architektur

Man unterscheidet abhängige und unabhängige Data Marts:

Abhängige Data Marts: Extraktion eines Teils des Data Warehouse zur Nutzung in einer Abteilung oder für eine bestimmte Benutzer*innengruppe/Anwendung. Zur Erinnerung: Das multidimensionale Datenmodell ergibt sich aus den Analyseanforderungen der Anwender*innen, ein Enterprise Data Warehouse sollte für verschiedene Anwendungen und Data Mining geeignet sein. (Virtuelle oder materialisierte) Data Marts können zur Erzeugung einer multidimensionalen Sicht auf das Enterprise-Datenmodell verwendet werden; vorberechnete Aggregate oder MDDB-Technologie sind nur in OLAP Data Marts nötig.
Unabhängige Data Marts: Unter unabhängigen Data Marts versteht man den Versuch der Verwendung eines Abteilungs-Data-Mart als Proof-of-Concept bzw. Prototyp für ein Data-Warehouse-Projekt. Problem: Der Aufwand für den Ladevorgang (Data Cleaning, Datenextraktion), die Hauptproblematik in einem DWH-Projekt, reduziert sich nicht. Unabhängige Data Marts bringen weitere Probleme mit sich, wenn sie später zusammengeführt werden sollen.

Referenzarchitekturen
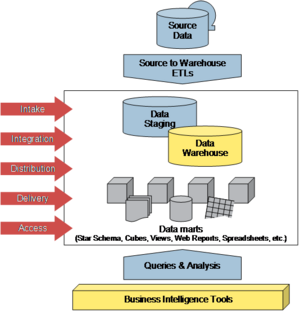
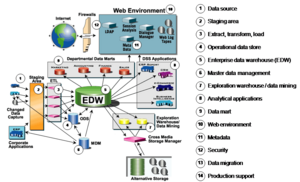
Die folgende Abbildung zeigt die Business-Intelligence-Referenzarchitektur des TDWI (The Data Warehouse Institute ^[4] ).

Referenzarchitektur des TDWI

Aufbauend auf dem Data-Warehouse-Konzept hat Bill Inmon eine Referenzarchitektur für eine Corporate Information Factory (CIF) definiert.

BI-Architektur basierend Bill Inmons Corporate Information Factory (CIF)

Datenmodellierung

Betrachtet man die dargestellte Architektur, lässt sich feststellen, dass für das Data Warehouse und OLAP Data Marts unterschiedliche Datenmodelle zum Einsatz kommen können. Da (Enterprise) Data Warehouses unabhängig von einer konkreten Analyseanwendung sein sollten, kommen hier ’normale’ ER-Modelle zur Modellierung zum Einsatz. Das daraus resultierende logische Datenmodell ergibt eine normalisierte (3. Normalform) relationale Datenbank.
OLAP-Anwendungen (i.e. Data Marts) hingegen basieren auf dem multidimensionalen Modell. Datenmodelle unterliegen daher gewissen Restriktionen um den intuitiven Zugriff auf die Daten durch OLAP-Analysewerkzeuge zu ermöglichen.

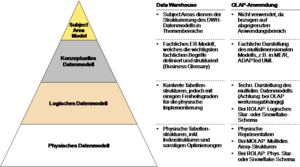
Diese Unterscheidung, inkl. Gliederung in die üblichen Abstraktionsebenen der Datenmodellierung (konzeptuelles, logisches und physisches Modell) ist in der folgenden Abbildung dargestellt.

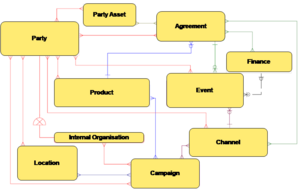
Data-Warehouse- und OLAP-Datenmodelle

Ein Subject Area Modell dient der groben Strukturierung des Data Warehouse in Themengebiete. Die folgende Abbildung zeigt das Subject Area Model eines Referenzdatenmodells für den Finanzdienstleistungssektor.

Subject Area Model für den Finanzdienstleistungssektor

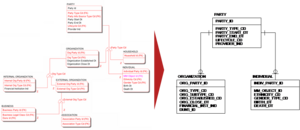
Im physischen Datenmodell werden Generalisierungshierarchien oft aufgelöst, um die Handhabbarkeit der entstehenden Tabellenstrukturen zu verbessern. Die folgende Abbildung zeigt einen Ausschnitt aus einem logischen DWH-Datenmodell und die zugehörige physische Umsetzung.

Auszug aus dem logischen Datenmodell und physische Umsetzung

Das multidimensionale Model
Es existiert keine einheitliche mutidimensionale Algebra wie in der relationalen Welt. Multidimensionale Modelle entwickelten sich aus den Implementierungen in kommerziellen OLAP- (oft ehem. EIS-) Produkten, sie unterscheiden sich in ihrer Unterstützung komplexer Dimensionenshierarchien, abgeleiteten Kennzahlen, etc.
Wissenschaftliche Arbeiten versuchten nachträglich eine Formalisierung und saubere Definition dieser bereits existierenden Implementierungen (anstatt umgekehrt). Inzwischen hat sich OLE DB for OLAP und MDX-Anfragesprache als De-Facto-Standard zum Zugriff auf multidimensionale Datenstrukturen etabliert.
Das MD-Modell von Cabibbo und Torlone bietet ein wissenschaftliches Standardmodell (aber nur eines von vielen). Formalismus ^[5] :

Dimension ist ein Tripel (L, ${\textstyle a\leq \ }$ b, R-UP) bestehend aus einer Menge von Levels L mit Halbordnung ${\textstyle a\leq \ }$ b und einer Menge von Roll-Up-Funktionen R-UP
Datenwürfel: n-dimensionale f-Tables f[A1:l1, …, An:ln]:l0 mit Namen von Attributen Ai und Levels li
Multidimensionales Schema (D, F) mit Menge von Dimensionen D und Menge von f-Tables F

Das Modell hat einige Einschränkungen. Es gibt keine Dimensionsattribute. Mehrere Kennzahlen müssen über mehrere f-Tables oder Kennzahlendimension abgebildet werden.

Beispielhalbordnung der Dimensionen im MD-Modell

Beispiel

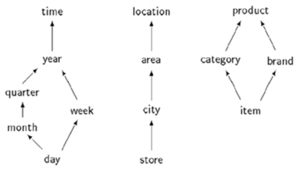
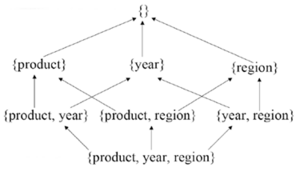
D = {time, location, product}
L ${\textstyle _{time}}$ , L ${\textstyle _{location}}$ , L ${\textstyle _{product}}$
R-UP ${\textstyle _{time}}$ = {R ${\textstyle _{day->month}}$ , R ${\textstyle _{month->quarter}}$ , R ${\textstyle _{quarter->year}}$ , R ${\textstyle _{day->week}}$ , R ${\textstyle _{week->year}}$ }, z.B. R ${\textstyle _{day->month}}$ (’27.06.2000’) = ’Juni 2000’
R-UP ${\textstyle _{location}}$ = {R ${\textstyle _{store->city}}$ , R ${\textstyle _{city->area}}$ }
R-UP ${\textstyle _{product}}$ = {R ${\textstyle _{item->category}}$ , R ${\textstyle _{item->brand}}$ }, z.B. R ${\textstyle _{item->category}}$ (’Lego’)=’Toys’

Multidimensionale Modellierung
Das multidimensionale Modell ist eine intuitive Repräsentation der Realwelt. Das ist wichtig, da Endbenutzer*innen durch das Datenmodell navigieren (dieses also verstehen) müssen.
Bei der multidimensionalen Modellierung stellt sich die Frage nach der Notation: Ist die ER-Notation ^[6] für multidimensionalen Entwurf geeignet? Problem: keine Unterscheidung zwischen qualifizierenden Entities (Dimensionen) und quantifizierenden Entities (Fakten). Es gibt viele Vorschläge für multidimensionale Notationen, es ist aber kein Standard in Sicht.

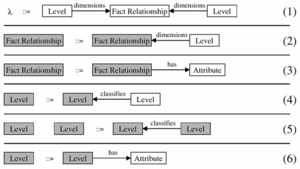
Multidimensional ER (ME/R) wurde am FORWISS, Technische Universität München entwickelt ^[7] . Es erweitert die ER-Notation um die drei Elemente Fact Relation, Dimension Level und Roll-up Relation.

Beispielhalbordnung der Dimensionen im MD-Modell

Graph-Grammatik von ME/R

Beispielmodell in ME/R

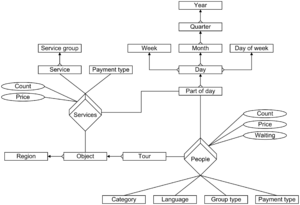
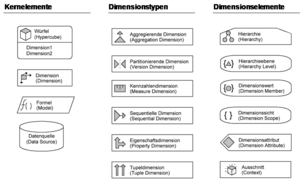
Application Design for Analytical Processing Technologies (ADAPT) ist ein proprietärer Ansatz (basiert nicht auf anderen Notationen) aus der Consulting-Praxis, entwickelt von Dan Bulos, Symmetry Corporation ^[8] . Er wird oft in Verbindung mit Oracle Express verwendet (erwähnt auf diversen Konferenzen der Oracle User Group). Erstmalig publiziert in der Zeitschrift Database Programming & Design, inzwischen auch diverse Reaktionen in wissenschaftlichen Veröffentlichungen.
Kritik: Fehlende formale Beschreibung, Semantik nur anhand von Beispielen; große Symbolvielfalt, hohe Komplexität.

Modellierungselemente in ADAPT

Beispielmodell in ADAPT

Speicherung multidimensionaler Daten
Multidimensionales Modell ist konzeptuell/logisch, nicht zwangsläufig physisch. Die multidimensionale Realisierung erfolgt mittels proprietärer MDBMS (MOLAP) oder relational mit herkömmlichen relationalen DBMS (ROLAP):

Multidimensionales OLAP (MOLAP): OLAP-Daten werden in speziellen Speicherstrukturen (d.h. multidimensionalen Arrays) gespeichert. Speichersystem und OLAP Engine sind stark miteinander verwoben, der Datenzugriff ist daher proprietär, aber schnell aufgrund optimierter Datenhaltung. Varianten von MOLAP sind Client OLAP oder Desktop OLAP (DOLAP). Der Trend geht in Richtung Hybrid OLAP (HOLAP) mit relationaler Speicherung der Detaildaten und multidimensionale Speicherung der Aggregate (eine Art Cache).
Relationales OLAP (ROLAP): ROLAP verwendet ein relationales logisches/physisches Datenmodell, ergänzt durch multidimensionale Metadaten. Eine multidimensionale Engine setzt OLAP-Operationen in SQL-Anfragen um.

MOLAP-Speicherung ist mit einigen Problemen verbunden. Oft müssen alle Aggregate vorberechnet werden, um die optimierte Speicherung nutzen zu können. Inkrementelle Datenbank-Aktualisierungen sind nicht möglich, da das multidimensionale Array jedes Mal komplett neu generiert werden muss, wenn sich die Struktur ändert. Ein weiteres Problem ist die Dünnbesetztheit (Sparsity): in typischen Datenwürfeln sind weniger als 5% der Zellen besetzt, leere Zellen benötigen jedoch ebenfalls Speicherplatz. Als Lösungsansatz dienen Kompressionsverfahren.

Mangelnde Skalierbarkeit: Multidimensionale Arrays werden durch die vorberechneten Aggregate und die Dünnbesetztheit sehr groß, die Technologie ist für hunderte Gigabytes dadurch ungeeignet. Aus diesen Gründen wird MOLAP üblicherweise nur für ’small-scale’ Anwendungen oder Data Marts verwendet, nicht zur Speicherung eines (Enterprise) Data Warehouse.
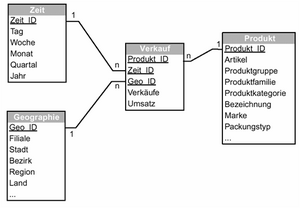
Bei ROLAP-Speicherung kommen als Datenmodell sog. Star- oder Snowflake-Schemata mit einer zentralen Fakttabelle und Dimensionstabellen zum Einsatz.

Ein Star-Schema besteht aus einer zentralen Fakttabelle zur Speicherung der quantifizierenden Daten (Kennzahlen) mit einem zusammengesetzten Primärschlüssel aus den Dimensionen. Die Fakttabelle hat wenige Spalten und (sehr) viele Tupel. Dimensionstabellen in Star-Schemata sind denormalisiert, sie haben relativ wenige Tupel und werden für Selektion und Aggregation (GROUP BY) verwendet.

Star-Schema

Bei Star-Schemata wird Redundanz in den Dimensionstabellen bewusst in Kauf genommen. Die Datenbank ist also nicht in 3. Normalform (3NF). Denormalisierung spart aufwendige Joins bei den Anfragen und erhöht die ’Browsing Performance’.

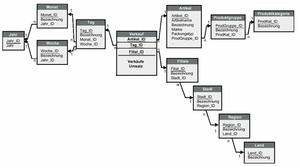
Beispieldimensionstabelle im Star-Schema

Im Gegensatz zum Star-Schema sind die Dimensionstabellen im Snowflake-Schema normalisiert (d.h. die Datenbank ist in 3NF). Das führt zu einer leichteren Aktualisierungsmöglichkeit, jedoch auch zu schlechterer Performance (mehr Joins). Die Speicherplatzeinsparung spielt keine Rolle (Dimensionstabellen sind im Vergleich Fakttabelle eher klein).

Snowflake-Schema

Ein Problem im multidimensionalen Modell sind die sog. Slow Changing Dimensions. Dimensionen (qualifizierende Daten) ändern sich mit der Zeit, z.B. Kund*innen ändern ihren Namen oder ziehen um, Produkte fallen weg, Produktgruppen, Organisationseinheiten werden umstrukturiert. Dies ist problematisch, da historische Daten im DWH existieren. Verglichen mit den quantifizierenden Kennzahlen sind die Dimensionen jedoch meist relativ statisch, daher spricht man von ’slow changing’. Designalternativen:

Überschreiben der Dimensionstabellen (UPDATE), Problem: alte Anfragen/Berichte sind nicht mehr nachvollziehbar
Versionierung/Historisierung der Dimensionstabellen, ggf. Abbildung der Versionierung als eigene Dimension

Datenbewirtschaftung

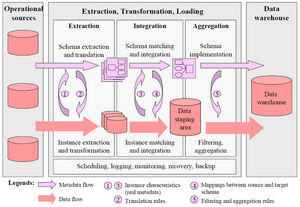
Die folgende Abbildung zeigt schematisch den Vorgang der Datenbewirtschaftung, sprich der Beladung des Data Warehouse (ETL – Extract ,Transform, Load).

Ladevorgang (ETL)

Daten werden temporär in der Staging Area gehalten, bevor sie in das DWH geladen werden. Alle Transformationen werden in der Staging Area durchgeführt. Das Preprocessing beeinflusst nicht die Datenquellen oder das DWH. Die Staging Area ist der zentrale Speicher für die ETL-Prozesse. Das Datenmodell der Staging Area entspricht dabei üblicherweise dem der Quellsysteme, von dort werden die Daten in das Zielmodell (Data-Warehouse-Datenmodell) transformiert.

ETL – Extract, Transform, Load
Es gibt unterschiedliche Verfahren zur Extraktion der Daten aus den Quellsystemen über Replika, Snapshots, Logfiles, Exports/Dumps, Datenbank APIs (ODBC), etc. Zu bedenken sind hierbei die begrenzten Zeitfenster, d.h. es werden meist nur relevante Daten (solche Tabellen/Felder, die ins DWH übernommen werden sollen) extrahiert. Die Verfügbarkeit und Performance des Quellsystems sollte nicht beeinträchtigt werden.

Extraktionsarten:

Periodisch
Manuelles Anstoßen
Ereignis-gesteuert
Sofort nach Veränderungen in den Quelldaten

Problem: OLTP-Systeme sind oft alt, schlecht dokumentiert und schwer zugänglich.

Die Transformation der Daten in eine integrierte Form (Data-Warehouse-Datenmodell) erfolgt im nächsten Schritt. Es muss sowohl die Struktur als auch die Inhalte transformiert werden.

Typische Transformationsformen:

Normalisierung, De-Normalisierung
Datentypumwandlung
Berechnungen, Aggregierung
Standardisierung
Umwandlung von Maßeinheiten
Data Cleansing
Anonymisierung
Historisierung

Beim Load werden die Daten aus der Staging Area in das DWH (und ggf. in Data Marts) transferiert. Daten im DWH werden selten ersetzt, stattdessen wird die Historie von Werten und Änderungen abgespeichert. Daten müssen an bereits existierende Tabellen hinzugefügt werden. Meistens geschieht das basierend auf Massenlade-Mechanismen des DBMS, um große Datenmengen zu bewegen.
Problem: Zugriff auf große Datenmengen in einem u.U. kurzen Zeitfenster; operative Systeme und DWH sollten während des Ladevorgangs aus Konsistenz- und Performance-Gründen möglichst offline sein, konkret die operativen Systeme während der jeweiligen Extraktion, das DWH während des Load.

Extract, Load, Transform (ELT)
Moderne relationale DBMS bieten mächtige Sprachen an (z.B. PL/SQL). Daher hat sich der ELT-Ansatz als Variante zum ETL entwickelt. Die Transformation findet dabei erst im DWH statt. Der Vorteil ist eine potentiell höhere Performance und die Tatsache, dass keine leistungsstarken und teuren ETL-Server benötigt werden (die Leistung der DWH-Datenbank wird auch zur Transformation verwendet).
Bei händischer Entwicklung ergibt sich jedoch das Problem, dass wichtige Funktionen zur Pflege und Verwaltung der Transformationsregeln (Metadaten) und Statistiken zur Bewertung der Datenqualität fehlen. Als Lösungsansatz dient hier die Generierung des SQL-Code durch ELT-Werkzeuge.

Historisierung
Daten werden in den operativen Datenbanken z.T. statisch (als Snapshot) gespeichert und müssen historisiert (versioniert) werden, um zeitliche Veränderungen analysieren zu können. Beim Update ist dafür zu sorgen, dass die Versionsführung ’sauber’ ist:

Keine Überschreibung von Werten
Keine Lücken
Keine Überschneidungen von Versionen einer Entität

Die Versionsführung von Entitäten wird von den Datenbanksystemen jedoch nicht direkt unterstützt. Der SQL-Befehl UPDATE überschreibt, der SQL-Befehl DELETE löscht. Beziehungen werden üblicherweise über Primärschlüssel hergestellt, referentielle Integrität wird über Constraints hergestellt, die auf Snapshots wirken. Das Problem ist daher auf Applikationsebene zu lösen, wird aber meist unterschätzt.

Häufigste Fehler:

Daten werden (absichtlich oder versehentlich) überschrieben
Es gibt Lücken oder Überschneidungen in den Versionen zu Objekten
Zeitlich nicht zusammenpassende Daten werden gemeinsam verwendet (’gejoint’)

Weitere Fehlerquellen in der Versionsführung liegen darin, dass Daten verspätet eintreffen, Eintritts- oder Wirksamkeitszeitpunkte von Zustandsänderungen sich nachträglich ändern oder Merkmale (Attribute) später anders beschrieben werden als ursprünglich konzipiert (Semantikänderungen).

In der temporalen Datenbanktheorie unterscheidet man drei Dimensionen der Zeit:

Gültigkeitszeit (Valid/Data Time): Zeitpunkt der Gültigkeit eines Objekts oder eines Ereignisses im betrachteten Realitätsausschnitt
Transaktionszeit (Transaction/Registration Time): Zeitpunkt, zu dem ein Ereignis oder Sachverhalt in die Datenbank aufgenommen wird
Benutzerdefinierte Zeit (User-defined Time): Zeit-Attribut, dessen Bedeutung von der Anwendung festgelegt wird (ist für das DBMS ein Attribut ohne besondere Bedeutung)

Eine temporale Erweiterung von SQL wurde als TSQL2 vorgeschlagen. ^[9] TSQL2 basierte auf einem bitemporalen Datenmodell (Gültigkeits- und Transaktionszeit) und einer Versionierung auf Tupelebene. z.B. Eingrenzung der Gültigkeitszeit im Rahmen der WHERE-Klausel:

Leider wurde die TSQL2 (auch SQL/Temporal) nicht weiterverfolgt und nie in den SQL-Standard aufgenommen.
’It was with some regret that the ANSI and ISO SQL groups withdrew the SQL/Temporal project from further development in late 2001, but some of us hope that […] standardization might continue in the future.’ ^[10]

Eine Methodik zur temporalen Datenhaltung in Data Warehouses ist das Continuous History Management. ^[11] Der konzeptuelle Rahmen sieht drei Arten von Entitätstypen vor: persistente Objekte, Ereignisse und Aufzählungstypen (diskrete, hierarchisch geordnete Wertevorräte). Es basiert auf einem bitemporalen Modell der Objektevolution mit zwei Zeitachsen (Zustand der Realität, Zustand der Datenbank). Dazu kommen Schemaevolutionsregeln zur Sicherstellung der Aufwärtskompatibilität des Datenmodells und Regeln zur Evolution von Aufzählungstypen.
Kund*innen, Produkte und alle Arten von Bestandsdaten sind persistente Objekte. Data Warehouses bestimmter Branchen (z.B. Versicherungen, Behörden) befassen sich überwiegend mit persistenten Objekten. Persistente Objekte sind in der Regel zeitlich veränderlich. Im Data Warehousing steht die Evolution der persistenten Objekte im Zentrum des Interesses (Beispiele: Bestandsoptimierung, Kostenmanagement, Yield Management).

Ein Datenmodell ist aufwärtskompatibel zu einem anderen Datenmodell, wenn alle Datenstrukturen und alle zulässigen Query-Ausdrücke des letzteren Modells in ersterem Modell enthalten sind.

’Damit ein Datenmodell aufwärtskompatibel mit einem anderen, vorher existierenden Datenmodell ist, müssen alle Queries, die im vorher existierenden Modell formulierbar sind, in beiden Modellen die gleichen Ergebnisse liefern.’ ^[12]

Neben der Nichtvolatilität nach Inmon wird die Aufwärtskompatibilität des Datenmodells und die Korrekturfähigkeit der Daten gefordert. Es ist kaum erreichbar, dass ein Data Warehouse, und sei es auch nur zu bestimmten Zeitpunkten und mit einem gewissen Zeitverzug, ein hundertprozentig vollständiges und korrektes Abbild der Realität darstellt. Nichtvolatilität und Korrekturfähigkeit sind jedoch auf den ersten Blick unvereinbare Forderungen, können jedoch durch geeignete Konventionen miteinander verträglich gemacht werden.

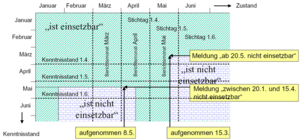
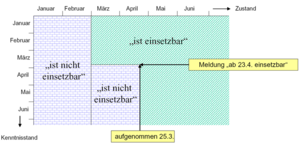
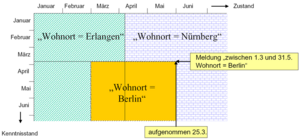
Die Lösung liegt im bitemporalen Modell:

Unterscheidung zwischen Wirksamkeitszeitpunkten und Aufnahmezeitpunkten (Transaktionszeitpunkten) von Ereignissen/Zustandsübergängen
Zwei Zeitachsen: Zustandsachse der realen Welt und Wissensachse (’bitemporales Modell’, Zeitebene)

Beispiel 1: Korrektur im Status einer Person

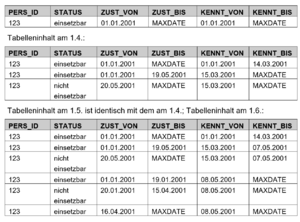
Das Beispiel stammt aus der Bundesagentur für Arbeit. Eine Person ist ’einsetzbar’, wenn sie arbeitslos ist. Bei einem bitemporalen Datenmodell gäbe es zwei Dimensionen (mit jeweils Von/Bis-Zeitstempeln), Zustand (z.B. ZUST_VON, ZUST_BIS) und Kenntnisstand (z.B. KENNT_VON und KENNT_BIS).

Am 1.3. sieht die entsprechende Datentabelle folgendermaßen aus (Annahme, Datensatz angelegt am 1.1.):

Beispiel 2: Korrektur eines Wirksamkeitszeitpunkts

Beispiel 3: Nachträgliches Einfügen eines Wohnorts

Vorberechnung von Aggregaten
Zur Optimierung der Abfrageperformance werden häufig verwendete Aggregate (z.B. Summierung der Verkäufe auf Monatsebene) oft vorberechnet und persistent gespeichert. Der Grundgedanke ist die Vorberechnung eines Join- oder Aggregationsergebnisses. Die höhere Geschwindigkeit der Anfrageverarbeitung gilt es dabei gegenüber den höheren Kosten zum Vorhalten und Aktualisieren der sog. materialisierten Sichten abzuwägen.

Man unterscheidet dabei eine explizite und implizite Speicherung:

Explizit: Die Speicherung erfolgt als zusätzliche (aggregierte Fakten-) Tabellen ohne direkte Verbindung zu den Detaildaten. Das Update erfolgt im ETL-Prozess, die Verwendung durch Abfragen auf Aggregate und Detaildaten getrennt.
Implizit: Aggregate sind als materialisierte Sichten direkt mit den Detaildaten verbunden. Das Update erfolgt durch das DBMS beim Verändern der Detaildaten, die Verwendung durch Abfrage auf die Detaildaten, das DBMS schreibt die Anfrage automatisch um (Query Rewriting).

Die Forschung beschäftigt sich bereits seit einigen Jahren mit der Fragestellung, welche materialisierten Sichten gespeichert werden sollen (Auswahlproblem). Die Anzahl möglicher Sichten ist dabei 2n bei n funktional unabhängigen Attributen (kombinatorische Explosion).

Mögliche materialisierte Sichten

Datenanalyse

Eines der Hauptanwendungsgebiete für Business Intelligence ist das Corporate Performance Management (CPM). Es unterstützt Unternehmen bei einer effizienten und kostensparenden Unternehmenssteuerung.
CPM steht für Prozesse, Methoden und analytische Anwendungen zur Unternehmenssteuerung.
CPM schafft die Verbindung zwischen Zielen, Metriken (KPIs) und Personen, um Verwaltung, Analysen und Maßnahmen im gesamten Unternehmen voranzubringen.
CPM hilft Transparenz zu schaffen, kritische Bereiche aufzuzeigen sowie Ergebnis, Planung und Forecasts zu optimieren. Daraus resultiert eine höhere Zuverlässigkeit der Prognosen und Forecasts. Durch intelligente Verknüpfung von Geschäftsanwendungen wird Zugang zu Informationen ermöglicht, um Antworten auf strategische und operative Fragen zu geben. Aus den gesammelten Daten wird über integrierte Planungs-und Konsolidierungs-Anwendungen ein Mehrwert geschaffen und Nutzen generiert. Ziel ist ein ’Single Point of Truth’ für sämtliche Kennzahlen und Reports sowie Zeit-und Kosteneinsparung.
Da auch der Mittelstand in einem globalisierten Marktumfeld wettbewerbsfähig sein muss, ist CPM ein immer wichtigerer Baustein. Die Kostenhürde wird durch konsequente Integration gesenkt. Weniger Anpassungsbedarf beschleunigt die Implementierung und senkt die Betriebskosten.

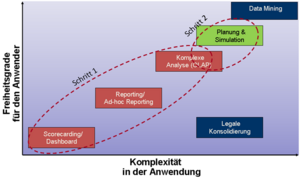
Die folgende Abbildung zeigt eine mögliche Kategorisierung der Funktionalität von BI-Werkzeugen.

Mögliche Kategorisierung der Funktionalität von BI Tools

Eine andere (ähnliche) Kategorisierung findet sich bei SAP/Business Objects zur Einordnung des Produktportfolios.

Reportingpyramide

Die Reportingpyramide unterscheidet drei Typen von Analysewerkzeugen und Nutzer*innengruppen:

Interaktive Dashboards/Entscheider: Hier kommen interaktive Analysen mit Auswahlboxen, Reglern, Drill, ’was-wäre-wenn’-Analysen zum Einsatz. Das Layout ist grafikorientiert, Output-Formate wie PowerPoint, Outlook, PDF und Web werden verwendet.
Ad-Hoc-Reporting/Analysten: Hier wird ein leistungsfähiges, webbasiertes Reporting mit intuitiver Drag&Drop-Funktionalität gefordert. Das Interface basiert auf semantischen Layers (multidimensionales Modell). Interaktive Analysen mit Drillen, Filtern, Sortieren, Gruppieren, Sektionen, Berechnungen und Formatieren sind möglich.
Reporting/Konsument*innen: Die dritte Kategorie bilden hochformatierte, interaktive Informationen für alle Anwender*innen mit listenorientierter Darstellung (GuV, Bilanzen, etc.). Informationen werden dargestellt, wann und so wie Anwender sie benötigen.

SQL für OLAP – Star Queries
Bei der Analyse in ROLAP-Anwendungen führt die Verwendung von Star- und Snowflake-Schemata zu Star Queries. Die Dimensionstabellen werden über Joins mit der Faktentabelle verbunden. Der Verdichtungsgrad und die Bildung von Aggregaten wird durch die GROUP-BY-Klausel gesteuert.

SQL SELECT Syntax

Beispiel – Wieviele Handies von welchem Hersteller haben junge Kund*innen in den bayrischen Filialen an Weihnachten 2001 gekauft:

Der frühe Sprachumfang von SQL weist dabei Defizite hinsichtlich Aggregations- und Gruppierungsmöglichkeiten auf. Ursprünglich werden nur die Standard-Aggregationsfunktionen SUM(), AVG(), COUNT(), MIN() und MAX() unterstützt. Herstellerabhängige Erweiterungen, z.B. STDDEV(), VARIANCE(), COVARIANCE() oder Funktionen zur linearen Regressionsanalyse kamen hinzu.
Seit SQL:99 gibt es für OLAP einige zusätzliche Konstrukte, wie ROLLUP, CUBE, GROUPING SETS, PERCENTILE, RANK, ...

Man unterscheidet folgende Funktionstypen in SQL:

Skalarfunktionen: Verknüpfung einzelner Attribute durch Operatoren zur Werteberechnung, Transformation einzelner Attribute, z.B. Nettopreis*Steuersatz, MONTH(Datum)
Aggregationsfunktionen: Werteverdichtung einer gebildeteten Gruppe, z.B. SUM(), MAX(), MIN(), COUNT(), …
OLAP-Funktionen: Erweiterung der Aggregationsfunktionen, OVER()-Klausel hinter einer Aggregationsoperation, z.B. Tagesstückzahlen und der Anteil an den Gesamtstückzahlen:

Beispieldatensatz

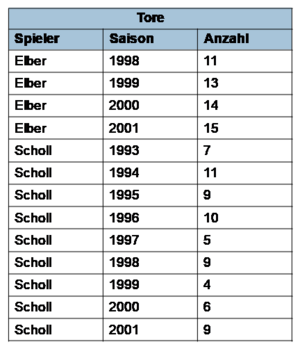
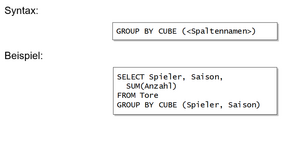
Die ROLLUP-Klausel errechnet n+1 (Unter-) Aggregate ausgehend von einer Liste mit n Spaltennamen, vom detailliertesten Level zur Gesamtsumme.

Ergebnis:

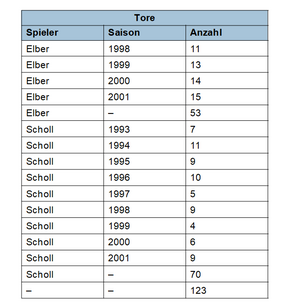
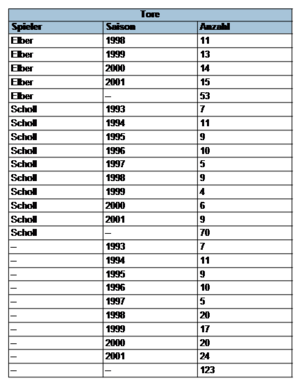
Beispielergebnis der ROLLUP-Klausel

Die CUBE-Klausel verallgemeinert ROLLUP und liefert die Aggregate aller 2n möglichen Gruppierungskombinationen.

Ergebnis:

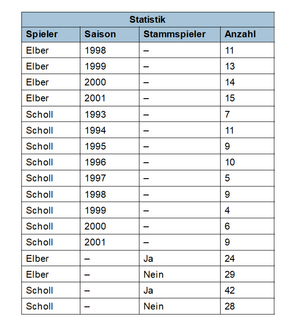
Beispielergebnis der CUBE-Klausel

Die GROUPING-SETS-Klausel erlaubt eine Gruppierung nach mehreren Kriterien innerhalb einer Anfrage.

Ergebnis:

Beispielergebnis der GROUPING-SETS-Klausel

Die OVER()-Klausel erlaubt die Berechnung von Aggregaten auf unterschiedlicher Aggregationsebene in einer Abfrage.
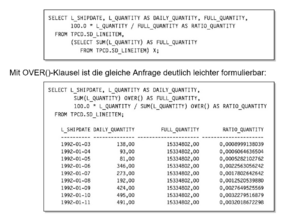
Beispiel: von Tagesstückzahlen und der Anteil an den Gesamtstückzahlen. Ohne OVER()-Klausel muss mit einer verschachtelten Anfrage gearbeitet werden:

Mit OVER()-Klausel ist die gleiche Anfrage deutlich leichter formulierbar:

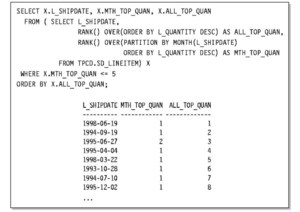
Die OVER()-Klausel erlaubt auch eine attributlokale Partitionierung pro Attribut der Ergebnisrelation, d.h. pro angewandter Aggregrationsoperation. Das ermöglicht eine individuelle Nachgruppierung der Ergebnisrelation.
Beispiel – Stückzahl und Anteil der Tagesproduktion an der Monats- und Jahresproduktion:

Weiters ist die Berechnung von kumulierten Werten möglich.
Beispiel – Berechnung kumulierter Lieferzahlen über Gesamtzeitraum, Lieferart und Liefermonat mit attributlokaler Ordnung durch ORDER-BY-Subklauseln:

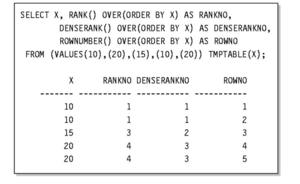
Schließlich existieren RANK-Operatoren zu Berechnung des Rangs eines Ergebnistupels innerhalb der Partitionsmenge.
Ohne RANK-Operator kann dies durch die COUNT-Klausel erfolgen:

Durch die Einführung von RANK- und DENSERANK-Operatoren ist die Semantik jedoch klarer definiert.
Beispiel für den RANK-Operator:

Tupel-Duplikate erhalten dabei den gleichen Rang mit Lückenbildung bei der Rangfolge zum Nachfolgetupel. DENSERANK arbeitet wie RANK, nur ohne Lückenbildung. ROWNUMBER liefert eine eindeutige Nummerierung der Tupel.
Beispiel für RANK, DENSERANK und ROWNUMBER

Beispiel für attributlokales Ranking:

Weiters ist die Bildung dynamischer Fenster möglich. Das Ziel ist dabei die Glättung ’verrauschter’ Datensätze.

Die Fenstergrößen kann einerseits über die Klauseln ROWS (Anzahl der Tupel) und RANGE (Anzahl der wertemäßig verschiedenen Tupel) explizit angegeben werden.
Für eine dynamische Festlegung der Fenstergröße gibt es zwei Möglichkeiten:

Ausgehend von definierten Startpunkt bis zum aktuellen Tupel über UNBOUNDED PRECEDING (erstes Tupel der jeweiligen Partition), n PRECEDING (n-ter Vorgänger relativ zur aktuellen Position), CURRENT ROW (aktuelles Tupel – nur mit RANGE und Duplikaten sinnvoll)
Angabe der unteren und oberen Schranken über BETWEEN untere Grenze AND obere Grenze, durch Spezifikation der Grenzen über UNBOUNDED PRECEDING, UNBOUNDED FOLLOWING, n PRECEDING, n FOLLOWING, CURRENT ROW (obere Grenze muss dabei eine höhere Position als untere Grenze spezifizieren)

Beispiel – gleitende Durchschnitte der Lieferzahlen (zentriertes 3-Tagesfenster, zwei asymmetrische Wochenfenster, retrospektives 30-Tagefenster):

Data Mining

Einführung

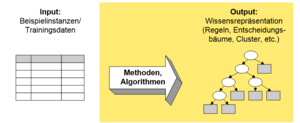
Data Mining bezeichnet das Entdecken interessanter Zusammenhänge und Trends in Daten mittels Mustererkennung sowie statistischer und mathematischer Verfahren.

Knowledge Discovery in Databases (KDD)
’Knowledge Discovery in Databases is the non-trivial process of identifying valid, novel, potentially useful, and ultimately understandable patterns in data’
’Data Mining is a step in the KDD process consisting of applying data analysis and discovery algorithms that, under acceptable computational efficiency limitations, produce a particular enumeration of patterns over the data’ ^[13]

Phasen des KDD-Prozesses

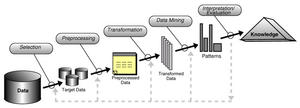
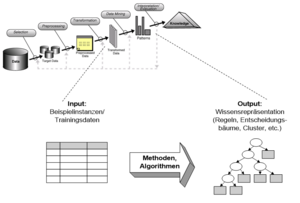
Phasen des KDD-Prozesses:

Selektion: Hierbei erfolgt die Auswahl relevanter Daten einer Datenbasis.
Preprocessing (Vorverarbeitung): Während dieses Schrittes werden Störungen wie Datenfehler oder Unvollständigkeit entfernt (Data Cleaning). Dieser Schritt entfällt unter Umständen bei Verwendung eines DWH als Datenquelle.
Transformation: In dieser Phase wird die Quantität der Daten durch Entfernung von Attributen ohne oder mit geringem Vorkommen in der Datenbasis verringert. Zusätzlich werden die Daten in eine geeignete Analyseform transformiert.
Data Mining (Kern des KDD-Prozesses): Hierbei kommen die eigentlichen Data-Mining-Techniken (Verfahren aus der Statistik und aus dem maschinellen Lernen) zum Einsatz.
Interpretation/Evaluation: Das Problem bei der Interpretation/Evaluation besteht darin, dass viele der erkannten Muster uninteressant und unpräzise sind.

Cross-Industry Standard Process for Data Mining (CRISP-DM)
Der Cross-Industry Standard Process for Data Mining (CRISP-DM) stellt ein im Rahmen eines EU-Projektes entwickeltes Data-Mining-Prozessmodell dar. Initiatoren hierbei waren unter anderem DaimlerCrysler, Integral Solutions Ltd. und NCR/Teradata.
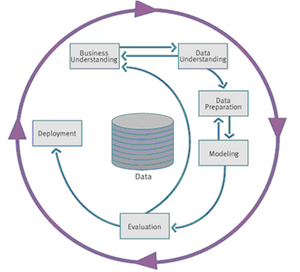
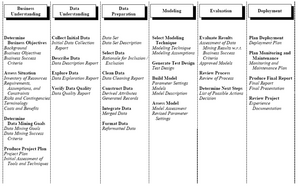
CRISP-DM teilt den Data-Mining-Prozess in sechs Phasen ein, nach denen man sich bei der Planung und Durchführung des Data-Mining-Projekts richten kann. CRISP-DM ist dabei breiter als das sich auf Technik fokussierende KDD-Prozessmodell.

Phasen des KDD-Prozesses

Die einzelen Phasen des CRISP-DM stellen sich wie folgt dar:

Business Understanding: In dieser Phase wird die Projektzielsetzung aus fachlicher Sicht festgelegt und die für die ausgemachte Problemstellung geeigneten Data-Mining-Techniken identifiziert.
Data Understanding: Hier werden Daten gesammelt, beschrieben und gesichtet. Darüber hinaus wird in dieser Phase zusätzlich die Datenqualität analysiert.
Data Preparation: Hierbei werden die Rohdaten so aufbereitet, wie sie für die Datenanalyse und für die Data Mining Tools benötigt werden
Modeling: In dieser Phase werden die ausgemachten Data-Mining-Techniken auf die Daten angewendet und die Parameter neu kalibiert. Bei Abweichungen erfolgt unter Umständen eine Rückkehr zu Phase 3.
Evaluation: Während der Evaluation wird das entwickelte Modell getestet und Entscheidungen bezüglich der Verwendung des Data-Mining-Ergebnisses getroffen.
Deployment: Hier wird der Plan für die Verwendung des entwickelten Modells, z.B. in einem operativen Softwaresystem, erstellt.

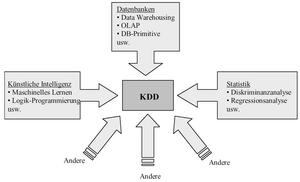
Aufgaben und Output im CRISP-DM-Referenzmodell

Data Mining/KDD kann als interdisziplinäre Wissenschaft bezeichnet werden. Im Data Mining/KDD treffen unter Anderem Methoden aus dem Bereich der Statistik, dem Bereich der Datenbanken oder dem Gebiet der künstlichen Intelligenz aufeinander.

Data Mining/KDD als interdisziplinäre Wissenschaft

Ziele des Data Mining
Allgemein besteht das Ziel des Data Mining in der Erkennung von Strukturen und Mustern anhand von Beispielen, um zukünftige Ergebnisse vorherzusagen oder Muster beschreiben bzw. erklären zu können, woraus sich eine Prognose ableitet. Die Trennung ist jedoch zum Teil unscharf, da z.B. eine Abhängigkeitsanalyse auch der Vorhersage dienen kann oder eine Klassifikation der Konzeptbeschreibung.

Ziele des Data Mining

Die Data-Mining-Ziele/-Methoden lassen sich wie folgt beschreiben:

Segmentierung/Clustering: Einteilung der Datenmenge in Gruppen (sog. Cluster) mit für diese Gruppe charakteristischen Attributwerten. Oft Kombination mit anderen Verfahren.
Klassifikation: Dient der Modellierung eines Klassifikators (a priori durch Trainingsdaten gegeben oder durch Clustering ermittelt). Beispiele sind Entscheidungsbäume und –regeln. Kann auch ein Beschreibungsziel verfolgen, z.B. Beschreibung der Konzepte ’treuer Kunde’ und ’untreuer Kunde’
Numerische Prognose: Vorhersage von numerischen Attributwerten. Ähnelt einer Klassifikation (mit numerischen ’Klassen’).
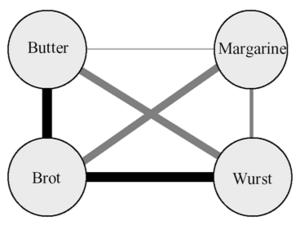
Abhängigkeitsanalyse: Auffinden signifikanter Abhängigkeiten zwischen Attributen. Klassisches Beispiel: Warenkorbanalyse
Sequenzanalyse: Erweiterung der Abhängigkeitsanalyse durch Beachtung von zeitlichen Beziehungen. z.B. Produktsequenzen bei der Warenkorbanalyse.
Abweichungsanalyse: Auffinden von ’abweichenden Instanzen’ (Ausreißern). z.B. zur Erkennung von fehlerhaften Daten.

Data Mining wird in vielfältigen Bereichen eingesetzt. Darunter gehören z.B. die Bearbeitung von Kreditanträgen, Risikoabschätzungen, die Erkennung von Versicherungsbetrug, die Lastvorhersage bei Stromversorgern oder im Telekommunikationsbereich oder auch diverse Bereiche im Marketing oder Customer Relationship Management. Weiterhin zählt auch die Anreicherung neu hinzuzufügender Daten oder die Unterstützung bei der Datenbereinigung im Zuge des ETL-Prozesses beim Data-Warehousing dazu.
Ein Beispiel ist die Bearbeitung von Kreditanträgen. Wenn man einen Kredit beantragen möchte, muss man zuerst einen Fragebogen mit relevanten finanziellen und persönlichen Informationen ausfüllen.
Dieser Fragebogen stellt die Grundlage für die Bewilligung oder die Ablehnung des Kredites dar. In 90% der Fälle kann durch eine einfache statistische Methode eine klare Entscheidung getroffen werden.
Die verbleibenden Grenzfälle werden von Sachbearbeiter*innen entschieden. Hierbei zeigen Untersuchungen, dass 50% der akzeptierten Grenzfälle jedoch in Zahlungsverzug geraten.
Eine komplette Ablehnung aller Grenzfälle stellt jedoch keine hinreichende Lösung dar, da Grenzfälle die aktivste Kund*innenguppe darstellen. Die Lösung des Problems wird durch maschinelles Lernen erreicht. Als Eingabe dienen 1000 Trainingsbeispiele von Grenzfällen mit 20 Attributen, wie unter anderem Alter, Jahre bei der/m momentanen Arbeitgeber*in, Jahre bei der aktuellen Adresse, Jahre bei der Bank oder Besitz anderer Kreditkarten.
Das Ergebnis dieses Lernprozesses stellt ein kleines Regelset dar, mit Hilfe dessen sich 2/3 der Grenzfälle korrekt prognostizieren lassen. Ein zusätzlicher Nebeneffekt besteht darin, dass die Regeln dazu genutzt werden können um den Kund*innen eine ablehnende Entscheidung zu erklären.
Ein weiteres Beispiel ist die Lastabschätzung bei Stromversorgern. Stromversorger benötigen eine Vorhersage für den zukünftigen Strombedarf, da korrekte Vorhersagen von minimaler und maximaler Last für jede Stunde immense Einsparungen ermöglichen.
Grundlage dieser Vorhersage war zunächst ein statisches Lastmodell, welches sich auf die letzten 15 Jahre bezieht, von normalen klimatischen Bedingungen ausgeht und sowohl aus Basislast des Jahres, Lastperiodizität über das Jahr als auch aus den Auswirkungen an Feiertagen besteht.
Eine Verfeinerung des Modells bestand darin, dass man klimatische Bedingungen mit in Betracht zog und die Prognose durch die Verwendung der ’ähnlichsten Tage’ der Vergangenheit korrigierte. Das statische Modell wurde hierbei um die durchschnittliche Abweichung der acht ähnlichsten Tage angepasst.
Weiterhin wurde eine Datenbank mit den Attributen Temperatur, Luftfeuchtigkeit, Windgeschwindigkeit und Messungen der Wolkendecke der letzten 15 Jahre, zusammen mit der Differenz zwischen tatsächlicher und prognostizierter Last angelegt.
Die Koeffizienten einer durchgeführten linearen Regressionsanalyse ergeben die Gewichte in der Ähnlichkeitsfunktion.
Das Resultat war, dass das neue System bei gleicher Performanz wesentlich weniger Zeit als ausgebildete menschliche Wetterexpert*innen zum Berechnen der Vorhersage benötigte.

Anwendungen im Marketing:

Kund*innentreue: Durch die Erkennung von Veränderungen in ihrem Verhalten (z.B. bei Banken, Telefongesellschaften) lassen sich potenziell abspringende Kund*innen identifizieren.
Spezielle Angebote: Identifizierung von profitträchtigen Kund*innen (z.B. zuverlässige Besitzer*innen von Kreditkarten, die zusätzliches Geld in der Weihnachtszeit benötigen)
Warenkorbanalyse: Abhängigkeitsanalyse, um Gruppen von Produkten zu finden, die oft zusammen in einer Transaktion vorkommen (meist Analyse von Kassenbondaten).

Weitere Anwendungen:

Sport: IBM Advanced Scout analysierte NBA-Spielestatistiken (Blocks, Fouls, etc.), um Vorteile für die New York Knicks und Miami Heat zu erreichen.
Astronomie: JPL und das Palomar Observatory entdeckten mit der Hilfe von Data Mining 22 neue ’Quasare’.
Web-Log Mining: Anwendung von Data-Mining-Algorithmen auf Web-Zugriffslogs zur Analyse des Navigationsverhaltens für die Verbesserung der Sitestruktur.

Die Verwendung von Daten, insbesondere von personenbezogenen Daten, für Data Mining bringt ernsthafte ethische Folgeerscheinungen mit sich. Während beispielsweise Informationen wie Geschlecht, Religion oder Abstammung bei den Entscheidungen über Kreditanträge zu Diskriminierungen führen können, sind die gleichen Informationen in medizinischen Anwendungen unproblematisch.
Ein weiterer Aspekt ist, dass Attribute indirekt problematische Informationen enthalten können. Zum Beispiel können durch Postleitzahlen eventuelle Rückschlüsse auf die Abstammung gezogen werden (z.B. Wohngebiete mit hohem Ausländer*innenanteil).
In Bezug auf die ethischen Aspekte müssen in der Praxis wichtige Fragen gestellt werden und die Ergebnisse von Analysen mit entsprechenden Warnungen versehen werden:

Zu welchem Zweck wurden die Daten gesammelt?
Wer hat Zugriff auf die Ergebnisse?
Welche Schlussfolgerungen können letztendlich aus den Ergebnissen gezogen werden?

Hierbei ist anzumerken, dass statistische Argumente niemals ausreichend sein können. Ein verwandtes Problem findet sich im Bereich des Datenschutzes wieder.
Der Fokus liegt im Folgenden auf ausgewählten Data-Mining-Zielen und -Methoden wie der Klassifikation, der Abhängigkeitsanalye, der Methode des Clusterings und der nummerischen Prognose. Die Beispieldaten zu den aufgeführten Zielen und Methoden entstammen größtenteils dem UCI Machine Learning Repository ^[14] .

Daten

Ziele/Methoden des Data Mining

Vorbereitung

Unter Datenvorbereitung versteht man die Bereitstellung des Inputs für die Ausführung von Data-Mining-Algorithmen. Die Datenvorbereitung stellt den aufwendigsten Teil im Data Mining Prozess dar.
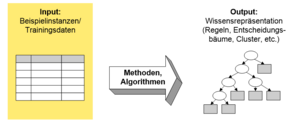
Es existieren verschiedene Typen an Output für verschiedene Lernprobleme (z.B. Klassifikation). Daher werden die Darstellungsformen zusammen mit den Methoden und Algorithmen behandelt.

Datenvorbereitung im Data-Mining-Prozess

Unter einer Instanz versteht man einen spezifischen Typ eines Beispiels, einen individuellen, unabhängigen Beispieldatensatz, der von einer bestimmten Menge an Attributen charakterisiert wird.
Eine Menge von Instanzen bzw. Datensätzen stellen den Input eines Data Mining Algorithmus (Learning Scheme) dar. Die Datensätze bzw. Instanzen werden zuvor denormalisiert (d.h. mehrere Relationen werden per Join verbunden) und danach als eine einzige Relation bzw. als Flatfile repräsentiert.
Problematisch hierbei ist, dass diese Denormalisierung zu Scheinunregelmäßigkeiten führen kann, die nur die Datenbankstruktur widerspiegeln (Beispiel: ’Lieferant’ prognostiziert ’Lieferantenadresse’).
Jede Instanz wird durch eine feste, vordefinierte Menge von Merkmalen, den sogenannten ’Attributen’, beschrieben. Die Anzahl dieser Attribute kann in der Praxis variieren. Eine mögliche Lösung bietet hier ein ’irrelevant’ Flag (siehe unten ’missing’ für fehlende Werte). Ein verwandtes Problem hierzu ist, dass die Existenz eines Attributes von dem Wert eines anderen abhängen kann.
Mögliche Attributtypen (’Skalentypen’) sind Nominal-, Ordinal-, Intervall- und Verhältnismaßzahlen.

Nominalwerte (lateinisch ’nomen’ = Name) sind unterschiedliche Symbole wobei die Werte selbst nur als Namen dienen. Zwischen den Nominalwerten bestehen keinerlei Beziehungen, weder Reihenfolge noch Distanzgröße und sie können nur auf Gleichheit getestet werden. Beispiel: Attribut ’outlook’ der Wetterdaten mit den Werten ’sunny’, ’overcast’ und ’rainy’.
Bei Ordinalwerten gibt es eine definierte Reihenfolge, aber keine Definition einer Distanz zwischen den Werten. Zusätzlich sei noch angemerkt, dass weder Addition noch Subtraktion sinnvoll ist.

Beispiel: Attribut ’temperature’ in den Wetterdaten oder die definierte Reihefolge der Werte: hot > mild > cool.
Beispielregel:

Weiterhin ist eine Unterscheidung zwischen nominal und ordinal nicht immer klar nachvollziehbar. So kann z.B. argumentiert werden, dass die Nominalwerte des verwendeten Beispiels ’outlook’ eine Ordnung aufweisen und somit als Ordinalwerte angesehen werden können. Overcast kann hierbei als Übergang zwischen ’sunny’ und ’rainy’ gesehen werden, d.h.: sunny > overcast > rainy.

Intervallmaßzahlen sind nicht nur geordnet, sondern werden in festen, gleichen Einheiten gemessen. Ein Beispiel für Intervallmaßzahlen stellen Jahreszahlen dar. Dabei macht es Sinn, sich über die Differenz zwischen zwei Jahreszahlen Gedanken zu machen (z.B. Differenz zwischen 1960 und 1976 -> 16 Jahre). Eine Summe oder ein Produkt macht hingegen keinen Sinn (z.B. 1960 + 1976 = 3936). Zudem gibt es bei Intervallmaßzahlen keinen Nullpunkt.
Verhältnismaßzahlen werden als reelle Zahlen gehandhabt, auf denen alle mathematischen Operationen erlaubt sind. Zudem definiert diese Maßmethode einen Nullpunkt. Die Frage nach einem von Natur aus gegebenen Nullpunkt erfordert jedoch (wissenschaftliches) Domänenwissen (z.B. kannte Fahrenheit keine untere Temperaturgrenze). Beispiel: Attribut ’distance’. Die Distanz zwischen einem Objekt und sich selbst ist Null.
Die meisten Data Mining Algorithmen (Learning Schemes) unterscheiden nur zwei Typen von Attributen: nominal und ordinal. Nominale Attribute werden auch kategorisch aufgezählt (’enumerated’) oder diskret genannt. Anzumerken ist, dass aufgezählt und diskret eine hier nicht geforderte Reihenfolge implizieren.
Einen Spezialfall stellt die Dichotomie (Boolsche Attribute) dar, die nur zwei Werte enthält (’true’ und ’false’ oder ’yes’ und ’no’).
Weiterhin erlaubt eine einfache Transformation die Kodierung ordinaler Attribute mit n Werten mit Hilfe von n-1 booleschen Attributen. Das Attribut ’temperature’ dient in folgender Abbildung als Beispiel.

Transformation ordinal nach boolesch

Die bereits angesprochene Denormalisierung stellt nicht das einzige Problem in der Vorbereitung der Quelldaten dar. Hinzu kommt, dass die Daten oft aus unterschiedlichen Datenquellen stammen (z.B. Verkaufsabteilung, Rechnungswesen, …). Ein weiteres Problem stellen unterschiedliche Datenerhebungsverfahren, bestimmte Namenskonventionen, andere semantische Unterschiede oder fehlerhafte Daten dar. Die Quelldaten müssen deshalb integriert, bereinigt und gegebenfalls ergänzt werden, wobei u.U. zusätzliche externe Daten („Overlay Daten“) benötigt werden.
Im Data Warehousing findet dieses sogenannte „Data Cleansing“ im ETL-Prozess statt und stellt sicher, dass das Data Warehouse als konsistente Datenquelle angesehen werden kann.
Kritisch ist jedoch die Form und der Grad der Datenaggregierung (vgl. Dimensionalität in OLAP).

Fehlende Werte und ungenaue/fehlerhafte Werte
Fehlende Werte werden oft als Einträge ausserhalb des Wertebereichs angezeigt (z.B. ’-1’) oder als Grund des fehlenden Eintrags (’unbekannt’, ’nicht erfasst’ oder ’irrelevant’). Die Gründe hierfür können in fehlerhaften Messgeräten, in Änderungen im Versuchsplan, in der Zusammenführung verschiedener Datenbestände oder in einer nicht möglichen Messung liegen. Jedoch können fehlende Werte eine eigene Aussagekraft haben (z.B. eine fehlende Messung in einer medizinischen Untersuchung).
Die meisten Data Mining Algorithmen gehen davon aber nicht aus und somit muss der Eintrag ’missing’ möglicherweise als gesonderter Wert kodiert werden.
Eine wichtige Aufgabe ist es, die Quelldaten auf fehlerhafte oder ungenaue Werte hin zu überprüfen. Der Grund für die Fehlerhaftigkeit oder die Ungenauigkeit liegt darin, dass die zugrunde liegenden Daten meist nicht zum Zwecke des Data Mining erfasst wurden. So kann es beispielsweise möglich sein, dass in der ursprünglichen Anwendung leer gelassene oder ungeprüfte Felder sich nicht auswirkten (z.B. Kund*innenalter).
Weiterhin können auf Tippfehler bei der Eingabe von Daten fehlerhafte Mess- und Erfassungfehler bei numerischen Attributen oder absichtlich entstandene Fehler (z.B. fehlerhafte Straßennamen/Hausnummern) als Fehlerquelle identifiziert werden. In Folge dessen ist es erforderlich, diese Daten einer Konsistenzprüfung zu unterziehen.
Ein weiteres Problem stellen Duplikate und veraltete Daten dar. So kann beispielsweise die Gewichtung eines Attributes bei maschineller Auswertung durch Duplikate beeinflusst werden.
Ein weiterer wichtiger Punkt ist, seine Daten kennenzulernen. Einfache Hilfsmittel sind beispielsweise Histogramme, die die Verteilung der Werte von nominalen Attributen anzeigen oder Graphen, die die Verteilung der Werte von ordinalen Attributen darstellen. Diese simplen grafischen Visualisierungen machen es einfach, Probleme zu identifizieren. 2D- und 3D-Visualisierungen zeigen zudem Abhängigkeiten zwischen Attributen auf. Um Abweichungen oder die Bedeutung von fehlenden Werten zu beurteilen, müssen Domänenexpert*innen konsultiert werden. Bei zu großen Datenmengen müssen zudem Stichproben genommen werden, um die Daten kennenzulernen.

Methoden und Algorithmen

In diesem Kapitel werden Methoden und Algorithmen mit ihren Ergebnistypen betrachtet.

Methoden und Algorithmen mit ihren Ergebnistypen

Grundsätzlich lassen sich folgende Anforderungen an praxistaugliche Algorithmen definieren:

Die Möglichkeit, numerische Attribute zu verarbeiten
Die Möglichkeit, fehlende Werte zu handhaben
Robustheit gegen verrauschte Daten (’Noise’)
Die Möglichkeit, (zumindest prinzipiell) jeden beliebigen Output zu erreichen

Zudem ist anzumerken, dass einfache Algorithmen oft überraschend gut arbeiten, beispielsweise die Verwendung eines einzelnen Attributes für eine Klassifikation (siehe 1R-Verfahren), Lineare Regression zur Prognose numerischer Werte, instanzbasiertes Lernen.

Klassifikation

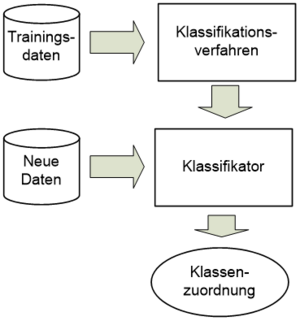
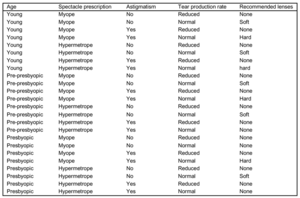
Die Klassifikation hat das Ziel der Vorhersage einer diskreten Klasse. Sie gehört zum Bereich des Supervised Learning (beaufsichtigtes Lernen). Das Ergebnis (die Klasse) wird für eine Menge von Beispielen (Trainingsdaten) vorgegeben, wobei der Erfolg anhand von weiteren Daten mit bekannten Klassen (Testdaten) gemessen werden kann. Im Folgenden werden Beispielprobleme in Form von Wetterdaten, Kontaktlinsendaten, Irisblumen oder Tarifverhandlungen vorgestellt.

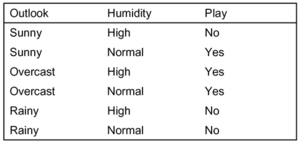
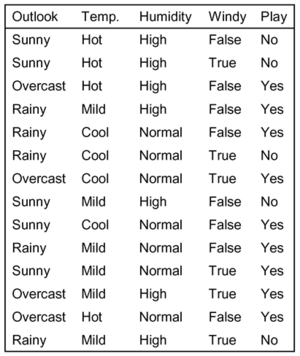
In der nachfolgenden Tabelle sind Bedingungen zum Spielen eines (nicht genauer spezifizierten) Spiels aufgelistet.

Wetterdaten und zugehörige Klassifikationsregeln

Ein Klassifikationsverfahren kann dabei die folgenden Klassifikationsregeln liefern:

Es können auch Attribute mit nummerischen Werten vorkommen. Nachfolgend Wetterdaten mit gemischten Attributen.

Wetterdaten mit gemischten Attributen

Diese Daten führen beispielsweise zu folgenden Klassifikationsregeln:

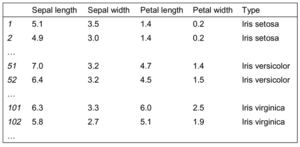
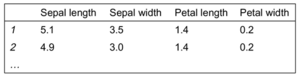
Das folgende Beispiel zur Klassifikation von Irisblumen bezieht sich auf Daten des Statistikers R.A. Fischer aus den 30er Jahren, einer beliebten Beispieldatenmenge für Data Mining.

Klassifikation von Irisblumen

Die Daten führen zu Klassifikationsregeln der folgenden Form:

Die Klassifikation hat zum Ziel, eine diskrete Klasse vorherzusagen (Vorhersageziel) bzw. zu beschreiben, wie sich diese woraus ableitet (Beschreibungsziel). Wie bereits angeführt, gehört die Klassifikation zum Supervised Learning (beaufsichtigtes Lernen). Das Ergebnis (die Klasse) wird für eine Menge von Beispielen (Trainingsdaten) vorgegeben.

Mögliche Repräsentationen der Modelle:

Entscheidungstabellen, -bäume, -regeln
Instanzbasiert

Formal lässt sich eine Klassifikation wie folgt darstellen. Gegeben seien:

Ein n-dimensionaler Raum S mit n Attributen
eine Menge C von k unterschiedlichen Klassen
eine Menge von Trainingsinstanzen mit bekannter Klasse aus C

Gesucht: Eine Funktion, die jedem Element aus S eine Klasse aus C zuordnet, d.h. K : S ${\textstyle \rightarrow }$ C (eine solche Funktion heißt Klassifikator).

Das Klassifikationsproblem

Entscheidungstabellen
Entscheidungstabellen stellen die rudimentärste Form des Outputs dar und verwenden das gleiche Format wie beim Input. Das Hauptproblem ist hierbei die Auswahl der richtigen Attribute, d.h. welche Attribute können weggelasssen werden, ohne die finale Entscheidung zu beeinflussen.

Entscheidungstabelle für das Wetterproblem

Entscheidungsbäume
Der ’Divide-and-Conquer’-Ansatz bezüglich des Problems des Lernens aus einem Set unabhängiger Instanzen führt zu einem sogenannten Entscheidungsbaum als Repräsentationsstil. Die Knoten repräsentieren den Test eines Attributs, meist den Vergleich mit einer Konstante. Weitere Möglichkeiten sind, dass die Knoten die Werte zweier Attribute miteinander vergleichen oder eine Funktion aus einem oder mehreren Attributen verwenden.
Die Blätter verweisen auf eine Klasse, eine Menge von Klassen oder eine Wahrscheinlichkeitsverteilung.

Kontaktlinsendaten

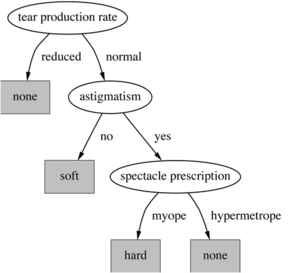
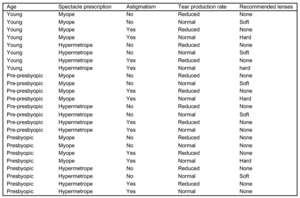
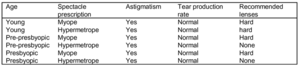
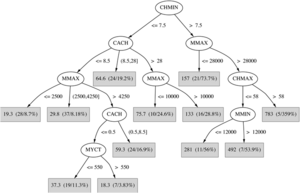
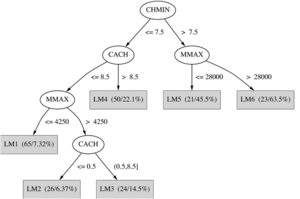
Nachfolgend die Darstellung eines Entscheidungsbaums für die Kontaktlinsendaten mit den Attributen ’tear production rate’, ’astigmatism’ und ’spectacle prescription’.

Entscheidungsbaum für die Kontaktlinsendaten

Enthalten die getesteten Knoten nominale Attribute, so entspricht die Anzahl der Kinder normalerweise der Anzahl der möglichen Werte. Jedes Attribut wird nur einmal getestet. Eine weitere Möglichkeit stellt die Aufteilung in zwei oder mehr Teilmengen dar.
Enthalten die Knoten numerische Attribute, so wird getestet ob der Wert größer oder kleiner als eine Konstante ist und es erfolgt ein Zwei-Wege-Split. Hierbei kann ein Attribut auch mehrmals getestet werden. Drei-Wege-Splits finden Verwendung, falls es mehrere Vergleichsmöglichkeiten gibt. So kann z.B. ein Integer auf ’kleiner als’, ’gleich’ oder ’größer als’ oder auf ’unterhalb’, ’innerhalb’ oder ’oberhalb’ eines Intervalls getestet werden.
Wenn das Fehlen eines Wertes eine eigene Aussagekraft hat, wird ’missing’ als eigener Wert kodiert. Ist das nicht der Fall so muss der fehlende Wert besonders behandelt werden. Eine mögliche Lösung stellt die Zuweisung zu dem ’beliebtesten’ Zweig dar.

Klassifikationsregeln
Eine beliebte Alternative zu Entscheidungsbäumen stellen Klassifikationsregeln dar. Sie setzen sich aus den Teilen Antecedent und Consequent zusammen, die meist mit einem logischen OR verbunden werden.
Der Antecedent-Teil (Prämisse, Bedingung) stellt eine Menge von Tests (wie die Tests an den Knoten eines Entscheidungsbaumes) dar, die üblicherweise mit einem logischen UND verbunden (auch andere logische Ausdrücke möglich) werden.
Als Consequent (Konklusion, Schlussfolgerung) bezeichnet man eine Klasse, eine Menge von Klassen oder eine Wahrscheinlichkeitsverteilung. Das Kontaktlinsenproblem lässt sich wie folgt mit Hilfe von Klassifikationsregeln abbilden:

Die Konvertierung eines Baumes in eine Menge von Regeln (eine Regel für jedes Blatt) gestaltet sich relativ einfach. Der Antecedentteil beinhaltet die Bedingung für jeden Knoten auf dem Pfad von der Wurzel zum Blatt während der Consequentteil die durch das Blatt zugewiesene Klasse repräsentiert.
Durch diese Transformation werden eindeutige Regeln erzeugt, deren Ausführungsreihenfolge keine Rolle spielt. Jedoch sind die resultierenden Regeln unnötig komplex und es ist erforderlich, redundante Regeln durch das sogenannte ’Pruning’ zu entfernen.
Die Transformation einer Regelmenge in einen Baum ist komplizierter als die Transformation von Bäumen in Regelmengen. So kann z.B. eine Disjunktion zwischen Regeln durch einen Baum nicht so einfach abgebildet werden. Im diesem Falle enthält der konstruierte Baum identische Teilbäume (’Replicated Subtree Problem’).
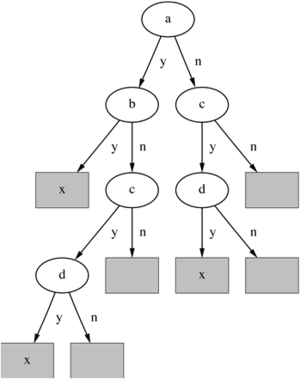
Beispiel – Regeln, die unterschiedliche Attribute testen:

Der zugehörige Baum für diese einfache Disjunktion:

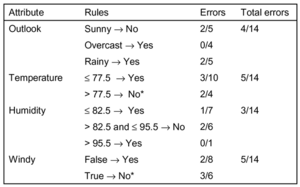
Entscheidungsbaum für eine Disjunktion

R – ein Klassifikationsalgorithmus zum Ableiten elementarer Regeln

Eine einfache Methode um einfache Klassifikationsregeln aus einem Set von Instanzen zu finden, stellt der 1R-Klassifikationsalgorithmus dar.
Der Algorithums lernt einen 1-Ebenen-Entscheidungsbaum. Anders ausgedrückt generiert er eine Menge von Regeln, die alle nur ein einzelnes Attribut testen.
In der Basisversion (ausgehend von nominalen Attributen) repräsentiert jeder Zweig einen anderen Attributwert. Jedem Zweig wird dabei die in den Trainingsdaten am häufigsten auftauchende Klasse zugewiesen. Die Fehlerrate ist das Verhältnis zwischen den Instanzen, die nicht in die Mehrheitsklasse des zugehörigen Zweiges und allen dem Zweig zugeordneten Instanzen gehören. Das Attribut mit der niedrigsten Fehlerrate wird ausgewählt. Zusätzlich ist darauf hinzuweisen, dass ’missing’ immer als separater Attributwert behandelt wird.
Pseudo-Code für 1R:

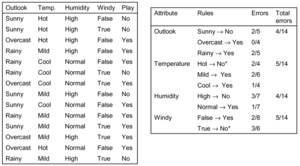
Beispiel:

Bewertung der Wetterattribute

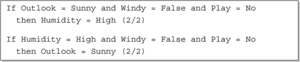
Das erste und das dritte Regelset werden ausgewählt. Es fällt auf, dass das Spiel nur gespielt wird, wenn es bewölkt ist oder regnet, hingegen nicht, wenn die Sonne scheint.

Verarbeiten numerischer Attribute in 1R
Bei der Verarbeitung von numerischen Attributen werden die numerischen Attribute durch eine Diskretisierungmethode in nominale Attribute umgewandelt. Der Wertebereich der Attribute wird dabei in Intervalle aufgeteilt. Im Anschluss werden die Instanzen nach den Werten des Attributs sortiert und die Intervallwechsel dort gesetzt, wo sich die (Mehrheits-) Klasse ändert so dass der Gesamtfehler minimiert wird.
Beispiel:

Wetterdaten mit numerischer Temperatur

Das Problem des ’Overfitting’
Die beim Verarbeiten von numerischen Attributen angewandte Diskretisierung ist sehr anfällig gegen verrauschte Daten. Eine einzige Instanz mit einem inkorrekten Klassenlabel wird vermutlich zu einem eigenen Intervall führen. Zudem wird z.B. ein Zeitstempelattribut immer einen Fehlerwert von 0 haben. Eine einfache Lösung ist das Erzwingen einer Mindestanzahl an Instanzen in der Mehrheitsklasse pro Intervall.
Beispiel:

Wetterdaten (mit einem Minimum von 3)

Ergebnis der Overfitting-Vermeidung für das Temperatur-Attribut

Die entsprechende Ergebnisregelmenge

Der 1R-Algorithmus wurde in einem Aufsatz von Holte (1993) beschrieben. Das Paper beinhaltet eine experimentelle Evaluation anhand von 16 Datenmengen (unter Verwendung von ’Cross-Validation’). Die Minimalanzahl an Instanzen wurde nach einigen Experimenten auf 6 gesetzt. Die einfachen 1R-Regeln lieferten kaum schlechtere Ergebnisse als deutlich komplexere Entscheidungsbäume. Die Schlussfolgerung daraus: Einfachheit lohnt sich!

ID3 – ein Klassifikationsalgorithmus zur Konstruktion von Entscheidungsbäumen

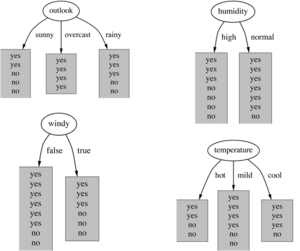
Das übliche Verfahren beim ID3-Algorithmus verläuft Top-down und rekursiv nach dem ’Divide-and-Conquer’ Prinzip. Zunächst wird das Attribut für die Wurzel selektiert und ein Zweig für jeden möglichen Wert wird erzeugt.
Dann werden für jeden von dem Knoten ausgehenden Zweig die Instanzen in Teilmengen aufgeteilt. Schließlich wird das Verfahren für jeden Zweig rekursiv mit den jeweiligen Instanzen wiederholt. Der Prozess terminiert, wenn alle Instanzen einer Teilmenge die gleiche Klasse haben, zum Split kein Attribut mehr übrig ist oder wenn es keine Instanzen für die vorzunehmende Aufteilung gibt.

Attributauswahl

Das beste Attribut ist das, welches zum kleinsten Baum führt. Die Heuristik hierzu: Wähle das Attribut, das die ’reinsten’ Knoten produziert.
Ein beliebtes Kriterium für ’Reinheit’ stellt der Information Gain (Informationsgewinn) dar. Der Information Gain wächst mit der durchschnittlichen Reinheit der Teilmengen, die ein Attribut erzeugt. Die Strategie hierfür ist, das Attribut zu wählen, das zum größten Information Gain führt.
Das Informationsmaß wird in Bits gemessen. Bei einer gegebenen Wahrscheinlichkeitsverteilung entspricht die Information, die zur Vorhersage eines Ereignisses benötigt wird, der Entropie der Verteilung. Die Entropie liefert die benötigten Informationen in Bits (Kann auch Teile eines Bits beinhalten!)
Die Formel zur Berechnung der Entropie lautet: ^[15]

Sie geht zurück auf Shannon und findet sich auch in anderen Anwendungen wie z.B. der Kryptographie. ^[16]
Beispiel – Attribut ’Outlook’:

’Outlook’ = ’Sunny’:

’Outlook’ = ’Overcast’:

’Outlook’ = ’Rainy’:

Das erwartete Informationsmaß für das Attribut:

Die Berechnung des Information Gains wird wie folgt vorgenommen. Information Gain = Informationsgehalt vor dem Split – Informationsgehalt nach dem Split:

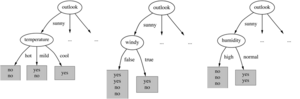
Beispiel – Information Gain für die Attribute der Wetterdaten:

Weitere Teilung:

Weitere Teilung

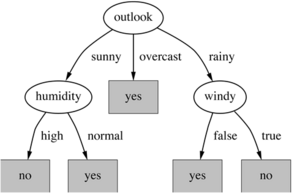
Ergebnis:

Der fertige Entscheidungsbaum:

Fertiger Entscheidungsbaum

Hinzuzufügen ist, dass nicht alle Blätter vollständig rein sein müssen. Manchmal haben identische Instanzen unterschiedliche Klassen. Die Teilung terminiert, wenn keine weitere Teilung möglich ist.

Die Gain Ratio ist eine Veränderung des Information Gains, die das Overfitting reduziert. Sie berücksichtigt die Anzahl und Größe der Zweige bei der Auswahl eines Attributes und berichtigt den Information Gain durch Berücksichtigung ’intrinsischer’ Informationen.
Eine ’Intrinsic Information’ stellt die Entropie der Verteilung der Instanzen auf die Zweige (d.h. wie viel Information wird benötigt, um zu entscheiden, zu welchem Zweig eine Instanz gehört) dar.
Der ID3-Algorithmus wurde zur Top-down Induktion von Entscheidungsbäumen von Ross Quinlan entwickelt. Die Verwendung der Gain Ratio ist nur eine Erweiterung dieses Basisalgorithmus. Er führte zu der Entwicklung von C4.5, der numerische Attribute, fehlende Werte und verrauschte Daten verarbeiten kann und ist zudem der bekannteste und (wahrscheinlich) der meistbenutzte Lernalgorithmus. Der kommerzielle Nachfolger ist C5.0. Einen ähnlichen Ansatz verfolgt auch CART (Classification And Regression Tree).

Erzeugung von Klassifikationsregeln
Ein Entscheidungsbaum kann in eine Regelmenge übersetzt werden. Bei einer einfachen Konvertierung wird die Regelmenge übermäßig komplex. Effektivere Konvertierungen sind jedoch nicht trivial.
Eine mögliche Strategie zur direkten Regelerzeugung ist für jede Klasse eine Regelmenge zu finden, die alle zugehörigen Instanzen einschließt (und keine Instanzen außerhalb der Klasse). Dieser Ansatz heißt ’Covering’, da in jedem Schritt eine Regel gefunden wird, die einen Teil der Instanzen ’abdeckt’.
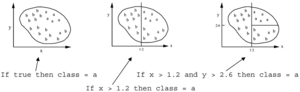
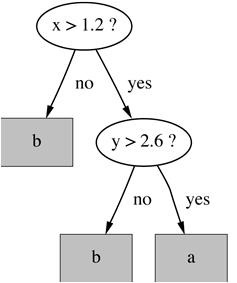
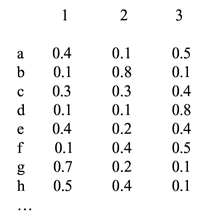
Beispiel – Erzeugen einer Regel:

Erzeugung einer Klassifikationsregel

Eine mögliche Regelmenge für Klasse ’b’:

Weitere Regeln können hinzugefügt werden, um zu einer ’perfekten’ Regelmenge zu gelangen.
Der zugehörige Entscheidungsbaum liefert exakt die gleichen Vorhersagen. Regelmengen können jedoch verständlicher sein. Bei mehreren Klassen behandelt ein Covering-Ansatz eine Klasse nach der anderen, während ein Algorithmus für Entscheidungsbäume alle Klassen auf einmal berücksichtigt.

Zugehöriger Entscheidungsbaum

PRISM – ein Klassifikationsalgorithmus zum Erzeugen von Klassifikationsregeln (Covering-Ansatz)

Der PRISM-Klassifikationsalgorithmus erzeugt eine Regel durch das Hinzufügen von Tests, die die Genauigkeit der Regel maximieren. Jeder neue Test reduziert die Abdeckung der Regel. Das Problem der Auswahl eines Attributes für den Split ist ähnlich der Situation bei Entscheidungsbäumen, wobei der Entscheidungsbaum-Algorithmus hingegen die Gesamtreinheit maximiert.
Das Ziel ist die maximale Genauigkeit der Regel. t steht dabei für die Gesamtzahl der durch die Regel abgedeckten Instanzen. p repräsentiert die Anzahl der positiven (richtig klassifizierten) Beispiele. t-p stellt Anzahl der Fehler (d.h. der Falsch-klassifizierungen) dar. Anschliessend wird der Test ausgewählt, der das Verhältnis p/t maximiert. Die Regel ist fertig, wenn p/t = 1 oder wenn die Instanzmenge nicht mehr weiter aufgeteilt werden kann.

Zur Erinnerung: Kontaktlinsendaten

Die gesuchte Regel:

Die möglichen Tests:

Die Regel nach Hinzufügen des besten Tests:

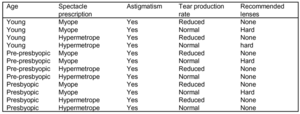
Die durch die Regel abgedeckte Instanzen:

Eine weitere Verfeinerung des aktuellen Stands:

Die möglichen Tests:

Die veränderte Regel nach Hinzufügen des besten Tests und den zugehörigen Daten:

Die nachfolgende Tabelle zeigt die durch die neue Regel abgedeckte Instanzen:

Eine weitere Verfeinerung des aktuellen Stands:

Mögliche Tests:

Es stellt sich raus, dass Gleichstand zwischen erstem und viertem Test herrscht. Deshalb wird derjenige mit der größeren Abdeckung ausgewählt.
Das Endergebnis und die fertige Regel lauten:

Die zweite Regel zur Empfehlung von ’hard lenses’ (mit den durch die erste Regel nicht abgedeckten Instanzen erzeugt):

Diese beiden Regeln decken alle ’hard lenses’ ab. Der gesamte Vorgang wird nun für die anderen beiden Klassen wiederholt.
Pseudo-Code für PRISM:

Methoden wie PRISM sind sog. ’Separate-and-Conquer’ Algorithmen mit folgendem Vorgehen:

Erst wird eine Regel identifiziert, dann werden alle Instanzen, die von der Regel abgedeckt werden, aussortiert. Schließlich werden die übrigen Instanzen ’erobert’. Der Unterschied zu ’Divide-and-Conquer’ Methoden ist, dass die von der Regel abgedeckte Teilmenge nicht mehr weiter untersucht werden müssen. Ein praxisüblicher Algorithmus ist CN2 .

k-NN – ein Klassifikationsalgorithmus für instanzbasiertes Lernen

Die einfachste Form des Lernens ist das sogenannte „Routinelernen“. Dabei werden die Trainingsdaten nach Instanzen durchsucht, die der neuen Instanz am ähnlichsten sind. Diese Instanzen selbst repräsentieren das Wissen.
Das ’Routinelernen’ wird auch instanzbasiertes Lernen (IBL), oder auch fallbasiertes Lernen/Schließen (’Case-based Reasoning’, CBR) genannt und fällt in den Bereich des ’Lazy Learning’.
Hierbei bestimmt die Ähnlichkeitsfunktion (Distanzfunktion) was ’gelernt’ wird. Die eingesetzten Methoden: Nächste-Nachbarn, k-Nächste-Nachbarn, …
Die einfachste Form der Distanzfunktion ist ein numerisches Attribut. Die Distanz ist die Differenz zwischen zwei Attributwerten oder eine Funktion davon. Bei mehreren numerischen Attributen wird normalerweise die „Euklidische Distanz“ verwendet und die Attribute werden normalisiert.
Bei nominalen Attributen ist die Distanz bei verschiedenen Werten 1 und bei gleichen Werten 0. Falls zudem nicht alle Attribute gleich wichtig sind, kann eine Gewichtung der Attribute notwendig sein.
Minkowski-Distanz – Gegeben seien zwei Instanzen a(1) und a(2) mit k Attributen:

q=1: City-Block Metric (auch: Manhattan-Distanz)
q=2: Euklidische Distanz (am häufigsten verwendet)
Das Ziehen der Wurzel ist nicht notwendig, wenn Distanzen nur verglichen werden sollen.
Bei numerischen Attributen werden verschiedene Attribute auf unterschiedlichen Skalen gemessen und müssen normalisiert werden:

vi: Wert des Attributes i
Bei nominalen Attributen ist die Distanz entweder 0 oder 1. Die übliche Vorgehensweise bei fehlenden Werten ist die Annahme der maximalen Distanz (bei normalisierten Attributen).
Zur Auswahl des Parameters k ist folgendes anzumerken. Falls k zu klein ist, ist die Empfindlichkeit gegenüber Ausreißern in den Daten zu hoch. Falls k zu groß ist, werden viele Instanzen aus anderen Klassen in die Entscheidung miteinbezogen. In vielen Fällen ist ein Wert zwischen 1 und 10 angemessen und erzielt gute Ergebnisse.
1-NN ist oft korrekt, aber langsam. Eine einfache Version durchsucht die gesamten Trainingsdaten, um eine Prognose abzuleiten.
Unter der Annahme, dass alle Attribute gleich wichtig sind, kann eine Lösung sein, eine Auswahl von Attributen oder der Gewichtung vorzunehmen. Eine mögliche Lösung bei verrauschten Daten stellt ein ’Mehrheitsentscheid’ der k nächsten Nachbarn dar. Zudem können Ausreißer aus den Daten entfernt werden, was sich jedoch meist nur schwer bewerkstelligen lässt.
In der Statistik wird k-NN seit den frühen 50er Jahren verwendet. Wenn n ${\textstyle \rightarrow }$ ${\textstyle \infty }$ und k/n ${\textstyle \rightarrow }$ 0, wird der Fehler minimal.

Evaluation von Klassifikationsverfahren

Evaluation ist der Schlüssel zum Erfolg im Data Mining. Die Fragestellung hierbei lautet, wie gut das erlernte Modell ist.
Die Fehlerrate in den Trainingsdaten ist kein guter Indikator für die Prognosegüte bei neuen Daten, sonst wäre 1-NN der beste Klassifikator.
Eine einfache Lösung, die verwendet werden kann, wenn viele Daten (mit zugehöriger Klasse) zur Verfügung stehen, ist das Aufteilen der Daten in eine Trainings- und eine Testmenge. Der Nachteil hierbei ist, dass klassifizierte Daten normalerweise rar sind.
Aspekte bei der Evaluation:

Statistische Verlässlichkeit der abgeschätzten Modellgüte (Signifikanztests)
Auswahl des Gütemaßes
Anzahl korrekter Klassifizierungen
Genauigkeit der geschätzten Wahrscheinlichkeiten
Fehler bei numerischen Prognosen
Unterschiedliche ’Kosten’ können verschiedenen Fehlertypen zugewiesen werden.

Die Fehlerrate ist ein natürliches Gütemaß für Klassifikationsprobleme. Der Klassifikator sagt die Klasse jeder Instanz voraus.
Wird die Klasse einer Instanz richtig prognostiziert, so zählt das als Erfolg. Wird hingegen die Klasse einer Instanz falsch prognostiziert, so zählt das als Fehler.
Das Verhältnis der Fehler zu der Gesamtzahl an getesteten Instanzen wird als Fehlerrate bezeichnet und misst die Performanz des Klassifikators. Der ’Resubstitution Error’ ist die Fehlerrate, die sich aus den Trainingsdaten ergibt (durch ’Ersetzen’ der zum Training verwendeten Klassen).
Anzumerken ist hierbei, dass der ’Resubstitution Error’ extrem optimistisch ist.
Die Testmenge stellt eine Menge unabhängiger Instanzen dar, die bei der Erzeugung des Klassifikators keine Rolle gespielt haben. Es wird angenommen, dass Trainings- und Testdaten repräsentative Stichproben des zugrunde liegenden Problems sind. Generell gilt, dass je größer die Trainingsdatenmenge, desto besser ist der Klassifikator. Ebenfalls gilt, dass je größer die Testdatenmenge, desto genauer ist die Fehlerabschätzung. Ideal wäre also beides, eine große Trainings- und eine große Testmenge.
Es ist wichtig, dass die Testdaten in keinster Weise bei der Erzeugung des Klassifikators verwendet werden. Einige Lernschemata beinhalten zwei Phasen: In Phase 1 wird die Basisstruktur erzeugt. In Phase 2 findet die Optimierung der Parameterwerte statt. Anzumerken ist, dass die Testdaten auch nicht zur Parameteroptimierung verwendet werden dürfen. Richtig ist hingegen die Verwendung von drei Datenmengen: Trainingsdaten, Validierungsdaten und Testdaten.
Die Trainingsdaten werden von einer oder mehreren Lernmethoden zusammen mit Klassifikatoren benutzt. Die Validierungsdaten werden zur Optimierung der Parameter verwendet und die Testdaten werden verwendet, um die Fehlerrate der finalen und optimierten Methode zu bestimmen.
Wenn die Datenmenge begrenzt ist, kommt die Holdout-Methode zum Einsatz. Sie reserviert einen Teil für das Testen und verwendet den Rest zum Training. Üblicherweise wird ein Drittel zum Testen und der Rest zum Training verwendet. Das Problem hierbei ist, dass die Stichproben möglicherweise nicht repräsentativ sind. So kann zum Beispiel eine Klasse in den Trainingsdaten fehlen.
Die erweiterte Version des Holdout-Verfahrens verwendet Stratifizierung. Sie stellt sicher, dass jede Klasse mit ungefähr gleichen Anteilen in beiden Teilmengen enthalten ist.
Die Zuverlässigkeit der Holdout-Abschätzung kann durch Wiederholung des Vorgangs mit unterschiedlichen Stichproben gesteigert werden. In jeder Iteration wird eine zufällige Stichprobe (ggf. mit Stratifizierung) gezogen. Die Gesamtfehlerrate wird dann als Durchschnitt der Fehlerraten der einzelnen Iterationen gebildet.
Diese Methode nennt man ’Repeated Holdout’. Sie ist aber immer noch nicht optimal, denn die einzelnen Testmengen überlappen.
Die Cross-Validation verhindert die überlappende Testmengen beim Holdout-Verfahren. Als erster Schritt werden die Daten in k Teilmengen gleicher Größe aufgeteilt. Im zweiten Schritt wird jede Teilmenge jeweils zum Testen verwendet und der Rest der Daten zum Training. Dieses Verfahren nennt man k-fache Cross-Validation.
Hierbei werden die Teilmengen oft vorher stratifiziert. Die Gesamtfehlerabschätzung ergibt sich wieder aus dem Durchschnitt der einzelnen Fehlerabschätzungen.
Das Standardverfahren zur Evaluation ist die stratifizierte zehnfache Cross-Validation. Zehnfach deshalb, da sich bei vielen Experimenten dieser Wert als die beste Wahl herausgestellt hat. Außerdem gibt es eine gewisse theoretische Grundlage dafür.
Die Leave-One-Out Cross-Validation ist eine besondere Form der Cross-Validation. Die Anzahl der Wiederholungen ist gleich der Anzahl aller Trainingsinstanzen, d.h. es muss n-mal ein Klassifikator erzeugt werden, wobei n die Anzahl der Trainingsinstanzen ist.
Die Leave-One-Out Cross-Validation macht maximalen Gebrauch von den Daten. Zudem gibt es keine zufälligen Stichproben. Ein Nachteil ist, dass ein sehr hoher Rechenaufwand (Ausnahme: NN) notwendig ist. Ein weiterer Nachteil von LOO-CV ist, dass eine Stratifizierung nicht möglich ist. Im Gegenteil, das Verfahren garantiert nicht-stratifizierte Stichproben, da die Testdaten aus jeweils nur einer Instanz bestehen.
Als Extrembeispiel dient eine vollständig zufällige Datenmenge mit zwei Klassen und gleichmäßiger Verteilung. Der beste Klassifikator prognostiziert die Mehrheitsklasse der Trainingsdaten (entspricht einer Fehlerrate von 50% bei frischen Daten mit gleichen Eigenschaften). Die durch LOO-CV abgeschätzte Fehlerrate dieses Klassifikators liegt aber bei 100%, da die verbleibende Testinstanz nie zur Mehrheitsklasse gehört.
Im Vergleich von Data-Mining-Verfahren steht die Frage im Mittelpunkt, welches von zwei Lernschemata besser arbeitet. Ein offensichtlicher Ansatz bietet ein Vergleich der 10-fachen Cross-Validation Abschätzungen. Das Problem ist die Varianz der Abschätzungen. Die Varianz kann aber durch wiederholte Cross-Validations reduziert werden. Jedoch ist die Zuverlässigkeit der Ergebnisse dann immer noch unbekannt. Die Durchführung von Signifikanztests ergibt, wie sicher man sein kann, dass tatsächlich Unterschiede existieren.

Abhängigkeitsanalyse

Das Erkennen von Abhängigkeiten zwischen Merkmalen realisiert man durch die sogenannte Abhängigkeitsanalyse. Sie kann angewendet werden, wenn keine Klasse verwendet werden kann und alle Strukturen als ’interessant’ angesehen werden.
Der Unterschied zur Klassifikationsanalyse besteht darin, dass mit Hilfe der Abhängigkeitsanalyse auch der Wert beliebiger Attribute (auch mehrerer) vorhergesagt werden kann, anstatt nur eine Klasse. Mit Hilfe von Klassifikationsregeln lässt sich somit der Wert eines vordefinierten Attributes (der Klasse eines Beispiels) vorhersagen bzw. erklären.
Mit Abhängigkeitsregeln (’Association Rules’) lässt sich hingegen der Wert eines beliebigen Attributes oder der Kombination eines Attributes vorhersagen bzw. erklären:

Da aus Datensätzen wesentlich mehr Abhängigkeitsregeln als Klassifikationsregeln abgeleitet werden können, sind die Einschränkungen minimaler Support (Abdeckung) und minimale Konfidenz (Genauigkeit) notwendig.
Die Abhängigkeitsanalyse kann verwendet werden, wenn keine Klasse angegeben werden kann und alle Strukturen als ’interessant’ angesehen werden. Sie zählt zum unbeaufsichtigten Lernen (’Unsupervised Learning’) und verfolgt ein Beschreibungsziel. Ein klassisches Beispiel ist die Warenkorbanalyse (die Attribute sind Produkte in einem Warenkorb). Der Output einer Anhängigkeitsanalyse sind Abhängigkeitsregeln bzw. Interdependenzgraphen.
Mit Hilfe von Abhängigkeitsregeln (’Association Rules’) kann ein Attribut oder eine Kombination von Attributen vorhergesagt werden.
Abhängigkeitsregeln sollen nicht als Regelmenge zusammen verwendet werden, sondern einzelne Regeln sind von Interesse. Ein Problem stellt hierbei die extrem große Anzahl an möglichen Abhängigkeiten dar. Der Output muss so eingeschränkt werden, dass nur die ’besten’ Abhängigkeiten ermittelt bzw. ausgegeben werden. Daraus folgen nur Regeln mit einem hohen Support und einer hohen Konfidenz.

Ein Item ist ein Paar aus Test und Attributwert. Eine Menge von Items wird als Item Set bezeichnet.
Der Support eines Item Set ist die Anzahl der Instanzen in der Trainingsmenge, die das Item Set enthalten (im Verhältnis zur Anzahl aller Instanzen in der Trainingsmenge). Die Konfidenz einer Regel ist die Anzahl der Instanzen, die die Regel (Bedingungs- und Schlussfolgerungsteil) erfüllen im Verhältnis zur Anzahl der Instanzen, die den Bedingungsteil erfüllen.

Ein Probem ist, dass bei vielen Elementen Zusammenhänge und Beziehungen aufgrund von mangelndem Support verloren gehen. Eine mögliche Lösung ist die Definition und das Speichern von Taxonomien.

Beispiel: ’Die Kund*innen, die Straßenschuhe kaufen, erwerben auch Jacken’. Wegen zu hoher Supportschranke gilt aber nicht: ’Die Kund*innen, die Stiefel kaufen, erwerben auch Jacken’. Die Aussagen werden wegen höherem Aggregationsniveau genereller.

Generalisierte Assoziationsregeln

APRIORI – ein Algorithmus zum Erlernen von Abhängigkeitsregeln

Der APRIORI-Algorithmus ist eine naive Methode zum Finden von Abhängigkeitsregeln. Er verwendet die Standard ’Separate-and-Conquer’ Methode, nur dass jede mögliche Kombination von Attributwerten als separate Klasse behandelt wird. Hierbei gibt es jedoch zwei Probleme. Zum einen ist der APRIORI-Algorithmus sehr aufwendig und komplex. Zum anderen gibt es eine große Anzahl an resultierenden Regeln, die anhand von Support und Konfidenz noch einem ’Pruning’ unterworfen werden müssen.
Vorteilhaft ist dabei, dass Regeln mit hohem Support direkt gefunden werden können. Man findet zunächst alle Item Sets mit dem gegebenen minimalen Support und generiert daraus dann Regeln.
Beispiel – Wetterdaten:

Zur Erinnerung: Wetterdaten

Item Sets für die Wetterdaten:

Item Sets für die Wetterdaten

Insgesamt entstehen 12 1-Item-Sets, 47 2-Item-Sets, 39 3-Item-Sets, 6 4-Item-Sets und keine 5-Item-Sets (mit einem minimalen Support von 2). Wenn alle Item Sets mit dem minimalen Support gefunden sind, können diese in Regeln umgewandelt werden.

Beispiel:

Es existieren sieben (2N-1) potenzielle Regeln:

Die resultierenden Regeln mit Support 2 und Konfidenz = 100%:

Resultierende Abhängigkeitsregeln

Es gibt 3 Regeln mit Support = 4, 5 mit Support = 3 und 50 mit Support = 2.

Effiziente Generierung der Item Sets

Es stellt sich die Frage, wie alle häufigen Item Sets gefunden werden können. Das Finden von 1-Item-Sets ist trivial. Zum Finden von k-Item-Sets gibt es folgende Idee
Man verwendet 1-Item-Sets, um 2-Item-Sets zu generieren, 2-Item-Sets, um 3-Item-Sets zu generieren, usw. Die Idee ist dass wenn (A B) ein häufiges Item Set ist, dass dann (A) und (B) ebenfalls häufige Item Sets sein müssen. Allgemein gilt dann:
Wenn X ein häufiges k-Item-Set ist, dann müssen alle darin enthaltenen (k-1)-Item-Sets ebenfalls häufig sein (sog. A-Priori-Eigenschaft). Die k-Item-Sets werden durch Zusammenfassen von (k-1)-Item-Sets berechnet.

Beispiel – Gegeben sind fünf 3-Item-Sets (Lexikographisch geordnet):

Kandidaten für 4-Item-Sets:

Abschließend findet eine Überprüfung durch Zählen der Instanzen statt und die (k-1)-Item-Sets werden in einer Hashtabelle gespeichert.
Zur effizienten Regelgenerierung werden alle Regeln mit hoher Konfidenz gesucht. Der Support des Antecedent kann aus der Hash Table ausgelesen werden, um Konfidenz zu berechnen. Der Nachteil hierbei ist, dass die Anwendung der Brute-Force-Methode (2^N-1) Versuche bedeutet.
Besser ist es, (c+1)-Consequent-Regeln aus c-Consequent-Regeln zu erzeugen. Die Beobachtung zeigt, dass eine (c+1)-Consequent-Regel nur gültig sein kann, wenn alle zugehörigen c-Consequent-Regeln ebenfalls gültig sind. Der resultierende Algorithmus ist ähnlich zu dem zum Finden der Item Sets.

Beispiel – 1-Consequent-Regeln:

Zugehörige 2-Consequent-Regel:

Abschließend erfolgt eine Prüfung des Antecedent in der Hash Table.
Die genannte Methode benötigt einen Durchlauf durch die Datenmenge für jede Item-Set-Größe. Eine andere Möglichkeit ist die Generierung von (k+2)-Item-Sets sofort nach der Generierung der (k+1)-Item-Sets ohne Überprüfung der (k+1)-Sets nach ihrer Erzeugung. Das Ergebnis ist, dass mehr (k+2)-Item-Sets als nötig berücksichtigt werden, aber weniger Durchläufe durch die Daten erfolgen. Diese Methode kann sinnvoll sein, wenn die Datenmenge zu groß ist, um in den Hauptspeicher zu passen.
Eine praktische Möglichkeit ist die Generierung einer bestimmten Anzahl von Regeln z.B. durch sukzessive Reduzierung des minimalen Supports.
Der Standardinput (flache Relation mit einer Zeile pro Instanz und einer Spalte pro Attribut) ist sehr ineffizient für typische Warenkorbdaten. Die Attribute repräsentieren Produkte in einem Warenkorb wobei üblicherweise die meisten Produkte fehlen. Die Instanzen werden in dem Zusammenhang auch Transaktionen genannt.
Zur graphischen Darstellung einfacher Abhängigkeitsregeln können sogenannte Interdependenzgraphen verwendet werden. Nachfolgende Grafik zeigt den Interdependenzgraphen einer Warenkorbanalyse.

Interdependenzgraph

Clustering

Unter Clustering, das zum Unsupervised Learning (unbeaufsichtigtes Lernen) gehört, versteht man die Gruppierung ähnlicher Instanzen in einer Menge (Cluster). Der Erfolg des Clusterings kann meist nur subjektiv gemessen werden.

Beispielproblem: Irisdaten ohne Klasse

Die Methode des Clusterings zählt zum Unsupervised Learning, d.h. es wird kein Zielwert vorgegeben.
Die Vorgaben sind:

Intra-Cluster-Ähnlichkeit der Instanzen soll möglichst hoch sein
Inter-Cluster-Ähnlichkeit der Instanzen soll möglichst gering sein

Die Unterschiede zwischen Modellen/Algorithmen:

Eindeutig vs. überlappend
Deterministisch vs. probabilistisch
Hierarchisch vs. Flach

Weiterhin gibt es eine Evaluationsproblematik. Eine Evaluierung ist üblicherweise nur durch manuelle Prüfung möglich, außer das Clustering wird als Dichteabschätzung verstanden. Dann kann es auf Testdaten evaluiert werden.

k-Means – ein Clustering-Algorithmus

Beim k-Means-Algorithmus werden die Daten in k Gruppen (mit vordefiniertem k) aufgeteilt. Die Vorgehensweise ist wie folgt:

Clustermitten werden gewählt (z.B. zufällig)
Instanzen werden den Clustern aufgrund ihrer Distanz zu den Clustermitten zugewiesen
die Schwerpunkte der Cluster werden berechnet und als neue Mitten verwendet
zurück zum ersten Schritt bis zur Konvergenz

Die Eigenschaften dabei sind, dass kein Cluster leer ist und jede Instanz genau einem Cluster angehört.
Die Ergebnisse des k-Means-Algorithmus können stark von der Auswahl der Anfangswerte abhängen. So kann der Algorithmus z.B. auf ein lokales Minimum ’hereinfallen’. Beispiel: Es gibt vier Instanzen an den Eckpunkten eines zweidimensionalen Rechtecks. Das lokale Minimum stellen zwei Clustermitten an den Mittelpunkten der langen Seiten des Rechtecks dar.
Eine einfache Möglichkeit, die Chance zum Auffinden des globalen Optimums zu erhöhen ist das wiederholte Ausführen mit unterschiedlichen Zufallsstartwerten.
Repräsentation von Clustern
Einfache 2D-Repräsentation:

Einfache 2D-Repräsentation

Probabilistische Zuweisung:

Probabilistische Zuweisung

Venn-Diagramm:

Überlappende Cluster

Dendrogramm ^[17] (hierarchisch):

Hierarchische Cluster

Zum hierarchischen Clustering werden beim Bottom-up (agglomerativen) Vorgehen in jedem Schritt die beiden ähnlichsten Cluster zusammengefasst (Beginn mit Einzelinstanz-Clustern), bis nur noch ein Cluster übrigbleibt.
Beim Top-down (divisiven) Vorgehen werden zwei Cluster gefunden und die Prozedur für die Teilmengen rekursiv fortgesetzt, bis Einzelinstanz-Cluster erreicht sind. Beide Methoden erzeugen ein Dendrogramm.
Gütemaße für Cluster – Gegeben seien zwei Cluster A und B.

Single-Link: Verwendet die minimale Distanz zwischen zwei Instanzen aus A und B und neigt zur Bildung von Ketten durch ’ungünstige’ Instanzen in den Clustern
Complete-Link: Verwendet die maximale Distanz zwischen zwei Instanzen aus A und B und ist empfindlich gegen Ausreißer.
Average-Link: Ist ein Kompromiss zwischen Single- und Complete-Link und verwendet den mittleren Abstand zwischen allen Instanzpaaren aus A und B.

Cluster können nachträglich mit Hilfe von Supervised Learning (Klassifikation) erklärt/ interpretiert werden. Ein Vorteil des probabilistischen Clustering-Verfahrens ist, dass Instanzen nur mit einer gewissen Wahrscheinlichkeit in einen bestimmten Cluster gehören. Zusätzlich kann das ’Likelihood’ der Daten abgeschätzt und zum Vergleich unterschiedlicher Clustering-Ergebnisse verwendet werden. Beispielalgorithmen sind: EM, Bayes’sches Clustering.

Numerische Prognose

Mit Hilfe der numerischen Prognose, die zum Supervised Learning zählt, lassen sich numerische Größen vorhersagen. Die numerische Prognose ist vergleichbar mit der Klassifikation, nur dass hier eine numerische ’Klasse’ gebildet wird. Der Erfolg wird, wie bei der Klassifikation, anhand von Testdaten (oder subjektiv) gemessen.

Beispiel: Angepasste Version der Wetterdaten

Ein weiteres Beispiel ist die Vorhersage der CPU-Performance bei 209 unterschiedlichen Computer-Konfigurationen.

Beispiel: Angepasste Version der CPU-Performancedaten

Die lineare Regressionsfunktion hierzu:

Die Standardmethode für die numerische Prognose ist die lineare Regression. Alle Klassifikationsverfahren können auch auf Regressionsprobleme angewandt werden (z.B. Regressionsbäume), was aber eine Diskretisierung der Daten erfordert. Umgekehrt kann die lineare Regression auch zur Prognose nominaler Attribute (also zur Klassifizierung) verwendet werden.

Regression zur numerischen Prognose

Regression nennt man die Ermittlung eines mathematischen Ausdrucks zur Vorhersage einer numerischen Größe. Die lineare Regression verwendet lineare Funktionen als Annäherung. Das Ergebnis der linearen Regression ist eine Linearkombination von Attributen:

Die Gewichte werden anhand der Trainingsdaten ermittelt. Der Prognosewert für die erste Trainingsinstanz a(1):

Die lineare Regression basiert auf der Methode der kleinsten Quadrate. Die k+1 Koeffizienten werden so gewählt, dass der quadrierte Fehler der n Trainingsinstanzen minimal wird.

Der quadrierte Fehler über alle n Instanzen:

Die Koeffizienten können durch Standard-Matrixoperationen ermittelt werden, wenn mehr Instanzen als Attribute existieren (vereinfacht ausgedrückt). Die Minimierung des absoluten Fehlers ist schwieriger.

Regression zur Klassifikation
Eine lineare Regression kann auch zur Klassifikation verwendet werden.
Training: Für jede Klasse wird eine Regression ausgeführt, das Ergebnis wird für Instanzen in der Klasse auf 1 gesetzt, für die anderen auf 0.

Prognose:
Wahl der Klasse des Modells mit dem größten Ergebniswert (’Membership Value’).
Bei der linearen Regression nennt man dieses Verfahren ’Multi-Response Linear Regression’. Erweiterungen hierzu sind die Pairwise Regression oder die Logistic Regression.
Ferner haben Minsky and Papert (1969) gezeigt, dass es bei linearen Klassifikatoren Einschränkungen gibt, sie können z.B. kein XOR lernen.

Bäume zur numerischen Prognose

Ein Regressionsbaum ist ein ’Entscheidungsbaum’, bei dem die Blätter numerische Größen darstellen. Ein Regressionsbaum dient der numerischen ’Klassifikation’. Der prognostizierte Wert ist der Durchschnittswert der Trainingsinstanzen, die das Blatt erreichen.
Ein Modellbaum ist ein ’Regressionsbaum’ mit linearen Regressionsmodellen als Blattknoten. Unter Umständen sind Bäume zur numerischen Prognose die bessere Wahl als eine einfache lineare Regression.
Regressionsbäume unterscheiden sich von Entscheidungsbäumen dadurch, dass der Teilungsprozess endet, wenn die Streuung in der Teilmenge ein Minimum erreicht hat (z.B. 5%). Das Pruning-Kriterium basiert auf einem numerischen Fehlermaß. Ein Blattknoten prognostiziert den durchschnittlichen ’Klassen’-Wert der Trainingsinstanzen, die den Knoten erreichen.
Der Vorteil von Regressionsbäumen liegen darin, dass sie konstante Funktionen stückweise annähern können und leicht zu interpretieren sind.

Beispiel – Regressionsbaum für die CPU-Daten:

Regressionsbaum für die CPU-Daten

Die erweitere Version von Regressionsbäumen stellen Modellbäume dar. Modellbäume sind Regressionsbäume mit einer linearen Regressionsfunktion an jedem Knoten. Die lineare Regression wird auf die Instanzen eines Knotens angewendet, wenn der gesamte Baum erzeugt ist. Für die lineare Regression wird nur eine Teilmenge der Attribute verwendet. Verwendung finden nur die Attribute, die in dem Teilbaum vorkommen und unter Umständen solche, die auf dem Pfad zur Wurzel liegen. Der Overhead für die lineare Regression ist gering, da üblicherweise nur ein kleiner Teil der Attribute im Baum verwendet wird. Deshalb ist dieses Verfahren sehr schnell.
Beispiel – Modellbaum für die CPU-Daten:

Modellbaum für die CPU-Daten

Einfache lineare Modelle sind unangebracht, wenn die Daten nicht-lineare Abhängigkeiten aufweisen. Sie können aber als Bausteine für komplexere Lernschemata (Modellbäume) verwendet werden.
Regressionsbäume wurden in CART (Classification And Regression Tree) ^[18] eingeführt. Quinlan entwickelte das M5 Modellbaum-Verfahren ^[19] . M5 ist eine leicht verbesserte veröffentlichte Version.

Evaluation von numerischer Prognose

Bei der Evaluation numerischer Prognosen kommen die gleichen Strategien zum Einsatz wie zum Beispiel unabhängige Testmenge, Cross-Validation, oder Signifikanztests. Der Unterschied liegt im Fehlermaß.
Ein beliebtestes Maß ist der Mittelwert des quadrierten Fehlers:

Die tatsächlichen Zielwerte sind a1, a2, …, an, die prognostizierten sind Zielwerte p1, p2, …, pn.
Die Wurzel des Mittelwertes der quadrierten Fehler:

Der Mittelwert des absoluten Fehlers ist weniger anfällig gegen Ausreißer:

Manchmal sind relative Fehlerwerte angebrachter (z.B. 10% für einen Fehler von 50, wenn 500 prognostiziert wird).

Oft ist es wissenswert, wie gut ein Schema den Mittelwert prognostiziert. Der relative quadrierte Fehler lautet (ā ist der Mittelwert):

Der relative absolute Fehler lautet:

Der Korrelationskoeffizient misst die statistische Korrelation zwischen den prognostizierten und den tatsächlichen Werten:

Er ist skalenunabhängig und zwischen -1 und +1. Eine gute Prognose führt im Gegensatz zu anderen Fehlermaßen zu großen Werten.
Es stellt sich die Frage, welche Bewertungsmaßzahl verwendet werden soll. Man betrachtet am besten alle, da es oft keine Rolle spielt.

Beispiel:

Data Warehousing und OLAP

Bair, J., Böhlen, M.H., Jensen, C.S., Snodgrass, R.T.: Notions of Upward Compatibility of Temporal Query Languages, in Wirtschaftsinformatik (WI), Volume 39, Number 1, 1997.

Bauer, A., Günzel, H.: Data-Warehouse-Systeme. Architektur, Entwicklung, Anwendung. 3. Auflage, dpunkt Verlag, 2008.

Bulos, D.: OLAP Database Design: A New Dimension, in Database Programming and Design, 1996.

Cabibbo, L., Torlone R.: A Systematic Approach to Multidimensional Databases, in Proc. SEBD 1997.

Chamoni, P., Gluchowski, P. (Hrsg.): Analytische Informationssysteme, 3. Auflage, Springer, 2006.

Chen, P.: The Entity-Relationship Model – Towards a Unified View of Data, ACM Transactions on Database Systems (TODS), 1976.

Inmon, W.H.: Building the Data Warehouse, 4. Auflage, Wiley, 2005.

Kemper, H.-G.: Business Intelligence – Grundlagen und praktische Anwendungen. Vieweg, 2004

Lehner, W.: Datenbanktechnologie für Data-Warehouse-Systeme, dpunkt Verlag, 2003.

Rahm, E. und Do, H.H.: Data Cleaning: Problems and Current Approaches, in IEEE Data Engineering Bulletin, Volume 23, Number 4, 2000.

Sapia, C., Blaschka, M., Höfling, G. und Dinter, B.: Extending the E/R Model for the Multidimensional Paradigm, in Proc. ER Workshops, Springer, 1998.

Snodgrass, R.T. et al.: A TSQL2 Tutorial, in SIGMOD Record, Volume 23, Number 3, 1994.

Data Mining

Breiman, L., Friedman, J.H., Olshen, R.A., Stone, C.J.: Classification and Regression Trees, Wadsworth, 1984.

Clark, P. und Niblett, T.: The CN2 Induction Algorithm, in Machine Learning (ML), Volume 3, 1989.

Cendrowska, J.: PRISM: An Algorithm for Inducing Modular Rules, in International Journal of Man-Machine Studies (IJMMS), Volume 27, Number 4, 1987.

Fayyad, U.M., Piatetsky-Shapiro, G. und Smyth, P.: From Data Mining to Knowledge Discovery in Databases, in AI Magazine (AIM), Volume 17, Number 3, 1996.

Quinlan, J.R.: C4.5: Programs for Machine Learning, Morgan Kaufmann, 1993.

Witten, I.H. und Frank, E.: Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations. 2. Auflage, Morgan Kaufmann Publishers, San Diego, 2005; Deutsche Übersetzung der 1. Auflage:

Witten, I.H. und Frank, E.: Data Mining: Praktische Werkzeuge und Techniken für das maschinelle Lernen. Carl Hanser Verlag, München, 2001

↑ Vgl. Gartner, 2006
↑ Vgl. Bauer und Günzel, 2008
↑ Hinweis: Das Paper wurde vor dem Aufkommen des Data Warehousing geschrieben; zu der Zeit arbeitete Codd für Arbor Software (später Hyperion), Hersteller von Essbase.
↑ Vgl. http://www.tdwi.org
↑ Vgl. Cabibbo und Torlone, 1997
↑ Vgl. Chen, 1976
↑ Vgl. Sapia, Blaschka, Höfling und Dinter, 1998
↑ Vgl. Bulos, 1996
↑ Vgl. Snodgrass et al., 1994
↑ Vgl. Gray, 2003
↑ Vgl. Zinke, 2002
↑ Vgl. Bair, Böhlen, Jensen, Snodgrass, 1997.
↑ Vgl. Fayyad, Piatetsky-Shapiro und Smyth, 1996
↑ Vgl: http://www.ics.uci.edu/ mlearn/MLSummary.html
↑ log = Logarithmus zur Basis 2
↑ Vgl. Shannon, 1948
↑ Griech. „dendron“ = Baum
↑ Vgl. Breiman et al., 1984
↑ Vgl. Quinlan, 1993

[1] Vgl. Gartner, 2006

[2] Vgl. Bauer und Günzel, 2008

[3] Hinweis: Das Paper wurde vor dem Aufkommen des Data Warehousing geschrieben; zu der Zeit arbeitete Codd für Arbor Software (später Hyperion), Hersteller von Essbase.

[4] Vgl. http://www.tdwi.org

[5] Vgl. Cabibbo und Torlone, 1997

[6] Vgl. Chen, 1976

[7] Vgl. Sapia, Blaschka, Höfling und Dinter, 1998

[8] Vgl. Bulos, 1996

[9] Vgl. Snodgrass et al., 1994

[10] Vgl. Gray, 2003

[11] Vgl. Zinke, 2002

[12] Vgl. Bair, Böhlen, Jensen, Snodgrass, 1997.

[13] Vgl. Fayyad, Piatetsky-Shapiro und Smyth, 1996

[14] Vgl: http://www.ics.uci.edu/ mlearn/MLSummary.html

[15] = Logarithmus zur Basis 2

[16] Vgl. Shannon, 1948

[17] Griech. „dendron“ = Baum

[18] Vgl. Breiman et al., 1984

[19] Vgl. Quinlan, 1993

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

Business & Competitive Intelligence Systems - Gesamt

Inhaltsverzeichnis

Data Warehousing & OLAP

Einführung

Architekturen

Datenmodellierung

Datenbewirtschaftung

Datenanalyse

Data Mining

Einführung

Daten

Vorbereitung

Methoden und Algorithmen

Klassifikation

R – ein Klassifikationsalgorithmus zum Ableiten elementarer Regeln

ID3 – ein Klassifikationsalgorithmus zur Konstruktion von Entscheidungsbäumen

PRISM – ein Klassifikationsalgorithmus zum Erzeugen von Klassifikationsregeln (Covering-Ansatz)

k-NN – ein Klassifikationsalgorithmus für instanzbasiertes Lernen

Evaluation von Klassifikationsverfahren

Abhängigkeitsanalyse

APRIORI – ein Algorithmus zum Erlernen von Abhängigkeitsregeln

Clustering

k-Means – ein Clustering-Algorithmus

Numerische Prognose

Regression zur numerischen Prognose

Bäume zur numerischen Prognose

Evaluation von numerischer Prognose

Navigationsmenü

Business & Competitive Intelligence Systems - Gesamt

Data Warehousing & OLAP

Einführung

Architekturen

Datenmodellierung

Datenbewirtschaftung

Datenanalyse

Data Mining

Einführung

Daten

Vorbereitung

Methoden und Algorithmen

Klassifikation

R – ein Klassifikationsalgorithmus zum Ableiten elementarer Regeln

ID3 – ein Klassifikationsalgorithmus zur Konstruktion von Entscheidungsbäumen

PRISM – ein Klassifikationsalgorithmus zum Erzeugen von Klassifikationsregeln (Covering-Ansatz)

k-NN – ein Klassifikationsalgorithmus für instanzbasiertes Lernen

Evaluation von Klassifikationsverfahren

Abhängigkeitsanalyse

APRIORI – ein Algorithmus zum Erlernen von Abhängigkeitsregeln

Clustering

k-Means – ein Clustering-Algorithmus

Numerische Prognose

Regression zur numerischen Prognose

Bäume zur numerischen Prognose

Evaluation von numerischer Prognose

Navigationsmenü

Suche