Dynamische Systeme - Dynamische Systeme
Dynamische Systeme
Dynamische Systeme In Lektion zwei ging es um die Optimierung eines Systems, indem die Zeit keine Rolle spielt: gesucht wurden Extremwerte einer Funktion oder , allenfalls unter Nebenbedingungen; die Zielfunktion war vorgegeben und unveränderlich, daher wird eine einmal gefundene optimale Lösung immer optimal bleiben. In der Praxis hat man es hingegen häufig mit Systemen zu tun, die sich im Wandel befinden, d.h., die Funktion in der freien Variablen verändert sich mit der Zeit und wird als beschrieben. Solche mit der Zeit veränderliche Systeme werden als dynamisch bezeichnet. Man unterscheidet zwischen deterministischen und stochastischen Systemen. Sind bei einem deterministischen System die Anfangsbedingungen bekannt, so ist der weitere Verlauf in alle Zukunft vorherbestimmt. Solche Systeme können oft mit Differential bzw. mit Differenzen-gleichungen beschrieben werden. Wir werden hier nur die einfachsten Fälle besprechen, um eine Idee von dieser Art der Modellierung zu bekommen. Speziell im Bereich der Finanzmathematik spielen stochastische Prozesse eine große Rolle, wo zusätzlich zur dynamischen Struktur des Systems auch noch zufällige Komponenten ins Spiel kommen. Die allgemeine mathematische Behandlung dieser Probleme ist sehr schwierig, nichts desto trotz sollen hier einige Grundlagen vermittelt werden.
Differentialgleichungen
Bei einer Differentialgleichung wird ein Zusammenhang zwischen einer (unbekannten) Funktion und ihren Ableitungen vorgegeben. „Eine Differentialgleichung lösen“ heißt: alle Funktionen finden, die diesen Zusammenhang erfüllen. Beginnen wir mit einem Beispiel, das uns bereits vertraut ist: in der Finanzmathematik wird gerne mit der exponentiellen Verzinsung begonnen, wo aufgrund der Zinseszinsen das Anfangskapital bei einem jährlichen Zinssatz von entsprechend der Formel wächst. Nehmen wir nun an, wir hätten eine monatliche Verzinsung zum Zinssatz . Das Kapital erhöht sich nun jeden Monat um den Faktor, d.h. nach einem Jahr gilt
In der Abbildung entspricht die horizontale Achse der unabhängigen Variable (der Zeit), und die vertikale Achse der abhängigen Variable (in unserem obigen Beispiel dem Kapital). Das Vektorfeld gibt an jedem Punkt die Steigung an, die eine Lösung der Differentialgleichung dort haben muss. Es ist speziell eine Lösung angegeben, die die Anfangsbedingung erfüllt. Beachte, wie diese Lösung den Pfeilen des Vektorfeldes folgt. Man kann sich leicht überzeugen, dass durch eine Lösung gegeben ist, die obige Differentialgleichung für und die Anfangsbedingung erfüllt. Näheres zur Lösung dieser Differentialgleichung folgt in den nächsten beiden Abschnitten.
Differentialgleichungen erster Ordnung
Eine explizite Differentialgleichung erster Ordnung hat die allgemeine Gestalt
Fall 1:
Beispiel 13:
Populationen, die über einen beliebig langen Zeitraum dem Gesetzt des natürlichen Wachstums folgen, könnten beliebig groß werden („exponentielles Wachstum“). Ein realistischeres Modell mit beschränktem Wachstum wird durch die sogenannte logistische Differentialgleichung beschrieben:
und daherFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} t\left(x\right)=\frac{1}{r}\int\left(\frac{1}{x}+\frac{1}{K-x}\right)\mathrm{dx}-C=\frac{1}{r}\left(\mathrm{log}\left(x\right)-\mathrm{log} \left(K-x\right)\right)-C=\frac{1}{r}\left(\mathrm{log}\left(\frac{x}{K-x}\right)\right)-C \end{aligned}}
Durch einfache Umformungen erhält man die Umkehrfunktion von t(x):Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(t\right)=K\frac{1}{1+\mathrm{exp}\left(-r\left(t+C\right)\right)}=K\frac{1}{1+c\mathrm{exp}\left(-\mathrm{rt}\right)} \end{aligned}}
wobei die Konstante auf die Integrationskonstante C des unbestimmten Integrals zurückgeht und so gewählt werden kann, dass eine etwaige AnfangsbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(0\right)=x_0 \end{aligned}}
erfüllt wird:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x_0=x\left(0\right)=K\frac{1}{1+c} \Rightarrow c=\frac{K-x_0}{x_0}. \end{aligned}}
Die folgende Abbildung zeigt Lösungen der logistischen Gleichung zu den Parametern Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle r = 1,K = 1} zu verschiedenen Anfangswerte . Die Lösung konvergiert jeweils gegen die Kapazitätsgrenze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K=1} .
Aufgabe 10:
Verwende die Methode aus Beispiel 13, um die Differentialgleichung des natürlichen Wachstums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^\prime\left(t\right)=\mathrm{rx}t}
allgemein zu lösen.
Finde die spezielle Lösung zur Anfangsbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(0\right)=x_0!}
Die Modelle von Beispiel 12 und Aufgabe 10 können herangezogen werden, um das Bevölkerungswachstum oder das Wachstum eines Marktes zu beschreiben. Beachte, dass wenn bei sehr kleinem Niveau begonnen wird, die Lösung der logistischen Gleichung sich zu Beginn ganz ähnlich verhält wie eine Exponentialfunktion (Abbildung 1.2, die unterste Kurve). Nichts desto trotz wird im Laufe der Zeit irgendwann das Wachstum begrenzt (wenn zum Beispiel die Marktsättigung eines neuen Produktes erreicht ist). Der Glaube an ein unbegrenztes exponentielles Wachstum ist in den meisten Fällen unbegründet, auch wenn viele Wirtschaftstreibende dies wohl gerne anders sehen würden.
Fall 3:
Die Ableitung der Funktion lässt sich als Produkt einer Funktion von x und einer Funktion von t schreiben. Fall 1 und von Fall 2 sind Spezialfälle von Fall 3. Eine Lösung lässt sich formal ähnlich wie im Fall 2 durch Trennung der Variablen finden:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\mathrm{dx}}{\mathrm{dt}}=f\left(t\right)g\left(x\right) \Leftrightarrow \frac{\mathrm{dx}}{g\left(x\right)}=f\left(t\right)\mathrm{dt} \Leftrightarrow \int\frac{\mathrm{dx}}{g\left(x\right)}=\int f\left(t\right)\mathrm{dt} +C\mathrm{.} \end{aligned}}
Beispiele dazu finden sich in den Wiederholungsaufgaben. Ein besonders wichtiger Fall tritt allerdings auf, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(x) = x} . Dann liegt eine sogenannte homogene lineare Differentialgleichung vor. Dem Typ der linearen Differentialgleichung widmen wir aufgrund seiner Wichtigkeit einen eigenen Abschnitt.
Lineare Differentialgleichungen
Darunter versteht man Gleichungen der FormFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^\prime\left(t\right)+f\left(t\right)x=h\left(t\right) \end{aligned}}
Im Falle von spricht man von einer inhomogenen Gleichung, ansonsten wie schon erwähnt, von einer homogenen (vgl. die Nomenklatur von linearen Gleichungssystemen in der linearen Algebra). Die Bezeichnung „linear“ bezieht sich darauf, dass das x nur mit dem Exponenten 1 vorkommt – erinnern Sie sich an die linearen Gleichungen, in denen gibt es auch keine quadratischen Terme, Wurzeln, Winkelfunktionen usw. in x. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(t\right)} hingegen darf beliebige Funktionen in t aufweisen! Für die Lösung einer linearen Differentialgleichung sucht man zuerst Lösungen der dazugehörigen homogenen Gleichung. Mit der Methode der Trennung der Variablen erhält man:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\mathrm{dx}}{\mathrm{dt}}=-f\left(t\right)x \Leftrightarrow \mathrm{log}x=\int\frac{\mathrm{dx}}{x}=-\int f\left(t\right)\mathrm{dt} +C \end{aligned}}
und daherFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(t\right)=\mathrm{exp}-ftdt+C=cexp-Ft \end{aligned}}
Damit haben wir für die homogene Gleichung eine allgemein gültige Lösungsformel gefunden, wobei eine beliebige Stammfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(t)} ist. Für die inhomogene Gleichung verwenden wir einen sogenannten Ansatz, d.h. man geht davon aus, dass die Lösung eine bestimmte Gestalt hat. Diese Technik wird sehr häufig zum Lösen von Differentialgleichungen verwendet. Hier benutzt man die Lösung der homogenen Gleichung, allerdings wird die unbestimmte Konstante c als Funktion von t gewählt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(t\right)=c\left(t\right)\mathrm{exp}-Ft \end{aligned}}
Was zu tun bleibt ist die Berechnung der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c\left(t\right)} Differenzieren liefert aufgrund der Produktregel und der Kettenregel
Andererseits soll ja die inhomogene Differentialgleichung erfüllt sein:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^\prime\left(t\right)=h\left(t\right)-x\left(t\right)f\left(t\right), \end{aligned}}
also sind die rechten Seiten der beiden letzten Gleichungen gleich:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} c^\prime\left(t\right)\mathrm{exp}-Ft-ctexp-Ftft=ht-xtft. \end{aligned}}
Der Vergleich ergibt, dass aufgrund des Ansatzes der zweite Term auf beiden Seiten bereits übereinstimmt, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c\left(t\right)} erhält man aus:
Damit haben wir die allgemeine Lösung der inhomogenen Gleichung erhalten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x(t)=\left(\int h(t) \exp (F(t)) \mathrm{dt}+k\right) \exp (-F(t)) }
Die Konstante k kann wiederum so gewählt werden, dass gegebenenfalls eine Anfangsbedingung erfüllt wird. Man bezeichnet diese Vorgangsweise zur Bestimmung der Lösung der inhomogenen linearen Differentialgleichung als Variation der Konstanten. Die Lösungsformel kann so interpretiert werden, dass zu einer PartikulärlösungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{exp}\left(-F\left(t\right)\right)\int h\left(t\right)\mathrm{exp} \left(F\left(t\right)\right)\mathrm{dt} \end{aligned}}
der inhomogenen Gleichung, eine beliebige LösungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} k\mathrm{exp}\left(-F\left(t\right)\right) \end{aligned}}
der homogenen Gleichung hinzuaddiert wird.
Lineare Differentialgleichungen – alternative Rechenmethode
Der oben angegebene Rechenweg erlaubt die Lösung der inhomogenen linearen Differenzialgleichung in einem Schritt; der Formalismus ist allerdings ein wenig sperrig; wir können aber die Methode der Trennung der Variablen auch etwas umständlicher, dafür aber nachvollziehbarer anwenden:
Betrachten wir etwa die inhomogene Differenzialgleichung
Zunächst lösen wir mithilfe der Trennung der Variablen die homogene Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} x^{\prime}(t)+2 \frac{x}{t}=0 \\ \frac{d x}{d t}=-\frac{2 x}{t} \\ \frac{d x}{x}=-2 \frac{d t}{t} \end{array} }
Wir integrieren beide Seiten und erhalten – Regeln für den Logarithmus bitte beachten! –Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \ln{x}=\ -2\ln{t}+c=\ln{\frac{1}{t^2}+c}\ \end{aligned}}
Wir nehmen links und rechts die Exponentialfunktion:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x_h=\frac{1}{t^2}e^c=\frac{C}{t^2} \end{aligned}}
(Die Exponentialfunktion einer Konstanten ist wieder eine Konstante!) Damit haben wir die allgemeine Lösung der homogenen Differenzialgleichung; um nun die inhomogene Gleichung zu lösen, reicht es, eine einzige partikuläre Lösung derselben zu finden, zu dieser kann dann jede beliebige Lösung der homogenen addiert werden. Der Witz ist nun, dass wir für diese partikuläre Lösung die Konstante C als Funktion in t betrachten – also:
diese Funktion setzen wir nun in die Differenzialgleichung ein – beachten aber, dass wir jetzt bei der Ableitung die Produktregel anwenden müssen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\frac{C(t)}{t^2}\right)^{\prime}=\frac{C^{\prime(t)}}{t^2}-2 \frac{C(t)}{t^3} } Diese Ausdrücke fürFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(t\right) \text{ und } x^\prime\left(t\right) \end{aligned}}
setzen wir nun in die Differenzialgleichung ein: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^{\prime}(t)+2 \frac{x}{t} &=4 t \\ \frac{C^{\prime(t)}}{t^2}-2 \frac{C(t)}{t^3}+2 \frac{C(t)}{t^3} &=4 t \end{aligned} } Nun bleibt von der linken Seite nur mehr der erste Ausdruck übrig – die beiden anderen heben sich weg; (das ist kein Zufall – wenn das in einer Rechnung nicht der Fall ist, dann haben Sie sich verrechnet!) Es bleibt also die Gleichung
Übrig. Diese formen wir um:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} C^{\prime\left(t\right)}=4t^3 \end{aligned}}
AlsoFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} C\left(t\right)=t^4 \end{aligned}}
(Wir brauchen nur eine partikulare Lösung – daher setzen wir die Integrationskonstante 0.) Für die partikuläre Lösung der Gleichung erhalten wir damit
Und für die allgemeine Lösung der inhomogenen Gleichung dürfen wir nun jede beliebige Lösung der homogenen hinzu addieren – alsoFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(t\right)=x_p\left(t\right)+x_h\left(t\right)=\frac{C}{t^2}+t^2. \end{aligned}}
Beispiel 14:
Ein weiteres sehr einfaches Wachstumsmodell ist gegeben durch die Gleichung
Äquivalent dazu istFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^\prime\left(t\right)+\mathrm{ax}t=aK \end{aligned}}
Hier ist das Wachstum der Population proportional zur Differenz zwischen der aktuellen Populationsgröße x und der Kapazität K des Habitats. Die homogene Gleichung entspricht im wesentlich dem Gesetz des natürlichen Wachstums, allerdings hier mit negativem Koeffizienten a. Einsetzen in die oben gegebene Lösungsformel mitFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(t\right)=a \end{aligned}}
undFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} h\left(t\right)=\mathrm{aK} \end{aligned}}
führt zur allgemeine Lösung
(Die konstante Partikulärlösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(t\right)=K} hätte wohl auch durch einfaches Raten gefunden werden können.) Falls zum Zeitpunkt t=0 eine Anfangsbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(0\right)=x_0} gegeben ist, so ergibt die Wahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k=x_0-K} die richtigen Lösung. Man erkennt klar, dass für kleine Anfangswerte die Konvergenz zur Kapazitätsgrenze wesentlich rascher verläuft als im logistischen Modell.
Aufgabe 11:
Löse die Differentialgleichung
zur AnfangsbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x\left(0\right)=1 \end{aligned}}
Wir haben in diesem Abschnitt Lösungsmethoden für die allereinfachsten gewöhnlichen Differentialgleichungen erster Ordnung kennen gelernt. Eine natürliche Erweiterung wären Differentialgleichungen höherer Ordnung. In diesen kommt nicht nur x’ vor, sondern auch höhere Ableitung von x. Eines der bekanntesten Beispiele ist die Schwingungsgleichung:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^{\prime\prime}\left(t\right)=-\lambda^2x\left(t\right). \end{aligned}}
Ebenso ist man häufig nicht nur an einer Variablen interessiert, die sich mit der Zeit verändert, sondern an vielen Variablen. Dies führt zu sogenannten Systemen von Differentialgleichungen. Ein System von linearen Differentialgleichungen mit konstanten Koeffizienten in Vektorform hat zum Beispiel die GestaltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}^\prime\left(t\right)=A\vec{x}\left(t\right) \end{aligned}}
Hier istFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}^\prime\left(t\right)=\left(x_1^\prime\left(t\right),\ldots,x_n^\prime\left(t\right)\right) \end{aligned}}
ein Vektor von n Funktion, die nach t abgeleitet werden, und A ist eine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n\times n} - Matrix. Für diese Art von Systemen gibt es explizite Lösungsformeln, in denen die Eigenwerte der Matrix A eine große Rolle spielen. Bereits das etwas allgemeinere lineare SystemFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}^\prime\left(t\right)=A\left(t\right)\vec{x}\left(t\right) \end{aligned}}
mit einer zeitabhängigen Koeffizentenmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle A\left(t\right)} lässt nicht immer eine geschlossene Darstellung der möglichen Lösungen zu. Die allgemeine Theorie nichtlinearer Systeme von Differentialgleichungen der FormFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}^\prime\left(t\right)=f\left(\vec{x}\left(t\right),t\right) \end{aligned}}
ist dementsprechend schwierig. Häufig ist das Ziel hier nicht mehr eine explizite Lösung zu finden, sondern das quantitative bzw. qualitative Langzeitverhalten von etwaigen Lösungen zu verstehen. Ein bekanntes Beispiel ist das sogenannte Räuber-Beute ModellFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} x^{\prime}(t)=x(t)(a-\mathrm{by}(t)) \\ y^{\prime}(t)=y(t)(-c+\mathrm{dx}(t)) \end{array}}
in dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)}
die Größe der Beute-Population und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y(t)}
die Größe der Räuber-Population angibt. Alle Konstanten a, b, c und d sind positiv. Je größer die Beutepopulation, desto stärker wächst sie selber (Faktor a), allerdings wächst dann auch die Räuberpopulation (Faktor d). Wenn die Räuberpopulation groß wird so verringert sich die Beutepopulation (Faktor -b), allerdings auch die Räuber-population (Faktor -c).
Bereits dieses relativ einfache Modell birgt sehr interessante Dynamiken in sich, die allerdings noch ziemlich gut zu verstehen sind. Nur minimal komplexere Modelle führen zu dynamischen Systemen mit mitunter recht eigenartigem Verhalten. In den 80-er und 90-erJahren war die Untersuchung solcher nichtlinearen Modelle unter dem Namen „Chaostheorie“ äußerst populär. Die mathematische Behandlung nichtlinearer Modelle ist schwierig, allerdings werden oft nur diese der Komplexität der Realität halbwegs gerecht. Zuletzt sei noch erwähnt, dass wir hier nur gewöhnliche Differentialgleichungen besprochen haben. Dies bedeutet, es gibt nur eine unabhängige Variable, nach der differenziert wird (in unseren Beispielen die Zeit t). Funktionen von mehreren Veränderlichen werden in der Theorie der partiellen Differentialgleichungen behandelt, ein Gebiet der Mathematik das noch um einiges schwieriger ist, als die ohnehin schon sehr komplexe Welt der gewöhnlichen Differentialgleichungen.
Differenzengleichungen
Differentialgleichungen behandeln dynamische Systeme in stetiger Zeit. Wir wollen uns nun dem Fall zuwenden, dass sich Systeme nicht stetig verändern, sondern nur in diskreten Zeiteinheiten. Wir werden typischerweise nur den Fall betrachten, dass die Zeitpunkte durch natürliche Zahlen wiedergegeben werden, und verwenden entsprechend Indizes, um den jeweiligen Zeitschritt anzugeben. Kehren wir zurück zum Beispiel am Beginn vom ersten Abschnitt, und betrachten wir nicht die kontinuierliche Verzinsung, sondern beschränken wir uns auf die jährliche Verzinsung. Nach einem Jahr wird dem Grundkapital die Verzinsung hinzugefügt, und wir haben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_1=K_0+{\mathrm{pK}}_0} . Allgemein gilt in jedem JahrFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} K_{n+1}-K_n={\mathrm{pK}}_n. \end{aligned}}
In dieser Form erkennen wir unschwer woher der Name Differenzengleichung rührt. Differenzengleichung sind formal ähnlich zu Differentialgleichungen, und auch in der Lösungstheorie gibt es gewisse Parallelen. Allerdings kann man in unserem Beispiel die Differenzengleichung umschreiben zuFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} K_{n+1}=K_n+{\mathrm{pK}}_n=\left(1+p\right)K_n \end{aligned}}
In dieser Form spricht man von einer Rekursionsgleichung, da die Folge der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_n} rekursiv definiert wird. Wie werden im Folgenden die Begriffe Rekursionsgleichung und Differenzengleichung synonym verwenden, da sie in den betrachteten Beispielen jeweils durch einfache Umformung ineinander übergeführt werden können. Gesucht werden nun wieder die Lösungen, d.h. im gegebenen Fall Funktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_n} , welche die Differenzengleichung erfüllen. Die obige Rekursionsgleichung wurde bereits in der Finanzmathematik explizit gelöst: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_n=K_0(1+p)^n} die Formel der exponentiellen Verzinsung. Vergleiche dies mit der Lösung der DifferentialgleichungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} K^\prime\left(t\right)=\mathrm{pK}t \end{aligned}}
dem natürlichen WachstumFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} K\left(t\right)=K_0e^{\mathrm{pt}} \end{aligned}}
Strukturell erscheinen die Lösungen der Differenzengleichung und der Differentialgleichung sehr ähnlich, und dies ist alles andere als ein Zufall.
Lineare Differenzengleichungen erster Ordnung
Im Gegensatz zu den Differentialgleichungen beschränken wir uns hier weitestgehend auf den Fall von linearen Differenzengleichungen. Wir beginnen mit zwei einfachen Beispielen für inhomogene Differenzengleichungen erster Ordnung (erster Ordnung heißt: es wird nur die Beziehung zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+1}}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n}
betrachtet).
Beispiel 15:
Betrachte die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+1}={\mathrm{ay}}_n+b}
, wobei a und b konstant seien. Es handelt sich demnach um eine inhomogene lineare Differenzengleichung mit Inhomogenität b. Die allgemeine Lösung des zugehörigen homogenen Gleichungssystems ist bereits bekannt als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\mathrm{ca}}^n}
mit beliebiger Konstante c. Des Weiteren se i Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a\neq1}
. Wir erinnern uns, dass die Lösung einer inhomogenen Differentialgleichung die Form hatte: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \text { Partikularlösung }+c}
(Lösung des homogenen Problems) Das Gleiche gilt auch hier. Es genügt eine einzige Partikulärlösung zu finden. Versuchen wir eine konstante Lösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y}
, so muss gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=\mathrm{ay}+b}
, und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=\ \frac{b}{1-a}}
. Die allgemeine Lösung lautet demnachFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} y_n=\frac{b}{1-a}+{\mathrm{ca}}^n \end{aligned}}
Ähnlich wie bei den Differentialgleichungen können wir auch hier eine Anfangsbedingung stellen, etwa dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_0} bekannt sei. Die Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c=y_0-\frac{b}{1-a}} liefert gerade die Erfüllung der Anfangsbedingung, und die Lösung lässt sich schreiben alsFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} y_n=\frac{\mathrm{\ \ } 1-a^n}{1-a}b+a^ny_0. \end{aligned}}
Wir können diese Lösung auch intuitiv verstehen: sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_0} das Kapital, das auf ein Sparbuch eingelegt wird, a=1+p wobei p der jährlichen Verzinsung entspricht, und b sei ein fester Geldbetrag der jedes Jahr zu Jahresbeginn auf das Sparbuch gelegt wird (ähnlich dem klassischen Bausparvertrag). Nach einem Jahr haben wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ y_1={\mathrm{ay}}_0+b} , nach zwei Jahren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_2={\mathrm{ay}}_1+b=a^2y_0+\mathrm{ab}++} , das heißt das Anfangskapital wurde zweimal verzinst und der Betrag, der nach einem Jahr auf das Sparbuch kam, wurde einmal verzinst. Entsprechend giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_n=a^n y_0+a^{n-1} b+a^{n-2} b+\ldots+\mathrm{ab}++=a^n y_0+\left(a^{n-1}+a^{n-2}+\ldots+a+1\right) b}
In der letzten Summe findet sich die Verzinsung der jährlich eingezahlten Beträge. Je später einbezahlt wurde, desto seltener wurde verzinst. Das formal hergeleitete Ergebnis erhält man schließlich aufgrund der bekannten Formel für eine geometrische Summe:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} a^{n-1}+a^{n-2}+\ldots+a+1 = \frac{\mathrm{\ \ }1-a^n}{1-a}. \end{aligned}}
Aufgabe 12:
Wie lautet die Lösung für obige Differenzengleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+1}={\mathrm{ay}}_n+b}
im Falle von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a=1}
?
Beispiel 16:
Ein einfaches Modell für Angebot und Nachfrage Nimm an die Nachfrage nach einem Produkt hängt linear von seinem Preis p ab:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} N\left(p\right)={\mathrm{\ N}}_{\mathrm{max}}\mathrm{\ -\ ap} \end{aligned}}
je höher der Preis, desto geringer die Nachfrage. Die Nachfrage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle N_{\mathrm{max}}} bei einem Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p=0} sei auf jeden Fall größer als das Angebot Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle A_{\mathrm{min}}} bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p=0} . Das Angebot hängt ebenfalls linear vom Preis ab, je höher der Preis ist, desto attraktiver wird die Produktion des Guts und desto größer damit das Angebot:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A\left(p\right)={\mathrm{\ A}}_{\mathrm{min}}+\mathrm{\ bp}. \end{aligned}}
Allerdings gibt es eine gewisse Verzögerung im Bereitstellen des Angebots, so dass das Angebot zum Zeitpunkt n+1 sich immer auf den Preis zum Zeitpunkt n bezieht. Die Nachfrage hingegen reagiert unmittelbar auf den gegebenen Preis.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A_{n+1}={\mathrm{\ A}}_{\mathrm{min}}+{\mathrm{\ bp}}_n N_{n+1}={\mathrm{\ N}}_{\mathrm{max}}{\mathrm{\ -ap}}_{n+1} \end{aligned}}
Ein Glaubensgrundsatz der Wirtschaftswissenschaft besagt, dass Angebot und Nachfrage zu jedem Zeitpunkt übereinstimmen, und diese Forderung liefert folgende Rekursionsgleichung für den Preis:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{\min }+\mathrm{bp}_n=N_{\max }-\mathrm{ap}_{n+1}}
oder auchFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} p_{n+1}=\frac{N_{\mathrm{max}}{\mathrm{-A}}_{\mathrm{min}}{\mathrm{\ -\ bp}}_n}{a} \end{aligned}}
Diese Gleichung hat die gleiche Gestalt wie jene in Beispiel 15 (nur mit anderen Konstanten), und wir erhalten unmittelbar die LösungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} p_n=\left(-\frac{\mathrm{\ b}}{a}\right)^np_0+\frac{\mathrm{1-} (\mathrm{-b/a} )^n}{a+b}\left(N_{\mathrm{max}}{\mathrm{-A}}_{\mathrm{min}}\right) \end{aligned}}
Es ist nun interessant in diesem Modell zu untersuchen, ob sich der Preis jemals seinem Gleichgewichtszustand annähert. Man spricht von einem Gleichgewicht, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{n+1}=p_n} . Falls dies erfüllt ist, so bleibt eine Lösung der Differenzengleichung für alle Zeiten konstant. Für Beispiel 16 bedeutet diesFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{p\ }=\frac{N_{\mathrm{max}}{\mathrm{-A}}_{\mathrm{min}}\mathrm{\ -\ bp} }{a} \end{aligned}}
Eine eindeutige Lösung dieser Gleichung ist gegeben durchFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{p\ }=\frac{N_{\mathrm{max}}{\mathrm{-A}}_{\mathrm{min}}}{a+b}. \end{aligned}}
Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b < a} , so konvergiert der Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(-\frac{\mathrm{\ b}}{a}\right)^n} in der Formel für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_n} gegen 0 und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_n} gegen das Gleichgewicht p (nachrechnen!), während dieser Faktor für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b > a} gegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \infty} konvergiert und aufgrund der alternierenden Vorzeichen der Preis mit immer größeren Schwankungen vom Gleichgewicht wegdivergiert, - das System aus Angebot und Nachfrage wird zunehmend instabil. Die folgende Abbildung veranschaulicht dieses Verhalten.
Die schwarzen Punkte geben den Preis zum Zeitpunkt n bei einem Verhältnis von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b/a = 0.9} an. Der Preis startet bei dem doppelten Wert des Gleichgewichts und pendelt dann jeweils um dieses, konvergiert aber langfristig gegen das Gleichgewicht. Der Preis war zu Beginn zu teuer, daher die Nachfrage zu gering, im nächsten Zeitpunkt war der Preis recht günstig und daher die Nachfrage sehr stark, was den Preis wieder in die Höher treibt, usw. Im Szenario wo Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b < a} pendelt sich die Situation langfristig beim Gleichgewicht ein. Ganz anders das Verhalten bei einem Verhältnis von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b/a = 1.1} , das in der Abbildung durch Sterne widergegeben wird. Obwohl der Preis sehr nahe am Gleichgewichtszustand startet, werden die Schwankungen von Jahr zu Jahr immer größer. Spätestens ab Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n = 40} ist die Gültigkeit dieses einfachen Modells höchst fragwürdig – die vorhergesagten Preise sind negativ! Eine mögliche Schlussfolgerung aus dieser Analyse ist, dass ein Preisgleichgewicht in diesem Modell nur dann erzielt werden kann, wenn die Steigung der Angebotskurve geringer ist als die Steigung der Nachfragekurve. In anderen Worten, die Anbieter müssen auf Preisschwankungen weniger sensibel reagieren als die Konsumenten. An dieser Stelle ist vielleicht eine allgemeine Bemerkung angebracht. Ein mathematisches Modell ist immer nur ein Modell und kein Naturgesetz. Selbst in der Physik wo von Naturgesetzen gesprochen wird, sind sich die Wissenschafter durchaus bewusst, dass ihre Gleichungen nur Modelle sind, welche gewisse Phänomene der Natur mehr oder weniger gut beschreiben, aber niemals die Wirklichkeit vollständig wiedergeben. In einer Wissenschaft wie der Ökonomie, die nicht unbedingt auf wiederholbaren Experimenten beruht, ist entsprechend noch höhere Vorsicht geboten. Das Modell aus Beispiel 15 kann als klassisch bezeichnet werden, aber man tut gut daran sich dessen Grenzen vor Augen zu halten. Offensichtlich ist die lineare Abhängigkeit der Nachfrage und des Angebots vom Preis eine recht starke Forderung, die wenn überhaupt nur in der Nähe eines Gleichgewichtspreises postuliert werden kann. Das Verhalten der Lösung im Falle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle b > a} für große n deutet darauf hin, dass das Modell in diesem Bereich nicht mehr sinnvoll ist. Eine grundlegendere Frage wäre zum Beispiel, bis zu welchem Grade überhaupt davon ausgegangen werden kann, dass sowohl das Angebot als auch die Nachfrage einzig und allein vom Preis abhängen. Die Voraussetzungen, die bei der mathematischen Modellierung eines Sachverhalts getroffen wurden, und die daraus resultierenden Beschränkungen eines Modells sollten niemals aus den Augen verloren werden.
Aufgabe 13:
Finde mögliche Gleichgewichtszustände für die nichtlineare Differenzengleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+1=}ay_n^2+b}
Lineare Differenzengleichungen höherer Ordnung
Die Rekursionsgleichungen im vorigen Abschnitt waren jeweils von erster Ordnung, das bedeutet, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+1}}
jeweils nur von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n}
abhängt, der Wert zu einem beliebigen Zeitpunkt hängt einzig und allein vom vorherigen Zeitpunkt ab. Bei Differenzengleichungen höherer Ordnung besteht ein funktionaler Zusammenhang, der sich über mehrere Zeitschritte erstreckt. Hier ein Beispiel für eine homogene Gleichung zweiter Ordnung:
Beispiel 17:
Löse die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+2}=2y_{n+1}+3y_n}
Als erste einfache Lösung erkennt man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=0}
. Um weitere Lösungen zu erhalten hilft ähnlich wie bei Differentialgleichungen wieder ein Ansatz: Versuche eine Lösung der Gestalt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\lambda^{n\ }}
und berechne Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
aus der Gleichung. Einsetzen liefert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^{n+2}=2\lambda^{n+1}+3\lambda^n}
Kürzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ \lambda^n}
gibt die quadratische Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-2\lambda-3=0}
mit den beiden Lösungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_1=-1, \lambda_1=3}
Zwei mögliche Lösungen sind also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n^{\left(1\right)}=(-1)^n}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n^{\left(2\right)}=3^n }
Die beiden so erhaltenen Lösungen bezeichnet man als Fundamentallösungen. Schreiben Sie von beiden Lösungen die ersten 4 Folgenglieder auf und kontrollieren Sie, dass die Gleichungen tatsächlich erfüllt sind! Aufgrund der Linearität der gegebenen Gleichungen sieht man leicht, dass ebenfalls jede Linearkombination der FundamentallösungenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} c_1y_n^{\left(1\right)}+c_2y_n^{\left(2\right)}=c_1(-1)^n+c_23^n \end{aligned}}
eine Lösung liefert. Man kann durch folgende Überlegungen zeigen, dass damit nun tatsächlich alle möglichen Lösungen gefunden wurden: Bei Differenzengleichungen erster Ordnung wird die Lösung durch eine einzige Anfangsbedingung eindeutig bestimmt. Dies ist völlig einleuchtend, wenn man sich das Rekursionsprinzip vor Augen führt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_0} bestimmt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1} , welches Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_2} bestimmt, usw. Für Differenzengleichungen zweiter Ordnung wird hingegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_2} sowohl durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_0} als auch durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1} bestimmt. Das heißt eine eindeutige Lösung wird durch zwei Anfangsbedingungen festgelegt, und die beiden Konstanten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c_2} können dann entsprechend gewählt werden. Die allgemeine homogene lineare Differenzengleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k-ter} Ordnung mit konstanten Koeffizienten hat folgende Gestalt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} y_{n+k}+a_{k-1}y_{n+k-1}+a_{k-2}y_{n+k-2}+\ldots+a_1y_{n-1}+a_0y_n=0 \end{aligned}}
Für Gleichungen dieser Form kann man immer zunächst den Ansatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\lambda^n} versuchen. Einsetzen des Ansatzes und Kürzen durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^n} liefert folgende Gleichung:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda^k+a_{k-1}\lambda^{k-1}+a_{k-2}\lambda^{k-2}+\ldots+a_1\lambda+a_0=0 \end{aligned}}
Die Bestimmung von Lösungen der Differenzengleichung reduziert sich somit auf das Finden von Nullstellen eines Polynoms, das wiederum als charakteristisches Polynom bezeichnet wird.
Aufgabe 14:
Eine Rekursionsgleichung zweiter Ordnung liefert die berühmten Fibonacci Zahlen: beginne zweimal mit der Zahl 1, und berechne jedes weitere Folgenglied als die Summe der beiden vorherigen. Formuliere dieses Problem als Differenzengleichung zweiter Ordnung mit Anfangsbedingungen und finde eine explizite Darstellung der n-ten Fibonacci Zahl!
Für inhomogene Differenzengleichungen genügt es wie bei Differentialgleichungen die homogene Gleichung zu lösen und eine Partikulärlösung der inhomogenen Gleichung zu finden. Die homogene Lösung wird so angepasst, dass die Anfangsbedingungen erfüllt werden.
Aufgabe 15:
Gegeben sei die DifferenzengleichungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{n+3}-6 y_{n+2}+11 y n+1-6 y n=2}
zu den AnfangsbedingungenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} y_1=0,y_2=-1,y_3=-4 \end{aligned}}
Bestimme die eindeutige Lösung dieser Gleichung. Hinweis: Versuche für die Partikulärlösung den Ansatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\mathrm{cn}}
Damit sind wir in der Lage, für gewisse lineare Differenzengleichungen mit konstanten Koeffizienten Lösungen zu bestimmen. Falls das charakteristische Polynom k verschiedene reelle Nullstellen hat liefert die vorgestellte Methode tatsächlich alle Lösungen. Es gibt zwei davon abweichende Fälle: Einerseits können sogenannte mehrfache Nullstellen auftreten, zum Beispiel hat das PolynomFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda^2-2\lambda+1=(\lambda-1)^2 \end{aligned}}
die zweifache NullstelleFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=1} . Andererseits gibt es mitunter komplexe Nullstellen, wie zum Beispiel beim Polynom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2+1} . Für die Vorgangsweise in diesen Fällen, sowie bei allgemeineren Differenzengleichungen sei auf die Literatur verwiesen. In den Wiederholungsaufgaben finden sich auch Beispiele für lineare Differenzengleichungen mit nichtkonstanten Koeffizienten.
Stochastische Prozesse
Wir haben nun dynamische Systeme sowohl in kontinuierlicher Zeit als auch in diskreter Zeit kennen gelernt. Sowohl für Differentialgleichungen als auch für Differenzengleichungen spricht man von sogenannten Anfangswertaufgaben. Sind zu einem bestimmten Zeitpunkt die Anfangsbedingungen festgelegt, so ist die Dynamik eindeutig vorherbestimmt (auch wenn die Berechnung in vielen Fällen äußerst schwierig bzw. nur näherungsweise möglich ist). In diesem abschließenden Kapitel betrachten wir – sehr oberflächlich! - dynamische Systeme, die sich qualitativ gänzlich anders verhalten. Bei stochastischen Prozessen wird das zeitliche Verhalten eines Systems von Zufällen bestimmt, die eine eindeutige Vorhersage verunmöglichen. Selbst, wenn man zu einem bestimmten Zeitpunkt alles über ein System wüsste, so könnte man für die Zukunft nur prognostizieren, mit welcher Wahrscheinlichkeit das System jeden der möglichen Zustände annimmt. Wir werden nur den einfachen Fall besprechen, dass ein System endlich viele Zustände annehmen kann. Stochastische Prozesse mit überabzählbar unendlichem Wertebereich sind in der modernen Finanzmathematik von immenser Bedeutung, würden aber den Rahmen dieses Lehrtextes bei weitem sprengen! Beginnen wir mit einem Beispiel. Angenommen ein System kann 3 verschiedene Zustände annehmen. Wenn es sich in Zustand 1 befindet, so kann es entweder dortbleiben, oder sich mit einer gewissen Wahrscheinlichkeit im nächsten Zeitschritt in Zustand 2 oder Zustand 3 begeben.
In der Abbildung sehen wir den Verlauf eines zufälligen Prozesses, der zwischen den Zuständen 1, 2 und 3 wechselt. Die Folge der ersten 20 Zustände lautet
2 1 3 1 3 3 3 3 2 2 1 2 1 3 3 2 3 1 2 3
Wir haben also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1= 2, y_2= 1}
, usw. Im Gegensatz zu den Lösungen der Differenzengleichungen aus dem vorigen Abschnitt gibt es hier keine Gesetzmäßigkeit, die angibt, wie die Folge sich fortsetzen wird. Im Gegenteil: die Folge ist vollständig zufällig. Sie wurde simuliert unter der Annahme, dass der Zustand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n}
des Prozesses zum Zeitpunkt n jeden der Werte 1, 2 und 3 mit gleicher Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p = 1/3}
annimmt, unabhängig davon, welche Zustände der Prozess an allen vorherigen Zeitpunkten annimmt. Im Vergleich zu den deterministischen Systemen des vorigen Abschnitts handelt sich also um das andere Extrem, wo keinerlei Vorhersage über die weitere Entwicklung des Prozesses aus seinem bisherigen Verlauf abgeleitet werden kann. Der folgende Abschnitt behandelt zufällige Prozesse, die etwas mehr innere Struktur besitzen können.
Markovketten
Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n} ein zufälliger Prozess der endlich viele Werte annehmen kann, d. h. für jedesFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} n\geq0\ \text{ gilt } y_n\in\left\{1,\ldots,k\right\} \end{aligned}}
wobei k die Anzahl der möglichen Zustände ist. Diese Werte werden zufällig angenommen, jedoch hängt die Wahrscheinlichkeit, mit der einen bestimmten Wert annimmt vom Zustand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n-1}} zum vorherigen Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n-1} ab – und zwar nur von diesem. Diese Markov-Eigenschaft lautet demgemäß:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=j \mid y_1=i_1, y_2=i_2, \ldots, y_{n-1}=i_{n-1}\right)=P\left(y_n=j \mid y_{n-1}=i_{n-1}\right)}
Die Wahrscheinlichkeit von einem Zustand in den Zustand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle j} zu gelangen bezeichnet man als ÜbergangswahrscheinlichkeitFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_{\mathrm{ij}}=P\left(y_n=j \mid y_{n-1}=i\right)}
Beachte die Reihenfolge der Indizes in der ÜbergangsmatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} P=\left(p_{\mathrm{ij}}\right) \end{aligned}}
In der i-ten Zeile und j-ten Spalte steht die Wahrscheinlichkeit vom Zustand i in den Zustand j zu gelangen. Im folgenden Beispiel werden die Übergangswahrscheinlichkeiten durch ein sogenanntes Markov-Diagramm veranschaulicht.
Beispiel 18:
Ein System kann 3 mögliche Zustände A, B und C annehmen. Die Übergangswahrscheinlichkeiten sind durch folgende Matrix gegeben:
Das entsprechende Markov-Diagramm hat folgende Gestalt:
In das Diagramm wurden nur die Übergangswahrscheinlichkeiten zwischen verschiedenen Zuständen eingetragen. Man könnte zusätzlich noch mit kleinen Schleifen für jeden Zustand die Übergangswahrscheinlichkeit in sich selbst eintragen. Dies wäre jedoch redundant, da sich diese Wahrscheinlichkeit aus den gegebenen Werten leicht berechnen lässt - das System nimmt zu jedem Zeitpunkt genau einen Zustand an, daher ist die Wahrscheinlichkeit, von einem Zustand in irgendeinen einen anderen Zustand zu gelangen, immer gleich 1. Diese Eigenschaft überträgt sich auf die Übergangsmatrizen, deren Zeilensummen immer grade 1 ergeben. Aus dem Diagramm erkennt man und und somit muss gelten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{\mathrm{AA}}=1-p_{\mathrm{AB}}-p_{\mathrm{AC}}=0\mathrm{.}2}
entsprechend dem Eintrag in der Matrix.
Nehmen wir an ein System befindet sich zum Zeitpunkt 0 in einem bestimmten Zustand i. Für deterministische Systeme erster Ordnung würde diese Information genügen, um den Zustand des Systems für seine gesamte Zukunft eindeutig vorherzusagen. Dies ist bei einem stochastischen Prozess nicht der Fall, aber unter Annahme der Markov-Eigenschaft kann man zumindest die Wahrscheinlichkeit berechnen, mit welcher sich das System zu einem späteren Zeitpunkt in einem bestimmten Zustand befinden wird.
Fortsetzung Beispiel 18:
Angenommen zum Zeitpunkt 0 befindet sich das System im Zustand A. Berechne die Wahrscheinlichkeit, dass sich das System zum Zeitpunkt 2 in einem bestimmten Zustand befindet. Identifiziere die Zustände A,B,C mit den Indices 1, 2 und 3. Aufgrund des Satzes von der totalen Wahrscheinlichkeit gilt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_2=j \mid y_0=1\right)=\sum_{i=1}^3 P\left(y_2=j \mid y_1=i\right) P\left(y_1=i \mid y_0=1\right)=\sum_{i=1}^3 p_{\mathrm{ij}} p_{1 i}}
Speziell:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &P\left(y_2=A \mid y_0=A\right)=p_{\mathrm{AA}} p_{\mathrm{AA}}+p_{\mathrm{AB}} p_{\mathrm{BA}}+p_{\mathrm{AC}} p_{\mathrm{CA}}=0.41 \\ &P\left(y_2=B \mid y_0=A\right)=p_{\mathrm{AA}} p_{\mathrm{AB}}+p_{\mathrm{AB}} p_{\mathrm{BB}}+p_{\mathrm{AC}} p_{\mathrm{CB}}=0.17 \\ &P\left(y_2=C \mid y_0=A\right)=p_{\mathrm{AAA}} p_{\mathrm{AC}}+p_{\mathrm{AB}} p_{\mathrm{BC}}+p_{\mathrm{AC}} p_{\mathrm{CC}}=0.42 \end{aligned}}
Beachte, dass die Berechnung vonFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_2=j \mid y_0=i\right)}
gerade auf das Element der i-ten Zeile und der j-ten Spalte der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle MatrixP^2} führt. Allgemein gilt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=j \mid y_0=i\right)=\left(P^n\right)_{\mathrm{ij}}}
Das heißt die Berechnung von Übergangswahrscheinlichkeiten für mehrere Zeitschritte erfolgt durch einfaches multiplizieren der Übergangsmatrix mit sich selbst. Am effizientesten berechnet man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P^n} mit Hilfe der Eigenwerte von P. Hat die Matrix k verschiedene reelle Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_i} , so lässt sich zeigen, dass der AnsatzFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=j \mid y_0=i\right)=\sum a_i \lambda_i^n}
verwendet werden kann. Für die ersten k Zeitpunkte ist die Berechnung der Überganswahrscheinlichkeiten oft sehr einfach (siehe Beispiel 18). Einsetzen in den Ansatz liefert ein System von k linearen Gleichungen mit k Variablen, durch dessen Lösung die Koeffizienten bestimmt werden können.
Aufgabe 16:
Gegeben sei die Übergangsmatrix einer MarkovketteFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} P=\left(\begin{matrix}0&1&0\\0&\frac{2}{3}&\frac{1}{3}\\\frac{1}{\mathrm{16}}&\frac{\mathrm{15}}{\mathrm{16}}&0\\\end{matrix}\right) \end{aligned}}
BerechneFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=1 \mid y_0=1\right)}
Für allgemeinere Eigenwertkonstellationen (komplexe Eigenwerte, mehrfache Eigenwerte) werden kompliziertere Ansätze verwendet um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P\left(y_n=j \mid y_0=i\right)} zu berechnen. Für Details sei auf die Literatur verwiesen. Die explizite Berechnung von Wahrscheinlichkeiten ist ein wesentlicher Aspekt bei der Modellierung von dynamischen Systemen mit Markovketten. Viele weitere interessante Probleme, wie die Berechnung von Absorptionswahrscheinlichkeiten und Absorptionszeiten, die Theorie der Random Walks, die Suche nach Gleichgewichtszuständen sowie das Langzeitverhalten von Markovketten können hier nicht erörtert werden. Es sei jedoch erwähnt, dass zur Bestimmung von diversen Wahrscheinlichkeiten die Techniken von Kapitel 3.2 eine große Rolle spielen. Aus mathematischer Sicht besteht also ein enger Zusammenhang zwischen Differenzengleichungen und Markovketten in diskreter Zeit. Für eine ausführliche Darstellung sei wiederum auf Norris (1997) verwiesen. Markovketten spielen in der mathematischen Modellierung eine große Rolle. Häufig finden sie Anwendung in komplexeren Modellen. Speziell seien hier die „Hidden Markov Models erwähnt, die ursprünglich als Modelle zur Spracherkennung entwickelt wurden , sich aber heute in immer mehr Gebieten großer Beliebtheit erfreuen - in letzter Zeit auch im Bereich Finance. Auch Markovketten in stetiger Zeit werden untersucht. Die wichtigsten Vertreter diese Klasse von Modellen sind die Poisson-Prozesse, die aus theoretischer und praktischer Sicht von fundamentaler Bedeutung sind. Typische Anwendungen betreffen die Wartezeit auf das Eintreten von bestimmten Ereignissen (Auftreten eines Defekts in einem Produktionsprozess, Anruf in einem Call-Center, etc.). Ebenfalls in diesen Rahmen, obwohl etwas komplizierter, fällt die Warteschlangentheorie, wo in stetiger Zeit zu einem zufälligen Zeitpunkt bestimmte Aufgaben anfallen, deren Abarbeitung selbst wiederum eine zufällige Zeitdauer in Anspruch nimmt. Für Details sei auch hier auf Norris (1997) verwiesen.
Zusammenfassung Wir haben in diesem Kapitel einige Aspekte von dynamischen Systemen besprochen. Speziell wurde die mathematische Modellierung von deterministischen Systemen in stetiger Zeit (Differentialgleichungen) und in diskreter Zeit (Differenzengleichungen) anhand von vergleichsweise einfachen Beispielen vorgestellt. Die Tatsache, dass alle hier besprochenen Gleichungen exakt lösbar waren soll nicht den Eindruck vermitteln, dass dies immer der Fall ist! Ganz im Gegenteil - der weitaus größte Teil der mathematischen Theorie von Differential- und Differenzengleichungen beschäftigt sich gerade mit der Situation, wo eine explizite Lösung nicht möglich ist. Numerische Methoden sind heute weit entwickelt, und falls überhaupt Lösungen existieren, so kann man häufig mit Hilfe von Computerberechnungen Näherungen zu finden. Zusätzlich wurde anhand von einfachsten Markovketten die Theorie der stochastischen Prozesse angerissen. Die stochastische Modellierung ist oft realistischer als ein deterministischer Ansatz, da nur in den seltensten Fällen alle Einflüsse auf ein System vollständig erfasst werden können. Allerdings wird auch die mathematische Analyse entsprechend schwieriger.
Wiederholungsaufgaben/Übungen
Aufgabe 1
Löse folgende Differentialgleichungen zur Anfangsbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^\prime\left(t\right)=\frac{x^2}{t^2} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^\prime\left(t\right)=\frac{t^2}{x^2} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^\prime\left(t\right)=t\mathrm{exp}\left(-x\right) }
Aufgabe 2
Gib die allgemeine Lösung folgender linearer Differentialgleichungen:
Aufgabe 3
Löse folgende linearen Differentialgleichungen zur Anfangsbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(0\right)=1}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^{\prime}(t)=5 x+7}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^\prime\left(t\right)=-\mathrm{tx}+e+\mathrm{p}\left(-\frac{t^2}{2}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^\prime\left(t\right)=x+t }
Aufgabe 4
Finde die allgemeine Lösung für folgende DifferenzengleichungenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(n+1\right)y_{n+1}-{\mathrm{ny}}_n=1 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (n+1)^2y_{n+1}-n^2y_n=1 }
Aufgabe 5
Finde die allgemeine Lösung für folgende Differenzengleichungen höherer OrdnungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{n+2}-2ay_{n+1}+a^2y_n=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2y_{n+3}-\mathrm{12}yn+2+27yn+1-17yn=0 }
Aufgabe 6
Eine Markovkette kann zwei mögliche Zustände (1 und 2) annehmen. Die Wahrscheinlichkeit in einem Zeitschritt von 1 nach 2 zu gelangen sei gegeben durch
Entsprechend sei
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=1 \mid y_{n-1}=2\right)=\beta .}
Bestimme die Übergansmatrix, zeichne das Markov-Diagramm und berechne die Wahrscheinlichkeiten
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=1 \mid y_0=1\right)}
sowie
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_n=1 \mid y_0=2\right)}
Aufgabe 7
Es sei
das Maximum der ersten n Ausgänge einer Folge unabhängiger Würfelexperimente mit einem fairen Würfel. Ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n}
eine Markovkette?
Berechne die Übergangsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P}
.
Lösungen der Wiederholungsaufgaben
Aufgabe 1
a) Separation der Variablen liefert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=\frac{t}{(\mathrm{Ct}+1)} }
Anfangsbedingung liefert und insgesamt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=\frac{\mathrm{kt}}{(1-k)t+k}}
Beachte, dass für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle k>1}
die Lösung zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t = k/(k-1)}
unbeschränkt wird.
b) Separation der Variablen liefert . Anfangsbedingung liefert und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=\sqrt[3]{t^3+k^3-1}}
c) Separation der Variablen liefert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(t\right)=\mathrm{log}(\frac{t^2}{2}+C)}
Anfangsbedingung liefert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle C=\mathrm{exp}k-\frac{1}{2}}
und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(t\right)=\mathrm{log}(\frac{t^2-1}{2}+\mathrm{exp}(k))}
Aufgabe 2
Gib die allgemeine Lösung folgender linearer Differentialgleichungen:
a) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^\prime(t)=5x+7}
homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=\mathrm{exp}((t)}
Variation der Konstanten:
b) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^\prime(t)=\frac{x}{t}+t^2}
homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=\mathrm{ct} }
(durch Separation der Variablen) Variation der Konstanten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^\prime(t)=c+c^\prime t=c+t^2 \Rightarrow x(t)=\frac{t^3}{2}+\mathrm{ct}}
c) homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\left(t\right)=c\mathrm{exp}\left(-\frac{1}{t}\right)}
(Separation der Variablen) Variation der Konstanten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c^\prime=1 \Rightarrow x\left(t\right)=\left(t+c\right)\mathrm{exp}-\frac{1}{t}}
Aufgabe 3
Löse folgende linearen Differentialgleichungen zur Anfangsbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(0)=1}
a)
homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=c\mathrm{exp}(-\frac{t^2}{2})}
(Separation der Variablen)
Variation der Konstanten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c^\prime=t\mathrm{exp}(\frac{t^2}{2}) \Rightarrow x(t)=1+c\mathrm{exp}(-\frac{t^2}{2})}
Anfangsbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(0)=1 \Rightarrow x(t)=1}
b)
homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=c\mathrm{exp}(-\frac{t^2}{2})}
(Separation der Variablen)
Variation der Konstanten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c^\prime=1 \Rightarrow x(t)=(t+c)\mathrm{exp}(\frac{t^2}{2})}
Anfangsbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(0)=1 \Rightarrow x(t)=(t+1)\mathrm{exp}((\frac{t^2}{2})}
c)
homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(t)=c\mathrm{exp}(t) }
Variation der Konstanten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c^\prime=t\mathrm{exp}(-t) \Rightarrow x(t)=-(t+1)+c\mathrm{exp}(t)}
Anfangsbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x(0)=1 \Rightarrow x(t)=-(t+1)+2\mathrm{exp}(t)}
Aufgabe 4
a)
homogen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\frac{1}{n}}
Partikulärlösung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=1}
(jeweils durch erraten) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Rightarrow}
allgemeine Lösung:
b) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\frac{n+1}{n-1}y_n }
Es handelt sich um eine lineare homogene Gleichung, direkt in Rekursionsform. Nimm an, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1=c}
. Die ersten Folgenglieder haben die Gestalt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_2=3c, y_3=\frac{4\ast3}{2}c, y_4=\frac{5\ast4}{2}c,y_5=\frac{6\ast5}{2}c}
Und man zeigt (mittels vollständiger Induktion oder durch einfaches Einsetzen in die Rekursionsformel), dass die allgemeine Lösung die Gestalt
hat.
(Man hätte auch die Aufgabe (a) systematisch auf die Art lösen können)
c) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (n+1)^2y_{n+1}-n^2y_n=1}
Homogen durch Rekursion wie in (b): Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\frac{1}{n^2}}
Partikulärlösung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\frac{1}{n}}
(vergleiche mit (a)
Allgemeine Lösung:
Aufgabe 5
Finde die allgemeine Lösung für folgende Differenzengleichungen höherer Ordnung
a) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_{n+2}-2ay_{n+1}+a^2y_n=0 }
Das charakteristische Polynom liefert nur einen zweifachen Eigenwert, nämlich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=a\mathrm{.}}
Der Ansatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\lambda^n}
liefert daher nur eine Lösung, nämlich (nur ein Eigenwert) Als zweite Lösung erhält man bei zweifachen reellen Eigenwerten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n={\mathrm{na}}^n\mathrm{.}}
Die allgemeine Lösung ist daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=c_1a^n+c_2{\mathrm{na}}^n}
b) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2y_{n+3}-\mathrm{12}y_{n+2}+27y_{n+1}-17y_n=0}
Ansatz , erster Eigenwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_1=1}
leicht zu erraten. Abspalten von Linearfaktor und Lösung von quadratischer Gleichung liefert folgende Lösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_{2,3}=\frac{5}{2}\pm\sqrt{-\frac{9}{4}}=\frac{5}{2}\pm\frac{3}{2}i}
wobei wir vor dem Problem stehen, dass die beiden restlichen Eigenwerte nun nur als komplexe Zahlen existieren. Ohne hier auf nähere Details über komplexe Zahlen eingehen zu wollen sei nur erwähnt, dass mit dem hier eingeführten Symbol Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle i=\sqrt{-1}}
weitgehend normal gerechnet werden kann. Die beiden Eigenwerte und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_3}
sind zueinander konjugiert komplex, und man kann zeigen, dass sowohl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_2^n+\lambda_3^n}
als auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {i\lambda}_2^n-{i\lambda}_3^n}
jeweils reelle Lösungen der Differenzengleichung bestimmen. Die allgemeine reelle Lösung lautet daher wobei zur expliziten Bestimmung dieser Lösung das Rechnen mit komplexen Zahlen beherrscht werden muss.
Aufgabe 6
Übergangsmatrix:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{matrix}1-\alpha&\alpha\\\beta&1-\beta\\\end{matrix}\right) }
Eigenwerte der Übergangsmatrix:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_1=1,\lambda_2=1-\alpha-\beta}
Abgesehen von dem trivialen Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \alpha=\beta=0}
gibt es daher zwei unterschiedliche Eigenwerte, und wir verfolgen den Ansatz
Aufgabe 7
Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_i}
das Ergebnis des i-ten Wurfes, das heißt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P(x_i=1)=\mathrm{...}=(x_i=6)=\frac{1}{6}}
. Weiters ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n=\max \left(x_1, \ldots, x_n\right)}
. Zunächst gilt und daher . Wie sieht es mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_2}
aus? Es gibt zwei Möglichkeiten:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{x}_2>x_1 \Rightarrow y_2=x_2 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 \leq x_1 \quad \Rightarrow \quad y_2=x_1 }
Die Wahrscheinlichkeit von hängt also von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1}
ab, und zwar in der Form
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\left(y_2=j \mid y_1=i\right)= \begin{cases}0, & j<i \\ \frac{i}{6}, & j=i \\ \frac{1}{6}, & j>i\end{cases} }
Wie man sich leicht überlegt gilt dieser Zusammenhang nicht nur für n=2, sondern für beliebiges n, und daher ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_n} tatsächlich eine Markovkette. Die Übergangsmatrix hat die Form




















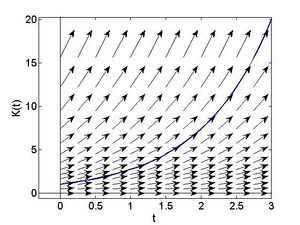


















![{\displaystyle {\begin{aligned}x^{\prime }(t)=\mathrm {rx} (t)[1-{\frac {x(t)}{K}}]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df768f9a00effe1c92febf8484905b09a9b994b7)





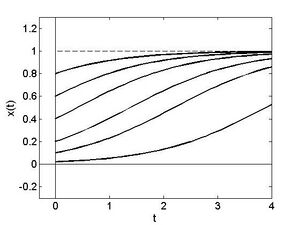












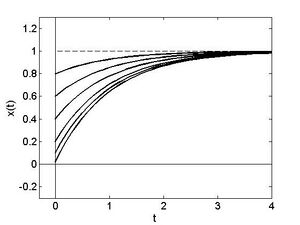
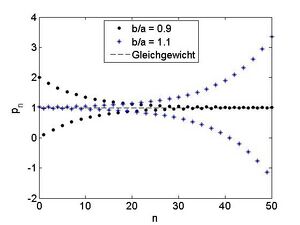
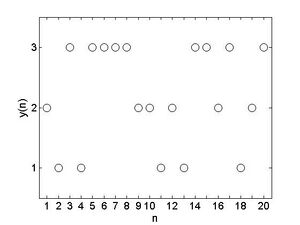



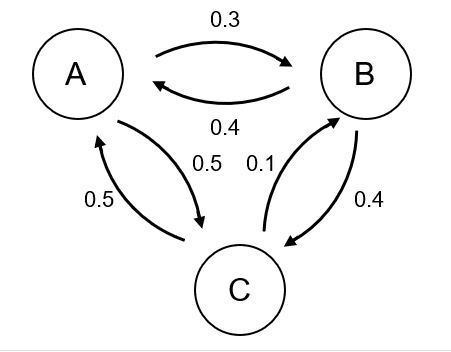









![{\textstyle x(t)={\sqrt[{3}]{t^{3}+3C}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4a5b1a675a6d870fcdd6fcbe40fcffde869f632)





















