Grundlagen der Modellierung - Einleitung

Einleitung

Modellierung und Modellierungssprachen sind ein essentieller Bestandteil der meisten Themenfelder der Wirtschafsinformatik. Die Modellierung bildet dabei einen existierenden, erwarteten oder geplanten Sachverhalt in Form eines Modells ab. Dabei handelt es sich um eine Darstellung, welche der betroffenen Zielgruppe und Zielsetzung angepasst wurde. In den nachfolgenden Lektionen werden der Modellbegriff und die ordnungsgemäße Modellierung, sowie die Grundlagen einzelner, in der Wirtschafsinformatik besonders relevanter, Modellierungsformen erläutert.

Der Modellbegriff

Bei einem Modell handelt es sich um eine vereinfachte Darstellung der Realität oder ihres Soll-Zustandes. Durch diese Abstraktion ist eine genauere Betrachtung oder Planung bestimmter Einzelaspekte möglich. Es betrachtet nur so viele Details wie nötig sind, um das zugrunde liegende Problem vollständig zu beschreiben. Der Begriff „Modell“ leitet sich aus dem lateinischen Wort „modulus“ ab und bezeichnete einen Maßstab im Bereich der Architektur. Laut dem deutschen Duden Fremdwörterbuch (2010), bedeutet Modell: Objekt, Gebilde, das die inneren Beziehungen und Funktionen von etwas abbildet bzw. [schematisch] veranschaulicht [und vereinfacht, idealisiert].

Für Wirtschaftsinformatiker und Wirtschaftsinformatikerinnen gehören Modelle und Modellierungstechniken zum unumgänglichen Handwerkszeug, insbesondere die Modelle, die in Informationssystemen abgebildet werden und jene, die wir in der Softwareentwicklung verwenden.

Modelle gibt es nicht nur in der Wirtschaftsinformatik, sondern auch in allen anderen Themenfeldern der Wissenschaft, Forschung und Entwicklung. So werden beispielsweise in der Wirtschaftsinformatik Datenmodelle verwendet und anatomische Modelle in der Medizin.

Die gängigen Modelle in der Wirtschaftsinformatik sind:

• Datenmodelle,
• Prozess- und Ablaufmodelle,
• Geschäftsprozessmodelle und
• objektorientierte Modelle.

Auf diese vier speziellen Modelle und ihre gängigsten Ausprägungen wird in den Lektionen Datenmodellierung bis Objektorientierte Modelle im Detail eingegangen.

Auch die Erstellung eines Test- oder Entwicklungssystems in der Software- und Systementwicklung ist ein (Soll-)Modell des Echtsystems. Meist hat es jedoch einen sehr geringen Abstrahierungsgrad, da es dem Echtsystem so nahe wie möglich kommen soll.

Die richtige Wahl eines Modells ist essentiell für den Erfolg der gewünschten Betrachtung, da es durch eine zu starke oder falsche Abstraktion der Darstellung auch zu fehlerhaften Annahmen und Resultaten führen kann.

Jedes Modell lässt sich selbst wiederum in einem Metamodell beschreiben, welches die Modellierung selbst definiert. Ein Metamodell definiert somit die einzelnen Bausteine eines Modells und wie sie anzuwenden sind.

Die drei Hauptmerkmale des allgemeinen Modellbegriffs nach Herbert Stachowiak, dem Begründer der allgemeinen Modelltheorie, sind (Stachowiak, 1973, S. 131ff):

• Abbildungsmerkmal: Modelle sind Abbildungen oder Repräsentationen natürlicher oder künstlicher Objekte, die selbst wiederum Modelle sein können. Es handelt sich dabei auch um die Zuordnung von Original-Attributen zu Modell-Attributen.
• Verkürzungsmerkmal: Modelle bestehen, in der Regel, nicht aus allen, sondern nur aus den relevanten, Attributen des betrachteten Objektes. Um die korrekten Attribute für ein Modell auszuwählen ist sowohl das Wissen über alle möglichen Attribute des Originalobjektes als auch über die Attribute des Modells notwendig.
• Pragmatisches Merkmal: Modelle sind nicht alleine einem Zweck, sondern auch einem bestimmten Anwenderkreis und Zeitraum zugeordnet. Eine pragmatisch vollständige Bestimmung des Modellbegriffs hat nicht nur die Frage zu berücksichtigen, wovon etwas Modell ist, sondern auch, für wen, wann und wozu bezüglich seiner je spezifischen Funktionen es Modell ist.

Ein Beispiel für ein einfaches Modell und seine Attribute ist das eines Smartphones:

Je nach Abstrahierungsgrad ändern sich die mögliche Darstellung und die relevanten Attribute. Eine mögliche Aufstellung der Attribute und Abbildungen unterschiedlicher Abstrahierungsgrade ist in der Tabelle "Einfaches Modell eines Smartphones" dargestellt.

Tabelle – Einfaches Modell eines Smartphones

Anwendungsfall:	Technischer Aufbau eines konkreten Smartphones	Abbildung eines konkreten Smartphones	Piktogramm für Smartphone
Attribute:	Gerätetyp Betriebssystem Hersteller Gehäuse Schrauben Kabel Platinen Speicher Anschlüsse …	Gerätetyp Betriebssystem Hersteller	Gerätetyp
Abbildung:

Modellbildung und Anforderungen an ein Modell

Bei der Modellbildung geht es um die ausreichende Abbildung eines realen Systems zur Beschreibung einer bestimmten Fragenstellung oder eines Zustandes. Dazu können entweder bestehende Modelle verwendet werden, oder ein eigenes, geeignetes, Metamodell geschaffen werden. Meist handelt es sich bei den gängigen Modellierungsaufgaben in der Wirtschaftsinformatik jedoch um Situationen, in denen bestehende Modellarten zur Anwendung kommen können und sollten. Die Verwendung eines weit verbreitenden, und im eigenen Fachbereich allgemein bekannten, Modells führt zu einem schnelleren Verständnis für alle beteiligten Personen.

Die Modellbildung lässt sich generell in vier Schritten beschreiben und durchführen (Oeser, 2012, S. 7):

• Schritt 1: Vereinfachung und Formulierung des Problems
• Schritt 2: Formalisierung und Quantifizierung des Problems
• Schritt 3: Verarbeitung des Datenmaterials und Erstellung des Modells
• Schritt 4: Interpretation und Rückschluss auf den ursprünglichen Sachverhalt

In Schritt 1 und 2 wird deutlich, dass die Anforderungen an ein Modell durch die Formulierung des zugrunde liegenden Problems definiert werden. Dieser Planungsschritt ist sehr wichtig, da die Modellauswahl für den weiteren Erfolg der Modellierung, und der damit verbundenen Behandlung der Problemstellung, essentiell ist.

Im 4. Schritt wird die Erfüllung der Zielsetzung des Modells nochmals überprüft und damit sichergestellt, dass es den Sachverhalt problemadäquat widerspiegelt.

Der Modellierer hat, durch seine Tätigkeit, eine hohe Verantwortung gegenüber der Zielsetzung des Modells. Durch eine zu hohe Abstrahierung kann es zu Fehlern in allen, anhand des Modells abgeleiteten, Folgerungen kommen. Diese Fehler wirken sich dann auf alle Bereiche aus, welche das Modell einsetzen. Wesentliche Fehler können in der Praxis auch sehr schlimme Folgen haben, wie das nachfolgende Beispiel beschreibt.

22.09.2006: 23 Menschen sterben in den Trümmern des Transrapid Bei dem schweren Transrapid-Unglück im emsländischen Lathen sind 23 Menschen getötet worden. Das teilte die Polizei am Freitag abend mit. Zehn Menschen sollen die Katastrophe verletzt überlebt haben. Der Transrapid war am Vormittag auf einen Reinigungswagen geprallt. Der Transrapid nutzt eine neue Antriebsform und ein spezielles Leitsystem mit einigen Sicherheitsmaßnahmen. Der Zug wird durch Magnete in der Schiene bewegt. Weiter umgreift das Fahrwerk des Zuges die Schiene und haltet ihn in Position, was wiederum ein entgleisen verhindert. Zusätzlich ist jeder Zug mit einem Ortungssystem ausgestattet, welches seine Daten kontinuierlich mit dem Leitsystem der Streckenanlage abgleicht. Ein Zusammenstoß zweier Züge ist daher, zumindest dem Modell nach, durch die zentrale Steuerung des Streckenantriebs und die Positionsbestimmung nicht möglich. Das System galt daher als enorm sicher. Leider gab es in diesem Modell eine Komponente, welche nicht beachtet wurde. Die Streckenfahrzeuge und Reinigungswagen sind mit herkömmlichen Dieselantrieben ausgestattet und verfügten über keine Ortungssysteme. Daher war es auch möglich, dass ein Reinigungsfahrzeug übersehen wurde und in dessen Folge 23 Menschen starben.

Die Grundsätze ordnungsmäßiger Modellierung (GoM)

Bei den Grundsätzen ordnungsgemäßer Modellierung (GoM) handelt es sich um semantische Empfehlungen zur bedarfsgerechten Informationsmodellierung. Damit wurde eine bewusste Einschränkung der Modellierungsfreiheit, zugunsten der Zielgerichtetheit der Modellierung selbst, eingeführt. Dies soll wiederum die Modellqualität erhöhen. Die GoM wurden von Becker, Rosemann und Schütte, in Anlehnung an den Grundsätzen ordnungsgemäßer Buchführung (GoB), entwickelt. (Becker, Rosemann, & Schütte, 1995, S. 437)

Die GoM definieren einen Ordnungsrahmen, bestehend aus sechs Grundsätzen, welchen wiederum ein Metamodell zugrunde liegt, in dem die einzelnen GoM Objekte, Attribute und ihre Beziehungen untereinander definiert werden (Becker, Rosemann, & Schütte, 1995, S. 437ff):

• Grundsatz der Richtigkeit,
• Grundsatz der Relevanz,
• Grundsatz der Wirtschaftlichkeit,
• Grundsatz der Klarheit,
• Grundsatz der Vergleichbarkeit und dem
• Grundsatz des systematischen Aufbaus.

Zusammengefasst sollen sie die Qualität von Informationsmodellen sicherstellen.

Grundsatz der Richtigkeit

Ein Modell kann sowohl semantisch, als auch syntaktisch richtig sein. Die syntaktische Richtigkeit bezieht sich dabei auf die korrekte Einhaltung der Vorgaben des Metamodells. Bei der semantischen Richtigkeit handelt es sich um die korrekte Abbildung des Modellierungsobjektes. Dies bedeutet nicht nur, dass das Modellierungsobjekt, dem Zweck entsprechend, vollständig abgebildet sein muss, sondern auch, dass es in sich keine Wiedersprüche aufweisen darf. Die Richtigkeit beinhaltet auch die eindeutige und korrekte Benennung von modellierten Objekten. Hierbei sollen Synonyme und Homonyme vermeiden werden.

Grundsatz der Relevanz

Bei der Modellierung müssen die mit ihr bezweckten Ziele eingehalten werden. Die in dem Modell enthaltenen Elemente und Beziehungen sind relevant, wenn das Modellierungsziel bei ihrer Reduzierung nicht mehr erfüllt werden würde. Das Modell muss sich wieder in eine Beschreibung des beschriebenen Objektes zurückführen lassen, ohne für die Betrachtung relevante Aspekte zu verlieren.

Grundsatz der Wirtschaftlichkeit

Der Grundsatz der Wirtschaftlichkeit limitiert die Tiefe und den Umfang eines Modells hinlänglich der, durch die Modellierung selbst, entstehenden Kosten. Es handelt sich dabei um eine Abwägung zwischen dem, durch die Modellierung entstehenden, Nutzen durch eine bessere Abbildbarkeit des zugrunde liegenden Problems und der Verbesserung der Interaktion zwischen den Modellnutzern und den Kosten, die durch die Modellierung entstehen. Je umfangreicher und tiefergehend ein Modell gebildet wird, desto mehr Aufwand muss in seine Erstellung investiert werden.

Grundsatz der Klarheit

Die Anwendbarkeit des Grundsatzes der Klarheit ist, ähnlich der Relevanz, stark von den Anwendern des Modells abhängig. So ist es nötig, die Darstellung eines Modells der Zielgruppe anzupassen. Analog zur syntaktischen Richtigkeit ist auch eine klare Darstellung des Modells essentiell. Dabei geht es insbesondere um die verwendeten Symbole auf Ebene des Metamodells, als auch um die Anordnung der Symbole innerhalb des Modells selbst. Dieser Grundsatz kann beispielsweise bedeuten, dass ein sehr komplexes Modell in weitere Abstrahierungsebenen geteilt werden muss, um für den Anwender verständlich zu bleiben. Hierfür werden meist die Möglichkeiten von Substitutionen und Detailmodellen geschaffen.

Grundsatz der Vergleichbarkeit

Ähnlich dem Grundsatz der Richtigkeit wird beim Grundsatz der Vergleichbarkeit in eine syntaktische und eine semantische Vergleichbarkeit unterschiedenen. Die beiden Grundsätze der Richtigkeit und Vergleichbarkeit lehnen sich dabei auch aneinander an. Bei der syntaktischen Vergleichbarkeit handelt es sich um eine Vergleichbarkeit unterschiedlicher Modelle, mit derselben zugrunde liegenden Modellierungsanforderung. Dadurch soll auch eine Überführung von Modellen mit unterschiedlichen Metamodellen ermöglicht werden. Die semantische Vergleichbarkeit bezieht sich auf die inhaltliche Vergleichbarkeit. Damit soll der Vergleich unterschiedlicher Modelle zueinander ermöglicht werden.

Grundsatz des systematischen Aufbaus

Bei in unterschiedlichen Sichten aufgebauten Modellen müssen die Sichten untereinander konsistent sein. Das bedeutet, dass die Bezüge der unterschiedlichen Sichten zueinander vorhanden sein müssen. So muss beispielsweise ein Ablaufmodell, welches auf ein Datenmodell referenziert, auch sicherstellen, dass das entsprechende Datenmodell entsprechend modelliert ist und umgekehrt. Um hierbei alle relevanten Sichten zu integrieren, liegen solchen Modellen übergreifende Architekturkonzepte zu Grunde.

Erweiterung der GoM

Die eingeführten Grundsätze ordnungsgemäßer Modellierung wurden von ihrem Mitbegründer Reinhard Schütte in Form der „neuen Grundsätze ordnungsgemäßer Modellierung“ überarbeitet. Diese erweiterten Grundsätze weichen von den herkömmlichen in einigen Teilen ab. Das Ziel der Überarbeitung war, die theoretische Begründung und die praktische Prüfbarkeit der Grundsätze zu verbessern.

Diese „neuen Grundsätze ordnungsgemäßer Modellierung“ sind (Schütte, 1997):

• Grundsatz der Konstruktionsadäquanz,
• Grundsatz der Sprachadäquanz,
• Grundsatz des systematischen Aufbaus,
• Grundsatz der Klarheit und der
• Grundsatz der Vergleichbarkeit.

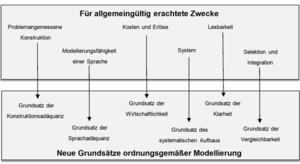
Die erweiterten Grundsätze selbst werden aus, als allgemeingültig erachteten, Zwecken abgeleitet, welche in Abbildung 1 dargestellt sind.

Zweckbezogene Ableitung der Grundsätze ordnungsmäßiger Modellierung (Schütte, 1997, S. 3)

Dabei unterscheiden sie sich primär in zwei Grundsätzen, von den ursprünglichen GoM:

• Grundsatz der Konstruktionsadäquanz und der
• Grundsatz der Sprachadäquanz.

Diese beiden sollten den Grundsatz der Richtigkeit und den Grundsatz der Relevanz ersetzen. Inhaltlich wurden jedoch auch bei den anderen Grundsätzen einige Ergänzungen durchgeführt.

Der Grundsatz der Konstruktionsadäquanz ist dabei als wichtigster Grundsatz definiert. Hierbei wird der Nutzen des Modells, für seinen jeweiligen Modellierungszweck, in den Vordergrund gestellt und der Konsens der Modellersteller herangezogen, da sie bewerten können, ob der Abstrahierungsgrad des Modells die Realität für die Aufgabenstellung angemessen abbildet. Es muss somit zwischen den Anwendern eine Einigkeit über die, ausreichend durch das Modell abgebildete, Problemstellung und die Art der gewählten Darstellung bestehen. Auch muss ein Konsens bezüglich einheitlicher Namenskonventionen herrschen. Ein inhaltlich identes Attribut oder Objekt muss auch in allen Modellen dieselbe Bezeichnung haben.

Der Grundsatz der Sprachadäquanz beschreibt dabei die Spracheignung und Sprachrichtigkeit in Relation zum Modellsystem. Die Spracheignung bezieht sich auf die Auswahl der geeigneten Modellierungstechnik für den jeweiligen Modellierungszweck. Die Sprachrichtigkeit bezieht sich dagegen auf die korrekte Anwendung der, im Metamodell definierten, Sprachsyntax.

Diese neuen GoM werden jedoch, im Gegensatz zu ihrer ursprünglichen Version, kaum angewendet, obwohl sie sich durch eine hohe theoretische Begründung und praktische Prüfbarkeit auszeichnen.