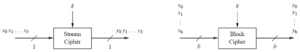Nachdruck – auch auszugsweise –, Weitergabe an Dritte und Benutzung für die Erteilung von Unterricht nur mit ausdrücklicher Zustimmung der Ferdinand Porsche Fernfachhochschule GmbH.

Es wird ausdrücklich erklärt, dass alle Angaben trotz sorgfältiger Bearbeitung ohne Gewähr erfolgen und eine Haftung des Autors/der Autorin oder des Verlegers/der Verlegerin ausgeschlossen ist.

Medieninhaberin (Verlegerin):

Ferdinand Porsche Fernfachhochschule GmbH

Ferdinand Porsche Ring 3

2700 Wiener Neustadt

Austria, Europe

Thomas Krabina

Thomas Krabina, geboren 1983, startete seine berufliche Laufbahn im Jahr 2003 als IT Freelancer neben einem Bachelor der Informatik an der TU-Wien. 2007 begann er in der Abteilung Informationstechologie und Service des Österreichischen Roten Kreuzes. Dort war er verantwortlich für den IT-Betrieb und entwickelte dort ¨auch die Security Maßnahmen weiter. 2009 wechselteer, aufgrund der besseren beruflichen Vereinbarkeit, von der TU-Wien auf ein berufsbegleitendes Bachelor Studium an der FH Technikum Wien, welches er 2011abschloss. Anschließend absolvierte er 2013 das Masterstudium Information Management and IT-Security ebenfalls an der FH Technikum Wien. Seit 2013 ist Thomas Krabina als Senior Security Consultant bei CoreTEC ITSecurity Solutions GmbH tätig, welche vollständig im ¨Bereich der Informationssicherheit und IT-Sicherheit tätig ist. Seine Schwerpunkte liegen dabei auf Firewall- und E-Mail Security Systemen, sowie der Multi-Faktor Authentifizierung. Bei CoreTEC leitet er auch die Managed Security Services.

Grundlagen der Kryptographie

Einleitung

Kryptographie ist an sich keine moderne Wissenschaft, sondern spielte schon in der Antike eine Rolle. Schon damals wurden vor allem im militärischen Bereich Nachrichten mit einfachen Methoden verschlüsselt. Mit Beginn des digitalen Zeitalters und durch starkes Vorantreiben durch militärische Organisationen entwickelte sich die Kryptographie zu einem der zentralen Themen in der heutigen Informationstechnologie.
Unter Kryptographie versteht man die Lehre der Methoden des Ver- und Entschlüsseln von Nachrichten . Als primäres Ziel gilt es, den Inhalt einer übertragenen Nachricht vor Dritten zu schützen. Die Kryptoanalyse beschäftigt sich hingegen mit der Entschlüsselung von Nachrichten ohne dabei Zugriff auf den verwendeten Schlüssel zu haben. Sie befasst sich somit mit dem Knacken von verschlüsseltem Text, der Aufdeckung von Schwachstellen und trägt somit dazu bei kryptographische Verfahren und Algorithmen sicherer zu machen. Kryptographie und Kryptoanalyse lassen sich zur Kryptologie zusammenfassen und sind eng miteinander verbunden. Ein weiterer Teilbereich der Kryptologie stellt die Steganografie dar. Diese zielt darauf ab eine geheime Nachricht zu verbergen. Sie teilt sich in die technische Steganographie, welche sich zum Beispiel mit verborgenen Copyright-Informationen innerhalb von digitalen Medien beschäftigt, und der linguistischen Steganographie die Geheimschriften und Semagramme im Fokus hat. Auf den Teilbereich der Steganographie wird allerdings nicht weiter eingegangen.

Begriffserklärungen

Um Verschlüsselungsverfahren zu erklären, bedarf es zunächst einiger Begriffserklärungen und Definitionen. Diese richten sich primär nach dem von der Internet Engineering Task Force (IETF) publiziertem RFC 4949 (Internet Security Glossary, Version 2) . In Fachbüchern, wie auch im Internet, werden oft unterschiedliche Begriffe und Nomenklaturen verwendet. Auch unterscheiden sich manchmal die deutschen Übersetzungen der englischen Begriffe. In der nachfolgenden Arbeit, wird versucht auf unterschiedliche Nomenklaturen und Bedeutungen hinzuweisen, sowie die englischen Begriffe ebenfalls anzuführen.

Die originale Nachricht, die es verschlüsselt zu übermitteln gilt, wird als Klartext ${\textstyle P}$ (engl. Plaintext) bezeichnet. Im mathematischen Kontext wird die unverschlüsselte Nachricht auch als Message ${\textstyle M}$ tituliert. In Kapitel [hashing], geht es nicht direkt darum Daten zu verschlüsseln, sondern ein Abbild der Daten zu generieren, daher einen sogenannten Hashwert (engl. Message Digest) zu bilden. Die verschlüsselte Nachricht nennt man Geheimtext ${\textstyle C}$ (engl. Ciphertext). Plaintext und Ciphertext setzen sich aus Zeichen aus zwei endlichen Zeichenmengen, den sogenannten Alphabeten (engl. alphabets) zusammen. Daher existiert ein Klartext-Alphabet und ein Geheimtext-Alphabet.
Der Vorgang, welcher den Klartext in den Geheimtext überführt, wird als Verschlüsselung (engl. Encryption) bezeichnet. Der umgekehrte Vorgang, welcher wiederum Geheimtext lesbar macht, heißt Entschlüsselung (engl. Decryption). Der mathematische Vorgang welcher ${\textstyle M}$ in ${\textstyle C}$ umwandelt, wird als Verschlüsselungs-Funktion ${\textstyle E}$ (eng. Encryption Function) bezeichnet. Daher muss gelten ${\textstyle E(M)=C}$ . Die Entschlüsselungs-Funktion ${\textstyle D}$ (engl. Decrypt Function) wandelt wieder um C in M um, daher ${\textstyle D(C)=M}$ . Für einen Algorithmus muss also gelten ${\textstyle D(E(M))=M}$ , ansonsten könnte man den ursprünglichen Klartext nicht mehr herstellen.

Ver- und Entschlusselungsvorgang (nach [3])

Der geheime Schlüssel (engl. Secret Key) ist eine entscheidende Variable eines Ver- beziehungsweise Entschlüsselungs - Algorithmus. Im Speziellen bezeichnet man den Encryption Key als ${\textstyle K_{E}}$ und den Decryption Key als ${\textstyle K_{D}}$ . Bei manchen Verfahren, wie vor allem bei den symmetrischen Verfahren (siehe Kapitel [symmetrischeVerfahren]), stellt der Decryption Key sogleich den Encryption Key dar. Bei anderen Verfahren können sich die Schlüssel natürlich auch unterscheiden. Der sogenannte Schlüsselraum (eng. keyspace) beinhaltet alle möglichen zur Verfügung stehenden Schlüssel. Die verwendete Methode zur Ver- und Entschlüsselung wird als Chiffre (engl. Cipher) bezeichnet.

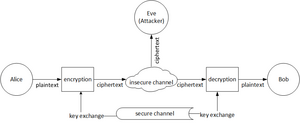
Alice, Bob und Eve

Um Protokolle und Verfahren zu erklären werden im Security Umfeld die fiktiven Personen Alice, Bob und Eve herangezogen . Im Normalfall wird Alice als jene Person beschrieben, von welcher ein Anfrage ausgeht beziehungsweise die eine Verbindung aufbaut. Bob ist die Person die auf diese Anfrage antwortet. Eve (von Eavesdropper) stellt die dritte Partei dar, welche Interesse an der Kommunikation von Alice und Bob hat. Sie stellt den Angreifer dar. Mit Hilfe dieser drei Personen werden in den nachfolgenden Kapiteln Sachverhalte dargestellt und Protokolle und Verfahren erklärt.

Kryptoanalyse

Die Kryptoanalyse befasst sich, wie schon bereits in Kapitel 1 erwähnt, mit Methoden um Informationen aus verschlüsselten Texten zu extrahieren. Angriffsszenarien gegen Verschlüsselungsmethoden liegen meist 4 grundlegenden Klassen zugrunde . Natürlich kann sich ein Angriff beziehungsweise eine Kryptoanalyse auch aus mehreren dieser Klassen zusammensetzen. Vorausgesetzt wird dabei das Kerckhoff’ sche Prinzip, welches in Kapitel [moderncrypto] vorgestellt wird.

Ciphertext-Only-Attack: Wird eine Attacke genannt, bei welcher der Angreifer oder Kryptoanalyst im Besitz eines oder mehrerer verschlüsselten Texte oder eines Auszuges davon ist. Die Beschaffung eines Ciphertexts ist in der Regel relativ leicht zu erhalten. Für einen erfolgreichen Angriff bedarf es allerdings einen großen Auszug des verschlüsselten Textes.
Known-Plaintext-Attack: Bei einer Known-Plaintext-Attack ist ein Angreifer sowohl im Besitz eines oder mehrerer Ciphertexte als auch des dazugehörigen Plaintextes.
Chosen-Plaintext-Attack: Bei der Chosen-Plaintext-Attack wird davon ausgegangen, dass sich der Angreifer zufällige Auszüge des Klartexte aussuchen kann, zu welchen er die entsprechenden verschlüsselten Texte erhält.
Chosen-Ciphertext-Attack: Im Gegensatz zu Chosen-Plaintext, kann sich der Angreifer hier verschlüsselte Auszüge des Textes aussuchen zu welchen er den Klartext erhält.

klassische Verschlüsselungsverfahren

Klassische Verschlüsselungsverfahren gelten heutzutage als nicht sicher. Dennoch sind sie hilfreich um die grundlegenden Attribute und Eigenschaften eines kryptographischen Systems darzustellen. Sie lassen sich in zwei Verfahren aufteilen, dem Substitutions-Verfahren und dem Transpositions-Verfahren. Bessere Verschlüsselungsverfahren kombinieren diese beiden Methoden miteinander und führen diese auch mehrmals hintereinander aus.

Substitutions-Verfahren

Beim Substitutions-Verfahren wird jedes Klartext-Zeichen durch ein Geheimtext-Zeichen ersetzt. Die Reihenfolge der einzelnen Zeichen bleibt dabei bestehen. In der klassischen Kryptographie gibt es vier Arten der Substitution :

monoalphabetische Substitution: Jedem Klartextzeichen wird genau ein Zeichen im Ciphertext zugeordnet. Das bekannteste Beispiel für eine monoalphabetische Substitution ist die Cäsar-Verschiebung, siehe dazu Kapitel 1.5.1.
homophone Substitution: Ein Zeichen im Klartext kann auf verschiedene Zeichen im Ciphertext abgebildet werden. Damit wird versucht Häufigkeitsverteilungen in der Sprache zu verschleiern. Häufig vorkommende Zeichen, wie zum Beispiel E und A, können jeweils einem anderen Zeichen im Ciphertext zugeordnet werden. Die homophone Substitution stellt somit eine Weiterentwicklung der monoalphabetischen Substitution dar.
polygraphische Substitution: Wie bei der homophonen Substitution wird versucht die Anfälligkeit für eine Häufigkeitsanalyse zu umgehen. Bei der polygraphischen Substitution werden allerdings gleich ganze Buchstabengruppen, sogenannte Polygramme, durch andere getauscht.
polyalphabetische Substitution: Wie der Name schon sagt, verwendet die polyalphabetische Substitution mehrere Geheimtext-Alphabete um den Klartext abzubilden. Das berühmteste Beispiel dafür ist die Viginière Verschlüsselung, siehe dazu Kapitel 1.5.3.

Cäsar-Verschiebung

Die Cäsar-Verschiebung (engl. Caesar Code) ist auch als Cäsar-Verschlüsselung oder als Cäsar-Chiffre bekannt. Er wurde von Julius Cäsar zur Verschlüsselung militärischer Nachrichten verwendet. Der Cäsar-Code gilt als einer der am Einfachsten zu knackenden Algorithmen. Trotzdem war er damals sehr wirksam, da ein Großteil der Bevölkerung nicht lesen und schreiben konnte.
Der Algorithmus basiert darauf, dass jeder Buchstabe um eine bestimmte Anzahl an Stellen im Alphabet zyklisch verschoben wird. Eine zyklische Verschiebung bedeutet an dieser Stelle, dass nach dem letzten Buchstaben im Alphabet wieder mit dem Ersten begonnen wird. Cäsar selbst verwendete eine Verschiebung um 3 Stellen.

Cäsar-Verschiebung um 3 Zeichen
plaintext	A	B	C	D	E	F	..	U	V	W	X	Y	Z
ciphertext	D	E	F	G	H	I	..	X	Y	Z	A	B	C

Der Cäsar-Code basiert auf einem einzigen festgesetzten Alphabet (monoalphabetisch). Jedes Zeichen des Klartext-Alphabets wird genau auf ein Zeichen im Geheimtext-Alphabet abgebildet (bijektiv). Somit wird jedes Zeichen mit einer Permutation von sich selbst ausgetauscht. Dies wird als einfache Substitution bezeichnet. Der Cäsar-Code ist somit eine monoalphabetische Substitution.

Ein mathematische Darstellung des Cäsar-Codes lässt sich wie folgt darstellen . Beachtet man Groß- und Kleinschreibung, sowie Sonderzeichen und Leerzeichen nicht, handelt es sich beim Cäsar-Code um ein Alphabet mit Länge 26, den Buchstaben von A bis Z. Die Buchstaben (A bis Z) werden durch ihre entsprechenden Stellen im Alphabet (0 bis 25) beschrieben. Da das Geheimtext-Alphabet ebenfalls aus den Buchstaben A bis Z besteht ist das Klartext-Alphabet ${\textstyle A_{1}}$ mit dem Geheimtext-Alphabet ${\textstyle A_{2}}$ ident. Daher ${\textstyle A_{1}=A_{2}=\{0,1,..,25\}}$ . Der geheime Schlüssel stellt die Anzahl der Verschiebungen dar. Der Decryption Key ${\textstyle K_{D}}$ und auch der Encryption Key ${\textstyle K_{E}}$ kann daher nur einen Wert innerhalb der Alphabete annehmen, daher ${\textstyle K_{D}=K_{E}=\{1,..,26\}}$ . Das Verfahren zur Verschlüsselung kann daher als Addition mit Modulo dargestellt werden. So sei ${\textstyle x}$ ein Klartext-Buchstabe, ${\textstyle y}$ ein Geheimtext-Buchstabe und ${\textstyle K_{E}}$ der Encryption Key beziehungsweise ${\textstyle K_{D}}$ der Decryption Key.

Encrypt:y=(x+K_{E})\mod 26

Eine Verschiebung ist einfach wieder rückgängig zu machen durch das umgekehrte Verfahren.

Decrypt:x=(y-K_{D})\mod 26

Um einen Ciphertext, der mit Cäsar-Code verschlüsselt wurde, zu knacken, ist natürlich die einfachste Variante alle verfügbaren Möglichkeiten zu probieren. In unserem Alphabet ist dies noch Recht überschaubar mit 26 möglichen Lösungen. Allerdings lässt auch ein Ausprobierenmöglicherweise Interpretationsspielraum besonders bei kurzen Nachrichten zu. So kann ein Ciphertext in mehrere mögliche Klartext-Nachrichten übersetzt werden.

Beispiel möglicher Klartexte einer Cäsar-Verschiebung
ciphertext	D	S	P
shift by 2	F	U	R
shift by 8	L	A	X
shift by 15	S	H	E

Die möglichen Lösungen machen für Außenstehende wenig Sinn, allerdings können auf diesem Weg zum Beispiel Codeworte übermittelt werden.

Ein besondere Form des Cäsar-Code wird sogar heute noch eingesetzt. ROT13 (Rotate by 13) stammt ursprünglich aus dem Usenet und wird dazu verwendet um Texte zu verschleiern beziehungsweise unlesbar zu machen, zum Beispiel für obszöne Witze oder sogenannten Spoilern. ROT13 verwendet eine Cäsar Verschiebung um 13 Stellen. Die Verwendung von 13 Stellen hat die Eigenschaft, dass eine Ver- beziehungsweise Entschlüsselung genau ident verläuft. Bei einer zweimaligen Verschlüsselung findet eine doppelte Verschiebung um 13 Stellen statt. In einem Alphabet mit 26 Buchstaben bringt dies wiederum den Klartextbuchstaben zum Vorschein. Zudem existieren weitere Versionen von ROT, bei welchen Sonderzeichen oder Zahlen miteinbezogen werden.

einfache Substitution

Eine einfache Substitution (engl. Simple Substitution) ersetzt einen Buchstaben des Klartext-Alphabets mit einer Permutation von sich selbst. Ein Buchstabe wird somit mit dem Buchstaben des Substitutions-Alphabets, dass an derselben Stelle steht, ersetzt. Ein Beispiel dafür ist in Tabelle [table: substitution] ersichtlich.

Ein Ausprobieren, wie beim Cäsar-Code, ist diesmal nicht so einfach möglich, da ${\textstyle 26!}$ Möglichkeiten bestehen um alle Permutationen abzudecken. Die einfache Substitution ist noch immer monoalphabetisch und basiert daher auf einem einzigen festgelegten Alphabet. Jeder Buchstabe für sich selbst verschlüsselt. Aus diesem Grund ist es möglich einen Ciphertext anhand statistischer Angriffe zu entschlüsseln . Die Buchstaben natürlicher Sprachen weisen unterschiedliche Häufungs-Verteilungen auf. Diese Häufungen können auf den Ciphertext umgelegt werden. Die Häufungen der deutschen Sprache sind in Tabelle [table: haeuffigkeiten] dargestellt.

Erforderlich für einen statistischen Angriff ist, dass der Klartext in einer natürlichen Sprache verfasst ist und ein genügend langer Ciphertext zur Verfügung steht, um die Buchstaben des Geheimtextes laut Statistik und Häufigkeitsverteilung einem Buchstaben im Klartextalphabet zuordnen zu können.
Um die Kryptoanalyse einer monoalphabetischen Verschlüsselung zu erschweren, können unterschiedliche Techniken angewendet werden. So wurden im ersten Weltkrieg Codebücher verwendet, um gebräuchliche Wörter mit einer Kunstsprache zu verschleiern. Außerdem wurden Homophone verwendet, sinnlose Zeichen eingefügt um Häufigkeiten zu verschleiern oder einem Klartextbuchstaben gleich eine Reihenfolge von Buchstaben zugeordnet.

Viginière-Verschlüsselung

Die Vigenière-Verschlüsselung ist eine polyalphabetische Verschlüsselung. Ein Buchstabe wird dabei nicht immer auf denselben Geheimtextbuchstaben abgebildet. Als Schlüssel wird ein Schlüsselwort gewählt, welches wiederholend über den Klartext gelegt wird . Im Beispiel der Tabelle 1.3 wird als Secret Key "BLAU" verwendet, welcher sich immer wiederholt.

Beispiel einer Vigenère-Verschlüsselung
plaintext	D	A	S	I	S	T	G	E	H	E	I	M
key	B	L	A	U	B	L	A	U	B	L	A	U
ciphertext	E	L	S	C	T	E	G	Y	I	P	I	G

Dies macht statistische Angriffe wie bei der einfachen Substitution in Kapitel 1.5.2 schwieriger aber nicht unmöglich. Der Knackpunkt der Vigenère-Verschlüsselung ist die Länge des eingesetzten Schlüssels. Es treten auch hier im Ciphertext Wiederholungen auf, welche auf die Länge des Schlüssels schließen lassen. Ist die Länge des Schlüssels wiederum bekannt, kann zur weiteren Kryptoanalyse ein statistischer Angriff erfolgen.
Theoretisch wäre die Vigenère-Verschlüsselung sicher, wenn die Länge des Keys gleich lang wie der Plaintext, nur einmalig verwendet wird und der Secret Key zufällig zusammengestellt ist. Somit gäbe es keine Wiederholungen und jeder Buchstabe wäre zufällig auf eine andere abgebildet. Dies wäre ein sogenanntes One Time Pad, siehe Kapitel 1.5.4. Dies ist natürlich nicht praktikabel, da bei einer Verschlüsselung von einem 1GB großen File, der Secret Key ebenfalls 1GB sein müsste und man unterschiedliche Keys jedes mal aufs Neue mit seinem Kommunikationspartner austauschen müsste.

One-Time Pad

Das One-Time Pad (OTP) ^[1] ist ein Theorem aus der Informationstheorie und wurde von Gilbert Vernam patentiert . Das OTP wird daher auch manchmal als Vernam Cipher bezeichnet. Ein One-Time Pad gilt als die perfekte Verschlüsselung da sie als beweisbar sicher gilt. Mehr zu beweisbarer Sicherheit ist in Kapitel [cryptoSec] zu finden.

OTP verwendet einen Secret Key, welcher gleich lang ist wie der Plaintext. Der Key wird nur einmal verwendet und ist durch einen echten Zahlenzufallsgenerator generiert (mehr zu Zufallsgeneratoren siehe Kapitel [moderncrypto]). Das OTP ist perfekt sicher. Das OTP kann nur durch Kenntnis des Secret Keys entschlüsselt werden. Diesen Secret Key zu erraten oder zu errechnen ist unmöglich, da jeder mögliche Schlüssel mit der selben Wahrscheinlichkeit auftreten kann. Leider ist ein OTP nicht praktikabel beziehungsweise durchführbar.

Transpositions-Verfahren

Bei der Transposition wird die Reihenfolge der Zeichen vertauscht, nicht aber die Zeichen selbst. Die Zeichen des Klartext bleiben somit an sich erhalten, sie werden nur an eine andere Stelle gesetzt. Somit bleibt auch die Anfälligkeit gegenüber Häufigkeitsanalysen bestehen. Die Sicherheit lässt sich etwas erhöhen, indem eine erneute Transposition durchgeführt wird.

Skytale

Das Skytale (oder auch Scytale) wurde ca. 500 vor Christus von den Spartanern entwickelt und verwendet um geheime Botschaften zu übermitteln . Das Skytale war ein einfacher Holzstab eines bestimmten Durchmessers. Um diesen Holzstab wurde ein Streifen Pergament gewickelt. Die Botschaft wurde längsseitig des Stabes auf das Pergament geschrieben und danach wieder abgewickelt. Um die Nachricht lesen zu können wurde daher ein Stab mit demselben Durchmesser benötigt. Der Durchmesser des Stabes stellt somit den Secret Key dar.

Skytale

Spaltentransposition

Bei der (einfachen) Spaltentransposition (engl. Simple Transposition) wird der Klartext in eine Tabelle eingetragen . Die Anzahl der Spalten wird durch die Länge des Schlüssels (oder der Keywords) bestimmt. Die Anzahl der Zeilen richtet sich nach der Länge des Klartextes.

Beispiel einer Spaltentransposition
2	4	5	1	3
D	A	S	T	R
E	F	F	E	N
F	I	N	D	E
T	A	M	F	R
E	I	T	A	G
S	T	A	T	T

Beispiel: Als Secret Key wird 2-4-5-1-3 verwendet. Der zu übertragende Klartext ist: "DASTREFFENFINDETAMFREITAGSTATT’. Die Anzahl der Spalten ist 5, da der Key die Länge 5 hat. Der Klartext wird nun, wie in 1.4 dargestellt in die Tabelle geschrieben:

Danach werden die Spalten aufgrund des Schlüssels in Blöcken dargestellt. Daher wird, wie in Tabelle 1.5 ersichtlich, bei Spalte 1 begonnen:

Auslesen der Spalten
ausgelesene Spalte	1	2	3	4	5
	TEDFAT	DEFTES	RNERGT	AFIAIT	SFNMTA

Um die Länge des Schlüssels nicht zu verraten können die Blöcke auch in Gruppen vorgegebener Länge eingeteilt werden. Die einfache Spaltentransposition kann durch die doppelte Spaltentransformation (engl. Double Transposition) erweitert werden. Hierzu wird der erhaltene Geheimtext erneut in eine neue Tabelle anderer Spaltengröße eingetragen.

Moderne Kryptographie

Mit moderner Kryptographie sind jene Methoden gemeint, welche nicht auf der Geheimhaltung des Verschlüsselungsverfahren beruhen um sicher zu sein. Sicherheit, welche durch Geheimhaltung der Funktionsweise erreicht wird, wird auch Security by Obscurity genannt. Im Gegensatz dazu steht das Kerckhoffs’sche Prinzip (engl. Kerckhoffs’ Maxime). Auguste Kerckhoff veröffentlichte im Jahr 1883 eine Arbeit über vertrauliche militärische Kommunikation (damals noch über Telegraphenleitungen), welche auch heute noch anwendbar sind. So besagt Kerckhoff’s zweite Regel:

The cipher method must not be required to be secret, and it must be able to fall into the hands of the enemy without inconvenience. ^[2]

Sinngemäß fordert diese Regel, dass die Sicherheit eines kryptographischen Systems nicht von der Geheimhaltung der Funktionsweise, sondern nur von der Geheimhaltung der verwendeten Schlüssel abhängen darf.

Es gibt immer wieder Diskussionen darüber ob Security by Obscurity einen validen Ansatz für ein sicheres kryptografisches System darstellt. Oft wird dies auch immer wieder so praktiziert. So konnte zum Beispiel die VoIP Software Skype aufgrund seines proprietären Protokolls und nicht zugänglichem Source Code lange seine Funktionsweise und Verschlüsselungsmethoden geheim halten. Durch Reverse Engineering gelang es aber die verwendeten Verschlüsselungsmethoden zu identifizieren. So wurde der VoIP Signaling Datenverkehr mittels einer abgewandelten RC4-Verschlüsselung versehen, die zum damaligen Zeitpunkt als nicht mehr sicher galt . Ein anderes Beispiel sind Mifare - Chipkarten, welche als kontaktloses Zahlungsmittel verwendet wurden und auf einem geheimen Algorithmus basierten. Nach Reverse-Engineering der Hardware wurden eklatante Sicherheitsmängel festgestellt .

Der bekannte Security Experte Bruce Schneier hat zum Thema Security by Obscuritybeziehungsweise Open Source / Closed Source auch folgende Argumentation:

"cryptography is hard to do right, and the only way to know if something was done right is to be able to examine it.. [..] .. Public algorithms are designed to be secure even though they are public; that’s how they’re made. So there’s no risk in making them public. If an algorithm is only secure if it remains secret, then it will only be secure until someone reverse-engineers and publishes the algorithms."

Security by Obscurity als Comic von [11]

Weitere Herausforderungen der Kryptographie sind zum einen das Mooresche Gesetz (engl. Moore’s Law) und zum anderen das Problem der Zufallsgeneratoren, mit welchem sich Kapitel 1.3 befasst. Das Mooersche Gesetz besagt, dass sich die Rechenkraft von Computern (je nach Quelle) alle 12 bis 24 Monate verdoppelt. Dies wirkt sich auch auf kryptographische Systeme aus . Werden beispielsweise heute noch Jahre für die Entschlüsselung eines Verfahrens benötigt, könnte man dafür in einigen Jahren nur noch kurze Zeit benötigen. Die Bit Anzahl für Verfahren müssen demnach regelmäßig erhöht werden beziehungsweise bessere Verfahren entwickelt werden, um weiterhin sicher zu sein.

Ziele und Anforderungen moderner Verfahren

Moderne kryptographische Systeme haben 4 fundamentale Ziele, die sie zu erreichen versuchen . Nicht jedes kryptographische System erreicht alle diese Ziele. Dies ist auch oft nicht notwendig, je nachdem für welchen Zweck das kryptographische System geschaffen wurde:

Vertraulichkeit (engl. Confidentiality): Die Information darf nur für berechtigten Personen zugänglich sein. Es soll sichergestellt sein, dass nur der die Nachricht empfangen und lesen kann, für den sie auch bestimmt war.
Integrität (engl. Integrity): Der Empfänger einer Nachricht muss feststellen können, ob die Nachricht nach der Erzeugung verändert worden ist. Somit muss die Nachricht vor Veränderungen geschützt sein. Beispiele hierfür sind die Integrität von Backups oder die Kommunikation von zwei Parteien.
Authentizität (engl. Authentication): Aus der Information oder Nachricht muss der Autor eindeutig hervorgehen. Dies muss für den Empfänger eindeutig nachprüfbar sein.
Nichtabbstreitbarkeit (engl. Non-repudiation): Wird auch als Verbindlichkeit bezeichnet. Der Autor einer Nachricht soll nicht abstreiten können, dass dieser auch die Nachricht verfasst hat. Dies ist vor allem wichtig beim Abschluss von elektronischen Verträgen. So soll für eine Nachricht weder der Versand für den Sender, noch der Erhalt für den Empfänger im Nachhinein bestreitbar sein.

Das Kapitel [Grundlagen] zeigte, dass klassische Verschlüsselungsverfahren wesentliche Nachteile aufweisen. So wird der Klartext zum einen nur zeichenweise in Ciphertext transformiert. Das Problem dabei ist, dass sich bei Änderung eines Klartextzeichens auch nur das entsprechende Zeichen im Ciphertext ändert, nicht aber der ganze oder zumindest ein Teil des Ciphertextes. Zweitens, sind klassische Verfahren durch Häufigkeitsverteilungen der Buchstaben und Worte vorhersagbar, auch wenn es Techniken gibt diese zu verschleiern. Aufgrund dieser Nachteile forderte Claude Shannon im Jahr 1949, dass ein guter Verschlüsselungsalgorithmus zwei grundlegende Eigenschaften erfüllen muss:

Diffusion: Jede noch so kleine Veränderung des Plaintext und / oder des Secret Keys sollen eine möglichst große Auswirkung auf den Ciphertext mit sich bringen. Damit verteilen sich die Redundanzen des Plaintexts über den Ciphertext.
Konfusion: Um eine Kryptoanalyse so schwer wie möglich zu machen, sollen Plaintext, Ciphertext und der Secret Key möglichst komplex sein um Zusammenhänge schwer erkennen zu können. Dies verkompliziert die Suche nach Redundanzen und statistischen Mustern im Ciphertext.

Moderne Verfahren erfüllen beide Eigenschaften. Diffusion und Konfusion werden dabei mehrmals hintereinander ausgeführt.

kryptographische Sicherheit

Eine absolute Sicherheit bietet nur das One-Time-Pad, welches in Kapitel [vernam] vorgestellt wurde. Das OTP bietet absolute Sicherheit, durch seine zwei grundlegenden Eigenschaften:

echte zufällig gewählte Schlüsselzeichen
der Schlüssel hat dieselbe Länge wie der Klartext

Dies allerdings nur, wenn das OTP nicht mehrmals verwendet wird und für jede Verschlüsselung ein neuer zufälliger Secret Key verwendet wird. Dann gilt das OTP als beweisbar sicher, da jeder mögliche Schlüssel mit der selben Wahrscheinlichkeit auftreten kann. Zur beweisbaren Sicherheit schreiben Paar und Pelzl:

A cryptosystem is unconditionally or information-theoretically secure if it cannot be broken even with infinite resources

Genau dies erfüllt das One-Time-Pad mit seinen Eigenschaften. Aber auch genau aufgrund dieser Eigenschaften ist es in der Praxis nicht tauglich. Stellen Sie sich vor Sie müssten ein 1GB größes File verschlüsseln. Hierzu müssten Sie einen Secret Key erzeugen und zum Empfänger bringen, der ebenfalls 1GB groß ist. Für jeden weiteren Empfänger müsste der Vorgang wiederholt werden. Somit ist das One-Time-Pad zwar perfekt sicher, aber untauglich in der Praxis. Es wird allerdings versucht sich diesen zwei Eigenschaften anzunähern.

Zufallszahlen

Zufallszahlen spielen eine große Rolle in der Kryptographie. Sei es beispielsweise ein Key Stream einer symmetrischen Chiffre (siehe Kapitel [symmetrischeVerfahren]) oder der Initialisierungsvektor eines Algorithmus. Leider sind Zufallszahlengeneratoren oft gar nicht so zufällig wie sie sein sollten und sehr einfach zu berechnen, da diese auch nur einem Algorithmus folgen. So schreibt Bruce Schneier folgende Erklärung:

"A computer can only be in a finite number of states (a large finite number, but a finite number nonetheless), and the stuff that comes out will always be a deterministic function of the stuff that went in and the computer’s current state. That means that any random-number generator on a computer (at least, on a finite-state machine) is, by definition, periodic. Anything that is periodic is, by definition, predictable. And if something is predictable, it can’t be random. A true random-number generator requires some random input; a computer can’t provide that."

Daher werden die meisten auf Software basierten Generatoren Pseudo - Zufallszahlen Generatoren (engl. Pseudo-Random Sequence Generator oder PRNG) genannt, welche eigentlich nur die Eigenschaft haben, dass sie zufällig aussehen. Sie erfüllen die Eigenschaft, dass die produzierten Zahlen statistisch gesehen zufällig sind. Für einen Angreifer beziehungsweise Kryptoanalysten stellen diese allerdings einen möglichen Angriffsvektor dar.

Ein kryptographisch sicherer Zufallszahlen - Generator (engl. Cryptographically Secure Pseudo-Random number generator oder CSPRNG) muss zudem die Anforderung erfüllen, dass die generierten Zahlen unvorhersagbar sind . Die erzeugten Zahlen dürfen nicht vorhersagbar sein, selbst wenn Algorithmus und/oder Hardware bekannt sind auf welcher sie generiert worden sind. Nur durch den initialen Seed ^[3] ist ein kryptographisch sicherer Zufallsgenerator kompromittierbar.

Ein echter Zufallszahlengenerator erfüllt noch eine dritte Eigenschaft. Die generierte Zahlenfolge kann nicht reproduziert werden . Wird unter gleichen Bedingungen und Startwerten eine weitere Folge an Zufallszahlen erzeugt, muss dieser eine komplett unabhängige zweite Zahlenfolge generieren. Natürlich ist es schwer zu sagen, was genau echter Zufall ist und was nicht. Zur Überprüfung von PRNGs existieren jedenfalls standardisierte Testverfahren.

Schlüsselmanagement

Der Secret Key ist einer der wichtigsten Bestandteile eins kryptographischen Verfahrens. Im Detail werden von einem Algorithmus allerdings noch andere Schlüssel benötigt, wie beispielsweise Rundenschlüssel oder Initialisierungsvektoren. Diese werden, wie in Kapitel 1.3 beschrieben, zumeist von einem Pseudo-Zufallszahlen Generator erzeugt . Je zufälliger Zahlen von einem Generator erzeugt werden, desto sicherer ist der Algorithmus. Beispielsweise verwendet /dev/random unter Linux zum einen Teil einen PRNG. Zum anderen Teil wird das Rauschen der Gerätetreiber addiert, um echte Zufallszahlen zu erhalten. Andere Möglichkeiten für die Schlüssel Generierung sind zum Beispiel die Messung der Zeitabstände von Tastaturanschlägen oder eine Analyse von Mausbewegungen. Meist wird eine Kombination mehrerer Komponenten, in welche zum Beispiel auch die aktuelle Systemzeit oder Teile der Hardware Identifikation mit einfließen, verwendet. Über teure und spezielle Hardware könnten Zufallszahlen auch über den radioaktiven Zerfall, Widerstandsrauschen oder Entladung von Kapazitäten generiert werden

Oft von Vorteil ist auch die Verwendung von kurzlebigen Schlüsseln, welche in regelmäßigen abständen erneuert werden müssen . Solche Schlüssel werden als Sitzungsschlüssel (engl. Session Keys) oder temporäre Schlüssel (engl. Ephemeral Keys) bezeichnet. Die Verwendung von zeitlich begrenzten Schlüsseln hat den Vorteil, dass bei Verlust eines Schlüssel nur ein begrenzter Teil des Ciphertextes betroffen ist.

Viele Protokolle und Verfahren erneuern in regelmäßigen Abständen den verwendeten Schlüssel. Dies ist am besten durch eine Einwegfunktion zu realisieren. Eine wichtige Anforderung für die Schlüsselerneuerung ist, dass der neue Secret Key nicht vom alten Key abhängen darf. Dies wird als perfekte Vorwärtssicherheit (engl. Perfect Forward Secrecy) (PFS) bezeichnet. Ansonsten wäre es bei Kompromittierung eines Secret Keys möglich, alle davor verwendeten Keys zu berechnen und damit die bisher stattgefundene Kommunikation zu entschlüsseln.

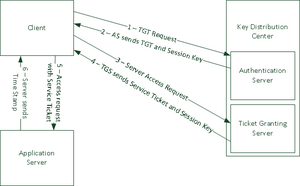
Um die generierten Schlüssel mit den Kommunikationsteilnehmern auszutauschen kann natürlich der Postweg verwendet werden, was in der Praxis natürlich nicht sehr praktisch ist. Vom Problem des sicheren Schlüssel Austausches sind vor allem symmetrische Verfahren betroffen. Um das Problem zu lösen, werden Schlüsselaustausch Protokolle verwendet, wie zum Beispiel das Diffie-Hellman Verfahren, welches in Kapitel [DH] vorgestellt wird. Verwendet ein Protokoll ein asymmetrisches Verfahren für den Austausch des Secret Keys, welcher dann in weiterer Folge für eine schnellere symmetrische Verschlüsselung verwendet wird, spricht man von einem hybriden Verfahren. Eine andere Möglichkeit um Schlüssel auszutauschen beziehungsweise zu Verwalten ist die Verwendung von zentralen Schlüsselservern (engl. Key Distribution Center) (KDC). Als Beispiel sei hier Kerberos angeführt, welches in Kapitel [Kerberos] beschrieben ist.

Angriffsvektoren

Bei kryptographischen Verfahren, gibt es natürlich auch immer Angriffspunkte, die für Kryptoanalysten beziehungsweise Angreifer besonders erfolgversprechend sind. Bei der klassischen Kryptoanalyse unterscheidet man einerseits zwischen einer vollständigen Schlüsselsuche, also dem Ausprobieren aller möglichen Schlüssel im Keyspace . Diese Methode ist besser bekannt als Brute-Force Angriff. Das Angriffsziel wird dabei als Blackbox betrachtet. Zweitens, werden analytische Angriffe verwendet. Diese betrachten die interne Struktur des Algorithmus um dessen Schwachstellen auszunutzen. Bekannte Angriffe sind zum Beispiel Side-Channel Attacks, also Seitenkanal Angriffe. Bei diesen wird anhand des Stromverbrauchs oder anhand der elektromagnetischen Abstrahlung und mit Hilfe der Signalverarbeitung versucht, den Schlüssel zu berechnen.
Eines der größten Risiken ist und bleibt immer der Mensch. Dies versuchen Angreifer durch Social Engineering Angriffe auszunutzen. Es wird versucht, unter Vortäuschung falscher Tatsachen und mittels der Gutgläubigkeit des Menschen, diesen geheime Informationen zu entlocken. Zu den klassischen Methoden des Social Engineering zählen Phishing oder Baiting. Unter Baiting wird das Platzieren von manipulierten Datenträgern verstanden, mit dem Ziel, dass Personen diese an ihren Computer öffnen.
Ein anderer Angriffsvektor sind sogenannte Protokollangriffe, die besonders bei RSA interessant sind. Bei Protokollangriffen werden Schwachstellen in der Implementierung des Verfahrens ausgenutzt. Beispielsweise, wenn die RSA Implementierung zu kleine oder zu nahe aneinander liegende Primzahlen verwendet und eine Berechnung der RSA Module ermöglicht, siehe dazu Kapitel [RSA]
Ein Angriff, der vor allem asymmetrische Verfahren trifft, ist die Man-in-the-Middle Attack. Die zu Grunde liegende Idee ist, dass ein Angreifer die öffentlichen Schlüssel von einem oder zwei Teilnehmern abfängt und gegen seine(n) eigenen tauscht. Dies ist möglich, wenn die Schlüssel nicht ausreichend geschützt sind. Als Gegenmaßnahme können die Public Keys mittels digitaler Signatur geschützt werden. Der Empfänger muss daher die Signatur auf Authentizität überprüfen bevor er den Public Key seines Kommunikationspartners verwendet.
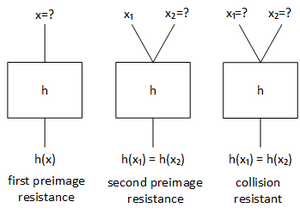
Bei Hash - Verfahren stellen Angriffe vor allem Kollisionsattacken und Urbild Angriffe (engl. Preimage Attacks) dar. Die Attacken zielen daher auf die Kollisionsresistenz des Algorithmus ab, siehe dazu Kapitel [collision-resistance]. Bei Kollisionsattacken (engl. Collision Attack) wird versucht zwei Dokumente zu finden, die denselben Hashwert bilden. Eine First Preimage Attack hingegen versucht zu einem vorgegebenen Hashwert eine Nachricht zu finden, die denselben Hashwert erzeugt. Eine Second Preimage Attack wiederum versucht zu einer gegebenen Nachricht eine zweite zu finden, die denselben Hashwert produziert. Der Vorteil den Kryptoanalysten beziehungsweise Angreifer auszunutzen zu versuchen ist das Geburtstagspradoxon aus Kapitel [geburtstagsparadoxon]. Solche Angriffe werden auch als Birthday - Attack bezeichnet.

Symmetrische Verfahren

Die wichtigste Eigenschaft eines symmetrischen Verfahrens ist, dass der Secret Key bei der Verschlüsselung gleich dem Key bei der Entschlüsselung ist, daher gilt ${\textstyle K_{E}=K_{D}}$ . Für die Entschlüsselung, benötigt der Empfänger den Secret Key des Absenders bzw. Erstellers. Daher muss der Schlüssel über einen sicheren Kanal zwischen Sender und Empfänger ausgetauscht werden.

Verschlusselung mittels symmetrischen Verfahren nach [6]

Symmetrische Algorithmen basieren auf einfachen Operationen wie Shifts oder Exclusive OR - Verknüpfungen (XOR) und sind somit dementsprechend schnell, da sie auch gut in Hard- und Software implementierbar sind. Sie treten entweder als Block- oder als Stromchiffren auf, die in den nachfolgenden Kapiteln 1.1 und 1.2 im Detail behandelt werden. Stromchiffren verschlüsseln jedes Bit des Plaintext Streams einzeln und kontinuierlich mit dem Key Stream. Blockchiffren hingegen verschlüsseln einen ganzen Block des Plaintextes mit dem Secret Key beziehungsweise einem Rundenschlüssel.

Unterschiede zwischen Stream- und Block Cipher aus [6]

Stromchiffren

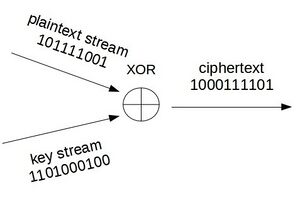
Bei Stromchiffren (engl. Stream Cipher) wird der Klartext als Stream kontinuierlich verschlüsselt. Das heißt, dass Klartext in der Größe von, zum Beispiel, 1-Bit, zeichenweise verschlüsselt wird. Der Klartext wird sequentiell abgearbeitet. Die Verschlüsselung geschieht anhand eines pseudozufälligen Bitstroms der mit dem Plaintext verknüpft wird (zum Beispiel durch XOR).

Funktionsweise einer Stream Cipher

Nach Verschlüsselung eines Zeichens kann dieses sofort an den Empfänger weitergeleitet werden. Daher eignen sich Stromchiffren auch sehr gut für Übertragungen die in Echtzeit ablaufen müssen, wie beispielsweise Telefonie.

RC4

Die RC4-Cipher (Ron’s Code 4) wurde im Jahr 1987 von Ronald Rivest, einem Mitarbeiter von RSA Data Security, entwickelt. Die Funktionsweise von RC4 wurde lange geheimgehalten. Aufgrund dessen konnte die Sicherheit von RC4 lange nicht geprüft werden. Um RC4 verwenden zu dürfen mussten auch Lizenzkosten an RSA gezahlt werden. 1994 fand der Algorithmus über eine anonyme Veröffentlichung in einer Mailingliste seinen Weg an die Öffentlichkeit. Um Streitigkeiten mit RSA zu vermeiden wurde der veröffentlichte Algorithmus ARCFOUR genannt. RC4 ist sehr einfach implementierbar und schnell. Sie erfreute sich hoher Beliebtheit und fand früher Anwendung im SSH, SSL beziehungsweise TLS und WEP Protokoll. Sie gilt aber mittlerweile als unsicher und von ihrer Verwendung wird abgeraten .

Funktionsweise:
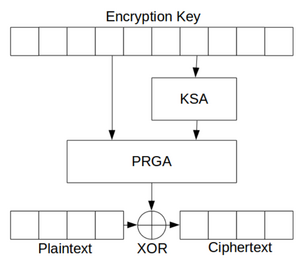
RC4 hat besteht aus zwei Elementen, dem Key - Scheduling Algorithm (KSA) und dem Pseudo Random Generation Algorithm (PRGA).

Schematische Darstellung der Funktionsweise von RC4

Der KSA befüllt ein Array von 0 bis 255. Anhand des Secret Keys mit variabler Länge (40 bis 256-Bit) wird dieses Array in eine pseudo-zufällige Reihenfolge gebracht. Dies geschieht anhand von Substitution, daher die Elemente innerhalb des Arrays werden untereinander vertauscht. Das Array wird auch als S-Box beziehungsweise Substitutions-Box bezeichnet. Ist die S-Box vollständig befüllt wird durch den PRGA eine weitere Substitution vorgenommen. Dabei werden die Elemente in der S-Box erneut mittels einem Array, das anhand des Secret Keys generiert wird, vertauscht. Als letzter Schritt wird der Cipherstream mit dem Plaintext bitweise XOR verknüpft.

Blockchiffren

Bei Blockchiffren (engl. Block Cipher) wird der Klartext vor der Verschlüsselung in Blöcke fester Größe eingeteilt. Typische Blockgrößen sind zum Beispiel 64-Bit, 128-Bit, etc. Die Größe des Blocks gibt der verwendete Algorithmus vor. Die Verschlüsselung findet dann blockweise und in mehreren Runden statt. Für eine Runde wird üblicherweise ein eigener Rundenschlüssel verwendet, um Konfusion zu erreichen. Außerdem wird innerhalb einer Runde eine Substitutions-Box (S-Box) verwendet. Dies erzeugt die gewünschte Diffusion. Der letzte Block wird dann mittels eines Füllmuster auf die entsprechende Blockgröße gefüllt. Dies wird als Padding bezeichnet. Der Paddingbereich wird durch eine definierte Bitfolge als solches gekennzeichnet, sonst gäbe es bei der Entschlüsselung Probleme. Blockchiffren können nur dann eingesetzt werden, wenn der gesamte Plaintext bereits vor der Verschlüsselung vorliegt. Anwendungsbereiche für Blockchiffren sind zum Beispiel Datei- oder E-Mail Verschlüsselung.

Betriebsmodi

Der Betriebsmodus (engl. Mode of Operation) gibt das Verfahren an, welches auf einen einzelnen Block angewendet wird. Die meisten der Betriebsmodi verwenden einen sich abwechselnden Initialisierungsvektor (IV) der in den Verschlüsselungsprozess einfließt . Damit wird sichergestellt, dass ein und der selbe Plaintext immer einen anderen Ciphertext ergibt.

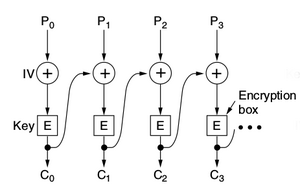
Electronic Code Book (ECB): Dies ist der einfachste Modus. Jeder Block wird auf dieselbe Art und Weise verschlüsselt. Daher ergibt ein und derselbe Plaintext auch immer den selben Ciphertext. ECB ist für die kryptographische Anwendung nicht empfohlen.
Cipher Block Chaining Mode (CBC): Bei CBC wird jeder Block der Reihe nach verschlüsselt. Vor der Verschlüsselung wird jedoch noch der Plaintext mit dem Ciphertext der letzten Runde XOR verknüpft. Für den ersten Block beziehungsweise die erste Runde wird ein Initialisierungsvektor verwendet. Dieser kann aus einem Zeitstempel oder einer zufälligen Zahlenfolge generiert werden.

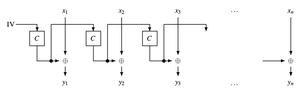
Verschlusselung mit Cipher Block Chaining Mode von [15] ¨
Output Feedback Mode (OFB): Beim OFB wird eine Blockchiffre dazu verwendet eine Stromchiffre zu erzeugen. Der Schlüsselstrom wird allerdings nicht Bit für Bit, sondern als Block generiert. Zu Beginn wird dafür ein Initialisierungsvektor mittels Blockchiffre verschlüsselt. Der Ausgabeblock dient als Stream und wird wieder als Eingangswert für die Blockchiffre verwendet (daher der Name Output Feedback). Der als Stream verwendete Block wird dann mit dem Plaintext XOR verknüpft.

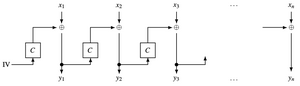
Verschlusselung mit Output Feedback Mode von [12]
Cipher-Feedback Mode (CFB): Der CFB ist wieder ein Betriebsmodus, welcher sich einer Blockchiffre zur Hilfe nimmt. Er ist sehr ähnlich dem OFB. Der wesentliche Unterschied ist, dass beim CFB der bereits verschlüsselte Block (daher der Name Cipher Feedback) als Eingabewert für den nächsten Block dient.

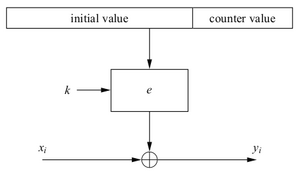
Verschlusselung mit Cipher Feedback Mode von [12]
Counter Mode (CTR): Der CTR Modus, verwendet wie OFB und CFB eine Blockcipher als Stromchiffre. Für die Berechnung des neuen Schlüsselstroms wird ein Zähler verwendet. Für die erste Runde dient wiederum ein Initialisierungsvektor.

Verschlusselung mit Counter Mode von [6] ¨
Galois Counter Mode (GCM): Der GCM hat neben seiner Verschlüsselungs - Funktion als Betriebsmodus auch die Möglichkeit einen MAC zu generieren (siehe Kapitel [MAC]). Mithilfe des MAC kann der Empfänger überprüfen, ob die Nachricht wirklich vom Absender stammt und ob die Nachricht manipuliert wurde. Mit anderen Worten, kann daher die Authentizität und die Integrität der Nachricht überprüft werden. Der GCM verschlüsselt die Daten nach dem Counter Mode (siehe oben). Anschließend wird der MAC berechnet. Dafür wird eine Blockgröße von 128-Bit verwendet. Somit könnte beispielsweise AES als AES-CGM verwendet werden. Der Berechnung des MAC liegt die Multiplikation im Galois Körper (endliche Körper) zugrunde.
Eine Variante von GCM wird als GMAC zur Berechnung von Hashwerten verwendet . Beim GMAC wird auf die Verschlüsselung verzichtet und nur der MAC berechnet. Durch die hohe Geschwindigkeit vom GMAC wird er oft in Bereichen eingesetzt in welchen eine schnelle Überprüfung der Datenintegrität zu gewährleisten ist, beispielsweise bei IPSec oder Fehlererkennungsverfahren.

Data Encryption Standard

Der Data Encryption Standard Algorithmus (DES) wurde in den 1970er Jahren von IBM, dem National Bureau of Standards (NBS) ^[4] und der NSA entwickelt . DES wurde nach seiner Veröffentlichung im Jahr 1977 zum Standard für alle US-Behörden erklärt. Durch die geringe Schlüssellänge von nur 56-Bit wurde vermutet, dass die NSA zu diesem Zeitpunkt bereits über ausreichend Rechenkapazität verfügte um DES durch einen Brute-Force Angriff zu entschlüsseln. Dazu müsste man alle möglichen ${\textstyle 2^{56}}$ (entspricht etwa 72 Billiarden) Schlüssel ausprobieren.

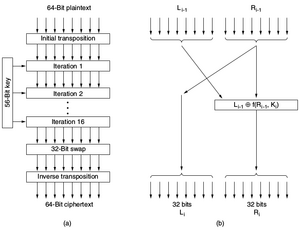
Generelle Ubersicht von DES (a) und Aufbau einer Runde (b) [ ¨ 15]

Funktionsweise:
DES arbeitet mit einer Blockgröße von 64-Bit. Allerdings wird jedes achte Bit als Paritätsbit verwendet. Als reale Blockgröße bleiben daher 56-Bit übrig. Der Algorithmus durchläuft insgesamt 16 Runden. Zuerst wird auf den gesamten 64-Bit Block wird eine initiale Substitution durchgeführt und anschließend der Block in zwei 32-Bit Hälfte aufgeteilt. Auf der rechten Hälfte wird die sogenannte Feistel-Funktion angewandt und anschließend mit der linken Hälfte XOR verknüpft. Das Ergebnis wird für die nächste Runde in der rechten Hälfte gespeichert. Die linke Hälfte der nächsten Runde beinhaltet die ursprüngliche rechte Hälfte. So werden alle 16 Runden durchlaufen. Nach der letzten Runde werden die beiden Hälften wieder zusammengeführt und eine finale Substitution durchgeführt. Im Jahr 1994 wurde eine theoretischer Angriff zu DES veröffentlicht, welcher auch 1998 praktisch durch Brute-Force nachgewiesen werden konnte . Dabei wurde DES in wenigen Stunden gebrochen.

3DES stellt eine Weiterentwicklung von DES dar. Bei 3DES wird DES dreimal, allerdings mit unterschiedlichen Schlüsseln durchgeführt.

Advanced Encryption Standard

DES wurde im Jahr 2001 durch den Advanced Encryption Standard (AES) durch die NIST abgelöst . Entwickelt wurde AES von den Belgiern Joan Daemon und Vincent Rijmen und wird deswegen auch als Rijndael-Cipher bezeichnet. Die Blockgrößen beziehungsweise Schlüssellängen bei AES sind variabel und voneinander unabhängig. Prinzipiell ist der Algorithmus so entworfen worden, dass die Blockgröße und die Schlüssellänge voneinander unabhängig die Werte 128, 160, 192, 224 oder 256-Bit annehmen können . Bei AES wurde die Blocklänge selbst wird auf 128-Bit beschränkt, die Schlüssellänge hingegen kann 128-, 192- oder 256-Bit lang sein.

Anzahl der Runden bei AES in Abhängigkeit von der Blockgröße ${\textstyle b}$ und der Schlüssellänge ${\textstyle k}$
rounds	b(128)	b(192)	b(256)
k(128)	10	12	14
k(192)	12	12	14
k(256)	14	14	14

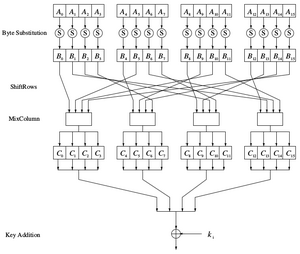
Funktionsweise:
AES basiert auf einem Prinzip, dass als Substitutions-Permutations-Netzwerk (SPN, engl. Substitution Permutation Network) bezeichnet wird . Zuerst werden die einzelnen Blöcke in zweidimensionale Tabellen mit 4 Zeilen geschrieben. Je nach Blockgröße variiert die Anzahl der Spalten von 4 (bei 128-Bit) und 8 (bei 256-Bit). In Runden werden nun Teile des Secret Keys mittels Transformationen auf den Klartextblock angewendet. Die Anzahl der Runden ist wiederum abhängig von der Schlüssellänge und der Blockgröße, siehe Tabelle 1.1. AES hat im Vergleich zu DES weniger Runden, da bei AES in jeder Runde die gesamte unterstützte Blockgröße von 128-Bit verschlüsselt wird. AES besteht aus 3 Schichten, die (mit Ausnahme der letzten, bei welcher MixColumns nicht durchgeführt wird) in jeder Runde angewendet werden.

Rundenfunktion von AES aus [6]

Die Schichten die pro Runde durchlaufen werden, sind folgende:

Key-Addition-Layer: Ein Rundenschlüssel mit 128-Bit wird mittels XOR auf die Daten angewendet. Der Rundenschlüssel wird aus dem Hauptschlüssel generiert.
Byte-Substitution-Layer: Hierbei handelt es sich um eine Substitutions-Box. Dabei wird jedes byte über eine nicht lineare Transformation durch ein anderes ersetzt. Es entsteht dadurch die gewünschte Konfusion.
Diffusion-Layer: Diese Schicht besteht aus zwei Elementen. Mittels ShiftRow werden die Daten permutiert. Mit MixColumn werden jeweils 4 bytes mittels einer Matrixoperation durchgewürfelt.

Asymmetrische Verfahren

Mitte der 1970er Jahre hatten Whitfield Diffie und Martin Hellman sowie Ralph Merkle unabhängig voneinander die Idee eines asymmetrischen Verfahrens beziehungsweise Public Key Systems . Das Prinzip beruht darauf, dass jeder Kommunikationspartner ein eigenes Schlüsselpaar besitzt, welches sich aus einem privaten und einem öffentlichen Schlüssel zusammensetzt. Der öffentliche Schlüssel kann natürlich öffentlich zugänglich gemacht werden. Der Plaintext wird vom Sender mit dem öffentlich zugänglichen Schlüssel des Empfängers verschlüsselt. Nur der Empfänger selbst ist mit seinem privaten Schlüssel in der Lage den Ciphertext wieder zu entschlüsseln. Die wesentlichen Vorteile und Nachteile von asymmetrischen Verfahren sind :

Es ist kein aufwendiger Schlüsselaustausch über unsichere Kanäle notwendig. Der öffentliche Schlüssel ist ohnehin nicht geheim. Es muss nur sichergestellt werden, dass der öffentliche Schlüssel auch nur jenem zuzuordnen ist, der auch im Besitz des privaten Schlüssels ist. Siehe dazu auch Kapitel [PGP].
Bei einem symmetrischen Verfahren musste mit jedem Kommunikationspartner ein eigener Schlüssel vereinbart beziehungsweise ausgetauscht werden. Mittels eines Public Key Verfahrens müssen keine geheimen Schlüssel verwaltet werden. Es ist ausreichend den öffentlichen Schlüssel des Kommunikationspartners zu kennen.
Asymmetrische Verfahren bieten eine relativ hohe Stufe der Sicherheit. Sie basieren auf einer sogenannten Falltür-Funktion. Diese sind in angemessener Zeit nicht invertierbar, außer man kennt den geheimen Schlüssel. Da es allerdings keinen mathematischen Beweis für Falltür-Funktionen gibt, wäre es aber in der Zukunft theoretisch möglich, dass ein schnelles Verfahren gefunden wird, welches eine Umkehrung ermöglicht.
Durch die Funktionsweise mit privaten und öffentlichen Schlüsseln bieten diese Verfahren auch die Möglichkeit für digitale Unterschriften beziehungsweise Signaturen, siehe dazu Kapitel [certificates].
Asymmetrische Verfahren sind durch den hohen Aufwand beim Ver- beziehungsweise Entschlüsseln im Gegensatz zu symmetrischen Verfahren sehr langsam. In der Praxis wird daher oft ein hybrider Ansatz gewählt. Der Schlüsselaustausch erfolgt asymmetrisch, die weitere Kommunikation wird symmetrisch verschlüsselt.

Diffie-Hellman Schlüsselaustausch

Der Diffie-Hellman Schlüsselaustausch (DH) (engl. Diffie Hellman Key Exchange, DHKE) ist ein Protokoll zum Austausch beziehungsweise zur Vereinbarung eines Secret Keys. Das Protokoll adressiert das Problem von symmetrischen Verfahren, dass zuerst ein gemeinsamer Schlüssel ausgetauscht werden muss, siehe Kapitel [symmetrischeVerfahren]. Mit dem DH - Verfahren ist es möglich einen Secret Key zwischen zwei Kommunikationspartnern über einen unsicheren Kanal hinweg auszutauschen. Das Verfahren wurde von 1976 von Diffie und Hellman veröffentlicht. Da auch Ralph Merkle Vorarbeit geleistet hat, wird es auch manchmal als Diffie-Hellman-Merkle Schlüsselaustausch (DHM) bezeichnet

Funktionsweise:
Der Diffie-Hellman Schlüsselaustausch verwendet eine Einweg-Funktion (ohne Falltür), welche auf dem diskreter Exponentialfunktion basiert. Für eine Umkehrung ist der diskrete Logarithmus notwendig, der dieses Problem allerdings nicht in polynomialer Laufzeit (und damit schnell genug) lösen könnte. Die Funktionsweise wird anhand eines Beispiels in Tabelle 1.1 erläutert.

Diffie-Hellman Schlüsselaustausch anhand eines Beispiels
	Alice und Bob haben gemeinsames Wissen über eine Primzahl ${\textstyle p=23}$
	und eine natürliche Zahl ${\textstyle g}$ , wobei ${\textstyle g<p}$ ist

	Alice	Bob

1.	Alice sucht sich eine geheime	Bob sucht sich eine geheime
	zufällige Zahl aus: ${\textstyle a=6}$	zufällige Zahl aus: ${\textstyle b=5}$

2.	Alice berechnet A:	Bob berechnet B:
	${\textstyle A=g^{a}\mod p}$	${\textstyle B=g^{b}\mod p}$
	${\textstyle A=11^{6}\mod 23=9}$	${\textstyle B=11^{5}\mod 23=5}$

3.	Alice übermittelt ${\textstyle A=9}$ an Bob	Bob übermittelt ${\textstyle B=5}$ an Alice

4.	Alice berechnet den secret key:	Bob berechnet den secret key:
	${\textstyle K=B^{a}\mod p}$	${\textstyle K=A^{b}\mod p}$
	${\textstyle K=5^{6}\mod 23=8}$	${\textstyle K=9^{5}\mod 23=8}$

RSA-Verfahren

Nachdem das Konzept zu asymmetrischen Verfahren von Whitfield Diffie und Martin Hellman beziehungsweise Ralph Merkle veröffentlicht wurde, wurde RSA als erstes Verfahren dazu entwickelt. Es wurde von Ronald Rivest, Adi Shamir und Leonard Adleman im Jahr 1978 publiziert. RSA ist mittlerweile defacto Standard und weit verbreitet.

RSA basiert auf dem Faktorisierungsproblem ^[5] großer natürlicher Zahlen. Es gilt als mathematisch sehr schwierig das Produkt zweier Primzahlen zu faktorisieren. Genau diese Tatsache macht man sich bei RSA zum Vorteil. Ein solches Problem wird auch als Einweg-Funktion mit Falltür oder Falltür-Funktion bezeichnet (engl. Trapdoor One Way Function). Um die Funktionsweise von RSA zu verstehen werden folgende mathematische Grundlagen benötigt:

Der Modulo Operator beziehungsweise das Rechnen mit Restklassen.
Die Eulersche ${\textstyle \varphi }$ - Funktion einer Zahl ${\textstyle N}$ , welche angibt wie viele natürliche es gibt die kleiner als ${\textstyle N}$ und teilerfremd zu ${\textstyle N}$ sind.
Der Satz von Euler - Fermat, welcher besagt, dass ${\textstyle a^{\varphi (N)}\equiv 1\mod N}$

Funktionsweise:
Die Funktionsweise wird anhand eines Beispiels mit kleinen Zahlen erklärt. Angenommen Bob will Alice eine Nachricht zukommen lassen, wird bei RSA vereinfacht wie folgt vorgegangen:

Alice wählt zwei Primzahlen ${\textstyle p}$ und ${\textstyle q}$ aus und ermittelt deren Produkt ${\textstyle n}$ :

$n=p*q$ Angenommen Alice wählt für ${\textstyle p=5}$ und für ${\textstyle q=13}$ aus, dann ist:
$n=5*13=65$

${\textstyle n}$ wird auch als RSA-Modul bezeichnet. In der Praxis verwendet man natürlich möglichst große und unterschiedliche Primzahlen.
Alice berechnet für ${\textstyle n}$ die Eulersche ${\textstyle \varphi }$ - Funktion mit der Formel:
$\varphi (n)=m=(p-1)*(q-1)$ $m=(5-1)*(13-1)=48$
Alice sucht sich nun eine zu ${\textstyle m}$ teilerfremde Zahl

Daher der größte gemeinsame Teiler ist 1
a aus, welche größer als 1 ist, daher ${\textstyle 1<a<m}$ . ${\textstyle a}$ wird auch als Verschlüsselungsexponent bezeichnet. In diesem Beispiel wählt Alice ${\textstyle a=7}$
Die Zahlen ${\textstyle n=65}$ und ${\textstyle a=7}$ stellen den öffentlichen Schlüssel von Alice dar. Diese kann sie nun Bob zur Verfügung stellen.
Bob möchte nun eine Nachricht an Alice schicken. Seine Nachricht ist eine Zahl kleiner als ${\textstyle n}$ , daher ${\textstyle x=19}$ .
Bob verschlüsselt seine Nachricht gemäß der Formel:
$y=x^{a}\mod n$ $y=19^{7}\mod 65$ $y=59$
Bob sendet seinen ciphertext ${\textstyle y=59}$ an Alice.
Alice berechnet mit Hilfe des erweiterten euklidischen Algorithmus das modulare Inverse, die Zahl ${\textstyle b}$ :
$b=a^{-1}\mod m$ $b=7^{-1}\mod 48$ $b=7$
Nun kann Alice die Nachricht von Bob mit dem Satz von Euler entschlüsseln:
$x=y^{b}\mod n$ $x=59^{7}\mod 65$ $x=19$

Kennt ein Angreifer nur den öffentlichen Schlüssel bestehend aus den Zahlen ${\textstyle n}$ und ${\textstyle a}$ , müsste dieser aus diesen zwei Zahlen den privaten Schlüssel errechnen. Das einzig bekannte Verfahren zurzeit ist die Primfaktorenzerlegung, mit welchem dies prinzipiell machbar wäre, allerdings nicht in angemessener Zeit. Zu beachten sind bei einer RSA Implementierung allerdings 2 Punkte:

die Wahl auf entsprechend große Primzahlen ${\textstyle p}$ und ${\textstyle q}$ .
${\textstyle p}$ und ${\textstyle q}$ sollen möglichst weit auseinander liegen. Eine sequentielle Suche nach Primzahlen kann auch bei hohen Primzahlen starten und rückwärts laufen. Ein klassischer Ausgangspunkt ist ${\textstyle {\sqrt[{}]{n}}}$ . Je näher sich die Zahlen ${\textstyle p}$ und ${\textstyle q}$ sind, desto näher befinden sie sich auch bei ${\textstyle {\sqrt[{}]{n}}}$ und desto kürzer wäre eine systematische Suche nach Primzahlen.

In der Praxis sollte auch sichergestellt werden, dass nach Generierung des RSA Moduls, die Variablen welche ${\textstyle p}$ und ${\textstyle q}$ enthalten, gelöscht werden. Sie werden in der weiteren Berechnung nicht mehr benötigt.

Für RSA beziehungsweise auch andere Verschlüsselungs-Verfahren, welche auf mathematischen Falltür-Funktionen basieren, ist zu beachten, dass es theoretisch auch Gefahren gibt. Zum einen könnte ein Algorithmus entwickelt werden, der ohne große Mühen das Problem der verwendeten Falltür-Funktion löst. Zum anderen auch technische Aspekte, wie die Entwicklung von Quantencomputern, für welche diese mathematischen Probleme wahrscheinlich weniger Aufwand bedeuten.

Elliptic Curve Cryptography

Im Bereich der Primfaktorenzerlegung wurden bessere und schnellere Verfahren entwickelt und auch die Hardware wurde schneller. So wurde klar, dass nach alternativen Falltür-Funktionen gesucht werden musste, falls eines Tages eine effiziente Umkehrfunktion gefunden wird. Im Jahr 1985 wurden von Victor Miller und Neil Koblitz unabhängig voneinander Elliptische Kurven über endlichen Körpern vorgeschlagen.

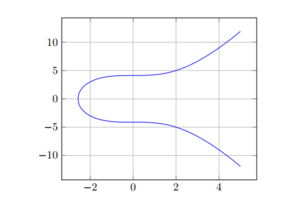
graphische Darstellung der elliptischen Kurve y2 = x3 + 17

Eine elliptische Kurve ist ein Menge an Punkten die eine spezielle mathematische Funktion erfüllen. Über diese Punkte lässt sich eine additive zyklische Gruppe bilden ^[6] . Innerhalb dieser Gruppe gelten bestimmte Rechenregeln. Die Verfahren aus dem diskreten Logarithmus lassen sich auf die Punkte einer elliptischen Kurve übertragen. Hier ist die nicht umkehrbare Funktion allerdings die Division eines Punktes.

Bei wesentlich kürzeren Operanden und Schlüsseln bietet ECC die gleiche Sicherheit wie bei Verfahren welche auf dem diskreten Logarithmus oder RSA beruhen . Als Vergleich, ein Verfahren mit 1024 bis 3072-Bit basierend auf dem diskreten Logarithmus oder RSA ist äquivalent mit ECC von 160 bis 256-Bit.

Vergleich des rechnerischen Aufwands von ECC, symmetrischen und asymmetrischen Verfahren aus [17]

Hash - Verfahren

Mit Hash - Verfahren ist es möglich die Integrität von Daten zu überprüfen . Eine große Anzahl an Eingabe - Zeichen (engl. Message) wird dabei auf eine fixe Anzahl an Ausgabe - Zeichen, dem Hashwert (engl. Message Digest) abgebildet. Daher ist eine Hash - Funktion eine nicht injektive Abbildung. Eine wichtige Voraussetzung ist, dass Hashwerte schnell und einfach zu berechnen sind, damit diese auch auf embedded devices lauffähig sind. Außerdem soll eine einige Änderung an einem Dokument eine größtmögliche Auswirkung auf den Hashwert haben, wie in Tabelle 1.1 ersichtlich.

Beispiel von zwei MD5 Hashwerten
Eingabe	md5sum
das ist ein test	babcdad51f89050112c127e206cddc3e
das ist ein test!	0c4fff19d6bd9dff8d43c8d113b80a1c

Anwendungsbereiche von Hash - Verfahren sind sehr vielfältig:

Überprüfung der Datenintegrität anhand eines Fingerabdrucks (sogenannte Prüfsummen)
Überprüfung der Authentizität des Datenursprungs
digitale Signaturen
digitale Zertifikate
Abbildung von Passwörtern
Such- und Zugriffsverfahren im Datenbankumfeld
Memory Adressierungs-Funktionen im Betriebssystem
Versionskontrollsysteme
Anti-Virus Signaturen, ..

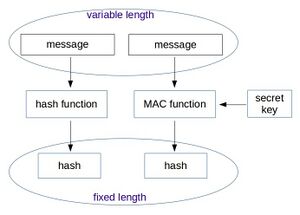
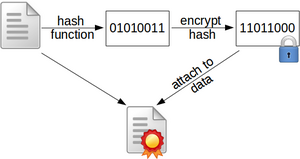
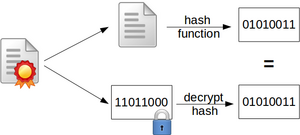
Hash - Verfahren können in zwei generelle Klassen unterteilt werden, siehe dazu auch Abbildung 1.1:

Schlüssellose Hash - Verfahren (engl. Hash Functions): Hierbei handelt es sich um jene Verfahren, welche rein die Überprüfung der Datenintegrität ermöglichen. Beispiele dafür sind in den nachfolgenden Kapitel 1.4 und 1.3 dargelegt.
Schlüsselabhängige Hash - Verfahren (engl. Message Authentication Codes beziehungsweise Keyed Hash Functions): Bei Message Authentication Codes (MAC) wird ein zusätzlicher Secret Key in den Algorithmus eingefügt. Damit ist es möglich neben der Integrität der Daten auch die Authentizität des Absenders zu überprüfen. Siehe dazu auch das Kapitel 1.5

Unterschiede zwischen Hash - Funktionen und Message Authentication Codes

Anforderungen an kryptographische Hash - Verfahren

Es muss zwischen herkömmlichenund kryptographischen Hash - Verfahren unterschieden werden. Herkömmliche Hash - Verfahren sind kryptographisch nicht sicher und werden in Anwendungsgebieten verwendet in denen diese Sicherheit auch nicht erforderlich ist. Diese sind zum Beispiel, CRC Überprüfungen (Cyclic Redundancy Check), Kompressionsfunktionen, Caches, Hash Tabellen, etc.. Hingegen haben kryptographische Hash - Verfahren folgende Anforderungen an die Sicherheit :

Es muss sich um eine Einweg - Funktion handeln. Daher muss es praktisch unmöglich sein, zu einem gegebenen Ausgabewert ${\textstyle y}$ einen Eingabewert ${\textstyle m}$ zu finden, welcher von der Hash-Funktion in ${\textstyle y}$ abgebildet wird, daher ${\textstyle h(m)=y}$ . Es darf daher kein ${\textstyle m'\neq m}$ mit ${\textstyle h(m')=h(m)}$ geben. Diese Anforderung wird auch als First Preimage Resistance (Urbildresistenz) bezeichnet und definiert die grundlegende Eigenschaft einer Einweg - Funktion.
Es muss praktisch unmöglich sein, für einen gegebenen Eingabewert ${\textstyle m}$ einen weiteren frei wählbaren Wert ${\textstyle m'}$ zu finden, welcher über den Hash - Algorithmus den selben Hashwert ergibt. Daher ${\textstyle h(m)=h(m')}$ mit ${\textstyle m\neq m'}$ . Diese Anforderung wird als Second Preimage Resistance oder auch als Weak Collision Resistance (schwach kollisionsresistent) bezeichnet.
Es muss praktisch unmöglich sein zwei verschiedene frei wählbare Eingabewerte ${\textstyle m}$ und ${\textstyle m'}$ mit ${\textstyle h(m)=h(m')}$ zu finden, welche den selben Hashwert ergeben. Hierbei würde es sich um ein Kollision zweier Eingabewerte handeln. Diese Anforderung wird daher als Collision Resistant (oder stark kollisionsresistent) bezeichnet

Als praktisch undurchführbar gilt ein Problem, wenn es kein bekanntes Verfahren gibt, das wesentlich schneller als das Durchprobieren aller Möglichkeiten ist.

Anforderungen an die Sicherheit von kryptographischen Hash - Funktionen nach [6]

Das Geburtstagsparadoxon

Das Geburtstagsparadoxon oder auch Geburtstagsproblem kommt oft in der Kryptoanalyse vor, da es einen Zusammenhang mit dem Finden von Kollisionen gibt . Die Frage die es zu beantworten gilt ist: Wie viele Personen müssen auf einer Geburtstagsparty anwesend sein, damit mit hoher Wahrscheinlichkeit (daher über 50 Prozent) mindestens zwei der Gäste am selben Tag Geburtstag haben?
Intuitiv würde man meinen, dass die Personenanzahl etwa die Hälfte von 365 möglichen Tagen (im Jahr) sein müsste. Jedenfalls über 100 Personen. Der Wahrscheinlichkeitsrechnung nach benötigt man allerdings viel weniger Personen, nämlich 23 . Dieses Paradoxon lässt sich auf das Finden von Kollisionen ummünzen. So ist es viel einfacher zwei Nachrichten zu finden, die denselben Hashwert ergeben, als beispielsweise zu einer gegeben Nachricht eine zweite mit demselben Hashwert zu finden. Ein Kryptoanalyst beziehungsweise Angreifer macht sich dieses Paradoxon zum Nutzen, da die Wahrscheinlichkeit höher ist eine Kollision zu finden. Er sucht daher eher nach zwei beliebigen Nachrichten, die denselben Hashwert erzeugen. Ein solcher Angriff wird als Birthday - Attack bezeichnet, ist generisch und kann auf jedes (schlüssellose) Hash - Verfahren angewendet werden.

Konstruktion von Hash - Funktionen

Kryptographisch sichere Hash - Algorithmen verwenden im Normalfall eine Folge von Kompressionsfunktionen, welche eine variable Zeichenfolge blockweise zu einem Hashwert umrechnet . Durch das Design des Kompressionsalgorithmus werden Hash - Verfahren in zwei Klassen unterteilt:

Hash - Funktionen welche als Basis symmetrische Blockchiffren verwenden: Dabei wird die Eingabefolge in Blöcke unterteilt welche dann in den Berechnungsschritten als Schlüssel verwendet werden. Der daraus resultierende Hashwert ist aber meist nur schwach kollisionsresistent. Mittels symmetrischer Blockchiffren lassen sich zwar auch stark kollisionsresistente Hash - Verfahren realisieren, allerdings setzt dies voraus, dass der Hashwert mindestens so groß wird, wie die doppelte Blockgröße. Deswegen werden großteils dezidierte Hashfunktionen verwendet.
dezidierte Hash - Funktionen: Diese Algorithmen wurden speziell für die Erzeugung von Hashwerten konstruiert und stehen in den nachfolgenden Kapiteln im Fokus. Das grundlegende Design von dezidierten Hash - Funktionen ist meist sehr ähnlich. Sie basieren auf den selben mathematischen Konstrukten, welche in Kapitel 1.2.1 und 1.2.2 näher betrachtet werden. Die Hash - Funktionen aus den Kapiteln 1.3 und 1.4 stammen aus dieser Klasse.

Merkle-Damgård Konstruktion

Viele Hash - Funktionen, wie MD4, MD5 und SHA-1, verwenden als Basis die sogenannte Merkle-Damgård Konstruktion (auch als Merkles Meta Methode bekannt). Sie wurde unabhängig voneinander von Ralph Merkle und Ivan Damgård entwickelt. Sie basiert auf einer Kompressionsfunktion ${\textstyle f}$ .

Funktionsweise der Merkle-Damgard Konstruktion ˚

Funktionsweise:

Die zu Eingabe Nachricht wird in gleich lange Blöcke ${\textstyle m_{1},m_{2},m_{3},..m_{n}}$ unterteilt. Der letzte Block wird mittels Padding aufgefüllt. Die Blöckgröße und in welcher Art und Weise das Padding konstruiert wird, sind Vorgabe des jeweiligen Hash - Verfahrens.
Die einzelnen ${\textstyle m_{i}}$ Blöcke werden nun nach der Reihe mit einer Kompressionsfunktion ${\textstyle f}$ abgearbeitet.
Die Funktion ${\textstyle f}$ verfügt über einen internen Zustand ${\textstyle x_{i-1}}$ des gerade behandelten Blocks ${\textstyle m_{i}}$ , welcher den Nachfolgezustand ${\textstyle x_{i}}$ des nächsten Blocks definiert, daher ${\textstyle x_{i}=f(x_{i-1},m_{i})}$ .
Die Funktion ${\textstyle f}$ und der initiale Zustand von ${\textstyle x_{0}}$ (in der Abbildung 1.3 als Initialisierungsvektor dargestellt) sind wiederum eine Konstruktionsvorgabe des jeweiligen Hash - Verfahrens und werden von diesem vorgegeben.
Der interne Zustand des letzten Blockes stellt den errechneten Hashwert dar.

Schwamm Konstruktion

Die Schwamm Konstruktion ist besser unter ihrem englischen Namen Sponge Construction bekannt. Sie ist der Merkle-Damgård Konstruktion ähnlich, verwendet aber anstelle einer Kompressionsfunktion eine Permutationsfunktion . Außerdem besitzt die Sponge Konstruktion keine fixe Ausgabegröße. Die Sponge Construction wurde von Guido Bertoni, Joan Daemen, Michaël Peeters und Gilles Van Assche im Zuge der SHA-3 Ausschreibung entwickelt, welche sie im Jahr 2012 auch gewinnen konnten . Siehe dazu auch Kapitel 1.4.3. Der Name Sponge resultiert aus den 2 Phasen, Absorb und Squeeze, welche durchlaufen werden.

Funktionsweise der Sponge Konstruktion aus [20]

Funktionsweise:

Die Sponge Konstruktion arbeitet mit einem internen Zustand ${\textstyle c}$ , der (Capacity). Dieser interne Zustand stellt den wichtigsten Sicherheitsparamter dar und wird nicht ausgegeben.
Über die Bitrate ${\textstyle r}$ erfolgt die Aus- und Eingabe des Schwammes. Sie stellt somit den äußeren Zustand dar. Die Bitrate ${\textstyle r}$ kommt nie direkt mit der Capacity ${\textstyle c}$ in Berührung.
Die Message wird zuerst in Blöcke mit Blockgröße ${\textstyle r}$ , der Bitrate, geteilt und auf den letzten Block ein Padding angehängt.
Die Absorbing Phase ist rundenbasiert und in dieser wird die Message eingelesen. In jeder Runde wird ein Block mit ${\textstyle r}$ Länge eingelesen und darauf eine Funktion ${\textstyle f}$ (eine Permutation mit XOR) angewendet. Das Ergebnis jeder Runde wird in den entsprechenden Capacity Bits ${\textstyle c}$ festgehalten.
Sind alle Blöcke abgearbeitet, wird mit der Phase Squeeze fortgesetzt. Blockweise werden die ersten ${\textstyle r}$ Bits mittels einer Funktion ${\textstyle f}$ verarbeitet und anschließend ausgegeben.

Message-Digest 5

MD5 wurde 1992 von Ronald Rivest als Nachfolger von MD4 entwickelt. MD5 war weit verbreitet bis Hans Dobbertin im Jahr 1996 eine Kollision in der Kompressionsfunktion von MD5 finden konnte . Die Hash - Funktion an sich war damit zwar nicht gebrochen, da sich die Kollision nur auf die Kompressionsfunktion bezog. Aber es entstanden Zweifel an der Sicherheit von MD5 und dessen Verwendung wurde fortan nicht mehr empfohlen. Im Jahr 2004 wurde dann eine vollständige Kollision nachgewiesen .
MD5 basiert auf der Merkle-Damgård Konstruktion und liefert einen 128-Bit Hashwert der folgendermaßen ermittelt wird :

Funktionsweise von MD5 aus [1]

Funktionsweise:

Die Eingabezeichen werden mittels Padding aufgefüllt bis ein Vielfaches von 512-Bit erreicht wird.
Danach werden Blöcke zu je 512-Bit gebildet, welche wiederum in 16 Stück 32-Bit Blöcke unterteilt werden. Daher jeder dieser Blöcke hat 32-Bit.
In 4 Runden werden die einzelnen Blöcke verarbeitet. In jeder dieser vier Runden wird einer der 32-Bit Blöcke durchlaufen. Somit ergeben sich pro Runde 16 Einzelschritte und insgesamt daher 64.
Die Runden selbst werden mit 4 fixen 32-Bit Variablen (A, B, C und D) initialisiert (die sogenannten Chaining Variables). Innerhalb einer Runde werden dann 16 Operationen auf die einzelnen Blöcke angewendet, welche sich pro Runde unterscheiden. Bei den Operationen handelt es sich um nicht-lineare Funktionen, modularer Addition und Linksrotation.
Das Ergebnis einer Runde dient als Eingabewert für die nächste Runde. Die Ergebnisse aller Runden ergeben dann den Hashwert.

Secure Hash Algorithm

Der Secure Hash Algorithm (auch als Secure Hash Standard bezeichnet) steht für eine Familie an Hash - Verfahren. SHA wurde 1993 von der National Security Agency (NSA) publiziert und als Federal Information Processing Standard (FIPS) von der NIST etabliert . Allerdings wurde kurz darauf, im Jahr 1995, bereits SHA-1 als Nachfolger, aufgrund einer Schwachstelle im SHA Algorithmus, präsentiert. SHA und SHA-1 unterscheiden sich hauptsächlich durch eine hinzugefügte Bit-Rotation in der Kompressions-Funktion. Der ursprüngliche SHA Algorithmus wurde fortan als SHA-0 bezeichnet.
SHA-2 wurde wieder von der NSA entwickelt, erstmals 2001 vorgestellt und 2002 zum neuen Standard erklärt. Die Unterschiede zu SHA-1 liegen vor allem in der Bitgröße des erzeugten Hashwertes. Mit SHA-2 wurden zudem mehrere Varianten eingeführt, welche unterschiedlich große Hashwerte erzeugen, siehe dazu Abbildung 1.4.2.

[[|Eigenschaften der SHA - Familie aus [24]]]

SHA-3 wurde nicht wie bei seinen Vorgängern von der NSA entwickelt. Die NIST entschloss sich aufgrund der Schwachstellen in SHA-1 zu einer öffentlichen Ausschreibung. 51 Algorithmen wurden dazu im Jahr 2008 eingereicht, von der NIST analysiert und bewertet. Im Jahr 2012 wurde der Algorithmus Keccak von Guido Bertoni, Joan Daemen, Michaël Peeters und Gilles Van Assche, welcher auf deren Sponge Konstruktion basiert, zum Sieger erklärt .

SHA-1

SHA-1 wurde im Jahr 1995 publiziert und gilt als Nachfolger von MD5. Wie MD5 zählt man auch SHA-1 zur Familie von MD4 Hash - Verfahren, da sich diese sehr ähneln (und nach der Merkle - Damgård Konstruktion arbeiten). Nachdem allerdings erste Zweifel an der Sicherheit von MD5 aufkamen, konkurrierten einige Zeit verschiedene Hash - Verfahren, wie Whirlepool, Tiger, RIPEMD-160 und SHA-1 miteinander. Im Jahr 2001 wurde SHA-1 jedoch durch den RFC 3174 als Internet Standard etabliert .

SHA-1 ähnelt in seiner Funktionsweise sehr MD5 beziehungsweise MD4. Beide basieren auch auf der Merkle-Damgård Konstruktion. SHA-1 erzeugt wie in Abbildung 1.6 ersichtlich einen 160-Bit Hashwert, im Gegensatz zu MD5, welcher nur 128-Bit Hashwerte erzeugt. Beide verwenden eine Blockgröße von 512-Bit. SHA-1 führt allerdings mehr Rundenoperationen durch als MD5. Anstelle von 64 Runden, werden bei SHA-1 80 Runden durchgeführt.

Funktionsweise der SHA-1 Kompressionsfunktion aus [6]

Funktionsweise:

Die zu hashende Nachricht wird um ein Padding verlängert, bis die Gesamtlänge ein Vielfaches von 512-Bit erreicht hat.
Die Nachricht wird in Blöcke von 512-Bit unterteilt. Jeder Block besteht dabei aus 16 Wörtern von 32-Bit Größe.
Diese 16 Wörter werden nun auf 80 Wörter erweitert. Dies wird durch XOR der einzelnen Wörter und einer Linksrotation ermöglicht.

SHA-1 verwendet 5 interne 32-Bit Variablen ${\textstyle A}$ , ${\textstyle B}$ , ${\textstyle C}$ , ${\textstyle D}$ und ${\textstyle E}$ , daher insgesamt 160-Bit. Diese sind fix vordefiniert und stellen den initialen Hashwert dar. Ihre Darstellung in Hexadezimal ist folgende:

{\textstyle A=H_{0}^{(0)}=67452301}

{\textstyle B=H_{0}^{(1)}=EFCDAB89}

{\textstyle C=H_{0}^{(2)}=98BADCFE}

{\textstyle D=H_{0}^{(3)}=10325476}

{\textstyle E=H_{0}^{(4)}=C3D2E1F0}

Jeder der 512-Bit Blöcke durchläuft nun 4 Stufen zu je 20 Runden, daher insgesamt 80 Runden.

In jeder Stufe wird auf einen Teil der Nachricht eine andere Funktion ${\textstyle f}$ angewendet. Zudem werden noch weitere Konstanten ${\textstyle K_{t}}$ verwendet, die ebenfalls pro Stufe wechseln.

Funktionen und Konstanten der SHA-1 Runden aus
stage ${\textstyle t}$	round ${\textstyle j}$	constant ${\textstyle K_{t}}$	function ${\textstyle f_{t}}$
1	0-19	${\textstyle K1=5A827999}$	${\textstyle f_{1}(B,C,D)=(B\wedge C)\vee (\neg B\wedge D)}$
2	20-39	${\textstyle K2=6ED9EBA1}$	${\textstyle f_{2}(B,C,D)=B\oplus C\oplus D}$
3	40-59	${\textstyle K3=8F1BBCDC}$	${\textstyle f_{3}(B,C,D)=(B\wedge C)\vee (B\wedge D)\vee (C\wedge D)}$
4	60-79	${\textstyle K4=CA62C1D6}$	${\textstyle f_{4}(B,C,D)=B\oplus C\oplus D}$

Der Ausgangswert der sich nach 80 Runden ergibt, wird dann noch mit dem Eingangswert modulo ${\textstyle 2^{32}}$ addiert.

Es ist seit 2005 bekannt, dass bei SHA-1 Kollisionen existieren, es gilt daher bereits seit längerem als unsicher. Es wurde dann im Februar 2017 die erste Kollision nachgewiesen .

SHA-2

SHA-2 steht für eine Gruppe von Algorithmen, die als Erweiterung von SHA-1 gelten. Unter dem Sammelbegriff SHA-2 werden die Verfahren SHA-224, SHA-256, SHA-384 und SHA-512 verstanden, siehe dazu auch Abbildung 1.6. Die angehängte dreistellige Zahl bezieht sich dabei immer auf Bitgröße des Hashwertes der ausgegeben wird. Die Algorithmen unterscheiden sich vor allem durch die verwendete Blockgröße, die Größe der Wörter (32 oder 64-Bit), die Anzahl der Konstanten ${\textstyle K_{T}}$ und der Funktion ${\textstyle f_{t}}$ . SHA-224 und SHA-384 werden analog wie bei SHA-256 beziehungsweise SHA-512 berechnet, nur werden nicht alle Wörter für den Hashwert verwendet. Bei SHA-224 wird das letzte 32-Bit Wort weggelassen. Bei SHA-384 werden die letzten zwei 64-Bit Wörter nicht berücksichtigt.

SHA-3

Wie schon in Kapitel 1.4 beschrieben, basiert SHA-3 auf dem Algorithmus Keccak. Dieser verwendet als unterliegende Architektur die Sponge Konstruktion, siehe Kapitel 1.2.2. SHA-3 ist von der NIST in 6 Varianten standardisiert . Diese sind SHA3-224, SHA3-256, SHA3-384 und SHA3-512, sowie 2 Varianten mit definierbarer Länge des Ausgabewertes (Extenable-Output Functions beziehungsweise XOF) namens SHAKE128 und SHAKE256. Bei den SHAKE Varianten bezieht sich der nachfolgende dreistellige Wert auf die sogenannte Security Strength. Für die XOF Algorithmen beschreibt die NIST:

"For XOFs, the length of the output can be chosen to meet the requirements of individual applications. The XOFs can be specialized to hash functions, subject to additional security considerations, or used in a variety of other applications."

Aufgrund der Flexibilität der Sponge Konstruktion wären natürlich noch viele andere Varianten möglich.

Darstellung des internen Zustands von Keccak aus [24]

Funktionsweise:
Die Funktionsweise folgt der Sponge Konstruktion aus 1.2.2. Keccak beziehungsweise SHA-3 arbeitet mit einem Zustand von 1600-Bit und kann graphisch als dreidimensionales Array dargestellt werden, siehe Abbildung 1.8. Keccak verwendet insgesamt 24 Runden innerhalb der Funktion ${\textstyle f}$ . Eine Rundenfunktion setzt sich aus 5 Einzelschritten zusammen, die als ${\textstyle \theta }$ (Theta), ${\textstyle \rho }$ (Roh), ${\textstyle \pi }$ (Pi), ${\textstyle \chi }$ (Chi) und ${\textstyle \iota }$ (Iota) definiert sind.

${\textstyle \theta }$ : Bits werden aufgrund ihrer Paritätssumme mittels XOR invertiert. Dies sorgt schon nach wenigen Runden für eine gute Diffusion.
${\textstyle \rho }$ : Durch Rotation werden die 25 64-Bit Wörter zyklisch durcheinander gewürfelt. Sorgt für eine Verbesserung der Diffusion in Kombination mit ${\textstyle \theta }$ .
${\textstyle \pi }$ : Durch diesen Schritt werden einzelne 64-Bit Wörter miteinander vertauscht. Dadurch wird ebenfalls die Diffusion verbessert.
${\textstyle \chi }$ : Ist der nicht lineare Teil einer Runde. ${\textstyle \chi }$ addiert mittels XOR die darauf folgenden 2 Worte.
${\textstyle \iota }$ : In der Lane (0,0) ^[7] werden mittels XOR die jeweilige Runden Indizes addiert. Dies hat den Effekt, dass eventuelle Symmetrien nach einigen Runden verschwinden und Keccak weniger Angriffsfläche bietet.

Message Authentication Codes

Ein Message Authentication Code verwendet einen zusätzlichen Secret Key der in die Berechnung eines Hashwertes einfließt , siehe dazu auch Abbildung 1.1. Sie werden daher auch Keyed One Way Functions genannt, also eine Einwegfunktion mit Secret Key. Ein MAC basiert daher auf einem symmetrischen Algorithmus zur Erstellung und Verifikation des Hashwertes. Die Vorteile von MAC sind die Überprüfbarkeit des Ursprungs, sowie der Integrität der Daten. Delfs und Knebl definieren den MAC und dessen Vorteile wie folgt:

"A very important application of hash functions is message authentication, which means to authenticate the origin of a message. At the same time, the integrity of the message is guaranted. If hash functions are used for message authentication, they are called message authentication codes, or MACs for short."

MACs können in zwei Gruppen unterteilt werden, je nach der Art ihrer Konstruktion :

Blockchiffren: MACs können mithilfe von Blockchiffren erzeugt werden, zum Beispiel mit AES mit dem Betriebsmodus CBC.
Hash - Verfahren: Die Methode ein gängiges Hash - Verfahren zur Konstruktion eines MAC zu verwenden ist in RFC 2104 , sowie dem FIPS 198-1 standardisiert. Diese Methode wird als Keyed-Hash Message Authentication Code (HMAC) bezeichnet und kommt zum Beispiel im SSL/TLS und SSH Protokoll zum Einsatz. Das folgende Kapitel 1.5.1 beschreibt die Funktionsweise näher.

Keyed-Hash Message Authentication Code

Ein HMAC besteht aus der Message ${\textstyle M}$ , dem Authentication Key ${\textstyle K}$ , sowie der verwendeten Hash - Funktion ${\textstyle H}$ . Der HMAC lässt sich folgendermaßen darstellen :

HMAC(M,K)=H(K\oplus opad,H(K\oplus ipad,M))

Funktionsweise:

Der key ${\textstyle K}$ wird durch Expansion durch den Wert 0 auf eine Länge gebracht, die der Blockgröße ${\textstyle b}$ der verwendeten Hash Funktion ${\textstyle H}$ entspricht. Ist der Secret Key ${\textstyle K}$ bereits größer als die Blockgröße ${\textstyle b}$ wird ein Hashwert von ${\textstyle K}$ verwendet, daher ${\textstyle K=H(K)}$ .
ipad und opad, zwei fixe unterschiedliche Strings werden für die weitere Berechnung verwendet. Das i und das o stehen für inner und outer.
ipad und der expandierte Secret Key ${\textstyle K}$ werden sodann XOR verknüpft.
Die Message ${\textstyle M}$ wird dem Ergebnis aus Punkt 3 angehängt.
Das Hashverfahren ${\textstyle H}$ wird auf den Stream aus Punkt 4 angewendet.
Der Key ${\textstyle K}$ wird mit dem opad definierten String XOR verknüpft.
Der Hashwert aus Punkt 5 wird dem Ergebnis aus Punkt 6 angehängt.
Die Hash - Funktion ${\textstyle H}$ wird auf den Stream aus Punkt 7 angewendet und das Ergebnis ausgegeben.

Digitale Signaturen und Zertifikate

Digitale Signaturen sind neben der Übertragung von geheimen Schlüsseln über unsichere Kanäle, die wichtigste Anwendung von asymmetrischen Verfahren (siehe Kapitel [asymmetrischeVerfahren]). Mittels digitaler Signaturen werden Webbrowser Sitzungen abgesichert, rechtlich bindende Verträge signiert oder Software sicher aktualisiert . An digitale Signaturen werden je nach Anwendung folgende Sicherheitsziele gestellt:

Vertraulichkeit (engl. Confidentiality)
Integrität (engl. Integrity)
Authentizität (engl. Message Authentication)
Nicht-Abstreitbarkeit (engl. Non-Repudiation)

Welche Sicherheitsziele erforderlich sind, hängt von der Art der Anwendung ab. So schreiben Paar und Pelzl:

"Different applications call for different sets of security services. For instance, for private e-mail the first three functions are desireable, whereas a corporate e-mail system might also require nonrepudiation. As another example, if we want to secure software updates for a cell phone, the chief objectives might be integrity and message authentication because the manufacturer primarily wants to assure that only orginal updates are loaded into the handheld device."

Außerdem gibt es neben den oben genannten Sicherheitszielen noch einige andere, abhängig von der Anwendung :

Identifikation (engl. Identification): eindeutige Ermittlung der Person oder des Gerätes.
Zugriffskontrolle (engl. Access Control): Zugriff auf Ressourcen wird nur für entsprechende Personen erlaubt.
Verfügbarkeit (engl. Availability): Sicherstellung das ein System verfügbar ist.
Physikalische Sicherheit (engl. Physical Security): Schutz gegen physikalische Manipulation.
Anonymität (engl. Anonymity): Schutz gegen die Offenlegung der Identität oder der Missbrauch einer solchen.

Funktionsweise:
Die Erstellung einer digitalen Signaturen erfolgt nicht durch das Signieren der Daten direkt. Stattdessen wird ein Hashwert des Dokuments signiert, siehe auch Abbildung 1.1.

Signieren eines Dokuments

Der Vorgang des Signierens ist allerdings nichts anderes als die (asymmetrische) Verschlüsslung des Hashwertes mit dem private Keys des Unterzeichners. Der verschlüsselte Hashwert stellt sodann die Signatur des Dokuments dar und wird diesem beigefügt.

Verifikation des signierten Dokuments

Erhält der Empfänger das signierte Dokument, muss dieser zwei Dinge tun, um die Signatur zu überprüfen, siehe dazu Abbildung 1.2. Erstens wird ebenfalls der Hashwert des Dokuments generiert. Zweitens wird mit Hilfe des Public Keys des Absenders der verschlüsselte Hashwert wieder entschlüsselt. Durch die Entschlüsselung erhält der Empfänger den durch den Absender berechneten Hashwert des Dokuments. Sind der entschlüsselte und der selbst berechnete Hashwert ident, handelt es sich um eine gültige Signatur.

Signatur mit RSA

Eine Signatur mit RSA wird nach den selben Prinzipien wie bei der Verschlüsselung mit RSA durchgeführt, siehe dazu auch Kapitel [RSA] .

Funktionsweise:

Bob möchte eine signierte Nachricht an Alice senden. Bob generiert ein RSA-Schlüsselpärchen. Er hat sodann einen privaten Schlüssel ${\textstyle k_{prv}=(d)}$ und einen öffentlichen Schlüssel bestehend aus ${\textstyle n}$ und ${\textstyle e}$ , daher ${\textstyle k_{pub}=(n,e)}$
Bob stellt Alice seinen öffentlichen Schlüssel ${\textstyle k_{pub}=(n,e)}$ zur Verfügung.
Bob berechnet die Signatur von ${\textstyle x}$ wie folgt: ${\textstyle s=sig_{k_{prv}}(x)\equiv x^{d}\mod n}$
Bob sendet die signierte Nachricht ${\textstyle x}$ sowie die Signatur ${\textstyle s}$ an Alice.
Alice kann die Signatur wie folgt verifizieren: ${\textstyle verify_{k_{pub}}(x,s)=x'\equiv s^{e}\mod n}$ . Falls ${\textstyle x'\equiv x\mod n}$ , dann sind ${\textstyle x}$ und ${\textstyle x'}$ ident und handelt es sich um eine gültige Signatur. Falls ${\textstyle x'\not \equiv x\mod n}$ ist die Signatur nicht gültig.

Digital Signature Algorithm

Der Digital Signature Algorithm (DSA) ist ein durch die NSA entwickelter und durch die NIST erstmals 1994 eingeführtes Signaturverfahren . Er wird im FIPS 186-4 spezifiziert und wird als Digital Signature Standard (DSS) bezeichnet. DSA stellt dabei den verwendeten Algorithmus dar.

Unterstützte Bitlängen beim Digital Signature Algorithmus in Abhängigkeit der Parameter ${\textstyle L}$ und ${\textstyle N}$ nach

${\textstyle L}$	${\textstyle N}$
1024	160
2048	224
2048	256
3072	256

Der DSA basiert wie RSA ebenfalls auf dem Problem des diskreten Logarithmus ^[8] , daher der Schwierigkeit ein Produkt zweier Primzahlen zu faktorisieren. Der DSA unterstützt unterschiedliche Bitlängen (siehe Tabelle 1.1) und besteht aus mehreren Komponenten beziehungsweise Parametern, die nachfolgend beschrieben sind .

Eine öffentlich bekannte Primzahl ${\textstyle p}$ , welche ${\textstyle L}$ Bit lang ist.
Ein öffentlich bekannter Primfaktor ${\textstyle q}$ von ${\textstyle p-1}$ , wobei ${\textstyle q}$ eine unterstützte Länge ${\textstyle N}$ haben.
Gibt die Länge von ${\textstyle q}$ an und muss ein Vielfaches von 64 sein, sowie ${\textstyle 512\leq L\leq 3072}$
Ein öffentlich bekannter Generator dessen Ordnung ${\textstyle q}$ ist, nach dem Satz von Lagrange
ein Secret Key mit ${\textstyle 0<x<q}$
ein Public Key mit ${\textstyle y=g^{x}\mod p}$
eine Hash - Funktion, zumeist wird SHA-1 oder auch SHA-2 verwendet

Funktionsweise:

Die Werte ${\textstyle p,q}$ und ${\textstyle g}$ sind öffentlich bekannt. Daher können sie in einer Gruppe von Personen benutzt werden.
Alice möchte ein Dokument ${\textstyle M}$ signieren. Sie besitzt dazu ein Schlüsselpaar, wobei ${\textstyle x_{A}}$ ihren privaten Schlüssel und ${\textstyle y_{A}}$ ihren öffentlichen Schlüssel darstellt.
Alice generiert eine zufällige Zahl ${\textstyle k}$ als ihren Secret Key, wobei ${\textstyle 0<k<q}$ .
Alice berechnet sodann die Signatur, welche sich aus ${\textstyle r}$ und ${\textstyle s}$ zusammensetzt: $r=(g^{k}\mod p)\mod q$ $s=(k^{-1}(H(M)+x_{A}*r))\mod q$
Alice schickt Dokument ${\textstyle M}$ und Signatur ${\textstyle (r,s)}$ an Bob.
Bob kann die Signatur nun wie folgt überprüfen. Er berechnet sich 3 Hilfswerte ${\textstyle w,u_{1}}$ und ${\textstyle u_{2}}$ . Mit Hilfe dieser Hilfswerte kann sich Bob dann ${\textstyle v}$ berechnen. $w=s^{-1}\mod q$ $u_{1}=w*H(M)\mod q$ $u_{2}=w*r\mod q$ $v=((g^{u_{1}}*y_{A}^{u_{2}})\mod p)\mod q$
Entspricht ${\textstyle v\equiv r}$ , dann ist die Signatur gültig.

X.509 und Public Key Infrastructure

X.509 spezifiziert das Format eines Public Key Zertifikates nach RFC 5280. . Public Key Zertifikate kommen vor allem im SSL/TLS Protokoll (siehe Kapitel [SSL] und zum Beispiel bei der E-Mail Verschlüsselung S/MIME (siehe Kapitel [SMIME]) zum Einsatz.

Zertifikat von onlinecampus.fernfh.ac.at

Der RFC 5280 spezifiziert folgende Attribute eines X.509 Zertifikats:

Version
Seriennummer
Algorithmus
Aussteller des Zertifikats
Gültigkeit (von Datum bis Datum)
Inhaber
Schlüsselinformation des Inhabers
Erweiterungen
Signaturalgorithmus
Signatur
optional eine eindeutige ID des Ausstellers und des Inhabers

Für die Verwaltung und Erzeugung von X.509 Zertifikaten wird eine sogenannte Public Key Infrastructure (PKI) verwendet. Eine PKI Umgebung ist hierarchisch aufgebaut. Diese besteht aus mehreren Komponenten :

hierarchischer Aufbau einer PKI aus [15]

Certificate Authority (CA): Die Zertifizierungsstelle hat die Aufgabe Zertifikate auszustellen und auch wieder zurückzurufen (Revoke). CAs können hierarchisch aufgebaut werden und sodann in eine Root-CA und ihre Intermediate CAs ^[9] unterteilt. Zwei oder mehrere CAs können sich gegenseitig vertrauen (Trust) und in einer Mesh Struktur aufgebaut sein. Näheres dazu ist in RFC 4158 zu finden
Registration Authority (RA): Die Registrierungsstelle hat die Aufgabe Zertifikatsanträge entgegenzunehmen (Certificate Signing Requests). Nach der eindeutigen Identifikation des Antragstellers wird der CSR an die CA zur Ausstellung weiterzugeben.
Trust Center: CA und RA arbeiten eng zusammen und werden als Trust Center zusammengefasst.
Certificate Revocation List (CRL): Werden Zertifikate vor Ablauf ihrer Gültigkeit von der CA zurückgerufen, werden diese in die CRL eingetragen. Diese wird in definierten Zeitabständen aktualisiert. Um gesperrte Zertifikate auszutauschen kann auch ein Protokoll wie das Online Certificate Status Protocol (OCSP) verwendet werden, siehe dazu den RFC 2560
Directory Service: Das Directory Service oder Verzeichnisdienst bietet eine Möglichkeit nach ausgestellten Zertifikaten zu suchen.

Hardware Security Module

Ein Hardware Security Module (HSM) ist eine Hardware, die speziell für den Schutz und der Berechnung von Schlüsselmaterial ausgelegt ist . Diese werden schon lange im Banken eingesetzt um die dort notwendigen kryptografischen Transaktionen sicherzustellen. Ein HSM muss folgende Anforderungen erfüllen:

Berechnung von echten Zufallszahlen.
Zur Verfügung Stellung aller benötigten kryptographischen Operationen, wie Signatur-, Verschlüsselungs- und Hashalgorithmen.
Es muss Schutz vor Seitenkanalangriffen vorhanden sein.
Es muss ein Schutz gegen Angriffe und Manipulation der Hardware vorhanden sein (engl. tamper resistant)

Um die Qualität und den Funktionsumfang von HSMs zu vergleichen hat das NIST den FIPS 140 entworfen. Dieser Standard zertifiziert eine HSM in vier unterschiedliche Sicherheitslevel, siehe dazu .

Zugriffskontrolle

Mit Hilfe von Zugriffskontrolle (engl. Access Control) kann der Zugriff von Usern (Subject) auf Ressourcen (Object) kontrolliert und somit gesteuert und geschützt werden. Access Control lässt sich in zwei Kategorien unterteilen, nämlich einerseits den physikalischen Schutz und andererseits den logischen Schutz. Mit physikalischen Schutz ist vor allem der Zutritt zu Ressourcen oder Systemen gemeint, zum Beispiel der Zutritt zu einem Rechenzentrum. Der logische Schutz bezieht sich auf Betriebssystem- beziehungsweise Applikations-Ebene. Die folgenden Kapitel beziehen sich auf den logischen Schutz von Ressourcen.

Autorisierung und Modelle

Access Control kann über verschiedene Modelle abgebildet werden. Das Modell bestimmt wann und wie ein Subject auf ein Objekt zugreifen kann. Die klassischen Zugriffsmodelle werden in den Kapiteln 1.1.1, 1.1.2 und 1.1.3 beschrieben.

Discretionary Access Control

Das Discretionary Access Control (DAC) Modell ist auf den Benutzer fokussiert . Der Benutzer ist der Eigentümer seiner Ressourcen und verfügt damit über vollen Zugriff auf diese. Somit kann er auch den Zugriff auf seine Ressourcen für andere erlauben. Es ergibt sich damit ein dezentrales System bezüglich der Rechtevergabe. Dieses Prinzip ist zum Beispiel im Unix Filesystem zu finden. Darstellbar ist DAC am besten durch eine Access Control Matrix, wie in Tabelle 1.1 ersichtlich.

Beispiel einer Access Control Matrix
	file 1	file 2	file 3
Alice	r	rwx	rw
Bob	rwx		r
Eve	rw	r	r

DAC ist auf der einen Seite sehr flexibel, hat aber zwei große Nachteile. Zum einen ist ein zugewiesener Lesezugriff transitiv. Das heißt, hat ein Subjekt Lesezugriff auf eine Datei hindert ihn nichts daran den Inhalt der Datei in eine neue Datei, welche unter seiner eigenen Kontrolle steht, zu kopieren und anschließend Rechte an andere subjekte zu verteilen. Zweitens, ist es durch die dezentrale Rechtevergabe kaum möglich eine systemweite Richtlinie zu definieren.

Mandatory Access Control

Mandatory Access Control (MAC) stammt ursprünglich aus dem militärischen Bereich und ist wesentlich restriktiver und strukturierter . MAC kann somit als Gegenteil von DAC betrachtet werden. Bei MAC werden Rechte von einer zentralen Verwaltungsinstanz vergeben. Eine Veränderung der Rechte durch ein Subjekt ist damit ausgeschlossen. Abgebildet wird dieses Modell meist durch Zuweisung von Klassifizierungen beziehungsweise Schutzstufen. Zum Beispiel darf ein Benutzer aus der Schutzstufe secret keine Dokumente aus der Schutzstufe top secret lesen. Es gibt zwei Ausprägungen von MAC Konzepten :

Multi-Level Sicherheitssysteme: Wie oben beschrieben, werden Ressourcen Schutzstufen zugeteilt. Die bekanntesten Modelle sind Bell-LaPadula und Biba.
multilaterale Sicherheitssysteme: Zusätzlich zu den Schutzstufen werden zudem noch Label vergeben. Diese ermöglichen neben der vertikalen auch eine horizontale Betrachtung. Die bekanntesten Vertreter sind das Lattrice Modell und das Chinese Wall Modell.

Role-based Access Control

Wie der Name schon sagt, werden bei Role-based Access Control (RBAC) den Subjekten unterschiedliche Rollen zugeteilt, welche eine bestimmte Funktion erfüllt . Durch diese Zuteilung erhält das Subjekt auch die entsprechenden Rechte auf die dafür notwendigen Objekte. Die Zugriffsberechtigungen erfolgen wie bei DAC mittels einer Access Control Matrix. Die Zuweisung der Rollen erfolgt allerdings durch eine zentrale Verwaltungsstelle, wie bei MAC. RBAC wird in verschiedenen Systemen, wie Microsoft Active Directory, SELinux, Solaris und diversen Datenbanksystemen umgesetzt.

Authentisierung auf Unix Systemen

Bei Unix beziehungsweise Linux Systemen werden die Credentials der Benutzer in der Datei /etc/passwd oder in die Datei /etc/shadow geschrieben . Diese Dateien sind in der Regel nur für Benutzer mit root Rechten beschreibbar beziehungsweise lesbar. In der Datei /etc/passwd erfolgt pro Zeile ein User Eintrag. Der User Eintrag umfasst mehrere Parameter welche durch Doppelpunkte getrennt sind.

myuser:x:1001:1001:User,,,:/home/myuser:/bin/bash

Folgende Attribute sind in der passwd Datei enthalten:

username: Der Loginname (myuser)
passwd: An dieser Stelle befindet sich das gehashte Passwort. Werden shadow Passwörter verwendet ist hier nur ein x angegeben. Das eigentliche Passwort ist dann in /etc/shadow zu finden.
UID: Die nummerische User ID (1001)
GID: Die nummerische Group ID des Users (1001)
full_name: Der vollständige Name des Users (User)
directory: Der Pfad zum Home Directory des Users (/home/myuser)
shell: Die eingestellte User Login Shell (/bin/bash)

Werden shadow Passwörter verwendet, bringt dies eine Sicherheitsvorteile. So ist die Datei für herkömmliche Benutzer nicht lesbar.

myuser:$6$0Hm6YF2C$6VxZAipdU8Qn8YZR5NqX1uH.P9J7DDz2gEXIvF0y/PpQy6lemTvWgBzYWFrFDcAQhajIYpjNJ8Q8e5trWq8Sd/:17291:0:99999:7:::

Die shadow Datei ist wiederum zeilenweise zu lesen und deren Attribute sind ebenfalls durch Doppelpunkte getrennt. Die angegebenen Attribute sind laut manual page von shadow ^[10] folgende:

Login Name: Ein gültiger Benutzer am System
encrypted password: Hier findet sich das "gesalzene" und gehashte Passwort des Users, mehr dazu später.
Datum des letzten Password Wechsels
minimum password age
maximum password age
password warning period: Die Anzahl der Tage befor ein Passwort ausläuft und der Benutzer gewarnt werden soll.
password inactivity period: Anzahl der Tage in denen ein bereits abgelaufenes Passwort noch akzeptiert wird.
account expiration date
reserved for future use

Das Encrypted Password Feld in der /etc/shadow Datei wird dabei im Format $id$salt$hash angegeben. $id bezieht sich dabei auf den Algorithmus der zum Hashen des Passwortes verwendet wird. So steht $1 für MD5, $2 für den Blowfish Algorithmus, $5 für SHA-256 und $5 für SHA-512 ^[11] . Der Wert $salt generiert sich aus der aktuellen Uhrzeit und der Prozessidentifikation. Der Salt beeinflusst die Verschlüsselung des unter $hash abgelegten Passwortes des Benutzers. Ein und dasselbe gehashte Passwort kann somit aufgrund des Salts unterschiedliche Repräsentationen annehmen. Somit können Angriffe nochmals erschwert werden.

Multi-Factor Authentication

Unter Multi-Factor Authentication wird die Authentisierung mit mehreren, dem Benutzer zugeordneten, Maßnahmen verstanden . Die hauptsächlichen Gründe für eine Verwendung von zwei oder mehreren Faktoren sind vor allem die Nachteile bei der alleinigen Verwendung von Passwörtern. So können Passwörter leicht vergessen oder weitergegeben und kompromittiert werden. Passwörter können erraten oder auch geknackt werden. In manchen Bereichen ist der Zugriff auf Ressourcen auch besonders schützenswert oder die Verwendung von MFA wird von einer Richtlinie vorgegeben, wie zum Beispiel PCI-DSS . Die Maßnahmen oder Möglichkeiten eine Authentisierung mit mehreren Faktoren sind vielfältig, lassen sich aber in drei Kategorien einteilen:

spezifisches Wissen: Passwort, PIN, Antworten auf bestimmte Fragen (Questions and Answers oder Sicherheitsabfrage), Zero-Knowledge Beweise, etc. Kurz gesagt: etwas, was man weiß.
persönlicher Besitz: Hardware-Token, Smartcard, physikalischer Schlüssel, Zertifikate, SmartPhone, RFID basierte Tokens, TAN-Liste, USB Stick oder andere USB Geräte, etc. Kurz gesagt: etwas, was man hat.
biometrische Merkmale: Fingerabdruck, Gesichtserkennung, Retina, Handschrifterkennung, etc. Kurz gesagt: etwas, das man ist.

Eine der bekanntesten Einsatzbereiche von Multi-Faktor Authentication (MFA) ist zum Beispiel der Überweisungsvorgang beim Online-Banking. Hier wird neben den Zugangsdaten mit Username und Passwort auch entweder ein One-Time-Password via SMS oder ein TAN aus einer TAN-Liste abgefragt. Dies stellt eine Authentisierung mit zwei Faktoren dar und wird auch 2 Factor Authentication (2FA) genannt. 2FA ist somit eine Form der Multi-Factor Authentication.

Bei der technischen Umsetzung werden Multi-Factor Mechanismen zum Beispiel über das RADIUS Protokoll (mittels Access-Challenge, siehe 1.5.2) oder über Kerberos Authentifizierungsmechanismen gelöst, sieh Kapitel 1.5.1.

One-Time Passwords

One-Time Passwords (OTP) sind Passwörter welche für den einmaligen Gebrauch (zum Beispiel einer Session oder Transaktion) von einem Generator generiert werden . Dies kann zum Beispiel ein Hardware Token sein. Der Validator ist die Serverseitige Software, welche den generierten Code auf seine Gültigkeit überprüft. Nach dem einmaligen Gebrauch ist der OTP nicht mehr gültig. OTPs haben den großen Vorteil, dass Replay Attacken nicht möglich sind. Aufgrund dessen werden OTPs gerne als Faktor für eine Multi-Faktor Authentifizierung, siehe Kapitel 1.3, verwendet. Für die Generierung von OTPs werden im allgemeinen drei mögliche Zugänge verwendet:

basierend auf Zeit: Der OTP wird unter Einbeziehung es aktuellen Timestamps berechnet. Dies setzt eine Zeit Synchronisation zwischen Server und Client voraus.
basierend auf dem letzten OTP: Der Algorithmus berechnet den nächsten OTP aufgrund des vorherigen. Dies heißt natürlich, dass alle OTPs in einer Kette berechenbar sind.
basierend auf einer Challenge: Der Algorithmus berechnet aufgrund einer Challenge (zum Beispiel einer Zufallszahl) den nächsten OTP.

Lange Zeit waren OTP-Algorithmen nicht standardisiert. Einige Unternehmen wie RSA Security und VASCO versuchten ihre eigenen Implementierungen als Standard zu etablieren und voranzutreiben. Im Jahre 2004 wurde dann die Initiative for Open AuTHentication (OATH) gegründet . Diese stellt einen Zusammenschluss von Unternehmen, wie ActiveIdentity, Gemalto und Symantec dar. Ziel der Initiative ist die Entwicklung von einheitlichen Standards für die Authentisierung, darunter auch Standards für die Generierung von One-Time Passwords. So wurde eine Referenz Architektur geschaffen, welche ein Framework für Open Authentication darstellt . Außerdem wurden einige Standards für die Generierung von OTPs entwickelt, welche als RFC verfügbar sind:

RFC 4226: HOTP: An HMAC-Based One-Time Password Algorithm : Der RFC spezifiziert einen OTP Algorithmus welcher einen HMAC-SHA-1 verwendet, siehe dazu Kapitel [MAC]. Generator und Validator einigen sich zuerst auf ein gemeinsames secret ${\textstyle K}$ , sowie einen Counter ${\textstyle C}$ . Mit diesen Informationen können auf beiden Seiten gleiche OTPs generiert werden. ${\textstyle C}$ wird nach jeder OTP Generierung inkrementiert: $HOTP(K,C)=Truncate(HMACSHA1(K,C))$ Die Funktion ${\textstyle Truncate}$ konvertiert dabei die Ausgabe des HMAC-SHA-1 von 160-Bit ^[12] in den endgültigen zumindest 6-stelligen HOTP.
RFC 6238: TOTP: Time-Based One-Time Password Algorithm : TOTP basiert auf den Grundprinzipien von HOTP. Der wesentliche Unterschied ist die Verwendung des Counters ${\textstyle C}$ . Bei TOTP wird anstelle von ${\textstyle C}$ , der Integer ${\textstyle T}$ verwendet. ${\textstyle T}$ gibt die Anzahl der Zeitschritte zwischen der Ausgangszeit ${\textstyle T0}$ und der aktuellen UnixTime an. Die Funktion ist ansonsten analog wie bei HOTP, daher: $TOTP=HOTP(K,T)$
RFC 6287: OCRA: OATH Challenge-Response Algorithm : Auch OCRA übernimmt die Funktionsweise von HOTP mit den folgenden Anpassungen. OCRA besteht aus einer kryptographische Funktion, dem gemeinsamen secret ${\textstyle K}$ und einer Menge an Eingabedaten ${\textstyle DataInput}$ . Eine OCRA Response berechnet sich durch $OCRA=CryptoFunction(K,DataInput)$ Als Standard für die ${\textstyle CryptoFunction}$ verwendet ORCA den SHA-1 Algorithmus. Mittels der Eingabedaten kann das Verhalten von OCRA angepasst werden. So unterstützt OCRA ein einseitiges und eine beidseitiges Challenge-Response Verfahren so wie die Möglichkeit einer Signatur von Daten.

AAA Systeme und Protokolle

AAA oder Triple A steht für Authentication, Autorisation und Accounting, also Authentisierung, Autorisierung und Abrechnung. AAA ist ein Framework welches diese 3 Verfahren beschreibt . Dabei werden keine spezifischen Methoden zur Verschlüsselung oder Authentication beschrieben, sondern ein generischer Ansatz zur Verfügung gestellt.

Kerberos

Kerberos ist ein Authentifizierungssystem welches vom MIT entwickelt wurde . Es ist ein Client - Server Modell welches symmetrische Verfahren einsetzt. Kerberos hat 2 primäre Aufgaben. Erstens die Subjekte, welche im Kerberos Kontext als Principals bezeichnet werden, zu authentifizieren. Zweitens werden über Kerberos Sitzungsschlüssel ausgetauscht. Zudem ist es möglich mit Kerberos Single-Sign On zu implementieren. Kerberos hat allerdings keine Funktion zur Autorisierung (daher Vergabe von Rechten) ihrer Principals. Kerberos schreibt auch nicht vor, wie die Authentifizierung zu erfolgen hat, daher kann ein Passwort als auch beispielsweise ein Token oder eine SmartCard verwendet werden. Kerberos verwendet zur Authentisierung sogenannte Tickets . Garman schreibt zur Aufgabe von Tickets:

"Tickets serve two purposes: to confirm identity of the end participants and to establish a short-lived encryption key that both parties can share for secure communication (called the session key)."

Tickets sind verschlüsselte Datenkonstrukte welche folgende Felder beinhalten:

Der Principal Name des User, welcher die Anfrage stellt.
Der Service Principal Name der Applikation, an welchem sich dieser authentisieren möchte.
Gültigkeitszeitraum des Tickets
Eine Liste von IP Adressen, von welchen das Ticket benutzt werden kann.
ein geteilter aber geheimer Schlüssel für die Kommunikation zwischen User und Service (Session Key)

Bei Kerberos ist es essentiell wichtig, dass eine Zeitsynchronisation zwischen Client und Server erfolgt. Tickets werden mit einem Zeitstempel versehen und es werden nur geringe Abweichungen akzeptiert.

Kerberos besteht im wesentlichen aus 3 logischen Komponenten, welche als Key Distribution Center (KDC) zusammengefasst werden:

Einer Datenbank mit allen Principals und deren verschlüsselten Keys
Einem Authentication Server (AS): Der AS stellt sogenannte Ticket Granting Tickets (TGT) an Clients aus.
Dem Ticket Granting Server (TGS): Der TGS überprüft TGTs und stellt Service Tickets für einzelne Applikationen bereit.

Ablauf einer Kerberos Authentifizierung

Funktionsweise:

Bei der Anmeldung des Users am Client stellt dieser einen Authentication Service Request für ein Ticket Granting Ticket (TGT) beim Authentication Server (AS).
Das Key Distribution Center überprüft die Credentials des Clients in seiner Datenbank. Der Authentication Server stellt dem Client ein Ticket Granting Ticket (TGT) aus und schickt dieses zusammen mit dem Logon Session Key, verschlüsselt mit dem Key des Clients, an den Client zurück.
Der Client entschlüsselt das TGT und den Logon Session Key und speichert diese in seinem Cache. Will der Client nun auf eine Applikation zugreifen, stellt er mittels dem TGT eine Anfrage für ein Service Ticket für das entsprechende Service an den Ticket Granting Server (TGS).
Der TGS validiert das TGS und retourniert ein verschlüsseltes Service Ticket zusammen mit dem Service Session Key.
Der Client kann sich nun mit dem ausgestellten Service Ticket und dem Session Key beim gewünschten Service anmelden und sendet diese Informationen an den Applikationsserver.
Das Applikationsserver sendet dem Client einen verschlüsselten Zeitstempel retour. Der Client kann diesen entschlüsseln und auf diese Weise feststellen, dass es sich um ein vertrauenswürdiges Service handelt.

Das RADIUS Protokoll

Die Abkürzung RADIUS steht für Remote Authentication Dial In User Service . Es handelt sich dabei um ein Client-Server Protokoll welches auf dem UDP Protokoll basiert. Es wird eingesetzt bei Service Providern für den Einwahldienst, aber auch im Unternehmensbereich zur Absicherung von Remote Access oder WLAN Lösungen. Ein Benutzer sendet über seinen Client Rechner seine Credentials an den sogenannten Network Access Server (NAS). Dieser agiert als RADIUS Client und erzeugt einen Access-Request, (welcher die Credentials des Users enthält) an den RADIUS Server. Das RADIUS Protokoll basiert auf einem Shared Secret ${\textstyle S}$ , welches zuvor zwischen dem RADIUS Client (NAS) und dem RADIUS Server vereinbart wurde. Nach Überprüfung der Anfrage erfolgt eine Rückmeldung an den RADIUS Clients entweder in Form einer Access-Denied oder Access-Accept (oder einer Access-Challenge) Nachricht. Das RADIUS Protokoll unterstützt mehrere Protokolle zur Authentifierung wie CHAP oder PAP .

Radius Authentifizierung

Funktionsweise:

Eine Client Rechner sendet eine Authentifizierung an den Network Access Server.
Der NAS agiert als RADIUS Client und erzeugt einen Access Request an den RADIUS Server. Erhält der RADIUS Client in einem definierten Zeitabstand keine Antwort wiederholt dieser seine Anfrage. Der Access Request enthält folgende Attribute:
- Die IP Adresse des RADIUS Clients.
- eine 8-Bit lange ID, über welchen der Request identifiziert wird.
- der sogenannte Request Authenticator (RA), welcher eine zufällig gewählte 128-Bit Zahl darstellt.
- Der Benutzername und Password. Das Passwort wird unter Berechnung des Request Authenticators und des Shared Secret als Hashwert übertragen. Dabei werden schrittweise die Werte ${\textstyle c_{1}=p_{1}\oplus MD5(S|RA)}$ bis ${\textstyle c_{n}=p_{n}\oplus MD5(S|c_{n}-1)}$ berechnet. ${\textstyle p_{i}}$ stellt dabei das ursprüngliche Passwort der Stelle ${\textstyle i}$ dar. Ist das ursprüngliche Passwort keine 128-Bit lang wird es mittels Padding aufgefüllt.
- zusätzlich sind noch weitere Attribute laut RFC 2865 möglich.
Der RADIUS Server empfängt den Access Request und berechnet aufgrund des shared secrets und des mitgelieferten Request Authenticators das ursprüngliche Passwort. Das Passwort kann dann zum Beispiel in einem externen User Directory auf Richtigkeit überprüft werden.
Anschließend wird eine Antwort vom RADIUS Server generiert. Hier bestehen drei Möglichkeiten:
- Access-Accept: Das Passwort ist korrekt und die Authentifizierung war erfolgreich. In diesem Fall wird eine Access Accept Meldung erzeugt, welche die ID des Requests und einen Response Authenticator enthält. Der Response Authenticator ist ein MAC des Access Requests. Mittels der MAC Berechnung wird die Authentiziät des Radius Servers bestätigt, da dieser in Kenntnis des Shared Secrets ${\textstyle s}$ ist.
- Access-Reject: Das Passwort ist nicht korrekt und ein Reject der Anfrage wird erteilt. Die Access Reject Meldung setzt sich wiederrum aus der ID und des Response Authenticators zusammen.
- Access-Challenge: Der RADIUS Server kann dem Client eine Challenge zusenden. Dies stellt eine erneute Aufforderung zur Generierung einer Access-Request Nachricht dar. Die Challenge kann einen frei definierbaren Text String enthalten, der vom RADIUS Client dem Benutzer anzuzeigen ist. Dies wird zum Beispiel bei Multi-Faktor beziehungsweise Strong Authentication verwendet (siehe Kapitel 1.3) um einen zweiten Faktor an den RADIUS Server zu senden.
Der RADIUS Client erhält die jeweilige Antwort und überprüft ob die ID zu seinem gesendeten Access-Request passt. Wenn ja, wird auch der Response Authenticator auf seine Richtigkeit überprüft. Anschließend wird das Ergebnis des Connection Requests dem ursprünglichen Client mitgeteilt.

Ein RADIUS Server kann auch als sogenannter Proxy fungieren und die erhaltenen Access-Request an einen oder mehrere RADIUS Server weiterleiten. Die Zuteilung des Access-Requests zu einem zuständigen RADIUS Server kann, zum Beispiel, durch die NAS IP-Adresse, den Benutzernamen oder durch Verwendung der zusätzlich definierbaren RADIUS Attribute abgebildet werden.

Zusätzlich bietet RADIUS auch ein optionales Accounting an, welches in RFC 2866 beschrieben ist. Wird RADIUS Accounting verwendet, wird nach einer erfolgreichen Access-Accept, vom NAS ein zusätzlicher Accounting-Request vom Typ Start zum RADIUS Server gesendet. In regelmäßigen Intervallen erfolgen dann Accounting Updates vom Client zum Server. Diese Updates enthalten die Session Dauer sowie die Informationen zum Datenverbrauch. Nach Beendigung der Verbindung wird ein Accounting Request vom Typ Stop, sowie Verbindungseigenschaften, wie zum Beispiel, die Gesamtdauer, Datenverbrauch oder Anzahl der übertragenen Pakete, an den RADIUS Server gesendet.

Sicherheit in Netzwerken

IPSec

Das IP Security Protocol (IPSec) ist eines der beliebtesten Protokolle um VPN Verbindungen aufzubauen. IPSec wurde von der IETF entwickelt und ist in RFC 4301 standardisiert . IPSec arbeitet auf Ebene der Netzwerkschicht des OSI-Modells und hat somit den Vorteil, dass es somit transparent für höhere Schichten ist. IPSec beinhaltet einige andere Protokolle, wie

dem IKE Protokoll für den Schlüsselaustausch,
dem ESP Protokoll für den verschlüsselten und integren Datenverkehr, sowie
dem AH Protokoll für den authentifizierten Datenverkehr.

IPSec kann in zwei Varianten eingesetzt werden . Erstens, den Transport Mode, bei welchem nur die Nutzdaten verschlüsselt werden. Dieser Modus kommt heutzutage praktisch kaum zur Anwendung und ist für Peer-to-Peer Kommunikation gedacht. Zweitens, den Tunnel Mode, bei welchem sämtliche Nutzdaten inklusive Verkehrsdaten verschlüsselt werden. Dies bietet ein höheres Maß an Sicherheit benötigt allerdings auch mehr Rechenleistung. Im Tunnel Mode werden die ursprünglichen IP-Header in ein neues IP Paket eingekapselt. Die neuen IP Header beinhalten die IP Adressen der Gateways welche den IPSec Tunnel aufbauen. Dies hat den Vorteil, dass die original IP Adressen während des Transports über den Tunnel verschlüsselt sind.

IPSec-Header nach
IP-Header	IPSec-Header	Data

Welches Verschlüsselungsverfahren und Schlüssel für einen IPSec Tunnel verwendet werden, wird in der sogenannten Security Association (SA) gespeichert. So beinhaltet eine SA die Parameter der IPSec Verbindung zwischen zwei oder mehreren Gateways. Jedes Gateway speichert sein SAs in einer Datenbank, der Security Association Database (SAD). IPSec Verbindungen sind unidirektional, deswegen werden für ein kommende und ausgehende Verbindungen jeweils eine eigene SAD geführt. Für die eindeutige Identifizierung einer Verbindung wird ein 32-Bit Wert, der Security Parameter Index (SPI) sowie der IP Adresse der Gegenstelle verwendend. Diese werden im IPSec Header mitgeschickt. In der Security Policy Database (SPD) werden zudem Strategien festgelegt, wie mit ein und ausgehenden IPSec Paket umgegangen werden soll. Zum Beispiel, ob IPSec angewendet werden soll, das Paket verworfen werden soll, oder ob es ohne weitere Sicherheitsüberprüfungen weitergeleitet werden soll.

Architektur von IPSec aus [17]

Internet Key Exchange Protocol

Das IKE Protokoll basiert auf dem Internet Security Association Key Management Protocol (ISAKMP) , einem Framework um SAs einzurichten, zu verhandeln und zu löschen. Die Funktionsweise von IKE ist in Abbildung 1.2 dargestellt. Die Aushandlung einer SA nach IKE erfolgt in 2 Phasen :

IKE Funktionsweise aus [1]

In der Phase 1 wird eine Verbindung zum Kommunikationspartner mittels der Diffie-Hellman Schlüsselaustausch Protokoll durchgeführt, siehe dazu [DH]. Diese Phase wird auch als Main Mode bezeichnet. Mit DH wird über Cookies ^[13] ein secret ausverhandelt mit welchem die weitere IKE Kommunikation verschlüsselt wird. Die Authentifizierung der beiden IPSec Gegenstellen, kann über einen preshared key, einem Zertifikat oder Public Key Encryption erfolgen. Durch diesen Vorgang wird ein einzelner SA generiert und gespeichert.
In der Phase 2 wird verschlüsselt über die IPSec Security Parameter, wie verwendete Algorithmen, Time-Outs, etc. verhandelt. Die Phase 2 wird auch als Quick Mode bezeichnet. In dieser tauschen sich beide Gegenstellen über ihre unterstützten Verschlüsselungsverfahren, Hashalgorithmen und Authentifizierungsmethoden aus. Im sogenannten Aggressive Mode, wird direkt die Krypto-Suite ausgewählt. Falls die Verbindung fehl schlägt besteht allerdings keine Möglichkeit zu erkennen welche Verfahren die Gegenstelle überhaupt anbietet. Nach Abschluss der Phase 2 werden mindestens 2 SAs (eingehend und ausgehend) erzeugt.

Authentication Header Protocol

Das Authentication Header Protokoll (AH) bietet eine transparente Überprüfung des Datenursprungs sowie des Datenpakets an . Daher kann mittels AH die Authentizität des Absenders und die Integrität der Daten überprüft werden. Optional ist eine Erkennung und Unterbindung von Replays möglich. Die Verschlüsselung der Daten ist nicht Aufgabe von AH, sondern von ESP, siehe Kapitel 1.1.3. Das AH Protokoll verwendet zur Überprüfung der Datenintegrität Message Authentication Codes, siehe dazu Kapitel [MAC]. Die dafür benötigten Informationen werden in jedem einzelnen IP Paket im Authentication Header, welcher ein Attribut des IPSec Headers darstellt, übermittelt. Der AH Header ist in Tabelle 1.2 dargestellt.

AH-Header nach
Next Header	AH Length	Reserved
Security Parameter Index (SPI)
Sequence Number
Authentication Data (MAC)

Der Next Header spezifiziert das nächste Paket. So kann eine Reihenfolge sichergestellt werden. Im Feld AH Length wird die Länge des AH Headers angegeben. Das Feld Reserved ist für zukünftige Verwendung reserviert, daher muss dieses Feld eine 0 enthalten. Der Security Parameter Index dient, wie im Kapitel 1.1 beschrieben zur Identifizierung der Security Association. Die Sequence Number ist optional und dient der Erkennung von Replays. Die Sequenznummer wird monoton inkrementiert. Im Feld Authentication Data befindet sich der über das gesamte Paket berechnete MAC Wert. Der Empfänger kann den MAC ebenfalls berechnen und kann, falls dieser nicht übereinstimmt, dieses Paket verwerfen.

Encapsulating Security Payload - Protocol

Zu den Eigenschaften des AH - Protokolls bietet das Encapsulating Security Payload (ESP) - Protokoll zusätzlich eine Verschlüsselung der Daten an. Der RFC 4303 beschreibt zwei Modi, entweder die Verschlüsselung des reinen Payloads (ohne Verkehrsdaten im Transport Mode) und zweitens die gesamte Verschlüsselung des IP Pakets im Tunnel Mode.

ESP-Format nach
Security Parameter Index (SPI)
Sequence Number
ESP Payload Data
Padding	Padding Length	Next Header

ESP Authentication Data

Ein ESP - Paket ist ähnlich dem AH - Paket aufgebaut. Er enthält einen SPI für die Identifizierung der Security Association und eine Sequenznummer. Diese beiden Teile des Headers, sowie ein Teil des ESP Authentication Data (ESP-Trailer) sind unverschlüsselt um eine Zuordnung zu ermöglichen. Der ESP - Trailer enthält den MAC Wert, um eine Überprüfung der Integrität zu ermöglichen.

SSL/TLS

Secure Socket Layer (SSL) und dessen Nachfolger das Transport Layer Security (TLS) Protokoll bieten eine Ende zu Ende Verschlüsselung an und hat sich zum Standard vor allem im Bereich der sicheren HTTP - Verbindungen, dem HTTPS - Protokoll, etabliert . SSL und TLS kann natürlich auch für andere auf TCP/IP basierende Dienste verwendet werden, wie zum Beispiel Telnet oder FTP. SSL/TLS arbeitet auf Ebene der Transportschicht des OSI Modells. Die Protokoll - Familie verwendet asymmetrische Verfahren (siehe Kapitel [asymmetrischeVerfahren]), sowie Zertifikate (siehe Kapitel [certificates]), um die Authentifikation der Kommunikationsteilnehmer durchzuführen. Es wird somit über ein asymmetrisches Verfahren eine gemeinsamer Schlüssel bestimmt, der für die weitere symmetrische Verschlüsselung verwendet wird. Die Integrität der ausgetauschten Pakte werden mittels Message Authentication Codes (siehe Kapitel [MAC]) sichergestellt.

Historie der SSL / TLS Versionen nach
1994	SSL v2	Netscape entwickelt die erste Version von SSL
1995	SSL v3	Wegen schwerer Sicherheitslücken von SSL v2 wird SSL v3 veröffentlicht (siehe RFC 6101)
1999	TLS v1.0	Die IETF standardisiert TLS v1.0, welches fast ident mit SSL v3 ist (siehe RFC 2246)
2006	TLS v1.1	Eine neue Version des TLS Protokolls wird aufgrund der BEAST Attacke veröffentlicht (siehe RFC 4346)
2008	TLS v1.2	In dieser TLS Version wird die Unterstützung für Stream und Block Verschlüsselungen entfernt, welche eine große Angriffsfläche bieten (siehe RFC 5246).
2013	TLS v1.3	Die Arbeit an Version 1.3 von TLS wurde begonnen.

SSL/TLS ist ein zustandsbehaftetes Protkoll und besteht aus zwei Bestandteilen, dem Record Protocol und dem Handshake Protocol, welche in den folgenden Kapiteln beschrieben werden.

Handshake Protocol

Das Handshake Protocol ist in RFC 5246 Section 7.3 definiert . Das Handshake Protocol hat die Aufgabe nach Verbindungseröffnung zwischen Client und Server die Verschlüsselungs - Parameter auszuhandeln.

vereinfachter Vorgang des SSL/TLS Handshakes aus [15]

Funktionsweise:

Der Client schickt im Klartext ein ClientHello an den Server. Dieses Hello enthält die kryptographischen Möglichkeiten des Clients, daher werden die höchste vom Client unterstützte Protokoll Version, eine Session ID, eine Liste von unterstützten Cipher Suiten, eine Liste der unterstützten Kompressions Methoden und ein zufällig generierter Wert, das ClientHello.random, an den Server gesendet.
Der Server schickt im Fehlerfall ein Handshake Failure und ansonsten ein ServerHello an den Client zurück. Das Hello besteht aus der Protokoll Version in Form der höchst möglichen unterstützten Version von Server und Client. Der Server sendet ebenfalls eine Session ID, eine ausgewählte Cipher Suite und Kompressions Methode aus der Liste des Clients, sowie einem ebenfalls zufällig und unabhängigen Zufallswert, dem ServerHello.random.
Nachdem der Server sein Hello gesendet hat, schickt dieser sein Zertifikat (normalerweise ein X.509 Zertifikat, siehe Kapitel [x509]) zur Authentifizierung an den Client. Falls der Server ein Client-Zertifikat zur Authentifizierung benötigt, schickt er einen entsprechenden Request an den diesen. Danach schickt der Server eine Server Hello Done Nachricht an den Client.
Der Client überprüft das erhaltene Server Zertifikat und die vom Server ausgewählten Verfahren. Sind die erhaltenen Daten korrekt, sendet der Client die sogenannte ClientKeyExchange Message an den Server. Diese enthält das PreMasterSecret, welches mit dem öffentlichen Schlüssel des Servers verschlüsselt wird. Das PreMasterSecret und die beiden Zufallswerte ClientHello.random und ServerHello.random werden von Client und Server dazu verwendet das MasterSecret zu berechnen. Dieses dient in weiterer Folge als Initialisierungswert für die Schlüsselerzeugung . Wurde vom Server ein Client-Zertifikat angefragt, sendet der Client zudem das Zertifikat oder generiert eine no certificate Fehlermeldung. Ausserdem sendet der Client ein ChangeCipherSpec Nachricht an den Server. Mit dieser wird die verwendete Cipher Suite bestätigt oder der Beginn einer neuen Methode angekündigt ^[14] . Zum Abschluss sendet der Client noch eine Finished Meldung an den Server, welche mit einem MAC mithilfe des Master Secrets verschlüsselt wurde.
Der Server sendet seinerseits eine ChangeCipherSpec Nachricht an den Client und das Handshake wird mit einer Finish Nachricht des Servers, wieder mit MAC und dem Master Secret verschlüsselt, abgeschlossen. Wenn die MACs der Finished Nachrichten auf beiden Seien übereinstimmen handelt es sich um eine akzeptierte Verbindung und der Austausch von Daten über das Record Protocol kann erfolgen.

Record Protocol

Die Aufgabe des Record Protokolls ist es Datenpakete aus dem Application Layer in sogenannte Records zu fragmentieren und wenn nötig zu komprimieren. Vom Record Protokoll werden zu den Daten werden entsprechende MAC - Hashwerte gebildet und MAC und Daten verschlüsselt. Die Generierung der MAC Schlüssel erfolgt dabei aus dem Master Secret. Dem verschlüsselten Paket wird ein Record Header vorangestellt und an den Transport Layer weitergegeben.

Operationen des Record Protocols aus [17]

Pretty Good Privacy und Web of Trust

Die Software Pretty Good Privacy (PGP) wurde 1991 von Phil Zimmerman entwickelt und stellt ein Möglichkeit bereit E-Mails und auch Dateien verschlüsselt und/oder signiert auszutauschen . PGP wurde 1998 als OpenPGP in RFC 2440 beziehungsweise RFC 4880 standardisiert und steht frei zum Download zur Verfügung. PGP verwendet für den Austausch eines symmetrischen Schlüssels das RSA beziehungsweise das DH Verfahren ein. Die Verschlüsselung des Plaintextes erfolgt dann symmetrisch mit dem ausgetauschten Schlüssel. Bei Verwendung einer digitalen Signatur wird die Integrität der Daten durch die Verwendung von HMACs sichergestellt. Für die Erstellung einer Signatur wird RSA als auch DSS unterstützt, siehe Kapitel [MAC].

Bei PGP wird eine Person über dessen Schlüssel ID und den Public Key, welche gewöhnlicherweise mit einer E-Mail Adresse verknüpft sind, identifiziert. Ein Beispiel eines Public Keys ist in Listing [lst: pgp] dargestellt. PGP speichert die eigenen Private Keys verschlüsselt in einer Datei ab, dem sogenannten Private-Key-Ring. Bei PGP ist es möglich mehrere asymmetrische Schlüsselpaare zu verwenden. Durch die Eingabe eines gesetzten Passwortes wird der Benutzer als Eigentümer des Private Keys authentifiziert. In einer weiteren Datei, dem Public-Key-Ring, werden zudem die öffentlichen Schlüssel der Empfänger und der eigene gespeichert.

Funktionsweise:

Alice möchte Bob eine mit PGP verschlüsselte E-Mail zukommen lassen. Sie generiert mit PGP einen symmetrischen Schlüssel ${\textstyle K}$ . Dafür verwendet PGP einen Pseudozufallszahlen - Generator.
Alice generiert über PGP einen Hashwert von ${\textstyle M}$ und signiert diesen mit ihrem Private Key und hängt diesen an ${\textstyle M}$ an.
Alice verschlüsselt die Nachricht ${\textstyle M}$ (welche auch den Hashwert enthält) mittels dem ausgewählten symmetrischen Verfahren und dem generierten Schlüssel. ${\textstyle K}$ ist ein Sitzungsschlüssel und nur für diese Kommunikation gültig. $C_{1}=EncSymm(M,K)$
Der Schlüssel ${\textstyle K}$ wird mit dem Public Key des Empfängers, also mit dem öffentlichen Schlüssel von Bob ${\textstyle K_{E}^{B}}$ , mit dem RSA Verfahren verschlüsselt. $C_{2}=EncAsym(K,K_{E}^{B})$
Alice schickt ${\textstyle C_{1}}$ und ${\textstyle C_{2}}$ an Bob.
Bob benötigt für die Entschlüsselung seinen privaten Schlüssel ${\textstyle K_{B}^{D}}$ . Dieser ist in PGP verschlüsselt abgelegt und Bob muss sich vor dessen Verwendung authentifizieren.
Nach erfolgreicher Authentifizierung kann Bob zuerst ${\textstyle C_{1}}$ entschlüsseln und erhält den Sitzungschlüssel ${\textstyle K}$ .
Mit dem erhaltenem Schlüssel ${\textstyle K}$ kann Bob dann ${\textstyle C_{2}}$ entschlüsseln und erhält die Nachricht ${\textstyle M}$ . Bob kann nun die eigentliche Nachricht ${\textstyle M}$ vom beigefügten Hashwert trennen. Er generiert sich nun selbst den Hashwert von ${\textstyle M}$ und kann beide Hashwerte vergleichen. Sind beide ident, kann er sich sicher sein, dass er die korrekte Nachricht erhalten hat. Dadurch dass der Hashwert von Alice signiert wurde, kann Bob mittels des öffentlichen Schlüssels von Alice auch überprüfen, ob dieser auch tatsächliche von Alice geschickt wurde.

PGP verwendet im Gegensatz zu hierarchischen Zertifikats - basierten Systemen eine dezentrale Struktur, die Web of Trust genannt wird. Um Vertrauen zu einem Public Key aufbauen zu können, können öffentliche Schlüssel von anderen signiert werden. Damit wird dem Besitzer des Public Keys vertraut (Owner Trust). So können Vertrauenspfade gebildet werden - zum Beispiel A vertraut B, B vertraut C, also kann A auch C vertrauen. Um die Vertrauenswürdigkeit eines Public Keys überprüfen zu können werden der Owner Trust und die Vertrauenswürdigkeit der Signatoren (Signatory Trust) im Attribut Key Legitimation Field (KLF) addiert. Die öffentlichen Schlüssel können auf Keyservern hochgeladen und für andere hinterlegt werden. Sie sind dann über ihre Schlüssel ID auffindbar.

Secure MIME

Secure MIME oder S/MIME erweitert den Multipurpose Internet Mail Extension (MIME) Standard um Sicherheitsfunktionen . Durch MIME wird das Datenformat von E-Mail Anhängen definiert. S/MIME ermöglicht zudem verschlüsselte und/oder digital signierte E-Mails zu verschicken. S/MIME ist in RFC 5751 spezifiziert und bietet Authentifizierung, Nachrichten Integrität, Nicht-Abstreitbarkeit des Ursprungs und Verschlüsselung der Daten für E-Mails an. Dafür wird einerseits ein asymmetrisches Verfahren, wie RSA verwendet und anderseits ein Signaturalgorithmus wie DSA eingesetzt. S/MIME ist vom Ablauf sehr ähnlich zu PGP, allerdings setzt S/MIME im Gegensatz zu PGP auf die X.509 Public Key Infrastructure. Daher muss vor der Verwendung von S/MIME ein Zertifikat einer Zertifizierungsstelle beantragt werden. Zertifizierungsstellen wie VeriSign bieten Zertifikaten an, welche nach 3 Vertrauensstufen unterschieden werden. Bei einem Klasse 1 Zertifikat, welches online beantragt werden kann, wird nur die Eindeutigkeit der E-Mail Adresse bestätigt. Bei Klasse 2 Zertifikaten wird dann auch postalisch eine Meldung an den Antragsteller geschickt, da dessen Name mit in das Zertifikat aufgenommen wird. Bei Klasse 3 muss der Antragssteller persönlich bei der Zertifizierungsstelle seine Identität vorweisen.

Secure Shell

Secure Shell (SSH) ist ein Client - Server Protokoll welches eine sichere Fernadministration von Computern über unsichere Netzwerke erlaubt . Es bietet folgende Funktionen:

eine sichere Shell auf einem entfernten Rechner
Port Forwarding beziehungsweise Tunneling von TCP/IP Verbindungen, auch über mehrere Rechnersysteme hinweg (Jumphosts)
Mittels dynamischen Port Fowarding kann ein SSH Server als SOCKS Proxy Server verwendet werden.
sicherer Dateitransfer mittels Secure copy (SCP) oder auch SFTP.
mittels Secure SHell FileSystem (SSHFS) kann das Filesystem eines entfernten Rechners gemountet werden.

SSH Architektur
SSH Connection Layer
SSH Authentication Layer
SSH Transport Layer

SSH arbeitet auf mehreren Layern und kann somit einerseits als Applikation als auch als Netzwerkprotokoll bezeichnet werden. Die einzelnen Schichten von unten nach oben sind:

Das SSH Transport Protocol ist in RFC 4253 definiert. Der Transport Layer setzt direkt auf TCP/IP auf und bietet eine sichere Verbindung für die darüber liegenden Schichten. Seine Aufgaben sind, die Aushandlung der verwendeten Algorithmen und Sitzungsschlüsseln, Serverauthentifizierung, Verschlüsselung und Sicherstellung der Integrität der Daten über HMAC.
Das SSH Authentication Protocol wird in RFC 4252 beschrieben und bietet 3 Möglichkeiten der Benutzerauthentifizierung. Die Authentifizierung kann mittels username/password, public key Verfahren (RSA, DSA) oder keyboard-interactive.
Das SSH Connection Protocol, standardisiert in RFC 4254 , führt die einzelnen Kanäle, die von SSH aufgebaut werden, zu einer einzigen SSH Verbindung durch. Durch den Austausch von Channel Requests können zudem Steuerinformationen ausgetauscht werden.

↑ nicht zu verwechseln mit One-Time Password, siehe Kapitel [OTP]
↑ Übersetzung aus der französischen Sprache
↑ Der Startwert eines Generators
↑ dem Vorgänger des National Institutes of Standards and Technology (NIST)
↑ die Zerlegung einer Zahl in ihre Primfaktoren
↑ wie über die Gruppe der Restklassen
↑ Das ist die Lane "links unten"
↑ Es gibt auch eine Variante mit Elliptic Curves
↑ Manchmal auch subordinate CAs genannt
↑ $ man shadow
↑ ersichtlich in der manual page für die Funktion crypt(3)
↑ in diesem Beispiel werden 160-Bit verwendet, der RFC 4226 definiert eine Mindest-Ausgabelänge von 128-Bit
↑ Das ist ein Hashwert aus Absender IP und Zeitstempel, nicht zu verwechseln mit einem Cookie aus dem HTTP Protokoll
↑ Das ChangeCipherSpec Protokoll stellt ein eigenständiges Protokoll dar und gehört nicht zum Handshake Protokoll

[1] t zu verwechseln mit One-Time Password, siehe Kapitel [OTP]

[2] Übersetzung aus der französischen Sprache

[3] Der Startwert eines Generators

[4] Vorgänger des National Institutes of Standards and Technology (NIST)

[5] Zerlegung einer Zahl in ihre Primfaktoren

[6] wie über die Gruppe der Restklassen

[7] Das ist die Lane "links unten"

[8] Es gibt auch eine Variante mit Elliptic Curves

[9] Manchmal auch subordinate CAs genannt

[10] $ man shadow

[11] rsichtlich in der manual page für die Funktion crypt(3)

[12] sem Beispiel werden 160-Bit verwendet, der RFC 4226 definiert eine Mindest-Ausgabelänge von 128-Bit

[13] Das ist ein Hashwert aus Absender IP und Zeitstempel, nicht zu verwechseln mit einem Cookie aus dem HTTP Protokoll

[14] Das ChangeCipherSpec Protokoll stellt ein eigenständiges Protokoll dar und gehört nicht zum Handshake Protokoll

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

Kryptographie und Zugriffskontrolle - Gesamt

Grundlagen der Kryptographie

Einleitung

Begriffserklärungen

Alice, Bob und Eve

Kryptoanalyse

klassische Verschlüsselungsverfahren

Substitutions-Verfahren

Cäsar-Verschiebung

einfache Substitution

Viginière-Verschlüsselung

One-Time Pad

Transpositions-Verfahren

Skytale

Spaltentransposition

Moderne Kryptographie

Ziele und Anforderungen moderner Verfahren

kryptographische Sicherheit

Zufallszahlen

Schlüsselmanagement

Angriffsvektoren

Symmetrische Verfahren

Stromchiffren

RC4

Blockchiffren

Betriebsmodi

Data Encryption Standard

Advanced Encryption Standard

Asymmetrische Verfahren

Diffie-Hellman Schlüsselaustausch

RSA-Verfahren

Elliptic Curve Cryptography

Hash - Verfahren

Anforderungen an kryptographische Hash - Verfahren

Das Geburtstagsparadoxon

Konstruktion von Hash - Funktionen

Merkle-Damgård Konstruktion

Schwamm Konstruktion

Message-Digest 5

Secure Hash Algorithm

SHA-1

SHA-2

SHA-3

Message Authentication Codes

Keyed-Hash Message Authentication Code

Digitale Signaturen und Zertifikate

Signatur mit RSA

Digital Signature Algorithm

X.509 und Public Key Infrastructure

Hardware Security Module

Zugriffskontrolle

Autorisierung und Modelle

Discretionary Access Control

Mandatory Access Control

Role-based Access Control

Authentisierung auf Unix Systemen

Multi-Factor Authentication

One-Time Passwords

AAA Systeme und Protokolle

Kerberos

Das RADIUS Protokoll

Sicherheit in Netzwerken

IPSec

Internet Key Exchange Protocol

Authentication Header Protocol

Encapsulating Security Payload - Protocol

SSL/TLS

Handshake Protocol

Record Protocol

Pretty Good Privacy und Web of Trust

Secure MIME

Secure Shell

Navigationsmenü

Suche