Kryptographie und Zugriffskontrolle - Hash - Verfahren

Hash - Verfahren

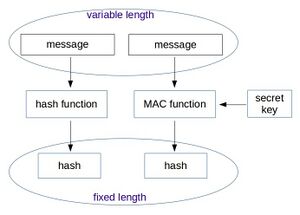
Mit Hash - Verfahren ist es möglich die Integrität von Daten zu überprüfen . Eine große Anzahl an Eingabe - Zeichen (engl. Message) wird dabei auf eine fixe Anzahl an Ausgabe - Zeichen, dem Hashwert (engl. Message Digest) abgebildet. Daher ist eine Hash - Funktion eine nicht injektive Abbildung. Eine wichtige Voraussetzung ist, dass Hashwerte schnell und einfach zu berechnen sind, damit diese auch auf embedded devices lauffähig sind. Außerdem soll eine einige Änderung an einem Dokument eine größtmögliche Auswirkung auf den Hashwert haben, wie in Tabelle 1.1 ersichtlich.

Beispiel von zwei MD5 Hashwerten

Eingabe	md5sum
das ist ein test	babcdad51f89050112c127e206cddc3e
das ist ein test!	0c4fff19d6bd9dff8d43c8d113b80a1c

Anwendungsbereiche von Hash - Verfahren sind sehr vielfältig:

• Überprüfung der Datenintegrität anhand eines Fingerabdrucks (sogenannte Prüfsummen)
• Überprüfung der Authentizität des Datenursprungs
• digitale Signaturen
• digitale Zertifikate
• Abbildung von Passwörtern
• Such- und Zugriffsverfahren im Datenbankumfeld
• Memory Adressierungs-Funktionen im Betriebssystem
• Versionskontrollsysteme
• Anti-Virus Signaturen, ..

Hash - Verfahren können in zwei generelle Klassen unterteilt werden, siehe dazu auch Abbildung 1.1:

• Schlüssellose Hash - Verfahren (engl. Hash Functions): Hierbei handelt es sich um jene Verfahren, welche rein die Überprüfung der Datenintegrität ermöglichen. Beispiele dafür sind in den nachfolgenden Kapitel 1.4 und 1.3 dargelegt.
• Schlüsselabhängige Hash - Verfahren (engl. Message Authentication Codes beziehungsweise Keyed Hash Functions): Bei Message Authentication Codes (MAC) wird ein zusätzlicher Secret Key in den Algorithmus eingefügt. Damit ist es möglich neben der Integrität der Daten auch die Authentizität des Absenders zu überprüfen. Siehe dazu auch das Kapitel 1.5

Unterschiede zwischen Hash - Funktionen und Message Authentication Codes

Anforderungen an kryptographische Hash - Verfahren

Es muss zwischen herkömmlichenund kryptographischen Hash - Verfahren unterschieden werden. Herkömmliche Hash - Verfahren sind kryptographisch nicht sicher und werden in Anwendungsgebieten verwendet in denen diese Sicherheit auch nicht erforderlich ist. Diese sind zum Beispiel, CRC Überprüfungen (Cyclic Redundancy Check), Kompressionsfunktionen, Caches, Hash Tabellen, etc.. Hingegen haben kryptographische Hash - Verfahren folgende Anforderungen an die Sicherheit :

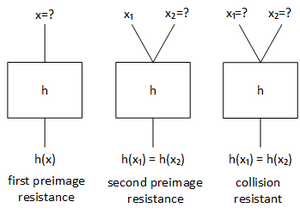
1. Es muss sich um eine Einweg - Funktion handeln. Daher muss es praktisch unmöglich sein, zu einem gegebenen Ausgabewert ${\textstyle y}$ einen Eingabewert ${\textstyle m}$ zu finden, welcher von der Hash-Funktion in ${\textstyle y}$ abgebildet wird, daher ${\textstyle h(m)=y}$. Es darf daher kein ${\textstyle m'\neq m}$ mit ${\textstyle h(m')=h(m)}$ geben. Diese Anforderung wird auch als First Preimage Resistance (Urbildresistenz) bezeichnet und definiert die grundlegende Eigenschaft einer Einweg - Funktion.
2. Es muss praktisch unmöglich sein, für einen gegebenen Eingabewert ${\textstyle m}$ einen weiteren frei wählbaren Wert ${\textstyle m'}$ zu finden, welcher über den Hash - Algorithmus den selben Hashwert ergibt. Daher ${\textstyle h(m)=h(m')}$ mit ${\textstyle m\neq m'}$. Diese Anforderung wird als Second Preimage Resistance oder auch als Weak Collision Resistance (schwach kollisionsresistent) bezeichnet.
3. Es muss praktisch unmöglich sein zwei verschiedene frei wählbare Eingabewerte ${\textstyle m}$ und ${\textstyle m'}$ mit ${\textstyle h(m)=h(m')}$ zu finden, welche den selben Hashwert ergeben. Hierbei würde es sich um ein Kollision zweier Eingabewerte handeln. Diese Anforderung wird daher als Collision Resistant (oder stark kollisionsresistent) bezeichnet

Als praktisch undurchführbar gilt ein Problem, wenn es kein bekanntes Verfahren gibt, das wesentlich schneller als das Durchprobieren aller Möglichkeiten ist.

Anforderungen an die Sicherheit von kryptographischen Hash - Funktionen nach [6]

Das Geburtstagsparadoxon

Das Geburtstagsparadoxon oder auch Geburtstagsproblem kommt oft in der Kryptoanalyse vor, da es einen Zusammenhang mit dem Finden von Kollisionen gibt . Die Frage die es zu beantworten gilt ist: Wie viele Personen müssen auf einer Geburtstagsparty anwesend sein, damit mit hoher Wahrscheinlichkeit (daher über 50 Prozent) mindestens zwei der Gäste am selben Tag Geburtstag haben?
Intuitiv würde man meinen, dass die Personenanzahl etwa die Hälfte von 365 möglichen Tagen (im Jahr) sein müsste. Jedenfalls über 100 Personen. Der Wahrscheinlichkeitsrechnung nach benötigt man allerdings viel weniger Personen, nämlich 23 . Dieses Paradoxon lässt sich auf das Finden von Kollisionen ummünzen. So ist es viel einfacher zwei Nachrichten zu finden, die denselben Hashwert ergeben, als beispielsweise zu einer gegeben Nachricht eine zweite mit demselben Hashwert zu finden. Ein Kryptoanalyst beziehungsweise Angreifer macht sich dieses Paradoxon zum Nutzen, da die Wahrscheinlichkeit höher ist eine Kollision zu finden. Er sucht daher eher nach zwei beliebigen Nachrichten, die denselben Hashwert erzeugen. Ein solcher Angriff wird als Birthday - Attack bezeichnet, ist generisch und kann auf jedes (schlüssellose) Hash - Verfahren angewendet werden.

Konstruktion von Hash - Funktionen

Kryptographisch sichere Hash - Algorithmen verwenden im Normalfall eine Folge von Kompressionsfunktionen, welche eine variable Zeichenfolge blockweise zu einem Hashwert umrechnet . Durch das Design des Kompressionsalgorithmus werden Hash - Verfahren in zwei Klassen unterteilt:

• Hash - Funktionen welche als Basis symmetrische Blockchiffren verwenden: Dabei wird die Eingabefolge in Blöcke unterteilt welche dann in den Berechnungsschritten als Schlüssel verwendet werden. Der daraus resultierende Hashwert ist aber meist nur schwach kollisionsresistent. Mittels symmetrischer Blockchiffren lassen sich zwar auch stark kollisionsresistente Hash - Verfahren realisieren, allerdings setzt dies voraus, dass der Hashwert mindestens so groß wird, wie die doppelte Blockgröße. Deswegen werden großteils dezidierte Hashfunktionen verwendet.
• dezidierte Hash - Funktionen: Diese Algorithmen wurden speziell für die Erzeugung von Hashwerten konstruiert und stehen in den nachfolgenden Kapiteln im Fokus. Das grundlegende Design von dezidierten Hash - Funktionen ist meist sehr ähnlich. Sie basieren auf den selben mathematischen Konstrukten, welche in Kapitel 1.2.1 und 1.2.2 näher betrachtet werden. Die Hash - Funktionen aus den Kapiteln 1.3 und 1.4 stammen aus dieser Klasse.

Merkle-Damgård Konstruktion

Viele Hash - Funktionen, wie MD4, MD5 und SHA-1, verwenden als Basis die sogenannte Merkle-Damgård Konstruktion (auch als Merkles Meta Methode bekannt). Sie wurde unabhängig voneinander von Ralph Merkle und Ivan Damgård entwickelt. Sie basiert auf einer Kompressionsfunktion ${\textstyle f}$.

Funktionsweise der Merkle-Damgard Konstruktion ˚

Funktionsweise:

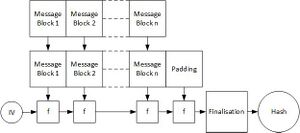
1. Die zu Eingabe Nachricht wird in gleich lange Blöcke ${\textstyle m_{1},m_{2},m_{3},..m_{n}}$ unterteilt. Der letzte Block wird mittels Padding aufgefüllt. Die Blöckgröße und in welcher Art und Weise das Padding konstruiert wird, sind Vorgabe des jeweiligen Hash - Verfahrens.
2. Die einzelnen ${\textstyle m_{i}}$ Blöcke werden nun nach der Reihe mit einer Kompressionsfunktion ${\textstyle f}$ abgearbeitet.
3. Die Funktion ${\textstyle f}$ verfügt über einen internen Zustand ${\textstyle x_{i-1}}$ des gerade behandelten Blocks ${\textstyle m_{i}}$, welcher den Nachfolgezustand ${\textstyle x_{i}}$ des nächsten Blocks definiert, daher ${\textstyle x_{i}=f(x_{i-1},m_{i})}$.
4. Die Funktion ${\textstyle f}$ und der initiale Zustand von ${\textstyle x_{0}}$ (in der Abbildung 1.3 als Initialisierungsvektor dargestellt) sind wiederum eine Konstruktionsvorgabe des jeweiligen Hash - Verfahrens und werden von diesem vorgegeben.
5. Der interne Zustand des letzten Blockes stellt den errechneten Hashwert dar.

Schwamm Konstruktion

Die Schwamm Konstruktion ist besser unter ihrem englischen Namen Sponge Construction bekannt. Sie ist der Merkle-Damgård Konstruktion ähnlich, verwendet aber anstelle einer Kompressionsfunktion eine Permutationsfunktion . Außerdem besitzt die Sponge Konstruktion keine fixe Ausgabegröße. Die Sponge Construction wurde von Guido Bertoni, Joan Daemen, Michaël Peeters und Gilles Van Assche im Zuge der SHA-3 Ausschreibung entwickelt, welche sie im Jahr 2012 auch gewinnen konnten . Siehe dazu auch Kapitel 1.4.3. Der Name Sponge resultiert aus den 2 Phasen, Absorb und Squeeze, welche durchlaufen werden.

Funktionsweise der Sponge Konstruktion aus [20]

Funktionsweise:

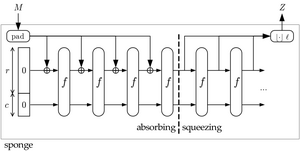
1. Die Sponge Konstruktion arbeitet mit einem internen Zustand ${\textstyle c}$, der (Capacity). Dieser interne Zustand stellt den wichtigsten Sicherheitsparamter dar und wird nicht ausgegeben.
2. Über die Bitrate ${\textstyle r}$ erfolgt die Aus- und Eingabe des Schwammes. Sie stellt somit den äußeren Zustand dar. Die Bitrate ${\textstyle r}$ kommt nie direkt mit der Capacity ${\textstyle c}$ in Berührung.
3. Die Message wird zuerst in Blöcke mit Blockgröße ${\textstyle r}$, der Bitrate, geteilt und auf den letzten Block ein Padding angehängt.
4. Die Absorbing Phase ist rundenbasiert und in dieser wird die Message eingelesen. In jeder Runde wird ein Block mit ${\textstyle r}$ Länge eingelesen und darauf eine Funktion ${\textstyle f}$ (eine Permutation mit XOR) angewendet. Das Ergebnis jeder Runde wird in den entsprechenden Capacity Bits ${\textstyle c}$ festgehalten.
5. Sind alle Blöcke abgearbeitet, wird mit der Phase Squeeze fortgesetzt. Blockweise werden die ersten ${\textstyle r}$ Bits mittels einer Funktion ${\textstyle f}$ verarbeitet und anschließend ausgegeben.

Message-Digest 5

MD5 wurde 1992 von Ronald Rivest als Nachfolger von MD4 entwickelt. MD5 war weit verbreitet bis Hans Dobbertin im Jahr 1996 eine Kollision in der Kompressionsfunktion von MD5 finden konnte . Die Hash - Funktion an sich war damit zwar nicht gebrochen, da sich die Kollision nur auf die Kompressionsfunktion bezog. Aber es entstanden Zweifel an der Sicherheit von MD5 und dessen Verwendung wurde fortan nicht mehr empfohlen. Im Jahr 2004 wurde dann eine vollständige Kollision nachgewiesen .
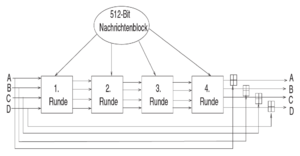
MD5 basiert auf der Merkle-Damgård Konstruktion und liefert einen 128-Bit Hashwert der folgendermaßen ermittelt wird :

Funktionsweise von MD5 aus [1]

Funktionsweise:

1. Die Eingabezeichen werden mittels Padding aufgefüllt bis ein Vielfaches von 512-Bit erreicht wird.
2. Danach werden Blöcke zu je 512-Bit gebildet, welche wiederum in 16 Stück 32-Bit Blöcke unterteilt werden. Daher jeder dieser Blöcke hat 32-Bit.
3. In 4 Runden werden die einzelnen Blöcke verarbeitet. In jeder dieser vier Runden wird einer der 32-Bit Blöcke durchlaufen. Somit ergeben sich pro Runde 16 Einzelschritte und insgesamt daher 64.
4. Die Runden selbst werden mit 4 fixen 32-Bit Variablen (A, B, C und D) initialisiert (die sogenannten Chaining Variables). Innerhalb einer Runde werden dann 16 Operationen auf die einzelnen Blöcke angewendet, welche sich pro Runde unterscheiden. Bei den Operationen handelt es sich um nicht-lineare Funktionen, modularer Addition und Linksrotation.
5. Das Ergebnis einer Runde dient als Eingabewert für die nächste Runde. Die Ergebnisse aller Runden ergeben dann den Hashwert.

Secure Hash Algorithm

Der Secure Hash Algorithm (auch als Secure Hash Standard bezeichnet) steht für eine Familie an Hash - Verfahren. SHA wurde 1993 von der National Security Agency (NSA) publiziert und als Federal Information Processing Standard (FIPS) von der NIST etabliert . Allerdings wurde kurz darauf, im Jahr 1995, bereits SHA-1 als Nachfolger, aufgrund einer Schwachstelle im SHA Algorithmus, präsentiert. SHA und SHA-1 unterscheiden sich hauptsächlich durch eine hinzugefügte Bit-Rotation in der Kompressions-Funktion. Der ursprüngliche SHA Algorithmus wurde fortan als SHA-0 bezeichnet.
SHA-2 wurde wieder von der NSA entwickelt, erstmals 2001 vorgestellt und 2002 zum neuen Standard erklärt. Die Unterschiede zu SHA-1 liegen vor allem in der Bitgröße des erzeugten Hashwertes. Mit SHA-2 wurden zudem mehrere Varianten eingeführt, welche unterschiedlich große Hashwerte erzeugen, siehe dazu Abbildung 1.4.2.

[[|Eigenschaften der SHA - Familie aus [24]]]

SHA-3 wurde nicht wie bei seinen Vorgängern von der NSA entwickelt. Die NIST entschloss sich aufgrund der Schwachstellen in SHA-1 zu einer öffentlichen Ausschreibung. 51 Algorithmen wurden dazu im Jahr 2008 eingereicht, von der NIST analysiert und bewertet. Im Jahr 2012 wurde der Algorithmus Keccak von Guido Bertoni, Joan Daemen, Michaël Peeters und Gilles Van Assche, welcher auf deren Sponge Konstruktion basiert, zum Sieger erklärt .

SHA-1

SHA-1 wurde im Jahr 1995 publiziert und gilt als Nachfolger von MD5. Wie MD5 zählt man auch SHA-1 zur Familie von MD4 Hash - Verfahren, da sich diese sehr ähneln (und nach der Merkle - Damgård Konstruktion arbeiten). Nachdem allerdings erste Zweifel an der Sicherheit von MD5 aufkamen, konkurrierten einige Zeit verschiedene Hash - Verfahren, wie Whirlepool, Tiger, RIPEMD-160 und SHA-1 miteinander. Im Jahr 2001 wurde SHA-1 jedoch durch den RFC 3174 als Internet Standard etabliert .

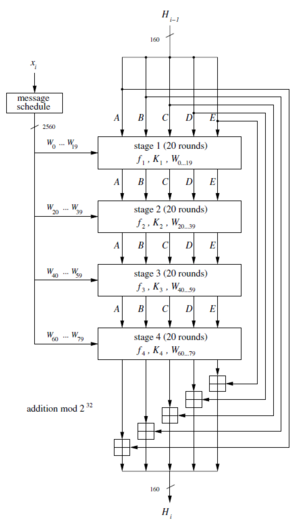
SHA-1 ähnelt in seiner Funktionsweise sehr MD5 beziehungsweise MD4. Beide basieren auch auf der Merkle-Damgård Konstruktion. SHA-1 erzeugt wie in Abbildung 1.6 ersichtlich einen 160-Bit Hashwert, im Gegensatz zu MD5, welcher nur 128-Bit Hashwerte erzeugt. Beide verwenden eine Blockgröße von 512-Bit. SHA-1 führt allerdings mehr Rundenoperationen durch als MD5. Anstelle von 64 Runden, werden bei SHA-1 80 Runden durchgeführt.

Funktionsweise der SHA-1 Kompressionsfunktion aus [6]

Funktionsweise:

1. Die zu hashende Nachricht wird um ein Padding verlängert, bis die Gesamtlänge ein Vielfaches von 512-Bit erreicht hat.

2. Die Nachricht wird in Blöcke von 512-Bit unterteilt. Jeder Block besteht dabei aus 16 Wörtern von 32-Bit Größe.

3. Diese 16 Wörter werden nun auf 80 Wörter erweitert. Dies wird durch XOR der einzelnen Wörter und einer Linksrotation ermöglicht.

4. SHA-1 verwendet 5 interne 32-Bit Variablen ${\textstyle A}$, ${\textstyle B}$, ${\textstyle C}$, ${\textstyle D}$ und ${\textstyle E}$, daher insgesamt 160-Bit. Diese sind fix vordefiniert und stellen den initialen Hashwert dar. Ihre Darstellung in Hexadezimal ist folgende:

   ${\textstyle A=H_{0}^{(0)}=67452301}$

   ${\textstyle B=H_{0}^{(1)}=EFCDAB89}$

   ${\textstyle C=H_{0}^{(2)}=98BADCFE}$

   ${\textstyle D=H_{0}^{(3)}=10325476}$

   ${\textstyle E=H_{0}^{(4)}=C3D2E1F0}$

   
   

5. Jeder der 512-Bit Blöcke durchläuft nun 4 Stufen zu je 20 Runden, daher insgesamt 80 Runden.

6. In jeder Stufe wird auf einen Teil der Nachricht eine andere Funktion ${\textstyle f}$ angewendet. Zudem werden noch weitere Konstanten ${\textstyle K_{t}}$ verwendet, die ebenfalls pro Stufe wechseln.

   Funktionen und Konstanten der SHA-1 Runden aus

   stage ${\textstyle t}$	round ${\textstyle j}$	constant ${\textstyle K_{t}}$	function ${\textstyle f_{t}}$
   1	0-19	${\textstyle K1=5A827999}$	${\textstyle f_{1}(B,C,D)=(B\wedge C)\vee (\neg B\wedge D)}$
   2	20-39	${\textstyle K2=6ED9EBA1}$	${\textstyle f_{2}(B,C,D)=B\oplus C\oplus D}$
   3	40-59	${\textstyle K3=8F1BBCDC}$	${\textstyle f_{3}(B,C,D)=(B\wedge C)\vee (B\wedge D)\vee (C\wedge D)}$
   4	60-79	${\textstyle K4=CA62C1D6}$	${\textstyle f_{4}(B,C,D)=B\oplus C\oplus D}$

   
   

7. Der Ausgangswert der sich nach 80 Runden ergibt, wird dann noch mit dem Eingangswert modulo ${\textstyle 2^{32}}$ addiert.

Es ist seit 2005 bekannt, dass bei SHA-1 Kollisionen existieren, es gilt daher bereits seit längerem als unsicher. Es wurde dann im Februar 2017 die erste Kollision nachgewiesen .

SHA-2

SHA-2 steht für eine Gruppe von Algorithmen, die als Erweiterung von SHA-1 gelten. Unter dem Sammelbegriff SHA-2 werden die Verfahren SHA-224, SHA-256, SHA-384 und SHA-512 verstanden, siehe dazu auch Abbildung 1.6. Die angehängte dreistellige Zahl bezieht sich dabei immer auf Bitgröße des Hashwertes der ausgegeben wird. Die Algorithmen unterscheiden sich vor allem durch die verwendete Blockgröße, die Größe der Wörter (32 oder 64-Bit), die Anzahl der Konstanten ${\textstyle K_{T}}$ und der Funktion ${\textstyle f_{t}}$. SHA-224 und SHA-384 werden analog wie bei SHA-256 beziehungsweise SHA-512 berechnet, nur werden nicht alle Wörter für den Hashwert verwendet. Bei SHA-224 wird das letzte 32-Bit Wort weggelassen. Bei SHA-384 werden die letzten zwei 64-Bit Wörter nicht berücksichtigt.

SHA-3

Wie schon in Kapitel 1.4 beschrieben, basiert SHA-3 auf dem Algorithmus Keccak. Dieser verwendet als unterliegende Architektur die Sponge Konstruktion, siehe Kapitel 1.2.2. SHA-3 ist von der NIST in 6 Varianten standardisiert . Diese sind SHA3-224, SHA3-256, SHA3-384 und SHA3-512, sowie 2 Varianten mit definierbarer Länge des Ausgabewertes (Extenable-Output Functions beziehungsweise XOF) namens SHAKE128 und SHAKE256. Bei den SHAKE Varianten bezieht sich der nachfolgende dreistellige Wert auf die sogenannte Security Strength. Für die XOF Algorithmen beschreibt die NIST:

"For XOFs, the length of the output can be chosen to meet the requirements of individual applications. The XOFs can be specialized to hash functions, subject to additional security considerations, or used in a variety of other applications."

Aufgrund der Flexibilität der Sponge Konstruktion wären natürlich noch viele andere Varianten möglich.

Darstellung des internen Zustands von Keccak aus [24]

Funktionsweise:
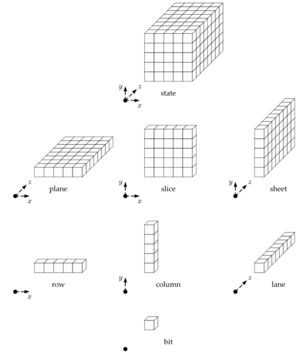
Die Funktionsweise folgt der Sponge Konstruktion aus 1.2.2. Keccak beziehungsweise SHA-3 arbeitet mit einem Zustand von 1600-Bit und kann graphisch als dreidimensionales Array dargestellt werden, siehe Abbildung 1.8. Keccak verwendet insgesamt 24 Runden innerhalb der Funktion ${\textstyle f}$ . Eine Rundenfunktion setzt sich aus 5 Einzelschritten zusammen, die als ${\textstyle \theta }$ (Theta), ${\textstyle \rho }$ (Roh), ${\textstyle \pi }$ (Pi), ${\textstyle \chi }$ (Chi) und ${\textstyle \iota }$ (Iota) definiert sind.

1. ${\textstyle \theta }$: Bits werden aufgrund ihrer Paritätssumme mittels XOR invertiert. Dies sorgt schon nach wenigen Runden für eine gute Diffusion.
2. ${\textstyle \rho }$: Durch Rotation werden die 25 64-Bit Wörter zyklisch durcheinander gewürfelt. Sorgt für eine Verbesserung der Diffusion in Kombination mit ${\textstyle \theta }$.
3. ${\textstyle \pi }$: Durch diesen Schritt werden einzelne 64-Bit Wörter miteinander vertauscht. Dadurch wird ebenfalls die Diffusion verbessert.
4. ${\textstyle \chi }$: Ist der nicht lineare Teil einer Runde. ${\textstyle \chi }$ addiert mittels XOR die darauf folgenden 2 Worte.
5. ${\textstyle \iota }$: In der Lane (0,0) werden mittels XOR die jeweilige Runden Indizes addiert. Dies hat den Effekt, dass eventuelle Symmetrien nach einigen Runden verschwinden und Keccak weniger Angriffsfläche bietet.

Message Authentication Codes

Ein Message Authentication Code verwendet einen zusätzlichen Secret Key der in die Berechnung eines Hashwertes einfließt , siehe dazu auch Abbildung 1.1. Sie werden daher auch Keyed One Way Functions genannt, also eine Einwegfunktion mit Secret Key. Ein MAC basiert daher auf einem symmetrischen Algorithmus zur Erstellung und Verifikation des Hashwertes. Die Vorteile von MAC sind die Überprüfbarkeit des Ursprungs, sowie der Integrität der Daten. Delfs und Knebl definieren den MAC und dessen Vorteile wie folgt:

"A very important application of hash functions is message authentication, which means to authenticate the origin of a message. At the same time, the integrity of the message is guaranted. If hash functions are used for message authentication, they are called message authentication codes, or MACs for short."

MACs können in zwei Gruppen unterteilt werden, je nach der Art ihrer Konstruktion :

• Blockchiffren: MACs können mithilfe von Blockchiffren erzeugt werden, zum Beispiel mit AES mit dem Betriebsmodus CBC.
• Hash - Verfahren: Die Methode ein gängiges Hash - Verfahren zur Konstruktion eines MAC zu verwenden ist in RFC 2104 , sowie dem FIPS 198-1 standardisiert. Diese Methode wird als Keyed-Hash Message Authentication Code (HMAC) bezeichnet und kommt zum Beispiel im SSL/TLS und SSH Protokoll zum Einsatz. Das folgende Kapitel 1.5.1 beschreibt die Funktionsweise näher.

Keyed-Hash Message Authentication Code

Ein HMAC besteht aus der Message ${\textstyle M}$, dem Authentication Key ${\textstyle K}$, sowie der verwendeten Hash - Funktion ${\textstyle H}$. Der HMAC lässt sich folgendermaßen darstellen :

$$HMAC(M,K)=H(K\oplus opad,H(K\oplus ipad,M))$$

Funktionsweise:

1. Der key ${\textstyle K}$ wird durch Expansion durch den Wert 0 auf eine Länge gebracht, die der Blockgröße ${\textstyle b}$ der verwendeten Hash Funktion ${\textstyle H}$ entspricht. Ist der Secret Key ${\textstyle K}$ bereits größer als die Blockgröße ${\textstyle b}$ wird ein Hashwert von ${\textstyle K}$ verwendet, daher ${\textstyle K=H(K)}$.
2. ipad und opad, zwei fixe unterschiedliche Strings werden für die weitere Berechnung verwendet. Das i und das o stehen für inner und outer.
3. ipad und der expandierte Secret Key ${\textstyle K}$ werden sodann XOR verknüpft.
4. Die Message ${\textstyle M}$ wird dem Ergebnis aus Punkt 3 angehängt.
5. Das Hashverfahren ${\textstyle H}$ wird auf den Stream aus Punkt 4 angewendet.
6. Der Key ${\textstyle K}$ wird mit dem opad definierten String XOR verknüpft.
7. Der Hashwert aus Punkt 5 wird dem Ergebnis aus Punkt 6 angehängt.
8. Die Hash - Funktion ${\textstyle H}$ wird auf den Stream aus Punkt 7 angewendet und das Ergebnis ausgegeben.