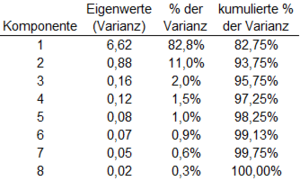
Methoden der Datenanalyse - Gesamt
Multiple Regression
Ziel dieser Lektion ist die Erweiterung des Konzepts des in der induktiven Statistik vorgestellten Konzeptes der einfachen linearen Regression (Anzur, 2007) auf mehrere erklärende Einflussgrößen.
Einleitung
Wie auch schon die einfache lineare Regression, ist die multiple lineare Regression ein Verfahren, um die (lineare) Beziehung verschiedener statistischer Merkmale abzuschätzen. Während bei der einfachen Regression nur eine erklärende und eine abhängige Variable vorhanden sind (daher auch der Name „Zwei-Variablen-Modell“), steht bei der multiplen Regression ein Satz von mehreren potentiellen erklärenden Variablen zur Verfügung. Lässt man auch mehr als eine abhängige Variable zu, spricht man üblicherweise von multivariater Regression, die aber hier nicht behandelt wird.
| Beispiel 1
Es soll nun mittels statistischer Analyse festgestellt werden, welche Variablen den Kaufpreis am besten erklären und welcher Art der Zusammenhang ist. |
|---|
Die Fragestellung könnte dadurch beantwortet werden, dass mehrere lineare Einfachregressionen berechnet werden, jedoch hängen die verschiedenen Variablen auch untereinander zusammen. Man kann hierbei die Korrelationen der verschiedenen Variablen zueinander aber nicht berücksichtigen. Beispielsweise hängen der Hubraum und die PS-Zahl eines Motors positiv miteinander zusammen und es können in einer Einfachregression nicht die getrennten Anteile beider Größen bei der Erklärung des Kaufpreises eruiert werden. Man will nun ein möglichst sparsames Modell finden, dass die wichtigsten Variablen auswählt und deren einzelne Beiträge zur Zielgröße (dem Preis) darstellt.
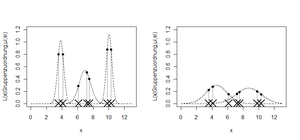
In einem ersten Schritt wird nun wie bei der Einfachregression versucht, die Zusammenhänge zwischen der Zielgröße und den verschiedenen erklärenden Variablen zu visualisieren.
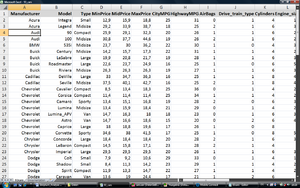
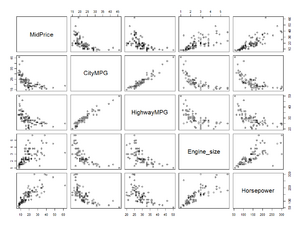
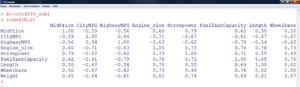
In Abbildung 2 und Abbildung 3 sind nun insgesamt acht Variablen ausgewählt, die einen mehr oder weniger inhaltlich begründeten Zusammenhang mit der Zielvariable „MidPrice“ [1] aufweisen. Der Scatterplot in Abbildung 3 rechts oben zeigt beispielsweise den Zusammenhang zwischen dem Preis und dem Gewicht des Wagens. Es zeigen sich mehrere einigermaßen lineare, jedenfalls monotone Zusammenhänge zur Zielvariable.
Modell und Schätzung der multiplen Regression
Das Modell der Daten lautet bei der multiplen Regression folgendermaßen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{i}=\beta_{0}+\beta_{1} x_{i 1}+\beta_{2} x_{i 2}+\cdots \beta_{k} x_{i k}+\varepsilon_{i}, (i=1, \ldots, n ; j=1, \ldots, k) ; }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{i}} die Werte der abhängigen Variablen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{i,j}} die Werte der erklärenden Variablen und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_{j}} die Regressionsparameter, die das Ausmaß des Einflusses der Variablen kennzeichnen, sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle +\varepsilon_{i}} die durch das lineare Modell nicht erklärten „Reste“ (=Fehler) sind.
Es wird üblicherweise angenommen, dass die Fehler Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle +\varepsilon_{i}} normalverteilt sind mit Erwartungswert gleich Null und Varianz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma^2} . Das bedeutet einerseits, dass das Modell verlangt, dass die Varianzen für alle Fehler gleich groß sind. Andererseits ist die Verteilungsannahme notwendig, um statistische Tests über die geschätzten Parameter durchführen zu können. Weiters wird auch noch angenommen, dass es keine Zusammenhänge (Korrelationen) zwischen beliebigen Fehlern gibt.
Wie im einfachen Modell werden die Werte für die Regressionsparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_{j}} ermittelt, indem das Kriterium der kleinsten Quadrate angewandt wird.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F\left(\beta_{0}, \beta_{1}, \ldots \beta_{k}\right)=\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\beta_{1} x_{i 1}-\beta_{2} x_{i 2}-\cdots \beta_{k} x_{i k}\right)^{2} \rightarrow \operatorname{Min} ! }
Die Lösung dieses Optimierungsproblemes sind nun die geschätzten Regressionsparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{0}}, \widehat{\beta}_{1}, \ldots \widehat{\beta_{k}}} .
Geometrisch bedeutet dies im Falle einer erklärenden Variable, dass die Gerade solange gedreht und verschoben wird, bis die Summe der Quadrate der vertikalen Abstände der Punkte zur Gerade im Scatterplot minimal wird. Im Falle zweier erklärender Variablen wird eine Ebene im dreidimensionalen Raum gedreht, bis sie „ideal passt“. Bei mehr als zwei erklärenden Variablen wäre es eine Hyperebene im Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} -dimensionalen Raum.
Auch hier ist es nun einfach, die durch die erklärenden Variablen prognostizierten Werte („fitted values“) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{y_{i}}} zu berechnen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{y_{i}}=\widehat{\beta_{0}}+\widehat{\beta_{1}} x_{i 1}+\widehat{\beta_{2}} x_{i 2}+\cdots \widehat{\beta_{k}} x_{i k} }
Die nicht erklärten Differenzen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\epsilon_{i}}= y_{i}- \widehat{y_{i}}} werden als „Residuen“ bezeichnet. Die Optimierungsaufgabe kann daher auch als Minimierung der Residuenquadratsumme bezeichnet werden.
| Fortsetzung Beispiel 1
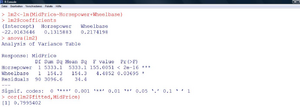
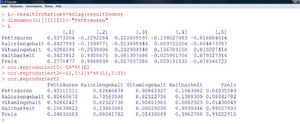
In R können die Koeffizienten folgendermaßen berechnet werden:
|
|---|
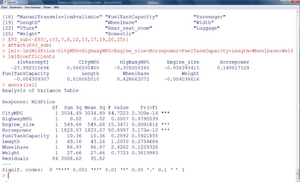
| Die Fortsetzung und die geschätzten Parameter sind nun in Abbildung 4 ersichtlich. |
Die erhaltene Gleichung zur Prognose des mittleren Preises eines Wagens lautet also folgendermaßen:
MidPrice (in T$)=
- 27,99 T$
- + Spritverbrauch in der Stadt (in “Miles“/Gallon) * 0,0865 T$
- - Spritverbrauch auf der Autobahn (in “Miles“/Gallon) * 0,3050 T$
- - Hubraum (in l) * 0,9364 T$
- + PS * 0,1498 T$
- - Tankgröße (in gallons) * 0,0043 T$
- + Länge (in inch) * 0,0181 T$
- + Radstand (in inch) * 0,4287 T$
- - Gewicht (in Pfund) * 0,0040 T$
Der prognostizierte Preis eines Buick Century Midsize wäre dann beispielsweise:
-27,99 T$ + 22 * 0,0865 T$ - 31 * 0,3050 T$ - 2,2 * 0,9364 T$ + 110 * 0,1498 T$ - 16,4 * 0,0043 T$ + 189 * 0,0181 T$ + 105 * 0,4287 T$ - 2880 * 0,0040 T$ =
-27,99 T$ + 1,90 T$ - 9,46 T$ - 2,06 T$ + 16,48 T$ - 0,07 T$ + 3,42 T$ + 45,01 T$ -11,52 T$ =15,71 T$
Der tatsächliche Preis dieses Wagens beträgt 15.700 $. Damit ist die Prognose auf 10 $ genau.
Das ausgewählte Beispiel vermittelt jedoch einen falschen Eindruck, da hier jener Wagen ausgewählt wurde, für den die Prognose am besten zugetroffen hat. Um einen Eindruck zu bekommen, wie gut das Modell zu den Daten passt, müssen nun verschiedene andere Kriterien herangezogen werden.
Interpretation und Beurteilung der Güte des Regressionsmodells
Korrelation und Bestimmtheitsmaß
Ein notwendiges, aber nicht hinreichendes Kriterium für ein gut passendes Regressionsmodell ist – wie schon im Zwei-Variablen-Modell – das Bestimmtheitsmaß.
Dieses ist definiert als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_{X, Y}^{2}=\frac{\sum_{i=1}^{n}\left(\hat{y}_{1}-\bar{y}\right)^{2}}{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}} .
Es sagt also aus, welcher Anteil an der Variabilität der Zielvariable einzig durch die erklärenden Variablen erklärt wird. So wie bei jedem Anteil errechnet sich hier eine Zahl zwischen 0 und 1 (=100%).
In Beispiel 1 kann man das Bestimmtheitsmaß aus der Aufstellung der Quadratsummen in der „Analysis of Variance“-Tabelle berechnen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}=3034,49+0,02+549,68+1823,07+10,36+43,16+86,97+27,66+3008,62=8584,33 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=1}^{n}\left(\widehat{y_{i}}-\bar{y}\right)^{2}=3034,49+0,02+549,68+1823,07+10,36+43,16+86,97+27,66 =5575,71 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_{X, Y}^{2}=\frac{5575,71}{8584,33}=65 \% }
Generell kann man sagen, dass eine Varianzerklärung von über 50% ganz gut ist. Das Bestimmtheitsmaß ist aber auch aus einer zweiten Sicht interessant, da es das Quadrat der linearen Korrelation der prognostizierten Werte mit der abhängigen Variable ist.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_{X, Y}^{2}=[\operatorname{cor}(\hat{Y}, Y)]^{2} }
Daher kann der Betrag dieser Korrelation ebenfalls errechnet werden. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{cor}(\hat{Y}, Y)=\sqrt{R_{X, Y}^{2}}=\sqrt{0,65}=0,81 }
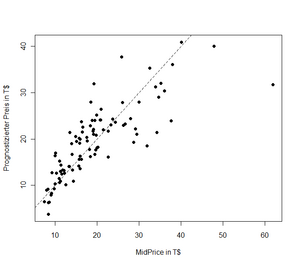
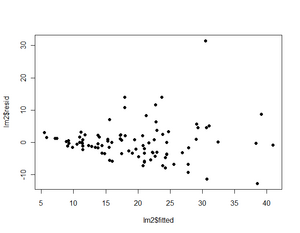
In der Gegenüberstellung der prognostizierten zu den tatsächlichen Preisen (Abbildung 5) kann man erkennen, welche Beobachtungen gut oder weniger gut geschätzt werden können. Hier sieht man auch beispielsweise sehr schön, dass der „Mercedes Benz 300E Midsize“ (ganz rechts) um ca. 30.000 $ teurer ist, als aufgrund seiner Leistungsdaten in diesem Beispiel prognostiziert.
Multikollinearität und Variablenselektion
Weder an der Tabelle in Abbildung 4, noch an den $-Beiträgen zum Gesamtpreis ist es aber möglich, festzustellen, welche Variablen nun die für den Preis wichtigsten sind. Die Komponenten der Varianz („Sum Sq“) sind davon abhängig, in welcher Reihenfolge das Modell spezifiziert wird. Es wird der Reihe nach untersucht, welchen Varianz-Anteil die jeweiligen Variablen an der Zielgröße haben. Nimmt man beispielsweise die „engine_size“ zuerst in das Modell, bleibt für die Variablen zum Spritverbrauch nicht mehr viel an Erklärung über, da dieser einigermaßen stark mit dem Motorvolumen korrelieren. Weiters führen viele hoch korrelierte Variablen dazu, dass schwerer bestimmbar ist, welchen Beitrag die einzelnen Variablen haben – die Varianzen dieser Schätzungen werden größer.
Gibt es potentielle erklärende Variablen, die sehr stark miteinander korrelieren (z.B. Spritverbrauch in der Stadt und auf der Autobahn), spricht man in diesem Zusammenhang von „beinaher Multikollinearität“, bei perfekter linearer Korrelation von „exakter Multikollinearität“. Ein Satz von erklärenden Variablen, der Multikollinearität aufweist, ist daher problematisch.
| Aufgabe 1
Berechnen Sie mit der Funktion „cor“ in R alle paarweisen Korrelationen der neun ausgewählten Variablen im obigen Regressionsmodell. |
|---|
Wie kann nun ein „brauchbarer“ Satz von Variablen zusammengestellt werden?
Besteht bei allen acht Variablen die Möglichkeit, ins Modell aufgenommen zu werden oder nicht, müssten 28-1=255 verschiedene Modelle miteinander verglichen werden (gegeben es wird zumindest eine Variable aufgenommen). Um diesen enormen Rechenaufwand zu vermindern gibt es nun verschiedene Methoden, die sich einer schrittweisen Vorgehensweise bedienen.
Ein weit verbreitetes Kriterium, dass die erklärte Varianz der Anzahl auf die Anzahl der verwendeten Variablen bezieht, ist das sogenannte „Akaike Information Criterion“ (AIC) von Akaike (1973, 1974, zitiert in Ripley, 1996, S. 34).
Fortsetzung Beispiel 1
Als Ergebnis erscheint nun eine Prozedur, die, ausgehend vom Modell mit allen acht erklärenden Variablen jeweils einzelne Variablen entfernt, solange das AIC vermindert werden kann. Im konkreten Fall ergeben sich nur mehr die „Horsepower“ und die „Wheelbase“ als relevante Einflussgrößen. |
|---|
Die erhaltene Gleichung zur Prognose des mittleren Preises eines Wagens lautet also nun:
MidPrice (in T$)= - 22,01 T$ + PS * 0,1316 T$ + Radstand (in inch) * 0,2174 T$
Der prognostizierte Preis des Buick Century Midsize wäre dann:
-22,01 T$ + 110 * 0,1316 T$ + 105 * 0,2174 T$ =15,30 T$
Wir erhalten also eine auf 400$ genaue Prognose, obwohl nun lediglich zwei statt acht Einflussgrößen im Modell sind.
Akzeptiert man dieses Modell, bedeutet dass, das ein Wagen mit 100 PS und 100 Inch Radstand im Mittel -22,01 T$ + 100 * 0,1316 T$ + 100 * 0,2174 T$ =12,89 T$ kostet. Jedes PS mehr oder weniger kostet/bringt im Mittel 131,6$ und jedes Inch mehr oder weniger beim Radstand kostet/bringt im Mittel 217,4$.
Abbildung 6 zeigt auch, dass die Korrelation zwischen dem Preis und der Prognose ebenfalls kaum merkbar gesunken ist (0,80 statt 0,81). Es findet daher quantitativ immer noch eine gute Erklärung durch das neue, deutlich sparsamere Modell statt.
Andere Variablenselektionskriterien nehmen, beginnend mit einem leeren Modell, die mit dem Zielkriterium jeweils am besten korrelierende Variable auf und prüfen, ob der Erklärungszuwachs noch statistisch signifikant ist („Vorwärtsselektion“; im Sinne eines statistischen Signifikanztests). Wieder andere Eliminieren aus dem vollen Satz an Variablen schrittweise jene, die nicht statistisch signifikant sind („Rückwärtsselektion“; ähnlich dem hier verendeten Verfahren). Das vorliegende Modell wäre auch mit den Standardeinstellungen der Vorwärts- und Rückwärtsselektion gewählt worden. Da die Korrelation zwischen Preis und PS-Stärke schon allein 0,79 beträgt, kann allerdings die PS-Stärke als weitaus wichtigere der beiden Variablen für die Erklärung des Preises identifiziert werden.
Residuenanalyse
Neben dem Bestimmtheitsmaß und der Sparsamkeit des Modells, ist es weiters bedeutend, die einzelnen Residuen der Regression zu untersuchen, und zwar in Hinblick auf
- Trend
- Ausreißer
- Heteroskedastizität
- Autokorrelation und
- Normalverteilung (NV)
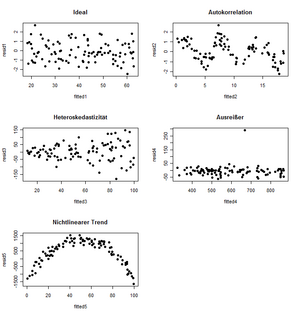
Eine Darstellung um die ersten vier genannten Punkte zu überprüfen ist in Abbildung 8 ersichtlich.
Trend
Es ist kein Trend zu erkennen. Mit wachsenden Prognosewerten bleibt das Niveau der Residuen im Mittel durchgehend auf Null.
Ausreißer
Hier sieht man wieder den Mercedes Benz von vorhin als größtes der Residuen. Es empfiehlt sich, eine Analyse ohne diesen Datenpunkt zu machen um zu sehen, wie sehr die Schätzungen beeinflusst werden.
| Aufgabe 2
Schätzen Sie die Koeffizienten des linearen Modells (Horsepower und Wheelbase) in R ohne den Mercedes 300E Midsize (Hinweis: Der Datensatz ohne die 59. Zeile – der entsprechende Wagen – wird in R folgendermaßen generiert: „X92_sub <- X93_sub[-59,]“). Wie stark ändern sich die Regressionskoeffizienten? Wie groß ist die Korrelation zwischen Preis und prognostiziertem Preis? |
|---|
Heteroskedastizität
Es ist ersichtlich, dass die mittleren Abweichungen der Daten von der Prognose umso größer werden, je teurer der Wagen ist. Sind für ähnliche Prognosewerte die Abweichungen nicht im Mittel gleich, spricht man von Heteroskedastizität. So das Ausmaß dieser Heteroskedastizität quantifiziert werden kann, sollte diese in die Modellschätzung einfließen. Die Schätzungen für die Regressionskoeffizienten unterliegen dann einer geringeren Variabilität.
Autokorrelation
Autokorrelation besteht dann, wenn Residuen von ähnlichen Datenpunkten in etwa gleich groß sind. Zum Beispiel ist die Abweichung der Temperatur am 26. und am 27. Juli von der Jahresdurchschnittstemperatur jedes Jahr in etwa gleich. Umgekehrt ist die Abweichung von der Durchschnittstemperatur im Jänner immer genau umgekehrt. Bei anderen Zeitreihen hat man ebenfalls solche Saisoneffekte (z.B. die Arbeitslosenrate) und das Ausmaß solcher Korrelationen sollte dort ebenfalls in die Modellschätzung einfließen.
Abbildung 9 zeigt nun nochmals zusammengefasst Darstellungen des „Idealfalles“ und verschiedene Modellverletzungen.
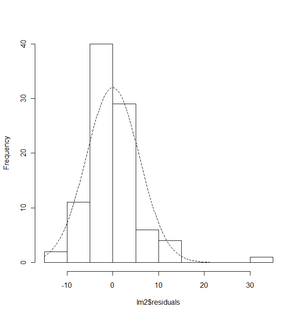
Die Annahme der Normalverteilung wird visuell mittels Histogramm (Abbildung 10) oder einem sogenannten Q-Q-Plot überprüft. Inferenzstatistisch wird der Kolmogorov-Smirnov-Anpassungstest verwendet.
Im Zuge der multiplen Regressionsanalyse können auch u.a. die einzelnen geschätzten Parameter auf Signifikanz geprüft werden, worauf aus Platzgründen hier verzichtet wird. Die Vorgehensweise ist in einführenden Büchern zu linearen Modellen beschrieben (z.B. Faraway, 2005, für eine Darstellung der Regressionsanalyse in R).
Fortsetzung Beispiel 1
Im vorliegenden Beispiel kann die NV-Annahme nicht widerlegt werden. |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Sie haben in ihrer Regression ein Bestimmtheitsmaß von 10% erhalten. Die Modellvoraussetzungen sind alle erfüllt. Was können Sie mit dieser Information anfangen?
- Was sagt ein Bestimmtheitsmaß von 100% über
a) die Korrelation zwischen prognostizierten Werten und Zielvariable,
b) über die Varianz der Residuen, und
c) über die geometrische Lage der Beobachtungspunkte aus?
Sie ziehen drei Stichproben aus einer Population und berechnen jedesmal dasselbe multiple Regressionsmodell. Folgende Parameterschätzer ergeben sich:
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{0}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{1}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{2}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{3}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{4}}} | |
|---|---|---|---|---|---|
| Stichprobe 1 | -0,3 | -0,07 | 18,1 | 44,5 | 2,2 |
| Stichprobe 2 | -0,29 | -0,09 | 22,4 | 21,9 | 1,7 |
| Stichprobe 3 | -0,32 | 0,04 | 19,3 | 2,6 | -2,5 |
Welche Variablen würden Sie aufgrund der Vorzeichen der Regressionskoeffizienten jedenfalls ausschließen? Welcher Koeffizient erscheint Ihnen weiters nicht statistisch bedeutsam?
Zusammenfassung
Die multiple Regressionsanalyse prüft das Vorhandensein einer linearen Beziehung zwischen einer abhängigen Größe und einem Satz erklärender Einflussvariablen. Es wird zunächst unterstellt, dass diese abhängige Größe von allen gewählten Einflussvariablen linear abhängt und es werden durch Optimierung jene Regressionsparameter ermittelt, welche die Summe der Quadrate der Differenzen zwischen beobachteten Werten und durch das Modell geschätzten Werten kleinstmöglich machen.
In weiteren Schritten muss nun analysiert werden, ob wirklich jede Variable für sich einen von den anderen Variablen unabhängigen Beitrag liefert. Falls dies nicht der Fall ist, wird diese eliminiert. Dazu bedient man sich neben inhaltlichen Überlegungen auch automatisierten Ansätzen, den verschiedenen statistischen Methoden der Variablenselektion.
Ist schließlich ein Modell gefunden, in dem jede Variable einen wichtigen linearen Beitrag zur Zielgröße liefert, wird üblicherweise mittels visueller Verfahren untersucht, ob Modellverletzungen vorliegen (Heteroskedastizität, Autokorrelation, Ausreißer oder nicht normalverteilte Residuen). Je nach Art einer gefundenen Modellverletzung müssen entweder komplexere Modelle mit weiteren Spezifikationen (Heteroskedastizität, Autokorrelation) gerechnet, Daten ausgeschlossen werden (Ausreißer) oder Transformationen in den Daten geschehen (nicht normalverteilte Residuen).
Varianzanalyse
Die Varianzanalyse stellt nicht nur ein spezielles Analyseverfahren, sondern eine generelle Methode dar, um Zusammenhänge zwischen verschiedenen Merkmalen inferenzstatistisch zu beurteilen. Ziel der Lektion ist das Grundmodell der Varianzanalyse sowie die wichtige Idee der Quadratsummenzerlegung darzustellen. Die Durchführung der Analysen der Modelle mit einem bzw. zwei Faktoren sowie die Umsetzung in der Software R sind die weiteren zentralen Punkte.
Begriffsabgrenzung
Die (univariate) Varianzanalyse („ANOVA“ = „analysis of variance“) wird ebenfalls dazu verwendet, den Einfluss einer oder mehrerer unabhängiger Variablen auf eine zumindest intervallskalierte (metrische) Zielvariable zu untersuchen. Im Gegensatz zur Regression sind die hier vorkommenden unabhängigen Variablen kategoriell. Es wird daher nicht eine lineare Funktion als Zusammenhang unterstellt, sondern die Varianzanalyse stellt eine Methode zur Analyse von Mittelwertsunterschieden in verschiedenen Versuchsgruppen dar. Der Name „Varianzanalyse“ kommt daher, dass zur Beurteilung der Signifikanz solcher Mittelwertsunterschiede Varianzen berechnet werden.
Liegt eine erklärende Gruppenvariable (ein „Faktor“) vor, spricht man von einer „einfachen“ bzw. „einfaktoriellen“ Varianzanalyse, ansonsten von zwei- oder mehrfaktoriellen Varianzanalysen. Im Gegensatz zur Regressionsanalyse werden üblicherweise auch Interaktionen zwischen (zwei oder mehreren) erklärenden Variablen im Modell berücksichtigt.
Die verschiedenen Ausprägungen eines jeden Faktors werden „Faktorstufen“ genannt. Hat man in jeder Faktorstufe gleich viele Daten zur Verfügung, spricht man von einem „balancierten Design“, sonst von einem „unbalancierten Design“. Gibt es (bei zumindest zwei vorhandenen Faktoren) nicht in jeder Kombination von Faktoren Beobachtungen, heißt die Versuchsanordnung „unvollständiges Design“.
Hat man als erklärende Variablen sowohl metrische, als auch kategorielle Variablen, wird eine Kovarianzanalyse durchgeführt, die aber hier nicht weiter behandelt wird. Ebenfalls nicht behandelt wird der Fall der multivariaten Varianzanalyse („MANOVA“) bei der mehrere abhängige, korrelierte Variablen vorkommen.
Typische Fragestellungen der ANOVA können sein:
- Ob und wie unterscheiden sich Mietkosten einer Wohnung in Bezug auf die Lage (Innen- vs. Außenbezirke) bzw. in Bezug auf die Zimmeranzahl?
- Gibt es Unterschiede im Ertrag bei verschiedenen Getreidesorten?
- Hängt der Absatz eines Produktes von der Platzierung im Supermarkt ab?
- Ist ein bestimmtes Training für eine Leistung förderlich?
- Ist eine Therapie in Bezug auf ein Kriterium erfolgreich?
Hinweis: Die einfaktorielle Varianzanalyse kann auch als die Verallgemeinerung des schon bekannten t-Tests (zum Vergleich zweier Erwartungswerte aus normalverteilten Grundgesamtheiten) für eine beliebige Anzahl an Erwartungswerten (Gruppen) gesehen werden.
Die einfache Varianzanalyse für unabhängige Stichproben
Modell der einfachen Varianzanalyse für unabhängige Stichproben
Formal lautet das Modell der einfachen Varianzanalyse:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{i j}=\mu+\alpha_{1}+\epsilon_{i j}, \qquad\left(i=1, \ldots, k ; j=1, \ldots, n_{i}\right) ; }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{i j}}
die Werte der metrischen Variable sind (j-ter Wert in Gruppe i), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu}
der unbedingte Erwartungswert (ohne Kenntnis der Gruppe), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_i}
der „Effekt“ von Gruppe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i}
ist (also der Unterschied des jeweiligen Gruppenerwartungswerts Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_i}
zu und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon_{i j}}
der durch die Gruppenvariable nicht erklärte Teil der abhängigen Variable – analog zur Regression, der Fehler – ist. Die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_i}
sind die Stichprobenumfänge der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k}
Gruppen.
Wie bei der Regression ist auch hier die Annahme, dass die Fehler Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon_{i j}} normalverteilt mit Erwartungswert Null und Varianz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma^2} und voneinander unabhängig sind (Varianzhomogenität und Unkorreliertheit der Fehler).
Schätzen und Testen bei der einfachen Varianzanalyse
| Beispiel 2
Es soll die Zugfestigkeit von drei Drahtsorten verglichen werden. Dazu werden von Sorte 1 sieben Proben, von Sorte 2 fünf Proben und von Sorte 3 sechs Proben auf ihre Zugfestigkeit überprüft. Es ergaben sich folgende Werte (in Newton/mm2):
Es soll die Frage untersucht werden, ob sich die einzelnen Drahtsorten hinsichtlich ihrer Festigkeit unterscheiden. |
|---|
Da in Beispiel 2 nur eine gruppierende Variable (in drei Ausprägungen) existiert, liegt eine einfache Varianzanalyse vor. Da nicht in jeder Gruppe gleich viele Beobachtungen sind, ist das Design unbalanciert.
Gemäß des Modells der einfachen Varianzanalyse haben wir also die Vorstellung: Die Zugfestigkeit einer Drahtsorte bei einem bestimmten Versuch setzt sich additiv zusammen aus
- einer mittleren Zugfestigkeit, die ein „durchschnittlicher“ Draht hat,
- einem Wert, um die die Zugfestigkeit einer speziellen Drahtsorte besser oder schlechter ist, als ein „durchschnittlicher“ Draht und
- einer Abweichung von der durchschnittlichen Zugfestigkeit dieser Drahtsorte, die in dem bestimmten Versuch beobachtet wurde und mangels anderer Erklärungsmöglichkeiten dem Zufall zugeordnet wird.
Dementsprechend werden auch die Parameter in diesem Modell geschätzt.
Schätzung der Zugfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} eines durchschnittlichen Drahts durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{\mu}=\frac{1}{\sum_{i=1}^{k} n_{i}} \sum_{i=1}^{k} \sum_{j=1}^{n_{i}} y_{i j} }
Schätzung des Effekts von Drahtsorte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_i} , durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{\alpha}_{i}=\hat{\mu}_{i}-\hat{\mu}=\frac{1}{n_{i}} \sum_{j=1}^{n_{i}} y_{i j}-\hat{\mu} }
Schätzung des Fehlers Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon_{i j}} durch das Residuum
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\epsilon_{i j}}=y_{i j}-\widehat{y_{i j}}=y_{i j}-\left(\hat{\mu}+\hat{a_{i}}\right) }
| Fortsetzung Beispiel 2
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{\mu}=\frac{1}{7+5+6}(9+15,4+\cdots+6,8+7,3+\cdots+9,7+18+\cdots+14,1)=11,717 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha_{1}}=\widehat{\mu_{1}}-\hat{\mu}=\frac{1}{7}(9+15,4+\cdots+6,8)-11,717=8,771-11,717=-2,945 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha_{2}}=\widehat{\mu_{2}}-\hat{\mu}=\frac{1}{5}(7,3+15,6+\cdots+9,7)-11,717=11,960-11,717=0,243 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha_{3}}=\widehat{\mu_{3}}-\hat{\mu}=\frac{1}{6}(18+9,6+\cdots+14,1)-11,717=14,950-11,717=3,233 } Kontrolle:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_{1} \widehat{\alpha_{1}}+n_{2} \widehat{\alpha_{2}}+n_{3} \widehat{\alpha_{3}}=0 ? \rightarrow 7 *(-2,945)+5 * 0,243+6 * 3,233=0} Residuum exemplarisch:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\varepsilon_{15}}=y_{15}-\widehat{\mu_{1}}=7,3-8,771=-1,471} |
|---|
| Aufgabe 3
Berechnen Sie für alle Beobachtungen aus Beispiel 2 die Residuen und bestimmen Sie jene Beobachtung, die durch das Modell am schlechtesten erklärt wird (d.h. das betragsmäßig größte Residuum aufweist). |
|---|
Die Schätzungen der einzelnen Parameter beschränken sich also immer nur auf die Berechnung von Mittelwerten und deren Differenzen. Aus den Berechnungen von Beispiel 2 wissen wir nun beispielsweise, dass Drahtsorte 3 eine um 3,233 Newton/mm2 größere Zugfestigkeit als der Durchschnitt aufweist. Das bezieht sich jedoch nur auf die beobachtete Stichprobe. Damit haben wir auf die ursprüngliche Frage „Unterscheiden sich die 3 Drahtsorten bezüglich der Zugfestigkeit“ nur eine deskriptivstatistische Antwort gegeben.
In der Regel ist aber von Interesse, ob wir durch die Daten genügend Evidenz dafür haben, dass sich auch die Mittelwerte der Grundgesamtheit (die Erwartungswerte) unterscheiden. Hier ist es nun wieder erforderlich, einen statistischen Test zu berechnen.
Das Hypothesenpaar bei der einfaktoriellen Varianzanalyse lautet folgendermaßen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{0}: \mu_{1}=\mu_{2}=\cdots=\mu_{k} \Leftrightarrow \alpha_{1}=\alpha_{2}=\cdots=\alpha_{k}=0 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{1}: \exists(i, j): \mu_{i} \neq \mu_{j} \Leftrightarrow \exists \alpha_{i} \neq 0 }
Getestet wird also, ob alle Erwartungswerte gleich sind, oder zumindest zwei Erwartungswerte existieren, die ungleich sind.
Beim t-Test (Anzur, 2007, S. 71) wurde als relevante Prüfgröße die Differenz der Mittelwerte der beiden Gruppen bezogen auf den Standardfehler der Mittelwertsdifferenz berechnet. Dieses Konzept ist nun nicht mehr möglich, da die Differenzen von mehr als zwei Gruppen berechnet werden müssten (die „mittlere“, die „maximale“, die „minimale“?). Anstelle der Differenz kommt nun das Konzept mit den Varianzen ins Spiel.
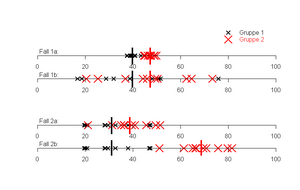
Abbildung 11 zeigt anhand von zwei Gruppen das Problem aber auch gleichzeitig die Lösung. Ziel der Varianzanalyse ist es, herauszufinden, ob die (durchschnittliche) Lage der Beobachtungen auf dem Zahlenstrahl in beiden Gruppen gleich ist. In Fall 1 besteht zwischen Gruppe 1 und Gruppe 2 bei a und b dieselbe Mittelwertsdifferenz. Es ist aber mit freiem Auge ersichtlich, dass in Fall 1a besser zwischen den beiden Gruppen getrennt werden kann, als in Fall 1b. Grund sind die größeren Varianzen innerhalb der beiden Gruppen im Fall 1b. Bei Fall 2 streuen nun die Werte aller Gruppen gleich um ihren Mittelwert. Demnach sind die Varianzen innerhalb der Gruppen jeweils gleich. Nun kann besser zwischen jenen Gruppen getrennt werden, die den größeren Mittelwertsunterschied haben. Zusammengefasst heißt das, dass umso mehr Evidenz für eine unterschiedliche Lage der Gruppen gegeben ist, je größer die Mittelwertsdifferenz ist und je kleiner die Streuung der Werte um ihren eigenen Mittelwert ist. Im Fall von mehr als zwei Gruppen wird die Mittelwertsdifferenz einfach durch die Streuung (Varianz) der Gruppenmittelwerte ersetzt.
Gegenübergestellt werden in der Varianzanalyse also die Varianzen (Quadratsummen [2] ) „innerhalb“ der Gruppen und „zwischen“ den Gruppen. Die Hilfsgrößen, um einen Test für oben genanntes Hypothesenpaar durchzuführen sind solche Quadratsummen. In der einfachen Varianzanalyse gilt immer folgende Quadratsummenzerlegung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underbrace{\sum_{i=1}^{k} \sum_{j=1}^{n_{1}}\left(y_{i j}-\hat{\mu}\right)^{2}}_{\mathrm{QT}}=\underbrace{\sum_{i=1}^{k} \sum_{j=1}^{n_{1}}\left(y_{i j}-\hat{\mu}_{i}\right)^{2}}_{\mathrm{QI}}+\underbrace{\sum_{i=1}^{k} n_{i}\left(\hat{\mu}_{i}-\hat{\mu}\right)^{2}}_{\mathrm{QZ}} }
QT…Quadratsumme „Total“
QI…Quadratsumme „Innerhalb“
QZ…Quadratsumme „Zwischen“
Die Gesamtvariabilität der Daten QT kann also in zwei additive Teile gespalten werden. Dadurch bietet sich als weitere deskriptive Größe analog zur Regressionsanalyse das Bestimmtheitsmaß an, welches als Quotient aus QZ und QT berechnet wird und wieder den Anteil an der durch das Modell erklärten Varianz an der Zielgröße angibt.
| Aufgabe 4
Denken Sie sich zwei Datensätze aus (je drei Gruppen mit je fünf Beobachtungen pro Gruppe). Einen, bei dem das Bestimmtheitsmaß 100% beträgt und einen, bei dem das Bestimmtheitsmaß 0% beträgt. Welche Charakteristik haben die Daten jeweils. |
|---|
Um nun inferenzstatistische Aussagen zu machen, wird nun die Quadratsumme „Zwischen“ nicht zur totalen Quadratsumme, sondern zur Quadratsumme „Innerhalb“ in Beziehung gesetzt. Dies liefert auch dann die Prüfgröße F [3] für unsere Hypothese:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F=\frac{M Q Z}{M Q I}=\frac{\frac{1}{k-1} Q Z}{\frac{1}{N-k} Q I}=\frac{(N-k) Q Z}{(k-1) Q I} \qquad {\left[N=n_{1}+n_{2}+n_{3}\right]} }
Es kann gezeigt werden, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F}
unter Gültigkeit der Nullhypothese (die Erwartungswerte aller Gruppen sind gleich) und den anderen vorher erwähnten Modellannahmen (Normalverteilung der Fehler) nach einer F-Verteilung mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k-1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N-k}
Freiheitsgraden verteilt ist. Dadurch werden Schranken definiert, bis zu welchen Werten von eine Entscheidung für die Nullhypothese und ab wann eine Entscheidung für die Alternativhypothese erfolgt. Was man weiters wie bei jedem statistischen Test benötigt, ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha}
, die “Irrtumswahrscheinlichkeit“ (=die Wahrscheinlichkeit, die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_0}
zu verwerfen, obwohl sie zutrifft).
| Fortsetzung Beispiel 2
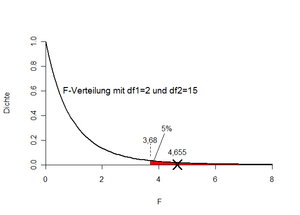
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q T=(9-11,717)^{2}+\cdots(14,1-11,717)^{2}=323,105 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q I=(9-8,771)^{2}+\cdots+(6,8-8,771)^{2}+\cdots+(14,1-14,950)^{2}=199,361 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q Z=Q T-Q I=323,105-199,361=123,744 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F=\frac{\frac{1}{3-1} * 123,744}{\frac{1}{18-3} * 199,361}=\frac{61,872}{13,291}=4,655 } |
|---|
|
|
| Aufgabe 5
Berechnen Sie für die Daten aus Beispiel 2 das Bestimmtheitsmaß. |
|---|
Soll bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F=4,655} nun für die H0 oder für die H1 entschieden werden? Bei kleinen Werten von F beobachten wir entweder kleine Werte für QZ und/oder große Werte für QI. Beides spricht eher für die H0. Umgekehrt sind große Werte für F eher Evidenz für H1. Um die Frage zu beantworten, wird nun der „kritische Wert“ in der Tabelle der F-Verteilung (oder z.B. in Excel) nachgeschlagen. Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=5%} am oberen Ende der Verteilung suchen wir de facto das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1-\alpha=95%} -Quantil der F-Verteilung mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=1=3-1=2} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N-k=18-3=15} Freiheitsgraden. In Excel kann dies mit der Funktion „FINV“ berechnet werden („=FINV(0,05;2;15)“). Dies liefert als maximal zulässigen F-Wert 3,68. Unser aus den Daten beobachtete F-Wert beträgt 4,655. Diese ist größer als der kritische Wert und daher wird die Nullhypothese verworfen. Ergebnis: Die drei Drahtsorten unterscheiden sich (bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=5%} ) signifikant voneinander bezüglich ihrer Zugfestigkeit. Abbildung 12 veranschaulicht die Entscheidungssituation nochmals.
In der Praxis rechnet man die Varianzanalyse natürlich wieder mit Software. In R kann wieder die Funktion „lm“ verwendet werden. Die unabhängige Variable muss aber als „Faktor“ spezifiziert werden, da sonst ein linearer Zusammenhang mit der Gruppennummer geschätzt wird.
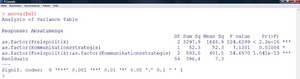
Abbildung 13 zeigt die Vorgehensweise in R, nachdem das csv-File eingelesen wurde (Name in R: „ZF“). Die geschätzten Koeffizienten sind hier nicht in der Effektkodierung angegeben (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha1, \alpha2, \alpha3} in Abschnitt 2.2.1), sondern in der sogenannten „Dummykodierung“. Die Mittelwerte der einzelnen Gruppen werden folgendermaßen reproduziert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\mu_{1}}=8,771 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\mu_{2}}=8,771+3,189=11,960 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\mu_{3}}=8,771+6,179=14,950 }
Da die Zugehörigkeit zu einer der drei Drahtsorten die einzige Information ist, die zur Prognose der Zugfestigkeit verwendet werden kann, entsprechen die geschätzten Werte für die einzelnen Daten („fitted values“) genau diesen Mittelwerten. Die „Tafel der Varianzanalyse“ liefert nun aus inferenzstatistischer Sicht die Kerninformation. Der p-Wert des Tests (siehe „Pr(>F); die Wahrscheinlichkeit, unter Gültigkeit der Nullhypothese den aus den Daten berechneten Wert für F oder einen noch größeren zu erhalten) ist kleiner als das üblicherweise gewählte Niveau des Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha}
-Fehlers (5%). Daher erfolgt auch mittels Software die Entscheidung für H1.
| Aufgabe 6
Abbildung 13 (unten) zeigt die typische „Tafel der Varianzanalyse“. Vergleichen Sie die darin vorkommenden Werte mit den bereits vorher berechneten, um die Berechnung nachzuvollziehen. In der Tafel ist statt des kritischen Wertes aus der F-Verteilung (3,68) der p-Wert ersichtlich. Versuchen Sie, die Berechnung des p-Werts in Excel mit der Funktion „FVERT“ nachzuvollziehen. Betrachten Sie dazu auch nochmals Abbildung 12. Argumentieren Sie, warum der p-Wert ausreichend ist, um für oder gegen H0 zu entscheiden und setzen Sie die Kriterien für die Testentscheidung, die in diesem Abschnitt auf zwei Wegen ermittelt wurde, zueinander in Beziehung. |
|---|
|
Aufgabe 7 Zu welcher Entscheidung würde man in Beispiel 2 bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=1%} kommen? |
|
Aufgabe 8 In welchem Verhältnis müssten in Beispiel 2 (bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=5%} bzw.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=1%} ) die Quadratsummen „Zwischen“ und „Innerhalb“ stehen, damit gerade noch für die H0 entschieden wird. Wie groß wäre dann jeweils das zugehörige Bestimmtheitsmaß? |
Prüfung der Modellvoraussetzungen, Residuenanalyse
Bei der Varianzanalyse beschränken sich die Prüfungen auf
- Ausreißer,
- Heteroskedastizität und
- Normalverteilung.
Diese werden gleich wie bei der Regressionsanalyse durchgeführt. Die Voraussetzung der Heteroskedastizität kann hier aber auch relativ einfach zusätzlich mit einem Test durchgeführt werden. Üblicherweise werden der Bartlett-Test (in R: Funktion „bartlett.test“) oder der Cochran-Test verwendet.
Multiple Mittelwertsvergleiche, Multiples Testen
Die Methode der einfaktoriellen Varianzanalyse liefert nur eine Antwort auf die Frage, ob es Unterschiede zwischen irgendwelchen zwei Gruppen gibt, aber nicht, zwischen welchen beiden Gruppen es diese Unterschiede gibt.
Um einzelne Unterschiede herauszufinden, müsste man theoretisch zwischen allen Gruppen paarweise t-Tests machen. Wie schon erwähnt, ist die einfaktorielle Varianzanalyse ja eine Verallgemeinerung des t-Tests. Man müsste dann allerdings Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{l}k 2 \end{array}\right)} solche t-Tests berechnen. Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=5} Gruppen wären das schon 10 t-Tests.
Die (neben der Notwendigkeit der zehnmaligen Durchführung eines Tests) auftretende Problematik ist, dass wenn bei jedem einzelnen Test eine 5%-Wahrscheinlichkeit besteht, einen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fehler zu begehen (d.h. die Nullhypothese fälschlicherweise zu verwerfen), die Wahrscheinlichkeit, bei 10 Tests zumindest einmal einen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fehler zu begehen, viel höher ist. Formal wäre diese Wahrscheinlichkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha^{*}=1-(1-\alpha)^{m}=1-(1-0,05)^{10}=40,1 \% }
Man kann sich das auch so vorstellen: Spielt man einmal eine Runde im Lotto mit, besteht nur eine sehr kleine Chance, einen Gewinn zu erzielen. Jedoch ist die Wahrscheinlichkeit, in 100 Lottorunden zumindest einmal zu gewinnen schon relativ hoch (wenngleich das zumeist auch die entstandenen Einsätze nicht ausgleicht…).
Die Lösung zum Testproblem ist nun, entweder den Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fehler jedes einzelnen Tests derart zu reduzieren, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} dem ursprünglich beabsichtigten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} entspricht, oder die Methode der Varianzanalyse zu verwenden, bei der nur ein Test durchgeführt wird.
In der Praxis berechnet man bei derartigen Fragestellungen zuerst eine Varianzanalyse. Fällt diese signifikant aus, werden anschließend sogenannte Post-Hoc-Tests gerechnet, die herausfinden sollen, zwischen welchen Gruppen die Unterschiede bestehen. In diesen Prozeduren werden die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fehler dann automatisch korrigiert.
Die zweifache Varianzanalyse für unabhängige Stichproben
| Beispiel 3
Der Marketingleiter eines Lebensmittelkonzerns steht vor der Frage, zu welchem empfohlenen Richtpreis eine neue Margarinemarke auf den Markt gebracht werden soll. Grundsätzlich stehen ihm drei Strategien zur Verfügung:
Neben der Preisstrategie (Faktor A) ist die Kommunikationsstrategie (Faktor B) von Interesse, und zwar in den alternativen Formen
Um die Wirkungen der Faktoren auf das Kaufverhalten zu untersuchen, wählt der Marketingleiter einen (3 x 2)-Versuchsplan, wobei auf die Kunden der ausgewählten Supermärkte jeweils eine unterschiedliche Kombination von Preis- und Kommunikationsstrategie wirken. An jeweils 10 zufällig ausgewählten Tagen werden die abgesetzten Mengeneinheiten der Margarine registriert. Die Resultate sind in der folgenden Tabelle wiedergegeben.
|
|---|
Modell der zweifachen Varianzanalyse für unabhängige Stichproben
Bei Vorliegen eines zweiten Faktors erweitert sich das einfaktorielle Modell zu
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{i j l}=\mu+\alpha_{i}+\beta_{j}+\alpha \beta_{i j}+\varepsilon_{i j l} \qquad(i=1, \ldots, k ; j=1, \ldots, m ; l=1, \ldots n) }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{i j l} }
die Werte der metrischen Variable sind (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l}
-ter Wert bei Preispolitik Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i}
und Kommunikationsstrategie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j}
), [Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu}
der unbedingte Erwartungswert (ohne Kenntnis der Gruppe), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha}
der Effekt der jeweiligen Preispolitik, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_{j}}
der Effekt der jeweiligen Kommunikationsstrategie, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha\beta_{j}}
jener Effekt ist, der sich aus der Kombination der Preispolitik Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i}
mit der Kommunikationsstrategie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j}
zusätzlich ergeben könnte und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{i j l}}
der durch die drei Effektgruppen nicht erklärte Teil der abhängigen Variable ist. Die Annahmen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{i j l}}
sind analog zum einfaktoriellen Modell.
Es kommen bei zwei erklärenden Faktoren also nicht zwei sondern drei Parametergruppen vor, weil es möglich ist, dass Kombinationen von Effekten andere Mittelwerte in der abhängigen Variable liefern. Dies wird im weiteren Verlauf der Analyse klarer.
Schätzen und Testen bei der zweifachen Varianzanalyse
Wie bei der einfachen Varianzanalyse können die einzelnen „Anteile“ an der Messung nun geschätzt werden.
Schätzung der durchschnittlichen Kaufmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{\mu}=\frac{1}{k * m * n} \sum_{i=1}^{k} \sum_{j=1}^{m} \sum_{l=1}^{n} y_{i j l} }
Schätzung des Effekts der Preispolitik i, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i, \alpha_i} , durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha_{i}}=\widehat{\mu_{l}}-\hat{\mu}=\frac{1}{m * n} \sum_{i=1}^{m} \sum_{l=1}^{n} y_{i j l}-\hat{\mu} }
Schätzung des Effekts der Kommunikationsstrategie j, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j, \beta_j} , durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{j}}=\widehat{\mu_{j}}-\hat{\mu}=\frac{1}{k * n} \sum_{i=1}^{k} \sum_{l=1}^{n} y_{i j l}-\hat{\mu} }
Schätzung des Interaktionseffektes (Preispolitik vs. Kommunikationsstrategie) durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha \beta_{\imath \jmath}}=\widehat{\mu_{\imath j}}-\left(\hat{\mu}+\widehat{\alpha_{\imath}}+\widehat{\beta_{j}}\right)=\frac{1}{n} \sum_{l=1}^{n} y_{i j l}-\left(\hat{\mu}+\widehat{\alpha_{\imath}}+\widehat{\beta_{j}}\right) }
Schätzung des Fehlers Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{i j l}} durch das Residuum
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\varepsilon_{i j l}}=y_{i j l}-\widehat{y_{i j l}}=y_{i j l}-\left(\hat{\mu}+\widehat{\alpha_{l}}+\widehat{\beta_{j}}+\widehat{\alpha \beta_{l j}}\right) }
| Aufgabe 9
Berechnen Sie die Schätzungen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{\mu}(1), \widehat{\alpha}_{i}(3) \widehat{\beta}_{j}(2) \text { und } \widehat{\alpha \beta_{i j}}\left(3^{*} 2=6\right) } |
|---|
Ob die in Aufgabe 9 berechneten deskriptiven Effekte signifikant sind, kann wieder analog obiger Vorgehensweise berechnet werden. Geprüft werden können nun drei Hypothesenpaare:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{ll} H_{0}^{(1)}: \alpha_{1}=\alpha_{2}=\alpha_{3}=0 & \rightarrow \text { Kein Einfluss der Preispolitik auf den Absatz } \\ H_{1}^{(1)}: \exists \alpha_{i} \neq 0 & \rightarrow \text { Einfluss der Preispolitik auf die Absatz } \\ H_{0}^{(2)}: \beta_{1}=\beta_{2}=0 & \rightarrow \text { Kein Einfluss der Komm.-Strategie auf den Absatz } \\ H_{1}^{(2)}: \exists \beta_{j} \neq 0 & \rightarrow \text { Einfluss der Komm.-Strategie auf den Absatz } \\ H_{0}^{(3)}: \alpha \beta_{11}=\alpha \beta_{12}=\alpha \beta_{21}=\alpha \beta_{22}=\alpha \beta_{31}=\alpha \beta_{32}=0 \\ H_{1}^{(3)}: \exists \alpha \beta_{i j} \neq 0 & \end{array} }
Interaktionen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(H_{1}^{(3)}\right)} ) bzw. keine Interaktionen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(H_{0}^{(3)}\right)} ) zwischen Preispolitik und Komm.-Strategie in Bezug auf den Absatz.
Für jede Hypothese kann nun wieder eine Quadratsumme, eine daraus abgeleitete, unter H0 F-verteilte Prüfgröße Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F} , sowie zur Bestimmung der Signifikanz ein p-Wert berechnet werden.
| Fortsetzung Beispiel 3
In R wird das lineare Modell nun so spezifiziert:
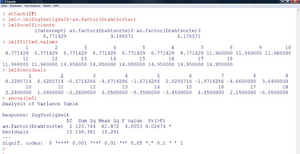
Man erhält dann folgende Tabelle (Abbildung 14): Alle p-Werte (Spalte rechts) sind kleiner als 5%. Daher wird in allen drei Fällen die Nullhypothese verworfen. Das Ergebnis ist (in Zusammenhang mit Aufgabe 9):
Die einzelnen Effekte (jene, die ausreichen, um das lineare Modell vollständig zu schätzen) können auch wieder mittels „lm1$coefficients“ ausgegeben werden. Folgender Befehl visualisiert diese Zusammenhänge schließlich noch in einem einfachen Liniendiagramm der Mittelwerte:
|
|---|
Ist ein balanciertes Design vorhanden (wie im Beispiel), macht es keinen Unterschied, in welcher Reihenfolge die Faktoren in die Gleichung eingegeben werden. Bei unbalancierten Designs ist die Interpretation der Signifikanzen schwieriger, da die Reihenfolge, in der die einzelnen Faktoren in die Gleichung eingehen, entscheidend ist.
Weitere Beispiele für varianzanalytische Designs
Varianzanalyse bei abhängigen Stichproben
Einfache Varianzanalyse für abhängige Stichproben
Wie beim t-Test für abhängige Stichproben kann auch eine Varianzanalyse für abhängige Stichproben berechnet werden. Beispielsweise, wenn Messung von Personen zu drei oder mehr Zeitpunkten vorliegen. In diesem Design können zwei Effekte geprüft werden: Unterschiede in der Versuchsbedingung (hier: Messzeitpunkt) und Unterschiede in den Versuchseinheiten (hier Personen).
Zweifache Varianzanalyse mit Messwiederholung
Hier können die Daten zum Beispiel zwei Gruppen von Personen (z.B. Männer und Frauen) sein, an denen je drei Messungen durchgeführt werden.
Unvollständige varianzanalytische Designs
Wenn nicht in allen Faktorkombinationen Daten erhoben werden, heißt das varianzanalytische Design „unvollständig“. Im folgenden werden zwei Beispiele für unvollständige Designs erwähnt.
Hierarchisches Design
Ein hierarchisches Design könnte sich beispielsweise dann ergeben, wenn man an der Wirkung eines Medikamentes, sowie am Behandlungserfolg verschiedener Spitäler interessiert ist. Sollen acht Medikamente und zwei Spitäler untersucht werden, ergibt sich ein Versuchsplan mit 2*8=12 Faktorkombinationen. Falls nun die Medikamente 1-4 nur in Spital 1 verwendet werden und die Medikamente 5-8 nur in Spital 2, dann können nicht wie in Beispiel 3 auch Wechselwirkungen auf Signifikanz getestet werden. Man sagt, dass der Faktor Medikament im Faktor Spital geschachtelt ist (auch „nested“). Dementsprechend müssen die Formeln der zweifaktoriellen ANOVA im vollständigen Design adaptiert werden.
Lateinisches Quadrat
Ein unvollständiges Design, das nicht durch mangelnde Verfügbarkeit der Daten, sondern vom Versuchsplaner selbst erzeugt wird, ist das „lateinische Quadrat“. Als Beispiel sei eine dreifaktorielle Varianzanalyse mit je drei Faktorstufen gegeben. Bei 10 Versuchseinheiten in jeder Kombination müsste man insgesamt 3*3*3*n Versuchseinheiten zur Verfügung haben. Stattdessen wird das Design auf z.B. 3*3 Faktorkombinationen gekürzt, sodass allerdings immer noch jede Faktorstufe und jede Kombination aus zwei Faktorstufen gleich oft vorkommt (Tabelle 1 und Tabelle 2). Der Vorteil dieses Designs liegt in der Kostenersparnis der Erhebung. Der Nachteil ist, dass nicht alle Hypothesen des vollständigen Designs prüfbar sind. Ist man ohnehin nur an den Einzelwirkungen der drei Faktoren und nicht an Interaktionen interessiert, fällt dieser Nachteil weg.
Tabelle 1: Übersicht über die gewählten Faktorkombinationen bei einer Kürzung
auf ein lateinisches Quadrat. Die Marker (X) geben an, welche Kombinationen tatsächlich gewählt werden
| B1 | B2 | B3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| A1 | X |
|
|
|
|
X |
|
X |
|
| A2 |
|
X |
|
X |
|
|
|
|
X |
| A3 |
|
|
X |
|
X |
|
X |
|
|
Tabelle 2: Lateinisches Quadrat aus Tabelle 1 in Kurzschreibweise
| C1 | C2 | C3 | |
|---|---|---|---|
| A1 | B1 | B3 | B2 |
| A2 | B2 | B1 | B3 |
| A3 | B3 | B2 | B1 |
Wiederholungsaufgaben und Zusammenfassung
- Welche Bedeutung kommt der Quadratsummenzerlegung in der Varianzanalyse zu?
- Warum ist es wichtig, dass die Fehler normalverteilt sind?
- Sie erhalten bei einer einfaktoriellen Varianzanalyse mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=5%} ein signifikantes Ergebnis. Wäre das Ergebnis auch signifikant, wenn Sie
- einen gleichgroßen Effekt (gleich große Mittelwertsdifferenzen) bei einem doppelt so großen Stichprobenumfang beobachten würden?
- einen gleichgroßen Effekt (gleich große Mittelwertsdifferenzen) bei einem halb so großen Stichprobenumfang beobachten würden?
- auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha=1%} testen?
Wie verändert sich der kritische Wert der F-Verteilung bei der Varianzanalyse, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} von 5% auf 1% gesenkt wird?
Zusammenfassung
Der Begriff „Varianzanalyse“ steht für eine große Zahl an Verfahren, bei denen mithilfe der Berechnung von Varianzen bzw. Quadratsummen inferenzstatistische Aussagen über Beziehungen verschiedener Variablen gemacht werden können („Quadratsummenzerlegung“). Dabei ist die Modellvorstellung immer, dass es eine oder mehrere gruppierende Variablen gibt, die auf eine metrische Variable einwirken (univariate ANOVA). Die Gruppeneinteilung kann „randomisiert“ erfolgen (indem die Versuchseinheiten zu verschiedenen Gruppen zugeordnet werden “Experiment“; Kausalschluss möglich) oder schon vorgegeben sein („Kranke vs. Gesunde“, „Männer vs. Frauen“, „Raucher vs. Nichtraucher“ „Beobachtungsstudie“; Kausalschluss nicht möglich).
Die Rechenschritte im Zuge einer Varianzanalyse betreffen einerseits die Parameterschätzungen des Modells welche auf die Berechnung von Gruppenmittelwerten und deren Differenzen hinauslaufen. Andererseits geschieht die Beurteilung, ob die in der Stichprobe gefundenen Unterschiede für die Grundgesmtheit verallgemeinert werden können, erst jeweils mittels des F-Tests, mittels Verteilungsannahmen, die sich aus der Forderung von normalverteilten Daten ableiten. Grundsätzlich gilt, dass soviele Hypothesen wie Effektgruppen vorhanden sind, getestet werden können.
Die Ergebnisse der Hypothesenprüfung werden jeweils in einer „Tafel der Varianzanalyse“ übersichtlich zusammengefasst.
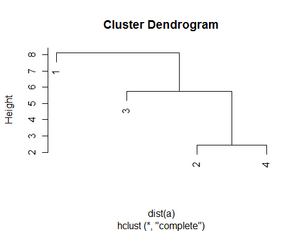
Clusteranalyse
Das Verständnis der Idee, die hinter clusteranalytischen Verfahren steckt, der Grundbegriffe und der Basis-Algorithmen, sowie die Durchführung einer Clusteranalyse in R sind die wesentlichen Ziele von Lektion 3.
Einführung und Beispielfragestellungen
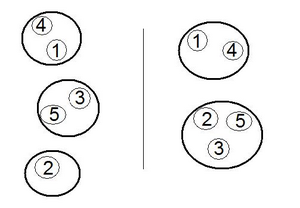
Während in den beiden vorangegangenen Kapiteln jeweils untersucht wurde, in welcher Form eine oder mehrere Merkmale von einer Reihe von weiteren Merkmalen abhängen, ist man bei der Clusteranalyse daran interessiert, die unterschiedlichen Beobachtungseinheiten (Personen, Unternehmen, Produkte,usw.) in einzelne Gruppen – die sogenannten „Cluster“ – zu teilen. Die Einteilung soll jeweils Beobachtungseinheiten zusammenfassen, die untereinander recht ähnlich und von Einheiten anderer Gruppen recht unterschiedlich sind.
Die Clusteranalyse untersucht nun im Wesentlichen,
- ob und wie gut eine solche Einteilung möglich ist,
- in wieviele Gruppen die beobachtete Stichprobe geteilt werden soll und
- wie die verschiedenen gefundenen Gruppen charakterisiert werden können.
Ziel ist es also, die Daten derart zu strukturieren, damit die einzelnen Merkmalsträger mit verschiedenen „Etiketten“ versehen werden können (“Typenbildung“). Während insbesondere mit der Varianzanalyse, aber auch mit der Regressionsanalyse bestehende Hypothesen geprüft werden können, wird die Clusteranalyse zu den hypothesengenerierenden („exploratorischen“) Verfahren gezählt. Die Daten werden hier meistens ohne Vorstellungen über die statistische Verteilung der einzelnen Gruppen analysiert. Auch können die Variablen der Clusteranalyse beliebiges Skalenniveau aufweisen.
Im folgenden einige Beispiele für den Einsatz von Methoden zur Cluster-Bildung:
- Klassifikation von Verkehrsunfällen anhand von 20 binären Merkmalen (Vogel, 1975), die zum jeweiligen Unfall erhoben wurden, unter anderen anhand der Merkmale „Werktag vs. Wochenende“, „Autobahn vs. Stadtgebiet“, „Alkoholeinfluss ja/nein“,usw..
- Ein Marktforschungsinstitut analysiert Lifestyle und Konsumentenprofile und ermittelt daraus verschiedene Kundensegmente. Die Personen werden dann beispielsweise in „Weltoffene Etablierte“, „Konsumeinsteiger“, „Bodenständige“, usw. eingeteilt. Weiters werden die Marktanteile der einzelnen Segmente berechnet.
- „Semantisches Differential“: Es kann bestimmt werden wie ähnlich sich bestimmte Worte bezüglich ihrer konnotativen Bedeutung sind. Die verschiedenen Dimensionen, die die konnotative Bedeutung beschreiben, werden mittels faktorenanalytischer Methoden (Lektion 5) anhand einer Stichprobe von wertenden Personen bestimmt.
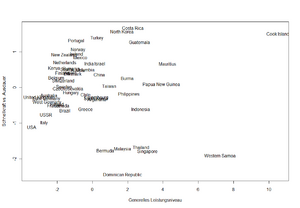
- Klassifikation verschiedener europäischer Länder nach Anteil der Angestellten in Landwirtschaft, Bauwirtschaft, Sozialarbeit, Finanzektor, usw..
- Biologie: Gruppierung von Bakterien und Mikroorganismen
Weitere Bezeichnungen für die Clusteranalyse sind „Klassifikationsverfahren“, „Unsupervised Learning“ oder auch „Pattern Recognition“.
Grundlagen der Clusteranalyse
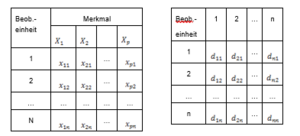
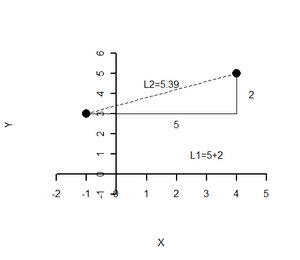
Ähnlichkeit und Distanzmaße
Um Beobachtungseinheiten gruppieren zu können, muss zunächst festgestellt werden, wie ähnlich sich die einzelnen Beobachtungen sind. Es muss also ein Maß für die Ähnlichkeit zwischen je zwei Beobachtungen definiert werden. Analog kann man statt Ähnlichkeiten auch Distanzen zwischen je zwei Beobachtungen angeben, die sich zu den Ähnlichkeiten in umgekehrter Relation verhalten. Der Ausgangspunkt einer Clusteranalyse ist bei den meisten Softwarepaketen daher entweder die Datenmatrix oder eine daraus abgeleitete Ähnlichkeits- oder Distanzmatrix (Abbildung 15). Da Ähnlichkeits- und Distanzmaße nur eine unterschiedliche Sicht des selben Sachverhalts ist, werden in weiterer Folge nur Distanzmaße betrachtet.
Die Forderungen für ein Distanzmaß sind folgende:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle - $d_{i i}=0 \forall i=1, \ldots, n$ - $d_{i j} \geq 0 \forall i \neq j=1, \ldots, n$ - $d_{i j}=d_{j i} \forall i, j=1, \ldots, n$ }
Weiters wird zumeist gefordert, dass das Distanzmaß invariant bezüglich einer Klasse von bestimmten Transformationen ist (Umskalierungen, Verschiebungen). Es soll ja keinen Unterschied machen ob Werte in cm oder m, in kg oder g, in Schilling oder Euro gemessen werden.
Bei metrischen Merkmalen werden nun am häufigsten die Minkowski-q-Metriken (Lq-Distanzen) als Distanzmaß verwendet. Diese sind gegeben durch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{m n}=\left(\sum_{i=1}^{p}\left|x_{i m}-x_{i n}\right|^{q}\right)^{1 / q} \text { für } q \geq 1 . }
Man beachte, dass alle Lq-Distanzen (außer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=2} ) nicht invariant gegenüber Drehungen des Koordinatenkreuzes (orthogonale lineare Transformationen) sind.
Ein alternatives Distanzmaß ist die „Mahalanobisdistanz“, der bei stark korrelierten Variablen der Vorzug gegeben wird.
Für einige Clusteralgorithmen ist nach Kenntnis der Distanzmatrix nur mehr die Reihenfolge der Distanzen zwischen je zwei Datenpunkten relevant.
| Aufgabe 10
Gegeben seien folgende vier Objekte, an denen jeweils drei Merkmale beobachtet wurden: (8/9/6), (6/2/3), (6/5/1), und (7/1/5). Berechnen Sie die L1- bzw. die L2-Distanzen und ordnen Sie die Objektpaare jeweils nach ihren Distanzen. Ist die Ordnung unterschiedlich? |
|---|
Im Falle von nominalskalierten Variablen müssen die Distanzen anders berechnet werden. Hier werden im wesentlichen die Übereinstimmungen zwischen je zwei Objekten gezählt und daraus Koeffizienten berechnet (siehe die entsprechenden Kapitel der vertiefenden Literatur).
Klassifikation - Partition
Wichtig im Zusammenhang mit der Clusteranalyse ist nun auch der Begriff der „Klassifikation“. Eine Klassifikation Ω ist ein System von Teilmengen (Klassen, Gruppen, Cluster) der Menge aller Beobachtungseinheiten (Objekte). In Bezug auf die Clusteranalyse fordert man zumeist, dass eine Klassifikation disjunkt und exhaustiv ist. Ersteres meint, dass jede Beobachtung zu höchstens einer Teilmenge zugeordnet wird. Zweiteres meint, dass jede Beobachtung zu mindestens einer Teilmenge zugeordnet wird. Eine Klassifikation, die disjunktiv und exhaustiv ist, nennt man „Partition“.
| Aufgabe 11
Welche Partitionen können zu den Daten in Aufgabe 10 gefunden werden? |
|---|
Die Anzahl der möglichen verschiedenen Partitionen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} Elementen ist durch die sogenannten BELLschen Zahlen [4] gegeben. Diese „explodieren“ bei wachsender Anzahl von Beobachtungseinheiten.
Tabelle 3: Bell'sche Zahlen
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| #Partitionen | 1 | 1 | 2 | 5 | 15 | 52 | 203 | 877 | 4140 | 21147 | 115975 |
| N | 20 |
|
|
|
|
50 |
|
|
|
|
|
| #Partitionen | 51724158235372 |
|
|
|
|
1,9*1047 |
|
|
|
|
|
Die „beste“ Partition zu finden ist nun die Aufgabe der Clusteranalyse und dies ist - in Anbetracht von Tabelle 3 - wenn nicht gerade drei bis fünf Objekte in Gruppen geteilt werden sollen, relativ schwierig. Analog zur Variablenselektion in der Regressionsanalyse gibt es aber nun Verfahren, die schrittweise durch Trennen oder Verbinden von Teilmengen eine möglichst gute Partitionen herausfinden sollen. Diese Methoden werden im folgenden Abschnitt diskutiert.
Hierarchische Verfahren
Grundbegriffe
Hierarchische Verfahren stellen Hierarchien von Partitionen auf. Bewegt man sich in eine Richtung der Hierarchie, unterscheiden sich „benachbarte“ Partitionen dadurch, dass entweder zwei Klassen miteinander „verschmolzen“ werden („Vergröberung“) oder eine Klasse in zwei aufgespalten wird („Verfeinerung“). In Abbildung 17 erhält man die Partition rechts durch Vergröberung der Partition links bzw. jene links durch Verfeinerung der rechten.
Je nachdem, ob das Verfahren kontinuierlich vergröbert oder verfeinert, spricht man von agglomerativen Verfahren bzw. divisiven Verfahren. Im weiteren Verlauf dieses Abschnitts soll nur auf agglomerative Verfahren eingegangen werden.
Bei agglomerativen Verfahren beginnt man mit jener Partition, in der jede Beobachtungseinheit eine Klasse definiert. Im weiteren Verlauf werden jeweils die beiden Klassen, die einander am ähnlichsten sind, miteinander zu einer Klasse verbunden. In jedem Schritt wird auch ein Heterogenitätsindex der erhaltenen Partition berechnet. Diese Prozedur geschieht solange, bis jene Klassifikation erreicht ist, die nur eine Klasse mit allen Werten enthält. Das Ergebnis eines agglomerativen Verfahrens ist eine Liste von durchgeführten Verbindungen und ein Vektor von Heterogenitätsmaßen.
Der Anwender hat nun zur genauen Durchführung der Analyse also zwei Fragen zu beantworten:
Frage 1: Was bedeutet „einander am ähnlichsten“ in Bezug auf Gruppen?
Frage 2: In wieviele und welche Gruppen sollen die Daten nun aufgeteilt werden?
Methoden zur Agglomeration
Frage 1 kann auf verschiedene Arten beantwortet werden und wieder hat der Anwender die Aufgabe, die Analyse genauer zu spezifizieren. Die Standardfunktion zur hierarchischen Clusteranalyse in R bietet beispielsweise sieben verschiedene Heterogenitätsmaße die die Unähnlichkeit zwischen je zwei Klassen ausdrücken.
Single Linkage, Complete Linkage und Average Linkage
Die Distanz zweier Klassen zueinander ist definiert als die kleinste („Single Linkage“), größte („Complete Linkage“) bzw. durchschnittliche („Average Linkage“) Distanz die zwischen beliebigen Paaren von Beobachtungen vorkommt. Die Paare bestehen dabei immer aus je einer Beobachtung aus beiden Klassen.
Median und Zentroid
Die Median- und die Zentroidmethode beziehen sich ebenfalls auf den „mittleren“ Abstand zwischen zwei Objektklassen. Der Nachteil ist hier, dass in Folge einer schrittweisen Fusionierung der Klassen das Heterogenitätsmaß nicht immer not-wendigerweise höher wird. So eine Hierarchie ist jedoch schwer zu interpretieren.
Ward
Das Ward-Kriterium fusioniert jene beiden Klassen, bei denen ein minimaler Zuwachs an Varianz innerhalb der Klassen erreicht wird.
| Beispiel 4
Betrachten wir nochmals die Daten aus Aufgabe 10. Ziel ist nun, eine hierarchische Clusteranalyse mit den Daten durchzuführen. Wir wählen als Abstand die L2-Distanz und als Agglomerations-Methode „Complete Linkage“. Zuerst Beginn besteht die Startpartition Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}_{1}=\{\{1\},\{2\},\{3\},\{4\}\}} . Nun wird die Distanzmatrix berechnet: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{12}=\sqrt{(8-6)^{2}+(9-2)^{2}+(6-3)^{2}}=\sqrt{62}}
Die Beobachtungen 2 und 4 sind jene mit dem geringsten Abstand zueinander. Diese werden zur folgenden Partition fusioniert. Damit hat die erste Vergröberung stattgefunden.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}_{1}=\{\{1\},\{2,4\},\{3\}\}} Der Heterogenitätsindex zu dieser Vergröberung ist gleich der maximal in einem Cluster vorkommenden Distanz. Daher: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{1}=\sqrt{6}} . Nach der „Complete Linkage“-Methode werden nun die neuen Abstände definiert, beispielsweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{1,(2,4)}=\max \left(d_{12}, d_{14}\right)}
Im letzten Schritt wird zur Partition Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}_{1}=\{\{1,2,3,4\}\}} fusioniert und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{3}=\max (\sqrt{66}, \sqrt{45}, \sqrt{33})=\sqrt{66}} . |
|---|
Heterogenitätsindex und Dendrogramm
Ehe Frage 2 des vorletzen Abschnitts beantwortet werden kann, sollte das Ergebnis der Analyse graphisch aufbereitet werden. Bei hierarchischen Clusteranalysen geschieht dies zumeist durch das Dendrogramm. Dies ist eine Darstellung, in welcher Reihenfolge welche Fusionsschritte vollzogen worden sind und wie heterogen die gefundenen Cluster sind. Dadurch fließt auch der jeweils protokollierte Heterogenitätsindex in die Grafik ein.
Die Entscheidung, wieviele Gruppen gebildet werden sollen, ist nun dem Anwender überlassen. Wie heterogen die Mitglieder der jeweils selben Gruppe sein sollen, hängt auch von der inhaltlichen Fragestellung ab. Daher kann in Beispiel 4 darüber keine Empfehlung gegeben werden (Abbildung 18).
| Fortsetzung Beispiel 4'''' |
|---|
Weitere Clusteralgorithmen
Partitionierende Verfahren
Die partitionierenden Verfahren unterscheiden sich von den hierarchischen Clusterverfahren dadurch, dass hier versucht wird, eine bereits bestehende Partition durch Umgruppieren einzelner Beobachtungen bezüglich festgelegten Kriteriums zu optimieren. Man sollte hier aber eine Vorstellung bezüglich der Clusteranzahl haben, da diese jeweils zu den Standard-Inputs solcher Verfahren gehören. Die Ausgangspartition kann zum Beispiel durch ein hierarchisches Verfahren ermittelt werden, aber auch durch Gruppierung um Kristallisationskerne (potentielle Klassenschwerpunkte) oder durch Verwendung zufälliger Anfangspartitionen.
Die Vorgehensweise ist weiters wie folgt:
- Definiere zusätzlich zur Startpartition ein Optimierungskriterium
Prüfe bei jeder Beobachtung, ob das Kriterium durch Zuordnung der Beobachtung in einen anderen Cluster verbessert werden kann
Ordne jene Beobachtung um, die die beste Verbesserung des Kriteriums erzielt
Wiederhole die Schritte 2 und 3 bis keine Verbesserung mehr möglich ist.
Verwendung finden oft Kriterien, die in irgendeiner Form die Streuung innerhalb der verschiedenen Gruppen minimieren (wie das schon besprochene „Ward“-Kriterium). Eine bekannte Methode stellt hierbei die (auch in R implementierte) k-Means-Methode dar.
Modellbasiertes Clustering
Im Gegensatz zu den bisherigen Verfahren, die eher auf heuristischen Überlegungen beruhen, legt man beim modellbasierten Clustering ein stochastisches Modell zugrunde. Man betrachtet die verschiedenen Gruppen als Realisierung von verschiedenen Populationen, denen jeweils eine bestimmte statistische Verteilung unterstellt wird – meist die Normalverteilung.
Bei den Modellen wird dann die Auftrittswahrscheinlichkeit gegeben eine Klassenzugehörigkeit und den Verteilungsparametern berechnet und die Klassenzuordnungen werden solange geändert, bis diese Auftrittswahrscheinlichkeit maximiert wird.
Abbildung 19 zeigt anhand einer Grafik, was hier passiert. Gegeben sind die sieben Datenpunkte, die auf der X-Achse mit einem Kreuz eingetragen sind. Es sollen nun zwei Kandidaten für eine Clustergruppierung gegenübergestellt werden. Auf der linken Seite wird die – intuitive – Lösung vorgeschlagen, eine Einteilung in drei Gruppen. Legt man die Einteilung fest, kann man daraus die Dichtefunktion der zugehörigen Normalverteilung schätzen. Führt man dies für alle drei Gruppen durch, erhält man nach Multiplikation der sieben Dichtefunktionswerte ein Maß für die Plausibilität der Stichprobe gegeben die Clustereinteilung, die „Likelihood“.
Sie beträgt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{1}\left(x \mid \text { Einteilung } 1 ; \widehat{\mu_{2}} ; \widehat{\sigma_{l}}\right)=0,80 \times 0,80 \times 0.29 \times 0.51 \times 0.4 \times 0.88 \times 0.88 \approx 0.03} .
Eine andere Partition wurde rechts gewählt. Dort wurden zwei Gruppen unterstellt (die kleinsten drei und die größten vier Beobachtungen). Wieder kann die Likelihood dieser Stichprobe berechnet werden. Diesmal ergibt sich:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_{2}\left(x \mid \text { Einteilung } 2 ; \hat{\mu}_{\nu} ; \widehat{\sigma}_{2}\right)=0,22 \times 0,28 \times 0.16 \times 0.16 \times 0.19 \times 0.20 \times 0.15 \approx 9 * 10^{-6}} .
Gewählt wird nun jene Partition, die die höchste Likelihood liefert. Für die Daten in Abbildung 19 ist die linke Gruppierung die bestmögliche.
Im multivariaten Fall (der für die Clusteranalyse relevant ist) gibt es viele Möglichkeiten, welche Annahmen über die Varianzen bzw. Kovarianzen gemacht werden (Alle Varianzen gleich oder nicht? Kovarianzen gleich Null oder nicht? usw.). Die Clusteranalyse mittels Modellannahme hat aber auch noch einen weiteren Nutzen. Es zeigt sich, dass verschiedene heuristische Verfahren implizit dieselbe Optimierung durchführen. Dadurch können diese Verfahren im Nachhinein gerechtfertigt werden.
Clusteranalyse in R
Um die Arbeitsweise eines Clusteralgorithmus besser nachzuvollziehen zu können, soll eine Analyse nun an einem Beispiel, an dem die Daten leicht visualisiert werden können (zwei Dimensionen) gerechnet werden. Im allgemeinen werden die Daten durch mehrere Variablen charakterisiert.
Die vorliegenden Daten haben fast schon sporthistorischen Wert, geht es doch um die jeweils nationalen Bestleistungen in acht olympischen Laufbewerben (100m, 200m, 400m, 800m, 1500m, 5000m, 10000m, Marathon) aus dem Jahr 1984, protokolliert vor den olympischen Spielen in Los Angeles. Ziel der Analyse ist herauszufinden, welche Länder ähnliche Bestzeiten und über ein ähnliches Leistungsniveau im Laufsport verfügen.
Mittels Hauptachsentransformation wurden bereits zwei Komponenten extrahiert, die über 90% an Varianz erklären. Diese können als „mittleres Leistungsniveau auf alle Strecken“ bzw. als „Ausdauer vs. Schnellkraft“ bezeichnet werden. Abbildung 20 zeigt die Länder in dem zweidimensionalen Raum. Nationen, die weit links stehen, haben ein hohes mittleres Leistungsniveau. Nationen, die oben stehen, haben bezogen auf ihr mittleres Leistungsniveau eine größere Bedeutung im Ausdauerbereich.
Die R-Sequenz, um aus den Daten Abbildung 20 zu erzeugen lautet wie folgt:
- Track.FA<-read.csv("C:\\...\\Track_FA.csv",header=TRUE,dec=",",sep=";")
- einlesen
- nam<-Track.FA[,1]
- dat<-Track.FA[,2:3]
- Trennung von Ländernamen und Werten
- plot(dat[,1],dat[,2],type="n",xlab="Generelles Leistungsniveau",ylab="Schnellkraft vs. Ausdauer")
- produziert einen XY-Scatterplot, allerdings ohne Punkte
- text(dat[,1], dat[,2],nam)
- trägt anschließend an den Stellen der Punkte die Ländernamen ein
Wieviele homogene Gruppen suggeriert Abbildung 20 nun? Wir haben einerseits zwei Ausreißern (Western Samoa und Cook Islands), sowie eine Gruppe von fünf Ländern im mittleren Leistungsniveau, die eher sprintstark bzw. schwach in Ausdauerbewerben sind (Dominikanische Republik, usw.). Die Topgruppe scheint vom Mittelfeld weniger gut trennbar.
Es wurde nun eine hierarchiche Clusteranalyse berechnet (Abbildung 21), die euklidische Distanzen und den „Complete-Linkage“-Algorithmus verwendet. Im Gegensatz zum „Single-Linkage“-Algorithmus, der zu bereits großen Gruppen immer noch einzelne Beobachtungen Schritt für Schritt dazuhängt, wachsen die Clustergrößen beim „Complete Linkage“ eher gleichmäßig.
Code-Fortsetzung:
Das erzeugte Objekt „result1“ ist vom Typ „hclust“, beinhaltet daher alle Informationen, die bei einer hierarchischen Clusteranalyse berechnet werden. Es können auf Wunsch mehrere Attribute ausgegeben werden. Wird so ein Objekt mit dem „plot“-Befehl versehen, entsteht das Dendrogramm (Abbildung 22). Die Gruppen sollen nun so gewählt werden, dass sie untereinander homogen und zueinander heterogen sind. Der hier gewählte Kompromiss ist jener, der das Dendrogramm horizontal an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3,1<h<4,2} schneidet und sechs Gruppen liefert. Dies wird durch die Funktion „cutree“ (Abbildung 21) erzeugt. Das Ergebnis der Gruppenzuordnung wird sodann unter „partition1“ abgespeichert.
Die beiden weiteren erstellten Partitionen wurden mit dem schon erwähnten k-Means-Algorithmus in R berechnet. Partition 2 verwendet die in Partition 1 gefundenen sechs Klassenschwerpunkte und ordnet jene Datenpunkte um, die näher zu einem anderen als dem eigenen Klassenschwerpunkt liegt. Nach einer Iteration werden die Schwerpunkte wieder neu berechnet. Das Verfahren konvergiert ziemlich schnell. Es müssen kaum Daten umgruppiert werden.
Partition 3 wählt ebenfalls die k-Means-Methode für sechs Gruppen, jedoch mit sechs zufällig gewählten Beobachtungen als Anfangsschwerpunkten. Das Verfahren wurde mehrere Male mit jeweils 1000 Iterationen durchgeführt. Die am häufigsten gefundene Gruppierung wurde hier als „partition3“ gespeichert. Die Konvergenz ist hier allerdings sehr langsam.
Die Unterschiede zwischen den drei Verfahren sind in Abbildung 23 ersichtlich. Zu beachten ist, das Partition 3 die beiden Ausreißer in eine Gruppe gibt. Unter dieser Voraussetzung wären wohl fünf Gruppen ausreichend. Am ehesten ist Einteilung 2 zu bevorzugen, da hier das Ergebnis einer hierarchischen Analyse weiter optimiert wurde und der Algorithmuss konvergiert. Jeder Datenpunkt ist dort dem Mittelpunkt seiner jeweiligen Gruppe näher als jedem anderen Mittelpunkt.
Abschließend sind die gefundenen Cluster nun noch zu charakterisieren. Tabelle 4 zeigt die Zuordnung der Länder zu den Clustern. Abbildung 24 stellt für alle acht Laufstrecken jeweils die Abweichung des Clustermittelwerts zum Gesamtmittelwert dar. Cluster 2 stellt sich als in jeder Disziplin überlegen heraus. Cluster 4 und 6 sind die beiden schwachen „Laufnationen“ am anderen Ende des Spektrums. Cluster 1 ist nach Cluster 2 die „zweite Leistungsgruppe“. Interessant sind nun Cluster 3 und 5. Cluster 3 ist in den beiden Sprintdistanzen besser als Cluster 1, in den drei längsten Distanzen jedoch nur besser als die beiden „Exoten“. Die Nationen von Cluster 5 sind bei diesen Distanzen am drittbesten, liegen aber beispielsweise auf 100m im Durchschnitt sogar hinter Western Samoa. Diese und weitere Erkenntnisse liefert also die durchgeführte Analyse.
Tabelle 4: Länderzuordnung zu den Clustern
| Cluster | Länder |
|---|---|
| 1 | Argentina, Austria, Chile, China, Columbia, Denmark, Greece, India, Ireland, Israel, Japan, South Korea, Luxembourg, Mexico, Norway, Portugal, Romania, Taiwan, Turkey |
| 2 | Australia, Belgium, Brazil, Canada, Czechoslovakia, Finland, France, East Germany, West Germany, United Kingdom, Hungary, Italy, Kenya, Netherlands, New Zealand, Poland, Spain, Sweden, Switzerland, USA, USSR |
| 3 | Bermuda, Dominican Republic, Malaysia, Singapore, Thailand |
| 4 | Cook Islands |
| 5 | Burma, Costa Rica, Guatemala, Indonesia, North Korea, Mauritius, Papua New Guinea, Philippines |
| 6 | Western Samoa |
Wiederholungsaufgaben und Zusammenfassung
- Was ist eine Partition?
Was ist eine Hierarchie?
Wie unterscheiden sich hierarchische Verfahren von partitionierenden Verfahren?
Wieviele Partitionen untersuchen Sie bei einem agglomerativen Verfahren mit gegebenen Algorithmus mit 20 Beobachtungen? Wieviele gibt es insgesamt?
Betrachten sie nochmals die vier Datenpunkte in Aufgabe 10. Führen Sie die „Average Linkage“-Methode unter Verwendung der L2-Distanzen durch und veranschaulichen Sie die Fusionsreihenfolge und die dazugehörigen Heterogenitätsindices anhand eines Dendrogramms.
Zusammenfassung
Die Clusteranalyse hat zum Ziel „ähnliche“ Objekte im Datensatz zu finden und diese dementsprechend in Gruppen (Cluster) zu ordnen. Diese Objekte sind Beobachtungseinheiten, von denen Messungen in mehreren Variablen vorhanden sind.
Zentrale Frage ist, wie „Abstand“ bzw. „Ähnlichkeit“ zwischen je zwei solcher Objekte definiert wird. Je nach Skalenniveau der Daten unterscheidet man zwischen Maßen, die die exakten Übereinstimmungen zählen oder Differenzen zwischen den einzelnen Komponenten der Beobachtungen messen. Zusätzlich muss jeweils ein Algorithmus gewählt werden, wie verschiedene Gruppierungen der Einheiten – Partitionen genannt – zu bewerten sind.
Die Gesamtzahl der Partitionen steigt rapide mit einem Zuwachs des Stichprobenumfangs. Daher ist es bereits bei Problemen mit moderaten Fallzahlen nicht möglich, alle möglichen Partitionen zu bewerten. Bei hierarchischen Verfahren werden verschiedene Partitionen schrittweise durch Verfeinerung bzw. Vergröberung erstellt. Hier wird nur ein sehr kleiner Bruchteil aller möglichen Partitionen bewertet. Bei partitionierenden Verfahren wird die Clusteranzahl festgelegt und dann ein Kriterium optimiert, das zumeist mit der Minimierung der Streuung der Datenpunkte innerhalb ihrer Cluster zu tun hat. Bei modellbasierten Verfahren verfolgt man einen stochastischen Ansatz.
Nachdem eine Partition gefunden ist, sind schließlich die gefundenen Gruppen auch zu charakterisieren und inhaltlich zu deuten.
Multidimensionale Skalierung
Die multidimensionale Skalierung bedient sich ähnlicher Techniken und Ideen wie die Clusteranalyse und die Faktorenanalyse. Ziel der Lektion ist es, Unterschiede und Gemeinsamkeiten herauszuarbeiten sowie exemplarisch in eine Analyse in R einzuführen.
Wir verlassen nun jene statistischen Analyseverfahren, die primär das Ziel haben, über die beobachteten Daten Voraussagen zu treffen und wechseln zu solchen, die auch latente (nicht messbare) Dimensionen („Faktoren“) zur Erklärung der beobachteten Daten zulassen.
Die Analyse mittels „multidimensionaler Skalierung“ (MDS) wird in diesem Skriptum nicht zufällig zwischen Clusteranalyse und Faktorenanalyse behandelt, sondern vereint auch Elemente aus beiden Analysemethoden in sich und nimmt damit eine Zwischenstellung ein.
Ziel des Verfahrens ist es, eine Anzahl von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} Objekten hinsichtlich ihrer Ähnlichkeit in der subjektiven Wahrnehmung durch eine oder mehrere Personen in einem für den Anwender übersichtlichen „Raum“ zu positionieren und abzubilden.
Merkmale, die einen Raum aufspannen, können hier nicht abgefragt werden, weil sie oft nicht bewusst sind und nur assoziativ angesprochen werden. Personen sollen lediglich Ähnlichkeits- und Distanzaussagen machen.
Die Gemeinsamkeit zur in der vorigen Lektion besprochenen Clusteranalyse besteht darin, dass Distanzen zwischen verschiedenen Objekten die zentrale Rolle in diesem Verfahren spielen. Der Unterschied ist jedoch, dass diese Distanzen oft nicht – wie in der Clusteranalyse – aufgrund von beobachtbaren Merkmalsausprägungen in verschiedenen Variablen objektiv berechnet werden können, sondern diese Distanzen nur in der Vorstellung der Personen existieren. Als Ergebnis einer MDS ist daher nicht nur die Darstellung von Objekten im Raum zu nennen, sondern ggf. auch die Interpretation der diesen Raum aufspannenden Dimensionen. Diese latenten Dimensionen bilden die Verbindung zur Faktorenanalyse, die im nächsten Abschnitt besprochen wird. Den Aspekt der Datenreduktion ist den beiden Verfahren ebenfalls gemein.
Grundlagen und Annahmen
Die Grundannahme besteht darin, dass ein Raum existiert, der durch orthogonale Achsen gebildet wird und die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} Objekte so darstellt, dass einander ähnliche Objekte beisammen liegen (eine niedrige Distanz aufweisen) und einander unähnliche Objekte weit voneinander entfernt sind. Idealerweise gilt für alle Paare von je zwei Objekten zueinander Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{i j} \leq d_{k l}} , falls die Objekte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j} als einander ähnlicher eingestuft werden als die Objekte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{i j} } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{k l} } sind die im gewählten Raum ersichtlichen Distanzen der Objekte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle j} bzw. und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} zueinander).
| Beispiel 5
Die beliebte Einordnung von politischen Parteien in Links- und Rechtsparteien könnte als eindimensionales Ergebnis einer MDS gesehen werden. Ergibt sich für eine Person z.B. die Einteilung „Grüne“ – „SPÖ“ – „ÖVP“ – „FPÖ“, so heißt dies, dass die „FPÖ“ der „ÖVP“ jedenfalls näher steht als der „SPÖ“. Wahlanalysen zeigen jedoch oft, dass gerade „SPÖ“ und „FPÖ“ oft ähnliche Wählerschichten ansprechen, was eine derartige Einteilung unzureichend machen würde. |
|---|
| Beispiel 6
Die MDS kann auch verwendet werden, um Marktlücken ausfindig zu machen. Hat man beispielsweise die in Abbildung 25 dargestellte Vorstellung über den Fast-Food-Markt in Österreich, können hier „freie Flecken“ identifiziert werden (z.B. rechts oben für eine neue Fastfood-Kette „Food 4 FUN“). |
|---|
Der Input bei dieser Analyse ist jeweils eine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N x N} Matrix, die entweder metrische Distanzen zwischen je zwei Objekten enthält (beispielsweise aufgrund des Ratings einer Person, die alle Paare von Objekten hinsichtlich ihrer Distanzen bewertet) – man spricht hier von metrischer MDS – oder schlichtweg die Reihenfolge der Ähnlichkeiten zwischen je zwei Objekten. Im letzten Fall spricht man von „nichtmetrischer MDS“. Ein Beispiel für eine metrische MDS könnte die örtliche Positionierung von Städten zueinander auf Basis der angegebenen Entfernungen der Städte zueinander sein (wie in einem Autoatlas ersichtlich). Die Verfahren, die metrische MDS durchführen, reduzieren sich im wesentlichen auf Fragestellungen, die in der Faktorenanalyse in der nächsten Lektion behandelt werden. In weiterer Folge wird hier daher auf die nichtmetrische MDS, die als Ziel die Optimierung der Ordnungsstruktur der Distanzen hat, eingegangen.
Etwas verkürzt kann man also sagen, dass eine Ordnung der Objektpaare als Input in diesem Verfahren übergeben wird und eine metrische Information das Ergebnis ist. Es findet damit eine Transformation auf eine Skala höherer Ordnung statt (metrisch statt ordinal). Bis jetzt ist noch unzureichend geklärt, ob es gerechtfertigt ist, aus empirisch ermittelten Ähnlichkeiten auf die Lage der Objekte im mehrdimensionalen Raum zu schließen.
Um die ordinale Information über die Ähnlichkeitsbeziehungen abzufragen, wird häufig eine der folgenden drei Methoden angewandt:
- Eine vollständige Rangordnung aller möglichen Paare. Die Person muss alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{c} N 2 \end{array}\right)} Paare von Beziehungen hinsichtlich ihrer Ähnlichkeit ordnen.
- Die Tetradenmethode: Bei allen Paaren von Objektpaaren muss bestimmt werden, welche einander ähnlicher sind.
- Die Ankerpunktmethode: Es werden einzelne Objekte herausgegriffen und die Ähnlichkeiten zu zumindest zwei anderen Objekten miteinander verglichen.
| Beispiel 7
Bei vier Objekten müssten folgende Kombinationen bewertet werden Vollständige Rangordnung: 12, 13, 14, 23, 24, 34 Tetradenmethode: 12 vs. 13, 12 vs. 14, 12 vs 23, 12 vs. 24, 12 vs. 34, 13 vs. 14, 13 vs. 23, 13 vs. 24, 13 vs. 34, 14 vs. 23, 14 vs. 24, 14 vs. 34, 23 vs. 24, 23 vs. 34, 24 vs. 34 Ankerpunktmethode mit drei Objekten: 12 vs. 13, 21 vs. 23, 31 vs. 32 12 vs. 14, 21 vs. 24, 41 vs. 42 13 vs. 14, 31 vs. 34, 41 vs. 43 23 vs. 24, 32 vs. 34, 42 vs. 43 |
|---|
| Aufgabe 12
Wieviele Relationen müssen bei 15 Objekten verglichen werden (nach der Methode der vollständigen Rangordnung bzw. der Tetradenmethode)? |
|---|
Sieht man von möglichen Problemen ab, die durch solche Bewertungen auftreten können – z.B. nicht transitive bzw. nicht symmetrische Ordnungen, die ein Hinweis sein können, dass Objekte nicht in einem metrischen Raum wahrgenommen werden – gestaltet sich die Aufgabe, aus einer solcherart gefundenen Ordnung die Lage der Punkte zueinander abzuleiten, relativ eindeutig.
Weiters zu entscheiden ist nun einerseits, in welcher Metrik das Ergebnis (die sogenannte „Konfiguration“) berechnet werden soll. Hier werden üblicherweise die schon erwähnten Minkowski-q-Metriken gewählt und unter diesen jene für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=2} (euklidische Distanz). Dies vor allem wegen der auch in der Faktorenanalyse wichtigen Invarianz der Lösung bezüglich Drehungen oder Spiegelungen [5] . Andererseits ist die Dimensionalität des zu erzeugenden Raumes zu wählen. Hier hat man zunächst keine Anhaltspunkte, da das finden von Dimensionen gerade die Aufgabe der MDS ist. Jedoch kommen die meisten Autoren aufgrund der Tatsache, dass die menschliche Vorstellung bei dreidimensionalen Räumen endet zu der Auffassung, dass zwei oder drei Dimensionen ausreichend sind. Hinweise, ob zwei oder drei Dimensionen besser sind, folgen noch. Das Vorgehen bei einer nichtlinearen MDS wird im folgenden Abschnitt beispielhaft demonstriert.
Konkretes Vorgehen bei der MDS
| Beispiel 8
Gegeben seien fünf Objekte A-E. Anhand folgender Ordnungsrelation der Ähnlichkeiten von je zwei Objekten soll eine MDS durchgeführt werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \overline{A D}<\overline{B E}<\overline{A C}<\overline{C D}<\overline{B C}<\overline{D E}<\overline{A E}<\overline{C E}<\overline{A B}<\overline{B D} } Die Angabe bedeutet, dass sich die Objekte A und D am ähnlichsten und die Objekte B und D am unähnlichsten sind. |
|---|
| Aufgabe 13
Zeigen Sie, dass die Objekte A bis E aus Beispiel 8 nicht in einer Dimension positioniert werden können, ohne zumindest eine der beschriebenen Ungleichungen zu verletzen. |
|---|
Wahl einer Startkonfiguration
Zu Beginn der Analyse wird die Dimension der Lösung, sowie die Metrik festgelegt. Wir entscheiden uns aufgrund der sehr geringen Anzahl an Objekten für eine zweidimensionale Lösung und für die euklidische Distanz. Es kann nun eine beliebige Positionierung der Punkte im zweidimensionalen Raum als Startlösung gewählt werden.
| Fortsetzung Beispiel 8
Wir wählen folgende Startkonfiguration:
Die sich daraus ergebenden quadrierten [6] euklidischen Distanzen lauten (vgl. Minkowski-Metrik in Abschnitt 3.2.1):
|
|---|
Monotoniebedingung und Disparitäten
Vergleicht man die Größenordnung der Distanzen mit der geforderten Größenordnung sorgfältig, erkennt man beispielsweise, dass die Distanz zwischen A und D – wie gefordert – die kleinste ist. Wir würden diese Tatsache mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{A D}=d_{A D}=1} notieren. Die Distanz zwischen B und E hingegen sollte die zweitkleinste sein (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{D E}=2} ), ist aber die größte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{B E}=2} . Einen Eindruck über die Gesamtanpassung bekommt man, wenn man die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u} - und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} -Werte einander im sogenannten „Shepard-Diagramm“ gegenüberstellt. Im Idealfall würden wir nun eine monoton nichtfallende Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u} sehen, was offensichtlich nicht der Fall ist.
Die Disparitäten sind mit „x“ gekennzeichnet
Die Disparitäten finden nun auf zweierlei Art Verwendung. Erstens kann aus ihnen eine Maßzahl für die Güte der Anpassung – ein Stressmaß – generiert werden. Ein weit verbreitetes Stressmaß ist folgendes:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{STRESS}_{1}=\sqrt{\frac{\sum_{k} \sum_{l}\left(d_{k l}-\widetilde{d_{k l}}\right)^{2}}{\sum_{k} \sum_{l} d_{k l}^{2}}} }
Die Anpassung ist umso besser, je kleiner das Stressmaß ist.
Zweitens hat Kruskal (1964, zitiert in Backhaus et al., 2003) einen Algorithmus vorgeschlagen, wie auf Basis der Disparitäten Richtungen ermittelt werden können, in die die Datenpunkte im Raum verschoben werden müssen, um das Stressmaß zu verbessern.
Die neuen Koordinaten berechnen sich folgendermaßen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{k r}^{+}=x_{k r}+\frac{a}{K-1} \sum_{l=1, l \neq k}^{N}\left(1-\frac{\widehat{d}_{k l}}{d_{k l}}\right) *\left(x_{l r}-x_{k r}\right) \quad(r=1, \ldots R) }
Hier ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K} die Anzahl der Objekte, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} das Objekt, dass verschoben werden soll, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} jene Koordinate, die neu berechnet wird und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} das Ausmaß in dem der Punkt entlang der Richtung verschoben wird.
| Fortsetzung Beispiel 8
Im folgenden sind die nach dem Kleinste-Quadrate-Kriterium berechneten Disparitäten, sowie das resultierende Stressmaß angegeben:
Die Monotonie ist noch lange nicht erreicht. Eine neue, bessere Positionierung wird mittels obiger Formel für a=2 berechnet. An dieser Stelle wird dies beispielhaft für die erste Koordinate von Punkt C skizziert: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{31}^{+}=x_{31}+\frac{2}{5-1} \sum_{l=1, l=3}^{5}\left(1-\frac{\widehat{d}_{3 l}}{d_{31}}\right) *\left(x_{l 1}-x_{31}\right)= 5+0,5\left[\left(1-\frac{5,4}{3}\right) *(7-5)+\left(1-\frac{5,4}{5}\right) *(10-5)+\left(1-\frac{5,4}{7}\right) *(9-5)+\left(1-\frac{7}{9}\right)\right. *(1-5)]=4,01 }
|
|---|
und der Ergebnisse nach der ersten Iteration
Beurteilung der Lösung
Die in Beispiel 8 schlussendlich erhaltene Lösung ist invariant gegenüber Drehungen von oder Spiegelungen an den Achsen.
Im konkreten Fall sind zwei Dimensionen mehr als ausreichend. In einer Analyse mit deutlich mehr Objekten gibt es folgende Kriterien, um die Frage der Dimensionszahl zu beantworten:
Beurteilung nach dem Stressmaß
Ein errechnetes Stressmaß kann laut Tabelle 5 klassifiziert werden. Zu beachten ist, dass sich das Stressmaß bei Hinzunahme einer weiteren Dimension nur verbessern kann. Dimensionen sollen nur dann hinzugefügt werden, wenn diese Verbesserung deutlich ausfällt.
Tabelle 5: Klassifikation des Stressmaßes
| Anpassung | Perfekt | Sehr gut | Gut | Ausreichend | Gering |
|---|---|---|---|---|---|
| Wert des Stressmaßes | <0,025 | 0,025-0,05 | 0,05-0,1 | 0,1-0,2 | >0,2 |
Beurteilung nach einem Datenverdichtungskoeffizient
Der Datenverdichtungskoeffizient setzt die Anzahl der Ähnlichkeiten zur Anzahl der Koordinaten im Output in Bezug. Im Beispiel 8 waren zehn Ähnlichkeiten in eine Reihenfolge zu bringen und zehn Koordinaten (5 mal 2) zu errechnen, was einen Koeffizient von 1 ergibt. Nach einer Faustregel sollte der Koeffizient größer oder gleich 2 sein.
| Aufgabe 14
Bestimmen Sie, ab welcher Anzahl an Objekten erst nach diesem Kriterium zwei, bzw. drei Dimensionen verwendet werden dürfen. |
|---|
Beurteilung nach Interpretierbarkeit der Dimensionen
Nachdem ein optionales Ziel der MDS darin besteht, die Dimensionen, die den Raum aufspannen, zu interpretieren, kann auch dies als Kriterium benutzt werden. Ermöglicht eine zwei- oder dreidimensionale Lösung eine bessere Interpretation der jeweiligen Konfiguration? Die Interpretierbarkeit der Dimensionen erhöht Anschaulichkeit und bestärkt jedenfalls die Validität der gefundenen Lösung.
Vorgehensweise bei Vorliegen der Daten von mehreren Personen
Die bisherige Vorgehensweise, bei der nur eine Person ein Ranking abgibt, wird auch „klassische MDs“ genannt. Fließen Urteile von mehreren Personen ein, bestehen grundsätzlich drei Möglichkeiten:
Aggregation der Urteile auf bekannte statistische Maßzahlen (Median, Mittelwert) – hier ist wichtig, dass die Personengruppen homogen sind
Getrennte MDs für jede einzelne Person und Aggregation der Ergebnisse
Eine gemeinsame Analyse der Ähnlichkeitsdaten (Replicated MDS)
Multidimensionale Skalierung in R
Die MDS kann beispielsweise in SPSS durchgeführt werden, oder auch mit Software, die auf MDS spezialisiert ist (MDSCAL, KYST, POLYCON). Wir verwenden aus Kontinuitätsgründen für unsere Analyse wieder R.
| Beispiel 9
Der vorliegende Datensatz ist im package „flexclust“ in R zu finden und beinhaltet die Daten über die Bestandteile der Milch von 25 verschiedenen Säugetieren („water“, „protein“, „fat“, „lactose“, „ash“) in Prozent. Ziel ist es, die Daten in zwei Dimensionen darzustellen, sodass Tiere, deren Milch ähnlich ist auch im XY-Scatterplot umso näher beisammen sind. Wir wählen die Funktion „isoMDS“ aus dem Package „MASS“, die eine nichtmetrische MDS durchführt, also die Rangordnung der Input-Distanzen zueinander verarbeitet.
Zuerst wird eine Distanzmatrix der L1-Distanzen („L1dist“) erzeugt. Diese ist Input für die nichtmetrische MDS, die in R mit der Funktion „isoMDS“ durchgeführt werden kann. Das Ergebnis wird im Objekt „result“ gespeichert. Ergebnis sind die Koordinaten in den gewünschten zwei Dimensionen. Der Stress-Wert wird in Prozent angegeben. Das Ergebnis ist lt. Tabelle 5 daher „ausgezeichnet“. Schließlich soll das Ergebnis noch mittels zweier Plots veranschaulicht werden:
Abbildung 30 zeigt also die Lage der Objekte zueinander im Raum. Beachtet werden muss hier, dass die X- und Y-Achse (aus Platzgründen) nicht gleich skaliert sind (um einen Faktor 4), was gerade bei der MDS wichtig wäre, da die Distanzen sonst verzerren. In diesem Fall ist die X-Achse viel bedeutender als die Y-Achse (Seehund und Delphin sind in Wirklichkeit viel weiter vom Rest entfernt, als der Elefant). Entweder Abbildung 30 müsste viermal so breit gezeichnet werden, oder man zieht die inhaltliche Konsequenz, dass möglicherweise sogar eine Dimension ausreichend ist. In der Tat ergibt sich mit einem Stress-Wert von 4,1% auch bei einer Dimension ein „sehr gutes“ Ergebnis. Der perfekte Zusammenhang zwischen Distanzen und Disparitäten ist ebenfalls ein Hinweis, dass eine Reduktion auf eine Dimension in Betracht kommen könnte. |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Wiederholen Sie die Begriffe Konfiguration, Distanzen und Disparitäten im Zusammenhang mit der MDS.
- Beschreiben Sie Unterschiede und Gemeinsamkeiten zwischen Clusteranalyse und MDS.
- Berechnen Sie für die in Abbildung 27 dargestellten Datenpunkte „D“ und „E“ die neuen Koordinaten (jeweils a=2).
- Gegeben sei ein nichtlineares MDS-Problem mit vier Objekten. Bestimmen Sie, ob (1) oder (2) die richtigen Disparitäten sind und berechnen Sie das Stressmaß.
| Paare k,l | 1,2 | 1,4 | 3,4 | 2,3 | 2,4 | 1,3 |
|---|---|---|---|---|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{k l}} | 1 | 2 | 3 | 4 | 5 | 6 |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_{k l}} | 3 | 1 | 2 | 4 | 6 | 5 |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1) \widehat{u_{k l}}}
|
2 | 2 | 2 | 4 | 5,5 | 5,5 |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (2) \widehat{u_{k l}}}
|
3 | 1,5 | 1,5 | 5 | 5 | 5 |
Zusammenfassung
Die multidimensionale Skalierung erweitert die Idee der Clusteranalyse dahingehend, dass anstelle von Distanzen zwischen beobachtbaren Merkmalen von Objekten hier Distanzen der Objekte in latenten Dimensionen die zentrale Rolle spielen. Diese bilden hier im Gegensatz zur Clusteranalyse den Output der Analyse. Die Vorstellung, dass Beurteilungen von Ähnlichkeit zwischen Objekten oft nicht durch objektive, beobachtbare Messungen ermittelt werden können, sondern teilweise unbewusst existieren, bildet das Grundgerüst dieser vor allem in der Psychologie, aber auch in der Ökologie unter dem Begriff „Ordination“ verbreiteten Methode.
Datengrundlage bildet bei den nichtmetrischen MDS-Verfahren eine Ordnung von Ähnlichkeiten zwischen den interessierenden Objekten. Mittels iterativer Optimierungsverfahren kann – ausgehend von einer Startlösung – eine bezüglich eines Stressmaßes optimale Lösung erzielt werden.
Bei der gefundenen Lösung ist die Lage der Punkte zueinander bei Wahl der euklidischen Distanz eindeutig. Die orthogonalen Achsen können schließlich beliebig gedreht werden, auch mit dem Ziel möglichst gut interpretierbare Dimensionen zu erhalten.
Faktorenanalyse
Wichtiges Ziel der Lektion ist die Erkenntnis, welche Aussagen über nichtbeobachtbare Merkmale aufgrund der Korrelationsstruktur eines Satzes von vorhandenen Variablen abgeleitet werden können. Die Grundlagen der Faktorenanalyse als Basis von Strukturmodellen und die Darstellung der subjektiven Entscheidungen, die im Zuge einer Faktorenanalyse getroffen werden müssen sind ebenso Schwerpunkte, wie die Analyse der Daten in R.
Einführung
Die in den ersten beiden Lektionen besprochenen Verfahren der Regressions- bzw. Varianzanalyse eignen sich, um den Zusammenhang zwischen einem Satz an ausgewählten Variablen und einer davon abhängigen Variable zu testen. Oft kommt es allerdings vor, dass die Menge an potentiellen Variablen relativ groß ist, einzelne Variablen hoch miteinander korrelieren, oder man nicht am Einfluss der Variablen auf eine abhängige Variable, sondern an der Korrelationsstruktur bzw. an latenten (=nicht beobachtbaren), den Daten zugrundeliegenden Faktoren interessiert ist. Den zweiten Fall haben wir bei Beispiel 1 gehabt. Hier waren Spritverbrauch in der Stadt bzw. auf der Autobahn klarerweise hoch korreliert und damit war schwer abzuschätzen, wie groß der Anteil jeder der beiden Variablen an der Erklärung des Preises ist (im gewählten Modell kam dann jedoch ohnehin keine der beiden Variablen vor). Für den Fall, dass man an latenten Faktoren interessiert ist, gibt es folgende Beispiele:
- Menschliches Verhalten ist beispielsweise von einer Vielzahl an Einflussfaktoren abhängig. In Fragebögen, die das Verhalten in bestimmten Situationen abfragen, werden oft viele ähnliche Fragen, die miteinander hoch korrelieren, gestellt. Letztendlich will man dabei aber latente Konstrukte, wie z.B. „Aggresionspotential“ oder „Verlässlichkeit“ erheben.
- Erhebung von Prädiktoren für die Kreditwürdigkeit von Kunden einer Bank. Bekannt sind zahlreiche Kundenvariablen, die hoch korreltiert sind und verdichtet werden können.
- Welche Fähigkeiten liegen Leistungen in Intelligenztests zugrunde? Es existieren viele verschiedene (ähnliche Tests), bei denen hochkorrelierte Leistungen zu beobachten sind. Welche (nicht beobachtbaren) Faktoren liegen diesen Leistungen zugrunde?
Die Faktorenanalyse bedient sich nun mathematischer Verfahren, die es ermöglichen, viele, miteinander hoch korrelierende Variablen auf einige wenige, nicht korrelierenden Faktoren umzurechnen, sodass die Information (Varianz) der Daten aber weitgehend vorhanden bleibt.
| Beispiel 10 (Extrembeispiel)
Angenommen Sie wollen den Umsatz von Speiseeis in Wien in Abhängigkeit von der jeweils um 12h in der Wiener Innenstadt gemessenen Temperatur vorhersagen. Sie messen die Temperatur in Grad Celsius, in Fahrenheit und in Kelvin. Anschließend führen Sie eine multiple lineare Regression des Speiseeisumsatzes, die alle drei Variablen als Erklärung enthält, durch. Aufgrund der Tatsache, dass zwischen den drei Skalen mittels Lineartransformation umgerechnet werden kann [7] (exakte Multikollinearität), ergeben sich für die Koeffizientenschätzungen unendlich große Varianzen und beliebige Werte. Die Information, die in allen drei Variablen steckt, kann ohne Verlust mit einer der drei Temperaturvariablen dargestellt werden. |
|---|
Die im folgenden dargestellten Methoden betreffen die explorative Faktorenanalyse. Mit ihrer Hilfe können keine Wirkzusammenhänge inferenzstatistisch geprüft werden, sondern es können nur Zusammenhangsstrukturen exploriert werden. Demgegenüber steht die konfirmatorische Faktorenanalyse, bei der hypothesenprüfend vorgegangen wird. Diese ist ein Spezialfall der in der folgenden Lektion vorgestellten Strukturgleichungsmodelle und wird dort betrachtet.
Für die explorative Faktorenanalyse gilt weiters, dass hier einige subjektive Entscheidungen des Anwenders im Analyseprozess erforderlich sind. Man ist mehr als bei anderen statistischen Verfahren auf Vermutungen angewiesen. Die Faktorenanalyse versteht sich eher als mathematisches Hilfsmittel, welches logisch begründeten Strukturtheorien zur Seite gestellt wird.
Die Faktorenanalyse geht zurück auf Spearman, der diese ursprünglich 1904 zum Zwecke der Intelligenzmessung verwendet hat. Das einleitende Beispiel im folgenden Abschnitt widmet sich daher diesem Thema.
Modellvorstellung
| Beispiel 11
Schulnoten sind Indikatoren für den unbekannten Faktor Intelligenz. Es werden aus Gründen der Einfachheit zwei voneinander unabhängige Intelligenzen (quantitative Intelligenz, Q, und verbale Intelligenz, V) postuliert. Folgende beispielhafte Annahme über das Zustandekommen der Noten in sechs verschiedenen Fächern werden getroffen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Math }=0,80 * Q+0,20 * V+A_{m}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Phys }=0,70 * Q+0,30 * V+A_{p}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Chem }=0,60 * Q+0,30 * V+A_{c}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Eng }=0,20 * Q+0,80 * V+A_{e}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Hist }=0,15 * Q+0,82 * V+A_{h}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { Fran }=0,25 * Q+0,85 * V+A_{f}} Die Noten setzen sich also mittels Linearkombination aus den beiden Intelligenzen plus einem spezifischen Faktor für das jeweilige Fach zusammen. |
|---|
Die Koeffizienten der Regressiongleichungen aus Beispiel 11 heißen „Ladungen“. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V} heißen „gemeinsame Faktoren“.
Wird nun ein derartiger Zusammenhang unterstellt, können auch die paarweisen Korrelationen zwischen je zwei Schulnoten (Fächern) daraus abgeleitet werden.
Bei der Faktorenanalyse kennt man die in Beispiel 11 getroffene Annahme nicht. Man beschreitet hier den umgekehrten Weg. Gegeben sind alle paarweisen Korrelationen (im Beispiel die Korrelationen zwischen den Schulnoten) und gesucht sind die (in Beispiel 11) gegebenen Ladungen.
Es werden dann einige mathematisch-statistische Restriktionen gemacht, um das Schätzproblem bei der Faktorenanalyse etwas genauer zu spezifizieren. Beispielsweise muss gefordert werden, dass die gemeinsamen Faktoren untereinander unabhängig sind. Das heißt, wenn jemand eine hohe quantitative Intelligenz hat, dann kann daraus keine Tendenz über die verbale Intelligenz geschlossen werden. Außerdem wir gefordert, dass die gemeinsamen Faktoren von den spezifischen Faktoren unabhängig sind.
Notiert wird das Modell der Faktorenanalyse in den gängigen Lehrbüchern in Matrixschreibweise (analog zu Beispiel 11):
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y=F L^{t}+E }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y}
die bereits spaltenweise auf Mittelwert Null zentrierte Datenmatrix (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n \times p, n}
Versuchseinheiten und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p}
Variablen), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F}
die Matrix (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (n \times k)}
), die die gemeinsamen Faktoren enthält, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L}
die Ladungsmatrix (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p \times k}
) und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E}
die (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n \times p}
)- Matrix der Einzelrestwerte ist. In Beispiel 11 ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=6}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K=2}
.
Aufgrund der vielen Unbekannten in diesem Modell ist dieses nicht empirisch überprüfbar bzw. uneindeutig. Durch die erwähnten mathematischen Annahmen lässt sich aber die für die Faktorenanalyse zentrale, unter bestimmten Umständen eindeutige Zerlegung bilden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\Sigma}=\mathbf{L} \mathbf{L}^{\mathrm{t}}+\mathbf{V}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Sigma} ist die sogenannte „Varianz-Kovarianzmatrix“ der Daten. Sie enthält in der Hauptdiagonale alle Varianzen der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} Variablen und abseits davon alle Kovarianzen. Die Varianz-Kovarianz-Matrix (bzw. bei standardisierten Variablen die Korrelationsmatrix) ist der wesentliche Input bei einer Faktorenanalyse, den es zu analysieren gilt. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} ist eine Diagonalmatrix mit den Varianzen der spezifischen Faktoren. Das wesentliche Ziel bei der Faktorenanalyse ist es nun, eine jener Matrizen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} zu finden, für die diese Zerlegung möglich ist, und zwar für eine minimale Anzahl an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} zugrundeliegenden gemeinsamen Faktoren.
Faktorextraktion
Es gibt nun verschiedene Schätzmethoden, um die Ladungsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} zu schätzen.
Die Maximum-Likelihood-Methode
Diese bedient sich einem in der Statistik weit verbreiteten Konzept zur Konstruktion von Schätzern. Es wird hier eine multivariate Normalverteilung der beobachteten Daten unterstellt. Als Folge davon kann analytisch jener Schätzer für die Ladungsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} ] ermittelt werden, der unter dieser Annahme am plausibelsten ist. Hier wird also stochastisch durch Verteilungsannahmen argumentiert. Die Wahl, wieviele Faktoren (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} ) gewählt werden, kann unter anderem durch statistische Hypothesentests erfolgen.
Die Hauptkomponentenanalyse
Die Ergebnisse der Hauptkomponentenanalyse erhält man ebenfalls durch Optimierung. Kriterium ist, dass die (zentrierte) Datenmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} durch Multiplikation mit einer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k \times k-} -Matrix (mit orthonormalen Spalten) derart transformiert wird, dass die Spalten der so transformierten Matrix jeweils schrittweise die höchste Varianz erzeugen. Dieser Vorgang wird Hauptachsentransformation genannt. Diese sehr theoretisch beschriebene Vorgehensweise soll anhand eines Beispieles skizziert werden (Abbildung 32).
| Beispiel 12
Abbildung 32 zeigt sieben Datenpunkte in zwei Variablen. In der linken Abbildung kann die Varianz in X- bzw. Y-Richtung durch Normalprojektion an die jeweiligen Achsen geschätzt werden. Die Daten sind so gewählt, dass sowohl die Varianz in X- als auch in Y-Richtung gleich 1 ist. Geometrisch gesehen wird bei der Hauptachsentransformation das Koordinatensystem solange gedreht, bis die größte der Varianzen der projizierten Datenpunkte auf die neuen Achsen maximal wird. Diese Drehung entspricht in diesem Beispiel 45 Grad und führt dazu, dass die Varianz der Daten auf der Achse von links unten nach rechts oben 1,501 beträgt. Dies ist die größte erzielbare Varianz auf einer Achse. Die Werte auf der zweiten Achse weisen eine Varianz von 0,499 auf. Nachdem die Daten nur zwei Dimensionen haben, bleibt für die zweite Achse nur mehr eine Richtung. Im allgemeinen wird jedoch für die zweite Achse jene Richtung gewählt, die ihrerseits wieder die maximale Varianz liefert. In Summe sind die Varianzen in beiden Richtungen sowohl in der Grafik links als auch rechts gleich 2. Sie teilen sich nur anders auf. Um wieder zu obigen Text zurückzukehren: Die hier angewandte Transformation bedeutet rechnerisch eine Multiplikation der Datenmatrix mit der Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{L}=\left(\begin{array}{cc} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right) } |
|---|
Wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=p} gewählt, heißt das, dass die volle Varianz erklärt wird (d.h. die volle Information erhalten bleibt). Die (bei hoher Korrelation in den Daten stark) ungleiche Varianzzerlegung macht man sich aber zunutze um nun die ersten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} interessierenden Achsen zu wählen und die anderen zu eliminieren. Damit erzielt man einen Kompromiss zwischen Datenreduktion und Informationsverlust. Der Anteil der Summe aller bis zur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} -ten Achse erklärten Varianzen an der Gesamtzahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} der Variablen im Originaldatensatz ist der erklärte Varianzanteil. Dieser ist ein Kriterium zur Bestimmung, auf wieviele Achsen die Daten reduziert werden sollen.
| Fortsetzung Beispiel 12
Die Varianz der Daten an der ersten transformierten Achse beträgt 1,501. Die Anzahl der Originalvariablen bzw. die Summe derer Varianzen beträgt 2. Daher beträgt der erklärte Varianzanteil bei alleiniger Datenreduktion auf eine Achse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1.501}{2}=75 \%} . |
|---|
| Aufgabe 15
Angenommen es liegt ein Satz von acht (auf Varianz gleich Eins) standardisierten, korrelierten Variablen vor, der mittels Hauptkomponentenmethode reduziert werden soll.
|
|---|
Die eben diskutierte Vorgehensweise nur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k<p} Achsen aus der transformierten Matrix zur Erklärung der Originaldaten auszuwählen, wird „Hauptkomponentenmethode“ genannt. Während bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=p} nur eine Lösung existiert, den gesamt erklärten Varianzanteil zu maximieren, ist die Lösung bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1<k<p} gewählten Achsen nicht eindeutig. Darauf wird in Abschnitt 5.6 eingegangen.
Die Lösung der Hauptkomponentenanalyse wird im Normalfall nicht graphisch durchgeführt, sondern reduziert sich – mathematisch gesehen – auf das Finden der Eigenwerte der Korrelations- bzw. Kovarianzmatrix der Daten. Deshalb liest man statt erklärten Varianzanteilen in Software-Outputs von Faktorenanalysen auch immer wieder von Eigenwerten. Die Varianzen der Daten in den einzelnen Richtungen sind gerade durch diese Eigenwerte gegeben.
Die Hauptkomponentenmethode ist die am häufigsten angewandte Methode zur Extraktion von Faktoren. Der Grund ist auch, dass hier im Gegensatz zu anderen Berechnungsmethoden kein iteratives Vorgehen benötigt wird. Im Hinblick zur eigentlichen Faktorenanalyse wird hier kein Modell zugrundegelegt, sondern es wird lediglich eine technische Optimierungsaufgabe zur Datenreduktion durchgeführt. Eine Methode, die die Hauptkomponentenmethode verwendet um in einem iterativen Prozess (wie vorher erwünscht) statt den Varianzen die Anpassung an die Korrelationsmatrix optimiert, ist die Hauptfaktorenanalyse. Auf diese wird aber aus Platzgründen nicht weiter eingegangen.
Bestimmung der Anzahl an Faktoren
Die wesentlichste Frage, wenn mittels Hauptkomponentenanalyse versucht wird, einen Satz von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k<p} Dimensionen – die „gemeinsamen Faktoren“ – zu ermitteln, ist, wie groß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} nun sein soll. Dazu gibt es drei häufig verwendete Kriterien.
Die erklärte Varianz
Ein mögliches Kriterium kann sein, dass man einen gewissen Anteil an erklärter Varianz nicht unterschreiten will, da man sonst nicht mehr das Gefühl hat, die ursprünglichen Daten mit dem reduzierten Datensatz gut zu beschreiben.
| Beispiel 13
Im diesem Beispiel (Backhaus et al., 2003) sind die mittels Fragebogen von mehreren Personen erhobenen Eigenschaften von sechs Margarinesorten erhoben. Die Daten beschreiben die Mittelwerte der Stichprobe, die auf einer Ratingskala zwischen 1 und 7 bewertet wurden.
In der ersten Spalte des Datensatzes sind die Markennamen. Diese werden gespeichert. Weitergerechnet wird dann ohne die erste Spalte.
Es zeigen sich hier sehr schön zwei untereinander jeweils hoch korrelierte Blöcke von Variablen. Auf Basis der Korrelationsmatrix könnte ein Faktor für die ersten drei und ein Faktor für die letzten zwei Variablen gewählt werden. Aufgrund der niedrigen Korrelationen abseits dieser Blöcke wäre die Unkorreliertheit der beiden Faktoren wohl auch einigermaßen sichergestellt.
Bei der Faktorenanalyse ist dieses Vorgehen durchaus üblich, da man im wesentlichen an der Korrelationsstruktur (statt an den Kovarianzen) interessiert ist. Die eigentliche Analyse geschieht nun mit der Funktion „prcomp“ (Abbildung 33). Der Output der Funktion liefert einerseits die Standardabweichungen der extrahierten Faktoren und andererseits die Hauptachsentransformation (unter „Rotation“). Dass die Methode schrittweise jene Richtungen extrahiert, die größtmögliche Varianz erklären, sieht man auch an der absteigenden Folge der Standardabweichungen. Die erste Komponente hat Standardabweichung 1,6264 und damit Varianz 1,62642=2,645. Nachdem eine Gesamtvarianz von 5 aufzuteilen ist, bedeutet das, dass die erste Komponente bereits 2,645/5=52,9% an Varianz erklärt. Die zweite Komponente hat eine Varianz von 1,39072=1,934 und liefert damit weitere 1,934/5=38,7% an Erklärung. Zusammen sind das bereits 91,6%. Mit dem Befehl „summary“ (siehe weiter Abbildung 33) bekommt man diese Varianzzerlegung ausgegeben. |
|---|
Hat man für sich selbst z.B. im Vorhinein bestimmt, dass jene Faktorenzahl gewählt wird, dass zumindest 80% der Varianz erklärt werden, würde man sich mittels dieses Kriteriums für zwei Variablen entscheiden.
Das Kaiser-Kriterium
Das Kaiser-Kriterium (Kaiser & Dickman, 1959, zitiert in Fahrmeir et al., 1996, S. 669) wählt jene Komponenten aus, die überdurchschnittlich an Varianz beitragen. Bei auf Varianz 1 skalierten Daten ist bei Variablen eine Varianz von aufzuteilen. Es werden daher jene Komponenten gewählt, deren Varianz größer als 1 ist.
| Fortsetzung Beispiel 13
Nur die ersten beiden Standardabweichungen/Varianzen (Eigenwerte) sind größer 1. Daher werden nach diesem Kriterium ebenfalls zwei Komponenten gewählt. |
|---|
Der Scree-Plot
Ein visuelles Kriterium stellt der Screeplot dar, der die einzelnen Varianzen absteigend nebeneinander aufträgt und mit Linien verbindet (Abbildung 34). Gewählt werden nun (von links) alle Komponenten bis zu jenem Punkt (exklusive), an dem der weitere Linienverlauf nach rechts im wesentlichen einer Gerade entspricht.
| Fortsetzung Beispiel 13
In Abbildung 34 ist ersichtlich, dass der größte Abfall von Komponente 2 auf Komponente 3 passiert. Dann fällt die Linie relativ flach weiter. Nach diesem Kriterium können zwei, eventuell auch drei Komponenten gewählt werden. |
|---|
Weitere Analyse und Interpretation
| Fortsetzung Beispiel 13
Laut der Analyse im letzten Abschnitt empfiehlt sich die Wahl von zwei Hauptkomponenten. Das heißt, dass in Abbildung 33 die ersten beiden Spalten der Transformationsmatrix gewählt und interpretiert werden müssen. Die Koeffizienten geben die relative Bedeutung an. Faktor 1 berechnet sich als 0,576 * Anteil ungesättigter Fettsäuren + 0,518 * Kaloriengehalt +0,571 * Vit.-Gehalt + 0,211 * Haltbarkeit + 0,170 * Preis. |
|---|
|
Demnach sind im ersten extrahierten Faktor eher die ersten drei Variablen in etwa gleicher Stärke ausgedrückt. Inhaltlich könnte dieser Faktor mit „Gesundheit“ bezeichnet werden. In Komponente 2 sind die letzten beiden Variablen stärker gewichtet. Daher kann Komponente 2 als „Wirtschaftlichkeit“ interpretiert werden. |
Der Zweck der Faktorenanalyse ist Datenreduktion. Daher ist das nächste Ziel, die (standardisierten) Originaldaten nun in den neuen gemeinsamen Faktoren darzustellen. Dazu wird die Datenmatrix mit den ersten Spalten der Transformationsmatrix multipliziert.
| Fortsetzung Beispiel 13
Die Werte der ursprünglichen Variablen in den neuen gemeinsamen Faktoren werden in der Matrix „Scores“ zusammengefasst (Abbildung 35). Hohe Werte stehen für gute Gesundheitswerte bzw. hohe Wirtschaftlichkeit. Man kann so die Datenpunkte im neuen Datenraum veranschaulichen und auch in einem XY-Scatterplot darstellen. Beispielsweise ist „Du darfst“ am „gesündesten“, und hat den niedrigsten Wert bzgl. Wirtschaftlichkeit, was geringem Preis und geringer Haltbarkeit entspricht. |
|---|
|
Berechnet man nun von beiden Faktoren die Varianzen, erhält man wieder die bekannten Werte von vorhin. |
Multipliziert man die Spalten der Transformationsmatrix mit der jeweiligen Standardabweichung (Abbildung 33), erhält man die Ladungsmatrix mit den Einträgen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{i j}} . Diese ist insofern interessant, als hier die Korrelationen der einzelnen Variablen mit den einzelnen Faktoren abgelesen werden können. Außerdem kann dort für jede Variable die sogenannte „Kommunalität“ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{i}^{2}} ermittelt werden. Diese gibt jeweils an, wieviel Prozent der Varianz der Variable durch den gewählten Satz gemeinsamer Faktoren erklärt wird. Die Formel lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{i}^{2}=\sum_{j=1}^{k} l_{i j}^{2} }
| Fortsetzung Beispiel 13
Abbildung 36 zeigt die Erzeugung der Ladungsmatrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} aus der Transformationsmatrix in R. Wir sehen, dass die ersten drei Variablen eine sehr hohe Korrelation mit dem ersten Faktor aufweisen. Haltbarkeit und Preis hingegen korrelieren mit dem zweiten gewählten Faktor zu 0,94 bzw. 0,96. Auch hier sieht man, dass ein dritter Faktor nicht mehr erforderlich ist, da hier kaum noch hohe Korrelationen zu den Variablen zu beobachten sind. Welche Variablen werden nun durch die ersten beiden Komponenten gut erklärt? Die Kommunalität des „Anteils ungesättigter Fettsäuren“ beträgt z.B. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{1}^{2}=0,937^{2}+(-0,229)^{2}=93,1 \%} . Also werden 93,1% der Varianz der Variable „Anteil ungesättigter Fettsäuren“ durch die beiden Komponenten erklärt. Der Kreis schließt sich nun wieder, da unser ursprüngliches Ziel war, die Korrelationsstruktur der Daten zu erklären. Wie gut das gelingt, kann durch die Matrix der durch die zwei gemeinsamen Faktoren reproduzierten Korrelationen ermittelt werden. Diese ist nun mit der ursprünglichen Korrelationsmatrix zu vergleichen. Beispielsweise beträgt die Korrelation zwischen Kalorien- und Vitamingehalt ursprünglich 0,704. Aufgrund der beiden gewählten Faktoren kommt man auf eine Korrelation von 0,823. Für diese Korrelation ergibt sich daher ein Residuum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,704-0,823=-0,119} . Die Residuen der Hauptdiagonalelemente (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(1-h_{i}^{2}\right)} ) sind die durch die Faktoren nicht erklärten Varianzanteile der Variablen. |
|---|
| Aufgabe 16
Berechnen Sie die Kommunalitäten für die restlichen vier Variablen aus Beispiel 13 und vergleichen Sie ihre Werte mit den Hauptdiagonalelementen der reproduzierten Korrelationsmatrix. |
|---|
Faktorrotation
Wie bereits erwähnt, gibt es für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1<k<p} mehrere (unendlich viele) Lösungen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} , die allesamt die maximale Varianz erklären. Diese unterscheiden sich wieder durch „Drehungen“ im Raum. Das heißt, die gefundene Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} kann durch Multiplikation einer beliebigen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k \times k} -Matrix mit orthonormalen Spalten transformiert werden, sodass die neue Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L^t} den gleichen maximal erklärten Varianzanteil liefert. Dies macht man sich zunutze, um jene Lösungen fürFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} auszuwählen, die besonders leicht zu interpretieren sind. Das ist dann möglich, wenn die Ladungen entweder nahe bei 1 oder nahe bei 0 sind. Mit anderen Worten heißt das, dass die Varianz der Koeffizienten maximiert werden soll. Die Faktorrotationsmethoden, die die Varianz der Ladungen spalten- bzw. zeilenweise maximieren, heißen Varimax bzw. Quartimax.
| Fortsetzung Beispiel 13
Die Ladungskoeffizienten in Beispiel 13 enthalten bereits inhaltlich gut interpretierbare Werte und müssen nicht weiter transformiert werden. Wird dennoch eine Transformation durchgeführt, heißt das, dass sich an der erklärten Varianz von 91,6% nichts ändert. Lediglich die Aufteilung 52,9%:38,7% ändert sich zugunsten des zweiten Faktors, da nicht mehr erforderlich ist, dass die erste Komponente die maximale Varianz erklärt. |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Berechnen Sie die Residuen der reproduzierten Korrelationen in Beispiel 13 und geben Sie an, welche Korrelation am schlechtesten durch die gefundene Faktorlösung dargestellt wird.
- Sie erhalten als Ergebnis einer Faktorenanalyse folgende erklärte Varianzen:
- Wieviele Faktoren müssen Sie nehmen, wenn Sie zumindest 90% der Varianz erklären wollen?
- Wieviele Faktoren müssen Sie nach dem Kaiser-Kriterium wählen?
- Für wieviele Faktoren würden Sie sich mittels zugehörigem Scree-Plot entscheiden?
Zeichnen Sie für die ersten beiden Spalten der Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} (Abbildung 36) einen XY-Scatterplot (in R: „plot(x,y)“) und beschreiben Sie verbal das Ergebnis der Analyse.
Zusammenfassung
Im Gegensatz zu den vorangegangenen Lektionen wird bei den Verfahren der Faktorenanalyse die (Korrelations-)Struktur eines Satzes von Variablen untersucht. Die Fragestellung ist, ob und wie diese Struktur durch einige wenige Variablen erklärt werden kann. Der Input bei diesen Verfahren ist daher die Kovarianz- bzw. Korrelationsmatrix, der Output im wesentlichen die Ladungsmatrix, die bestimmt, in welcher Art und Weise die gefundenen Faktoren durch die Originalvariablen bestimmt werden.
Es existieren viele Methoden, Faktoren zu bestimmen. Neben der Maximum-Likelihood-Faktorenanalyse hat sich die Hauptkomponentenanalyse als beliebtes und häufig verwendetes Verfahren herausgestellt. In deren Rahmen wird zunächst eine Hauptachsentransformation in Komponenten, die schrittweise maximale Varianz an den Originaldaten erklären, durchgeführt. Setzt man dieses Verfahren dazu ein, um einen guten Satz an Variablen zu bekommen, wird dies die „Hauptkomponentenmethode“ genannt. Eine weitere sich aus dem Verfahren ableitende, iterative Vorgehensweise, bei der das Gewicht stärker auf der Erklärung der Kovarianzen anstelle der Varianzen liegt, ist die Hauptfaktorenanalyse.
Die Anzahl an ausgewählten Faktoren wird zumeist durch einen vorgegebenen minimal erforderlichen, erklärten Varianzanteil, durch das Kaiser-Kriterium oder den Scree-Plot ermittelt und sind daher teilweise subjektiv. Die vollständige Darstellung der Faktorenanalyse umfasst schließlich noch eine Darstellung der Beobachtungseinheiten im neu transformierten Raum sowie weiteren, die Güte der Analyse beschreibenden Darstellungen, wie z.B. der Matrix der reproduzierten Korrelationen.
Wichtig ist nochmals zu erwähnen, dass die Verfahren der (exploratorischen) Faktorenanalyse praktisch keine Hypothesenprüfungen zulassen. Die Ergebnisse sind auch nicht „richtig“ oder „falsch“, sondern bieten eine mathematische Unterstützung zur Dokumentation von Zusammenhangsstrukturen.
Strukturgleichungsmodelle
Die abschließende Lektion dient vor allem als Ausblick, wie die bestehenden Verfahren kombiniert bzw. erweitert werden können. Dies geschieht in der Theorie hinter Strukturgleichungsmodellen. Die Basiskomponenten und deren Darstellung, sowie eine überblicksartige Beschreibung des Prozesses vom Aufstellen von Hypothesen bis zur Schätzung des gewählten Modells sind Kernpunkt und Ziel dieser letzten Lektion.
Einführung und Begriffsabgrenzung
Die Strukturgleichungsmodelle stellen eine Kombination zweier in diesem Skriptum behandelter Verfahren dar. Wie in der Faktorenanalyse soll hier eine Korrelationsstruktur von manifesten Variablen durch latente Faktoren erklärt werden. Weiters sollen aber die Beziehungen zwischen verschiedenen latenten Faktoren durch regressionsanalytische Methoden festgestellt werden. Das ist hier gewissermaßen die Besonderheit. Wichtig ist dabei, dass die Art des kausalen Zusammenhanges identifiziert wird. Daher werden derartige Methoden auch als Kausalanalyse bezeichnet. Andere Bezeichnungen sind „Kovarianzstrukturanalyse“ oder auch Pfadanalyse, wobei letztere ein Spezialfall ist, da dort nur manifeste Variablen („Indikatoren“) im Kausalmodell zugelassen sind. Daher steht die Pfadanalyse auch der schon besprochenen Regressionsanalyse näher. Die „Latent Structure Analyse“ – ein ebenfalls verwandter Begriff – ist hingegen eine übergeordnete Bezeichnung für Verfahren, die auch diskrete, ordinale oder sogar dichotome Variablen zulassen.
Die Feststellung der Kausalität ist wichtig, da eine hohe Korrelation nur für „immer wenn, dann“ und nicht notwendig für „deswegen, weil“ steht. Mögliche Entsprechungen einer hohen Korrelation zwischen zwei Variablen X und Y können sein (vgl. Bortz, 1999, S. 226):
- X beeinflusst Y kausal
- Y beeinflusst X kausal
- X und Y werden von einer dritten Variable kausal beeinflusst
- X und Y beeinflussen sich wechselseitig kausal
Im Rahmen von Strukturgleichungsmodellen wird die Faktorenanalyse konfirmatorisch (im Gegensatz zur exploratorischen FA in Lektion 5) durchgeführt, d.h. es wird bereits konkret unterstellt von welchen latenten Variablen die manifesten abhängen. Mehr als bei anderen Verfahren ist der Anwender hier – auch in Hinblick auf Identifizierbarkeit und Eindeutigkeit der Schätzungen – gefordert, sich zu überlegen, welcher Art die Zusammenhänge sein könnten. Es fließen hier sehr viele unbekannte Größen in die Modellierung ein.
In der folgenden Darstellung geht es weniger um den komplexen mathematischen Hintergrund der Methode – dies würde den Rahmen deutlich sprengen – sondern um die Vorstellung der Idee dahinter.
Grundlagen und Beispiele
Modelldarstellung, Terminologie und Notation
Die Datengrundlage für die Analyse mittels Strukturgleichungsmodellen sind wie in der Faktorenanalyse Kovarianzen bzw. Korrelationen zwischen den beobachtbaren Variablen. Output des Verfahrens sind wieder Modellparameter, zu denen in diesem Fall auch Signifikanzen berechnet werden können. Es kann also (wie übrigens auch bei der Regression) statistisch getestet werden, welche Parameter überzufällig von Null verschieden sind. Das Modell gilt dann als durch die Daten “bestätigt”, wenn sich die Korrelationen durch die Modellparameter (direkte oder indirekte Pfadkoeffizienten) rekonstruieren lässt.
Die Modelle werden üblicherweise in Pfaddiagrammen dargestellt, wobei die Variablen als Knoten und die Wirkungen zwischen den Variablen als Kanten eingezeichnet werden. Manifeste Variablen („Indikatoren“) werden oft als Rechtecke und latente Variablen („Faktoren“) als Ellipsen gezeichnet. Abbildung 37 zeigt die Regressionsanalyse und die Faktorenanalyse als solches Pfaddiagramm. Für jeden Pfeil wird in den Verfahren ein Parameter geschätzt.
Die Erweiterung der Regressions- und Faktorenanalyse zu allgemeinen Strukturgleichungsmodellen besteht nun darin, dass Wirkungen zwischen latenten Variablen untersucht werden können, also auch „Pfeile zwischen Ellipsen“ zugelassen werden. Beispielsweise könnte man daran interessiert sein, inwiefern die Einstellung zu einem Produkt das Kaufverhalten beeinflusst. Die latente Variable „Einstellung zum Produkt“ kann durch verschiedene psychologische Einstellungsskalen z.B. mittels Fragebogen (manifest) erhoben werden, das Kaufverhalten womöglich am ehesten durch die Zahl der Käufe (manifest). Abbildung 38 zeigt das Pfaddiagramm eines solchen Modells (Backhaus et al., 2003).
Die dort dargestellte Struktur ist prototypisch für die Darstellung von Strukturgleichungsmodellen. Die Komponenten sind einerseits die Messmodelle der latenten Variablen. In ihnen wird spezifiziert, in welcher Form die entscheidenden latenten Variablen von den manifesten abhängen, also wie das, was von Interesse ist, gemessen wird. Es werden die latent endogenen Variablen (Zielvariablen, erklärten Variablen) und die latent exogenen Variablen (erklärenden Variablen) unterschieden. Die zweite Komponente ist das Strukturmodell, das angibt, wie die latenten Variablen untereinander zusammenhängen. Im vorliegenden Fall ist die Einstellung die verursachende Variable und das Kaufverhalten die davon abhängige Variable. Ein vollständiges Strukturgleichungsmodell besteht immer aus einem Strukturmodell und zwei Messmodellen.
Wie in Abbildung 38 ersichtlich, müssen auch die in den Gleichungen vorkommenden Fehler- bzw. Residualvariablen eingetragen werden. Hierfür werden die griechischen Buchstaben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} („Delta“; Fehlerterm für Indikatoren der exogenen Variablen), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon} („Epsilon“; Fehlerterm für die Indikatoren der endogenen Variablen) und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta} („Zeta“; Fehlerterm für die latenten endogenen Variablen) verwendet. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi} („Ksi“) und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta} („Eta“) stehen für die latenten Variablen selbst.
Aus der Darstellung der Wirkweise der Variablen zueinander folgen die resultierenden Gleichungen, die im Zuge der Analyse geschätzt werden müssen. Für das Beispiel in Abbildung 38 bedeutet das konkret:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_{1}=\lambda_{x 1} * \xi_{1}+\delta_{1} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_{2}=\lambda_{x 2} * \xi_{1}+\delta_{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{1}=\lambda_{y 1} * \eta_{1}+\varepsilon_{1} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_{1}=\gamma * \xi_{1}+\zeta}
Auf die übliche Notation in Matrixschreibweise wird an dieser Stelle verzichtet. Man beachte, dass in den Gleichungen lediglich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_1} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_2} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_3} bekannt sind. Die Möglichkeit, die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda} - und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma} -Parameter dennoch zu schätzen ergibt sich aus der Erweiterung der einfachen Korrelation (vgl. Anzur, 2007) zur „partiellen Korrelation“.
Wichtig ist hier, nochmals zu betonen, dass die Zusammenhänge und das daraus resultierende Gleichungssystem aus intensiven sachlogischen Überlegungen zustandekommen sollen. Dies erleichtert im Anschluss an die Parameterschätzungen das Auffinden etwaiger Widersprüche.
Partielle Korrelation
Um zu widerlegen, dass zwei Variablen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} , vollständig kausal [8] miteinander in Zusammenhang stehen, muss eine Korrelation zwischen den beiden Variablen unter Ausschaltung potentieller Störvariablen berechnet werden. Im Falle einer Störvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} kann dies durch Berechnung der „partiellen Korrelation zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} unter Auspartialisierung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z^{\prime \prime}} “ mittels folgender Formel erreicht werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{X Y, Z}=\frac{r_{X Y}-r_{X Z} r_{Y Z}}{\sqrt{\left(1-r_{X Z}^{2}\right) *\left(1-r_{Y Z}^{2}\right)}} }
| Beispiel 14
Zwischen Pro-Kopf-BIP (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} ) und Lebenserwartung ([Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} ) sei in verschiedenen Ländern eine Korrelation von 0,57 beobachtet worden. Bekannt sind aber auch Daten über die Bildung, beispielsweise die Analphabetenquote (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} ). Hier sei weiters bekannt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{X Z}=-0,43} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{Y Z}=-0,76} . Will man nun den Einfluss von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} ausschalten, berechnet man in Wirklichkeit so etwas wie die mittlere Korrelation zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} für Gruppen von Länder, die jeweils dieselben (konstanten) [9] Analphabetenquoten haben. Konkret ergibt sich: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{X Y . Z}=\frac{0,57-(-0,43) *(-0,76)}{\sqrt{\left(1-(-0,43)^{2}\right) *\left(1-(-0,76)^{2}\right)}}=0,41 }
|
|---|
Das Konzept der partiellen Korrelation kann für beliebig viele auszuschaltende Variablen verallgemeinert werden.
Beispielfragestellungen
Nachdem nun das Grundprinzip und die Bauart von Strukturgleichungsmodellen skizziert wurde, sollen nun einige Beispiele deren Einsatz zeigen:
- Welche Auswirkung haben Familie und Schule auf die Schulleistung eines Kindes?
- Latente Variablen: Familie und Schule (exogen); Schulleistung (endogen)
- Indikatoren: Beruf und Schulbildung der Eltern, Ausmaß an Nachhilfe, Ausbildungsniveau des Lehrers, Wissenstest, Interessentest
- Inwieweit nehmen Rollenunsicherheit und Arbeitsmotivation eines Verkäufers Einfluss auf seine Selbstwertschätzung, seine Berufszufriedenheit und den erzielten Umsatz?
- Latente Variablen: Rollenverständnis und Arbeitsmotivation (exogen); Selbstwertschätzung, Berufszufriedenheit und Leistung (endogen)
- Indikatoren: Verschiedene Messmodelle, Umsatz
- Wie beeinflussen bestimmte Rahmenbedingungen das Interaktionsverhalten bei Verhandlungsprozessen im Investitionsgüter-Marketing?
Latente Variablen: Kaufsituation, Unternehmensgröße (exogen); Buying Center-Struktur, Geschäftsbeziehungen, Transaktionsprozess (endogen)
Indikatoren: Konjunktur, Produktwert, Größe, Technikerzahl (für die exogenen Variablen); Buying-Center-Größe, Umsatz, Aufträge, Verhandlungsdauer, Telefonkontakt (für die endogenen Variablen)
Durchführung
Vorgehen nach Vorliegen des Pfaddiagrammes
Nach Aufstellen von Hypothesen und der Spezifikation des Modells müssen – wie bei den meisten hier vorgestellten Verfahren – Zusatzannahmen getroffen werden. Auch hier ist die Unkorreliertheit der Fehler wieder eine entscheidende Annahme, sowohl untereinander (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} ) als auch mit den jeweils zugehörigen latenten Variablen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi} , sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta} ).
Bevor nun Parameter geschätzt werden können, ist weiters erforderlich, zu untersuchen, ob das vorliegende Gleichungssystem überhaupt gelöst werden kann. Hierfür muss sichergestellt sein, dass genügend viele Indikatoren in Bezug auf die Zahl der zu schätzenden Parameter im Modell enthalten sind. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} die Anzahl der verwendeten Indikatorvariablen, so darf die Anzahl der zu schätzenden Parameter maximal Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{n(n+1)}{2}} sein. Für das Pfaddiagramm in Abbildung 38 ergeben sich maximal Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2} * 3 * 4=6} Parameter. Daher sind die vier Parameter eindeutig schätzbar.
Parameterschätzung
Ziel ist es nun, die Parameter derart zu schätzen, dass die durch die geschätzten Parameterwerte resultierenden Kovarianzen (Korrelationen) bestmöglich zur empirischen Varianz-Kovarianz-Matrix (Korrelationsmatrix) passt. Dieses Vorgehen ist schon aus der Faktorenanalyse bekannt. Dafür, was jedoch „bestmöglich“ heißen kann, gibt es ebenfalls wieder verschiedene Vorschläge, die aber überwiegend in den wichtigsten statistischen Schätzprinzipien „Kleinste quadrierte Abweichungen“ bzw. „Maximum Likelihood“ [10] resultieren. Kriterien für die Wahl des Verfahrens sind (lt. Adler, 1996, zitiert in Backhaus et al., 2003) die Annahme der multivariaten Normalverteilung der Daten, die Skaleninvarianz der Schätzfunktion, der erforderliche Stichprobenumfang und ob Inferenzstatistiken verfügbar sein sollen.
Inferenzstatistische Beurteilung des geschätzten Modells
Hinweise, ob das geschätzte Modell die Daten gut beschreibt gibt es einige. Zuerst sollten die Schätzergebnisse auf Plausibilität überprüft werden. Korrelationen, die betragsmäßig größer als 1 sind, negative Varianzen, Koeffizienten, deren Vorzeichen umgekehrt zum postulierten Zusammenhang sind oder nicht positiv definite Korrelationsmatrizen sind einige Indikatoren, die auf eine Fehlspezifikation des Modells hinweisen.
Ist offensichtlich keine der Minimalforderungen verletzt, kann man für dieses Setting verschiedene prototypische statistische Tests, wie beispielsweise den t-Test oder den Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^{2}} -Test (Anzur, 2007) adaptieren. Während der t-Test Hypothesen über einzelne Parameter testet ([Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{0}: \lambda_{i}=0 \text { versus } H_{1}: \lambda_{i} \neq 0} ), führt der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^{2}} -Test einen globalen Test durch (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{0}} „Die empirische Kovarianzmatrix entspricht dem Modell“ versus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{1}} „Die empirische Kovarianzmatrix entspricht nicht dem Modell“).
Als Maßzahlen für die Zuverlässigkeit können außerdem noch das aus Lektion 1 bekannte Bestimmtheitsmaß (wie zuverlässig werden die latenten Variablen gemessen) sowie die paarweise Korrelationen zwischen den Parameterschätzungen angegeben werden. Falls sehr hohe Werte vorkommen, müssen einzelne Parameter entfernt werden.
All diese Prüfungen (und einige mehr) bestimmen letztendlich, ob das gewählte Modell die Daten und damit den Sachverhalt gut erklärt. Abschließend sei hier nun nochmals der Gesamtablauf während der Analyse mit Strukturgleichungsmodellen schematisch dargestellt (Reinecke, 2005, S. 11):
Strukturgleichungsmodelle in R
Zwei häufig in der Literatur genannten Softwarepakete zur Schätzung von Strukturgleichungsmodellen sind AMOS und LISREL, jedoch können derartige Analysen auch mit R durchgeführt werden. Wir werden uns nun ein kurzes Beispiel ansehen, wie ein Modelle in R spezifiziert und geschätzt werden kann.
| Beispiel 15
Die Daten stammen aus einer Untersuchung des Einflusses von Freunden („peer group“) und Familie auf den beruflichen Ehrgeiz (Duncan, Haller und Portes, 1968). In diesem einfachen Beispiel sollen die Zusammenhangsstrukturen von sechs manifesten Variablen untersucht werden. Gemessen wurde der berufliche Ehrgeiz („occupational aspiration“) der Respondenten („R“) bzw. des besten Freundes/der besten Freundin („F“) des/der Respondenten/in. Der Index korreliert u.a. mit persönliche Erfolgsorientierung, dem Selbstkonzept zur Zielerreichung und der „Wertigkeit“ des tatsächlich realisierten Berufes. Für beide „Ehrgeiz“-Variablen gibt es je zwei erklärende Variablen, den Intelligenzquotienten („IQ“) und den sozioökonomische Status („SES“) der Familie der betreffenden Person. Folgendes Pfaddiagramm (Abbildung 40) veranschaulicht das zu spezifizierende Modell:
' . Für das Modell ergeben sich folgende Gleichungen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { ROccAsp }=\lambda_{51} * R I Q+\lambda_{52} * R S E S+\gamma_{56} * \text { FOccAsp }+\varepsilon_{7} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text { FOccAsp }=\lambda_{63} * \text { FIQ }+\lambda_{64} * \text { FSES }+\gamma_{65} * \text { ROccAsp }+\varepsilon_{8} }
Die Berechnung der Parameter erfolgt hernach durch die Funktion „sem“, die als Input das spezifizierte Modell, den Stichprobenumfang (zur Bestimmung von Signifikanzen) und die Information, welches die manifesten exogenen Variablen sind, verlangt. Für sie müssen keine Varianzen und Kovarianzen spezifiziert werden. Das Ergebnis wird dem Objekt „sem.DHP.1“ zugewiesen:
Die Zusammenfassung des Modells erscheint mittels der generischen Funktion „summary“ (Abbildung 42). Diese kann auf die verschiedensten R-Objekte angewandt werden. Ausgegeben werden zunächst die gängigen globalen Fit-Statistiken. Der oben erwähnte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^{2}} -Test erzielt einen p-Wert von 0,245. Dieser ist größer als der übliche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fehler von 0,05 und damit entscheidet der Test für die Nullhypothese, dass die Varianz-Kovarianz-Matrix der Daten durch das Modell adäquat abgebildet wird. Unterhalb stehen die t-Tests für jeden einzelnen Koeffizienten. Die p-Werte sind allesamt kleiner als 0,05, daher sind alle Koeffizienten signifikant von Null verschieden. Die geschätzten Gleichungen lauten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R O C C A s p=0,24 * R I Q+0,18 * R S E S+0,40 * F O C C A s p+\varepsilon_{7} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F O C C A s p=0,22 * F I Q+0,31 * F S E S+0,42 * R O C C A s p+\varepsilon_{8} }
Als Kovarianzschätzung für die Fehlerterme ergibt sich: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{78}=-0,50} |
|---|
Wiederholungsaufgaben und Zusammenfassung
- Wiederholen Sie die Schritte bei der Analyse eines Strukturgleichungsmodells
- Was ist ein Messmodell? Was ein Strukturmodell?
- Zeigen Sie anhand der Bedingung für die maximale Parameteranzahl, dass das Beispiel 15 lösbar ist.
Zusammenfassung
In der statistischen Analyse mittels Strukturgleichungsmodellen (SEM) steht wie in keinem anderen der in diesem Studienheft vorgestellten Verfahren die Bildung von Hypothesen über die Wirkzusammenhänge zwischen manifesten und latenten Variablen im Vordergrund. Dieses konfirmatorische Vorgehen unterscheidet sich wesentlich von der (explorativen) Faktorenanalyse, die sich „blind“ auf die Daten stürzt. Es können komplexe Abhängigkeitsstrukturen unterstellt werden und durch ein Pfaddiagramm beschrieben werden. Dies enthält im Allgemeinen sowohl Messmodelle für latente Variablen, als auch ein Strukturmodell für den Zusammenhang zwischen latenten Variablen. Für die Lösbarkeit des dadurch entstehenden Gleichungssystems ist es von Bedeutung, dass – bezogen auf die Zahl der zu schätzenden Parameter – genügend Daten in Form von Kovarianzen zwischen beobachtbaren Merkmalen verfügbar sind. Geschätzt werden die Gleichungssysteme dann mit der in der Statistik üblichen Methode der Kleinsten-Quadrate- bzw. der Maximum-Likelihood-Schätzung. Wesentlicher Unterschied zur Faktorenanalyse ist auch, dass Hypothesen über die geschätzten Parameter getestet werden können.
Lösungen zu den Aufgaben und zu den Wiederholungsaufgaben
Lösungen zu den Aufgaben
Aufgabe 1
Wie auch schon Abbildung 2 vermuten lässt, ist – wenig überraschend – der lineare Zusammenhang zwischen dem Benzinverbrauch in der Stadt und auf der Autobahn betragsmäßig am größten (0,94).
Aufgabe 2
Die Regressionskoeffizienten ändern sich geringfügig. Die lineare Korrelation zwischen den Vorhersagewerten und der Originalvariable verändert sich durch Wegnahme einer einzigen Beobachtung immerhin von 0,80 auf 0,83.
Aufgabe 3
Analog zum Beispiel:
| Versuch | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Sorte 1 | 0,229 | 6,629 | -0,571 | -4,871 | -1,471 | 2,029 | -1,971 |
| Sorte 2 | -4,660 | 3,640 | 2,240 | 1,040 | -2,260 | - | - |
| Sorte 3 | 3,050 | -5,350 | -3,450 | 4,450 | 2,150 | -0,850 | - |
Draht Nr. 2 von Sorte 1 weicht am stärksten von der Prognose ab.
Aufgabe 4
| Datensatz 1 | Datensatz 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Beobachtung Nr. |
|
X1 | X2 | X3 | Beobachtung Nr. | X1 | X2 | X3 |
| 1 |
|
3 | 14 | 5 | 1 | 4 | 14 | 7 |
| 2 |
|
3 | 14 | 5 | 2 | 5 | 2 | 3 |
| 3 |
|
3 | 14 | 5 | 3 | 6 | 8 | 3 |
| 4 |
|
3 | 14 | 5 | 4 | 7 | 1 | 7 |
| 5 |
|
3 | 14 | 5 | 5 | 8 | 5 | 10 |
Datensatz 1 hat Bestimmtheitsmaß 100%, da alle drei Spalten (Variablen) keine Varianz aufweisen und die Mittelwerte unterschiedlich sind. Die Gesamtstreuung der Daten entfällt daher vollständig auf die Streuung zwischen den Gruppen(mittelwerten). Datensatz 2 hat Bestimmtheitsmaß 0, da alle drei Spalten den gleichen Mittelwert und Varianzen größer als Null aufweisen. Die Gesamtstreuung der Daten entfällt daher vollständig auf die Streuung innerhalb der einzelnen Gruppen.
Aufgabe 5
Bestimmtheitsmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R^{2}=\frac{Q Z}{Q T}=\frac{Q Z}{Q Z+Q I}=\frac{123,744}{123,744+199,361}=38,3 \%}
Aufgabe 6
Die Testentscheidung, ob H0 oder H1 gewählt werden soll, kann auf zwei Arten erfolgen.
Entweder es wird die Prüfgröße (im Beispiel 4,655) mit einem kritischen Wert, der von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} abhängt und einer Verteilungstabelle entstammt verglichen (im Beispiel 3,68). In diesem Fall wird für H1 entschieden, da 4,655>3,68. Im umgekehrten Fall wäre für H0 entschieden worden.
Die von Softwarepaketen durchgeführte, äquivalente Vorgehensweise dazu ist die Berechnung des p-Werts. Es wird also berechnet, mit welcher Wahrscheinlichkeit die F-Verteilung (im Beispiel mit 2 und 15 Freiheitsgraden) einen Wert größer als die Prüfgröße erzielt (in Excel: „FVERT(4,655;2;15)“ was als p-Wert 0,0267 liefert). Anschließend erfolgt die Testentscheidung, indem der p-Wert mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} verglichen wird. Im vorliegenden Fall gilt: p-WertFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle <\alpha=5%} , daher Entscheidung für H1. Der Vorteil nach letzterer Methode ist, dass auf einen Blick bestimmt werden kann, ab welchem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} der Test für H1 entscheidet. Der p-Wert wird auch bei Publikationen verwendet.
Aufgabe 7
Der p-Wert der Varianzanalyse ist 0,0264. Testet man auf 1%-Niveau, muss der p-Wert mit 1% verglichen werden. Da 0,0264>0,01 wird in diesem Fall die Nullhypothese H0 beibehalten.
Aufgabe 8
Alpha=5%: in Excel: „FINV(0,05;2;15)“ liefert 3,68 (vgl. Aufgabe 6)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{Q Z}{Q I}=3,68 \Leftrightarrow \frac{Q Z}{Q Z+Q I}=\frac{3,68}{3,68+1}=78,6 \%=R^{2} }
Alpha=1%: in Excel: „FINV(0,01;2;15)“ liefert 6,36
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{Q Z}{Q I}=6,36 \Leftrightarrow \frac{Q Z}{Q Z+Q I}=\frac{6,36}{6,36+1}=86,4 \%=R^{2} }
Aufgabe 9
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{\mu}=49,80 ; \widehat{\alpha_{1}}=59,05-49,80=9,25} (PP niedrig) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha_{2}}=49,45-49,80=-0,35} (PP mittel) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha_{3}}=40,90-49,80=-8,90} (PP hoch) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{1}}=50,73-49,80=0,93} (Postwurf) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{2}}=48,87-49,80=-0,93} (Anzeigen)
Interaktionen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\alpha \beta_{11}}=63,80-(49,80+9,25+0,93)=3,82; \widehat{\alpha \beta_{12}}=54,30-(49,80+9,25-0,93)=-3,82; \widehat{\alpha \beta_{21}}=51,50-(49,80-0,35+0,93)=1,12; \widehat{\alpha \beta_{22}}=47,40-(49,80-0,35-0,93)=-1,12; \widehat{\alpha \beta_{31}}=36,90-(49,80-8,90+0,93)=-4,93; \widehat{\alpha \beta_{32}}=44,90-(49,80-8,90-0,93)=4,93 } Interpretation (Beispiel): Bei Hochpreispolitik und Anzeigenwerbung werden durchschnittlich um 4,93 Stück mehr verkauft als aufgrund der getrennten Effekte zu erwarten gewesen wäre (d.h. der reduzierte Verkauf bei Hochpreispolitik wirkt sich eher bei der Werbeart „Postwurfsendung“) aus.
Aufgabe 10
| Objektpaar | |||||||
|---|---|---|---|---|---|---|---|
|
|
|
12 | 13 | 14 | 23 | 24 | 34 |
| L1-Distanz | Wert | 12 | 11 | 10 | 5 | 4 | 9 |
|
|
Rang | 6 | 5 | 4 | 2 | 1 | 3 |
| L2-Distanz | Wert | 7,87 | 6,71 | 8,12 | 3,61 | 2,45 | 5,74 |
|
|
Rang | 5 | 4 | 6 | 2 | 1 | 3 |
Die Rangfolgen der Distanzen zwischen den Objektpaaren sind nicht für beide Distanzmaße ident.
Aufgabe 11
Bei vier Objekten sind lt. Bell’schen Zahlen 15 Partitionen möglich:
| 1 / 2 / 3 / 4 | 12 / 3 / 4 | 13 / 2 / 4 | 14 / 2 / 3 | 23 / 1 / 4 |
|---|---|---|---|---|
| 24 / 1 / 3 | 34 / 1 / 2 | 12 / 34 | 13 / 24 | 14 / 23 |
| 123 / 4 | 124 / 3 | 134 / 2 | 234 / 1 | 1234 |
Aufgabe 12
Vollständige Rangordnung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{c} 15 \\ 2 \end{array}\right)=105} ]; Tetradenmethode: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{c}\left(\begin{array}{c} 15 \\ 2 \\ \end{array}\right) 2 \end{array}\right)=\left(\begin{array}{c} 105 \\ 2 \end{array}\right)=5460}
Bei 105 Vergleichen werden die Paare schrittweise sortiert (alle Paare werden z.B. auf Kärtchen präsentiert; diese werden vorerst in ähnliche und unähnliche Paare geteilt; die Untergruppen werden weiter geteilt). Bei 5460 Vergleichen muss jede Person nur einige Vergleiche durchführen.
Aufgabe 13
Die Distanz zwischen B und D ist am größten, jene zwischen A und D am kleinsten. Daher müssen die drei Objekte beispielsweise wie folgt liegen:
| B | A | D |
|---|
C und E müssten an den freien Stellen eingetragen werden. Nachdem die Distanz AE lt. Angabe größer als DE sein muss, ergibt sich hier ein Widerspruch.
Aufgabe 14
Bei 2 Dimensionen muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{l} K \\ 2 \end{array}\right) \geq 2 * K * 2} gelten, also muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K \geq 9} sein.
Bei 3 Dimensionen muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\begin{array}{l} K \\ 2 \end{array}\right) \geq 2 * K * 3} , also muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K \geq 13} sein.
Aufgabe 15
Standardisierte Variablen haben Varianzen gleich Eins; die mittels Hauptachsentransformation rotierten Komponenten haben daher ebenfalls im Durchschnitt eine Varianz gleich Eins; es wird daher eine Varianzsumme gleich Acht aufgeteilt; die drei Achsen mit der höchsten Varianz haben demnach zumindest eine Varianzsumme größer als Drei, und…
…erklären damit mindestens Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{3}{8}=37,5 \%} der Varianzsumme. Bei hochkorrelierten Variablen sollte die Varianzerklärung jedoch wesentlich höher liegen.
Eine Varianzerklärung von 74% bedeutet, dass maximal fünf Achsen gewählt werden, da bei den besten sechs Achsen der erklärte Anteil jedenfalls zumindest Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{6}{8}=75 \%} wäre.
Aufgabe 16
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{lr} h_{2}^{2}=0,843^{2}+(-0,160)^{2}=73,6 \% ; & h_{3}^{2}=0,929^{2}+(-0,254)^{2}=92,7 \% \\ h_{4}^{2}=0,342^{2}+0,936^{2}=99,3 \% ; h_{5}^{2}=0,277^{2}+0,957^{2}=99,2 \% & \end{array} }
Die errechneten Kommunalitäten finden sich alle in der Hauptdiagonale der reproduzierten Korrelationsmatrix. „Haltbarkeit“ wird durch die gewählten Komponenten am besten erklärt (99,3%).
Lösungen zu den Wiederholungsaufgaben
Lektion 1
Aufgabe 1
Da die Modellvoraussetzungen erfüllt sind, kann die geschätzte lineare Beziehung grundsätzlich vernünftig interpretiert werden, jedoch weist das niedrige Bestimmtheitsmaß auf eine schlechte Voraussage durch die erklärenden Variablen hin. Die Korrelation zwischen beobachteten Werten der Zielvariable und den geschätzten Werten beträgt lediglich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pm \sqrt{0,1}=\pm 0,32} .
Aufgabe 2
Die Korrelation ist 1
Die Varianz der Residuen ist gleich Null
Alle Punkte liegen in einer (Hyper-)Ebene
Aufgabe 3
Grundsätzlich ist der Einfluss einer Variablen, die einmal ein positives und einmal ein negatives Vorzeichen annimmt, fraglich. Man weiß nicht, ob der Einfluss nun positiv oder negativ ist (oder überhaupt Null?). Das trifft für die Variablen, zu denen die Koeffizienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{1}}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{2}}} geschätzt worden sind, zu. Auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{3}}} ist fraglich. Objektiv lässt sich das nachprüfen, indem jeweils der Mittelwert über die drei Stichproben der Standardabweichung gegenübergestellt wird:
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{0}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{1}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{2}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{3}}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \widehat{\beta_{4}}} | |
|---|---|---|---|---|---|
| Mittelwert | -0,30 | -0,04 | 19,93 | 23,00 | 0,47 |
| Standardabweichung | 0,02 | 0,07 | 2,22 | 20,97 | 2,58 |
| Mittelwert/Standardabweichung | -19,86 | -0,57 | 8,98 | 1,10 | 0,18 |
Die letzte Zeile zeigt auch die Prüfgröße, die üblicherweise bei einem statistischen Test für die Regressionsschätzer verwendet wird. Alle Zahlen nahe Null (insbesondere zwischen -2 und 2) deuten daraufhin, dass der zugrundeliegende Populations-Parameter eventuell nicht von Null verschieden ist.
Lektion 2
Aufgabe 1
Einerseits kann durch die Aufspaltung der gesamten Quadratsumme angegeben werden, welcher Anteil an der Gesamtstreuung durch die Faktoren erklärt wird (deskriptiv). Andererseits bilden die aufgespaltenen Quadratsummen „Zwischen“ und „Innerhalb“ die Basis für den statistischen Test, ob überzufällige Mittelwertsunterschiede existieren (induktiv).
Aufgabe 2
Weil sonst (insbesondere bei kleinen Stichproben) die Prüfgröße nicht F-verteilt ist und die Varianzanalyse ungültig ist.
Aufgabe 3
- Ja. Ein signifikanter Effekt ist bei einer größeren Stichprobe jedenfalls auch signifikant.
- Müsste konkret nachgeprüft werden. Je kleiner der Stichprobenumfang, desto eher wird für H0 entschieden, wenn alles andere konstant gehalten wird.
- Falls der p-Wert des Tests zwischen 1% und 5% liegt, wäre das Ergebnis nicht signifikant. Wenn er kleiner ist, schon.
Aufgabe 4
Der kritische Wert wird größer, da das 99%-Quantil größer als das 95%-Quantil ist. Dies führt dazu, dass H0 eher beibehalten wird.
Lektion 3
Aufgabe 1
Eine Partition ist ein System von Teilmengen der zu untersuchenden Objekte, wobei alle paarweisen Schnittmengen leer sind und die Vereinigung dieser Teilmengen die Objektmenge ergibt. Das Auffinden der in gewissen Sinne besten Partition ist das Ziel der Clusteranalyse.
Aufgabe 2
Eine Hierarchie ist eine Art Stammbaum, der angibt, in welcher Reihenfolge die Partitionen bei hierarchischen Clusterverfahren vergröbert bzw. verfeinert werden. In der Clusteranalyse ist die übliche Darstellungsform einer Hierarchie ein Dendrogramm.
Aufgabe 3
Bei hierarchischen Verfahren wird ein „Pfad“ abgesucht, der entweder von der Menge aller einelementigen Teilmengen der Untersuchungsobjekte zur Vereinigungsmenge (agglomerative Verfahren) führt, oder den umgekehrten Weg (divisive Verfahren). Hierbei werden der Reihe nach immer zwei Cluster vereinigt (Vergröberung) oder ein Cluster in zwei Teile aufgespalten (Verfeinerung). Damit wird untersucht, welche Clusteranzahl die beste ist. Bei partitionierenden Verfahren wird im vorhinein festgelegt, wieviele Cluster gewünscht sind und es werden verschiedene Partitionen derselben Clusteranzahl bezüglich eines Kriteriums optimiert.
Aufgabe 4
Von der Startpartition, die 20 Cluster zu je einem Element enthält, bis zur Zielpartition, die einen Cluster mit 20 Elementen enthält werden bei einem agglomerativen Verfahren insgesamt 20 Partitionen untersucht. Gesamt gibt es bei 20 Elementen 51724158235372 Partitionen.
Aufgabe 5
| Schritt Nr. | Partition | Heterogenität |
|---|---|---|
| 0 | 1 / 2 / 3 / 4 | 0 |
| 1 | 1 / 3 / 24 | 2,45 |
| 2 | 1 / 234 | 4,68 |
| 3 | 1234 | 7,57 |
Lektion 4
Aufgabe 1
Die Konfiguration ist die Anordnung der Beobachtungseinheiten in einem gewählten, meist zwei- oder dreidimensionalen Raum. Eine optimale Konfiguration zu finden, sodass ähnliche Objekte nahe bzw. unähnliche Objekte weit entfernt voneinander dargestellt werden ist das Ziel der MDS.
Die Distanz zwischen je zwei Objekten ist ein quantifiziertes Maß für ihre Unähnlichkeit. Je verschiedener eine Person zwei Objekte beurteilt bzw. je größer die Differenz zwischen einzelnen Merkmalen der Objekte sind, desto größer ist ihre Distanz zueinander.
Die Disparitäten sind Rechenhilfsgrößen bei der MDS. Sie modifizieren jede einzelne Distanz in der aktuellen Konfiguration um die kleinstmögliche Differenz, sodass die geforderte Distanzordnung eingehalten werden kann. Bei einer perfekt erstellten Ordnung gibt es keinen Unterschied zwischen den Disparitäten und den Distanzen.
Aufgabe 2
Sowohl die Clusteranalyse, als auch die MDS bewerten Distanzen der Objekte zueinander. Beide Verfahren benötigen nicht die Daten selbst, sondern kommen ausschließlich mit einer Distanzmatrix als Input aus. Die Clusteranalyse versucht, in bestehenden Daten homogene Gruppen zu finden. Ziel der MDS hingegen ist vor allem die Visualisierung der Abstände von Objekten zueinander.
Aufgabe 3
D: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{41}^{+}=8,69 ; x_{42}^{+}=-12,34} ;
E: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{51}^{+}=0,04 ; x_{52}^{+}=5,00}
Aufgabe 4
Die Disparitäten bilden eine monoton nicht fallende Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_{k l}} . Daher sind (1) die richtigen Disparitäten.
Das Stressmaß beträgt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S T R E S S_{1}=\sqrt{\frac{\sum\left(d_{k !}-\alpha_{k !}^{2}\right)^{2}}{\sum d_{k !}^{2}}}=\sqrt{\frac{2,5}{91}}=0,17} .
Daher kann die gefundene Konfiguration nur als „ausreichend“ bezeichnet werden.
Lektion 5
Aufgabe 1
Die Residuen der Korrelationen sind wie folgt:
| Kaloriengehalt | Vitamingehalt | Haltbarkeit | Preis | |
|---|---|---|---|---|
| Fettsäuren | 0,115 | -0,033 | -0,003 | -0,003 |
| Kaloriengehalt |
|
0,119 | 0,001 | 0,014 |
| Vitamingehalt |
|
|
0,002 | -0,009 |
| Haltbarkeit |
|
|
|
0,007 |
Die Korrelation zwischen Kaloriengehalt und Vitamingehalt wird mittels der beiden gewählten Komponenten am schlechtesten erklärt.
Aufgabe 2
Für zumindest 90% der Varianz sind zwei Komponenten notwendig.
Nach dem Kaiser-Kriterium werden nur Komponenten gewählt, die einen Eigenwert größer Eins haben, also überdurchschnittlich beitragen. Im Beispiel wäre das nur die erste Komponente.
Screeplot: Von rechts kommend wird der Linienverlauf erstmals merkbar an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=3} abgelenkt. Das würde für zwei Komponenten sprechen.
Aufgabe 3
Die Darstellung zeigt, welche Variablen in den beiden Komponenten hoch laden. Komponente 1 fasst im wesentlichen die Variablen „Fettsäuren“, „Vitamingehalt“ und „Kaloriengehalt“, die untereinander hoch korrelieren zusammen. Haltbarkeit und Preis sind hier vernachlässigbar, jedoch am ehesten für Komponente 2 repräsentativ. Hier wird deutlich, was hohe bzw. niedrige Werte der beiden Komponenten bei den verschiedenen Produkten bedeuten.
Lektion 6
Aufgabe 1
Vgl. Abbildung 39.
Aufgabe 2
Mess- und Strukturmodell sind die Komponenten eines allgemeinen Strukturgleichungsmodells. Das Messmodell gibt an, in welcher Form die latenten Faktoren durch die beobachteten Merkmale beschrieben/ gemessen werden können. Das Strukturmodellgibt an, wie die latenten Variablen untereinander wirken.
Aufgabe 3
In Beispiel 15 werden die paarweisen Kovarianzen/Korrelationen von sechs verschiedenen Variablen verwertet. Dies sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{6 *(6+1)}{2}=21} . Da nur 9 Parameter geschätzt werden, ist das Gleichungssystem lösbar.
- ↑ „MidPrice“ ist die in der Regression gewählte Zielvariable. Sie ist definiert als der arithmetische Mittelwert zwischen den Preisen für Basis- und Premiumversium des jeweiligen Modells.
- ↑ Unter Quadratsumme wird die Summe von quadrierten Zahlen verstanden. In der Varianzanalyse geht es immer um die Summe von quadrierten Abweichungen von Mittelwerten. Im Prinzip ist eine Quadratsumme eine Varianz, die nicht durch den Stichprobenumfang dividiert wurde.
- ↑ Die Prüfgröße F bzw. die Prüfverteilung ist benannt nach Sir Ronald A. Fisher, der erstmals im Jahre 1935 mit Erscheinen seines Buches „The Design of Experiments“ eine ausführliche Darstellung von Varianzanalyse und Versuchsplanung veröffentlichte (Hartung, 1998, S.12).
- ↑ Benannt nach dem schottisch-amerikanischen Mathematiker Eric Temple Bell. Berechenbar nach der Rekursionsformel <math>B_{n+1}=\sum_{k=0}^{n}\left(\begin{array}{l} n k \end{array}\right) B_{k} \text { mit } B_{0}=B_{1}=1
- ↑ Man kann die Achsen in einem Koordinatensystem beliebig drehen, ohne dass sich die L2-Distanz (Luftlinie) ändert..
- ↑ Da nur die Reihenfolge der Distanzen eine Rolle spielt, können auch – um „Wurzel“-Zahlen zu vermeiden – quadrierte euklidische Distanzen verwendet werden.
- ↑ Kelvin= Celsius+273,15 bzw. Fahrenheit=32+9/5*Celsius.
- ↑ Vgl. dazu auch die Beispiele von Anzur (2007, S.95).
- ↑ Man spricht daher auch von „partieller Korrelation unter Konstanthaltung einer weiteren Variablen.
- ↑ Vgl. ein grundlegendes Statistik-Lehrbuch (z.B. Bortz, 1999, Abschnitt 3.4).