Optimierung - Funktionen mehrerer Veränderlicher

Funktionen mehrerer Veränderlicher

Um Extremwerte von Funktionen in mehreren freien Variablen zu finden ist es erforderlich, die Kriterien für Extremwerten für höherdimensionale Definitionsbereiche zu verallgemeinern. Hier werden Gradient und Hessematrix die gleichen Rollen spielen wie 1. und 2. Ableitung im Eindimensionalen. Während die Bedingung an den Gradienten – er muss gleich dem Nullvektor sein, d.h., die Richtungsableitung muss in jeder Richtung verschwinden, sich ganz unmittelbar übertragen lässt, brauchen wir für die 2. Ableitungen etwas lineare Algebra – schließlich wollen wir der Matrix ansehen, ob die 2. Richtungsableitungen in jeder Richtung positiv oder negativ sind, oder ob das Krümmungsverhalten in den verschiedenen Richtungen unterschiedlich ist.

Determinante einer Matrix

Eine nxn-Matrix A entspricht einer linearen Abbildung:

$${\begin{aligned}{\begin{matrix}f:&\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}\\\ &{\vec {x}}\mapsto A{\vec {x}}\\\end{matrix}}\ \end{aligned}}$$

D.h., jeder Vektor aus dem ${\textstyle \mathbb {R} ^{n}}$ wird durch die Abbildung gedreht und/oder gestreckt oder gestaucht, so dass sein Bild wieder ein Vektor aus dem ${\textstyle \mathbb {R} ^{n}}$ ist. Nun sprengt eine ausführliche Abhandlung der linearen Funktionen den Rahmen dieses Kurses; eine Größe, die wir aber im Weiteren brauchen werden, ist die Determinante der Matrix. Sie errechnet sich für eine 2x2 Matrix

$${\begin{aligned}\ A=\left({\begin{matrix}a&b\\c&d\\\end{matrix}}\right)\end{aligned}}$$

nach der Formel

$${\begin{aligned}\det {\left(A\right)}=ad-bc,\end{aligned}}$$

für eine 3x3 Matrix

$${\begin{aligned}A=\left({\begin{matrix}a&b&c\\d&e&f\\g&h&i\\\end{matrix}}\right)\end{aligned}}$$

nach der Formel

$${\begin{aligned}\det {\left(A\right)}=aei+bfg+cdh-afh-bdi-ceg\end{aligned}}$$

(Regel von Sarrus), für höherdimensionale Matrizen mithilfe des Entwicklungssatzes und in der Praxis mit einem Algebra-Programm; Spezialfälle von Matrizen mit leicht ermittelbaren Determinanten sind Matrizen, die nur in der Diagonale Einträge ungleich 0 haben, sowie Matrizen, die entweder oberhalb oder unterhalb der Diagonale nur Nullen stehen haben; in beiden Fällen ist die Determinante das Produkt der Diagonal-Elemente. Ist die Determinante einer Matrix 0, so heißt das, dass zumindest eine Gerade von der Matrix auf den Nullvektor abgebildet wird; d.h., die Ebene wird auf eine Gerade abgebildet, der dreidimensionale Raum auf eine Ebene (oder eine Gerade) usw. Diese Eigenschaft macht man sich zunutze, um die sogenannten Eigenwerte der Matrix zu finden.

Eigenwerte und Eigenvektoren einer Matrix

Für eine ${\textstyle n\times n}$ Matrix A nennt man einen Vektor ${\textstyle {\vec {x}}\in \mathbb {R} ^{n}}$ einen Eigenvektor zum Eigenwert ${\textstyle \lambda }$, falls die sogenannte Eigenwertgleichung

$${\begin{aligned}A{\vec {x}}=\lambda {\vec {x}}\end{aligned}}$$

erfüllt ist. Dies bedeutet, dass der Eigenvektor x durch Multiplikation mit A einfach um den Faktor ${\textstyle \lambda }$ gestreckt (oder gestaucht) wird, ohne dabei gedreht zu werden; ist ${\textstyle \lambda }$ negativ, so wird der Vektor zusätzlich noch am Koordinaten-Ursprung gespiegelt – d.h., er zeigt nun in die entgegengesetzte Richtung.
Beispiel 7:
Gegeben sei die Matrix

$${\begin{aligned}A=\left({\begin{matrix}3&2\\-3&-4\\\end{matrix}}\right)\end{aligned}}$$

Es gilt

$${\begin{aligned}\left({\begin{matrix}3&2\\-3&-4\\\end{matrix}}\right)\left({\begin{matrix}1\\-3\\\end{matrix}}\right)=\left({\begin{matrix}-3\\\mathrm {\ \ } 9\\\end{matrix}}\right)\end{aligned}}$$

und

$${\begin{aligned}\left({\begin{matrix}3&2\\-3&-4\\\end{matrix}}\right)\left({\begin{matrix}2\\-1\\\end{matrix}}\right)=\left({\begin{matrix}4\\-2\\\end{matrix}}\right)\end{aligned}}$$

Somit ist

$${\begin{aligned}\left({\begin{matrix}1\\-3\\\end{matrix}}\right)\end{aligned}}$$

ein Eigenvektor zum Eigenwert -3,

$${\begin{aligned}\left({\begin{matrix}\mathrm {\ \ } 2\\-1\\\end{matrix}}\right)\end{aligned}}$$

Eigenvektor zum Eigenwert 2.

Wie kann man Eigenwerte und Eigenvektoren berechnen? Die Eigenwertgleichung bei bekanntem ${\textstyle \lambda }$ ist ein lineares Gleichungssystem mit ${\textstyle n}$ Gleichungen in ${\textstyle n}$ Variablen. Allerdings sind auch die Eigenwerte ${\textstyle \lambda _{i}}$ zunächst unbekannt, und müssen erst bestimmt werden: wenn ein Vektor ${\textstyle {\vec {x}}}$ Lösung Lösung der Eigenwertgleichung ${\textstyle \ A{\vec {x}}=\lambda {\vec {x}}}$ ist, so können wir diese Gleichung umformen zu ${\textstyle \left(A-\lambda I\right){\vec {x}}={\vec {o}}}$, (Hier ist I die Einheitsmatrix und ${\textstyle {\vec {o}}}$ der Nullvektor.) Daher ist die Matrix ${\textstyle A-\lambda I}$ singulär und hat die Determinante 0 – schließlich wird ja nicht nur ${\textstyle {\vec {x}}}$ auf den Nullvektor abgebildet, sondern auch jedes Vielfache, also die ganze Gerade, die durch diesen Vektor läuft. Es gilt:

$${\begin{aligned}det(A-\lambda I)=(-\lambda )^{n}+a_{n-1}\lambda ^{n-1}+\cdots +a_{1}\lambda +a_{0}=0\end{aligned}}$$

(Die Koeffizienten ${\textstyle a_{i}}$ ergeben sich dabei aus der Berechnung der Determinante, wie weiter unten ausgeführt.) Man bezeichnet ${\textstyle det\left(A-\lambda I\right)}$ als das charakteristische Polynom von A, die Eigenwerte sind die Nullstellen dieses Polynom. Die Suche nach allen Nullstellen erfolgt für großes n im Normalfall durch die im vorigen Abschnitt besprochenen numerischen Methoden. Für n=2 können Nullstellen sogar als Lösung einer quadratischen Gleichung unmittelbar gefunden werden, für n=3 häufig durch Erraten einer Nullstelle und anschließendes Aufspalten des Polynoms in Linearfaktoren (s. Beispiel 10).

Fortsetzung Beispiel 7:
Die charakteristische Gleichung lautet

$${\begin{aligned}\left|A-\lambda I\right|=\left|{\begin{matrix}3-\lambda &2\\-3&-4-\lambda \\\end{matrix}}\right|=\lambda ^{2}+\lambda -6=0\end{aligned}}$$

Lösen der quadratischen Gleichung

$${\begin{aligned}\lambda =-{\frac {1}{2}}\pm {\sqrt {{\frac {1}{4}}+6}}=-{\frac {1}{2}}\pm {\frac {5}{2}}\end{aligned}}$$

liefert die Nullstellen ${\textstyle \lambda _{1}=-3}$ und ${\textstyle \lambda _{2}=2}$.

Die zugehörigen Eigenvektoren erhält man durch Lösen der jeweiligen Eigenwertgleichungen. Beachte, dass die Eigenvektoren nur bis auf einen multiplikativen Faktor festgelegt sind.
Aufgabe 6:
Berechne alle Eigenwerte und Eigenvektoren für folgende Matrizen:

$${\begin{aligned}A=\left({\begin{matrix}\mathrm {\ 8} &7\\1&2\\\end{matrix}}\right)\\\ B=\left({\begin{matrix}1&-1\\-1&1\\\end{matrix}}\right)\\\ C=\left({\begin{matrix}1&-2&2\\-2&-2&4\\1&4&-6\\\end{matrix}}\right)\end{aligned}}$$

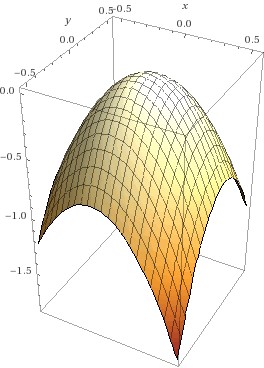
Die Theorie der Eigenwerte und Eigenvektoren spielt in vielen Anwendungsbereichen eine wesentliche Rolle . Ein Polynom n-ten Grades hat genau n Null-stellen, allerdings müssen diese nicht unbedingt verschieden sein – das Polynom ${\textstyle x^{2}-2x+1}$ hat die beiden Nullstellen ${\textstyle x_{1}=x_{2}=1}$ Man sagt: 1 ist eine Nullstelle mit Vielfachheit 2. Nullstellen können auch komplexe Zahlen sein. Für symmetrische Matrizen (d.h. AT = A), kann man zeigen, dass alle Eigenwerte reell sind. Zu den Eigenwerten mit Vielfachheit n gehören dann n linear unabhängige Eigenvektoren. Um uns die Bedeutung dieser Größen im Zusammenhang mit mehrdimensionalen Funktionen vor Augen zu führen, betrachten wir die Abbildung

$${\begin{aligned}f\left(x,y\right)=\left(x+y\right)^{2}+1.5\left(x-y\right)^{2}\end{aligned}}$$

Konvexe Funktion in zwei Veränderlichen

Konvexe Funktion in zwei Veränderlichen

Konvexe Funktion in zwei Veränderlichen

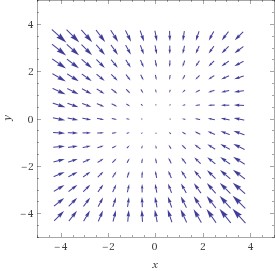
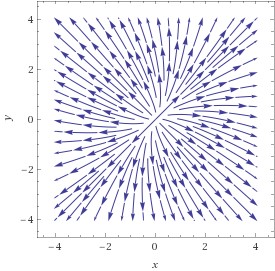
Die erste Graphik zeigt den (ziemlich faden …) Funktionsgraphen – ein Paraboloid; die zweite Graphik zeigt das Gradientenfeld – in jedem Punkt zeigt der Vektorpfeil in die Richtung des steilsten Anstiegs; die letzte Graphik zeigt nun die möglichen Wege einer Kugel, die wir am Scheitelpunkt absetzen: genau am Scheitelpunkt ist der Gradient null, d.h., die Richtungsableitung in jeder Richtung ist 0 und die Kugel bleibt einfach liegen. Geben wir ihr aber einen winzig kleinen Schubs, so ist der Gradient ungleich 0 und sie rollt sie nun in jedem Punkt dem Gradienten entgegen – schließlich will sie so schnell wie möglich nach unten und der Gradient zeigt den schnellsten Weg nach oben; die meisten möglichen Bahnen sind daher gekrümmt, d.h., der Gradient ändert ständig seine Richtung; es gibt allerdings zwei Richtungen, in denen die Bahnen Geraden sind – und das sind nun genau die Richtungen der Eigenvektoren der Hessematrix: in jedem Punkt auf dieser Geraden ändert sich der Gradient genau in der Richtung der Verbindung des Punktes mit dem Koordinaten-Ursprung; in unserem Fall zeigen die Pfeile auf diesen Trajektorien-Geraden jeweils vom Ursprung weg – damit ist klar: der Punkt ist ein Maximum – d.h., die Kugel wird in jeder Richtung vom Scheitel wegrollen. Das wiederum bedeutet für die Funktion, die die Höhe des Paraboloids für jeden Punkt der ${\textstyle x,y}$ – Ebene angibt, dass ihre 2. Richtungsableitung im Scheitelpunkt in jeder Richtung negativ sein muss.
Daraus ergibt sich folgendes Kriterium für Extremalstellen: der Gradient muss dort verschwinden; sind alle Eigenwerte der Hessematrix negativ, so ist der Punkt ein Maximum, sind sie positiv, ein Minimum, gibt es sowohl positive als auch negative, so haben wir einen Sattelpunkt. Die Vorzeichen der Eigenwerte bestimmt man mit den Definitheitskriterien:
Definitheit
Wir werden in diesem Abschnitt immer davon ausgehen, dass A eine symmetrische Matrix ist. Für die Anwendung, die wir letztendlich betrachten wollen, nämlich für die Hessematrix, ist dies natürlich der Fall, da ja gilt:

$${\begin{aligned}{\frac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}={\frac {\partial ^{2}f}{\partial x_{j}\partial x_{i}}}.\end{aligned}}$$

Im Zusammenhang mit symmetrischen Matrizen sind quadratische Formen von besonderem Interesse, dabei handelt es sich um die zur Matrix A gehörende Funktion

$${\begin{aligned}{\begin{matrix}q:&\mathbb {R} ^{n}\rightarrow \mathbb {R} \\\ &{\vec {x}}\mapsto {\vec {x}}^{T}A{\vec {x}}\\\end{matrix}}\end{aligned}}$$

Beispiel 8:
Gegeben sei die symmetrische Matrix

$${\begin{aligned}A=\left({\begin{matrix}1&2\\2&-4\\\end{matrix}}\right)\end{aligned}}$$

Die zu A gehörende quadratische Form ${\textstyle q}$ ordnet jedem zweidimensionalen Vektor den Wert zu.

$${\begin{array}{r}{\vec {x}}=\left({\begin{array}{l}x_{1}\\x_{2}\end{array}}\right)\\{\vec {x}}^{T}A{\vec {x}}=x_{1}^{2}+4x_{1}x_{2}-4x_{2}^{2}\end{array}}$$

Eine quadratische Form heißt
positiv definit, falls ${\textstyle {\vec {x}}^{T}A{\vec {x}}>{\vec {0}}}$ für alle x 0
positiv semidefinit, falls ${\textstyle {\vec {x}}^{T}A{\vec {x}}\geq {\vec {0}}}$ für alle x 0
negativ definit, falls ${\textstyle {\vec {x}}^{T}A{\vec {x}}<{\vec {0}}}$ für alle x 0
negativ semidefinit, falls ${\textstyle {\vec {x}}^{T}A{\vec {x}}\leq {\vec {0}}}$ für alle x 0
indefinit, falls ${\textstyle {\vec {x}}^{T}A{\vec {x}}>0}$ für einige x und ${\textstyle {\vec {y}}^{T}A{\vec {y}}<0}$ für einige y.

Diese Definitheitseigenschaften stehen in unmittelbarem Zusammenhang mit den Eigenwerten der Matrix A. Man kann zeigen, eine quadratische Form ${\textstyle {\vec {x}}^{T}A{\vec {x}}}$ ist
positiv definit, falls alle Eigenwerte > 0
positiv semidefinit, falls alle Eigenwerte ${\textstyle \geq }$ 0
negativ definit, falls alle Eigenwerte < 0
negativ semidefinit, falls alle Eigenwerte ${\textstyle \leq }$ 0
indefinit, falls einige Eigenwerte ${\textstyle >}$ 0 und einige Eigenwerte ${\textstyle <}$ 0 sind.
 

Die dazugehörigen Matrizen werden dann ebenfalls als positiv (semi-) definit usw. bezeichnet. In der Praxis kann die Definitheit von Matrizen oft mit dem Hauptminorenkriterium bestimmt werden. Als i-ten führenden Hauptminor einer Matrix bezeichnet man die Determinante der Matrix, die man gewinnt, wenn man nur die ersten i Zeilen und Spalten betrachtet; für eine Matrix

$${\begin{aligned}A=\left({\begin{matrix}a_{1,1}&\cdots &a_{1,n}\\\vdots &\ddots &\vdots \\a_{n,1}&\cdots &a_{n,n}\\\end{matrix}}\right)\end{aligned}}$$

lauten sie also (die senkrechten Striche sind eine alternative Schreibweise für die Berechnung der Determinante der Matrix zwischen den Strichen):

$${\tilde {\Delta }}_{1}(A)=a_{1,1},\quad {\tilde {\Delta }}_{2}(A)=\left({\begin{array}{cc}a_{1,1}&a_{1,2}\\a_{2,1}a_{2,2}\end{array}}\right),\ldots ,{\tilde {\Delta }}_{n}=\operatorname {det} A$$

Es gilt nun: sind alle führenden Hauptminoren positiv, so ist die Matrix positiv definit; sind die Vorzeichen der führenden Hauptminoren abwechselnd positiv und negativ – beginnend mit negativ – so ist die Matrix negativ definit. Weiters ist die Determinante der Matrix das Produkt der Eigenwerte - ist also die Determinante 0, so ist die Matrix indefinit, ist sie ungleich 0, sind alle Eigenwerte ungleich 0. Viele Fälle können mit diesen Kriterien durch Ausschluss bestimmt werden; nur wenn einer oder mehrere führende Hauptminoren 0 sind, ist keine eindeutige Aussage möglich. Wir können nun allgemeine Kriterien dafür aufstellen, wann eine zweimal differenzierbare mehrdimensionale nichtlineare Funktion ein lokales Extremum aufweist. Eine notwendige Bedingung ist wie bereits erwähnt ${\textstyle \mathrm {\nabla f} =0}$.Für Funktionen in einer Variablen bedeutet das: die Ableitung verschwindet. Ist die zweite Ableitung positiv, so findet sich dort ein Minimum. Diese Bedingung für Minima lässt sich auf Funktionen in mehreren Variablen erweitern: Wenn der Gradient in einem Punkt verschwindet und die zweite Ableitung in jeder Richtung negativ ist, so handelt es sich um ein lokales Minimum. Dafür genügt es, dass die zweite Ableitung in Richtung der Eigenvektoren der Hessematrix negativ ist, d.h., dass alle Eigenwerte der Hessematrix negativ sind und diese daher negativ definit ist; analoges gilt für die Maxima.

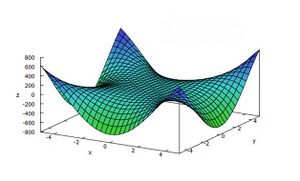
Achtung! Ein naheliegender Irrtum: man könnte glauben, dass es reicht, wenn wir uns das Krümmungsverhalten in x und y Richtung anschauen – also die zweiten partiellen Ableitungen; das ist aber nicht der Fall: die Abbildung zeigt eine Funktion, die entlang x und der y-Achse konkav ist; trotzdem ist der Nullpunkt – in dem der Gradient verschwindet – ein Sattelpunkt – es gibt nämlich auch Richtungen, in denen die Funktion konvex ist - die Diagonalen.

Beispiel für einen Sattelpunkt

Basierend auf den Definitheitseigenschaften der Hessematrix Hf gelten folgende hinreichenden Bedingungen für Extremwerte: Sei

$${\begin{aligned}\mathrm {\nabla f} \left({\vec {x}}_{0}\right)=0.\end{aligned}}$$

 Falls Hf an der Stelle ${\textstyle {\vec {x}}_{0}}$ positiv definit, so hat f dort ein lokales Minimum.
 Falls Hf an der Stelle ${\textstyle {\vec {x}}_{0}}$ negativ definit, so hat f dort ein lokales Maximum.
 Falls Hf an der Stelle ${\textstyle {\vec {x}}_{0}}$ indefinit, so handelt es sich an der Stelle weder um ein lokales Maximum noch um ein Minimum, sondern um einen sogenannten Sattelpunkt.
 Im Falle von ${\textstyle H_{f}}$ positiv semidefinit oder negativ semidefinit kann keine Aussage getroffen werden (vgl. die Situation im eindimensionalen, wenn die zweite Ableitung verschwindet).
 

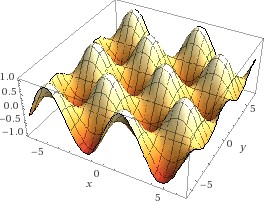
Die folgende Eierkarton-Funktion ${\textstyle \sin {x\cos {y\ }}}$ hat Bereiche, in denen sie in jeder Richtung kokav ist – dort finden sich die Maxima, also die Gipfel - andere, in denen sie in jeder Richtung konvex ist – dort sind die Minima, also die Gruben, und weitere Beriche, in denen sie in einer Richtung konvex ist, in einer anderen konkav – dort finden sich die Sattelpunkte. Stellen sie sich einen Bewohner einer dieser Gruben vor, der eine Freundin in der benachbarten Grube besuchen möchte; dabei muss er über einen Pass wandern – und dieser Pass ist dann der Sattelpunkt.

Eierkarton-Funktion

Beispiel 9:
Der linke Graph in Abbildung 1.3 zeigt einen Oberflächenplot der Funktion ${\textstyle x^{2}-y^{2}}$:
 

$${\begin{aligned}{\begin{matrix}f:&\mathbb {R} ^{2}\rightarrow \mathbb {R} \\\ &\left(x,y\right)\mapsto x^{2}-y^{2}\\\end{matrix}}.\end{aligned}}$$

Es gilt

$${\begin{aligned}\mathrm {\nabla f} \left(x,y\right)=\left({\begin{matrix}\mathrm {\ \ } 2x\\-2y\\\end{matrix}}\right)\end{aligned}}$$

und daher ist der Ursprung x=0, y=0 Kandidat für eine Extremstelle. Allerdings gilt

$${\begin{aligned}H_{f}\left(x,y\right)=\left({\begin{matrix}2&0\\0&-2\\\end{matrix}}\right)\end{aligned}}$$

mit den offensichtlichen Eigenwerten -2 und 2. Die Hessematrix ist indefinit, und der Ursprung ist keine Extremstelle, sondern ein Sattelpunkt. Die Abbildung veranschaulicht, woher dieser Name kommt: die zweite Ableitung der Funktion in Richtung der x-Achse ist überall positiv, daher insbesondere im Punkt (0,0); ebenso ist die zweite Ableitung in Richtung der y – Achse überall negativ, d.h. der Punkt (0,0) ist ein lokales Minimum, wenn wir ihn in Richtung der x-Achse queren und ein lokales Maximum, wenn wir ihn in Richtung y – Achse überqueren. Ein lokales Minimum müsste aber in jeder Richtung Minimum sein, daher kann (0,0) keines sein, und aus dem analogen Grund ebenso wenig ein Maximum.

Aufgabe 7:
Untersuche die folgenden beiden Funktionen auf lokale Extrema:

$${\begin{array}{r}f_{1}(x,y,z)=4x-2x^{2}+6y-y^{2}-z^{2}+3\\f_{2}(x,y,z)=3x^{2}-4xy+3y^{2}+10z-z^{2}\end{array}}$$