Optimierung - Gesamt
Christoph Krall studierte Genetik und Mathematik an den Universitäten Innsbruck, Salzburg und Wien und ist Lektor für Statistik an der Universität Wien sowie an der Technischen Universität Wien.
Derzeit arbeitet er am Institut für Medizinische Statistik der Medizinischen Universität Wien.
Wiederholung Analysis
In der einführenden Lektion werden grundlegende Konzepte der Analysis besprochen, die an sich bereits vom Schulunterricht und vom Bachelor Studium vertraut sein sollten, deren Wiederholung allerdings sicherlich nicht schadet. Zur Vorbereitung auf die späteren Kapitel, welche auf den hier vorgestellten Begriffen basieren, wird ein etwas formalerer Zugang gewählt als im Bachelor Studium.
Reelle Funktionen einer Veränderlichen
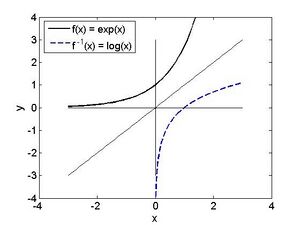
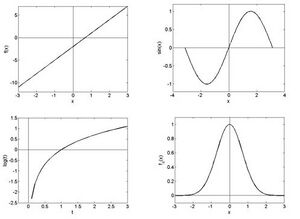
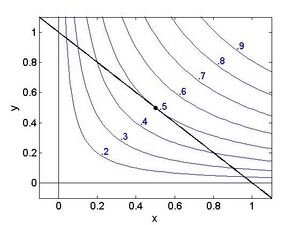
In der Finanzmathematik wurden bereits verschiedenste reelle Funktionen besprochen, etwa die Abhängigkeit des Kapitals von der Zeit , wenn Verzinsung erfolgt. Abbildung 1.1 zeigt den Graphen von zwei Funktionen.
In diesem Beispiel wäre die Zeit t (in Jahren) die unabhängige Variable, und wir haben zwei verschiedene Funktionen: das Kapital unter einfacher Verzinsung, und unter Berücksichtigung der Zinseszinsen. Dabei wird jedem Wert aus dem Intervall [0,40] eine Zahl bzw. zugeordnet. Üblicherweise wird die Funktion der Verzinsung nur für natürliche Zahlen ausgewertet. Wir möchten hier die entsprechenden Funktionen auf beliebige reelle Zahlen im Intervall [0,40] fortsetzen. Im Allgemeinen versteht man unter einer reellen Funktion, bzw. einer reellen Abbildung eine Zuordnungsvorschrift, wo jedem Wert der unabhängigen Variablen genau ein Wert der abhängigen Variable zugeordnet wird. Mitunter ist die Funktion nicht für alle reellen Zahlen definiert, sondern hat einen eingeschränkten Definitionsbereich. So ist zum Beispiel der Logarithmus nur für positive reelle Zahlen definiert. Um eine Funktion vollständig zu charakterisieren schreibt man
wobei in der ersten Zeile festgelegt wird für welche Werte von x die Abbildung definiert ist (Definitionsbereich ), und dass der Bildbereich in den reellen Zahlen liegt. Die zweite Zeile gibt konkret die Rechenvorschrift an.
Beispiel 1: In Abbildung 1 haben wir
Zu den wichtigsten Funktionen gehören lineare Funktionen, Polynome, trigonometrische Funktionen, die Exponentialfunktion und die Logarithmusfunktion, deren Gestalt als bekannt vorausgesetzt wird.
Aufgabe 1 Zeichne mit R und Maxima ähnlich zu Abbildung 1.1 die Graphen folgender Funktionen:
Bei der Bildung einer zusammengesetzten Funktion ist darauf zu achten, dass der Bildbereich von f im Definitionsbereich von liegt.
Umkehrabbildung
Ein wesentliches Merkmal einer Funktion ist, dass jedem Wert von genau eine reelle Zahl zugeordnet wird. Manchmal ist es der Fall, dass auch umgekehrt jeder Bildwert genau einem Urbildwert entspricht. Dies gilt speziell dann, wenn eine Funktion streng monoton steigend bzw. streng monoton fallend ist. Dies bedeutet, dass für jedes entweder (steigend) oder (fallend). In diesen Fällen kann die sogenannte Umkehrabbildung gebildet werden, die jedem Bildwert den entsprechenden Urbildwert zuordnet. Es gilt
Beispiel 2: In Abbildung 2 finden wir ein wichtiges Beispiel: Die streng monoton steigende Funktion und deren Umkehrfunktion Beachte, dass man im Graphen die Umkehrfunktion durch Spiegelung an der ersten Hauptdiagonale erhält. Klarerweise gilt . Andererseits gilt auch für , ansonsten liegt nicht im Definitionsbereich der Logarithmus-Funktion.
Ein Beispiel für eine Funktion die sich nicht umkehren lässt wäre .
Aufgabe 2 Skizziere ähnlich zu Abbildung 2 den Graphen von
\begin{aligned}f^+:&\mathbb{R}^+\rightarrow\mathbb{R}\\\ &x\mapsto x^2\\\end{aligned} und überlege, warum es keine eindeutige Umkehrfunktion gibt. Zeichne die beiden Umkehrfunktionen zu und
Löse algebraisch die Gleichung nach und vergleiche mit den graphischen Lösungen
Differentiation
Als nächstes wollen wir uns mit Glattheitseigenschaften von Funktionen beschäftigen. Als erstes wäre da der Begriff der Stetigkeit. Eine Funktion ist an einem Punkt x im Wesentlichen dann stetig, wenn sie dort nicht springt.
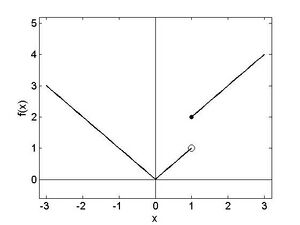
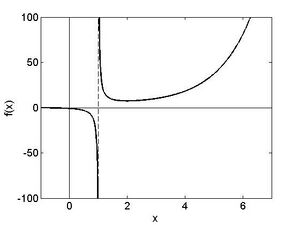
Beispiel 3: In Abbildung 3 ist folgende Funktion gezeichnet:
Die Funktion ist überall stetig außer an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=1} wo sie einen Sprung der Höhe 1 hat.
Formal wird die Stetigkeit dadurch definiert, dass an einer bestimmten Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_0} sowohl der rechtsseitige Limes als auch der linksseitige Limes mit dem Funktionswert übereinstimmt. AlsoFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{x_n \rightarrow x_0}f\left(x_n\right)=f\left(x_0\right) }
sowohl für beliebige Folgen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_n < x_0} als auch für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_n > x_0} .
In Beispiel 3 bedeutet dies, dass an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_0 = 1} zwar der rechts-seitige Limes mit dem Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(1) = 2} übereinstimmt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{x_n\rightarrow1^+}f\left(x_n\right)= \lim\limits_{h \rightarrow 0, h \rightarrow 0} f(1+h)= 1+1+\lim\limits_{h \rightarrow 0, h \rightarrow 0}|h|= 1=f\left(1\right) }
Hingegen gilt für den linksseitigen Limes:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{x_n\rightarrow1^-}f\left(x_n\right)=1 }
(nachrechnen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h < 0} !) Daher ist die Funktion an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_0 = 1} nicht stetig. In Abbildung 1.3 ist der rechtsseitige Limes durch einen Punkt, der linksseitige Limes durch einen Ring gekennzeichnet.
Differenzierbarkeit hängt nun damit zusammen, ob eine Funktion an einem Punkt einigermaßen glatt ist und nicht etwa einen Knick aufweist. Anschaulich gesprochen bedeutet dies, dass man im Graphen der Funktion an einem Punkt eine Tangente anpassen kann. Stetigkeit ist dafür eine notwendige Voraussetzung, allerdings nicht hinreichend. Die Funktion aus Abbildung 1.3 etwa ist an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=0} zwar stetig, aber nicht differenzierbar. Die Theorie der Differentialrechnung wurde in der Finanzmathematik ausführlich besprochen.
Rechenregeln
Wir wollen nur die wichtigsten Rechenregeln der Differentialrechnung wiederholen. Die folgende Tabelle beinhaltet die Ableitungen der gängigsten Funktionen, wobei hier a eine beliebige reelle Zahl sein kann:
Zusätzlich von Bedeutung sindFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} Produktregel: (f g)^{\prime}=f^{\prime} g+f g^{\prime} \\ Quotientenregel: \left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime} g-f g^{\prime}}{g^2} \\ Kettenregel: (g \circ f)^{\prime}=\left(g^{\prime} \circ f\right) \cdot f^{\prime \prime} \\ \end{array} }
Die Kettenregel kann auch in folgender Form geschrieben werden:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{d}{{dx}}g\left(f\left(x\right)\right)=g^\prime\left(f\left(x\right)\right)\cdot f^\prime\left(x\right) } Durch konsequente Anwendung dieser Regeln lassen sich bereits viele praktische Aufgaben lösen.
Aufgabe 3 Differenziere folgende Funktionen und überprüfe das Ergebnis mit Maxima!Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} f_1(x)=\exp (-x 2) \\ f_2(x)=\tan x=\sin (x) \cdot \cos (x) \\ f_3(x)=\sqrt{1+x^3} \end{array} }
Die erste Ableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{'}(x)} ist wiederum eine Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}} , deren Ableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{''}(x)} man als Ableitung zweiter Ordnung bezeichnet. Entsprechend können Ableitungen höherer Ordnung definiert werden. Die erste Ableitung einer Funktion gibt deren Steigung an. Die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{'}(x)=0} bestimmt potentielle lokale Extremstellen der Funktion. Die Ableitung zweiter Ordnung beschreibt die Krümmung einer Kurve und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{''}(x)=0} definiert potentielle Wendepunkte. All diese Überlegungen fließen bei der wohlbekannten Diskussion von Kurven ein.
Integration
Geometrisch gesehen dient das Integrieren zum Berechnen von Flächen.
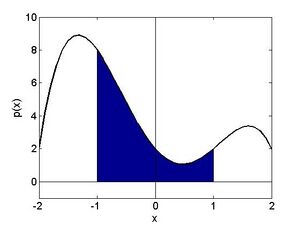
Beispiel 4: In Abbildung 1.4 ist das Polynom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(x) = -x^4+x^3+4x^2-4x+2} geplottet. Es soll die Fläche zwischen der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(x)} und der x-Achse im Bereich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-1,1)} berechnet werden, die in der Abbildung hervorgehoben wurde. Die Berechnung erfolgt mit einem sogenannten bestimmten Integral, bei dem die obere und die untere Grenze des Integrationsbereichs feststehen (im Beispiel eben die Grenzen -1 und 1).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{x=-1}^1 p(x) \mathrm{dx} &=\int_{x=-1}^1\left(-x^4+x^3+4 x^2-4 x+2\right) \mathrm{dx}=\\ &=-\frac{x^5}{5}+\frac{x^4}{4}+\frac{4 x^3}{3}-\frac{4 x^2}{2}+\left.2 \mathrm{x}\right|_{-1} ^1=\frac{94}{15} \end{aligned} }
Im folgenden Abschnitt werden wir die Details zu dieser Berechnung genau erläutern. Für die allgemeine Integrationstheorie ist der Zusammenhang zwischen Integralrechnung und Differentialrechnung von entscheidender Bedeutung:
Hauptsatz der Analysis
Dieser fundamentale Satz besagt, dass Integrieren und Differenzieren zueinander inverse Operationen sind. Um dies zu verstehen brauchen wir zunächst folgende Begriffe: Das unbestimmte Integral einer Funktion f sowie deren Stammfunktion. Ein unbestimmtes Integral von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} erhält man, indem man die untere Grenze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} des Integrals festhält, während man die obere Grenze variieren lässt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_a\left(x\right)=\int_{y=a}^{x}f\left(y\right)\mathrm{dy} }
Für jedes feste Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} wird dadurch eine Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} definiert. Unter eine Stammfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} versteht man eine differenzierbare Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle F(x)} für die giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F^\prime\left(x\right)=f\left(x\right) }
Es gibt davon unendlich viele, da man zu jeder Stammfunktion eine Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} addieren kann und wiederum giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (F(x)+c)^\prime=f(x) }
D.h. die Stammfunktion ist nur bis auf eine Konstante eindeutig bestimmbar. Der Hauptsatz der Analysis besagt nun, dass jedes unbestimmte Integral von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} gerade eine Stammfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} ist:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{d}{\mathrm{dx}}I_a\left(x\right)=\frac{d}{\mathrm{dx}}\int_{y=a}^{x}f\left(y\right)\mathrm{dy} =f\left(x\right) }
Umgekehrt erhalte ich alle Stammfunktionen mittels unbestimmter IntegraleFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F\left(x\right)=\int_{y=a}^{x}f\left(y\right)\mathrm{dy} +c }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} als Integrationskonstante bezeichnet wird. Die folgende Tabelle gibt die Stammfunktionen der wichtigsten einfachen Funktionen, wobei hier Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} jede beliebige reelle Zahl mit Ausnahme von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -1} sein kann.
Die Tabelle ist gerade die Umkehrung von jener der Differentiation.
Ist die Stammfunktion F(x) einer Funktion f(x) bekannt, so können bestimmte Integrale für ein Intervall [a,b] recht einfach berechnet werden:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=a}^{b}f\left(x\right)\mathrm{dx} =F\left(b\right)-F\left(a\right) }
Die Integrationskonstante des unbestimmten Integrals kürzt sich weg, und daher genügt es eine einzige Stammfunktion zu kennen um beliebige bestimmte Integrale von f zu berechnen. Man verwendet häufig die NotationFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=a}^{b}f\left(x\right)\mathrm{dx} =F\left(x\right)|_a^b=F\left(b\right)-F\left(a\right) }
um in einem Zwischenschritt zu verdeutlichen, wie die Stammfunktion explizit aussieht. Nun sollte die Berechnung des Integrals in Beispiel 4 kein Problem mehr machen.
Aufgabe 4:
Das Berechnen von Wahrscheinlichkeiten entspricht hier gerade der Integration. Eine in der Praxis häufig auftretende Verteilung ist die Exponentialverteilung, mit DichteFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\left(x\right)=\left\{\begin{aligned}\lambda\mathrm{\ exp}\left(-\lambda x\right)\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ } x>0\\\mathrm{\ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sonst}\\\end{aligned}\right. }
Berechne die Wahrscheinlichkeit, dass eine exponentialverteilte Zufallsvariable mit Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda} Werte zwischen 1 und 2 annimmt.
Partielle Integration, Substitution
Während das Differenzieren nach Erlernen der Grundtechniken weitgehend mechanisch abläuft ist dies beim Integrieren leider nicht der Fall. Im Gegenteil, häufig gleicht die Suche nach einer Stammfunktion einer höheren Kunstform, und in vielen Fällen ist eine geschlossene Darstellung eines unbestimmten Integrals gar nicht möglich. So besitzt beispielsweise die Dichte der Normalverteilung keine einfach darstellbare Stammfunktion, und zur Berechnung von Wahrscheinlichkeiten ist man hier entweder auf Tabellen oder auf numerische Integration angewiesen. Zwei Basistechniken zur Bestimmung von Stammfunktionen sollen hier allerdings Erwähnung finden:
Partielle Integration:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int{{f}^\prime g}={fg}-{fg}' }
Dies ist das Pendant zur Produktregel, was durch Differenzieren unter Verwendung des Hauptsatzes der Analysis unmittelbar klar wird:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {f}^\prime {g}=\left({fg}\right)^\prime-{{fg}}^\prime }
Substitution:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int g\left(x\right)\mathrm{dx} =\left|\begin{aligned}y=h\left(x\right)\\\mathrm{dy}=h^\prime\left(x\right)\mathrm{dx} \\\end{aligned}\right|=\int{g(h}^{-1}(y))\frac{\mathrm{dy} }{h^\prime\left(x\right)} }
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h(x)} streng monoton steigend.
Man kann zeigen, dass es sich hier um das Pendant zur Kettenregel beim Differenzieren handelt. Wir wollen beide Techniken anhand eines konkreten Beispiels vorführen. In den Wiederholungsaufgaben gibt es einige weitere Beispiele.
Beispiel 5: Der Erwartungswert einer Zufallsvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle X} mit Dichte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} ist definiert alsFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E\left(X\right)=\int_{x=-\infty}^{\infty}\mathrm{xf}\left(x\right)\mathrm{dx} }
Für die Exponentialverteilung (aus Aufgabe 4) erhält manFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=0}^{\infty} x \lambda \exp (-\lambda x) \mathrm{d} x= \int_{y=0}^{\infty} y \lambda \exp (-\lambda y) \mathrm{d} y= -\left.\frac{1}{\lambda} y \exp (-y)\right|_0 ^{\infty}+\frac{1}{\lambda} \int_{y=0}^{\infty} \exp (-y) \mathrm{d} y=\frac{1}{\lambda} } Die zweite Gleichung mittels partieller Integration:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f^\prime\left(y\right)=\mathrm{exp}-y, gy=y }
Man beachte, dassFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{y\rightarrow\infty}y\mathrm{\ exp}\left(\mathrm{-y}\right)=0 }
weil die Exponentialfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{exp}(-y)} wesentlich rascher gegen 0 konvergiert als der Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} wächst.
Reelle Funktionen mehrerer Veränderlicher
Vorbemerkung: in diesem Abschnitt wird mit Vektoren und Matrizen gerechnet; zwar werden die einzelnen Schritte erläutert, - falls diese Schritte aber große Schwierigkeiten bereiten, sollten Sie die erforderlichen Grundlagen der Linearen Algebra rekapitulieren. Bislang haben wir uns auf Funktionen einer freien Variablen beschränkt, d.h. der Definitionsbereich und der Bildbereich waren jeweils Teilmengen der Zahlengerade. Allgemeiner betrachtet kann man Abbildungen mit n Veränderlichen studieren; diese schreibt man in der Form:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f:\ \ D\ \subseteq\mathbb{R}^n\ \rightarrow\ \mathbb{R} \ \ \ \ \ \ \left(x_1,\ \ldots x_n\right)\rightarrow f\left(x_1,\ \ldots x_n\right) }
Nun ist diese Verallgemeinerung – trotz der etwas sperrigen Notation (und es wird noch schlimmer!) durchaus naheliegend: in der Praxis wird eine Zielvariable ja häufig nicht nur von einer einzigen Einflussvariablen bestimmt, sondern von mehreren – nehmen wir etwa die Nachfrage nach Bier in einem Gastgarten: sie wird vom Preis des Bieres abhängen, von der Temperatur und vom Datum zu Monatsbeginn haben viele Gäste noch mehr Geld zur Verfügung als gegen Monatsende; diese drei freien Variablen können wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P,T,d} nennen – oder eben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1,x_2,x_3} . Funktionen mit eindimensionalem Definitionsbereich konnten wir durch den Graphen veranschaulichen – auf der x-Achse wird die freie Variable aufgetragen, auf der y-Achse die Abhängige – dann erhalten wir bei einer stetigen Funktion eine Kurve (oder Gerade) im Raum. Bei Funktionen mit mehrdimensionalem Definitionsbereich ist eine solche Veranschaulichung im Allgemeinen nicht mehr möglich; eine Ausnahme sind die FunktionenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ f:\ \ D\ \subseteq\mathbb{R}^2\ \rightarrow\ \mathbb{R}: }
hier ist der Definitionsbereich ein Teilbereich der (zweidimensionalen) Ebene, und jedem Punkt aus diesem Ebenen-Bereich wird ein Funktionswert zugeordnet – den wir uns als Höhe vorstellen können. Der Graph der Funktion wird also eine – möglicherweise sehr unebene – Fläche im Raum sein; als Beispiel können Sie sich eine Landschaft vorstellen: jeder Punkt hat eine x- und eine y- Koordinate in der Ebene, und diesem Punkt wird eine Höhe zugeordnet; je nachdem wie stetig die Funktion nun ist, wird die Landschaft glatt oder zerklüftet sein. Funktionen mit höherdimensionalem Definitionsbereich kann man sich nicht mehr so einfach veranschaulichen. Die Definition der Stetigkeit wird nun etwas komplizierter, da man sich einem Punkt in der Ebene – oder einem höherdimensionalen Raum – nicht nur aus zwei Richtungen, sondern aus beliebig vielen Richtungen nähern kann. Das Konzept bleibt ansonsten aber das Gleiche. Eine Funktion f ist an einer Stelle stetig, falls für jede Folge von Punkten, die gegen diesen Punkt konvergiert die entsprechende Folge der Funktionswerte gegengegen den Funktionswert dieses Punktes konvergiert.
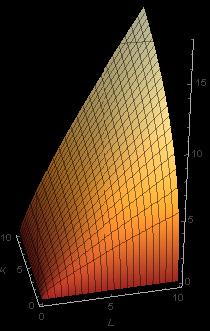
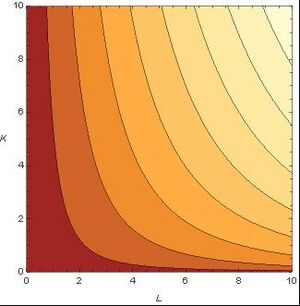
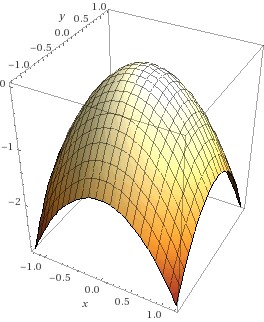
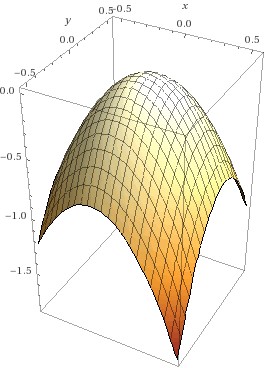
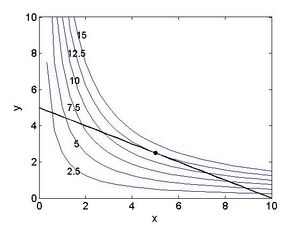
Beispiel 6: Großer Beliebtheit erfreut sich in den Wirtschaftswissenschaften die Cobb-Douglas Funktion, die den Einfluss von mehreren Faktoren auf die Produktion modelliert. So ließ sich in den Jahren 1960 bis 1975 die Produktion Y der Beiersdorf AG in Abhängigkeitn von den beiden Faktoren L (Arbeit) und K (Kapital) durch die FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y=Y\left(L,K\right)=e^{0.04}L^{0.84}K^{0.39} }
gut beschreiben. Die Abbildung zeigt den Graphen der Funktion: der Definitionsbereich ist die Menge aller Punkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (L,K),L>=0,K>=0} , also der positive Quadrant der Ebene; jedem dieser Punkte wird nun eine Funktionswert zugeordnet. Ist einer der beiden Faktoren 0, so ist die Produktivität auch 0; für jeden anderen Wert des einen Faktors ist die Funktion streng monoton steigend im anderen – das sehen wir an den Gitterlinien auf dem Graphen; diese sind die Bilder von Geraden parallel zur K- bzw. zur L-Achse. Offensichtlich ist die Funktion auf jeder dieser Gitterlinien streng monoton steigend. Die Abbildung daneben zeigt die Höhenschichtlinien der Funktion; sie verbinden Punkte aus dem Definitionsbereich mit jeweils gleichem Funktionswert. Im Wikipedia – Eintrag zur Cobb-Douglas Funktion finden Sie eine schöne Animation!
Funktionen in mehreren Variablen können wir uns im Allgemeinen nicht vorstellen; wir können aber versuchen, jede dieser Variablen „getrennt“ zu betrachten, d.h., wir weisen allen anderen einen konstanten Wert zu – dann nehmen diese in der Funktionsgleichung die Rolle von Konstanten ein – und betrachten die Änderung des Funktionswertes bei Änderung der einen Variablen im Fokus.
Beispiel 6 (Fortsetzung): Nehmen wir an, wir wissen, wir wollen nur wissen, wie sich die Produktivität bei konstanter Arbeitsleistung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1} entwickelt, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} variiert. Dann können wirFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y=Y\left(K,1\right)=e^{0.04}\cdot1\ K^{0.39} }
schreiben – also die Funktion nur noch abhängig von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} betrachten. In der linken Graphik würde das heißen, dass wir uns jene Gitterlinie suchen, die zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1} gehört, und auf dieser variable Werte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} betrachten. In dieser Betrachtung können wir nun das Werkzeug aus der eindimensionalen Analysis einsetzen; z.B. können wir Ableitungen in Richtung einer Variablen definieren, wenn alle anderen Festgehalten werden – formal:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial x_i}f\left(x_1,\ldots,x_n\right)=\lim\limits_{h\rightarrow0}\frac{f\left(x_1,\ldots,x_i+h,\ldots x_n\right)-f\left(x_1,\ldots,x_i,\ldots x_n\right)}{h} }
Beispiel 6 (Fortsetzung): Bilden wir die partiellen Ableitungen der Cobb-Douglas-Funktion, so erhalten wir:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial Y}{\partial L}={0.84e}^{0.04}L^{-0.16}K^{0.39},\ \ \frac{\partial Y}{\partial K}={0.39e}^{0.04}L^{0.84}K^{-0.61} }
Der Zeilen-Vektor aus den partiellen Ableitungen wird als Jacobi-Matrix bezeichnet,Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\left(f\right)=\left(\frac{\partial f}{\partial x_1},\ \ldots\frac{\partial f}{\partial x_n}\right) }
Der Spalten-Vektor bestehend aus allen partiellen Ableitungen wird als Gradient bezeichnet,Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla\left(f\right)=\left(\frac{\partial f}{\partial x_1},\ \ldots\frac{\partial f}{\partial x_n}\right)^t=: \begin{pmatrix}\frac{\partial f}{\partial x_1} \\\frac{\partial f}{\partial x_2} \end{pmatrix} }
Existieren die partiellen Ableitungen für alle Variablen und sind ihrerseits stetig, so bezeichnet man die Funktion als differenzierbar. Der Gradientenvektor steht in jedem Punkt normal auf die Höhenschichtlinie durch den Punkt und zeigt in die Richtung des steilsten Anstiegs.
Beispiel 6 (Fortsetzung): Die Jacobi Matrix der Cobb-Douglas Funktion, ausgewertet für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1,K=2} :Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\left(f\right)\left(1,2\right)=\left(1.15,0.27\right) }
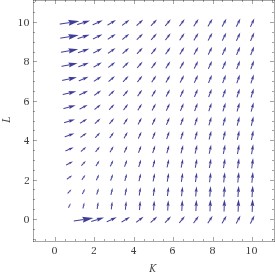
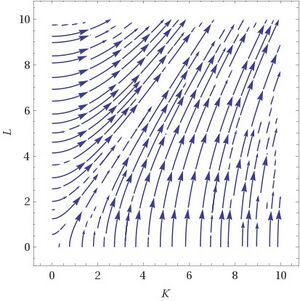
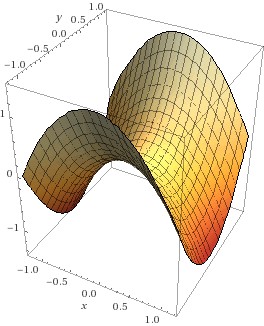
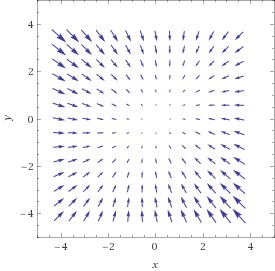
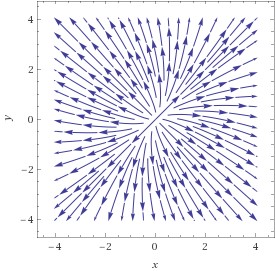
Die untere Abbildung zeigt den Gradienten der Cobb-Douglas Funktion als Vektorfeld; in jedem Punkt zeigt die horizontale Komponente des Pfeils die partielle Ableitung nach K, die vertikale die partielle Ableitung nach L. Sie stehen normal auf die Höhenschichtlinien. Die rechte Graphik stückelt diese Gradienten-Vektoren zu Trajektorien zusammen – jene Wege, auf denen man von einem gegebenen Startpunkt aus am schnellsten steigt. Auf diesen werden wir bei der Suche nach Maxima bewegen – zumindest annähernd.
In der Jacobi-Matrix stehen die Richtungsableitungen in Richtung jeder einzelnen Variablen – d.h., sie gibt die Steigung der Tangenten an den Funktionsgraph in jeder dieser Richtungen an. Gibt es nur zwei freie Variable, dann ist der Graph einer stetigen Funktion eine Fläche im Raum, und die Tangenten an einen Punkt spannen eine Ebene aus – die Tangentialebene; bei höherdimensionalen Funktionen spricht man von Hyperebenen. Mithilfe der Jacobi-Matrix lässt sich nun die Richtungsableitung in beliebiger Richtung definieren. Die partiellen Ableitungen geben ja an, wie sich der Funktionswert auf der Tangentialebene verändert, wenn man eine Einheit in Richtung jeder einzelnen Variablen geht. Will man nun in eine beliebige Richtung gehen, so sucht man deren Einheitsvektor und multipliziert jede Komponente mit der entsprechenden partiellen Ableitung – man bildet das Matrix-Produkt der Jacobi-Matrix mit dem Richtungsvektor der Veränderung.
Beispiel 6 (Fortsetzung): Die Jacobi Matrix der Cobb-Douglas Funktion, ausgewertet für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1,K=2} :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\left(f\right)\left(1,2\right)=\left(1.15,0.27\right) }
D.h. Wenn ich über dem Punkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P=(1,2)} eine Tangentialebene anlege, so hat diese über dem Punkt die Höhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Y(1,2)=1.37} , verändere ich nun die erste Komponente, so erhöht sich die Höhe der Tangentialebene um einen Betrag von 1.15; gehen wir stattdessen von P eine Einheit in Richtung der 2. Komponente, so ergibt sich ein Zuwachs von 0.27.
Wie aber verändert sich der Funktionswert, wenn wir uns in beliebiger Richtung vom Punkt P fortbewegen? Dann brauchen wir den Einheitsvektor dieser Richtung: z.B. in Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (3,1)} : Die Länge des Vektors istFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt{3^2+1^2}=\sqrt{10} }
D.h.: der VektorFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{\sqrt{10}}\left(3,1\right)= \begin{pmatrix} \frac{3}{\sqrt{10}} \\\ \frac{1}{\sqrt{10}}) \end{pmatrix} }
ist der Einheitsvektor in dieser Richtung. Wenn wir als vom Punkt P eine Einheit in diese Richtung gehen, so ergibt sich ein Höhenzuwachs von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ \frac{3}{\sqrt{10}}.1.15} aus der Bewegung in die erste Richtung, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ \frac{3}{\sqrt{10}}.0.27} aus der Bewegung in der zweiten Richtung – und der gesamte Höhenzuwachs ist die Summe dieser beiden.
Mathematisch ausgedrückt erhalten wir die Richtungsableitung als Produkt der Jacobi-Matrix mit dem Richtungsvektor, oder – äquivalent – als inneres Produkt des Gradientenvektors mit dem Richtungsvektor. Die folgenden Schreibweisen sind äquivalent – die letzte nicht ganz exakt aber gebräuchlich:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &(0.27,1.15)\left(\begin{array}{c}\frac{3}{\sqrt{10}} \\ \frac{1}{\sqrt{10}}\end{array}\right)=\left(\left(\begin{array}{c}1.15 \\ 0.27\end{array}\right),\left(\begin{array}{c}\frac{3}{\sqrt{10}} \\ \frac{1}{\sqrt{10}}\end{array}\right)\right)=\\=&\left(\left(\begin{array}{c}1.15 \\ 0.27\end{array}\right) \cdot\left(\begin{array}{c}\frac{3}{\sqrt{10}} \\ \frac{1}{\sqrt{10}}\end{array}\right)\right)=1.15 \cdot \frac{3}{\sqrt{10}}+0.27 \cdot \frac{1}{\sqrt{10}} \end{aligned} } Der Gradient bzw. die Jacobi-Matrix entsprechen den ersten Ableitungen von Funktion mit eindimensionalem Definitionsbereich; lassen sich einige Aussagen aus dem Eindimensionalen umformulieren – z.B. die Definition einer streng monoton wachsenden Funktion: im eindimensionalen Fall hieß das, dass die 1. Ableitung strikt positiv ist. Ebenso bezeichnen wir eine Funktion aus dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}^n} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}} als streng monton wachsend, wenn alle partiellen Ableitungen strikt positiv sind. Ebenso können wir die Kriterien für Extremwerte ins Mehrdimensionale übertragen. Hier muss gelten: wenn eine Funktion aus dem Mehrdimensionalen einen Extremwert in einem Punkt hat, so müssen in diesem Punkt alle partiellen Ableitungen 0 sein – dann sind auch alle Richtungsableitungen in beliebiger Richtung 0; allerdings war das Verschwinden der ersten Ableitung schon im Eindimensionalen eine notwendige, aber keine hinreichende Bedingung für das Vorliegen eines Extremwertes – wir mussten noch die zweite Ableitung befragen. Nun wird die Verallgemeinerung der 2. Ableitung ins mehrdimensionale allerdings formal etwas sperriger werden und zur sogenannten Hesse-Matrix führen. Das Gegenstück zur ersten Ableitung war nämlich der Gradient, in dem sich die partiellen ersten Ableitungen befanden. Aus diesem gewinnen wir nun die Hessematrix, indem wir die Jacobi-Matrix von jeder Komponente dieses Gradienten bilden.
Beispiel 6 (Fortsetzung): Der Gradient der Cobb-Douglas Funktion warFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla Y=\left(\begin{array}{c} Y \\ L \\ Y \end{array}\right)=\left(\begin{array}{c} 0.84 e^{0.04} L^{-0.16} K^{0.39} \\ 0.39 e^{0.04} L^{0.84} K^{-0.61} \end{array}\right) }
Die partiellen zweiten Ableitungen werden nun wieder nach beiden Variablen abgeleitet – analog zu den ersten:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial L}\left(\frac{\partial Y}{\partial L}\right)=:\ \frac{\partial^2Y}{\left(\partial L\right)^2}=\ -0.16\cdot0.84e^{0.04}L^{-1.16}K^{0.39} }
Für die Hessematrix ergibt sich daher:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_f\left(L,K\right)=\left(\begin{aligned}-0.14L^{-1.16}K^{0.39}&0.34L^{-0.16}K^{-0.61}\\0.34L^{-0.16}K^{-0.61}&-0.25L^{0.84}K^{-1.61}\\\end{aligned}\right) }
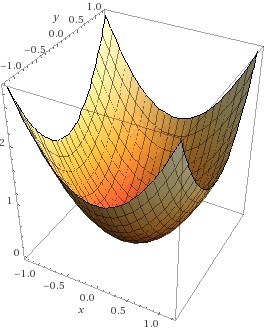
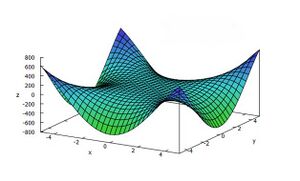
Die gemischten 2. Ableitungen sind immer gleich unabhängig von der Reihenfolge, in der abgeleitet wird – d.h., die Matrix ist symmetrisch. Mit dieser Hessematrix kann nun die 2. Ableitung in jeder beliebigen Richtung bestimmt werden: die zweite Ableitung in Richtung eines Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{v}} der Länge 1 ergibt sich durch die sogenannte quadratische Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ {\vec{v}}^t\vec{H_f}\vec{v}\ } Ist nun diese 2. Ableitung in jeder Richtung positiv, so heißt das, die Funktion ist in jeder Richtung konvex – d.h., ein Punkt, an dem alle partiellen Ableitungen 0 sind (und damit auch der Gradient der Nullvektor) ist ein Minimum. Ist die 2. Richtungsableitung in allen Richtungen negativ, so ist die Funktion in allen Richtungen konkav – d.h., der kritische Punkt ist ein Maximizer. Und gibt es Richtungen, in denen die 2. Richtungsableitung positiv ist, ander, in denen sie negativ ist, so handelt es sich um einen Sattelpunkt. Beispiele finden Sie in der Abbildung:
Beispiel 6 (Fortsetzung): Für die Hessematrix der Cobb-Douglas-Funktion im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1,2)} ist:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_f\left(1,2\right)=\left(\begin{aligned}-0.18&0.22\\0.22&-0.08\\\end{aligned}\right) }
Für die 2 Richtungsableitung in Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{v}=(\frac{3}{\sqrt{10}},\ \frac{1}{\sqrt{10}})} bilden wir zunächst das Matrix-Vektor Produkt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{H}_f \vec{v}=\left(\begin{array}{cc}-0.18 & 0.22 \\ 0.22 & -0.08\end{array}\right)\left(\begin{array}{c}\frac{3}{\sqrt{10}} \\ \frac{1}{\sqrt{10}}\end{array}\right)=\left(\begin{array}{c}-0.18 \cdot \frac{3}{\sqrt{10}}+0.22 \cdot \frac{1}{\sqrt{10}} \\ 0.22 \cdot \frac{3}{\sqrt{10}}-0.08 \frac{1}{\sqrt{10}}\end{array}\right)=\left(\begin{array}{c}-0.10 \\ 0.18\end{array}\right) } Der Vektor auf der rechten Seite hat eine anschauliche Interpretation: er gibt an, in welcher Richtung und wie stark sich der Gradient verändert, wenn wir vom Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1,2)} in der Richtung des Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(\frac{3}{\sqrt{10}},\frac{1}{\sqrt{10}}\right)} gehen. Für die Quadratische Form wird nun das innere ProduktFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{pmatrix}\frac{3}{\sqrt{10}}\\\ \frac{1}{\sqrt{10}}\end{pmatrix}. \begin{pmatrix} -0.10 \\\ 0.18\end{pmatrix} =-0.04 }
gebildet. Es gibt uns die 2. Richtungsableitung in dieser Richtung an. Es ist negativ – d.h. die Funktion ist in diesem Punkt in dieser Richtung konkav. (Die Cobb-Douglas Funktion ist in jedem Punkt in jeder Richtung konkav)
Ein Kriterium, anhand dessen wir diese Eigenschaften der Hessematrix bestimmen können, findet sich in der 2 Lektion (Definitheitskriterien).
Einige Beispiele dazu finden sich in den Wiederholungsaufgaben.
Zusammenfassung Ziel dieses Kapitels war es, in sehr komprimierter Weise grundlegendes mathematisches Basiswissen zu wiederholen, das zum Teil bereits von der Mittelschule bekannt sein sollte, und zum Teil im Bachelor Studium erworben wurde. Speziell die Techniken des Differenzierens und Integrierens sollten beherrscht werden, können aber aufgrund von Platzmangel in diesem Skriptum nicht ausführlicher behandelt werden. Für eine umfangreiche und sehr lesbare Quelle zum Thema mit konkretem Bezug zu den Wirtschaftswissenschaften empfehle ich zum Beispiel das Buch von Sydsaeter und Hammond (2004).
Wiederholungsaufgaben/Übungen
Aufgabe 1 Differenziere folgende Funktionen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=x^{\mathrm{exp}\left(x\right)}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{x^2+\sqrt x}{3x-2}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\sqrt x\mathrm{cos}x^2}
Aufgabe 2 Führe für die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{\mathrm{exp} \left(x\right)}{x-1}} eine Kurvendiskussion durch! (d.h. Definitionsbereich, Nullstellen, Extremwerte, Wendepunkte, Zeichnung)
Aufgabe 3 Suche die Stammfunktionen folgender Funktionen mittels Substitution: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=e^{3x+4}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=x\mathrm{log}\left(x^2\right)} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\mathrm{sin}(4x-3)}
Aufgabe 4 Berechne folgende Integrale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \int_{x=0}^{1}x^2e^{-x}\mathrm{dx}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \int_{x=1}^{2}\mathrm{log}\left(\frac{x}{2}\right)\mathrm{dx}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \int_{x=2}^{4}\left|x-3\right|\mathrm{dx}}
Aufgabe 5 Bestimme den Definitionsbereich folgender Funktionen und berechne Gradienten und Hessematrix: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=\mathrm{log}(x^2-y^2)} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=\frac{\mathrm{xy} }{x-y}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y,z\right)=\mathrm{xyz}+x^2y+y^2z+z^2x}
Optimierung
Ziel dieser Lektion ist es die nichtlineare Optimierung auf Funktionen mit mehreren Variablen zu erweitern. Dazu wird die Theorie der Eigenwerte aus der linearen Algebra benötigt. Neben der theoretischen Abhandlung sollen hier auch algorithmische Ansätze besprochen werden. Ein wesentlicher Punkt ist die Suche nach Extremwerten unter der Einhaltung von gewissen Nebenbedingungen. Als notwendige Kriterien werden die Lagrange–Methode sowie die Karush–Kuhn–Tucker Bedingungen besprochen.
Lokale Extrema von reellen Funktionen
Wir erinnern uns, dass für Funktionen mit einer Veränderlichen eine notwendige Bedingung für lokale Extrema darin besteht, dass die erste Ableitung verschwindet, i.e. durch Lösen der Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^\prime\left(x\right)=0}
erhält man mögliche Kandidaten für ein Maximum bzw. ein Minimum einer Funktion.
Beispiel 6: Betrachte das Polynom aus Beispiel 4:
Ableitung liefert
Die Suche nach Nullstellen von liefert potenzielle Kandidaten für lokale Maxima und Minima. Für ein Polynom dritten Grades gibt es geschlossene Formeln, um die Nullstellen zu bestimmen, man erhält näherungsweise
Der Vergleich lässt erkennen, dass an der Stelle das absolute Maximum der Funktion liegt, während es sich bei um ein lokales Minimum und bei um ein lokales Maximum handelt.
Bereits für eine solch einfache Funktion wie ein Polynom dritten Grades ist die Bestimmung der Nullstellen nicht ganz trivial. Für die meisten Funktionen ist eine explizite Lösung überhaupt nicht möglich, und man ist auf numerische Methoden angewiesen. Die wichtigste wird im folgenden Abschnitt vorgestellt:
Das Newton Verfahren
Wir wollen die Nullstelle einer Funktion finden. (In Zusammenhang mit den Optimierungsaufgaben dieses Kapitels ist die Ableitung der Funktion, deren Extremwerte gesucht werden; das Verfahren kann aber selbstverständlich für beliebige einmal differenzierbare Funktionen angewandt werden.) Das Newton-Verfahren ist ein Iterationsverfahren. Wir beginnen mit einer Stelle , die hoffentlich bereits in der Nähe der Nullstelle liegt. Grundidee ist nun die Funktion durch ihre Tangente an der Stelle zu ersetzen, und anschließend die Nullstelle der Tangente zu suchen. Die Lösung liefert den nächsten Punkt der Iteration:
Anschließend wird diese Prozedur so lange wiederholt, bis das Verfahren konvergiert, d.h. (bis auf numerische Genauigkeit) eine Nullstelle gefunden wurde. Es kann gezeigt werden, dass das Newton Verfahren extrem rasch (quadratisch) konvergiert, sobald man sich in der Nähe einer Nullstelle befindet. Die deutsche Wikipedia Seite bietet eine sehr schöne Animation, die verdeutlich wie das Newton Verfahren in der Praxis funktioniert. Um Kandidaten für lokale Extrema von zu erhalten sucht man Nullstellen der Ableitung von f, und das Iterationsverfahren hat daher die Gestalt
Das bedeutet eine Funktion muss mindestens zweimal differenzierbar sein, damit diese Methode verwendet werden kann. In der Literatur findet man eine Unzahl an weiteren Methoden zur numerischen Bestimmung von Nullstellen.
Aufgabe 5:
Berechne für das Polynom aus Beispiel 6 die ersten beiden Newtonschritte mit Startwert . Schreib ein kleines Programm in der Programmiersprache deiner Wahl. Versuche auch andere Startwerte und beobachte wie sich das Verfahren verhält.
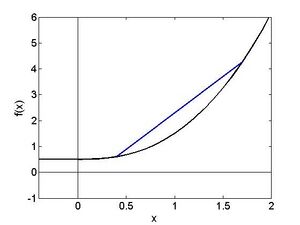
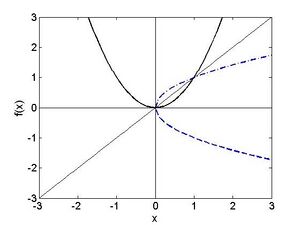
Die Bestimmung von globalen Extrema ist typischerweise wesentlich komplizierter als die Suche nach lokalen Extrema. Auch müssen diese nicht zwangsläufig existieren; die Funktion besitzt unendlich lokale Minima und Maxima, die gleichzeitig globale Extremwerte sind, die Funktion besitzt unendlich viele lokale Extremwerte, aber keinen globalen. Plotten Sie die beiden Funktionen, um sich diese Tatsache vor Augen zu führen! Für eine gewisse Klasse von Funktionen kann man jedoch von lokaler Optimalität auf globale Optimalität schließen. Speziell nennt man eine Funktion f konvex (konkav), falls die Funktionswerte zwischen zwei Werten x und y jeweils unterhalb der Verbindungsgeraden der beiden Funktionswerte an x und y – der sogenannten Sekante - liegen. D.h. für jede Zahl t zwischen 0 und 1 gilt
Die Abbildung zeigt eine konvexe Funktion und deren Sekante für zwei ausgewählte Werte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_2} . Die Sekante liegt oberhalb des Graphen der Funktion. Falls die zweite Ableitung existiert so gilt für eine konvexe FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^{\prime\prime}\left(x\right)\geq0 \end{aligned}}
und für eine konkave FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^{\prime\prime}\left(x\right)\le0 \end{aligned}}
Für eine konvexe (konkave) Funktion gibt es höchstens ein lokales Extremum, und dies ist dann das globale Minimum (Maximum).
Funktionen mehrerer Veränderlicher
Um Extremwerte von Funktionen in mehreren freien Variablen zu finden ist es erforderlich, die Kriterien für Extremwerten für höherdimensionale Definitionsbereiche zu verallgemeinern. Hier werden Gradient und Hessematrix die gleichen Rollen spielen wie 1. und 2. Ableitung im Eindimensionalen. Während die Bedingung an den Gradienten – er muss gleich dem Nullvektor sein, d.h., die Richtungsableitung muss in jeder Richtung verschwinden, sich ganz unmittelbar übertragen lässt, brauchen wir für die 2. Ableitungen etwas lineare Algebra – schließlich wollen wir der Matrix ansehen, ob die 2. Richtungsableitungen in jeder Richtung positiv oder negativ sind, oder ob das Krümmungsverhalten in den verschiedenen Richtungen unterschiedlich ist.
Determinante einer Matrix
Eine nxn-Matrix A entspricht einer linearen Abbildung:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{matrix}f:&\mathbb{R}^n\rightarrow\mathbb{R}^n\\\ &\vec{x}\mapsto A\vec{x}\\\end{matrix}\ \end{aligned}}
D.h., jeder Vektor aus dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}^n} wird durch die Abbildung gedreht und/oder gestreckt oder gestaucht, so dass sein Bild wieder ein Vektor aus dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}^n} ist. Nun sprengt eine ausführliche Abhandlung der linearen Funktionen den Rahmen dieses Kurses; eine Größe, die wir aber im Weiteren brauchen werden, ist die Determinante der Matrix. Sie errechnet sich für eine 2x2 MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \ A=\left(\begin{matrix}a&b\\c&d\\\end{matrix}\right) \end{aligned}}
nach der FormelFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \det{\left(A\right)}=ad-bc, \end{aligned}}
für eine 3x3 MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}a&b&c\\d&e&f\\g&h&i\\\end{matrix}\right) \end{aligned}}
nach der FormelFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \det{\left(A\right)}=aei+bfg+cdh-afh-bdi-ceg \end{aligned}}
(Regel von Sarrus), für höherdimensionale Matrizen mithilfe des Entwicklungssatzes und in der Praxis mit einem Algebra-Programm; Spezialfälle von Matrizen mit leicht ermittelbaren Determinanten sind Matrizen, die nur in der Diagonale Einträge ungleich 0 haben, sowie Matrizen, die entweder oberhalb oder unterhalb der Diagonale nur Nullen stehen haben; in beiden Fällen ist die Determinante das Produkt der Diagonal-Elemente. Ist die Determinante einer Matrix 0, so heißt das, dass zumindest eine Gerade von der Matrix auf den Nullvektor abgebildet wird; d.h., die Ebene wird auf eine Gerade abgebildet, der dreidimensionale Raum auf eine Ebene (oder eine Gerade) usw. Diese Eigenschaft macht man sich zunutze, um die sogenannten Eigenwerte der Matrix zu finden.
Eigenwerte und Eigenvektoren einer Matrix
Für eine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n\times n} Matrix A nennt man einen Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}\in\mathbb{R}^n} einen Eigenvektor zum Eigenwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda} , falls die sogenannte EigenwertgleichungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A\vec{x}=\lambda\vec{x} \end{aligned}}
erfüllt ist. Dies bedeutet, dass der Eigenvektor x durch Multiplikation mit A einfach um den Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
gestreckt (oder gestaucht) wird, ohne dabei gedreht zu werden; ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
negativ, so wird der Vektor zusätzlich noch am Koordinaten-Ursprung gespiegelt – d.h., er zeigt nun in die entgegengesetzte Richtung.
Beispiel 7:
Gegeben sei die MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}3&2\\-3&-4\\\end{matrix}\right) \end{aligned}}
Es giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}3&2\\-3&-4\\\end{matrix}\right)\left(\begin{matrix}1\\-3\\\end{matrix}\right)=\left(\begin{matrix}-3\\\mathrm{\ \ }9\\\end{matrix}\right) \end{aligned}}
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}3&2\\-3&-4\\\end{matrix}\right)\left(\begin{matrix}2\\-1\\\end{matrix}\right)=\left(\begin{matrix}4\\-2\\\end{matrix}\right)\end{aligned}}
Somit ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}1\\-3\\\end{matrix}\right) \end{aligned}}
ein Eigenvektor zum Eigenwert -3,
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(\begin{matrix}\mathrm{\ \ }2\\-1\\\end{matrix}\right) \end{aligned}}
Eigenvektor zum Eigenwert 2.
Wie kann man Eigenwerte und Eigenvektoren berechnen? Die Eigenwertgleichung bei bekanntem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda} ist ein lineares Gleichungssystem mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} Gleichungen in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle n} Variablen. Allerdings sind auch die Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_i} zunächst unbekannt, und müssen erst bestimmt werden: wenn ein Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}} Lösung Lösung der Eigenwertgleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ A\vec{x}=\lambda\vec{x}} ist, so können wir diese Gleichung umformen zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(A-\lambda I\right)\vec{x}=\vec{o}} , (Hier ist I die Einheitsmatrix und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{o}} der Nullvektor.) Daher ist die Matrix Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle A-\lambda I} singulär und hat die Determinante 0 – schließlich wird ja nicht nur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}} auf den Nullvektor abgebildet, sondern auch jedes Vielfache, also die ganze Gerade, die durch diesen Vektor läuft. Es gilt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} det(A-\lambda I)=(-\lambda)^n+a_{n-1}\lambda^{n-1}+\cdots+a_1\lambda+a_0=0 \end{aligned}}
(Die Koeffizienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a_i} ergeben sich dabei aus der Berechnung der Determinante, wie weiter unten ausgeführt.) Man bezeichnet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle det\left(A-\lambda I\right)} als das charakteristische Polynom von A, die Eigenwerte sind die Nullstellen dieses Polynom. Die Suche nach allen Nullstellen erfolgt für großes n im Normalfall durch die im vorigen Abschnitt besprochenen numerischen Methoden. Für n=2 können Nullstellen sogar als Lösung einer quadratischen Gleichung unmittelbar gefunden werden, für n=3 häufig durch Erraten einer Nullstelle und anschließendes Aufspalten des Polynoms in Linearfaktoren (s. Beispiel 10).
Fortsetzung Beispiel 7:
Die charakteristische Gleichung lautetFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left|A-\lambda I\right|=\left|\begin{matrix}3-\lambda&2\\-3&-4-\lambda\\\end{matrix}\right|=\lambda^2+\lambda-6=0 \end{aligned}}
Lösen der quadratischen GleichungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda=-\frac{1}{2}\pm\sqrt{\frac{1}{4}+6}=-\frac{1}{2}\pm\frac{5}{2} \end{aligned}}
liefert die Nullstellen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_1=-3} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda_2=2} .
Die zugehörigen Eigenvektoren erhält man durch Lösen der jeweiligen Eigenwertgleichungen. Beachte, dass die Eigenvektoren nur bis auf einen multiplikativen Faktor festgelegt sind.
Aufgabe 6:
Berechne alle Eigenwerte und Eigenvektoren für folgende Matrizen:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}\mathrm{\ 8}&7\\1&2\\\end{matrix}\right) \\\ B=\left(\begin{matrix}1&-1\\-1&1\\\end{matrix}\right) \\\ C=\left(\begin{matrix}1&-2&2\\-2&-2&4\\1&4&-6\\\end{matrix}\right) \end{aligned}}
Die Theorie der Eigenwerte und Eigenvektoren spielt in vielen Anwendungsbereichen eine wesentliche Rolle . Ein Polynom n-ten Grades hat genau n Null-stellen, allerdings müssen diese nicht unbedingt verschieden sein – das Polynom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2-2x+1} hat die beiden Nullstellen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1=x_2=1} Man sagt: 1 ist eine Nullstelle mit Vielfachheit 2. Nullstellen können auch komplexe Zahlen sein. Für symmetrische Matrizen (d.h. AT = A), kann man zeigen, dass alle Eigenwerte reell sind. Zu den Eigenwerten mit Vielfachheit n gehören dann n linear unabhängige Eigenvektoren. Um uns die Bedeutung dieser Größen im Zusammenhang mit mehrdimensionalen Funktionen vor Augen zu führen, betrachten wir die AbbildungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\left(x+y\right)^2+1.5\left(x-y\right)^2 \end{aligned}}
Die erste Graphik zeigt den (ziemlich faden …) Funktionsgraphen – ein Paraboloid; die zweite Graphik zeigt das Gradientenfeld – in jedem Punkt zeigt der Vektorpfeil in die Richtung des steilsten Anstiegs; die letzte Graphik zeigt nun die möglichen Wege einer Kugel, die wir am Scheitelpunkt absetzen: genau am Scheitelpunkt ist der Gradient null, d.h., die Richtungsableitung in jeder Richtung ist 0 und die Kugel bleibt einfach liegen. Geben wir ihr aber einen winzig kleinen Schubs, so ist der Gradient ungleich 0 und sie rollt sie nun in jedem Punkt dem Gradienten entgegen – schließlich will sie so schnell wie möglich nach unten und der Gradient zeigt den schnellsten Weg nach oben; die meisten möglichen Bahnen sind daher gekrümmt, d.h., der Gradient ändert ständig seine Richtung; es gibt allerdings zwei Richtungen, in denen die Bahnen Geraden sind – und das sind nun genau die Richtungen der Eigenvektoren der Hessematrix: in jedem Punkt auf dieser Geraden ändert sich der Gradient genau in der Richtung der Verbindung des Punktes mit dem Koordinaten-Ursprung; in unserem Fall zeigen die Pfeile auf diesen Trajektorien-Geraden jeweils vom Ursprung weg – damit ist klar: der Punkt ist ein Maximum – d.h., die Kugel wird in jeder Richtung vom Scheitel wegrollen. Das wiederum bedeutet für die Funktion, die die Höhe des Paraboloids für jeden Punkt der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x,y}
– Ebene angibt, dass ihre 2. Richtungsableitung im Scheitelpunkt in jeder Richtung negativ sein muss.
Daraus ergibt sich folgendes Kriterium für Extremalstellen: der Gradient muss dort verschwinden; sind alle Eigenwerte der Hessematrix negativ, so ist der Punkt ein Maximum, sind sie positiv, ein Minimum, gibt es sowohl positive als auch negative, so haben wir einen Sattelpunkt. Die Vorzeichen der Eigenwerte bestimmt man mit den Definitheitskriterien:
Definitheit
Wir werden in diesem Abschnitt immer davon ausgehen, dass A eine symmetrische Matrix ist. Für die Anwendung, die wir letztendlich betrachten wollen, nämlich für die Hessematrix, ist dies natürlich der Fall, da ja gilt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial^2f}{\partial x_i\partial x_j}=\frac{\partial^2f}{\partial x_j\partial x_i}. \end{aligned}}
Im Zusammenhang mit symmetrischen Matrizen sind quadratische Formen von besonderem Interesse, dabei handelt es sich um die zur Matrix A gehörende FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{matrix}q:&\mathbb{R}^n\rightarrow\mathbb{R}\\\ &\vec{x}\mapsto{\vec{x}}^TA\vec{x}\\\end{matrix} \end{aligned}}
Beispiel 8:
Gegeben sei die symmetrische MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}1&2\\2&-4\\\end{matrix}\right) \end{aligned}}
Die zu A gehörende quadratische Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q} ordnet jedem zweidimensionalen Vektor den Wert zu.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} \vec{x}=\left(\begin{array}{l} x_1 \\ x_2 \end{array}\right) \\ \vec{x}^T A \vec{x}=x_1^2+4 x_1 x_2-4 x_2^2 \end{array} }
Eine quadratische Form heißt
positiv definit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} > \vec{0} }
für alle x 0
positiv semidefinit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} \geq \vec{0} }
für alle x 0
negativ definit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} < \vec{0} }
für alle x 0
negativ semidefinit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} \leq \vec{0} }
für alle x 0
indefinit, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}^TA\vec{x} > 0 }
für einige x und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{y}}^TA\vec{y} < 0 }
für einige y.
Diese Definitheitseigenschaften stehen in unmittelbarem Zusammenhang mit den Eigenwerten der Matrix A. Man kann zeigen, eine quadratische Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{x}^TA\vec{x}}
ist
positiv definit, falls alle Eigenwerte > 0
positiv semidefinit, falls alle Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \geq}
0
negativ definit, falls alle Eigenwerte < 0
negativ semidefinit, falls alle Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \leq}
0
indefinit, falls einige Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle >}
0 und einige Eigenwerte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle <}
0 sind.
Die dazugehörigen Matrizen werden dann ebenfalls als positiv (semi-) definit usw. bezeichnet. In der Praxis kann die Definitheit von Matrizen oft mit dem Hauptminorenkriterium bestimmt werden. Als i-ten führenden Hauptminor einer Matrix bezeichnet man die Determinante der Matrix, die man gewinnt, wenn man nur die ersten i Zeilen und Spalten betrachtet; für eine MatrixFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} A=\left(\begin{matrix}a_{1,1}&\cdots&a_{1,n}\\\vdots&\ddots&\vdots\\a_{n,1}&\cdots&a_{n,n}\\\end{matrix}\right) \end{aligned}}
lauten sie also (die senkrechten Striche sind eine alternative Schreibweise für die Berechnung der Determinante der Matrix zwischen den Strichen): Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\Delta}_1(A)=a_{1,1}, \quad \tilde{\Delta}_2(A)=\left(\begin{array}{cc} a_{1,1} & a_{1,2} \\ a_{2,1} a_{2,2} \end{array}\right), \ldots, \tilde{\Delta}_n=\operatorname{det} A }
Es gilt nun: sind alle führenden Hauptminoren positiv, so ist die Matrix positiv definit; sind die Vorzeichen der führenden Hauptminoren abwechselnd positiv und negativ – beginnend mit negativ – so ist die Matrix negativ definit. Weiters ist die Determinante der Matrix das Produkt der Eigenwerte - ist also die Determinante 0, so ist die Matrix indefinit, ist sie ungleich 0, sind alle Eigenwerte ungleich 0. Viele Fälle können mit diesen Kriterien durch Ausschluss bestimmt werden; nur wenn einer oder mehrere führende Hauptminoren 0 sind, ist keine eindeutige Aussage möglich. Wir können nun allgemeine Kriterien dafür aufstellen, wann eine zweimal differenzierbare mehrdimensionale nichtlineare Funktion ein lokales Extremum aufweist. Eine notwendige Bedingung ist wie bereits erwähnt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla f}=0} .Für Funktionen in einer Variablen bedeutet das: die Ableitung verschwindet. Ist die zweite Ableitung positiv, so findet sich dort ein Minimum. Diese Bedingung für Minima lässt sich auf Funktionen in mehreren Variablen erweitern: Wenn der Gradient in einem Punkt verschwindet und die zweite Ableitung in jeder Richtung negativ ist, so handelt es sich um ein lokales Minimum. Dafür genügt es, dass die zweite Ableitung in Richtung der Eigenvektoren der Hessematrix negativ ist, d.h., dass alle Eigenwerte der Hessematrix negativ sind und diese daher negativ definit ist; analoges gilt für die Maxima.
Achtung! Ein naheliegender Irrtum: man könnte glauben, dass es reicht, wenn wir uns das Krümmungsverhalten in x und y Richtung anschauen – also die zweiten partiellen Ableitungen; das ist aber nicht der Fall: die Abbildung zeigt eine Funktion, die entlang x und der y-Achse konkav ist; trotzdem ist der Nullpunkt – in dem der Gradient verschwindet – ein Sattelpunkt – es gibt nämlich auch Richtungen, in denen die Funktion konvex ist - die Diagonalen.
Basierend auf den Definitheitseigenschaften der Hessematrix Hf gelten folgende hinreichenden Bedingungen für Extremwerte: SeiFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{\nabla f}\left({\vec{x}}_0\right)=0. \end{aligned}}
Falls Hf an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_0}
positiv definit, so hat f dort ein lokales Minimum.
Falls Hf an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_0}
negativ definit, so hat f dort ein lokales Maximum.
Falls Hf an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_0}
indefinit, so handelt es sich an der Stelle weder um ein lokales Maximum noch um ein Minimum, sondern um einen sogenannten Sattelpunkt.
Im Falle von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle H_f}
positiv semidefinit oder negativ semidefinit kann keine Aussage getroffen werden (vgl. die Situation im eindimensionalen, wenn die zweite Ableitung verschwindet).
Die folgende Eierkarton-Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \sin{x\cos{y\ }}} hat Bereiche, in denen sie in jeder Richtung kokav ist – dort finden sich die Maxima, also die Gipfel - andere, in denen sie in jeder Richtung konvex ist – dort sind die Minima, also die Gruben, und weitere Beriche, in denen sie in einer Richtung konvex ist, in einer anderen konkav – dort finden sich die Sattelpunkte. Stellen sie sich einen Bewohner einer dieser Gruben vor, der eine Freundin in der benachbarten Grube besuchen möchte; dabei muss er über einen Pass wandern – und dieser Pass ist dann der Sattelpunkt.
Beispiel 9:
Der linke Graph in Abbildung 1.3 zeigt einen Oberflächenplot der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2-y^2}
:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{matrix}f:&\mathbb{R}^2\rightarrow\mathbb{R}\\\ &\left(x,y\right)\mapsto x^2-y^2\\\end{matrix}. \end{aligned}}
Es giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{\nabla f}\left(x,y\right)=\left(\begin{matrix}\mathrm{\ \ }2x\\-2y\\\end{matrix}\right) \end{aligned}}
und daher ist der Ursprung x=0, y=0 Kandidat für eine Extremstelle. Allerdings giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_f\left(x,y\right)=\left(\begin{matrix}2&0\\0&-2\\\end{matrix}\right) \end{aligned}}
mit den offensichtlichen Eigenwerten -2 und 2. Die Hessematrix ist indefinit, und der Ursprung ist keine Extremstelle, sondern ein Sattelpunkt. Die Abbildung veranschaulicht, woher dieser Name kommt: die zweite Ableitung der Funktion in Richtung der x-Achse ist überall positiv, daher insbesondere im Punkt (0,0); ebenso ist die zweite Ableitung in Richtung der y – Achse überall negativ, d.h. der Punkt (0,0) ist ein lokales Minimum, wenn wir ihn in Richtung der x-Achse queren und ein lokales Maximum, wenn wir ihn in Richtung y – Achse überqueren. Ein lokales Minimum müsste aber in jeder Richtung Minimum sein, daher kann (0,0) keines sein, und aus dem analogen Grund ebenso wenig ein Maximum.
Aufgabe 7:
Untersuche die folgenden beiden Funktionen auf lokale Extrema:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} f_1(x, y, z)=4 x-2 x^2+6 y-y^2-z^2+3 \\ f_2(x, y, z)=3 x^2-4 x y+3 y^2+10 z-z^2 \end{array} }
Algorithmen zur Optimierung
Bisher haben wir nur notwendige und hinreichende Bedingungen für lokale Extremstellen kennen gelernt. Bereits im Eindimensionalen war die aktuelle Berechnung der Stelle nicht immer einfach. Für die in der Praxis so wichtigen Funktionen mehrerer Veränderlicher ist dieses Problem häufig um ein Vielfaches komplizierter – schließlich muss in der Iteration in jedem Schritt die Richtung, in der weitergesucht wird, neu bestimmt werden. Man ist oft auf numerische Lösungsmethoden angewiesen. Dieses Gebiet ist ein aktiver Forschungszweig, und nach wie vor sind bei weitem nicht alle Fragestellungen gelöst. Wir wollen an dieser Stelle nur zwei grundlegende Verfahren besprechen. Eine Umsetzung dieser Verfahren mithilfe von R finden Sie in den Videos auf der Homepage erläutert.
Das Newton Verfahren in mehreren Dimensionen
Das in Abschnitt davor bereits erwähnte Newton-Verfahren kann recht einfach auf mehrere Dimensionen verallgemeinert werden. Die Grundidee bleibt dabei gleich, man sucht nach Nullstellen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla f}\left(\vec{x}\right)} und ersetzt mit Hilfe dieses Gradienten die Funktion durch eine lineare Approximation. Man erhält das IterationsverfahrenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}_{k+1}={\vec{x}}_k-\left[H_f\left({\vec{x}}_k\right)\right]^{-1}\mathrm{\nabla f}\left({\vec{x}}_k\right) \end{aligned}}
Verfolgen wir die Analogie zum bekannten eindimensionalen Fall: sucht man dort einen Extremwert, so kann mithilfe des eindimensionalen Newton-Verfahrens die Nullstellen der Ableitung bestimmen; dazu wird der Wert der ersten Ableitung an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_i} durch die zweite Ableitung dividiert, dieser Quotient gibt dann an, wie weit auf der x-Achse weitergegangen werden muss. Ist die Funktion, deren Extremwert gesucht wird, eine quadratische Funktion, dann ist das Verfahren nach einem Schritt am Ziel – dann ist nämlich die Ableitung eine lineare Funktion, deren Nullstelle in einem Schritt gefunden wird; für jede andere Funktion entspricht das Newton-Verfahren dann der Approximation durch quadratische Funktionen. Formal sieht die Iterationsvorschrift im Mehrdimensionalen genauso aus wie im eindimensionalen. Allerdings approximieren wir jetzt den Gradienten durch eine lineare Funktion, und die Division durch die zweite Ableitung im eindimensionalen entspricht der Multiplikation mit der Inversen der Hessematrix. Wenn die zu optimierende Funktion eine quadratische Funktion ist, so führt das Verfahren bereits in einem Schritt zum Ziel – wie im eindimensionalen. Die Hesse-Matrix muss im Allgemeinen nach jedem Iterationsschritt für jedes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_k} neu berechnet und invertiert werden, was bei großer Dimension n recht zeitaufwendig ist. In der Praxis wird dieses Update der Hesse-Matrix daher nicht in jedem Schritt durchgeführt, dies führt zu sogenannten Quasi-Newton Verfahren . Das Newtonverfahren konvergiert äußerst rasch, sobald man sich in der Nähe eines lokalen Minimums befindet. Allerdings ist es noch schwieriger als in einer Dimension, überhaupt in die Nähe eines Minimums zu kommen. Oft werden dazu Verfahren wie das folgende verwendet, die zwar nicht so rasch konvergieren, sich dafür aber mit Sicherheit in Richtung Minimum bewegen.
Das Gradientenverfahren
Die Idee hier ist, dass zunächst eine Suchrichtung festgelegt wird, und dann in diese Richtung ein eindimensionales Optimierungsverfahren angewendet wird. Bei der Suche nach einem Minimum ist es natürlich, dass man eine Richtung sucht, in der die Werte der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} kleiner werden, eine sogenannte Abstiegsrichtung. Mathematisch gesprochen verringern sich die Werte der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(\vec{x}\right)} in Richtung des Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{d}} , fallsFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(\vec{x}+c\vec{d}\right)<f\left(\vec{x}\right) \end{aligned}}
für kleine Werte von c > 0. Dies hat zur Folge, dassFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left[\mathrm{\nabla f}\left(\vec{x}\right)\right]^T\vec{d}<0 \end{aligned}}
Das heißt wenn das innere Produkt des Gradienten mit einem Richtungsvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{d}} negativ ist, so handelt es sich um eine Abstiegsrichtung. Wie man leicht zeigen kann erfolgt der steilste Abstieg gerade in die entgegengesetzte Richtung des Gradientenvektors, d.h.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \vec{d}=-\frac{{\nabla f}(\vec{x})}{||{{\nabla f}(\vec{x})}||} \end{aligned}}
ist der normierte Vektor, der die Richtung des optimalen Abstiegs angibt. Die Idee des Gradientenverfahrens besteht nun darin, dass man wieder mit einem beliebigen Startvektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_1} beginnt und die SuchtrichtungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \vec{d_1}=-\frac{{\nabla f}(\vec{x_1})}{||{{\nabla f}(\vec{x_1})}||} \end{aligned}}
festlegt. (Für die Rechnung einfacher und im Ergebnis äquivalent ist es, wenn der Vektor nicht normiert wird; es ist zwar dann kein Richtungsvektor mehr – aber der nächste Iterationspunkt ist genau derselbe.) Definiere die eindimensionale FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(y\right)=f\left({\vec{x}}_1+y{\vec{d}}_1\right) \end{aligned}}
deren Minimum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y_1} nun zum Beispiel mit dem eindimensionalen Newtonverfahren bestimmt werden kann. Dieses liefert den nächsten IterationspunktFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} {\vec{x}}_2={\vec{x}}_1+y_1{\vec{d}}_1 \end{aligned}}
Bestimme an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_2} eine neue Suchrichtung, und wiederhole das Verfahren so lange, bis ein lokales Minimum gefunden wurde. Dies ist dann der Fall, wenn der Gradient von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle {\vec{x}}_k} sich kaum mehr vom Nullvektor unterscheidet. Das Gradientenverfahren konvergiert zwangsläufig gegen einen kritischen Punkt, d.h. gegen einen Punkt mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla f}\left(\vec{x}\right)= 0} . Allerdings kann es in der Nähe eines Minimums zum sogenannten Zickzackphänomen kommen. Dabei ändert sich die Suchrichtung in jedem Iterationsschritt in drastischer Weise, während kaum mehr eine Verminderung des Wertes der Zielfunktion zu beobachten ist. Es empfiehlt sich häufig in der Nähe des Minimums zu anderen Verfahren überzugehen, etwa zu einem Quasi-Newton Verfahren. Für weitere Details sei hier wiederum auf die Literatur verwiesen (Bomze, Grossmann 1993, Nocedal, Wright 1999, etc.)
Optimierung unter Nebenbedingungen
Häufig treten in ökonomischen Anwendungen Optimierungsprobleme auf, bei denen gewisse Nebenbedingungen erfüllt werden müssen. Das bedeutet, das nicht mehr der ganze Definitionsbereich einer Funktion betrachtet wird, sondern nur eine Teilmenge; deren genaue Gestalt hängt von den Nebenbedingungen ab; maximieren wir etwa eine Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} unter der Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=x^2+y^2=4} , so wird das Maximum auf dem Kreis mit Radius 2 gesucht. Dieser ist die Höhenschichtline der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)} zum Niveau 4. Wenn wir statt der Gleichung die Ungleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=x^2+y^2\le1} als Nebenbedingung vorgeben, so wird das Maximum auf der ganzen Kreisscheibe gesucht (also auch im Inneren des Kreises). Für den Spezialfall der Optimierung von linearen Funktionen unter linearen Nebenbedingungen gibt es das sogenannte Simplex-Verfahren, das hier nicht behandelt wird; es gibt dafür inzwischen leicht auffindbare Internetresourcen (z.B. www.phpsimplex.com oder LINDO); wir behandeln die weitaus schwierigere Fragestellung der nichtlinearen Optimierung unter Nebenbedingungen, die selbst linear oder nichtlinear sein können. Die wichtigste Methode zur Behandlung von Optimierungsaufgaben unter Nebenbedingungen besteht darin, diese auf Optimierungsprobleme ohne Nebenbedingungen zurückzuführen. Der Einfachheit halber werden wir diese Theorie hier nur für Funktionen in zwei Veränderlichen vorstellen, die Verallgemeinerung auf mehrere Veränderliche erfordert zwar mehr Rechenaufwand, jedoch keine neuen Konzepte. Wir beschreiben nur die Suche nach einem lokalen Minimum, für Maxima läuft alles völlig analog, bzw. kann man das Minimum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -f\left(x,y\right)} suchen um das Maximum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} zu erhalten.
Lagrange – Multiplikatoren – Gleichungen als Nebenbedingung
Wir wollen folgende Aufgabe lösen:Finde
unterFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=c \end{aligned}}
d.h., wir suchen das Minimum der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} über der Höhenschichtline zum Niveau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} der Funktion , wobei wir voraussetzen, dass sowohl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} als auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} differenzierbar sind. Im ersten Schritt der Methode wird ein Lagrange-Multiplikator, zumeist mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda} bezeichnet (hat nichts mit den Eigenwerten einer Matrix zu tun!), eingeführt. Man definiert die Lagrange-Funktion als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y,\lambda\right)=f\left(x,y\right)+\lambda\left(g\left(x,y\right)-c\right) \end{aligned}}
und sucht jene Paare Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x_0,y_0\right)}
, für das es ein Lambda gibt, mit dem die Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x_0,y_0,\lambda(x_0,y_0\right))}
ein Minimum annimmt. Die Nebenbedingung steckt nun implizit in der Lagrange-Funktion. Falls die Nebenbedingung erfüllt ist so gilt . Falls die Nebenbedingung nicht erfüllt ist und zum Beispiel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x_0,y_0\right)>c}
, so wird die Lagrange-Funktion für diesen Punkt für hinreichen kleines Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
beliebig klein, und und die Lagrangefunktion kann in diesem Punkt für kein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
ein Minimum annehmen. Beachten Sie auch: das Kriterium ist etwas anderes als die Suche nach Tripeln , welche die Lagrangefunktion minimieren – solche wird man im Allgemeinen nicht finden: gilt nämlich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(g\left(x,y\right)-c\right)\neq0}
, dann gibt es aus den genannten Gründen kein optimales Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
!
Das Lagrange-Theorem besagt nun folgendes: falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x_0,y_0\right)}
ein lokales Minimum von unter der Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c}
ist, und falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla g}(x_0,y_0)\neq(0,0)^T }
so gibt es eine eindeutige Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
, für welche die Lagrange-Funktion einen stationären Punkt in hat, d.h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{\nabla L}(x_0,y_0)=(0,0)^T}
unter Beibehaltung der Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c}
. Um Kandidaten zur Lösung der ursprünglichen Aufgabe zu erhalten, muss also das folgende System von Gleichungen gelöst werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\frac{\partial}{\partial x} L(x, y, \lambda)=\frac{\partial}{\partial x} f(x, y)+\lambda \frac{\partial}{\partial x} g(x, y)=0\\ &\frac{\partial}{\partial y} L(x, y, \lambda)=\frac{\partial}{\partial y} f(x, y)+\lambda \frac{\partial}{\partial y} g(x, y)=0\\ &\frac{\partial}{\partial \lambda} L(x, y, \lambda)=g(x, y)-c=0 \end{aligned} }
d.h., der Gradient der Zielfunktion ist ein lineares Vielfaches des Gradienten der Funktion, die die Nebenbedingung angibt. Nun zeigt uns der Gradient die Richtung des stärksten Anstiegs an und steht normal auf die Höhenschichtlinie. Stellen wir uns den Graphen der Zielfunktion als hügelige Landschaft vor, so wird durch die Nebenbedingung ein Weg durch diese Landschaft gelegt, und gesucht werden die höchsten bzw. tiefsten Punkte auf diesem Weg. An diesen fällt das Gelände senkrecht zum Weg am steilsten ab.
Beispiel 11:
Ein Verbraucher habe die Nutzenfunktion
Maximiere die Nutzenfunktion unter der BudgetbeschränkungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=x+2y=\mathrm{10}. \end{aligned}}
Die Lagrange Funktion lautet:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y,\lambda\right)=\mathrm{xy}+\left(x+2y-\mathrm{10}\right) \end{aligned}}
Null setzen der partiellen Ableitungen gibtFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x} L(x, y, \lambda) &=y+\lambda=0 \\ \frac{\partial}{\partial y} L(x, y, \lambda)=x+2 \lambda &=0 \end{aligned} }
Elimination von aus diese beiden Gleichungen liefert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x-2y=0} Und wir haben die NebenbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x+2y=\mathrm{10} \end{aligned}}
Dieses lineare Gleichungssystem mit zwei Variablen hat eine eindeutige Lösung:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x = 5, y = 2.5 \end{aligned}}
und schließlich
An sich haben wir bisher nur eine notwendige Bedingung für ein lokales Extremum und es sollte noch gezeigt werden, dass es sich tatsächlich um ein Maximum handelt. Ähnlich wie im Falle der Optimierung ohne Nebenbedingung gibt es entsprechende Kriterien an die zweiten Ableitungen von und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} , anhand derer man entscheiden kann ob es sich um ein Maximum oder ein Minimum handelt. Wir wollen uns zunächst auf eine graphische Darstellung des Sachverhalts beschränken:
Abbildung 1.4 zeigt einerseits ausgewählte Niveaulinien der Zielfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=\mathrm{xy}}
, anderseits die Gerade Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=5-\frac{x}{2}}
welche gerade die Budget-beschränkung beschreibt. Sinnvoller weise sind beide Investitionen x und y positiv. Entsprechende Ungleichungs-Nebenbedingungen werden im nächsten Abschnitt besprochen. Am Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (x_0 = 5, y_0 = 2.5)}
berührt die Gerade die Niveaulinie zum Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle xy = 12.5}
. Es ist klar ersichtlich, dass an allen anderen Punkten die Gerade jene Niveaulinien schneidet, die einem geringeren Wert der Zielfunktion entsprechen. Daher handelt es sich bei dem Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (x_0, y_0)}
um ein lokales Maximum der Zielfunktion unter der gegebenen Budgetbeschränkung. Dass an dieser Stelle die Nebenbedingungsgerade tangential an die Niveaulinie liegt ist typisch, und der geometrische Grund dafür, dass die Lagrange-Methode funktioniert. Abbildung 1.5 ist eine dreidimensionale Veranschaulichung des Sachverhaltes; die stark ausgezogene Kurve ist der Graph der Funktion unter der Nebenbedingung (der „Weg durch das hügelige Gelände“, um beim Bild zu bleiben). An seinem höchsten Punkt ist er tangential zum Graphen der Höhenschichtlinien, d.h., das Gelände fällt dort senkrecht zum Weg am steilsten ab.
Für eine allgemeine Klassifizierung von Punkten, die mithilfe der Lagrage Funktion gefunden wurden, steht die Methode der berandeten Hessematrizen zur Verfügung; im zweidimensionalen Fall: Sei
Ist die Determinante dieser Matrix positiv, so haben wir ein lokales Maximum, ist sie negativ, ein Minimum, ist die Determinante Null, so ist die Frage nicht entscheidbar.
Einen Sonderfall stellen Nebenbedingungen dar, die eine beschränkte Menge beschreiben – z.B. einen geschlossenen Kreis, eine Ellipse oder ein Streckenstück; auf einer solchen Menge können wir einfach alle kritischen Punkte der Reihe nach betrachten – der mit dem größten Funktionswert ist das Maximum, der mit dem kleinsten das Minimum.
Aufgabe 8:
Finde die beiden Extremstellen von
unter der NebenbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=x^2+\mathrm{xy}+2=3 \end{aligned}}
Die vorgestellte Theorie lässt sich weitgehend unverändert auf Funktionen mit mehr als zwei unabhängigen Variablen erweitern. Häufig gibt es in der Anwendung mehr als eine Nebenbedingung, und die Lagrange-Methode besteht dann darin, dass für jede Nebenbedingung ein eigener Lagrange-Multiplikator hinzugefügt wird. Bei einem Optimierungsproblem in n Variablen mit m Nebenbedingungen erhält man demnach eine Lagrange-Funktion L in n+m Variablen. Kandidaten für lokale Extrema erhält man wiederum indem man nach stationären Punkten von L sucht, wobei es nun gilt n+m Gleichungen in n+m Variablen zu lösen.
Karush Kuhn Tucker Bedingungen
Häufig tauchen Nebenbedingungen nicht in Gleichungsform, sondern in Ungleichungsform auf, z.B., dass eine Variable x nur positive Werte annehmen kann, also die Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\geq0} erfüllen muss. Das allgemeine Problem in zwei Variablen mit einer Nebenbedingung hat die Form: FindeFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{max\ (}f(x,y)) \end{aligned}}
unter
D.h., wir suchen das Minimum der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)} über einem Bereich, der von der Höhenschichtline zum Niveau c der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)} begrenzt wird, wobei wir wieder voraussetzen, dass sowohl f als auch g differenzierbar sind. Die Menge aller Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x,y\right)} welche die Nebenbedingung erfüllen, wird als zulässige Menge bezeichnet. Im Prinzip kann dieses Problem mit den bereits gelernten Methoden behandelt werden, indem man einerseits nach lokalen Extremstellen im Inneren des zulässigen Bereichs sucht (Optimierung ohne Nebenbedingung), und andererseits den Rand des zulässigen Bereichs mit Hilfe der Lagrange-Methode untersucht. Unter gewissen Voraussetzungen an die Randbedingungen (den sogenannten constraint qualifications ) lassen sich allerdings notwendige Bedingungen für lokale Extremwerte im gesamten zulässigen Bereich angeben. Dazu wird wiederum die Lagrange-FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y,\lambda\right)=f\left(x,y\right)+\lambda\left(g\left(x,y\right)-c\right) \end{aligned}}
definiert, allerdings gilt hier für die Lagrange Multiplikatoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda\le0} . Entscheidend ist nun die sogenannte komplementäre Schlaffheitsbedingung (complementary slackness). Man fordert, dass entweder die Nebenbedingung exakt erfüllt ist (d.h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x,y\right)=c} ), oder aber der Lagrange Multiplikator. Diese Bedingung ist erfüllt fallsFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda\left(g\left(x,y\right)-c\right)=0 \end{aligned}}
Die complementary slackness Bedingung beinhaltet in sehr eleganter Form dass ein lokaler Extremwert direkt am Rande des zulässigen Bereiches andere Bedingungen erfüllen muss als im Inneren: für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
erhält man die lokalen Maxima im Inneren, diese sind die gleichen, die wir auch ohne Nebenbedingung gefunden hätte. Am Rand hingegen müssen die Gradienten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)}
und (anti-) parallel sein, d.h., wenn wir der Richtung des steilsten Angstiegs der Zielfunktion folgen würden, würden wir den von der Nebenbedingung erlaubten Bereich verlassen. Zusammenfassend liefert dies die sogenannten Karush Kuhn Tucker (KKT) Bedingungen als notwendige Bedingungen für lokale Extrema unter Ungleichheits-Nebenbedingungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x} L(x, y, \lambda)=\frac{\partial}{\partial x} f(x, y)+\lambda \frac{\partial}{\partial x} g(x, y) &=0 \\ \frac{\partial}{\partial y} L(x, y, \lambda)=\frac{\partial}{\partial y} f(x, y)+\lambda \frac{\partial}{\partial y} g(x, y) &=0 \\ g(x, y) \leq c \; \; \; \; \; \; \; \lambda & \leq 0 \\ \lambda(g(x, y)-c) &=0 \end{aligned} }
Beispiel 12:
Ein Unternehmen hat die Möglichkeit zwei Güter zu produzieren. Bei beiden Produkten ist der erzielbare Preis jeweils proportional zur Qualität x bzw. y, während der Aufwand zur Qualitätssteigerung quadratisch wächst. D.h.:
Produkt 1: Für Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle ax}
bedarf es Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Ax^2}
Arbeitseinheiten
Produkt 2: Für Preis bedarf es Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle By^2}
Arbeitseinheiten
wobei alle Konstanten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (a,b, A,B)}
größer als 0 sein sollen.
Das Unternehmen hat insgesamt höchstens L Einheiten an Arbeit pro Woche zur Verfügung, die es der Produktion der beiden Güter zuordnen kann. Bestimme welche Qualität Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x}
bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y}
den Erlös maximiert, wenn der wöchentliche Absatz auf jeden Fall gewährleistet ist. Lösung: Der erzielbare Erlös beträgtFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\mathrm{ax}+b \end{aligned}}
Die Gesamtarbeitsleitung ist beschränkt:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)={\mathrm{Ax}}^2+{\mathrm{By}}^2\le L \end{aligned}}
Die KKT Bedingungen lauten also: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial}{\partial x} L(x, y) &=a+2 \lambda \mathrm{Ax}=0 \\ \frac{\partial}{\partial y} L(x, y)=b+2 \lambda \mathrm{By}=0 &=\\ \lambda\left(\mathrm{Ax}^2+\mathrm{By}^2-L\right) &=0 \end{aligned} } wobeiFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda\le0 {\mathrm{Ax}}^2+{\mathrm{By}}^2\le L \end{aligned}}
Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0} folgt aus den ersten beiden Gleichungen unmittelbar Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a=b=0} , im Widerspruch zur Angabe. Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda<0} folgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x>0,y>0} , und daherFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \lambda=\frac{-a}{2Ax}=\frac{-b}{2By} \end{aligned}}
Somit gilt auchFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} y=\frac{\mathrm{Ab}}{\mathrm{Ba}}x \end{aligned}}
Andererseits muss gelten (complementary slackness)Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{Ax}^2+\mathrm{By}^2=L \end{aligned}}
und wir folgern, dass insgesamt die optimale Lösung erreicht wird fürFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x=\sqrt{\frac{L}{a^2B+b^2A}}\cdot\frac{a\sqrt{B}}{\sqrt{A}} y=\sqrt{\frac{L}{a^2B+b^2A}}\cdot\frac{b\sqrt{A}}{\sqrt{B}} \end{aligned}}
Aufgabe 9: Untersuche die FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y+1 \end{aligned}}
auf Extremwerte unter der NebenbedingungFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,y\right)=x+y\le4 \end{aligned}}
Zusammenfassung
Wir haben einige Aspekte der nichtlinearen Optimierung kennen gelernt. Speziell wurden zur Lösung von mehrdimensionalen Optimierungsaufgaben als hinreichende Bedingungen für lokale Maxima und Minima die Definitheitseigenschaften der Hessematrix angegeben. Für Optimierungsaufgaben mit Nebenbedingungen wurden nur notwendige Bedingungen zum Finden von lokalen Extremstellen besprochen, und zwar die Lagrange-Methode im Falle von Gleichheits-nebenbedingungen, und die Karush-Kuhn-Tucker Bedingungen für Ungleichheits-nebenbedingungen. Als einfache Algorithmen zum Lösen von nichtlinearen Optimierungsaufgaben wurden das Newton-Verfahren und das Gradientenverfahren kurz diskutiert.
Optimierung ist ein weites Feld, und viele interessante Gebiete konnten hier nicht einmal kurz angerissen werden. Eine Liste von gängigen Fragestellungen umfasst Transportprobleme, Zuordnungsprobleme, Netzplantechnik oder das weitläufige Gebiet der ganzzahligen und kombinatorischen Optimierung. Die dort benötigten Techniken unterscheiden sich oft wesentlich von denen die in diesem Kapitel erwähnt wurden, und oftmals finden Konzepte der Graphentheorie Verwendung. Für eine elementare deutschsprachige Einführung sei etwa auf das Buch von Domschke und Drexl (1995) verwiesen.
Wiederholungsaufgaben/Übungen
Aufgabe 1
Untersuche folgende Funktionen auf Extremwerte bzw. Sattelstellen (verwende die Definitheit der Hessematrix, um Entscheidung zu treffen).Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y^2 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f(x,y)=(1+x)^2-(1-y)^2 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=\mathrm{xy} \end{aligned}}
Aufgabe 2
Führe zu den Funktionen aus Aufgabe 1 jeweils die erste Iteration des Gradientenverfahrens aus, wobei im Punkt (1,1) gestartet wird. Für welche der drei Aufgaben ist die Suche nach einem (lokalen oder globalen) Minimum überhaupt sinnvoll?
Aufgabe 3
Führe für die FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^4+y^4 \end{aligned}}
die ersten beiden Schritte des Newtonverfahrens aus, wenn im Punkt (1,1) gestartet wird.
Aufgabe 4
Finde die Extremwerte der folgenden Funktionen unter den angegebenen Nebenbedingungen:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=4x+3y\\\ NB:g\left(x,y\right)=x^2+y^2=1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+y^2\\\ NB:g\left(x,y\right)=2\mathrm{xy}=1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} f(x, y)=e^{x y} \\ N B: g(x, y)=x+y=1 \end{array} }
(Gib jeweils Skizzen mit den Niveaulinien an um zu klären, ob es sich um ein Maximum oder ein Minimum handelt).
Aufgabe 5
Ermittle mit Hilfe der KKT-Bedingungen alle Extremstellen der folgenden Funktionen unter den gegebenen NebenbedingungenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f(x,y)=(x-1)^2+(y-2)^2-1\\\ NB:g\left(x,y\right)=x^2+y^2\le1 \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(x,y\right)=x^2+3\mathrm{xy}+y^2 \\\ NB: g\left(x,y\right)=x+y\le1 \end{aligned}}
Stelle die Lösungen wiederum graphisch dar!
Lösungen der Aufgaben
Aufgabe 1:
Aufgabe 2:
Die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2 = y}
hat natürlich zwei Lösungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1=\sqrt{y} \text { und } x_2=-\sqrt{y}}
Dementsprechend ist die Umkehrabbildung über ganz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}}
nicht eindeutig definierbar, sehr wohl aber für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x \in \mathbb{R}^{+}}
(strichpunktiert) bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{x}\in\mathbb{R}^-}
(strichliert). Aufgabe 3:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_1^\prime(x)=-2x\mathbb{exp}{(}-x^2) \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_2^\prime(x)=\left(\frac{\mathbb{sin}{x}}{\mathbb{cos}{x}}\right)^\prime=1+{\mathbb{tan}}^2{(}x)=\frac{1}{{\mathbb{cos}}^2{(}x)} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_3^\prime\left(x\right)=\frac{3x^2}{2\sqrt{1+x^3}} \end{aligned}}
Aufgabe 4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{\mathbb{x}=1}^{2}\lambda\mathrm{\ exp}\left(-\lambda\mathbb{x}\right)\ dx=\mathrm{\ \ }-\left.\mathrm{\ exp}\left(-\lambda\mathbb{x}\right)\right|_1^2=\ e^{-\lambda}-e^{\mathrm{-2}\lambda} \end{aligned}}
Aufgabe 5:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} x_2=0-\frac{p^{\prime}(0)}{p^{(0)}} \\ x_3=\frac{1}{2}-\frac{p^{\prime}(1 / 2)}{p^{\prime}(1 / 2)}=\frac{1}{2}-\frac{1}{32}=0.4688 \end{array}}
Vergleicht man diesen Wert mit der tatsächlichen Stelle des lokalen Minimums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 0.4691} , so erkennt man, wie nahe das Newton Verfahren bereits nach zwei Iterationen gekommen ist.
Aufgabe 6:
Matrix A – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-10\lambda+9=0}
Eigenwerte: 1 und 9 (positiv definit)
Eigenvektoren: (1,-1)T und (7,1)T
Matrix B – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^2-2\lambda=0}
Eigenwerte: 2 und 0 (positiv semidefinit)
Eigenvektoren: (1,-1)T und (1,1)T
Matrix C – charakteristische Gleichung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda^3+7\lambda^2-18\lambda=0}
Eigenwerte: -9, 2 und 0 (indefinit)
Eigenvektoren: (1,2,-3)T , (-4,3,1)T und (2,4,3) T
Aufgabe 7:
a)Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f_1\left(x,y,z\right)=\left(\begin{matrix}4-4x\\6-2y\\-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) \end{aligned}}
Kandidat für Extremum: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=1, y=3, z=0} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_{f_1}\left(x,y,z\right)=\left(\begin{matrix}-4&0&0\\0&-2&0\\0&0&-2\\\end{matrix}\right) \end{aligned}}
negativ definit ⇒ (1,3,0)T ist ein lokales Maximum
b)Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f_2\left(x,y,z\right)=\left(\begin{matrix}6x-4y\\6y-4x\\10-2z\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\0\\\end{matrix}\right) \end{aligned}}
Kandidat für Extremum: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=0, y=0, z=5}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} H_{f_2}\left(x,y,z\right)=\left(\begin{matrix}6&-4&0\\-4&6&0\\0&0&-2\\\end{matrix}\right) \end{aligned}}
ist indefinit (Eigenwerte -2, 2 und 10) (0,0,5)T ist ein Sattelpunkt und kein lokaler Extremwert
Aufgabe 8:
Die Lagrange Funktion lautet:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L\left(x,y\right)=x^2+y^2+\lambda\left(x^2+xy+y^2-3\right) \end{aligned}}
Null setzen der partiellen Ableitungen gibtFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\frac{\partial}{\partial x} L(x, y)=2 x+\lambda(2 x+y)=0 \\ &\frac{\partial}{\partial y} L(x, y)=2 y+\lambda(2 y+x)=0 \end{aligned}}
Addieren wir diese beiden Gleichungen so erhalten wirFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 2\left(x+y\right)+\lambda\left(3x+3y\right)=0 \end{aligned}}
oder äquivalent dazuFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(x+y\right)\left(2+3\lambda\right)=0 \end{aligned}}
Das bedeutet entweder der erste Faktor oder der zweite Faktor verschwindet.
Fall1: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y=0, d.h. y = -x}
.
Die Nebenbedingung lautet dannFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,-x\right)=x^2=3 \end{aligned}}
Und wir erhalten die beiden Lösungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=\sqrt{3}, y=-\sqrt{3} x=-\sqrt{3}, y=\sqrt{3}}
Fall2: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2+3\lambda = 0, d.h. \lambda = -2/3}
.
Die erste Gleichung lautetFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=2x-\frac{2}{3}\left(2x+y\right)=0 \end{aligned}}
und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y} . Die Nebenbedingung wird zuFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} g\left(x,x\right)=3x^2=3 \end{aligned}}
und wir erhalten die beiden Lösungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=-\sqrt{3}, y=\sqrt{3} x=-1, y=-1}
Vergleichen wir die Funktionswerte: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(\sqrt{3},-\sqrt{3})=f(-\sqrt{3}, \sqrt{3})=6 f(1,1) = f(-1,-1)=2} Die ersten beiden Punkte liefern jeweils ein Maximum, die zweiten Punkte ein Minimum unter der Nebenbedingung. Die folgende Abbildung veranschaulicht die Zusammenhänge.
Die konzentrischen Kreise geben einige Niveaulinien der Zielfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=x^2+y^2} . Beachte wiederum wie an den 4 extremalen Punkten die Kurve der Nebenbedingungen dazu tangential liegt.
Aufgabe 9: Die Lagrange Funktion lautetFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(x, y)=x^2+y+1+\lambda(x+y-4) } Null setzen der partiellen Ableitungen gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial x} L(x, y)=2 x+\lambda=0 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial y} L(x, y)=1+\lambda=0 } und von den KKT Bedingungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda(x+y-4)=0 } Im Inneren des zulässigen Bereiches muss gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0} , und daher wird die zweite Gleichung oben zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 1=0} , offensichtlich ein Widerspruch, Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda<0} muss gelten liefert die zweite Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=-1} , und daher die erste Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda\left(x+y-4\right)=0} . Die KKT Bedingung gibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x+y-4\right)=0} , und daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x+y-4\right)=0} . Der Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} ist somit eine potentielle lokale Extremstelle, um zu erkennen worum es sich tatsächlich handelt betrachte folgende Abbildung, die wiederum die Niveaulinien der Zielfunktion sowie den Rand des zulässigen Bereichs zeigt.
Der zulässige Bereich befindet sich unterhalb der Geraden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=4-x} . Am kritischen Punkt nimmt die Funktion den Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 19/4} an, in unmittelbarer Umgebung davon gibt es sowohl Punkte mit größeren als auch mit kleineren Funktionswerten. Es handelt sich bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} also um kein lokales Extremum, sondern um eine Art Sattelpunkt, allerdings nur wenn die Nebenbedingung in Betracht gezogen wird. Entlang der Geraden ist der Punkt ein Minimum. Für alle Werte die in einem zugespitzten Kegel mit Spitze bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1/2, 7/2)} liegen (Siehe Abbildung) liegt ein Maximum vor.
Lösungen der Wiederholungsaufgaben
Aufgabe 1.1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \begin{array}{r} f(x)=x^{\exp (x)}=\exp \left[\log (x) e^x\right] \\ f^{\prime}(x)=\exp \left[\log (x) e^x\right] \cdot\left[\frac{1}{x} e^x+\log (x) e^x\right]= \\ x^{\exp (x)}\left[\frac{1}{x} e^x+\log (x) e^x\right] \end{array} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^\prime\left(x\right)=\frac{\left(3x-2\right)\left(2x+\frac{1}{2\sqrt x}\right)-3\left(x^2+\sqrt x\right)}{(3x-2)^2} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^\prime\left(x\right)=\frac{1}{\sqrt{2x}}\mathrm{cos}\left(x^2\right)-\sqrt x\mathrm{sin}x^22x \end{aligned}}
Aufgabe 1.2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{\mathrm{exp} \left(x\right)}{x-1}}
an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 1}
nicht definiert. Linksseitiger Limes ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -\infty}
, rechtsseitiger Limes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle +\infty}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)}
hat keine Nullstellen, allerdings konvergiert es gegen 0 für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x\rightarrow-\infty}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^\prime\left(x\right)=\frac{\left(x-2\right)\mathrm{exp} \left(x\right)}{(x-1)^2}}
, Nullstelle nur bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 2}
(potentielles lokales Extremum)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{\prime\prime}\left(x\right)=\frac{\left(x^2-4x+5\right)\mathrm{exp} \left(x\right)}{(x-1)^3}}
keine reellen Nullstellen, daher keine Wendepunkte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{\prime\prime}\left(2\right)=\mathrm{exp}2>0}
, daher ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 2}
ein lokales Minimum
Aufgabe 1.3
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=\frac{1}{3} e^{3 x+4}(\text { Substitution } y=3 x+4) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=\left(x^2 \log \left(x^2\right)-x^2\right) / 2\left(\right. Substitution y=x^2 und partielle Integration ) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=-\frac{1}{4} \cos (4 x-3)(\text { Substitution } y=4 x-3) }
Aufgabe 1.4
Berechnung der Integrale
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} -\left(x^2+2x+2\right)e^{-x}|_0^1=2-5e^{-1} \end{aligned}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left.x(\log (x 2)-1)\right|_1 ^2=\log 2-1}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \int_{x=2}^{3}\left(3-x\right)+\int_{x=3}^{4}\left(x-3\right)\mathrm{dx}=1 \end{aligned}}
Aufgabe 1.5
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D=\left\{(x, y) \in R^2: x^2>y^2\right\}=\{(x, y):|x|>|y|\}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla \mathrm{f}=\frac{1}{x^2-y^2}\left(\begin{array}{c} 2 x \\ -2 y \end{array}\right), H_f=\frac{1}{\left(x^2-y^2\right)^2}\left(\begin{array}{cc} -2\left(x^2+y^2\right) & 4 \mathrm{xy} \\ 4 \mathrm{xy} & -2\left(x^2+y^2\right) \end{array}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D=\left\{(x, y) \in \mathbb{R}^2: x \neq y\right\} \nabla f=\frac{1}{(x-y)^2}\left(\begin{array}{c} -y^2 \\ x^2 \end{array}\right), H_f=\frac{1}{(x-y)^3}\left(\begin{array}{cc} 2 y^2 & -2 \mathrm{xy} \\ -2 \mathrm{xy} & 2 x^2 \end{array}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &\nabla f=\left(\begin{array}{l} 2 x \\ 2 y \end{array}\right) \text { kritischerWert }(x, y)=(0,0) \\ &H_f=\left(\begin{array}{ll} 2 & 0 \\ 0 & 2 \end{array}\right) \text { positivde finit }(\text { konvex })(0,0) \text { ist globales Minimum } \\ &\nabla \mathrm{f}=\left(\begin{array}{cc} 2(x+1) \\ 2(1-y) \end{array}\right) \text { kritischer Wert }(x, y)=(-1,1) \\ &H_f=\left(\begin{array}{cc} 2 & 0 \\ 0 & -2 \end{array}\right) \text { indefinit }(-1,1) \text { ist Sattelpunkt } \\ &\nabla \mathrm{f}=\left(\begin{array}{l} y \\ x \end{array}\right) \text { kritischerWert }(x, y)=(0,0) \\ &H_f=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right) \text { indefinit }(E W \pm 1)(0,0) \text { ist Sattelpunkt } \end{aligned} }
Aufgabe 2.2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a) \nabla \mathrm{f}=\left(\begin{array}{l}2 x \\ 2 y\end{array}\right), \vec{x}_1=\left(\begin{array}{l}1 \\ 1\end{array}\right) }
Abstiegsrichtung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{d}_1=-\left(\begin{array}{l} 2 \\ 2 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(h)=f\left(\begin{array}{l} 1 \\ 1 \end{array}\right) -h\left(\begin{array}{l} 2 \\ 2 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle =2(1-2 h)^2 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g^{\prime}(h)=-8(1-2 h)=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h=12 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}_2=\left(\begin{array}{l} 1 \\ 1 \end{array}\right)- }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2}\left(\begin{array}{l} 2 \\ 2 \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla \mathrm{f}=\left(\begin{array}{l} 2(x+1) \\ 2(1-y) \end{array}\right), \vec{x}_1=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) }
Abstiegsrichtung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{d}_1=-\left(\begin{array}{l} 4 \\ 0 \end{array}\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(h)=f\left(\left(\begin{array}{l} 1 \\ 1 \end{array}\right)-h\left(\begin{array}{l} 4 \\ 0 \end{array}\right)\right)=(2-4 h)^2 g^{\prime}(h)=-8(2-4 h)=0 h=12 \vec{x}_2=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) }
In allen 3 Fällen landet man bereits nach einem Iterationsschritt im kritischen Punkt. Dies ist für allgemeine Funktionen nicht der Fall, sondern stammt daher, dass wir es hier jeweils mit quadratischen Funktionen zu tun haben. Im Beispiel a) haben wir somit nach einer Iteration bereits das globale Minimum gefunden. Aber Achtung! In Beispiel b) und c) sind wir jeweils in einem Sattelpunkt gelandet, und das Gradientenverfahren würde hier einfach abbrechen, weil der Gradient an einem kritischen Punkt natürlich gerade 0 ist. Würden wir in Beispiel b) etwa im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-1,-1)}
starten so erhält man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(h)=f\left(\left(\begin{matrix}-1\\-1\\\end{matrix}\right)-h\left(\begin{matrix}0\\4\\\end{matrix}\right)\right)=-(2+4h)^2}
und man erkennt, dass für wachsendes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h}
der Funktionswert gegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -\infty}
strebt.
Aufgabe 2.3:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla f=\left(\begin{array}{l} 4 x^3 \\ 4 y^3 \end{array}\right), \quad H_f=\left(\begin{array}{cc} 12 x^2 & 0 \\ 0 & 12 y^2 \end{array}\right) \quad, \vec{x}_1=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) }
1. Schritt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f\left(\vec{x}_1\right)=\left(\begin{array}{l} 4 \\ 4 \end{array}\right), \quad H_f\left(\vec{x}_1\right)=\left(\begin{array}{cc} 12 & 0 \\ 0 & 12 \end{array}\right) \\ \vec{x}_2=\left(\begin{array}{l} 1 \\ 1 \end{array}\right)-\left(\begin{array}{cc} 1 / 12 & 0 \\ 0 & 1 / 12 \end{array}\right)\left(\begin{array}{l} 4 \\ 4 \end{array}\right)=\left(\begin{array}{l} 2 / 3 \\ 2 / 3 \end{array}\right) \end{aligned} }
2. Schritt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f\left(\vec{x}_2\right)= & \left(\begin{array}{l} 32 / 27 \\ 32 / 27 \end{array}\right), \quad H_f\left(\vec{x}_1\right)=\left(\begin{array}{cc} 16 / 3 & 0 \\ 0 & 16 / 3 \end{array}\right) \\ & \vec{x}_3=\left(\begin{array}{l} 2 / 3 \\ 2 / 3 \end{array}\right)-\left(\begin{array}{cc} 3 / 16 & 0 \\ 0 & 3 / 16 \end{array}\right)\left(\begin{array}{l} 32 / 27 \\ 32 / 27 \end{array}\right)=\left(\begin{array}{l} 4 / 9 \\ 4 / 9 \end{array}\right) \end{aligned} }
3. Schritt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \nabla f\left(\vec{x}_3\right)= & \left(\begin{array}{l} 4^4 / 9^3 \\ 4^4 / 9^3 \end{array}\right), \quad H_f\left(\vec{x}_1\right)=\left(\begin{array}{cc} 4^3 / 3^3 & 0 \\ 0 & 4^3 / 3^3 \end{array}\right) \\ & \vec{x}_4=\left(\begin{array}{l} 4 / 9 \\ 4 / 9 \end{array}\right)-\left(\begin{array}{cc} 3^3 / 4^3 & 0 \\ 0 & 3^3 / 4^3 \end{array}\right)\left(\begin{array}{l} 4^4 / 9^3 \\ 4^4 / 9^3 \end{array}\right)=\left(\begin{array}{l} 8 / 27 \\ 8 / 27 \end{array}\right) \end{aligned} }
Aufgabe 2.4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=4 x+3 y+\lambda\left(x^2+y^2-1\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial x}=4+2 x \lambda=0 }
Multipliziere mit -x
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial y}=3+2 y \lambda=0 }
Multipliziere mit y
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 4 y-3 x=0, \text { oder } y=\frac{3}{4} x }
Nebenbedingung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+y^2=1}
Zwei Lösungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (4/5, 3/5)}
ist Maximum (Funktionswert 5)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-4/5, -3/5)}
ist Minimum (Funktionswert -5)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=x^2+y^2+\lambda\left(2\mathrm{xy}-1\right) \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=2x+2y\lambda=0 \end{aligned}}
Multipliziere mit xFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=2y+2x\lambda=0 \end{aligned}}
Multipliziere mit -yFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} 2x^2-2y^2=0 \end{aligned}}
Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y=\frac{1}{2x}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x^4=\frac{1}{4} \end{aligned}}
Zwei reelle Lösungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(\frac{1}{\sqrt2},\frac{1}{\sqrt2}\right)}
sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(-\frac{1}{\sqrt2},-\frac{1}{\sqrt2}\right)}
jeweils mit Funktionswert 1.
Die Zeichnung zeigt, dass es sich jeweils um ein Minimum handelt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} L=\mathrm{exp}(xy)+\lambda(x+y-1) \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial x}=y\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 \end{aligned}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \frac{\partial L}{\partial y}=x\mathrm{exp}\left(\mathrm{xy}\right)+\lambda=0 \end{aligned}}
Bilde Differenz der beidenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \left(x-y\right)\mathrm{exp}xy=0 \end{aligned}}
also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
Nebenbedingung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y=1}
Eindeutige Lösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y = 1/2}
mit FunktionswertFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} \mathrm{exp}\left(\frac{1}{4}\right) \end{aligned}}
Die Zeichnung zeigt, dass es sich wiederum um ein Minimum handelt:
Die Werte in der Zeichnung geben den Logarithmus der Wurzel der entsprechende Wertes der Funktion an. Z. Bsp ist das Minimum der Funktion unter der Nebenbedingung gegeben durchFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f\left(0\mathrm{.}5,0\mathrm{.}5\right)=\mathrm{exp}(0.5^2) \end{aligned}}
Aufgabe 2.5:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=(x-1)^2+(y-2)^2-1+\lambda\left(x^2+y^2-1\right) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K K T: \frac{\partial L}{\partial x}=2(x-1)+2 x \lambda=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial y}=2(y-2)+2 y \lambda=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda\left(x^2+y^2-1\right)=0(\text { Comp. Slack. }) }
Fall 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
(Lösung im inneren des zulässigen Bereichs)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 1}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = 2}
einzige formale Lösung, liegt nicht im zulässigen Bereich!
Fall 2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+y^2-1=0}
(Lösung am Rand)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(x-1\right)y-\left(y-2\right)x=2x-y=0}
, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 2x = y}
(ähnlich wie in Aufgabe 2.4)
Einsetzen in NB liefert zwei Lösungen:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right) \text { mit Funktionswert } 5-\frac{10}{\sqrt{5}}(\text { Minimum unter } N B) \\ \left(-\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}}\right) \text { mit Funktionswert } 5+\frac{10}{\sqrt{5}}(\text { Maximum unter } N B) \end{array}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} L=x^2+3 x y++2++y-1 \\ K K T: \frac{\partial L}{\partial x}=2 x+3 y+\lambda=0 \\ \frac{\partial L}{\partial y}=3 x+2 y+\lambda=0 \\ \lambda(x+y-1)=0(\text { Comp. Slack. }) \end{array}}
Fall 1:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda=0}
(Lösung im inneren des zulässigen Bereichs)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = 0}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = 0}
einzige formale Lösung, Hessematrix indefinit
Sattelpunkt
Fall 2:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x+y-1=0}
(Lösung am Rand)
Eliminiere Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x-y=0}
, also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x = y}
(ähnlich wie in Aufgabe 2.4)
Einsetzen in NB liefert eindeutige Lösung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x = y = 1/2 \end{aligned}}
mit Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle 5/4} Die Grafik zeigt, dass es sich um ein Maximum handelt:
Die Niveaulinien entsprechen Hyperbeln: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^2+3\mathrm{xy}+2=const.} Je weiter man sich vom Ursprung nach rechts oben bewegt, desto größer sind die Werte die die Funktion entlang der Niveaulinie annimmt. Je weiter man sich vom Ursprung nach links oben (bzw. rechts unten) bewegt, desto kleiner sind die entsprechenden Funktionswerte.
Bartholomew-Biggs, M. (2005): Nonlinear Optimization with Financial Applications, Kluwer Academic Publishers
Beutelspacher, A. (2003): Lineare Algebra, 6. Auflage, Vieweg-Verlag,
Bomze I.M., Grossmann W. (1993), Optimierung – Theorie und Algorithmen, Eine Einführung in Operations Research für Wirtschaftsinformatiker, BI-Verlag, Mannheim.
Christmann A.(1990): Anwendungen der Synergetik und Chaostheorie in der Ökonomie. Doktorarbeit, Karlsruhe;
Domschke W., Drexl A., (1995): Einführung in Operations Research, 3. verb. und erw. Auflage, Springer, Berlin
Fischer, G. (2005): Lineare Algebra, 15. Auflage, Vieweg-Verlag
Heuser, H. (2004): Gewöhnliche Differentialgleichungen. 4. Auflage, Teubner, Wiesbaden
Lawrence R. Rabiner (1989): A tutorial on Hidden Markov Models and selected applications in speech recognition. Proceedings of the IEEE 77 (2): 257-286.
Loistl O., Iro B. (1993): Chaostheorie. Zur Theorie nichtlinearer dynamischer Systeme. Oldenbourg R. Verlag, München
Luenberger D.G. (1979): Introduction to Dynamic Systems, Theory, Models & Applications, Wiley
Nocedal, J., Wright, S. J. (1999): Numerical Optimization, Springer-Verlag
Nørlund, N. E. (1924): Vorlesungen über Differenzenrechnung, Springer, Berlin
Norris, J.R. (1997): Markov Chains, Camebridge University Press
Sydsaeter K., Hammond P. (2004), Mathematik für Wirtschaftswissenschaftler, Pearson Studium
Walter W. (1991): Gewöhnliche Differentialgleichungen. 5. Auflage, Springer-Verlag, Berlin Heidelberg New York



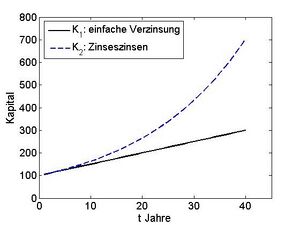










![{\displaystyle {\begin{aligned}K1:[0,40]\rightarrow \mathbb {R} \\t&\mapsto 100+0.05*\mathrm {t} \\K2:[0,40]\rightarrow \mathbb {R} \\t&\mapsto 100*1.05^{t}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b68ee9dc0c0192e3afb96d26917757baa6007a7)
![{\displaystyle {\begin{aligned}f_{1}:[-3,3]\rightarrow \mathbb {R} \\x\mapsto 3\mathrm {x} -2\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bfd6a469d498d52cb8624353d6bdf041f824baa)
![{\displaystyle {\begin{aligned}f_{2}:[-\pi ,\pi ]\rightarrow \mathbb {R} \\x\mapsto \sin x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/905d765441158c2576d25383a303c67a5362b358)
![{\displaystyle {\begin{aligned}f_{3}:\quad [0.1,3]\rightarrow \mathbb {R} \\t\mapsto \log(t)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16fbd8384df1d19bee7db114a8f1cc66cd1d0e01)
![{\displaystyle {\begin{aligned}f_{4}:&{[-3,3]\rightarrow \mathbb {R} }\\&x\mapsto \exp \left(-x^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14c7b75b95652c8c4f25480acbcb087fdd047538)