Optimierung - Lokale Extrema von reellen Funktionen

Lokale Extrema von reellen Funktionen

Wir erinnern uns, dass für Funktionen mit einer Veränderlichen eine notwendige Bedingung für lokale Extrema darin besteht, dass die erste Ableitung verschwindet, i.e. durch Lösen der Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^\prime\left(x\right)=0} erhält man mögliche Kandidaten für ein Maximum bzw. ein Minimum einer Funktion.
Beispiel 6: Betrachte das Polynom aus Beispiel 4:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(x) = -x^4+x^3+4x^2-4x+2}
Ableitung liefert
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p^{\prime}(x)=-4 x^3+3 x^2+8 x-4}
Die Suche nach Nullstellen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p^{\prime}(x)} liefert potenzielle Kandidaten für lokale Maxima und Minima. Für ein Polynom dritten Grades gibt es geschlossene Formeln, um die Nullstellen zu bestimmen, man erhält näherungsweise
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1 = -1.3263, x_2 = 1.6073, x_3 = 0.4691} Der Vergleich lässt erkennen, dass an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1} das absolute Maximum der Funktion liegt, während es sich bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_2} um ein lokales Minimum und bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_3} um ein lokales Maximum handelt.
Bereits für eine solch einfache Funktion wie ein Polynom dritten Grades ist die Bestimmung der Nullstellen nicht ganz trivial. Für die meisten Funktionen ist eine explizite Lösung überhaupt nicht möglich, und man ist auf numerische Methoden angewiesen. Die wichtigste wird im folgenden Abschnitt vorgestellt:

Das Newton Verfahren

Wir wollen die Nullstelle einer Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(x)} finden. (In Zusammenhang mit den Optimierungsaufgaben dieses Kapitels ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\left(x\right)=f^\prime\left(x\right)} die Ableitung der Funktion, deren Extremwerte gesucht werden; das Verfahren kann aber selbstverständlich für beliebige einmal differenzierbare Funktionen angewandt werden.) Das Newton-Verfahren ist ein Iterationsverfahren. Wir beginnen mit einer Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1} , die hoffentlich bereits in der Nähe der Nullstelle liegt. Grundidee ist nun die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(x)} durch ihre Tangente an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1)} zu ersetzen, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t(x) = g(x_1) + g\prime(x_1)(x- x_1)} und anschließend die Nullstelle der Tangente zu suchen. Die Lösung liefert den nächsten Punkt der Iteration:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x_2=x_1-\frac{g\left(x_1\right)}{g^\prime\left(x_1\right)} \end{aligned}}

Anschließend wird diese Prozedur so lange wiederholt, bis das Verfahren konvergiert, d.h. (bis auf numerische Genauigkeit) eine Nullstelle gefunden wurde. Es kann gezeigt werden, dass das Newton Verfahren extrem rasch (quadratisch) konvergiert, sobald man sich in der Nähe einer Nullstelle befindet. Die deutsche Wikipedia Seite bietet eine sehr schöne Animation, die verdeutlich wie das Newton Verfahren in der Praxis funktioniert. Um Kandidaten für lokale Extrema von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} zu erhalten sucht man Nullstellen der Ableitung von f, und das Iterationsverfahren hat daher die GestaltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} x_{k+1}=x_k-\frac{f^\prime\left(x_k\right)}{f^{\prime\prime}\left(x_k\right)} \end{aligned}}

Das bedeutet eine Funktion muss mindestens zweimal differenzierbar sein, damit diese Methode verwendet werden kann. In der Literatur findet man eine Unzahl an weiteren Methoden zur numerischen Bestimmung von Nullstellen.
Aufgabe 5:
Berechne für das Polynom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p^{\prime}(x)} aus Beispiel 6 die ersten beiden Newtonschritte mit Startwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1 = 0} . Schreib ein kleines Programm in der Programmiersprache deiner Wahl. Versuche auch andere Startwerte und beobachte wie sich das Verfahren verhält.

Die Bestimmung von globalen Extrema ist typischerweise wesentlich komplizierter als die Suche nach lokalen Extrema. Auch müssen diese nicht zwangsläufig existieren; die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x) = sin(x)} besitzt unendlich lokale Minima und Maxima, die gleichzeitig globale Extremwerte sind, die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x) = x sin(x)} besitzt unendlich viele lokale Extremwerte, aber keinen globalen. Plotten Sie die beiden Funktionen, um sich diese Tatsache vor Augen zu führen! Für eine gewisse Klasse von Funktionen kann man jedoch von lokaler Optimalität auf globale Optimalität schließen. Speziell nennt man eine Funktion f konvex (konkav), falls die Funktionswerte zwischen zwei Werten x und y jeweils unterhalb der Verbindungsgeraden der beiden Funktionswerte an x und y – der sogenannten Sekante - liegen. D.h. für jede Zahl t zwischen 0 und 1 giltFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} &f(t x+(1-t) y) \leq t f(x)+(1-t) f(y) \text { (konvex) } \\ &f(t x+(1-t) y) \geq t f(x)+(1-t) f(y)(\text { konkav) } \end{aligned}}

Konvexe Funktion

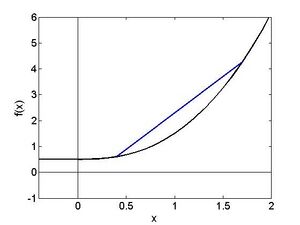
Die Abbildung zeigt eine konvexe Funktion und deren Sekante für zwei ausgewählte Werte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_2} . Die Sekante liegt oberhalb des Graphen der Funktion. Falls die zweite Ableitung existiert so gilt für eine konvexe FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^{\prime\prime}\left(x\right)\geq0 \end{aligned}}

und für eine konkave FunktionFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f^{\prime\prime}\left(x\right)\le0 \end{aligned}}

Für eine konvexe (konkave) Funktion gibt es höchstens ein lokales Extremum, und dies ist dann das globale Minimum (Maximum).