Optimierung - Wiederholung Analysis

Wiederholung Analysis

In der einführenden Lektion werden grundlegende Konzepte der Analysis besprochen, die an sich bereits vom Schulunterricht und vom Bachelor Studium vertraut sein sollten, deren Wiederholung allerdings sicherlich nicht schadet. Zur Vorbereitung auf die späteren Kapitel, welche auf den hier vorgestellten Begriffen basieren, wird ein etwas formalerer Zugang gewählt als im Bachelor Studium.

Reelle Funktionen einer Veränderlichen

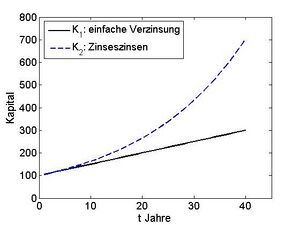
In der Finanzmathematik wurden bereits verschiedenste reelle Funktionen besprochen, etwa die Abhängigkeit des Kapitals ${\textstyle K}$ von der Zeit ${\textstyle t}$, wenn Verzinsung erfolgt. Abbildung 1.1 zeigt den Graphen von zwei Funktionen.

Beispiele für reelle Funktionen

In diesem Beispiel wäre die Zeit t (in Jahren) die unabhängige Variable, und wir haben zwei verschiedene Funktionen: das Kapital ${\textstyle K_{1}}$ unter einfacher Verzinsung, und ${\textstyle K_{2}}$ unter Berücksichtigung der Zinseszinsen. Dabei wird jedem Wert ${\textstyle t}$ aus dem Intervall [0,40] eine Zahl ${\textstyle K_{1}(t)}$ bzw. ${\textstyle K_{2}(t)}$ zugeordnet. Üblicherweise wird die Funktion der Verzinsung nur für natürliche Zahlen ausgewertet. Wir möchten hier die entsprechenden Funktionen auf beliebige reelle Zahlen im Intervall [0,40] fortsetzen. Im Allgemeinen versteht man unter einer reellen Funktion, bzw. einer reellen Abbildung eine Zuordnungsvorschrift, wo jedem Wert der unabhängigen Variablen ${\textstyle x}$ genau ein Wert der abhängigen Variable ${\textstyle f(x)}$ zugeordnet wird. Mitunter ist die Funktion ${\textstyle f}$ nicht für alle reellen Zahlen definiert, sondern hat einen eingeschränkten Definitionsbereich. So ist zum Beispiel der Logarithmus nur für positive reelle Zahlen definiert. Um eine Funktion vollständig zu charakterisieren schreibt man

$${\begin{aligned}f:D&\rightarrow \mathbb {R} \\x&\mapsto f(x)\end{aligned}}$$

wobei in der ersten Zeile festgelegt wird für welche Werte von x die Abbildung definiert ist (Definitionsbereich ${\textstyle D}$), und dass der Bildbereich in den reellen Zahlen ${\textstyle {R}}$ liegt. Die zweite Zeile gibt konkret die Rechenvorschrift an.

Beispiel 1: In Abbildung 1 haben wir

$${\begin{aligned}K1:[0,40]\rightarrow \mathbb {R} \\t&\mapsto 100+0.05*\mathrm {t} \\K2:[0,40]\rightarrow \mathbb {R} \\t&\mapsto 100*1.05^{t}\end{aligned}}$$

Zu den wichtigsten Funktionen gehören lineare Funktionen, Polynome, trigonometrische Funktionen, die Exponentialfunktion und die Logarithmusfunktion, deren Gestalt als bekannt vorausgesetzt wird.

Aufgabe 1 Zeichne mit R und Maxima ähnlich zu Abbildung 1.1 die Graphen folgender Funktionen:

$${\begin{aligned}f_{1}:[-3,3]\rightarrow \mathbb {R} \\x\mapsto 3\mathrm {x} -2\end{aligned}}$$

$${\begin{aligned}f_{2}:[-\pi ,\pi ]\rightarrow \mathbb {R} \\x\mapsto \sin x\end{aligned}}$$

$${\begin{aligned}f_{3}:\quad [0.1,3]\rightarrow \mathbb {R} \\t\mapsto \log(t)\end{aligned}}$$

$${\begin{aligned}f_{4}:&{[-3,3]\rightarrow \mathbb {R} }\\&x\mapsto \exp \left(-x^{2}\right)\end{aligned}}$$

In der Funktion ${\textstyle f_{4}}$ von Aufgabe 1 wurden zwei einfache Funktionen zusammengesetzt. Sei ${\textstyle f(x)=x^{2}}$ und ${\textstyle g(x)=exp(-x)}$, so ergibt sich ${\textstyle f_{4}}$ als Zusammensetzung von g und f:

$$f_{4}(x)=exp{(}-x^{2})=exp{(}-f(x))=g(f(x))=g\circ f(x)$$

Bei der Bildung einer zusammengesetzten Funktion ${\textstyle g\circ f(x)}$ ist darauf zu achten, dass der Bildbereich von f im Definitionsbereich von ${\textstyle g}$ liegt.

Umkehrabbildung

Ein wesentliches Merkmal einer Funktion ist, dass jedem Wert von ${\textstyle x}$ genau eine reelle Zahl ${\textstyle y=f(x)}$ zugeordnet wird. Manchmal ist es der Fall, dass auch umgekehrt jeder Bildwert ${\textstyle y}$ genau einem Urbildwert ${\textstyle x}$ entspricht. Dies gilt speziell dann, wenn eine Funktion streng monoton steigend bzw. streng monoton fallend ist. Dies bedeutet, dass für jedes ${\textstyle x1>x2}$ entweder ${\textstyle f(x_{1})>f(x_{2})}$ (steigend) oder ${\textstyle f(x_{1})<f(x_{2})}$ (fallend). In diesen Fällen kann die sogenannte Umkehrabbildung ${\textstyle f^{-}1(y)}$ gebildet werden, die jedem Bildwert ${\textstyle y}$ den entsprechenden Urbildwert ${\textstyle x}$ zuordnet. Es gilt

$$f^{-1}\circ f\left(x\right)=f^{-1}\left(f\left(x\right)\right)=x$$

$$f\circ f^{-1}\left(y\right)=f\left(f^{-1}\left(y\right)\right)=y$$

Funktion und Umkehrfunktion

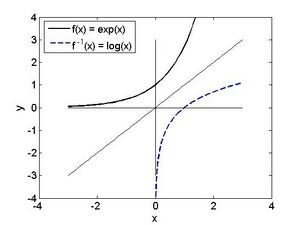
Beispiel 2: In Abbildung 2 finden wir ein wichtiges Beispiel: Die streng monoton steigende Funktion ${\textstyle f(x)=\exp(x)}$ und deren Umkehrfunktion ${\textstyle g(x)=f^{-}1(x)=log(x)}$ Beachte, dass man im Graphen die Umkehrfunktion durch Spiegelung an der ersten Hauptdiagonale erhält. Klarerweise gilt ${\textstyle log(exp(x))=x}$. Andererseits gilt auch ${\textstyle exp(log(x))=x}$ für ${\textstyle x>0}$, ansonsten liegt ${\textstyle x}$ nicht im Definitionsbereich der Logarithmus-Funktion.

Ein Beispiel für eine Funktion die sich nicht umkehren lässt wäre ${\textstyle f(x)=x^{2}}$.

Aufgabe 2 Skizziere ähnlich zu Abbildung 2 den Graphen von

$${\begin{aligned}f:&\mathbb {R} \rightarrow \mathbb {R} \\&x\mapsto x^{2}\end{aligned}}$$

\begin{aligned}f^+:&\mathbb{R}^+\rightarrow\mathbb{R}\\\ &x\mapsto x^2\\\end{aligned} und überlege, warum es keine eindeutige Umkehrfunktion gibt. Zeichne die beiden Umkehrfunktionen zu und

$${\begin{aligned}f^{-}:&\mathbb {R} ^{-}\rightarrow \mathbb {R} \\\ &x\mapsto x^{2}\\\end{aligned}}$$

Löse algebraisch die Gleichung ${\textstyle y=x^{2}}$ nach ${\textstyle x}$ und vergleiche mit den graphischen Lösungen

Differentiation

Als nächstes wollen wir uns mit Glattheitseigenschaften von Funktionen beschäftigen. Als erstes wäre da der Begriff der Stetigkeit. Eine Funktion ist an einem Punkt x im Wesentlichen dann stetig, wenn sie dort nicht springt.

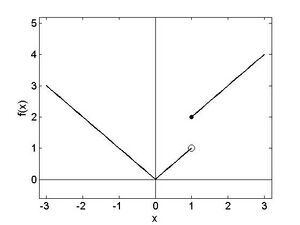
Beispiel 3: In Abbildung 3 ist folgende Funktion ${\textstyle f(x)}$ gezeichnet:

$$f\left(x\right)=\left\{{\begin{aligned}\mathrm {\ \ \ \ \ } \left|x\right|\mathrm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } x<1\\\mathrm {\ \ \ \ } \left|x\right|+1\mathrm {\ \ \ \ \ \ \ \ \ \ } x\geq 1\\\end{aligned}}\right.$$

Die Funktion ist überall stetig außer an ${\textstyle x=1}$ wo sie einen Sprung der Höhe 1 hat.

Formal wird die Stetigkeit dadurch definiert, dass an einer bestimmten Stelle ${\textstyle x_{0}}$ sowohl der rechtsseitige Limes als auch der linksseitige Limes mit dem Funktionswert übereinstimmt. Also

$$\lim \limits _{x_{n}\rightarrow x_{0}}f\left(x_{n}\right)=f\left(x_{0}\right)$$

sowohl für beliebige Folgen mit ${\textstyle x_{n}<x_{0}}$ als auch für ${\textstyle x_{n}>x_{0}}$.

In Beispiel 3 bedeutet dies, dass an der Stelle ${\textstyle x_{0}=1}$ zwar der rechts-seitige Limes mit dem Funktionswert ${\textstyle f(1)=2}$ übereinstimmt:

$$\lim \limits _{x_{n}\rightarrow 1^{+}}f\left(x_{n}\right)=\lim \limits _{h\rightarrow 0,h\rightarrow 0}f(1+h)=1+1+\lim \limits _{h\rightarrow 0,h\rightarrow 0}|h|=1=f\left(1\right)$$

Hingegen gilt für den linksseitigen Limes:

$$\lim \limits _{x_{n}\rightarrow 1^{-}}f\left(x_{n}\right)=1$$

(nachrechnen mit ${\textstyle h<0}$!) Daher ist die Funktion an der Stelle ${\textstyle x_{0}=1}$ nicht stetig. In Abbildung 1.3 ist der rechtsseitige Limes durch einen Punkt, der linksseitige Limes durch einen Ring gekennzeichnet.

Funktion mit Sprungstelle bei x = 1

Differenzierbarkeit hängt nun damit zusammen, ob eine Funktion an einem Punkt einigermaßen glatt ist und nicht etwa einen Knick aufweist. Anschaulich gesprochen bedeutet dies, dass man im Graphen der Funktion an einem Punkt eine Tangente anpassen kann. Stetigkeit ist dafür eine notwendige Voraussetzung, allerdings nicht hinreichend. Die Funktion aus Abbildung 1.3 etwa ist an der Stelle ${\textstyle x=0}$ zwar stetig, aber nicht differenzierbar. Die Theorie der Differentialrechnung wurde in der Finanzmathematik ausführlich besprochen.

Rechenregeln

Wir wollen nur die wichtigsten Rechenregeln der Differentialrechnung wiederholen. Die folgende Tabelle beinhaltet die Ableitungen der gängigsten Funktionen, wobei hier a eine beliebige reelle Zahl sein kann:

Zusätzlich von Bedeutung sind

$${\begin{array}{r}Produktregel:(fg)^{\prime }=f^{\prime }g+fg^{\prime }\\Quotientenregel:\left({\frac {f}{g}}\right)^{\prime }={\frac {f^{\prime }g-fg^{\prime }}{g^{2}}}\\Kettenregel:(g\circ f)^{\prime }=\left(g^{\prime }\circ f\right)\cdot f^{\prime \prime }\\\end{array}}$$

Die Kettenregel kann auch in folgender Form geschrieben werden:

$${\frac {d}{dx}}g\left(f\left(x\right)\right)=g^{\prime }\left(f\left(x\right)\right)\cdot f^{\prime }\left(x\right)$$

Durch konsequente Anwendung dieser Regeln lassen sich bereits viele praktische Aufgaben lösen.

Aufgabe 3 Differenziere folgende Funktionen und überprüfe das Ergebnis mit Maxima!

$${\begin{array}{r}f_{1}(x)=\exp(-x2)\\f_{2}(x)=\tan x=\sin(x)\cdot \cos(x)\\f_{3}(x)={\sqrt {1+x^{3}}}\end{array}}$$

Die erste Ableitung ${\textstyle f^{'}(x)}$ ist wiederum eine Funktion von ${\textstyle \mathbb {R} }$ nach ${\textstyle \mathbb {R} }$, deren Ableitung ${\textstyle f^{''}(x)}$ man als Ableitung zweiter Ordnung bezeichnet. Entsprechend können Ableitungen höherer Ordnung definiert werden. Die erste Ableitung einer Funktion gibt deren Steigung an. Die Gleichung ${\textstyle f^{'}(x)=0}$ bestimmt potentielle lokale Extremstellen der Funktion. Die Ableitung zweiter Ordnung beschreibt die Krümmung einer Kurve und ${\textstyle f^{''}(x)=0}$ definiert potentielle Wendepunkte. All diese Überlegungen fließen bei der wohlbekannten Diskussion von Kurven ein.

Integration

Geometrisch gesehen dient das Integrieren zum Berechnen von Flächen.

Beispiel für Integration

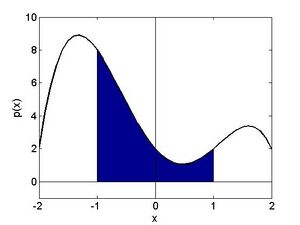
Beispiel 4: In Abbildung 1.4 ist das Polynom ${\textstyle p(x)=-x^{4}+x^{3}+4x^{2}-4x+2}$ geplottet. Es soll die Fläche zwischen der Funktion ${\textstyle p(x)}$ und der x-Achse im Bereich ${\textstyle (-1,1)}$ berechnet werden, die in der Abbildung hervorgehoben wurde. Die Berechnung erfolgt mit einem sogenannten bestimmten Integral, bei dem die obere und die untere Grenze des Integrationsbereichs feststehen (im Beispiel eben die Grenzen -1 und 1).

$${\begin{aligned}\int _{x=-1}^{1}p(x)\mathrm {dx} &=\int _{x=-1}^{1}\left(-x^{4}+x^{3}+4x^{2}-4x+2\right)\mathrm {dx} =\\&=-{\frac {x^{5}}{5}}+{\frac {x^{4}}{4}}+{\frac {4x^{3}}{3}}-{\frac {4x^{2}}{2}}+\left.2\mathrm {x} \right|_{-1}^{1}={\frac {94}{15}}\end{aligned}}$$

Im folgenden Abschnitt werden wir die Details zu dieser Berechnung genau erläutern. Für die allgemeine Integrationstheorie ist der Zusammenhang zwischen Integralrechnung und Differentialrechnung von entscheidender Bedeutung:

Hauptsatz der Analysis

Dieser fundamentale Satz besagt, dass Integrieren und Differenzieren zueinander inverse Operationen sind. Um dies zu verstehen brauchen wir zunächst folgende Begriffe: Das unbestimmte Integral einer Funktion f sowie deren Stammfunktion. Ein unbestimmtes Integral von ${\textstyle f(x)}$ erhält man, indem man die untere Grenze ${\textstyle a}$ des Integrals festhält, während man die obere Grenze variieren lässt:

$$I_{a}\left(x\right)=\int _{y=a}^{x}f\left(y\right)\mathrm {dy}$$

Für jedes feste ${\textstyle a}$ wird dadurch eine Funktion in ${\textstyle x}$ definiert. Unter eine Stammfunktion von ${\textstyle f(x)}$ versteht man eine differenzierbare Funktion ${\textstyle F(x)}$ für die gilt

$$F^{\prime }\left(x\right)=f\left(x\right)$$

Es gibt davon unendlich viele, da man zu jeder Stammfunktion eine Konstante ${\textstyle c}$ addieren kann und wiederum gilt

$$(F(x)+c)^{\prime }=f(x)$$

D.h. die Stammfunktion ist nur bis auf eine Konstante eindeutig bestimmbar. Der Hauptsatz der Analysis besagt nun, dass jedes unbestimmte Integral von ${\textstyle f}$ gerade eine Stammfunktion von ${\textstyle f}$ ist:

$${\frac {d}{\mathrm {dx} }}I_{a}\left(x\right)={\frac {d}{\mathrm {dx} }}\int _{y=a}^{x}f\left(y\right)\mathrm {dy} =f\left(x\right)$$

Umgekehrt erhalte ich alle Stammfunktionen mittels unbestimmter Integrale

$$F\left(x\right)=\int _{y=a}^{x}f\left(y\right)\mathrm {dy} +c$$

wobei ${\textstyle c}$ als Integrationskonstante bezeichnet wird. Die folgende Tabelle gibt die Stammfunktionen der wichtigsten einfachen Funktionen, wobei hier ${\textstyle a}$ jede beliebige reelle Zahl mit Ausnahme von ${\textstyle -1}$ sein kann.

Die Tabelle ist gerade die Umkehrung von jener der Differentiation.
Ist die Stammfunktion F(x) einer Funktion f(x) bekannt, so können bestimmte Integrale für ein Intervall [a,b] recht einfach berechnet werden:

$$\int _{x=a}^{b}f\left(x\right)\mathrm {dx} =F\left(b\right)-F\left(a\right)$$

Die Integrationskonstante des unbestimmten Integrals kürzt sich weg, und daher genügt es eine einzige Stammfunktion zu kennen um beliebige bestimmte Integrale von f zu berechnen. Man verwendet häufig die Notation

$$\int _{x=a}^{b}f\left(x\right)\mathrm {dx} =F\left(x\right)|_{a}^{b}=F\left(b\right)-F\left(a\right)$$

um in einem Zwischenschritt zu verdeutlichen, wie die Stammfunktion explizit aussieht. Nun sollte die Berechnung des Integrals in Beispiel 4 kein Problem mehr machen.

Aufgabe 4:
Das Berechnen von Wahrscheinlichkeiten entspricht hier gerade der Integration. Eine in der Praxis häufig auftretende Verteilung ist die Exponentialverteilung, mit Dichte

$$f\left(x\right)=\left\{{\begin{aligned}\lambda \mathrm {\ exp} \left(-\lambda x\right)\mathrm {\ \ \ \ \ \ \ \ \ \ \ \ \ } x>0\\\mathrm {\ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sonst} \\\end{aligned}}\right.$$

Berechne die Wahrscheinlichkeit, dass eine exponentialverteilte Zufallsvariable mit Parameter ${\textstyle \lambda }$ Werte zwischen 1 und 2 annimmt.

Partielle Integration, Substitution

Während das Differenzieren nach Erlernen der Grundtechniken weitgehend mechanisch abläuft ist dies beim Integrieren leider nicht der Fall. Im Gegenteil, häufig gleicht die Suche nach einer Stammfunktion einer höheren Kunstform, und in vielen Fällen ist eine geschlossene Darstellung eines unbestimmten Integrals gar nicht möglich. So besitzt beispielsweise die Dichte der Normalverteilung keine einfach darstellbare Stammfunktion, und zur Berechnung von Wahrscheinlichkeiten ist man hier entweder auf Tabellen oder auf numerische Integration angewiesen. Zwei Basistechniken zur Bestimmung von Stammfunktionen sollen hier allerdings Erwähnung finden:
Partielle Integration:

$$\int {{f}^{\prime }g}={fg}-{fg}'$$

Dies ist das Pendant zur Produktregel, was durch Differenzieren unter Verwendung des Hauptsatzes der Analysis unmittelbar klar wird:

$${f}^{\prime }{g}=\left({fg}\right)^{\prime }-{fg}^{\prime }$$

Substitution:

$$\int g\left(x\right)\mathrm {dx} =\left|{\begin{aligned}y=h\left(x\right)\\\mathrm {dy} =h^{\prime }\left(x\right)\mathrm {dx} \\\end{aligned}}\right|=\int {g(h}^{-1}(y)){\frac {\mathrm {dy} }{h^{\prime }\left(x\right)}}$$

für ${\textstyle h(x)}$ streng monoton steigend.

Man kann zeigen, dass es sich hier um das Pendant zur Kettenregel beim Differenzieren handelt. Wir wollen beide Techniken anhand eines konkreten Beispiels vorführen. In den Wiederholungsaufgaben gibt es einige weitere Beispiele.

Beispiel 5: Der Erwartungswert einer Zufallsvariable ${\textstyle X}$ mit Dichte ${\textstyle f}$ ist definiert als

$$E\left(X\right)=\int _{x=-\infty }^{\infty }\mathrm {xf} \left(x\right)\mathrm {dx}$$

Für die Exponentialverteilung (aus Aufgabe 4) erhält man

$$\int _{x=0}^{\infty }x\lambda \exp(-\lambda x)\mathrm {d} x=\int _{y=0}^{\infty }y\lambda \exp(-\lambda y)\mathrm {d} y=-\left.{\frac {1}{\lambda }}y\exp(-y)\right|_{0}^{\infty }+{\frac {1}{\lambda }}\int _{y=0}^{\infty }\exp(-y)\mathrm {d} y={\frac {1}{\lambda }}$$

Die zweite Gleichung mittels partieller Integration:

$$f^{\prime }\left(y\right)=\mathrm {exp} -y,gy=y$$

Man beachte, dass

$$\lim \limits _{y\rightarrow \infty }y\mathrm {\ exp} \left(\mathrm {-y} \right)=0$$

weil die Exponentialfunktion ${\textstyle \mathrm {exp} (-y)}$ wesentlich rascher gegen 0 konvergiert als der Faktor ${\textstyle y}$ wächst.

Reelle Funktionen mehrerer Veränderlicher

Vorbemerkung: in diesem Abschnitt wird mit Vektoren und Matrizen gerechnet; zwar werden die einzelnen Schritte erläutert, - falls diese Schritte aber große Schwierigkeiten bereiten, sollten Sie die erforderlichen Grundlagen der Linearen Algebra rekapitulieren. Bislang haben wir uns auf Funktionen einer freien Variablen beschränkt, d.h. der Definitionsbereich und der Bildbereich waren jeweils Teilmengen der Zahlengerade. Allgemeiner betrachtet kann man Abbildungen mit n Veränderlichen studieren; diese schreibt man in der Form:

$$f:\ \ D\ \subseteq \mathbb {R} ^{n}\ \rightarrow \ \mathbb {R} \ \ \ \ \ \ \left(x_{1},\ \ldots x_{n}\right)\rightarrow f\left(x_{1},\ \ldots x_{n}\right)$$

Nun ist diese Verallgemeinerung – trotz der etwas sperrigen Notation (und es wird noch schlimmer!) durchaus naheliegend: in der Praxis wird eine Zielvariable ja häufig nicht nur von einer einzigen Einflussvariablen bestimmt, sondern von mehreren – nehmen wir etwa die Nachfrage nach Bier in einem Gastgarten: sie wird vom Preis des Bieres abhängen, von der Temperatur und vom Datum zu Monatsbeginn haben viele Gäste noch mehr Geld zur Verfügung als gegen Monatsende; diese drei freien Variablen können wir ${\textstyle P,T,d}$ nennen – oder eben ${\textstyle x_{1},x_{2},x_{3}}$. Funktionen mit eindimensionalem Definitionsbereich konnten wir durch den Graphen veranschaulichen – auf der x-Achse wird die freie Variable aufgetragen, auf der y-Achse die Abhängige – dann erhalten wir bei einer stetigen Funktion eine Kurve (oder Gerade) im Raum. Bei Funktionen mit mehrdimensionalem Definitionsbereich ist eine solche Veranschaulichung im Allgemeinen nicht mehr möglich; eine Ausnahme sind die Funktionen

$$\ f:\ \ D\ \subseteq \mathbb {R} ^{2}\ \rightarrow \ \mathbb {R} :$$

hier ist der Definitionsbereich ein Teilbereich der (zweidimensionalen) Ebene, und jedem Punkt aus diesem Ebenen-Bereich wird ein Funktionswert zugeordnet – den wir uns als Höhe vorstellen können. Der Graph der Funktion wird also eine – möglicherweise sehr unebene – Fläche im Raum sein; als Beispiel können Sie sich eine Landschaft vorstellen: jeder Punkt hat eine x- und eine y- Koordinate in der Ebene, und diesem Punkt wird eine Höhe zugeordnet; je nachdem wie stetig die Funktion nun ist, wird die Landschaft glatt oder zerklüftet sein. Funktionen mit höherdimensionalem Definitionsbereich kann man sich nicht mehr so einfach veranschaulichen. Die Definition der Stetigkeit wird nun etwas komplizierter, da man sich einem Punkt in der Ebene – oder einem höherdimensionalen Raum – nicht nur aus zwei Richtungen, sondern aus beliebig vielen Richtungen nähern kann. Das Konzept bleibt ansonsten aber das Gleiche. Eine Funktion f ist an einer Stelle stetig, falls für jede Folge von Punkten, die gegen diesen Punkt konvergiert die entsprechende Folge der Funktionswerte gegengegen den Funktionswert dieses Punktes konvergiert.

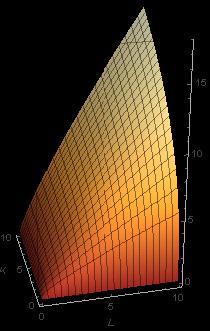
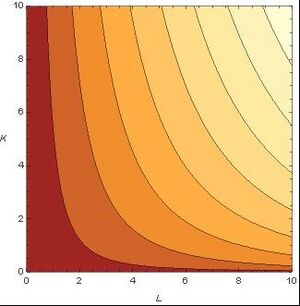
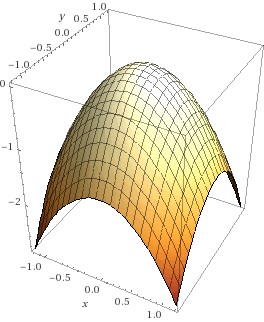
Beispiel 6: Großer Beliebtheit erfreut sich in den Wirtschaftswissenschaften die Cobb-Douglas Funktion, die den Einfluss von mehreren Faktoren auf die Produktion modelliert. So ließ sich in den Jahren 1960 bis 1975 die Produktion Y der Beiersdorf AG in Abhängigkeitn von den beiden Faktoren L (Arbeit) und K (Kapital) durch die Funktion

$$Y=Y\left(L,K\right)=e^{0.04}L^{0.84}K^{0.39}$$

gut beschreiben. Die Abbildung zeigt den Graphen der Funktion: der Definitionsbereich ist die Menge aller Punkte ${\textstyle (L,K),L>=0,K>=0}$, also der positive Quadrant der Ebene; jedem dieser Punkte wird nun eine Funktionswert zugeordnet. Ist einer der beiden Faktoren 0, so ist die Produktivität auch 0; für jeden anderen Wert des einen Faktors ist die Funktion streng monoton steigend im anderen – das sehen wir an den Gitterlinien auf dem Graphen; diese sind die Bilder von Geraden parallel zur K- bzw. zur L-Achse. Offensichtlich ist die Funktion auf jeder dieser Gitterlinien streng monoton steigend. Die Abbildung daneben zeigt die Höhenschichtlinien der Funktion; sie verbinden Punkte aus dem Definitionsbereich mit jeweils gleichem Funktionswert. Im Wikipedia – Eintrag zur Cobb-Douglas Funktion finden Sie eine schöne Animation!

Cobb-Douglas Funktion mit Höhenschichtlinien

Funktionen in mehreren Variablen können wir uns im Allgemeinen nicht vorstellen; wir können aber versuchen, jede dieser Variablen „getrennt“ zu betrachten, d.h., wir weisen allen anderen einen konstanten Wert zu – dann nehmen diese in der Funktionsgleichung die Rolle von Konstanten ein – und betrachten die Änderung des Funktionswertes bei Änderung der einen Variablen im Fokus.

Beispiel 6 (Fortsetzung): Nehmen wir an, wir wissen, wir wollen nur wissen, wie sich die Produktivität bei konstanter Arbeitsleistung ${\textstyle L=1}$ entwickelt, wenn ${\textstyle K}$ variiert. Dann können wir

$$Y=Y\left(K,1\right)=e^{0.04}\cdot 1\ K^{0.39}$$

schreiben – also die Funktion nur noch abhängig von ${\textstyle K}$ betrachten. In der linken Graphik würde das heißen, dass wir uns jene Gitterlinie suchen, die zu ${\textstyle L=1}$ gehört, und auf dieser variable Werte von ${\textstyle K}$ betrachten. In dieser Betrachtung können wir nun das Werkzeug aus der eindimensionalen Analysis einsetzen; z.B. können wir Ableitungen in Richtung einer Variablen definieren, wenn alle anderen Festgehalten werden – formal:

$${\frac {\partial }{\partial x_{i}}}f\left(x_{1},\ldots ,x_{n}\right)=\lim \limits _{h\rightarrow 0}{\frac {f\left(x_{1},\ldots ,x_{i}+h,\ldots x_{n}\right)-f\left(x_{1},\ldots ,x_{i},\ldots x_{n}\right)}{h}}$$

Beispiel 6 (Fortsetzung): Bilden wir die partiellen Ableitungen der Cobb-Douglas-Funktion, so erhalten wir:

$${\frac {\partial Y}{\partial L}}={0.84e}^{0.04}L^{-0.16}K^{0.39},\ \ {\frac {\partial Y}{\partial K}}={0.39e}^{0.04}L^{0.84}K^{-0.61}$$

Der Zeilen-Vektor aus den partiellen Ableitungen wird als Jacobi-Matrix bezeichnet,

$$J\left(f\right)=\left({\frac {\partial f}{\partial x_{1}}},\ \ldots {\frac {\partial f}{\partial x_{n}}}\right)$$

Der Spalten-Vektor bestehend aus allen partiellen Ableitungen wird als Gradient bezeichnet,

$$\nabla \left(f\right)=\left({\frac {\partial f}{\partial x_{1}}},\ \ldots {\frac {\partial f}{\partial x_{n}}}\right)^{t}=:{\begin{pmatrix}{\frac {\partial f}{\partial x_{1}}}\\{\frac {\partial f}{\partial x_{2}}}\end{pmatrix}}$$

Existieren die partiellen Ableitungen für alle Variablen und sind ihrerseits stetig, so bezeichnet man die Funktion als differenzierbar. Der Gradientenvektor steht in jedem Punkt normal auf die Höhenschichtlinie durch den Punkt und zeigt in die Richtung des steilsten Anstiegs.

Beispiel 6 (Fortsetzung): Die Jacobi Matrix der Cobb-Douglas Funktion, ausgewertet für ${\textstyle L=1,K=2}$ :

$$J\left(f\right)\left(1,2\right)=\left(1.15,0.27\right)$$

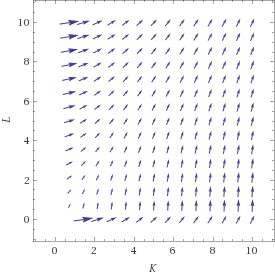
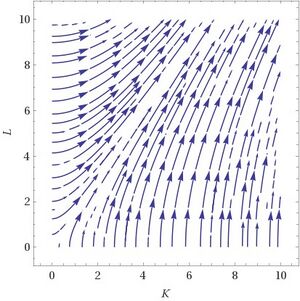
Die untere Abbildung zeigt den Gradienten der Cobb-Douglas Funktion als Vektorfeld; in jedem Punkt zeigt die horizontale Komponente des Pfeils die partielle Ableitung nach K, die vertikale die partielle Ableitung nach L. Sie stehen normal auf die Höhenschichtlinien. Die rechte Graphik stückelt diese Gradienten-Vektoren zu Trajektorien zusammen – jene Wege, auf denen man von einem gegebenen Startpunkt aus am schnellsten steigt. Auf diesen werden wir bei der Suche nach Maxima bewegen – zumindest annähernd.

Gradient der Cobb – Douglas Funktion

Gradient der Cobb – Douglas Funktion

In der Jacobi-Matrix stehen die Richtungsableitungen in Richtung jeder einzelnen Variablen – d.h., sie gibt die Steigung der Tangenten an den Funktionsgraph in jeder dieser Richtungen an. Gibt es nur zwei freie Variable, dann ist der Graph einer stetigen Funktion eine Fläche im Raum, und die Tangenten an einen Punkt spannen eine Ebene aus – die Tangentialebene; bei höherdimensionalen Funktionen spricht man von Hyperebenen. Mithilfe der Jacobi-Matrix lässt sich nun die Richtungsableitung in beliebiger Richtung definieren. Die partiellen Ableitungen geben ja an, wie sich der Funktionswert auf der Tangentialebene verändert, wenn man eine Einheit in Richtung jeder einzelnen Variablen geht. Will man nun in eine beliebige Richtung gehen, so sucht man deren Einheitsvektor und multipliziert jede Komponente mit der entsprechenden partiellen Ableitung – man bildet das Matrix-Produkt der Jacobi-Matrix mit dem Richtungsvektor der Veränderung.

Beispiel 6 (Fortsetzung): Die Jacobi Matrix der Cobb-Douglas Funktion, ausgewertet für ${\textstyle L=1,K=2}$:

$$J\left(f\right)\left(1,2\right)=\left(1.15,0.27\right)$$

D.h. Wenn ich über dem Punkte ${\textstyle P=(1,2)}$ eine Tangentialebene anlege, so hat diese über dem Punkt die Höhe ${\textstyle Y(1,2)=1.37}$, verändere ich nun die erste Komponente, so erhöht sich die Höhe der Tangentialebene um einen Betrag von 1.15; gehen wir stattdessen von P eine Einheit in Richtung der 2. Komponente, so ergibt sich ein Zuwachs von 0.27.

Wie aber verändert sich der Funktionswert, wenn wir uns in beliebiger Richtung vom Punkt P fortbewegen? Dann brauchen wir den Einheitsvektor dieser Richtung: z.B. in Richtung ${\textstyle (3,1)}$: Die Länge des Vektors ist

$${\sqrt {3^{2}+1^{2}}}={\sqrt {10}}$$

D.h.: der Vektor

$${\frac {1}{\sqrt {10}}}\left(3,1\right)={\begin{pmatrix}{\frac {3}{\sqrt {10}}}\\\ {\frac {1}{\sqrt {10}}})\end{pmatrix}}$$

ist der Einheitsvektor in dieser Richtung. Wenn wir als vom Punkt P eine Einheit in diese Richtung gehen, so ergibt sich ein Höhenzuwachs von ${\textstyle \ {\frac {3}{\sqrt {10}}}.1.15}$ aus der Bewegung in die erste Richtung, ${\textstyle \ {\frac {3}{\sqrt {10}}}.0.27}$ aus der Bewegung in der zweiten Richtung – und der gesamte Höhenzuwachs ist die Summe dieser beiden.

Mathematisch ausgedrückt erhalten wir die Richtungsableitung als Produkt der Jacobi-Matrix mit dem Richtungsvektor, oder – äquivalent – als inneres Produkt des Gradientenvektors mit dem Richtungsvektor. Die folgenden Schreibweisen sind äquivalent – die letzte nicht ganz exakt aber gebräuchlich:

$${\begin{aligned}&(0.27,1.15)\left({\begin{array}{c}{\frac {3}{\sqrt {10}}}\\{\frac {1}{\sqrt {10}}}\end{array}}\right)=\left(\left({\begin{array}{c}1.15\\0.27\end{array}}\right),\left({\begin{array}{c}{\frac {3}{\sqrt {10}}}\\{\frac {1}{\sqrt {10}}}\end{array}}\right)\right)=\\=&\left(\left({\begin{array}{c}1.15\\0.27\end{array}}\right)\cdot \left({\begin{array}{c}{\frac {3}{\sqrt {10}}}\\{\frac {1}{\sqrt {10}}}\end{array}}\right)\right)=1.15\cdot {\frac {3}{\sqrt {10}}}+0.27\cdot {\frac {1}{\sqrt {10}}}\end{aligned}}$$

Der Gradient bzw. die Jacobi-Matrix entsprechen den ersten Ableitungen von Funktion mit eindimensionalem Definitionsbereich; lassen sich einige Aussagen aus dem Eindimensionalen umformulieren – z.B. die Definition einer streng monoton wachsenden Funktion: im eindimensionalen Fall hieß das, dass die 1. Ableitung strikt positiv ist. Ebenso bezeichnen wir eine Funktion aus dem ${\textstyle \mathbb {R} ^{n}}$ nach ${\textstyle \mathbb {R} }$ als streng monton wachsend, wenn alle partiellen Ableitungen strikt positiv sind. Ebenso können wir die Kriterien für Extremwerte ins Mehrdimensionale übertragen. Hier muss gelten: wenn eine Funktion aus dem Mehrdimensionalen einen Extremwert in einem Punkt hat, so müssen in diesem Punkt alle partiellen Ableitungen 0 sein – dann sind auch alle Richtungsableitungen in beliebiger Richtung 0; allerdings war das Verschwinden der ersten Ableitung schon im Eindimensionalen eine notwendige, aber keine hinreichende Bedingung für das Vorliegen eines Extremwertes – wir mussten noch die zweite Ableitung befragen. Nun wird die Verallgemeinerung der 2. Ableitung ins mehrdimensionale allerdings formal etwas sperriger werden und zur sogenannten Hesse-Matrix führen. Das Gegenstück zur ersten Ableitung war nämlich der Gradient, in dem sich die partiellen ersten Ableitungen befanden. Aus diesem gewinnen wir nun die Hessematrix, indem wir die Jacobi-Matrix von jeder Komponente dieses Gradienten bilden.

Beispiel 6 (Fortsetzung): Der Gradient der Cobb-Douglas Funktion war

$$\nabla Y=\left({\begin{array}{c}Y\\L\\Y\end{array}}\right)=\left({\begin{array}{c}0.84e^{0.04}L^{-0.16}K^{0.39}\\0.39e^{0.04}L^{0.84}K^{-0.61}\end{array}}\right)$$

Die partiellen zweiten Ableitungen werden nun wieder nach beiden Variablen abgeleitet – analog zu den ersten:

$${\frac {\partial }{\partial L}}\left({\frac {\partial Y}{\partial L}}\right)=:\ {\frac {\partial ^{2}Y}{\left(\partial L\right)^{2}}}=\ -0.16\cdot 0.84e^{0.04}L^{-1.16}K^{0.39}$$

Für die Hessematrix ergibt sich daher:

$$H_{f}\left(L,K\right)=\left({\begin{aligned}-0.14L^{-1.16}K^{0.39}&0.34L^{-0.16}K^{-0.61}\\0.34L^{-0.16}K^{-0.61}&-0.25L^{0.84}K^{-1.61}\\\end{aligned}}\right)$$

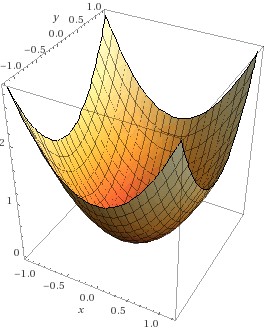
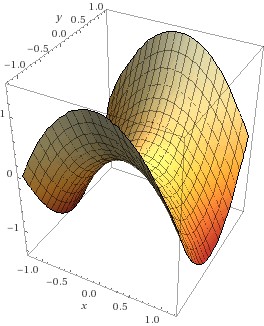
Die gemischten 2. Ableitungen sind immer gleich unabhängig von der Reihenfolge, in der abgeleitet wird – d.h., die Matrix ist symmetrisch. Mit dieser Hessematrix kann nun die 2. Ableitung in jeder beliebigen Richtung bestimmt werden: die zweite Ableitung in Richtung eines Vektors ${\textstyle {\vec {v}}}$ der Länge 1 ergibt sich durch die sogenannte quadratische Form ${\textstyle \ {\vec {v}}^{t}{\vec {H_{f}}}{\vec {v}}\ }$ Ist nun diese 2. Ableitung in jeder Richtung positiv, so heißt das, die Funktion ist in jeder Richtung konvex – d.h., ein Punkt, an dem alle partiellen Ableitungen 0 sind (und damit auch der Gradient der Nullvektor) ist ein Minimum. Ist die 2. Richtungsableitung in allen Richtungen negativ, so ist die Funktion in allen Richtungen konkav – d.h., der kritische Punkt ist ein Maximizer. Und gibt es Richtungen, in denen die 2. Richtungsableitung positiv ist, ander, in denen sie negativ ist, so handelt es sich um einen Sattelpunkt. Beispiele finden Sie in der Abbildung:

Minimum

Maximum

Sattelpunkt

Beispiel 6 (Fortsetzung): Für die Hessematrix der Cobb-Douglas-Funktion im Punkt ${\textstyle (1,2)}$ ist:

$$H_{f}\left(1,2\right)=\left({\begin{aligned}-0.18&0.22\\0.22&-0.08\\\end{aligned}}\right)$$

Für die 2 Richtungsableitung in Richtung ${\textstyle {\vec {v}}=({\frac {3}{\sqrt {10}}},\ {\frac {1}{\sqrt {10}}})}$ bilden wir zunächst das Matrix-Vektor Produkt:

$$\mathrm {H} _{f}{\vec {v}}=\left({\begin{array}{cc}-0.18&0.22\\0.22&-0.08\end{array}}\right)\left({\begin{array}{c}{\frac {3}{\sqrt {10}}}\\{\frac {1}{\sqrt {10}}}\end{array}}\right)=\left({\begin{array}{c}-0.18\cdot {\frac {3}{\sqrt {10}}}+0.22\cdot {\frac {1}{\sqrt {10}}}\\0.22\cdot {\frac {3}{\sqrt {10}}}-0.08{\frac {1}{\sqrt {10}}}\end{array}}\right)=\left({\begin{array}{c}-0.10\\0.18\end{array}}\right)$$

Der Vektor auf der rechten Seite hat eine anschauliche Interpretation: er gibt an, in welcher Richtung und wie stark sich der Gradient verändert, wenn wir vom Punkt ${\textstyle (1,2)}$ in der Richtung des Vektors ${\textstyle \left({\frac {3}{\sqrt {10}}},{\frac {1}{\sqrt {10}}}\right)}$ gehen. Für die Quadratische Form wird nun das innere Produkt

$${\begin{pmatrix}{\frac {3}{\sqrt {10}}}\\\ {\frac {1}{\sqrt {10}}}\end{pmatrix}}.{\begin{pmatrix}-0.10\\\ 0.18\end{pmatrix}}=-0.04$$

gebildet. Es gibt uns die 2. Richtungsableitung in dieser Richtung an. Es ist negativ – d.h. die Funktion ist in diesem Punkt in dieser Richtung konkav. (Die Cobb-Douglas Funktion ist in jedem Punkt in jeder Richtung konkav)

Ein Kriterium, anhand dessen wir diese Eigenschaften der Hessematrix bestimmen können, findet sich in der 2 Lektion (Definitheitskriterien).

Einige Beispiele dazu finden sich in den Wiederholungsaufgaben.

Zusammenfassung Ziel dieses Kapitels war es, in sehr komprimierter Weise grundlegendes mathematisches Basiswissen zu wiederholen, das zum Teil bereits von der Mittelschule bekannt sein sollte, und zum Teil im Bachelor Studium erworben wurde. Speziell die Techniken des Differenzierens und Integrierens sollten beherrscht werden, können aber aufgrund von Platzmangel in diesem Skriptum nicht ausführlicher behandelt werden. Für eine umfangreiche und sehr lesbare Quelle zum Thema mit konkretem Bezug zu den Wirtschaftswissenschaften empfehle ich zum Beispiel das Buch von Sydsaeter und Hammond (2004).

Wiederholungsaufgaben/Übungen

Aufgabe 1 Differenziere folgende Funktionen: ${\textstyle f\left(x\right)=x^{\mathrm {exp} \left(x\right)}}$ ${\textstyle f\left(x\right)={\frac {x^{2}+{\sqrt {x}}}{3x-2}}}$ ${\textstyle f\left(x\right)={\sqrt {x}}\mathrm {cos} x^{2}}$

Aufgabe 2 Führe für die Funktion ${\textstyle f\left(x\right)={\frac {\mathrm {exp} \left(x\right)}{x-1}}}$ eine Kurvendiskussion durch! (d.h. Definitionsbereich, Nullstellen, Extremwerte, Wendepunkte, Zeichnung)

Aufgabe 3 Suche die Stammfunktionen folgender Funktionen mittels Substitution: ${\textstyle f\left(x\right)=e^{3x+4}}$ ${\textstyle f\left(x\right)=x\mathrm {log} \left(x^{2}\right)}$ ${\textstyle f\left(x\right)=\mathrm {sin} (4x-3)}$

Aufgabe 4 Berechne folgende Integrale ${\textstyle \int _{x=0}^{1}x^{2}e^{-x}\mathrm {dx} }$ ${\textstyle \int _{x=1}^{2}\mathrm {log} \left({\frac {x}{2}}\right)\mathrm {dx} }$ ${\textstyle \int _{x=2}^{4}\left|x-3\right|\mathrm {dx} }$

Aufgabe 5 Bestimme den Definitionsbereich folgender Funktionen und berechne Gradienten und Hessematrix: ${\textstyle f\left(x,y\right)=\mathrm {log} (x^{2}-y^{2})}$ ${\textstyle f\left(x,y\right)={\frac {\mathrm {xy} }{x-y}}}$ ${\textstyle f\left(x,y,z\right)=\mathrm {xyz} +x^{2}y+y^{2}z+z^{2}x}$