Optimierung - Wiederholung Analysis
Wiederholung Analysis
In der einführenden Lektion werden grundlegende Konzepte der Analysis besprochen, die an sich bereits vom Schulunterricht und vom Bachelor Studium vertraut sein sollten, deren Wiederholung allerdings sicherlich nicht schadet. Zur Vorbereitung auf die späteren Kapitel, welche auf den hier vorgestellten Begriffen basieren, wird ein etwas formalerer Zugang gewählt als im Bachelor Studium.
Reelle Funktionen einer Veränderlichen
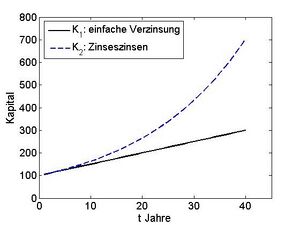
In der Finanzmathematik wurden bereits verschiedenste reelle Funktionen besprochen, etwa die Abhängigkeit des Kapitals Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} von der Zeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t} , wenn Verzinsung erfolgt. Abbildung 1.1 zeigt den Graphen von zwei Funktionen.
In diesem Beispiel wäre die Zeit t (in Jahren) die unabhängige Variable, und wir haben zwei verschiedene Funktionen: das Kapital Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_1} unter einfacher Verzinsung, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_2} unter Berücksichtigung der Zinseszinsen. Dabei wird jedem Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle t} aus dem Intervall [0,40] eine Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_1(t)} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K_2(t)} zugeordnet. Üblicherweise wird die Funktion der Verzinsung nur für natürliche Zahlen ausgewertet. Wir möchten hier die entsprechenden Funktionen auf beliebige reelle Zahlen im Intervall [0,40] fortsetzen. Im Allgemeinen versteht man unter einer reellen Funktion, bzw. einer reellen Abbildung eine Zuordnungsvorschrift, wo jedem Wert der unabhängigen Variablen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} genau ein Wert der abhängigen Variable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} zugeordnet wird. Mitunter ist die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} nicht für alle reellen Zahlen definiert, sondern hat einen eingeschränkten Definitionsbereich. So ist zum Beispiel der Logarithmus nur für positive reelle Zahlen definiert. Um eine Funktion vollständig zu charakterisieren schreibt man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f: D & \rightarrow \mathbb{R} \\ x & \mapsto f(x) \end{aligned} } wobei in der ersten Zeile festgelegt wird für welche Werte von x die Abbildung definiert ist (Definitionsbereich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle D} ), und dass der Bildbereich in den reellen Zahlen liegt. Die zweite Zeile gibt konkret die Rechenvorschrift an.
Beispiel 1: In Abbildung 1 haben wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} K 1:[0,40] \rightarrow \mathbb{R} \\ t & \mapsto 100+0.05 * \mathrm{t} \\ K 2:[0,40] \rightarrow \mathbb{R} \\ t & \mapsto 100 * 1.05^t \end{aligned} }
Zu den wichtigsten Funktionen gehören lineare Funktionen, Polynome, trigonometrische Funktionen, die Exponentialfunktion und die Logarithmusfunktion, deren Gestalt als bekannt vorausgesetzt wird.
Aufgabe 1 Zeichne mit R und Maxima ähnlich zu Abbildung 1.1 die Graphen folgender Funktionen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_1:[-3,3] \rightarrow \mathbb{R} \\ x \mapsto 3 \mathrm{x}-2 \end{aligned} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_2:[-\pi, \pi] \rightarrow \mathbb{R} \\ x \mapsto \sin x \end{aligned} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_3: \quad[0.1,3] \rightarrow \mathbb{R} \\ t \mapsto \log (t) \end{aligned} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f_4: & {[-3,3] \rightarrow \mathbb{R} } \\ & x \mapsto \exp \left(-x^2\right) \end{aligned} } In der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f_4} von Aufgabe 1 wurden zwei einfache Funktionen zusammengesetzt. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x) = x^2} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(x) = exp(-x)} , so ergibt sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f_4} als Zusammensetzung von g und f: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_4(x)=exp{(}-x^2)=exp{(}-f(x))=g(f(x))=g\circ f(x) } Bei der Bildung einer zusammengesetzten Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g\circ f(x)} ist darauf zu achten, dass der Bildbereich von f im Definitionsbereich von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g} liegt.
Umkehrabbildung
Ein wesentliches Merkmal einer Funktion ist, dass jedem Wert von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} genau eine reelle Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = f(x)} zugeordnet wird. Manchmal ist es der Fall, dass auch umgekehrt jeder Bildwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} genau einem Urbildwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} entspricht. Dies gilt speziell dann, wenn eine Funktion streng monoton steigend bzw. streng monoton fallend ist. Dies bedeutet, dass für jedes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x1 > x2} entweder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x_1) > f(x_2)} (steigend) oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x_1) < f(x_2)} (fallend). In diesen Fällen kann die sogenannte Umkehrabbildung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^-1(y)} gebildet werden, die jedem Bildwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} den entsprechenden Urbildwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} zuordnet. Es gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f^{-1}\circ f\left(x\right)=f^{-1}\left(f\left(x\right)\right)=x } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\circ f^{-1}\left(y\right)=f\left(f^{-1}\left(y\right)\right)=y }
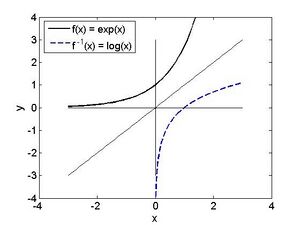
Beispiel 2: In Abbildung 2 finden wir ein wichtiges Beispiel: Die streng monoton steigende Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)=\exp (x)} und deren Umkehrfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle g(x)=f^-1(x)=log(x)} Beachte, dass man im Graphen die Umkehrfunktion durch Spiegelung an der ersten Hauptdiagonale erhält. Klarerweise gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle log(exp(x))=x} . Andererseits gilt auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle exp(log(x))=x} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x > 0} , ansonsten liegt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} nicht im Definitionsbereich der Logarithmus-Funktion.
Ein Beispiel für eine Funktion die sich nicht umkehren lässt wäre Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x) = x^2} .
Aufgabe 2 Skizziere ähnlich zu Abbildung 2 den Graphen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned} f: & \mathbb{R} \rightarrow \mathbb{R} \\ & x \mapsto x^2 \end{aligned} }
\begin{aligned}f^+:&\mathbb{R}^+\rightarrow\mathbb{R}\\\ &x\mapsto x^2\\\end{aligned} und überlege, warum es keine eindeutige Umkehrfunktion gibt. Zeichne die beiden Umkehrfunktionen zu und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{aligned}f^-:&\mathbb{R}^-\rightarrow\mathbb{R}\\\ &x\mapsto x^2\\\end{aligned} } Löse algebraisch die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y = x^2} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} und vergleiche mit den graphischen Lösungen
Differentiation
Als nächstes wollen wir uns mit Glattheitseigenschaften von Funktionen beschäftigen. Als erstes wäre da der Begriff der Stetigkeit. Eine Funktion ist an einem Punkt x im Wesentlichen dann stetig, wenn sie dort nicht springt.
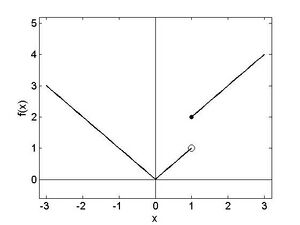
Beispiel 3: In Abbildung 3 ist folgende Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} gezeichnet: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\left(x\right)=\left\{\begin{aligned}\mathrm{\ \ \ \ \ }\left|x\right|\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } x<1\\\mathrm{\ \ \ \ }\left|x\right|+1\mathrm{\ \ \ \ \ \ \ \ \ \ } x\geq1\\\end{aligned}\right. } Die Funktion ist überall stetig außer an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=1} wo sie einen Sprung der Höhe 1 hat.
Formal wird die Stetigkeit dadurch definiert, dass an einer bestimmten Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_0} sowohl der rechtsseitige Limes als auch der linksseitige Limes mit dem Funktionswert übereinstimmt. Also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{x_n \rightarrow x_0}f\left(x_n\right)=f\left(x_0\right) } sowohl für beliebige Folgen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_n < x_0} als auch für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_n > x_0} .
In Beispiel 3 bedeutet dies, dass an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_0 = 1} zwar der rechts-seitige Limes mit dem Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(1) = 2} übereinstimmt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{x_n\rightarrow1^+}f\left(x_n\right)= \lim\limits_{h \rightarrow 0, h \rightarrow 0} f(1+h)= 1+1+\lim\limits_{h \rightarrow 0, h \rightarrow 0}|h|= 1=f\left(1\right) }
Hingegen gilt für den linksseitigen Limes: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{x_n\rightarrow1^-}f\left(x_n\right)=1 } (nachrechnen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h < 0} !) Daher ist die Funktion an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_0 = 1} nicht stetig. In Abbildung 1.3 ist der rechtsseitige Limes durch einen Punkt, der linksseitige Limes durch einen Ring gekennzeichnet.
Differenzierbarkeit hängt nun damit zusammen, ob eine Funktion an einem Punkt einigermaßen glatt ist und nicht etwa einen Knick aufweist. Anschaulich gesprochen bedeutet dies, dass man im Graphen der Funktion an einem Punkt eine Tangente anpassen kann. Stetigkeit ist dafür eine notwendige Voraussetzung, allerdings nicht hinreichend. Die Funktion aus Abbildung 1.3 etwa ist an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x=0} zwar stetig, aber nicht differenzierbar. Die Theorie der Differentialrechnung wurde in der Finanzmathematik ausführlich besprochen.
Rechenregeln
Wir wollen nur die wichtigsten Rechenregeln der Differentialrechnung wiederholen. Die folgende Tabelle beinhaltet die Ableitungen der gängigsten Funktionen, wobei hier a eine beliebige reelle Zahl sein kann:
Zusätzlich von Bedeutung sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} Produktregel: (f g)^{\prime}=f^{\prime} g+f g^{\prime} \\ Quotientenregel: \left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime} g-f g^{\prime}}{g^2} \\ Kettenregel: (g \circ f)^{\prime}=\left(g^{\prime} \circ f\right) \cdot f^{\prime \prime} \\ \end{array} <math display="block"> \frac{d}{{dx}}g\left(f\left(x\right)\right)=g^\prime\left(f\left(x\right)\right)\cdot f^\prime\left(x\right) } Durch konsequente Anwendung dieser Regeln lassen sich bereits viele praktische Aufgaben lösen.
Aufgabe 3 Differenziere folgende Funktionen und überprüfe das Ergebnis mit Maxima! Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{r} f_1(x)=\exp (-x 2) \\ f_2(x)=\tan x=\sin (x) \cdot \cos (x) \\ f_3(x)=\sqrt{1+x^3} \end{array} }
Die erste Ableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{'}(x)} ist wiederum eine Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}} , deren Ableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{''}(x)} man als Ableitung zweiter Ordnung bezeichnet. Entsprechend können Ableitungen höherer Ordnung definiert werden. Die erste Ableitung einer Funktion gibt deren Steigung an. Die Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{'}(x)=0} bestimmt potentielle lokale Extremstellen der Funktion. Die Ableitung zweiter Ordnung beschreibt die Krümmung einer Kurve und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f^{''}(x)=0} definiert potentielle Wendepunkte. All diese Überlegungen fließen bei der wohlbekannten Diskussion von Kurven ein.
Integration
Geometrisch gesehen dient das Integrieren zum Berechnen von Flächen.
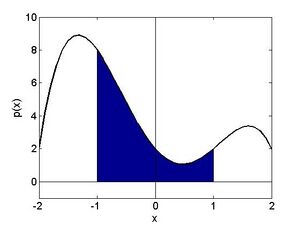
Beispiel 4: In Abbildung 1.4 ist das Polynom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(x) = -x^4+x^3+4x^2-4x+2} geplottet. Es soll die Fläche zwischen der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p(x)} und der x-Achse im Bereich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (-1,1)} berechnet werden, die in der Abbildung hervorgehoben wurde. Die Berechnung erfolgt mit einem sogenannten bestimmten Integral, bei dem die obere und die untere Grenze des Integrationsbereichs feststehen (im Beispiel eben die Grenzen -1 und 1).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=-1}^{1}{p\left(x\right)\mathrm{dx} =}\int_{x=-1}^{1}{\left(-x^4+x^3+4x^2\mathrm{-4} x+2\right)\mathrm{dx} =}\\\ =-\frac{x^5}{5}+\frac{x^4}{4}+\frac{4x^3}{3}-\frac{4x^2}{2}+\mathrm{2x\ }|_{-1}^1=\frac{\mathrm{94} }{\mathrm{15}} }
Im folgenden Abschnitt werden wir die Details zu dieser Berechnung genau erläutern. Für die allgemeine Integrationstheorie ist der Zusammenhang zwischen Integralrechnung und Differentialrechnung von entscheidender Bedeutung:
Hauptsatz der Analysis
Dieser fundamentale Satz besagt, dass Integrieren und Differenzieren zueinander inverse Operationen sind. Um dies zu verstehen brauchen wir zunächst folgende Begriffe: Das unbestimmte Integral einer Funktion f sowie deren Stammfunktion. Ein unbestimmtes Integral von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} erhält man, indem man die untere Grenze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} des Integrals festhält, während man die obere Grenze variieren lässt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_a\left(x\right)=\int_{y=a}^{x}f\left(y\right)\mathrm{dy} } Für jedes feste Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} wird dadurch eine Funktion in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x} definiert. Unter eine Stammfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f(x)} versteht man eine differenzierbare Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle F(x)} für die gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F^\prime\left(x\right)=f\left(x\right) }
Es gibt davon unendlich viele, da man zu jeder Stammfunktion eine Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} addieren kann und wiederum gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (F(x)+c)^\prime=f(x) } D.h. die Stammfunktion ist nur bis auf eine Konstante eindeutig bestimmbar. Der Hauptsatz der Analysis besagt nun, dass jedes unbestimmte Integral von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} gerade eine Stammfunktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} ist: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{d}{\mathrm{dx}}I_a\left(x\right)=\frac{d}{\mathrm{dx}}\int_{y=a}^{x}f\left(y\right)\mathrm{dy} =f\left(x\right) }
Umgekehrt erhalte ich alle Stammfunktionen mittels unbestimmter Integrale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F\left(x\right)=\int_{y=a}^{x}f\left(y\right)\mathrm{dy} +c }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle c} als Integrationskonstante bezeichnet wird. Die folgende Tabelle gibt die Stammfunktionen der wichtigsten einfachen Funktionen, wobei hier Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle a} jede beliebige reelle Zahl mit Ausnahme von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -1} sein kann.
Die Tabelle ist gerade die Umkehrung von jener der Differentiation.
Ist die Stammfunktion F(x) einer Funktion f(x) bekannt, so können bestimmte Integrale für ein Intervall [a,b] recht einfach berechnet werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=a}^{b}f\left(x\right)\mathrm{dx} =F\left(b\right)-F\left(a\right) }
Die Integrationskonstante des unbestimmten Integrals kürzt sich weg, und daher genügt es eine einzige Stammfunktion zu kennen um beliebige bestimmte Integrale von f zu berechnen. Man verwendet häufig die Notation Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=a}^{b}f\left(x\right)\mathrm{dx} =F\left(x\right)|_a^b=F\left(b\right)-F\left(a\right) }
um in einem Zwischenschritt zu verdeutlichen, wie die Stammfunktion explizit aussieht. Nun sollte die Berechnung des Integrals in Beispiel 4 kein Problem mehr machen.
Aufgabe 4:
Das Berechnen von Wahrscheinlichkeiten entspricht hier gerade der Integration. Eine in der Praxis häufig auftretende Verteilung ist die Exponentialverteilung, mit Dichte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\left(x\right)=\left\{\begin{aligned}\lambda\mathrm{\ exp}\left(-\lambda x\right)\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ } x>0\\\mathrm{\ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sonst}\\\end{aligned}\right. }
Berechne die Wahrscheinlichkeit, dass eine exponentialverteilte Zufallsvariable mit Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \lambda}
Werte zwischen 1 und 2 annimmt.
Partielle Integration, Substitution
Während das Differenzieren nach Erlernen der Grundtechniken weitgehend mechanisch abläuft ist dies beim Integrieren leider nicht der Fall. Im Gegenteil, häufig gleicht die Suche nach einer Stammfunktion einer höheren Kunstform, und in vielen Fällen ist eine geschlossene Darstellung eines unbestimmten Integrals gar nicht möglich. So besitzt beispielsweise die Dichte der Normalverteilung keine einfach darstellbare Stammfunktion, und zur Berechnung von Wahrscheinlichkeiten ist man hier entweder auf Tabellen oder auf numerische Integration angewiesen. Zwei Basistechniken zur Bestimmung von Stammfunktionen sollen hier allerdings Erwähnung finden:
Partielle Integration:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int{{f}^\prime g}={fg}-{fg}' }
Dies ist das Pendant zur Produktregel, was durch Differenzieren unter Verwendung des Hauptsatzes der Analysis unmittelbar klar wird: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {f}^\prime {g}=\left({fg}\right)^\prime-{{fg}}^\prime }
Substitution:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int g\left(x\right)\mathrm{dx} =\left|\begin{aligned}y=h\left(x\right)\\\mathrm{dy}=h^\prime\left(x\right)\mathrm{dx} \\\end{aligned}\right|=\int{g(h}^{-1}(y))\frac{\mathrm{dy} }{h^\prime\left(x\right)} }
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle h(x)}
streng monoton steigend.
Man kann zeigen, dass es sich hier um das Pendant zur Kettenregel beim Differenzieren handelt. Wir wollen beide Techniken anhand eines konkreten Beispiels vorführen. In den Wiederholungsaufgaben gibt es einige weitere Beispiele.
Beispiel 5: Der Erwartungswert einer Zufallsvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle X} mit Dichte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f} ist definiert als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E\left(X\right)=\int_{x=-\infty}^{\infty}\mathrm{xf}\left(x\right)\mathrm{dx} } Für die Exponentialverteilung (aus Aufgabe 4) erhält man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{x=0}^{\infty}x\lambda\mathrm{\ exp}\left(-\lambda x\right)\mathrm{dx}=\\\ \int_{y=0}^{\infty}y\lambda\mathrm{\ exp}\left(-\lambda y\right)\mathrm{dy}=\\\ -\frac{1}{\lambda}y\mathrm{\ exp}\left(\mathrm{-y}\right)|_0^\infty +\frac{1}{\lambda}\int_{y=0}^{\infty}\mathrm{\ exp}\left(\mathrm{-y}\right)\mathrm{dy}=\frac{1}{\lambda} } Die erste Gleichung erhält man mit Substitution: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left|\begin{aligned}y=\lambda x\\\mathrm{dy}=\lambda\mathrm{dx}\\\end{aligned}\right| } Die zweite Gleichung mittels partieller Integration: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f^\prime\left(y\right)=\mathrm{exp}-y, gy=y } Man beachte, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{y\rightarrow\infty}y\mathrm{\ exp}\left(\mathrm{-y}\right)=0 } weil die Exponentialfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathrm{exp}(-y)} wesentlich rascher gegen 0 konvergiert als der Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y} wächst.
Reelle Funktionen mehrerer Veränderlicher
Vorbemerkung: in diesem Abschnitt wird mit Vektoren und Matrizen gerechnet; zwar werden die einzelnen Schritte erläutert, - falls diese Schritte aber große Schwierigkeiten bereiten, sollten Sie die erforderlichen Grundlagen der Linearen Algebra rekapitulieren. Bislang haben wir uns auf Funktionen einer freien Variablen beschränkt, d.h. der Definitionsbereich und der Bildbereich waren jeweils Teilmengen der Zahlengerade. Allgemeiner betrachtet kann man Abbildungen mit n Veränderlichen studieren; diese schreibt man in der Form: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f:\ \ D\ \subseteq\mathbb{R}^n\ \rightarrow\ \mathbb{R} \ \ \ \ \ \ \left(x_1,\ \ldots x_n\right)\rightarrow f\left(x_1,\ \ldots x_n\right) } Nun ist diese Verallgemeinerung – trotz der etwas sperrigen Notation (und es wird noch schlimmer!) durchaus naheliegend: in der Praxis wird eine Zielvariable ja häufig nicht nur von einer einzigen Einflussvariablen bestimmt, sondern von mehreren – nehmen wir etwa die Nachfrage nach Bier in einem Gastgarten: sie wird vom Preis des Bieres abhängen, von der Temperatur und vom Datum zu Monatsbeginn haben viele Gäste noch mehr Geld zur Verfügung als gegen Monatsende; diese drei freien Variablen können wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P,T,d} nennen – oder eben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_1,x_2,x_3} . Funktionen mit eindimensionalem Definitionsbereich konnten wir durch den Graphen veranschaulichen – auf der x-Achse wird die freie Variable aufgetragen, auf der y-Achse die Abhängige – dann erhalten wir bei einer stetigen Funktion eine Kurve (oder Gerade) im Raum. Bei Funktionen mit mehrdimensionalem Definitionsbereich ist eine solche Veranschaulichung im Allgemeinen nicht mehr möglich; eine Ausnahme sind die Funktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ f:\ \ D\ \subseteq\mathbb{R}^2\ \rightarrow\ \mathbb{R}: } hier ist der Definitionsbereich ein Teilbereich der (zweidimensionalen) Ebene, und jedem Punkt aus diesem Ebenen-Bereich wird ein Funktionswert zugeordnet – den wir uns als Höhe vorstellen können. Der Graph der Funktion wird also eine – möglicherweise sehr unebene – Fläche im Raum sein; als Beispiel können Sie sich eine Landschaft vorstellen: jeder Punkt hat eine x- und eine y- Koordinate in der Ebene, und diesem Punkt wird eine Höhe zugeordnet; je nachdem wie stetig die Funktion nun ist, wird die Landschaft glatt oder zerklüftet sein. Funktionen mit höherdimensionalem Definitionsbereich kann man sich nicht mehr so einfach veranschaulichen. Die Definition der Stetigkeit wird nun etwas komplizierter, da man sich einem Punkt in der Ebene – oder einem höherdimensionalen Raum – nicht nur aus zwei Richtungen, sondern aus beliebig vielen Richtungen nähern kann. Das Konzept bleibt ansonsten aber das Gleiche. Eine Funktion f ist an einer Stelle stetig, falls für jede Folge von Punkten, die gegen diesen Punkt konvergiert die entsprechende Folge der Funktionswerte gegengegen den Funktionswert dieses Punktes konvergiert.
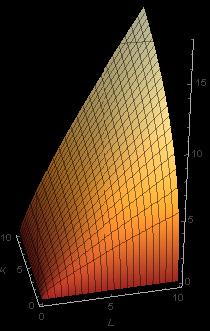
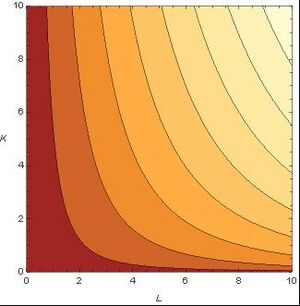
Beispiel 6: Großer Beliebtheit erfreut sich in den Wirtschaftswissenschaften die Cobb-Douglas Funktion, die den Einfluss von mehreren Faktoren auf die Produktion modelliert. So ließ sich in den Jahren 1960 bis 1975 die Produktion Y der Beiersdorf AG in Abhängigkeitn von den beiden Faktoren L (Arbeit) und K (Kapital) durch die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y=Y\left(L,K\right)=e^{0.04}L^{0.84}K^{0.39} } gut beschreiben. Die Abbildung zeigt den Graphen der Funktion: der Definitionsbereich ist die Menge aller Punkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (L,K),L>=0,K>=0} , also der positive Quadrant der Ebene; jedem dieser Punkte wird nun eine Funktionswert zugeordnet. Ist einer der beiden Faktoren 0, so ist die Produktivität auch 0; für jeden anderen Wert des einen Faktors ist die Funktion streng monoton steigend im anderen – das sehen wir an den Gitterlinien auf dem Graphen; diese sind die Bilder von Geraden parallel zur K- bzw. zur L-Achse. Offensichtlich ist die Funktion auf jeder dieser Gitterlinien streng monoton steigend. Die Abbildung daneben zeigt die Höhenschichtlinien der Funktion; sie verbinden Punkte aus dem Definitionsbereich mit jeweils gleichem Funktionswert. Im Wikipedia – Eintrag zur Cobb-Douglas Funktion finden Sie eine schöne Animation!
Funktionen in mehreren Variablen können wir uns im Allgemeinen nicht vorstellen; wir können aber versuchen, jede dieser Variablen „getrennt“ zu betrachten, d.h., wir weisen allen anderen einen konstanten Wert zu – dann nehmen diese in der Funktionsgleichung die Rolle von Konstanten ein – und betrachten die Änderung des Funktionswertes bei Änderung der einen Variablen im Fokus.
Beispiel 6 (Fortsetzung): Nehmen wir an, wir wissen, wir wollen nur wissen, wie sich die Produktivität bei konstanter Arbeitsleistung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1} entwickelt, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} variiert. Dann können wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y=Y\left(K,1\right)=e^{0.04}\cdot1\ K^{0.39} } schreiben – also die Funktion nur noch abhängig von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} betrachten. In der linken Graphik würde das heißen, dass wir uns jene Gitterlinie suchen, die zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1} gehört, und auf dieser variable Werte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle K} betrachten. In dieser Betrachtung können wir nun das Werkzeug aus der eindimensionalen Analysis einsetzen; z.B. können wir Ableitungen in Richtung einer Variablen definieren, wenn alle anderen Festgehalten werden – formal:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial x_i}f\left(x_1,\ldots,x_n\right)=\lim\limits_{h\rightarrow0}\frac{f\left(x_1,\ldots,x_i+h,\ldots x_n\right)-f\left(x_1,\ldots,x_i,\ldots x_n\right)}{h} }
Beispiel 6 (Fortsetzung): Bilden wir die partiellen Ableitungen der Cobb-Douglas-Funktion, so erhalten wir: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial Y}{\partial L}={0.84e}^{0.04}L^{-0.16}K^{0.39},\ \ \frac{\partial Y}{\partial K}={0.39e}^{0.04}L^{0.84}K^{-0.61} }
Der Zeilen-Vektor aus den partiellen Ableitungen wird als Jacobi-Matrix bezeichnet, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\left(f\right)=\left(\frac{\partial f}{\partial x_1},\ \ldots\frac{\partial f}{\partial x_n}\right) }
Der Spalten-Vektor bestehend aus allen partiellen Ableitungen wird als Gradient bezeichnet, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla\left(f\right)=\left(\frac{\partial f}{\partial x_1},\ \ldots\frac{\partial f}{\partial x_n}\right)^t=: \begin{pmatrix}\frac{\partial f}{\partial x_1} \\\frac{\partial f}{\partial x_2} \end{pmatrix} }
Existieren die partiellen Ableitungen für alle Variablen und sind ihrerseits stetig, so bezeichnet man die Funktion als differenzierbar. Der Gradientenvektor steht in jedem Punkt normal auf die Höhenschichtlinie durch den Punkt und zeigt in die Richtung des steilsten Anstiegs.
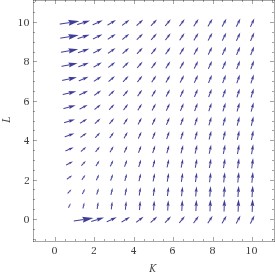
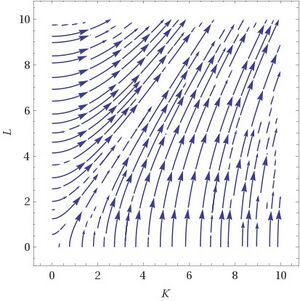
Beispiel 6 (Fortsetzung): Die Jacobi Matrix der Cobb-Douglas Funktion, ausgewertet für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1,K=2} : Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\left(f\right)\left(1,2\right)=\left(1.15,0.27\right) } Die untere Abbildung zeigt den Gradienten der Cobb-Douglas Funktion als Vektorfeld; in jedem Punkt zeigt die horizontale Komponente des Pfeils die partielle Ableitung nach K, die vertikale die partielle Ableitung nach L. Sie stehen normal auf die Höhenschichtlinien. Die rechte Graphik stückelt diese Gradienten-Vektoren zu Trajektorien zusammen – jene Wege, auf denen man von einem gegebenen Startpunkt aus am schnellsten steigt. Auf diesen werden wir bei der Suche nach Maxima bewegen – zumindest annähernd.
In der Jacobi-Matrix stehen die Richtungsableitungen in Richtung jeder einzelnen Variablen – d.h., sie gibt die Steigung der Tangenten an den Funktionsgraph in jeder dieser Richtungen an. Gibt es nur zwei freie Variable, dann ist der Graph einer stetigen Funktion eine Fläche im Raum, und die Tangenten an einen Punkt spannen eine Ebene aus – die Tangentialebene; bei höherdimensionalen Funktionen spricht man von Hyperebenen. Mithilfe der Jacobi-Matrix lässt sich nun die Richtungsableitung in beliebiger Richtung definieren. Die partiellen Ableitungen geben ja an, wie sich der Funktionswert auf der Tangentialebene verändert, wenn man eine Einheit in Richtung jeder einzelnen Variablen geht. Will man nun in eine beliebige Richtung gehen, so sucht man deren Einheitsvektor und multipliziert jede Komponente mit der entsprechenden partiellen Ableitung – man bildet das Matrix-Produkt der Jacobi-Matrix mit dem Richtungsvektor der Veränderung.
Beispiel 6 (Fortsetzung): Die Jacobi Matrix der Cobb-Douglas Funktion, ausgewertet für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle L=1,K=2} :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J\left(f\right)\left(1,2\right)=\left(1.15,0.27\right) }
D.h. Wenn ich über dem Punkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle P=(1,2)} eine Tangentialebene anlege, so hat diese über dem Punkt die Höhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Y(1,2)=1.37} , verändere ich nun die erste Komponente, so erhöht sich die Höhe der Tangentialebene um einen Betrag von 1.15; gehen wir stattdessen von P eine Einheit in Richtung der 2. Komponente, so ergibt sich ein Zuwachs von 0.27.
Wie aber verändert sich der Funktionswert, wenn wir uns in beliebiger Richtung vom Punkt P fortbewegen? Dann brauchen wir den Einheitsvektor dieser Richtung: z.B. in Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (3,1)} : Die Länge des Vektors ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt{3^2+1^2}=\sqrt{10} } D.h.: der Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{\sqrt{10}}\left(3,1\right)= \begin{pmatrix} \frac{3}{\sqrt{10}} \\\ \frac{1}{\sqrt{10}}) \end{pmatrix} } ist der Einheitsvektor in dieser Richtung. Wenn wir als vom Punkt P eine Einheit in diese Richtung gehen, so ergibt sich ein Höhenzuwachs von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ \frac{3}{\sqrt{10}}.1.15} aus der Bewegung in die erste Richtung, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ \frac{3}{\sqrt{10}}.0.27} aus der Bewegung in der zweiten Richtung – und der gesamte Höhenzuwachs ist die Summe dieser beiden.
Mathematisch ausgedrückt erhalten wir die Richtungsableitung als Produkt der Jacobi-Matrix mit dem Richtungsvektor, oder – äquivalent – als inneres Produkt des Gradientenvektors mit dem Richtungsvektor. Die folgenden Schreibweisen sind äquivalent – die letzte nicht ganz exakt aber gebräuchlich: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(0.27,\ 1.15\right) \begin{pmatrix}\frac{3}{\sqrt{10}} \\\ \frac{1}{\sqrt{10}} \end{pmatrix} =(\begin{pmatrix}1.15 \\\ 0.27\end{pmatrix}, \begin{pmatrix}\frac{3}{\sqrt{10}} \\\ \frac{1}{\sqrt{10}} \end{pmatrix})=\\\ =(\begin{pmatrix}1.15 \\\ 0.27\end{pmatrix}\cdot \begin{pmatrix}\frac{3}{\sqrt{10}} \\\ \frac{1}{\sqrt{10}} \end{pmatrix}) =1.15\cdot\frac{3}{\sqrt{10}}+0.27\cdot\frac{1}{\sqrt{10}} } Der Gradient bzw. die Jacobi-Matrix entsprechen den ersten Ableitungen von Funktion mit eindimensionalem Definitionsbereich; lassen sich einige Aussagen aus dem Eindimensionalen umformulieren – z.B. die Definition einer streng monoton wachsenden Funktion: im eindimensionalen Fall hieß das, dass die 1. Ableitung strikt positiv ist. Ebenso bezeichnen wir eine Funktion aus dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}^n} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \mathbb{R}} als streng monton wachsend, wenn alle partiellen Ableitungen strikt positiv sind. Ebenso können wir die Kriterien für Extremwerte ins Mehrdimensionale übertragen. Hier muss gelten: wenn eine Funktion aus dem Mehrdimensionalen einen Extremwert in einem Punkt hat, so müssen in diesem Punkt alle partiellen Ableitungen 0 sein – dann sind auch alle Richtungsableitungen in beliebiger Richtung 0; allerdings war das Verschwinden der ersten Ableitung schon im Eindimensionalen eine notwendige, aber keine hinreichende Bedingung für das Vorliegen eines Extremwertes – wir mussten noch die zweite Ableitung befragen. Nun wird die Verallgemeinerung der 2. Ableitung ins mehrdimensionale allerdings formal etwas sperriger werden und zur sogenannten Hesse-Matrix führen. Das Gegenstück zur ersten Ableitung war nämlich der Gradient, in dem sich die partiellen ersten Ableitungen befanden. Aus diesem gewinnen wir nun die Hessematrix, indem wir die Jacobi-Matrix von jeder Komponente dieses Gradienten bilden.
Beispiel 6 (Fortsetzung): Der Gradient der Cobb-Douglas Funktion war Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla Y=\begin{pmatrix} \frac{\partial Y}{\partial L} \\\ \frac{\partial Y}{\partial K}\end{pmatrix}= \begin{pmatrix} {0.84e}^{0.04}L^{-0.16}K^{0.39}\\\ {0.39e}^{0.04}L^{0.84}K^{-0.61}\end{pmatrix} }
Die partiellen zweiten Ableitungen werden nun wieder nach beiden Variablen abgeleitet – analog zu den ersten: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial L}\left(\frac{\partial Y}{\partial L}\right)=:\ \frac{\partial^2Y}{\left(\partial L\right)^2}=\ -0.16\cdot0.84e^{0.04}L^{-1.16}K^{0.39} } Für die Hessematrix ergibt sich daher: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_f\left(L,K\right)=\left(\begin{aligned}-0.14L^{-1.16}K^{0.39}&0.34L^{-0.16}K^{-0.61}\\0.34L^{-0.16}K^{-0.61}&-0.25L^{0.84}K^{-1.61}\\\end{aligned}\right) }
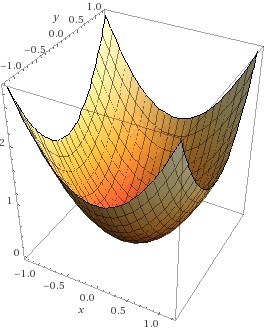
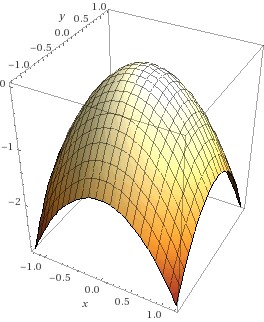
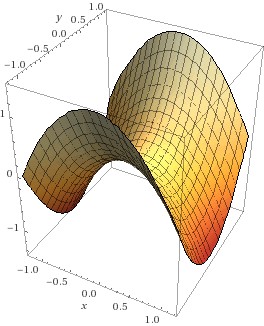
Die gemischten 2. Ableitungen sind immer gleich unabhängig von der Reihenfolge, in der abgeleitet wird – d.h., die Matrix ist symmetrisch. Mit dieser Hessematrix kann nun die 2. Ableitung in jeder beliebigen Richtung bestimmt werden: die zweite Ableitung in Richtung eines Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{v}} der Länge 1 ergibt sich durch die sogenannte quadratische Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \ {\vec{v}}^t\vec{H_f}\vec{v}\ } Ist nun diese 2. Ableitung in jeder Richtung positiv, so heißt das, die Funktion ist in jeder Richtung konvex – d.h., ein Punkt, an dem alle partiellen Ableitungen 0 sind (und damit auch der Gradient der Nullvektor) ist ein Minimum. Ist die 2. Richtungsableitung in allen Richtungen negativ, so ist die Funktion in allen Richtungen konkav – d.h., der kritische Punkt ist ein Maximizer. Und gibt es Richtungen, in denen die 2. Richtungsableitung positiv ist, ander, in denen sie negativ ist, so handelt es sich um einen Sattelpunkt. Beispiele finden Sie in der Abbildung:
Beispiel 6 (Fortsetzung): Für die Hessematrix der Cobb-Douglas-Funktion im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1,2)} ist: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_f\left(1,2\right)=\left(\begin{aligned}-0.18&0.22\\0.22&-0.08\\\end{aligned}\right) } Für die 2 Richtungsableitung in Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \vec{v}=(\frac{3}{\sqrt{10}},\ \frac{1}{\sqrt{10}})} bilden wir zunächst das Matrix-Vektor Produkt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_f\vec{v}=\left(\begin{aligned}-0.18 \:0.22\\0.22\:-0.08\\\end{aligned}\right) \begin{pmatrix}\frac{3}{\sqrt{10}}\\\ \frac{1}{\sqrt{10}}\end{pmatrix}= \begin{pmatrix} -0.18\cdot\frac{3}{\sqrt{10}}+0.22\cdot\frac{1}{\sqrt{10}} \\\ 0.22\cdot\frac{3}{\sqrt{10}}-0.08\frac{1}{\sqrt{10}} \end{pmatrix} =\begin{pmatrix} -0.10 \\\ 0.18\end{pmatrix} } Der Vektor auf der rechten Seite hat eine anschauliche Interpretation: er gibt an, in welcher Richtung und wie stark sich der Gradient verändert, wenn wir vom Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle (1,2)} in der Richtung des Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \left(\frac{3}{\sqrt{10}},\frac{1}{\sqrt{10}}\right)} gehen. Für die Quadratische Form wird nun das innere Produkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{pmatrix}\frac{3}{\sqrt{10}}\\\ \frac{1}{\sqrt{10}}\end{pmatrix}. \begin{pmatrix} -0.10 \\\ 0.18\end{pmatrix} =-0.04 }
gebildet. Es gibt uns die 2. Richtungsableitung in dieser Richtung an. Es ist negativ – d.h. die Funktion ist in diesem Punkt in dieser Richtung konkav. (Die Cobb-Douglas Funktion ist in jedem Punkt in jeder Richtung konkav)
Ein Kriterium, anhand dessen wir diese Eigenschaften der Hessematrix bestimmen können, findet sich in der 2 Lektion (Definitheitskriterien).
Einige Beispiele dazu finden sich in den Wiederholungsaufgaben.
Zusammenfassung Ziel dieses Kapitels war es, in sehr komprimierter Weise grundlegendes mathematisches Basiswissen zu wiederholen, das zum Teil bereits von der Mittelschule bekannt sein sollte, und zum Teil im Bachelor Studium erworben wurde. Speziell die Techniken des Differenzierens und Integrierens sollten beherrscht werden, können aber aufgrund von Platzmangel in diesem Skriptum nicht ausführlicher behandelt werden. Für eine umfangreiche und sehr lesbare Quelle zum Thema mit konkretem Bezug zu den Wirtschaftswissenschaften empfehle ich zum Beispiel das Buch von Sydsaeter und Hammond (2004).
Wiederholungsaufgaben/Übungen
Aufgabe 1 Differenziere folgende Funktionen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=x^{\mathrm{exp}\left(x\right)}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{x^2+\sqrt x}{3x-2}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\sqrt x\mathrm{cos}x^2}
Aufgabe 2 Führe für die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\frac{\mathrm{exp} \left(x\right)}{x-1}} eine Kurvendiskussion durch! (d.h. Definitionsbereich, Nullstellen, Extremwerte, Wendepunkte, Zeichnung)
Aufgabe 3 Suche die Stammfunktionen folgender Funktionen mittels Substitution: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=e^{3x+4}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=x\mathrm{log}\left(x^2\right)} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x\right)=\mathrm{sin}(4x-3)}
Aufgabe 4 Berechne folgende Integrale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \int_{x=0}^{1}x^2e^{-x}\mathrm{dx}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \int_{x=1}^{2}\mathrm{log}\left(\frac{x}{2}\right)\mathrm{dx}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \int_{x=2}^{4}\left|x-3\right|\mathrm{dx}}
Aufgabe 5 Bestimme den Definitionsbereich folgender Funktionen und berechne Gradienten und Hessematrix: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=\mathrm{log}(x^2-y^2)} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y\right)=\frac{\mathrm{xy} }{x-y}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle f\left(x,y,z\right)=\mathrm{xyz}+x^2y+y^2z+z^2x}